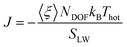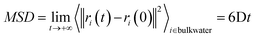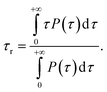Open Access Article
Open Access ArticleWater dynamics affects thermal transport at the surface of hydrophobic and hydrophilic irradiated nanoparticles†
Sebastian
Salassi
 a,
Annalisa
Cardellini
a,
Annalisa
Cardellini
 b,
Pietro
Asinari
b,
Pietro
Asinari
 b,
Riccardo
Ferrando
b,
Riccardo
Ferrando
 a and
Giulia
Rossi
a and
Giulia
Rossi
 *a
*a
aPhysics Department, University of Genoa, via Dodecaneso 33, 16146 Genoa, Italy
bDepartment of Energy, Politecnico di Torino, Corso Duca degli Abruzzi 24, 10129 Torino, Italy. E-mail: rossig@fisica.unige.it
First published on 15th April 2020
Abstract
Plasmonic nanoparticles, such as Au nanoparticles (NPs) coated with bio-compatible ligands, are largely studied and tested in nanomedicine for photothermal therapies. Nevertheless, no clear physical interpretation is currently available to explain thermal transport at the nanoparticle surface, where a solid–liquid (core–ligand) interface is coupled to a liquid–liquid (ligand–solvent) interface. This lack of understanding makes it difficult to control the temperature increase imposed by the irradiated NPs to the surrounding biological environment, and it has so far hindered the rational design of the NP surface chemistry. Here, atomistic molecular dynamics simulations are used to show that thermal transport at the nanoparticle surface depends dramatically on solvent diffusivity at the ligand–solvent interface. Furthermore, using physical indicators of water confinement around hydrophobic and hydrophilic ligands, a predictive model is developed to allow the engineering of NP coatings with the desired thermal conductivities at the nanoscale.
Introduction
Plasmonic nanoparticles (NPs) functionalized with bio-compatible ligands have attracted enormous interest in the biomedical field.1,2 The localized surface plasmon resonance upon irradiation of light in the ultraviolet-visible-near infrared region has been largely exploited to improve the performances of bio-sensing applications3 and photothermal therapies.4 In photoporation set-ups,5 plasmonic gold nanoparticles (Au NPs) coated by organic ligands are heated up by short-laser pulses, inducing nanoscale transient pores in cell membranes, allowing for drug/siRNA penetration into cells in vitro.6 Laser-irradiated Au NPs have been also tested to favor a more systematic nuclear envelope rupture (NER) and allow a rigorous study of the related diseases.7Regardless of the specific application, the ability to control the temperature profile developed in the core of8 and around plasmonic NPs9 would guarantee their optimal design. Plasmonic NPs in biomedicine are usually coated by organic ligands to achieve solubility, long circulating time in the bloodstream, and biocompatibility. As a matter of fact, the presence of ligands influences the thermal conductance of the nano-bio interface, altering the temperature profile developed around the NP. Therefore, tuning the NP ligand composition to achieve the desired temperature increase at the NP surface, and to limit the damage on the healthy tissues,10 is the ultimate objective for final designing and exploiting plasmonic coated NPs in biomedicine.
The direct experimental measurement of the temperature profile at NP surface is challenging, and it has been attempted by means of the ad hoc covalent binding of polymers or quantum dots to the NPs.11,12 A less direct approach consists in the measurement of the interface thermal conductance via optical pump and probe techniques, such as time-domain thermo-reflectance, often applied to extended surfaces. It has been shown that the presence of a ligand layer enhances the thermal conductivity with respect to the bare solid surface in contact with the solvent.13–15 The seminal works by Braun and Cahill16–18 suggested the dependence of the interfacial conductance on the hydrophobic or hydrophilic nature of the coating ligand layer.18 The nature of the solvent,17 the density of covalent bonds at the metal surface19 and the work of adhesion needed to separate the liquid from the solid20 are all factors that have been shown to affect thermal conductance. There is a general consensus that in the presence of a three-component interface, namely metal–ligand–solvent, the ligand–solvent interface offers the largest thermal resistance,21 thereby playing a major role in the study of heat transfer mechanisms. However, this interface cannot be classified as an ideal solid–liquid nor as liquid–liquid interface, instead it strictly preserves a soft matter nature whose thermal properties are likely to be explained only considering its chemical and physical features at the molecular scale. For this reason, molecular modelling techniques have been adopted to clarify and unveil the most critical phenomena ruling the heat transfer at the ligand–water nanoscale interface.
Molecular dynamics (MD) in particular, has demonstrated a considerable potential to distinguish the specific molecular mechanisms which influence heat conduction and the formation of thermal gradients around NPs. MD studies have proved that stronger van der Waals interactions favor heat conduction, both at metal–solvent22,23 and ligand–solvent interfaces.21,24 The collaborative effects of van der Waals and electrostatic forces, which contribute to the formation of hydrogen bonds between the ligands and the solvent, have also shown to increase thermal conductance at ligand–solvent interfaces.25 Heat conduction can be enhanced also by the reciprocal alignment of ligands and intercalating solvent molecules.26
Based on the acoustic and diffusive mismatch models of the thermal conductance at solid–solid interfaces, several MD studies have related interfacial temperature drops to the overlap of the vibrational spectra,27 even for solid–liquid and liquid–liquid interfaces. For example, the overlap of the vibrational density of states (vDOS) between Au NPs and rigid or flexible water models has been invoked to explain a little difference in the thermal conductance at the Au–water interface.28 Similar considerations hold for three-component interfaces. Gezelter and collaborators have found positive correlation between the overlap of the vibrational power spectra of the interface components and the thermal conductance, in different systems including Au surface/butanethiol/organic solvent,29 CdSe surface/hexylamine/hexane,30 Au NP/alkane (or alkene) thiols/hexane.26 Organic ligands with long saturated carbon tails are expected to have a good vibrational overlap with organic alkane solvents.21 However, relating the temperature drops at solid–liquid and liquid–liquid interfaces with the spectra overlapping between the involved materials is not always straightforward, and often only qualitative trends can be derived from this kind of analysis.21 No correlation between spectral overlap and thermal conductance was found by Alexeev et al. for graphene–water interfaces.23 For thiolated Au surfaces in water, Hung et al. found lower thermal conductance for hydrophobic self-assembled monolayers (SAMs) than for hydrophilic, –OH-terminated SAMs, but no correlation with the overlap between their vibrational spectra and that of water.31 Overall, the reliability of this approach to characterize soft interfaces remains unclear.
Here we use MD simulations to investigate the thermal gradient developed around hot thiolated Au NP in cold bulk water. The NP ligands have different degrees of hydrophobicity: we consider fully hydrophobic carbon chains, polyethylene glycol chains, and carbon chains terminated by hydrophilic, charged groups. We show that the temperature profile developing around the hot NP can be explained in terms of interfacial water structure and dynamics. Our results reveal that the shape of the temperature profile, and in particular the ligand capability to retain the NP temperature in the coating volume, is correlated to the self-diffusion coefficient of water. When ligands are hydrophobic, water molecules do not spend enough time at the ligand interface to cool down the coating volume, which remains hot. On the contrary, water resides for longer time at the interface with hydrophilic ligands, allowing for an efficient thermal exchange. In order to give a predictive estimation of the thermal gradients, herein we suggest, and validate, a quantitative model relating interfacial water confinement to the temperature drops at the interfaces, allowing a fast and preliminary screening for the best ligands to coat NPs in tailored biomedical applications.
Results and discussion
Au NP models
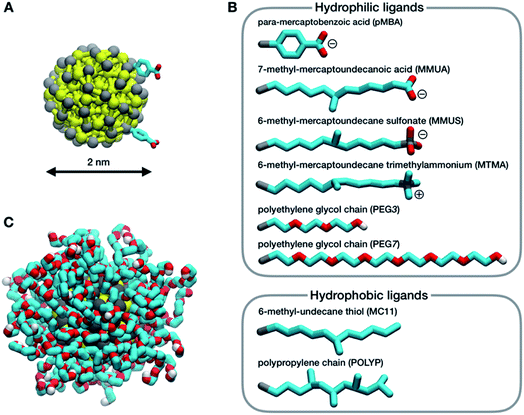
In this work, we consider a single Au NP with a diameter of 2 nm, covalently functionalized by different organic thiols. In Fig. 1B, from top to bottom, the first, second and third ligand are negatively charged: para-mercaptobenzoic acid (pMBA), 7-methyl-mercaptoundecanoic acid (MMUA) and 6-methyl-mercaptoundecanesulfonic acid (MMUS). 6-Methyl-mercapto-undecane trimethylammonium (MTMA) is positively charged. The fifth and sixth ligands are two neutral but hydrophilic polyethylene glycol (PEG) chains terminated with a –OH group, made with 3 and 7 PEG monomers, respectively. The last two ligands are completely hydrophobic carbon chains, the 6-methyl-undecane thiol (MC11) and a polypropylene oligomer (POLYP). The addition of the methyl group in the MMUA, MMUS, MTMA and MC11 ligands assure that the final configuration assumed by the functionalized NP in the water phase (Fig. 1C) is, as much as possible, isotropic and spherical, i.e. the methyl group is needed to prevent the ordered packing of the alkane chains on the NP surface, as shown in Fig. S1 of the ESI† for the MC11 case. Fig. 1C shows the configuration assumed by the PEG7–Au NP in the water phase; the other Au NP configurations are shown in Fig. S2 of the ESI.† The system is modeled with the OPLS united-atom (UA) force-field32–36 in explicit rigid simple point charge (SPC/E) water model,37 as better described in the Methods section.Non-equilibrium MD set-up
The temperature profiles generated by the hot Au NPs, are obtained from non-equilibrium MD simulations consisting of one thiol protected Au NP constrained in a simulation box of about 2000 nm3 (left panel of Fig. 2). As in Tascini et al.,38 temperature is controlled in only two spatial regions, hot and cold, by two independent thermostats, while the rest of the system is left un-thermostated. The heat source is represented by the Au atoms of the NP, thermostated at an average temperature of Thot = 380 K. The heat sink corresponds to a group of 500 water molecules, constrained to move outside a sphere of 6 nm from the Au NP center of mass (COM) (Fig. 2, blue) and thermostated at Tcold = 300 K. The constrained water molecules do not affect the dynamics nor the structural properties of water, as better detailed in the next paragraph and in the ESI (see Fig. S5†).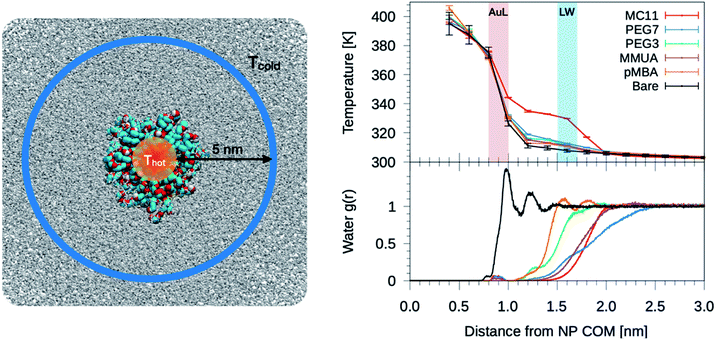 | ||
| Fig. 2 Left: simulation box used for the non-equilibrium MD simulations. A Au NP is placed at the center of the box and solvated with water. Color code as in Fig. 1, water is shown as gray-stick representation. Au atoms are the heat source, while the sink is constituted by a group of 500 cold water molecules constrained to move outside a sphere of 6 nm from the NP COM. Top-right: plot of the temperature profile for the different ligand types as a function of the distance from the NP COM, r. The light red shaded area corresponds to the Au–ligand interface (AuL); the light blue one corresponds to the ligand–water interfaces (LW) for the MC11 case. The protocol to compute the interface is detailed in the Method section. Right-bottom: plot of the radial distribution function, g(r), of water molecules as a function of r. | ||
We also tested an alternative set-up, as described in the ESI,† in which the heat sink is represented by a solid sphere of 7 nm in diameter and verified that the resulting temperature profile around the Au NPs does not depend on the choice of the non-equilibrium MD scheme.
Temperature profiles
We start analyzing the behavior of our training set of NPs, functionalized with MC11, PEG7, PEG3, MMUA and pMBA. The training set comprises also the reference bare Au NP. For the bare Au NP, the only thermally conductive interface is the Au–water interface. For the functionalized NPs there are two interfaces, Au–ligand and ligand–water. The spatial extension of ligand–water interfaces depends on the type of ligand, as better described in the Methods section. In the top right panel of Fig. 2, we show the temperature profiles as a function of the distance from the NP COM. The bare NP case, as expected, shows a single large temperature drop at the Au–water interface, ΔTAuW = 48.7 ± 0.7 K. When the NP is functionalized by ligands, we can distinguish two main behaviors depending on the hydrophobicity of the ligand: in presence of a hydrophilic ligand, the largest temperature drop is recorded at the Au–ligand interface, ΔTAuL (light-red shaded area in Fig. 2). The temperature drop at the ligand–water interface, ΔTLW (light-blue shaded area for the MC11 case in Fig. 2), in contrast, is smaller by an order of magnitude. For example, for the pMBA ligand (orange line) ΔTAuL = 39.8 ± 0.7 K > ΔTLW = 2.1 ± 0.4 K. The hydrophobic MC11 ligand, instead, shows two almost equal temperature drops at the Au–ligand and ligand–water interfaces (ΔTAuL = 31.6 ± 0.4 K and ΔTLW = 24.3 ± 0.3 K), separated by a temperature plateau. The temperature drops for all ligands are reported in Table S1 of the ESI.† A similar behavior is also shown in the work of Hung et al.31 for the temperature drops at the interface between a Au(111)-supported SAM and water: using a hydrophilic SAM they observe ΔTAuL > ΔTLW and vice versa for the hydrophobic case. We also measured the thermal conductance obtained at the ligand–water interface, as better described in the Methods section, and obtained values in close agreement with the experimental data by Ge et al.18To quantitatively rank the temperature profiles, we have defined the following dimensionless quantity:
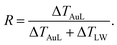 | (1) |
For the bare case, R = 1 since ΔTLW = 0. The lower the R value, the more the ligand acts as a thermal insulator, increasing ΔTLW and lowering ΔTAuL.
Overlap of core, ligand and water vDOS
We calculated the vDOS of the different materials composing the interface (Au and S atoms, ligand atoms and water molecules at ligand–water interface), for the MC11 and MMUA cases, as better detailed in the Methods section. We found, as shown in Fig. S6 of the ESI,† that there is no appreciable difference between the overlap of solvent and ligand vDOS in the MC11 and MMUA cases, despite the temperature profiles are quite different. We thus explored in more detail other physical parameters characterizing the hydrophobic and hydrophilic ligand–water interfaces.Dynamics and structure of interfacial water
Since hydrophobicity seems to be an important driving force shaping the temperature profile around the NP, we have investigated water penetration into the shell of the different ligand types. The bottom-right panel of Fig. 2 shows the radial distribution functions (RDFs) of the water molecules as a function of the distance from the NP COM. Despite the different chemico–physical nature of the ligands, there is no clear correlation between the water RDFs and the temperature profiles. For instance, the RDFs of water for MMUA and MC11 are quite similar while the temperature profiles differ significantly. This suggests that, if water molecules play a role in the heat transfer, this may not be related to the number of water molecules inside the ligand shell or at the ligand–water interface but rather to water dynamics or to the specific interaction between water molecules and the functionalizing ligands.We thus investigated if and how the thermal gradients are correlated to the mobility of interfacial water. We classify as interfacial water all water molecules having non-bonded interactions with the ligand atoms (Lennard-Jones and Coulomb energy terms) larger than the thermal energy of the fluid at interface (∝kBT), as described in detail in the Methods section and in Chiavazzo et al.39 From equilibrium MD simulations, we computed the self-diffusion coefficient of bulk water (that is, water far from the NP) Dbulk, and that of the interfacial water molecules, Dint. The results are shown in Fig. 3 and also reported in Table S2 of the ESI.† The diffusion coefficient for bulk water is compatible with the one obtained for the SPC/E water model.40,41 The diffusion coefficient of water at the ligand–water interface is substantially reduced with respect to the bulk molecules, as also shown in ref. 39 for water confined around a wide class of NPs. Most interestingly, the reduction of the diffusion coefficient depends on the functionalization of the Au NP: we recorded the lowest value of the diffusion coefficient for the pMBA ligand, Dint = 0.74 ± 0.03 10−5 cm2 s−1, and the highest Dint = 1.72 ± 0.06 10−5 cm2 s−1 is found in presence of the hydrophobic MC11 ligand type. Dint visibly clusters into three groups identified as weakly, moderately and highly confined water corresponding to the transition from hydrophobic to hydrophilic ligands and eventually to the bare Au surface (panel A and C of Fig. 3). We also quantified the residence time of interfacial water around the different types of ligands, τr (panel D of Fig. 3), as defined in the Methods section. The residence time depends on the functionalization of the Au NP: the lowest value is recorded for the MC11 (τr = 0.7 ps) and the largest for the pMBA (τr = 42 ps). Fig. 3 distinctly emphasizes that a large water mobility at hydrophobic ligand interface prevents the heat release at the ligand–water interface. Hydrophobic ligands are thus acting as a thermal insulator. On the other hand, a more confined water state registered around the hydrophilic ligands is the promoter of a more efficient thermal transport across the interface (highest R).
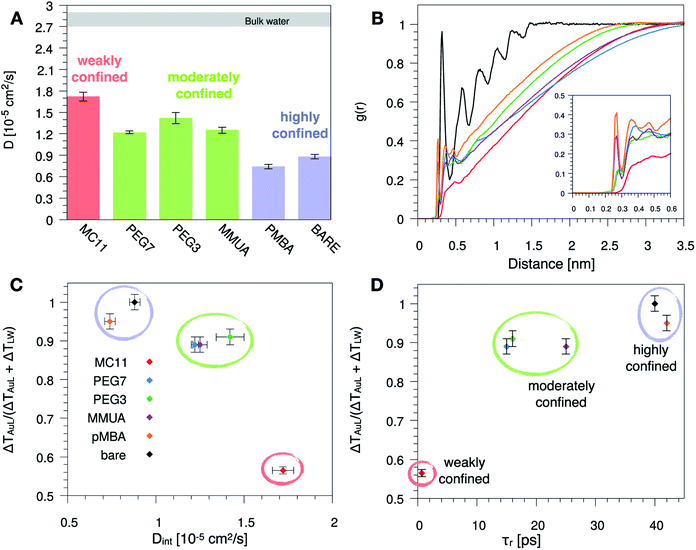 | ||
| Fig. 3 (A) Self-diffusion coefficient of the water molecules confined at the ligand–water interface, Dint, for the different ligand types. The grey area corresponds to the range of the self-diffusion coefficient of bulk water, far from the NP (Dbulk), obtained for the different ligands, compatible with the SPC/E self-diffusion coefficient.40,41 (B) Radial distribution function, g(r), of the water oxygens as a function of the distance between the oxygen and any atom of the Au NP and ligands. (C) and (D) Plot of the R parameter (see eqn (1)) as a function of Dint (C) or as a function of the water characteristic residence time τr (D), at ligand–water interface. Colored bars and circles indicate the degree of water confinement: red for weakly confined water at the interface of hydrophobic MC11, green for moderately confined water in proximity of hydrophilic PEG7, PEG3 and MMUA and purple for highly confined water close to charged pMBA and bare Au NP. | ||
To characterize the water structuring and density at interface we calculated the RDF of the water oxygens as a function of the distance between the oxygen and any atom of the Au NP and ligands. As confirmed by Fig. 3B, the MC11 coated Au NP shows, at ligand–water interface, the lowest density and oxygen structuring. The hydrophilic NPs, instead, exhibit a typical layering profile around highly interacting moieties.
A predictive model based on energetic and structural data
We then tested if the different behavior of interfacial water could be related to the strength and spatial extent of the ligand–water interaction. Indeed, energy and structural data are accessible via equilibrium MD simulations without recurring to non-equilibrium set-ups and to the extensive sampling that is required to quantify water dynamics or temperature profiles. As proposed by Chiavazzo et al.39 we characterized the water confinement around a NP by means of a spatial and an energetic parameter, δ and ε. Fig. 4A provides a graphical explanation of the physical meaning of δ and ε. Their definition relies on the identification of a single-well effective potential interaction between water and the NP surface. The characteristic length of water nanolayer δ can be explained as a measurement of the thickness of the layer in which the non-bonded interaction energy between water and the ligands is larger than thermal energy (∝kBT), thus causing the typically reduced solvent mobility at the interface.42 The water confinement energy ε instead represents the binding energy of the effective potential between interfacial water and the NP (core and ligands). We have then computed these two parameters for all the considered Au NPs, as reported in Fig. 4 and in Table S1 of the ESI.†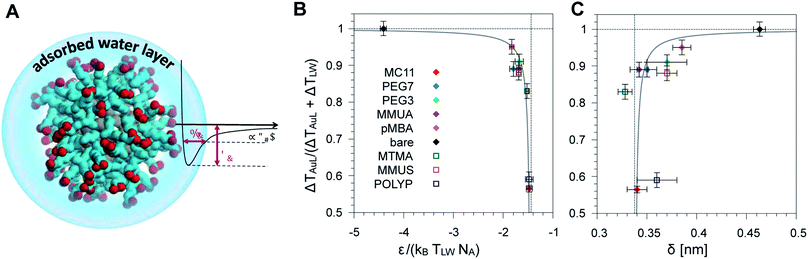 | ||
| Fig. 4 (A) Schematic representation of the adsorbed water layer (i.e. interfacial water molecules). Color code as Fig. 1. (B) Dimensionless parameter R (see eqn (1)) as a function of the parameter ε normalized with respect to the thermal energy associated to the temperature at ligand–water interface. Ligands used to derive the fit parameters are shown with full symbols, while the ligands used for model validation are indicated by empty symbols. (C) Plot of the same parameter R as a function of the characteristic water confinement length, δ. | ||
The water confinement energy ε, which is expressed in kJ mol−1, is divided by the thermal energy associated to the temperature at the ligand–water interface, in order to obtain a dimensionless parameter, the normalized-ε. In Fig. 4 the parameter R (see eqn (1)) is plotted as a function of normalized-ε (panel B); and as a function of the characteristic water confinement length, δ (panel C). The normalized-ε and δ parameters are distributed in three main regions. For R < 0.8, we only find the MC11 ligand that is characterized by the smallest R and the feeblest interaction with water (normalized-ε = −1.48 ± 0.06 and δ = 0.34 ± 0.01 nm). All the hydrophilic ligands (PEG7, MMUA, PEG3 and pMBA), instead, show similar values of the normalized-ε and δ (see Table S1†). Finally, for R = 1 we have the bare Au NP with the strongest interaction with water (normalized-ε = −4.41 ± 0.06) and the largest δ = 0.463 ± 0.006 nm. We thus observe that ligands with a feebler interaction with water lead to the formation of a thick hot layer around the NP, which is further evidence of a poor heat conduction on the solvent side. The R data vs. normalized-ε and δ are well fitted by a hyperbolic function (solid grey line in the plots of Fig. 4B and C, fitting parameters in Table S3†). Our results suggest that short equilibrium MD simulations could be used to screen a large set of ligands with different degrees of hydrophobicity. We obtained the values of the normalized-ε and δ with 25 ns MD simulations, while we had to sample at least 150 ns in order to derive the temperature profiles shown in Fig. 2.
Ligand validation set
We have validated our approach by testing the reliability of the model on three ligands that were not included in the fitting procedure, namely POLYP (hydrophobic), MMUS and MTMA (hydrophilic, see Fig. 1). Fig. 4 shows that their R, normalized-ε and δ parameters fall well within the hydrophilic and hydrophobic clusters previously identified and can allow for the prediction of the temperature gradients arising at the NP–solvent interface. The corresponding temperature profiles are shown in Fig. S8.†Methods
Au NP core model
The core of the NP is made of 144 Au atoms with icosahedral symmetry and 60 S atoms bound to Au atoms, as predicted via ab initio calculations43 and resolved with X-ray spectroscopy.44 A total of 60 ligands are bound to the NP core via Au–S bonds. The AuS core model relies on our previous work.10,45,46 The classical Lennard-Jones pair potential describing the Au–Au and Au–S interactions within the OPLS model suffers from intrinsic limitations at describing the many-body character of the metal bonding, and thus it may fail at reproducing the transfer of heat from the hot Au core to the ligands via atomic vibrations. We solved this issue by modeling Au–Au and Au–S interactions with an elastic network parameterized using as a target the harmonic vibrational spectrum of the Au NP given by a more reliable many-body model.47,48 The optimized elastic network uses two different elastic constants: 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 kJ mol−1 nm−1 for surface Au atoms and 11
500 kJ mol−1 nm−1 for surface Au atoms and 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 nm−1 for bulk Au atoms. The S atoms are bound to Au atoms via harmonic bonds with equilibrium distances from ref. 43 and elastic constant of 32
000 kJ mol−1 nm−1 for bulk Au atoms. The S atoms are bound to Au atoms via harmonic bonds with equilibrium distances from ref. 43 and elastic constant of 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 kJ mol−1 nm−1. To maintain the structure of S atoms stable, an elastic network is added also between S–S atoms with an elastic constant of 25
500 kJ mol−1 nm−1. To maintain the structure of S atoms stable, an elastic network is added also between S–S atoms with an elastic constant of 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 nm−1. Moreover, to prevent the overlap between S and Au atoms a purely repulsive Lennard-Jones potential is added between Au and S atoms (ε = 0.2324 10−6 kJ mol−1). The non-bonded parameters for Au atoms are from Heinz et al.49 For the S atoms the standard OPLS parameters are used.
000 kJ mol−1 nm−1. Moreover, to prevent the overlap between S and Au atoms a purely repulsive Lennard-Jones potential is added between Au and S atoms (ε = 0.2324 10−6 kJ mol−1). The non-bonded parameters for Au atoms are from Heinz et al.49 For the S atoms the standard OPLS parameters are used.
Water model
SPC/E model is the most widely used in combination with the OPLS force field. It has already been used successfully for the study of thermal transport at the interface between different organic compounds and water.23,31,50–52 Also, the SPC/E model is designed to well reproduce the self-diffusion coefficient of water41,53 and it is also able to well reproduce the thermal conductance at room temperature, with a small deviation from experiments53–55 (about 10 to 20%).We also tested a different water model. As we found that the self-diffusion coefficient of water plays a crucial role in determining the heat flow from the hot nanoparticle to the cold-water bath, we tested the TIP4P-2005 water model41,56,57 that perfectly matches water self-diffusion coefficient, with a deviation from experiments of less than 1%. For what concerns the thermal conductance, its behavior is similar to the SPC/E model.53 On the computational side, the TIP4P-2005 model is about 1.5 times slower than the SPC/E model. We have calculated a new temperature profile for the TIP4P-2005 water model with the hydrophobic MC11 ligand type and we found that the temperature profile, within the errors, is the same as that calculated with the SPC/E water model.
Ligand models
The topology of all ligands was derived following the standard OPLS-UA rules32–36 and our previous work,10,46,58 with missing parameters taken from the AMBER forcefield.59 For what concerns the PEG chains, three OPLS-compatible parameters were tested, from Fuchs et al.,60 Fischer et al.61 and Weiner et al.32 For each parameter set, a MD simulation was performed with one PEG molecule composed by 28 monomers, solvated with about 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 SPC/E water molecules. We calculated the chain radius of gyration and compared it, via extrapolation at low molecular weight, with the experimental data by Kawaguchi et al.62 The model based on Weiner is able to reproduce well the experimental data. The cationic trimethylammonium terminal group of the MTMA ligand rely on the modified-Berger parameters for lipids63 while the anionic terminal group of the MMUS ligand are taken from ref. 64. All the topology files of the ligands and of the functionalized Au NPs used in this work are freely available in our online repository.65 For what concerns the generation of the functionalized Au NPs the reader is addressed to the ESI.†
000 SPC/E water molecules. We calculated the chain radius of gyration and compared it, via extrapolation at low molecular weight, with the experimental data by Kawaguchi et al.62 The model based on Weiner is able to reproduce well the experimental data. The cationic trimethylammonium terminal group of the MTMA ligand rely on the modified-Berger parameters for lipids63 while the anionic terminal group of the MMUS ligand are taken from ref. 64. All the topology files of the ligands and of the functionalized Au NPs used in this work are freely available in our online repository.65 For what concerns the generation of the functionalized Au NPs the reader is addressed to the ESI.†
MD simulation set-up
All non-equilibrium simulations were performed with a time step of 2 fs. The pressure was kept constant at 1 bar with Parrinello–Rahman barostat66 (τP = 0.1 ps). The temperature of the two thermostated regions were kept constant with two Nose–Hoover thermostats.67 The heat source was set at 380 K (τT = 0.5 ps) and the heat sink at 300 K (τT = 1 ps). The Thot temperature we chose is lower than the typical melting temperature of Au NPs of this size,68 while Tcold is the reference room temperature. The NP was restrained at the center of the box by applying a position restraint at one of the most internal Au atoms with an elastic constant of 5000 kJ mol−1 nm−1 in the three directions. The group of 500 water molecules associated with the heat sink was constrained to move outside a sphere of radius 6 nm centered at the center of the box, with a spherical flat-bottom position restraint and an elastic constant of 1000 kJ mol−1 nm−1. Each water molecule in this group is subject to a harmonic repulsive potential only if its distance from the NP COM is less than 6 nm, otherwise it moves unperturbed. All non-equilibrium simulations were pre-equilibrated with the same parameters for 5 ns. Then, 80 ns long production runs, for each NP, were performed and used to calculate the temperature profiles.All equilibrium MD simulations to calculate water properties were performed in the NPTNP ensemble with a time step of 1 fs and a verlet-buffer-tolerance of 0.0001 kJ mol−1 ps−1. These simulations were pre-equilibrated in the NPT ensemble with a time step of 2 fs, Berendsen barostat69 and v-rescale thermostat70 to maintain constant, respectively, pressure (1 bar) and temperature of the system (300 K). Then, the barostat was switched to Parrinello–Rahman (τP = 0.1 ps) and the v-rescale thermostat (τT = 0.2 ps), with a reference temperature of 300 K, was applied only on the NP atoms while the rest of the system was left un-thermostated, in order not to affect the properties of water at the interface. In this case two independent 5 ns runs were performed for each NP.
In all simulations the rigid SPC/E37 water model and the PME method, with a grid spacing of 0.12 nm for long-range electrostatics, was used. All H-bonds were constrained with the LINCS (linear constraint solver) algorithm.71 All simulations were performed with Gromacs v. 2018.72
Temperature profiles
The temperature profiles in function of the distance from the NP COM, were calculated with an in house Gromacs tool, freely downloadable from our online repository.65 To calculate the local temperature, the system was divided in spherical shells of fixed thickness (Δr = 0.2 nm) and the kinetic energy (Ki) for the ith shell was calculated according to the equipartition theorem as Ti = NDOFiKi/2. NDOFi is the total number of degrees of freedom (DOF) in the ith shell, taking appropriately into account the presence of constrained bonds.In order to obtain a smooth temperature profile, as shown in Fig. 2, each profile is obtained by averaging, along the 80 ns trajectory, the temperature profiles collected every 2 ns; this time interval was chosen in such a way as to average independent temperature profiles, coherently with the longest decorrelation time of the temperature of a given shell, as we have calculated with the error estimation option of the gmx analyze tool. The error on temperature was computed as the standard error associated to the mean.
Core–ligand and ligand–water interfaces
The temperature drop at the sharp Au–ligand interface (and Au–water in the case of the bare NP), ΔTAuL, was calculated as ΔTAuL = T(r = 1 nm) − T(r = 0.8 nm). Since the ligand–water interface is not sharp, we defined the temperature drop at the ligand–water interface as ΔTLW = T(rW) − T(rL). Where rL is the radius, from the NP COM, that gives 75% of the integral of the ligand RDF, while rW gives 95%. The values of rL and rW are reported in Table S1.†Thermal conductance
The thermal conductance G at the interface between NP ligands and water was quantified via:73| G = J/ΔT |
where 〈ξ〉 is the time average of the thermostat heat bath parameter, NDOF and Thot are, respectively, the number of degrees of freedom and temperature of the hot thermostat, kB is the Boltzmann constant and SLW is the surface area of the ligand–water interface. We performed two simulations in order to obtain the G value for a hydrophilic and a hydrophobic ligand differing only for their terminal group, namely MMUS (from the new Validation set) and MC11. We obtained G = 470 ± 54 MW m−2 K−1 for the hydrophilic MMUS ligand, and G = 123 ± 15 MW m−2 K−1 for the hydrophobic MC11 ligand. These data are in good agreement with the experimental data by Ge et al.,18 related to flat surfaces functionalized by SAMs of different hydrophobicity.
Solvent accessible surface area (SASA)
The SASA estimation, needed for the calculation of ε and δ, was obtained from a 5 ns long simulation, for each NP, with the gmx sasa tool.77Self-diffusion coefficient
The self-diffusion coefficient of bulk water, Dbulk, was calculated following the Einstein relationship with the mean square displacement (MSD) calculated as:the MSD was calculated by the gmx msd tool. The error was computed as the standard deviation of the self-diffusion obtained from independent simulations.
The self-diffusion coefficient of water at the ligand-water interface, Dint, was calculated with a homemade Gromacs tool, freely downloadable from our online repository.65 The input trajectory, with 1 frame every 5 ps, was divided into stretches of 150 ps. For each stretch, the MSD was calculated only for the water molecules that were in contact (within a cut-off equal to the value of δ) with at least one atom of the NP + ligands system (i.e. those water molecules within δ from the NP + ligands SASA) in the first frame of that stretch. Then, the MSD was averaged between all stretches and Dint was calculated with the Einstein relationship. The error was computed in the same way as for Dbulk.
Characteristic confinement estimator
The concept of interfacial water, also known as hydration layer, has been largely studied because of its structural and thermodynamic properties, which are found significantly different from those of bulk water. Essentially, the collective non-bonded interactions between interfacial water molecules and the adjacent atoms of the solute induce a more confined and ordered state of water, with remarkable consequences on nanoparticle or protein stability, self-assembly, nanofluidic, and heat transport. The characteristic water confinement length δ and water confinement energy ε were defined by Chiavazzo et al.39 The spatial δ parameters defines the thickness of a shell of influence of the NP on water. Water molecules that are found within a distance δ from the solvent accessible area can be considered as bound to the NP, and as such they may exhibit a different dynamic with respect to bulk water. The ε parameter quantifies the binding energy of the NP-bound water molecules. These parameters, which are experimentally validated by Diallo et al.,78,79 were calculated using our modified version of the Matlab script, freely downloadable from our online repository.65 The error estimation to ε and δ is described in the ESI.†Characteristic residence time
The water characteristic residence time, τr, is calculated with a homemade Gromacs tool, available in our online repository.65 For each frame of the trajectory, a shell of thickness τ around each atom of the NP is defined. Each water molecule for each frame is tracked to record the time, τ, for which the water molecule is continuously inside the shell, i.e. continuously in contact with an atom of the NP. A frequency histogram P(τ) is built. The characteristic residence time, τr, is defined as80,81Vibrational density of states
The vDOS spectra are calculated by means of the double precision version of the Gromacs gmx dos tool82 using the Fourier transform of the mass-weighted velocity autocorrelation function.83Conclusions
In this work, we have unveiled the role of water dynamics on the thermal conductance at the three-component Au NP–ligand–water interface. In particular, we have investigated via MD simulations the interfacial water physics driving the thermal transport from a hot ligand coated Au NP to a cold-water bath. For bare NPs and hydrophilic ligand-coated NPs, the temperature profile exhibits a single steep descent at the Au–ligand interface. Instead, a different temperature profile is found in the case of fully hydrophobic ligands coating the hot Au NP. We observe a first temperature drop at the Au–ligand interface, a temperature plateau, and a second large drop of at the ligand–water interface.We thus propose an interpretation of the data based on the dynamics of water at the ligand–water interface. The large water mobility registered only in the case of completely hydrophobic ligands prevents interfacial water from exchanging heat with the hot NP, thereby increasing the thermal resistance at the ligand–water interface and causing a significant heating of the ligand shell. On the contrary, water is more effectively confined at the interface with hydrophilic ligands, promoting NP-to-solvent heat transfer and reducing the thermal resistance at the ligand–water interface. This mechanism, which we have described for the case of thiolated Au NPs, can also explain the dependence of thermal conductance on the hydrophobicity of the self-assembled monolayers adsorbed at different planar interfaces.18
Beyond the physical insight, our study can contribute to the engineering of coated NPs with controlled thermal behavior in presence of intense, short laser pulses.9 The proposed computational approach could indeed be used to predict which functionalization would be more efficient at creating a spatially confined hot region around the NP. As this approach is based on the use of short equilibrium molecular dynamics runs, it could be easily exported to the case of larger NPs, coated by more massive organic ligands.12 These results, together with the knowledge of the NP absorbance, could finally allow the estimation of the temperature rise occurring in those biological components in direct contact with theranostic Au NPs, such as the lipids and the plasma membrane proteins in photoporation applications.
Author contributions
P. A., R. F. and G. R. conceived the idea and supervised the work. S. S. performed all the simulations, developed the analysis tools and the script to create the NP, and, together with A. C. and G. R., analyzed the data. S. S, A. C. and G. R. wrote the article with the collaboration of the other authors. All the authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Giulia Rossi acknowledges funding from the ERC Starting Grant BioMNP – 677513. The authors thank Matteo Fasano, Eliodoro Chiavazzo and Davide Bochicchio for fruitful discussions and Andrea Torchi for having designed and developed the first version of the tool to compute the temperature profile. G. R., S. S. and R. F. acknowledge funding for computational equipment from the MIUR grant “Dipartimento di eccellenza” 2018-2022.Notes and references
- H. H. Jeong, E. Choi, E. Ellis and T. C. Lee, J. Mater. Chem. B, 2019, 7, 3480–3496 RSC.
- J. J. Giner-Casares, M. Henriksen-Lacey, M. Coronado-Puchau and L. M. Liz-Marzán, Mater. Today, 2016, 19, 19–28 CrossRef CAS.
- X. Huang, Z. Xu, Y. Mao, Y. Ji, H. Xu, Y. Xiong and Y. Li, Biosens. Bioelectron., 2015, 66, 184–190 CrossRef CAS PubMed.
- S.-M. Lee, H. J. Kim, S. Y. Kim, M.-K. Kwon, S. Kim, A. Cho, M. Yun, J.-S. Shin and K.-H. Yoo, Biomaterials, 2014, 35, 2272–2282 CrossRef CAS PubMed.
- R. Xiong, K. Raemdonck, K. Peynshaert, I. Lentacker, I. De Cock, J. Demeester, S. C. De Smedt, A. G. Skirtach and K. Braeckmans, ACS Nano, 2014, 8, 6288–6296 CrossRef CAS PubMed.
- E. Teirlinck, R. Xiong, T. Brans, K. Forier, J. Fraire, H. Van Acker, N. Matthijs, R. De Rycke, S. C. De Smedt, T. Coenye and K. Braeckmans, Nat. Commun., 2018, 9, 1–12 CrossRef CAS PubMed.
- G. Houthaeve, R. Xiong, J. Robijns, B. Luyckx, Y. Beulque, T. Brans, C. Campsteijn, S. K. Samal, S. Stremersch, S. C. De Smedt, K. Braeckmans and W. H. De Vos, ACS Nano, 2018, 12, 7791–7802 CrossRef CAS PubMed.
- A. Carattino, M. Caldarola and M. Orrit, Nano Lett., 2018, 18, 874–880 CrossRef CAS PubMed.
- P. Keblinski, D. G. Cahill, A. Bodapati, C. R. Sullivan and T. A. Taton, J. Appl. Phys., 2006, 100, 054305 CrossRef.
- A. Torchi, F. Simonelli, R. Ferrando and G. Rossi, ACS Nano, 2017, 11, 12553–12561 CrossRef CAS PubMed.
- A. Gupta, R. S. Kane and D. A. Borca-Tasciuc, J. Appl. Phys., 2010, 108, 06490 Search PubMed.
- A. Riedinger, P. Guardia, A. Curcio, M. A. Garcia, R. Cingolani, L. Manna and T. Pellegrino, Nano Lett., 2013, 13, 2399–2406 CrossRef CAS PubMed.
- D. C. Hannah, J. D. Gezelter, R. D. Schaller and G. C. Schatz, ACS Nano, 2015, 9, 6278–6287 CrossRef CAS PubMed.
- J. Soussi, S. Volz, B. Palpant and Y. Chalopin, Appl. Phys. Lett., 2015, 106, 093113 CrossRef.
- T. Zhang, F. Sun, Z. Guo, D. Tang, Z. Zheng, S. Ptasinska, X. Zhang, M. M. Jobbins and T. Luo, Adv. Mater., 2014, 26, 6093–6099 CrossRef PubMed.
- O. M. Wilson, X. Hu, D. G. Cahill and P. V. Braun, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 2243011–2243016 CrossRef.
- Z. Ge, D. G. Cahill and P. V. Braun, J. Phys. Chem. B, 2004, 108, 18870–18875 CrossRef CAS.
- Z. Ge, D. G. Cahill and P. V. Braun, Phys. Rev. Lett., 2006, 96, 1–4 CrossRef PubMed.
- M. D. Losego, M. E. Grady, N. R. Sottos, D. G. Cahill and P. V Braun, Nat. Mater., 2012, 11, 502–506 CrossRef CAS PubMed.
- J. Park and D. G. Cahill, J. Phys. Chem. C, 2016, 120, 2814–2821 CrossRef CAS.
- H. A. Patel, S. Garde and P. Keblinski, Nano Lett., 2005, 5, 2225–2231 CrossRef CAS PubMed.
- A. S. Tascini, E. Chiavazzo, M. Fasano, P. Asinari and F. Bresme, Phys. Chem. Chem. Phys., 2017, 19, 3244–3253 RSC.
- D. Alexeev, J. Chen, J. H. Walther, K. P. Giapis, P. Angelikopoulos and P. Koumoutsakos, Nano Lett., 2015, 15, 5744–5749 CrossRef CAS PubMed.
- D. Huang, R. Ma, T. Zhang and T. Luo, ACS Appl. Mater. Interfaces, 2018, 10, 28159–28165 CrossRef CAS PubMed.
- T. Zhang, A. R. Gans-Forrest, E. Lee, X. Zhang, C. Qu, Y. Pang, F. Sun and T. Luo, ACS Appl. Mater. Interfaces, 2016, 8, 33326–33334 CrossRef CAS PubMed.
- K. M. Stocker, S. M. Neidhart and J. D. Gezelter, J. Appl. Phys., 2016, 119(2), 025106 CrossRef.
- E. T. Swartz and R. O. Pohl, Rev. Mod. Phys., 1989, 61, 605–668 CrossRef.
- X. Chen, A. Munjiza, K. Zhang and D. Wen, J. Phys. Chem. C, 2014, 118, 1285–1293 CrossRef CAS.
- S. Kuang and J. D. Gezelter, J. Phys. Chem. C, 2011, 115, 22475–22483 CrossRef CAS.
- E. S. Melby, S. E. Lohse, J. E. Park, A. M. Vartanian, R. A. Putans, H. B. Abbott, R. J. Hamers, C. J. Murphy and J. A. Pedersen, ACS Nano, 2017, 11, 5489–5499 CrossRef CAS PubMed.
- S. W. Hung, G. Kikugawa and J. Shiomi, J. Phys. Chem. C, 2016, 120, 26678–26685 CrossRef CAS.
- S. J. Weiner, P. A. Kollman, D. A. Case, U. C. Singh, C. Ghio, G. G. G. Alagona, S. Profeta, P. Weiner, P. Weinerl and P. Weiner, J. Am. Chem. Soc., 1984, 106, 765–784 CrossRef CAS.
- W. L. Jorgensen, J. D. Madura and C. J. Swenson, J. Am. Chem. Soc., 1984, 106, 6638–6646 CrossRef CAS.
- W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657–1666 CrossRef CAS PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197 CrossRef CAS.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- A. S. Tascini, E. Chiavazzo, M. Fasano, P. Asinari, F. Bresme, J. Armstrong, E. Chiavazzo, M. Fasano, P. Asinari and F. Bresme, Phys. Chem. Chem. Phys., 2017, 19, 3244–3253 RSC.
- E. Chiavazzo, M. Fasano, P. Asinari and P. Decuzzi, Nat. Commun., 2014, 5, 1–11 Search PubMed.
- P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960 CrossRef CAS.
- S. Tazi, A. Boţan, M. Salanne, V. Marry, P. Turq and B. Rotenberg, J. Phys.: Condens. Matter, 2012, 24, 284117 CrossRef PubMed.
- A. Cardellini, M. Fasano, E. Chiavazzo and P. Asinari, Phys. Lett. A, 2016, 380, 1735–1740 CrossRef CAS.
- O. Lopez-Acevedo, J. Akola, R. L. Whetten, H. Grönbeck and H. Häkkinen, J. Phys. Chem. C, 2009, 113, 5035–5038 CrossRef CAS.
- N. Yan, N. Xia, L. Liao, M. Zhu, F. Jin, R. Jin and Z. Wu, Sci. Adv., 2018, 4, eaat7259 CrossRef CAS PubMed.
- F. Simonelli, D. Bochicchio, R. Ferrando and G. Rossi, J. Phys. Chem. Lett., 2015, 6, 3175–3179 CrossRef CAS.
- S. Salassi, F. Simonelli, D. Bochicchio, R. Ferrando and G. Rossi, J. Phys. Chem. C, 2017, 121, 10927–10935 CrossRef CAS.
- R. P. Gupta, Phys. Rev. B, 1981, 23, 6265–6270 CrossRef CAS.
- R. Ferrando, J. Jellinek and R. L. Johnston, Chem. Rev., 2008, 108, 845–910 CrossRef CAS PubMed.
- H. Heinz, R. A. Vaia, B. L. Farmer and R. R. Naik, J. Phys. Chem. C, 2008, 112, 17281–17290 CrossRef CAS.
- N. Shenogina, R. Godawat, P. Keblinski and S. Garde, Phys. Rev. Lett., 2009, 102, 1–4 CrossRef PubMed.
- E. Chiavazzo and P. Asinari, Nanoscale Res. Lett., 2011, 6, 249 CrossRef PubMed.
- F. Grunewald, G. Rossi, A. H. De Vries, S. J. Marrink and L. Monticelli, J. Phys. Chem. B, 2018, 122, 7436–7449 CrossRef CAS PubMed.
- S. H. Lee and J. Kim, Mol. Phys., 2019, 117, 1926–1933 CrossRef CAS.
- D. Bertolini and A. Tani, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 4135–4151 CrossRef CAS.
- D. Bedrov and G. D. Smith, J. Chem. Phys., 2000, 113, 8080–8084 CrossRef CAS.
- I. N. Tsimpanogiannis, O. A. Moultos, L. F. M. Franco, M. B. d. M. Spera, M. Erdős and I. G. Economou, Mol. Simul., 2019, 45, 425–453 CrossRef CAS.
- J. L. F. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef CAS PubMed.
- S. Salassi, F. Simonelli, A. Bartocci and G. Rossi, J. Phys. D: Appl. Phys., 2018, 51, 384002 CrossRef.
- S. J. Weiner, P. A. Kollman, U. C. Singh, D. A. Case, C. Ghio, G. Alagona, S. Profeta and P. Weiner, J. Am. Chem. Soc., 1984, 106, 765–784 CrossRef CAS.
- P. F. J. Fuchs, H. S. Hansen, P. H. Hünenberger and B. A. C. Horta, J. Chem. Theory Comput., 2012, 8, 3943–3963 CrossRef CAS PubMed.
- J. Fischer, D. Paschek, A. Geiger and G. Sadowski, J. Phys. Chem. B, 2008, 112, 2388–2398 CrossRef CAS PubMed.
- S. Kawaguchi, G. Imai, J. Suzuki, A. Miyahara, T. Kitano and K. Ito, Polymer, 1997, 38, 2885–2891 CrossRef CAS.
- D. P. Tieleman, J. L. MacCallum, W. L. Ash, C. Kandt, Z. Xu and L. Monticelli, J. Phys.: Condens. Matter, 2006, 18, S1221–S1234 CrossRef CAS PubMed.
- J. N. Canongia Lopes, A. A. H. Pádua and K. Shimizu, J. Phys. Chem. B, 2008, 112, 5039–5046 CrossRef CAS PubMed.
- https://bitbucket.org/biomembnp/biomembnp, BioMembNP repository, https://bitbucket.org/biomembnp/biomembnp.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef PubMed.
- R. Ferrando and F. Baletto, Rev. Mod. Phys., 2005, 77, 371–423 CrossRef.
- H. J. C. Berendsen, J. P. M. Postma, W. F. Van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindah, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- L. Hu, T. Desai and P. Keblinski, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 1–5 Search PubMed.
- M. Fasano, M. Bozorg Bigdeli, M. R. Vaziri Sereshk, E. Chiavazzo and P. Asinari, Renewable Sustainable Energy Rev., 2015, 41, 1028–1036 CrossRef CAS.
- R. A. Shelly, K. Toprak and Y. Bayazitoglu, Int. J. Heat Mass Transfer, 2010, 53, 5884–5887 CrossRef CAS.
- W. G. Hoover and C. G. Hoover, Mol. Phys., 2003, 101, 1559–1573 CrossRef CAS.
- F. Eisenhaber, P. Lijnzaad, P. Argos, C. Sander and M. Scharf, J. Comput. Chem., 1995, 16, 273–284 CrossRef CAS.
- S. O. Diallo, Phys. Rev. E, 2015, 92, 012312 CrossRef CAS PubMed.
- N. C. Osti, A. Coté, E. Mamontov, A. Ramirez-Cuesta, D. J. Wesolowski and S. O. Diallo, Chem. Phys., 2016, 465–466, 1–8 CrossRef CAS.
- A. Luzar, J. Chem. Phys., 2000, 113, 10663–10675 CrossRef CAS.
- V. P. Voloshin and Y. I. Naberukhin, J. Struct. Chem., 2009, 50, 78–89 CrossRef CAS.
- T. A. Pascal, S. T. Lin and W. A. Goddard, Phys. Chem. Chem. Phys., 2011, 13, 169–181 RSC.
- S. T. Lin, M. Blanco and W. A. Goddard, J. Chem. Phys., 2003, 119, 11792–11805 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: All the topology information (gro and itp files) used to perform the simulations and all tools and scripts made to analyse the simulations and to create the NPs are available. See DOI: 10.1039/d0na00094a |
| This journal is © The Royal Society of Chemistry 2020 |