Open Access Article
Open Access ArticleMo2B, an MBene member with high electrical and thermal conductivities, and satisfactory performances in lithium ion batteries†
Xian-Hu
Zha
 *a,
Pengxiang
Xu
a,
Qing
Huang
*a,
Pengxiang
Xu
a,
Qing
Huang
 b,
Shiyu
Du
b,
Shiyu
Du
 *b and
Rui-Qin
Zhang
*b and
Rui-Qin
Zhang
 c
c
aCenter for Quantum Computing, Peng Cheng Laboratory, Shenzhen, 518055, China. E-mail: zhaxh@pcl.ac.cn
bEngineering Laboratory of Advanced Energy Materials, Ningbo Institute of Materials Technology and Engineering, Chinese Academy of Sciences, Ningbo, Zhejiang 315201, China. E-mail: dushiyu@nimte.ac.cn
cDepartment of Physics, City University of Hong Kong, Hong Kong SAR, China
First published on 12th November 2019
Abstract
Owing to their high specific area, good flexibility and many other unique properties, two-dimensional (2D) materials have attracted extensive attention in the recent two decades. As an analogy to the well-studied MXenes, MBenes also emerged. In this work, Mo2B, an MBene member, is predicted both in H- and T-type configurations from first-principles calculations. Structural, mechanical, electronic, and thermal properties, and performances in lithium ion batteries (LIBs) for both configurations are investigated. The H-type Mo2B is found to be the stable structure, which can be transformed into the T-type by applying strains. The elastic constants c11 in the H- and T-type Mo2B are respectively calculated to be 187.5 and 157.6 N m−1, which are higher than that in the previously reported Mo2C. The electronic thermal conductivity and electrical conductivity are investigated based on the semiclassical Boltzmann transport theory. The electrical conductivities for both structures are of the order of 106 Ω−1 m−1. Because of the large phonon contributions, the thermal conductivities in the H- and T-type Mo2B are much higher than that of the synthesized Mo2C. Based on a 5 μm flake length, the phonon thermal conductivities at room temperature are calculated to be 146 and 141 W m−1 K−1 respectively for the H- and T-type configurations. The T-type Mo2B shows promising performances in LIBs. The theoretical volumetric capacity is as high as 2424 mA h cm−3, and the migration energy barrier is as low as 0.0372 eV. These data imply that Mo2B has widespread applications, such as in conductive films and anode materials.
Introduction
Since the discovery of graphene,1 two-dimensional (2D) materials have attracted extensive attention.2,3 Especially, the high specific surface area and great flexibility of the 2D configuration meet the increasing technological demands for paper displays and wearable electronics.4,5 To date, a large number of 2D configurations have been predicted and synthesized,6,7 such as the high-profile molybdenum disulfide8 and phosphorene.9 Since 2011, MXenes have generally stood out owing to their abundant configurations and adjustable properties.10–12 Different from graphene, MXenes are a large family, which were initially synthesized by the selective etching of Mn+1AXn phases (or abbreviated to MAX phases). Here, M denotes an early transition metal, A is an A-group element (mostly in the IIIA or IVA group), X is carbon and/or nitrogen,13 and n is a number normally ranging from one to three. Since M–A bonds are generally weaker than M–X bonds in the MAX phases, the A atomic layer is normally etched out in adequate etchants. Therefore, the synthesized MXene generally has the formula Mn+1XnTx, where Tx denotes surface groups.12 Later, non-MAX layered carbides, such as Zr3Al3C5 and Hf3(Al,Si)4C6, were also employed as precursors for Zr3C2Tx14 and Hf3C2Tx MXenes.15 Moreover, non-stoichiometric Mo1.33CTx (ref. 16) and W1.33CTx (ref. 17) were also developed through selective etching of (Mo2/3Sc1/3)2AlC and (W2/3M1/3)2AlC (M = Sc, Y), respectively. Until now, approximately thirty MXene members have been synthesized,18 which have been demonstrated to show widespread applications, such as energy storage,19–21 electromagnetic shielding,22 sewage treatment,23 nuclide adsorption,24 photothermal therapy,25 multicolor cellular imaging,26 electrocatalysts,27,28etc.MBene, by replacing the X element of MXene with the neighboring B, naturally aroused increasing attention in the recent three years.29–33 Moreover, most boron-containing compounds are high-temperature refractory materials.34,35 With respect to the formula Mn+1XnTx for MXenes, MBenes have more adjustable space. For instance, M2B2Tx with two boron atomic layers intercalated in the transition metals are reported based on existing bulk precursors MAB, such as MoAlB.32 Theoretically, Guo et al. found that Mo2B2 and Fe2B2 show good electrical conductivities, small migration energy barriers, and high storage capacities for lithium ion batteries (LIBs). Moreover, Fe2B2 was determined to be a potential catalyst for hydrogen evolution.31 Furthermore, Bo et al. reported a new type of M2B2 MBenes with two boron atoms forming a planar honeycomb sandwiched by two M atomic planes. Six M2B2 (M = Sc, Ti, V, Cr, Y, Zr, Mo) members were determined to be the global minimum structures. Ti2B2 was determined to be a candidate anode material for LIBs and SIBs.29 Using a high-throughput structural search, Jiang et al. determined twelve metastable MBenes, MnB, HfB, ZrB, Au2B, Mo2B, Nb5B2, Nb3B4, Ta3B4, V3B4, OsB2, FeB2, and RuB2, and they found that bare or functionalized MnB compounds are ferromagnets with high Curie temperatures.30 Although H-type Mo2B has been predicted,30 this structure was not discussed in detail. In their experiment, Alameda et al. used MoAlB as the precursor to synthesize MBene, but they obtained MoAlB slabs of nanoscale thickness in their first attempt.32 Furthermore, they performed etching of MoAlB in two steps, and they identified isolated MoB layers inside the etched cavities.33 Based on the discussions above, MBenes have potential applications, which have been shown to be feasible in experiments. Thus, an in-depth investigation on MBene is justified.
Previously, Xu et al. synthesized the bare Mo2C configuration by chemical vapor deposition (CVD), which was proven to show superconductivity36 and oscillatory magnetoresistance.37 Theoretically, the synthesized Mo2C was also found to show high storage capacities and low migration energy barriers for Li, Na and K ions. Specifically, the storage capacity was determined to be 263 mA h g−1, and the migration barrier is calculated to be as low as 0.043 eV for Li ion.38 In addition, Mo2C is determined to be robust under varying temperatures and strains since it possesses relatively low thermal expansion coefficient and high mechanical strength.39 In analogy to Mo2C, Mo2B, both in the H- and T-type configurations, is predicted in this work. The structural, mechanical and thermal properties, and the performances in LIBs are studied. Compared with Mo2C, both the H- and T-type Mo2B are found to show comparable electrical conductivities, and much higher thermal conductivities. In addition to a relatively low migration energy barrier and a high storage capacity, the T-type Mo2B is a potential candidate anode material for LIBs.
Methods
The first-principles calculations are implemented in the plane-wave VASP code40 in this work. Based on the projected augmented wave (PAW) pseudopotential, the generalized gradient approximation (GGA) by Purdew–Burke–Ernzerhof (PBE)41 is employed for description of the exchange and correlation functional. A plane-wave cutoff energy of 500 eV is adopted for describing the ion–electron interaction, in which the Mo 4p6, 5s1, 4d5 and B 2s2, 2p1 electrons are considered as valence electrons. All the structures are relaxed until the force on each atom is less than 1.0 × 10−3 eV Å−1, and the criterion for energy convergence is set as 1.0 × 10−6 eV per cell. A Γ-centered sampling of 12 × 12 × 1 k-point mesh is adopted for the Brillouin zone (BZ) of the Mo2B unit cell. In order to eliminate the layer interaction, a vacuum layer larger than 23 Å is employed parallel to the Mo2B surface. In order to test the stable configuration for Mo2B, the local particle swarm optimization for 2D structures is performed combined with the CALYPSO package42 and the VASP code. All the structures are visualized in the VESTA3 code.43 In order to investigate the elastic constants, the stress–strain relationship44 is employed as implemented in the VASP code. Spin-polarization is considered in the calculation. To investigate the electrical conductivity and electronic thermal conductivity, the semiclassical Boltzmann transport calculations are performed based on constant relaxation time approximation, which are undertaken in the BoltzTraP code.45 The electronic structure for transport properties is calculated based on a very fine k-point mesh of 42 × 42 × 1, and the mesh is interpolated to a dense one of 20 times in the BoltzTraP calculation. The obtained transport parameters from BoltzTraP are rescaled using h/d, where h denotes the lattice parameter in the c-axis, and d represents the layer thickness, which is equal to the monomer thickness in its multilayer configuration.39,46Regarding the thermal properties, the specific heat, thermal expansion coefficient, and phonon thermal conductivity are calculated. The phonon dispersions are calculated based on density functional perturbation theory (DFPT),47 which is implemented by a combination of the VASP and Phonopy48 softwares. For calculating the dynamical matrix, a 4 × 4 × 1 supercell with a 6 × 6 × 1 Γ-centered k-point mesh is employed. The phonon dispersions are plotted using a 120 k-point grid for various directions and the entire BZ. The specific heat and thermal expansion coefficient are calculated based on the Grüneisen approximation.39,49–51 The phonon thermal conductivity is calculated according to the Klemens theory.39,52–55 The details are presented in eqn (S1)–(S3) in the ESI.†
Regarding the Mo2B performance in LIBs, 4 × 4 × 1 supercells for both H- and T-type Mo2B are optimized. Diffusion energy barriers for Li atom on the supercells are calculated according to the climbing-image nudge elastic-band (CI-NEB) method.56 The binding energies of Li atoms on the 4 × 4 × 1 supercells are calculated according to the following equation:
| Ebinding = (EMo2B + xELi − EMo2BLix)/x | (1) |
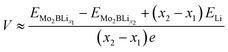 | (2) |
Results and discussion
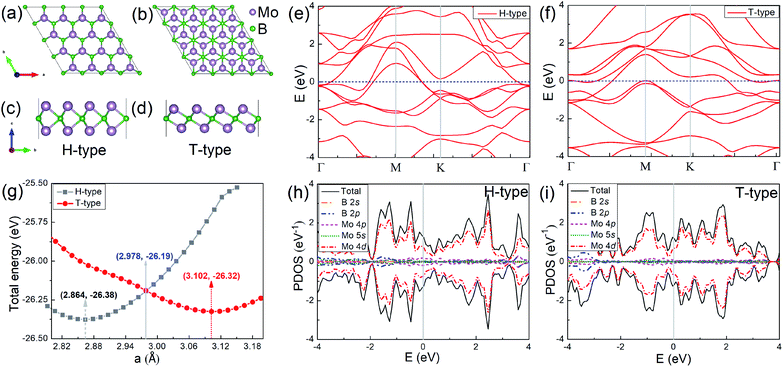
In order to investigate the physical properties of the H- and T-type Mo2B, their structures are investigated firstly. Fig. 1(a) and (c) show the top- and side-view of H-type Mo2B, whose structure is similar to that of the well-studied MoS2.58 A boron atomic layer is sandwiched by two Mo layers, and the Mo atoms in the top-layer are on the top-sites of those in the bottom layer. The corresponding space group is 187. Fig. 1(b) and (d) present the top- and side-view of the T-type Mo2B. This configuration is similar to that of Mo2C reported previously,38,39 with a space group of 164. The difference is that the carbon in Mo2C is replaced by boron in the T-type Mo2B. In addition, other possible metastable configurations for the chemical formula Mo2B are also studied from the local particle swarm optimization, and some structures and corresponding relative total energies are provided in Fig. S1 and Table S1 in the ESI.† Evidently, the H-type Mo2B is determined to be the most stable structure in this chemical formula, and the T-type is the second most stable one. The relationships between the total energy and lattice parameter for both H- and T-type Mo2B are presented in Fig. 1(g). The total energy of the H-type Mo2B is 0.06 eV lower than that of the T-type configuration based on their unit cells after relaxation. However, the H-type can be transformed to the T-type by applying tensile strains. According to this figure, the optimal lattice parameters for the H- and T-type Mo2B in the basal plane are determined to be 2.864 and 3.102 Å, respectively. The T-type configuration becomes more stable since the lattice parameter increases to 2.978 Å. The lattice parameters, bond lengths, layer thicknesses, and the elastic constants for these two configurations are provided in Table 1. From the table, the T-type configuration shows a smaller layer thickness compared to that in the H-type configuration. Both the T- and H-type Mo2B show higher c11 values compared to that of the synthesized Mo2C (143.8 N m−1).39 In addition, the H-type also presents a large c12 value of 124.1 N m−1. The discrepant mechanical strengths in the H- and T-type Mo2B could be ascribed to their structural differences. In the H-type configuration, a tensile strain needs to overcome the interatomic attraction between the neighbouring Mo and B atoms, and the atomic repulsion between the counter Mo atoms. In the T-type structure, the interatomic attraction between the neighbouring Mo and B atoms could be the main resistance to the tensile strain. Based on the two independent elastic constants c11 and c12, the Young's moduli for both the H- and T-type Mo2B are further calculated according to Y2D = (c112 − c122)/c11,59 the corresponding values are also provided in Table 1. These high elastic constants imply that both configurations are robust under strains. Fig. 1(e) and (f) present the electronic energy bands of the H- and T-type Mo2B, respectively. Fig. 1(h) and (i) show the corresponding projected density of states (PDOS). Both structures are nonmagnetic metals with large DOS in the vicinity of their Fermi levels. The DOS around Fermi levels are mainly contributed by the electrons in the Mo 4d orbitals. The electronic energy bands and PDOS imply that both the H- and T-type Mo2B could possess favorable electrical conductivities.| Mo2B | a | h | d | Mo–B | Mo–Mo | c 11 | c 12 | Y 2D |
|---|---|---|---|---|---|---|---|---|
| H-Type | 2.864 | 33.04 | 5.443 | 2.176 | 2.830 | 187.5 | 124.1 | 105.4 |
| T-Type | 3.102 | 28.16 | 4.713 | 2.115 | 2.876 | 157.6 | 28.95 | 152.3 |
Regarding the transport properties of the H- and T-type Mo2B, the electrical conductivities and the electronic thermal conductivities are further investigated based on constant relaxation time approximation. It is found that these transport coefficients are isotropic in the basal plane regardless of temperatures and chemical potentials. Therefore, σxx/τ and κxx/τ for both configurations are adopted to present the transport properties, as provided in Fig. 2. Here σxx and κxx respectively denote the electrical conductivity and electronic thermal conductivity along the x-axis direction, τ represents the electron relaxation time. According to this figure, temperature has a relatively weak influence on the electrical conductivity. In contrast, the electronic thermal conductivity is proportional to the increasing temperatures, and the shape of the relationship between the values of the electrical conductivity and electronic thermal conductivity meets the Wiedemann–Franz law.60 For the H-type Mo2B, σxx/τ is determined to be 12.78 × 1020 Ω−1 m−1 s−1 at room temperature at μ = 0.0 eV, where the transport coefficient slightly decreases with increasing chemical potential. This behavior could be explained by the similar trend of PDOS with increasing energy presented in Fig. 1(h), since the electrical conductivity is approximately proportional to the PDOS. In the chemical potential range presented, the largest σxx/τ at room temperature is calculated to be 14.30 × 1020 Ω−1 m−1 s−1 at μ = −0.473 eV. From Fig. 2(b), κxx/τ of zero chemical potential is calculated to be 93.35 × 1014 W−1 m−1 K−1 s−1 at room temperature, which is increased to 155.7 × 1014 W−1 m−1 K−1 s−1 at 500 K. For the T-type configuration, σxx/τ and κxx/τ generally show minimum values at the zero chemical potential, which imply that one can enhance these transport coefficients by employing both n- and p-doping. At room temperature, σxx/τ and κxx/τ are respectively determined to be 4.121 × 1020 Ω−1 m−1 s−1 and 30.87 × 1014 W−1 m−1 K−1 s−1 when μ = 0.0 eV. To be more intuitive, the electrical conductivity and electronic thermal conductivity calculated are compared with those of Mo2C, based on the same electron relaxation time (τ = 5.52 × 10−15s) determined in experiments for Mo2C.36 At zero chemical potential and at room temperature, the electrical conductivity and electronic thermal conductivity of Mo2C have been previously calculated to be 3.590 × 106 Ω−1 m−1 and 26.4 W−1 m−1 K−1 s−1.39 Under the same conditions, the electrical conductivity and electronic thermal conductivity of the H-type Mo2B are determined to be 7.546 × 106 Ω−1 m−1 and 51.53 W−1 m−1 K−1, respectively. Regarding the T-type Mo2B, the corresponding values are determined to be 2.275 × 106 Ω−1 m−1 and 17.07 W−1 m−1 K−1. Moreover, the electron relaxation time ranging from 1.00 × 10−15 s to 1.00 × 10−14 s is also considered for Mo2B. Based on τ = 1.00 × 10−15s, σxx and κxx in the H-type Mo2B at room temperature are calculated to be 1.278 × 106 Ω−1 m−1 and 9.335 W−1 m−1 K−1 at zero chemical potential. With τ = 1.00 × 10−14s, the corresponding σxx and κxx are an order of magnitude larger. Obviously, both H-type and T-type Mo2B are promising electrical conductors.
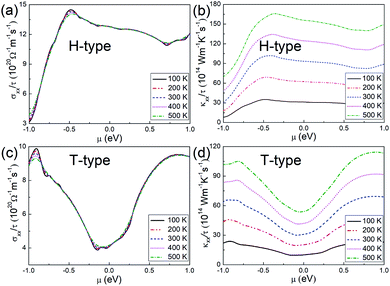 | ||
| Fig. 2 (a) and (b) Transport coefficients σxx/τ and κxx/τ, respectively, for the H-type Mo2B. (c) and (d) Corresponding transport coefficients σxx/τ and κxx/τ for the T-type Mo2B. | ||
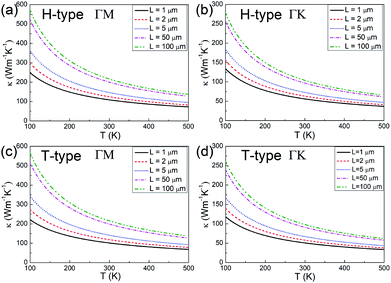
Since the thermal conductivity comprises electron and phonon contributions, the phonon thermal conductivity is further investigated. The phonon dispersions for both the H- and T-type Mo2B are provided in Fig. S1 in the ESI,† where ZA, TA and LA respectively denote the out-of-plane, transversal and longitudinal acoustic modes. The phonon dispersions are predicted without an imaginary frequency, which implies that both structures are dynamically stable. According to the method described in the Methods section,39,54,55 the phonon thermal conductivities along the ΓM and ΓK directions are calculated, where the high-symmetry directions ΓM and ΓK in BZs respectively correspond to the armchair and zigzag directions in the real spaces of both H- and T-type Mo2B, as shown in Fig. S2 in the ESI.† The calculated values with increasing temperatures based on various flake lengths are provided in Fig. 3. Since the size of the synthesized Mo2C is approximately 100 μm,36 the flake lengths of Mo2B ranging from 1 to 100 μm are studied here. Apparently, the phonon thermal conductivity increases with a larger flake length when the flake length is smaller than 100 μm, and decreases with increasing temperature in the range from 100 to 500 K. Fig. 3(a) shows the phonon thermal conductivity along the armchair direction in the H-type Mo2B. Based on the different flake lengths of 1, 2, 5, 50 and 100 μm, the phonon thermal conductivities are respectively determined to be 108.7, 125.0, 146.4, 200.2 and 216.4 W m−1 K−1 at room temperature. Regarding the increasing temperatures, the values based on the 5 μm flake length are calculated to be 362.1, 205.4, 146.4, 114.8 and 95.00 W m−1 K−1, respectively at 100, 200, 300, 400 and 500 K. Fig. 3(b) shows the corresponding phonon thermal conductivity along the zigzag direction. Obviously, the phonon thermal conductivity is anisotropic, with much lower values in the zigzag direction. At room temperature, the phonon thermal conductivity with the flake length of 5 μm is determined to be 72.78 W m−1 K−1. Fig. 3(c) and (d) respectively present the phonon thermal conductivities along the armchair and zigzag directions in the T-type configuration, whose values are generally similar to those in the H-type Mo2B. Based on the 5 μm flake length, the phonon thermal conductivities along the armchair and zigzag directions at room temperature are 141.3 and 67.14 W m−1 K−1. In a word, both the H- and T-type Mo2B possess high phonon thermal conductivities, especially along their armchair direction. These calculated values are much higher than those of many well-known metals,61 and those in the reported Mo2C.39
In order to understand the high phonon thermal conductivities, each acoustic mode contribution is calculated and provided in Fig. S3 in the ESI.† According to this figure, each acoustic mode presents evident contribution to its phonon thermal conductivity in the H-type Mo2B, although the ZA mode contribution is relatively smaller in the armchair direction. Regarding the T-type configuration, the phonon thermal conductivity is mainly dominated by the LA mode. The ZA mode presents little contribution in both directions. This behaviour could be explained from their phonon dispersions, where the frequency magnitude of the ZA mode is much smaller in the T-type configuration. Based on the low phonon frequency, the phonon velocity is smaller, which induces the small phonon thermal conductivity contribution. Compared with the reported Mo2C, the larger phonon thermal conductivity of Mo2B is mainly caused by its larger phonon group velocities and lower Grüneisen parameters(GPs). Since the T-type Mo2B and Mo2C possess the same space group, and their phonon thermal conductivities are both mainly dominated by the LA modes, the phonon thermal conductivities in the armchair directions of these two configurations are compared. In Mo2B, the phonon group velocity and the square of the GP of the LA mode are respectively determined to be 2.967 × 103 m s−1 and 1.454, while the corresponding values in Mo2C are determined to be 2.167 × 103 m s−1 and 53.88, respectively. According to eqn (S2) in the ESI,† the thermal conductivity of Mo2B is naturally much higher than that in Mo2C.
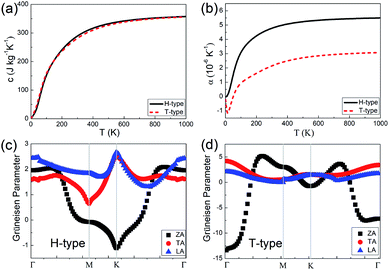
Combined with the electron and phonon contributions, both the H- and T-type Mo2B could have outstanding thermal conductivities in a wide temperature range, since the electron part increases and the phonon part decreases with increasing temperature. Based on the 5 μm flake length and the constant electron relaxation time τ = 5.52 × 10−15 s, the thermal conductivities in the armchair direction in the H-type Mo2B are determined to be 379.3, 239.8, 197.9, 183.5 and 180.9 W m−1 K−1, respectively at 100, 200, 300, 400 and 500 K. Correspondingly, the values in the armchair direction of the T-type Mo2B are 347.4, 208.0, 158.3, 134.6 and 122.3 W m−1 K−1. These high thermal conductivities enable both the H- and T-type Mo2B applications in thermal conductive materials. In addition, the specific heat and thermal expansion coefficients (TECs) of these two configurations are studied, and corresponding results are provided in Fig. 4. From Fig. 4(a), the specific heats of the H- and T-type Mo2B are generally equivalent in the entire range of temperature investigated. The room temperature values are calculated to be 289.4 and 281.8 J kg−1 K−1, respectively. Regarding the thermal expansion behaviors as shown in Fig. 4(b), the TEC of the H-type Mo2B increases with increasing temperature. The value at room temperature is calculated to be 4.780 × 10−6 K−1, which increases to 5.498 × 10−6 K−1 at 1000 K. For the T-type configuration, its TEC is much smaller than that in the H-type, and the corresponding value at room temperature is determined to be 2.148 × 10−6 K−1. Interestingly, the TEC of the T-type configuration is negative under 50 K, and the negative TEC with the largest absolute value is determined to be −1.153 × 10−6 K−1 at 14 K. In order to understand the different thermal expansion behaviors between the H- and T-type Mo2B, the GPs of the acoustic modes in the BZs of both configurations are calculated and provided in Fig. 4(c) and (d). From these figures, the GPs of the TA and LA are positive in the entire BZs for both H- and T-type configurations, which imply that both the TA and LA modes contribute to thermal expansion.50,51,62 The GP of the ZA mode in the H-type Mo2B is generally positive, although it shows small negative values around the high symmetry K point. Consequently, the TEC of the H-type Mo2B increases with increasing temperature. In the T-type configuration, the ZA mode shows large negative GPs, especially around its BZ center. The large negative value implies that the amplitude of ZA mode is significant, which contributes to the thermal contraction. As a result, this structure shows negative TEC in the low temperature range. For in-depth understanding, the different behaviors of the ZA modes in the H- and T-type Mo2B are ascribed to the different layer thickness and mechanical strength of these two configurations.51 The configuration with a thinner layer thickness and weaker mechanical strength could be more flexible, and the amplitude of the ZA mode is more significant. In addition, the GP values in Fig. 4(c) and (d) could also explain the magnitude of the phonon thermal conductivity. For instance, the ZA mode in the T-type Mo2B makes little contribution to its thermal conductivity, ascribed to the large absolute value of GP, since the phonon thermal conductivity is inversely proportional to the square of GPs.54,55,63 Based on the different thermal expansion behaviors of the H- and T-type Mo2B, it is possible to obtain a zero TEC intuitively by combining these two phases, since two competitive phases can be obtained concurrently by applying strains or other techniques.64 This could be an interesting topic for future work.
Based on the high mechanical strength, promising electrical and thermal conductivities, and low TECs calculated above, both the H- and T-type Mo2B could have widespread applications. In the following, the performances in LIBs of both configurations are further investigated. The key parameters, i.e., theoretical storage capacity and migration energy barrier are studied. Based on 4 × 4 supercells, the stable adsorption sites for the Li ion on both H- and T-type Mo2B are investigated firstly. According to Fig. S4 and S5,† three possible locations for each configuration are considered, and corresponding relative total energies are provided in Table S2 in the ESI.† From the table, the Li atom is stabilized on the top-site of the hexagonal centre of the H-type Mo2B, as shown in Fig. S4(c) and (f).† The distance between the Li atom and the MXene surface is calculated to be 2.416 Å. The corresponding total energy is 0.0263 eV lower than that of the structure with Li on the top-site of Mo atom. In the T-type Mo2B, the Li atom is found to stabilize on the top-site of the bottom Mo atom, and its location is 2.311 Å higher than that of the MXene surface. The top- and side-views for the stable location are presented in Fig. S5(c) and (f),† respectively. The corresponding total energy is 0.0125 eV lower than that of the configuration with Li on the top-site of the middle B atom.
Since the migration energy barrier is a key parameter in determining the rates of charging and discharging, it is studied after the stable location of Li is determined. The migration barrier profiles for Li on the H- and T-type Mo2B are respectively shown in Fig. 5(a) and (b), respectively. For each configuration, three possible migration pathways are studied. In the H-type Mo2B, PATH I denotes the diffusion of the Li atom directly from the top-site of the hexagonal centre to the neighbouring top-site of the hexagonal centre. PATH II represents the diffusion of the Li atom from the top-site of the hexagonal centre to the top-site of neighbouring boron, and then moves to the neighbouring top-site of the neighbouring hexagonal centre. PATH III shows the diffusion path from the top-site of the hexagonal centre to the top-site of neighbouring molybdenum, and then moves to the top-site of the neighbouring hexagonal centre. The energy barriers for PATH I, PATH II and PATH III are determined to be 0.130, 0.050 and 0.188 eV, respectively. To give a clear view, only the two lower energy barriers are provided in Fig. 5(a). Based on the different stable locations for Li atom on the T-type configuration, PATH I shows the diffusion route directly from the top-site of the bottom Mo atom to the top-site of a neighbouring bottom Mo atom. PATH II shows that the Li diffuses from the top-site of the bottom Mo atom to the top-site of the middle boron atom, and then moves to the stable top-site of the neighbouring bottom Mo atom. PATH III is the route from the top-site of the bottom molybdenum to the neighbouring top-site of top molybdenum, and then diffuses to the top-site of bottom molybdenum. The corresponding energy barriers for PATH I, PATH II and PATH III are calculated to be 0.110, 0.037 and 0.152 eV, respectively. The energy barriers for PATH I and II are given in Fig. 5(b). Evidently, the diffusion energy barrier of PATH II is generally lower than those for PATH I and PATH III in both H- and T-type Mo2B. The energy barriers of PATH II in both configurations are comparable to that in Mo2C (0.043 eV).38 Moreover, these values are much smaller than that (0.35–0.65 eV) in the commercially used anode material TiO2.65 Based on the relatively low diffusion energy barriers, both the H- and T-type Mo2B could show rapid charge and discharge rate when applied as anode materials for LIBs.38
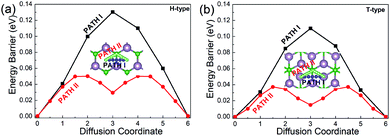 | ||
| Fig. 5 Diffusion barrier profiles for Li on (a) the H-type Mo2B and (b) the T-type Mo2B. The insets show the two migration pathways with low energy barriers on each configuration. | ||
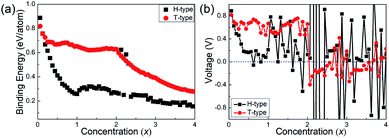
After the diffusion energy barrier is calculated, the binding energy and open-circuit-voltage for LIBs are further studied. Based on the 4 × 4 × 1 supercells, increasing number of Li atoms from one to sixty-four are studied. From the previous discussion, the Li atom could prefer the top-site of the hexagonal centre in the H-type Mo2B until its number reaches thirty-two, with both sides of Mo2B adsorbing one atomic layer of Li atoms. If more Li atoms are adsorbed, an additional Li atomic layer will be formed based on the 4 × 4 × 1 supercells, and thus the stable location for the additional atomic layer must be investigated. As shown in Fig. S6,† three possible locations for the thirty-three Li atoms on the H-type Mo2B are studied, and their relative total energies are provided in Table S3.† From the table, the second Li atomic layer is stabilized on the top-site of the Mo atomic layer. The top- and side-views for the stable location are provided in Fig. S6(a) and (d),† respectively. With a similar procedure, the second Li atomic layer is found to locate on the top-site of the neighbouring Mo atomic layer in the T-type Mo2B, and the corresponding structures are provided in Fig. S7(a) and (d).† After all the structures with increasing Li atoms are optimized, the binding energies and open-circuit voltages for the adsorbed Li atoms are calculated according to eqn (1) and (2) in the Methods section. To facilitate elaboration, Mo2BLix is adopted to denote the Li-adsorbed Mo2B. Since sixty-four Li atoms are studied based on the 4 × 4 × 1 supercells, the x value ranges from zero to four. The corresponding binding energies and voltage profiles for Li atoms on both H- and T-type Mo2B are provided in Fig. 6. From Fig. 6(a), the binding energies of Li on both H- and T-type Mo2B are positive in the entire range of concentration x investigated, which imply that both configurations could adsorb at least four Li atomic layers on their surfaces. The binding energy for Li on the T-type Mo2B is generally large than that on the H-type Mo2B, which could be ascribed to the larger specific area of the T-type configuration. The three large binding energies around the Li concentration x = 2.0 on the H-type Mo2B are due to structural distortion. It is noteworthy that, although the binding energies calculated are positive, it is better to estimate the theoretical storage capacity by inspecting the open voltage.38,66Fig. 6(b) presents the corresponding voltage profiles. Obviously, the voltage varies significantly with the increasing concentration of Li atoms. Moreover, the first negative value appears at x = 0.625 (the number of Li atoms is 10) on the H-type Mo2B, and x = 2.062 (the number of Li atoms is 33) on the T-type configuration. Based on the binding energies and open voltages calculated, the theoretical storage capacities for the H- and T-type Mo2B are calculated to be 74.18 and 264.0 mA h g−1, respectively (corresponding x values are 0.562 and 2.00, respectively). Based on the volumes of the bare H- and T-type Mo2B, corresponding volumetric capacities are respectively calculated to be 647.8 and 2424 mA h cm−3. Obviously, the volumetric capacity in the T-type configuration is much higher than those in commercial carbon-based electrodes.67 Therefore, Mo2B could be a candidate anode material, especially for applications where size matters. Regarding the volume changes of the lithium adopted configurations, the volumes of the H-type Mo2BLi0.562 and T-type Mo2BLi2 are respectively 1.408 and 1.845 times of those for the bare H- and T-type Mo2B. The averaged voltage in the range of 0 ≤ x ≤ 0.562 is calculated to be 0.386 V in the H-type Mo2B. Similarly, in the T-type configuration, the averaged voltage averaged over 0 ≤ x ≤ 2.00 is calculated to be 0.628 V. As reported previously, the potential voltage range for an anode material is from 0.1 to 1.0 V.38 Both the average voltages for the H- and T-type Mo2B fall in this potential range, which imply that both configurations are favourable anode materials.
Conclusions
In summary, we have investigated an MBene member Mo2B in both H- and T-type configurations in this work. Compared with the synthesized Mo2C, Mo2B shows higher mechanical strength and comparable electrical conductivities. More importantly, both the H- and T-type configurations show relatively higher thermal conductivities. Based on a 5 μm flake length, the thermal conductivities along the armchair direction of the H- and T-type Mo2B are respectively determined to be 197.9 and 158.3 W m−1 K−1 at room temperature. In addition, the specific heat and thermal expansion behavior are studied. Low TECs are determined, and thermal contraction is determined in the T-type configuration. Based on the high mechanical strength, favorable electrical and thermal conductivities, and low TECs, both the H-and T-type Mo2B could be promising conductive materials in 2D electronic devices. Moreover, the performances in LIBs are studied. The storage capacity in the T-type configuration is comparable with that in the synthesized Mo2C, and the migration energy barrier is even lower. Based on the data calculated, Mo2B could be a candidate anode material in LIBs. We look forward to the synthesis of this MBene in the near future.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the support of the National Key Research and Development Program of China (No. 2016YFB0700100), the National Natural Science of Foundation of China (No. 11604346, 21671195, 21875271), Key Research Program of Frontier Sciences, CAS (Grant No. QYZDB-SSW-JSC037), K.C. Wong Education Foundation (rczx0800), and the key technology of nuclear energy, 2014, CAS Interdisciplinary Innovation Team.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666 CrossRef CAS PubMed.
- K. S. Novoselov, Z. Jiang, Y. Zhang, S. V. Morozov, H. L. Stormer, U. Zeitler, J. C. Maan, G. S. Boebinger, P. Kim and A. K. Geim, Science, 2007, 315, 1379 CrossRef CAS PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197 CrossRef CAS PubMed.
- H. E. A. Huitema, G. H. Gelinck, J. B. P. H. van der Putten, K. E. Kuijk, C. M. Hart, E. Cantatore, P. T. Herwig, A. J. J. M. van Breemen and D. M. de Leeuw, Nature, 2001, 414, 599 CrossRef CAS.
- K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim, J. H. Ahn, P. Kim, J. Y. Choi and B. H. Hong, Nature, 2009, 457, 706 CrossRef CAS PubMed.
- C. Tan, X. Cao, X.-J. Wu, Q. He, J. Yang, X. Zhang, J. Chen, W. Zhao, S. Han, G.-H. Nam, M. Sindoro and H. Zhang, Chem. Rev., 2017, 117, 6225 CrossRef CAS PubMed.
- N. Mounet, M. Gibertini, P. Schwaller, D. Campi, A. Merkys, A. Marrazzo, T. Sohier, I. E. Castelli, A. Cepellotti, G. Pizzi and N. Marzari, Nat. Nanotechnol., 2018, 13, 246 CrossRef CAS.
- K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105, 136805 CrossRef PubMed.
- L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2014, 9, 372 CrossRef CAS.
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248 CrossRef CAS PubMed.
- M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2014, 26, 992 CrossRef CAS PubMed.
- B. Anasori, M. R. Lukatskaya and Y. Gogotsi, Nat. Rev. Mater., 2017, 2, 16098 CrossRef CAS.
- M. W. Barsoum, Prog. Solid State Chem., 2000, 28, 201 CrossRef CAS.
- J. Zhou, X. –H. Zha, F. Y. Chen, Q. Ye, P. Eklund, S. Du and Q. Huang, Angew.Chem., Int. Ed., 2016, 55, 5008 CrossRef CAS PubMed.
- J. Zhou, X. –H. Zha, X. Zhou, F. Chen, G. Gao, S. Wang, C. Shen, T. Chen, C. Zhi, P. Eklund, S. Du, J. Xue, W. Shi, Z. Chai and Q. Huang, ACS Nano, 2017, 11, 3841 CrossRef CAS PubMed.
- Q. Tao, M. Dahlqvist, J. Lu, S. Kota, R. Meshkian, J. Halim, J. Palisaitis, L. Hultman, M. W. Barsoum, P. O. Å. Persson and J. Rosen, Nat. Commun., 2017, 8, 14949 CrossRef PubMed.
- R. Meshkian, M. Dahlqvist, J. Lu, B. Wickman, J. Halim, J. Thörnberg, Q. Tao, S. Li, S. Intikhab, J. Snyder, W. Barsoum Michel, M. Yildizhan, J. Palisaitis, L. Hultman, O. Å. Persson Per and J. Rosen, Adv. Mater., 2018, 30, 1706409 CrossRef PubMed.
- K. Hantanasirisakul and Y. Gogotsi, Adv. Mater., 2018, 30, 1804779 CrossRef PubMed.
- M. R. Lukatskaya, O. Mashtalir, C. E. Ren, Y. Dall'Agnese, P. Rozier, P. L. Taberna, M. Naguib, P. Simon, M. W. Barsoum and Y. Gogotsi, Science, 2013, 341, 1502 CrossRef CAS PubMed.
- M. Ghidiu, M. R. Lukatskaya, M.-Q. Zhao, Y. Gogotsi and M. W. Barsoum, Nature, 2014, 516, 78 CrossRef CAS PubMed.
- Y. Xia, T. S. Mathis, M.-Q. Zhao, B. Anasori, A. Dang, Z. Zhou, H. Cho, Y. Gogotsi and S. Yang, Nature, 2018, 557, 409 CrossRef CAS PubMed.
- F. Shahzad, M. Alhabeb, C. B. Hatter, B. Anasori, S. Man Hong, C. M. Koo and Y. Gogotsi, Science, 2016, 353, 1137 CrossRef CAS PubMed.
- Q. Peng, J. Guo, Q. Zhang, J. Xiang, B. Liu, A. Zhou, R. Liu and Y. Tian, J. Am. Chem. Soc., 2014, 136, 4113 CrossRef CAS PubMed.
- L. Wang, L. Yuan, K. Chen, Y. Zhang, Q. Deng, S. Du, Q. Huang, L. Zheng, J. Zhang, Z. Chai, M. W. Barsoum, X. Wang and W. Shi, ACS Appl. Mater. Interfaces, 2016, 8, 16396 CrossRef CAS PubMed.
- J. N. Xuan, Z. Q. Wang, Y. Y. Chen, D. J. Liang, L. Cheng, X. J. Yang, Z. Liu, R. Z. Ma, T. Sasaki and F. X. Geng, Angew. Chem., Int. Ed., 2016, 55, 14569 CrossRef CAS PubMed.
- Q. Xue, H. Zhang, M. Zhu, Z. Pei, H. Li, Z. Wang, Y. Huang, Y. Huang, Q. Deng, J. Zhou, S. Du, Q. Huang and C. Zhi, Adv. Mater., 2017, 29, 1604847 CrossRef PubMed.
- L. Li, X. Wang, H. Guo, G. Yao, H. Yu, Z. Tian, B. Li and L. Chen, Small Methods, 2019, 1900337 CrossRef.
- S. Wang, L. Chen, Y. Wu and Q. Zhang, ChemPhysChem, 2018, 19, 3380 CrossRef CAS PubMed.
- T. Bo, P.-F. Liu, J. Xu, J. Zhang, Y. Chen, O. Eriksson, F. Wang and B.-T. Wang, Phys. Chem. Chem. Phys., 2018, 20, 22168 RSC.
- Z. Jiang, P. Wang, X. Jiang and J. Zhao, NanoscaleHoriz., 2018, 3, 335 RSC.
- Z. Guo, J. Zhou and Z. Sun, J. Mater. Chem.A, 2017, 5, 23530 RSC.
- L. T. Alameda, C. F. Holder, J. L. Fenton and R. E. Schaak, Chem. Mater., 2017, 29, 8953 CrossRef CAS.
- L. T. Alameda, P. Moradifar, Z. P. Metzger, N. Alem and R. E. Schaak, J. Am. Chem. Soc., 2018, 140, 8833 CrossRef CAS PubMed.
- S. Kota, E. Zapata-Solvas, A. Ly, J. Lu, O. Elkassabany, A. Huon, W. E. Lee, L. Hultman, S. J. May and M. W. Barsoum, Sci. Rep., 2016, 6, 26475 CrossRef CAS PubMed.
- W. G. Fahrenholtz, G. E. Hilmas, I. G. Talmy and J. A. Zaykoski, J. Am. Ceram. Soc., 2007, 90, 1347 CrossRef CAS.
- C. Xu, L. B. Wang, Z. B. Liu, L. Chen, J. K. Guo, N. Kang, X. L. Ma, H. M. Cheng and W. C. Ren, Nat. Mater., 2015, 14, 1135 CrossRef CAS PubMed.
- L. Wang, C. Xu, Z. Liu, L. Chen, X. Ma, H.-M. Cheng, W. Ren and N. Kang, ACS Nano, 2016, 10, 4504 CrossRef CAS PubMed.
- D. Cakir, C. Sevik, O. Gulseren and F. M. Peeters, J. Mater. Chem.A, 2016, 4, 6029 RSC.
- X.-H. Zha, J. Yin, Y. Zhou, Q. Huang, K. Luo, J. Lang, J. S. Francisco, J. He and S. Du, J. Phys. Chem. C, 2016, 120, 15082 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- Y. Wang, M. Miao, J. Lv, L. Zhu, K. Yin, H. Liu and Y. Ma, J. Chem. Phys., 2012, 137, 224108 CrossRef PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272 CrossRef CAS.
- Y. Le Page and P. Saxe, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104104 CrossRef.
- G. K. H. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67 CrossRef CAS.
- X.-H. Zha, J. Zhou, K. Luo, J. Lang, Q. Huang, X. Zhou, J. S. Francisco, J. He and S. Du, J. Phys.: Condens. Matter, 2017, 29, 165701 CrossRef PubMed.
- X. Gonze and C. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10355 CrossRef CAS.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- N. Mounet and N. Marzari, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 205214 CrossRef.
- X.-H. Zha, R.-Q. Zhang and Z. Lin, J. Chem. Phys., 2014, 141, 064705 CrossRef PubMed.
- X.-H. Zha, R.-Q. Zhang and Z. Lin, Europhys. Lett., 2014, 107, 26007 CrossRef.
- P. G. Klemens and D. F. Pedraza, Carbon, 1994, 32, 735 CrossRef CAS.
- P. G. Klemens, Int. J. Thermophys., 2001, 22, 265 CrossRef CAS.
- X.-H. Zha, Q. Huang, J. He, H. He, J. Zhai, J. S. Francisco and S. Du, Sci. Rep., 2016, 6, 27971 CrossRef PubMed.
- X.-H. Zha, J. Zhou, Y. Zhou, Q. Huang, J. He, J. S. Francisco, K. Luo and S. Du, Nanoscale, 2016, 8, 6110 RSC.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- B. Radisavljevic, A. Radenovic, J. Brivio, V. Giacometti and A. Kis, Nat. Nanotechnol., 2011, 6, 147 CrossRef CAS PubMed.
- R. C. Andrew, R. E. Mapasha, A. M. Ukpong and N. Chetty, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125428 CrossRef.
- W. Kim and J. P. Carbotte, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 033104 CrossRef.
- D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press, Boca Raton, FL, 84th edn, 2003 Search PubMed.
- X.-H. Zha, S. Li, R.-Q. Zhang and Z. Lin, Commun. Comput.Phys., 2014, 16, 201 CrossRef.
- P. G. Klemens, J. Wide Bandgap Mater., 2000, 7, 332–339 CrossRef CAS.
- X. Wang, R. Zang, J. Gao, C. Liu, L. Wang, W. Gong, X. –H. Zha, X. Chen, F. Huang, K. Javaid, Z. Xu, H. Cao and A. A. Rogachev, Adv. Mater. Interfaces, 2019, 6, 1900031 CrossRef.
- S. Lunell, A. Stashans, L. Ojamae, H. Lindstrom and A. Hagfeldt, J. Am. Chem. Soc., 1997, 119, 7374 CrossRef CAS.
- Q. Tang, Z. Zhou and P. Shen, J. Am. Chem. Soc., 2012, 134, 16909 CrossRef CAS PubMed.
- M. –Q. Zhao, C. E. Ren, Z. Ling, M. R. Lukatskaya, C. Zhang, K. L. Van Aken, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2015, 27, 339 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9na00610a |
| This journal is © The Royal Society of Chemistry 2020 |