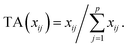Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Choosing proper normalization is essential for discovery of sparse glycan biomarkers†
Hae-Won
Uh
 *a,
Lucija
Klarić
*a,
Lucija
Klarić
 bc,
Ivo
Ugrina
bde,
Gordan
Lauc
bf,
Age K.
Smilde
g and
Jeanine J.
Houwing-Duistermaat
ah
bc,
Ivo
Ugrina
bde,
Gordan
Lauc
bf,
Age K.
Smilde
g and
Jeanine J.
Houwing-Duistermaat
ah
aDepartment of Biostatistics and Research Support, University Medical Center Utrecht, Utrecht, Netherlands. E-mail: h.w.uh@umcutrecht.nl
bGenos Glycoscience Research Laboratory, Zagreb, Croatia
cMRC Human Genetics Unit, MRC Institute of Genetics and Molecular Medicine, University of Edinburgh, Edinburgh, UK
dUniversity of Split, Faculty of Science, Split, Croatia
eIntellomics Ltd, Croatia
fFaculty of Pharmacy and Biochemistry, University of Zagreb, Zagreb, Croatia
gBiosystems Data Analysis, Swammerdam Institute for Life Sciences, University of Amsterdam, Amsterdam, The Netherlands
hDepartment of Statistics, University of Leeds, Leeds, UK
First published on 10th March 2020
Abstract
Rapid progress in high-throughput glycomics analysis enables the researchers to conduct large sample studies. Typically, the between-subject differences in total abundance of raw glycomics data are very large, and it is necessary to reduce the differences, making measurements comparable across samples. Essentially there are two ways to approach this issue: row-wise and column-wise normalization. In glycomics, the differences per subject are usually forced to be exactly zero, by scaling each sample having the sum of all glycan intensities equal to 100%. This total area (row-wise) normalization (TA) results in so-called compositional data, rendering many standard multivariate statistical methods inappropriate or inapplicable. Ignoring the compositional nature of the data, moreover, may lead to spurious results. Alternatively, a log-transformation to the raw data can be performed prior to column-wise normalization and implementing standard statistical tools. Until now, there is no clear consensus on the appropriate normalization method applied to glycomics data. Nor is systematic investigation of impact of TA on downstream analysis available to justify the choice of TA. Our motivation lies in efficient variable selection to identify glycan biomarkers with regard to accurate prediction as well as interpretability of the model chosen. Via extensive simulations we investigate how different normalization methods affect the performance of variable selection, and compare their performance. We also address the effect of various types of measurement error in glycans: additive, multiplicative and two-component error. We show that when sample-wise differences are not large row-wise normalization (like TA) can have deleterious effects on variable selection and prediction.
1. Introduction
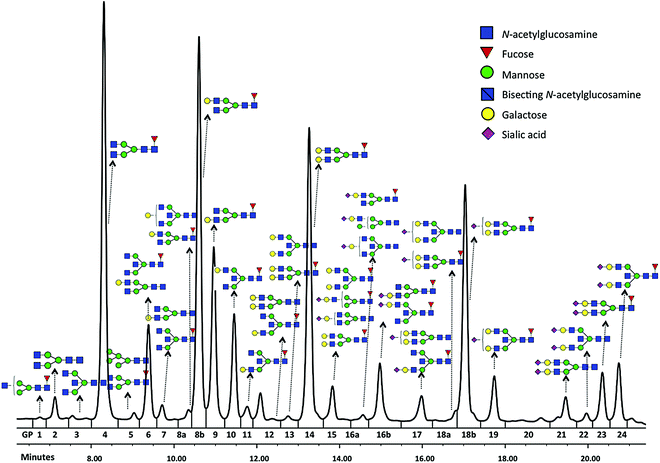
Glycomics is an emerging omics field. The majority of proteins are glycosylated and glycomics changes may well be a hallmark of human disease.1 The structural complexity of glycans, however, has slowed down the development of high-throughput quantification methods, and technical improvements are still ongoing. Keeping pace with technological progress we here examine appropriate handling of glycomics data in large sample studies. The motivating example of the present work is based on data from Orkney Islands in Scotland,2 where we assess prediction of age from immunoglobulin G (IgG) glycans. Fig. 1 shows twenty four glycans bound to IgG measured by ultra-performance liquid chromatography (UPLC). It is reported that IgG glycosylation appears to be closely linked with chronological and biological ages.2–4 Prior to exploring the potential of glycan biomarkers of ageing, several steps of data pre-processing are required (Fig. 2). Our interest here is to minimize unwanted biases and variances. In this paper pre-processing refers to various techniques used for extracting clean data from raw instrumental data, and pre-treatment to methods that transform the cleaned raw data for downstream statistical analysis.5 Normalization of the raw data is needed to transform glycomics measurements or abundances to comparable scales, and improper normalization methods can significantly impair the data.6,7 In this work we systematically investigate the impact of different normalization methods on variable selection using lasso regression with glycan covariates.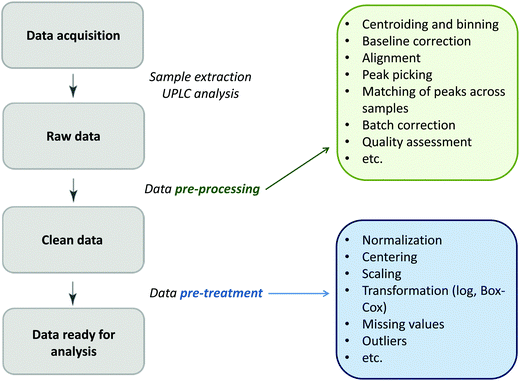 | ||
| Fig. 2 The flow diagram identifying the steps involved in a preparation of data for statistical analysis. | ||
In general, between-subject differences in total abundance of raw glycomics data are large, and even technical replicates show substantial differences due to measurement errors. To reduce these differences (or variances), applying a log-transformation to the cleaned raw data is by far the easiest way, as in other omics data analysis. Traditionally, however, the difference in total abundance per subject is forced to be exactly zero by scaling each sample to have the sum of all glycan intensities equal to 1 (or 100%). This results in so-called compositional data, also present in microbiome data analysis. Until now, there is no clear consensus on the appropriate normalization method for glycomics data.
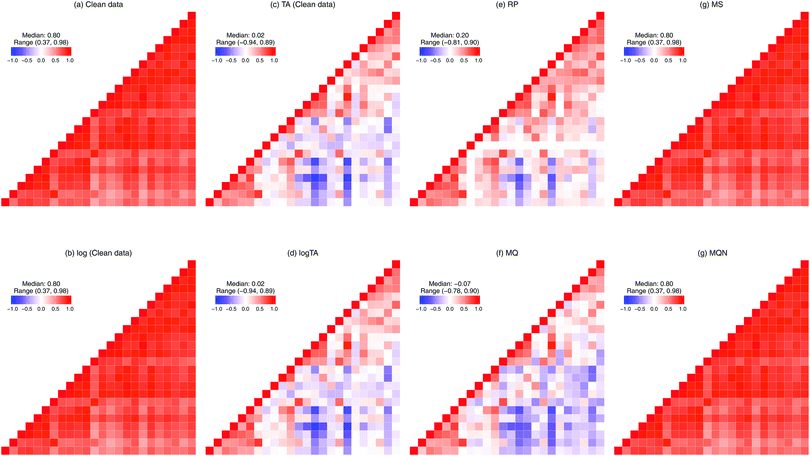
The compositional nature of the data renders many standard multivariate statistical methods inappropriate or inapplicable, and the complications from such data are well recognized in the statistics literature.8,9 For example, one cannot simply calculate the Pearson's correlations between two compositional components. To illustrate this problem, consider a simple, toy example of only two glycans representing a whole glycome of a person. Because of the constraint to the sum of a 100%, when the level of one glycan increases, the level of another must decrease. These two glycans are therefore negatively correlated.10 Such changes in correlation structure are shown in Fig. 3. In Table 1, we divide the six normalization methods considered here into two classes: row-wise (making samples comparable, Fig. 3(c)–(f)), and column-wise (making glycans comparable, Fig. 3(g) and (h)). Moreover, as can be seen in Fig. 3(a), glycans are highly correlated. To avoid overfitting and the multicollinearity problem, penalized regression can be considered. The effects of column-wise normalization such as centering and scaling will lead to a corresponding change in the scale of the coefficients and standard errors, but no change in the significance or interpretation. In contrast, if the compositional glycan data is used as covariates in regression analysis, the lasso regression should not be directly applied.11
| Class | Normalization | Abbreviation | Description |
|---|---|---|---|
| a Aitchison12 introduced transformations based on ratios: the additive log-ratio transformation (ALR) and the centred log-ratio transformation (CLR). b By taking the logarithm of RP, the additive log-ratio (ALR) transformation is obtained. | |||
| Row-wise | Total area | TA | Each glycan peak is divided by total abundance per subject, resulting compositional data. |
| Log-transform of TA | logTA | To achieve less-skewed distribution. When centering is applied to each sample, it is equivalent to the centred log-ratio (CLR) transformation.a | |
| Reference peakb | RP | Each glycan peak is divided by the most abundant glycan peak per subject. | |
| Median quotient | MQ | To remove the bias due to the relative abundance of glycan intensities. | |
| Column-wise | Median scaling | MS | Each glycan peak is subtracted by its median and divided by the interquartile range (IQR). |
| Multivariate quantile normalization | MQN | Column-wise adaptation of quantile normalization in gene expression data. | |
Another important issue to be addressed is measurement error in glycans. Compared to more abundant glycans, IgG glycans of low-abundance appear to be measured with up to 50% of measurement error, indicating an additive error (unpublished data). In gene expression data, where measurement error is approximately constant over a range of intensity levels near zero, it appears to be proportional to intensity level at large intensity levels,13,14 which might imply multiplicative error. Since the specific measurement error structure in the real data is not well studied, we consider three models: additive, multiplicative, and two-component measurement error in glycan measurements, the last containing both additive and multiplicative error components. We study the effects caused by measurement error in our simulation studies. Given that the real correlation structure between glycans is not known, to assess the influence of different normalizations on discovery of glycan biomarkers we simulated the data to mimic the real data and simulated association with an outcome. In short, we first generate the glycans that mimic the correlation structure of real glycan data, namely the log-transformed glycan measurements from the Orkney Complex Disease Study (ORCADES).15 Next, outcome variables are generated assuming that different sets of glycan combinations are associated with the outcome. In addition, based on different error models the corresponding error-contaminated datasets are generated. For each of simulated glycan datasets (with or without error) six different normalization methods are applied, and variable selection is employed. Finally, the impact of normalization on the performance of variable selection is assessed via extensive simulations reflecting various scenarios as described in Section 3.
The structure of the paper is as follows. In the next section, a detailed description of the considered normalization methods is given, followed by discussion on measurement error in glycomics data. In Section 3 we present our simulation study and evaluate the robustness and efficiency of the normalization methods regarding variable selection. Next, the analysis of glycan measurements from the ORCADES study15 is considered in Section 4, where glycan variable selection is performed with age as an outcome. Finally, in the last section we give some insights and recommendations based on the conducted simulation study.
2. Methods
2.1. Normalization methods
Let us first introduce some notation. Matrices are represented with bold upper case (X) and column vectors as bold lower case (x) letters. Let an n × p matrix X = (xij), where i = 1,…,n represents samples and j = 1,…,p glycan variables of the cleaned raw data. Following the order presented in Table 1, the total area normalization (TA) can be written as follows:From this formula it is obvious that TA introduces constraint that
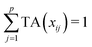 . TA does not entirely correct for highly skewed distribution of glycans, and can add additional skewing to glycan intensity distributions. Therefore, the TA-normalized data TA(xij) is often log-transformed
. TA does not entirely correct for highly skewed distribution of glycans, and can add additional skewing to glycan intensity distributions. Therefore, the TA-normalized data TA(xij) is often log-transformed| logTA(xij) = log(TA(xij)). |
| RP(xij) = xij/xis. |
| MQ(xij) = xqij/median(xmqi). |
| MS(xij) = {xij − median(xj)}/IQR(xj). |
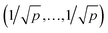 . For further computational details we refer to ref. 19.
. For further computational details we refer to ref. 19.
2.2. Normalization can change correlation structure
Let X denote an n × p matrix containing glycan measurements for n samples and p glycans. Without loss of generality we assume that X has a multivariate normal distribution with mean μ and covariance matrix Σ. The transformation performed by TA on a row (sample) is given by(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) 1,…, 1,…,![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) p) = (x1,…,xp)/(x1 +⋯+ xp), p) = (x1,…,xp)/(x1 +⋯+ xp), |
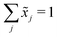 . This, unfortunately, leads to the problem of losing the possibility to interpret the correlation coefficients between the original components, commonly referred to as the negative bias problem.10 This means that for a p-part composition (
. This, unfortunately, leads to the problem of losing the possibility to interpret the correlation coefficients between the original components, commonly referred to as the negative bias problem.10 This means that for a p-part composition (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) 1,…,
1,…,![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) p) we have
p) we haveCov(![[x with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0078_0303.gif) 1, 1, ![[x with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0078_0303.gif) 1 +⋯+ xp) = 0. 1 +⋯+ xp) = 0. |
Cov(![[x with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0078_0303.gif) 1, 1, ![[x with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0078_0303.gif) 2) +⋯+ Cov( 2) +⋯+ Cov(![[x with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0078_0303.gif) 1, 1, ![[x with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0078_0303.gif) p) = −Var( p) = −Var(![[x with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0078_0303.gif) 1). 1). |
2.3. Measurement error models
Standard regression models assume that the covariates have been measured precisely, or observed without error. In contrast, the so-called errors-in-variables models or measurement error models are regression models that account for measurement errors in the independent variables (i.e. covariates, predictors).21 We use measurement error models to generate glycomics datasets that contain measurement errors for our simulation study.Assuming X has a multivariate normal distribution with mean μ and covariance matrix Σ, we consider a regression of a response Y on a predictor or covariate X. Instead of observing X, we observe W: i.e., error-free data (Y, X) versus the error-contaminated data (Y, W). First, for additive error we have WA = X + U1, where U1 is additive error independent of X. U1 is normally distributed and has mean zero and covariance matrix ΣU1. For simple linear regression the effect of having additive measurement error in a covariate is said to be an underestimate of the coefficient, known as the attenuation bias. The effects can vary depending on simple or multiple regression, and whether a covariate measured with error is univariate or multivariate. For our simulation study, we consider a diagonal matrix for uncorrelated error as well as a full matrix for correlated errors. For the multiplicative measurement error, we have WM = XU2, where U2 is multiplicative error. It indicates that the largest observed values are very far from the true values. If 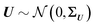 and U2,j = exp(Uj), for j = 1,…,p, then U2 has a multivariate log-normal distribution with mean zero and covariance matrix ΣU. Lastly, the two-component model or Rocke–Lorenzato model13,22 containing both additive and multiplicative error is as follows: WMA = XU2 + U1, where U1 and U2 are independent errors. In the univariate case, w = xσ22 + σ12, and this implies Var(w|x) = x2σ22 + σ12. For sufficiently small values of x, Var(w|x) is similar to σ12, while for sufficiently large values of x, Var(w|x) is similar to σ22.21 This behaviour in the multivariate case will be studied using simulations.
and U2,j = exp(Uj), for j = 1,…,p, then U2 has a multivariate log-normal distribution with mean zero and covariance matrix ΣU. Lastly, the two-component model or Rocke–Lorenzato model13,22 containing both additive and multiplicative error is as follows: WMA = XU2 + U1, where U1 and U2 are independent errors. In the univariate case, w = xσ22 + σ12, and this implies Var(w|x) = x2σ22 + σ12. For sufficiently small values of x, Var(w|x) is similar to σ12, while for sufficiently large values of x, Var(w|x) is similar to σ22.21 This behaviour in the multivariate case will be studied using simulations.
2.4. Variable selection and prediction
We consider a multiple linear regression model with n observations on a dependent variable y = (y1,…,yn)T and p glycans as predictors (or covariates). Let 1n denote a vector of ones of length n, and I an identity matrix. In matrix notation the linear regression model can be written as:| y = Xβ + ε, | (1) |
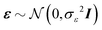 . Often when we are given a large number of covariates and due to different reasons (like the high cost of measuring all these covariates or inability to interpret results with many covariates), we would like to obtain a reduced set of covariates including only those that are necessary to obtain a “good enough” model. Also, we may have some domain knowledge telling us that only a few predictors should indeed be important for an outcome and therefore our “good enough” model is the best model. In other words, it is frequently assumed that most regression coefficients βj are zero. Variable selection aims to identify all important variables whose regression coefficients are not zero and to provide effective estimates of those coefficients. These variable selection features can lead to finding smaller groups of variables with good prediction accuracy. A potentially simple and effective tool for variable selection is the stepwise selection. However, it has severe problems in the presence of collinearity.
. Often when we are given a large number of covariates and due to different reasons (like the high cost of measuring all these covariates or inability to interpret results with many covariates), we would like to obtain a reduced set of covariates including only those that are necessary to obtain a “good enough” model. Also, we may have some domain knowledge telling us that only a few predictors should indeed be important for an outcome and therefore our “good enough” model is the best model. In other words, it is frequently assumed that most regression coefficients βj are zero. Variable selection aims to identify all important variables whose regression coefficients are not zero and to provide effective estimates of those coefficients. These variable selection features can lead to finding smaller groups of variables with good prediction accuracy. A potentially simple and effective tool for variable selection is the stepwise selection. However, it has severe problems in the presence of collinearity.
Among many methods, to achieve good prediction, to avoid overfitting, and to obtain an interpretable model, we consider the Least Absolute Shrinkage and Selection Operator (lasso) proposed by Tibshirani.23 This method considers both continuous shrinkage and variable selection. The lasso is a penalized least squares procedure that minimizes RSS = (ỹ − Xβ)T(ỹ − Xβ) where ỹ = y − y1n, subject to the non-differentiable constraint expressed in terms of the L1 norm. The lasso estimator is given by
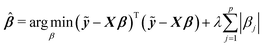 | (2) |
To assess how the results of different scenarios will generalize to external datasets, we investigate performance of predictive model through estimating accuracy of a predictive model applied to a new independent data. We therefore first build the model (or perform variable selection) using a training and test dataset, and then validate the model composed of the selected variables using an external validation dataset. To summarize the results, we report the numbers of correctly and incorrectly selected variables, and we quantify the prediction error,24 defined by squared root of the average error in the prediction of y given X for future cases not used in the construction of a prediction equation. Formally, if ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) (X) is the predicted values constructed using the present data, the prediction error can be written as
(X) is the predicted values constructed using the present data, the prediction error can be written as
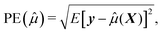 | (3) |
3. Simulation study
3.1. Simulation schemes
(i) Generate the glycan data X based on the correlation structure of real data. We simulate 1000 datasets consisting of 2n (n = 1000, for n model building set and n validation set) observations. The p glycans (p = 24) are drawn from multivariate normal distribution with mean μ and covariance matrix Σ. Details such as μ and Σ of real data and X are shown in Table S1 (ESI†). To mimic the skewed clean data exp(X) is used.(ii) Generate the error-contaminated glycan data W. We simulate 1000 datasets consisting of 2n observations and p glycans generated with three different error models – additive, multiplicative, two-component. The parameters of the covariance matrix Σ are shown in Table 2. The diagonal elements are denoted as σii = σi2, and the off-diagonal elements as σij(i ≠ j). We consider both correlated and uncorrelated covariance matrices.
| Error type | Additive | Multiplicative | |||
|---|---|---|---|---|---|
| σ ii | σ ij | σ ii | σ ij | ||
| Correlated | E1 | 1/4 | 1/8 | 0.1 | 0.05 |
| E2 | 1 | 0.5 | 0.01 | 0.005 | |
| Uncorrelated | E1un | 1/4 | 0 | 0.1 | 0 |
| E2un | 1 | 0 | 0.01 | 0 | |
(iii) Simulation of trait (y). Based on linear regression y = Xβ + ε (eqn (1)) with 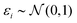 , and the coefficients β were set as follows:
, and the coefficients β were set as follows:
• 3 coefficients fixed: βj∈{1,2,10} = (1,0.5,2)T and all other βj{1,2,10} = 0.
• 6 coefficients fixed: βj∈{1,2,10,15,16,17} = c(1,0.5,2,3,0.5,1)T and all others are set to zero.
The descriptives of y are given in Table S1 (ESI†).
(iv) Six normalization methods. For each of the error-free and -contaminated glycan datasets – glycan data generated from the steps (i) and (ii) – the TA, logTA, RP, MS, MQ, or MQN transformation is applied.
(v) Regression. Using n training sets we apply lasso penalized regression for variable selection and prediction. The effect estimates ![[small beta, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e114.gif) are compared to the true β.
are compared to the true β.
(vi) Prediction. Using n (independent) validation or test sets, ![[small beta, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e114.gif) estimates from the variable selection (step v) are plugged in the model, and the fitted outcome ŷ are compared to the true y.
estimates from the variable selection (step v) are plugged in the model, and the fitted outcome ŷ are compared to the true y.
(vii) To assess the performance of variable selection, the average number of the correctly and incorrectly (falsely) selected variables is computed. For prediction performance the root mean squared prediction error (eqn (3)) is computed.
3.2. Distribution of error-contaminated glycans
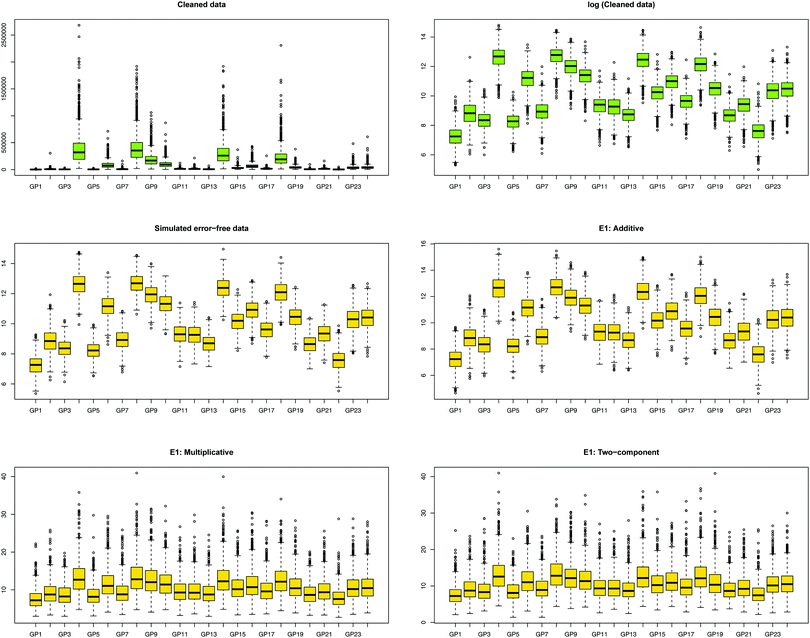
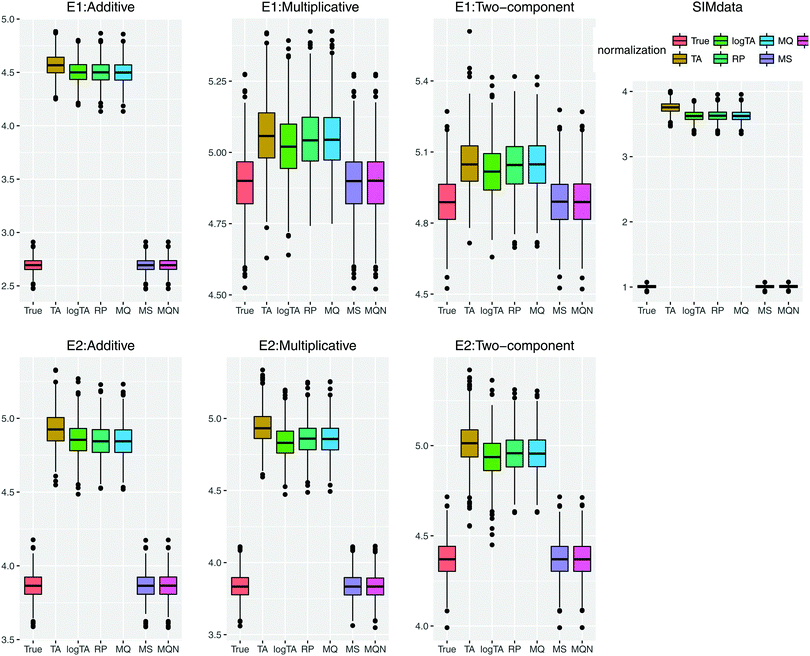
We first show how the different error models change the distribution of simulated glycan data. Fig. 4 shows the glycan distributions of such simulated data with and without the correlated error E1 in Table 2. The first row depicts the distribution of the highly skewed cleaned raw data, and that of the log-transformed data, which induces relative symmetry of glycan distributions, still having the same correlation structure. The second row, the left figure shows the error-free simulated data, SIMdata, based on the real log-transformed data. The rest depicts the distribution of the simulated data under additive, multiplicative, and two-component error model. While data with additive error showed similar distribution and correlation patterns, introducing multiplicative error in glycans makes the distribution skewed. Moreover, multiplicative error dominates additive error.3.3. Results of variable selection and prediction of multiple glycan predictors
Tables 3 and 4 show the results based on correlated errors under E1 and E2, respectively. The results of each table are averaged across 1000 simulations: for six normalization methods, two sets of fixed coefficients (3 and 6 βs), and four different error models (data without additional measurement error, and with additive, multiplicative, and two-component). For evaluation of the performance of normalization methods we considered (i) the number of the correctly selected variables, namely 3 or 6, (ii) the number of falsely selected variables (should be zero), and (iii) prediction error as defined in (3).| Error model | 3 beta'sa | 6 beta'sb | |||||
|---|---|---|---|---|---|---|---|
| Nr correctc | Nr falsed | PEe | Nr correct | Nr false | PE | ||
| a The glycans 1, 2, and 10 were assumed to have non-zero effects, and all other 21 glycans no effect. b The glycans 1, 2, 10, 15, 16 and 17 were assumed to have non-zero effects, and all other 18 glycans no effect. c The average number of correctly selected glycans. d The average number of falsely selected glycans, which should be close to zero. e The root mean squared error of prediction with respect to the new observations. f The rows in italics show the results of simulated data without additional error in glycans, which can be interpreted as the best achievable results under the correct models. | |||||||
| Error-free | SIMdata | 3.00 | 4.46 | 1.00 | 5.94 | 5.12 | 1.01 |
| MS | 3.00 | 4.47 | 1.00 | 5.94 | 5.10 | 1.01 | |
| MQN | 3.00 | 4.52 | 1.00 | 5.94 | 5.29 | 1.01 | |
| TA | 2.83 | 17.96 | 1.88 | 5.18 | 15.7 | 3.75 | |
| logTA | 2.97 | 19.86 | 1.83 | 5.75 | 17.2 | 3.62 | |
| RP | 1.83 | 13.21 | 2.33 | 5.73 | 17.13 | 3.63 | |
| MQ | 1.88 | 12.99 | 2.33 | 5.71 | 16.19 | 3.62 | |
| Additive | SIMdata | 3.00 | 13.57 | 1.50 | 5.38 | 15.31 | 2.69 |
| MS | 3.00 | 13.63 | 1.50 | 5.37 | 15.32 | 2.69 | |
| MQN | 3.00 | 13.58 | 1.50 | 5.37 | 15.29 | 2.70 | |
| TA | 2.42 | 16.46 | 2.18 | 4.91 | 14.63 | 4.57 | |
| logTA | 2.61 | 17.19 | 2.16 | 5.24 | 15.47 | 4.50 | |
| RP | 2.61 | 17.25 | 2.16 | 5.18 | 15.82 | 4.50 | |
| MQ | 2.70 | 16.98 | 2.16 | 5.44 | 15.56 | 4.50 | |
| Multiplicative | SIMdata | 2.12 | 8.90 | 2.29 | 3.03 | 8.50 | 4.90 |
| MS | 2.14 | 8.89 | 2.29 | 3.02 | 8.46 | 4.90 | |
| MQN | 2.12 | 8.76 | 2.29 | 3.03 | 8.46 | 4.90 | |
| TA | 0.29 | 1.68 | 2.36 | 0.45 | 1.32 | 5.06 | |
| logTA | 0.61 | 6.50 | 2.35 | 1.62 | 6.15 | 5.02 | |
| RP | 0.64 | 4.27 | 2.36 | 1.54 | 4.36 | 5.05 | |
| MQ | 0.54 | 4.14 | 2.36 | 1.46 | 4.09 | 5.05 | |
| Two-component | SIMdata | 2.06 | 9.07 | 2.30 | 3.01 | 8.30 | 4.89 |
| MS | 2.06 | 9.09 | 2.30 | 3.02 | 8.40 | 4.89 | |
| MQN | 2.07 | 9.13 | 2.30 | 3.00 | 8.29 | 4.89 | |
| TA | 0.23 | 1.66 | 2.36 | 0.49 | 1.38 | 5.05 | |
| logTA | 0.63 | 6.68 | 2.35 | 1.63 | 5.93 | 5.02 | |
| RP | 0.64 | 4.37 | 2.36 | 1.59 | 4.19 | 5.04 | |
| MQ | 0.55 | 4.26 | 2.36 | 1.57 | 4.27 | 5.05 | |
| Error model | 3 beta'sa | 6 beta'sb | |||||
|---|---|---|---|---|---|---|---|
| Nr correctc | Nr falsed | PEe | Nr correct | Nr false | PE | ||
| a The glycans 1, 2, and 10 were assumed to have non-zero effects, and all other 21 glycans no effect. b The glycans 1, 2, 10, 15, 16 and 17 were assumed to have non-zero effects, and all other 18 glycans no effect. c The average number of correctly selected glycans. d The average number of falsely selected glycans, which should be close to zero. e The root mean squared error of prediction with respect to the new observations. f The rows in italics show the results of simulated data without additional error in glycans, which can be interpreted as the best achievable results under the correct models. | |||||||
| Additive | Simdata | 2.74 | 13.91 | 1.92 | 5.26 | 15.02 | 3.87 |
| TA | 1.82 | 14.00 | 2.31 | 3.82 | 11.57 | 4.93 | |
| logTA | 2.26 | 15.68 | 2.29 | 4.62 | 13.86 | 4.86 | |
| RP | 2.34 | 15.81 | 2.29 | 4.84 | 4.94 | 4.85 | |
| MQ | 2.45 | 15.48 | 2.29 | 5.01 | 14.77 | 4.85 | |
| Multiplicative | Simdata | 2.65 | 16.06 | 1.87 | 5.07 | 15.05 | 3.83 |
| TA | 1.83 | 13.80 | 2.32 | 4.00 | 11.75 | 4.94 | |
| logTA | 2.00 | 16.10 | 2.28 | 4.51 | 14.63 | 4.84 | |
| RP | 2.22 | 15.50 | 2.29 | 4.65 | 14.01 | 4.86 | |
| MQ | 2.30 | 15.28 | 2.29 | 4.96 | 13.96 | 4.86 | |
| Two-component | Simdata | 2.67 | 12.25 | 2.10 | 4.32 | 10.99 | 4.37 |
| TA | 1.08 | 8.77 | 2.35 | 2.49 | 7.58 | 5.01 | |
| logTA | 1.66 | 13.25 | 2.33 | 3.64 | 11.64 | 4.94 | |
| RP | 1.81 | 12.35 | 2.10 | 4.05 | 11.87 | 4.96 | |
| MQ | 1.84 | 12.24 | 2.10 | 4.36 | 12.25 | 4.96 | |
The first row of each error model in Table 3, SIMdata, serves as a reference point and can be interpreted as the best achievable results under the correct model. Even when glycans were simulated without additional measurement error, the number of the falsely selected variables was non-zero: 4.46 for 3 fixed coefficients, and 5.12 for 6 fixed coefficients in average. When additive error in the data, the number of the falsely selected (13.57 and 15.31, respectively) becomes large, indicating a poor performance of variable selection. When multiplicative error was introduced the number of both correctly and incorrectly selected variables decreased and prediction error increased. The results of two-component error were close to those of multiplicative error, which indicates that in this parameter setting multiplicative error dominates additive one. Among row-wise normalization methods, TA and logTA perform poorly for variable selection when multiplicative error was involved. For multiplicative and two-component error the performance of all normalization methods was comparable; variable selection and prediction became exceedingly difficult. Overall, the column-wise normalizations outperformed the row-wise normalizations. Moreover, the results from two column-wise normalization, MS and MQN, were similar to SIMdata under all error models of Table 2.
Based on the error model E2 (Table 4), in which multiplicative errors have very small variances compared to additive ones, the number of incorrectly selected variables for the benchmark, SIMdata, was very large across all error types, leading to a poor variable selection performance. Prediction error seemed more controllable than under E1.
Fig. 5 highlights the prediction performance. Since the results of the models including 3 and 6 β's were similar, only the performance based on the models with 6 β's under E1 and E2 is shown. In case of uncorrelated error, compared to Table 3, the effects of the error in glycans became more marked (data not shown). Comparison of the correlated and uncorrelated error based on 6 βs in the model and the two-component error model is depicted in Fig. S1 (ESI†). The correlated error caused a poorer performance in variable selection.
To summarize the simulation results, even without additional measurement error the row-wise normalization appeared to perform poorly based on simulated glycan data, in terms of false positives and accurate prediction. Adding error caused perturbation of correlation structure, and especially introducing multiplicative error resulted in smaller number of variables in the model (less correctly- and incorrectly selected variables) and larger prediction error.
4. Data application
Glycans have been previously reported as biomarkers of both chronological and biological ages.2–4 These results were obtained using single-point analysis where the association between each glycan and ageing outcome was studied one at a time. Here we aim to detect multiple biomarkers associated with ageing, all in one go. Considering high correlation shown among glycan variables, to avoid overfitting and to obtain an interpretable model, the lasso regression23 in Section 2.4 is applied to the data from Scottish island of Orkney.15Glycan traits bound to immunoglobulin G (IgG) (Fig. 1) were measured by ultra-performance liquid chromatography (UPLC) in 2035 individuals from the ORCADES study, as described in Kristic et al.2 As can be seen in Fig. 1, 24 different glycan peaks are quantified using UPLC, with each glycan peak containing one or more glycan structures. Abundance of individual glycan structures in every glycan peak can be found in Pucic, et al.25 Participants were men and women (797; 1238) aged between 17 and 100 years (median age, 54). To explore effects of different normalization on biomarker selection of age, the glycan abundance was transformed using six normalization methods shown in Table 1, and additional logRP (log-transformation of RP). To remove strong batch effects in the glycomics data, following different normalization, we performed batch correction using empirical Bayes method26 as implemented in the ComBat function of sva package for R.27 To determine the ‘best’ model, applying the lasso requires selecting a value for the tuning parameter λ in eqn (2). For this training and testing of the model, ten-fold cross-validation was applied to the lasso fits in two third of the dataset. Then, the selected model was re-fitted for predicting age to the remaining one-third of the data (validation set). For comparison of the performance of each normalization, variable selection (in terms of non-zero coefficients) and accuracy in prediction are presented in Table 5.
| Glycan | Row-wise | Column-wise | |||||
|---|---|---|---|---|---|---|---|
| TA | logTA | RP | logRPa | MQ | MS | MQN | |
| Effect sizes (coefficients) | |||||||
| a Log-transformation of RP is included, which is equivalent to the ALR transformation.12 b The number of non-zero coefficients (selected variables). c As defined in eqn (3). The smaller, the better performance. | |||||||
| GP1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GP2 | 0.00 | 1.36 | 32.53 | 12.27 | 2.26 | 2.28 | 2.82 |
| GP3 | 0.00 | 0.00 | 0.00 | 0.00 | 0.55 | 0.00 | 0.00 |
| GP4 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GP5 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GP6 | 2.06 | 12.05 | 123.14 | 129.56 | 9.97 | 13.33 | 14.14 |
| GP7 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GP8 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GP9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GP10 | 0.63 | 2.55 | 90.74 | 0.00 | 8.14 | 0.00 | 1.43 |
| GP11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GP12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GP13 | 0.00 | 0.00 | −58.53 | 0.00 | −7.38 | 0.00 | 0.00 |
| GP14 | −1.72 | −20.65 | −259.85 | −212.61 | −14.76 | −16.56 | −20.00 |
| GP15 | 0.00 | 0.00 | 0.00 | 0.00 | −2.76 | 0.00 | 0.00 |
| GP16 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GP17 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GP18 | 0.00 | 0.00 | 0.00 | 0.00 | −0.63 | 0.00 | 0.00 |
| GP19 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GP20 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GP21 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GP22 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GP23 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GP24 | 0.00 | 0.48 | 9.39 | 0.00 | 0.00 | 1.41 | 2.14 |
| Variable selectionb | 3 | 5 | 6 | 3 | 8 | 4 | 5 |
| Prediction errorc | 10.52 | 10.40 | 10.45 | 10.83 | 10.46 | 10.40 | 10.36 |
Here, the results of variable selection is presented as (bold-faced) non-zero coefficients (effect size). For example, if you use TA normalization, 3 glycans (GP6, GP10, and GP14) will be selected as potential biomarkers with prediction error 10.52. In contrast, the smallest prediction error (10.36) is obtained using MQN, which selects 5 glycans (GP2, GP6, GP10, GP14, and GP24). GP6 and GP14 are the stable associated glycans, which are selected using every normalization methods. RP and log RP selected 6 and 3 glycans, respectively. However, the absolute effect size of the ‘stable’ glycans (GP6 and GP14) is ca. 10-fold greater than that of other normalizations, indicating biased results. Less robust (with smaller effect size), but evidence of association of GP2, GP10, and GP24, can be found using the majority of the normalization methods (represented by the bold-faced glycans in the first column).
To summarize, with regard to the accuracy of prediction, MQN showed the smallest prediction error, followed by logTA and MS. In terms of variable selection, MQ selected the largest number of the variables, thereby failing to provide sparse model. In particular, the strong effect size of GP14 appears to influence the selection of neighbouring GP13 and GP15. The other row-wise normalization, TA and RP (including logRP), results in seemingly ‘out-of-range’ values, which lacks model interpretability. Based on the magnitude of the effect sizes as well as variable selection, logTA (row-wise) and MS and MQN (both column-wise) seem to agree on the selected glycans.
5. Discussion
It is often claimed that glycans are by their nature compositions, and that percentage of glycan species in the whole is biologically relevant information.28 To dispute such claims is not of our interest; our intention is to increase the awareness of spurious correlations caused by row-wise normalization. In this work, we did not try to disentangle the true correlation structure in view of biochemical pathways, but rather demonstrated that choosing one normalization method can cause several potential issues and problems for downstream analysis. In particular, we focused here on variable selection by implementing standard statistical learning. When sample-wise differences are non-ignorable, more investigation for the choice of normalization method is needed. One of the challenges is how to generate or simulate such data to study statistical properties. Moreover, platform differences between measurement technologies such as ultra-performance liquid chromatography (UPLC) or nano liquid chromatography-electrospray ionization-mass spectrometry (nanoLC-ESI-MS) cannot be ignored. At this moment we do not have sufficient knowledge to deal with these issues.In this work we also addressed the effect of possible measurement error present in glycans. In general, introducing error caused decrease in the strength of correlations, and in particular multiplicative error produced more perturbation in correlation structure. In case of two-component error, the tendency of decreasing correlation was more pronounced. Moreover, even with very small multiplicative error, multiplicative error dominated additive one. Our simulation study clearly indicates that understanding measurement error structure is crucial, not only to extract real signals from noise-ridden data, but also to improve accuracy and efficiency of variable selection and prediction for finding glycan biomarkers. In statistics, measurement error models or errors-in-variables models are regression models that account for measurement errors in independent variables.21 Here, given that the real-life data measurement error is not well studied, we did not consider how to correct for the attenuation bias in multivariate errors-in-variables regression, but applied measurement error model to generate datasets contaminated with various types of error. We also included here an arbitrary correlated error structure, assuming that the highly correlated glycan data will have correlated errors. Nevertheless, replicates are more and more used in quantification of glycans and it will soon be possible to estimate the correlated measurement error for glycan data, which will greatly improve data pre-processing of glycan measurements.
Via simulation we have shown the row-wise normalization methods can have deleterious effects on variable selection based on multiple regression with the glycans covariates. When applied to the real data, two column-wise (MS and MQN) and logTA gave similar results in terms of variable selection, prediction, and the magnitude of effect estimates. For argument's sake, assuming the glycomics data resembles the microbiome count data and is compositional, what are the possibilities to obtain valid results? Although compositional data are proven difficult to handle statistically – the covariance matrix is not positive-semi-definite (or singular) and the level of the variance depends on the mean of the distribution – statistical methods for such data have been developed. For principal component analysis, Aitchison proposed a log linear contrast form to deal with compositional data,29 Regarding the variable selection problem, Lin et al.30 addressed this in high-dimensional regression with compositional covariates, motivated by research problems arising in the analysis of gut microbiome and metagenomic data. They considered the linear log-contrast model of Aitchison and Bacon-Shone.31 Whether any of these approaches would be beneficial for glycomics data analysis is yet to be determined. In particular, for network analysis where the analysis is based on correlation structure, it is not at all clear how to perform analysis based on the TA normalized data.32
With regard to biomarker discovery, it might be a better strategy to analyse glycans jointly. New groups of a few glycans, called derived traits, can be constructed, which represent groups of glycan structures that have similar structural and chemical properties. Up until now, these derived traits often exhibited stronger associations with studied outcome. Alternatively, we investigated here well-established variable selection and prediction method to discover multiple glycans that might be jointly responsible for association with disease trait. As shown in application to the real data (Table 5), the glycan biomarkers with large effect were selected, regardless which method was applied. To identify glycans with smaller effect and to avoid false positive and biased results, a few normalization methods (such as logTA, MS and MQN) can be employed to check the robustness of variable selection. Our simulation study clearly demonstrated that incorrect pre-processing steps might hamper discovery of reliable biomarkers. Another non-ignorable issue emerged from simulation study was the large amount of false positives (or falsely selected), due to the highly correlated nature of glycan measurements. In various scenarios many false positives were found, and therefore the task of variable selection failed. Hence, robustness of glycan biomarkers is of utmost importance for further investigation.
Regardless of the correlation structure or glycan measurement technology used, row-wise normalizations introduce spurious correlations and can therefore have an effect on downstream statistical analyses. The specific effects of other normalization methods on biomarker discovery not assessed in this paper should be studied before being implemented in measurement technology specific preprocessing procedures.
6. Conclusion
Modern high-throughput glycomics data measured by UPLC typically shows (i) that the between-subject differences in total abundance are very large, and (ii) that the glycans are highly correlated. Therefore, glycomics abundances should be normalized to comparable scales, and to avoid overfitting special care is needed for jointly selecting multiple biomarkers. Here, we assessed the impact of various normalization methods on glycomics biomarker selection using lasso regression. Through an extensive simulation study, we demonstrated that the widely used row-wise total area (TA) normalization method performs poorly compared to the column-wise normalization methods – glycans were falsely selected (false positives) and the prediction error was large. The column-wise normalization methods, such as MS and MQN, not only outperformed the row-wise methods but also have an advantage of preserving the correlation structure. Measurements error in glycan abundances, moreover, caused perturbation of correlation structure and diluted the signals in the data, which led to decreased accuracy in variable selection. Further application to the real data problem of glycan biomarker selection for biological ageing, confirmed these findings. To identify glycans with smaller association effects and to avoid false positives and biased results, we recommend to apply several normalization methods, such as logTA, MS and MQN, and report the association results that are detected by majority of them. This procedure will assist in identifying robust and reproducible glycan biomarkers.Conflicts of interest
Gordan Lauc is a founder and owner of the Genos Glycoscience Research Laboratory, a private research organization that specializes in high-throughput glycomic analysis and has several patents in this field. The other authors declare that they have no competing interests.Acknowledgements
The research leading to these results has received funding from the European Union's Seventh Framework Programme (FP7-Health-F5-2012) under grant agreement number 305280 (MIMOmics), and from the European Union's Horizon 2020 research and innovation programme IMforFUTURE under H2020-MSCA-ITN grant agreement number 721815. Authors thank to Gordan Lauc and James F. Wilson for providing ORCADES data that were the basis for simulation study and prediction of age. The work of LK was supported by an RCUK Innovation Fellowship from the National Productivity Investment Fund (MR/R026408/1). The Orkney Complex Disease Study (ORCADES) was supported by the Chief Scientist Office of the Scottish Government (CZB/4/276, CZB/4/710), a Royal Society URF to J. F. W., the MRC Human Genetics Unit quinquennial programme “QTL in Health and Disease”, Arthritis Research UK and the European Union framework program 6 EUROSPAN project (contract no. LSHG-CT-2006-018947).References
- D. Walt, Transforming Glycoscience: A roadmap for the future, The National Academic Press, Washington DC, 2012 Search PubMed.
- J. Krištić, F. Vučković, C. Menni, L. Klarić, T. Keser, I. Beceheli, M. Pučić-Baković, M. Novokmet, M. Mangino, K. Thaqi, P. Rudan, N. Novokmet, J. Sarac, S. Missoni, I. Kolčić, O. Polašek, I. Rudan, H. Campbell, C. Hayward, Y. Aulchenko, A. Valdes, J. F. Wilson, O. Gornik, D. Primorac, V. Zoldoš, T. Spector and G. Lauc, Glycans are a novel biomarker of chronological and biological ages, J. Gerontol., Ser. A, 2014, 69(7), 779–789, DOI:10.1093/gerona/glt190.
- L. R. Ruhaak, H.-W. Uh, M. Beekman, C. H. Hokke, R. G. J. Westendorp, J. Houwing-Duistermaat, M. Wuhrer, A. M. Deelder and P. E. Slagboom, Plasma protein N-glycan profiles are associated with calendar age, familial longevity and health, J. Proteome Res., 2011, 10(4), 1667–1674, DOI:10.1021/pr1009959.
- V. Vanhooren, X.-E. Liu, C. Franceschi, C.-F. Gao, C. Libert, R. Contreras and C. Chen, N-glycan profiles as tools in diagnosis of hepatocellular carcinoma and prediction of healthy human ageing, Mech. Ageing Dev., 2009, 130(1–2), 92–97, DOI:10.1016/j.mad.2008.11.008.
- R. Goodacre, D. Broadhurst, A. K. Smilde, B. S. Kristal, J. D. Baker, R. Beger, C. Bessant, S. Connor, G. Capuani, A. Craig, T. Ebbels, D. B. Kell, C. Manetti, J. Newton, G. Paternostro, R. Somorjai, M. Sjostrom, J. Trygg and F. Wulfert, Proposed minimum reporting standards for data analysis in metabolomics, Metabolomics, 2007, 231–241 CrossRef CAS.
- S. M. Kohl, M. S. Klein, J. Hochrein, P. J. Oefner, R. Spang and W. Gronwald, State-of-the art data normalization methods improve NMR-based metabolomic analysis, Metabolomics, 2012, 8(1), 146–160 CrossRef CAS PubMed.
- M.-A. Dillies, A. Rau, J. Aubert, C. Hennequet-Antier, M. Jeanmougin, N. Servant, C. Keime, G. Marot, D. Castel, J. Estelle, G. Guernec, B. Jagla, L. Jouneau, D. Laloë, C. Le Gall, B. Schaëffer, S. Le Crom, M. Guedj, F. Jaffrézic and FS Consortium, A comprehensive evaluation of normalization methods for Illumina high-throughput RNA sequencing data analysis, Briefings Bioinf., 2013, 14(6), 671–683 CrossRef CAS PubMed.
- J. Atchison, The statistical analysis of compositional data (with Discussion), J. R. Stat. Soc. B, 1982, 44, 139–177 Search PubMed.
- V. Pawlowsky-Glahn, J. J. Egozcue and R. Tolosana-Delgado, Modelling and analysis of compositional data, John Wiley & Sons, Ltd., Hoboken, NJ, 2015, https://www.wiley.com/en-nl/Modeling+and+Analysis+of+Compositional+Data-p-9781118443064 Search PubMed.
- K. Pearson, Mathematical contributions to the theory of evolution: on a form of spurious correlation which may arise when indices are used in the measurements of organs, Proc. R. Soc. London, 1897, 60, 489–498 CrossRef.
- H. Li, Microbiome, Metagenomics, and High-Dimensional Compositional Data Analysis, Annu. Rev. Stat. Appl., 2015, 2(1), 73–94, DOI:10.1146/annurev-statistics-010814-020351.
- J. Aitchison, The statistical analysis of compositional data, Blackburn Press, 2003 Search PubMed.
- D. M. Rocke and B. Durbin, A model for measurement error for gene expression arrays, J. Comput. Biol., 2001, 8(6), 557–569, DOI:10.1089/106652701753307485.
- M. F. Van Batenburg, L. Coulier, F. van Eeuwijk, A. K. Smilde and J. A. Westerhuis, New figures of merit for comprehensive functional genomics data: the metabolomics case, Anal. Chem., 2011, 83, 3267–3274 CrossRef CAS PubMed.
- R. McQuillan, A. L. Leutenegger, R. Abdel-Rahman, C. S. Franklin, M. Pericic, L. Barac-Lauc, N. Smolej-Narancic, B. Janicijevic, O. Polasek, A. Tenesa, A. K. MacLeod, S. M. Farrington, P. Rudan, C. Hayward, V. Vitart, I. Rudan, S. H. Wild, M. G. Dunlop, A. F. Wright, H. Campbell and J. F. Wilson, Runs of Homozygosity in European Populations, Am. J. Hum. Genet., 2008, 83(3), 359–372, DOI:10.1016/j.ajhg.2008.08.007.
- L. R. Ruhaak, H.-W. Uh, M. Beekman, C. A. M. Koeleman, C. H. Hokke, R. G. J. Westendorp, M. Wuhrer, J. J. Houwing-Duistermaat, P. E. Slagboom and A. M. Deelder, Decreased levels of bisecting GlcNAc glycoforms of IgG are associated with human longevity, PLoS One, 2010, 5(9), e12566, DOI:10.1371/journalpone0012566.
- F. Dieterle, A. Ross, H. Schlotterbeck and G. Senn, Probabilistic quotient normalization as robust method to account for dilution of complex biological mixtures Application to 1H NMR metabolomics, Anal. Chem., 2006, 78, 4281–4290 CrossRef CAS PubMed.
- R. A. van den Berg, H. C. J. Hoefsloot, J. A. Westerhuis, A. K. Smilde and M. J. van der Werf, Centering, scaling, and transformations: improving the biological information content of metabolomics data, BMC Genomics, 2006, 7, 142 CrossRef PubMed.
- B. M. Bolstad, Pre-processing DNA microarray data, Fundamentals of data mining in genomics and proteomics, Springer, 2007, pp. 51–78 Search PubMed.
- J. Aitchison, A concise guide to compositional data analysis, 1999 Search PubMed.
- R. J. Carroll, D. Ruppert, L. A. Stefanski and C. M. Crainiceanu, Measurement Error in Nonlinear Models, A Modern Perspective, Chapman and Hall/CRC, 2nd edn, 2006 Search PubMed.
- D. M. Rocke and S. Lorenzato, A two-Component model for measurement error in analytical chemistry, Technometrics, 1995, 37, 176–184 CrossRef.
- R. Tibshirani, Regression shrinkage and selection via the lasso, J. R. Stat. Soc. B, 1996, 58, 267–288 Search PubMed.
- J. Fan and R. Li, Variable Selection via Nonconcave Penalized Likelihood and its Oracle Properties, J. Am. Stat. Assoc., 2001, 96(456), 1348–1360, DOI:10.1198/016214501753382273.
- M. Pučić, A. Knežević, J. Vidič, B. Adamczyk, M. Novokmet, O. Polašek, O. Gornik, S. Šupraha-Goreta, M. R. Wormald, I. Redžić, H. Campbell, A. Wright, N. D. Hastie, J. F. Wilson, I. Rudan, M. Wuhrer, P. M. Rudd, D. Josić and G. Lauc, High Throughput Isolation and Glycosylation Analysis of Ig-Variability and Heritability of the IgG Glycome in Three Isolated Human Populations, Mol. Cell. Proteomics, 2011, 10(10), M111.010090, DOI:10.1074/MCP.M111.010090.
- W. E. Johnson, C. Li and A. Rabinovic, Adjusting batch effects in microarray expression data using empirical Bayes methods, Biostatistics, 2007, 8(1), 118–127, DOI:10.1093/biostatistics/kxj037.
- J. T. Leek, W. E. Johnson, H. S. Parker, A. E. Jaffe and J. D. Storey, The sva package for removing batch effects and other unwanted variation in high-throughput experiments, Bioinformatics, 2012, 28(6), 882–883, DOI:10.1093/bioinformatics/bts034.
- M. C. Galligan, R. Saldova, M. P. Campbell, P. M. Rudd and T. B. Murphy, Greedy feature selection for glycan chromatography data with the generalized Dirichlet distribution, BMC Bioinf., 2013, 14, 155 CrossRef CAS PubMed.
- J. Aitchison, Principal component analysis of compositional data, Biometrika, 1983, 70(1), 57–65 CrossRef.
- W. Lin, P. Shi, R. Feng and H. Li, Variable selection in regression with compositional covariates, Biometrika, 2014, 101(4), 785–797 CrossRef.
- J. Aitchison and J. Bacon-Shone, Log contrast models for experimentswith mixtures, Biometrika, 1984, 71, 323–330 CrossRef.
- J. J. Houwing-Duistermaat, H. W. Uh and A. Gusnanto, Discussion on the paper ‘Statistical contributions to bioinformatics: design, modelling, structure learning and integration’ by Jeffrey S. Morris and Veerabhadran Baladandayuthapani, Stat. Modell., 2017, 17(4–5), 319–326, DOI:10.1177/1471082x17706135.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9mo00174c |
| This journal is © The Royal Society of Chemistry 2020 |