Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dynamic intermolecular interactions through hydrogen bonding of water promote heat conduction in hydrogels
Jiawei
Zhou
 a,
Shaoting
Lin
a,
Shaoting
Lin
 a,
Hongxia
Zeng
a,
Ji
Liu†
a,
Hongxia
Zeng
a,
Ji
Liu†
 a,
Buxuan
Li
a,
Yanfei
Xu‡
a,
Xuanhe
Zhao
a,
Buxuan
Li
a,
Yanfei
Xu‡
a,
Xuanhe
Zhao
 *ab and
Gang
Chen
*a
*ab and
Gang
Chen
*a
aDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: zhaox@mit.edu; gchen2@mit.edu
bDepartment of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 10th August 2020
Abstract
Heat-conducting polymers provide a new opportunity to tackle thermal management challenges in advanced technologies such as wearable electronics and soft robotics. One strategy to enhance heat conduction in amorphous polymers has been tuning their intermolecular interactions. These intermolecular forces are often static in nature as the participating molecules are anchored on the polymer chains. In this work, using hydrogel as a model system, we demonstrate how dynamic intermolecular forces, which break and re-form constantly, can also enhance thermal transport. Utilizing calorimetric and spectroscopic measurements, we show that this arises from the hydrogen bonds formed between water and nearby polymer chains, which enhances the inter-chain heat transfer efficiency. This mechanism may potentially allow the design of heat-conducting polymers with self-healing or adaptability functionalities.
New conceptsWe demonstrate how dynamic intermolecular forces – fundamental to adaptable materials – can be explored to enhance thermal transport in polymer networks. Recent progress in engineering heat conduction in polymers through chain alignment or intermolecular interaction enhancement has achieved thermal conductivities orders of magnitude larger than typical bulk polymers, with potential applications from wearable devices to soft robotics. A hitherto unexplored area is how to apply these concepts to adaptable materials, which allow intriguing functionalities from self-healing to dynamic control. Using hydrogel as a material system, we show that dynamic intermolecular forces, which break and re-form constantly, can enhance the thermal conductivity of a polymer network beyond the prediction of effective medium theory. Combining calorimetric and spectroscopic studies, we clarify how this enhancement originates from the hydrogen bonding interactions of bound water, which facilitate the heat transfer across adjacent polymer chains. This mechanism potentially allows the design of heat-conducting polymers with adaptability or self-healing functionalities. |
Introduction
Soft materials such as polymers and gels have found wide applications in recent years in advanced technologies such as wearable electronics, soft robotics and three-dimensional printing.1 As heat is generated in these devices, however, their low thermal conductivity becomes an undesirable property,2 which hinders the further improvement of the device performance. The low thermal conductivity of polymers and gels is generally understood as a result of the atomic structural disorder and weak intermolecular interactions,2,3 which are intrinsic to soft materials because the energy scales of the intermolecular bonding strengths are comparable to the thermal fluctuation energy at room temperature and impose a large impact on their physical properties. By creating aligned polymer chains through stretching,4–12 electro-spinning,13,14 spin-coating,15 template-guided growth,16,17etc., past work has shown that the thermal conductivity of polymers can be increased by orders of magnitude compared to their typical values around 0.1–0.5 W m−1 K−1. More specifically, ultradrawn polyethylene nanofibers have been shown to reach thermal conductivity over 100 W m−1 K−1. Later on, polyethylene films drawn by up to 100 times were demonstrated to possess thermal conductivities over 60 W m−1 K−1.10–12 Polythiophene nanofibers grown via electropolymerization assisted by nanoscale templates also exhibit a thermal conductivity up to ∼4.4 W m−1 K−1.16 These results demonstrated that reduced atomic structural disorder can be beneficial for enhancing the heat conduction in polymers. As an ideal scenario, crystalline polymers with simple backbone moieties should possess high thermal conductivity because they support long-wavelength phonon modes which carry significant heat as in crystalline solids.18,19 Bulk polymers are not fully crystalline and contain amorphous regions. Nevertheless, by increasing the alignment of the polymer chains and reducing the structural disorder in the polymer network, more phonon-like modes are potentially allowed to exist and thus contribute to the heat conduction.Another strategy to enhance the thermal conductivity of a disordered polymer system is to enhance the intermolecular interaction strengths between polymer chains through various ways, such as hydrogen bonding,20,21 electrostatic interactions,22,23 or π–π interactions.24,25 These approaches have led to polymers with a thermal conductivity in the range of 1–2 W m−1 K−1, nearly one order of magnitude higher than most bulk polymers. These intermolecular forces are often static in nature, because the molecules involved in these forces are anchored on the polymer backbones. Dynamic intermolecular forces, which can reversibly break and re-form, represent another opportunity to be explored for engineering thermal conductivity of polymers. Such dynamic interactions have recently been utilized to design adaptable or self-healing polymer materials.26,27 The advantage of dynamic interactions is that when the material is significantly deformed, the interactions can remain effective because as the bonds break the molecules can re-arrange themselves to form new bonds.27 In contrast, static intermolecular interactions are not suitable in such a case because the intermolecular bonds contributing to heat transport will break. Consequently, heat-conducting materials designed with dynamic interactions can be useful for applications where mechanical compliance is a requirement, for example, in stretchable electronics or soft robotics.28 Hydrogels are one representative example possessing such dynamic intermolecular interactions. This is because in hydrogels, water molecules which participate in the hydrogen bonds with the hydrophilic groups on the polymer chains can readily rotate. In bulk water, the time scale for hydrogen bond randomization and water reorientation is on the order of 1 ps.29 The water reorientation is slowed down near the polymer chains, due to the hydrogen bond and the structuring effect. Even so, molecular dynamics simulation has indicated that for hydrophilic polymers the water reorientational dynamics is still fast near the polymer chains30 (on the order of picosecond). This means the hydrogen bonds between polymer chains and water survive only for a short period. Nonetheless, the bond strengths are comparable to the intermolecular forces in rigid polymers, indicating the possibility to enhance the thermal conductivity of a polymer network.
Heat conduction in hydrogels has been studied recently, with the focus mostly on the high water fraction regime where polymer chains are separated from each other by water.31,32 In this work, we studied the thermal transport within a hydrogel, particularly focusing on the low water fraction regime when the polymer chains are only separated by a few water molecules. We observe that the thermal conductivity value in this regime is beyond the prediction of effective medium theories. Combining differential scanning calorimetry and Raman scattering measurements, we discuss how this enhancement arises from the dynamic intermolecular interactions between polymer chains introduced by the hydrogen bonding of water molecules.
Main text
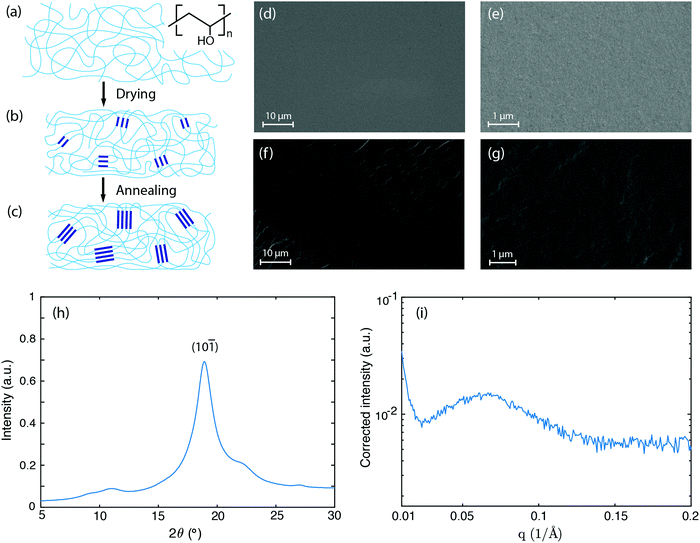
We choose polyvinyl alcohol (PVA) as our material system owing to PVA's simplest polymer backbone among water soluble polymers (chemical structure indicated in Fig. 1a), as well as their tunable hydrogen bonding between PVA chains and water molecules. First, 10 wt% PVA solution is prepared by dissolving PVA (molecular weight, 89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 98
000 to 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000; 99+% hydrolyzed; Sigma Aldrich) in deionized water and stirring at 90 °C overnight. The PVA solution is then degassed by centrifugation and poured into a plastic mold with a disk shape. The solution is allowed to evaporate inside an oven at 40 °C under high humidity so that water evaporation from the solution is well controlled and slowed down, otherwise the top layer will dry out first, leading to an inhomogeneous material. The residual water remaining is finally removed by further annealing the material at 90 °C for one hour. The above steps ensure that the obtained dry PVA has a dense structure, as confirmed by scanning electron microscopy images (Fig. 1d–g). The dry PVA sample has a disk shape with a thickness around 0.1 mm.
000; 99+% hydrolyzed; Sigma Aldrich) in deionized water and stirring at 90 °C overnight. The PVA solution is then degassed by centrifugation and poured into a plastic mold with a disk shape. The solution is allowed to evaporate inside an oven at 40 °C under high humidity so that water evaporation from the solution is well controlled and slowed down, otherwise the top layer will dry out first, leading to an inhomogeneous material. The residual water remaining is finally removed by further annealing the material at 90 °C for one hour. The above steps ensure that the obtained dry PVA has a dense structure, as confirmed by scanning electron microscopy images (Fig. 1d–g). The dry PVA sample has a disk shape with a thickness around 0.1 mm.
As water evaporates away, the PVA solution becomes more concentrated. As the concentration continues to increase, hydroxyl groups from separate PVA chains form associations (Fig. 1a), followed by crystallization due to the strong hydrogen bonding interactions among them.33,34 These crystalline domains hold polymer chains at one location and serve as physical crosslinkers. After most water is evaporated, a physically cross-linked PVA network is obtained (Fig. 1b). During the annealing process, the polymer chains acquire higher mobility and the crystalline domains grow in size accordingly35 (Fig. 1c). When this annealed PVA material absorbs water, only the amorphous regions swell because the crystalline domains are held by the strong cooperative hydrogen bonding forces and do not dissolve.
The growth of the crystalline domains is strongly hindered by the difficulty in re-organizing the entangled polymer chains. Previous studies have attributed this process to a kinetically frustrated crystallization process, suggesting that the entanglement of the polymer chains hinders the crystallites from further growing.33 To characterize the microstructure of the as-annealed PVA sample, we performed X-ray scattering experiments. Fig. 1h shows the wide-angle X-ray scattering (WAXS) data. The strong diffraction peak at 2θ = 18.9° indicates the semi-crystalline nature of the PVA sample, corresponding to the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) reflection plane of PVA crystals.36 Based on Scherrer's equation,37 the peak width Δ (full width at half maximum in radians, after subtracting the instrumental broadening) can be related to the crystal size D via D = kλ/(Δcos
) reflection plane of PVA crystals.36 Based on Scherrer's equation,37 the peak width Δ (full width at half maximum in radians, after subtracting the instrumental broadening) can be related to the crystal size D via D = kλ/(Δcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), where k is a dimensionless factor characterizing the shape of crystals, λ is X-ray wavelength (1.54 Å from CuKα1 radiation), and θ is the Bragg diffraction angle. The structural dimensionless factor usually varies from 0.9 to 1.1, and for estimation here we take k = 1.38 The measured peak width for the (10
θ), where k is a dimensionless factor characterizing the shape of crystals, λ is X-ray wavelength (1.54 Å from CuKα1 radiation), and θ is the Bragg diffraction angle. The structural dimensionless factor usually varies from 0.9 to 1.1, and for estimation here we take k = 1.38 The measured peak width for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) plane diffraction peak is ≈1.3° after subtracting the amorphous background, which corresponds to a crystal size of D ≈ 6.8 nm.
) plane diffraction peak is ≈1.3° after subtracting the amorphous background, which corresponds to a crystal size of D ≈ 6.8 nm.
These nanometer sized crystalline domains are separated in space. The average spatial separation can be investigated by small-angle X-ray scatterings (SAXS). To better reveal the structure factor, we correct the measured intensity I by the Lorentz factor:38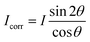 . In Fig. 1i, the peak arising at q ≈ 0.071 Å−1 indicates a periodic structure with a periodicity of
. In Fig. 1i, the peak arising at q ≈ 0.071 Å−1 indicates a periodic structure with a periodicity of 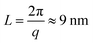 . The crystallinity is also estimated by comparing the melting enthalpy of the PVA sample to that of PVA crystals:
. The crystallinity is also estimated by comparing the melting enthalpy of the PVA sample to that of PVA crystals: 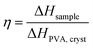 .39 The estimated crystallinity is 45% for the as-annealed sample. Even though the material has a high degree of crystallinity in its dry state, the crystalline domains are still separated by the amorphous region, which is the limiting factor for heat conduction.
.39 The estimated crystallinity is 45% for the as-annealed sample. Even though the material has a high degree of crystallinity in its dry state, the crystalline domains are still separated by the amorphous region, which is the limiting factor for heat conduction.
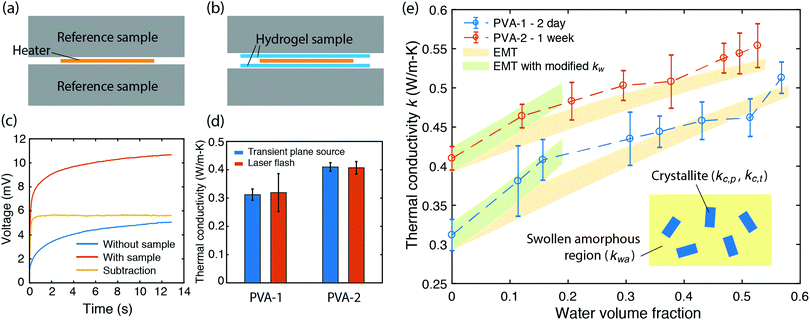
As the PVA sample swells in water, water molecules may potentially mediate the intermolecular interactions between polymer chains and enhance the thermal transport. To investigate whether this mechanism is effective, we measure the thermal conductivity of the PVA sample at different water fractions. The principle of the thermal conductivity measurement is illustrated in Fig. 2, and is based on the transient plane source (TPS) method.40,41 A heater is placed between two identical samples (Fig. 2a). As the current flows through the heater, the transient temperature increase at the heater is recorded by the resistance change in the heater. The measurement takes two steps. The first measurement is taken on reference materials (stainless steel) for a fixed current (Fig. 2a), with the resulting data denoted as T0(t). In the second measurement, two identical PVA samples are placed in between the heater and the reference samples (Fig. 2b), with the new data denoted as T1(t). To ensure good thermal contact, silicone oil is added at the interfaces for the two measurements. The additional temperature increase in the second case compared to the first one is due to the temperature drop across the thin sample layer. Because the layer thickness is much smaller than the thermal penetration depth (∼1 mm) within the acquisition time (a few seconds), the temperature profile inside the sample can be approximated to be linear. The corresponding temperature drop can thus be estimated to be 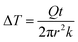 , where Q is the heating power of the heater, r the radius of the heater, t the sample thickness, and k the sample thermal conductivity. The factor of two takes into account the two sides of the heater. This temperature drop equates with the temperature difference between the two measurements T1 − T0, and therefore we have
, where Q is the heating power of the heater, r the radius of the heater, t the sample thickness, and k the sample thermal conductivity. The factor of two takes into account the two sides of the heater. This temperature drop equates with the temperature difference between the two measurements T1 − T0, and therefore we have 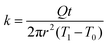 .41
.41
A commercial TPS system (Thermal Conductivity Kit, C-Therm Technologies) has been adapted for measuring the thermal conductivity of hydrogels. A Keithley sourcemeter is used to acquire data with a time resolution of around 1 ms for up to 13 seconds. The heater resistance is measured each time before the experiments by passing a small current through the heater. For the thermal measurement, the current is set at 0.2 A, which is found to give good signal-to-noise ratio while minimizing the sample heating (temperature increase is less than 1 K). Fig. 2c shows the measurement data of the as-annealed sample with and without the sample, and their difference. While both signals show a continuous increase, their difference reaches the plateau in less than one second, indicating that a linear temperature profile is established within the sample layer. The voltage difference during this period is converted to temperature difference by calibration, and used to calculate the thermal conductivity, as shown in Fig. 2e for different water volume fractions. Water volume fractions are calculated based on the weight difference between the swollen state (mwet) and the dry state (mdry), 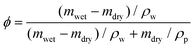 , where ρp and ρw are the density of the polymer and water respectively. Two polymer samples are prepared with different drying times. The first one (PVA-1) is dried for 2 days before annealing while the second one (PVA-2) is dried for one week. The longer drying time for PVA-2 allows the polymer chains to equilibrate towards a more stable and ordered configuration, and consequently a higher thermal conductivity is observed. The measured thermal conductivity of the as-annealed dry PVA is around 0.3–0.4 W m−1 K−1, consistent with the previous literature. These values have been further confirmed by independent measurements of thermal diffusivity using commercial laser flash equipment (Netzsch LFA 457), which are converted to thermal conductivities based on the literature data of heat capacity (1.55 kJ (kg T)−1) and density (1.25 g cm−3) of PVA at room temperature42 (Fig. 2d).
, where ρp and ρw are the density of the polymer and water respectively. Two polymer samples are prepared with different drying times. The first one (PVA-1) is dried for 2 days before annealing while the second one (PVA-2) is dried for one week. The longer drying time for PVA-2 allows the polymer chains to equilibrate towards a more stable and ordered configuration, and consequently a higher thermal conductivity is observed. The measured thermal conductivity of the as-annealed dry PVA is around 0.3–0.4 W m−1 K−1, consistent with the previous literature. These values have been further confirmed by independent measurements of thermal diffusivity using commercial laser flash equipment (Netzsch LFA 457), which are converted to thermal conductivities based on the literature data of heat capacity (1.55 kJ (kg T)−1) and density (1.25 g cm−3) of PVA at room temperature42 (Fig. 2d).
If water only served as a filler in the PVA polymer matrix, the thermal conductivity of the hydrogel should follow an increasing curve as expected from effective medium theories (EMT). Indeed, as water fraction increases the thermal conductivity also increases, because water has a higher thermal conductivity (0.6 W m−1 K−1) at room temperature than the polymer. However, we also observed a larger slope for the thermal conductivity increase when the water volume fraction is less than 20%. To emphasize this deviation, the thermal conductivity predicted by EMT is also shown in the plot as shaded regions (in yellow). The EMT takes the thermal conductivity of the dry state as the only input, and also considers the measurement uncertainty. To construct the EMT for thermal transport in hydrogels, we proceed in two steps. PVA hydrogel has three phases – crystalline PVA domains, amorphous PVA domains, and water. Because crystalline domains do not swell in water,39 the increase in the total thermal conductivity thus comes from the amorphous region. As an approximation, we assume that water is uniformly distributed in the amorphous PVA domain with a volume fraction EQ, which is related to the water fraction in the entire volume (ϕ) by the crystallinity (η) via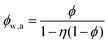 (in deriving this relation, we ignore the density difference between crystalline and amorphous PVA domains). The effective thermal conductivity of the swollen amorphous region (kwa) can be estimated based on EMT, once the thermal conductivities for water (kw) and amorphous PVA (ka) are known. The two most widely employed effective medium theories are the Maxwell-Garnett EMT43 and the self-consistent EMT,44 corresponding to isolated particles in a matrix, and randomly distributed particles, respectively.45 For the amorphous region, as water diffuses into the polymer network, the self-consistent EMT is more applicable. This implies
(in deriving this relation, we ignore the density difference between crystalline and amorphous PVA domains). The effective thermal conductivity of the swollen amorphous region (kwa) can be estimated based on EMT, once the thermal conductivities for water (kw) and amorphous PVA (ka) are known. The two most widely employed effective medium theories are the Maxwell-Garnett EMT43 and the self-consistent EMT,44 corresponding to isolated particles in a matrix, and randomly distributed particles, respectively.45 For the amorphous region, as water diffuses into the polymer network, the self-consistent EMT is more applicable. This implies
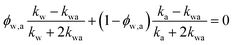 | (1) |
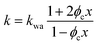 | (2) |
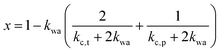 and kwa is solved from eqn (1).
and kwa is solved from eqn (1).
The above formalism requires thermal conductivities of each phase. The thermal conductivity in the crystalline domain along the chain direction is taken from recent molecular dynamics simulations for the PVA single chain47 (kc,p = 6 W m−1 K−1). Due to substantially less phase space for phonon scatterings to occur, the single chain could possess higher thermal conductivity than a bulk crystal, and the simulated value thus serves as an approximate upper bound.48 The thermal conductivity of water is taken from the literature data on bulk water (kw = 0.6 W m−1 K−1). The remaining two unknown values (kc,t and ka) are expected to be small because they are not along the chain direction and heat is transported via weak interactions. For simplicity, we take kc,t to be the same as the amorphous thermal conductivity ka, leaving only one variable unknown. For each sample, this variable is determined by fitting to the thermal conductivity value of the dry state. Given this, the EMT can then predict the thermal conductivity across the entire water fraction range, as shown by the shaded region (in yellow) in Fig. 2e. The fitted ka ranges from 0.2 to 0.3 W m−1 K−1, as expected for amorphous polymers.49 We should note that kc,t can be larger than ka as the crystallites are held by hydrogen bonds. However, we have found that fitting kc,t and ka independently would give almost identical EMT predictions as long as the thermal conductivity of the dry state is correctly reproduced.
The EMT formalism takes no fitting parameters except ka to reproduce the thermal conductivity in the dry state (zero water fraction). For higher water fractions, experiments agree reasonably well with the theory, which is expected because as water fraction increases, water behaves more like bulk water and the effective medium approach is justified. The slight increasing trend near the highest water fraction point could result from the fact that polymer chains are swollen in water and therefore adopt an extended conformation, which is favorable for heat conduction. Due to the limited extension, however, the enhancement in thermal conductivity is small compared to the EMT prediction. On the other hand, when water fractions are low, water molecules are strongly affected by their interactions with polymer chains and do not behave as bulk water. Intriguingly, in this range water molecules behave as if they have a higher thermal conductivity. Better agreement can be obtained for the low water fraction region if the thermal conductivity of water arbitrarily increases to 0.8–0.9 W m−1 K−1, as shown in the shaded regions in green in Fig. 2e.
It is well known that for water soluble polymers, the first layer of water molecules is strongly bound to polymer chains, known as bound water.50,51 These water molecules have much less degrees of freedom compared to bulk water (also known as ‘free’ water). For PVA in particular, this results from the hydrogen bonding interactions between water and the hydroxyl groups on the PVA chains. Despite the strong interactions, these intermolecular forces are dynamic in nature because the hydrogen bonds can constantly break and re-form. This dynamic interaction can be studied via simulating the orientational relaxation time of water molecules.30 Indeed, molecular dynamics simulation on the PVA–water system has shown that the orientational relaxation time of water near the –OH group of the PVA chains is around a few picoseconds,30 a short time that is on the same order of magnitude with bulk water.29 The studied system has a water content of 50 wt%, for which a major portion of water is bound water as we demonstrate below. The simulation result thus indicates that the bound water in PVA forms dynamic hydrogen bonding interactions with the polymer chains. These hydrogen bonds can effectively enhance the intermolecular interactions between separate polymer chains, potentially contributing to an enhanced thermal conductivity at low water volume fractions.
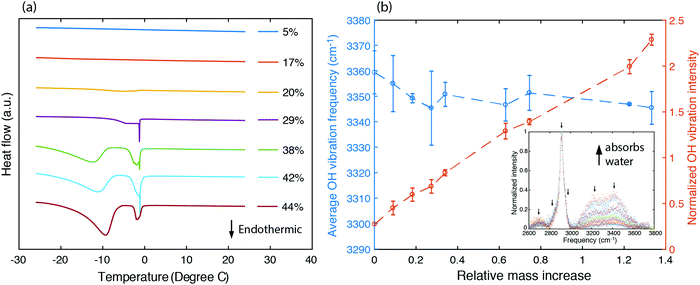
To understand the states of water and their interactions with polymer chains, we first characterized the fraction of bound water existing in the sample by studying the melting behavior of frozen hydrogels using differential scanning calorimetry. Frozen water typically exhibits an endothermic peak as the temperature passes 0 °C. Instead, no such endothermic peak is found for samples having a water volume fraction as high as 20% (Fig. 3a). This unfreezing behavior in PVA has been understood as resulting from bound water losing their ability to interact with nearby water molecules to crystallize below 0 °C,50 which also suggests that in this range water molecules exhibit strong interactions with PVA chains. Indeed, the enhancement in thermal conductivity is most significant for water volume fractions less than 20% (Fig. 2e). As water fraction continues to increase, endothermic peaks are observed, indicating the existence of freezable water with more degrees of freedom inside the sample. The appearance of an endothermic peak below 0 °C has been ascribed to freezable bound water to distinguish from the non-freezable bound water that dominates at low water fractions.52 As the bound water molecules have local environments different from the bulk water, they acquire a different phase transition temperature.52 The endothermic peak occurring near 0 °C results from bulk-like free water at locations away from the polymer chains. The increasing fraction of freezable water implies that there is more bulk-like water separating the polymer chains. Consequently, at larger water fractions, the thermal conductivity approaches the values described by the EMT (Fig. 2e).
To further understand how strongly the water molecules bind to the polymer chains, we measured the Raman spectrum for PVA hydrogels with different water fractions, as shown in the inset of Fig. 3b. The peaks around 2900 cm−1 are due to C–H stretching vibrations in the polymer backbone, and the broader feature from 3000 cm−1 to 3600 cm−1 containing two major peaks at around 3200 cm−1 and 3400 cm−1 corresponds to O–H stretching vibrations (including those from both the polymer and water). We have deconvoluted the Raman spectrum assuming that the peaks have Gaussian shapes, with peak positions indicated by arrows. The area under the peaks is added up to give the total intensity for C–H and O–H stretching vibrations respectively (ICH and IOH). We further define normalized OH vibration intensity as ĪOH = IOH/ICH, which eliminates the variation in the scattering cross section between samples. Fig. 3b shows that ĪOH increases linearly with the relative mass increase, indicating that the additional Raman signal increase for the OH vibration peaks indeed comes from water molecules.
O–H vibration frequencies of water molecules are sensitive to their environment. When water molecules form strong hydrogen bonds with nearby molecules, the participating O–H bond will be elongated, and consequently have smaller restoring forces and lower vibrational frequencies.53 We calculated the intensity averaged O–H vibration frequency as 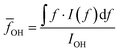 , where the integration covers the O–H vibration spectrum and f is the frequency. As seen in Fig. 3b,
, where the integration covers the O–H vibration spectrum and f is the frequency. As seen in Fig. 3b, ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) OH decreases with increasing relative mass, indicating that the water molecules are involved in strong interactions with nearby molecules. The large frequency decrease for a small mass increase below 30% indicates that the hydroxyl groups of bound water have stronger intermolecular interactions with nearby molecules than the hydroxyl groups on the polymer backbones, consistent with the range where thermal conductivity is enhanced. Some of the bound water will strongly bind to one polymer chain, but others can interact with more than one chain, the latter of which is the dominant factor that mediates the intermolecular interactions between polymer chains. Although the frequency shift is small compared to the uncertainty, one can observe that a non-monotonic behavior emerges near 30%. This can be explained as follows. At low water fractions, some water molecules are bound to two polymer chains, serving as a ‘bridge’ to enhance inter-chain heat transfer. As water fraction further increases, the polymer chains are separated apart and each water molecule only binds to one polymer chain. Because their orientations are restricted by the hydrogen bonds with the polymer, it becomes difficult for these water molecules to form hydrogen bonds with each other, thus leaving a weaker hydrogen bonding interaction on average. Together with thermal transport measurement, this result demonstrates that, instead of only serving as fillers, the water molecules can improve thermal transport in the polymer network by enhancing the inter-chain intermolecular interactions.
OH decreases with increasing relative mass, indicating that the water molecules are involved in strong interactions with nearby molecules. The large frequency decrease for a small mass increase below 30% indicates that the hydroxyl groups of bound water have stronger intermolecular interactions with nearby molecules than the hydroxyl groups on the polymer backbones, consistent with the range where thermal conductivity is enhanced. Some of the bound water will strongly bind to one polymer chain, but others can interact with more than one chain, the latter of which is the dominant factor that mediates the intermolecular interactions between polymer chains. Although the frequency shift is small compared to the uncertainty, one can observe that a non-monotonic behavior emerges near 30%. This can be explained as follows. At low water fractions, some water molecules are bound to two polymer chains, serving as a ‘bridge’ to enhance inter-chain heat transfer. As water fraction further increases, the polymer chains are separated apart and each water molecule only binds to one polymer chain. Because their orientations are restricted by the hydrogen bonds with the polymer, it becomes difficult for these water molecules to form hydrogen bonds with each other, thus leaving a weaker hydrogen bonding interaction on average. Together with thermal transport measurement, this result demonstrates that, instead of only serving as fillers, the water molecules can improve thermal transport in the polymer network by enhancing the inter-chain intermolecular interactions.
Conclusions
For water soluble polymers that are slightly hydrated, the water molecules are strongly bound to the polymer chains through hydrogen bonds, which are intrinsically dynamic due to the constant rotational motions of water molecules. We found that these dynamic intermolecular interactions can effectively enhance inter-chain heat transfer and promote the heat conduction in a PVA polymer network beyond the predictions of effective medium theory. Calorimetric and spectroscopy measurements were taken to demonstrate that the enhanced thermal conductivity originates from bound water, which forms strong hydrogen bonds with nearby polymer chains. Though the observed enhancement is small on absolute scales, this mechanism can potentially be useful for developing heat conducting materials with self-healing or reconfigurable functionalities using dynamic intermolecular forces as the building blocks. Moreover, we note that as water fraction increases the modulus of the hydrogel also decreases. Hydrogels are well known for their mechanical deformability, partly owing to the dynamic nature of the intermolecular forces within the material. In this regard, dynamic intermolecular interactions can also help design materials with simultaneously higher thermal conductivity and lower elastic modulus. As one example, we highlight the thermal management in the operation of thermally responsive soft actuators for robotic applications. These thermally responsive actuators have usually employed temperature-induced phase transitions, which are typically triggered by variation in the external temperature.28 Consequently, the response time of the soft actuators can be limited by the heat diffusion, with a characteristic time of t ∼ l2/α, where l is the characteristic actuator length (e.g. thickness for sheet-like actuator) and α is the thermal diffusivity, which is proportional to the thermal conductivity of the soft material used. Most of the current soft actuators are based on polymers which have low thermal conductivities. If the thermal conductivity can be increased, the actuator can then potentially respond in a faster speed. Materials with simultaneously high thermal conductivity and low elastic modulus are therefore ideal for such a case because they are mechanically compatible with soft actuators. In general, these materials will be desirable for thermal management applications where mechanical compliance is important.Conflicts of interest
There are no competing interests to declare.Acknowledgements
We thank G. Mahan and G. Rutledge for discussions on the heat conduction mechanisms, and Y. Tu for discussions on the polymer structure. The X-ray scattering experiments were performed using the shared facility at the MIT Material Research Science and Engineering Center (MRSEC). This work was supported by the U.S. Department of Energy (DOE)–Basic Energy Sciences (Award No. DE-FG02-02ER45977).References
- M. Peplow, The plastics revolution: how chemists are pushing polymers to new limits, Nat. News, 2016, 536, 266 CrossRef CAS PubMed.
- A. Henry, Thermal transport in polymers, Annu. Rev. Heat Transfer, 2014, 17, 485–520 CrossRef.
- R. J. Young and P. A. Lovell, Introduction to Polymers, CRC Press, 3rd edn, 2011 Search PubMed.
- C. L. Choy, Thermal conductivity of polymers, Polymer, 1977, 18, 984–1004 CrossRef CAS.
- B. Poulaert, R. Legras, J. C. Chielens, C. Vandenhende and J. P. Issi, Thermal-conductivity of highly oriented polyethylene fibers, Polym. Commun., 1990, 31, 148 CAS.
- H. Fujishiro, M. Ikebe, T. Kashima and A. Yamanaka, Thermal conductivity and diffusivity of high-strength polymer fibers, Jpn. J. Appl. Phys., 1997, 36, 5633 CrossRef CAS.
- S. Shen, A. Henry, J. Tong, R. Zheng and G. Chen, Polyethylene nanofibres with very high thermal conductivities, Nat. Nano, 2010, 5, 251–255 CrossRef CAS PubMed.
- X. Wang, V. Ho, R. A. Segalman and D. G. Cahill, Thermal conductivity of high-modulus polymer fibers, Macromolecules, 2013, 46, 4937–4943 CrossRef CAS.
- R. Shrestha, et al., Crystalline polymer nanofibers with ultra-high strength and thermal conductivity, Nat. Commun., 2018, 9, 1–9 CrossRef CAS PubMed.
- Y. Xu, et al., Nanostructured polymer films with metal-like thermal conductivity, Nat. Commun., 2019, 10, 1771 CrossRef PubMed.
- S. Ronca, T. Igarashi, G. Forte and S. Rastogi, Metallic-like thermal conductivity in a lightweight insulator: solid-state processed ultra high molecular weight polyethylene tapes and films, Polymer, 2017, 123, 203–210 CrossRef CAS.
- B. Zhu, et al., Novel polyethylene fibers of very high thermal conductivity enabled by amorphous restructuring, ACS Omega, 2017, 2, 3931–3944 CrossRef CAS PubMed.
- J. Ma, et al., Thermal conductivity of electrospun polyethylene nanofibers, Nanoscale, 2015, 7, 16899–16908 RSC.
- C. Lu, et al., Thermal conductivity of electrospinning chain-aligned polyethylene oxide (PEO), Polymer, 2017, 115, 52–59 CrossRef CAS.
- K. Kurabayashi, M. Asheghi, M. Touzelbaev and K. E. Goodson, Measurement of the thermal conductivity anisotropy in polyimide films, J. Microelectromech. Syst., 1999, 8, 180–191 CrossRef CAS.
- V. Singh, et al., High thermal conductivity of chain-oriented amorphous polythiophene, Nat. Nano, 2014, 9, 384–390 CrossRef CAS PubMed.
- M. K. Smith, V. Singh, K. Kalaitzidou and B. A. Cola, Poly(3-hexylthiophene) nanotube array surfaces with tunable wetting and contact thermal energy transport, ACS Nano, 2015, 9, 1080–1088 CrossRef CAS PubMed.
- J. G. Kirkwood, The skeletal modes of vibration of long chain molecules, J. Chem. Phys., 1939, 7, 506–509 CrossRef CAS.
- C. L. Choy, S. P. Wong and K. Young, Model calculation of the thermal conductivity of polymer crystals, J. Polym. Sci., Polym. Phys. Ed., 1985, 23, 1495–1504 CrossRef CAS.
- G.-H. Kim, et al., High thermal conductivity in amorphous polymer blends by engineered interchain interactions, Nat. Mater., 2015, 14, 295–300 CrossRef CAS PubMed.
- L. Mu, et al., Molecular origin of efficient phonon transfer in modulated polymer blends: effect of hydrogen bonding on polymer coil size and assembled microstructure, J. Phys. Chem. C, 2017, 121, 14204–14212 CrossRef CAS.
- A. Shanker, et al., High thermal conductivity in electrostatically engineered amorphous polymers, Sci. Adv., 2017, 3, e1700342 CrossRef.
- X. Xie, et al., High and low thermal conductivity of amorphous macromolecules, Phys. Rev. B, 2017, 95, 035406 CrossRef.
- K. Fukushima, et al., High thermal conductive epoxy resins with controlled high-order structure. in 340–343 (IEEE, 2004), DOI: 10.1109/CEIDP.2004.1364257.
- Y. Xu, et al., Molecular engineered conjugated polymer with high thermal conductivity, Sci. Adv., 2018, 4, eaar3031 CrossRef.
- J.-M. Lehn, From supramolecular chemistry towards constitutional dynamic chemistry and adaptive chemistry, Chem. Soc. Rev., 2007, 36, 151–160 RSC.
- Z. Wei, et al., Self-healing gels based on constitutional dynamic chemistry and their potential applications, Chem. Soc. Rev., 2014, 43, 8114–8131 RSC.
- L. Hines, K. Petersen, G. Z. Lum and M. Sitti, Soft actuators for small-scale robotics, Adv. Mater., 2017, 29, 1603483 CrossRef.
- M. D. Fayer, Dynamics of water interacting with interfaces, molecules, and ions, Acc. Chem. Res., 2012, 45, 3–14 CrossRef CAS PubMed.
- Y. Tamai, H. Tanaka and K. Nakanishi, Molecular dynamics study of polymer–water interaction in hydrogels. 2. hydrogen-bond dynamics, Macromolecules, 1996, 29, 6761–6769 CrossRef CAS.
- N. Tang, et al., Thermal transport in soft PAAm hydrogels, Polymers, 2017, 9, 688 CrossRef PubMed.
- S. Xu, S. Cai and Z. Liu, Thermal conductivity of polyacrylamide hydrogels at the nanoscale, ACS Appl. Mater. Interfaces, 2018, 10, 36352–36360 CrossRef CAS PubMed.
- P. J. Willcox, et al., Microstructure of poly(vinyl alcohol) hydrogels produced by freeze/thaw cycling, J. Polym. Sci., Part B: Polym. Phys., 1999, 37, 3438–3454 CrossRef CAS.
- C. M. Hassan and N. A. Peppas, Structure and applications of poly(vinyl alcohol) hydrogels produced by conventional crosslinking or by freezing/thawing methods, in Biopolymers PVA Hydrogels, Anionic Polymerisation Nanocomposites, Springer, 2000, pp. 37–65 DOI:10.1007/3-540-46414-X_2.
- H. E. Assender and A. H. Windle, Crystallinity in poly(vinyl alcohol). 1. An X-ray diffraction study of atactic PVOH, Polymer, 1998, 39, 4295–4302 CrossRef CAS.
- R. Ricciardi, F. Auriemma, C. De Rosa and F. Lauprêtre, X-ray diffraction analysis of poly(vinyl alcohol) hydrogels, obtained by freezing and thawing techniques, Macromolecules, 2004, 37, 1921–1927 CrossRef CAS.
- A. L. Patterson, The Scherrer formula for X-ray particle size determination, Phys. Rev., 1939, 56, 978–982 CrossRef CAS.
- B. Cullity and S. Stock, Elements of X Ray Diffraction, Pearson, 2001 Search PubMed.
- N. A. Peppas and E. W. Merrill, Differential scanning calorimetry of crystallized PVA hydrogels, J. Appl. Polym. Sci., 1976, 20, 1457–1465 CrossRef CAS.
- S. E. Gustafsson, Transient plane source techniques for thermal conductivity and thermal diffusivity measurements of solid materials, Rev. Sci. Instrum., 1991, 62, 797–804 CrossRef CAS.
- H. Zhang, et al., A numerical study on the theoretical accuracy of film thermal conductivity using transient plane source method, Appl. Therm. Eng., 2014, 72, 62–69 CrossRef.
- J. E. Mark, Physical Properties of Polymers Handbook, Springer-Verlag, 2007 Search PubMed.
- J. C. M. Garnett and J. Larmor XII, Colours in metal glasses and in metallic films, Philosophical Transactions of the Royal Society of London, Series A, Containing Papers of a Mathematical or Physical Character, 1904, vol. 203, pp. 385–420.
- D. a. G. Bruggeman, Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. I. Dielektrizitätskonstanten und Leitfähigkeiten der Mischkörper aus isotropen Substanzen, Ann. Phys., 1935, 416, 636–664 CrossRef.
- G. A. Niklasson, C. G. Granqvist and O. Hunderi, Effective medium models for the optical properties of inhomogeneous materials, Appl. Opt., 1981, 20, 26–30 CrossRef CAS.
- C.-W. Nan, Physics of inhomogeneous inorganic materials, Prog. Mater. Sci., 1993, 37, 1–116 CrossRef CAS.
- Q. Liao, L. Zeng, Z. Liu and W. Liu, Tailoring thermal conductivity of single-stranded carbon-chain polymers through atomic mass modification, Sci. Rep., 2016, 6, 34999 CrossRef CAS.
- A. Henry, G. Chen, S. J. Plimpton and A. Thompson, 1D-to-3D transition of phonon heat conduction in polyethylene using molecular dynamics simulations, Phys. Rev. B: Condens Matter Mater. Phys., 2010, 82, 144308 CrossRef.
- L. H. Sperling, Introduction to Physical Polymer Science, John Wiley & Sons, 2005 Search PubMed.
- T. Hatakeyema, A. Yamauchi and H. Hatakeyema, Studies on bound water in poly(vinyl alcohol) hydrogel by DSC and FT-NMR, Eur. Polym. J., 1984, 20, 61–64 CrossRef CAS.
- A. S. Hoffman, Hydrogels for biomedical applications, Adv. Drug Delivery Rev., 2012, 64, 18–23 CrossRef.
- A. Higuchi and T. Iijima, D.s.c. investigation of the states of water in poly(vinyl alcohol) membranes, Polymer, 1985, 26, 1207–1211 CrossRef CAS.
- K. Kudo, J. Ishida, G. Syuu, Y. Sekine and T. Ikeda-Fukazawa, Structural changes of water in poly(vinyl alcohol) hydrogel during dehydration, J. Chem. Phys., 2014, 140, 044909 CrossRef.
Footnotes |
| † Current address: Department of Mechanical and Energy Engineering, Southern University of Science and Technology, China. |
| ‡ Current address: Department of Mechanical and Industrial Engineering, University of Massachusetts, Amherst, USA. |
| This journal is © The Royal Society of Chemistry 2020 |