Open Access Article
Open Access ArticleLocal manipulation of metamagnetism by strain nanopatterning†
Michael
Foerster
a,
Enric
Menéndez
b,
Emerson
Coy
 c,
Alberto
Quintana
b,
Carles
Gómez-Olivella
c,
Alberto
Quintana
b,
Carles
Gómez-Olivella
 d,
Daniel
Esqué de los Ojos
b,
Oriol
Vallcorba
d,
Daniel
Esqué de los Ojos
b,
Oriol
Vallcorba
 a,
Carlos
Frontera
a,
Carlos
Frontera
 e,
Lucia
Aballe
a,
Josep
Nogués
fg,
Jordi
Sort
e,
Lucia
Aballe
a,
Josep
Nogués
fg,
Jordi
Sort
 *bg and
Ignasi
Fina
*bg and
Ignasi
Fina
 *e
*e
aALBA Synchrotron Light Facility, Cerdanyola del Vallès, Carrer de la Llum 2-26, Barcelona E-08290, Spain
bDepartament de Física, Universitat Autònoma de Barcelona, Bellaterra, Barcelona E-08193, Spain. E-mail: jordi.sort@uab.cat
cNanoBioMedical Centre, Adam Mickiewicz University, Wszechnicy Piastowskiej 3, 61-614, Poznan, Poland
dDepartament Física Aplicada i Òptica, Universitat de Barcelona, Martí i Franquès 1, 08028 Barcelona, Spain
eInstitut de Ciència de Materials de Barcelona (ICMAB-CSIC), Campus UAB, Bellaterra E-08193, Catalonia, Spain. E-mail: ifina@icmab.es
fCatalan Institute of Nanoscience and Nanotechnology (ICN2), CSIC and BIST, Campus UAB, Bellaterra, E-08193 Barcelona, Spain
gICREA, Pg. Lluís Companys 23, E-08010 Barcelona, Spain
First published on 14th May 2020
Abstract
Among metamagnetic materials, FeRh alloys are technologically appealing due to their uncommon antiferromagnetic-to-ferromagnetic metamagnetic transition which occurs at a temperature T* just above room temperature. Here, a controlled increase of T* (ΔT* ∼ 20 °C) is induced in pre-selected regions of FeRh films via mechanical strain nanopatterning. Compressive stresses generated at the vicinity of pre-defined nanoindentation imprints cause a local reduction of the FeRh crystallographic unit cell parameter, which leads to an increase of T* in these confined micro-/nanometric areas. This enhances the stability of the antiferromagnetic phase in these localized regions. Remarkably, generation of periodic arrays of nanopatterned features also allows modifying the overall magnetic and electric transport properties across large areas of the FeRh films. This approach is highly appealing for the design of new memory architectures or other AFM-spintronic devices.
New conceptsControl of the transition temperature (T*) in metamagnetic materials, such as the transition from antiferromagnetic to ferromagnetic states in FeRh, has been so far realized by means of different approaches: voltage-driven piezo-strain, application of strong magnetic fields (spin–flip or spin-flop transitions) or chemical doping, amongst others. These methods typically affect the entire FeRh films, causing global changes in their magnetic properties. Here, a straightforward alternative concept, which allows for a large enhancement of the stability of the AFM phase both locally and globally, is presented. Nanoindentation patterning (i.e., localized generation of compressive mechanical stress in pre-selected micro- and nanoscale actuated regions) is shown to induce a significant shift of T* in these pre-defined areas of the FeRh films. This method results in an array of confined regions which exhibit an enhanced antiferromagnetic stability with respect to the adjacent non-stressed film. By properly tuning the heating conditions (and not far from room temperature) it is possible to obtain an array of antiferromagnetic dots embedded in a ferromagnetic matrix. The concept can be extrapolated to other materials displaying functional properties that are dependent on the crystallographic unit cell volume. Therefore, this method constitutes an interesting approach towards functional nanostructuration of physical properties, eventually breaking the light diffraction limits, and allowing for the implementation of novel micro-/nano-device architectures. |
Introduction
Nanopatterning of magnetic structures is an ubiquitous approach widely used in applications involving magnetic materials,1–4 particularly in storage media. Nanopatterning is also interesting for the basic understanding of effects such as exchange bias, current-induced magnetic switching and other spintronic phenomena.5–8 From the broad range of methods to perform nanopatterning, mechanical nanoimprinting, which uses local stress applied by means of a tip, is a convenient technique because, in spite of its simplicity, it allows generating structures eventually smaller than those of standard optical methods which cannot easily go below the light diffraction limit. Via mechanical nanopatterning, properties such as crystallinity,9,10 nanoparticle arrangement,11 ferroelectricity,12,13 electric transport13 or metal-insulator transitions,14 amongst others, can be controlled at the nanoscale. Remarkably, mechanical nanopatterning of non-ferromagnetic alloys can also be used to obtain nanomagnetic motifs (i.e., magnetic nanolithography).15–17FeRh in its α phase shows an antiferromagnetic (AFM)-to-ferromagnetic (FM) phase transition slightly above room temperature.18 This particular functionality makes FeRh interesting for magnetic and spintronic applications, such as heat-assisted recording,19–23 tunneling24 and AFM-based memory devices,25–27 magnetocalorics and barocalorics.28,29 This AFM–FM transition has been widely studied as well from a fundamental point of view.30–33 The temperature at which the AFM order disappears (metamagnetic transition temperature, T*) can be tailored by the application of external magnetic fields,34 changing composition/doping,35,36 electrochemical processes,37 hydrostatic pressure38 or biaxial strain imposed by the substrate.39–46 The two latter effects are related to the change of the FeRh unit cell across the transition, being the unit cell parameter smaller in the low temperature AFM phase than in the high temperature FM phase.47 Thus, when the FeRh unit cell is reduced by external stimuli, the AFM phase is stabilized and, consequently, T* increases.
In the present work, we use mechanical nanopatterning in FeRh films to induce, locally, a shift of T* towards higher temperatures. This is different from previous studies in which strain is induced in the entire FeRh film, often through application of voltage across an adjacent piezoelectric substrate.39–46 The local increase of T* is evidenced using results from photo-emission electron microscopy (PEEM). Finite element modelling reveals that the T* increase is not solely induced by the imposed nanoindentation stresses but also mediated by the mechanical properties of the substrate (MgO), which are transmitted to FeRh by epitaxial strain. Finally, by using Kerr magnetometry and electric transport characterization, we show that arrays of mechanically patterned structures can be used to selectively tune the average T* of large areas within in the FeRh films.
Results
Sample structural and magnetic properties and mechanical patterning
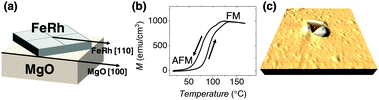
An epitaxial 55 nm FeRh film is grown on a MgO(001) substrate by RF sputtering (see Materials and methods in ESI†). The structural characterization (see Fig. S1 and S2, ESI†),48,49 reveals that the as-deposited film grows in the α phase and it has a slight tetragonal distortion [a = 2.98(1) Å and c = 2.99(1) Å lattice parameters] compared to its bulk value.47 The FeRh film grows epitaxially on the MgO substrate with a [100]FeRh(001)//[110]MgO(001) epitaxial relation. Namely, the FeRh pseudo-cube grows with a 45° rotation with respect to the MgO cubic structure, as sketched in Fig. 1(a).19The as-grown FeRh film exhibits the conventional magnetic properties of this alloy,22 where the temperature dependence of the magnetization, M(T), displays an abrupt transition from near zero magnetization at room temperature, in the AFM phase, to about 1000 emu cm−3 at high temperature, in the FM phase (Fig. 1(b)). As expected, the system shows thermal hysteresis,22 where the transition temperature (T*) during heating is 90 °C, whereas it is 80 °C upon cooling.
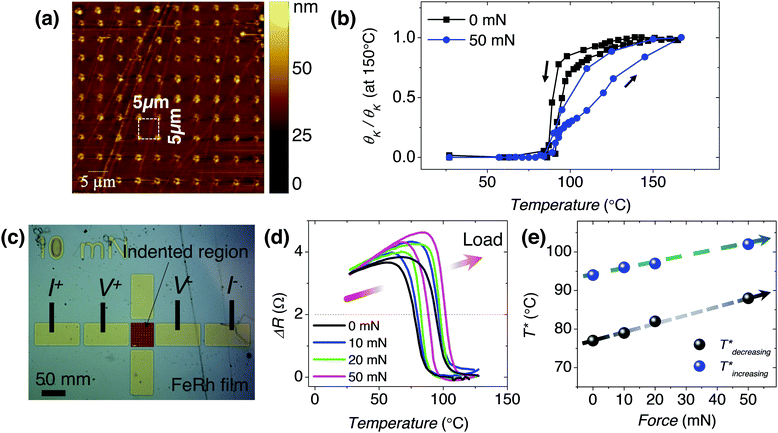
To locally adjust the magnetic properties of the FeRh films, we apply nanoindentations using different loads (see Materials and methods in ESI†). As it can be seen in Fig. 1(c), the indentations produce triangular-shaped depressions on the film and do not induce any important changes on the overall sample morphology except for the typical pile-up effect near the indentation imprint. The compression in the FeRh film produced by the mechanical indentation is expected to stabilize the AFM phase due to the smaller unit cell volume, resulting in a T* increase.
Local distribution of the AFM phase near the indented regions
In order to gain insight into the changes produced in the magnetic properties of the material near the indented region, we use X-ray Magnetic Circular Dichroism (XMCD) in combination with PEEM50 (XMCD-PEEM, Fig. 2(a); see Materials and methods in ESI†). In these experiments, black and white regions account for FM domains and grey regions can account for either AFM domains or domains with net magnetization perpendicular to the incident light.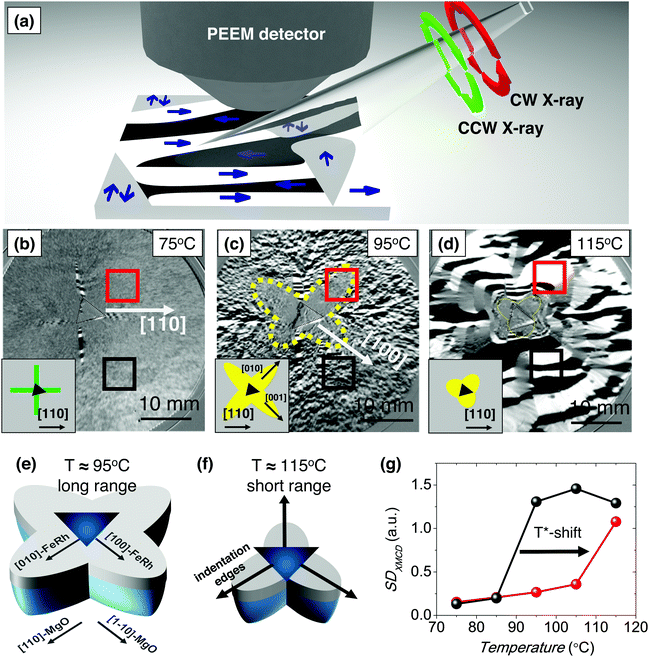 | ||
| Fig. 2 (a) Schematic representation of the experimental set-up for XMCD-PEEM experiments. The black and white areas account for domains with net magnetization along and opposite to the direction of the incident light, respectively. Grey regions correspond to either domains without net magnetization (in our case AFM domains), or domains with net magnetization perpendicular to the incident light. CCW and CW correspond to anticlockwise and clockwise X-ray light, respectively. (b)–(d) XMCD-PEEM magnetic domain images of the FeRh film region with a 300 mN indentation measured at 75 °C, 95 °C and 105 °C, respectively. Insets show schematic representations of the image symmetry. (e) and (f) Sketch of the AFM regions after indentation in the FeRh/MgO system, as deduced from the XMCD-PEEM characterization, at the indicated temperatures. (g) Magnetic contrast of the XMCD images (SDXMCD) of the regions enclosed in red (near indentation) and black (far from the indentation) in (b)–(d) and Fig. S8, ESI.† | ||
First, we focus on an indented region where the applied load force is 300 mN. This force is strong enough to ensure that the tip reached the MgO substrate (see Fig. S3, ESI†). Shown in Fig. 2(b)–(d) are the XMCD-PEEM images collected while heating at 75 °C, 95 °C, and 115 °C, respectively, where the dashed triangle encloses the indentation region (i.e., a 6.5 μm triangle for a 300 mN indentation). At low temperatures, in regions both “far” from (black square) and “near” (red square) the indentation, the magnetic contrast is negligible (grey contrast), indicating the absence of FM domains in both regions. The absence of FM domains is in agreement with the predominant AFM state of the sample at this temperature (Fig. 1(b)). Only starting at the vertexes of the triangular indentation and along the [110], [1−10], [−110], [−1110] FeRh-directions, needles of black/white domains, which account for FM regions, are found at 75 °C (Fig. 2(b)), schematically depicted in green in the inset of Fig. 2(b). This indicates that near these particular directions there is unit cell expansion, probably resulting from cracks in the film, favouring locally the FM phase, which results in a very confined reduction of T*. At intermediate temperatures (e.g., 95 °C, Fig. 2(c)), where the AFM-to-FM transition starts, black/white domains corresponding to FM regions are observed in areas far (black square) from the indentation. Conversely, near the indentation (red square) the contrast is virtually inexistent. These regions with lower contrast indicate the predominance of the AFM phase. Therefore, in these particular regions, the transition to the FM state has not yet started at this temperature. The gradual evolution of the magnetic contrast (domain pattern) with increasing temperature is shown in Video S1, ESI.† Indentations with 5 mN, 10 mN and 20 mN display similar features, although the AFM areas at high temperature are smaller (see Fig. S4, ESI†). Importantly, in all cases, the grey regions have 4-fold symmetry and they are mainly confined along the [100], [010], [−100] and [0−10] FeRh-directions, schematically depicted in yellow in the inset of Fig. 2(c). At high temperature (Fig. 2(d)), where the FM state should be predominant throughout the sample, large black/white domains corresponding to FM regions are found both far and near the indentation. Only very close to the indentation the contrast remains grey. In this case, one can infer that the grey region is a mixture of 4-fold with 3-fold symmetries along the directions normal to the sides of the triangular indentation, dictated by the indenter shape (dashed yellow line). The 3-fold symmetry is schematically depicted in yellow in the inset of Fig. 2(d).
The 4-fold shape of the grey region of Fig. 2(c) along the [100], [010], [−100] and [0−10] FeRh-directions is in agreement with the maximum compression of the {110} planes reported for MgO,51,52 as sketched in Fig. 2(e). Notably, according to the FeRh mechanical parameters,53 the maximum deformation of a stand-alone FeRh film is expected to be along the {110} FeRh planes, as demonstrated by finite-element calculations (see Fig. S5, ESI,† based on low-load indentation data54 of Fig. S6, ESI†). This is in contrast with our results, which show that the maximum deformation in FeRh is along the [100], [010], [−100] and [0−10]. This indicates that the mechanical properties of the FeRh itself do not play a crucial role in the overall behaviour; instead, it is the deformation of the MgO substrate and its propagation to the FeRh film what governs the shift in T*. Given the epitaxial growth of the FeRh layer on the MgO, the larger strain along the {110} MgO planes is transmitted to the {100} planes of the FeRh, originating the observed 4-fold symmetry (Fig. 2(e)). Nevertheless, the mechanical properties of the FeRh and the film interaction with the Berkovich indentation tip are relevant very close to the indentation as evidenced by the 3-fold symmetry of the remaining “grey domains” at high temperatures sketched in Fig. 2(f), in this case in agreement with the finite element simulations of the pure FeRh (Fig. S7, ESI†). In fact, very close to the indentation, T* is even higher than 115 °C (note the remaining grey contrast in Fig. 2(d)). Hence, the enhanced T* originates from a complex interplay of the mechanical properties of the film and the substrate. The AFM–FM transition in the non-indented regions takes place isotropically (see Fig. S4 and S8, ESI†), thus ruling out any contribution from the intrinsic crystalline directions in the anisotropic AFM–FM transition of indented regions (Fig. 2).
The evolution of the magnetic contrast of the XMCD images (SDXMCD; see Methods in ESI†) collected at several temperatures (see Fig. S8, ESI,† for the whole set of images) is plotted as a function of temperature in Fig. 2(g). The figure reveals that the SDXMCD value, which is indicative of the magnetization, increases at around T* = 90 °C for the region far from the indentation (black line), in agreement with the M(T) of the as-grown films (Fig. 1(b)). On the other hand, the SDXMCD for the region near the indentation increases at a higher temperature, T* = 110 °C (see Video S1, ESI†). Thus, the indentation-induced residual strain produces a clear 20 °C increase of the transition temperature.
Large-area effects for device functionalization
In order to understand the effects of indentation in larger areas (50 × 50 μm2) of the film, arrays of indentations (Fig. 3(a)) are studied by magneto-optic Kerr effect (MOKE) and electrical resistance. The temperature dependence of the Kerr rotation (proportional to M), θK(T), in the as-obtained film (black line in Fig. 3(b)) shows a similar temperature dependence as the M(T) measured by vibrating sample magnetometer (Fig. 1(b)), although the transition obtained by MOKE is more abrupt, probably due to the improved crystallinity of the sample surface (MOKE probes mainly the film top surface; ≈first tens of nm in depth) in this 50 × 50 μm2 region. As seen in Fig. 3(b), in the array of indentations (blue line), the transition occurs at a higher temperature and it is less abrupt. Note that the abruptness of the transition is reduced in the arrays due to the strain gradients surrounding each indentation imprint.Since the AFM-to-FM phase transition in FeRh films is accompanied by an important decrease (increase) of the electric resistance upon heating (cooling),34 we next study the transport properties of the indented FeRh (arrays with different maximum indentation loads of 0 mN, 10 mN, 20 mN and 50 mN) using the contact configuration shown in Fig. 3(c) (see Methods in ESI†). Similar to the magnetic measurements, the transition can be also clearly observed in the resistance dependence on temperature (Fig. 3(d)). Interestingly, the normalized resistance curves (ΔR) at different indentation loads (Fig. 3(d)) reveal a progressive increase of T*. This difference is more clearly seen in Fig. 3(e), where the T* for the cooling and heating branches is plotted as a function of the indentation load. Note that the increase of T* with indentation load is only about 10 °C (for the 50 mN region), whereas the XMCD-PEEM and MOKE characterization revealed changes in T* of at least 20 °C. This can be understood by the higher surface sensitivity of XMCD-PEEM and MOKE with respect to transport measurements. This suggests that the temperature shift is larger at the surface than in the bulk of the film, coherent with previous findings of different behaviour of the bulk and the surface of FeRh films.55 Thus, although the FM domains are large (micron size, Fig. 2(d)), they are expected to be inhomogeneous along the thickness, as shown by Gatel et al.55 for equivalent FeRh thin films. This inhomogeneity can be easily solved by reducing the film thickness. Note also that the width of the transition increases in the MOKE experiments, whereas in the transport experiments it is roughly constant, with a slight decrease. The higher surface sensitivity of MOKE experiments results in their higher sensitivity to strain gradients produced by indentation, which induce an increase in the width of the transition, whereas the transition width variations in transport experiments are not significant and probably masked by small lateral inhomogeneity in the film composition.56
Conclusions
We demonstrate the possibility to locally modify the AFM-to-FM transition temperature in FeRh films by means of nanoindentation. We show that nanoindentation stresses induce compressive strains (mediated by the underlying compression of the MgO substrate), which cause a shift of T* by at least 20 °C. In addition, we show that the developed methodology can be used to globally increase T*, across large areas, as evidenced by Kerr magnetometry and transport measurements. Interestingly, this approach can be potentially extrapolated to other metamagnetic materials or, in general, to any system in which a magnetic order phase transition is accompanied by a structural transformation. The T* increase by nanoindentation is, at first instance, an irreversible process, however, annealing or other procedures could, at least partially, recover the initial state.The presented results are relevant for memory devices based on the lateral co-existence of contiguous antiferromagnetic-ferromagnetic regions, or for devices based on AFM materials, such as those where magnetic information must be locally stored in an AFM phase.
Author contributions
I. F and J. S. planned the study. M. F., A. Q., L. A. and I. F. carried out the XMCD-PEEM experiments. A. Q., E. M. and I. F. carried out the MOKE experiments under assistance of J. N. E. C. and E. M. carried out the nanoindentations. O. V., C. G.-O. and C. F. carried out the X-ray characterization experiments. I. F. wrote the manuscript with input from M. F., E. M., J. N. and J. S.Data and materials availability
Data and materials are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Dr Patxi López-Barberá is acknowledged for his assistance with the MOKE experiments. Vicente García-Juez from Real Casa de la Moneda – Fábrica Nacional de Moneda y Timbre is acknowledged for his scientific advice. Dr Florencio Sánchez is acknowledged for the growth of the samples. Dr Bernat Bozzo is acknowledged for the electric transport characterization. ALBA synchrotron is acknowledged for the provision of beamtime at the MSPD (proposal number 2017092412) and CIRCE (proposal numbers 2017092462 and 2018022818) beamlines. Financial support from the Spanish Ministry of Economy and Competitiveness, through the “Severo Ochoa” Programme for Centres of Excellence in R&D (SEV-2015-0496 and SEV-2017-0706) and the MAT2017-85232-R, RTI2018-095303-B-C53. MAT2014-56063-C2-1-R, MAT2017-86357-C3-1-R (and associated FEDER) and MAT2015-73839-JIN projects, the Generalitat de Catalunya (2014 SGR 734 and 2017 SGR 292), AGAUR (2018 LLAV 00032 and 2019 LLAV 00050) and the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 665919 is acknowledged. This work was supported by the European Research Council under the SPIN-PORICS 2014-Consolidator Grant, Agreement No. 648454 and the MAGIC-SWITCH 2019-Proof of Concept Grant, Agreement No. 875018. ICN2 is funded by the CERCA Programme/Generalitat de Catalunya. I. F. acknowledges his RyC contract RYC-2017-22531. E. C. acknowledges the partial financial support from the National Science Centre of Poland (NCN) by the PRELUDIUM project UMO-2015/17/N/ST5/01988 and the SONATA Project No. UMO-2016/23/D/ST3/02121. We acknowledge support of the publication fee by the CSIC Open Access Publication Support Initiative through its Unit of Information Resources for Research (URICI).Notes and references
- J. I. Martín, J. Nogues, K. Liu, J. L. Vicent and I. K. Schuller, J. Magn. Magn. Mater., 2003, 256, 449–501 CrossRef.
- A. Kosiorek, W. Kandulski, H. Glaczynska and M. Giersig, Small, 2005, 1, 439–444 CrossRef CAS PubMed.
- J. R. Jeong, S. Kim, S. H. Kim, J. Bland, S. C. Shin and S. M. Yang, Small, 2007, 3, 1529–1533 CrossRef CAS PubMed.
- J. Fassbender and J. McCord, J. Magn. Magn. Mater., 2008, 320, 579–596 CrossRef CAS.
- P. Grünberg, J. Magn. Magn. Mater., 2001, 226, 1688–1693 CrossRef.
- S. Wolf, D. Awschalom, R. Buhrman, J. Daughton, S. Von Molnar, M. Roukes, A. Y. Chtchelkanova and D. Treger, Science, 2001, 294, 1488–1495 CrossRef CAS PubMed.
- J. Nogués, J. Sort, V. Langlais, V. Skumryev, S. Suriñach, J. Muñoz and M. Baró, Phys. Rep., 2005, 422, 65–117 CrossRef.
- S. S. Parkin, M. Hayashi and L. Thomas, Science, 2008, 320, 190–194 CrossRef CAS PubMed.
- J.-J. Kim, Y. Choi, S. Suresh and A. Argon, Science, 2002, 295, 654–657 CAS.
- J. Fornell, E. Rossinyol, S. Surinach, M. D. Baró, W. H. Li and J. Sort, Scr. Mater., 2010, 62, 13–16 CrossRef CAS.
- J. A. Lefever, T. D. Jacobs, Q. Tam, J. L. Hor, Y.-R. Huang, D. Lee and R. W. Carpick, Nano Lett., 2016, 16, 2455–2462 CrossRef CAS PubMed.
- H. Lu, C.-W. Bark, D. E. De Los Ojos, J. Alcala, C.-B. Eom, G. Catalan and A. Gruverman, Science, 2012, 336, 59–61 CrossRef CAS PubMed.
- A. Gómez, J. M. Vila-Fungueiriño, R. Moalla, G. Saint-Girons, J. Gázquez, M. Varela, R. Bachelet, M. Gich, F. Rivadulla and A. Carretero-Genevrier, Small, 2017, 13, 1701614 CrossRef PubMed.
- Y. Kim, S. J. Kelly, A. Morozovska, E. K. Rahani, E. Strelcov, E. Eliseev, S. Jesse, M. D. Biegalski, N. Balke and N. Benedek, Nano Lett., 2013, 13, 4068–4074 CrossRef CAS PubMed.
- J. Sort, A. Concustell, E. Menéndez, S. Suriñach, K. V. Rao, S. C. Deevi, M. D. Baró and J. Nogués, Adv. Mater., 2006, 18, 1717–1720 CrossRef CAS.
- J. Sort, A. Concustell, E. Menéndez, S. Suriñach, M. Baró, J. Farran and J. Nogués, Appl. Phys. Lett., 2006, 89, 032509 CrossRef.
- J. Sort, L. F. Bonavina, A. Varea, C. Souza, W. J. Botta, C. S. Kiminami, C. Bolfarini, S. Surinach, M. D. Baró and J. Nogués, Small, 2010, 6, 1543–1549 CrossRef CAS PubMed.
- J. Kouvel and C. Hartelius, J. Appl. Phys., 1962, 33, 1343–1344 CrossRef CAS.
- J.-U. Thiele, S. Maat and E. E. Fullerton, Appl. Phys. Lett., 2003, 82, 2859–2861 CrossRef CAS.
- J.-U. Thiele, S. Maat, J. L. Robertson and E. E. Fullerton, IEEE Trans. Magn., 2004, 40, 2537–2542 CrossRef CAS.
- G. Ju, J. Hohlfeld, B. Bergman, R. J. van de Veerdonk, O. N. Mryasov, J.-Y. Kim, X. Wu, D. Weller and B. Koopmans, Phys. Rev. Lett., 2004, 93, 197403 CrossRef PubMed.
- S. Maat, J.-U. Thiele and E. E. Fullerton, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 214432 CrossRef.
- E. E. Fullerton, S. Maat and J.-U. Thiele, US Pat., 7372116 B2, 2008 Search PubMed.
- X. Chen, J. Feng, Z. Wang, J. Zhang, X. Zhong, C. Song, L. Jin, B. Zhang, F. Li and M. Jiang, Nat. Commun., 2017, 8, 449 CrossRef CAS PubMed.
- X. Marti, I. Fina, C. Frontera, J. Liu, P. Wadley, Q. He, R. J. Paull, J. D. Clarkson, J. Kudrnovsky, I. Turek, J. Kunes, D. Yi, J.-H. Chu, C. T. Nelson, L. You, E. Arenholz, S. Salahuddin, J. Fontcuberta, T. Jungwirth and R. Ramesh, Nat. Mater., 2014, 13, 367–374 CrossRef CAS PubMed.
- T. Moriyama, N. Matsuzaki, K.-J. Kim, I. Suzuki, T. Taniyama and T. Ono, Appl. Phys. Lett., 2015, 107, 122403 CrossRef.
- I. Fina, N. Dix, E. Menéndez, A. Crespi, M. Foerster, L. Aballe, F. Sánchez and J. Fontcuberta, ACS Appl. Mater. Interfaces, 2020, 12, 15389–15395 CrossRef CAS PubMed.
- Y. Liu, L. C. Phillips, R. Mattana, M. Bibes, A. Barthélémy and B. Dkhil, Nat. Commun., 2016, 7, 11614 CrossRef CAS PubMed.
- Q. Hu, J. Li, C. Wang, Z. Zhou, Q. Cao, T. Zhou, D. Wang and Y. Du, Appl. Phys. Lett., 2017, 110, 222408 CrossRef.
- V. Uhlíř, J. A. Arregi and E. E. Fullerton, Nat. Commun., 2016, 7, 13113 CrossRef PubMed.
- T. Seifert, U. Martens, S. Günther, M. A. W. Schoen, F. Radu, X. Z. Chen, I. Lucas, R. Ramos, M. H. Aguirre, P. A. Algarabel, A. Anadón, H. S. Körner, J. Walowski, C. Back, M. R. Ibarra, L. Morellón, E. Saitoh, M. Wolf, C. Song, K. Uchida, M. Münzenberg, I. Radu and T. Kampfrath, Spin, 2017, 7, 1740010 CrossRef CAS.
- S. Bennett, A. Herklotz, C. Cress, A. Ievlev, C. Rouleau, I. Mazin and V. Lauter, Mater. Res. Lett., 2018, 6, 106–112 CrossRef CAS.
- Y. Wang, M. M. Decker, T. N. Meier, X. Chen, C. Song, T. Grünbaum, W. Zhao, J. Zhang, L. Chen and C. H. Back, Nat. Commun., 2020, 11, 275 CrossRef CAS PubMed.
- L. Lewis, C. Marrows and S. Langridge, J. Phys. D: Appl. Phys., 2016, 49, 323002 CrossRef.
- N. Baranov and E. Barabanova, J. Alloys Compd., 1995, 219, 139–148 CrossRef CAS.
- W. Lu, J. Fan and B. Yan, Sci. China: Phys., Mech. Astron., 2011, 54, 1223–1226 CAS.
- M. Jiang, X. Chen, X. Zhou, B. Cui, Y. Yan, H. Wu, F. Pan and C. Song, Appl. Phys. Lett., 2016, 108, 202404 CrossRef.
- R. Wayne, Phys. Rev., 1968, 170, 523 CrossRef CAS.
- R. Cherifi, V. Ivanovskaya, L. Phillips, A. Zobelli, I. Infante, E. Jacquet, V. Garcia, S. Fusil, P. Briddon and N. Guiblin, Nat. Mater., 2014, 13, 345 CrossRef CAS PubMed.
- Y. Lee, Z. Liu, J. Heron, J. Clarkson, J. Hong, C. Ko, M. Biegalski, U. Aschauer, S.-L. Hsu and M. Nowakowski, Nat. Commun., 2015, 6, 5959 CrossRef CAS PubMed.
- Z. Liu, L. Li, Z. Gai, J. Clarkson, S. Hsu, A. Wong, L. Fan, M.-W. Lin, C. Rouleau and T. Ward, Phys. Rev. Lett., 2016, 116, 97203 CrossRef CAS PubMed.
- M. Loving, R. Barua, C. Le Graët, C. Kinane, D. Heiman, S. Langridge, C. Marrows and L. Lewis, J. Phys. D: Appl. Phys., 2017, 51, 024003 CrossRef.
- J. Clarkson, I. Fina, Z. Liu, Y. Lee, J. Kim, C. Frontera, K. Cordero, S. Wisotzki, F. Sanchez and J. Sort, Sci. Rep., 2017, 7, 15460 CrossRef CAS PubMed.
- I. Fina, A. Quintana, J. Padilla-Pantoja, X. Marti, F. Macia, F. Sanchez, M. Foerster, L. Aballe, J. Fontcuberta and J. Sort, ACS Appl. Mater. Interfaces, 2017, 9, 15577–15582 CrossRef CAS PubMed.
- I. Fina, A. Quintana, X. Marti, F. Sanchez, M. Foerster, L. Aballe, J. Sort and J. Fontcuberta, Appl. Phys. Lett., 2018, 113, 152901 CrossRef.
- I. Fina and J. Fontcuberta, J. Phys. D: Appl. Phys., 2019, 53, 023002 CrossRef.
- A. Zakharov, A. Kadomtseva, R. Levitin and E. Ponyatovskii, Sov. Phys. JETP, 1964, 19, 1348–1353 Search PubMed.
- F. Fauth, I. Peral, C. Popescu and M. Knapp, Powder Diffr., 2013, 28, S360–S370 CrossRef CAS.
- O. Vallcorba and J. Rius, J. Appl. Crystallogr., 2019, 52, 478 CrossRef CAS.
- L. Aballe, M. Foerster, E. Pellegrin, J. Nicolas and S. Ferrer, J. Synchrotron Radiat., 2015, 22, 745–752 CrossRef CAS PubMed.
- J. Amodeo, S. Merkel, C. Tromas, P. Carrez, S. Korte-Kerzel, P. Cordier and J. Chevalier, Crystals, 2018, 8, 240 CrossRef.
- T. Nazarova and M. Nazarov, Philos. Mag. A, 1996, 74, 1311–1318 CAS.
- U. Aschauer, R. Braddell, S. A. Brechbühl, P. M. Derlet and N. A. Spaldin, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 014109 CrossRef.
- E. Coy, L. Yate, Z. Kabacińska, M. Jancelewicz, S. Jurga and I. Iatsunskyi, Mater. Des., 2016, 111, 584–591 CrossRef CAS.
- C. Gatel, B. Warot-Fonrose, N. Biziere, L. Rodríguez, D. Reyes, R. Cours, M. Castiella and M.-J. Casanove, Nat. Commun., 2017, 8, 15703 CrossRef CAS PubMed.
- V. Saidl, M. Brajer, L. Horak, H. Reichlova, K. Vyborny, M. Veis, T. Janda, F. Trojanek, M. Marysko, I. Fina, X. Marti, T. Jungwirth and P. Nemec, New J. Phys., 2016, 18, 083017 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Supplementary materials includes materials and methods and Fig. S1–S8. Supplementary materials Video S1 corresponds to direct PEEM image at Fe L3 absorption edge at ca. 707 eV while increasing temperature to the video was recorded on the same region shown in Fig. 2. The temperature ranges from 85 °C and 115 °C. Topographic contribution has not been subtracted. See DOI: 10.1039/d0mh00601g |
| This journal is © The Royal Society of Chemistry 2020 |