Open Access Article
Open Access ArticleTemperature dependence of the spectral line-width of charge-transfer state emission in organic solar cells; static vs. dynamic disorder†
Kristofer
Tvingstedt
 *a,
Johannes
Benduhn
*a,
Johannes
Benduhn
 b and
Koen
Vandewal
b and
Koen
Vandewal
 c
c
aExperimental Physics VI, Julius-Maximilian University of Würzburg, Am Hubland, 97074 Würzburg, Germany. E-mail: ktvingstedt@physik.uni-wuerzburg.de
bDresden Integrated Center for Applied Physics and Photonic Materials (IAPP) and Institute for Applied Physics, Technische Universität Dresden, Nöthnitzer Str. 61, 01187 Dresden, Germany
cInstitute for Materials Research (IMO-IMOMEC), Hasselt University, Wetenschapspark 1, 3590 Diepenbeek, Belgium
First published on 18th May 2020
Abstract
The origin of energetic disorder in organic semiconductors and its impact on opto-electronic properties remains a topic of intense controversy. Particularly the disorder at electron donor–acceptor interfaces for organic photovoltaics is pivotal to understand as it is expected to affect photo-carrier generation, recombination and consequently device efficiency parameters. In this work we evaluate the temperature dependence of the line-shape of the photoluminescence (PL) and electroluminescence (EL) spectra of small molecule:fullerene blend devices, with the ambition to disentangle dynamic and static disorder contributions. The EL emission spectra are dominated by charge-transfer (CT) state emission and are confirmed to be of Gaussian character and almost completely voltage independent. More importantly, a strong line-width narrowing is persistently observed upon cooling, down to a certain material specific low temperature, below which the line-width remains constant. It is consequently clear that the main portion of the line-width measured at operating conditions of room temperature or higher, is originating from thermally activated, or dynamic, disorder. The observed temperature dependence of the high-energy emission tail can be fully described by taking into account high and low frequency molecular vibrational modes, without having to rely on static disorder. The presence of low frequency molecular modes with large Huang–Rhys factors results in a Gaussian line-shape, which is additionally broadened at high temperature by thermal population of high frequency intra-molecular modes. We therefore cast strong doubts regarding the commonly used assumption that single temperature optical measurements of absorption or emission tails are able to provide meaningful information regarding the shape of a static density of states tail.
New conceptsAbsorption and emission tails of semiconducting materials are often considered a probe of energetic disorder. For photovoltaic materials, a broad energetic distribution of the density of states limits both open-circuit voltage and charge transport properties. In organic semiconductors and their blends, the origin of absorption and emission tails and their relation to the density of states is however still unclear. As the high-energy emission tail is often easier to measure than the absorption tail, we here perform a highly sensitive study of the temperature dependence of the emission spectra of a multitude of organic solar cells. Our main ambition is to explain and disentangle the contribution from static disorder (inhomogeneous) and vibrational (dynamic or homogeneous) broadening. Our measured emission spectra are dominated by charge-transfer-state emission, and we persistently observe a pronounced line-width narrowing upon cooling, down to a certain material specific low temperature below which the line-width remains constant. We rationalize these experimental observations with a Franck–Condon vibrational picture without having to account for any contribution from static disorder. We therefore also cast strong doubts regarding the now commonly used assumption that single temperature optical measurements provides meaningful information regarding the shape of a static density of states tail. |
1. Introduction
Charge carrier generation and recombination at donor–acceptor interfaces in organic solar cells (OPVs) are now well known to involve charge-transfer states. These intermolecular electronic states have been quite well characterized and are recognized to lead to additional weak absorption and emission features below the optical gaps of the individual donor and acceptor material constituting the blend. However, a pronounced riddle lies unresolved on the correct assignment of the true origin of the width of the absorption tail and the, by reciprocity relations related,1 corresponding spectral line-width of the high-energy emission tail. Broad low-energy absorption tails and consequently broad high-energy tails in the emission spectra, as well as large Stokes shifts, are always undesired properties for a solar cell to possess, as they are a sign of a large energetic disorder, detrimental for charge transport, recombination and open-circuit voltage. However, the microscopic origin of the absorption- and emission-tails in most solar cells, including OPVs, is actually not clear. Earlier measurements and models on a multitude of different materials have often demonstrated exponential absorption tails with slopes usually referred to as the Urbach edge with an associated Urbach energy (EU(T)) or Urbach slope (σU). Such tails are fitted by the following expression: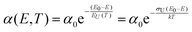 | (1) |
| EU(T) = EstatU(0) + EdynU(T) | (2) |
A direct consequence of purely static localized exponential tail state distribution is that the EL emission peak must10,11 display a pronounced voltage dependence, as a direct consequence of the fact that upon increasing carrier concentration, higher localized energy states within the exponential DOS are filled. However, Gong et al.12 showed that this did not really seem to be the case for a majority of OPV cells evaluated. Hörmann et al. recently showed noticeable bias dependent EL peak shifts in metaloxide:organic solar cells, and has argued that its origin could both be due to tail state filling13 but could also be assigned to a Stark effect14 (internal field dependence of polarizable molecules).
Contrary to a picture where static disorder dominates, we suggested earlier15 that the absorption tail and the corresponding emission line-width of organic solar cells can be quite well described in the framework of classical molecular Marcus theory. In this picture, the observed (often Gaussian) spectral shape of both the emission and the absorption tails are instead exclusively described by a reorganization energy (λ) associated with the interfacial charge-transfer state. Instead of absorption/emission being ruled by the temperature independent shape (tail) of a static DOS, optical transitions are in this model determined only by the vibrational wave-function overlap between thermally populated vibrational ground/excited state levels and any vibrational excited/ground state level, respectively. This type of broadening related to vibrations is therefore referred to as dynamic disorder broadening.
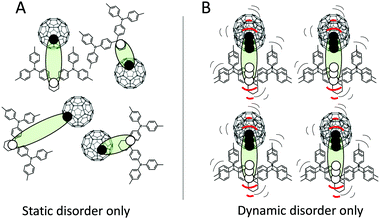
Fig. 1 outlines a sketch of the two extreme cases of pure static disorder and pure dynamic disorder of charge-transfer excitons at the interface between donor and acceptor molecules. In general, both static and dynamic contributions to the total absorption tail and the emission line-width are to be expected, and combinations of the two cases in Fig. 1 should hence be anticipated. If a static Gaussian disorder is described simply by a temperature independent energetic variance σS and the dynamic disorder parameter described by a temperature dependent σD(T), the sum of these two simultaneous contributions add up to the total variance σT quadratically:
| σT2(T) = σS2 + σD2(T) | (3) |
| σD2(T) = 2λkT | (4) |
First attempts to disentangle the contributions of σS and σD were presented in the work of Burke et al.,21 who found that the CT-state absorption tail of regio-random P3HT:PCBM could be described using a σS ≈ 104 meV and a σD of 48 meV at 300 K. Further recent analysis of EQE tails combined with theoretical work suggested23 on the contrary that the contribution from static disorder however did not appear to constitute a major part of the tail width in small molecule:C60 samples. It was also concluded from DFT simulations that low frequency intra-molecular vibrations on donor and acceptor molecules are the main contributors to the CT-state absorption tails. Very recently, Kahle et al.24 however questioned this description and pointed out that a complete quantum mechanical Frank–Condon (F–C) picture (or Levitch–Jortner formalism25) should be employed, taking into account both low and high frequency vibrations. In line with Burke's EQE measurements, the static temperature independent energetic disorder of their studied system (MeLPPP:PCBM60) was also concluded to dominate the spectral line-width of emission. As only weak alteration of the CT emission spectra was observed over a large temperature range, the assigned energetic disorder amounted to σS = 67 meV and the 300 K dynamic disorder σD = 45 meV. This renders the static line-width contribution according to eqn (3) more than twice that of the dynamic 300 K contribution. We notice that the general temperature independence of their measured CT emission line-width seems to be in accordance with previous PL CT measurements by Jarzab26 on PCPDTBT:PCBM, but in strong contrast to the work by Riisnes27 on F8T2:PCBM. Along with Burke et al., it was thus strongly emphasized that the contribution from static energetic disorder (inhomogeneous broadening) should not be neglected. Although we fully agree with the interpretations made, and the need of a complete F–C model, we will here demonstrate for a series of small molecule:fullerene and polymer:fullerene samples that the relative contributions of σS and σD as determined from optical measurements, does not really appear to be represented by the results provided by neither Kahle et al.,24 Street et al.9 nor Burke et al.21
As the energetic distribution of the emission is reciprocal with the absorption tail, it allows straightforward access to the relevant properties ruling the sought-after optical transitions. Herein we will therefore focus our study on (intermolecular) CT-state emission and show, for a multitude of different organic bulk heterojunction PV systems that the dominant part of the spectral line-width does in fact not appear to be subjugated to static energetic disorder. We instead find a clearly temperature dependent emission line-width defined by vibrational modes of the bulk heterojunction molecules. We first show that our T dependent observations can be quite well described by a system governed by low energy vibrations (<20 meV). A more complete description however requires a full quantum mechanical treatment that accounts also for combinations of both low and high-energy vibrational modes. Our results therefore cast strong doubt on the common practice to extract a static DOS from optical tail measurements.
2. Results
Before presenting experimental results and interpreting temperature dependent emission spectral measurements, we want to make a note on the effect of thin film optical interference. As recently pointed out by List et al.,28 thin film optical interference effects lead to a wavelength dependent light outcoupling efficiency, which can disrupt the spectral shape as well as the peak position of emission, complicating the assignment of the sought after dependence of internal energetic transitions. The absolute values of peak positions as well as line-widths are thus expected to be slightly inaccurate according to the vindicated claims by List et al., but, as optical interference and outcoupling efficiency is not expected to be temperature dependent, the overall measured and presented temperature-dependence in this work is expected to preserve the true behaviour of the internal transitions. Although we cannot fully rule out the combined effect of EL emission-zone shifts and potential altered out-coupling efficiency with temperature, we deem the voltage independence of the spectra from devices and the overall similar behavior of the EL spectra of devices and PL spectra of films (vide infra) a strong gauge against this effect.We start by a brief recapitulation of charge-transfer state emission in relation to the excitonic emission of the pure organic material constituents in OPV blends. Fig. 2 shows an archetypal example of the relationship between the emission of two OPV blends and the two materials constituting these blends, in this case the prior OPV working horses MDMO-PPV:PCBM60 and PCDTBT:PCBM70. In line with a majority of other (later and better) OPV cells, the pure acceptor peaks are redshifted with respect to the pure donors, and the CT-state peaks (from the blends) are further redshifted into the NIR region.
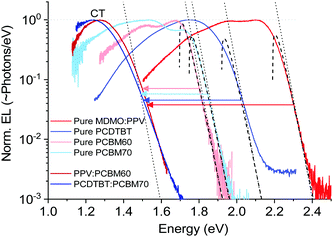 | ||
| Fig. 2 Normalized electroluminescence spectra of some classical pure OPV materials and blends on logarithmic scale, emphasizing the varying slope of the high-energy tail. Dashed lines are fits to the well-known relation in eqn (5), whereas the dotted lines are accounting only for the exponential part of the same equation. | ||
The important feature worth highlighting in Fig. 2 is the overall slope of the high-energy tail of the emission peaks, which represents the main studied parameter of this work. Three of the pure materials all show quite steep slopes that can be fairly well approximated by a simple exponential function over more than two decades of measured data. The exponential shape is here fitted by a simple Boltzmann population of a three dimensional square-root shaped DOS whose band to band distribution of high energy emission is regularly given by:29,30
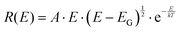 | (5) |
2.1. Temperature dependence of neat C60 photoluminescence
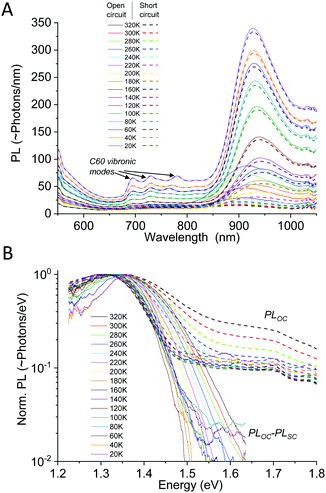
As a counterexample to the thermal behavior of interfacial CT-state line-widths, we proceed by showing the highly structured spectra of pure C60, demonstrating archetypal and assignable high-energy (intra-molecular) organic vibronic progressions. The pure Buckminster fullerene molecule has been intensively studied since it was first31 observed. A plethora of prior studies32–35 has already dealt with the assignment of its temperature dependent spectral features, although the conclusions have varied somewhat throughout the decades. It is by now however well recognized that peak narrowing always occur upon cooling C60 films or crystals, whereas the reproducibility of the energetic position of these peaks have been somewhat poorer. It has later been settled that even within an individual film, there is often a large spectral variability and accordingly, site-specific molecular packing appear to play a non-negligible role in spectral peak distribution. Even so, the C60 fullerene represents an archetypal molecule that always displays very characteristic molecular bond stretching vibronic features when cooled. To put the ensuing measurement of CT-state emission line-width in perspective to what is known for the temperature dependence of emission of pure organic materials,36–38 we in Fig. 3A present the case of C60 photoluminescence (PL) and line-width narrowing behavior upon cooling. Fig. 3B plots the transition moment squared (determining the spectra in 3A) obtained by39 dividing the measured spectra by E3. This slightly altered energetic distribution properly displays the low temperature resolved vibronic progression from transitions involving at least three clearly identifiable vibrating modes. We can compare our data with the intra-molecular vibrational modes reported by Menéndez and Page35 and conclude that the large 182 meV http://www.public.asu.edu/~cosmen/C60_vibrations/Mode_gifs/ag2.htm mode is easily identified. We also identify intermediate and as well as lower energy vibrational modes in the C60 spectra. These could be the http://www.public.asu.edu/~cosmen/C60_vibrations/Mode_gifs/hg2.htm and the http://www.public.asu.edu/~cosmen/C60_vibrations/Mode_gifs/hg1.htm mode respectively, but their values differs marginally from the stated values. The low temperature spectra in Fig. 3B accordingly shows the case of a material whose transition moment is very rich in features and shaped by both higher and lower frequency vibrational modes.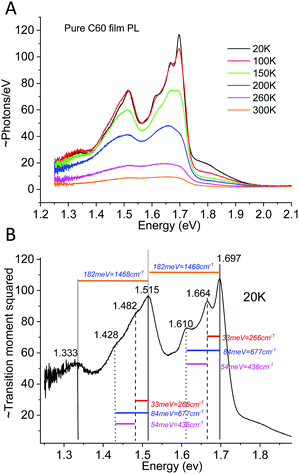 | ||
| Fig. 3 (A) Temperature dependent PL emission (photon flux per eV) from pure films of C60. (B) 20 K spectra divided by E3 rendering the relevant distribution proportional to the transition moment squared. The stiff intra-molecular bond stretching completely governs the vibrational progression35 of the spectra, whose dominant vibrational energies are designated. | ||
2.2. Temperature dependence of the CT-state emission line-width
Measuring the correct temperature of samples inside a cryostat may seem easy but is actually not so straightforward when the carrier concentration needs to be pronouncedly out of equilibrium to generate a detectable radiative recombination rate. Accordingly, our efforts to minimize the effects of sample Joule heating due to optical or electrical input power are summarized in the ESI.† There, we also show in Fig. S1 and S2 (ESI†) the voltage dependence of the charge-transfer state electroluminescence spectra and observe, in accordance with Gong12et al., no noticeable peak shift with increased injection. Although these results stand as an indication that static disorder does not seem to dictate the emission, the solid proof of the pudding can only be found in detailed and accurate temperature dependent measurements of the spectral line-width.To not make any initial physical presumptions regarding the origin of the measured spectral line-width and its temperature dependence, we here first choose to fit the reduced CT-state PL spectra simply with a Gaussian distribution function:
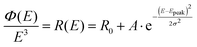 | (6) |
In the classical Marcus description of CT-state emission line-widths, the variance σ2 comprises only the dynamic contribution that corresponds to σD2 = 2kTλ (eqn (4)). The obtained Gaussian variance σ2 of the line-width is here therefore always normalized to 2k and plotted in Fig. 5, which allows a direct assessment of the reorganization energy λ by simply dividing with the temperature that the spectra was measured at. The obtained values for λ are shown in the inset of Fig. 5. As the measured spectra are still not 100% perfect Gaussians, the determined variance (and λ) is to a certain extent also depending on which energy range is selected for the Gaussian fitting. An uncertainty of the variance is therefore included by evaluating a set of different energy ranges. The difficulty of correctly assigning the baseline value R0 in eqn (6) for the PL at VOC also highlights the benefit of evaluating the PLOC–PLSC spectra. Irrespective if we decide to evaluate the PL spectra at OC conditions (with a best attempt non-zero baseline R0) or the PLOC–PLSC difference spectra, it is obvious that the variance is strongly depending on temperature for T > 120 K. Here, a more linearly dependent Gaussian variance on temperature (or correspondingly a more temperature independent apparent reorganization energy) indicates that thermal line-width broadening appears to be governing, at least at elevated temperatures. The observed temperature trend in CT-state PL line-width is a thus a first gauge that the classical Marcus approximation, without having to take into account static disorder, appears to be valid at higher temperatures. At lower temperatures, a saturation of the variance is however identified, and the correspondingly determined apparent reorganization energies accordingly start to increase rapidly.
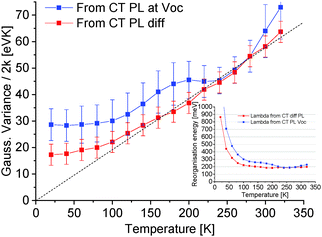 | ||
| Fig. 5 Normalized variance of Gaussian fits from the TAPC(6%):C60 CT-state dominated emission obtained from the PL at OC or the spectra obtained from evaluating the difference between PLOC–PLSC as shown in Fig. 4. Inset shows the corresponding apparent reorganization energies obtained by dividing the normalized Gaussian variance by the temperature. For the subtracted spectra, a fairly constant reorganization energy is found for T > 120 K. | ||
In addition to the complications of pure phase emission, a set of further concerns prevails when aiming to evaluate CT-state PL peaks, as stressed in the ESI.† Our main concern regarding CT-state PL as a probe of tail state disorder is that PL is generally not reciprocal with absorption or EQE measurements, meaning that it is not possible to relate the shape of the CT-state emission spectra to the absorption tails and vice versa by neither conventional van Roosbroek–Shockley1 nor Rau's45 electro-optical reciprocity relation. The redshifted42 peak of CT-state EL has, on the other hand, repeatedly and unwaveringly demonstrated adherence to reciprocity19,46 and we therefore chose to weigh our following studies on evaluating low injection electroluminescence spectra, as electrical injection better allows for population of low energy CT-states only.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PCBM70 cell in 1
PCBM70 cell in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 stoichiometric weight-ratio. More materials studied are presented in Fig. S3 of the ESI,† together with the molecular structures of all studied materials (Fig. S4, ESI†). The devices in Fig. 6A–C are evaluated at constant current (and thus with a linearly increasing voltage with temperature to sustain the set current). To certify that our observations is not influenced by the electric field47,48 which is determined by the applied voltage in the EL experiment, the PCDTBT:PCBM70 cell is instead shown at constant voltage, where accordingly the injection current decreases exponentially with reduced temperature. For this device, we moreover only apply 950 mV, noticeably lower than the energetic peak of emission at 1.23 eV. At this voltage, it was not possible to sustain a large enough injection current to provide any detectable emission for temperatures lower than 220 K (where merely 311 μA cm−2 was injected).
4 stoichiometric weight-ratio. More materials studied are presented in Fig. S3 of the ESI,† together with the molecular structures of all studied materials (Fig. S4, ESI†). The devices in Fig. 6A–C are evaluated at constant current (and thus with a linearly increasing voltage with temperature to sustain the set current). To certify that our observations is not influenced by the electric field47,48 which is determined by the applied voltage in the EL experiment, the PCDTBT:PCBM70 cell is instead shown at constant voltage, where accordingly the injection current decreases exponentially with reduced temperature. For this device, we moreover only apply 950 mV, noticeably lower than the energetic peak of emission at 1.23 eV. At this voltage, it was not possible to sustain a large enough injection current to provide any detectable emission for temperatures lower than 220 K (where merely 311 μA cm−2 was injected).
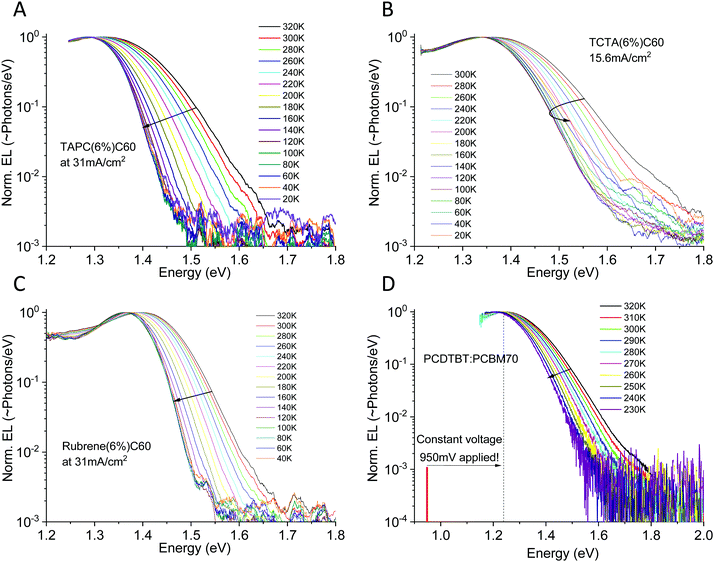 | ||
| Fig. 6 Electroluminescence spectra vs. temperature for four different organic solar cells. (A), (B) and (C) shows small molecule diluted donor devices based on TAPC:C60, TCTA:C60 and rubrene:C60 run at constant current, whereas (D) shows a polymer PCDTBT:PCBM70 device instead evaluated at constant voltage. All devices show noticeable CT-state line-width narrowing as well as a small, but detectable, EL peak red-shift upon cooling. More materials studied are presented in the ESI,† in Fig. S3. | ||
The benefit of EL as compared to PL is very obvious. As all electroluminescence spectra are now entirely dominated by interfacial low energy CT-state radiative recombination, we can easily cover a CT-state intensity range of 3–4 decades. All devices show a very broad EL-spectra apart from the rubrene:C60 device, which is noticeably narrower. For all devices, independent of being evaluated under constant current or constant voltage mode, we observe a substantial narrowing of the CT-state EL spectra upon cooling.
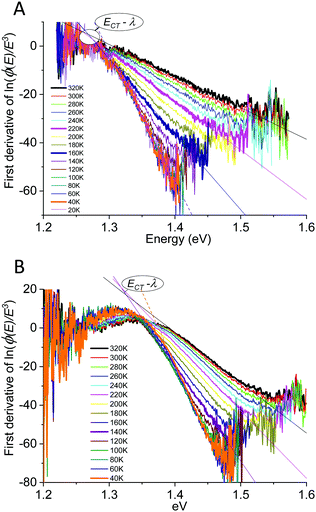
With EL allowing access to a larger logarithmic intensity range, a superior approach, compared to Gaussian functional fitting (as implemented above for PL) becomes straightforwardly available to determine the correct value of the Gaussian variance. If the line-shape is perfectly Gaussian, the first derivative of ln(ϕ(E)/E3) is equal to −(E − Epeak)/σ2 and the second derivative equates the inverse of the variance and is consequently a constant, fully independent of E;
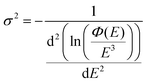 | (7) |
The straight lines covering a few hundreds of millivolts first quite clearly confirm that a majority of the measured line-shapes indeed are of true Gaussian shape. The lowest temperature data however also start to display noticeable deviations from linearity, as the line-widths are here no longer truly Gaussians (vide infra). The data in Fig. 6 and 7 accordingly provides the most decisive experimental quantification of the true CT-state line-width dependency on temperature. Following this method for the EL spectra of the other devices, allows us to in Fig. 8A present the 2k normalized variance from all evaluated data, together with the results previously found by Kahle et al. and Burke et al.Fig. 8B shows the corresponding total (or “apparent”21) reorganization energies (λ). From the EL data we can now clearly confirm a variance which is quite linear with temperature for T > 120 K for the TAPC and rubrene devices. The TCTA cell shows instead what seems to comprise two different linear regions, with a bending point at ∼200 K. At lower temperatures, a saturation of the variance is again clearly identified in all three samples, and the correspondingly determined apparent reorganization energies accordingly start to increase rapidly. We remind the reader though at these lowest temperatures the variance is no longer truly Gaussian. The observed high temperature trend in CT-state EL line-width thus appears to corroborate the classical Marcus approximation, without having to account for any noticeable static disorder, whereas the low temperature saturated line-width data implies something else. The pronounced line-width narrowing upon cooling is thus in quite strong experimental contrast to the recent observations by Kahle et al., Burke et al. and earlier Jarzab et al. These prior works observed no significant CT-state line-width narrowing, and thus concluded that static disorder contribution is strongly dictating the spectra (orange and purple dashed lines in graph). From our data, we note instead that when extrapolating the linear variance from the high temperature regime towards zero Kelvin, we are in fact not able to confirm any pronounced positive deviation from zero. According to eqn (3), this shows that the static disorder broadening does not seem to be of any significance to the measured line-width, at least in our fairly large set of evaluated samples. What is however also evident from Fig. 8A is the apparent negative values obtained when extrapolating the high temperature linear variance regime towards zero Kelvin, particularly perceptible for the TAPC and TCTA data (PCDTBT having a larger error margin). Having re-measured these spectra and re-evaluated the data carefully it is clear that this is not within the experimental error-margin, and truly that “negative static disorder” would be implied for those materials. This, at first highly puzzling observation, does therefore not at all seem to fit with the prior description of the simple summation of a static and a dynamic variance as suggested previously21 and offered above in eqn (3). As also the clearly observed saturation of the line-width variance at lower temperatures is not possible to reconcile with neither classical Marcus nor the simple summation of the two disorder contributions, we here therefore judge that a F–C treatment beyond the classical Marcus picture is utterly necessary. Below, we show that both the line-width saturation at low temperatures as well as the negative extrapolated values at zero K, from the high temperature regime, are indeed present in a full F–C treatment.
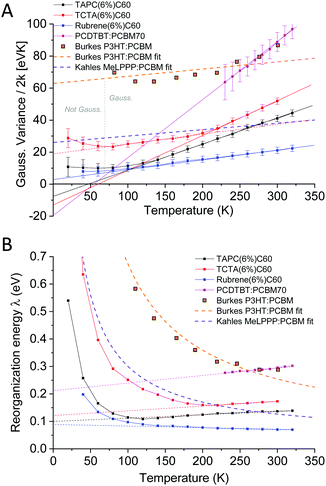 | ||
| Fig. 8 (A) Temperature dependence of the obtained Gaussian variance of the E3 reduced spectra from the electroluminescence in Fig. 6. (B) The corresponding (“apparent”) reorganization energy, determined by dividing the data in (A) with the temperature. Whereas Burke's EQE and Kahle's PL data showed strongly T-dependent reorganization energies (almost constant variance dominated by static disorder) our data do not indicate any pronounced contribution to line-width broadening from static disorder. | ||
2.3. Theory on line-width saturation and Keil's equation
In a full quantum mechanical treatment, the impact of harmonic vibrations with characteristic energy ħω on the emission spectrum is reflected in the following complete Franck–Condon formula:49,50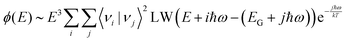 | (8) |
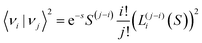 | (9) |
As outlined above in the analysis of the experimental data in Fig. 7, if the line-shape is perfectly Gaussian, the first derivative of the logarithm of the data should be a straight line. For the calculated high temperature curves in Fig. 9A and B, with S = 10 and ħω = 15 meV, this is indeed the case. However, at the lowest temperatures the line-shape deviates considerably from Gaussian and assumes instead the so-called Pekarian shape. For all temperatures, the second derivative is evaluated at E − Egap = 0 and is plotted as a function of temperature in Fig. 9C. As can be seen the obtained temperature dependence of both the first derivative and the variance display quite the same behavior as the measured ones presented in Fig. 7 and 8.
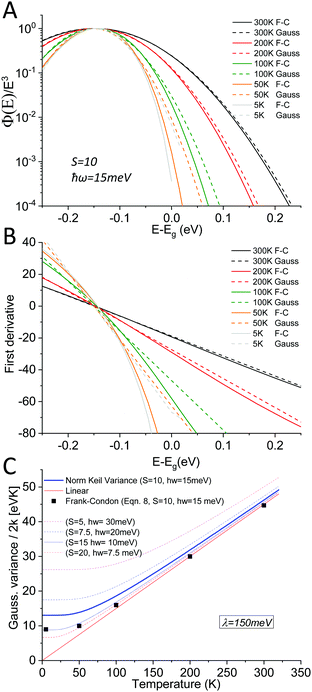 | ||
| Fig. 9 (A) shows eqn (8) plotted for S = 10, ħω = 15 meV (λ = 150 meV) at a set of selected temperatures. The dashed lines are Gaussians with their variance given by the Keil equation (eqn (9)). (B) shows the first derivate of the logarithm of the data in (A). The high temperatures are nicely represented by Gaussians (straight lines) whereas it is clear that the low T data are not. Note the similarity to the derivative of the experimental data in Fig. 7. (C) shows the corresponding variance from the calculated spectra, as obtained viaeqn (8) as well as from the semi-classical Keil equation (eqn (10)). | ||
As the variance shows a saturation at low temperature and a linear behavior at higher temperatures, its behavior corresponds rather well with the semi-classical formula for the variance σD2 of the line-shape as derived in the 1965 seminal work (eqn (3.11)) by Thomas Keil:51
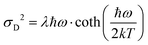 | (10) |
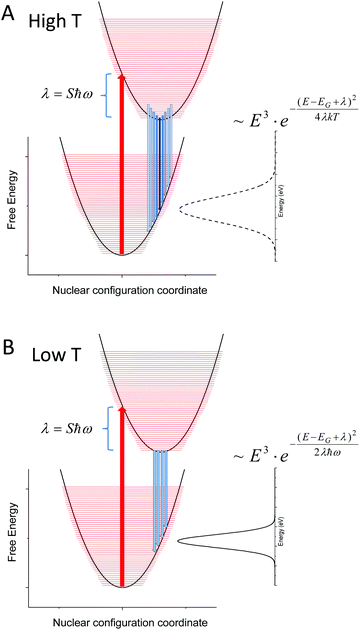
Fig. 10 sketches the corresponding potential energy configuration coordinate diagram for the ground and excited state for such a modeled system with moderately large Huang–Rhys factors (and thus a large reorganization energy (λ) in combination with small vibrational (densely spaced) energy levels (ħω)).
As our data are in quite decent agreement with Keil's equation, with an almost constant non-zero line-width observed at lower temperatures (<120 K), we therefore argue that the spectral line-width of the CT-state emission should be treated as experiencing a transition from the classical high temperature Marcus regime, where several of the higher vibronic levels of the exited state are thermally populated (Fig. 10A), to a low temperature regime where only the lowest vibrational level of the excited state is populated (Fig. 10B). When reducing the temperature further, no more narrowing is possible as no further reduction of populated vibrational energy levels of the excited state can occur. The constant line-width (given by λħω), is then governed only by the shape of the potential energy parabola according to Keil's equation. The two resulting line-width equations are inserted for the two limiting cases presented in panel (A) and (B) of Fig. 10. A linear temperature dependence at elevated temperatures therefore suggest that the classical Marcus approximation implemented previously (at high temperatures) is well justified for bulk heterojunction solar cells whose transitions are governed by interfacial CT-states, whereas Keil's semi-classical equation outlines better what takes place in the entire temperature range.
The classical approximation stipulates that the relevant vibronic energy levels are so densely spaced, that there is no argument for invoking the quantum mechanical description for the high-energy part of the emission tails at room temperature. The question to resolve is consequently; how to justify the observed presence of such small and densely spaced vibronic energy levels also in the solid state? Bearing in mind that the CT emission in OPV blends is per definition occurring at the interface between (rather large) molecules, it is well justified to assume that the intermolecular motions should play a more dominant role, and not only the intra-molecular (C–C, C–H) high-energy modes of the molecules themselves. Merely the motion of extended parts of the molecules may be dominating the low frequency interface interactions. These may comprise extremities such as single bond attached rings present in most of our studied small molecules, or even just sidechains as present in the soluble polymers. Accordingly, at higher temperatures, the thermal energy of a system ruled by interface interaction can be considered high with respect to the low frequency vibrations originating from these slow and small movements that appears to govern the CT-state spectra, and the classical approximation accordingly becomes justified. This picture might however be less valid for significantly stiffer molecules, such as the MeLPPP combined with PCBM60, which e.g. Kahle et al. focused on.
The observed transition of spectral line-width from a low temperature constant value to a temperature dependent line-width at higher temperatures, along with Keil's equation, has in fact been identified several times throughout the history of material spectroscopy, and for vastly different materials. Meyer,52 Dexter,53 Toyozawa,54 Keil,55 Mahr56 and Kurik2,57 have all confirmed the above observed temperature behavior, but in completely different materials, and often with an exponential tail instead of a Gaussian. Recalling the Urbach tail introduction of the manuscript, we here therefore also stress the almost identical expression as Keil's equation, frequently found for the temperature dependence of the exponential tail slope; namely the dynamic part of the Urbach energy.2,57
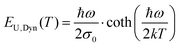 | (11) |
2.4. Explanation of negative extrapolated variance values; a multimode analysis
Having first settled the occurrence of line-width saturation at low temperatures with Keil's semi-classical description, we also need to understand the perplexing observation of the 0 K extrapolated negative linewidth values in Fig. 8A. An explanation for this is found in the fact that in real systems, multiple vibrational modes with different energies are expected to be present. Let us therefore now consider the simplest case where one high and one low frequency mode are present simultaneously. As shown above, the low frequency modes are responsible for a Gaussian like line-width. Including high frequency modes can be done by again using the general eqn (8). This time we however let 〈νi|νj〉 represent the overlap integral between the i:th ground state vibrational level and the j:th excited state vibration level of a high frequency mode. In this example, presented in Fig. 11A, we take this high frequency mode to have a large value ħω = 0.15 eV, and a typical low value of the Huang–Rhys factor S = 1, representative for a classic C–C vibration (as also seen to dominate the pure fullerene case of Fig. 3). The LW function is this time taken to instead be a Gaussian with its line-width determined by the Keil formula (eqn (10)) with the S and ħω parameters of a low frequency mode. The low frequency mode is, as above, taken to be ħω = 0.015 eV and with S = 10. This parameter selection leads to emission spectra peaking at a value of 150 meV below Egap. In a classical picture, a single reorganization energy of 150 meV would thus be assigned if a single measurement at room temperature would be performed. The LW function as well as the full Frank–Condon expression, according to eqn (8), is therefore again plotted for several temperatures in the figure, allowing us to discriminate the influence of both modes.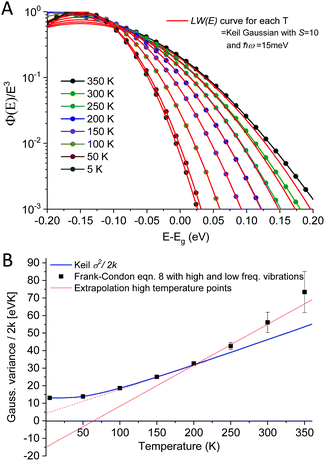 | ||
| Fig. 11 (A) shows eqn (8) now accounting for both high and low frequency vibrational modes. The red lines represents the line-width associated with only the low frequency modes, whose behavior is now set to be defined by Keil's equation. (B) shows the corresponding calculated normalized Gaussian variance, as determined from the second derivative. At low temperatures the variance is governed by the low frequency modes, whereas at higher temperatures also the high frequency mode is populated, further broadening the spectra (and increasing the variance). | ||
One sees that at low T, the full expression (8) is almost identical to the low frequency mode LW function. At high T however, higher energy vibrational states of the high frequency mode start to become populated, leading to an additional steeper broadening with T. When again determining σ2 from the second derivative approach as outlined above, we obtain the line-widths with associated variance as presented in Fig. 11B and once more confirm that at low T, the line-width equals that of the low frequency mode. At higher temperatures, the line-width broadens further, due to additional thermal population of the high frequency modes. We therefore argue that Fig. 11 may very well represent the theoretical case of the experimental measurements, of for example the TCTA(6%):C60 device, which showed similar behavior and is thus expected to have pronounced influence of both high and low vibrational modes. We believe that also the other devices that too showed negative extrapolation therefore likely are governed by combinations of different energy modes. Although rubrene is the only material that appears to indicate a (very small) positive static disorder in Fig. 8b, we want to emphasize that, as its low frequency reorganization energy is much smaller than the other materials, one would have to measure emission with even higher sensitivity to detect the effect of the present high frequency modes. Accordingly, our work strongly supports the theoretical approach taken by Kahle et al., arguing that a complete Frank–Condon picture is indeed needed to account for the entire temperature dependence of the CT-state line-width. Our experimental observations on the other hand do not corroborate Kahle's claim on the strong influence of static disorder. We finally note the very recent manuscript by Linderl et al.,58 who observed a very similar behavior in DBP:C60 devices as we have done herein.
3. Conclusions
The broad room temperature spectral line-width of interfacial charge-transfer-state emission of organic solar cells does not appear to be an effect of energetic static disorder. Instead, the larger part of the line-width at 300 K is originating from thermally activated molecular motion, which can be quite well described by the reorganization energy in the classical Marcus formalism. The spectral line-width of CT-state transitions at room temperature is thus mainly broadened by strong coupling to molecular vibrations, and not by static disorder broadening. Our conclusion on these matters is based on a very strong experimental observable; the emission line-width at high temperatures is a linear function that does not extrapolate to noticeable positive values at zero Kelvin. At lower temperatures, we however clearly observe a saturation of the line-width and thus a breakdown of the classical Marcus picture. Below this temperature, the line-width is no longer broadened by recombination from higher vibronic levels of the excited state, but instead more ruled by the shape of the potential parabola of the harmonic oscillator. A full quantum mechanical treatment is in line with Thomas Keil's semi-classical expression of line-width broadening as presented in eqn (10), bearing a strong similarity to the dynamic Urbach tail expressions.2 From this, we conclude that low energy vibrations in combination with moderately large Huang–Rhys factors are most likely responsible for the observed temperature dependence of the line-width broadening. To be able to fully reconcile the sometimes-steeper temperature dependence at higher temperatures, we also outlined the inclusion of simultaneous low and high energy vibrational contribution in a Frank–Condon framework. Considering our observations on overall vibrational dominance to the emission line-width and accordingly to the, from reciprocity relations corresponding, absorption tail, we conclude that any Gaussian disorder parameters (or equivalent exponential Urbach energies) obtained from pure optical measurements is unlikely to be directly defined by only the tail shape of a static DOS of the material blend. As such, any static disorder parameter linked to the DOS shape cannot be determined from single temperature absorption tail measurements. As a final concluding note on this matter, we would also like to make it clear that although we cannot find any evidence of discernable static disorder contribution to CT-state emission broadening, we do not want to argue that static disorder is not present in organic semiconductors, as our data provides no evidence for such a more general statement. It is still very possible that tail states that are not associated with an optical transition moment (oscillator) are still present. As these dark states do not couple to absorption or emission events, they do not affect the measurements performed herein but would still be able to play a role in the transport of charge carriers.Author contribution
J. B. manufactured the small molecules co-evaporated diluted donor cells in Dresden. K. T. manufactured the solution processed polymer devices in Würzburg. K. T. measured the T-dependent EL and PL spectra and the corresponding L–I–V curves of all devices in Würzburg. All authors analyzed the data (multiple times) and discussed the results. K. V. conducted the Franck–Condon calculations. K. T. wrote the paper, to which K. V. and J. B. provided feedback and amendments. The study was designed collectively by all authors.Conflicts of interest
There are no conflict to declare.Acknowledgements
K. T. acknowledges the German Research Foundation (DFG) through project 382633022 (RECOLPER) and the Experimental Physics VI chair of Prof. Vladimir Dyakonov at Würzburg University. J. B. acknowledges the DFG project VA 1035/5-1 (Photogen) and the Sächsische Aufbaubank through project no. 100325708 (Infrakart). The authors also acknowledge discussion on the topic with Robert Street, Thomas Kirchartz, Frank Ortmann and Carsten Deibel.Notes and references
- W. van Roosbroeck and W. Shockley, Phys. Rev., 1954, 94, 1558 CrossRef CAS.
- I. Studenyak, M. Kranjcec and M. Kurik, Int. J. Opt., 2014, 4, 76–83 Search PubMed.
- D. Redfield, Phys. Rev., 1963, 130, 916 CrossRef CAS.
- T. Tiedje, B. Abeles and J. M. Cebulka, Solid State Commun., 1983, 47, 493–496 CrossRef CAS.
- H. Oheda, Jpn. J. Appl. Phys., 1979, 18, 1973–1978 CrossRef CAS.
- G. D. Cody, T. Tiedje, B. Abeles, B. Brooks and Y. Goldstein, Phys. Rev. Lett., 1981, 47, 1480–1483 CrossRef CAS.
- F. Urbach, Phys. Rev., 1953, 92, 1324 CrossRef CAS.
- C. W. Greeff and H. R. Glyde, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 1778–1783 CrossRef CAS PubMed.
- R. A. Street, K. W. Song, J. E. Northrup and S. Cowan, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 165207 CrossRef.
- B. E. Pieters, T. Kirchartz, T. Merdzhanova and R. Carius, Sol. Energy Mater. Sol. Cells, 2010, 94, 1851–1854 CrossRef CAS.
- J. Krustok, H. Collan, M. Yakushev and K. Hjelt, Phys. Scr., T, 1999, 79, 179–182 CrossRef.
- W. Gong, M. A. Faist, N. J. Ekins-Daukes, Z. Xu, D. D. C. Bradley, J. Nelson and T. Kirchartz, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 024201 CrossRef.
- U. Hörmann, S. Zeiske, S. Park, T. Schultz, S. Kickhofel, U. Scherf, S. Blumstengel, N. Koch and D. Neher, Appl. Phys. Lett., 2019, 114, 183301 CrossRef.
- U. Hörmann, S. Zeiske, F. Piersimoni, L. Hoffmann, R. Schlesinger, N. Koch, T. Riedl, D. Andrienko and D. Neher, Phys. Rev. B, 2018, 98, 155312 CrossRef.
- K. Vandewal, K. Tvingstedt, A. Gadisa, O. Inganäs and J. V. Manca, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125204 CrossRef.
- R. S. Crandall, Phys. Rev. Lett., 1980, 44, 749–752 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- I. R. Gould, D. Noukakis, L. Gomezjahn, R. H. Young, J. L. Goodman and S. Farid, Chem. Phys., 1993, 176, 439–456 CrossRef CAS.
- K. Vandewal, K. Tvingstedt, A. Gadisa, O. Inganäs and J. V. Manca, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125204 CrossRef.
- K. Vandewal, K. Tvingstedt and O. Inganäs, Semiconductors and Semimetals, Elsevier, 2011, vol. 85, pp. 261–295 Search PubMed.
- T. M. Burke, S. Sweetnam, K. Vandewal and M. D. McGehee, Adv. Energy Mater., 2015, 5, 1500123 CrossRef.
- V. Coropceanu, J. Cornil, D. A. da Silva, Y. Olivier, R. Silbey and J. L. Bredas, Chem. Rev., 2007, 107, 926–952 CrossRef CAS PubMed.
- K. Vandewal, J. Benduhn, K. S. Schellhammer, T. Vangerven, J. E. Ruckert, F. Piersimoni, R. Scholz, O. Zeika, Y. L. Fan, S. Barlow, D. Neher, S. R. Marder, J. Manca, D. Spoltore, G. Cuniberti and F. Ortmann, J. Am. Chem. Soc., 2017, 139, 1699–1704 CrossRef CAS PubMed.
- F. J. Kahle, A. Rudnick, H. Bässler and A. Köhler, Mater. Horiz., 2018, 5, 837–848 RSC.
- J. Jortner, J. Chem. Phys., 1976, 64, 4860–4867 CrossRef CAS.
- D. Jarzab, F. Cordella, J. Gao, M. Scharber, H. J. Egelhaaf and M. A. Loi, Adv. Energy Mater., 2011, 1, 604–609 CrossRef CAS.
- I. Riisness and M. J. Gordon, Appl. Phys. Lett., 2013, 102, 113302 CrossRef.
- M. List, T. Sarkar, P. Perkhun, J. Ackermann, C. Luo and U. Wurfel, Nat. Commun., 2018, 9, 3631 CrossRef PubMed.
- Z. Vaitonis, P. Vitta and A. Zukauskas, J. Appl. Phys., 2008, 103, 093110 CrossRef.
- E. F. Schubert, Light-Emitting Diodes, Cambridge University Press, 2nd edn, 2006 Search PubMed.
- H. W. Kroto, J. R. Heath, S. C. O'Brian, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162 CrossRef CAS.
- P. M. Pippenger, R. D. Averitt, V. O. Papanyan, P. Nordlander and N. J. Halas, J. Phys. Chem., 1996, 100, 2854–2861 CrossRef CAS.
- E. J. Shin, J. H. Park, M. Y. Lee, D. H. Kim, Y. D. Suh, S. I. Yang, S. M. Jin and S. K. Kim, Chem. Phys. Lett., 1993, 209, 427–433 CrossRef CAS.
- V. Capozzi, M. Santoro, G. Perna, G. Celentano, A. Minafra and G. Casamassima, Eur. Phys. J.: Appl. Phys., 2001, 14, 3–11 CrossRef CAS.
- J. Menéndez and J. B. Page, Vibrational spectroscopy of C60, in Light Scattering in Solids VIII. Fullerenes, Semiconductor Surfaces, Coherent Phonons, ed. M. Cardona and G. Güntherodt, Topics in Applied Physics, Springer, Berlin, Heidelberg, 2006, vol. 76, pp. 27–95 Search PubMed.
- P. J. Brown, D. S. Thomas, A. Köhler, J. S. Wilson, J. S. Kim, C. M. Ramsdale, H. Sirringhaus and R. H. Friend, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 064203 CrossRef.
- S. Guha, J. D. Rice, Y. T. Yau, C. M. Martin, M. Chandrasekhar, H. R. Chandrasekhar, R. Guentner, P. S. de Freitas and U. Scherf, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 125204 CrossRef.
- S. T. Hoffmann, H. Bässler and A. Köhler, J. Phys. Chem. B, 2010, 114, 17037–17048 CrossRef CAS PubMed.
- J. Mooney and P. Kambhampati, J. Phys. Chem. Lett., 2013, 4, 3316–3318 CrossRef CAS.
- S. S. Chen, Y. M. Wang, L. Zhang, J. B. Zhao, Y. Z. Chen, D. L. Zhu, H. T. Yao, G. Y. Zhang, W. Ma, R. H. Friend, P. C. Y. Chow, F. Gao and H. Yan, Adv. Mater., 2018, 30, 1804215 CrossRef PubMed.
- L. Perdigon-Toro, H. T. Zhang, A. S. Markina, J. Yuan, S. M. Hosseini, C. M. Wolff, G. Z. Zuo, M. Stolterfoht, Y. P. Zou, F. Gao, D. Andrienko, S. Shoaee and D. Neher, Adv. Mater., 2020, 32, 1906763 CrossRef CAS PubMed.
- K. Tvingstedt, K. Vandewal, F. Zhang and O. Inganäs, J. Phys. Chem. C, 2010, 114, 21824–21832 CrossRef CAS.
- K. Tvingstedt, O. Malinkiewicz, A. Baumann, C. Deibel, H. J. Snaith, V. Dyakonov and H. J. Bolink, Sci. Rep., 2014, 4, 6071 CrossRef CAS PubMed.
- M. de Jong, L. Seijo, A. Meijerink and F. T. Rabouw, Phys. Chem. Chem. Phys., 2015, 17, 16959–16969 RSC.
- U. Rau, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 085303 CrossRef.
- K. Vandewal, K. Tvingstedt, A. Gadisa, O. Inganäs and J. V. Manca, Nat. Mater., 2009, 8, 904–909 CrossRef CAS PubMed.
- W. Franz, Z. Naturforsch., A: Phys. Sci., 1958, 13, 484–489 Search PubMed.
- R. Williams, Phys. Rev., 1962, 126, 442 CrossRef CAS.
- P. K. H. Ho, J. S. Kim, N. Tessler and R. H. Friend, J. Chem. Phys., 2001, 115, 2709–2720 CrossRef CAS.
- M. Malagoli, V. Coropceanu, D. A. da Silva and J. L. Bredas, J. Chem. Phys., 2004, 120, 7490–7496 CrossRef CAS PubMed.
- T. H. Keil, Phys. Rev., 1965, 140, A601 CrossRef.
- H. J. G. Meyer, Physica, 1954, 20, 1016–1020 CrossRef CAS.
- D. L. Dexter, Nuovo Cimento, Suppl., 1958, 7, 245–286 CrossRef.
- Y. Toyozawa, Prog. Theor. Phys., 1959, 22, 455–457 CrossRef.
- T. H. Keil, Phys. Rev., 1966, 144, 582 CrossRef CAS.
- H. Mahr, Phys. Rev., 1963, 132, 1880 CrossRef.
- M. V. Kurik, Phys. Status Solidi A, 1971, 8, 9 CrossRef CAS.
- T. Linderl, T. Zechel, A. Hofmann, T. Sato, K. Shimizu, H. Ishii and W. Brütting, Phys. Rev. Appl., 2020, 13, 024061 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0mh00385a |
| This journal is © The Royal Society of Chemistry 2020 |