Open Access Article
Open Access ArticleWhen nanocellulose meets diffraction grating: freestanding photonic paper with programmable optical coupling†
Guang
Chu
 ab,
Dan
Qu
a,
Andrea
Camposeo
*c,
Dario
Pisignano
ab,
Dan
Qu
a,
Andrea
Camposeo
*c,
Dario
Pisignano
 *cd and
Eyal
Zussman
*cd and
Eyal
Zussman
 *a
*a
aNanoEngineering Group, Faculty of Mechanical Engineering, Technion-Israel Institute of Technology, Haifa 3200003, Israel. E-mail: meeyal@technion.ac.il
bBio-based Colloids and Materials, Department of Bioproducts and Biosystems, School of Chemical Engineering, Aalto University, P.O. Box 16300, FI-00076 Aalto, Espoo, Finland
cNEST, Istituto Nanoscienze-CNR, Piazza S. Silvestro 12, I-56127 Pisa, Italy. E-mail: andrea.camposeo@nano.cnr.it
dDipartimento di Fisica, Università di Pisa, Largo B. Pontecorvo 3, I-56127 Pisa, Italy. E-mail: dario.pisignano@unipi.it
First published on 2nd October 2019
Abstract
Photonic crystals based on plasmonic or dielectric periodic structures have attracted considerable interest owing to their capabilities to control light–matter interactions with tailored precision. By using a nanocellulose derived chiral liquid crystal as a building block, here we demonstrate a bio-inspired dual photonic structure that contains the combination of microscopic periodic 1D surface grating and nanoscopic helical organization, giving rise to programmable colour mixing and polarization rotation. We show that a variation in the photonic band-gap in the bulk matrix leads to simultaneous control over the reflection and diffraction of light with controllable iridescence.
New conceptsNature's light manipulation strategies, especially those at the origin of bright structural colours, have fascinated humans for centuries. Typically, many arthropods display polarization sensitive iridescent colours for communication and aid in their camouflage against predators. This structural coloration usually contains hierarchical Bouligand-type structures that exhibit helical organization and periodic surface structure. Inspired by the beetle of Chalcothea smaragdina, here we demonstrated a scalable route for the manufacture of custom-tailored cellulose paper with a hierarchical photonic architecture: in particular, we combined the nanoscale self-assembly of cellulose nanocrystals with microscale surface grating-like structures, exhibiting dual structural colour that is derived from the helical matrix and circularly polarized light diffraction. Owing to the structural flexibility, the photonic band-gap of the cellulose matrix can be precisely controlled to couple with the diffraction peaks of the surface grating, giving rise to hierarchical photonic structures with strong grating efficiency. The current communication is particularly important to understand how hierarchy affects the properties of chiral light–matter interactions in living organisms, not only providing inspiration for designing bio-mimetic artificial counterparts, but also allowing further understanding of their biological significance in nature. |
Introduction
Colours play essential roles in the evolution and survival of plants and animals.1 Depending on the basic optical mechanism, colours and colour appearance in living creatures can be classified into three classes: absorption, bioluminescence and interference. These mechanisms, alone or combined, generate the palette of the colourful biological world.2 While the first two mechanisms strongly rely on the chemical composition of the molecules that compose the organisms, structural colour is mainly the result of light interference in approximately micro- or nanometre-scaled periodic structures.3 Some of the photonic structures in nature are chiral, namely, the organization of bio-derived building blocks in plants or insects is spatially assembled to form a helicoid architecture, known as a Bouligand structure or a twisted plywood structure.4,5 The attractive feature of this chiral structure is its circular polarized light–matter interaction, which selectively reflects the circularly polarized light with the same handedness, whereas light with opposite handedness is transmitted and experiences no phase change.6 Apart from helicoid ordering, the origin of such brilliant chiral structural colours in natural materials is quite complex: they are often organised into hierarchical architectures and combined with other optical materials such as pigments to enhance or modulate their response, leading to vivid colours which perform signalling functions within or between species.7–9 For example, in the fruit of Pollia condensata, the colour is originated by the helical organization of cellulose fibrils with a spherical geometry on top of a layer of brown tannin pigments, which exhibits intense blue colour reflection.10 In other cases such as scarab beetle Chalcothea smaragdina, the metallic green colour appearance results from the combination of helical fibrous chitin with periodic blazed diffraction grating-like surface structures, yielding morphology-induced light scattering as well as helical matrix derived structural colour, named as multiple photonic–photonic colour mixing.11 Knowledge of the interplay between the morphology, composition and optical appearance of biological photonic systems can provide inspiration for novel artificial photonic materials with a wide range of applications.12–14Cellulose is an inexhaustible biopolymer on earth that can be easily found in plants and bacteria.15,16 When the bulk cellulose material is subjected to controlled sulfuric acid assisted hydrolysis, it transforms into a well-defined rigid rod-like morphology with excellent dispersibility in water.17,18 The residues are termed as cellulose nanocrystals (CNCs). It is well known that CNCs can self-assemble into a chiral nematic liquid crystal phase with its ordering preserved in a solid film after evaporation, producing vivid structural colour as observed in plants and certain animals when its helical pitch is on the order of the visible light wavelength.19–21 Up to now, copious studies on CNC liquid crystals have been presented from the perspective of their templating,22,23 colloidal assembly,24–27 drying dynamics28–30 and optical coupling with guest nanoparticles,31–34 however, their potential uses as building blocks to fabricate periodic grating-like surface patterned films which have programmable photonic–photonic couplings still remain relatively unexplored, i.e., two spatial structures with different scales (micro and nano) coexist and modulate the light independently, showing hierarchical photonic structures.
The mimicry of biological species to produce photonic materials has raised increasing interest in the scientific community. However, the edge of knowledge in this research topic is today settled by the limitation that scientists face in the fabrication of materials with similar structural complexity to biological nanostructures. In fact, the fabrication of nano-scale structures on large area with additional control on their micro-scale morphology is very demanding. Drawing inspiration from Chalcothea smaragdina, here we develop a hierarchical structured photonic paper that contains both chiral nematic organization of a CNC matrix and periodic grating lines on its surface, showing dual photonic colours. The patterned photonic film is prepared by confining the CNC suspension into highly aligned microgrooves through soft nanoimprinting lithography followed by evaporation induced self-assembly processes. After drying, these films are peeled off from the template with highly ordered grating lines imprinted onto the lower surface of the films, showing precisely controlled microstructures not only with a surface morphology but also with a bulk phase with deformed helical organization.35 In particular, we describe that tuning the composition of initial CNC ink can be used to manipulate the photonic band-gap in the helical matrix which couples with diffraction derived from surface grating lines, showing programmable photonic–photonic colour mixing in reflection mode and affecting the diffuse appearance of the dual photonic paper. These bio-inspired films offer a convenient opportunity for the production of coupled photonic structures with complex polarization control, which may be of value in advanced optical devices.
Results and discussion
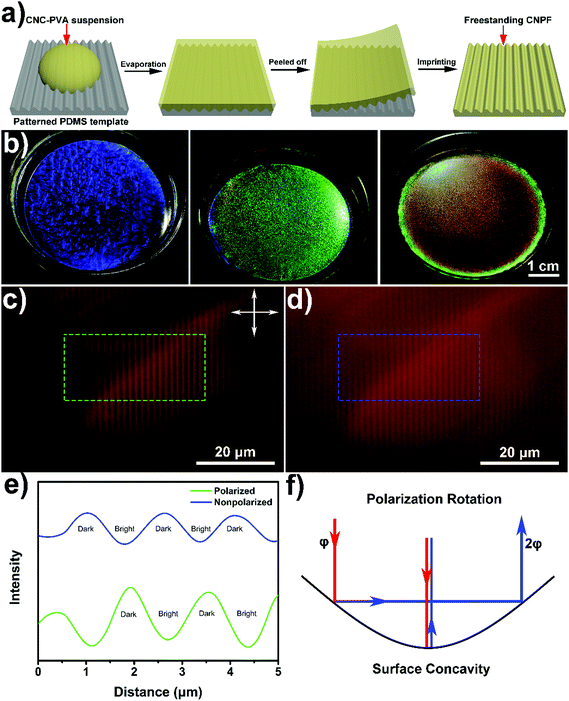
The CNC used in this study was produced by sulfuric acid hydrolysis of bleached cotton pulp, which exhibited rod-like morphology with an average length and diameter of 300 nm and 16 nm, respectively (Fig. S1, ESI†). Before drying, the as prepared CNC colloid suspension was diluted to the desired concentration (5.0 wt%, zeta potential −53 mV) and mixed with varying amounts of water-soluble polymers (polyvinyl alcohol, PVA) to generate homogeneous mixtures without disrupting the ability of the CNC to form the chiral nematic phase. Then, these mixtures were cast onto a hydrophilic polydimethylsiloxane (PDMS) template with periodic surface microgrooves (Fig. 1a). After evaporation, iridescent composite films were obtained with vivid structural colour, which were tunable from blue to green and red, due to the increase of helical pitch (Fig. 1b). Finally, a centimetre-scaled composite film (3 × 5 cm2) was carefully peeled off from the template with a Janus layer, i.e., a film with an upper smooth surface and a bottom patterned surface. This chiral nematic patterned film was denoted as CNPF which revealed rainbow-like bistructural colour and high mechanical strength (Fig. S2 and S3, ESI†).In order to test the influence of surface topography on CNPF, the optical details were first obtained from polarized optical microscopy (POM) images in reflection mode. For normal light incidence, when the sample was placed between crossed polarizers, it exhibited alternately dark and bright stripes with the width of dark stripes similar to the grating distance. However, removing the polarizers led to a reverse of the optical pattern compared with crossed polarizers, namely, the center of the grating line concavity turned bright while the edge of the stripes became dark (Fig. 1c–e). This phenomenon is a result of the geometry induced double reflection and polarization rotation.36 In a regular reflection mode without polarizers, light from the cavity center is directly reflected with the strongest reflection intensity, while at the grating line edge retro-reflection of incident light occurs by double reflection off the cavity multilayer. On the other hand, if the incident light is linearly polarized with angle ϕ to the initial incident plane, it will be retro-reflected by the double bounce and undergoes a polarization rotation of 2ϕ at each interface (Fig. 1f). Therefore, under crossed polarization state light reflected off the center of the grating line is suppressed, whereas only retro-reflected light from the grating line edges passes through the analyzer and is detected.37 Besides, for the transmission mode the optical images of the same sample showed no sign of reversing dark and bright stripes (Fig. S4, ESI†), indicative of lacking double reflection and polarization rotation.
Visually, as well as by large area optical microscopy and small area scanning electron microscopy (SEM) tests, the chiral nematic patterned film showed periodic grating lines that fully replicate the microstructure of the template (Fig. 2a and b). Fig. 2c shows the low magnification SEM image of CNPF3 with an oblique view of the film which shows three different parts, i.e., a periodic surface grating region, the interface between the surface and the bulk and an extensive periodic bulk phase. Looking at the cross sections, a deformed helical layered structure was present near its patterned surface where the helix axis of the CNC remained parallel to the curved surface (Fig. 2d), implying the planar anchoring of the CNC at the water–PDMS interface during evaporation. At the nanoscale, CNC nanorods in bulk phase were rotated in a counter-clockwise direction, giving rise to a long-range helical structure (Fig. 2e). The distance between two adjacent layers was termed as the helical pitch for a chiral nematic structure, which was 195, 365 and 475 nm for CNPF1–3, as estimated by SEM analysis (Fig. S5, ESI†). Surface profiles of the CNPF samples demonstrated a groove depth of 275 nm and a grating distance of 2.5 μm as observed in atomic force microscopy (AFM) images (Fig. S6, ESI†), similar to the surface profile of the PDMS template (260 nm and 2.4 μm, respectively). Besides, tuning the surface profile of the PDMS template by controlled plasma treatment could also manipulate the surface morphology of the corresponding CNPF composites (Tables S1 and S2, ESI†). All of these data above clearly displayed the coexistence of hierarchical micro- and nanoscale features with the periodic surface grating lines and chiral nematic organization (Fig. 2f). Previous reports demonstrated that an individual CNC could be highly aligned into the microgrooves of the PDMS template with periodic line arrangement.38 Through evaporation, due to the elastic interplays between a liquid crystalline CNC and a PDMS template, the patterned template will deform the interface of liquid crystals into a hilly topography, with each hill accommodating a chiral nematic spiral, generating a nontrivial interfacial curvature with bend-splay orientation distortions along the template surface.39,40 In the end, this deformed helical ordering will be preserved as a solid film, with the distance and amplitude of these grating lines imprinted and determined by the PDMS template.35
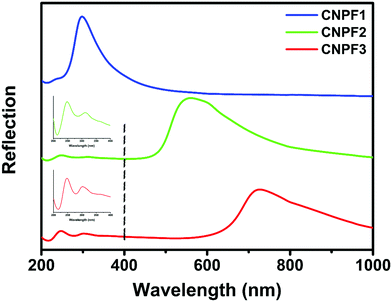
In the chiral nematic film, the position of its photonic band-gap is optically tunable from UV-blue to visible regions by tuning the helical pitch.20 By changing the CNC–PVA composition in its initial ink, we can easily manipulate the helix derived photonic band-gap in CNPF.41Fig. 3 shows the reflection spectra of CNPF1–3 consisting of varied photonic–photonic coupling. A series of photonic band-gaps were obtained with their positions centered at 297, 562 and 722 nm, respectively, which resulted from the increase of helical pitch, typical for the chiral nematic organization. For the sample of CNPF2 and CNPF3, a double-peak spectral feature was observed in the UV-blue range centered at 245 and 300 nm, which resulted from the surface grating line induced photonic structure and almost remained constant without the influence of the surface morphology (also confirmed by a chiral nematic-free patterned CNC film, Fig. S7 and S8, ESI†). When the photonic band-gap in the host CNC matrix was blue-shifted to smaller wavelength (from 722 to 297 nm), there occurred a strong photonic–photonic coupling between the CNC matrix and surface grating lines, leading to an enhanced coupled optical signal with vivid blue structural colour appearance (see Fig. S2, ESI†). Hence, both the chiral nematic ordering in the bulk CNC phase and surface grating lines on the film surface can individually be termed as a photonic crystal, showing programmable photonic–photonic coupling. More interestingly, the optical property of the CNPF film could be further tuned by varying the light incident angle (Fig. S9, ESI†). During the increase of rotation angle, the photonic band-gaps of these two samples were blue-shifted to smaller wavelength which could be attributed to changes in diffraction related to incidence angles. However, the band-gap shifting in CNPF2 showed a monotonic linear relationship whereas the peak shifting in CNPF1 followed a non-linear trend, which implied that the photonic–photonic coupling between the helical matrix and surface gratings exhibited strong influences on the angle-dependence spectra behaviour.
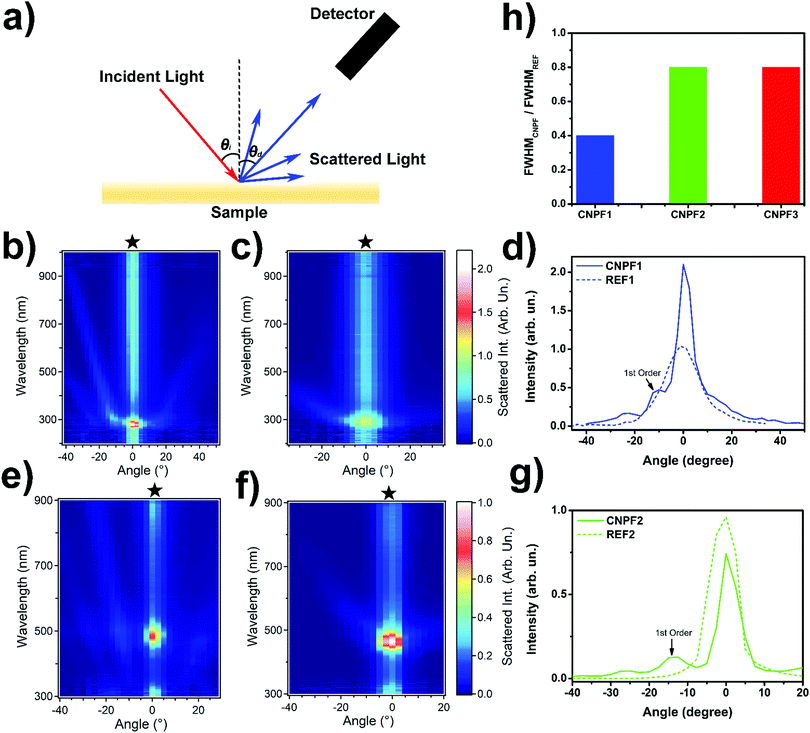
To quantify the diffraction induced photonic property in CNPF, angle-resolved scattering measurements were performed (Fig. 4a). The set-up contained a broadband deuterium-halogen light source (mod. DH-2000, Ocean Optics) for a fixed incident light beam (incident angle: 35°), a rotating sample stage and a rotating detector. The output beam was first collimated by a quartz lens, giving rise to a spot size of 3 mm on the sample surface. Then, the light diffused signal was collected by a multimode optical fibre on a rotation stage. The reflected and scattered light was detected at varying detection angles between 0° and 70° in 2.5° steps. Fig. 4b–h exhibit the diffraction results for the sample of CNPF1, 2 and their corresponding grating-free reference (REF) samples. For patterned samples, the presence of surface grating lines generated a series of diffraction peaks in different angular directions, thus, resulting in the first, second and third-order diffractions which located in a wide range of angles, a characteristic of grating-derived iridescence (Fig. 4b and e). Compared with a CNPF sample, the scattering orders in REF resulting due to the surface topography were not obvious, and they only demonstrated a broad scattering band at 0° which was ascribed to the zero-order reflection with the highest intensity located at their corresponding photonic band-gaps (Fig. 4c and f). As a 1D photonic crystal, the optical property in the chiral nematic structure itself is angle-dependent.42 During scattering measurement, illumination at an oblique angle leads to iridescence manifested as a blue-shift in the reflected structural colour with the Bragg reflection peak given by λ = navgP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, where navg and P are the refractive index and helical pitch, respectively, and θ is the angle between the incident direction and the helical axis.43 Therefore, the zero-order reflection bands in CNPF and REF showed the strongest scattering intensity at the position of the photonic band-gap and then decreased to further wavelengths due to the increasing incident angle.
θ, where navg and P are the refractive index and helical pitch, respectively, and θ is the angle between the incident direction and the helical axis.43 Therefore, the zero-order reflection bands in CNPF and REF showed the strongest scattering intensity at the position of the photonic band-gap and then decreased to further wavelengths due to the increasing incident angle.
In addition, we found that the interplay between the helical CNC matrix and imprinted surface gratings could provide dramatic effects on the resulting scattering properties. A significant increase of the reflection and diffraction in CNPF1 was achieved by shifting the band-gap toward the UV-blue spectral band. The specular reflectivity at 280 nm was enhanced by 2 factors in CNPF1 compared to the pattern-free one (Fig. 4d), whereas for CNPF2 and CNPF3 the addition of surface gratings did not affect the reflection peaks at 480 and 630 nm, respectively (Fig. 4g and Fig. S10, ESI†). Calculations of the first-order diffraction efficiency for CNPF1 and CNPF2 were 0.47 and 0.12, respectively, demonstrating an effective boosting of optical properties in hierarchical photonic structures in CNPF1 through the interplay of photonic–photonic coupling. As a consequence, we concluded that the chiral nematic photonic band-gap could enhance the iridescence response that derived from the periodic surface grating lines. The ensemble structural colour appearance is attributed to the sum of the scattered helicoidal photonic reflections with additional interference resulting from the periodic surface topography.44 Interestingly, the presence of the photonic–photonic coupling between the grating structure and the helical matrix also decreased the angular width of the reflectance peak in CNPF1, whereas the bandwidth was almost unchanged in samples of CNPF2 and CNPF3 (Fig. 4h). The total angular distribution of the light intensity reflected from CNPF samples was the result of the convolution of the angular distribution of the intensity reflected by the bulk CNC cholesteric structures and surface diffraction grating. The latter generated a characteristic angular distribution of the intensity of the reflected light composed by consecutive intensity maxima and minima, whose separation depended on the wavelength of light and the periodic grating period.45 While for CNPF2 and CNPF3 the first diffraction order was well separated from the zero order (helical induced photonic band-gap) peak, for CNPF1 the first diffraction order was within the angular width of the reflected light beam. This in turn led to a decrease of the intensity of light between the zero and the first diffraction order, in correspondence with the first intensity minimum of the diffracted light pattern, thus determining a decrease in the angular width of the zero order diffracted beam.
In nature, the green colour appearance of Chalcothea smaragdina is anticipated to be used as protective coloration and aids in its camouflage against predators.11 The beetle is visibly vivid green when observed through a left-handed circularly polarized (LCP) filter and totally loses its characteristic bright green reflection under a right-handed circularly polarized (RCP) filter, exhibiting selective reflection of the LCP light exclusively, which is due to the anticlockwise rotation of helicoidal chitin fibrils within the beetle's elytron exocuticle (Fig. 5a). The measured average pitch and refractive index of the helicoid beetle cuticle are about 340 nm and 1.647, respectively. Thus, a helical structure derived Bragg reflection occurs at 560 nm in normal incidence which fits well with its saturated green colour appearance. On the other hand, the surface structure of the beetle exocuticle reveals parallel surface striations that possess a fine irregular sawtooth-shaped profile parallel to the surface plane (Fig. 5b). And the beetle surface topography is further explored to show a quasi-regular surface periodicity manifested by a distinct acclivity and declivity at the edge of the striation, forming a step structure similar to a blazed grating structure (Fig. 5b, inset).11 The measured spacing between neighbouring striations is 5.07 μm with a blaze angle θb of 3.1°. The blaze angle is optimized with maximum efficiency for all the incident light, which gives rise to the metallic appearance of the beetle exocuticle. The grating equation for the reflective blazed grating can be found as: d(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α + sin
α + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β) = mλ, where α and β are the incidence and diffraction angles, respectively, d is the periodicity of the grating lines, λ is the diffracted incident light wavelength and m is the diffraction order (Fig. 5c). In particular, if the incidence angle and diffraction angle are identical (α = β = θb) which refers to a specific geometry for blazed grating named as the Littrow configuration, the grating equation can be transformed into 2d
β) = mλ, where α and β are the incidence and diffraction angles, respectively, d is the periodicity of the grating lines, λ is the diffracted incident light wavelength and m is the diffraction order (Fig. 5c). In particular, if the incidence angle and diffraction angle are identical (α = β = θb) which refers to a specific geometry for blazed grating named as the Littrow configuration, the grating equation can be transformed into 2d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θb = mλ.46 The grating efficiency of the Littrow configuration is mainly dependent on the most intense order (m = 1), thus, the light wavelength for which scattering is optimized in Chalcothea smaragdina is calculated as 548 nm, coinciding with a green spectral range and overlapping with the reflection peak of an internal helical structure. The dual structural coloration in Chalcothea smaragdina is therefore the result of the combination of helical matrix derived photonic colour and surface blade grating induced interference of reflected light, creating an additive effect on the sum colour appearance and leading to strong photonic–photonic coupling.
θb = mλ.46 The grating efficiency of the Littrow configuration is mainly dependent on the most intense order (m = 1), thus, the light wavelength for which scattering is optimized in Chalcothea smaragdina is calculated as 548 nm, coinciding with a green spectral range and overlapping with the reflection peak of an internal helical structure. The dual structural coloration in Chalcothea smaragdina is therefore the result of the combination of helical matrix derived photonic colour and surface blade grating induced interference of reflected light, creating an additive effect on the sum colour appearance and leading to strong photonic–photonic coupling.
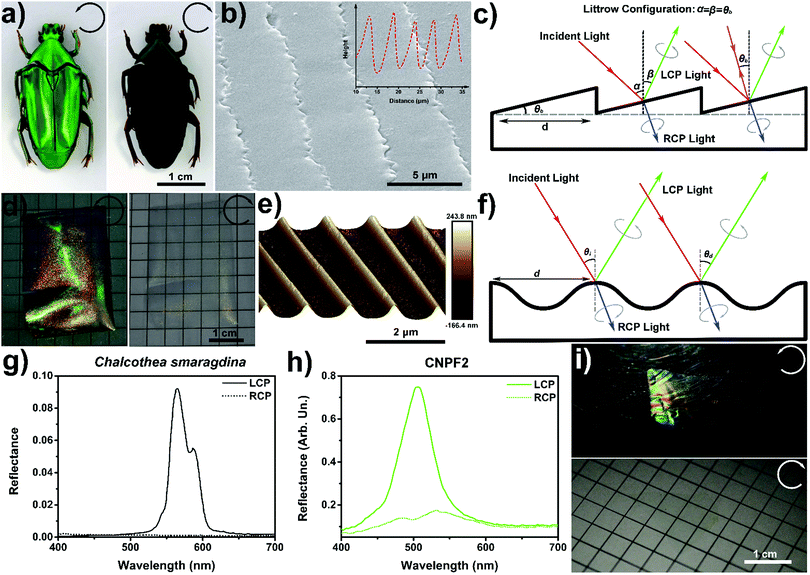 | ||
| Fig. 5 (a) Photographs of the beetle Chalcothea smaragdina captured in a LCP (left) and a RCP (right) filter, respectively. (b) SEM image of the periodic surface structure for the beetle. The inset represents the AFM surface profile of the beetle surface, which reveals a blazed grating surface topography. (c) Schematic representation of the polarization-selective surface blazed grating for the beetle exocuticle in which the diffracted LCP light generates constructive interference, whereas for the Littrow configuration (purple lines) the incidence angle and diffraction angle are identical, leading to a special specular reflection. (d) Photographs of CNPF2 captured using a LCP (left) and a RCP (right) filter, respectively. (e) Three-dimensional AFM image of CNPF2 that exhibits a smooth sinusoidal surface profile. (f) Schematic description of the chiral nematic ordered holographic surface grating with selective constructive interference for LCP light. (g and h) LCP and RCP reflectance spectra for the beetle of Chalcothea smaragdina (g) and CNPF2 (h), respectively. (i) Photographs of CNPF1 with strong photonic–photonic coupling captured in a LCP and RCP filter. (a), (b) and (g) were adopted with permission from ref. 11. | ||
To better compare the similarities and differences (structure and optics) between Chalcothea smaragdina and our mimetic patterned sample, we choose CNPF2 with the same green structural colour appearance that has both periodic surface topography and a helicoidal ultrastructure. In agreement with the circularly polarized response associated with the beetle, upon illumination the captured photographs of CNPF2 exhibit bright green appearance under a LCP filter which completely extinguishes through a RCP filter, indicative of the selective reflection of circularly polarized light and optical scattering from the sample (Fig. 5d). Closer inspection of the film surface by AFM images reveals a 3D sinusoidal surface pattern with a smooth profile (Fig. 5e), which can be classified into holographic grating, responsible for a diffraction-induced rainbow-like appearance in an oblique view (Fig. S11, ESI†). Blazed gratings can offer extremely high diffraction efficiency at the designed wavelength, whilst they suffer from periodic optical errors and ghosts.46 When compared with the blazed gratings, the holographic grating can reduce and eliminate these errors, only with the drawback of reduced diffraction efficiency. According to the grating equation d(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi − sin
θi − sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θd) = mλ, θi and θd are the incidence and diffraction angles, respectively.47 When the incident light with a wavelength of λ impinges on the grating surface at a given value of θi, the diffracted light scatters in different angular directions with constructive interference (Fig. 5f). The scattering maps of CNPF2 for circularly polarized light diffractions showed that the diffracted signals remained strong under LCP illumination while being almost extinguished under RCP illumination (Fig. S12, ESI†), which exhibited a close agreement with the circularly polarized optical images. In both cases, Chalcothea smaragdina with blazed grating and CNPF2 with holographic grating, the diffractive scattering resulting due to the patterned chiral nematic structure reflects a half proportion of incident light with LCP handedness away from the grating surface while the remaining with RCP state is transmitted. As a result, the scatterings imparted by surface topography (blade or sinusoidal) can be switched on/off under different circularly polarized illuminations, displaying vivid colour appearance only with LCP light.
θd) = mλ, θi and θd are the incidence and diffraction angles, respectively.47 When the incident light with a wavelength of λ impinges on the grating surface at a given value of θi, the diffracted light scatters in different angular directions with constructive interference (Fig. 5f). The scattering maps of CNPF2 for circularly polarized light diffractions showed that the diffracted signals remained strong under LCP illumination while being almost extinguished under RCP illumination (Fig. S12, ESI†), which exhibited a close agreement with the circularly polarized optical images. In both cases, Chalcothea smaragdina with blazed grating and CNPF2 with holographic grating, the diffractive scattering resulting due to the patterned chiral nematic structure reflects a half proportion of incident light with LCP handedness away from the grating surface while the remaining with RCP state is transmitted. As a result, the scatterings imparted by surface topography (blade or sinusoidal) can be switched on/off under different circularly polarized illuminations, displaying vivid colour appearance only with LCP light.
Furthermore, we also presented the circularly polarized spectral comparison of Chalcothea smaragdina and the sample of CNPF2. Typically, the LCP specular reflection spectrum derived from the beetle surface showed a pronounced double-peak photonic band-gap with the principal reflection peak centred at 565 nm and less intense feature at 585 nm, which was due to the pitch undulations of helicoid structures. Meanwhile, the RCP spectrum exhibited an absence of distinguishable optical features, implying the extinction of RCP reflection (Fig. 5g). It should be noted that the surface blazed grating induced reflection feature also vanished during RCP measurement which proved the LCP state of reflected light under Littrow configuration, showing full photonic–photonic coupling inside the dual photonic structures. By contrast, the reflection spectrum of CNPF2 exhibited a distinct peak reflectance at 506 nm for LCP light, which was significantly suppressed under RCP measurement (Fig. 5h), which resulted from the left-handed chiral nematic CNC matrix. Unlike Chalcothea smaragdina, the surface grating induced reflection peaks in CNPF2 were located at the UV-blue spectral range (245 and 300 nm, see Fig. 3), far away from its corresponding helicoid derived photonic band-gap and lacking photonic–photonic coupling. However, blue shifting the photonic band-gap led to a strong coupling effect between the helicoid organized CNCs and holographic surface grating, showing saturated blue colour appearance (Fig. S2, ESI†). This metallic blue structural colouration was attributed to the combination of helicoid matrix and surface grating induced photonic coupling, which was sensitive to both the circular polarization state and incident angle of light illumination (Fig. 5i and Fig. S13, ESI†). It should be pointed out that the blue structural colouration totally extinguished and became transparent under a RCP filter, implying that the surface grating induced diffuse appearance was fully coupled with helical photonic band-gaps and kept in a circular polarization state, similar to the colouring mechanism of the beetle exocuticle.
Conclusions
In conclusion, here we have studied the chiral nematic organization and surface topography relations governing dual structural colorations in a CNPF sample, showing the possibility to engineer photonic colour in a custom-made cellulose paper by patterning the liquid crystalline CNCs. Our observations shed light on the colour appearance of CNPF arising from the selective Bragg reflection as well as further scattering of LCP light which related to the hierarchical structure, presenting programmable photonic–photonic coupling similar to the exocuticle of Chalcothea smaragdina. In addition, because of the 3D sinusoidal fluctuation on the film surface and tuneable chiral anisotropic bulk phase in the matrix, the reflected light underwent a polarization rotation along with a directional sensitive constructive interference. We believe that the present finding of nanoimprinting a self-assembled CNC helicoid with a precise spatial structure (micro- and nanoscopic scales) will provide knowledge regarding the designing and fabrication of future metamaterials and metasurfaces with cost-effective and eco-friendly procedures, which can also be introduced into other self-organized systems, e.g., block-co-polymers, liquid crystal colloids and functional nanoparticles.Author contribution
G. C. prepared the samples and carried out POM, SEM and part of the optical measurements. A. C. and D. P. carried out the light scattering measurement. G. C. and E. Z. designed and led the project. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by the Russell Berrie Nanotechnology Institute (RBNI), the Israel Science Foundation (ISF Grant No. 286/15). All the authors acknowledge funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement No. 682157, “xPRINT”).References
- A. G. Dumanli and T. Savin, Chem. Soc. Rev., 2016, 45, 6698–6724 RSC.
- A. R. Parker, J. Opt. A: Pure Appl. Opt., 2000, 2, R15–R28 CrossRef.
- P. Vukusic, J. Sambles and C. Lawrence, Nature, 2000, 404, 457 CrossRef CAS.
- D. Raabe, P. Romano, C. Sachs, A. Al-Sawalmih, H.-G. Brokmeier, S. B. Yi, G. Servos and H. Hartwig, J. Cryst. Growth, 2005, 283, 1–7 CrossRef CAS.
- M. Giraud, J. Castanet, F. Meunier and Y. Bouligand, Tissue Cell, 1978, 10, 671–686 CrossRef CAS.
- Z. Bian, K. Li, W. Huang, H. Cao, H. Yang and H. Zhang, Appl. Phys. Lett., 2007, 91, 201908 CrossRef.
- T. H. Chiou, S. Kleinlogel, T. Cronin, R. Caldwell, B. Loeffler, A. Siddiqi, A. Goldizen and J. Marshall, Curr. Biol., 2008, 18, 429–434 CrossRef CAS.
- V. Sharma, M. Crne, J. O. Park and M. Srinivasarao, Science, 2009, 325, 449–451 CrossRef CAS.
- I. M. Daly, M. J. How, J. C. Partridge, S. E. Temple, N. J. Marshall, T. W. Cronin and N. W. Roberts, Nat. Commun., 2016, 7, 12140 CrossRef CAS.
- S. Vignolini, P. J. Rudall, A. V. Rowland, A. Reed, E. Moyroud, R. B. Faden, J. J. Baumberg, B. J. Glover and U. Steiner, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15712–15715 CrossRef CAS.
- L. T. McDonald, E. D. Finlayson, B. D. Wilts and P. Vukusic, Interface Focus, 2017, 7, 20160129 CrossRef.
- Z. G. Zheng, Y. Li, H. K. Bisoyi, L. Wang, T. J. Bunning and Q. Li, Nature, 2016, 531, 352–356 CrossRef CAS PubMed.
- W. Huang, C. l. Yuan, D. Shen and Z. G. Zheng, J. Mater. Chem. C, 2017, 5, 6923–6928 RSC.
- Z. G. Zheng, R. S. Zola, H. K. Bisoyi, L. Wang, Y. Li, T. J. Bunning and Q. Li, Adv. Mater., 2017, 29, 1701903 CrossRef.
- D. Klemm, B. Heublein, H. P. Fink and A. Bohn, Angew. Chem., Int. Ed., 2005, 44, 3358–3393 CrossRef CAS.
- Y. Habibi, L. A. Lucia and O. J. Rojas, Chem. Rev., 2010, 110, 3479–3500 CrossRef CAS.
- B. G. Rånby, Discuss. Faraday Soc., 1951, 11, 158–164 RSC.
- S. Mukherjee and H. Woods, Biochim. Biophys. Acta, 1953, 10, 499–511 CrossRef CAS.
- J. F. Revol, H. Bradford, J. Giasson, R. Marchessault and D. Gray, Int. J. Biol. Macromol., 1992, 14, 170–172 CrossRef CAS.
- S. Beck, J. Bouchard and R. Berry, Biomacromolecules, 2010, 12, 167–172 CrossRef.
- A. G. M. Dumanli, H. M. van der Kooij, G. Kamita, E. Reisner, J. J. Baumberg, U. Steiner and S. Vignolini, ACS Appl. Mater. Interfaces, 2014, 6, 12302–12306 CrossRef CAS.
- K. E. Shopsowitz, H. Qi, W. Y. Hamad and M. J. MacLachlan, Nature, 2010, 468, 422–425 CrossRef CAS PubMed.
- M. K. Khan, M. Giese, M. Yu, J. A. Kelly, W. Y. Hamad and M. J. MacLachlan, Angew. Chem., Int. Ed., 2013, 52, 8921–8924 CrossRef CAS PubMed.
- R. M. Parker, B. Frka-Petesic, G. Guidetti, G. Kamita, G. Consani, C. Abell and S. Vignolini, ACS Nano, 2016, 10, 8443–8449 CrossRef CAS.
- Y. Li, E. Prince, S. Cho, A. Salari, Y. M. Golestani, O. D. Lavrentovich and E. Kumacheva, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 2137–2142 CrossRef CAS PubMed.
- G. Chu, R. Vilensky, G. Vasilyev, S. Deng, D. Qu, Y. Xu and E. Zussman, Angew. Chem., 2017, 129, 8877–8881 CrossRef.
- G. Chu, G. Vasilyev, R. Vilensky, M. Boaz, R. Zhang, P. Martin, N. Dahan, S. Deng and E. Zussman, Langmuir, 2018, 34, 13263–13273 CrossRef CAS.
- G. Chu, R. Vilensky, G. Vasilyev, P. Martin, R. Zhang and E. Zussman, J. Phys. Chem. Lett., 2018, 9, 1845–1851 CrossRef CAS PubMed.
- A. Gençer, C. Schütz and W. Thielemans, Langmuir, 2016, 33, 228–234 CrossRef PubMed.
- J. P. Lagerwall, C. Schütz, M. Salajkova, J. Noh, J. H. Park, G. Scalia and L. Bergström, NPG Asia Mater., 2014, 6, e80 CrossRef CAS.
- G. Chu, H. Yin, H. Jiang, D. Qu, Y. Shi, D. Ding and Y. Xu, J. Phys. Chem. C, 2016, 120, 27541–27547 CrossRef CAS.
- G. Chu, X. Wang, H. Yin, Y. Shi, H. Jiang, T. Chen, J. Gao, D. Qu, Y. Xu and D. Ding, ACS Appl. Mater. Interfaces, 2015, 7, 21797–21806 CrossRef CAS.
- A. Querejeta-Fernández, G. G. Chauve, M. Methot, J. Bouchard and E. Kumacheva, J. Am. Chem. Soc., 2014, 136, 4788–4793 CrossRef.
- J. Majoinen, J. Hassinen, J. S. Haataja, H. T. Rekola, E. Kontturi, M. A. Kostiainen, R. H. Ras, P. Törmä and O. Ikkala, Adv. Mater., 2016, 28, 5262–5267 CrossRef CAS.
- G. Chu, A. Camposeo, R. Vilensky, G. Vasilyev, P. Martin, D. Pisignano and E. Zussman, Matter, 2019, 1, 988–1000 CrossRef.
- M. Kolle, P. M. Salgard-Cunha, M. R. Scherer, F. Huang, P. Vukusic, S. Mahajan, J. J. Baumberg and U. Steiner, Nat. Nanotechnol., 2010, 5, 511–515 CrossRef CAS.
- S. Coyle, G. Prakash, J. Baumberg and M. Abdelsalam, Appl. Phys. Lett., 2003, 83, 767–769 CrossRef CAS.
- G. Nyström, A. B. Fall, L. Carlsson and L. Wågberg, Cellulose, 2014, 21, 1591–1599 CrossRef.
- R. Meister, H. Dumoulin, M. A. Hallé and P. Pieranski, J. Phys. II, 1996, 6, 827–844 CrossRef CAS.
- R. Meister, M. A. Hallé, H. Dumoulin and P. Pieranski, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 3771 CrossRef CAS PubMed.
- B. Wang and A. Walther, ACS Nano, 2015, 9, 10637–10646 CrossRef CAS.
- G. Chu, W. Xu, D. Qu, Y. Wang, H. Song and Y. Xu, J. Mater. Chem. C, 2014, 2, 9189–9195 RSC.
- H. De Vries, Acta Crystallogr., 1951, 4, 219–226 CrossRef CAS.
- R. S. Zola, H. K. Bisoyi, H. Wang, A. M. Urbas, T. J. Bunning and Q. Li, Adv. Mater., 2019, 31, 1806172 CrossRef.
- M. Born and E. Wolf, Principles of Optics, Cambridge University Press, Cambridge, 1999, pp. 595–606 Search PubMed.
- E. Loewen, M. Nevière and D. Maystre, Appl. Opt., 1977, 16, 2711–2721 CrossRef CAS.
- M. Kolle, Photonic structures inspired by nature, Springer, New York, 2011 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9mh01485c |
| This journal is © The Royal Society of Chemistry 2020 |