Open Access Article
Open Access ArticleAutomated microfluidic screening of ligand interactions during the synthesis of cesium lead bromide nanocrystals†
Shangkun
Li
a,
Robert W.
Baker
b,
Ioannis
Lignos‡
 a,
Zhibo
Yang§
a,
Stavros
Stavrakis
a,
Zhibo
Yang§
a,
Stavros
Stavrakis
 a,
Philip D.
Howes
a,
Philip D.
Howes
 *a and
Andrew J.
deMello
*a and
Andrew J.
deMello
 *a
*a
aInstitute for Chemical and Bioengineering, Department of Chemistry and Applied Biosciences, ETH Zürich, Vladimir Prelog Weg 1, 8093 Zürich, Switzerland. E-mail: philip.howes@chem.ethz.ch; andrew.demello@chem.ethz.ch
bDepartment of Chemistry, University of Bath, Claverton Down, Bath, UK
First published on 2nd March 2020
Abstract
Varying the nature of the molecular surface ligands used to synthesize and stabilize lead halide perovskite nanocrystals provides a facile way of tuning and optimizing particle properties. However, the inherently complex reaction parameter space associated with perovskite nanocrystal synthesis complicates this, necessitating long-term and laborious experimentation to optimize conditions for a specific ligand set, and to compare nanoparticle properties across different ligand sets. In the current work, we present an automated microfluidic-based strategy for multidimensional parameter screening, seeking to maximize luminescence intensities and minimize emission bandwidths from quantum confined nanostructures, by monitoring variations in photoluminescence as a function of reaction temperature, base-to-acid ligand ratio, and ligand alkyl chain structure (linear versus branched). For a linear ligand pair (octylamine and octanoic acid), we find two reaction parameter sets that yield bright and narrow emission from nanosheets emitting at 460 nm (synthesized at 100 °C with a low base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio, FWHM = 25 nm) and nanowires emitting at 497 nm (synthesized at 140 °C with a high base
acid ratio, FWHM = 25 nm) and nanowires emitting at 497 nm (synthesized at 140 °C with a high base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio, FWHM = 17 nm). Introducing branched ligands (2-ethylhexylamine and/or 2-ethylhexanoic acid) induces a red shift in emission and shows that bright and narrow emission can only be obtained from weakly quantum-confined nanostructures, within the reaction conditions studied. This work represents the first use of a rapid automated microfluidic system for the screening of ligand interactions during the synthesis lead halide perovskite nanocrystals.
acid ratio, FWHM = 17 nm). Introducing branched ligands (2-ethylhexylamine and/or 2-ethylhexanoic acid) induces a red shift in emission and shows that bright and narrow emission can only be obtained from weakly quantum-confined nanostructures, within the reaction conditions studied. This work represents the first use of a rapid automated microfluidic system for the screening of ligand interactions during the synthesis lead halide perovskite nanocrystals.
Design, System, ApplicationIn this work we employ rapid multidimensional reaction parameter screening in the design optimization of cesium lead bromide nanocrystals, with a focus on how changes in molecular surface ligand structure, base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio and reaction temperature affect resultant photoluminescence properties of the nanocrystals. The system revolves around the use of an automated droplet microfluidic reactor with integrated photoluminescence collection, which allows rapid progression through a user-defined set of synthesis parameters covering the parameter space of interest. While we apply this to the design optimization of cesium lead bromide nanocrystals in a binary organic amine/acid ligand system, the approach could be used for scanning a wide variety of reaction input and output variables, and shows much promise for application in the discovery and optimization of many different functional nanoparticles compositions and reaction formulations. acid ratio and reaction temperature affect resultant photoluminescence properties of the nanocrystals. The system revolves around the use of an automated droplet microfluidic reactor with integrated photoluminescence collection, which allows rapid progression through a user-defined set of synthesis parameters covering the parameter space of interest. While we apply this to the design optimization of cesium lead bromide nanocrystals in a binary organic amine/acid ligand system, the approach could be used for scanning a wide variety of reaction input and output variables, and shows much promise for application in the discovery and optimization of many different functional nanoparticles compositions and reaction formulations.
|
1. Introduction
The surface ligands of colloidal nanocrystals are fundamental in defining material properties, including size, shape, crystal phase, electronic character and colloidal stability.1–3 The ability to tune and rationally design nanocrystal properties as a function of surface ligand character requires a deep understanding of their molecular properties, behaviour and interactions, before, during and after the growth of the nanocrystal product. Tools that facilitate more efficient screening and characterization of surface ligands in nanocrystal synthesis are vital in expediting the transfer of these promising materials into target applications, including optoelectronics4,5 (photovoltaics, displays, lighting) and biomedicine6,7 (diagnostics, therapeutics, imaging).Interest in lead halide perovskite (LHP) nanocrystals has exploded in the half decade since their first reports,8,9 with particular excitement surrounding their application in optoelectronics.5,10 This has been driven by their exceptional properties, including high photoluminescence quantum yields (PLQYs, routinely >95%), widely tuneable optical characteristics and facile solution-processibility,11,12 along with the general advantages of metal halide perovskites that include strong optical absorption, high charge-carrier mobilities and extremely high defect tolerance.13 Given humanity's drastic need to increase sustainable and clean energy, much hope has been pinned on LHP nanocrystals in yielding next-generation photovoltaics and electroluminescent diodes.5,10,14
The propensity of organic–inorganic hybrid LHPs to degrade over time has shifted interest to more stable all-inorganic analogues, in particular CsPbX3 (X = halide).15–17 With a view to further improving stability, a major focus has fallen on understanding nanocrystal surface chemistry,12,15,18 since structural and optical instabilities during isolation, purification and handling are still major issues.10 Such instability is seen in both the colloidal state and after casting into solid-state devices, where exposure to heat, light, moisture and oxygen severely accelerates physical and optical degradation.19 The unique challenges presented by LHP nanocrystals have meant that the plethora of knowledge gathered around more traditional semiconductor nanocrystals has not been wholly translatable to these new systems.20 Therefore, developing an improved understanding of surface stability in LHP nanocrystals has become a primary challenge for researchers in the field.21
LHP nanocrystals are commonly synthesized in non-polar solvents, with a binary ligand system comprising aliphatic carboxylic acids and primary amines of various chain lengths.9,22,23 The dynamic interplay between the ligands themselves (acid–base chemistry), with the reaction precursors, with the nucleating and growing nanocrystals and with the final (rapidly generated) reaction products results in a complex synthetic system, containing various potent surface binding species (such as lead carboxylate and aliphatic ammonium halides, acids and amines20) and also complex mechanisms, such as Ostwald ripening.22 Further, literature results indicate that relatively minor modifications to ligands can yield significant shifts in nanocrystal properties. For example, Chen et al. recently showed that by mixing C8 and C18 alkylamine and carboxylic acid ligands in the synthesis of CsPbI3, QDs exhibiting improved optical properties, long-term stability and enhanced charge transport rates when compared to QDs capped only with C18 ligands.24 Furthermore, Shamsi and coworkers have reported the growth of CsPbBr3 nanosheets with lateral dimensions up to micrometers using a mixed C8/C18 alkylamine and carboxylic acid system.25
Branched capping ligands have commonly been used in solution-phase nanocrystal synthesis (e.g. trioctylphosphine oxide for quantum dots26), owing to steric effects. These have also been investigated in the context of LHP nanocrystals. For example, Wu et al. used trioctylphosphine oxide (TOPO) as an additive in the common oleic acid/oleylamine system, and observed that TOPO allows for higher temperature syntheses owing to its strong surface adsorption and dramatically improved stability of CsPbX3 nanocrystals against ethanol treatment.27 Additionally, Luo and coworkers used the branched capping ligand (3-aminopropyl)triethoxysilane to improve the stability of CH3NH3PbBr3 perovskite nanocrystals in polar solvents.27 Further, Huang et al. treated CsPbX3 nanocrystals with polyhedral oligomeric silsesquioxane and observed enhanced stability in water for several months.28 In general, long chain surface ligands impede efficient charge recombination,29 favouring the use of shorter ligands.23 However, it has been observed that changing the length of the aliphatic chains, and changing the base–acid ratio in the reaction medium yields drastic variations in the size, shape, crystal phase and optical properties of the final products, which can assume varied morphologies including spheres, cubes, plates, sheets, rods, and wires.23,30,31 Introducing branched ligands introduces an additional modality to exert control over these properties. For example, Yan et al. recently demonstrated improved colloidal stability and optical stability under ambient conditions, and enhanced amplified spontaneous emission (ASE) performance, by substituting the commonly-used oleic acid for the branched 2-hexyldecanoic acid.29 Further, although interpenetration of ligands on colliding nanocrystals can lead to particle aggregation due to attractive van der Waals forces, branched or unsaturated ligands can restrict this due to a disruption of ligand alignment. This effect has been explored by Krieg et al. in their development of zwitterionic capping ligands for CsPbX3 nanocrystal synthesis,32,33 and by Yang et al. in studying the colloidal stability of CdSe nanocrystals with n-alkanoate ligands.34,35
It is important to note that large scale screening and mapping of reaction parameter spaces in the synthesis of LHP nanocrystals is hindered by the low throughput of traditional flask-based synthetic approaches.23,30,31 In this regard, microfluidic technologies possesses significant advantages when compared to batch syntheses.36,37 Indeed, the last decade has seen significant developments in the use of microfluidic reactors for nanocrystal synthesis, with many studies reporting improved reaction control and the rapid production of a wide range of products with tailored chemical and photophysical properties.38–42 Of particular current interest are segmented flow microfluidic reactors, where the reaction is split into discreet droplets separated by a continuous carrier phase.43 Such formats confer additional advantages when compared to continuous flow approaches; most prominently rapid mixing (that yields nanocrystals with lower polydispersity) and negligible reactor fouling. Additionally, improved heat and mass transfer provides for unrivalled control over reaction parameters, ensuring excellent product-to-product reproducibility.44 A key capability of microfluidic reactors of this kind is the capacity to scan large and multidimensional reaction parameter spaces via automated reaction control (of precursor dosing, reaction times and temperature) and in situ product characterization (by absorption and emission spectroscopies).45 Put simply, such approaches allow for a dramatic increase in the rate of information generation/collection, with a concurrent and dramatic decrease in reagent usage, when compared to standard flask-based synthesis methods.
In regard to the synthesis of LHP nanocrystals in segmented-flow microfluidics, significant developments have recently been reported by us,46–51 and Abolhasani.52,53 Whilst these studies have been instrumental in revealing the nature of growth kinetics of LHP nanocrystals,47,52,54 and of compositional tuning for optical and morphological character,46,48,49,53 they have not yet been applied to the study of surface ligand effects during the synthesis of nanocrystals.
Herein, we show how an automated microfluidic reactor with integrated photoluminescence detection can be used to perform detailed parametric scans (temperature versus base–acid ratio) for defined ligand sets, and critical comparisons between different ligand sets. We study the model case of how ligand structure affects CsPbBr3 nanocrystal growth in a binary organic acid/amine ligand system. The four tested ligands all possess eight carbons in the alkyl chain, but one set is branched, and the other linear. By repeating the multidimensional parameter scans under identical conditions but substituting in the different ligands, it is possible to conduct a detailed comparison between different conditions and elucidate the effect of alkyl structure on the resultant nanocrystal properties. To our knowledge, this is the first demonstration of a microfluidic platform able to perform high-throughput screening of ligand activities in nanocrystal synthesis, and serves as an important demonstration of the power of multiparametric scanning in the characterization of ligand effects in nanocrystal systems.
2. Materials & methods
2.1 Materials
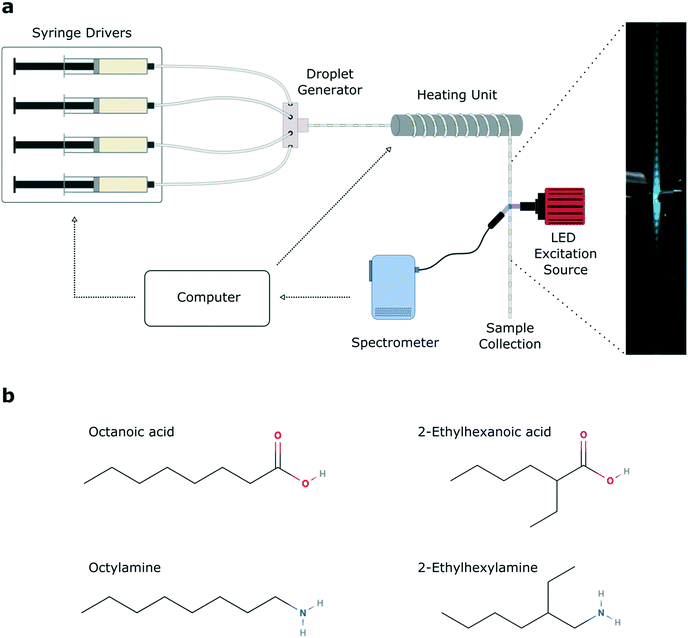
Cesium carbonate (Cs2CO3, Aldrich, 99.9%), lead bromide (PbBr2, ABCR, 98%), 1-octadecene (ODE, Sigma-Aldrich, 90%), octanoic acid (Sigma-Aldrich, ≥99%), octylamine (Sigma-Aldrich, 99%), 2-ethylhexanoic acid (TCI, >99%), 2-ethylhexylamine (TCI, >98%) were used as received.2.2 Preparation of precursor solutions
Cesium precursor: Cs2CO3 (51 mg) was loaded into a 20 ml Schlenk flask together with 10 ml of ODE and 0.625 ml of organic acid (octanoic or 2-ethylhexanoic acid), dried for 1 h at 120 °C, and then cooled to room temperature under N2. For the subsequent microfluidic synthesis, the precursor was loaded into a 10 mL Hamilton glass syringe.Lead bromide precursor: PbBr2 (138 mg) was loaded into a 20 ml Schlenk flask along with 10 ml of ODE. The cloudy mixture was heated to 120 °C under vacuum, and then the total 7.5 mmol of ligands (base plus acid at 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 1
1 or 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 base
1 base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid) were added under a N2 atmosphere. After the PbBr2 dissolved completely, the solution was cooled to room temperature under N2 before being loaded into a 10 ml Hamilton glass syringe.
acid) were added under a N2 atmosphere. After the PbBr2 dissolved completely, the solution was cooled to room temperature under N2 before being loaded into a 10 ml Hamilton glass syringe.
2.3 Microfluidic synthesis of nanocrystals
The precursor-loaded syringes were positioned on precision syringe pumps (neMESYS, Cetoni GmbH, Germany). Two syringes were filled with PbBr2 precursor with different ratios of ligands. One syringe was used to inject the carrier fluid (Galden Fluorinated Fluid, Blaser Swisslube AG, Germany) while another was used to injected Cs precursor. The precursors and oil were all conveyed separately through polytetrafluoroethylene (PTFE) tubing (1/16′′ OD, 0.5 mm ID, IDEX Health & Science, USA) into a polyether ether ketone (PEEK) 7-port manifold (0.5 mm thru-hole, IDEX Health & Science, USA), where they combined to form a segmented flow. The ratio of carrier phase (oil) to dispersed phase (ODE) could be controlled precisely, along with the exact base–acid ligand ratio within the dispersed phase, by varying the pump rates of the four separate syringes. Droplets were conveyed through the tubing onto a heating module, where the tubing was wrapped around a copper rod heated to a user-defined reaction temperature. After exiting the heating unit, inline fluorescence measurements were performed on droplets using a 365 nm LED light source (M365LP1, Thorlabs, Germany) and a fiber coupled spectrometer (QE 65 Pro, Ocean Optics, USA) for detection, with an integration time of 30 milliseconds. Each parameter set was run for 2 minutes, and data was recorded for the last 30 seconds of this to allow for reactor pressure equilibration. All reactor units are controlled and systematically linked together using an in-house-developed LabVIEW program, which automatically adjusts the temperature, flow rate, and residence time while managing data logging. All photoluminescence spectra were measured inline without any product purification.2.4 Data analysis
Each experimental run yielded 121 .csv files containing 335 spectra each. These were processed using a custom Python script to average the data in each file, to compile all data, to perform calculations of dominant peak position, median, interquartile range and peak intensity, and to plot all spectra, scatter, and contour plots.2.5 Offline characterization
Selected reaction products were collected at the exit of the reactor for later analysis by transmission electron microscopy (TEM) (Hitachi HT7700, accelerating voltage 100 kV). TEM samples were prepared using crude products without further processing.3. Results
General system description
Cesium lead bromide nanocrystals were synthesized following literature protocols,54 with some modifications. The cesium, lead and bromine precursors were maintained at a constant concentration (yielding a Cs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pb
Pb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Br ratio of 1
Br ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.9
2.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.8), whilst the reaction temperature and the ratio between the amine and acid ligands was varied during experiment (between 90 and 190 °C, and a base
5.8), whilst the reaction temperature and the ratio between the amine and acid ligands was varied during experiment (between 90 and 190 °C, and a base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio of 0.7
acid ratio of 0.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1.2
1 to 1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Accordingly, changes in photoluminescence and size/morphology within a single experimental run occurred as a function of ligand base
1). Accordingly, changes in photoluminescence and size/morphology within a single experimental run occurred as a function of ligand base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio and temperature. The ligand ratio was varied during experiment by maintaining the cesium precursor at a constant flow rate, and by keeping the total flow rate of the two lead sources constant while altering the individual flow rates to yield different ratios of base to acid. It is important to note that this ligand base
acid ratio and temperature. The ligand ratio was varied during experiment by maintaining the cesium precursor at a constant flow rate, and by keeping the total flow rate of the two lead sources constant while altering the individual flow rates to yield different ratios of base to acid. It is important to note that this ligand base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio considers the carboxylic acid delivered in both the lead and cesium precursors.
acid ratio considers the carboxylic acid delivered in both the lead and cesium precursors.
The automated microfluidic platform is shown in Fig. 1a. A key component of the system is a LabVIEW script which controls the flow rate of the precursor and oil syringe pumps, and collects inline photoluminescence data from the spectrometer. Within a single experimental run, 11 temperatures and 11 different base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ligand ratios were sampled, yielding 121 unique reaction parameter sets per experiment, for four unique ligand sets (see Fig. S1† for full spectral data sets). Between different experimental runs, the ligands were exchanged, varying the aliphatic branching (Fig. 1b). We chose four ligands, namely the linear ligands octanoic acid (C8A) and octylamine (C8B), and branched ligands 2-ethylhexanoic acid (C8Ab) and 2-ethylhexylamine (C8Bb). Growth rates of cesium lead bromide nanocrystals are typically high, owing to the rapidity of the ionic metathesis reaction, therefore induction of and control over the growth focussing phase is challenging. As a result, it is common to observe multiple peaks in the PL spectra of crude reaction solutions, arising from variable levels of quantum confinement in the different sized nanocrystals.55 This often necessitates careful post-synthetic processing to isolate a monodisperse population,32 with the purification procedure (typically using polar solvents) commonly leading to degradation of the ligand shell and therefore the nanocrystals.56,57
acid ligand ratios were sampled, yielding 121 unique reaction parameter sets per experiment, for four unique ligand sets (see Fig. S1† for full spectral data sets). Between different experimental runs, the ligands were exchanged, varying the aliphatic branching (Fig. 1b). We chose four ligands, namely the linear ligands octanoic acid (C8A) and octylamine (C8B), and branched ligands 2-ethylhexanoic acid (C8Ab) and 2-ethylhexylamine (C8Bb). Growth rates of cesium lead bromide nanocrystals are typically high, owing to the rapidity of the ionic metathesis reaction, therefore induction of and control over the growth focussing phase is challenging. As a result, it is common to observe multiple peaks in the PL spectra of crude reaction solutions, arising from variable levels of quantum confinement in the different sized nanocrystals.55 This often necessitates careful post-synthetic processing to isolate a monodisperse population,32 with the purification procedure (typically using polar solvents) commonly leading to degradation of the ligand shell and therefore the nanocrystals.56,57
When analysing spectral data, we report the dominant peak position, the median peak position, the peak intensity and the interquartile range (see Fig. S2†). The dominant peak position indicates the dominant emitting species in the reaction solution, but ignores any subpeaks present. The median emission wavelength is used as an indicator of average emission wavelength weighted by intensity (note, although the value itself does not correspond to a specific excited state, for spectra containing only one peak, the value tends towards the peak emission wavelength). The peak intensity is used as a measure of the brightness of the dominant reaction product. It should be noted that we do not compare the peak emission intensities between ligand sets, as excitation intensities vary between experiments. Furthermore, the interquartile range (IQR) is used in preference to the full width at half maximum (FWHM), since many of the spectra contain several convoluted peaks; the IQR yields a single value as an indicator of the spread of emission wavelengths in a sample.
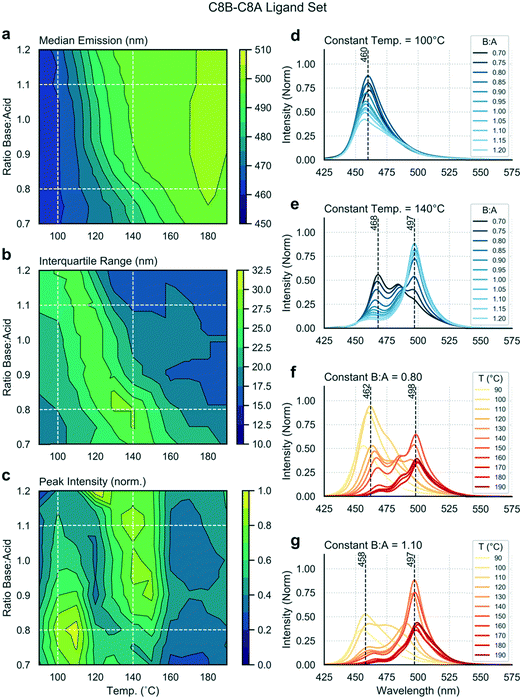
Mapping trends within a single experiment
Multiple input and output variables are used to map the parameter space and to identify the optimal conditions for a given ligand set. Using the linear ligand set C8B–C8A, we sought to find reaction conditions that yield high emission intensities and low spectral widths (or IQRs). Fig. 2 presents extracted data as a series of contour plots (a–c) and spectral series (d–g) extracted along lines of interest in the contour plots. In this way, it is possible to use the contour plots for a broad survey of the reaction parameter space, and then to extract specific spectra of interest for further study. A general shift in the median emission towards the red is observed as a function of reaction temperature, within the range 460 to 500 nm. As the bulk emission of CsPbBr3 occurs at approximately 525 nm (well above the indicated range), we see that all nanostructures synthesized in this parameter space are quantum confined.58 There is a smaller dependence of the median emission on base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio. The distinct spectral peaks do not shift continuously, but instead rise or fall within relatively narrow ranges (Fig. 2d–g), suggesting the presence of several distinct species. There is a clear relationship between input variables and peak intensity, with two distinct regions of high intensity being visible in Fig. 2c and occurring at approximately 110 °C and 140 °C. At 110 °C, a lower base
acid ratio. The distinct spectral peaks do not shift continuously, but instead rise or fall within relatively narrow ranges (Fig. 2d–g), suggesting the presence of several distinct species. There is a clear relationship between input variables and peak intensity, with two distinct regions of high intensity being visible in Fig. 2c and occurring at approximately 110 °C and 140 °C. At 110 °C, a lower base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio yields a higher peak intensity, whereas at 140 °C a higher base
acid ratio yields a higher peak intensity, whereas at 140 °C a higher base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio yields a higher peak intensity. There is clear relationship between the “valley” separating these high intensity regions and the region where the IQR reaches a maximum, as emission is shared between two distinct species emitting at 460 or 497 nm in the intermediate zone. Accordingly, the maximum intensity is less than in neighbouring regions, where emission is dominated by single emitting species. The region of high IQR represents a transition zone which is undesirable when targeting a specific reaction product with minimal size (and emission) dispersity.
acid ratio yields a higher peak intensity. There is clear relationship between the “valley” separating these high intensity regions and the region where the IQR reaches a maximum, as emission is shared between two distinct species emitting at 460 or 497 nm in the intermediate zone. Accordingly, the maximum intensity is less than in neighbouring regions, where emission is dominated by single emitting species. The region of high IQR represents a transition zone which is undesirable when targeting a specific reaction product with minimal size (and emission) dispersity.
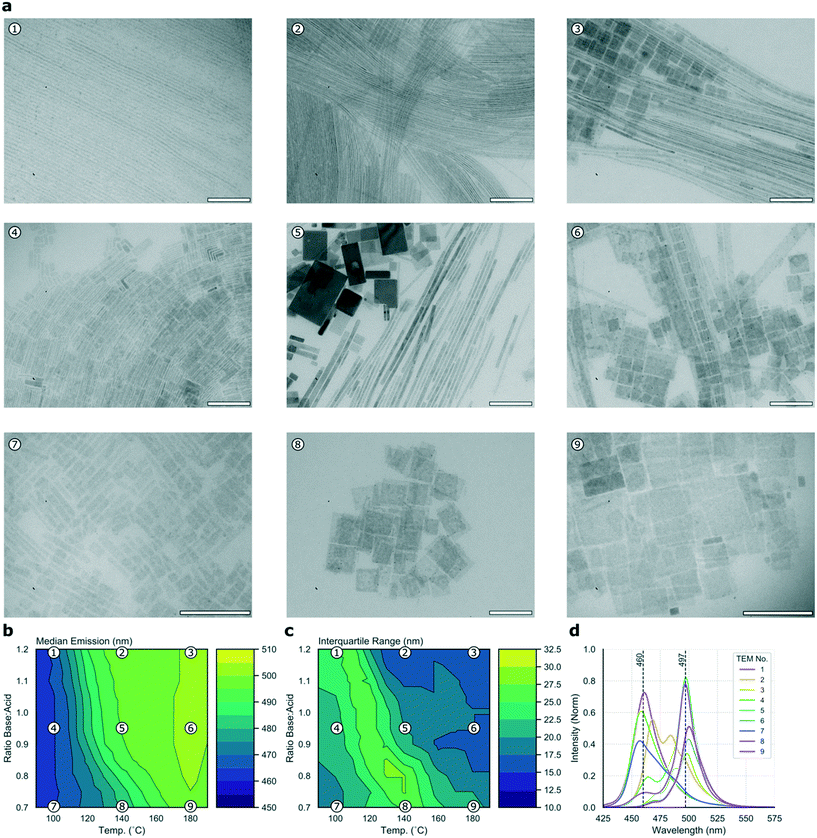
To cast further light on the large data set collected during the high-throughput microfluidic experiments, it is possible to collect a subset of samples for detailed offline analysis. Fig. 3a presents nine TEM micrographs of samples collected for the C8B–C8A experiment, sampled from points dispersed equidistantly through the parameter space and mapped in relation to the median and IQR contour plots in Fig. 3b and c, respectively, with the corresponding emission spectra shown in Fig. 3d. It should be noted that TEM imaging can be problematic for LHP nanocrystals, as the high energy electron beam can degrade samples.59 Further, studying the crude reaction product means that there are often many different structures visible in the micrographs (e.g.Fig. 3a5). These two issues make quantitative assessment of the different populations challenging, however the images do provide an indication of types of morphologies present, which can be related to the experimental data. In the current study, micrographs revealed two distinct species—nanoplates and nanowires, albeit with widely ranging dimensions. High base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratios appear to favour nanowire formation, with products tending towards nanosheets at higher temperatures and lower base
acid ratios appear to favour nanowire formation, with products tending towards nanosheets at higher temperatures and lower base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratios, an observation that is in agreement with previous results.22,60Fig. 3 shows that the two highly emissive species highlighted above correspond to nanowires emitting at 497 nm (synthesized at 140 °C with high base
acid ratios, an observation that is in agreement with previous results.22,60Fig. 3 shows that the two highly emissive species highlighted above correspond to nanowires emitting at 497 nm (synthesized at 140 °C with high base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio) and nanosheets emitting at 460 nm (synthesized at 100 °C with low base
acid ratio) and nanosheets emitting at 460 nm (synthesized at 100 °C with low base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio). Although products synthesized at 110 °C with low base
acid ratio). Although products synthesized at 110 °C with low base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio exhibit slightly higher emission intensities, this is at the expense of a higher IQR, so we suggest that the 100 °C condition offers a better overall result. Fig. S3a† shows the position of the two species within the parameter space, and their full emission spectra. Nanoplates emitting at 460 nm have a full width at half maximum (FWHM) of 25 nm, while nanowires emitting at 497 nm have a FWHM of 17 nm. Previous studies of CsPbBr3 nanocrystals have revealed a strong correlation between the thickness of nanostructures (in terms of crystalline unit cells) and the emission wavelength, due to quantum confinement of excitons.9 Bulk emission occurs at approximately 2.36 eV (525 nm), with higher energy emission occurring in the quantum confinement regime with nanostructures below the excitonic Bohr diameter (which is 7 nm for CsPbBr3).9,58 As the two major peaks in the spectral series of the linear ligands experiment occur at 460 and 497 nm, they can be ascribed to quantum-confined structures of CsPbBr3. The 460 and 497 nm peaks map to nanostructures of 3 and 11 unit cells, respectively.58,61 In summary, this experiment demonstrates how simultaneously scanning several input variables, and studying several output variables in concert allows ready visualization and selection of optimal reaction conditions, here revealing two distinct regions of useful emission characteristics from quantum confined nanostructures.
acid ratio exhibit slightly higher emission intensities, this is at the expense of a higher IQR, so we suggest that the 100 °C condition offers a better overall result. Fig. S3a† shows the position of the two species within the parameter space, and their full emission spectra. Nanoplates emitting at 460 nm have a full width at half maximum (FWHM) of 25 nm, while nanowires emitting at 497 nm have a FWHM of 17 nm. Previous studies of CsPbBr3 nanocrystals have revealed a strong correlation between the thickness of nanostructures (in terms of crystalline unit cells) and the emission wavelength, due to quantum confinement of excitons.9 Bulk emission occurs at approximately 2.36 eV (525 nm), with higher energy emission occurring in the quantum confinement regime with nanostructures below the excitonic Bohr diameter (which is 7 nm for CsPbBr3).9,58 As the two major peaks in the spectral series of the linear ligands experiment occur at 460 and 497 nm, they can be ascribed to quantum-confined structures of CsPbBr3. The 460 and 497 nm peaks map to nanostructures of 3 and 11 unit cells, respectively.58,61 In summary, this experiment demonstrates how simultaneously scanning several input variables, and studying several output variables in concert allows ready visualization and selection of optimal reaction conditions, here revealing two distinct regions of useful emission characteristics from quantum confined nanostructures.
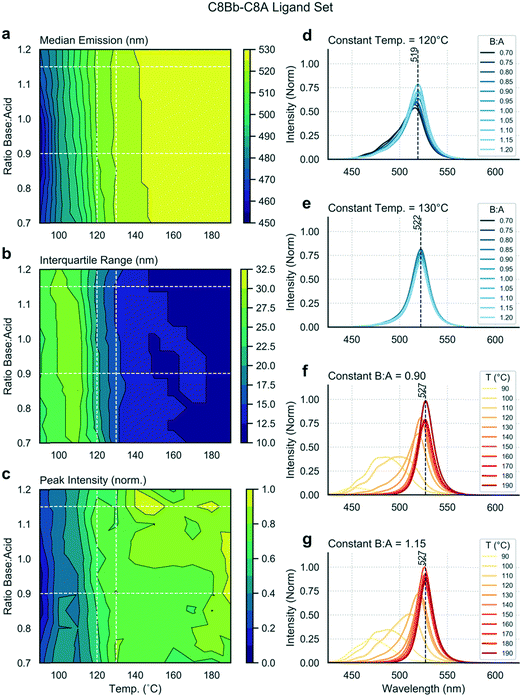
Next, we exchanged the octylamine (C8B) for 2-ethylhexamine (C8Bb), and ran the same analysis. Data shown in Fig. 4 are distinctly different from the linear ligand case (Fig. 2), showing the stark effect of amine ligand branching on output variables. Firstly, the median emission and IQR are now independent of the base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio (Fig. 4a and b). At lower temperatures, broader and lower intensity spectra are observed (Fig. 4f and g). As the temperature is increased, spectra shift towards the red and the IQR drops. At 190 °C, narrow emission spectra centred at 527 nm are obtained. Such emission corresponds to bulk material emission,58 showing that these nanostructures are no longer in the quantum confinement regime, and thus that it cannot be concluded that the sample is monodisperse. Interestingly, there is a dependence of the peak intensity on the base
acid ratio (Fig. 4a and b). At lower temperatures, broader and lower intensity spectra are observed (Fig. 4f and g). As the temperature is increased, spectra shift towards the red and the IQR drops. At 190 °C, narrow emission spectra centred at 527 nm are obtained. Such emission corresponds to bulk material emission,58 showing that these nanostructures are no longer in the quantum confinement regime, and thus that it cannot be concluded that the sample is monodisperse. Interestingly, there is a dependence of the peak intensity on the base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio at higher temperatures (>140 °C), with higher base content favouring higher fluorescence intensities (Fig. 4c). From these results, it is evident that there exists a narrow temperature range (between 120 and 130 °C) in which bright and narrow emission can be obtained (Fig. 4d and e) from very weakly quantum-confined nanostructures (519 to 522 nm emission), with only a mild dependence on base
acid ratio at higher temperatures (>140 °C), with higher base content favouring higher fluorescence intensities (Fig. 4c). From these results, it is evident that there exists a narrow temperature range (between 120 and 130 °C) in which bright and narrow emission can be obtained (Fig. 4d and e) from very weakly quantum-confined nanostructures (519 to 522 nm emission), with only a mild dependence on base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio. Fig. S3b† shows the position of two species in this range in parameter space, and their full emission spectra. Above 130 °C, emission arises from non-confined excitons, emitting above 525 nm. The TEM map of this experiment (Fig. S4†) shows the formation of nanosheets under all sampled reaction conditions. The three samples at 100 °C are less distinct and more aggregated, and correspond to the three lower wavelength spectra shown in Fig. S4d.† However, at 140 and 180 °C, the products are consistent, with all resulting in narrow spectral peaks centred at 527 nm, albeit with products that vary quite markedly in their lateral dimensions.
acid ratio. Fig. S3b† shows the position of two species in this range in parameter space, and their full emission spectra. Above 130 °C, emission arises from non-confined excitons, emitting above 525 nm. The TEM map of this experiment (Fig. S4†) shows the formation of nanosheets under all sampled reaction conditions. The three samples at 100 °C are less distinct and more aggregated, and correspond to the three lower wavelength spectra shown in Fig. S4d.† However, at 140 and 180 °C, the products are consistent, with all resulting in narrow spectral peaks centred at 527 nm, albeit with products that vary quite markedly in their lateral dimensions.
The remaining two ligand sets (C8B–C8Ab and C8Bb–C8Ab) showed less variation in emission character within each experiment, so they are now reviewed only briefly. For the C8B–C8Ab ligand set, we observe a dependence of median emission and IQR on temperature, with spectra red-shifting and narrowing with increasing temperature; but less of a dependence on the base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio (Fig. S5a and b†). However, as shown in Fig. S5c,† the peak fluorescence intensity does show a dependence on base
acid ratio (Fig. S5a and b†). However, as shown in Fig. S5c,† the peak fluorescence intensity does show a dependence on base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio, with a lower ratio favouring higher intensities, and a maximum occurring at high temperatures and low base
acid ratio, with a lower ratio favouring higher intensities, and a maximum occurring at high temperatures and low base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratios. Inspection of the three contour plots together indicates that there is a region that yields products in the weak quantum confinement regime (emission between 500 and 525 nm), with relatively bright and narrow emission, corresponding to the center and lower left portions of the parameter space as plotted. Within this region, bright and narrow quantum-confined emission is observed along the base
acid ratios. Inspection of the three contour plots together indicates that there is a region that yields products in the weak quantum confinement regime (emission between 500 and 525 nm), with relatively bright and narrow emission, corresponding to the center and lower left portions of the parameter space as plotted. Within this region, bright and narrow quantum-confined emission is observed along the base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio 0.7 line (Fig. S5f†), below a temperature of 140 °C (Fig. S5e†). Fig. S3c† shows the position of three products in this region of parameter space, and their full emission spectra. The TEM map shown in Fig. S6† exhibits a variety of nanostructures, including nanosheets with large lateral dimensions, similar to those synthesized by Shamsi et al. using a mixed C8/C18 binary ligand system.25 Further, under reaction conditions of 140 °C and base
acid ratio 0.7 line (Fig. S5f†), below a temperature of 140 °C (Fig. S5e†). Fig. S3c† shows the position of three products in this region of parameter space, and their full emission spectra. The TEM map shown in Fig. S6† exhibits a variety of nanostructures, including nanosheets with large lateral dimensions, similar to those synthesized by Shamsi et al. using a mixed C8/C18 binary ligand system.25 Further, under reaction conditions of 140 °C and base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio of 0.95, nanocubes are obtained with an emission peak in weak confinement, at 515 nm.
acid ratio of 0.95, nanocubes are obtained with an emission peak in weak confinement, at 515 nm.
Finally, Fig. S7† presents a detailed analysis of the C8Bb–C8Ab ligand set, where all of the reaction products yield peaks above 519 nm, with low IQR in all cases. However, the peak intensity does vary considerably across the data set. There is a narrow temperature range (between 90 and 100 °C) that yields emission peaks at approximately 520 nm, with maximum intensity occurring at 0.95 base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio at 100 °C. Fig. S3d† shows the position of four products in this region of the parameter space, with their full emission spectra. Emission at 520 nm suggests very weak quantum confinement. Fig. S8† shows the TEM map for the branched ligand set, exhibiting a mixture of nanocubes and nanospheres, and some larger aggregates.
acid ratio at 100 °C. Fig. S3d† shows the position of four products in this region of the parameter space, with their full emission spectra. Emission at 520 nm suggests very weak quantum confinement. Fig. S8† shows the TEM map for the branched ligand set, exhibiting a mixture of nanocubes and nanospheres, and some larger aggregates.
Mapping trends between experiments
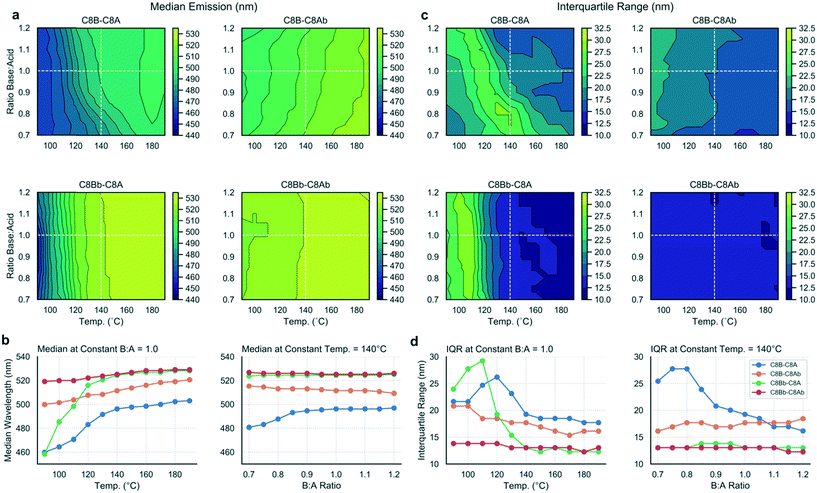
Using the methodology outlined herein, it is possible to make detailed comparisons between experiments and elucidate the effects of different ligands on the reaction output variables. To compare the data sets for the four ligand combinations studied in this work, the contour plots were directly compared (Fig. 5a and c) and data extracted to visualize the differing effects between the ligand sets (Fig. 5b and d). Fig. 5a contrasts the median emission wavelength contour plots for the four ligand sets, while Fig. 5b shows two scatter plots with data series extracted at a constant base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio (1.0), and a constant temperature (140 °C), corresponding to the dashed white lines on the contour plots and chosen as instructive lines of comparison.
acid ratio (1.0), and a constant temperature (140 °C), corresponding to the dashed white lines on the contour plots and chosen as instructive lines of comparison.
From the median emission contour plots, we can see that the C8Bb–C8Ab ligand set (i.e. both branched ligands) yields the most consistent result across the data set, with no dependence on base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio and little temperature dependence, which is shown in the corresponding scatter plots in Fig. 5b (red line). In contrast, the C8B–C8A ligand set (i.e. where both ligands are linear) shows a dependency on both base content and temperature. The C8Bb–C8A set shows the biggest shift in emission, as a function of temperature, but no dependence on base
acid ratio and little temperature dependence, which is shown in the corresponding scatter plots in Fig. 5b (red line). In contrast, the C8B–C8A ligand set (i.e. where both ligands are linear) shows a dependency on both base content and temperature. The C8Bb–C8A set shows the biggest shift in emission, as a function of temperature, but no dependence on base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio (green line). For the IQR contour plots (Fig. 5c), again the biggest contrast is between the C8B–C8A and C8Bb–C8Ab data sets, with the branched ligands showing constant IQR in all conditions, but the linear ligands allowing a large range of IQRs reflective of the varied reaction products as discussed above. The most striking shift in IQR is seen for the C8Bb–C8A as a function of temperature (Fig. 5d), with the C8B–C8A set also showing a pronounced reduction with increasing temperature. Overall, the scatter plots indicate that changing the temperature has a more pronounced effect on the median and IQR than changing the base
acid ratio (green line). For the IQR contour plots (Fig. 5c), again the biggest contrast is between the C8B–C8A and C8Bb–C8Ab data sets, with the branched ligands showing constant IQR in all conditions, but the linear ligands allowing a large range of IQRs reflective of the varied reaction products as discussed above. The most striking shift in IQR is seen for the C8Bb–C8A as a function of temperature (Fig. 5d), with the C8B–C8A set also showing a pronounced reduction with increasing temperature. Overall, the scatter plots indicate that changing the temperature has a more pronounced effect on the median and IQR than changing the base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio.
acid ratio.
4. Discussion
In this work we have demonstrated how a microfluidic platform can be used to investigate the effect of input variables, including ligand structure, ligand base–acid ratio and temperature, on the nature of the reaction products in the synthesis of cesium lead bromide nanocrystals, with a view to accelerating the search for reaction conditions that yield bright and narrow emission from quantum confined nanostructures. We have observed a variety of nanostructures, predominantly nanosheets and nanowires. Such anisotropic growth of CsPbBr3 nanocrystals is common with alkylammonium ligands as they preferentially bind to the basal plane of the structure, restricting growth in the vertical axis and more readily permitting lateral growth.62 Further, reaction solutions rich in aliphatic ammonium ions encourage anisotropic growth due to competition between the RNH3+ and Cs+ ions.22Additionally, we have observed that, in the case of the linear ligand set C8B–C8A, there are two distinct regions in the reaction parameter space that yield high intensity emission and low emission width. The regions correspond to distinct products emitting at two different wavelengths, both in the quantum confined regime (i.e. dimensional confinement below the exciton Bohr diameter of 7 nm for CsPbBr3). Synthesis at 100 °C with lower base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio yields nanosheets with intense emission at 460 nm with FWHM = 25 nm, and synthesis 140 °C at higher base
acid ratio yields nanosheets with intense emission at 460 nm with FWHM = 25 nm, and synthesis 140 °C at higher base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio yields nanowires with intense emission at 497 nm with FWHM = 17 nm (Fig. S3a†). In contrast, we have observed that when either the organic acid or amine ligand possesses a branched alkyl chain, emission is on average significantly shifted towards the red, with weaker and wider peaks in the strong quantum confinement regime (emission <500 nm), indicating less control over growth and the production of larger nanostructures. In the case where both ligands are branched, very weak or no quantum confinement is observed, indicating that the branched ligands are less suited to controlling growth or stabilizing smaller nanostructures in the conditions studied (Fig. S1†).
acid ratio yields nanowires with intense emission at 497 nm with FWHM = 17 nm (Fig. S3a†). In contrast, we have observed that when either the organic acid or amine ligand possesses a branched alkyl chain, emission is on average significantly shifted towards the red, with weaker and wider peaks in the strong quantum confinement regime (emission <500 nm), indicating less control over growth and the production of larger nanostructures. In the case where both ligands are branched, very weak or no quantum confinement is observed, indicating that the branched ligands are less suited to controlling growth or stabilizing smaller nanostructures in the conditions studied (Fig. S1†).
The rate of addition of monomers to growing LHP nanocrystals, and therefore the final size of the reaction products and extent of quantum confinement, is known to depend strongly on both the packing of the monolayer of ligand molecules on the crystal surface, and the dynamic equilibrium of surface-bound and free ligands in solution.62,63 These, in turn, depend on the ligand structure, ligand concentration and reaction temperature. Ligand shells with less regular packing and/or lower packing densities, allow faster monomer addition, resulting in the growth of larger nanostructures.55 In our study, the use of relatively short C8 alkyl ligands likely leads to well-ordered ligand monolayers,64 but the relatively short chain length provides less inhibition of monomer diffusion versus longer chain ligands.62 With increasing temperature, increased kinetic energy of monomers then facilitates faster diffusion and addition of material to the growing nanocrystals, leading to an increased particle size with increasing temperature under all conditions. This is in accord with previous observations that LHP nanostructure thickness increases with increasing growth temperature regardless of the alkyl chain length of the alkylammonium ligand.62
Although introducing branched ligands can offer a steric effect to hinder monomer diffusion, our studies demonstrate the opposite effect, yielding larger nanostructures with more red-shifted emission. We suggest that the disruptive effect of the branched ligands on ligand packing dominates over steric hindrance of monomer diffusion, allowing increased monomer addition, increased growth rates and larger final structures. This is likely a consequence of the short alkyl chain lengths used in this study. Interestingly, introducing the branched acid (C8B–C8Ab) yielded a greater red shift with fewer blue emitting species compared to introducing the branched amine (C8Bb–C8A). This is somewhat counterintuitive given the common presumption that the dominant surface ligand is alkylammonium. However, several studies have suggested that carboxylic acid and carboxylate ligands are in fact present in significant amounts on the surface of CsPbBr3 nanocrystals,20,21,23 with the amine and carboxylic acids showing facet-dependent binding.30 Further, the multiple states and roles of each ligand before, during and after the reaction,21,65 make this effect hard to disentangle in the context of the current study. However, we note that the effects of ligand branching are evidently not restricted to sterics, but also have implications in the diffusion of ligands in solution, and of ligand stabilized monomers (e.g. alkylammonium bromide and cesium carboxylate) in solution and, critically, through the ligand shell. For example, previous studies have observed that organic acid concentration has a strong effect on particle growth rate, which was ascribed to chain-length-dependent protonation rates (with the carboxylic acid protonating the amine),22 an effect that is exacerbated by the rapid nucleation and growth kinetics of LHP nanocrystals.
The acid–base chemistry of a binary aliphatic amine–acid ligand system is critical in determining the morphology and optical properties of cesium lead bromide nanocrystals both during and after synthesis.22,65 Which ligand species are binding the surface, and by what mechanism, is highly dependent not just on the nature of the surface, but also on the interactions between the ligands and precursors in solution.20 In our system, by scanning the molar ligand concentration range 0.7 to 1.2 base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid, we move from a regime of excess acid to excess amine, which should have a distinct effect upon the ratio of the different specifies present (amine versus ammonium, carboxylic acid versus carboxylate). NMR studies have demonstrated that oleic acid protonates oleylamine in aprotic solvents, leading to the formation of ammonium carboxylate salts.21,22 The equilibrium of this reaction is affected by temperature, with higher temperatures pushing the equilibrium towards the reactants.22 Further, an increased concentration of carboxylic acid leads to an increased concentration of ammonium ions, and a lower temperature also leads to an increased ammonium ion concentration.22 Our results have shown that, within the bounds of ligand ratios and combinations that we have studied, the dominant peak position and median emission show a much stronger dependence on reaction temperature versus base
acid, we move from a regime of excess acid to excess amine, which should have a distinct effect upon the ratio of the different specifies present (amine versus ammonium, carboxylic acid versus carboxylate). NMR studies have demonstrated that oleic acid protonates oleylamine in aprotic solvents, leading to the formation of ammonium carboxylate salts.21,22 The equilibrium of this reaction is affected by temperature, with higher temperatures pushing the equilibrium towards the reactants.22 Further, an increased concentration of carboxylic acid leads to an increased concentration of ammonium ions, and a lower temperature also leads to an increased ammonium ion concentration.22 Our results have shown that, within the bounds of ligand ratios and combinations that we have studied, the dominant peak position and median emission show a much stronger dependence on reaction temperature versus base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio (Fig. S2†). The peak emission intensity shows a stronger dependence on base
acid ratio (Fig. S2†). The peak emission intensity shows a stronger dependence on base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio, though with no clear relationship across the data set. For example, the peak intensity for C8B–C8Ab occurs at a low base
acid ratio, though with no clear relationship across the data set. For example, the peak intensity for C8B–C8Ab occurs at a low base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio (<0.9), whilst for C8Bb–C8A it occurs at higher base
acid ratio (<0.9), whilst for C8Bb–C8A it occurs at higher base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratios (>1.0). This again suggest that the ligand branching, affecting surface packing and ligand diffusion in solution and through the ligand monolayer, is a critical factor. Further, as it is known that surface trap states in LHP nanocrystals,57 and the crystal phase,66 both strongly affect photoluminescence brightness, it seems that the changing base
acid ratios (>1.0). This again suggest that the ligand branching, affecting surface packing and ligand diffusion in solution and through the ligand monolayer, is a critical factor. Further, as it is known that surface trap states in LHP nanocrystals,57 and the crystal phase,66 both strongly affect photoluminescence brightness, it seems that the changing base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio in our study is having a significant effect on surface structure, passivation and/or crystal structure, but a lesser effect on the overall size of the nanocrystals.
acid ratio in our study is having a significant effect on surface structure, passivation and/or crystal structure, but a lesser effect on the overall size of the nanocrystals.
It is also important to note that a limitation of fluorescence spectra is that little information can be discerned for nanoparticles above the quantum confinement regime (7 nm here, with emission around 525 nm), as changes in size and shape do not yield changes in emission, therefore structural characteristics outside the quantum confinement regime cannot be discerned. Accordingly, it would be highly beneficial to include also inline absorption spectroscopy in future studies, as such analyses reveal additional information, for example on crystal structure, which are not discernible from the photoluminescence spectra alone. An important reaction variable that was not studied in the current work, but could readily be integrated, is the reaction time. For example, it was previously shown that by extending the reaction time under the conditions previously used for CsPbBr3 nanocube synthesis, nanowires with diameters below 12 nm and lengths up to 5 μm were obtained.67 It is evident that the more the reaction parameter space can be expanded (including further input variables and output variables), the more powerful this data driven approach to product optimization will be. This will be the focus of future work.
We note that there are some mechanistic differences in how the synthesis of LHP nanocrystals proceeds in our microreactor as opposed to the flask-based approach. Following the hot-injection approach developed by Kovalenko and co-workers,9 CsPbX3 nanocrystals form after the injection of a Cs-oleate solution into a hot octadecene solution of PbX2 (from 140–200 °C), followed by rapid quenching in an ice bath after five seconds. In contrast, in our microfluidic reactor precursors are mixed at room temperature in a microfluidic manifold, and then conveyed to a rod which heats the reaction solution to the desired reaction temperature (90–190 °C herein), with a residence time of 30 seconds before cooling to room temperature. Despite these differences, our previous studies have demonstrated excellent agreement in results obtained using equivalent reaction conditions in the microfluidic and bulk approaches.46 This is an important observation, as it makes comparisons between literature data using the hot-injection approach and our microfluidic data meaningful. However, it should not be forgotten that the microfluidic approach has inherent advantages (such as rapid mixing and heat transfer leading to lower polydispersity,37 excellent batch-to-batch reproducibility36 and potential for industrial scale-up68) that mark it as a desirable synthesis methodology in itself, and not solely as a means of performing high-throughput screening.
5. Conclusions
Herein, we have demonstrated how an automated microfluidic reactor with in situ photoluminescence characterisation can be used to map a two dimensional parameter space (scanning base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ligand ratio and reaction temperature), in search of reaction conditions that yield quantum confined nanostructures with bright and narrow emission properties. Our results demonstrate the time and material efficiency of automated multidimensional parameter screening versus a one-factor-at-a-time optimization approach normally undertaken in conventional synthesis routes.
acid ligand ratio and reaction temperature), in search of reaction conditions that yield quantum confined nanostructures with bright and narrow emission properties. Our results demonstrate the time and material efficiency of automated multidimensional parameter screening versus a one-factor-at-a-time optimization approach normally undertaken in conventional synthesis routes.
We feel this approach shows potential for impact in some areas of study that are pertinent to the advancement of the LHP nanocrystal field. First, it is desirable to discover and employ reaction conditions that yield inherently low polydispersity, rather than relying on post hoc product purification to isolate specific products, which is both involved and inefficient. We have demonstrated this by identifying two reaction parameters sets in the C8B–C8A experiment that both yield bright and narrow emission. Second, it evident from the literature that the binary organic amine–acid ligand system has some disadvantages (e.g. poor surface binding20) that inherently limit the product stability. Our study herein has demonstrated the complexity of the parameter space for even a relatively simple binary ligand system, with a strong dependence on reaction temperature and ligand ratio. The discovery and optimization of new ligands, and formulations in multinary ligands systems, will likely require such advanced experimental approaches to aid new discoveries. Third, as we enter a data-driven era of nanomaterials discovery and optimization,55,69 we feel approaches such as the one presented herein may yield extraordinary gains when combined with advanced tools such as machine learning and directed evolution.70–72
Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
S. L. would like to thank Richard Maceiczyk and Leonard Bezinge for kind advice in using and developing the microfluidic platform. P. D. H. and S. S. would like to thank the Swiss National Science Foundation (SNSF) for support via a Spark Grant (Project No. CRSK-2_190750). The authors are grateful to the ScopeM center at ETH for technical assistance in TEM imaging. Finally, the authors would like to thank Kane Shenton for help in developing the Python scripts used in this work.References
- M. A. Boles, D. Ling, T. Hyeon and D. V. Talapin, Nat. Mater., 2016, 15, 141–153 CrossRef CAS PubMed.
- A. Heuer-Jungemann, N. Feliu, I. Bakaimi, M. Hamaly, A. Alkilany, I. Chakraborty, A. Masood, M. F. Casula, A. Kostopoulou, E. Oh, K. Susumu, M. H. Stewart, I. L. Medintz, E. Stratakis, W. J. Parak and A. G. Kanaras, Chem. Rev., 2019, 119, 4819–4880 CrossRef CAS PubMed.
- S. Lazzari, P. M. Theiler, Y. Shen, C. W. Coley, A. Stemmer and K. F. Jensen, Langmuir, 2018, 34, 3307–3315 CrossRef CAS PubMed.
- S. V. Kershaw, L. Jing, X. Huang, M. Gao and A. L. Rogach, Mater. Horiz., 2017, 4, 155–205 RSC.
- Y. Fu, H. Zhu, J. Chen, M. P. Hautzinger, X.-Y. Zhu and S. Jin, Nat. Rev. Mater., 2019, 4, 169–188 CrossRef CAS.
- H. Kim, S. Beack, S. Han, M. Shin, T. Lee, Y. Park, K. S. Kim, A. K. Yetisen, S. H. Yun, W. Kwon and S. K. Hahn, Adv. Mater., 2018, 30, 1701460 CrossRef PubMed.
- D. Kim, K. Shin, S. G. Kwon and T. Hyeon, Adv. Mater., 2018, 30, 1802309 CrossRef PubMed.
- L. C. Schmidt, A. Pertegás, S. González-Carrero, O. Malinkiewicz, S. Agouram, G. Mínguez Espallargas, H. J. Bolink, R. E. Galian and J. Pérez-Prieto, J. Am. Chem. Soc., 2014, 136, 850–853 CrossRef CAS PubMed.
- L. Protesescu, S. Yakunin, M. I. Bodnarchuk, F. Krieg, R. Caputo, C. H. Hendon, R. X. Yang, A. Walsh and M. V. Kovalenko, Nano Lett., 2015, 15, 3692–3696 CrossRef CAS PubMed.
- Q. A. Akkerman, G. Rainò, M. V. Kovalenko and L. Manna, Nat. Mater., 2018, 17, 394–405 CrossRef CAS PubMed.
- D. Aldakov and P. Reiss, J. Phys. Chem. C, 2019, 123, 12527–12541 CAS.
- J. Shamsi, A. S. Urban, M. Imran, L. De Trizio and L. Manna, Chem. Rev., 2019, 119, 3296–3348 CrossRef CAS PubMed.
- D. H. Fabini, J. G. Labram, A. J. Lehner, J. S. Bechtel, H. A. Evans, A. Van der Ven, F. Wudl, M. L. Chabinyc and R. Seshadri, Inorg. Chem., 2017, 56, 11–25 CrossRef CAS PubMed.
- H. Fu, J. Mater. Chem. A, 2019, 7, 14357–14379 RSC.
- D. Yang, X. Li and H. Zeng, Adv. Mater. Interfaces, 2018, 5, 1701662 CrossRef.
- J. Yin, G. H. Ahmed, O. M. Bakr, J.-L. Brédas and O. F. Mohammed, ACS Energy Lett., 2019, 4, 789–795 CrossRef CAS.
- M. Gong, R. Sakidja, R. Goul, D. Ewing, M. Casper, A. Stramel, A. Elliot and J. Z. Wu, ACS Nano, 2019, 13, 1772–1783 CrossRef CAS PubMed.
- B. Luo, S. B. Naghadeh and J. Z. Zhang, ChemNanoMat, 2017, 3, 456–465 CrossRef CAS.
- T. A. Berhe, W.-N. Su, C.-H. Chen, C.-J. Pan, J.-H. Cheng, H.-M. Chen, M.-C. Tsai, L.-Y. Chen, A. A. Dubale and B.-J. Hwang, Energy Environ. Sci., 2016, 9, 323–356 RSC.
- J. De Roo, M. Ibáñez, P. Geiregat, G. Nedelcu, W. Walravens, J. Maes, J. C. Martins, I. Van Driessche, M. V. Kovalenko and Z. Hens, ACS Nano, 2016, 10, 2071–2081 CrossRef CAS PubMed.
- R. Grisorio, M. E. Di Clemente, E. Fanizza, I. Allegretta, D. Altamura, M. Striccoli, R. Terzano, C. Giannini, M. Irimia-Vladu and G. P. Suranna, Nanoscale, 2019, 11, 986–999 RSC.
- G. Almeida, L. Goldoni, Q. Akkerman, Z. Dang, A. H. Khan, S. Marras, I. Moreels and L. Manna, ACS Nano, 2018, 12, 1704–1711 CrossRef CAS PubMed.
- A. Pan, B. He, X. Fan, Z. Liu, J. J. Urban, A. P. Alivisatos, L. He and Y. Liu, ACS Nano, 2016, 10, 7943–7954 CrossRef CAS PubMed.
- K. Chen, Q. Zhong, W. Chen, B. Sang, Y. Wang, T. Yang, Y. Liu, Y. Zhang and H. Zhang, Adv. Funct. Mater., 2019, 29, 1900991 CrossRef.
- J. Shamsi, Z. Dang, P. Bianchini, C. Canale, F. Di Stasio, R. Brescia, M. Prato and L. Manna, J. Am. Chem. Soc., 2016, 138, 7240–7243 CrossRef CAS PubMed.
- C. B. Murray, D. J. Norris and M. G. Bawendi, J. Am. Chem. Soc., 1993, 115, 8706–8715 CrossRef CAS.
- B. Luo, Y.-C. Pu, S. A. Lindley, Y. Yang, L. Lu, Y. Li, X. Li and J. Z. Zhang, Angew. Chem., Int. Ed., 2016, 55, 8864–8868 CrossRef CAS PubMed.
- H. Huang, B. Chen, Z. Wang, T. F. Hung, A. S. Susha, H. Zhong and A. L. Rogach, Chem. Sci., 2016, 7, 5699–5703 RSC.
- D. Yan, T. Shi, Z. Zang, T. Zhou, Z. Liu, Z. Zhang, J. Du, Y. Leng and X. Tang, Small, 2019, 15, 1901173 CrossRef PubMed.
- S. Sun, D. Yuan, Y. Xu, A. Wang and Z. Deng, ACS Nano, 2016, 10, 3648–3657 CrossRef CAS PubMed.
- Z. Liang, S. Zhao, Z. Xu, B. Qiao, P. Song, D. Gao and X. Xu, ACS Appl. Mater. Interfaces, 2016, 8, 28824–28830 CrossRef CAS PubMed.
- F. Krieg, Q. K. Ong, M. Burian, G. Rainò, D. Naumenko, H. Amenitsch, A. Süess, M. J. Grotevent, F. Krumeich, M. I. Bodnarchuk, I. Shorubalko, F. Stellacci and M. V. Kovalenko, J. Am. Chem. Soc., 2019, 141, 19839–19849 CrossRef CAS PubMed.
- F. Krieg, S. T. Ochsenbein, S. Yakunin, S. ten Brinck, P. Aellen, A. Süess, B. Clerc, D. Guggisberg, O. Nazarenko, Y. Shynkarenko, S. Kumar, C.-J. Shih, I. Infante and M. V. Kovalenko, ACS Energy Lett., 2018, 3, 641–646 CrossRef CAS PubMed.
- Y. Yang, H. Qin and X. Peng, Nano Lett., 2016, 16, 2127–2132 CrossRef CAS PubMed.
- Y. Yang, H. Qin, M. Jiang, L. Lin, T. Fu, X. Dai, Z. Zhang, Y. Niu, H. Cao, Y. Jin, F. Zhao and X. Peng, Nano Lett., 2016, 16, 2133–2138 CrossRef CAS PubMed.
- S. Kubendhiran, Z. Bao, K. Dave and R.-S. Liu, ACS Appl. Nano Mater., 2019, 2, 1773–1790 CrossRef CAS.
- I. Lignos, R. Maceiczyk and A. J. deMello, Acc. Chem. Res., 2017, 50, 1248–1257 CrossRef CAS PubMed.
- S. Duraiswamy and S. A. Khan, Small, 2009, 5, 2828–2834 CrossRef CAS PubMed.
- A. Toyota, H. Nakamura, H. Ozono, K. Yamashita, M. Uehara and H. Maeda, J. Phys. Chem. C, 2010, 114, 7527–7534 CrossRef CAS.
- Y. Roig, S. Marre, T. Cardinal and C. Aymonier, Angew. Chem., Int. Ed., 2011, 50, 12071–12074 CrossRef CAS PubMed.
- T. Gendrineau, S. Marre, M. Vaultier, M. Pucheault and C. Aymonier, Angew. Chem., Int. Ed., 2012, 51, 8525–8528 CrossRef CAS PubMed.
- J. Baek, Y. Shen, I. Lignos, M. G. Bawendi and K. F. Jensen, Angew. Chem., 2018, 130, 11081–11084 CrossRef.
- A. Suea-Ngam, P. D. Howes, M. Srisa-Art and A. J. Demello, Chem. Commun., 2019, 55, 9895–9903 RSC.
- T. W. Phillips, I. G. Lignos, R. M. Maceiczyk, A. J. deMello and J. C. deMello, Lab Chip, 2014, 14, 3172–3180 RSC.
- R. M. Maceiczyk, I. G. Lignos and A. J. deMello, Curr. Opin. Chem. Eng., 2015, 8, 29–35 CrossRef.
- I. Lignos, V. Morad, Y. Shynkarenko, C. Bernasconi, R. M. Maceiczyk, L. Protesescu, F. Bertolotti, S. Kumar, S. T. Ochsenbein, N. Masciocchi, A. Guagliardi, C.-J. Shih, M. I. Bodnarchuk, A. J. deMello and M. V. Kovalenko, ACS Nano, 2018, 12, 5504–5517 CrossRef CAS PubMed.
- R. M. Maceiczyk, K. Dümbgen, I. Lignos, L. Protesescu, M. V. Kovalenko and A. J. deMello, Chem. Mater., 2017, 29, 8433–8439 CrossRef CAS.
- L. Bezinge, R. M. Maceiczyk, I. Lignos, M. V. Kovalenko and A. J. deMello, ACS Appl. Mater. Interfaces, 2018, 10, 18869–18878 CrossRef CAS PubMed.
- I. Lignos, L. Protesescu, D. B. Emiroglu, R. Maceiczyk, S. Schneider, M. V. Kovalenko and A. J. deMello, Nano Lett., 2018, 18, 1246–1252 CrossRef CAS PubMed.
- I. Lignos, S. Stavrakis, G. Nedelcu, L. Protesescu, A. J. deMello and M. V. Kovalenko, Nano Lett., 2016, 16, 1869–1877 CrossRef CAS PubMed.
- I. Lignos, R. M. Maceiczyk, M. V. Kovalenko and S. Stavrakis, Chem. Mater., 2020, 32, 27–37 CrossRef CAS.
- R. W. Epps, K. C. Felton, C. W. Coley and M. Abolhasani, Lab Chip, 2017, 17, 4040–4047 RSC.
- K. Abdel-Latif, R. W. Epps, C. B. Kerr, C. M. Papa, F. N. Castellano and M. Abolhasani, Adv. Funct. Mater., 2019, 29, 1900712 CrossRef.
- I. Lignos, S. Stavrakis, G. Nedelcu, L. Protesescu, A. J. DeMello and M. V. Kovalenko, Nano Lett., 2016, 16, 1869–1877 CrossRef CAS PubMed.
- E. J. Braham, J. Cho, K. M. Forlano, D. F. Watson, R. Arròyave and S. Banerjee, Chem. Mater., 2019, 31, 3281–3292 CrossRef CAS.
- L. Wu, Q. Zhong, D. Yang, M. Chen, H. Hu, Q. Pan, H. Liu, M. Cao, Y. Xu, B. Sun and Q. Zhang, Langmuir, 2017, 33, 12689–12696 CrossRef CAS PubMed.
- M. I. Bodnarchuk, S. C. Boehme, S. ten Brinck, C. Bernasconi, Y. Shynkarenko, F. Krieg, R. Widmer, B. Aeschlimann, D. Günther, M. V. Kovalenko and I. Infante, ACS Energy Lett., 2019, 4, 63–74 CrossRef CAS PubMed.
- Q. A. Akkerman, S. G. Motti, A. R. Srimath Kandada, E. Mosconi, V. D'Innocenzo, G. Bertoni, S. Marras, B. A. Kamino, L. Miranda, F. De Angelis, A. Petrozza, M. Prato and L. Manna, J. Am. Chem. Soc., 2016, 138, 1010–1016 CrossRef CAS PubMed.
- Z. Dang, J. Shamsi, F. Palazon, M. Imran, Q. A. Akkerman, S. Park, G. Bertoni, M. Prato, R. Brescia and L. Manna, ACS Nano, 2017, 11, 2124–2132 CrossRef CAS PubMed.
- C. Wang, Y. Zhang, A. Wang, Q. Wang, H. Tang, W. Shen, Z. Li and Z. Deng, Chem. Mater., 2017, 29, 2157–2166 CrossRef CAS.
- Y. Bekenstein, B. A. Koscher, S. W. Eaton, P. Yang and A. P. Alivisatos, J. Am. Chem. Soc., 2015, 137, 16008–16011 CrossRef CAS PubMed.
- J. Cho, H. Jin, D. G. Sellers, D. F. Watson, D. H. Son and S. Banerjee, J. Mater. Chem. C, 2017, 5, 8810–8818 RSC.
- J. Cho, Y. H. Choi, T. E. O'Loughlin, L. De Jesus and S. Banerjee, Chem. Mater., 2016, 28, 6909–6916 CrossRef CAS.
- A. Ulman, Chem. Rev., 1996, 96, 1533–1554 CrossRef CAS PubMed.
- E. Fanizza, F. Cascella, D. Altamura, C. Giannini, A. Panniello, L. Triggiani, F. Panzarea, N. Depalo, R. Grisorio, G. P. Suranna, A. Agostiano, M. L. Curri and M. Striccoli, Nano Res., 2019, 12, 1155–1166 CrossRef CAS.
- T. Udayabhaskararao, L. Houben, H. Cohen, M. Menahem, I. Pinkas, L. Avram, T. Wolf, A. Teitelboim, M. Leskes, O. Yaffe, D. Oron and M. Kazes, Chem. Mater., 2018, 30, 84–93 CrossRef CAS.
- D. Zhang, S. W. Eaton, Y. Yu, L. Dou and P. Yang, J. Am. Chem. Soc., 2015, 137, 9230–9233 CrossRef CAS PubMed.
- J. Sui, J. Yan, D. Liu, K. Wang and G. Luo, Small, 2019, 1902828 CrossRef PubMed.
- O. Voznyy, L. Levina, J. Z. Fan, M. Askerka, A. Jain, M.-J. Choi, O. Ouellette, P. Todorović, L. K. Sagar and E. H. Sargent, ACS Nano, 2019, 13, 11122–11128 CrossRef CAS PubMed.
- B. Lambert, A. J. Gillen, N. Schuergers, S.-J. Wu and A. A. Boghossian, Chem. Commun., 2019, 55, 3239–3242 RSC.
- R. Ramprasad, R. Batra, G. Pilania, A. Mannodi-Kanakkithodi and C. Kim, npj Comput. Mater., 2017, 3, 54 CrossRef.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0me00008f |
| ‡ Current address: Department of Chemical Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA. |
| § Current address: Department of Chemistry, University of California, Berkeley, California 94720, USA. |
| This journal is © The Royal Society of Chemistry 2020 |