Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Modeling of stimuli-responsive nanoreactors: rational rate control towards the design of colloidal enzymes
Matej
Kanduč
 *a,
Won Kyu
Kim
*a,
Won Kyu
Kim
 *b,
Rafael
Roa
*b,
Rafael
Roa
 *c and
Joachim
Dzubiella
*c and
Joachim
Dzubiella
 *de
*de
aJožef Stefan Institute, Jamova 39, SI-1000 Ljubljana, Slovenia. E-mail: matej.kanduc@ijs.si
bKorea Institute for Advanced Study, 85 Hoegiro, Seoul 02455, Republic of Korea. E-mail: wonkyukim@kias.re.kr
cDepartamento de Física Aplicada I, Facultad de Ciencias, Universidad de Málaga, Campus de Teatinos s/n, E-29071 Málaga, Spain. E-mail: rafaroa@uma.es
dResearch Group for Simulations of Energy Materials, Helmholtz-Zentrum Berlin, Hahn-Meitner-Platz 1, D-14109 Berlin, Germany
eInstitut für Physik, Albert-Ludwigs-Universität Freiburg, Hermann-Herder-Str. 3, D-79104 Freiburg, Germany. E-mail: joachim.dzubiella@physik.uni-freiburg.de
First published on 5th November 2019
Abstract
In modern applications of heterogeneous liquid-phase nanocatalysis, the catalysts (e.g., metal nanoparticles) need to be typically affixed to a colloidal carrier system for stability and easy handling. “Passive carriers” (e.g., simple polyelectrolytes) serve for a controlled synthesis of the nanoparticles and prevent coagulation during catalysis. Recently, however, hybrid conjugates of nanoparticles and synthetic thermosensitive polymers have been developed that enable to change the catalytic activity of the nanoparticles by external triggers. In particular, nanoparticles embedded in a stimuli-responsive network made from poly (N-isopropylacrylamide) (PNIPAM) have become the most-studied examples of such hybrids. It has been demonstrated that the permeability of the polymer network and thus the reactant flux can be switched and controlled by external stimuli. Such “active carriers” may thus be viewed as true nanoreactors that open up new design routes in nano-catalysis and elevate synthesis to create highly selective, programmable “colloidal enzymes”. However, only a comprehensive understanding of these materials on all time and length scales can lead to a rational design of future, highly functional materials. Here we review the current state of the theoretical and multi-scale simulation approaches, aiming at a fundamental understanding of these nanoreactors. In particular, we summarize a theoretical approach for reaction rates of surface-catalyzed bimolecular reactions in responsive nanoreactors in terms of the key material parameters, the polymer shell permeability 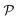 and the reactant partition ratio
and the reactant partition ratio 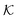 . We discuss recent computer simulation studies of both atomistic and coarse-grained polymer models in which these quantities have been characterized in some detail. We conclude with an outlook on selected open questions and future theoretical challenges in nanoreactor modeling.
. We discuss recent computer simulation studies of both atomistic and coarse-grained polymer models in which these quantities have been characterized in some detail. We conclude with an outlook on selected open questions and future theoretical challenges in nanoreactor modeling.
Design, System, ApplicationIn liquid phase catalysis, catalytic nanoparticles need to be stabilized by polymeric or colloidal carrier systems. If the nanoparticles are embedded within a thermosensitive, permeable polymer matrix, stimuli-responsive nanoreactors can be created based on the phenomenon that the polymer properties can respond to environmental triggers, such as the local pH or osmotic pressure, thereby modifying the catalytic processes. Two of the key control parameters are the partition ratio of the reactants within the polymer matrix as well as the polymer permeability, which are both defined by the molecular topology of the polymer matrix, e.g., a cross-linked hydrogel, and the microscopic interactions of the polymers with the reactant. Rational design rules must thus be based on a microscopic understanding on how molecular details and polymer structure relate to macroscopic thermodynamic and transport properties and how they enter continuum rate theory. Based on such a multi-scale understanding, ‘programmable’ nanoreactors can potentially be designed to create catalytic devices that, like enzymes, are highly selective, adaptive and interactive with their environment, and can accelerate, decelerate, or even switch on and off a specific reaction, e.g., for the purpose of locally deceasing or increasing the concentration of a toxic or functionally important substance, respectively. |
1 Introduction
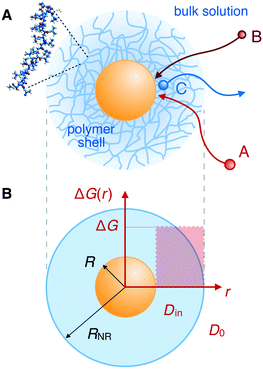
Synthetic nanoreactors are an emerging and promising new nanotechnology for liquid-phase heterogenous catalysis. In these nanoreactors, the catalysts are confined in a permeable nanostructure, which acts as a carrier and can be used to shelter and control the catalytic processes. In particular, the catalysis can be made selective and responsive if the nanoreactor permeability differentiates among molecules and can be modulated by external stimuli.1–14 These nanoreactors can be used for a large variety of applications, ranging from analytical tools to study chemical reactions1–12 to biosensors for the diagnosis of diseases.10–14 Examples of natural nanoreactors are lipid-based membranes (e.g., liposomes), cage-like proteins (e.g., ferritins), protein-based bacterial microcompartments, and viruses.11–13,15 Artificial nanoreactors (based on spherical polyelectrolyte brushes, dendrimers, ligands, or even DNA) are simpler than the natural ones and thus easier to control for targeted applications.4–12,16,17In particular, nanoreactors containing metal nanoparticles have emerged as a promising catalytic system.4–9,18–21 For example, gold becomes an active catalyst when divided down to the nanophase.22–27 However, the handling of the particles in the liquid phase is an important problem: the surface of the particles should be easily accessible for the mixture of the reactants. This condition would require the nanoparticles to be freely suspended in the solution, and coagulation or any type of Ostwald ripening of the nanoparticles should not occur during the catalytic reaction. Also, leaching of metal or loss of nanoparticles from the carrier must be prevented to ensure a meaningful and repeated use of the catalyst. The latter requirements necessitate a suitable carrier that ensures a safe and repeated handling of the nanoparticles.28,29 It was demonstrated that suitable carrier systems include colloidal particles,30,31 dendrimers,32–42 mesoporous materials,43–45 spherical polyelectrolyte brushes,46,47 and other systems48 structured on a length scale between one and a few hundred nm.
In recent years, the concept of such carrier systems has been further advanced with the synthesis of hydrogel-based nanoreactors, for which rate control by external stimuli has become possible.6,7,10,12,15,18,49–57 Thermosensitive hydrogels made from a network of poly(N-isopropylacrylamide) (PNIPAM) and its copolymers provide a good example:4–8,18–21,58–67 typical colloidal carrier architectures are of core–shell or yolk–shell type where the polymer gel constitutes a permeable shell around a solid core (core–shell) or around a hollow void (yolk–shell).6 The core can be the nanoparticle itself, cf.Fig. 1, or, for example, a polystyrene core. The catalytic nanoparticles can be located during synthesis in a well controlled fashion, e.g., into the voids, onto the cores, or distributed within the polymer shell. Sometimes simply a pure hydrogel (nano- or microgel) particle is the carrier for the catalysts. In this case, carrier and polymer shell in our context are essentially the same. A survey of selected but very typical experimental architectures and results for polymer-based nanoreactor carriers is provided in Table 1.
| Ref. | Architecture | Core–polymer | Catalyst | Reaction | Result |
|---|---|---|---|---|---|
| 7 | Yolk–shell | Au–PNIPAM | Au | Reduction: NP → AP & NB → AB | T-Dependence on gel swelling and reaction rate |
| 5, 6 | Core–shell | Au–PNIPAM | Au | Reduction: HCF → HCF2 | T-Dependence on gel swelling and reaction rate, rate dependence on nanoreactor concentration and cross-linking density |
| 6, 67 | Core–shell | Pt/Au–PNIPAM | Pt/Au | Reduction: NP → AP | Rate dependence on reactant concentration |
| 8 | Core–shell | Cu2O–PNIPAM | Cu2O | Decomposition by visible light: methyl orange | T-Dependence on gel swelling and reaction rate |
| 21 | Core–shell | Au–PNIPAM | Ag | Reduction: NP → AP | Photoresponsive gel size and reaction rate |
| 65 | Core–shell | Au–P(VPBA-NIPAM-AAm) | Au | Reduction: NP → AP & NB → AB | Glucose concentration dependence on gel swelling and reaction rate |
| 4, 51 | Core–shell | PS–PNIPAM | Au/Pt/Rh | Oxidation: benzyl alcohol → benzaldehyde | T-Dependence on gel swelling and reaction rate |
| 4, 56 | Core–shell | PS–PNIPAM | β-D-Glucosidase | Hydrolysis: oNPG → D-glucose + o-nitrophenol | T-Dependence on gel swelling and reaction rate |
| 57 | Core–shell | PS–PNIPAM | Ag | Reduction: NP → AP | T-Dependence on gel swelling and reaction rate |
| 59 | Core–shell | P(S-NIPAM)–P(NIPAM-co-MAA) | Ag | Reduction: NP → AP & NB → AB | T-Dependence on gel swelling and reaction rate |
| 19 | Microgel | PNIPAM/MACACS | Ag | Reduction: NP → AP | T-Dependence on gel swelling and reaction rate |
| 55 | Microgel | PVCL-α-cyclodextrin | Au | Reduction: NP → AP | T-Dependence on gel swelling and reaction rate |
| 60 | Microgel | P(NIPAM-co-MAA) | Au | Reduction: NP → AP | T-Dependence on gel swelling and reaction rate |
| 61 | Microgel | Cellulose | Cellulase (enzyme) | Hydrolysis: cellulose → glucose | T-Dependence on gel swelling and time-dependent product concentration |
| 62 | Hydrogel | P(NIPAM-co-AMPS) | Ni | Reduction: NP → AP | T-Dependence on gel swelling and reaction rate |
| 63 | Microgel | P(NIPAM-co-AMPS) | Ag | Reduction: methylene blue | T-Dependence on gel swelling and reaction rate, pH-dependence on gel swelling |
The responsive polymer shell is in a swollen hydrophilic state at low temperature, but sharply collapses into a rather hydrophobic state above the critical solution temperature.68 The sharp volume transition of the gel is reversible69–75 and depends on the temperature,76,77 or more generally, solvent quality. This has substantial influence on reactant partitioning close to the catalysts as well as reactant transport towards it.78 Hence, there are two key roles of the polymer shell. On the one hand, the shell acts as an integral part of the whole carrier that protects nanoparticles from aggregation and hinders chemical degradation processes, e.g., oxidation.8 On the other hand, the polymer ability to switch between states with different physicochemical properties upon changes in environmental parameters, e.g., temperature, pH, or concentration of certain solutes, provides a handle to actively control the nanoreactor's catalytic properties.78
A quantitative study and understanding of a nanoreactor requires kinetic data measured with the highest precision possible. Up to now, most of the testing of the catalytic activity of nanoparticles in aqueous phase has been done using the reduction of 4-nitrophenol by borohydride. Pal et al.79 and Esumi et al.36 have been the first who have demonstrated the usefulness of this reaction. In the meantime, the reduction of 4-nitrophenol has become the most used model reaction for the quantitative testing and analyzing of the catalytic activity of nanoparticles in the liquid phase.80,81 Further examples of catalytic reactions in aqueous solution studied in this system are the reductions of nitrobenzene and hexacyanoferrate (III) by borohydride ions6,7,18,19 and the decomposition of methyl orange under visible light.8
All the aforementioned examples deal with surface-catalyzed bimolecular reactions, being a very common type. As pointed out before,5–7,78 pseudo-unimolecular surface-catalyzed reactions in responsive nanoreactors can be described by combining a thermodynamic two-state model for the polymer volume transition with the appropriate reaction–diffusion equations. In particular, the important effect of a change of the shell permeability on the reactants' approach to the catalyst's surface can be described by theory of diffusion through an energy landscape,7,78,82,83 in the spirit of Debye–Smoluchowski diffusion-controlled rate theory.84–88 Importantly, the latter also takes into account the local reactant concentration, i.e., the partitioning inside the polymer shell close to the catalyst. Recently, we have presented an extended theory of diffusion-limited bimolecular reactions in nanoreactors, which can be employed to rationally design the activity and selectivity of a nanoreactor.78,83 The main result of our consideration was the following formula for the total catalytic rate in bimolecular reactions in core–shell nanoreactors (cf.Fig. 1):
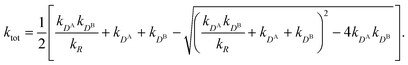 | (1) |
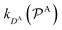 and
and 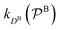 are the diffusion rates of the reactants A and B, which explicitly depend on the shell permeability
are the diffusion rates of the reactants A and B, which explicitly depend on the shell permeability 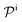 , and
, and 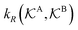 is the surface reaction rate, explicitly depending on partitioning
is the surface reaction rate, explicitly depending on partitioning 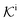 as defined below.
as defined below.
In general, permeability of a material defines the ability of the penetrating molecules (e.g., gas, ligands, reactants, etc.) to permeate and flow through a given medium under the action of an external field or chemical gradient. It is thus without doubt one of the most fundamental transport descriptors employed in the physical sciences and material engineering. In the standard ‘solution–diffusion' picture for permeable membranes, it is commonly defined on the linear response level by89–99
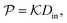 | (2) |
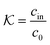 | (3) |
Hence, in the last couple of years many quantitative concepts have emerged both on the continuum and the microscopic level that will eventually lead to a more fundamental understanding of nanoreactors in the future. The possibility arises to optimize responsive nanoreactors to reach the high recognition, selectivity, and feedback control as found for enzymes,115,116 to create “colloidal enzymes”. Here we review the state-of-the-art of the current understanding of the intricate links between nanoreactor reaction rate and polymer permeability. Most of the results presented here are based on our recent research endeavor of multi-scale modeling schemes of hydrogel systems in order to establish rational design principles of responsive nanoreactors. We start in section 2 by summarizing the rate theory for nanoparticle-catalyzed bimolecular reactions including partitioning and permeability of the polymer shell. The key property to be tuned and ‘programmed’ during the synthesis in order to select and switch catalytic activity is the permeability. In section 3 we thus proceed with mesoscale coarse-grained computer models, which give fundamental insights on partition–diffusion correlations in the permeability and how they can be tuned qualitatively by microscopic interactions. In the last part we turn to atomistically-resolved molecular simulations of the PNIPAM hydrogel models in swollen and collapsed state. There we address the question of the influence of the ‘chemistry’ of the interactions, e.g., role of (temperature-dependent) hydration, polarity, reactant type and size, etc. Obviously, there are many open questions, missing connections, and remaining challenges to overcome to obtain a comprehensive multi-scale model. We will briefly discuss those and give an outlook in the final, concluding section.
2 Bimolecular reactions in nanoreactors
2.1 Macroscopic rates and dependence on permeability
We review the rate theory for nanoreactors for the case of surface-catalyzed bimolecular reactions in one of the simplest nanoreactor geometries, a core–shell nanoreactor,83 depicted in Fig. 1A, where a catalytically active metal nanoparticle of radius R is embedded in a thermoresponsive hydrogel matrix of outer radius R. In this spherically symmetric system, we consider that two species A and B diffuse from a bulk solution with respective (initial) concentration cA0 and cB0 through the polymer shell towards the catalyst nanoparticle. A fraction of the reactants arriving at the surface combines with each other to produce a third molecular species C. Assuming a total concentration of nanoreactors cNR, the experimentalist would measure the transformation of a reactant (say reactant A) per time, according to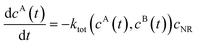 | (4) |
To derive the functional form of the total catalytic rate, we assume ktot (number of molecules reacting per unit of time) is equal to the radial flux of reactants at the nanoparticle surface. In bimolecular reactions, the fraction of molecules A reacting is then proportional to the number of molecules B at the same location, and vice versa. Thus, ktot can be estimated through the standard mean-field relation78,117
| ktot = KvolcA(R)cB(R), | (5) |
| ∇·Ji = 0 | (6) |
In their diffusive approach to the catalyst nanoparticle, reactants have to permeate the shell. The kinetics of this process is thus governed by the shell permeability, which depends on the diffusivity profile, Di(r), and on the thermodynamic barrier, i.e., the transfer free energy between bulk and shell, ΔGi(r). For simplicity, we take both profiles to be shell-centered step functions of the width equal to the polymer shell width (see Fig. 1B), i.e.
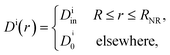 | (7) |
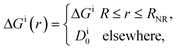 | (8) |
| Ji = −Dici∇βμi, | (9) |
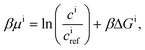 | (10) |
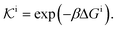 | (11) |
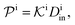 | (12) |
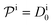 .
.
We found83 that the total catalytic rate for bimolecular reactions in responsive nanoreactors is obtained as in eqn (1). In this expression,
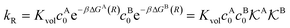 | (13) |
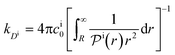 | (14) |
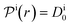 , and the diffusion rate turns into the Smoluchowski rate
, and the diffusion rate turns into the Smoluchowski rate 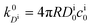 . For the core–shell configuration depicted in Fig. 1B the step profiles in eqn (7) and eqn (8) apply and the relation between the shell permeability and the diffusion rate, eqn (14), simplifies to
. For the core–shell configuration depicted in Fig. 1B the step profiles in eqn (7) and eqn (8) apply and the relation between the shell permeability and the diffusion rate, eqn (14), simplifies to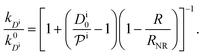 | (15) |
Eqn (1) is the main analytical result for nanoparticle surface-catalyzed bimolecular reactions. It shows that, in the fully bimolecular case, the diffusional fluxes of the different reactants are coupled. Thus, ktot depends in a non-trivial way on the surface and the diffusion rates and nanoreactor shell permeability, in contrast to the simple unimolecular case (i.e., in general ktot−1 ≠ kD−1 + kR−1 in bimolecular reactions).
Eqn (1) together with eqn (13) and (15) can be used to predict the total catalytic rate once the nanoreactor shell permeability and the reactant partition ratios are known (e.g., from experiments, or from simulations, see sections 3 and 4), or, conversely, to extract the parameters by fitting to experimental data. Carregal-Romero et al.5 investigated the bimolecular electron-transfer reaction between hexacyanoferrate(III), Fe(CN)63− (HCF), and borohydride BH4− ions in Au–PNIPAM core–shell nanoreactors. In a previous work83 we demonstrated that this bimolecular reaction is diffusion-controlled and can be treated as pseudo-unimolecular (see also next section 2.2), that is, dcHCF(t)/dt = −kobscHCF(t).
The temperature dependence of the measured pseudo-first-order constant is shown by blue filled squares in Fig. 2A. We observe that the reaction rate decreases by one order of magnitude when the temperature of the solution exceeds the lower critical solution temperature (LCST) of the PNIPAM polymer. The measured nanoreactor hydrodynamic radius data, displayed by orange open circles in Fig. 2A, exhibit the well-known volume transition between the swollen and the collapsed states below and above the LCST, respectively. As we pointed out before, this transition changes the physicochemical properties of the polymer, which leads to different reactant diffusivity and transfer free energy values resulting in a nanoreactor permeability switch at the LCST. In the diffusion-controlled limit for pseudo-unimolecular kinetics we can identify kobs = kHCFDcNR/cHCF0. The cHCF0 is the initial bulk concentration, which can be replaced by the instantaneous cHCF(t) in the equations during the reaction because of the stationarity assumption. Using eqn (15) together with the experimental data from Fig. 2A, we estimate the temperature dependence of the nanoreactor shell permeability for HCF (Fig. 2B) and clearly observe the aforementioned permeability switch below and above the LCST. The permeability decreases around one order of magnitude from the swollen to the collapsed state. By comparing Fig. 2A and B we clearly see that the nanoreactor shell permeability is the essential ingredient to understand the reaction rate response of nanoreactors in diffusion-controlled reactions. Detailed mesoscopic and microscopic insights on the influence of effective interaction potentials, hydrogel density, and chemistry on the permeability of polymer shells is presented in sections 3 and 4.
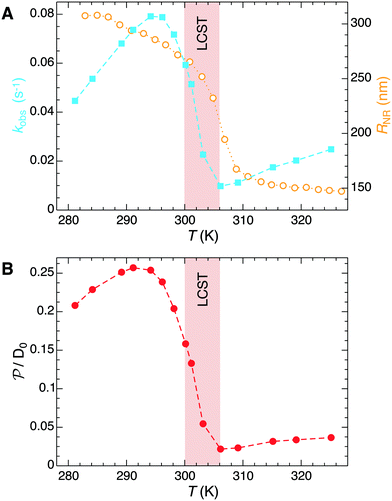 | ||
| Fig. 2 (A) Temperature dependence of the measured pseudo-first-order constant kobs (blue filled squares) of the electron-transfer reaction between HCF and borohydride ions in Au–PNIPAM nanoreactors. The measured temperature dependence of the nanoreactor hydrodynamic radius is shown by orange opened circles. All data were taken from ref. 5. (B) Temperature dependent nanoreactor shell permeability for HCF estimated using eqn (15). | ||
2.2 Pseudo-unimolecular reactions in nanoreactors
Bimolecular reactions are typically treated as pseudo-unimolecular when one of the reactants is in large excess with respect to the other. The reasoning behind this assumption is that, according to the simple Smoluchowski rate, the reactant in larger concentration would diffuse towards the nanoparticle surface at a much larger rate than the other one. Therefore, when the reactant in limiting concentration arrives to the catalyst, it will always find a reactant of the other species to combine with. However, this is not always true when considering nanoreactors. In this case, the diffusion rate, eqn (14), not only depends on the bulk reactant concentration but also on the shell permeability and thus on the molecular interactions of reactants with the shell. It is thus the combination of both quantities that determines whether a bimolecular reaction can be treated as pseudo-unimolecular or not.If one of the reactants has a much larger diffusion rate than the other one, e.g., kDB ≫ kDA, the total reaction rate, eqn (1), reduces to (see ESI in ref. 83)
| ktot → k1tot = (kDA−1 + kR−1)−1, | (16) |
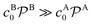 . This means that one of the reactants should be in a much higher bulk concentration and/or subject to a much larger shell permeability than the other.
. This means that one of the reactants should be in a much higher bulk concentration and/or subject to a much larger shell permeability than the other.
In Fig. 3 we analyze how large should be the excess of reactant B for the pseudo-unimolecular reaction limit to be valid. This value depends on the relative nanoreactor shell permeability, 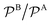 . For simplicity, we consider that the surface rate is equal to the diffusion rate of the reactant in limiting concentration (kR = kDA, diffusion-influenced reaction). When both reactants have the same permeability (red line), the concentration of reactant B should be roughly 10 times larger than the one of A to have a unimolecular reaction. If we then decrease the shell permeability to the reactant B by 10 times, its concentration has thus to become 100 times higher with respect to that of A to keep this limit. Fig. 3 also shows that the catalytic rate predicted for a pseudo-unimolecular reaction for the reactant in limiting concentration may differ from the fully bimolecular one by orders of magnitude. Thus, when dealing with nanoreactors, it is necessary to consider not only the difference between the bulk concentrations of the reactants but also the difference in the shell permeability to the reactants.
. For simplicity, we consider that the surface rate is equal to the diffusion rate of the reactant in limiting concentration (kR = kDA, diffusion-influenced reaction). When both reactants have the same permeability (red line), the concentration of reactant B should be roughly 10 times larger than the one of A to have a unimolecular reaction. If we then decrease the shell permeability to the reactant B by 10 times, its concentration has thus to become 100 times higher with respect to that of A to keep this limit. Fig. 3 also shows that the catalytic rate predicted for a pseudo-unimolecular reaction for the reactant in limiting concentration may differ from the fully bimolecular one by orders of magnitude. Thus, when dealing with nanoreactors, it is necessary to consider not only the difference between the bulk concentrations of the reactants but also the difference in the shell permeability to the reactants.
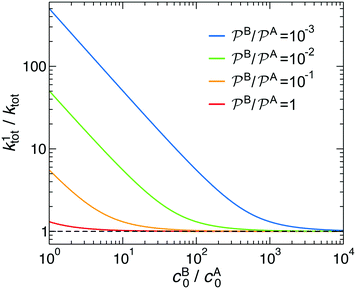 | ||
Fig. 3 Total rate for unimolecular reactions ktot1, eqn (16), divided by the total reaction rate ktot for bimolecular reactions, eqn (1), as a function of the relative reactant bulk concentration, cB0/cA0. The lines stand for different relative nanoreactor shell permeabilities to the reactants, 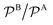 . We assume kR = kDA. . We assume kR = kDA. | ||
Hence, when considering nanoreactors, care should be taken since in these systems it is not the bulk mobility and concentration that determine the reaction type (diffusion versus surface control), but the values in the polymer shell, which can be the limiting factor. The latter is defined by the shell permeability 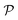 and can thus strongly differ from the bulk value. Because of the responsive nature of the gating shell of nanoreactors, this dependence crucially implies that the identity of the limiting reactant can switch upon a change in the external stimulus. Failure to recognize this fact can lead to very large discrepancies between the correct and the approximate rate. This theoretical framework for pseudo-unimolecular reactions qualitatively rationalizes the large and sharp variations in catalytic rate observed in the relevant nanoreactor experiments.6–8,78
and can thus strongly differ from the bulk value. Because of the responsive nature of the gating shell of nanoreactors, this dependence crucially implies that the identity of the limiting reactant can switch upon a change in the external stimulus. Failure to recognize this fact can lead to very large discrepancies between the correct and the approximate rate. This theoretical framework for pseudo-unimolecular reactions qualitatively rationalizes the large and sharp variations in catalytic rate observed in the relevant nanoreactor experiments.6–8,78
3 Partitioning and diffusion: coarse-grained simulations
As we have just described, key parameters to understand a nanoreactor's selectivity and rate response to stimuli are the permeability of its polymeric shell and the reactant partitioning within. In the following, we review two selected coarse-grained (CG) simulation studies of partitioning, diffusion, and permeability in model membranes.109,110 Mesoscopic models, neglecting chemical resolution, play a pivotal role not only as a bridge between the aforementioned macroscopic reaction model and the following microscopic all-atom models but also for the deeper understanding of essential physics, e.g., of molecular adsorption and transport in polymer systems. Particle-based simulations on various scales with increasing complexity and chemical detail are now emerging. For the convenience of the reader, we have summarized selected relevant simulation efforts in Table 2.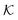 , permeability
, permeability 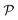 , or related adsorption or transport phenomena of (co)solutes in polymers. Abbreviations: all-atom (AA), coarse-grained (CG), molecular dynamics (MD), Monte-Carlo (MC), Langevin dynamics (LD), Brownian dynamics (BD), dissipative particle dynamics (DPD)
, or related adsorption or transport phenomena of (co)solutes in polymers. Abbreviations: all-atom (AA), coarse-grained (CG), molecular dynamics (MD), Monte-Carlo (MC), Langevin dynamics (LD), Brownian dynamics (BD), dissipative particle dynamics (DPD)
| Ref. | Simulation methods | Architecture | Polymer | Resulting quantity | Comment |
|---|---|---|---|---|---|
| 145 | AA-MD | Swollen cross-linked network | Polyethyleneglycole | Diffusivity of water, ions, rhodamine | Water content: 75–91%, mesh size: 2.3–5.5 nm |
| 146 | AA-MD | Collapsed | Polyethylene | Diffusivity and partitioning of oxygen and water | Permeability for oxygen 5–6 orders of magnitude larger than for water |
| 147 | AA-MD | Collapsed | Poly(vinyl alcohol) | Diffusivity of O2 | Water uniformly distributes |
| 148, 149 | AA-MD | Collapsed | Poly(vinyl alcohol) | Diffusivity of water | Hydrogel with 4–40% water |
| 150 | AA-MD | Collapsed | Polydimethylsiloxane | Diffusivity of water and ethanol | Water/ethanol mixtures; water molecules faster than ethanol |
| 151 | AA-MD + transition state approach | Collapsed | Polystyrene and its copolymers | Diffusivity and partitioning of gas and water molecules | |
| 152 | AA-MD | Single chain | PNIPAM | Adsorption of urea | Studying volume phase transition |
| 153 | AA-MD | Single chain | PNIPAM | Adsorption of TMAO, urea | Studying volume phase transition |
| 154 | AA-MD | Collapsed and solvent phase | PNIPAM | Partitioning of ions | Thin core–shell membrane, direct measuring of partitioning |
| 155 | AA-MD | Cross-linked network | PNIPAM | Diffusivity of water; volume transition | Studying volume transition; cross-linking inhibits the collapse |
| 156 | AA-MD | Collapsed and solvent phase | PNIPAM (3mer) | Water–polymer coexistence | Also 30mer of PNIPAM: no conclusions on chain configuration |
| 157 | AA-MD | Swollen & collapsed finite aggregate | PNIPAM | Partitioning of large ions | Umbrella sampling of the potential of mean force of the ions |
| 158 | Gibbs-ensemble CG-MD | Cubic network | Bead-spring | Solvent sorption and swelling isotherm | Effects of solvents on swelling |
| 119 | Two-box–particle-transfer CG-MD | Cubic network | Bead-spring | Solvent sorption and swelling isotherm | Effects of cross-linkers on swelling |
| 159, 160 | CG-MC | Tetra-functional network | Bead-spring | Solvent sorption and swelling isotherm | Effects of polymer network density and deformation on swelling |
| 120 | CG-MC | Cubic network | Rigid rod | Cosolute diffusivity | Effects of cosolute size and polymer density on cosolute diffusivity |
| 121 | CG-LD | Cubic network | Charged bead-spring | Energy conversion | Effects of compression and solvents on energy contribution |
| 122 | CG-LD | Highly swollen cubic network | Charged bead-spring | Adsorption and conformational response | Counterion-induced deformation |
| 123 | LD | Cubic network | Charged bead-spring | Ion transport | Effects of electrostatic coupling between polymer and ions on ion transport |
| 136 | CG-MC | Tetra-functional network | Bead-spring | Cosolute partitioning | Effects of polymer density on partitioning |
| 139 | CG-MD | Polymer melt | Semi-flexible | Gas partitioning, diffusivity and permeability | Effect of gas size and polymer semi-flexibility on gas transport |
| 161 | CG-BD | Cubic network | Bead-spring | Cosolute diffusivity | Effects of cosolute density on cosolute diffusivity |
| 162 | CG-DPD | Random network | Semi-flexible | Permeability and cosolute diffusivity | Effects of porosity and deformation on permeability |
| 163–165 | CG-BD | Cubic network | Rigid rod | Cosolute diffusivity | Effects of interactions, hydrodynamics, and network heterogeneity on cosolute diffusivity |
| 166 | CG-BD | Random cubic network | Rigid rod | Cosolute diffusivity | Effects of network porosity, flexibility, degree of cross linking, and electrostatic interaction on cosolute diffusivity |
3.1 Influence of gel volume transition on reactant partitioning in a model polymeric membrane
Responsive polymers feature a sharp volume transition where the density of the polymer drastically changes. The partitioning of reactants across the volume transition and the feedback of the polymer to the permeation is complex and poorly understood. We thus first discuss a CG simulation model with details described previously109 consisting of permeating reactants in a polymer-based thin membrane (Fig. 4A), where we aim at a qualitative study of the effects of structural transitions of gels on the reactant partitioning and its back-coupling to the volume transition. In the following, we refer to the permeating reactants generally as ‘solutes’.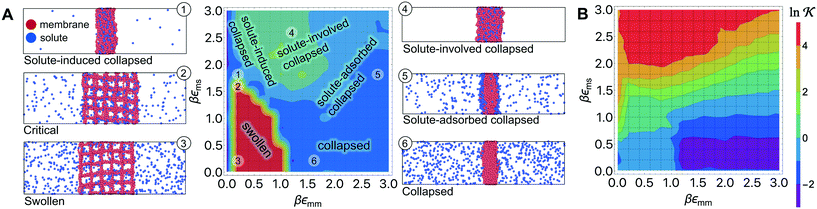 | ||
Fig. 4 (A) Various conformational states and regimes in the mesoscopic network membrane–solute system from CG computer simulations are depicted in the main phase diagram (center) depending on the Lennard-Jones (LJ) interactions εmm and εms: (1) is a ‘solute-induced collapsed’ state, (2) is a ‘critical’ transition line (yellow contour) between the intrinsic (3) ‘swollen' and (6) ‘collapsed’ states. (4) is a ‘solute-involved collapsed’ state, while (5) is a ‘solute-adsorbed’ collapsed state where solutes adsorb mostly on the membrane surface. For details see text. Reprinted with permission from ref. 109, copyright 2017 American Chemical Society. (B) Solute partitioning landscape 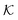 depending on εmm and εms. depending on εmm and εms. | ||
The membrane is constructed as cross-linked semi-flexible network of polymers formed on a regular cubic lattice,118–123 and the solutes can diffuse throughout the membrane and the bulk regions. This enables a direct sampling of the solute partitioning from the simulations simply according to eqn (3). We use the Lennard-Jones (LJ) pair potential and its size unit σ as the diameter for all particles and the monomer–monomer (bonded) distance in the polymers. In order to model such a gel in the presence of various solutes, we employ inter- and intra-particle interactions in terms of LJ pair potentials. We focus on two key interaction parameters: the membrane–membrane interaction εmm controls the solvent quality, turning it from good to poor upon the increase of εmm. The membrane–solute interaction εms governs the membrane–solute coupling and thus models different kinds of solutes. For the solute–solute interaction we always use εss = 0.1kBT, essentially being a steep (r−12) repulsion.
In Fig. 4A we show the landscape of the gel structural phases, depending on both interaction parameters. The red region depicts swollen states, where the gel volume is relatively large, while the blue region indicates collapsed states. Without the solutes (εms = 0) our model exhibits a collapse transition at around εms ≃ 1.0kBT. In the presence of the solutes, however, the picture becomes more complex: the ‘critical’ transition line (yellow contour line) between swollen and collapsed states depends substantially on the membrane–solute interaction, as shown by the label (2). The stark color contrast around this critical line signifies the sharp transition. In addition, one can identify in total five distinct phase regions (or states), classified into (1) “solute-induced collapsed”, (3) “swollen”, (4) “solute-involved collapsed”, (5) “solute-adsorbed collapsed”, and (6) “collapsed” states, indexed by the numbers in the colored center panel of Fig. 4A. Interestingly, the “solute-induced collapsed” state (state 1) can occur even in good solvent conditions, where the membrane undergoes a relatively sharp collapse transition induced by a strong ‘bridging’ attraction between the solutes and the network monomers. The effect has been reported in computer simulations before but only on the single polymer level.124–131 The “solute-involved” collapsed state (state 4) occurs at the intermediate solvent quality where the membrane collapses with most of the internal solutes embedded, yielding a bulkier collapsed gel than the intrinsically collapsed case. The “solute-adsorbed collapsed” state (state 5) is an example for the limiting case, where both of the membrane–membrane and membrane–solute attractions are strong, but the first one dominates and excludes the solutes, therefore leading to a strong surface accumulation of those.
The solute partitioning 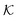 (on a log-scale) averaged over the membrane slab is shown in Fig. 4B in a 2D-landscape plot, and is related to the transfer free energy from the bulk into the network,
(on a log-scale) averaged over the membrane slab is shown in Fig. 4B in a 2D-landscape plot, and is related to the transfer free energy from the bulk into the network, 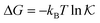 , which quantifies the average transfer free energy for the solute transfer from bulk to the membrane. The partitioning varies by several orders of magnitude, depending not only on the membrane–solute interaction but also significantly on the solvent quality. The partitioning overall becomes large (i.e., higher adsorption) as the membrane–solute attraction, εms, increases, while it has large regions of unity in the swollen states (light blue-greenish areas). Note that when compared with the structural landscape in Fig. 4A, both extrema of
, which quantifies the average transfer free energy for the solute transfer from bulk to the membrane. The partitioning varies by several orders of magnitude, depending not only on the membrane–solute interaction but also significantly on the solvent quality. The partitioning overall becomes large (i.e., higher adsorption) as the membrane–solute attraction, εms, increases, while it has large regions of unity in the swollen states (light blue-greenish areas). Note that when compared with the structural landscape in Fig. 4A, both extrema of 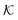 (i.e., the minimum and the maximum) are in the collapsed regions, indicating that the collapsed phase can relate to extremely different partitionings and there is no unique mapping. Moreover, at intermediate values of εms,
(i.e., the minimum and the maximum) are in the collapsed regions, indicating that the collapsed phase can relate to extremely different partitionings and there is no unique mapping. Moreover, at intermediate values of εms, 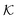 is a nonmonotonic function of the solvent quality, meaning that it can be maximized by an optimal solvent quality. The maximization of the partitioning is in fact a quite general feature in attractive but crowded systems as we will discuss in the following section.
is a nonmonotonic function of the solvent quality, meaning that it can be maximized by an optimal solvent quality. The maximization of the partitioning is in fact a quite general feature in attractive but crowded systems as we will discuss in the following section.
To sum up, the CG simulation model of a polymer network in the presence of solutes reveals a rich topology of structure phases and their relation to solute partitioning, entering the rate equations eqn (13) and (15). In particular, for very attractive solute–membrane interactions (εms ≳ 1kBT) the network structure and partitioning are coupled. The mesoscopic model thus provides a landscape of the partitioning, thereby bridging the macroscopic continuum model and microscopic discrete data in terms of the generic interaction parameters. In addition, the results will be helpful for the interpretation of experiments for certain polymer–reactant systems and could also be useful to design feedback-systems where the local reactant (or product) concentration may couple back to polymer structure in a prescribed way.
3.2 Partitioning, diffusion, and permeability in a model lattice membrane
Now we present a related but different CG model110 of a membrane–solute system (Fig. 5A) in order to study permeability in dense media qualitatively on a generic level. We demonstrate how the permeability can be tuned massively in magnitude by systematically varying the membrane–solute interactions and the density of the membrane. The study also gives important insights about how partitioning and diffusion are correlated.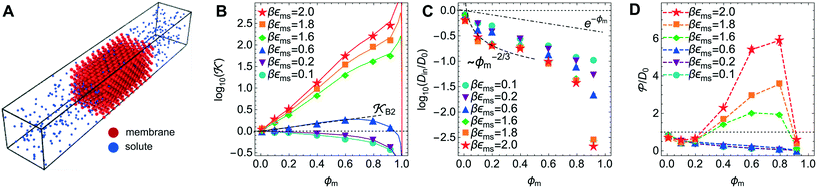 | ||
Fig. 5 (A) Snapshot of the mesoscopic lattice membrane–solute system. The membrane sites (red) are fixed on a face-centered-cubic (fcc) lattice with the volume fraction ϕm, and the penetrating solutes (blue) are diffusing and interacting via the LJ potentials with εms. (B) Solute partitioning 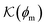 at different εms. The solid lines depict the exact relation, eqn (17), and the dashed line depicts the approximated partitioning at different εms. The solid lines depict the exact relation, eqn (17), and the dashed line depicts the approximated partitioning 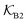 with βεms = 0.6 (see text for details). (C) Solute diffusivity Din(ϕm)/D0 with different εms. The dashed lines depict the approximation Din/D0 = exp(−ϕm) valid for low εms and ϕm, and the scaling Din/D0 ∼ ϕm−2/3 valid for high εms and low ϕm. (D) Permeability with βεms = 0.6 (see text for details). (C) Solute diffusivity Din(ϕm)/D0 with different εms. The dashed lines depict the approximation Din/D0 = exp(−ϕm) valid for low εms and ϕm, and the scaling Din/D0 ∼ ϕm−2/3 valid for high εms and low ϕm. (D) Permeability 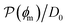 at different εms. Reprinted with permission from ref. 110, copyright 2019 American Physical Society. at different εms. Reprinted with permission from ref. 110, copyright 2019 American Physical Society. | ||
The permeability is defined following the solution–diffusion theory89–91,94–99 by eqn (2). There have been pioneering theoretical models to elucidate the transport phenomena in membranes89–91,94,132–135 based on simple theories for either partitioning or diffusion. Recently, a simulation study revealed maximization of partitioning of penetrating solutes in polymer membranes tuned by the polymer volume fraction.136 Diffusion in dense membranes is usually quite complex and highly dependent on details of the interaction potentials.102,103,113,137–141 Nevertheless, there have been no comprehensive studies on the permeability 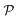 , being a product of partitioning and diffusion.
, being a product of partitioning and diffusion.
In the CG model membrane–solute system as shown in Fig. 5A the diffusive solutes are ideal (εss = σss = 0), and the membrane consists of immobile interaction sites, located on a face-centered-cubic (fcc) lattice with a fixed unit cell size l, variation of which tunes the monomer packing fraction ϕm. The simplicity of such an ordered and rigid model membrane with ideal solutes renders the problem easier for interpretation and perhaps theoretically tractable. The ideal solutes diffuse throughout the simulation box but interact only with the membrane sites via the LJ potential with the coupling strength εms. For the ideal solutes the partitioning can be exactly computed via the transfer free energy shown in eqn (11). In our case 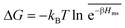 ,142 where Hms(r) = ∑iUms(∣r − ri∣) is the total Hamiltonian (summing over all membrane sites i), and
,142 where Hms(r) = ∑iUms(∣r − ri∣) is the total Hamiltonian (summing over all membrane sites i), and ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = ∫dVx/Vm is the volume average, yielding
= ∫dVx/Vm is the volume average, yielding
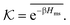 | (17) |
The computed partitioning as a function of the membrane volume fraction ϕm is shown in Fig. 5B for various εms. For relatively low membrane–solute couplings (βεms ≲ 0.3), the LJ interaction between solutes and membrane sites is essentially repulsive (signified by a positive second virial coefficient), and the partitioning monotonically decreases as the membrane becomes dense, owing to the dominant exclusion by the membrane. For intermediate couplings around βεms = 0.6, which is moderately attractive, partitioning reaches a maximum at an optimal membrane density around ϕm = 0.6. The partitioning maximization is attributed to a balance between adsorption and steric exclusion. In addition, a leading order approximation of 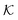 on a two-body level,
on a two-body level, 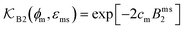 for βεms = 0.6 is depicted by the dashed line, where cm ∝ ϕm is the membrane concentration, and Bms2 is the second virial coefficient. Fig. 5C shows the solute diffusivity Din/D0 in the membrane as a function of ϕm, rescaled by the free diffusivity in the bulk. As the membrane becomes dense, Din tends to exponentially decrease, showing more complex behavior with higher couplings. We compare the simulation results with scaling theories for diffusion in two limiting cases. The upper dashed line indicates the limiting law Din/D0 = exp(−ϕm) based on the ‘volume-exclusion’ theory.102,134,135,143,144 It is indeed valid only for low couplings, which acts essentially repulsive. For high membrane–solute attractions and low membrane density, the diffusivity follows the power law Din/D0 ∼ ϕm−2/3. The scaling relation is derived by the limiting law from the Kramers' barrier crossing over the distance l ∼ ϕ−1/3, and therefore Din ∼ l2/τ ∼ ϕm−2/3.110
for βεms = 0.6 is depicted by the dashed line, where cm ∝ ϕm is the membrane concentration, and Bms2 is the second virial coefficient. Fig. 5C shows the solute diffusivity Din/D0 in the membrane as a function of ϕm, rescaled by the free diffusivity in the bulk. As the membrane becomes dense, Din tends to exponentially decrease, showing more complex behavior with higher couplings. We compare the simulation results with scaling theories for diffusion in two limiting cases. The upper dashed line indicates the limiting law Din/D0 = exp(−ϕm) based on the ‘volume-exclusion’ theory.102,134,135,143,144 It is indeed valid only for low couplings, which acts essentially repulsive. For high membrane–solute attractions and low membrane density, the diffusivity follows the power law Din/D0 ∼ ϕm−2/3. The scaling relation is derived by the limiting law from the Kramers' barrier crossing over the distance l ∼ ϕ−1/3, and therefore Din ∼ l2/τ ∼ ϕm−2/3.110
The resulting permeability, the product of 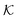 and Din, shown in Fig. 5D, exhibits intriguing features. For essentially repulsive solutes,
and Din, shown in Fig. 5D, exhibits intriguing features. For essentially repulsive solutes, 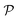 decreases monotonically as the membrane density increases, and the overall magnitude is below unity, almost approaching zero for very dense membranes. We speculate that this essentially repulsive case maybe the scenario in the experiments with the highly charged reactant HCF in section 2.1, which probably does not like to enter the collapsed gel, but this suspicion needs further scrutiny. On the other hand, for high couplings (attraction) the permeability is first minimal around ϕm = 0.1, then maximized at large membrane densities ϕm ≃ 0.8. The permeability vanishes at the maximum overlapping density (ϕm ∼ 1), where no percolating holes for diffusion are present anymore. This demonstrates a clear maximization of permeability when the system is highly attractive and dense. The nonmonotonic behavior of permeability results from drastic nontrivial cancellations between the partitioning and the diffusivity, which exponentially increase and decrease, respectively. The massive cancellation between two largely varying functions over several orders of magnitude yields a permeability of the order of unity,110 implying a high potential for fine-tuning of the permeability behavior in experiments by small changes in density or interactions.
decreases monotonically as the membrane density increases, and the overall magnitude is below unity, almost approaching zero for very dense membranes. We speculate that this essentially repulsive case maybe the scenario in the experiments with the highly charged reactant HCF in section 2.1, which probably does not like to enter the collapsed gel, but this suspicion needs further scrutiny. On the other hand, for high couplings (attraction) the permeability is first minimal around ϕm = 0.1, then maximized at large membrane densities ϕm ≃ 0.8. The permeability vanishes at the maximum overlapping density (ϕm ∼ 1), where no percolating holes for diffusion are present anymore. This demonstrates a clear maximization of permeability when the system is highly attractive and dense. The nonmonotonic behavior of permeability results from drastic nontrivial cancellations between the partitioning and the diffusivity, which exponentially increase and decrease, respectively. The massive cancellation between two largely varying functions over several orders of magnitude yields a permeability of the order of unity,110 implying a high potential for fine-tuning of the permeability behavior in experiments by small changes in density or interactions.
Mesoscopic models of membrane–solute systems demonstrate that the permeability, typically resulting from large cancellation effects of partitioning and diffusion, is very sensitively tuned by the effective interaction potentials and the membrane density. The results indicate that most drastic selectivity effects are at high membrane densities and significant (≳kBT) membrane–solute attractions. The effective potentials in realistic material design assemblies can be somewhat controlled by various external parameters, such as temperature, ionic strength, pH, and possibly various additives in the solution. The results from the mesoscopic models thus provide useful physical insight and may bear important applications in design and engineering of molecular systems to achieve a selective transport by fine-tuning interactions and topologies, particularly in highly attractive membrane systems.
4 Partitioning and diffusion: all-atom simulations
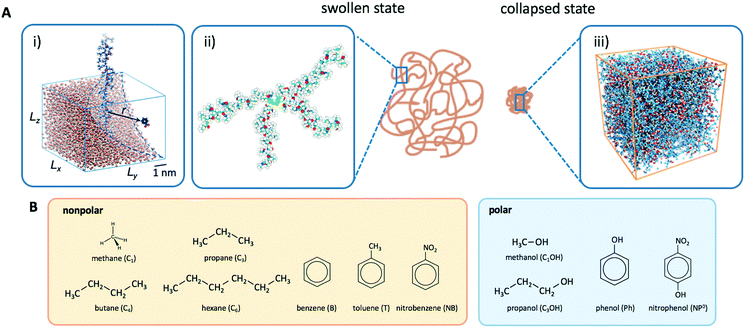
The advantage of the mesoscopic simulations in the previous section is that we can obtain fundamental and qualitative insights on how permeability depends on basic input parameters such as interaction energies, lattice geometry, and single solute diffusion. However, in experiments we deal with specific, chemical systems, where the effects of interactions are highly convoluted and solvation, polarity, electrostatics, and specific steric constraints come explicitly into play. Hence, for a more detailed insight and quantitative numbers for the continuum approach to reaction rates in section 2, we need to resort to higher resolution, molecular dynamics computer simulations. All-atom simulation studies of partitioning and diffusion through polymer networks with increasing complexity and chemical detail are now emerging and growing in the literature. Selected works in this field are given in Table 2. In the following, we will review our recent efforts to understand partitioning and diffusion of solutes in swollen and collapsed PNIPAM hydrogels by all-atom MD simulations.111–1144.1 Swollen state
In order to model the swollen state of a hydrogel shell one can focus on one elongated PNIPAM chain, as shown in Fig. 6A.i, where the chain is replicated through periodic boundary conditions. The cylindrical geometry allows for a simple extraction of adsorption properties111 of solvated molecules in the solution. The first step is to evaluate the cylindrical radial distribution function (RDF) of the solute molecules from the backbone, g2D(r), as shown in an example for nitrobenzene (NB) in Fig. 7A. The adsorption coefficient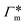 per monomer of the polymer is then obtained by integration along the spatial coordinates,167
per monomer of the polymer is then obtained by integration along the spatial coordinates,167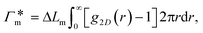 | (18) |
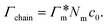 | (19) |
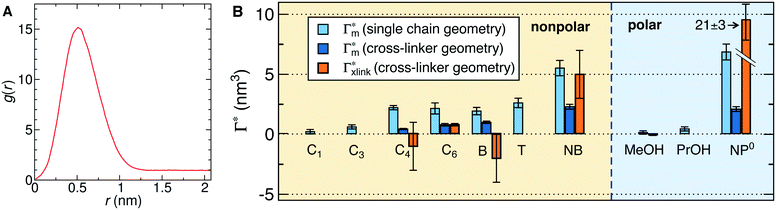 | ||
Fig. 7 (A) Cylindrical RDF of backbone–NB for an extended PNIPAM chain111 (see Fig. 6A.i). (B) Adsorption coefficients of various solutes (see Fig. 6B) to a PNIPAM monomer 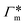 (from single-chain geometry and the OPLS111 force field, and from cross-linker geometry using the OPLS-QM2 (ref. 112) force field) and to a cross-linker (from single-chain geometry and the OPLS111 force field, and from cross-linker geometry using the OPLS-QM2 (ref. 112) force field) and to a cross-linker  112 (OPLS-QM2 force field) at 300 K. 112 (OPLS-QM2 force field) at 300 K. | ||
Another setup of swollen hydrogels, shown in Fig. 6.ii, mimics the cross-linker unit of a hydrogel network, and thus lends itself to study the influence of cross-linkers on adsorption of molecules. In our previous study,112 we considered a very common N,N′-methylenebisacrylamide (BIS) cross-linker, connecting four PNIPAM chains with their ends tethered in a tetrahedral geometry. The solute molecules in general adsorb in different proportions to the chain regions and the cross-linker neighborhood. The overall adsorption in the radial interval [r1,r2] from the cross-linker is obtained in a straightforward manner by integrating the (spherical) RDF g(r) of the solutes
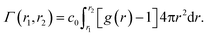 | (20) |
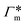 , as in the single-chain geometry. Finally, the total adsorption can be decomposed into two contributions,
, as in the single-chain geometry. Finally, the total adsorption can be decomposed into two contributions,| Γtot = Γchain + Γxlink. | (21) |
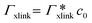 , where
, where 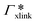 is the adsorption coefficient of the cross-linker.
is the adsorption coefficient of the cross-linker.
The resulting adsorption coefficients 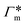 are shown in Fig. 7B (blue shaded bars), from the single-chain111 and cross-linker112 geometries. Quite generally, the adsorption grows with the molecular size. The effect of the cross-linker,
are shown in Fig. 7B (blue shaded bars), from the single-chain111 and cross-linker112 geometries. Quite generally, the adsorption grows with the molecular size. The effect of the cross-linker, 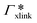 , is shown in Fig. 7B by orange bars: the apolar compounds C4, C6, and B show a low affinity to the cross-linker. In contrast, the adsorption of nitro-aromatic solutes to the cross-linker is significant, in particular for NP0.112 NB shows more than doubled and NP0 even an order of magnitude higher adsorption to the cross-linker region than to a monomer of the polymer. Note that the BIS cross-linker has two amide groups and is slightly more hydrophilic than the PNIPAM chain, hence favoring polar molecules.
, is shown in Fig. 7B by orange bars: the apolar compounds C4, C6, and B show a low affinity to the cross-linker. In contrast, the adsorption of nitro-aromatic solutes to the cross-linker is significant, in particular for NP0.112 NB shows more than doubled and NP0 even an order of magnitude higher adsorption to the cross-linker region than to a monomer of the polymer. Note that the BIS cross-linker has two amide groups and is slightly more hydrophilic than the PNIPAM chain, hence favoring polar molecules.
From the known adsorptions on individual chains and cross-linkers we can predict the partitioning in extensive hypothetical swollen polymer architectures, such as hydrogels. The partitioning follows from 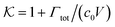 , where V is the volume of the gel and Γtot the total adsorption of molecules on all the chains and cross-linkers [eqn (21)], which leads to
, where V is the volume of the gel and Γtot the total adsorption of molecules on all the chains and cross-linkers [eqn (21)], which leads to
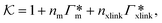 | (22) |
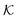 for several solutes from the obtained MD parameters in Fig. 8. The values range around unity,
for several solutes from the obtained MD parameters in Fig. 8. The values range around unity, 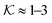 , as also resulted from the CG models in Fig. 5B for this polymer fraction range. As we will see in the following, the collapsed state can give rise to much higher partitioning.
, as also resulted from the CG models in Fig. 5B for this polymer fraction range. As we will see in the following, the collapsed state can give rise to much higher partitioning.
 | ||
| Fig. 8 Partitioning of several molecules resulting from the atomistic models of a swollen (at 300 K and polymer fraction of ϕm = 0.1) and collapsed (at 340 K and ϕm = 0.8) state of a PNIPAM gel. The values for the swollen state are computed from eqn (22) and assuming polymer volume fraction ϕm = 0.1, whereas the values for the collapsed state are computed from eqn (11). | ||
4.2 Collapsed state
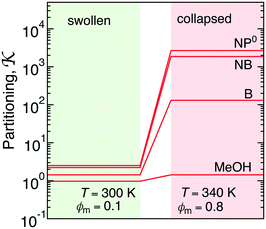
The collapsed state of the PNIPAM hydrogel can be modeled as a bulk of aggregated polymeric chains (in our case 20 monomeric units long) at 340 K (above the LCST), where cross-linkers are ignored. The amount of sorbed water between the polymeric chains is chosen such that it corresponds to the chemical equilibrium with bulk water.113 The amount of water in the collapsed state depends on temperature, and amounts to around 20 wt% (somehow less than experimental estimates of around 30 wt% (ref. 168–172)), which roughly correspond to the polymer volume fraction of ϕm = 0.8. Note that this is in the range of packing fractions for which we observed the most interesting behavior of permeability in the CG simulations in section 3.Water molecules are very non-uniformly distributed throughout the phase and tend to flock together into irregular clusters of various nanoscopic sizes, which were observed also in simulations of other amorphous polymer structures.151,173–176 This water–polymer spatial heterogeneity is a crucial player in the solvation of small molecules, whereby the nature of the solute (being polar, nonpolar, or ionic177) is a decisive property. Two representative snapshots in Fig. 9A, showing a benzene (nonpolar) and a phenol (polar) molecule, demonstrate that nonpolar solutes are preferentially expelled from water clusters and tend to reside in ‘dryer’ regions of the gel, whereas polar molecules tend to partition closer to or inside water clusters. Thus, the “dual” character of the gel can favorably accommodate both polar and nonpolar species.
 | ||
| Fig. 9 (A) Snapshots of benzene and phenol molecules solvated in the PNIPAM phase. Hydrophobic parts of the solutes are shown in yellow, the hydroxyl groups in green, PNIPAM polymers in blue, and water in red-white. (B) Transfer free energies from water to PNIPAM versus the molecular surface area. The dashed line is a fit of eqn (23) to the data points of nonpolar solutes. (C) Microsecond-long trajectory sequence of a NP0 molecule projected on a 2D plane (color coded from blue at t = 0 to red at t = 1000 ns). The green bubbles schematically depict the hopping transition with a transient pore opening. (D) Diffusion coefficients of molecules in the collapsed PNIPAM polymer versus their Stokes radii in water. The dashed line shows a fit of eqn (24) to the data points. | ||
The transfer free energy for a given molecule is obtained as the difference between the solvation free energy in PNIPAM (Gg) and in water (Gw), ΔG = ΔGg − ΔGw, both evaluated via the thermodynamic integration procedure.114Fig. 9B shows ΔG for various solutes plotted versus the molecular surface area Am of the solutes (defined as the envelope area of the fused union of the atoms178). The results follow a clear linear trend for the groups of nonpolar and aromatic solutes as well as alcohols and water. The linearity in the very heterogeneous polymer–water medium is rather surprising. The results can be conveniently described in terms of an effective molecular surface tension γm,179,180
| ΔG = ΔG0 + γmAm. | (23) |
Using eqn (11), we show the partitioning in the collapsed state in Fig. 8. In general, the partitioning of our neutral molecules is larger in the collapsed state. Also, the larger the partitioning in the swollen state, the progressively larger it is in the collapsed state. With some heuristic arguments, we showed that the partitioning roughly follows the relation  .114 This is in line with the universal observation from our CG model (section 3.1), namely that a collapsed state can have much more extreme effects on partitioning than a swollen state.
.114 This is in line with the universal observation from our CG model (section 3.1), namely that a collapsed state can have much more extreme effects on partitioning than a swollen state.
Moving on to the diffusion properties of solutes in the collapsed PNIPAM, we first look at the projected trajectory of a NP0 molecule in Fig. 9C. Its connected blob-like structure suggests that the diffusion advances via the hopping mechanism:182,183 a penetrating solute resides for longer time in a local cavity and suddenly performs a longer jump into a neighboring cavity through a transient water channel113 that forms between the chains (schematically illustrated in the bubbles in Fig. 9C). We plot the diffusion coefficients versus the size of the solutes aw (defined as the Stokes radius in pure water) in Fig. 9D. As the size of a solute increases by a factor of 7, the diffusion coefficients decreases by dramatic 5 orders of magnitude. The diffusion coefficients depend on the solute size aw roughly exponentially,
D = D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−aw/λ. e−aw/λ. | (24) |
Note that the rate-determining step in the hopping diffusion is the opening of a channel, which is associated with a free energy barrier ΔFa and can be via Boltzmann probability related to the diffusion coefficient as D ∼ exp(−ΔFa/kBT). In conjunction with the empirically obtained diffusion relation [eqn (24)], this implies
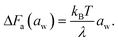 | (25) |
In conclusion, all-atom MD simulations offer insights into the molecular nature of the transport and solvation properties of molecules in hydrogels. These mechanisms are not only important for PNIPAM hydrogels, but most probably play important roles also in other responsive hydrogels, and their understanding is important for the rational design of novel materials. Notably, we see drastically larger effects for 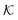 and D in the collapsed phase than in the swollen states, but apparently also a large anti-correlation between them, like in the coarse-grained simulations in section 3. The dense, collapsed state is thus more decisive for nanoreactor design and control. Very recent studies indicate that in particular for charged molecular reactants, the presence of water clusters and resulting substantial interfacial effects within a dense hydrogel may decisively affect their permeability behavior.117
and D in the collapsed phase than in the swollen states, but apparently also a large anti-correlation between them, like in the coarse-grained simulations in section 3. The dense, collapsed state is thus more decisive for nanoreactor design and control. Very recent studies indicate that in particular for charged molecular reactants, the presence of water clusters and resulting substantial interfacial effects within a dense hydrogel may decisively affect their permeability behavior.117
5 Concluding remarks
Stimuli-responsive nanoreactors are of high potential for the design of programmable and selective nano-devices for controlled catalysis and can therefore serve as candidates to create novel synthetic enzymes on the colloidal scale. However, they constitute complex devices with non-equilibrium processes starting at the electronic scale, defining the chemical surface reactions, coupled to those at the polymer network scale with all the intrinsic complexity of polymer–reactant interactions, including the feedback of responsive polymers, up to the device scale where reactants diffuse and react in a suspension of colloids. Here we reviewed the recent theoretical attempts of understanding some parts of the processes by focussing mostly on the key roles played by the permeability of the polymer shell and the reactant partitioning in order to control activity and selectivity, and how those enter the continuum rate predictions for the nanoreactors.As an important general result, we see substantial variations and correlations among 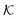 and D in the dense, collapsed polymer phases, in both coarse-grained and atomistically-resolved simulations, which are thus more decisive and tuneable for nanoreactor rate control than for the swollen states. Results for the temperature-induced rate switch observed in reference experiments, like the HCF reduction briefly discussed in section 2.1, can be thus traced back to, for example, the large exclusion (low partition ratio) and significant slowing down (low diffusion) of reactants in the collapsed state of neutral PNIPAM. However, a quantification of partitioning and diffusion of molecular ions by simulation approaches remains a challenge because of the water heterogeneities in the collapsed states.177
and D in the dense, collapsed polymer phases, in both coarse-grained and atomistically-resolved simulations, which are thus more decisive and tuneable for nanoreactor rate control than for the swollen states. Results for the temperature-induced rate switch observed in reference experiments, like the HCF reduction briefly discussed in section 2.1, can be thus traced back to, for example, the large exclusion (low partition ratio) and significant slowing down (low diffusion) of reactants in the collapsed state of neutral PNIPAM. However, a quantification of partitioning and diffusion of molecular ions by simulation approaches remains a challenge because of the water heterogeneities in the collapsed states.177
A large number of challenges and questions remain, which we try to tackle currently or leave open for future studies. For example, continuum approaches to diffusion- and permeability-influenced rates in confinement are often based on mean-field theories (like presented here), but more elaborate and accurate treatments, like Green's-function approaches,185 are yet to be devised.
The polymer permeability and the knowledge of how reactants partition in the polymer are the keys to program the desired function and response into a nanoreactor. Clearly, the number of experimental and chemical ways to synthesize a responsive hydrogel shell (e.g., with various combinations of copolymerization) is basically infinite. Modeling the features of diverse polymer systems on various scales is therefore out of reach. Our CG and all-atom studies so far delivered some basic but important insights into the physics of these systems. However, we are continuing the endeavors towards even more refined notions of the general response features of hydrogels both experimentally and theoretically. Some of such features are ions, charged reactants,6,177 and even charged (pH-responsive) hydrogels,2 which we ignored in this review, but are of high practical relevance. Combining all the simulations with continuum-based approaches will help devising models, or at least semi-empirical rules how the hydrogel properties, in particular the permeability of certain molecular species, are connected and can be tuned by stimuli.
In order to formulate improved rate equations that carry more physical information, also the chemical processes on the nanoparticle surface in the solvent/polymer environment have to be better understood, which we did not touch in this review. For instance, rate-limiting chemical intermediates67 could be present. It would be also important to know whether and how strong the (often charged) reactants and products adsorb and diffuse on the nanoparticle surface in the crowded polymer environment. In some cases this may lead to steric hindrance and reaction inhibition on the reactive surface by both reactants and products and highly nonlinear rate behavior.186 Here, particle-based reaction–diffusion simulations may also help illuminating dynamical transitions and collective effects during the reaction.187
Only the fundamental understanding on all scales will enable us to reach the high recognition, selectivity, and feedback behavior in these colloidal devices as found for the nano-sized enzymes.115,116 On the other hand, the large scale and diverse building blocks that constitute the nanoreactors in various architectures establish the opportunity to develop many new design directions within the goal of programmable, ‘intelligent’ nanoparticle catalysis in the liquid phase.
Author contribution
All authors contributed equally to this manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Richard Chudoba, Karol Palczynski, Sebastian Milster, Arturo Moncho-Jordá, Stefano Angioletti-Uberti, Daniel Besold, Yan Lu, and Matthias Ballauff for inspiring discussions. This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (Grant Agreement No. 646659-NANOREACTOR). M.K. acknowledges the financial support from the Slovenian Research Agency (research core funding No. P1-0055). The simulations were performed with resources provided by the North-German Supercomputing Alliance (HLRN).References
- S. H. Petrosko, R. Johnson, H. White and C. A. Mirkin, J. Am. Chem. Soc., 2016, 138, 7443–7445 CrossRef CAS.
- M. A. C. Stuart, W. T. S. Huck, J. Genzer, M. Müller, C. Ober, M. Stamm, G. B. Sukhorukov, I. Szleifer, V. V. Tsukruk, M. Urban, F. Winnik, S. Zauscher, I. Luzinov and S. Minko, Nat. Mater., 2010, 9, 101–113 CrossRef PubMed.
- S. Campisi, M. Schiavoni, C. Chan-Thaw and A. Villa, Catalysts, 2016, 6, 185 CrossRef.
- Y. Lu and M. Ballauff, Prog. Polym. Sci., 2011, 36, 767–792 CrossRef CAS.
- S. Carregal-Romero, N. J. Buurma, J. Pérez-Juste, L. M. Liz-Marzán and P. Hervés, Chem. Mater., 2010, 22, 3051–3059 CrossRef CAS.
- P. Hervés, M. Pérez-Lorenzo, L. M. Liz-Marzán, J. Dzubiella, Y. Lu and M. Ballauff, Chem. Soc. Rev., 2012, 41, 5577–5587 RSC.
- S. Wu, J. Dzubiella, J. Kaiser, M. Drechsler, X. Guo, M. Ballauff and Y. Lu, Angew. Chem., Int. Ed., 2012, 51, 2229–2233 CrossRef CAS.
- H. Jia, R. Roa, S. Angioletti-Uberti, K. Henzler, A. Ott, X. Lin, J. Möser, Z. Kochovski, A. Schnegg, J. Dzubiella, M. Ballauff and Y. Lu, J. Mater. Chem. A, 2016, 4, 9677–9684 RSC.
- G. Prieto, H. Tüysüz, N. Duyckaerts, J. Knossalla, G.-H. Wang and F. Schüth, Chem. Rev., 2016, 116, 14056–14119 CrossRef CAS.
- J. Gaitzsch, X. Huang and B. Voit, Chem. Rev., 2015, 116, 1053–1093 CrossRef PubMed.
- D. M. Vriezema, M. Comellas Aragonès, J. A. A. W. Elemans, J. J. L. M. Cornelissen, A. E. Rowan and R. J. M. Nolte, Chem. Rev., 2005, 105, 1445–1490 CrossRef CAS PubMed.
- K. Renggli, P. Baumann, K. Langowska, O. Onaca, N. Bruns and W. Meier, Adv. Funct. Mater., 2011, 21, 1241–1259 CrossRef CAS.
- P. Tanner, P. Baumann, R. Enea, O. Onaca, C. Palivan and W. Meier, Acc. Chem. Res., 2011, 44, 1039–1049 CrossRef CAS.
- Y. Guan and Y. Zhang, Soft Matter, 2011, 7, 6375–6384 RSC.
- A. Liu, C. H. H. Traulsen and J. J. L. M. Cornelissen, ACS Catal., 2016, 6, 3084–3091 CrossRef CAS.
- S. Montolio, C. Vicent, V. Aseyev, I. Alfonso, M. I. Burguete, H. Tenhu, E. García-Verdugo and S. V. Luis, ACS Catal., 2016, 6, 7230–7237 CrossRef CAS.
- A. Zinchenko, Y. Che, S. Taniguchi, L. I. Lopatina, V. Sergeyev and S. Murata, J. Nanopart. Res., 2016, 18, 1–9 CrossRef CAS.
- Y. Lu, Y. Mei, M. Drechsler and M. Ballauff, Angew. Chem., Int. Ed., 2006, 45, 813–816 CrossRef CAS.
- J.-T. Zhang, G. Wei, T. F. Keller, H. Gallagher, C. Stötzel, F. A. Müller, M. Gottschaldt, U. S. Schubert and K. D. Jandt, Macromol. Mater. Eng., 2010, 295, 1049–1057 CrossRef CAS.
- R. Contreras-Cáceres, A. Sánchez-Iglesias, M. Karg, I. Pastoriza-Santos, J. Pérez-Juste, J. Pacifico, T. Hellweg, A. Fernández-Barbero and L. M. Liz-Marzán, Adv. Mater., 2008, 20, 1666–1670 CrossRef.
- S. Li, D. Lin, J. Zhou and L. Zha, J. Phys. Chem. C, 2016, 120, 4902–4908 CrossRef CAS.
- M. Haruta, Chem. Rec., 2003, 3, 75–87 CrossRef CAS.
- G. J. Hutchings and M. Haruta, Appl. Catal., A, 2005, 291, 2–5 CrossRef CAS.
- Y. Zhang, X. Cui, F. Shi and Y. Deng, Chem. Rev., 2012, 112, 2467–2505 CrossRef CAS PubMed.
- D. Astruc, in Nanoparticles and Catalysis, ed. D. Astruc, Wiley-VCH Verlag GmbH, Weinheim, Germany, 2008, ch. 1, pp. 1–48 Search PubMed.
- P. Zhao, N. Li and D. Astruc, Coord. Chem. Rev., 2013, 257, 638–665 CrossRef CAS.
- N. Li, P. Zhao and D. Astruc, Angew. Chem., Int. Ed., 2014, 53, 1756–1789 CrossRef CAS.
- E. Boisselier and D. Astruc, Chem. Soc. Rev., 2009, 38, 1759–1782 RSC.
- U. Taylor, C. Rehbock, C. Streich, D. Rath and S. Barcikowski, Nanomedicine, 2014, 9, 1971–1989 CrossRef CAS.
- G. Sharma and M. Ballauff, Macromol. Rapid Commun., 2004, 25, 547–552 CrossRef CAS.
- Y. Mei, G. Sharma, Y. Lu, M. Ballauff, M. Drechsler, T. Irrgang and R. Kempe, Langmuir, 2005, 21, 12229–12234 CrossRef CAS PubMed.
- N. C. Antonels and R. Meijboom, Langmuir, 2013, 29, 13433–13442 CrossRef CAS PubMed.
- R. M. Crooks, M. Zhao, L. Sun, V. Chechik and L. K. Yeung, Acc. Chem. Res., 2001, 34, 181–190 CrossRef CAS PubMed.
- R. M. Anderson, D. F. Yancey, L. Zhang, S. T. Chill, G. Henkelman and R. M. Crooks, Acc. Chem. Res., 2015, 48, 1351–1357 CrossRef CAS PubMed.
- C. Deraedt, N. Pinaud and D. Astruc, J. Am. Chem. Soc., 2014, 136, 12092–12098 CrossRef CAS PubMed.
- K. Esumi, K. Miyamoto and T. Yoshimura, J. Colloid Interface Sci., 2002, 254, 402–405 CrossRef CAS PubMed.
- N. Bingwa and R. Meijboom, J. Phys. Chem. C, 2014, 118, 19849–19858 CrossRef CAS.
- N. Bingwa and R. Meijboom, J. Mol. Catal. A: Chem., 2015, 396, 1–7 CrossRef CAS.
- J.-H. Noh and R. Meijboom, Appl. Surf. Sci., 2014, 320, 400–413 CrossRef CAS.
- J.-H. Noh and R. Meijboom, Appl. Catal., A, 2015, 497, 107–120 CrossRef CAS.
- Z. D. Pozun, S. E. Rodenbusch, E. Keller, K. Tran, W. Tang, K. J. Stevenson and G. Henkelman, J. Phys. Chem. C, 2013, 117, 7598–7604 CrossRef CAS PubMed.
- J. A. Johnson, J. J. Makis, K. A. Marvin, S. E. Rodenbusch and K. J. Stevenson, J. Phys. Chem. C, 2013, 117, 22644–22651 CrossRef CAS.
- E. Gross and G. A. Somorjai, Top. Catal., 2014, 57, 812–821 CrossRef CAS.
- A. Calvo, M. C. Fuertes, B. Yameen, F. J. Williams, O. Azzaroni and G. J. A. A. Soler-Illia, Langmuir, 2010, 26, 5559–5567 CrossRef CAS.
- S. L. Brock, N. Duan, Z. R. Tian, O. Giraldo, H. Zhou and S. L. Suib, Chem. Mater., 1998, 10, 2619–2628 CrossRef CAS.
- M. Ballauff and O. Borisov, Curr. Opin. Colloid Interface Sci., 2006, 11, 316–323 CrossRef CAS.
- M. Ballauff, Prog. Polym. Sci., 2007, 32, 1135–1151 CrossRef CAS.
- J. Cao, S. Mei, H. Jia, A. Ott, M. Ballauff and Y. Lu, Langmuir, 2015, 31, 9483–9491 CrossRef CAS PubMed.
- Y. Lu, M. Hoffmann, R. S. Yelamanchili, A. Terrenoire, M. Schrinner, M. Drechsler, M. W. Möller, J. Breu and M. Ballauff, Macromol. Chem. Phys., 2009, 210, 377–386 CrossRef CAS.
- M. Ballauff and Y. Lu, Polymer, 2007, 48, 1815–1823 CrossRef CAS.
- Y. Lu, S. Proch, M. Schrinner, M. Drechsler, R. Kempe and M. Ballauff, J. Mater. Chem., 2009, 19, 3955–3961 RSC.
- S. Wu, J. Kaiser, X. Guo, L. Li, Y. Lu and M. Ballauff, Ind. Eng. Chem. Res., 2012, 51, 5608–5614 CrossRef CAS.
- A. Lu and R. K. O'Reilly, Curr. Opin. Biotechnol., 2013, 24, 639–645 CrossRef CAS PubMed.
- M. Resmini, K. Flavin and D. Carboni, in Molecular Imprinting, Springer, 2010, pp. 307–342 Search PubMed.
- H. Jia, D. Schmitz, A. Ott, A. Pich and Y. Lu, J. Mater. Chem. A, 2015, 3, 6187–6195 RSC.
- N. Welsch, A. Wittemann and M. Ballauff, J. Phys. Chem. B, 2009, 113, 16039–16045 CrossRef CAS.
- Y. Lu, Y. Mei, M. Drechsler and M. Ballauff, Angew. Chem., Int. Ed., 2006, 45, 813–816 CrossRef CAS PubMed.
- Y. Lu, Y. Mei, M. Ballauff and M. Drechsler, J. Phys. Chem. B, 2006, 110, 3930–3937 CrossRef CAS PubMed.
- L.-Q. Yang, M.-M. Hao, H.-Y. Wang and Y. Zhang, Colloid Polym. Sci., 2015, 293, 2405–2417 CrossRef CAS.
- S. Shi, Q. Wang, T. Wang, S. Ren, Y. Gao and N. Wang, J. Phys. Chem. B, 2014, 118, 7177–7186 CrossRef CAS PubMed.
- A. Chang, Q. Wu, W. Xu, J. Xie and W. Wu, Chem. Commun., 2015, 51, 10502–10505 RSC.
- J. Liu, J. Wang, Y. Wang, C. Liu, M. Jin, Y. Xu, L. Li, X. Guo, A. Hu, T. Liu, S. F. Lincoln and R. K. Prud'homme, Colloid Interface Sci. Commun., 2015, 4, 1–4 CrossRef.
- Y. Tang, T. Wu, B. Hu, Q. Yang, L. Liu, B. Yu, Y. Ding and S. Ye, Mater. Chem. Phys., 2015, 149, 460–466 CrossRef.
- J. Plazas-Tuttle, L. S. Rowles, H. Chen, J. H. Bisesi, T. Sabo-Attwood and N. B. Saleh, Nanomaterials, 2015, 5, 1102–1123 CrossRef CAS PubMed.
- Q. Wu, H. Cheng, A. Chang, W. Xu, F. Lu and W. Wu, Chem. Commun., 2015, 51, 16068–16071 RSC.
- F. A. Plamper and W. Richtering, Acc. Chem. Res., 2017, 50, 131–140 CrossRef CAS PubMed.
- S. Gu, S. Wunder, Y. Lu, M. Ballauff, R. Fenger, K. Rademann, B. Jaquet and A. Zaccone, J. Phys. Chem. C, 2014, 118, 18618–18625 CrossRef CAS.
- R. Pelton, Adv. Colloid Interface Sci., 2000, 85, 1–33 CrossRef CAS PubMed.
- A. Khokhlov, Polymer, 1980, 21, 376–380 CrossRef CAS.
- B. Erman and P. Flory, Macromolecules, 1986, 19, 2342–2353 CrossRef CAS.
- A. Khokhlov, S. Starodubtzev and V. Vasilevskaya, in Responsive gels: Volume transitions I, Springer, 1993, pp. 123–171 Search PubMed.
- T. M. Barenbrug, J. Smit and D. Bedeaux, Polym. Gels Networks, 1995, 3, 331–373 CrossRef CAS.
- M. Heskins and J. E. Guillet, J. Macromol. Sci., Chem., 1968, 2, 1441–1455 CrossRef CAS.
- K. Dušek and D. Patterson, J. Polym. Sci., Polym. Phys. Ed., 1968, 6, 1209–1216 Search PubMed.
- A. Habicht, W. Schmolke, G. Goerigk, F. Lange, K. Saalwächter, M. Ballauff and S. Seiffert, J. Polym. Sci., Part B: Polym. Phys., 2015, 53, 1112–1122 CrossRef CAS.
- S. Zhou and C. Wu, Macromolecules, 1996, 29, 4998–5001 CrossRef CAS.
- C. Wu and S. Zhou, Macromolecules, 1997, 30, 574–576 CrossRef CAS.
- S. Angioletti-Uberti, Y. Lu, M. Ballauff and J. Dzubiella, J. Phys. Chem. C, 2015, 119, 15723–15730 CrossRef CAS.
- N. Pradhan, A. Pal and T. Pal, Colloids Surf., A, 2002, 196, 247–257 CrossRef CAS.
- T. Aditya, A. Pal and T. Pal, Chem. Commun., 2015, 51, 9410–9431 RSC.
- P. Zhao, X. Feng, D. Huang, G. Yang and D. Astruc, Coord. Chem. Rev., 2015, 287, 114–136 CrossRef CAS.
- M. Galanti, D. Fanelli, S. Angioletti-Uberti, M. Ballauff, J. Dzubiella and F. Piazza, Phys. Chem. Chem. Phys., 2016, 18, 20758–20767 RSC.
- R. Roa, W. K. Kim, M. Kanduč, J. Dzubiella and S. Angioletti-Uberti, ACS Catal., 2017, 7, 5604–5611 CrossRef CAS PubMed.
- M. v. Smoluchowski, Z. Phys. Chem., 1917, 92, 129–168 Search PubMed.
- P. Debye, Trans. Electrochem. Soc., 1942, 82, 265–272 CrossRef.
- G. Wilemski and M. Fixman, J. Chem. Phys., 1973, 58, 4009–4019 CrossRef CAS.
- D. F. Calef and J. M. Deutch, Annu. Rev. Phys. Chem., 1983, 34, 493–524 CrossRef CAS.
- P. Hänggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251–341 CrossRef.
- H. Yasuda, A. Peterlin, C. Colton, K. Smith and E. Merrill, Makromol. Chem., 1969, 126, 177–186 CrossRef CAS.
- L. M. Robeson, J. Membr. Sci., 1991, 62, 165–185 CrossRef CAS.
- J. Williams and R. W. Baker, J. Membr. Sci., 1995, 107, 1–21 CrossRef.
- J. M. Diamond and Y. Katz, J. Membr. Biol., 1974, 17, 121–154 CrossRef CAS PubMed.
- M. Palasis and S. H. Gehrke, J. Controlled Release, 1992, 18, 1–11 CrossRef CAS.
- S. Gehrke, J. Fisher, M. Palasis and M. E. Lund, Ann. N. Y. Acad. Sci., 1997, 831, 179–207 CrossRef CAS PubMed.
- P. Pandey and R. Chauhan, Prog. Polym. Sci., 2001, 26, 853–893 CrossRef CAS.
- S. C. George and S. Thomas, Prog. Polym. Sci., 2001, 26, 985–1017 CrossRef CAS.
- M. Ulbricht, Polymer, 2006, 47, 2217–2262 CrossRef CAS.
- R. W. Baker and B. T. Low, Macromolecules, 2014, 47, 6999–7013 CrossRef CAS.
- H. B. Park, J. Kamcev, L. M. Robeson, M. Elimelech and B. D. Freeman, Science, 2017, 356, 1137 CrossRef CAS PubMed.
- J. K. Guesta and J. H. Prévost, Comput. Methods Appl. Mech. Eng., 2007, 196, 1006–1017 CrossRef.
- E. Atci, I. Erucar and S. Keskin, J. Phys. Chem. C, 2011, 115, 6833–6840 CrossRef CAS.
- K. Falk, B. Coasne, R. Pellenq, F.-J. Ulm and L. Bocquet, Nat. Commun., 2015, 6, 6949 CrossRef CAS PubMed.
- A. Obliger, R. Pellenq, F.-J. Ulm and B. Coasne, J. Phys. Chem. Lett., 2016, 7, 3712–3717 CrossRef CAS PubMed.
- M. A. Shannon, P. W. Bohn, M. Elimelech, J. G. Georgiadis, B. J. Mariñas and A. M. Mayes, Nature, 2008, 452, 301–310 CrossRef CAS PubMed.
- G. M. Geise, H. B. Park, A. C. Sagle, B. D. Freeman and J. E. McGrath, J. Membr. Sci., 2011, 369, 130–138 CrossRef CAS.
- B. Tansel, J. Sager, T. Rector, J. Garland, R. F. Strayer, L. Levine, M. Roberts, M. Hummerick and J. Bauer, Sep. Purif. Technol., 2006, 51, 40–47 CrossRef CAS.
- C. S. Brazel and N. A. Peppas, Polymer, 1999, 40, 3383–3398 CrossRef CAS.
- D. F. Stamatialis, B. J. Papenburg, M. Gironés, S. Saiful, S. N. M. Bettahalli, S. Schmitmeier and M. Wessling, J. Membr. Sci., 2008, 308, 1–34 CrossRef CAS.
- W. K. Kim, A. Moncho-Jordá, R. Roa, M. Kanduč and J. Dzubiella, Macromolecules, 2017, 50, 6227–6237 CrossRef CAS.
- W. K. Kim, M. Kanduč, R. Roa and J. Dzubiella, Phys. Rev. Lett., 2019, 122, 108001 CrossRef CAS PubMed.
- M. Kanduč, R. Chudoba, K. Palczynski, W. K. Kim, R. Roa and J. Dzubiella, Phys. Chem. Chem. Phys., 2017, 19, 5906–5916 RSC.
- S. Milster, R. Chudoba, M. Kanduč and J. Dzubiella, Phys. Chem. Chem. Phys., 2019, 21, 6588 RSC.
- M. Kanduč, W. K. Kim, R. Roa and J. Dzubiella, Macromolecules, 2018, 51, 4853–4864 CrossRef.
- M. Kanduč, W. K. Kim, R. Roa and J. Dzubiella, J. Phys. Chem. B, 2019, 123, 720–728 CrossRef PubMed.
- M. Garcia-Viloca, J. Gao, M. Karplus and D. G. Truhlar, Science, 2004, 303, 186–195 CrossRef CAS PubMed.
- K. M. Ramsey, J. Yoshino, C. S. Brace, D. Abrassart, Y. Kobayashi, B. Marcheva, H.-K. Hong, J. L. Chong, E. D. Buhr, C. Lee, J. S. Takahashi, S. Ichiro Imai and J. Bass, Science, 2009, 324, 651–654 CrossRef CAS PubMed.
- P. Atkins and J. de Paula, Physical Chemistry, ed. W. H. Freeman and Company, 2010 Search PubMed.
- E. Aydt and R. Hentschke, J. Chem. Phys., 2000, 112, 5480–5487 CrossRef CAS.
- Z. Y. Lu and R. Hentschke, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 1–8 Search PubMed.
- P. A. Netz and T. Dorfmüller, J. Chem. Phys., 1997, 107, 9221–9233 CrossRef CAS.
- A. Erbaş and M. Olvera de la Cruz, ACS Macro Lett., 2015, 4, 857–861 CrossRef.
- A. Erbaş and M. Olvera de la Cruz, Macromolecules, 2016, 49, 9026–9034 CrossRef.
- H. Li, A. Erbaş, J. Zwanikken and M. Olvera de la Cruz, Macromolecules, 2016, 49, 9239–9246 CrossRef CAS.
- J. Heyda, A. Muzdalo and J. Dzubiella, Macromolecules, 2013, 46, 1231–1238 CrossRef CAS.
- D. Mukherji and K. Kremer, Macromolecules, 2013, 46, 9158–9163 CrossRef CAS.
- D. Mukherji, C. M. Marques and K. Kremer, Nat. Commun., 2014, 5, 4882 CrossRef PubMed.
- F. Rodríguez-Ropero, T. Hajari and N. F. van der Vegt, J. Phys. Chem. B, 2015, 119, 15780–15788 CrossRef PubMed.
- F. Rodríguez-Ropero and N. F. van der Vegt, Phys. Chem. Chem. Phys., 2015, 17, 8491–8498 RSC.
- J. Rika, M. Meewes, R. Nyffenegger and T. Binkert, Phys. Rev. Lett., 1990, 65, 657 CrossRef PubMed.
- L.-T. Lee and B. Cabane, Macromolecules, 1997, 30, 6559–6566 CrossRef CAS.
- J. Heyda, H. I. Okur, J. Hladílková, K. B. Rembert, W. Hunn, T. Yang, J. Dzubiella, P. Jungwirth and P. S. Cremer, J. Am. Chem. Soc., 2017, 139, 863–870 CrossRef CAS PubMed.
- H. Yasuda, C. Lamaze and L. D. Ikenberry, Makromol. Chem., 1968, 118, 19–35 CrossRef CAS.
- H. Yasuda, L. Ikenberry and C. Lamaze, Makromol. Chem., 1969, 125, 108–118 CrossRef CAS.
- L. Masaro and X. Zhu, Prog. Polym. Sci., 1999, 24, 731–775 CrossRef CAS.
- B. Amsden, Macromolecules, 1998, 31, 8382–8395 CrossRef CAS.
- L. Pérez-Mas, A. Martín-Molina, M. Quesada-Pérez and A. Moncho-Jordá, Phys. Chem. Chem. Phys., 2018, 20, 2814–2825 RSC.
- L.-H. Cai, S. Panyukov and M. Rubinstein, Macromolecules, 2015, 48, 847–862 CrossRef CAS PubMed.
- B. Rotenberg, J.-F. Dufreche, B. Bagchi, E. Giffaut, J.-P. Hansen and P. Turq, J. Chem. Phys., 2006, 124, 154701 CrossRef CAS PubMed.
- K. Zhang and S. K. Kumar, ACS Macro Lett., 2017, 6, 864–868 CrossRef CAS.
- R. Zhang and K. S. Schweizer, J. Chem. Phys., 2017, 146, 194906 CrossRef PubMed.
- P. M. Kekenes-Huskey, C. E. Scott and S. Atalay, J. Phys. Chem. B, 2016, 120, 8696–8706 CrossRef CAS PubMed.
- A. Leo, C. Hansch and D. Elkins, Chem. Rev., 1971, 71, 525–616 CrossRef CAS.
- J. Haus and K. Kehr, Phys. Rep., 1987, 150, 263–406 CrossRef CAS.
- S. K. Ghosh, A. G. Cherstvy and R. Metzler, Phys. Chem. Chem. Phys., 2014, 17, 1847–1858 RSC.
- Y. Wu, S. Joseph and N. R. Aluru, J. Phys. Chem. B, 2009, 113, 3512–3520 CrossRef CAS PubMed.
- A. Börjesson, E. Erdtman, P. Ahlström, M. Berlin, T. Andersson and K. Bolton, Polymer, 2013, 54, 2988–2998 CrossRef.
- G. E. Karlsson, U. W. Gedde and M. S. Hedenqvist, Polymer, 2004, 45, 3893–3900 CrossRef CAS.
- F. Müller-Plathe, Ber. Bunsenges. Phys. Chem., 1998, 102, 1679–1682 CrossRef.
- F. Müller-Plathe, J. Membr. Sci., 1998, 141, 147–154 CrossRef.
- L. Fritz and D. Hofmann, Polymer, 1997, 38, 1035–1045 CrossRef CAS.
- E. Kucukpinar and P. Doruker, Polymer, 2003, 44, 3607–3620 CrossRef CAS.
- F. Rodríguez-Ropero and N. F. van der Vegt, J. Phys. Chem. B, 2014, 118, 7327–7334 CrossRef PubMed.
- M. A. Schroer, J. Michalowsky, B. Fischer, J. Smiatek and G. Grübel, Phys. Chem. Chem. Phys., 2016, 18, 31459–31470 RSC.
- I. Adroher-Benítez, A. Moncho-Jordá and G. Odriozola, J. Chem. Phys., 2017, 146, 194905 CrossRef PubMed.
- S. Deshmukh, D. A. Mooney, T. McDermott, S. Kulkarni and J. D. MacElroy, Soft Matter, 2009, 5, 1514–1521 RSC.
- V. Boţan, V. Ustach, R. Faller and K. Leonhard, J. Phys. Chem. B, 2016, 120, 3434–3440 CrossRef PubMed.
- L. Pérez-Fuentes, C. Drummond, J. Faraudo and D. Bastos-González, Soft Matter, 2015, 11, 5077–5086 RSC.
- E. Aydt and R. Hentschke, J. Chem. Phys., 2000, 112, 5480–5487 CrossRef CAS.
- F. A. Escobedo and J. J. de Pablo, J. Chem. Phys., 1997, 106, 793–810 CrossRef CAS.
- F. A. Escobedo and J. J. De Pablo, Phys. Rep., 1999, 318, 85–112 CrossRef CAS.
- D. Sandrin, D. Wagner, C. Sitta, R. Thoma, S. Felekyan, H. Hermes, C. Janiak, N. de Sousa Amadeu, R. Kühnemuth and H. Löwen, et al. , Phys. Chem. Chem. Phys., 2016, 18, 12860–12876 RSC.
- H. Masoud and A. Alexeev, Macromolecules, 2010, 43, 10117–10122 CrossRef CAS.
- J. Hansing and R. R. Netz, Macromolecules, 2018, 51, 7608–7620 CrossRef CAS.
- J. Hansing and R. R. Netz, Biophys. J., 2018, 114, 2653–2664 CrossRef CAS PubMed.
- J. Hansing, J. R. Duke III, E. B. Fryman, J. E. DeRouchey and R. R. Netz, Nano Lett., 2018, 18, 5248–5256 CrossRef CAS PubMed.
- H. Zhou and S. B. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 021801 CrossRef PubMed.
- D. Horinek and R. R. Netz, J. Phys. Chem. A, 2011, 115, 6125–6136 CrossRef CAS PubMed.
- L.-C. Dong and A. S. Hoffman, J. Controlled Release, 1990, 13, 21–31 CrossRef CAS.
- S. Sasaki, S. Koga and H. Maeda, Macromolecules, 1999, 32, 4619–4624 CrossRef CAS.
- R. Raccis, R. Roskamp, I. Hopp, B. Menges, K. Koynov, U. Jonas, W. Knoll, H.-J. Butt and G. Fytas, Soft Matter, 2011, 7, 7042–7053 RSC.
- Y. Kaneko, R. Yoshida, K. Sakai, Y. Sakurai and T. Okano, J. Membr. Sci., 1995, 101, 13–22 CrossRef CAS.
- L. C. Dong and A. S. Hoffman, J. Controlled Release, 1986, 4, 223–227 CrossRef CAS.
- Y. Tamai, H. Tanaka and K. Nakanishi, Macromolecules, 1994, 27, 4498–4508 CrossRef CAS.
- M. Fukuda, J. Chem. Phys., 1998, 109, 6476–6485 CrossRef CAS.
- S. Goudeau, M. Charlot, C. Vergelati and F. Müller-Plathe, Macromolecules, 2004, 37, 8072–8081 CrossRef CAS.
- G. Marque, S. Neyertz, J. Verdu, V. Prunier and D. Brown, Macromolecules, 2008, 41, 3349–3362 CrossRef CAS.
- M. Kanduç, W. K. Kim, R. Roa and J. Dzubiella, ACS Nano, 2019, 13, 11224–11234 CrossRef PubMed.
- M. Karelson, Molecular Descriptors in QSAR/QSPR, Wiley-Interscience, 2000 Search PubMed.
- C. Tanford, Proc. Natl. Acad. Sci. U. S. A., 1979, 76, 4175–4176 CrossRef CAS PubMed.
- H. S. Ashbaugh and L. R. Pratt, Rev. Mod. Phys., 2006, 78, 159 CrossRef CAS.
- C. Hansch, A. Leo and R. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
- H. Takeuchi, J. Chem. Phys., 1990, 93, 2062–2067 CrossRef CAS.
- F. Müller-Plathe, J. Chem. Phys., 1991, 94, 3192–3199 CrossRef.
- L.-H. Cai, S. Panyukov and M. Rubinstein, Macromolecules, 2011, 44, 7853–7863 CrossRef CAS PubMed.
- O. Bénichou, M. Coppey, M. Moreau and G. Oshanin, J. Chem. Phys., 2005, 123, 194506 CrossRef PubMed.
- R. Roa, T. Siegl, W. K. Kim and J. Dzubiella, J. Chem. Phys., 2018, 148, 065705 CrossRef PubMed.
- M. J. del Razo, H. Qian and F. Noé, J. Chem. Phys., 2018, 149, 044102 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2020 |