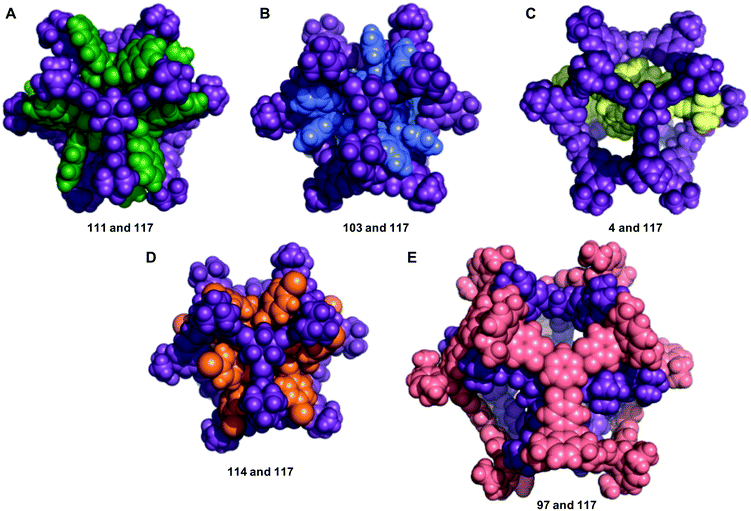Computational screening for nested organic cage complexes†
Enrico
Berardo
 a,
Rebecca L.
Greenaway
a,
Rebecca L.
Greenaway
 b,
Marcin
Miklitz
b,
Marcin
Miklitz
 a,
Andrew I.
Cooper
a,
Andrew I.
Cooper
 b and
Kim E.
Jelfs
b and
Kim E.
Jelfs
 *a
*a
aDepartment of Chemistry, Imperial College London, Molecular Sciences Research Hub, White City Campus, Wood Lane, London W12 0BZ, UK. E-mail: k.jelfs@imperial.ac.uk; Tel: +44 (0)2075943438
bDepartment of Chemistry and Materials Innovation Factory, University of Liverpool, 51 Oxford Street, Liverpool L7 3NY, UK
First published on 13th August 2019
Abstract
Supramolecular self-assembly has allowed the synthesis of beautiful and complex molecular architectures, such as cages, macrocycles, knots, catenanes, and rotaxanes. We focus here on porous organic cages, which are molecules that have an intrinsic cavity and multiple windows. These cages have been shown to be highly effective at molecular separations and encapsulations. We investigate the possibility of complexes where one cage sits within the cavity of another. We term this a ‘nested cage’ complex. The design of such complexes is highly challenging, so we use computational screening to explore 8712 different pair combinations, running almost 0.5 million calculations to sample the phase space of the cage conformations. Through analysing the binding energies of the assemblies, we identify highly energetically favourable pairs of cages in nested cage complexes. The vast majority of the most favourable complexes include the large imine cage reported by Gawroński and co-workers using a [8 + 12] reaction of 4-tert-butyl-2,6-diformylphenol and cis,cis-1,3,5-triaminocyclohexane. The most energetically favourable nested cage complex combines the Gawroński cage with a dodecaamide cage that has six vertices, which can sit in the six windows of the larger cage. We also identify cages that have favourable binding energies for self-catenation.
Design, System, ApplicationThe ultimate goal of chemists is to be able to design and then control the assembly of complex molecules and architectures. Computer-aided design allows us to screen hundreds to millions of possibilities, a scale that is not feasible in the laboratory, even using high-throughput automation. Here, we use simulations to focus on a specific type of supramolecular material, porous organic cages, which are discrete organic molecules that contain an internal cavity. These cavities, and the multiple entry and exit routes to these cavities, allow for potential application of these systems in catalysis, separation and encapsulation. In this paper, we aim to control the encapsulation such that we form nested cages where one cage sits within the internal cavity of a larger cage. To do this, we use simulations to trial 8712 different combinations of cage pairs, to discover systems that have highly favourable binding energies and are thus therefore the most likely to form. We are therefore able to predict not only the most promising nested cage pair systems, but also the systems that have a preference for self-catenation. These predictions can be used for future synthetic realisation. |
Supramolecular chemistry involves ‘chemistry beyond the molecule’ and can enable the assembly of incredibly complex, and beautiful, structures. Examples include cages,1–3 macrocycles,4 and more complex, interlocked, structures such as catenanes,5 rotaxanes,6 knots,7 and molecular machines.8,9 The potential possible combinations of organic building blocks to form these complex architectures is vast, and therefore the design of these molecules is challenging and normally based on the chemical experience of synthetic chemists and small changes to existing structures. While many interlocked organic species such as catenanes have been reported, no example of an organic cage completely encapsulated inside the cavity of a second organic cage has been reported to date. Even considering other species beyond organic cages, there are few examples of ‘nested cages’ or ‘Russian doll complexes’. There are examples of macrocycle-in-a-macrocycle complexes,10–13 including Russian doll concentric porphyrin nanorings,14 and fullerene/macrocycle complexes.15,16 Some metal–organic nested cage complexes have been reported;17 perhaps the most relevant are those complexes that involve the encapsulation of a small organic cage within a metal-organic cage,18,19 or the formation of multi-layered DNA nanocages.20 However, the nesting of an organic cage within another organic cage remains a challenging target, and if realised would demonstrate fine control over supramolecular assembly.
Porous organic cages (POCs) are an example of a porous molecular material where the porosity of the material originates in the intrinsic cavity of the cage molecule. A POC can be defined as having an internal cavity with multiple entry and exit routes through which guests can access the central cavity.3 POCs have been reported in a variety of sizes, shapes and topologies (see examples in Fig. 1), although the total number reported is only on the order of 200 molecules. The majority of POCs are made through the use of dynamic covalent chemistry (DCC), in particular imine condensation reactions, the reversible nature of which allows for error correction during the synthesis of these high symmetry products, often in high yield. There are also examples of POCs catenating to form interlocked structures with another molecule of the same cage species.21–25 This catenation can typically be controlled by the functionalisation of the cage; for instance, the position of the alkyl groups, which can introduce multiple pores of different sizes within a single complex.22 Potential applications of POCs include their use as encapsulants,26 in catalysis,27 molecular separations,28–31 as sensors,32,33 and in porous liquids.34
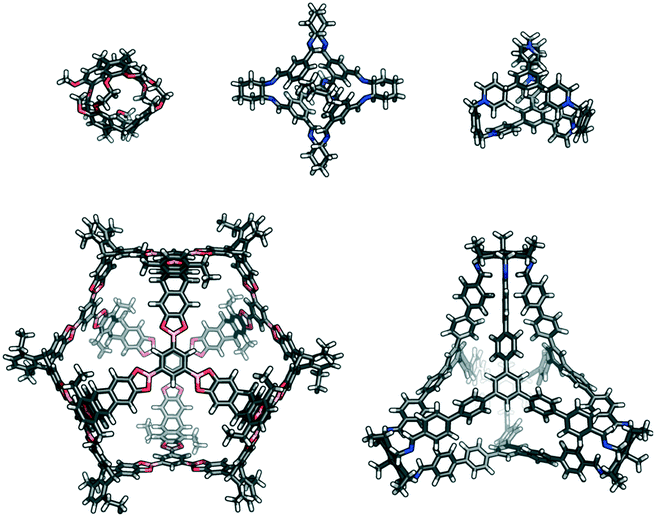 | ||
| Fig. 1 Examples of previously reported porous organic cages that are a variety of sizes, shapes, and topologies; (top left) cryptophane;35 (top centre) CC3;36 (top right) ExCage;37 (bottom left) a giant boronate cage,22 and (bottom right) C26.23 | ||
It is possible to use computer simulations to assist in the design and discovery of porous organic cages.38 First, starting from the precursors of the cage synthesis reaction, the outcome in terms of the molecular mass and topology of the cage can be hard to predict, since small changes in the precursors are known to have led to large changes in topology and consequently the properties of the cages.39 It has been shown that it is possible to predict the topology by examining the relative energies of the different possible assemblies,40,41 or further, by considering the formation mechanisms of the cage products.42 While most studies to date have focused upon a posteriori rationalisation of previously reported systems, we have recently shown it is possible to identify trends in the reaction outcomes and therefore assist in the discovery process during a larger-scale robotic screening of 78 potential cage reactions.23 It is also possible to predict shape persistency, the ability for a cage to maintain an internal void in the absence of solvent.43,44 The solid-state structure of materials and their properties can be predicted from molecular structures using crystal structure prediction (CSP) techniques.45–49 Molecular-level calculations of binding energies of dimer pairs can also assist in predicting the preferential binding modes in the solid-state, for example the preference to racemise or form enantiopure structures.50 The properties of the materials can be also understood or predicted a priori once the structures are known.38,51,52
We report here a computational screening study where we conduct almost 0.5 million calculations in order to search for elusive nested organic cage complexes. Through an examination of binding energies, we identify the most promising candidate cages for forming such complexes and analyse which systems are the most suitable for targeting for synthesis. Alongside this, we compare the competing pathways of self-catenation of the cages, which further identifies promising candidates for that type of assembly.
Methods
Through a literature search of reported intrinsically porous molecules,2,53 we constructed a database of 132 candidate molecules. A complete list of the included cages, including images of the molecules, is given in Table S1,† together with their numbering from 1 to 132. The set consists of 78 cages from a recently reported combined high-throughput robotic and computational screening study from Greenaway et al.,23 three [6 + 12] TCC cages from Stackhouse et al.,54 the carbon nanocage of Matsui et al.,55 cucurbiturils CB[5], CB[6] and CB[7],56 ExCage,37 seven cages from Mastalerz and co-workers,22,57–60 two hemicarceplexes from Cram and co-workers,61 twenty-four imine and amide cages from Cooper and co-workers,36,39,46,62–69 the triazine cage of Ding et al.,70 BlueCage,71 noria,72 the alkyne cage from Doonan and co-workers,73 cryptophane,35 a fluorescent cage from Mukherjee and co-workers,33 a boronate cage from Iwasawa and co-workers,74 an imine cage from Gawroński and co-workers,75 and four cages from Beuerle and co-workers.76,77 These molecules cover the full range of topologies and shapes reported for porous organic cages to date and range in maximum dimension from 13 to 47 Å and internal cavity diameter of 0 to 26 Å.The cage structures were taken from reported crystal structures, or constructed manually for those structures where no X-ray diffraction structure was reported. The manual construction involved a short molecular dynamics (MD) simulation that sampled several hundred conformations and selected the lowest energy conformation for further simulations. For a few cases where more than one enantiomer of the cage is possible, we used only the enantiomer that was reported in the crystal structure. If there was positional isomerism, for example in methyl position for CC2, a random isomer was constructed to keep the number of calculations required feasible. The structural properties of the cages and their voids and windows are given in Table S2.† All void sizes and window sizes were calculated with our pywindow software, with void sizes calculated as the diameter of the largest sphere that can fit in the cavity and window size as the diameter of the largest circle that can fit in a window.78 The maximum diameter of a molecule was defined as the distance between the edges of the van der Waals spheres of the two atoms at the greatest distance from each other in the molecule. The average diameter of a molecule was determined as a mean distance from the centre of mass of a molecule to its van der Waals surface. The latter value can match the experimentally determined solvodynamic diameters.23
Pairing each molecule with every other molecule in our data set, including the self-catenation combination, made a total of 8712 pair combinations to be considered. To sample the possible relative orientations of each molecular pair, we considered 56 different but evenly spaced relative orientations by carrying out rotations of the polar and azimuthal angles of one cage while keeping the other in a fixed position. Each of these structures was geometry optimised so that the lowest energy orientation could be analysed further. Thus, we conducted a total of 487![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 872 calculations (8712 molecule pairs, each in 56 orientations). For all forcefield calculations, we used the OPLS3 forcefield79 which we have previously shown effectively predicts the structure of flexible porous imine cages,41 and is designed to be transferable to new organic systems. The calculations were carried out in Macromodel, using a conjugate gradient minimisation with a convergence criteria of a root mean square force below 0.05 kJ mol−1 Å−1. The individual cage structures were geometry optimised in isolation with the same setup. The binding energy for the lowest energy conformation of each cage pairing was then calculated as:
872 calculations (8712 molecule pairs, each in 56 orientations). For all forcefield calculations, we used the OPLS3 forcefield79 which we have previously shown effectively predicts the structure of flexible porous imine cages,41 and is designed to be transferable to new organic systems. The calculations were carried out in Macromodel, using a conjugate gradient minimisation with a convergence criteria of a root mean square force below 0.05 kJ mol−1 Å−1. The individual cage structures were geometry optimised in isolation with the same setup. The binding energy for the lowest energy conformation of each cage pairing was then calculated as:
| Eb = Ecage pair − Ecage1 − Ecage2 | (1) |
Results and discussion
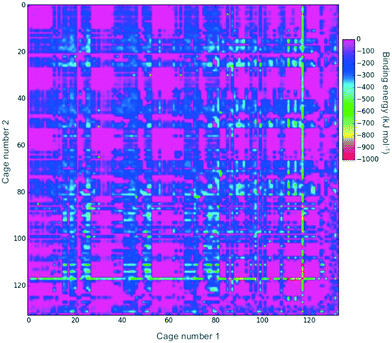
Fig. 2 shows a heat-map of the binding energies of all the possible pairings of the 132 organic cages. A total of 4947 pairings have a favourable (negative) binding energy, which equates to 57% of the possible pairings. Highly unfavourable pairings, for instance combining two small capsular cages that have very small internal cavities, can be seen in several regions; for example, the pink region for cages both numbered 27 to 36. It is also possible to pick out “sweet-spots” where there are many favourable binding energies, and in particular cage 117 can be clearly identified as being selected in many of the most highly favourable binding energy pairs. Cage 117 is a large imine cage synthesised from an [8 + 12] reaction of 4-tert-butyl-2,6-diformylphenol and cis,cis-1,3,5-triaminocyclohexane by Gawroński and co-workers.75117 has an approximately cuboctahedral shape, a maximum dimension of 34 Å, a void diameter of 13 Å, and six equally sized windows of 9 Å in diameter.In theory, a favourable binding energy should be found in cases where there is a good match of the void size of the larger cage in the pairing with the dimensions of the smaller cage. However, in Fig. S1,† a heat-map of the difference in the void size of the larger cage to the maximum dimension of the smaller cage does not show any correlation with the binding energies in Fig. 2. Similarly, there appears to be no correlation between the difference in those sizes and the binding energy (Fig. S2†). This suggests that there are many other factors, for instance symmetry and the intermolecular bonding available for a given cage pairing, that are influencing the binding energy.
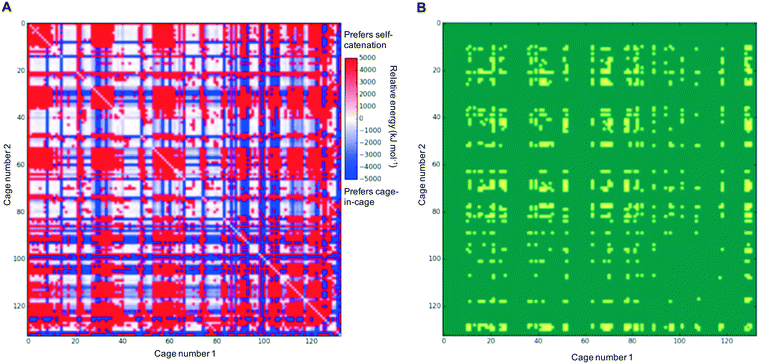
In each case of pairing two different cages, there would be competition with each of the individual cages preferring to self-catenate instead, which might be due to that potentially being thermodynamically favoured over forming a nested cage complex. We therefore compared the binding energies against the comparable self-catenation energies, and in Fig. 3A we plot a heat-map that shows which pairings would energetically favour self-catenation (red) and which would favour forming a nested cage complex (blue). We find that all the pairings where self-catenation is preferred correspond to regions in Fig. 2 where the binding energy for a nested cage pairing was unfavourable (pink). Therefore, if we replot Fig. 2 with any pairings that would prefer self-catenation shown as energetically unfavourable, then there is no visual difference in the heat-map. Further, many of the pairings that might favour self-catenation over a nested cage complex are instances where even the self-catenation is energetically unfavourable. In Fig. 3B, we show a heat-map of which pairings actually truly prefer self-catenation (yellow); i.e., have both an energetically favourable binding energy for self-catenation and self-catenation is energetically preferred over a nested cage complex. It is clear that it is very rare for the pairings to prefer self-catenation.
Cage pairings that prefer self-catenation
We will now examine the cage pairings that most preferred to self-catenate. The binding energies of all the favourable self-catenations are shown in Fig. S3† and the energies and structural features of the top 20 self-catenating molecules are shown in Table 1. The most favourable binding energy for self-catenation was −505 kJ mol−1, found for cage 81, although this falls to −291 kJ mol−1 by the 20th best self-catenating cage. These binding energies are considerably less favourable than the best 20 nested cage complexes, which range in energy from −1023 to −660 kJ mol−1. Cage 97, a large boronate ester cage reported by Mastalerz and co-workers,80 which is ranked 13th by binding energy is closely related (differing only in the position of solubilising groups) to the boronate ester cage reported to self-catenate by Mastelerz and co-workers in 2014.22 Whilst we did not include the exact molecule that Mastelerz reported in this study, the finding that 97 is energetically favourable towards self-catenation is very encouraging for our approach.| Rank | Cage number | Binding energy (kJ mol−1) | Remaining cavity diameter (Å) | Number of windows | Degree of interlocking |
|---|---|---|---|---|---|
| 1 | 81 | −505 | 10.5 | 8 | 4 |
| 2 | 52 | −477 | 11.8 | 6 | 6 |
| 3 | 78 | −473 | 9.5 | 6 | 6 |
| 4 | 89 | −453 | 2.1 | 3 | 2 |
| 5 | 26 | −453 | 12.1 | 6 | 6 |
| 6 | 25 | −427 | 9.1 | 6 | 6 |
| 7 | 51 | −387 | 8.7 | 6 | 6 |
| 8 | 77 | −377 | 9.9 | 6 | 6 |
| 9 | 15 | −365 | 8.3 | 4 | 3 |
| 10 | 71 | −346 | 10.8 | 4 | 3 |
| 11 | 18 | −345 | 9.8 | 4 | 2 |
| 12 | 69 | −333 | 8.0 | 4 | 3 |
| 13 | 97 | −325 | 15.7 | 6 | 6 |
| 14 | 20 | −325 | 7.5 | 4 | 3 |
| 15 | 68 | −320 | 8.2 | 4 | 3 |
| 16 | 45 | −311 | 11.3 | 4 | 3 |
| 17 | 70 | −309 | 7.8 | 4 | 3 |
| 18 | 19 | −306 | 12.2 | 4 | 3 |
| 19 | 43 | −303 | 8.7 | 4 | 3 |
| 20 | 41 | −291 | 8.6 | 4 | 3 |
In all cases, the self-catenated complex is left with a considerable internal cavity, which could still host further guests. The cavities range from 7.5–15.7 Å, with the exception of cage 89 which has a much smaller cavity of 2.1 Å when self-catenated. We can examine the extent to which the structures are interlocked and compare this to the number of windows (Table 1). The number of windows in these best self-catenation pairs ranges from 3 to 8. In theory, a self-catenation that is maximally interlocked will have the same degree of interlocking as the number of windows, and this is also likely to lead to a more symmetric structure. This maximal interlocking occurs in 6 of the 20 best self-catenation pairs, and in all cases, these are instances where the individual cage has six windows.
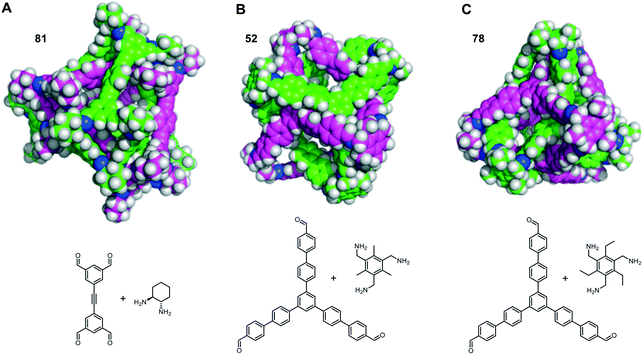
The self-catenated structures of the three most energetically favoured combinations are shown in Fig. 4, along with the chemical structures of the precursors for those cages. The images for the remaining structures in the top 20 are shown in Fig. S4.† All three of the best self-catenating cages approximate to (truncated) tetrahedrons, with 81 being a TCC1[6+12] cage reported by Stackhouse et al.,54 and 52 and 78 being two [4 + 4] cages recently reported by Greenaway et al.23 The latter two cages differ only by the fact that the aromatic triamine of 52 is decorated with three methyl groups, whilst 78 is decorated with three ethyl groups. Only in the case of 78 are all of the windows interlocked. Due to this difference in interlocking between 52 and 78, this may be indicative that despite our best efforts for the large numbers of structures, we have not been able to fully sample the potential energy surface for every pair. However, we still believe it is sufficient to identify favourable pairings (such as cage 97). We also note the large size of all of the ‘best’ cages for self-catenation, naturally, with additional atoms, they are likely to have higher binding energies than smaller molecules. Indeed, this is the case for three smaller cages previously reported to self-catenate experimentally, cages 102 (imine cage CC2), 110 (imine cage CC1) and 112 (imine cage CC4),21 which all had much less favourable binding energies for self-catenation than the top 20 reported in Table 1.
Cage pairings that prefer nested cage complexes
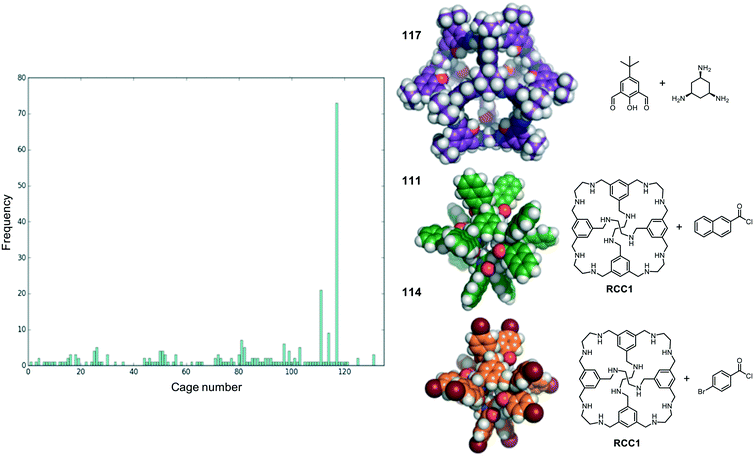
We now return to the energetically favourable nested cage complexes. First, we examined which cages are most frequently found in energetically favourable pairings. In Fig. 5 there is a histogram of cages that are found in nested cage complexes with highly favourable binding energies, Eb < 500 kJ mol−1. The equivalent histogram for all binding energies that are negative is shown in Fig. S5.† The structures of the three most frequently found cages, and their precursors, are shown on the right of Fig. 5. It is clear that cage 117 is found in highly favourable pairings many more times than any other cage (73 times), with the next most frequently found being cage 111 (21 times) and cage 114 (9 times), which are two very similar cages formed by reducing the imine [4 + 6] cage CC1 (cage 110) and functionalising with different acid chlorides to form the corresponding dodecaamide cages. 117 is a relatively large cage, with an internal cavity diameter of 12.9 Å, and is typically found as the outer cage in nested cage complexes. By contrast, cages 111 and 114 are smaller with internal cavity diameters of 4.2 and 4.1 Å, respectively, and are always found as the inner cage in the complexes.The binding energies and structural features of the top 20 nested cage complexes are shown in Table 2. In none of these instances is self-catenation energetically competitive. The most favourable binding energy for a nested cage complex was −1023 kJ mol−1, found for combining cages 111 and 117, which were also the two cages most frequently found in energetically favourable pairings. This pairing is 148 kJ mol−1 more favourable than the next best pairing, and by the 20th best pairing the binding energy has fallen to −660 kJ mol−1, although that is still more favourable than the best self-catenation pairing (−505 kJ mol−1). There are only 3 of the top 20 pairings where cage 117 is not involved. In the majority of cases, the space filling of a smaller cage inside a larger cage is relatively efficient, and only a small cavity remains in the complex, typically below 2.5 Å. However, there are exceptions; for example, the pairing of 97 and 117, which has a remaining cavity of 6.7 Å, where 117 is now the inner cage.
| Rank | Inner cage | Outer cage | Binding energy (kJ mol−1) | Remaining cavity diameter (Å) | List 1 | List 2 | High symmetry |
|---|---|---|---|---|---|---|---|
| 1 | 111 | 117 | −1023 | 2.2 | ✓ | ✓ | ✓ |
| 2 | 103 | 117 | −875 | 2.5 | ✓ | ✓ | |
| 3 | 4 | 117 | −862 | 0.7 | ✓ | ||
| 4 | 114 | 117 | −852 | 2.0 | ✓ | ✓ | ✓ |
| 5 | 117 | 97 | −807 | 6.7 | ✓ | ✓ | ✓ |
| 6 | 91 | 117 | −782 | 0.0 | |||
| 7 | 116 | 117 | −781 | 2.1 | ✓ | ✓ | ✓ |
| 8 | 86 | 117 | −775 | 1.4 | |||
| 9 | 113 | 117 | −732 | 2.4 | ✓ | ✓ | |
| 10 | 89 | 117 | −718 | 1.8 | ✓ | ||
| 11 | 56 | 117 | −714 | 0.5 | ✓ | ✓ | |
| 12 | 26 | 117 | −714 | 3.9 | ✓ | ||
| 13 | 71 | 117 | −690 | 0.3 | ✓ | ||
| 14 | 117 | 81 | −688 | 6.6 | ✓ | ||
| 15 | 30 | 52 | −678 | 1.0 | ✓ | ✓ | |
| 16 | 90 | 117 | −674 | 2.2 | ✓ | ✓ | |
| 17 | 111 | 50 | −666 | 2.5 | ✓ | ✓ | ✓ |
| 18 | 48 | 117 | −664 | 3.0 | ✓ | ||
| 19 | 111 | 52 | −661 | 2.4 | ✓ | ✓ | ✓ |
| 20 | 28 | 117 | −660 | 0.0 | ✓ | ✓ |
The structures of the five most energetically favoured nested cage complexes are shown in Fig. 6, with the rest of the top 20 shown in Fig. S6.† All of the top 5 complexes involve cage 117, which is shown in purple in the figures. It is likely that 117 is found in so many favourable complexes due to the large internal cavity of the cage (diameter 12.9 Å), and the fact that it has six relatively large windows (diameter 8.7 Å). The large size of the window diameter means that many of the inner cages can have their vertices aligned so as to sit inside or through the window, forming favourable intermolecular interactions with the windows of 117. The fact that 117 has six windows is also significant, as 45% of the cages in our data set are formed from [4 + 6] reactions into structures that have six vertices. Each of these vertices can then sit in one of the six windows of 117, as is the case in many of the best structures, including the top two hits (Fig. 6).
As our goal in making these computational predictions is the eventual synthetic realisation of the nested cage complexes, we now consider the synthetic route to realisation of the top 20 pairings. This will allow us to suggest the most promising targets for synthesis. We considered both the availability and ease of synthesis of the precursors, and how readily and with what yield the cages have been reported to be synthesised. With that in mind, we considered whether the cages met two separate sets of criteria. The first set of criteria includes cages that could be synthesised from commercially available precursors or precursors that are readily synthesisable in a reasonable number of steps (“List 1”). This does not consider how readily and cleanly cage formation has been reported, allowing us to include cages from our recent high-throughput screen23 that were attempted but either did not form or formed mixtures experimentally. We still include them here as it could be the case that the synthesis in a nested cage complex allows templating of the cage that did not previously form. The second set of criteria is more stringent, using all the initial criteria with the additional requirement that the cages have been reported to be synthesised readily and cleanly, eliminating all failed syntheses, reports of mixtures forming, and low yielding reactions (“List 2”). The complete characterisation of each individual cage into these criteria is given in Table S3,† and which list criteria are met for each of the top 20 nested cage complexes are given in Table 2. We also visually inspected the complexes for their symmetry, denoting the complexes as high symmetry if there were similar arrangements of the molecules at each window of the outer cage (Table 2). We would expect that high symmetry complexes would be particularly favoured and therefore might have a higher chance of synthetic realisation.
The vast majority of the nested cage complexes meet the initial criteria (95%), whereas only 56% of the complexes meet the more stringent criteria. Only 40% of the cage pairings are deemed to be high symmetry, and overall only 6 of the complexes (30%) meet both the stringent criteria and are high symmetry. We would expect these six complexes to be the most promising for synthetic realisation of a nested cage complex. These complexes were ranked 1st, 4th, 5th, 7th, 17th, and 19th purely based on binding energies. Therefore, the most promising nested cage complex still remains the combination of cages 111 and 117. Further, the best four of these six complexes all include 117 as the outer cage, but the last two complexes include cage 111 as the inner cage with two different outer cages.
Conclusions
To our knowledge, an organic nested cage complex has not been previously reported. Here, we have screened 132 organic cage molecules for their potential in forming energetically favourable nested cage complexes. We have also considered which cages are energetically favourable for self-catenation instead. The large number of possible combinations and the need to sample many different relative orientations of the cages in each pairing meant that we conducted almost half a million calculations in this study. Through calculating the binding energy of the cage pairings, we were then able to identify which self-catenated complexes and which nested cage complexes were most energetically favourable. We also considered the degree of interlocking, symmetry of the arrangements, and the ease of synthesis of the precursors and of the individual cage molecules to analyse which are the most promising candidates for attempts at synthesis.The three most favourable cages for self-catenation were found to be a TCC1[6+12] large truncated tetrahedron (cage 81),54 and two related large tetrahedral cages formed from a [4 + 4] imine reaction, that differ only in the alkyl functionalisation of the triamine vertex (52 and 78).23 Of these, cages 52 and 78 would be the most promising for synthesis because they were formed cleanly and in good yield. The nested cage complexes were found to be energetically much more favourable than the self-catenation reactions, and in all of the top nested cage complexes, the alternative self-catenation reactions were never found to be energetically competitive. The large [8 + 12] imine cage from Gawroński and co-workers (cage 117),75 was found to be involved in the largest number of favourable nested cage complexes by a considerable margin, typically as the outer cage. The frequency that 117 was involved in favourable nested cage complexes can in large part be attributed to the fact that it has six large windows, which are a good symmetry match for encapsulating inner cages that have six vertices that can sit in each of the windows of 117, which is the case for 45% of the cages in our data set. The next most frequently found cage in the complexes was cage 111, which is a dodecaamide cage that has six vertices. The highest binding energy pairing involves cages 111 and 117, in an arrangement where pairs of naphthalene arms at each vertex of 111 sit in the windows of 117, with intermolecular interactions that make the binding energy particularly favourable.
We can now suggest the most promising routes for synthetic realisation of a nested cage complex. The most promising complex is that containing 111 and 117. Given the irreversible nature of the inner cage 111, there are two viable approaches to synthesising the nested cage complex with 117. The first would be to use the inner cage 111 as a template and attempt a one-pot reaction with the precursors for the outer cage 117 or, alternatively, the reversible outer cage could be formed separately and then mixed with the inner cage and allowed to equilibrate. A range of different solvents and additives could be trialled for both of these approaches, as well as recrystallisation screens, which is how previous organic cage catenanes were initially discovered.
Due to the high frequency with which 117 occurred in energetically favourable complexes however, we would also suggest that it is worth screening for complexes combining 117 with a wider range of potential cages, particularly smaller cages with six vertices that we find to be good partner cages for 117. It will be important to take into consideration the reversible nature of alternative organic cage partners, particularly those formed through imine condensations, where competing reactions to form new species may occur over forming a nested cage complex, such as scrambled statistical distributions81 or socially self-sorted structures.82 Furthermore, a similar screen could also be attempted with cage 111, which was found to partner favourably with many cages. We hope that by narrowing down the thousands of possibilities for nested cage complexes to just a handful, this computational study stimulates synthetic work and assists in the realisation of the first organic nested cage complex.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Royal Society for a University Research Fellowship (K. E. J.), the EPSRC (EP/M017257/1, EP/P005543/1, EP/R005710/1 and EP/N004884/1) and the ERC through grant agreement no. 758370 (ERC-StG-PE5-CoMMaD) for funding. We thank Dr. Filip Szczypiński for valuable discussions.References
- F. Beuerle and B. Gole, Angew. Chem., Int. Ed., 2018, 57, 4850–4878 CrossRef CAS.
- T. Hasell and A. I. Cooper, Nat. Rev. Mater., 2016, 1, 10686 Search PubMed.
- M. Mastalerz, Angew. Chem., Int. Ed., 2010, 49, 5042–5053 CrossRef CAS.
- Z. Liu, S. K. M. Nalluri and J. F. Stoddart, Chem. Soc. Rev., 2017, 46, 2459–2478 RSC.
- G. Gil-Ramírez, D. A. Leigh and A. J. Stephens, Angew. Chem., 2015, 127, 6208–6249 CrossRef.
- M. Xue, Y. Yang, X. Chi, X. Yan and F. Huang, Chem. Rev., 2015, 115, 7398–7501 CrossRef CAS PubMed.
- S. D. P. Fielden, D. A. Leigh and S. L. Woltering, Angew. Chem., Int. Ed., 2017, 56, 11166–11194 CrossRef CAS.
- S. Erbas-Cakmak, D. A. Leigh, C. T. McTernan and A. L. Nussbaumer, Chem. Rev., 2015, 115, 10081–10206 CrossRef CAS.
- S. Kassem, T. van Leeuwen, A. S. Lubbe, M. R. Wilson, B. L. Feringa and D. A. Leigh, Chem. Soc. Rev., 2017, 46, 2592–2621 RSC.
- S. Y. Kim, I. S. Jung, E. Lee, J. Kim, S. Sakamoto, K. Yamaguchi and K. Kim, Angew. Chem., Int. Ed., 2001, 40, 2119–2121 CrossRef CAS.
- H. Danjo, Y. Hashimoto, Y. Kidena, A. Nogamine, K. Katagiri, M. Kawahata, T. Miyazawa and K. Yamaguchi, Org. Lett., 2015, 17, 2154–2157 CrossRef CAS.
- W. Gong, X. Yang, P. Y. Zavalij, L. Isaacs, Z. Zhao and S. Liu, Chem. – Eur. J., 2016, 22, 17612–17618 CrossRef CAS.
- K. Cai, M. C. Lipke, Z. Liu, J. Nelson, T. Cheng, Y. Shi, C. Cheng, D. Shen, J.-M. Han, S. Vemuri, Y. Feng, C. L. Stern, W. A. Goddard, M. R. Wasielewski and J. F. Stoddart, Nat. Commun., 2018, 9, 5275–528–52833 CrossRef.
- S. A. L. Rousseaux, J. Q. Gong, R. Haver, B. Odell, T. D. W. Claridge, L. M. Herz and H. L. Anderson, J. Am. Chem. Soc., 2015, 137, 12713–12718 CrossRef CAS.
- T. Kawase, K. Tanaka, N. Shiono, Y. Seirai and M. Oda, Angew. Chem., Int. Ed., 2004, 43, 1722–1724 CrossRef CAS.
- H. Ueno, T. Nishihara, Y. Segawa and K. Itami, Angew. Chem., Int. Ed., 2015, 54, 3707–3711 CrossRef CAS.
- B. Sun, M. Wang, Z. Lou, M. Huang, C. Xu, X. Li, L.-J. Chen, Y. Yu, G. L. Davis, B. Xu, H.-B. Yang and X. Li, J. Am. Chem. Soc., 2015, 137, 1556–1564 CrossRef CAS.
- D. Zhang, T. K. Ronson, J. L. Greenfield, T. Brotin, P. Berthault, E. Léonce, J.-L. Zhu, L. Xu and J. R. Nitschke, J. Am. Chem. Soc., 2019, 141, 8339–8345 CAS.
- T. Sawada, H. Hisada and M. Fujita, J. Am. Chem. Soc., 2014, 136, 4449–4451 CrossRef CAS.
- Z. Liu, C. Tian, J. Yu, Y. Li, W. Jiang and C. Mao, J. Am. Chem. Soc., 2015, 137, 1730–1733 CrossRef CAS PubMed.
- T. Hasell, X. Wu, J. T. A. Jones, J. Bacsa, A. Steiner, T. Mitra, A. Trewin, D. J. Adams and A. I. Cooper, Nat. Mater., 2010, 2, 750–755 CAS.
- G. Zhang, O. Presly, F. White, I. M. Oppel and M. Mastalerz, Angew. Chem., Int. Ed., 2014, 53, 5126–5130 CAS.
- R. L. Greenaway, V. Santolini, M. J. Bennison, B. M. Alston, C. J. Pugh, M. A. Little, M. Miklitz, E. G. B. Eden-Rump, R. Clowes, A. Shakil, H. J. Cuthbertson, H. Armstrong, M. E. Briggs, K. E. Jelfs and A. I. Cooper, Nat. Commun., 2018, 9, 2849 CrossRef CAS.
- Y. Li, K. M. Mullen, T. D. W. Claridge, P. J. Costa, V. Felix and P. D. Beer, Chem. Commun., 2009, 7134–71373 RSC.
- H. Li, H. Zhang, A. D. Lammer, M. Wang, X. Li, V. M. Lynch and J. L. Sessler, Nat. Chem., 2015, 7, 1003–1008 CrossRef CAS.
- M. Yoshizawa, M. Yoshizawa, J. K. Klosterman, J. K. Klosterman, M. Fujita, M. Fujita and M. Fujita, Angew. Chem., Int. Ed., 2009, 48, 3418–3438 CrossRef CAS.
- T.-C. Lee, E. Kalenius, A. I. Lazar, K. I. Assaf, N. Kuhnert, C. H. Grün, J. Jänis, O. A. Scherman and W. M. Nau, Nat. Chem., 2013, 5, 376–382 CrossRef CAS.
- A. Kewley, A. Stephenson, L. Chen, M. E. Briggs, T. Hasell and A. I. Cooper, Chem. Mater., 2015, 27, 3207–3210 CrossRef CAS.
- T. Mitra, K. E. Jelfs, M. Schmidtmann, A. Ahmed, S. Y. Chong, D. J. Adams and A. I. Cooper, Nat. Chem., 2013, 5, 276–281 CrossRef CAS.
- T. Hasell, M. Miklitz, A. Stephenson, M. A. Little, S. Y. Chong, R. Clowes, L. Chen, D. Holden, G. A. Tribello, K. E. Jelfs and A. I. Cooper, J. Am. Chem. Soc., 2016, 138(5), 1653–1659 CrossRef CAS.
- L. Chen, P. S. Reiss, S. Y. Chong, D. Holden, K. E. Jelfs, T. Hasell, M. A. Little, A. Kewley, M. E. Briggs, A. Stephenson, K. M. Thomas, J. A. Armstrong, J. Bell, J. Busto, R. Noel, J. Liu, D. M. Strachan, P. K. Thallapally and A. I. Cooper, Nat. Mater., 2014, 13, 954–960 CrossRef CAS PubMed.
- M. Brutschy, M. W. Schneider, M. Mastalerz and S. R. Waldvogel, Adv. Mater., 2012, 24, 6049–6052 CrossRef CAS PubMed.
- K. Acharyya and P. S. Mukherjee, Chem. Commun., 2014, 50, 15788–15791 RSC.
- N. Giri, M. G. Del Pópolo, G. Melaugh, R. L. Greenaway, K. Rätzke, T. Koschine, L. Pison, M. F. C. Gomes, A. I. Cooper and S. L. James, Nature, 2015, 527, 216–220 CrossRef CAS.
- T. Brotin and J.-P. Dutasta, Chem. Rev., 2009, 109, 88–130 CrossRef CAS.
- T. Tozawa, J. T. A. Jones, S. I. Swamy, S. Jiang, D. J. Adams, S. Shakespeare, D. Bradshaw, T. Hasell, S. Y. Chong, C. Tang, S. Thompson, J. Parker, A. Trewin, J. Bacsa, A. M. Z. Slawin, A. Steiner and A. I. Cooper, Nat. Mater., 2009, 8, 973–978 CrossRef CAS.
- E. J. Dale, N. A. Vermeulen, A. A. Thomas, J. C. Barnes, M. Juríček, A. K. Blackburn, N. L. Strutt, A. A. Sarjeant, C. L. Stern, S. E. Denmark and J. F. Stoddart, J. Am. Chem. Soc., 2014, 136, 10669–10682 CrossRef CAS.
- J. D. Evans, K. E. Jelfs, G. M. Day and C. J. Doonan, Chem. Soc. Rev., 2017, 46, 3286–3301 RSC.
- K. E. Jelfs, X. Wu, M. Schmidtmann, J. T. A. Jones, J. E. Warren, D. J. Adams and A. I. Cooper, Angew. Chem., Int. Ed., 2011, 50, 10653–10656 CrossRef CAS.
- K. E. Jelfs, E. Eden, J. L. Culshaw, S. Shakespeare, E. O. Pyzer-Knapp, H. P. G. Thompson, J. Bacsa, G. M. Day and D. J. Adams, J. Am. Chem. Soc., 2013, 135, 9307–9310 CrossRef CAS.
- V. Santolini, M. Miklitz, E. Berardo and K. E. Jelfs, Nanoscale, 2017, 9, 5280–5298 RSC.
- G. Zhu, Y. Liu, L. Flores, Z. R. Lee, C. W. Jones, D. A. Dixon, D. S. Sholl and R. P. Lively, Chem. Mater., 2017, 30, 262–272 CrossRef.
- V. Santolini, G. A. Tribello and K. E. Jelfs, Chem. Commun., 2015, 51, 15542–15545 RSC.
- L. Turcani, R. L. Greenaway and K. E. Jelfs, Chem. Mater., 2019, 31, 714–727 CrossRef CAS.
- A. J. Cruz-Cabeza, G. M. Day and W. Jones, Chem. – Eur. J., 2009, 15, 13033–13040 CrossRef CAS.
- J. T. A. Jones, T. Hasell, X. Wu, J. Bacsa, K. E. Jelfs, M. Schmidtmann, S. Y. Chong, D. J. Adams, A. Trewin, F. Schiffman, F. Cora, B. Slater, A. Steiner, G. M. Day and A. I. Cooper, Nature, 2011, 474, 367–371 CrossRef CAS.
- E. O. Pyzer-Knapp, H. P. G. Thompson, F. Schiffmann, K. E. Jelfs, A. I. Cooper and G. M. Day, Chem. Sci., 2014, 5, 2235–2245 RSC.
- A. G. Slater, P. S. Reiss, A. Pulido, M. A. Little, D. L. Holden, L. Chen, S. Y. Chong, B. M. Alston, R. Clowes, M. Haranczyk, M. E. Briggs, T. Hasell, G. M. Day and A. I. Cooper, ACS Cent. Sci., 2017, 3, 734–742 CrossRef CAS.
- M. Bernabei, R. Pérez-Soto, I. Gomez Garcia and M. Haranczyk, Mol. Syst. Des. Eng., 2019, 4, 912–920 RSC.
- T. Hasell, S. Y. Chong, K. E. Jelfs, D. J. Adams and A. I. Cooper, J. Am. Chem. Soc., 2012, 134, 588–598 CrossRef CAS.
- M. Miklitz, S. Jiang, R. Clowes, M. E. Briggs, A. I. Cooper and K. E. Jelfs, J. Phys. Chem. C, 2017, 121, 15211–15222 CrossRef CAS.
- J. S. Camp and D. S. Sholl, J. Phys. Chem. C, 2016, 120, 1110–1120 CrossRef CAS.
- G. Zhang and M. Mastalerz, Chem. Soc. Rev., 2014, 43, 1934–1947 RSC.
- C. Stackhouse, V. Santolini, R. Greenaway, M. A. Little, M. E. Briggs, K. E. Jelfs and A. I. Cooper, Cryst. Growth Des., 2018, 18, 2759–2764 CrossRef.
- K. Matsui, Y. Segawa and K. Itami, J. Am. Chem. Soc., 2014, 136, 16452–16458 CrossRef CAS.
- J. Kim, I.-S. Jung, S.-Y. Kim, E. Lee, J.-K. Kang, S. Sakamoto, K. Yamaguchi and K. Kim, J. Am. Chem. Soc., 2000, 122, 540–541 CrossRef CAS.
- M. Mastalerz, M. W. Schneider, I. M. Oppel and O. Presly, Angew. Chem., Int. Ed., 2011, 50, 1046–1051 CrossRef CAS.
- M. W. Schneider, I. M. Oppel and M. Mastalerz, Chem. – Eur. J., 2012, 18, 4156–4160 CrossRef CAS PubMed.
- M. Mastalerz, Chem. Commun., 2008, 4756–4758 RSC.
- M. W. Schneider, H.-J. Siegfried Hauswald, R. Stoll and M. Mastalerz, Chem. Commun., 2012, 48, 9861–9863 RSC.
- B. S. Park, C. B. Knobler and D. J. Cram, Chem. Commun., 1998, 55–56 RSC.
- N. Giri, C. E. Davidson, G. Melaugh, M. G. Del Pópolo, J. T. A. Jones, T. Hasell, A. I. Cooper, P. N. Horton, M. B. Hursthouse and S. L. James, Chem. Sci., 2012, 3, 2153–2158 RSC.
- M. Liu, M. A. Little, K. E. Jelfs, J. T. A. Jones, M. Schmidtmann, S. Y. Chong, T. Hasell and A. I. Cooper, J. Am. Chem. Soc., 2014, 136, 7583–7586 CrossRef CAS.
- M. J. Bojdys, M. E. Briggs, J. T. A. Jones, D. J. Adams, S. Y. Chong, M. Schmidtmann and A. I. Cooper, J. Am. Chem. Soc., 2011, 133, 16566–16571 CrossRef CAS.
- J. L. Culshaw, G. Cheng, M. Schmidtmann, T. Hasell, M. Liu, D. J. Adams and A. I. Cooper, J. Am. Chem. Soc., 2013, 135, 9307–9310 CrossRef PubMed.
- M. E. Briggs, K. E. Jelfs, S. Y. Chong and C. Lester, Cryst. Growth Des., 2013, 13, 4993–5000 CrossRef CAS.
- A. G. Slater, M. A. Little, A. Pulido, S. Y. Chong, D. Holden, L. Chen, C. Morgan, X. Wu, G. Cheng, R. Clowes, M. E. Briggs, T. Hasell, K. E. Jelfs, G. M. Day and A. I. Cooper, Nat. Chem., 2016, 9, 17–25 CrossRef PubMed.
- S. Jiang, J. Bacsa, X. Wu, J. T. A. Jones, R. Dawson, A. Trewin, D. J. Adams and A. I. Cooper, Chem. Commun., 2011, 47, 8919–8922 RSC.
- T. Hasell, J. L. Culshaw, S. Y. Chong, M. Schmidtmann, M. A. Little, K. E. Jelfs, E. O. Pyzer-Knapp, H. Shepherd, D. J. Adams, G. M. Day and A. I. Cooper, J. Am. Chem. Soc., 2014, 136, 1438–1448 CrossRef CAS PubMed.
- H. Ding, Y. Yang, B. Li, F. Pan, G. Zhu, M. Zeller, D. Yuan and C. Wang, Chem. Commun., 2015, 51, 1976–1979 RSC.
- N. Hafezi, J. M. Holcroft, K. J. Hartlieb, E. J. Dale, N. A. Vermeulen, C. L. Stern, A. A. Sarjeant and J. F. Stoddart, Angew. Chem., Int. Ed., 2015, 54, 456–461 CAS.
- H. Kudo, H. Kudo, R. Hayashi, R. Hayashi, K. Mitani, K. Mitani, T. Yokozawa, T. Yokozawa, N. C. Kasuga, N. C. Kasuga, T. Nishikubo and T. Nishikubo, Angew. Chem., Int. Ed., 2006, 45, 7948–7952 CrossRef CAS PubMed.
- C. J. Doonan, C. J. Sumby, J. D. Evans, D. M. Huang, P. Valente and A. Burgun, Chem. Commun., 2016, 52, 8850–8853 RSC.
- K. Ono, R. Aizawa, T. Yamano, S. Ito, N. Yasuda, K. Johmoto, H. Uekusa and N. Iwasawa, Chem. Commun., 2014, 50, 13683–13686 RSC.
- P. Skowronek, B. Warżajtis, U. Rychlewska and J. Gawroński, Chem. Commun., 2013, 49, 2524–2526 RSC.
- S. Klotzbach and F. Beuerle, Angew. Chem., Int. Ed., 2015, 127, 10497–10502 CrossRef.
- S. Klotzbach, T. Scherpf and F. Beuerle, Chem. Commun., 2014, 50, 12454–12457 RSC.
- M. Miklitz and K. E. Jelfs, J. Chem. Inf. Model., 2018, 58, 2387–2391 CrossRef CAS PubMed.
- E. Harder, W. Damm, J. Maple, C. Wu, M. Reboul, J. Y. Xiang, L. Wang, D. Lupyan, M. K. Dahlgren, J. L. Knight, J. W. Kaus, D. S. Cerutti, G. Krilov, W. L. Jorgensen, R. Abel and R. A. Friesner, J. Chem. Theory Comput., 2016, 12, 281–296 CrossRef CAS PubMed.
- G. Zhang, O. Presly, F. White, I. M. Oppel and M. Mastalerz, Angew. Chem., Int. Ed., 2014, 53, 1516–1520 CrossRef CAS.
- S. Lee, A. Yang, T. P. Moneypenny and J. S. Moore, J. Am. Chem. Soc., 2016, 138, 2182–2185 CrossRef CAS.
- F. Beuerle, S. Klotzbach and A. Dhara, Synlett, 2016, 27, 1133–1138 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional figures and tables. The structures of the individual cage molecules and the best self-catenation and nested cage complexes are provided at https://github.com/JelfsMaterialsGroup/Nested-cages. See DOI: 10.1039/c9me00085b |
| This journal is © The Royal Society of Chemistry 2020 |