Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Emergence of non-monotonic deep cavity cavitand assembly with increasing portal methylation†
Alexander
Saltzman
 a,
Du
Tang
a,
Du
Tang
 a,
Bruce C.
Gibb
a,
Bruce C.
Gibb
 b and
Henry S.
Ashbaugh
b and
Henry S.
Ashbaugh
 *a
*a
aDepartment of Chemical and Biomolecular Engineering, Tulane University, New Orleans, LA 70118, USA. E-mail: hanka@tulane.edu
bDepartment of Chemistry, Tulane University, New Orleans, LA 70118, USA
First published on 27th September 2019
Abstract
Octa-acid (OA) and tetra-endo-methyl octa-acid (TEMOA) are deep cavity cavitands that readily form multimeric complexes with hydrophobic guests, like n-alkanes, in aqueous solution. Experimentally, OA displays a monotonic progression from monomeric to dimeric complexes with n-alkanes of increasing length, while TEMOA exhibits a non-monotonic progression from monomeric, to dimeric, to monomeric, to dimeric complexes over the same range of guest sizes. Previously we have conducted simulations demonstrating this curious behavior arises from the methyl units ringing TEMOA's portal to its hydrophobic pocket barring the possibility for two alkane chains to simultaneously bridge between two hosts in a dimer. Here we expand our prior simulation study to consider the partially methylated hosts mono-endo-methyl octa-acid, 1,3-di-endo-methyl octa-acid, and tri-endo-methyl octa-acid to examine the emergence of non-monotonic assembly behavior. Our simulations demonstrate a systematic progression of non-monotonic assembly with increasing portal methylation. This behavior is traced to the progressive destabilization of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes (two hosts assembled with two guests) rather than stabilizing other potential host/guest complexes that could be formed.
2 complexes (two hosts assembled with two guests) rather than stabilizing other potential host/guest complexes that could be formed.
Design, System, ApplicationThe programming of aqueous phase assembly processes constitutes a grand challenge in soft matter physics. Deep-cavity cavitands, a class of water-soluble, bowl-like supramolecular hosts, readily bind non-polar guests via hydrophobic interactions to build well-defined complexes. Here we report a molecular simulation study of the impact of methylation about the rim of cavitand host pockets on the stoichiometry of their assemblies with n-alkanes. While non-methylated hosts exhibit a monotonic assembly pattern with increasing n-alkane size from monomeric to dimeric host complexes, increasing rim methylation progressively leads to the onset of non-monotonic assembly patterns, where the monomeric complex is reemergent for intermediate guest chain lengths. The effective use of a “throttle” between dimerized hosts hints at a novel route for manipulating host/guest assembly, forcing guests to thread constrictions that stabilize/destabilize specific complex structures. |
1 Introduction
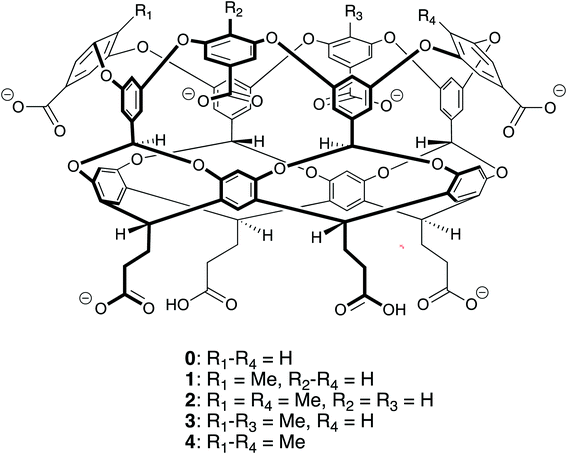
The ability to self-assemble supramolecular complexes into discrete, well-defined structures is a grand research challenge. While metal/ligand1 and hydrogen bonding2–4 offer strong, specific interactions to direct self-assembly processes, the toxicity of heavy metals and promiscuity of hydrogen bonds in polar solvents limits the ability to utilize these interactions in aqueous systems with potential biological applications. Driven by the meager solubility of non-polar moieties in water, hydrophobic interactions offer a potentially useful route toward supramolecular assembly in water. In difference to metal/ligand and hydrogen bonding, hydrophobic interactions are non-specific; making it difficult to build directed structures in solution. In this case, the complex interplay between supramolecular shape, potential host/guest packing effects, and hydrophobic interactions offers a potentially large landscape to explore for building discrete assemblies.Motivated by these challenges, Gibb has explored the relationship between the functionalization of water-soluble deep cavity cavitand hosts and the complexes formed with n-alkane guests.5–8 Specifically, his group has examined octa-acid (host 0 in Fig. 1) and tetra-methyl-endo-octa-acid (host 4 in Fig. 1), which differ only by the presence of four methyl units that ring the portal to the hydrophobic, guest binding pocket of the cavitand. The n-alkane complexes of host 0 display a straightforward progression of assembly states with increasing guest length: methane (C1, where the subscript indicates the number of carbons in the n-alkane) does not bind the host; ethane (C2) forms a monomeric 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex (denoted i
1 complex (denoted i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j, where i and j indicate the number of host and guest molecules in a complex. Complexes with one host are referred to as simple, monomeric host–guest complexes, while those with two hosts are referred to as dimeric capsular complexes. These host/guest complexes are illustrated in Fig. 2); propane (C3) through octane (C8) form dimeric 2
j, where i and j indicate the number of host and guest molecules in a complex. Complexes with one host are referred to as simple, monomeric host–guest complexes, while those with two hosts are referred to as dimeric capsular complexes. These host/guest complexes are illustrated in Fig. 2); propane (C3) through octane (C8) form dimeric 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes; while larger guests form dimeric 2
2 complexes; while larger guests form dimeric 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes. This progression from monomeric to dimeric assemblies is a monotonic assembly pattern. Host 4, on the other hand, exhibits a decidedly non-monotonic progression of assemblies with increasing guest length: C1 and C2 form monomeric 1
1 complexes. This progression from monomeric to dimeric assemblies is a monotonic assembly pattern. Host 4, on the other hand, exhibits a decidedly non-monotonic progression of assemblies with increasing guest length: C1 and C2 form monomeric 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes; C3 through C6 form dimeric 2
1 complexes; C3 through C6 form dimeric 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes; C7 and C8 form monomeric 1
2 complexes; C7 and C8 form monomeric 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes; while C9 and longer guests form dimeric 2
1 complexes; while C9 and longer guests form dimeric 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes. In difference to host 0, that at most only forms dimeric complexes, host 4 can also form tetrameric and hexameric complexes with alkanes C17 and longer.8
1 complexes. In difference to host 0, that at most only forms dimeric complexes, host 4 can also form tetrameric and hexameric complexes with alkanes C17 and longer.8
Ashbaugh and Gibb reported molecular simulation studies of cavitand assembly with n-alkanes in water,9 breaking down the association process into elementary steps to understand the factors stabilizing distinct host/guest complexes. These simulations accurately captured the distinct monotonic versus non-monotonic assembly patterns of hosts 0 and 4. The non-monotonic assembly of 4 was found to arise from destabilization of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex. This destabilization was shown to result from the added methyl groups choking the portal region at the equator of the complex dimer, and limiting the ability of two alkane guests to thread between the hosts. 2
2 complex. This destabilization was shown to result from the added methyl groups choking the portal region at the equator of the complex dimer, and limiting the ability of two alkane guests to thread between the hosts. 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex destabilization begins with guest C6, which is comparable in length to the depth of an individual host pocket. The 1
2 complex destabilization begins with guest C6, which is comparable in length to the depth of an individual host pocket. The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex subsequently reemerges over the 2
1 complex subsequently reemerges over the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex since the 2
1 complex since the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex requires alkanes C9 and longer to bridge between two hosts. Within host 0, guests longer than ∼C15 must adopt a J-shaped conformational motif with a reverse turn in their main-chain. Interestingly however, simulations demonstrated that due to the portal narrowing within dimers of 4, alkanes cannot adopt such motifs.10,11 As a result, 2
1 complex requires alkanes C9 and longer to bridge between two hosts. Within host 0, guests longer than ∼C15 must adopt a J-shaped conformational motif with a reverse turn in their main-chain. Interestingly however, simulations demonstrated that due to the portal narrowing within dimers of 4, alkanes cannot adopt such motifs.10,11 As a result, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes with guests C16 or larger are destabilized relative to the corresponding capsular complex with 0. A follow up simulation study of the transfer of alkanes into tetrameric and hexameric complexes of host 4 demonstrated that guest packing preferences can tilt the assembly equilibrium towards those larger assemblies,12 in agreement with experiment. These molecular simulations subsequently highlighted guest packing within confined host/guest complexes as a useful strategy for directing the stabilization of distinct assembly morphologies.
1 complexes with guests C16 or larger are destabilized relative to the corresponding capsular complex with 0. A follow up simulation study of the transfer of alkanes into tetrameric and hexameric complexes of host 4 demonstrated that guest packing preferences can tilt the assembly equilibrium towards those larger assemblies,12 in agreement with experiment. These molecular simulations subsequently highlighted guest packing within confined host/guest complexes as a useful strategy for directing the stabilization of distinct assembly morphologies.
A question that follows from our previous studies is: what is the impact of partial methylation of the cavitand portal on their assemblies with n-alkanes? To address this question, we have performed a theoretical study of mono-endo-methyl-octa-acid (1), 1,3-di-endo-methyl-octa-acid (2), and tri-endo-methyl-octa-acid (3) (Fig. 1) complexed with n-alkanes from C1 to C14 to form 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 2
1, and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes in aqueous solution. Molecular dynamics simulations were conducted to evaluate free energies for forming 1
2 complexes in aqueous solution. Molecular dynamics simulations were conducted to evaluate free energies for forming 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 2
1, and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 host/guest complexes along the association pathways illustrated in Fig. 2. These association free energies are subsequently utilized by a reaction network model we previously developed to predict the distribution for host/guest complexes formed as a function of the host methylation and guest length. While hosts 1 through 3 can in principle be synthesized, the cavitands would be formed in statistical yields and could not be readily purified. Here then, theory offers insight into the origin of the non-monotonic assembly in this interesting class of supramolecular complexes that cannot be met by synthetic means.
2 host/guest complexes along the association pathways illustrated in Fig. 2. These association free energies are subsequently utilized by a reaction network model we previously developed to predict the distribution for host/guest complexes formed as a function of the host methylation and guest length. While hosts 1 through 3 can in principle be synthesized, the cavitands would be formed in statistical yields and could not be readily purified. Here then, theory offers insight into the origin of the non-monotonic assembly in this interesting class of supramolecular complexes that cannot be met by synthetic means.
2 Methods
2.1 Molecular dynamics simulations
Molecular dynamics simulations of n-alkanes complexed with hosts 0, 1, 2, 3, and 4 (Fig. 1) were performed using GROMACS 5.13 The simulations for hosts 0 and 4 were previously reported in ref. 9. Here we extend that study to consider hosts with intermediate degrees of methylation following the same simulation procedures as the previous study. The alkanes were modeled using the L-OPLS all-atom force field, which accurately reproduces the thermodynamic and conformational properties of long alkanes.14 In difference to models that predict longer alkanes that are too rigid, we find the L-OPLS force field more freely explores the conformational landscapes of the confined guests. While we cannot guarantee that the guests have exhaustively explore their entire landscape over the course of our simulations, we obtain reproducible, experimentally consistent results using the simulation protocols described below. The series of n-alkane guests from methane (C1) to tetradecane (C14) were considered. The hosts were simulated using the generalized Amber force field (GAFF)15 with partial charges obtained from the AM1-BCC calculations.16 The net charge of each cavitand was set to −6e to match the expected protonation state at pH 7.17 This charge state was obtained by deprotonating the four benzoic acid groups around the rim of the cavitand and two of the four groups at the base of the hosts (Fig. 1). Six sodium cations per host, modeled using GAFF, were included to neutralize the host charge. Water was modeled using the TIP4P/EW potential.18 GROMACS topology files for hosts 0–4 are provided in the ESI.† Non-bonded Lennard-Jones interactions were truncated beyond a separation of 9 Å with a mean-field dispersion correction for longer-range contributions to the energy and pressure. Electrostatic interactions were evaluated using the particle mesh Ewald summation method with a real space cutoff of 9 Å.19 Simulations were conducted in the isothermal–isobaric ensemble at 25 °C and 1 bar, where the temperature and pressure were controlled using the Nosé–Hoover thermostat20,21 and Parrinello–Rahman barostat,22 respectively. Bonds involving hydrogens for the hosts and guests were constrained using the LINCS algorithm,23 while water was held rigid using the SETTLE algorithm.24 The equations of motion were integrated using a time step of 2 fs.Complex stability was characterized by evaluating potentials-of-mean force (PMF) between hosts and guests. A PMF quantifies the interaction free energy between components along a designated reaction trajectory, which here lies along the host's four-fold (C4) rotational axis of symmetry.9 We consider three distinct PMFs (Fig. 2): the interaction between a single alkane and cavitand to form a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex; the interaction between an empty cavitand (1
1 complex; the interaction between an empty cavitand (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0) and a 1
0) and a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 alkane/cavitand complex to form a 2
1 alkane/cavitand complex to form a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex; and the interaction between two 1
1 complex; and the interaction between two 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 alkane/cavitand complexes to form the corresponding 2
1 alkane/cavitand complexes to form the corresponding 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex. In the first set of simulations, we determined the PMF between a host and guest (C1 to C14) from bulk water. In these simulations the cavitand and guest were solvated by 2600 water molecules in a cubic simulation box. Restraint potentials were applied to two dummy atoms along the C4-axis of each host to align the cavitand along the z-axis of the simulation box. The first “bottom” dummy atom was determined by the average position of the four atoms connecting the four feet of the cavitand to the bottom row of aromatic rings, while the second “top” dummy atom was determined by the average positions of the four carbon atoms on the second row of aromatic rings closest to the cavitand portal (see ESI† Fig. S1). The dummy atom at the bottom of the binding pocket was spatially restrained with a harmonic force constant of 100
2 complex. In the first set of simulations, we determined the PMF between a host and guest (C1 to C14) from bulk water. In these simulations the cavitand and guest were solvated by 2600 water molecules in a cubic simulation box. Restraint potentials were applied to two dummy atoms along the C4-axis of each host to align the cavitand along the z-axis of the simulation box. The first “bottom” dummy atom was determined by the average position of the four atoms connecting the four feet of the cavitand to the bottom row of aromatic rings, while the second “top” dummy atom was determined by the average positions of the four carbon atoms on the second row of aromatic rings closest to the cavitand portal (see ESI† Fig. S1). The dummy atom at the bottom of the binding pocket was spatially restrained with a harmonic force constant of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 nm−2, while the vector connecting the bottom atom to the top was fixed along the z-axis using a harmonic constraint of 50
000 kJ mol−1 nm−2, while the vector connecting the bottom atom to the top was fixed along the z-axis using a harmonic constraint of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 nm−2. The PMF was determined over a series of overlapping windows spanning from bulk water into the host pocket using umbrella sampling.25 The guest center was restrained to the C4-axis of the host using a harmonic potential acting normal to the symmetry axis with a force constant of 100
000 kJ mol−1 nm−2. The PMF was determined over a series of overlapping windows spanning from bulk water into the host pocket using umbrella sampling.25 The guest center was restrained to the C4-axis of the host using a harmonic potential acting normal to the symmetry axis with a force constant of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 nm−2. In the case of guests with an odd number of carbon atoms, the center was taken as the middle carbon along the chain backbone (i.e., carbon number (n + 1)/2). For guests with an even number of carbons, a dummy atom was placed between the n/2 and n/2 + 1 carbons to serve as the restraint center. Sample windows were simulated from 5 Å deep-inside the cavitand pocket, measured from the center of the top plane defined by the four carbon atoms on the second row of aromatic rings closest to the cavitand mouth, to 15 Å out into bulk solvent. Forty overlapping windows were used along the z-axis with the harmonic umbrella potential minimum separated in 0.5 Å increments and a force constant of 15
000 kJ mol−1 nm−2. In the case of guests with an odd number of carbon atoms, the center was taken as the middle carbon along the chain backbone (i.e., carbon number (n + 1)/2). For guests with an even number of carbons, a dummy atom was placed between the n/2 and n/2 + 1 carbons to serve as the restraint center. Sample windows were simulated from 5 Å deep-inside the cavitand pocket, measured from the center of the top plane defined by the four carbon atoms on the second row of aromatic rings closest to the cavitand mouth, to 15 Å out into bulk solvent. Forty overlapping windows were used along the z-axis with the harmonic umbrella potential minimum separated in 0.5 Å increments and a force constant of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ (mol−1 nm−2).25 Each simulation window was equilibrated for 1 ns, followed by a 15 ns production run. We have found in our previous simulations of cavitand/alkane interactions that this simulation time is sufficient to obtain reproducible, converged results,9,10,12 suggesting the guest conformational landscape has been well explored. System configurations were saved every 0.2 ps for post-simulation analysis. The PMF for forming the 1
000 kJ (mol−1 nm−2).25 Each simulation window was equilibrated for 1 ns, followed by a 15 ns production run. We have found in our previous simulations of cavitand/alkane interactions that this simulation time is sufficient to obtain reproducible, converged results,9,10,12 suggesting the guest conformational landscape has been well explored. System configurations were saved every 0.2 ps for post-simulation analysis. The PMF for forming the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex was reconstructed from the overlapping windows using the weighted histogram analysis method.26
1 complex was reconstructed from the overlapping windows using the weighted histogram analysis method.26
In the second set of simulations, we evaluated the PMF between an empty cavitand (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0) and a second cavitand in a 1
0) and a second cavitand in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex with a C1 to C14 guest in water. The two cavitands were oriented with their binding pockets facing one another aligned along their C4-axes to form a dimeric 2
1 complex with a C1 to C14 guest in water. The two cavitands were oriented with their binding pockets facing one another aligned along their C4-axes to form a dimeric 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 host/guest assembly. Both hosts were aligned with the simulation box's z-axis, using the same restraints as in the 1
1 host/guest assembly. Both hosts were aligned with the simulation box's z-axis, using the same restraints as in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexation simulations. No restraint was applied to the guest, however, which was held within its host pocket via hydrophobic interactions. Sample windows were simulated from distances ranging from the center of the two cavitand faces, which established a separation of zero, to 13 Å into the bulk water. Twenty-seven overlapping windows were simulated, with the harmonic umbrella potential minimum separated in 0.5 Å increments and a force constant of 15
1 complexation simulations. No restraint was applied to the guest, however, which was held within its host pocket via hydrophobic interactions. Sample windows were simulated from distances ranging from the center of the two cavitand faces, which established a separation of zero, to 13 Å into the bulk water. Twenty-seven overlapping windows were simulated, with the harmonic umbrella potential minimum separated in 0.5 Å increments and a force constant of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ (mol−1 nm−2). The same simulation procedures and PMF reconstruction methods were used here as for the 1
000 kJ (mol−1 nm−2). The same simulation procedures and PMF reconstruction methods were used here as for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexation study. In addition, we considered the PMF between two empty hosts devoid of guests to form a 2
1 complexation study. In addition, we considered the PMF between two empty hosts devoid of guests to form a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 dimer. Approximately 3000 TIP4P/EW water molecules were used to solvate these complexes.
0 dimer. Approximately 3000 TIP4P/EW water molecules were used to solvate these complexes.
In the third set of simulations, we evaluated the PMF between two 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 host/guest complexes to form a 2
1 host/guest complexes to form a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex (Fig. 2). As in the 2
2 complex (Fig. 2). As in the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexation simulations, the cavitands were oriented with their binding pockets facing one another aligned along their C4-axes. For host 1, 2, and 3 we simulated alkane guests up to C11, C10, and C10 in length, respectively. Longer guests exhibited increasingly destabilizing repulsive interactions. As above, no restraints were placed on the guests. The same simulation procedures, PMF reconstruction methods, and numbers of hydration waters were used here as for the 2
1 complexation simulations, the cavitands were oriented with their binding pockets facing one another aligned along their C4-axes. For host 1, 2, and 3 we simulated alkane guests up to C11, C10, and C10 in length, respectively. Longer guests exhibited increasingly destabilizing repulsive interactions. As above, no restraints were placed on the guests. The same simulation procedures, PMF reconstruction methods, and numbers of hydration waters were used here as for the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexation study.
1 complexation study.
2.2 Host/guest assembly model
We previously developed a reaction network model to predict the distribution of monomeric and dimeric host/guest assembly states as a function of the alkane guest length. Here we outline the essential elements of that model. A complete development of the model can be found in ref. 9. The host/guest assembly process is broken down into a series of four reactions (Fig. 2) that dictates the assembly equilibrium between guests (G) and the possible monomeric and dimeric host/guest complexes (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, 1
0, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, 2
0, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 2
1, and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 assemblies)
2 assemblies)1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 + G ⇌ 1 0 + G ⇌ 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1, | (1a) |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 + 1 0 + 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 ⇌ 2 0 ⇌ 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, 0, | (1b) |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 + 1 1 + 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 ⇌ 2 0 ⇌ 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1, | (1c) |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 + 1 1 + 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ⇌ 2 1 ⇌ 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. 2. | (1d) |
The equilibrium constants for these reactions, K1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, K2
1, K2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, K2
0, K2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and K2
1, and K2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, are evaluated as a Boltzmann weighting of the minima in the PMFs (ωi
2, are evaluated as a Boltzmann weighting of the minima in the PMFs (ωi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j) evaluated from the corresponding simulations described above. The equilibrium constants for the monomeric and dimeric host/guest assembly reactions subsequently are
j) evaluated from the corresponding simulations described above. The equilibrium constants for the monomeric and dimeric host/guest assembly reactions subsequently are
K1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 = α 1 = α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ω1 exp(−ω1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1/RT) and K2 1/RT) and K2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j = β j = β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ω2 exp(−ω2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j/RT), j/RT), | (2) |
The free host concentration, [1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0], is determined from the solution of a quadratic equation (see ESI† for full derivation)
0], is determined from the solution of a quadratic equation (see ESI† for full derivation)
2(K2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 + K2 0 + K2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1K1 1K1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1[G] + K2 1[G] + K2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1K21 1K21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1[G]2)[1 1[G]2)[1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0]2 + (1 + K1 0]2 + (1 + K1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1[G])[1 1[G])[1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0] − [1]total = 0. 0] − [1]total = 0. | (3) |
The total host concentration, [1]total, corresponds to the amount of host added to solution distributed amongst all potential assembly states, i.e., [1]total = [1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0] + [1
0] + [1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1] + 2([2
1] + 2([2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0] + [2
0] + [2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1] + [2
1] + [2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2]). We assume [1]total = 3 mM, which corresponds to a typical experimental concentration. The alkane guest concentration was assumed to be saturated as described by the relationship
2]). We assume [1]total = 3 mM, which corresponds to a typical experimental concentration. The alkane guest concentration was assumed to be saturated as described by the relationship
 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1] = K1
1] = K1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [1
1 [1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0][G].
0][G].
3 Results & discussion
Pairwise PMFs for formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 2
1, and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
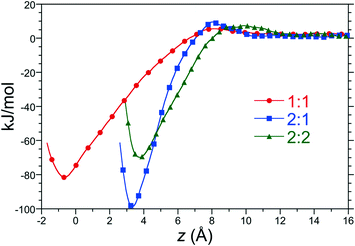
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes in water as a function of distance along the reaction coordinate between host 2 and C8 at 25 °C and 1 atm are reported in Fig. 3. Each of these free energy profiles exhibit minima at least 70 kJ mol−1 (28 RT) deep as a result of significant hydrophobic interactions between the hosts and guests. The strength of these interactions suggest that these complexes are long lived once assembled. The minimum of the 1
2 complexes in water as a function of distance along the reaction coordinate between host 2 and C8 at 25 °C and 1 atm are reported in Fig. 3. Each of these free energy profiles exhibit minima at least 70 kJ mol−1 (28 RT) deep as a result of significant hydrophobic interactions between the hosts and guests. The strength of these interactions suggest that these complexes are long lived once assembled. The minimum of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PMF falls at distance slightly less than zero since the center-of-mass of C8 can enter the binding pocket below the rim of the pocket's portal. The minima of the dimeric complexes sits 3 to 4 Å above the rim of the portal, roughly corresponding to the distance of closest approach between the rim carbons of opposing host “hemispheres”. The minimum of the 2
1 PMF falls at distance slightly less than zero since the center-of-mass of C8 can enter the binding pocket below the rim of the pocket's portal. The minima of the dimeric complexes sits 3 to 4 Å above the rim of the portal, roughly corresponding to the distance of closest approach between the rim carbons of opposing host “hemispheres”. The minimum of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex lies slightly to the right of that of the 2
2 complex lies slightly to the right of that of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, however, due to tight packing of two guests within the capsule interior. The 1
1, however, due to tight packing of two guests within the capsule interior. The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 2
1, and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 PMFs for all host/guest pairs examined here are qualitatively similar to those for host 2 and C8, though differ in quantitative detail.
2 PMFs for all host/guest pairs examined here are qualitatively similar to those for host 2 and C8, though differ in quantitative detail.
As previously demonstrated, the relative stability of the distinct host/guest assembly states is dominated by the free energy minima of the PMFs, denoted ω1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, ω2
1, ω2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and ω2
1, and ω2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, respectively. The 1
2, respectively. The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 2
1, and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
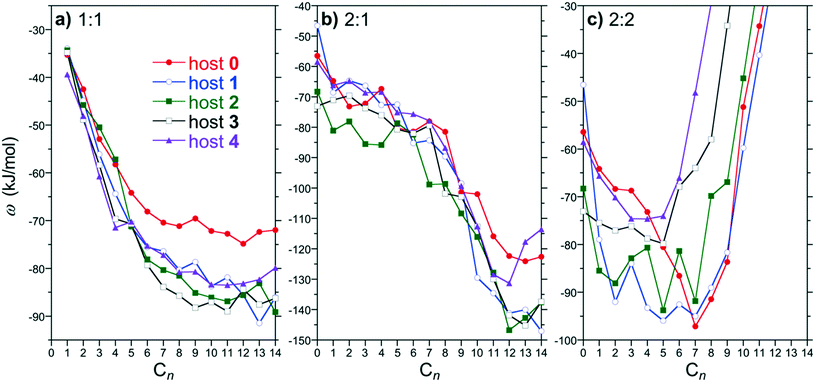
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 PMF minima for hosts 0 through 4 as a function of the alkane guest chain length are compared in Fig. 4. The PMF minima for 1
2 PMF minima for hosts 0 through 4 as a function of the alkane guest chain length are compared in Fig. 4. The PMF minima for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex formation for all the hosts exhibit an increasing attraction with guest chain length beginning with methane that plateaus for guests approximately longer than pentane (Fig. 4a). The PMF minima for the shorter guests (∼C4 and shorter) examined are comparable for all the hosts simulated. The plateau begins roughly for guests longer than the depth of the binding pocket. Longer guests subsequently are unable to stuff more methylene units within the pocket away from water and thereby do not gain any additional benefit for forming a 1
1 complex formation for all the hosts exhibit an increasing attraction with guest chain length beginning with methane that plateaus for guests approximately longer than pentane (Fig. 4a). The PMF minima for the shorter guests (∼C4 and shorter) examined are comparable for all the hosts simulated. The plateau begins roughly for guests longer than the depth of the binding pocket. Longer guests subsequently are unable to stuff more methylene units within the pocket away from water and thereby do not gain any additional benefit for forming a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex. Interestingly, the plateau for the methyl functionalized hosts (1 through 4) is more attractive than that for host 0, but are approximately the same as one another. Previously, we attributed the greater attraction between host 4 for longer guests compared to host 0 to increased van der Waals interactions between the methyl units of host 4 and the guests.9 We might then expect the plateau for hosts 1 through 3 to systematically deepen with increasing methylation between the host 0 and 4 limits, which we do not observe. This interpretation, however, does not consider the solvent's role on directing hydrophobic host/guest interactions. Moreover, we do not observe systematic variations with host methylation for the PMF minima of the short guests despite the systematic chains in host/guest van der Waals interactions. A definitive conclusion regarding the dependence of the 1
1 complex. Interestingly, the plateau for the methyl functionalized hosts (1 through 4) is more attractive than that for host 0, but are approximately the same as one another. Previously, we attributed the greater attraction between host 4 for longer guests compared to host 0 to increased van der Waals interactions between the methyl units of host 4 and the guests.9 We might then expect the plateau for hosts 1 through 3 to systematically deepen with increasing methylation between the host 0 and 4 limits, which we do not observe. This interpretation, however, does not consider the solvent's role on directing hydrophobic host/guest interactions. Moreover, we do not observe systematic variations with host methylation for the PMF minima of the short guests despite the systematic chains in host/guest van der Waals interactions. A definitive conclusion regarding the dependence of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexation plateau on host methylation is thus not immediately apparent.
1 complexation plateau on host methylation is thus not immediately apparent.
The 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PMF minima are attractive for all guest/host combinations considered (Fig. 4b). For guests up to C8, ω2
1 PMF minima are attractive for all guest/host combinations considered (Fig. 4b). For guests up to C8, ω2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weakly decreases with increasing alkane chain length with little distinction between the free energies for any of the hosts within the simulation noise. Beginning with C9, ω2
1 weakly decreases with increasing alkane chain length with little distinction between the free energies for any of the hosts within the simulation noise. Beginning with C9, ω2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 drops precipitously with increasing chain length further stabilizing the 2
1 drops precipitously with increasing chain length further stabilizing the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes. This guest size corresponds to the point at which a guest readily spans between the two hosts to gain additional favorable van der Waals interactions to stabilize the complex. Similar to the 1
1 complexes. This guest size corresponds to the point at which a guest readily spans between the two hosts to gain additional favorable van der Waals interactions to stabilize the complex. Similar to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 free energies, ω2
1 free energies, ω2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 drops to lower levels with increasing chain lengths for the methylated hosts (1 through 4) compared to that for host 0. While ω2
1 drops to lower levels with increasing chain lengths for the methylated hosts (1 through 4) compared to that for host 0. While ω2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for hosts 1 through 3 are practically indistinguishable, ω2
1 for hosts 1 through 3 are practically indistinguishable, ω2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for host 4 exhibits a minimum at C12 after which the complexation free energy increases with increasing guest length. In our previous work considering guests up to C16 the 2
1 for host 4 exhibits a minimum at C12 after which the complexation free energy increases with increasing guest length. In our previous work considering guests up to C16 the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex of host 4 ultimately becomes unstable.9 Experimentally8 and from simulation12 this host transitions from a dimeric 2
1 complex of host 4 ultimately becomes unstable.9 Experimentally8 and from simulation12 this host transitions from a dimeric 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex to a tetrameric 4
1 complex to a tetrameric 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex for sufficiently long guests. Host 0, on the other hand, only forms dimeric complexes with increasing guest length. Based on these observations, we may anticipate that ω2
2 complex for sufficiently long guests. Host 0, on the other hand, only forms dimeric complexes with increasing guest length. Based on these observations, we may anticipate that ω2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for hosts 1, 2, or 3 may exhibit a free energy minimum with increasing alkane chain length that destabilizes the dimer in favor of a tetramer. That lies beyond the scope of the present study, however.
1 for hosts 1, 2, or 3 may exhibit a free energy minimum with increasing alkane chain length that destabilizes the dimer in favor of a tetramer. That lies beyond the scope of the present study, however.
The most significant assembly PMF changes are observed for 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexation (Fig. 4c). Generally, ω2
2 complexation (Fig. 4c). Generally, ω2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 for all hosts is attractive for shorter chains and then dramatically diverges towards more positive free energies beyond a characteristic alkane chain length. This divergence was previously demonstrated to be correlated with constriction of the portal region at the dimeric complex equator by the endo-methyl rim groups. That is the endo-methyls choke the portal region between hosts blocking guests in opposing hosts threading through the portal. The divergence begins for guests C6 and longer for the host 4 dimer, which has the narrowest portal. This guest length corresponds to the depth of an individual host pocket as inferred from the ω1
2 for all hosts is attractive for shorter chains and then dramatically diverges towards more positive free energies beyond a characteristic alkane chain length. This divergence was previously demonstrated to be correlated with constriction of the portal region at the dimeric complex equator by the endo-methyl rim groups. That is the endo-methyls choke the portal region between hosts blocking guests in opposing hosts threading through the portal. The divergence begins for guests C6 and longer for the host 4 dimer, which has the narrowest portal. This guest length corresponds to the depth of an individual host pocket as inferred from the ω1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 plateau (Fig. 4a). While the divergence length for hosts 0 and 1 are similar, the divergence systematically shifts to increasingly shorter guest lengths for 2, 3, and 4. This observation agrees with the interpretation of the portal region becoming progressively constricted as more endo-methyls are added. We may anticipate then that the 2
1 plateau (Fig. 4a). While the divergence length for hosts 0 and 1 are similar, the divergence systematically shifts to increasingly shorter guest lengths for 2, 3, and 4. This observation agrees with the interpretation of the portal region becoming progressively constricted as more endo-methyls are added. We may anticipate then that the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes will become increasingly unstable with increasing methylation, tipping the balance towards other assemblies.
2 complexes will become increasingly unstable with increasing methylation, tipping the balance towards other assemblies.
The PMF minima reported in Fig. 4 can be utilized within the host/guest assembly model described above to predict the distribution of complexes between 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, 1
0, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, 2
0, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 2
1, and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 for a given guest. The predicted population of assemblies for host 3 as a function of the alkane chain length is reported in Fig. 5. This host/guest system exhibits non-monotonic assembly characteristics with increasing guest chain length. Specifically, the dimeric 2
2 for a given guest. The predicted population of assemblies for host 3 as a function of the alkane chain length is reported in Fig. 5. This host/guest system exhibits non-monotonic assembly characteristics with increasing guest chain length. Specifically, the dimeric 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex dominates for guests from C2 to C5, the monomeric 1
2 complex dominates for guests from C2 to C5, the monomeric 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex dominates for guests C6 to C8, and the dimeric 2
1 complex dominates for guests C6 to C8, and the dimeric 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex dominates for guests C9 and longer. Interestingly, even in the absence of any guest (C0), the dimeric 2
1 complex dominates for guests C9 and longer. Interestingly, even in the absence of any guest (C0), the dimeric 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 complex is predicted to exhibit a population comparable to the free 1
0 complex is predicted to exhibit a population comparable to the free 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 host within the simulation error. Guest free dimers are not observed experimentally. Moreover, our previous study of hosts 0 and 4 predicted a negligible population of 2
0 host within the simulation error. Guest free dimers are not observed experimentally. Moreover, our previous study of hosts 0 and 4 predicted a negligible population of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 complexes. Based on the expectation that the guest is a necessary element of the assembly to draw the two hosts together, it is likely that that the predicted population of 2
0 complexes. Based on the expectation that the guest is a necessary element of the assembly to draw the two hosts together, it is likely that that the predicted population of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 complexes is erroneous. Indeed, no 2
0 complexes is erroneous. Indeed, no 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 complexes are predicted for guests longer than C1. We attribute this prediction to the fact that small errors on the order of RT are sufficient to shift the populations of complexes observed, especially for the shorter guests. Examining the 2
0 complexes are predicted for guests longer than C1. We attribute this prediction to the fact that small errors on the order of RT are sufficient to shift the populations of complexes observed, especially for the shorter guests. Examining the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 PMF minimum for hosts 2 and 3 we observe predicted free energies ∼10 kJ mol−1 (4 RT) more stable than those for hosts 0, 1, and 4 (Fig. 4c). Given the lack of systematic variation in the PMF minimum with increasing hosts methylation, it appears the predicted overstabilization may be diminished with increasing simulation run times. Another potential source of error may result from the simplified reaction coordinate along the principle axis of host symmetry assumed to evaluate the equilibrium constants within the host/guest assembly model (eqn (2)). To alleviate this difficulty here after we assume K2
0 PMF minimum for hosts 2 and 3 we observe predicted free energies ∼10 kJ mol−1 (4 RT) more stable than those for hosts 0, 1, and 4 (Fig. 4c). Given the lack of systematic variation in the PMF minimum with increasing hosts methylation, it appears the predicted overstabilization may be diminished with increasing simulation run times. Another potential source of error may result from the simplified reaction coordinate along the principle axis of host symmetry assumed to evaluate the equilibrium constants within the host/guest assembly model (eqn (2)). To alleviate this difficulty here after we assume K2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 = 0 within the host guest assembly model, eliminating the potential for forming 2
0 = 0 within the host guest assembly model, eliminating the potential for forming 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 complexes. The impact of this assumption is to redistribute the population of assembly states amongst the 1
0 complexes. The impact of this assumption is to redistribute the population of assembly states amongst the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, 1
0, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 2
1, and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes for C0 (no guest) and C1. No complex population differences were observed for longer alkanes. Thus, this assumption has no impact on the onset of non-monotonic dimer-to-monomeric-to dimeric complex assembly patterns for longer guests.
2 complexes for C0 (no guest) and C1. No complex population differences were observed for longer alkanes. Thus, this assumption has no impact on the onset of non-monotonic dimer-to-monomeric-to dimeric complex assembly patterns for longer guests.
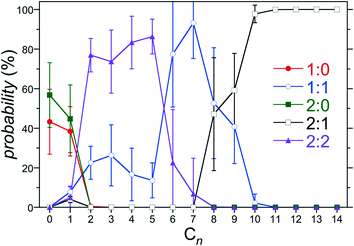 | ||
Fig. 5 Population of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, 1 0, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2 1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, 2 0, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 2 1, and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes for host 3 as a function of the alkane guest chain length predicted from the host/guest assembly model using the free energies reported in Fig. 4. The symbols for each complex are defined in the legend. The error bars indicate one standard error. 2 complexes for host 3 as a function of the alkane guest chain length predicted from the host/guest assembly model using the free energies reported in Fig. 4. The symbols for each complex are defined in the legend. The error bars indicate one standard error. | ||
The predicted distributions of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, 1
0, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 2
1, and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes as a function of the alkane guest chain length are reported in Fig. 6 for hosts 0 through 4. As previously documented, the dominant (most populous) complexes observed for host 0 progresses from 1
2 complexes as a function of the alkane guest chain length are reported in Fig. 6 for hosts 0 through 4. As previously documented, the dominant (most populous) complexes observed for host 0 progresses from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 for C1; to 1
0 for C1; to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for C2 and C3; to 2
1 for C2 and C3; to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 for C4 through C8; to 2
2 for C4 through C8; to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for C9 and longer guests (Fig. 6a). Thus host 0 is predicted to exhibit monotonic assembly from monomeric to dimeric complexes with increasing alkane chain length, as observed experimentally. Similar monotonic assembly is observed for host 1, although the population of 1
1 for C9 and longer guests (Fig. 6a). Thus host 0 is predicted to exhibit monotonic assembly from monomeric to dimeric complexes with increasing alkane chain length, as observed experimentally. Similar monotonic assembly is observed for host 1, although the population of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 assemblies is suppressed for the shortest guests (Fig. 6b). Interestingly, a small (∼10%) population of 1
1 assemblies is suppressed for the shortest guests (Fig. 6b). Interestingly, a small (∼10%) population of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex is observed for C9 near the transition between 2
1 complex is observed for C9 near the transition between 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 2
2 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 assemblies, hinting at the potential of a reemergent population of monomeric complex. This population of 1
1 assemblies, hinting at the potential of a reemergent population of monomeric complex. This population of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex near the 2
1 complex near the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 to 2
2 to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 transition grows to ∼40% of the total for 2 (Fig. 6c), albeit with its peak maximum shifted to C8. This population of 1
1 transition grows to ∼40% of the total for 2 (Fig. 6c), albeit with its peak maximum shifted to C8. This population of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex finally becomes dominant for guests from C6 through C8 complexed with 3 (Fig. 6d). The host subsequently exhibits full non-monotonic assembly from monomeric, to dimeric, to monomeric, then back to dimeric complexation with increasing alkane chain length. Interestingly, the reemergence of the 1
1 complex finally becomes dominant for guests from C6 through C8 complexed with 3 (Fig. 6d). The host subsequently exhibits full non-monotonic assembly from monomeric, to dimeric, to monomeric, then back to dimeric complexation with increasing alkane chain length. Interestingly, the reemergence of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 population for longer guests is accompanied with growth in the 1
1 population for longer guests is accompanied with growth in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 population for shorter guests as well, with a minimum between the short and long chain peaks. This trend continues for host 4, which exhibits a progression from 1
1 population for shorter guests as well, with a minimum between the short and long chain peaks. This trend continues for host 4, which exhibits a progression from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes for C1 and C2; to 2
1 complexes for C1 and C2; to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes for C3 through C5, to 1
2 complexes for C3 through C5, to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes for C6–C8; to 2
1 complexes for C6–C8; to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes for C9 and longer guests (Fig. 6e). The 1
1 complexes for C9 and longer guests (Fig. 6e). The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 population minimum between the short and long chain guests is more clearly defined for host 4 than for host 3, continuing the systematic trends observed with increasing host methylation.
1 population minimum between the short and long chain guests is more clearly defined for host 4 than for host 3, continuing the systematic trends observed with increasing host methylation.
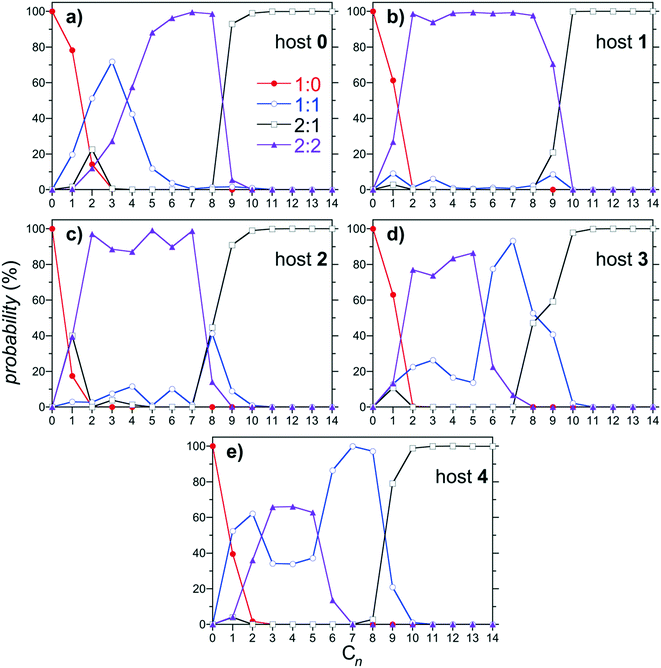 | ||
Fig. 6 Population of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, 1 0, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2:1, and 2 1, 2:1, and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes as a function of the alkane guest chain length predicted from the host/guest assembly model using the free energies reported in Fig. 4. Figures a, b, c, d, and e report results for hosts 0, 1, 2, 3, and 4, respectively. The symbols for each complex are defined in the legend in a. Error bars, which are comparable to those reported in Fig. 4, are neglected for clarity. 2 complexes as a function of the alkane guest chain length predicted from the host/guest assembly model using the free energies reported in Fig. 4. Figures a, b, c, d, and e report results for hosts 0, 1, 2, 3, and 4, respectively. The symbols for each complex are defined in the legend in a. Error bars, which are comparable to those reported in Fig. 4, are neglected for clarity. | ||
The emergence of the non-monotonic assembly pattern can be more directly visualized by evaluating the mean host aggregation number as
〈N〉 = p1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 + p1 0 + p1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 + 2(p2 1 + 2(p2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 + p2 1 + p2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2), 2), | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j is the probability a host is in an i
j is the probability a host is in an i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j complex (note that 2
j complex (note that 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 complexes were neglected, but could be included within the parentheses if they contributed substantively to the dimer population). The host aggregation numbers are plotted in Fig. 7. Host 0 displays a near monotonic progression from monomers to dimers with increasing guest chain length. Beginning with host 1 a dimple in the dimer population appears at intermediate length guests, which gets deeper with increasing host methylation. By host 4 the dimer population for guest C7 is zero, for all intents and purposes, and the monomer population is fully reemergent. Interestingly, for hosts 1 through 4 the population of dimers from ∼C2 to ∼C5, associated with 2
0 complexes were neglected, but could be included within the parentheses if they contributed substantively to the dimer population). The host aggregation numbers are plotted in Fig. 7. Host 0 displays a near monotonic progression from monomers to dimers with increasing guest chain length. Beginning with host 1 a dimple in the dimer population appears at intermediate length guests, which gets deeper with increasing host methylation. By host 4 the dimer population for guest C7 is zero, for all intents and purposes, and the monomer population is fully reemergent. Interestingly, for hosts 1 through 4 the population of dimers from ∼C2 to ∼C5, associated with 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes, becomes progressively suppressed with increasing methylation. We might surmise in this case that the 2
2 complexes, becomes progressively suppressed with increasing methylation. We might surmise in this case that the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex population could be further suppressed with increased methylation, barring the fact the host 4 has the greatest possible endo-methylation for this class of hosts.
2 complex population could be further suppressed with increased methylation, barring the fact the host 4 has the greatest possible endo-methylation for this class of hosts.
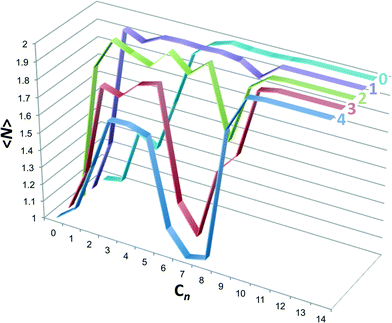 | ||
| Fig. 7 Host aggregation number, 〈N〉, as a function of the alkane guest chain length predicted from the probabilities reported in Fig. 6. Graphs for each host are identified by the text at the top right-hand side. | ||
4 Conclusions
We have presented a molecular simulation and reaction network modeling study of the complexation of deep cavity cavitand hosts with n-alkane guests to examine the onset of non-monotonic assembly patterns in biomimetic materials. Beginning with the unmethylated cavitand (host 0), which displays a monotonic transformation from monomeric to dimeric complexes with increasing alkane length, successive hosts from 1 through 4 exhibit progressively non-monotonic assembly patterns with increasing host methylation, transforming from monomeric, to dimeric, to monomeric, to dimeric complexes with increasing alkane length. The reentrance of the monomeric assembly morphology at intermediate guest lengths (C6 to C8) is associated with the systematic destabilization of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex association free energy rather than stabilization of the 1
2 complex association free energy rather than stabilization of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 2
1 or 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes. We attribute 2
1 complexes. We attribute 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex destabilization to increasing methylation constricting the portal region between dimerized hosts diminishing the ability for two guests to thread between opposing sides of the complex. For the maximally narrowed portal of 4, a fully reemergent monomeric 1
2 complex destabilization to increasing methylation constricting the portal region between dimerized hosts diminishing the ability for two guests to thread between opposing sides of the complex. For the maximally narrowed portal of 4, a fully reemergent monomeric 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex is observed, while only partially reemergent monomers are observed for the intermediately methylated hosts (1 through 3). These results hint at potential routes for manipulating host/guest assembly patterns that force guests to navigate narrow host portal constrictions to either stabilize or destabilize distinct complexes.
1 complex is observed, while only partially reemergent monomers are observed for the intermediately methylated hosts (1 through 3). These results hint at potential routes for manipulating host/guest assembly patterns that force guests to navigate narrow host portal constrictions to either stabilize or destabilize distinct complexes.
Conflicts of interest
No potential conflicts of interest were reported by the authors.Acknowledgements
We gratefully acknowledge financial support from the NSF (CBET-1403167). We also thank the Louisiana Optical Network Initiative who provided computational support.References
- D. Fujita, Y. Ueda, S. Sato, N. Mizuno, T. Kumasaka and M. Fujita, Self-assembly of tetravalent Goldberg polyhedra from 144 small components, Nature, 2016, 540, 563–567 CrossRef CAS PubMed.
- L. R. MacGillivray and J. L. Atwood, A chiral spherical molecular assembly held together by 60 hydrogen bonds, Nature, 1997, 389, 469–472 CrossRef CAS.
- D. Ajami and J. Rebek, Longer guests drive the reversible assembly of hyperextended capsules, Angew. Chem., Int. Ed., 2007, 46, 9283–9286 CrossRef CAS PubMed.
- K. Tiefenbacher, D. Ajami and J. Rebek, Self-Assembled Capsules of Unprecedented Shapes, Angew. Chem., Int. Ed., 2011, 50, 12003–12007 CrossRef CAS PubMed.
- C. L. D. Gibb and B. C. Gibb, Well-defined, organic nanoenvironments in water: The hydrophobic effect drives a capsular assembly, J. Am. Chem. Soc., 2004, 126, 11408–11409 CrossRef CAS PubMed.
- C. L. D. Gibb and B. C. Gibb, Straight-chain alkanes template the assembly of water-soluble nano-capsules, Chem. Commun., 2007, 1635–1637 RSC.
- H. Y. Gan, C. J. Benjamin and B. C. Gibb, Nonmonotonic assembly of a deep-cavity cavitand, J. Am. Chem. Soc., 2011, 133, 4770–4773 CrossRef CAS PubMed.
- H. Y. Gan and B. C. Gibb, Guest-mediated switching of the assembly state of a water-soluble deep-cavity cavitand, Chem. Commun., 2013, 49, 1395–1397 RSC.
- D. Tang, J. W. Barnett, B. C. Gibb and H. S. Ashbaugh, Guest controlled nonmonotonic deep cavity cavitand assembly state switching, J. Phys. Chem. B., 2017, 121, 10717–10725 CrossRef CAS.
- J. W. Barnett, B. C. Gibb and H. S. Ashbaugh, Succession of alkane conformational motifs bound within hydrophobic supramolecular capsular assemblies, J. Phys. Chem. B., 2016, 120, 10394–10402 CrossRef CAS.
- S. M. Liu, D. H. Russell, N. F. Zinnel and B. C. Gibb, Guest packing motifs within a supramolecular nanocapsule and a covalent analogue, J. Am. Chem. Soc., 2013, 135, 4314–4324 CrossRef CAS PubMed.
- J. W. Barnett, D. Tang, B. C. Gibb and H. S. Ashbaugh, Alkane guest packing drives switching between multimeric deep-cavity cavitand assembly states, Chem. Commun., 2018, 54, 2639–2642 RSC.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1-2, 19–25 CrossRef.
- S. W. I. Siu, K. Pluhackova and R. A. Bockmann, Optimization of the OPLS-AA force field for long hydrocarbons, J. Chem. Theory Comput., 2012, 8, 1459–1470 CrossRef CAS PubMed.
- J. M. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Phys., 2004, 25, 1157–1174 CAS.
- A. Jakalian, D. B. Jack and C. I. Bayly, Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation, J. Comput. Chem., 2002, 23, 1623–1641 CrossRef CAS PubMed.
- J. Ewell, B. C. Gibb and S. W. Rick, Water inside a hydrophobic cavitand molecule, J. Phys. Chem. B., 2008, 112, 10272–10279 CrossRef CAS PubMed.
- H. W. Horn, W. C. Swope, J. W. Pitera, J. D. Madura, T. J. Dick, G. L. Hura and T. Head-Gordon, Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew, J. Chem. Phys., 2004, 120, 9665–9678 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, Particle mesh Ewald - An N.log(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- S. Nosé, A unified formulation of the constant temperature molecular-dynamics methods, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Canonical dynamics - Equilibrium phase-space distributions, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef.
- M. Parrinello and A. Rahman, Polymorphic transitions in single-crystals - A new molecular-dynamics method, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. Fraaije, LINCS: A linear constraint solver for molecular simulations, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- S. Miyamoto and P. A. Kollman, SETTLE - An analytical version of the shake and rattle algorithm for rigid water models, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS.
- G. M. Torrie and J. P. Valleau, Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- S. Kumar, D. Bouzida, R. H. Swendsen, P. A. Kollman and J. M. Rosenberg, The weighted histogram analysis method for free-energy calculation on biomolecules. 1. The method, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- H. B. Luo and K. Sharp, On the calculation of absolute macromolecular binding free energies, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 10399–10404 CrossRef CAS.
- H. J. Woo and B. Roux, Calculation of absolute protein-ligand binding free energy from computer simulations, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6825–6830 CrossRef CAS PubMed.
- B. Widom, Potential-distribution theory and the statistical mechanics of fluids, J Phys Chem, 1982, 86, 869–872 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Full derivation of eqn (3); dummy atom placement to align cavitands and guests along their reaction coordinate; GROMACS topology files for simulating hosts 0–4. See DOI: 10.1039/c9me00076c |
| This journal is © The Royal Society of Chemistry 2020 |