Differences in the morphology and vibrational dynamics of crystalline, glassy and amorphous silica – commercial implications

Abstract

Quartz, bentonite, sodium silicate, precipitated and pyrogenic synthetic amorphous silica (SAS) were compared using high-resolution transmission electron microscopy and neutron vibrational spectroscopy. These materials span the full gamut of structures of silica: crystalline, disordered crystalline, glassy and completely amorphous respectively. Traces of water, together with the silanol groups, are of paramount importance for commercial applications, particularly the catalytic influence on the reaction kinetics of surface silanisation of SAS in tyre technology. The reaction of a bifunctional silane, (bis(3-triethoxysilylpropyl)-tetrasulfide), with precipitated silica eliminates accessible surface-silanol groups to improve SAS/polymer interaction and removes traces of water. The degree of reaction of ethoxy-functions was quantified. The removal of reactive protons by the silanisation reaction is even more effective than drying of SAS at 120 °C, however, residual traces of isolated silanols were detected in the interior structure of SAS, even after silanisation or high temperature (750 °C) drying. Some minor residual translational periodicity present in the bulk piece of amorphous solid water glass is completely missing in amorphous SAS powders.

---

1. Introduction

Synthetic amorphous silicas (SAS) are widely used on an industrial scale. They are produced via water glass by wet precipitation processes or by the controlled high temperature hydrolysis of silicon chlorides in hydrogen/oxygen flames.^1,2 These finely divided materials are widely used in free-flow regulation, anti-caking of numerous products, as a thickening agent, for thermal insulation and as reinforcing filler materials for lacquers and paints, various polymers, silicon rubber (pyrogenic SAS) and many other applications. Precipitated silicas have become the most important white reinforcing fillers for the rubber industry.^1b

A major application of precipitated SAS in the rubber industry is for ‘green tyre’ technology, where the tread compound contains grades of silica that are surface-modified by sulphur-containing organosilanes to simultaneously improve the tyre tread abrasion resistance, to lower the rolling resistance but also to improve the wet skid behaviour, all of which translates into better long term performance, fuel economy and safety.

The major difference between these SAS and many of the silica minerals that are encountered in nature is that they are completely X-ray amorphous and show only short range order effects in the range 0.8–1.2 nm.^3–7 In previous work,⁸ we have used inelastic incoherent neutron scattering (IINS) to follow the variations of the vibrational density of states of amorphous and crystalline silicas, and changes in the spectra of pyrogenic SAS after different post-treatments including wetting, pelletisation and calcination, in the production of high purity catalyst supports. High resolution transmission electron microscopy (HR-TEM) and, especially, electron tomography,⁹ together with 3D-TEM,^9–11 have been shown to be well-suited to complement the information on amorphicity from X-ray diffraction data by direct imaging of the nano-structure. The short range geometry, down to the molecular scale of two-dimensional mono-/bi-layers, of amorphous and crystalline silica and a crystalline/vitreous interface were studied by means of atomic force microscopy (AFM) and evaluated in order of Si–O–Si ring sizes,^12–15 confirming the Zachariasen model.⁵ The relative energies of hydroxylated double silica rings of different geometry were reported.¹³ Electron imaging at varying focus planes by successive small steps in z-direction is able to qualitatively study and compare amorphicity/short range order in SAS.⁹

Owing to the surface area of hydrophilic and hydrophobic SAS being in the range 25–700 m² g⁻¹, the adsorption properties are of major relevance. An important parameter is the silanol group density and the specific interaction with water in precipitated SAS. For the application of SAS as a reinforcing agent in tyres, the dispersibility in the polymer matrix has to be adjusted. This can be chemically improved by conversion of the polar silanol groups to non-polar entities by reaction with sulfur-containing bifunctional silanes. These also contribute to the vulcanisation reaction by cross-linking the silica via the silane to the polymer chains via sulfur bridges. The ca. 4–7% of residual water in dried SAS from the wet-production process is essential to, and has a beneficial catalytic influence on, the reaction kinetics of the silanisation processes. To better understand, how the water and silanols interact and are distributed in the silica, a bulk, non-destructive technique with good sensitivity and selectivity to hydrogen is needed. Previous work on carbon blacks revealed that, because of the very high sensitivity to protons, IINS is particularly suitable for spectroscopic studies on the hydrogen bonding of strongly adsorbed water at the surface and even inside micropores of finely divided, post-oxidized, electrically conductive gas blacks.¹⁶ Disordered water in confined geometry of strongly oxidized gas blacks can be discriminated from ordered water structures at the outer surfaces of these materials by the position of the leading edge of the intermolecular librational modes of condensed water in the ice-like state (as measured by IINS at T < 20 K).¹⁷

The sensitivity of IINS¹⁸ to hydrogen arises from the dependence of the measured intensity on the incoherent cross section of the scattering atom. For ¹H, this is almost an order of magnitude larger than for any other atom of interest (C, O, Si). This means that it is possible to observe the entire 0–4000 cm⁻¹ range and allows the low energy silanol deformations and water librations to be detected. This is not usually possible by infrared spectroscopy because of the intense absorption by the silica. Methyl torsions are rarely detected by infrared or Raman spectroscopy; with IINS they are often the strongest bands in the spectrum. IINS is also sensitive to all wavevectors (k, Å⁻¹), thus allows a complete vibrational density of states to be obtained. This is in contrast to infrared and Raman spectroscopy that only detect modes with k ∼ 0.

Fumed and precipitated SAS as nanostructured materials show different amounts of silanol groups. These may enhance the interactions between moisture either picked up accidentally from ambient air or that is retained from the precipitation/drying process:

Na₂SiO₃ + H₂SO₄ → SiO₂ + Na₂SO₄ + H₂O (1)

It was anticipated that, as in the case of carbon blacks, IINS measurements would allow direct study of the interactions between traces of water and the active sites of precipitated silica. This would include the outer surface and the intergranular volume of silica aggregates and agglomerates as well as trace amounts of trapped water. According to R. K. Iler,^6,7 it is generally agreed that on the smooth, non-porous heat-stabilised amorphous precipitated SAS surface that is fully hydroxylated, there are about 4–5 Si–OH groups per nm² which remain when the sample is dried at 120–150 °C. For pyrogenic SAS only about 1.5 SiOH per nm² are detected, mostly isolated SiOH, since high temperatures are involved in the production process from the hydrogen/oxygen flame:

SiCl₄ + 2H₂ + O₂ → SiO₂ + 4HCl (2)

However, for the topmost atomic layers this value can change with time and storage conditions due to adsorption phenomena.¹

The silanols are also important in a different context: namely for gas storage. Methane hydrate is an enormous energy reserve¹⁹ that is preferentially formed in sandy i.e. siliceous environments.²⁰ Experiments show that conversion to methane hydrate was found to be minimal in solid silica and maximal in hollow silica.²¹ This is presumably a surface area effect: the hollow silica enables more significant hydrogen-bonding interactions with the water. Computational studies of a hydroxylated silica interacting with methane hydrate confirm the crucial role of hydroxyls.²² Molecular dynamics simulations show pore size dependent behaviour of methane in montmorillonite, which is used as a model for shale.²³

2. Experimental

2.1 Materials

Quartz sand (Nivelstein, Herzogenrath, Germany, sieve fraction, Fig. 1a and b) SiO₂ content 99.77%, containing only traces of Al. The bentonite clay (Clariant, Germany) was a pure grade for catalyst support purposes. A bulk piece (100 g) of glass-like solid sodium silicate with a high alkaline element content was chosen for comparison (SiO₂ > 75.0 mass%, Na₂O > 22.4 mass%, measured by potentiometric titration). The total hydrogen content was 220 ppm (0.022%). For the topmost atomic layers X-ray photoelectron spectroscopy (XPS) revealed the presence of some surface-shielding of the silicate by enrichment with Na₂O, surface carbonate (289.2 eV, C 1s) and humidity/surface hydroxide (ca. 17% of the surface-oxygen, ca. 535 eV, O 2p) by partial surface-hydrolysis of this hygroscopic alkaline material. Commercial quality SAS of Evonik Industries were used: dry pyrogenic Aerosil® and precipitated ULTRASIL® grades. Table 1 summarizes results from surface-related characterisation of three different ULTRASIL® grades. The values illustrate that typical rubber technology grades of SAS are used in this study. A COUPSIL® powder sample, Silica I, surface-modified by silanisation treatment with the bifunctional silane Si 69®, was also studied. The pure silane reference was prepared as a liquid in a Viton-sealed square-shaped Al-sample holder, shock-frozen and measured as a macroscopic plan-parallel sheet of solid matter (14.2 g sample). Two commercial hydrophobic SAS products based on Aerosil®200, after silanisation with dimethyldichlorosilane and octylsilane were also investigated. For comparison, pure polydimethylsiloxane (PDMS) was also measured.

Fig. 1 Light microscopy survey images of the sequence: quartz crystals → bulk sodium silicate piece → finely divided precipitated SAS powder, dried (105 °C). (a) Quartz sand particles, crystalline as indicated by (b) polarization contrast imaging, (c) solid sodium silicate as obtained from crystalline quartz by alkaline-treatment and (d) finely divided, amorphous silica powder (SAS) obtained by precipitation from liquid sodium silicate solution, after elution, drying via chamber filter press and finely ground.

Table 1 Analytical parameters of precipitated SAS: physical and chemical surface area and weight loss at standard testing treatment at 105 °C

	Silica I	Silica II	Silica III	Aerosil®
a BET: Brunauer/Emmett/Teller physical surface area. Polymer-related surface parameters. b DBP dibutyl phthalate adsorption. c CTAB cetyl-trimethylammonium-bromide adsorption. d Sears number (titration of silanols with NaOH).
BET surface area^a/(m^2 g^−1)	166	168	178	210
pH-value	6.6	6.6	6.6	4.2
DBP water free^b/(g (100 g)^−1)	239	224	212
CTAB surface area ASTM D 3765^c/(m^2 g^−1)	160	164	171
Sears V2^d/(ml (5 g)^−1)	15.6	19.7	26.4
Volatiles (2 h at 105 °C)/(wt%)	3.9	4.9	5.8

---

2.2 Methods

2.2.1 High-resolution-transmission electron microscopy HR-TEM. Compact SiO₂ particles were carefully fractioned and small pieces were transferred onto standard TEM-sample holders (200 mesh copper grids, coated with Holey carbon foil). Using a precision tilt sample manipulator in the TEM column electron-transparent areas of such entities were characterized. The aggregates of pyrogenic and precipitated SAS⁹ were dispersed in isopropanol/water, treated in an ultrasonic bath together with energy input by an ultrasonic finger (sonotrode) for three minutes and afterwards transferred onto Holey carbon foil using an Eppendorf pipette. A Jeol 2010F HR-TEM was operated at 200 keV primary electron beam energy. The quality, stability and calibration of the field emission TEM system were maintained by the use of the Magical No. 641 standard (Norrox Scientific Ltd, Beaver Pond, Ontario, Canada). HR-TEM images were taken by measuring electron-transparent ultrathin regions of fragments of crystalline, partly amorphous and glass-like bulky silica and of very finely divided aggregates of SAS at the nanoscale on Holey carbon foil.

2.2.2 Inelastic incoherent neutron scattering (IINS), infrared and Raman spectroscopy. IINS spectra were recorded using the TOSCA,²⁴ MARI²⁵ and MAPS²⁶ spectrometers at the spallation neutron source ISIS of the STFC Rutherford Appleton Laboratory, Chilton, U.K. TOSCA is complementary to MARI and MAPS. As explained in detail elsewhere,²⁶ TOSCA is optimum for the 0–1600 cm⁻¹, while MARI and MAPS provide access to the region above 2000 cm⁻¹, which allows observation of the crucial O–H stretch modes. The samples were sealed into thin-walled aluminium cans (wall thickness <0.5 mm) and evacuated by a turbomolecular pump at room temperature. Details on cuvette design are given in ref. 27. The highly penetrating nature of neutrons enables information on silica-filled aluminum-cans to be obtained non-destructively from macroscopic samples. Sample weights were: 170 g for the quartz sand, 60 g for the bentonite, 100 g for the single solid piece of sodium silicate, and ca. 20–30 g for the powder type SAS samples. A sample was quenched with liquid nitrogen to 77 K followed by cooling to T < 20 K using a closed cycle helium cryostat. The spectra have been normalised to 1 g SiO₂, thus relative intensities are directly comparable:

For the COUPSIL® sample, the amount of bound Si 69® (estimated as 0.42 g by subtraction of a Si 69® reference spectrum) was first subtracted from the sample weight. Note that the normalization assumes that the samples dried at 750 C are hydrogen-free. We will show later that this assumption is not completely correct for at least one of the samples.

Infrared spectra of the glass-like solid sodium silicate were measured at room temperature using a Bruker Vertex70 FTIR spectrometer, over the range 150 to 4000 cm⁻¹ at 4 cm⁻¹ resolution with a DLaTGS detector using 64 scans and the Bruker Diamond ATR. The use of the ultra-wide range beamsplitter enabled the entire spectral range to be recorded without the need to change beamsplitters. Raman spectra were recorded at 7 K using an upgraded version of a Renishaw InVia spectrometer, that has been previously described.²⁸ The upgrade consists of an additional laser operating at 532 nm and improved laser rejection filters with a low energy cut-off of ∼40 cm⁻¹.

3. Results and discussion

The samples, see Fig. 1, were chosen so as to cover the full range of silica: crystalline, glassy and amorphous. Quartz sand was used as an example of a pure, crystalline silica material, (the IINS spectra of this material have been previously shown⁸). Bentonite as a natural clay-type silicate mineral with a layered structure, containing mostly crystalline but also some disordered structures, was selected to probe for the influence of moderate bulk mismatch. The glass-like solid sodium silicate was used as an example of a glassy, predominantly amorphous silica with only trace amounts of silanols and water. Commercial quality SAS were measured as examples of very finely divided completely amorphous powders consisting of aggregates^1,2,6–10 to compare with dry pyrogenic (Aerosil® 200) and precipitated SAS. Thus Fig. 1 visualizes the evolution of the macromorphology from quartz crystals (digestion by alkaline oxide) over bulky solid sodium silicate glass to a final amorphous precipitated dried pure SAS powder (by removal of sodium and water). TEM results on the characteristic micro- and nanostructure of SAS aggregates are available.⁹

The water and hydroxyl content as a function of temperature is of particular interest. In Table 2 the weight losses are compared: (a) 120 °C (standard: 105 °C) and (b) 750 °C (which is still below an ignition loss test at T > 1000 °C). This includes the removal of water and, partly, of silanol groups by formation of siloxane bonds.^6,7 Some of the SAS samples were also measured after silanisation.

Table 2 Weight loss at different steps of the removal of traces of water

Silica sample	Wt.-loss (wt%)
Silica I original
Silica I 120 °C	−5.57
Silica I 750 °C	−8.36 (total)
Silica II original
Silica II 120 °C	−6.22
Silica II 750 °C	−9.61 (total)
Silica III original
Silica III 120 °C	−5.95
Silica III 750 °C	−9.24 (total)
Silica 1 + 5.4 phf Si 69®	−13.95 (total, 750 °C)

---

3.1 HR-TEM

In Fig. 2 examples of HR-TEM imaging of crystalline and amorphous silica at the nanoscale are compared. The average amplitudes between maximum and minimum brightness (peak/valley) show considerable differences with increasing disorder/amorphicity. Some results of grey scale analysis by digital evaluation of TEM images via line scans (software tool “analysis Add-Inn”, Fa. M. A. S., Freiburg, Germany) are included. Numerical values which were obtained by accumulating the results of 10 line scans per sample from different areas of an image as taken at a certain focus plane are summarized in Table 3. The distance between two adjacent maxima in brightness are determined as a first rough approximation in the qualitative comparison of apparent electron optical differences between crystalline and amorphous silica. Note that this is only a qualitative two-dimensional estimate derived from one single focus plane in imaging electron optical sections of three-dimensional objects (crystallites or amorphous entities). A detailed numerical evaluation as shown for the ideal case of a flat sheet, a two-dimensional bi-layer of vitreous amorphous silica as reported in ref. 13–15 by analyzing AFM-images, and for 2D-models derived from aberration-corrected TEM,²⁹ for the case of three dimensions is out of the scope of this study. This would require further developments in high resolution electron tomography, aberration-corrected TEM and atomic coordinate analysis dedicated to amorphous matter.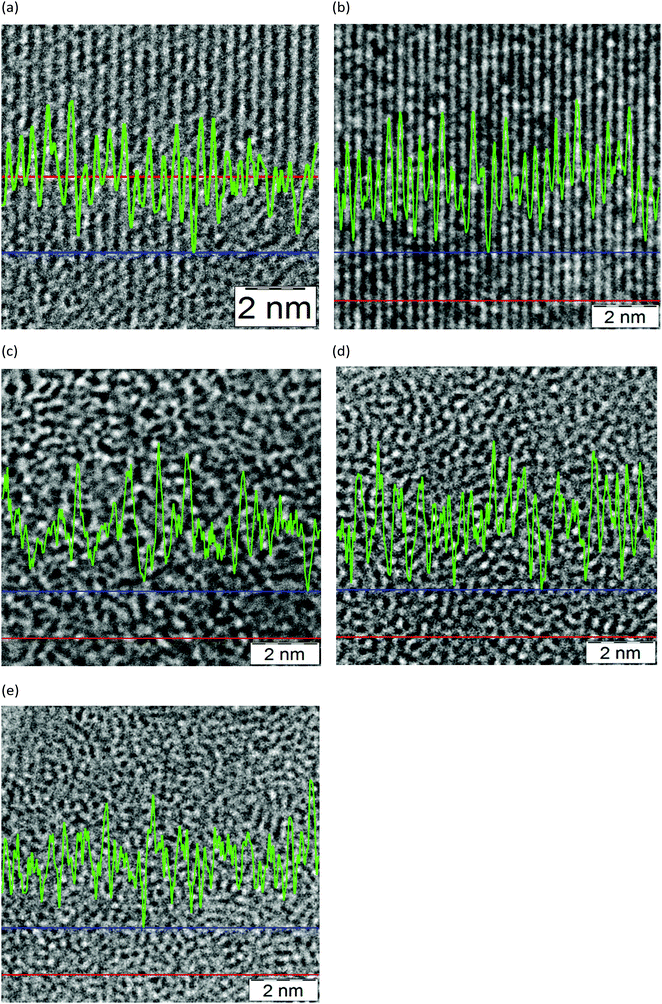

Fig. 2 High resolution TEM images of crystalline (a) and (b) silica, sodium silicate glass (c) and amorphous silica (d) and (e) evaluation by line scan analysis; red: marked position of one single line scan, green: results of grey scale variation, blue: base line. See Table 3.

Table 3 Numerical results from line scan analyses of the grey scale variation in a HR-TEM-image of different silica; distance between two adjacent maxima, average value (nm) accumulated over 10 line scans per sample

Image number (Fig. 2) material	Average distance/nm	Standard deviation/nm
(a) Bentonite	0.22	0.06
(b) Quartz	0.16	0.03
(c) Sodium silicate	0.16	0.05
(d) Precipitated silica	0.15	0.04
(e) Pyrogenic silica	0.14	0.04

---

In Fig. 2 the TEM images of an ordered crystalline lattice are apparent in (a) (bentonite, (220)) and (b) (quartz (211)), whereas (c)–(e) have an amorphous appearance with different fine features and a decrease in average distance (sodium silicate, precipitated and pyrogenic SAS) in the grey scale analysis, Table 3. However, the numerical differences are very small. Considering the bulk chemical composition a tentative interpretation could be: the higher average value for (c) compared to (d) or (e) can be explained by the high sodium oxide content in the network of the sodium silicate (SiO₂ > 75.0 mass%, Na₂O > 22.4 mass%). The change from short range order after about the 3^rd tetrahedral coordination sphere to disorder is reported at ca. 0.8 nm for pyrogenic and 1.2 nm for precipitated material.^1b This is also influenced by significant variability in the Si–O–Si bonding angle (120–180°, maximum 144°) as derived for vitreous silica (random network model) and an Si–O distance close to 0.162 nm.³⁰ For the >99.8% SiO₂ SAS samples (d) and (e), some average contraction of the three-dimensional molecular network of SiO₄-tetrahedra according to Warren³ and Evans and King⁴ and to the Zachariasen⁵ model appears, however, there are some differences in fine-structure and short-range order. A qualitative difference in the nanostructure of (d) and (e) can be explained by varying silanol group densities and traces of residual water on/in the highly dispersed powders from wet-precipitation and high-temperature hydrogen/oxygen flame processes, respectively. This is supported by the IINS results in the next section.

3.2 Inelastic incoherent neutron scattering

3.2.1 Residual water and silanols in precipitated SAS. To probe the properties of traces of water and of silanol groups in 20–30 g quantities of freshly prepared precipitated SAS and their behavior as a function of temperature (although still below the conversion temperatures of amorphous to crystalline silica) three grades were used: Silica I–III. Each SAS was run on TOSCA: as received, after drying at 120 °C and after drying at 750 °C, Table 1 and Fig. 3. The three Silica I samples were also run on MARI, Fig. 4. The different treatments were expected to provide a mixture of adsorbed water and silanols, just silanols and a hydrogen-free reference material, respectively.

Fig. 3 TOSCA IINS spectra of: Silica I (top panel), Silica II (middle panel) and Silica III (bottom panel). In each panel, (a) is the silica “as received”, (b) after drying at 120 °C and (c) after drying at 750 °C. Note the scale factors in the (b) and (c) spectra.

Fig. 4 MARI IINS spectra of Silica I recorded with an incident energy of 5240 cm⁻¹ (top panel) and 2820 cm⁻¹ (bottom panel). In each panel, (a) is the silica “as received”, (b) after drying at 120 °C and (c) after drying at 750 °C.

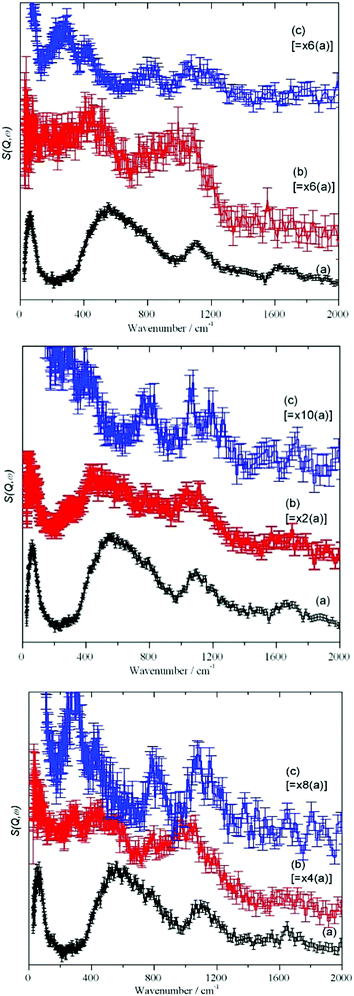
For each stage of the drying process, Fig. 3, the spectra show a remarkable similarity. The as received “original” samples all show bands characteristic of water (65, 540, 1650 cm⁻¹) and hydroxyls (1100 cm⁻¹). After drying at 120 °C, there is a considerable reduction in the integrated intensity (see Table 4 and the scale factors on the figures), however, most of the features still remain. The intensity of the hydroxyl bending mode at 1100 cm⁻¹ has increased relative to that of the water librational modes at 540 cm⁻¹, consistent with removal of water by drying but it is clear that there is still residual water present. With increasing Sears number (indicating silanols, Table 1) the 1100 cm⁻¹ band increases as well. Drying at 750 °C apparently removes all the hydrogenous material and just leaves a spectrum typical of silica.

Table 4 Normalized integrated intensities and assignments for the silica (n.b.: Silica I was measured on both TOSCA and MARI)

Property	Silica I original	Silica I dried 120 °C	Silica I dried 750 °C	Silica II original	Silica II dried 120 °C	Silica II dried 750 °C	Silica III original, GR2BB	Silica III dried 120 °C	Silica III dried 750 °C	COUPSIL (Silica I + Si 69®)
Normalised to 1 g integrated intensity (TOSCA)	123.4	42.5	17.5	118.1	45.9	17.9	123.4	68.1	14.7	31.7
O–H stretch (hydroxyl)/cm^−1	3650	3715	3730
O–H stretch (water)/cm^−1	3462	3471
H–O–H bend/cm^−1	1659	1659		1655			1661
Si–O–H bend (in-plane)/cm^−1	1100	1037	826	1096	1025		1091	1081		1045
H2O librations/cm^−1	550	452		569	432		547	470		615
H2O translations/cm^−1	51	58		56	40		61	51		40
Si–O–H bend (out-of-plane)/cm^−1			268			284
SiO2 modes/cm^−1			788, 1092, 1204			807, 1060, 1148			786, 1085, 1195

---

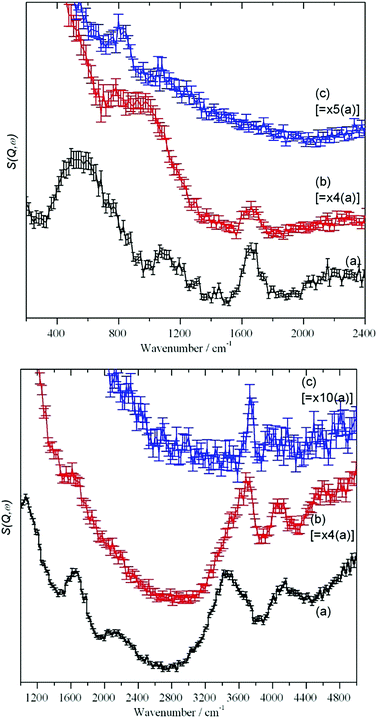
The MARI spectra for the original and 120 °C samples are in agreement with the TOSCA spectra. MARI allows access to the O–H stretch region and a broad stretching band at 3400 cm⁻¹ and a (stretch + libration) combination at 4100 cm⁻¹ are apparent consistent with the presence of water and hydroxyls. On drying there is a loss of intensity at 3400 cm⁻¹ and a band at 3730 cm⁻¹ typical of isolated hydroxyls is discernible. In Fig. 4 (top, (a) and (b)) the water scissors mode at 1650 cm⁻¹ is clearly seen in both spectra. This mode is characteristic of water, so provides unambiguous evidence for the presence of residual water. This band is not apparent in Fig. 3 (top) and this is explained in the ESI.† The dry sample provides a surprise in that a small number of isolated hydroxyls are still present, Fig. 4 (top, (c)). An isolated terminal hydroxyl has three modes: an O–H stretch, and in-plane and out-of-plane Si–O–H bends (torsions). In Fig. 4 (bottom) there is a weak band at 820 cm⁻¹ which is assigned to the in-plane bend. In Fig. 4 (top), there is a very weak feature at 4031 cm⁻¹ which is assigned to the (stretch + out-of-plane bend) combination. This would predict that the out-of-plane Si–O–H bend fundamental is at 290 cm⁻¹ and a band at this energy is apparent in the TOSCA spectrum, Fig. 3 (top, (c)).

The shape of the broad librational water band that extends from 400–1000 cm⁻¹ in Fig. 3 ((a) in top, middle and bottom), is similar to that of the literature data on high density amorphous (HDA) ice,³¹ both having a sloping leading edge with an asymmetric broadening and shift to lower wavenumbers (ca. 430 cm⁻¹), as compared to ice I_h. It follows that the water traces on/in the SAS are disordered^32,33 and increased oxygen–oxygen distances are weakening the hydrogen bonding between water molecules. This can be explained by the influence of silanol groups and distinct differences in the silanol/water and water/water interactions on the precipitated silica. The weakening of the water/water interactions due to the silanol groups explains the catalytic effect and diffusivity of residual traces of water on the kinetics of silanisation: the water molecules associated with the silanol group reaction centers is readily available for the chemical reactions and formation of new covalent Si–O–Si bonds in hydrolysis of the ethoxy-functions in Si 69®, see the following section. This is in agreement with observations on the interaction of single water molecules with silanols in mesoporous silica: it is reported that the hydrogen bond of the water proton with the oxygen of the silanol group is much stronger than the hydrogen bonds of bulk water.³⁴ Also, the impact of surface silanol density and, therefore, the average silanol spacing³⁵ on surface water diffusivity showing a sharp change at 2.0–2.9 nm⁻² is of relevance, together with differences in the pH-values of pyrogenic and precipitated SAS.^1b,36

The result that after drying at 120 °C (standard 105 °C)³⁶ residual water and hydroxyls are still present and even after high temperature drying (750 °C) isolated hydroxyls are detected (Fig. 4) supports the interpretation of differences in the nano-morphology of precipitated and pyrogenic SAS (Fig. 2, TEM-images (d), (e) and Table 3). The corresponding surface-related differences in drying characteristics, pH value,¹ hygroscopic behaviour have been discussed in terms of Sears number.³⁷

3.2.2 Effect of silanisation. Si 69® (bis(3-triethoxysilylpropyl)-tetrasulfide) is a bifunctional compound that is used to improve the dispersion of silica in rubber.³⁸ The thermoxidative stability, ageing properties and service life of the rubber matrix are considerably improved.³⁹ In Fig. 5a the spectrum of the pure silane (sample of 14.2 g) is dominated by the low energy methyl torsional modes of the six ethoxy functions at 265 cm⁻¹ and the rocking mode of these CH₃-groups at 809 cm⁻¹. In the range of 600–1600 cm⁻¹ the CH₂-deformational modes of the ethoxy- and propyl-segments occur (with increasing wavenumber: rocking, wagging, twisting and scissor modes). All these signals are missing on the untreated SAS-sample, Fig. 3 (top). Due to the strong methyl torsion of the ethoxy-groups at 265 cm⁻¹ a semi-quantitative evaluation of the spectrum in Fig. 5b is possible in order to detect residues of non-hydrolysed ethoxy functions in the topmost atomic layers of the very finely divided SAS. We find that for the given macroscopic sample, about 10% of the ethoxy groups are left intact. Usually it is assumed that for steric reasons 4 of the 6 ethoxy functions of the silane react with the silanols at the SAS surface and the water, and that two may be left (Fig. 5, bottom) to react with adjacent functions in process. Contrary to this view, the present result indicates that at the 20 g average, 5.4 ethoxy-groups of the silane were reacted and 0.6 remained unreacted. This underlines the influence of water in catalyzing the surface reactions with the silane and its participation in the hydrolysis of residual silane.

Fig. 5 Top panel: (a) Si 69® (pure compound), (b) Silica I after reaction with Si 69® to give COUPSIL® and (c) COUPSIL® after subtraction of the spectrum of Si 69®. Bottom panel: a sketch of the reacted silane.

Comparison of Fig. 5c and 3 confirms that the reaction with silica removes accessible surface silanol groups and traces of water. From Table 4 and Fig. 5, it can be seen from the normalized integrated intensity that, in total, its effect is even larger than that of drying SAS at 120 C. However, both water and hydroxyls are still present and this supports the idea that there is a population of intra-network traces of −OH and H₂O that is largely inaccessible to chemical agents of significant molecular size. This will contribute to the small differences in appearance of the HR-TEM-images Fig. 2(d) and (e) in at the nanoscale for precipitated as compared to pyrogenic SAS.

As shown elsewhere,⁴⁰ the methyl torsion transition energy is sensitive to both the intra- and intermolecular environment. Table 5 compares the position of the methyl torsion in different chemical surroundings. Additional peak splitting effects observed for the 700–900 cm⁻¹ signals of pure PDMS (ca. 584, 739, 805, 866 cm⁻¹) and of dimethylsilyl on SAS (ca. 720, 760, 833, 875 cm⁻¹) can be explained by the fact that the three protons in the methyl groups are inequivalent as already known for PDMS.⁴¹ This is due to differences in the steric interactions between the methyl protons and the oxygen in the adjacent Si–O–Si structures for the pure molecule and the reacted structures on the SAS aggregates. From the transition energies, it is clear that the methyl groups are still attached to the alkyl chains and not bonded to the silica.

Table 5 Position of the methyl torsional mode

	Functionality	cm^−1
Pure Si 69®	Ethoxy	264
Pure PDMS	Dimethylsiloxane	177
SiO2 reacted with Si 69®	Residual ethoxy	272
SiO2 reacted with dimethyldichlorosilane	Dimethylsilyl	153
SiO2 reacted with octylsilane	Octyl	244

---

3.2.3 Low frequency vibrational dynamics. Complementary to the TEM-results in Fig. 2 and Table 3 the lower energy vibrational dynamics of the samples show distinct differences, Fig. 6. The ideally crystalline quartz sample shows strong sharp bands at 77, (103), 130/shoulder 141 cm⁻¹, and bands or weaker features at ca. 176, 207, 245, 302, 420/458, 544, 616, 802, 954, 1092, 1188 cm⁻¹. The higher energy bands resemble the vibrational modes of HNa-Y-zeolite,^42,43 as previously measured down to 290 cm⁻¹.

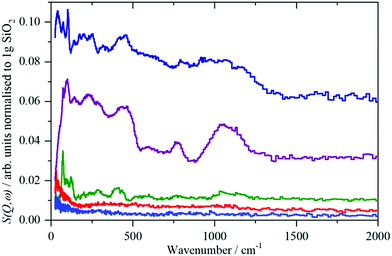Fig. 6 From top to bottom: bentonite, sodium silicate, quartz, precipitated silica, pyrogenic silica; traces green, red and blue taken from ref. 8.

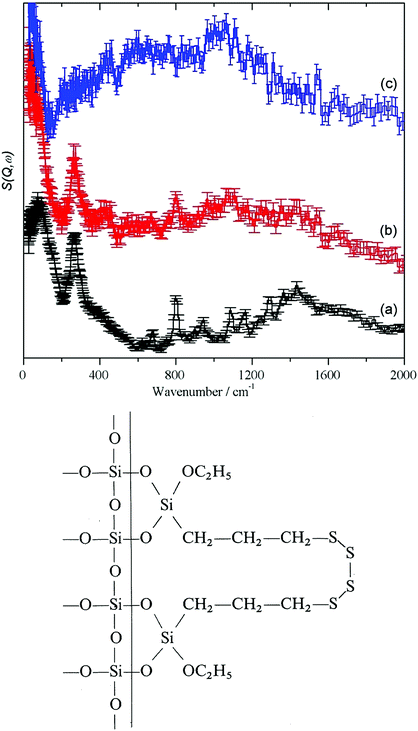
For the crystalline and partly amorphous bentonite sample and the highly alkaline silica glass the dominating 77 cm⁻¹ signal is much lower in relative intensity than the 130 cm⁻¹ signal. An out-of-plane Si–O–H bend mode of Si–OH can be expected at this energy.⁴⁴ However, the hydrogen content of the bulk water glass is very low (220 ppm, Section 2.1), making detection very difficult. Neutron scattering studies of vitreous silica led to the conclusion that bands at about 800–1200 cm⁻¹ are due to Si–O stretching modes and those at 300–400 cm⁻¹ to Si–O bending modes.⁴⁵ With decreasing crystallinity (Fig. 1, 2 and Table 3) the low energy modes are affected by the decrease in long range and short range order.

In the IINS-spectra of the SAS powders these sharp vibrational lines of the crystalline silica are either completely missing or strongly altered by distinct broadening and shifting towards very low energy (<60 cm⁻¹) to form a broad band of low energy translational motions. The IINS spectra now resemble the vibrational density of states previously seen of a vitreous i.e. amorphous silica sample.⁴⁵ From the comparison of the spectra in Fig. 6 and 7, it follows that the three-dimensional network of the SiO₄ units of the fumed and of the precipitated silica is not rigid and ordered enough to accommodate the sharp vibrational modes observed for crystalline silica or as calculated for glass-like SiO₂. According to calculations by Taraskin and Elliot,⁴⁶ the vibrations of the SiO₄ units are expected to be composed of the rocking, bending and stretching contributions of Si–O–Si units in “glass-like”, “vitreous” SiO₂ and comprise a broad but sub-structured vibrational band spreading from about 65–940 cm⁻¹. This comprises of translational and rotational motions of the SiO₄ structural units at the lower end of the range and the T₂ and E O–Si–O bending modes peaking at ∼435 and ∼740 cm⁻¹. A double-structured band at about 1005–1340 cm⁻¹ is assigned to the asymmetric (T₂) and symmetric (A₁) and Si–O stretching modes. The bands centered at about 250, 490, 750 cm⁻¹ and the band extending from ca. 1070–1200 cm⁻¹ in the IINS spectrum of the sodium silicate glass (Fig. 7) are in qualitative agreement with this model of the partial VDOS of the SiO₄ structural units. The infrared and Raman spectra in Fig. 7 show that the E and T₂ O–Si–O bending modes of the SiO₄ structural units are at 430 and 770 cm⁻¹ and the T₂ and A₁ Si–O stretching modes are at 980 and 1100 cm⁻¹. The infrared spectrum also shows a weak O–H stretch mode at 3460 cm⁻¹ with a tail to lower energy. The IINS spectrum in the O–H stretch recorded with MAPS, Fig. 7d, does not show these features as the compact shape (Fig. 1, image (c)) ensures that mostly bulk properties of the silicate are detected by the highly penetrating neutrons. This suggests that the hydroxyls are located on the outer surfaces of the material as indicated by XPS and consistent with the limited penetration depth of infrared radiation with ATR.

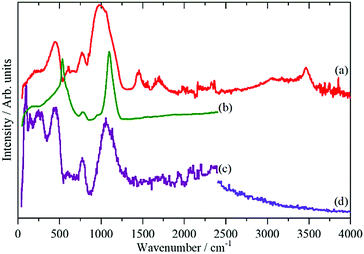Fig. 7 Vibrational spectra of solid sodium silicate: (a) ATR infrared at room temperature, (b) Raman at 8 K using 532 nm excitation, (c) IINS (TOSCA) at 20 K and (d) IINS (MAPS) at 5 K.

Fig. 6 and 7 indicate that some residual translational periodicity^47,48 in the bulk piece of amorphous solid water glass is completely missing in amorphous SAS powders (Fig. 1 image (d) and Fig. 2 TEM (c)–(e)). This leads to further softening of the translational modes of the amorphous Si–O–Si–O molecular network.

It is still a challenge for future work to specify and evaluate a degree of “amorphicity” in bulk solid glasses, “vitreous silica” and highly dispersed, amorphous high purity silica powders of fluffy appearance from varying production technologies in three dimensions, following the work on 2D silica (e.g.ref. 12–14). HR-TEM at the nanoscale, together with spectroscopic evidence from INS on bulk quantities of silica are needed, synergetically, to evaluate differences of nanostructure and low frequency translational dynamics.

3.2.4 Comparison to computational studies. Unsurprisingly, owing to the commercial importance of silicas, the silanol–water interaction has been extensively investigated by computational methods.

Attempts to simulate silicas by using clusters are generally unsuccessful⁴⁹ because of the amorphous nature of the material; small parts of the material are not representative of the totality. This means that large scale simulations are required.^50–54 Simulation of the infrared spectrum in the O–H stretch region⁵² shows the isolated silanol O–H shifting to progressively higher energy as the surface is dehydroxylated. However, the calculated shift is small: 3735 to 3780 cm⁻¹. This is in good agreement with that found here, 3650 to 3730 cm⁻¹ (Fig. 4 (top) and Table 4).

4. Conclusions

Crystalline, disordered crystalline, glassy and completely amorphous silica show differences in the macro- and nanostructure that are visible to optical and electron microscopy. However, they are also expressed in the low frequency vibrational and translational dynamics, as measured by IINS.

The use of IINS enables a coherent picture of the properties and interactions between traces of water and silanol groups to be obtained. Due to the influence of surface silanols a weakening of the hydrogen bonding between the adsorbed water molecules is indicated by enhanced oxygen–oxygen distances and disorder. More isolated water molecules are present which have a positive catalytic influence on the reactivity of the associated silanol groups of SAS with organosilanes. Accessible surface silanol groups and traces of water are reacted. In total, the effect of surface silanisation is even stronger than that of drying SAS at 120 °C. Residual intra-network traces of isolated hydroxyl-groups are left, largely inaccessible to chemical agents of significant molecular size.

As described in the Introduction, SAS have many, and varied, industrial applications: from pharmaceutical additives to reinforcing agents in composites. All of the applications depend on the interaction between the surface of the SAS and the product. The interactions are all mediated by the silanols in some way; either directly via hydrogen-bonding or by providing sites for chemical derivatisation. This work provides new insights into these interactions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Dr Manfred Ettlinger (formerly Degussa AG Hanau, Germany) and Dr Günther Michael are gratefully acknowledged for many helpful discussions on the properties and applied technology of high performance amorphous silicas. André Wehmeier and Dr Jens Kiesewetter, Evonik Resource Efficiency GmbH, D-50389 Wesseling, Germany are thanked for supplying the samples. The workshop team of Evonik Technology & Infrastructure GmbH (Hanau/Wolfgang) is cordially thanked for the manufacture of the thin-walled aluminum cuvettes for handling and measuring large quantities of finely divided silica. The STFC Rutherford Appleton Laboratory is thanked for access to the neutron beam facilities of TOSCA, MARI and MAPS.

References

1. (a) O. W. Flörke, H. Graetsch, F. Brunk, L. Benda, S. Paschen, H. E. Bergna, W. O. Roberts, W. A. Welsh, D. M. Chapman, M. Ettlinger, D. Kerner, M. Maier, W. Meon, R. Schmoll, H. Gies and D. Schiffmann, Ullmann's Encylopedia of Industrial Chemistry, Wiley-VCH, Weinheim, 6th edn, vol. 32, 2003, pp. 273–359; (b) Basic Characteristics of AEROSIL® Fumed Silica, Technical Bulletin Fine Particles Number 11 (Ed. Evonik Industries, Applied Technology AEROSIL®), and literature cited therein; https://www.silica-specialist.com/product/aerosil/downloads/technical-overview-aerosil-fumed-silica-en.pdf.
2. E. F. Vansant, P. Van Der Voort and K. C. Vranken, Characterization and chemical modification of the silica surface, in Studies in Surface Science and Catalysis, ed. B. Delmon and J. T. Yates, Elsevier, Amsterdam, vol. 93, 1995.
3. B. E. Warren, Fiz. Krist., 1933, 86, 349.
4. L. D. Evans and S. V. King, Nature, 1966, 212, 1353.
5. W. H. Zarachiasen, J. Am. Chem. Soc., 1932, 54, 3841.
6. R. K. Iler, The Colloid Chemistry of Silica and Silicates, Cornell University Press, USA, 1955.
7. R. K. Iler, The Chemistry of Silica, Wiley, New York, USA, 1979.
8. P. W. Albers, G. Michael, H. Lansink Rotgerink, M. Reisinger and S. F. Parker, Z. Naturforsch., 2012, 67b, 1016.
9. P. Albers, M. Maier, M. Reisinger, B. Hannebauer and R. Weinand, Cryst. Res. Technol., 2015, 50, 846–865.
10. E. A. F. Van Doren, P.-J. R. H. De Temmerman, M. A. D. Francisco and J. Mast, J. Nanobiotechnol., 2011, 9, 17.
11. T. Altantzis, B. Goris, A. Sánchez-Iglesias, M. Grzelczak, L. M. Liz-Marzán and S. Bals, Part. Part. Syst. Charact., 2013, 30, 84.
12. C. Büchner, L. Lichtenstein and M. Heyde, Nachr. Chem., 2012, 60, 861.
13. L. Lichtenstein, C. Büchner, B. Yang, S. Shaikutdinov, M. Heyde, M. Sierka, R. Wloddarczyk, J. Sauer and H.-J. Freund, Angew. Chem., Int. Ed., 2012, 51, 404.
14. L. Lichtenstein, M. Heyde and H.-J. Freund, Phys. Rev. Lett., 2012, 109, 106101.
15. L. Lichtenstein, M. Heyde and H.-J. Freund, J. Phys. Chem. C, 2012, 116, 20426–20432.
16. P. Albers, A. Karl, J. Mathias, D. K. Ross and S. F. Parker, Carbon, 2001, 39, 1663–1676.
17. J.-C. Li, J. D. London, D. K. Ross, J. L. Finney, J. Tomkinson and W. F. Sherman, J. Chem. Phys., 1991, 94, 6770.
18. P. C. H. Mitchell, S. F. Parker, A. J. Ramirez-Cuesta and J. Tomkinson, Vibrational spectroscopy with neutrons, with applications in chemistry, biology, materials science and catalysis, World Scientific, Singapore, 2005.
19. Z. R. Chong, S. H. B. Yanga, P. Babua, P. Linga and X.-S. Li, Appl. Energy, 2016, 162, 1633–1652.
20. M. Riedel, T. Collet, M. Malone, F. Akiba, M. Blanc-Valleron, M. Ellis, G. Guerin, Y. Hashimoto, V. Heuer, Y. Higashi, M. Holland, P. Jackson, M. Kaneko, M. Kastner, J.-H. Kim, H. Kitajima, P. Long, A. Malinverno, G. Myers, L. Palekar, J. Pohlman, P. Schultheiss, B. Teichert, M. Torres, A. Tréhu, J. Wang, U. Wortmann and H. Yoshioka, Trans., Am. Geophys. Union, 2006, 87, 325.
21. V. D. Chari, P. S. R. Prasad and S. R. Murthy, Oil Gas Sci. Technol., 2015, 70, 1125–1132.
22. S. A. Bagherzadeh, P. Englezos, S. Alavi and J. A. Ripmeester, J. Phys. Chem. B, 2012, 116, 3188–3197.
23. C. Chen, W. Hu, J. Sun, W. Lia and Y. Song, Int. J. Heat Mass Transfer, 2019, 141, 367–378.
24. S. F. Parker, F. Fernandez-Alonso, A. J. Ramirez-Cuesta, J. Tomkinson, S. Rudić, R. S. Pinna, G. Gorini and J. Fernández Castañon, J. Phys.: Conf. Ser., 2014, 554, 012003.
25. M. Arai, A. D. Taylor, S. M. Bennington and Z. A. Bowden, in Recent Developments in the Physics of Fluids, ed. W. S. Howells and A. K. Soper, Adam Hilger, 1992, p. 291.
26. S. F. Parker, D. Lennon and P. W. Albers, Appl. Spectrosc., 2011, 65, 1325.
27. P. W. Albers, D. Lennon and S. F. Parker, in Neutron Scattering: Applications in Chemistry, Materials Science, and Biology, Experimental Methods in the Physical Sciences, Neutron Scattering, ed. F. Fernandez-Alonso and D. L. Price, Academic Press, vol. 49, 2017, p. 285.
28. M. A. Adams, S. F. Parker, F. Fernandez-Alonso, D. J. Cutler, C. Hodges and A. King, Appl. Spectrosc., 2009, 63, 727–732.
29. P. Y. Huang, S. Kurasch, J. S. Alden, A. Shekhawat, A. A. Alemi, P. L. McEuen, J. P. Sethna, U. Kaiser and D. A. Muller, Science, 2013, 342, 224–227.
30. R. L. Mozzi and B. E. Warren, J. Appl. Crystallogr., 1969, 2, 164.
31. A. I. Kolesnikov, J.-C. Li, S. F. Parker, R. S. Eccleston and C.-K. Loong, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 3569–3578.
32. J.-C. Li, J. Chem. Phys., 1996, 105, 6733–6755.
33. J.-C. Li and A. I. Kolesnikov, J. Mol. Liq., 2002, 100, 1–39.
34. C. Pantalei, R. Senesi, C. Andreani, P. Sozziani, A. Comotti, S. Bracco, M. Beretta, P. E. Sokol and G. Reiter, Phys. Chem. Chem. Phys., 2011, 13, 6022–6028.
35. A. M. Schrader, J. I. Monroe, R. Shell, H. A. Dobbs, T. J. Keller, Y. Li, S. Jain, M. Scott Shell, J. N. Israelachvili and S. Han, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 2890–2895.
36. https://www.silica-specialist.com/product/aerosil/downloads/ib-279-precipitated-silica-for-the-rubber-industry-en.pdf .
37. F. Heinroth, R. Münnekhoff, C. Panz, R. Schmoll, J. Behnisch and P. Behrens, Microporous Mesoporous Mater., 2008, 116, 95–100.
38. https://www.silica-specialist.com/en/products/search-products/pages/product-details.aspx?productId=47655; https://www.silica-specialist.com/product/aerosil/downloads/silica-silan-system-for-the-rubber-industry-en.pdf.
39. A. Adhikary, R. Mukhopadhyay and A. S. Deuri, J. Mater. Sci., 1995, 30, 4112.
40. A. Zachariou, A. P. Hawkins, P. Collier, R. F. Howe, D. Lennon and S. F. Parker, ACS Omega, 2020, 5, 2755–2765.
41. A. P. Hard, S. F. Parker and U. A. Jayasooriya, Appl. Spectrosc., 2007, 61, 314–320.
42. H. Jobic, J. Catal., 1991, 131, 289–293.
43. W. P. J. H. Jacobs, J. H. M. C. Wolput, R. A. van Santen and H. Jobic, Zeolites, 1994, 14, 117–125.
44. B. A. Morrow and A. J. McFarlan, J. Phys. Chem., 1992, 96, 1395–1400.
45. M. Arai, A. C. Hannon, A. D. Taylor, T. Otomo, A. C. Wright, R. N. Sinclair and D. L. Price, Trans. Am. Crystallogr. Assoc., 1991, 27, 113–131.
46. S. N. Taraskin and S. R. Elliot, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 8605–8622.
47. W. A. Weyl and E. C. Marboe, J. Soc. Glass Technol., 1959, 43, 191.
48. B. Friede, W. Hoffbauer, M. Jansen, K. Schulmeister, W. Assenmacher and W. Mader, Z. Anorg. Allg. Chem., 2000, 626, 2269.
49. V. D. Khavryuchenko, O. V. Khavryuchenko and V. V. Lisnyak, Mol. Simul., 2007, 33, 531–540.
50. T. Bakos, S. N. Rashkeev and S. T. Pantelides, Phys. Rev. Lett., 2002, 88, 055508.
51. M. Sulpizi, M.-P. Gaigeot and M. Sprik, J. Chem. Theory Comput., 2012, 8, 1037–1047.
52. A. Comas-Vives, Phys. Chem. Chem. Phys., 2016, 18, 7475–7482.
53. S. A. Bagherzadeh, P. Englezos, S. Alavi and J. A. Ripmeester, J. Phys. Chem. B, 2012, 116, 3188–3197.
54. C. Chen, W. Hu, J. Sun, W. Li and Y. Song, Int. J. Heat Mass Transfer, 2019, 141, 367–378.

---

Footnote

† Electronic supplementary information (ESI) available: Explanation of the differences between Fig. S3 and S4. See DOI: 10.1039/d0ma00158a

---