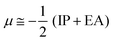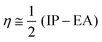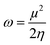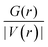DOI:
10.1039/D0MA00018C
(Paper)
Mater. Adv., 2020,
1, 1909-1919
In the search of active nanocarriers for delivery of mitomycin C drug†
Received
10th February 2020
, Accepted 21st July 2020
First published on 18th August 2020
Abstract
Recently, the application of nanomaterials in medicine and more specifically controlled drug delivery systems has been spreading rapidly. The present study provides a theoretical investigation on the application of chitosan (CS), poly-caprolactone (PCL), carbon nanotubes (CNTs), and boron nitride nanotubes (BNNTs) as potential nanocarriers for the delivery of mitomycin C (MMC) drug. First, the chemical reactivities of these carriers are evaluated by the use of global and local reactivity descriptors. Then, the obtained reactivity pattern is evaluated by the explicit adsorption of MMC over each carrier. The calculated enthalpy and Gibbs free energies indicate that the MMC adsorptions over all examined carriers are exothermic and spontaneous. However, it is found that the polymeric carriers can load the MMC drug more effectively than the nanotubes. Analyzing the adsorption mechanism for different carriers reveals that the interaction between MMC and polymeric carriers occurs just through hydrogen bonding, while in the case of nanotubes, the π–π stacking has a cooperative effect. To determine how much the interactions between the MMC drug and carriers are medium-dependent, we have also calculated the adsorption in aqueous solution and evaluated the impact of solvation on the adsorption strength.
1. Introduction
The advances in nanoscience, on the one side, and the progress in computational methods, on the other side, have led to a route toward rational design of improved nanomaterials for biomedical applications. In particular, nanoparticles represent unique physicochemical and biological properties such as small size, large specific surface, enhanced reactive area, and good biocompatibility that make them favorable materials for drug delivery applications.1,2 These properties enable nanoparticles to bind, adsorb and carry the drug to the target tissue. The drug delivery system reduces undesirable side effects and protects the drug from fast degradation. Different types of nanoparticles have been applied so far for the targeted delivery, such as polymeric nanoparticles (PNPs),3 nanotubes (NTs),4,5 liposomes,6 and quantum dots.7,8 Among these, polymer-based and carbon allotropes including graphene and carbon nanotubes (CNTs) have attracted more attention. PNPs can be obtained from synthetic polymers, such as poly-caprolactone,9 poly-acrylate,10 and poly-acrylamide11 or natural polymers such as albumin,12 gelatin,13 and chitosan.14 PNPs can be utilized to supply controlled release profiles or they can be combined with ligands for targeted drug delivery. On the other hand, the well-ordered molecular structure brings CNTs high surface area and excellent mechanic strength and renders them effective for drug carrier systems. Like CNTs, boron nitride nanotubes (BNNTs) exhibit good chemical and thermal stability, excellent oxidation resistance, and high biocompatibility for different biomedical applications.15,16
There are many experimental and theoretical investigations on the application of PNPs and NTs in drug delivery systems.17–20 In the context of computational studies, Hong et al. explored the capability of CNTs and BNNTs as delivery vehicles of efavirenz (EFV), an antiretroviral medication, by density functional theory (DFT) calculations.21 They found that the π–π stacking interaction of EFV with CNTs is larger than that on BNNTs, which explains the stronger interaction of EFV on the CNTs. In another theoretical study, the application of boron nitride oxide nanosheets as potential carriers for the delivery of doxorubicin (DOX) as an anticancer drug has been investigated by DFT and molecular dynamic (MD) simulation methods.22 Moreover, Eslami et al. performed MD calculations to explore the compatibility of poly(n-butylcyanoacrylate) and chitosan polymers with different degrees of polymerization versus a tacrine unit as the most well-known drug for the treatment of Alzheimer's disease.23 In another attempt, the adsorption of curcumin anticancer drug on montmorillonite nanoparticles in the presence of poly(lactic-co-glycolic acid) (PLGA) has been systematically studied.24 It was found that the inclusion of clay minerals into the PLGA containing nanoparticles enhances the interaction of drugs and the release control. Furthermore, the application of graphene quantum dots and their doped structures has been investigated as potential carriers for the delivery of isoniazid drug.25
In the context of designing delivery system, the present research has been conducted to study potential candidates for the delivery of mitomycin C (MMC) drug. MMC is a chemotherapy drug used to treat different cancers such as bladder, breast, stomach, pancreas, lung, and liver cancers.26 In the case of bladder cancer, the therapeutic effect is limited by the periodical voiding of urine that washes out the drug and reduces its residence time in the bladder. To overcome this problem, frequent treatments with repeated catheterizations are required, leading in many cases to irritation during voiding, bladder fibrosis, and infections.27,28 Hence, developing a suitable drug delivery system that provides prolonged contact between the MMC drug and the bladder tissues is of vital importance. Bilensoy et al. have designed cationic nanoparticles of chitosan (CS), poly caprolactone (PCL) attached to chitosan, and poly-lysine coated poly-caprolactone for the delivery of MMC. They found that coating PCL with bioadhesive polymer CS results in promising drug loading and release profiles.29 In another study, a novel formulation of phytosomes was developed as an effective system for MMC drug delivery and cancer therapy.30 Sun et al. introduced an in situ forming depot consisting of CS, β-glycerophosphate, and Fe3O4 magnetic nanoparticles for MMC loading.31 It has also been shown that co-encapsulation of MMC and DOX anticancer drug within polymer-lipid hybrid nanoparticles leads to a synergetic effect in co-delivery of both drugs to human breast cancer cells.32 Taking inspiration from experimental evidence, in the present study, we explore the mechanistic details to compare the performance of CS, PCL, PCL coated with chitosan (PCL/CS), CNT, and BNNT as potential carriers for delivery of the MMC drug. CS and PCL are selected because of their abundance, biocompatibility, and cost-effectiveness. We have used first-principles calculations to gain insight into the reactivity and site selectivity of the considered carriers toward MMC. The reactivity of the carrier systems has been evaluated using the reactivity descriptors such as chemical hardness and the Fukui function as well as the interaction energy.
2. Computational details
DFT calculations have been performed based on the hybrid generalized gradient approximation (hybrid-GGA) in the M06-2X functional33 and the TZV basis set. All quantum chemical calculations were carried out by the use of the Gaussian 09 package.34 The reliability of the M06-2X density functional has been assessed for reproducing the experimental MMC absorption spectrum. To this end, we have performed time-dependent DFT calculations to obtain the maximum absorption wavelength for MMC. It is found that the predicted λmax by the M06-2X method (335 nm), is in close agreement with its experimental value (350 nm).35 Therefore, the M06-2X/TZV level of theory has been adopted for all calculations. The impact of solvation on the interactions between MMC and carriers has also been explored by employing the polarizable continuum model (PCM) within a water medium.36
The stability of the MMC–carrier complexes has been quantitatively evaluated by calculating the binding energies (Ebind) using the following equation:
| | | Ebind = E(MMC–carrier) − E(MMC) − E(carrier) | (1) |
where
E(MMC),
E(carrier), and
E(MMC–carrier) refer to the total energies of free-standing MMC, carrier, and the MMC–carrier complex, respectively. We found that in some cases, the drug adsorption is accompanied by significant geometrical restructuring of the interacting fragments. Thus, it is necessary to take into account the deformation of the species to describe the interactions correctly. Accordingly, the interaction energy (
Eint) is defined by
where Δ
Edef is the sum of deformation energies of carriers and MMC. For each fragment, the deformation energy is calculated as the difference between the energy of the isolated and deformed fragment in the complex geometries. The basis set superposition error (BSSE) is eliminated by the standard counterpoise correction method of Boys and Bernardi.
37 Frequency calculations have been carried out for all MMC–carrier complexes to assure that they are in their minimum energy structures with no imaginary frequency. The nature of interactions between the carriers and MMC has been scrutinized by means of quantum theory of atoms in molecules (QTAIM).
38
The chemical reactivity of the considered systems are studied by the use of global reactivity descriptors such as chemical potential (μ), chemical hardness (η), and electrophilicity index (ω) which are defined as below,39
| | 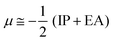 | (3) |
| | 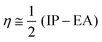 | (4) |
| | 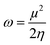 | (5) |
where EA and IP are the ground state electron affinity and ionization potential, respectively. Chemical hardness is a helpful quantity for understanding the global reactivity of molecules. The higher chemical hardness indicates greater stability and less reactivity. Nonetheless, it is more preferred to interpret chemical reactivity in terms of the atoms composing the molecular structure. Accordingly, in order to evaluate the local reactivity at different sites in the considered systems, we have also calculated the atom condensed Fukui function which shows the change in the atomic electron density of an atom with respect to the number of electrons. Applying the finite difference method,
40 the Fukui functions are approximated as
where
ρaN,
ρaN−1, and
ρaN+1 are the atomic charge densities in neutral, cationic, and anionic systems, respectively.
Finally, it should be mentioned that for the case of CS and PCL, we have considered a dimeric model because earlier molecular modeling calculations showed that the dimeric framework can be a well-defined prototype that can reproduce the polymeric properties.41,42 In the case of CNT and BNNT we have considered the zigzag (5,0) configuration because the zigzag orientation is a preferred growth for NTs and the (5,0) tubes have moderate diameters and suitable curvature. Earlier experimental studies indicate that NTs with short length are more suitable to functionalize them for biomedical applications and obtain composites with high mechanical resistance.43,44 Nonetheless, to investigate the effect of NT length on the drug adsorption, we have examined four CNTs with lengths 8.43, 12.72, 16.95, and 21.18 Å which are named CNT-8, CNT-12, CNT-17, and CNT-21, respectively, all over the article. Similarly, four BNNTs with lengths of 8.59, 12.88, 17.17, and 21.47 Å are considered and named BNNT-8, BNNT-12, BNNT-17, and BNNT-21, respectively.
3. Results and discussion
3.1. Electronic structures of the carriers
The optimized structures of the carriers and the MMC drug are displayed in Fig. 1 and the calculated electronic properties and global reactivity indices are collected in Table 1. These results show that, regardless of their length, CNTs have remarkably smaller energy gaps and chemical hardness than other carriers. The energy gap and the chemical hardness of BNNTs are much higher than those of CNTs, however, they still exhibit higher reactivity compared with PNPs. From the perspective of global descriptors, the chemical reactivity of the considered carriers follows the trend: CNTs > BNNTs > CS > PCL. Although the chemical hardness and electrophilicity index give a general picture for the reactivity of the carriers, they do not have the capability to specify the nucleophilic and electrophilic regions in the molecules. In the case of nanotubes, all constituent atoms are equivalent from the perspective of chemical reactivity and there is no preference for local reactivity. On the other hand, the CS and PCL carriers can interact with the MMC through their electrophilic sites (H atoms) or nucleophilic sites (O, N atoms). To evaluate the reactivity of different sites in these carriers, we have calculated the condensed Fukui indices for all reactive sites (Table S1, ESI†). These results indicate that in CS, the condensed nucleophilicity (f−) indices for all O atoms are less than 0.1 and almost in the same order but the N atom of the –NH2 group has a larger f− value (∼0.467) indicating its susceptibility for interaction with electrophilic sites. The condensed electrophilicity (f+) values vary in the range between 0.005 and 0.039 with the highest value for H atoms of –NH2 groups. In the case of PCL, the highest values of f− and f+ belong to the oxygen and hydrogen of the terminal carbonyl groups, respectively.
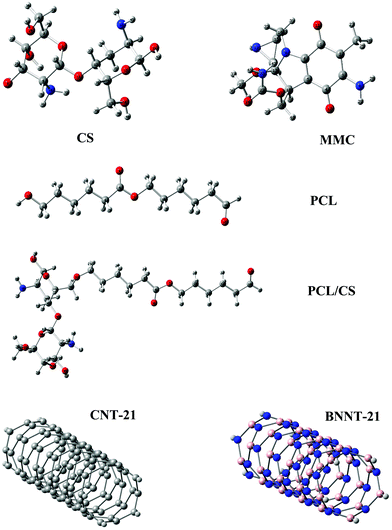 |
| | Fig. 1 Structural representations of the MMC drug and investigated carriers. | |
Table 1 Calculated dipole moment (D, Debye), energies of frontier molecular orbitals (EHOMO, ELUMO, eV), the energy gap (Eg, eV), global hardness (η, eV), and global electrophilicity index (ω, eV) of the studied carriers
| Carrier |
D
|
E
HOMO
|
E
LUMO
|
E
g
|
η
|
ω
|
| CS |
2.09 |
−7.73 |
0.97 |
8.69 |
5.15 |
1.70 |
| PCL |
0.88 |
−9.22 |
0.10 |
9.32 |
5.64 |
1.19 |
| PCL/CS |
1.65 |
−7.95 |
0.09 |
8.04 |
4.97 |
1.41 |
| CNT-8 |
0.00 |
−5.28 |
−2.94 |
2.34 |
1.66 |
5.19 |
| CNT-12 |
0.00 |
−4.45 |
−2.56 |
1.88 |
1.29 |
5.11 |
| CNT-17 |
0.00 |
−4.87 |
−2.77 |
2.09 |
1.05 |
6.98 |
| CNT-21 |
0.03 |
−5.17 |
−2.93 |
2.23 |
1.12 |
7.33 |
| BBNT-8 |
3.80 |
−8.06 |
−1.97 |
6.09 |
3.58 |
3.52 |
| BNNT-12 |
2.00 |
−7.99 |
−2.16 |
5.83 |
3.41 |
3.80 |
| BNNT-17 |
0.07 |
−7.94 |
−2.28 |
5.66 |
2.83 |
4.61 |
| BNNT-21 |
2.47 |
−7.90 |
−2.36 |
5.54 |
2.77 |
4.75 |
Further evidence for the most reactive sites of these carriers can be obtained from the spatial distribution of the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) as presented in Fig. 2. It is observed that the spatial distribution of electron density in the HOMO goes hand in hand with the preferred binding sites as predicted by the Fukui indices. In CS, the HOMO and LUMO are mostly distributed over the carrier molecular backbone with the greater contribution of the –NH2 group in the HOMO. For PCL, the HOMO and LUMO are mainly localized on the terminal carbonyl group. Irrespective of their length, for CNTs the HOMO and LUMO are highly delocalized over the entire tube length, while in BNNTs the edge atoms have greater contribution in spatial distribution of frontier orbitals.
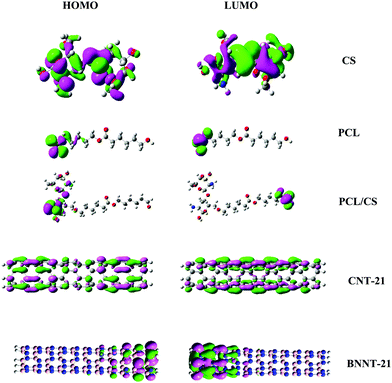 |
| | Fig. 2 Spatial distributions of the HOMO and LUMO for the investigated carriers. | |
3.2. Drug-carrier complexes
After identifying the most reactive sites in the carriers, we turn our attention to validate the anticipated reactivity pattern for the carriers by the explicit adsorption of MMC drug. Due to the existence of oxygen, –OH, and –NH2 groups in the structure of MMC, the drug adsorption on the PNPs occurs through hydrogen bonding. Accordingly, the initial interaction configurations were constructed by aligning the OH or NH of MMC on top or parallel to different adsorption sites of CS, PCL and PCL/CS. Then, for each initial configuration, full geometrical optimizations without any symmetry constraint were performed and after relaxation the most stable complexes were identified by comparing the calculated interaction energies. The stable complexes with the lowest interaction energy values are presented in Fig. 3–7. As shown in Fig. 3, five stable MMC–CS complexes are obtained with the interaction energies in the range from −7.49 to −23.25 kcal mol−1. Similarly, for the adsorption of MMC on the PCL, five stable configurations are found and the interaction energies range between −6.80 and −19.16 kcal mol−1 (Fig. 4). Comparing binding and interaction energies reveals that the deformation energies correlate with the strength of the MMC–carrier interaction and are the largest for the most stable configurations. However, for CS and PCL carriers, the calculated binding and interaction energies are very close implying small geometrical distortion upon the MMC adsorption. Coating PCL with CS reduces reactive sites of CS due to steric hindrance (Fig. 5). In the most stable complex, the MMC has interaction with both CS and PCL leading to interaction energy of −24.47 kcal mol−1 which is more than the most stable MMC–PCL and MMC–CS complexes (Fig. 5). The calculated harmonic frequencies show that all the stable configurations are true stationary points on the potential energy surface with the frequency values being in the range of 13–377 cm−1. For the cases of CNT and BNNT carriers, the MMC is initially placed either above the open ends of the tube or on the outer side of the tubes with different orientations such as OH or NH on top of the carbon atoms in the CNTs, boron and nitrogen in the BNNTs, on the middle of the C–C or B–N bond, and above the center of a hexagonal ring. Furthermore, to model an infinite nanotube length under real conditions, we have performed drug adsorption on nanotubes with different lengths in the range from 8 to 21 Å. The length dependents of the drug interaction energies are shown in Fig. 6 and 7 for CNTs and BNNTs, respectively. As shown in Fig. 6, the adsorption of MMC over CNTs is almost insensitive to the tube length. The calculations show that, after the inclusion of deformation correction, the interaction energies for CNT-8 and CNT-21 differ only by about 1.3 kcal mol−1. This implies that due to delocalization of frontier orbitals over the whole tube length, the nature of interaction between the drug and the CNT is almost independent of the tube length. In contrast, for the BNNT system, considerable deformation energies up to 28.0 kcal mol−1 demonstrate that the drug adsorption is accompanied by the severe geometrical distortion of the BNNTs. An important point to remark is that in BNNTs with short length, the MMC drug tends to adsorb on the tube edge. Increasing the tube length moves the drug toward the middle of the tube and the artificial interaction with the edge atoms disappeared. Hence, a decrease in the deformation energy indicates that for longer tubes the electronic reorganization and structural relaxation can easily take place upon the drug adsorption. For longer tubes, the interaction energies roughly converge and seem to become less sensitive to the tube length. Thus, it can be concluded that CNT-21 and BNNT-21 are long enough to model the drug adsorption over the infinite nanotube in a real system. For this reason, in the rest of the article, we just report the data corresponding to MMC–CNT-21 and MMC–BNNT-21.
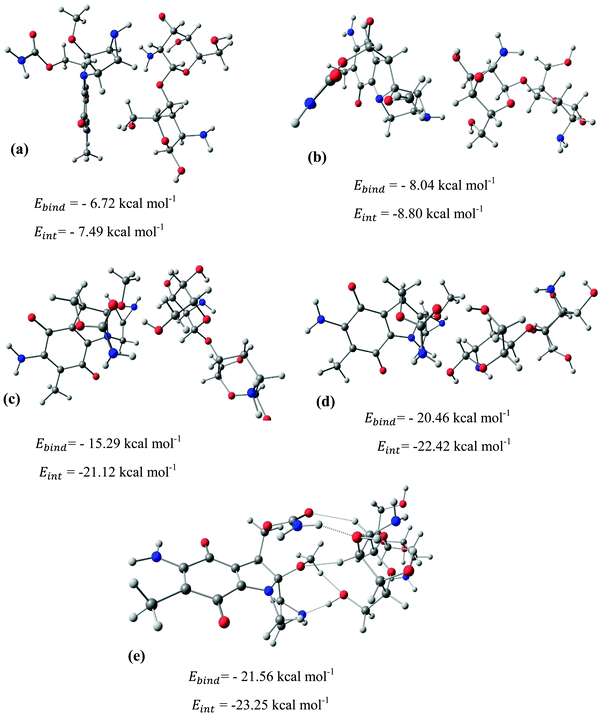 |
| | Fig. 3 Stable configurations for the adsorption of MMC drug over the CS carrier together with corresponding binding and interaction energies. For the most stable configuration, the hydrogen bonding interactions are shown by dotted lines. | |
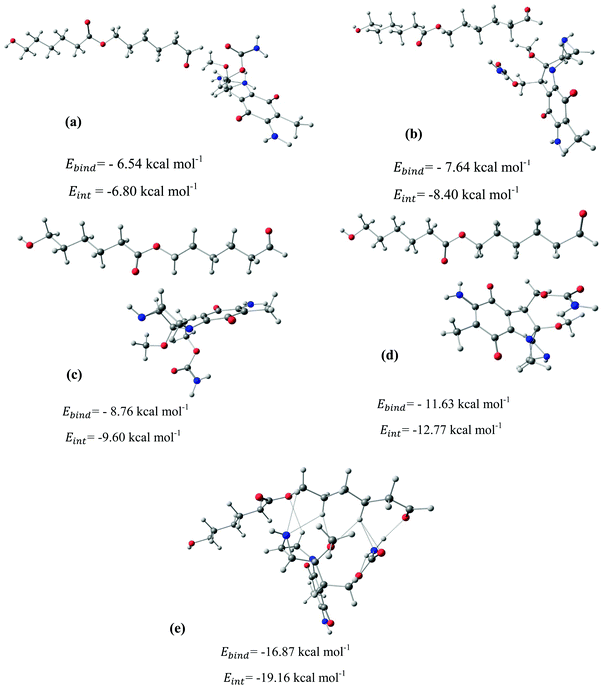 |
| | Fig. 4 Stable configurations for the adsorption of MMC drug over the PCL carrier together with corresponding binding and interaction energies. For the most stable configuration, the hydrogen bonding interactions are shown by dotted lines. | |
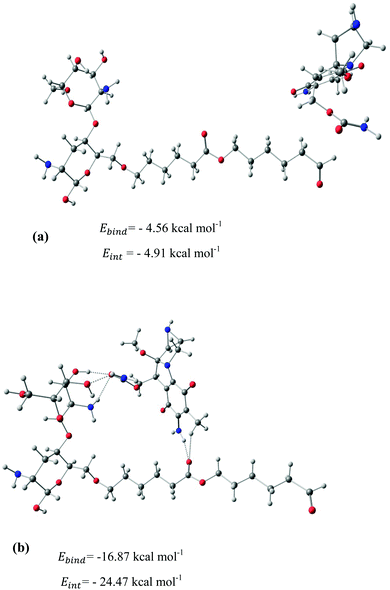 |
| | Fig. 5 Stable configurations for the adsorption of MMC drug over the PCL/CS carrier together with the corresponding binding and interaction energies. For the most stable configuration, the hydrogen bonding interactions are shown by dotted lines. | |
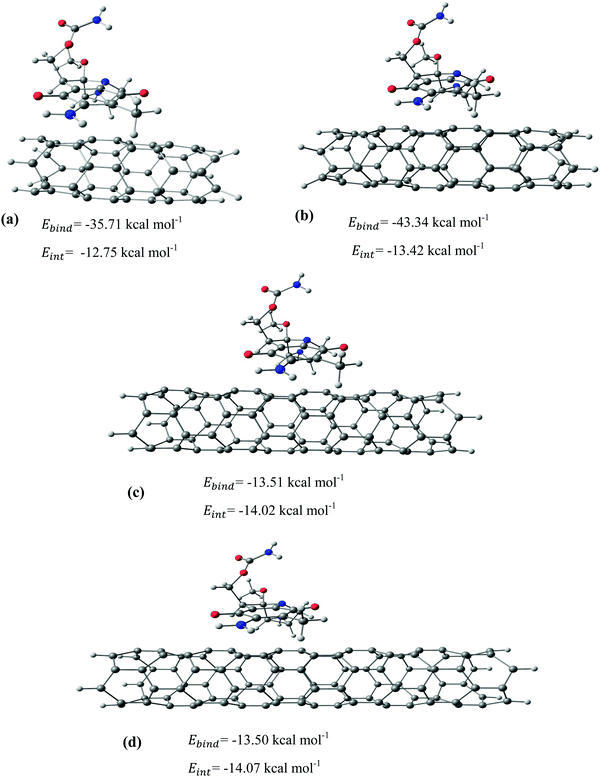 |
| | Fig. 6 The most stable configurations together with the corresponding binding and interaction energies for the adsorption of MMC drug over the (a) CNT-8, (b) CNT-12, (c) CNT-17, and (d) CNT-21. | |
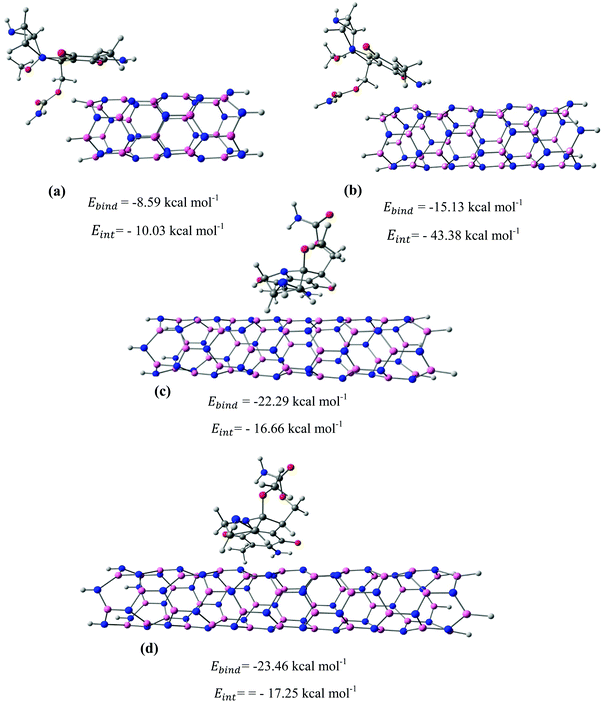 |
| | Fig. 7 The most stable configurations together with the corresponding binding and interaction energies for the adsorption of MMC drug over the (a) BNNT-8, (b) BNNT-12, (c) BNNT-17, and (d) BNNT-21. | |
To assure that the adsorption strength of MMC on the PNPs or NTs is more likely than the interaction between two MMC molecules, we have also carried out the calculations for the interaction between two MMCs (MMC–MMC). All possible orientations are considered and full geometry optimizations are performed. The interaction energies and the optimized structures are given in the ESI.† The results indicate that the MMC–carrier interactions are about 1.0–11.0 kcal mol−1 stronger than MMC–MMC interactions. Thus, in the case of more than a single MMC drug that can be adsorbed on the carriers, the MMCs tend to adsorb on the carriers instead of aggregate.
Table 2 collects the interaction energies and the thermodynamic properties, including the changes in enthalpy (ΔHint) and Gibbs free energy (ΔGint) for the most stable MMC–carrier complexes. Inspection of the results reveals that for the PNPs, the trend in interaction energies is consistent with the obtained pattern for the electrophilicity index. The CS carrier that has greater electrophilicity than PCL exhibits stronger interaction with the MMC drug. Nonetheless, this is not true for the case of NT carriers suggesting that the nature of the interactions between the drug and NTs is different from that of the drug and PNPs. The negative ΔHint values indicate that the adsorption of MMC on these carriers is exothermic. Moreover, the results in Table 2 show that all ΔGint values are negative; hence, the adsorption of MMC drug on the tested carriers is thermodynamically favorable. The highest negative ΔGint belongs to the MMC–CNT complex implying that the MMC drug can be loaded on the surface of CNTs, effectively.
Table 2 Calculated interaction energies in the gas phase and aqueous solution (kcal mol−1), enthalpy changes (kcal mol−1), and Gibbs free energy changes at 298 K (kcal mol−1) for the most stable configurations of MMC adsorption on different carriers
| Complex |
E
int (g) |
E
int (eq.) |
ΔHint |
ΔGint |
| MMC–CS |
−23.25 |
−19.30 |
−21.02 |
−6.86 |
| MMC–PCL |
−19.16 |
−13.05 |
−16.50 |
−1.80 |
| MMC–PCL/CS |
−24.47 |
−17.37 |
−22.69 |
−7.62 |
| MMC–CNT-21 |
−14.07 |
−16.95 |
−12.84 |
−0.77 |
| MMC–BNNT-21 |
−17.25 |
−24.21 |
−15.68 |
−1.23 |
To verify the impact of MMC adsorption on the electronic properties of the carriers, we have collected the electronic properties for the MMC–carrier complexes in Table 3. These results show that the drug adsorption induces a significant increase in the dipole moment relative to the free standing carrier. For example, after the adsorption of MMC on the non-polar CNT-21, the dipole moment of MMC–CNT-21 becomes 6.45 Debye. This increase in the polarity enhances the solubility of the drug-carrier complex in biological matrices. Moreover, the results indicate that, except for CNT-21, for other carriers the HOMO–LUMO gaps undergo considerable reduction after the adsorption of MMC. The amounts of reduction in the Eg values are about 50% for CS and PCL and 13% for BNNT-21. In contrast, upon the MMC adsorption on CNT-21, the energy gap increases by about 2.9 eV. However, the variation in energy gap would be helpful for tracking the drug trajectory by fluorescence imaging. The global hardness for CS, PCL, and BNNT-21 decreases after adsorption of the MMC drug, but an increase is observed in the MMC–CNT-21 complex.
Table 3 The same properties as in Table 1 for the MMC–carrier complexes
| Complex |
D
|
E
HOMO
|
E
LUMO
|
E
g
|
η
|
ω
|
| MMC–CS |
9.86 |
−7.50 |
−2.55 |
4.95 |
3.10 |
4.06 |
| MMC–PCL |
3.42 |
−7.23 |
−2.30 |
4.94 |
3.07 |
3.67 |
| MMC–PCL/CS |
5.47 |
−6.90 |
−2.02 |
4.89 |
3.04 |
3.29 |
| MMC–CNT-21 |
6.45 |
−5.26 |
−0.11 |
5.15 |
2.58 |
1.40 |
| MMC–BNNT-21 |
3.37 |
−7.25 |
−2.34 |
4.91 |
2.45 |
4.68 |
To gain deeper insight into the nature of the interactions between the MMC drug and carriers, we have derived the topological parameters based on the QTAIM approach. The existence of a critical point (CP) in the region between the MMC and the carrier not only permits the establishing of the intermolecular interactions but also helps quantitatively estimate their strength. The molecular graphs for all MMC–carrier systems in their lowest energy configurations are given in the ESI† and the corresponding properties for bond critical points (BCP) and cage critical points (CCP) are reported in Table 4. The considered topological properties include electron density (ρ(r)), the Laplacian of electron density (∇2ρ(r)), the total electron energy density (H(r)), and the ratio of kinetic energy density to potential energy density (G(r)/|V(r)|). Although MMC can be adsorbed over all tested carriers, however, the nature of its interactions is different for various carriers. Topological analysis of electron density identifies the existence of O⋯H and N⋯H hydrogen bonding interactions through bond paths for the MMC–CS, MMC–PCL and MMC–PCL/CS complexes. In a system with a single hydrogen bond, the value of ρ(r) at BCP is correlated with the hydrogen bond strength, while for a complex having multiple hydrogen bonds the sum of electron densities at BCPs (Σρ(r)) can be correlated with the whole stability of the complex. Fig. 8 shows that for MMC–PNP complexes, the Σρ(r) values correlate with the calculated interaction energies. The greatest Σρ(r), 0.1035 a.u., belongs to MMC–PCL/CS which has the highest interaction energy (−24.47 kcal mol−1). As evident from Table 4, all Laplacian values are positive and span in the range of 0.0203–0.1431 a.u., and 0.0230–0.1166 a.u. for O⋯H and N⋯H interactions which are lying within the commonly accepted values of normal hydrogen bonding.38 Positive ∇2ρ(r) indicates the depletion of charge density away from the interatomic surface toward each of the interaction species. More detailed information concerning the nature of interaction can be provided through using the energetic properties at BCPs. Except for three interactions, for the rest, the H(r) values are positive and the G(r)/|V(r)| ratios are greater than unity, which are indicators of non-covalent interactions. For two interactions in MMC–CS and one in MMC–PCL/CS, the negative H(r) goes along with the G(r)/|V(r)| < 1. This implies an enhancement of the covalent character in these interactions, which in turn is responsible for the greater adsorption strength of MMC over the CS and PCL/CS carriers.
Table 4 QTAIM topological parameters at BCPs of interaction contacts in the considered systems (au)
| Complex |
BCP |
R
|
ρ(r) |
∇2ρ(r) |
G(r) |
V(r) |
H(r) |
|
| MMC–CS |
N⋯H |
1.63 |
0.044 |
0.1166 |
0.0353 |
−0.0415 |
−0.0062 |
0.8506 |
| O⋯H |
2.27 |
0.012 |
0.0577 |
0.0121 |
−0.0099 |
0.0023 |
1.2313 |
| O⋯H |
1.96 |
0.033 |
0.1431 |
0.0367 |
−0.0377 |
−0.0009 |
0.9752 |
| O⋯H |
2.63 |
0.0065 |
0.0334 |
0.0066 |
−0.0048 |
0.0018 |
1.3711 |
| O⋯H |
2.55 |
0.0066 |
0.0272 |
0.0052 |
−0.0036 |
0.0016 |
1.4405 |
| MMC–PCL |
N⋯H |
2.68 |
0.0077 |
0.0294 |
0.0060 |
−0.0046 |
0.0014 |
1.2955 |
| N⋯H |
2.83 |
0.0067 |
0.0230 |
0.0046 |
−0.0035 |
0.0011 |
1.3233 |
| N⋯H |
2.71 |
0.0085 |
0.0307 |
0.0065 |
−0.0052 |
0.0012 |
1.2332 |
| O⋯H |
1.93 |
0.0243 |
0.1094 |
0.0250 |
−0.0227 |
0.0023 |
1.1019 |
| O⋯H |
2.57 |
0.0088 |
0.0342 |
0.0069 |
−0.0053 |
0.0016 |
1.2998 |
| O⋯H |
2.76 |
0.0057 |
0.0205 |
0.0041 |
−0.0030 |
0.0011 |
1.3508 |
| O⋯H |
2.37 |
0.0120 |
0.0479 |
0.0098 |
−0.0076 |
0.0022 |
1.2854 |
| O⋯H |
2.55 |
0.0077 |
0.0310 |
0.0062 |
−0.0046 |
0.0016 |
1.3500 |
| MMC–PCL/CS |
O⋯H |
2.79 |
0.0063 |
0.0239 |
0.0047 |
−0.0035 |
0.0012 |
1.3482 |
| O⋯H |
1.90 |
0.0243 |
0.1154 |
0.0264 |
−0.0238 |
0.0025 |
1.1051 |
| O⋯H |
2.28 |
0.0135 |
0.0591 |
0.0121 |
−0.0095 |
0.0026 |
1.2792 |
| O⋯H |
1.82 |
0.0321 |
0.1245 |
0.0319 |
−0.0327 |
−0.0008 |
0.9752 |
| O⋯H |
1.91 |
0.0273 |
0.1229 |
0.0287 |
−0.0267 |
0.0020 |
1.0751 |
| MMC–CNT-21 |
C⋯H |
2.84 |
0.0064 |
0.0211 |
0.0042 |
−0.0032 |
0.0010 |
1.3250 |
| C⋯H |
2.92 |
0.0054 |
0.0167 |
0.0034 |
−0.0025 |
0.0008 |
1.3252 |
| C⋯H |
2.77 |
0.0075 |
0.0246 |
0.0051 |
−0.0042 |
0.0010 |
1.2398 |
| C⋯H |
2.93 |
0.0056 |
0.0171 |
0.0035 |
−0.0026 |
0.0008 |
1.3182 |
| C⋯H |
2.68 |
0.0075 |
0.0243 |
0.0050 |
−0.0040 |
0.0011 |
1.2675 |
| C⋯H |
2.79 |
0.0072 |
0.0218 |
0.0045 |
−0.0035 |
0.0010 |
1.2863 |
| CCP(1) |
— |
0.0023 |
0.0075 |
0.0014 |
−0.0009 |
0.0005 |
1.4968 |
| CCP(2) |
— |
0.0042 |
0.0141 |
0.0028 |
−0.0021 |
0.0007 |
1.3495 |
| CCP(3) |
— |
0.0059 |
0.0205 |
0.0042 |
−0.0032 |
0.0010 |
1.3009 |
| MMC–BNNT-21 |
N⋯O |
3.06 |
0.0090 |
0.0362 |
0.0072 |
−0.0054 |
0.0018 |
1.3430 |
| N⋯H |
3.05 |
0.0049 |
0.0179 |
0.0035 |
−0.0025 |
0.0010 |
1.4114 |
| N⋯H |
2.97 |
0.0050 |
0.0171 |
0.0033 |
−0.0024 |
0.0009 |
1.3941 |
| N⋯H |
2.77 |
0.0072 |
0.0242 |
0.0049 |
−0.0037 |
0.0012 |
1.3123 |
| N⋯H |
3.16 |
0.0048 |
0.0156 |
0.0031 |
−0.0023 |
0.0008 |
1.3313 |
| N⋯H |
3.02 |
0.0048 |
0.0152 |
0.0030 |
−0.0021 |
0.0008 |
1.3877 |
| N⋯H |
2.94 |
0.0051 |
0.0174 |
0.0034 |
−0.0025 |
0.0009 |
1.3788 |
| N⋯H |
2.77 |
0.0078 |
0.0255 |
0.0052 |
−0.0040 |
0.0012 |
1.3007 |
| N⋯H |
2.63 |
0.0097 |
0.0337 |
0.0070 |
−0.0056 |
0.0014 |
1.2563 |
| CCP(1) |
— |
0.0036 |
0.0133 |
0.0026 |
−0.0018 |
0.0007 |
1.4104 |
| CCP(2) |
— |
0.0061 |
0.0206 |
0.0044 |
−0.0037 |
0.0007 |
1.2014 |
| CCP(3) |
— |
0.0032 |
0.0109 |
0.0021 |
−0.0015 |
0.0006 |
1.3947 |
| CCP(4) |
— |
0.0036 |
0.0134 |
0.0026 |
−0.0018 |
0.0008 |
1.4088 |
| CCP(5) |
— |
0.0046 |
0.0164 |
0.0033 |
−0.0025 |
0.0008 |
1.3163 |
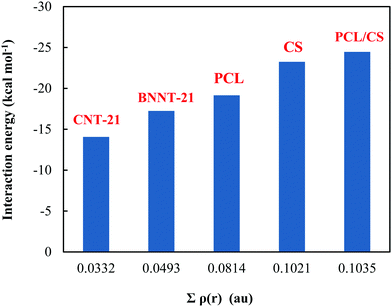 |
| | Fig. 8 Plot of interaction energy versus the sum of electron densities for MMC–carrier complexes. | |
In contrast to PNPs, no strong bonding interaction occurs for the case of MMC adsorption on the CNTs. There are six C⋯H BCPs in the region between MMC and the CNT-21 surface associated with the interaction between carbon atoms of the CNTs and hydrogens of MMC. The sum of electron densities at these BCPs (Σρ(r) = 0.0332 a.u.) is much smaller than those we obtained for normal hydrogen bonds. Topological analysis of the electron density further confirms the presence of π–π interactions in the MMC–CNT-21. To be specific, for MMC–CNT-21 the π–π interaction has been evidenced by the presence of CCP which is a typical feature of stacking interaction. The electron density and its Laplacian at the CCPs are helpful for determining and evaluating the strength of π–π interactions. As shown in Table 4, three CCPs describe π–π stacking interactions in an MMC–CNT complex with the sum of electron densities (Σρ(r) = 0.0124 a.u.). The distances between the centroid of the two stacking rings are in the range of 3.18–3.76 Å. When the sum of the electron densities at all intermolecular BCPs is considered, the total electron density becomes 0.0456 a.u., which is still less than that of MMC–PNP systems. However, the cooperativity between stacking and C⋯H interaction leads to stable adsorption. It should be pointed out that due to the mixed interactions in the MMC–CNT complex, in Fig. 8 we just considered the sum over the densities at the BCP of the C⋯H bonds. The dominant interactions between the MMC and BNNT-21 are N⋯H hydrogen bonds and π–π stacking. As evident from Table 4, there exist eight BCPs associated with N⋯H hydrogen bonds. Furthermore, there is pnicogen O⋯N bonding that could be regarded as a consequence of interaction between the lone pair of the oxygen atom of MMC and the π-hole above the nitrogen atom at the outer surface of BNNT. The sum of electron densities over all N⋯H BCPs between MMC and BNNT is 0.0493 a.u. which well supports the interaction energy of −17.25 kcal mol−1.
Although the biologically-relevant interactions can be reasonably treated using gas-phase calculations, it would be interesting to investigate how much the interactions between the drug and carriers are medium-dependent. Accordingly, to simulate a medium which reasonably mimics the human cell environment, we have performed the calculations in a water medium. To reduce the computational costs, we just considered those initial geometries which correspond to the most stable configurations in terms of interaction energy. The calculated water-mediated interaction energies are given in Table 2. It is known that the aqueous solubility of the drug and carrier is an important factor affecting their usability in biological systems. Accordingly, we have also determined the solubility of the isolated drug and carriers as well as the drug-carrier complexes by calculating the solvation energy defined as the difference between the total energy of the system in the solvent and gas phases. A graphical representation for the calculated solvation energies is presented in Fig. 9. Among the considered carriers, the PCL/CS exhibits higher solubility, which can be attributed to the presence of several –OH, –NH2, and –O groups in its structure that assists hydrogen bonding interactions with water. It can be observed that the solubilities of MMC–carrier systems are higher than the free standing carriers. Thus, the attachment of the MMC drug leads to solubility enhancement of the carriers which is a prerequisite in drug-delivery systems.
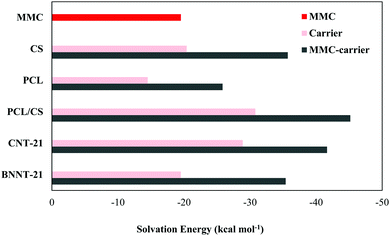 |
| | Fig. 9 A graphical comparison of the solvation energy for MMC, free standing carriers and MMC–carrier complexes. | |
4. Conclusions
The adsorption of MMC drug on CS, PCL, PCL/CS, CNT and BNNT carriers has been theoretically investigated using DFT methods. We found that CNT has remarkably smaller chemical hardness and electrophilicity index, which are crucial for binding to the MMC drug. In the context of global reactivity descriptors, the chemical reactivity of the considered carriers follows the trend: CNT > BNNT > CS > PCL. This reactivity pattern has also been evaluated by explicit adsorption of MMC on the considered carriers. The results indicate that all the MMC–carrier complexes are stable and the adsorptions are exothermic in both vacuum and aqueous media. However, the comparison between the interaction energy values reveals that PCL coated with CS can adsorb the MMC drug stronger than isolated CS and PCL. Upon the adsorption, the energy gaps of the carriers vary between 20 and 50%, which is beneficial for tracking the drug trajectory by fluorescence imaging. The nature of intermolecular interactions between the MMC drug and the carriers has also been investigated by QTAIM analysis. It is found that the adsorption of MMC on PNPs is mainly governed by hydrogen bond interactions, while in the case of NT carriers the π–π stacking interaction dominates. Furthermore, examining the impact of nanotube length on the drug adsorption reveals that, the nature of interaction between the MMC and the CNT is almost independent of the tube length. By contrast, the MMC tends to adsorb on the edge of shorter BNNTs, while in the case of longer BNNTs, the drug moves toward the middle. Our results also manifested that all MMC–carrier complexes have greater polarity and solubility as compared to isolated MMC drug and carriers. Overall, we have shown that a deep discernment on the electronic structure and reactivity descriptors of nanomaterials offers a promising route toward designing efficient carriers for drug delivery applications.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
The authors thank the Supercomputing Center of Shiraz University for providing the computational resources and software.
References
- D. Jong, H. Wim and P. J. A. Borm, Int. J. Nanomedicine, 2008, 3, 133 CrossRef PubMed.
- W. Z. Agnieszka, K. Niemirowicz, K. H. Markiewicz and H. Car, Pharmacol. Rep., 2012, 64, 1020 CrossRef.
- K. S. Soppimath, T. M. Aminabhavi, A. R. Kulkarni and W. E. Rudzinski, J. Controlled Release, 2001, 70, 1 CrossRef CAS PubMed.
- M. S. Digge, R. S. Moon and S. G. Gattani, Int. J. PharmTech Res., 2012, 4, 839 CAS.
- J. H. Kim, T. V. Pham, J. H. Hwang, C. S. Kim and M. J. Kim, Nano Convergence, 2018, 5, 17 CrossRef PubMed.
- M. Çağdaş, A. D. Sezer and S. Bucak, Appl. Nanotechnol. Drug Delivery, 2014, 25, 1 Search PubMed.
- C. T. Matea, T. Mocan, F. Tabaran, T. Pop, O. Mosteanu, C. Puia, C. Iancu and L. Mocan, Int. J. Nanomed., 2017, 12, 5421 CrossRef CAS PubMed.
- M. X. Zhao and B. J. Zhu, Nanoscale Res. Lett., 2016, 11, 207 CrossRef PubMed.
- E. Bilensoy, C. Sarisozen, G. Esendağlı, A. L. Doğan, Y. Aktaş, M. Şen and N. A. Mungan, Int. J. Pharm., 2009, 371, 170 CrossRef CAS PubMed.
- E. Turos, J. Y. Shim, Y. Wang, K. Greenhalgh, G. S. Reddy, S. Dickey and D. V. Lim, Bioorg. Med. Chem. Lett., 2007, 17, 53 CrossRef CAS PubMed.
- J. Bai, Y. Li, J. Du, S. Wang, J. Zheng, Q. Yang and X. Chen, Mater. Chem. Phys., 2007, 106, 412 CrossRef CAS.
- A. Martínez, I. Iglesias, R. Lozano, J. M. Teijón and M. D. Blanco, Carbohydr. Polym., 2011, 83, 1311 CrossRef.
- G. K. Saraogi, P. Gupta, U. D. Gupta, N. K. Jain and G. P. Agrawal, Int. J. Pharm., 2010, 385, 143 CrossRef CAS PubMed.
- H. Q. Mao, K. Roy, V. L. Troung-Le, K. A. Janes, K. Y. Lin, Y. Wang, J. T. August and K. W. Leong, J. Controlled Release, 2001, 70, 399 CrossRef CAS PubMed.
- W. Shao, P. Arghya, M. Yiyong, L. Rodes and S. Prakash, Synth. Appl. Carbon Nanotubes Their Compos., 2013, 13, 285 Search PubMed.
- C. Lee, S. Bhandari, B. Tiwari, N. Yapici, D. Zhang and Y. Yap, Molecules, 2016, 21, 922 CrossRef PubMed.
- S. K. S. Kushwaha, S. Ghoshal, A. K. Rai and S. Singh, J. Pharm. Sci., 2013, 49, 629 CAS.
- Ö. Şen, Z. Çobandede, M. Emanet, Ö. F. Bayrak and M. Çulha, Biochim. Biophys. Acta, Gen. Subj., 2017, 1861, 2391 CrossRef PubMed.
- G. Ciofani, V. Raffa, A. Menciassi and A. Cuschieri, Nanoscale Res. Lett., 2009, 4, 113 CrossRef CAS PubMed.
- R. Kumar, M. Dhanawat, S. Kumar, N. S. Brahma, K. P. Jayant and R. S. Vivek, Recent Pat. Drug Delivery Formulation, 2014, 8, 12 CrossRef CAS PubMed.
- H. Xu, L. Li, G. Fan and X. Chu, Comput. Theor. Chem., 2018, 1131, 57 CrossRef CAS.
- E. Duverger, S. Balme, M. Bechelany, P. Miele and F. Picaud, Appl. Surf. Sci., 2019, 475, 666 CrossRef CAS.
- M. Eslami, S. J. Nikkhah, S. M. Hashemianzadeh and S. A. Sajadi, Eur. J. Pharm. Sci., 2016, 82, 79 CrossRef CAS PubMed.
- D. Karataş, A. Tekin, F. Bahadori and M. S. Çelik, J. Mater. Chem. B, 2017, 5, 8070 RSC.
- M. Vatanparast and Z. Shariatinia, Struct. Chem., 2018, 29, 1427 CrossRef CAS.
- J. Verweij and H. M. Pinedo, Anticancer Drugs, 1990, 1, 5 CrossRef CAS PubMed.
- M. Burjak, M. Bogataj, M. Velnar, I. Grabnar and A. Mrhar, Int. J. Pharm., 2001, 224, 123 CrossRef CAS PubMed.
- S. GuhaSarkar and R. Banerjee, J. Controlled Release, 2010, 148, 147 CrossRef CAS PubMed.
- E. Bilensoy, C. Sarisozen, G. Esendağlı, A. L. Doğan, Y. Aktaş, M. Şen and N. A. Mungan, Int. J. Pharm., 2009, 371, 170 CrossRef CAS PubMed.
- Z. Hou, Y. Li, Y. Huang, C. Zhou, J. Lin, Y. Wang, F. Cui, S. Zhou, M. Jia, S. Ye and Q. Zhang, Mol. Pharmaceutics, 2013, 10, 90 CrossRef CAS PubMed.
- X. Sun, P. Sun, B. Li, Y. Liu, M. Wang, N. Suo, M. Yang, D. Zhang and X. Jin, Mater. Des., 2016, 110, 849 CrossRef CAS.
- R. X. Zhang MSc, P. Cai, T. Zhang, K. Chen, J. Li, J. Cheng, K. Sandy Pang, H. A. Adissu, A. M. Rauth and X. Yu Wu, Nanomedicine, 2016, 12, 1279 CrossRef PubMed.
- Y. Zhao and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215 Search PubMed.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. J. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision D.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- L. M. Fischer, J. L. Vasquez, J. Gehl, G. G. Hermann and N. B. Larsen, Biol. Proced. Online, 2013, 15, 12 Search PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999 CrossRef CAS PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553 CrossRef CAS.
-
C. F. Matta and R. J. Boyd, The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design, John Wiley & Sons, Weinham, 2007 Search PubMed.
- W. Yang and W. J. Mortier, J. Am. Chem. Soc., 1986, 108, 5708 CrossRef CAS PubMed; R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512 CrossRef.
- U. Koch and P. L. Popelier, J. Phys. Chem., 1995, 99, 9747 CrossRef CAS.
- L. V. Schueren, T. Meyer, I. Steyaert, Ö. Ceylan, K. Hemelsoet, V. V. Speybroeck and K. D. Clerck, Carbohydr. Polym., 2013, 91, 284 CrossRef PubMed.
- N. C. Braier and R. A. Jishi, J. Mol. Struct., 2000, 499, 51 CrossRef CAS.
- V. Raffa, C. Riggio, M. W. Smith, K. C. W. Jordan, W. Cao and A. Cuschieri, Technol. Cancer Res. Treat., 2012, 11, 459 CrossRef CAS PubMed.
- M. D. Ellison, M. J. Crotty, D. Koh, R. L. Spray and K. E. Tate, J. Phys. Chem. B, 2004, 108, 7938 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The optimized structures for MMC–MMC interaction, the QTAIM molecular graphs for the most stable complexes between MMC and carriers and the condensed Fukui indices for the carriers are given in Fig S1, S2 and Table S1, respectively. See DOI: 10.1039/d0ma00018c |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article * and
Soode
Amigh
* and
Soode
Amigh