Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Microfluidic devices powered by integrated elasto-magnetic pumps†
Jacob L.
Binsley
 *a,
Elizabeth L.
Martin
*a,
Elizabeth L.
Martin
 a,
Thomas O.
Myers
a,
Thomas O.
Myers
 b,
Stefano
Pagliara
b,
Stefano
Pagliara
 c and
Feodor Y.
Ogrin
c and
Feodor Y.
Ogrin
 a
a
aDepartment of Physics and Astronomy, University of Exeter, Physics Building, Stocker Road, Exeter, EX4 4QL, UK. E-mail: jb778@exeter.ac.uk; Tel: +44 (0)1392 725018
bPlatform Kinetics Limited, Pegholme, Wharfebank Mills, Otley, LS21 3JP, UK
cDepartment of Biosciences, University of Exeter, Living Systems Institute, Stocker Road, Exeter, EX4 4QD, UK
First published on 23rd October 2020
Abstract
We show how an asymmetric elasto-magnetic system provides a novel integrated pumping solution for lab-on-a-chip and point of care devices. This monolithic pumping solution, inspired by Purcell's 3-link swimmer, is integrated within a simple microfluidic device, bypassing the requirement of external connections. We experimentally prove that this system can provide tuneable fluid flow with a flow rate of up to 600 μL h−1. This fluid flow is achieved by actuating the pump using a weak, uniform, uniaxial, oscillating magnetic field, with field amplitudes in the range of 3–6 mT. Crucially, the fluid flow can be reversed by adjusting the driving frequency. We experimentally prove that this device can successfully operate on fluids with a range of viscosities, where pumping at higher viscosity correlates with a decreasing optimal driving frequency. The fluid flow produced by this device is understood here by examining the non-reciprocal motion of the elasto-magnetic component. This device has the capability to replace external pumping systems with a simple, integrated, lab-on-a-chip component.
1 Introduction
Lab-on-a-chip microfluidic devices are a promising solution to progressing point-of-care testing (POCT)1–4 and biomedical applications.5–8 Miniaturising and integrating a range of processes onto one small chip allows fast, sensitive tests to be distributed and used outside of the laboratory. As such there is significant research focusing on the development of devices for use in the field.3,9 However, while some POCT devices can be designed to operate using capillary flow, many still require bulky and expensive pumping systems10,11 which can be prohibitive to their potential widespread use.Manufacturing a self-contained, chip-based pumping system would allow for actively pumped POCT devices to be used more widely. However, there are significant challenges to overcome when producing net fluid flow on microscopic length scales. Creating effective swimming or pumping requires actuation which is non-symmetrical in time and is therefore non-trivial.12
Generating net motion in the Stokes regime has been a lively area of study over the last few decades, underpinned by the work of Purcell13 and Taylor,14 and has grown into a diverse field with a multitude of swimming and pumping mechanisms being developed both theoretically and experimentally. Research in this field has explored a vast array of driving mechanisms, including magnetic torque,15–23 electric fields,24,25 light,26,27 acoustic waves28–30 and chemical energy.31–33
Many of these driving mechanisms have been studied in the context of microscopic pumping solutions.19,20,24,34–46 While there is no formal way of comparing these systems directly, it is clear that many of these integrated pumping designs do not offer optimal solutions for use in a broad range of low-cost, portable POCT devices. For example, a device utilising capillary flow45 can be fabricated and operated easily, although cannot produce tuneable or reversible fluid flow and is not appropriate for prolonged or repeated use. Meanwhile Sawetzki's self-assembled pumping and valving devices,40 again requiring only simple fabrication techniques, offers a great degree of control over fluid behaviour, although is limited by a complex actuation method. The inverse of this is the magneto-elastic membranes utilised by Martin et al.46 relying on a long and complex fabrication, limiting its implementation even though the actuation method is simple.
Therefore, during the development of many self-contained POCT devices, the choice of pumping mechanism requires just as much consideration as the functional components of the chip. This can be a time consuming and expensive distraction from the primary aims of the project which presents a significant barrier to the development of POCT devices. A modular standard which can be calibrated post-integration to be utilised in a broad range of applications, would do much to advance the prevalence of self-contained lab-on-a-chip devices.
An appropriate general purpose integrated pumping solution should be able to produce consistent, precise, tuneable and reversible flow rates appropriate for repeated or prolonged use. It should be implemented using simple, accessible and repeatable actuation methods, requiring no external connections or manual intervention, and thus be capable of being used by an untrained third party. Finally, it should be fabricated using only standard techniques, materials and expertise as currently used in the production of microfluidic devices, minimising the potential expense of manufacture. Satisfying all three of these criteria fully and simultaneously is a difficult challenge which has yet to be fulfilled by an integrated pumping solution.
This paper introduces a device which aims to overcome the limitations above. The research pursues the development of a multipurpose, modular micropump by exploring the validity of a design inspired by Purcell's 3-link swimmer,13 the simplest possible swimming solution in the Stokes regime. This design is integrated within a self-contained module at the time of manufacture, requiring only soft lithography, utilising a simple external actuation method and producing highly tuneable and reversible fluid flow.
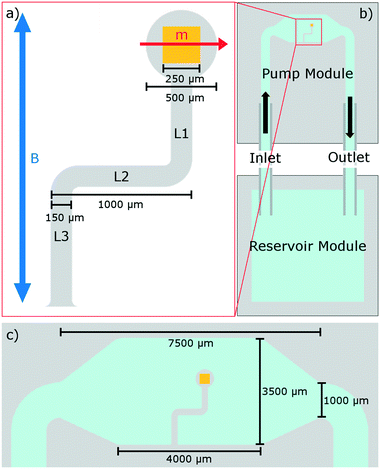
The pump design (Fig. 1) represents a simple, planar, elasto-magnetic device with an elastic geometry similar to that of Purcell's 3-link swimmer, where in this case the action of Purcell's hinges is replaced by an elastic deformation of the links L1 to L3. Due to an embedded magnet, the application of a weak, uniaxial magnetic field can be used to drive the required elastic deformation. The result is a device that is capable of performing non-reciprocal, time-irreversible motion which generates a strong net fluid flow. Fabricated through simple, single stage lithography, this planar design is within the bounds of fabrication of many microfluidic laboratories. The pump is integrated into the device at the time of fabrication without requiring extra assembly and represents the first realisation of an asymmetric pumping system based on Purcell's 3-link swimmer. The elastic geometry is formed of polydimethylsiloxane (PDMS) and the embedded magnet is neodymium iron boron (NdFeB).
This research provides a general purpose, integrated pumping solution which can be readily and cheaply fabricated by most well-equipped microfluidic laboratories. In this way, research into POCT devices has greater freedom and flexibility to move towards more portable and self-contained lab-on-a-chip devices, with fewer barriers to their full implementation.
2 Experimental
2.1 Working principles
In lab-on-a-chip devices, where length scales and velocities are small compared to fluid viscosity, the Reynolds number can become much less than one, resulting in the valid use of the Stokes approximation to the Navier–Stokes equation. The resulting equations of motion of the system are,47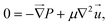 | (1) |
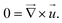 | (2) |
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) represents velocity.
represents velocity.
In this inertia-less, quasistatic regime, fluid flow is time independent. This implies that a swimmer which performs a reciprocal motion consisting of an action followed immediately by the inverse of that action, returns the system to its original state with zero residual flow production, regardless of any time difference taken to perform each action.
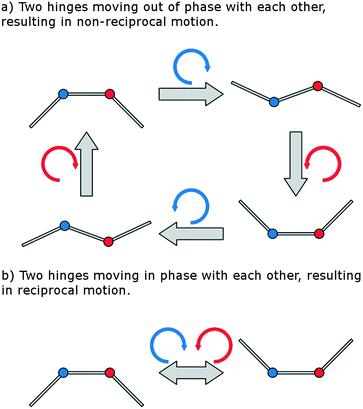
In 1977, Purcell13 suggested the simplest possible swimming mechanism in the Stokes regime, known as the 3-link swimmer. The 3-link swimmer is a device consisting of 3-links attached via two hinges, where the rotation angles of the hinges are controlled. Due to viscous forces, a rotation of a hinge also induces a translation of the body. Rotations and translations are non-commutative and therefore the motion of the swimmer is dictated by the order of rotation of the two hinges.48 Provided the two hinges are rotated out of phase with each other, the resultant motion is capable of being non-symmetric in time and can produce net translation of the body (Fig. 2). If both hinges were to move in phase with each other, the system would become degenerate with that of a single hinged swimmer. Opening a single hinge is identical to the time-inverse of closing a single hinge and therefore there is no time-irreversible series of single hinge rotations capable of producing net motion, known as scallop theorem.49
However, only one hinge of a 3-link swimmer needs to be actively driven to produce net motion, provided the second hinge has an elastic restoring force. This system will also produce non-reciprocal motion, with the elasticated hinge following in phase behind the driven hinge. Elasticated microswimmers have been of theoretical interest50,51 and would be much more experimentally convenient due to the fact that a net fluid motion can be produced by controlling the rotation of a single component.
The behaviour of this style of swimmer has been studied analytically through the application of slender body theory. Slender body theory considers thin filaments moving through viscous fluids, far from any boundaries.52 When examining a sperm-like swimmer with a magnetic head and a flexible tail analytically through the use of slender body theory, performing small amplitude motion, the sperm compliance number is introduced as,51,53
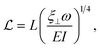 | (3) |
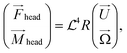 | (4) |
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) head and
head and ![[M with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004d_20d1.gif) head represent the viscous drag force at the head and the magnetic moment of the head, R is the dimensionless grand resistance matrix of the head,
head represent the viscous drag force at the head and the magnetic moment of the head, R is the dimensionless grand resistance matrix of the head, ![[U with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0055_20d1.gif) and
and 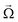 represent the head velocity field.
represent the head velocity field.
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) therefore mediates the effect of a driving force on the resultant motion in the Stokes regime. The sperm compliance number is vital in understanding how these flexible systems behave. While inappropriate to apply to many real experimental systems due to the necessary approximation of the system to be a series of high aspect ratio filaments, it still gives an understanding of how the motion of the swimmer is expected to depend on the geometric parameters, the viscosity of the fluid and the driving frequency. Altering the sperm compliance number will alter the behaviour of the swimmer and the resultant fluid flow produced. Altering the driving force in isolation does not alter the sperm compliance number but will have secondary impacts on flow production.51 The simplest way to alter the sperm compliance number dynamically in an experimental system would be to alter the driving frequency.
therefore mediates the effect of a driving force on the resultant motion in the Stokes regime. The sperm compliance number is vital in understanding how these flexible systems behave. While inappropriate to apply to many real experimental systems due to the necessary approximation of the system to be a series of high aspect ratio filaments, it still gives an understanding of how the motion of the swimmer is expected to depend on the geometric parameters, the viscosity of the fluid and the driving frequency. Altering the sperm compliance number will alter the behaviour of the swimmer and the resultant fluid flow produced. Altering the driving force in isolation does not alter the sperm compliance number but will have secondary impacts on flow production.51 The simplest way to alter the sperm compliance number dynamically in an experimental system would be to alter the driving frequency.
These theoretical investigations into the principles of swimming in this regime can be harnessed to produce a pumping system, as the difference between swimming and pumping depend solely on the frame of reference. A symmetric 3-link swimmer produces the strongest net flow parallel to its length and so if such a swimmer were constrained by its tail, the resulting pump would also produce net flow in the same manner. However, in nature we find that cilia produce an asymmetric motion which allows for efficient pumping perpendicular to their length.54 This enables cilia to be arrayed on large flat surfaces and produce efficient fluid flow, particularly when beating patterns are coordinated.55 Therefore, taking inspiration from nature, the optimal pumping solution would exhibit an asymmetric response where each full cycle is composed of a pump stroke and recovery stroke.
An asymmetric response can be achieved experimentally in bio-mimetic cilia by actuating a symmetric system using a driving torque which is asymmetric in time.37,38 However, in the interest of limiting the complexity of any external equipment used to power the device, the optimal solution is to actuate a geometrically asymmetric pump using a simple symmetric driving torque. The direction of stable flow production from a Purcell-like system driven by a periodic driving torque about its hinges is dependent on its symmetry axes.56 An asymmetric elastic 3-link swimmer, where the equilibrium configuration is offset from the traditional rest configuration, breaking symmetry perpendicular to its length, should therefore be capable of producing stable fluid flow similarly perpendicular to its length. This hypothesis can be understood in the system depicted in Fig. 1a by recognising that the application of a clockwise torque about the magnet will not only bend the pump towards the right, but also increase the angle between links L1 and L2, describing a length extension of the system. Conversely, the application of an anti-clockwise torque about the magnet will simultaneously bend the pump towards the left, as well as decrease the angle between links L1 and L2, describing a length contraction of the system. Provided the bending occurs at a different rate to the extension/contraction, this describes a hysteretic behaviour and the desired asymmetric response will be observed.
The result is a distinct power stroke and recovery stroke as observed in the biological solution of cilia.54 It can be shown that the area enclosed within the closed loop path difference between these two strokes of motile cilia is proportional to the volume of fluid pumped per cycle, and this area is therefore an important figure of merit with respect to the pump response.57
The Purcell 3-link swimmer is capable of producing tuneable flow rates when altering the phase difference of the two hinges,49,50,58,59 and has been theorised to be capable of producing flow in the reverse direction,60 however achieving reverse flow rates in this manner is experimentally impractical as it would require high amplitude deformation which has not yet been achieved experimentally. Hamilton et al.20 has shown that placing restrictions on the near-field fluid vortices around an elasto-magnetic pump can constrain the resultant fluid flows into producing strong flow in the negative direction without altering the motion of the pump. In this manner, the flow direction can be controlled through much smaller changes in pump behaviour. By introducing channel walls in close proximity to the pump, the flow direction can be controlled much more readily by simple adjustment of the driving frequency. Therefore, the driving frequency will dictate not only the sperm compliance number, the behaviour of the pump and the production of fluid flow, but also the direction of fluid flow.
The choice of power delivery mechanism is important in the design of any pumping device. It has been theorised that the most effective way to deliver power remotely to a system is through the use of magnetic fields.61 As such, the optimal design for a microfluidic pump should be an elasto-magnetic device with power delivered through the production of a magnetic torque. In this instance, torque, 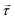 , is provided to the elastic structure remotely by coupling an embedded magnet, with magnetisation,
, is provided to the elastic structure remotely by coupling an embedded magnet, with magnetisation, ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) , to an external driving field with magnetic flux density,
, to an external driving field with magnetic flux density, ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) , utilising the commonly used equation,
, utilising the commonly used equation, 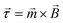 . This external driving field can be the simplest possible, uniform, uniaxial, oscillating magnetic field since the hysteretic pump motion is a property of the asymmetric elastic geometry.
. This external driving field can be the simplest possible, uniform, uniaxial, oscillating magnetic field since the hysteretic pump motion is a property of the asymmetric elastic geometry.
Through these working principles, the first experimental application of an elasto-magnetic Purcell-like system is employed as a fully operational microfluidic pump with parallels to the behaviour of biological cilia. The behaviour of this pump can be controlled through the manipulation of driving frequency alone, simplifying the equipment required to operate the device.
2.2 Design overview and actuation
The proposed pump is integrated within a segregated pumping module with an inlet and outlet (Fig. 1). The pumping module is constructed of three layers of PDMS bonded in a vertical stack (Fig. 3): the middle layer containing the integrated pump, with the top and bottom layers extending the depth of the channel, additionally acting as capping layers to fully enclose the device.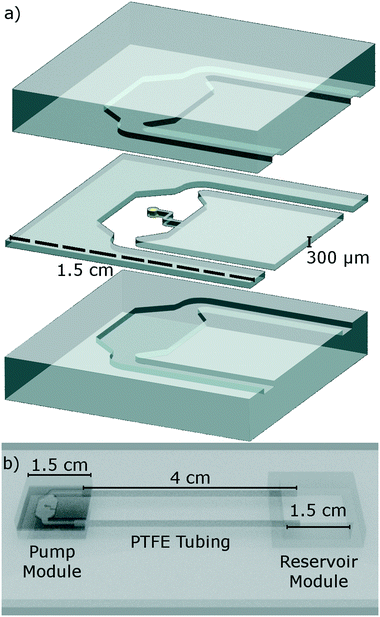 | ||
| Fig. 3 A 3D rendering of the device. a) Is an exploded projection of the pump module. We see the pump module is made from three distinct layers. The middle layer contains the integrated pump (Fig. 1), the upper and lower layers act to extend the height of the microfluidic channels by 300 μm each side, while also acting as capping layers. b) Shows that the pump module and reservoir module are assembled onto a microscope slide and connected via PTFE tubing as in the experiments. | ||
This pump is fully made from PDMS with an embedded NdFeB magnet. The pumping module is fully enclosed, with enough internal volume to allow for the pump to move out of plane without stalling against the bounding channel walls. In this way, the pump operates in the bulk, distinct from similar previous studies on elasto-magnetic pumps investigating surface flows produced in open channels.19–22,62 The inlet and outlet channels are 1000 μm in width, and 900 μm in depth. This pumping module is connected via polytetrafluoroethylene (PTFE) tubing, of length 4 cm and internal diameter 860 μm, to a separate reservoir module. This reservoir module is a large, open cup structure with internal side-length of 1.5 cm which is not fully enclosed and allows for fluid and tracer particles to be readily introduced, removed or replaced in this system.
The cubic NdFeB magnet of side length 250 μm is set in the “head” of the pump (Fig. 1) and provides torque, 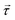 , when driven by a weak, uniaxial external magnetic field,
, when driven by a weak, uniaxial external magnetic field, ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) , provided by a Helmholtz coil. The magnet provides magnetisation,
, provided by a Helmholtz coil. The magnet provides magnetisation, ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) , in a direction perpendicular to the external driving field to maximise torque (and elastic deformation) in accordance to the common equation,
, in a direction perpendicular to the external driving field to maximise torque (and elastic deformation) in accordance to the common equation, 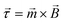 . The remnant flux density of the NdFeB magnet is 1390–1440 mT, with a coercivity of 835 mT.63 This magnetic material is coated in a thin protective nickel layer with thickness 12–25 μm.
. The remnant flux density of the NdFeB magnet is 1390–1440 mT, with a coercivity of 835 mT.63 This magnetic material is coated in a thin protective nickel layer with thickness 12–25 μm.
2.3 Device fabrication
The middle layer of the pumping module with the integral pump was created with an SU-8 mould constructed using standard photolithographic techniques.64 A photomask was designed in AutoCAD and printed on an emulsion film by JD Photodata. A hexamethyldisilazane (HMDS) based primer was spin coated onto a 2 cm square silicon wafer at 4000 rpm and baked on a hot plate at 95 °C for 10 minutes. SU-8 3050 photoresist was then spin coated on top of the primer at 1500 rpm to a thickness of 300 μm and baked on a hot plate at 95 °C for 45 minutes. The photomask was aligned with the wafer using a Kloe UV-Kub 2 masking optical system and exposed to UV (365 nm wavelength and 40 mW cm−2 irradiance) for 15 seconds. The wafer was then baked on a hot plate again at 95 °C for 5 minutes and developed with propylene glycol methyl ether acetate (PGMEA) in a sonicator for 20 minutes. This was then washed with isopropanol and blow dried with N2. This negative mould was then spin coated with polymethylmethacrylate (PMMA) 950K A4 at 4000 rpm and baked on a hot plate at 100 °C for 10 minutes.The upper and lower capping layers were both created using one acrylic mould which was CNC machined. A mould for the reservoir module was produced by 3D printing due to its larger feature sizes.
PDMS was mixed 10 parts to 1, oligomer to curing agent and then degassed. This uncured PDMS was introduced into these moulds and cured at 50 °C in an oven for 11 hours, giving the elastic material a final elastic modulus of 1.6 MPa.65 During the curing process, the NdFeB magnet, dip coated in PMMA and dried at room temperature, was manually inserted into the head of the pump. The magnet was then rotated to the specified orientation (Fig. 1) through the application of an external magnetic field.
Once cured, the three distinct layers of the pumping module were removed from their moulds and manually aligned in a vertical stack under a microscope. Uncured PDMS was used as an adhesive between each of the layers, utilising the “stamp-and-stick” method.66 This was then cured for 48 hours at room temperature to avoid further heating the pump: maintaining a low elastic modulus. The completed pumping module and reservoir module were bonded to opposite ends of a glass slide through treatment with oxygen plasma.67
PTFE tubing with an inner diameter of 860 μm was then inserted into both modules and sealed using a further application of uncured PDMS. The assembled device was then cured at room temperature for an additional 48 hours. The completed device was then filled with fluid through the reservoir module using a syringe to begin measurements.
2.4 Device handling
The device is filled with a mixture of water and glycerol. The fluid viscosity is subsequently controlled by varying the relative proportions of these two fluids.The measurements were taken using the ABIOMATER system provided by Platform Kinetics Limited, consisting of an optical microscope equipped with an Olympus MPLFLN10×, 10× magnification optic and an Olympus MPLFLN2.5×, 2.5× magnification optic, a MotionBLITZ EoSens mini1 monochromatic high speed camera operating at 1000 frames per second, single axis Helmholtz coil and XY-stage. The pump is actuated by the Helmholtz coil providing a sinusoidal, oscillating magnetic field perpendicular to the orientation of the NdFeB magnet (Fig. 1). The amplitude of the driving field is varied in the range of 3 mT to 6 mT and the frequency is varied in the range of 1 Hz to 60 Hz.
The flow rates produced by the pump are measured as follows: 15 μm diameter polystyrene microbeads (Sigma-Aldrich, 74964) are introduced into the channel via the reservoir module. The bead motion is observed with the ABIOMATER optical microscope equipped with the 10× magnification optic and recorded with the high speed camera. This data is then analysed with the open source software, Tracker68 and is discussed in section 2.5. The motion of the pump is also measured with the same apparatus using the 2.5× magnification optic. This motion is also analysed using Tracker.
2.5 Measurement of fluid motion
When tracking the microbeads as mentioned in section 2.4, the initial position of a given bead is recorded in the tracking software. The position of this bead is then automatically tracked by the software between frames as its position evolves in time, until a final frame. This final frame is determined to be an integer number of periods of the driving field, from the initial frame, and is typically 1000 frames (1 second) unless otherwise restricted. The velocity of this bead is taken as the distance travelled over this integer number of periods. A minimum of three high speed videos are recorded for each data point, and a selection of beads are tracked in each video.The motion of the pump is tracked in a similar manner. The initial position of the centre of the pump “head” is recorded and then automatically tracked by the software as its position evolves in time until a final frame, capturing multiple periods of oscillation. At higher frequencies, fewer data points can be captured per oscillation period: for example, at a driving frequency of 50 Hz, only 20 data points will be recorded per pump cycle. The data is therefore interpolated using a smoothing spline to better represent physically realistic pump motion for analysis in section 2.6.
2.6 Analysis of fluid motion
The peak fluid velocity, vpeak, is taken to be equal to the peak bead velocity as recorded in section 2.5, since the beads are assumed to have equal velocity to the surrounding fluid. vpeak is used in this study because it must occur ata known, consistent position at the very centre of the channel and is therefore a consistent point of reference, producing consistent measurements. vpeak can be obtained from measurements as long as the centre of the channel is captured within the depth of field of the microscope used in this study. The standard deviation of the recorded velocities is taken as the uncertainty.The volumetric flow rate, Q, can then be calculated from vpeak due to the known channel cross section. For the rectangular channels used in this study, this can be performed using the following two equations:69
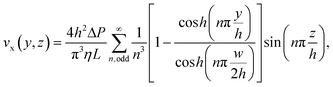 | (5) |
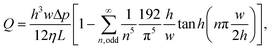 | (6) |
From these two equations we can calculate the constant ratio, Q/vpeak, for this particular channel geometry to be ∼775/2104. As such, our peak velocity measurements need only be multiplied by this ratio to obtain the volumetric flow rate.
When analysing the motion of the pump, the resultant motion as measured in section 2.5 is hysteretic, forming a closed loop (Fig. S1†). The area contained within this closed loop is taken to be indicative of the non-reciprocal motion of the pump.57 This area is calculated as the median area over multiple pump cycles, with the standard deviation between these cycles being taken as the uncertainty in the measurement. Due to the nature of the path taken by the pump, if too few data points are taken during a cycle, then linearly interpolating between them will result in under predicting the value of the enclosed area. Therefore it is necessary to interpolate between the data points with a smooth function, such as a smoothing spline. The standard deviation of the recorded areas is taken as the uncertainty.
3 Results and discussion
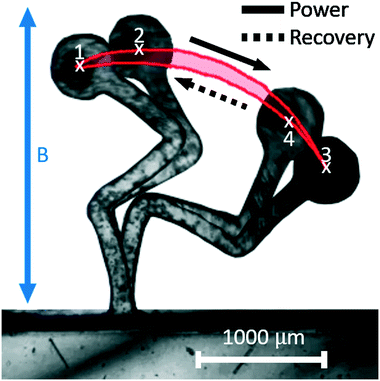
We begin by measuring the motion of the pump. When actuated through the application of the external magnetic field, the elastic geometry is deformed, with the 3-links deforming out of phase with each other. The top-most link, L1, responds before L2, leading in phase, and again L2 leads in phase over L3. The desired non-reciprocal motion is observed and can be clearly represented when observing the motion of the pump head as it moves in a closed loop path exhibiting hysteretic behaviour, being reminiscent of biological cilia (Fig. 4 and S1†).We clearly see an extension/contraction of the pump in accordance with the direction of the provided magnetic torque (Fig. 4 and S1†). When a clockwise torque is provided, through points 1 → 2 → 3, a length extension is observed as the pump deforms towards the right. When an anti-clockwise torque is provided, through points 3 → 4 → 1, a length contraction is observed as the pump deforms towards the left. When tracing the path taken by the pump head, a closed loop is obtained representing the path difference and resultant hysteresis. This motion exhibits a distinct power stroke and recovery stroke as predicted in section 2.1, where fluid is expected to be pumped more effectively in the direction of the power stroke than the recovery stroke.
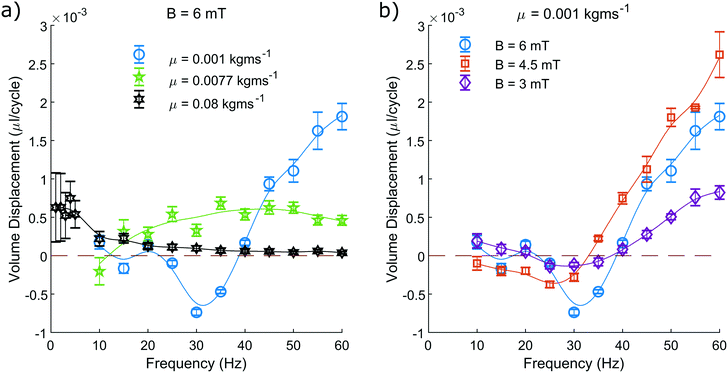
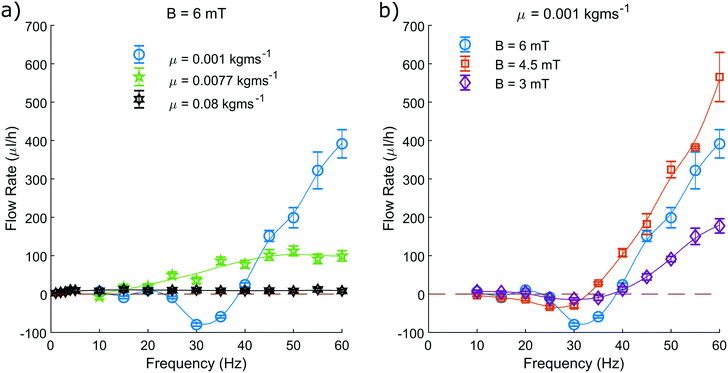
We measure the area contained within this closed loop path as a function of frequency for various driving field amplitudes and fluid viscosities (Fig. 5). From these measurements we can determine that increasing the driving frequency results in increasing the measured hysteretic area, until a maximum value. Beyond this value, increasing the driving frequency further causes the hysteretic area to decay towards zero. From the green curve representing a viscosity of 0.0077 kg ms−1 (Fig. 5a), we can see most clearly the characteristic frequency dependence of the pump motion.
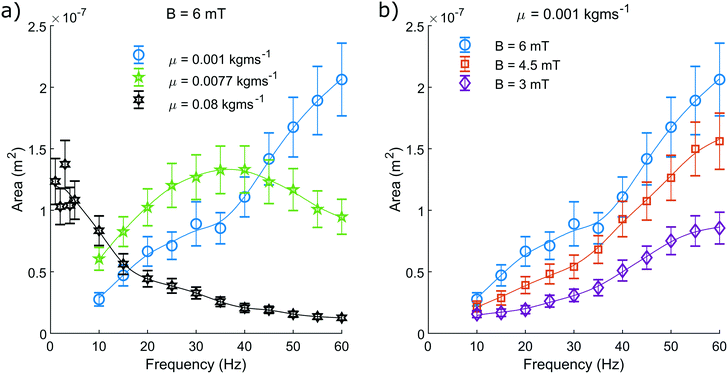 | ||
| Fig. 5 The pump motion as a function of frequency. a) Depicts the dependence on fluid viscosity with a constant field amplitude of 6 mT and b) depicts how the motion depends on field amplitude with a constant dynamic viscosity of 0.001 kg ms−1. The blue curve is duplicated between both a) and b) for reference. The median area contained within the closed loop path traced by the non-reciprocal motion of the magnetic head of the pump, as suggested in Fig. 4, is shown. This is recorded as a function of driving frequency and repeated for a range of dynamic viscosities and driving field amplitudes. The plotted line is a simple smoothing spline between the data points to act as a visual guide. | ||
The optimal driving frequency of this system is shown to be strongly dependent on fluid viscosity. When altering the fluid viscosity (Fig. 5a) we notice two key points. Firstly, that lower viscosities offer a maximum hysteretic area at a higher frequency. Secondly, that the maximum hysteretic area appears to increase with decreasing viscosity in the measured range.
The difference between these curves is understood here by discussing the behaviour of eqn (3). Increasing the frequency will increase the sperm compliance number, as will increasing the viscosity of the fluid. Therefore, a greater fluid viscosity will compound with the increasing driving frequency to accelerate the increasing sperm compliance number. A system with greater fluid viscosity will therefore exhibit higher sperm compliance number behaviour at lower driving frequencies.
The optimal driving frequency of this system is shown to not be strongly dependent on field amplitude. We show that altering the driving field amplitude (Fig. 5b) does not alter the trend of the curve and only serves to alter the amplitude of the response at all points. A greater field amplitude allows for greater maximum displacement of the pump from its rest position, widening and broadening the hysteresis (Fig. 4), for all frequencies.
We have limited the maximum driving frequency in these experiments to 60 Hz. This is due to the increasing power required to maintain the maximum field amplitude at higher driving frequencies. The maximum hysteretic area is therefore not captured in this study for the measurements taken at the lowest viscosity of 0.001 kg ms−1.
When observing the system with the highest viscosity of 0.08 kg ms−1 we find that the optimal driving frequency appears to be in the range of a few Hertz with recorded area similar to that of the green curve at 0.0077 kg ms−1 (Fig. 5a). We know that as the driving frequency tends to zero, the hysteretic area must also tend to zero. We can be confident therefore that the trend of the curve is unchanged, rising from zero to an optimal value, before decaying back towards zero at higher frequencies.
By analogy to a comparable system of cilia, we should expect a linear relationship between the area swept by the pump and the volume displacement of the fluid per cycle.57 When measuring the volume of the fluid displaced per cycle (Fig. 6 and S2†) we observe a number of key points. Much like our measurements of pump motion, the fluid volume displaced per cycle must tend to zero as the driving frequency tends to zero or infinity. A maximum volume displacement is observed at the same frequency as with the maximum area traced by the pump.
When altering the amplitude of the driving field, we also observe in correlation with the measurements of pump motion, that the trend of the curves is unchanged (Fig. 6a). Instead, altering the amplitude of the driving field serves to scale the net displacement of the fluid at all points. Interestingly, we also note a divergence from the linear relationship between the pump motion and the net volume displacement. The maximum volume displacement is observed at an intermediate driving field amplitude, rather than at the maximum amplitude as might be expected.
An increased field amplitude reduces the phase lag of the motion of the head behind the driving field,51 altering the point in the cycle when the stored elastic energy is released. Therefore, an optimal driving field amplitude is likely to exist in the context of maximising flow production within this system.
Crucially, in these measurements we also observe an undocumented phenomena for an experimental Purcell-like system: a consistent region of negative flow production due to the flow restrictions imposed on the system due to the close proximity of the bounding walls, as outlined in section 2.1. By placing these restrictions, the net flow direction becomes discretised and flow in the negative direction becomes favourable under the conditions provided. The ability of this system to dynamically change the pumping direction through no alteration of the geometry is an important property to consider when contemplating potential applications.
The same dependence on viscosity is also recorded for the fluid displacement as with the pump motion (Fig. 6a). By increasing the fluid viscosity, the maximum volume displacement occurs at lower driving frequencies, with the lowest viscosity measurements recorded here exhibiting an inflated maximum value. These correlations confirm that taking the area enclosed within the motion path traced by the pump is an important figure of merit when characterising the system. The flow produced is not steady, but oscillates in both the positive and negative direction throughout each full cycle. This is because during the recovery stroke, the pump moves fluid in the reverse direction, only less effectively than in the forward direction. The net volume displacement per cycle is recorded here.
Now that we have discussed the net volume displacement per cycle, and the strong relationship this has with the motion of the pump, we will also discuss how this translates into usable volumetric flow rate (Fig. 7). This pumping system is capable of producing flows in the range of −100 to +600 μL h−1 for the measured frequencies at the lowest viscosity tested.
The trend of these curves is much as expected when considering their relationship with the net volume displacement per cycle (Fig. 6). We find that the peak flow rate is more biased towards higher frequencies than for the volume displacement per cycle. This is most visible for the measurements using a viscosity of 0.0077 kg ms−1, represented by the green curve (Fig. 7a). This can be understood since at frequencies greater than the optimal frequency, the pump completes more cycles in a given time period, counteracting the decrease in fluid displaced per cycle at these higher frequencies.
The behaviour of the system described here agrees with the previous theoretical work on its free swimming counterpart.49–51,58,59 When the phase difference between the two hinges of Purcell's 3-link swimmer is varied, a maximum fluid velocity is observed at an optimal, finite phase difference. The result is replicated in this study, with the peak fluid flow produced at an optimal, finite driving frequency which can be related to the phase difference between the actuation of the links.
This demonstrates the first experimental application of an asymmetric Purcell-like system. Moreover, this system is capable of providing tuneable, reversible fluid flow when integrated within a microfluidic device. The device is capable of being manufactured using only existing, standard methods of fabrication in the field, and can be implemented with the employment of the simplest actuation method. This device can therefore be considered for general purpose use in low-cost, portable POCT devices.
When comparing its operation to alternative integrated micropumping solutions, a number of advantages can be ascertained. It is shown to operate on a fully enclosed bulk fluid rather than just surface flows as is shown previously for a number of elasto-magnetic devices.19–22,46 The pumping mechanism does not alter the fluid in any way through chemical interactions such as found in studies exploring Janus particles or diodes.24,31–33 This system does not rely on the maintenance of phase separated fluids, as found in some acoustic actuation methods29 which may be adversely effected by long term storage or transport. It can be utilised for prolonged periods of time and used repeatedly unlike systems which rely on capillary forces,70 low pressure43 or otherwise depend on the advancement of a fluid–air interface.35,36,71 The system requires no physical external connections and is completely self-contained.34 The device is actuated using the simplest transient magnetic field commanding only a single degree of freedom unlike those used by other bio-mimetic, cilia-like systems,37,38 minimizing the complexity of the actuation equipment. The pump can be fabricated as one piece with the rest of the microfluidic device, integrated at the time of manufacture with minimal extra assembly required.
The oscillatory flow produced should have no impact on the functionality of the device, due to the time reversibility of flow in the Stokes regime, only the net flow is significant when evaluating pumping performance. While the fabrication time is relatively long, this is mostly due to prolonged curing times and so lends itself to batch production, requiring minimal input from the manufacturer.
Therefore, we can confidently introduce a general purpose micropump capable of being applied to a large variety of portable, low-cost, actively pumped POCT devices with broad ranging applications, circumventing the specific drawbacks of many alternative solutions.
4 Conclusions
This work successfully implements the first asymmetric elasto-magnetic integrated pumping system based on Purcell's 3-link swimmer. Effective, tuneable, bidirectional fluid flow is produced for microfluidic applications without manually altering the pumping system. The oscillatory nature of the flow produced will have no appreciable impact on simple low Reynolds systems.The device requires no physical connection to external systems and can be fabricated using only what is already commonplace in the production of microfluidic devices, relying on nothing more complex than single stage monolithography. Actuation is achieved through equally accessible equipment, requiring only a single input with one degree of freedom: the application of the simplest possible, uniaxial, oscillating magnetic field. This design therefore serves to reduce or remove barriers to the development and implementation of fully self-contained POCT devices.
Author contributions
Experimental data was collected by J. L. Binsley with the support of E. L. Martin and supervision from S. Pagliara and F. Y. Ogrin. The magneto-optical equipment was provided by T. O. Myers and the manuscript was drafted by J. L. Binsley. All authors contributed to the revision of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by the EPSRC Centre for Doctoral Training in Metamaterials under Grant EP/L015331/1 and in part by the European Union's HORIZON2020 Research and Innovation Program under projects 665440 (ABIOMATA) and 801374 (MagElastic). This work was also supported by a MRC Proximity to Discovery EXCITEME2 grant (MCPC17189), a Royal Society Research Grant (RG180007), a Wellcome Trust Strategic Seed Corn Fund (WT097835/Z/11/Z) and a Marie Skłodowska-Curie grant (H2020-MSCA-ITN-2015-675752). The authors would like to thank Platform Kinetics Ltd., for providing the magneto-optic equipment. The authors would also like to thank Mark Heath for useful discussions.References
- W. Jung, J. Han, J.-W. Choi and C. H. Ahn, Microelectron. Eng., 2015, 132, 46–57 CrossRef CAS.
- U. Hassan, T. Ghonge, B. Reddy Jr, M. Patel, M. Rappleye, I. Taneja, A. Tanna, R. Healey, N. Manusry and Z. Price, et al. , Nat. Commun., 2017, 8, 1–12 CrossRef.
- P. Abgrall and A. Gue, J. Micromech. Microeng., 2007, 17, R15 CrossRef.
- W. Jung, J. Han, J. Kai, J.-Y. Lim, D. Sul and C. H. Ahn, Lab Chip, 2013, 13, 4653–4662 RSC.
- R. A. Bamford, A. Smith, J. Metz, G. Glover, R. W. Titball and S. Pagliara, BMC Biol., 2017, 15, 1–12 CrossRef.
- F. J. Hol and C. Dekker, Science, 2014, 346(6208), 1251821 CrossRef.
- E. K. Sackmann, A. L. Fulton and D. J. Beebe, Nature, 2014, 507, 181–189 CrossRef CAS.
- U. Łapińska, G. Glover, P. Capilla-Lasheras, A. J. Young and S. Pagliara, Philos. Trans. R. Soc., B, 2019, 374, 20180442 CrossRef.
- B. Ngamsom, E. A. Wandera, A. Iles, R. Kimani, F. Muregi, J. Gitaka and N. Pamme, Analyst, 2019, 144, 6889–6897 RSC.
- K. F. Lei, J. Lab. Autom., 2012, 17, 330–347 CrossRef CAS.
- N.-T. Nguyen, X. Huang and T. K. Chuan, J. Fluids Eng., 2002, 124, 384–392 CrossRef.
- P. Garstecki and M. Cieplak, J. Phys.: Condens. Matter, 2009, 21, 200301 CrossRef.
- E. M. Purcell, Am. J. Phys., 1977, 45, 3–11 CrossRef.
- G. I. Taylor, Proc. R. Soc. London, Ser. A, 1951, 209, 447–461 Search PubMed.
- M. Medina-Sánchez, L. Schwarz, A. K. Meyer, F. Hebenstreit and O. G. Schmidt, Nano Lett., 2016, 16, 555–561 CrossRef.
- R. M. Erb, J. J. Martin, R. Soheilian, C. Pan and J. R. Barber, Adv. Funct. Mater., 2016, 26, 3859–3880 CrossRef CAS.
- A. Barbot, D. Decanini and G. Hwang, Sci. Rep., 2016, 6, 19041 CrossRef CAS.
- H.-W. Huang, M. S. Sakar, A. J. Petruska, S. Pané and B. J. Nelson, Nat. Commun., 2016, 7, 1–10 Search PubMed.
- M. Bryan, J. Garcia-Torres, E. Martin, J. Hamilton, C. Calero, P. Petrov, C. Winlove, I. Pagonabarraga, P. Tierno and F. Sagués, et al. , Phys. Rev. Appl., 2019, 11, 044019 CrossRef CAS.
- J. K. Hamilton, M. T. Bryan, A. D. Gilbert, F. Y. Ogrin and T. O. Myers, Sci. Rep., 2018, 8, 1–12 CrossRef.
- J. K. Hamilton, A. D. Gilbert, P. G. Petrov and F. Y. Ogrin, Phys. Fluids, 2018, 30, 092001 CrossRef.
- J. K. Hamilton, P. G. Petrov, C. P. Winlove, A. D. Gilbert, M. T. Bryan and F. Y. Ogrin, Sci. Rep., 2017, 7, 44142 CrossRef.
- A. M. Maier, C. Weig, P. Oswald, E. Frey, P. Fischer and T. Liedl, Nano Lett., 2016, 16, 906–910 CrossRef CAS.
- S. T. Chang, V. N. Paunov, D. N. Petsev and O. D. Velev, Nat. Mater., 2007, 6, 235–240 CrossRef CAS.
- G. Loget and A. Kuhn, Nat. Commun., 2011, 2, 1–6 Search PubMed.
- M. Camacho-Lopez, H. Finkelmann, P. Palffy-Muhoray and M. Shelley, Nat. Mater., 2004, 3, 307–310 CrossRef CAS.
- W. Li, X. Wu, H. Qin, Z. Zhao and H. Liu, Adv. Funct. Mater., 2016, 26, 3164–3171 CrossRef CAS.
- K. J. Rao, F. Li, L. Meng, H. Zheng, F. Cai and W. Wang, Small, 2015, 11, 2836–2846 CrossRef CAS.
- A. R. Tovar, M. V. Patel and A. P. Lee, Microfluid. Nanofluid., 2011, 10, 1269–1278 CrossRef CAS.
- M. Kaynak, A. Ozcelik, A. Nourhani, P. E. Lammert, V. H. Crespi and T. J. Huang, Lab Chip, 2017, 17, 395–400 RSC.
- A. Walther and A. H. Müller, Soft Matter, 2008, 4, 663–668 RSC.
- S. J. Ebbens and J. R. Howse, Soft Matter, 2010, 6, 726–738 RSC.
- A. A. Solovev, W. Xi, D. H. Gracias, S. M. Harazim, C. Deneke, S. Sanchez and O. G. Schmidt, ACS Nano, 2012, 6, 1751–1756 CrossRef CAS.
- M. A. Unger, H.-P. Chou, T. Thorsen, A. Scherer and S. R. Quake, Science, 2000, 288, 113–116 CrossRef CAS.
- S. Girardo, M. Cecchini, F. Beltram, R. Cingolani and D. Pisignano, Lab Chip, 2008, 8, 1557–1563 RSC.
- L. Masini, M. Cecchini, S. Girardo, R. Cingolani, D. Pisignano and F. Beltram, Lab Chip, 2010, 10, 1997–2000 RSC.
- F. Fahrni, M. W. Prins and L. J. van IJzendoorn, Lab Chip, 2009, 9, 3413–3421 RSC.
- A. Shields, B. Fiser, B. Evans, M. Falvo, S. Washburn and R. Superfine, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 15670–15675 CrossRef CAS.
- K. S. Ryu, K. Shaikh, E. Goluch, Z. Fan and C. Liu, Lab Chip, 2004, 4, 608–613 RSC.
- T. Sawetzki, S. Rahmouni, C. Bechinger and D. W. Marr, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 20141–20145 CrossRef CAS.
- A. R. Tovar, M. V. Patel and A. P. Lee, Microfluid. Nanofluid., 2011, 10, 1269–1278 CrossRef CAS.
- A. K. Au, H. Lai, B. R. Utela and A. Folch, Micromachines, 2011, 2, 179–220 CrossRef.
- K. Hosokawa, K. Sato, N. Ichikawa and M. Maeda, Lab Chip, 2004, 4, 181–185 RSC.
- J. Park and J.-K. Park, Lab Chip, 2019, 19, 2973–2977 RSC.
- M. Zimmermann, H. Schmid, P. Hunziker and E. Delamarche, Lab Chip, 2007, 7, 119–125 RSC.
- E. L. Martin, M. T. Bryan, S. Pagliara and F. Y. Ogrin, IEEE Trans. Magn., 2019, 55, 1–6 Search PubMed.
- L. D. Landau and E. M. Lifshitz, Fluid Mechanics, 1963, pp. 63–64 Search PubMed.
- E. Gutman and Y. Or, IEEE Trans. Robot., 2015, 32, 53–69 Search PubMed.
- L. E. Becker, S. A. Koehler and H. A. Stone, J. Fluid Mech., 2003, 490, 15–35 CrossRef.
- E. Passov and Y. Or, Eur. Phys. J. E: Soft Matter Biol. Phys., 2012, 35, 1–9 CrossRef.
- H. Gadêlha, Regul. Chaotic Dyn., 2013, 18, 75–84 CrossRef.
- G. Batchelor, J. Fluid Mech., 1970, 44, 419–440 CrossRef.
- H. Gadêlha, E. Gaffney, D. Smith and J. Kirkman-Brown, J. R. Soc., Interface, 2010, 7, 1689–1697 CrossRef.
- M. A. Chilvers and C. O'Callaghan, Thorax, 2000, 55, 314–317 CrossRef CAS.
- L. Gheber and Z. Priel, Cell Motil. Cytoskeleton, 1990, 16, 167–181 CrossRef CAS.
- Y. Or, Phys. Rev. Lett., 2012, 108, 258101 CrossRef.
- S. Hanasoge, M. Ballard, P. J. Hesketh and A. Alexeev, Lab Chip, 2017, 17, 3138–3145 RSC.
- D. Tam and A. E. Hosoi, Phys. Rev. Lett., 2007, 98, 068105 CrossRef.
- J. E. Avron and O. Raz, New J. Phys., 2008, 10, 063016 CrossRef.
- M. S. Kumar and P. Philominathan, Int. J. Autom. Comput., 2012, 9, 325–330 CrossRef.
- R. M. Erb, J. J. Martin, R. Soheilian, C. Pan and J. R. Barber, Adv. Funct. Mater., 2016, 26, 3859–3880 CrossRef CAS.
- D. Matsunaga, J. K. Hamilton, F. Meng, N. Bukin, E. L. Martin, F. Y. Ogrin, J. M. Yeomans and R. Golestanian, Nat. Commun., 2019, 10, 1–9 CrossRef CAS.
- SM Magnetics, Materials and Tables, https://smmagnetics.com/pages/magnetic-materials-tables, accessed 11.3. 2020 Search PubMed.
- A. del Campo and C. Greiner, J. Micromech. Microeng., 2007, 17, R81 CrossRef CAS.
- I. Johnston, D. McCluskey, C. Tan and M. Tracey, J. Micromech. Microeng., 2014, 24, 035017 CrossRef.
- S. Satyanarayana, R. N. Karnik and A. Majumdar, J. Microelectromech. Syst., 2005, 14, 392–399 Search PubMed.
- S. Bhattacharya, A. Datta, J. M. Berg and S. Gangopadhyay, J. Microelectromech. Syst., 2005, 14, 590–597 CAS.
- D. Brown, Tracker (v 5.0.6), https://physlets.org/tracker/, accessed 11.3. 2020 Search PubMed.
- H. Bruus, Theoretical Microfluidics, 2006, pp. 43–47 Search PubMed.
- K. K. Lee and C. H. Ahn, Lab Chip, 2013, 13, 3261–3267 RSC.
- F. Villafiorita-Monteleone, E. Mele, G. Caputo, F. Spano, S. Girardo, P. D. Cozzoli, D. Pisignano, R. Cingolani, D. Fragouli and A. Athanassiou, RSC Adv., 2012, 2, 9543–9550 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0lc00935k |
| This journal is © The Royal Society of Chemistry 2020 |