Acoustofluidic generation of droplets with tunable chemical concentrations†
Abstract
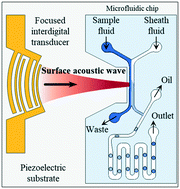
The dynamic control of the chemical concentration within droplets is required in numerous droplet microfluidic applications. Here, we propose an acoustofluidic method for the generation of a library of aqueous droplets with the desired chemical concentrations in a continuous oil phase. Surface acoustic waves produced by a focused interdigital transducer interact with two parallel laminar streams with different chemical compositions. Coupling the acoustic waves with the flow streams results in the controlled acoustofluidic mixing of the aqueous solutions through the formation of acoustic streaming flow-induced microvortices. The mixed streams are split at a bifurcation, and one of the streams with a precisely controlled chemical concentration is fed into a T-junction to produce droplets with tunable chemical concentrations. The periodic acoustofluidic mixing of the aqueous streams enables the generation of a droplet library with a well-defined inter-droplet concentration gradient. The proposed method is a promising tool for the on-chip dynamic control of in-droplet chemical concentrations and for next-generation droplet microfluidic applications.


 Please wait while we load your content...
Please wait while we load your content...