Everything in its right place: controlling the local composition of hydrogels using microfluidic traps†
Abstract
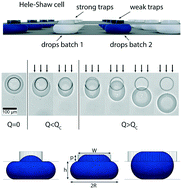
Many natural materials display locally varying compositions that impart unique mechanical properties to them which are still unmatched by manmade counterparts. Synthetic materials often possess structures that are well-defined on the molecular level, but poorly defined on the microscale. A fundamental difference that leads to this dissimilarity between natural and synthetic materials is their processing. Many natural materials are assembled from compartmentalized reagents that are released in well-defined and spatially confined regions, resulting in locally varying compositions. By contrast, synthetic materials are typically processed in bulk. Inspired by nature, we introduce a drop-based technique that enables the design of microstructured hydrogel sheets possessing tuneable locally varying compositions. This control in the spatial composition and microstructure is achieved with a microfluidic Hele-Shaw cell that possesses traps with varying trapping strengths to selectively immobilize different types of drops. This modular platform is not limited to the fabrication of hydrogels but can be employed for any material that can be processed into drops and solidified within them. It likely opens up new possibilities for the design of structured, load-bearing hydrogels, as well as for the next generation of soft actuators and sensors.
- This article is part of the themed collection: Lab on a Chip Recent HOT Articles


 Please wait while we load your content...
Please wait while we load your content...