Metachronal actuation of microscopic magnetic artificial cilia generates strong microfluidic pumping

Abstract

Biological cilia that generate fluid flow or propulsion are often found to exhibit a collective wavelike metachronal motion, i.e. neighboring cilia beat slightly out-of-phase rather than synchronously. Inspired by this observation, this article experimentally demonstrates that microscopic magnetic artificial cilia (μMAC) performing a metachronal motion can generate strong microfluidic flows, though, interestingly, the mechanism is different from that in biological cilia, as is found through a systematic experimental study. The μMAC are actuated by a facile magnetic setup, consisting of an array of rod-shaped magnets. This arrangement imposes a time-dependent non-uniform magnetic field on the μMAC array, resulting in a phase difference between the beatings of adjacent μMAC, while each cilium exhibits a two-dimensional whip-like motion. By performing the metachronal 2D motion, the μMAC are able to generate a strong flow in a microfluidic chip, with velocities of up to 3000 μm s⁻¹ in water, which, different from biological cilia, is found to be a result of combined metachronal and inertial effects, in addition to the effect of asymmetric beating. The pumping performance of the metachronal μMAC outperforms all previously reported microscopic artificial cilia, and is competitive with that of most of the existing microfluidic pumping methods, while the proposed platform requires no physical connection to peripheral equipment, reduces the usage of reagents by minimizing “dead volumes”, avoids undesirable electrical effects, and accommodates a wide range of different fluids. The 2D metachronal motion can also generate a flow with velocities up to 60 μm s⁻¹ in pure glycerol, where Reynolds number is less than 0.05 and the flow is primarily caused by the metachronal motion of the μMAC. These findings offer a novel solution to not only create on-chip integrated micropumps, but also design swimming and walking microrobots, as well as self-cleaning and antifouling surfaces.

---

1 Introduction

Biological cilia are slender microscopic hair-like protrusions of cells,¹ which exist ubiquitously in nature as a versatile means for fluid pumping,² cell transportation,³ mucus cleaning,⁴ assisting feeding⁵ and self-cleaning and antifouling,⁶ among others. For example, the collective asymmetric motion of active cilia covering the body of a paramecium is able to propel the aquatic micro-organism forward at a speed of 10 times its body length per second.² The asymmetric motion of each cilium has a whip-like shape with an effective stroke when the cilium beats more straight and a recovery stroke when the cilium beats more close to the body surface.⁷ Inspired by the impressive functionalities of biological cilia, researchers have been exploring the capabilities of artificial cilia in applications such as microrobots,^8,9 microsensors,^10,11 light, droplet and particle manipulation,^12,13 self-cleaning and antifouling surfaces,^14–16 microfluidic mixing,¹⁷ and predominantly, microfluidic pumping as integrated on-chip actuators in microfluidic devices.¹⁸ Most of the studies on artificial cilia for microfluidic pumping, including our own work, have focused on synchronous motion of artificial cilia,^19–25 where the artificial cilia perform a three-dimensional tilted conical motion. Among these studies, the reported maximum cilia-motion induced flow speed and volumetric flow rate is approximately 1350 μm s⁻¹ (ref. 24) and 40 μL min⁻¹,²⁵ respectively. Although some biological cilia do perform such tilted conical motion (e.g. in the embryonic node),²⁶ most natural cilia exhibit the whip-like motion described above and, moreover, they beat in a metachronal fashion, where neighboring cilia move slightly out-of-phase, to facilitate fluid transportation.^27–29 The specific metachrony is termed symplectic, antiplectic and laeoplectic when the metachronal wave travels in the same, opposite and perpendicular direction as the effective stroke, respectively.⁷ Numerical research has unveiled the advantages of metachronal motion by cilia, showing that both symplectic and antiplectic metachrony results in enhanced fluid flow compared to synchronous beating.^30–32 One numerical study has demonstrated that metachronal motion can lead to a 3-fold increase in propulsion velocity and a 10-fold increase in efficiency compared to synchronous motion.³³

The advantages of metachronal motion over synchronous motion have motivated researchers to explore manmade analogs of natural cilia that are capable of performing metachronal motion.^9,34–36 The mechanism for creating metachronal motion can be generalized into two categories: (a) applying different forcing to each cilium among an array of cilia, and (b) design an array of cilia with different responses to a uniformly applied forcing. In 2015, Gorissen et al. experimentally created metachronal motion for the first time using a pneumatically actuated array of artificial cilia that could be addressed separately using a sequential forcing mode, demonstrating an improved fluid pumping capability compared to synchronous motion.³⁴ These artificial cilia are of millimeter size which limits their integration in microfluidic devices, and the actuation setup is complex since each cilium needs a separate actuator with a physical connection by a tube. In 2016, Tsumori et al. designed an array of magnetic artificial cilia in which the direction of magnetization of adjacent cilia was different, by controlling the orientation of the magnetic particle distribution within the cilia.³⁵ Thus, these cilia responded differently to an applied uniform magnetic field, and consequently a metachronal motion was realized. Fluid flow experiments were however not reported. Moreover, these cilia (2 mm) are also too large to incorporate them into a typical microfluidic device. In addition, the fabrication process of these cilia is sophisticated and time consuming. Employing a similar design principle but a simpler fabrication process, in 2020, Gu et al. demonstrated programmable metachronal waves of magnetic cilia, and showed their capability of fluid pumping and creating soft walking robots.⁹ These cilia were also quite large (4 mm) limiting their incorporation into typical microfluidic devices. In 2018, Hanasoge et al. reported metachronal motion of an array of magnetic artificial cilia in which the cilia length was varied so that the cilia had a varying elastic stiffness, and they responded out-of-phase to a uniform rotating magnetic field.³⁶ The metachronal wave traveled perpendicularly to the effective stroke (laeoplectic metachrony). Fluid flow measurements were not reported by Hanasoge et al.³⁶ Taking together these studies, we conclude that to date, experimental research on the fluid pumping by metachronal motion of artificial cilia, especially with microscopic sizes, is still at an embryonic stage.

In this paper, we create metachronal motion of microscopic magnetic artificial cilia (μMAC), compatible with typical lab-on-a-chip devices. We analyze the cilia behavior as well as the generated fluid flow in depth, and we demonstrate that the metachronal μMAC can create strong fluid pumping in a microfluidic device, though the mechanism is different from that in biological cilia. The metachronal motion of the μMAC is realized using a simple actuation setup, composed of an array of rod-shaped magnets in which adjacent magnets have opposite magnetic dipole orientations. This configuration of alternating dipoles generates a non-uniform but periodic magnetic field. When translating this magnet array like a conveyer belt underneath the cilia array, the μMAC in the array move out of phase exhibiting metachrony, because the long axis of each μMAC continuously tends to align with the local magnetic field due to the magnetic torque.²⁵ Due to this actuation, each individual cilium exhibits a two-dimensional whip-like motion. For comparison and as a benchmark, we have also carried out experiments with an existing method, in which all the μMAC perform a synchronous three-dimensional tilted conical motion. We show that the metachronal whip-like motion of the μMAC is able to induce a strong water flow with a net velocity of up to 3000 μm s⁻¹ in a circular microfluidic channel, which is 30 times higher than that generated by the synchronous tilted conical motion, and is stronger than that generated by all previously reported microscopic artificial cilia. For glycerol, with a viscosity 1000 times that of water and thus ensuring a low Reynolds number (Re < 0.05) environment, a flow velocity of up to 60 μm s⁻¹ is reached, being somewhat less than that generated by the synchronous tilted conical motion. We show that, different from biological cilia, the fluid flow generation is caused by the combination of metachrony, inertial effects, and effects of asymmetric cilia motion; these three mechanisms are balanced differently for the different actuation modes, propelled liquids and frequencies. Since low viscous liquids such as water are often used in microfluidic applications, the reported metachronal motion offers an attractive novel solution for microfluidic pumping. Moreover, the metachronal motion of the μMAC may potentially facilitate the design of swimming and walking mini-robots.

2 Results and discussion

2.1 μMAC and actuation setup

The μMAC used in this article are fabricated from a magnetic composition of polydimethylsiloxane (PDMS) and carbonyl iron powder, using a facile and highly reproducible micro-molding process (Fig. 1A, details are available in the Experimental section).²⁵ In all experiments reported in this paper, the fabricated μMAC have a cylindrical shape with a diameter of 50 μm and a height of 350 μm (Fig. 1B), standing on a transparent non-magnetic PDMS substrate. The μMAC array consists of 10 × 10 + 9 × 9 = 181 cilia, and they are arranged in a staggered configuration with a pitch of 450 μm (Fig. 1C); the total ciliated area is therefore 4.1 mm by 4.1 mm, which can be appropriately adjusted to targeted applications. The reproducibility and uniformity of the produced μMAC are very good; analysis using scanning electron microscopy revealed only slight differences in dimension and shape between neighboring cilia, see Fig. 1B and C. These μMAC previously have been demonstrated to possess superior magnetic and actuation properties. These grant the μMAC various capabilities, when actuated in the conventional way, namely synchronously to perform a tilted conical motion, including generating versatile microfluidic flows in a microfluidic channel network,²⁵ creating self-cleaning and anti-fouling surfaces,^15,16 and directionally transporting single particles in a controlled manner in both water and air.³⁷

Fig. 1 Microscopic magnetic artificial cilia (μMAC) and actuation scheme for metachronal 2D whip-like motion. (A) Schematic illustration of the fabrication process of the μMAC. Details are available in the Experimental section. Illustrations are not to scale. (B) Side-view and (C) top-view scanning electron microscopy (SEM) images of the fabricated μMAC. The cylindrical μMAC have a diameter, a height and a pitch of 50, 350 and 450 μm, respectively. (D) Schematic drawing of the home-built magnetic actuation setup, which consists of a belt of rod-shaped magnets arranged with alternating dipole orientation between consecutive magnets as indicated in the figure. This setup is termed the “magnet–belt”. The rod-shaped magnets have a diameter of d_m = 4 mm and a length of 10 mm, and they have a remnant magnetic flux density of 1.2 T. The magnet–belt system contains 92 magnets in total, and the total width of the belt system is approximately 17 cm. The μMAC, supported by a glass plate with a thickness of 1 mm, are positioned 1.1 mm above the surface of the magnets. Illustrations are not to scale. (E) Snapshot of the magnetic flux density B induced by the rod-shaped magnets from a COMSOL simulation. The horizontal blue line indicates the position of the μMAC array. The red arrows indicate the direction of B at the μMAC level, i.e. 1.1 mm above the top surface of the magnets. (F) Magnetic field generated by the rod-shaped magnets from a COMSOL simulation, along the horizontal μMAC level line in panel E. (G) Side-view schematic diagram of the theoretically expected orientation of one row of μMAC at one specific instant, by assuming that the long axes of the μMAC align with the applied magnetic field and the μMAC are rigid rods that only bend at the anchor points. The blue line segments represent the μMAC, and y = 3.1 represents the PDMS substrate. (H) The angle between the μMAC and the PDMS substrate when the μMAC are assumed to align with the applied magnetic field in panel F. The phase difference is the angle difference between adjacent cilia, which is constant and approximately 20°.

A home-built magnetic actuation setup (Fig. 1D) consisting of a belt with magnets that is driven by an electric motor is used to actuate the μMAC to perform a metachronal 2D whip-like motion. This setup is termed the “magnet–belt”. The rod-shaped magnets have a diameter of d_m = 4 mm and a length of 10 mm, and are arranged to have alternating dipole orientation between consecutive magnets. In this way, a non-uniform but periodic magnetic field is generated (Fig. 1E). The μMAC array is positioned 1.1 mm above the surface of the magnets (indicated by the horizontal blue line in Fig. 1E), where the directions of the magnetic flux density B experienced by the μMAC are indicated by the red arrows. The details of the imposed magnetic field on the μMAC are depicted in Fig. 1F. As the long axes of the μMAC tend to align with the applied magnetic field, the μMAC array is predicted to perform a metachronal motion. The theoretically predicted μMAC orientation at one specific time instant is depicted in Fig. 1G, where the long axis of each cilium is assumed to align with the local magnetic field and the μMAC are regarded as rigid rods that only bend at the anchor points. In practice, obviously, the μMAC will not move into the substrate, like is suggested in this figure. It makes however clear that, when the magnetic field is now translated horizontally, which is done when translating the magnet–belt, the μMAC array is indeed expected to move in a metachronal fashion. The phase difference between adjacent cilia is approximately 20° for the whole cilia array when it is defined as the angle between the magnetic flux density B experienced by the adjacent cilia (Fig. 1H). The phase difference can be easily tuned by changing the cilia pitch, the distance between the rod-shaped magnets, and/or the diameter of the rod-shaped magnets. Table S1† shows an example of altering the phase difference through the aforementioned means. Note that the COMSOL simulation is a calculation of the magnetic field only, and does not include elastic or fluid considerations. The validation of the simulation results using the experimental results can be found in ESI† 2.

A circular microfluidic chip (Fig. 2A), with a rectangular cross-section with a width of 5 mm and a height of 660 μm, is used to characterize the flow pumping properties of the μMAC. A synchronous tilted conical motion of the same μMAC array is also realized using another home-built magnetic actuation setup (Fig. 2B) in order to compare the pumping efficiency of the two different cilia motions. Such an actuation mode is commonly reported for artificial cilia, so this synchronous motion functions as a benchmark. The setup contains a rotating magnet positioned at an offset r with respect to its rotating axis, while the center of the μMAC array is offset by the same distance d relative to the rotating axis, i.e. d = r = 6.5 mm. As a result, relative to the rotating magnet, the trajectory of the center of the μMAC array is a circle as indicated by the blue circle in Fig. 2C (details about the calculation of the cilia trajectory can be found in an earlier paper²⁵), where the red arrows indicate the generated magnetic flux density B at the level of the μMAC array, i.e. at h = 2 mm above the surface of the magnet, projected on the horizontal xy-plane. Details of the generated magnetic field can be found in Fig. S1.† All μMAC in the ciliated area of 4.1 mm by 4.1 mm experience almost the same magnetic field at each instant, and therefore the motion is synchronous.^15,25 In this way, each cilium is expected to perform a three-dimensional tilted conical motion (Fig. 2D) if it is assumed that the μMAC follow the applied magnetic field instantaneously and the μMAC are constantly straight, which mimics the motion of the cilia in the embryonic node.²⁶ This bio-inspired asymmetric motion consists of an effective stroke when the cilia beat more straight and a recovery stroke when the cilia beat more close to the substrate, which was previously demonstrated to be a simple yet effective asymmetric nonreciprocal motion to generate a net fluid flow in the same direction as the effective stroke.³⁸

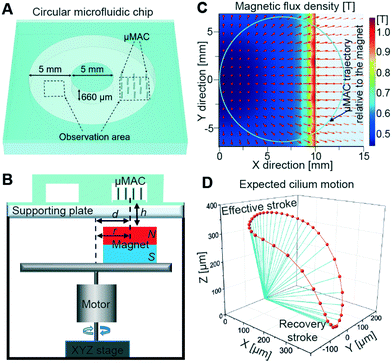Fig. 2 Microfluidic chip and synchronous 3D tilted conical motion. (A) A top-view schematic diagram of the microfluidic chip used to characterize the fluid pumping efficiency of the μMAC. The area containing the cilia array and the observation area for fluid flow are indicated. (B) Schematics of the homebuilt rotating magnetic setup (details are available in the Experimental section). Illustration is not to scale. (C) The distribution of the magnetic flux density B induced by the offset magnet, obtained from a COMSOL simulation. The center of the magnet (size 20 mm by 20 mm) is at the origin of the plot. The magnitude of the flux density is only shown in the area right above the magnet. The blue circle indicates the trajectory of the cilia relative to the center of the rotating magnet in a full beating cycle (details about the calculation of the cilia trajectory can be found in an earlier paper²⁵). The red arrows indicate the direction of B projected on the horizontal plane at the μMAC level, i.e. 2 mm above the top surface of the magnet. (D) A perspective view of the expected cilium motion by assuming that the long axis of the cilium continuously aligns with the applied magnetic field and the cilium is always straight. The blue line segments represent the cilium at various times with equal time intervals, and the red curve is the trajectory of the cilium tip. The cilium motion exhibits a titled cone.

2.2 μMAC motion

A side view of the resulting μMAC motion from the magnet–belt actuation is shown in Fig. 3A, where one row of μMAC performs an out of phase motion, exhibiting a metachronal wave, with each μMAC making a 2D motion in the vertical plane. Note that the rotating direction of the magnet–belt is always counterclockwise as indicated in Fig. 1D. The wavelength of the metachrony is 4 mm, corresponding to the diameter of the individual magnets on the belt (d_m), which also equals the period of the induced periodical magnetic field. The beating frequency of the μMAC (f) is determined by the traveling speed of the metachronal wave U_w that equals the translation speed of the belt, through

f = U_w/d_m (1)

The propagating metachronal wave in both water and glycerol can be clearly seen from both side view and top view in Movie ESI† 1. This metachrony is similar to that in Fig. 1G except that the μMAC do not move into the PDMS substrate, which obviously cannot happen in reality since the solid substrate prevents the μMAC from moving further upon touching it. Fig. 3B shows that each cilium performs a 2D asymmetric whip-like motion, consisting of (i) a magnetic stroke when the cilium mostly follows the applied magnetic field and bends to the right, thereby accumulating elastic energy (indicated by the blue dashed line), (ii) a sliding stroke when the cilium tip reaches its rightmost position and starts to move to the left, (almost) touching the surface, accumulating additional elastic energy (indicated by the orange line), and (iii) an elastic stroke when the cilium tip starts to move upwards and whips back to its upright position by releasing the accumulated elastic energy (indicated by the red dashed line). This motion is more complex than for biological cilia and therefore it cannot be unequivocally described in terms of ‘effective’ and ‘recovery’ strokes. A high-speed video of the elastic stroke part of the 2D asymmetric motion in both water and glycerol is available in Movie ESI† 2. This movie shows that the cilium vibrates for a certain time at the end of the elastic stroke before it reaches its equilibrium state in water, but not in glycerol. This is a result of the competition between the elastic forces, magnetic forces and the fluidic viscous drag, the latter being around 1000 times larger in glycerol based on Stokes' law. It has been demonstrated in previous studies that a net flow can be induced in the same direction as the so-called effective stroke when the cilia perform a 2D asymmetric motion, under the condition that Stokes conditions prevail.^21,24,39 The latter means that the Reynolds number (Re), characterizing the local flow at the position of the cilia, is small. In this 2D asymmetric motion under Stokes conditions, the effective stroke is defined as the stroke during which the cilium sweeps a larger area than during the other stroke in one beating cycle. According to this definition, the effective stroke of our μMAC corresponds to the magnetic stroke in Fig. 3B. It is shown in Fig. 3A and Movie ESI† 1 that the metachronal wave induced by the magnet–belt travels in the opposite direction to the magnetic stroke, thus the metachrony is antiplectic. Note, even when the rotating direction of the magnet–belt is reversed, the metachronal wave will remain travelling in the opposite direction to the magnetic stroke. In another words, we can only create antiplectic metachrony using the proposed platform. It can also be seen in Fig. 3B that the μMAC motion remains almost the same for all frequencies in water, whereas the μMAC motion dramatically reduces in glycerol when the beating frequency increases. This can be explained using the dimensionless quantity – the sperm number,⁴⁰ which is the ratio of the viscous to the elastic/bending forces on a cilium, through

Sp = L[8π²ηf/EI]^1/4 (2)

where L = 350 μm is the length of the cilia, η is the viscosity of the liquid (1 mPa s for water and 1.4 Pa s for glycerol), f is the beating frequency of the cilia (i.e., the actuation frequency, 1–100 Hz), E is the Young's modulus of the cilia (here we use 2 MPa),⁴¹ and I = πd⁴/4 is the area moment of inertia of the cilia with d = 50 μm the diameter of the cilia. The calculated Sp ∈ [0.1, 0.33] in water, and Sp ∈ [0.63, 2.1] in glycerol with Sp = 1 at a beating frequency of approximately 6 Hz. This means that in water the elastic/bending forces always dominate, and that in glycerol the viscous forces dominate at beating frequencies over 6 Hz. Consequently, the cilia motion is independent of the actuation frequency in water, while the cilia motion is hampered by the viscous forces in glycerol at actuation frequencies over 6 Hz as observed in Fig. 3B.

Fig. 3 μMAC motion. (A) Side-view snapshots of the μMAC motion resulting from the magnet–belt actuation at 1 Hz in glycerol, showing a metachronal wave. A video of the motion is available in Movie ESI† 1. (B) Side-view time-lapse images of cilium motion activated by the magnet–belt at different actuation frequencies in both water and glycerol, showing a 2D asymmetric motion. OA means the opening angle of the cilium motion in a complete cycle. The top row images are overlays of 50 000/f frames during one beating cycle, where f is the actuation frequency. The blue dashed line, the orange line and the red dashed line indicate the tip trajectory during the magnetic stroke, sliding stroke and elastic stroke, respectively. A video of the cilium motion in both water and glycerol is available in Movie ESI† 2. (C) Top-view time-lapse images of the μMAC motion resulting from the rotating magnet at different actuation frequencies in both water and glycerol, showing a 3D tilted conical motion. The images are composed of 25 frames in one rotating cycle. OA means the opening angle of the μMAC motion in a complete cycle. The red arrow indicates the effective stroke, and the blue arrow indicates the recovery stroke. A video of the tilted conical motion in both water and glycerol is available in Movie ESI† 3. (D) The projected tilted conical motion on the XY plane from Fig. 2D, which matches well with the experimental results in panel C.

A top view of the 3D synchronous μMAC motion actuated by the rotating magnet is depicted in Fig. 3C. A top-view high-speed video of this synchronous μMAC motion in both water and glycerol is available in Movie ESI† 3. It is clear that there is no obvious motion difference among the whole cilia array, and thus the μMAC are indeed actuated to perform a synchronous 3D tilted conical motion with a maximum bending angle of 75° (details are given in ESI† 4). Moreover, the μMAC motion only slightly changes in both water and glycerol when the actuation frequency increases (up to 50 Hz in this article). The experimental results are well predicted by the simulation as shown in Fig. 2D and 3D, except for the obvious difference in the recovery stroke during which the experimental bending angle is smaller than the simulated results which have a maximum bending angle of 90°. This is due to the fact that in the simulation the cilia are assumed to be always straight including during the recovery stroke, which is not the case in reality.

2.3 Microfluidic pumping

The generated flow speed of water and glycerol by both the metachronal 2D motion and the synchronous 3D tilted conical motion, measured at the geometrical center of the microfluidic channel (where the velocity is maximal), is depicted in Fig. 4A. A positive result means that the flow is in the same direction as the traveling direction of the metachronal wave or the direction of the effective stroke of the synchronous 3D motion. Fig. 4C shows some examples of the trajectories of the tracked tracer particle over a certain period of time at a specific actuation frequency made with ImageJ, indicating the speed and direction of the generated flow. Note that as the cilia are performing cyclic motions, cyclically reversing flow may occur, which we indeed observed in the recorded movies for glycerol. The flow reversal is not visible in Fig. 4C since the reversed motion is directed exactly opposite to the forward flow, and in the color streaks the two can therefore not be distinguished. Flow reversal was not observed for the water experiments at a recording frame rate of 200 fps. This is likely due to the fact that inertia plays an important role for the water experiments, or our recording rate is not high enough to detect the reversed flow.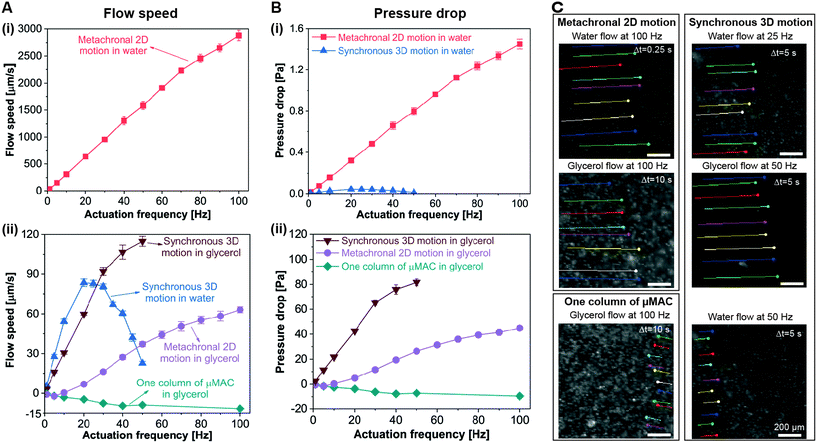

Fig. 4 Fluid pumping capability of the μMAC. (A) Generated flow speed as a function of the actuation frequency, measured at the geometrical center of the microfluidic channel, where the velocity is maximal. As the flow speed of water generated by the metachronal 2D motion is approximately two orders of magnitude higher than that of the other conditions, we plotted it in a separate figure, namely panel (i). A positive result represents a flow in the same direction as the traveling direction of the metachronal wave or the direction of the effective stroke for the synchronous 3D motion. (B) Corresponding pressure drop generated by the μMAC. Details about the calculation of the volumetric flow rate and the pressure drop are available in ESI† 5. All error bars are standard deviations of the obtained data of at least five measurements. (C) Trajectories of the tracked tracer particles over a period of time Δt at a specific actuation frequency, which indicate the speed and direction of the generated flow. The color streaks are the trajectories of the tracked tracer particles made with ImageJ. All scale bars are 200 μm.

Several observations can be made from the results, which we will list first and discuss further later. First, the metachronal motion generates a strong water flow and the flow velocity is always positive, i.e. in the direction of the metachronal wave, and approximately proportional to the actuation frequency. The maximum water flow velocity generated by the metachronal motion is around 3000 μm s⁻¹ at an actuation frequency of 100 Hz. Second, the glycerol flow generated by the metachronal motion is in the opposite direction to the traveling direction of the metachronal wave up to 10 Hz and hence in the magnetic stroke direction (since the velocity is slightly negative). Beyond 10 Hz, it turns positive, i.e. it changes direction, and increases proportionally to the actuation frequency until 50 Hz, after which it increases less than linearly with the actuation frequency. Finally, it reaches a maximum of around 60 μm s⁻¹ at an actuation frequency of 100 Hz. Third, results for a single column of 10 μMAC actuated in glycerol with the magnetic–belt setup are included in the Fig. as well; since the column is aligned perpendicularly to the belt motion (and hence parallel to the long axis of the rod-shaped magnets), all these μMAC move synchronously exhibiting the 2D whip-like motion, but metachrony is by definition absent. In this case, a negative glycerol flow is induced, which means that the generated flow is in the same direction as the magnetic stroke. Fourth, the water flow generated by the synchronous 3D tilted conical motion is in the direction of the effective stroke, and initially increases linearly with the actuation frequency before reaching a maximum of around 90 μm s⁻¹ at an actuation frequency of 20 Hz, after which it drops with the actuation frequency. Fifth, the glycerol flow generated by the synchronous 3D conical motion initially increases linearly with the actuation frequency up to 30 Hz, subsequently the increase is less than linear, and the velocity reaches a maximum of around 120 μm s⁻¹ at an actuation frequency of 50 Hz (the limit of the rotating magnet). Sixth, comparing the flow velocities for the two fluids due to the synchronous 3D motion, Fig. 4A shows that the water velocity is larger than that of glycerol up to 25 Hz, around which frequency the water velocity drops as we have seen above, but the glycerol velocity continues to increase and exceeds the water velocity. Finally, we compare the metachronal 2D results with the synchronous 3D observations. For glycerol, the flow velocity is substantially higher for the synchronous 3D tilted conical motion than for the metachronal 2D actuation, i.e. about a factor of three larger at 50 Hz. For water, on the other hand, the maximum speed generated by the metachronal motion is more than 30 times higher than that generated by the synchronous 3D tilted conical motion.

The corresponding volumetric flow rate and pressure drop (which is the pressure difference between the locations right before and after the ciliated area) are plotted in Fig. S3† and 4B, respectively (details of the calculation are given in ESI† 5). Both the volumetric flow rate and the pressure drop show a similar trend as the flow speed. Specifically, in our circular microchannel, the metachronal 2D motion can generate a water and glycerol flow rate of around 350 μL min⁻¹ and 8 μL min⁻¹, respectively, and it can generate a water and glycerol pressure drop of around 1.5 Pa and 45 Pa, respectively. The synchronous 3D motion is able to generate a water and glycerol flow rate of around 10 μL min⁻¹ and 14 μL min⁻¹, respectively, and it can generate a water and glycerol pressure drop of around 0.04 Pa and 80 Pa, respectively. Both motions outperform most of the previously published artificial cilia in terms of fluid pumping (see ESI† 6 for a detailed comparison between the μMAC reported in this article and previously published artificial cilia). Especially, the metachronal 2D motion outperforms all of the previously reported artificial cilia except for the millimeter-size pneumatic cilia (see Table S2†).³⁴ Moreover, the pumping performance of the μMAC is competitive with that of most of the existing microfluidic pumping methods including electro-hydrodynamic, piezoelectric, electroosmotic and electrostatic micropumps as shown in ESI† 6,^42–44 while the proposed platform requires no physical connection to peripheral equipment, reduces the usage of reagents by minimizing “dead volumes”, avoids undesirable electrical effects, and accommodates a wide range of different fluids.

To explain the results shown in Fig. 4A on the flow speeds, we note that several mechanisms can be at play in fluid flow generation by artificial cilia.¹ In general, most artificial cilia reported up to date, just like biological cilia, operate in the low Reynolds number (Re) regime, also called the Stokes flow regime. This means that inertial effects are not important, and the flow is dominated by viscous effects. Consequently, to generate any net flow, an individual cilium needs to move asymmetrically, i.e. having a different forward trajectory compared to backward trajectory during one beating cycle. For a 2D motion, like in our metachronal configuration, the asymmetry is achieved when the swept area in one beating direction is larger than that in the other direction due to the varying curvature of the beating cilium, which is indeed the case as shown in Fig. 3B: the swept area of the magnetic stroke is larger which is why we call it the effective stroke. For the 3D tilted conical motion, the asymmetry is achieved by the cilium moving straight-up in one direction, and more closely to the substrate in the other direction. The former is called the effective stroke since then the cilium effect on the fluid will be larger. In the Stokes regime, a net flow will always be generated in the direction of the effective stroke, and temporal asymmetry (i.e. the cilium moving faster in one direction than in the other) does not have an effect due to the absence of inertia. However, when the cilium motion is so fast that the local Reynolds number Re, based on cilia dimensions and local velocity, becomes substantially larger than 1, inertial effects become important, and in that case temporal asymmetry may start to dominate over the effect of spatial asymmetry, i.e. the net flow generation is in the direction of the fastest stroke. This regime was for example reached in electrostatically actuated artificial cilia we reported previously.¹⁷ Finally, as mentioned earlier, in the case of metachrony the collective motion of cilia can have an additional effect on the net fluid flow generation. In our various experiments, these three effects (spatial asymmetry, temporal asymmetry and metachrony) are balanced differently as we will see in the following.

With this in mind, the positive water flow generation by the metachronal motion (the first observation mentioned earlier), i.e. in the direction of the metachronal wave and the elastic stroke, but opposite to the magnetic (‘effective’) stroke, can be explained as follows. First, as shown in Fig. 5A, the μMAC beat much faster during the elastic stroke than during the other strokes. In case of Stokes flow, this should not make a difference, and the flow generation is expected to be in the direction of the ‘effective’ magnetic stroke (i.e. the negative direction) since the area swept during the magnetic stroke is larger than during the elastic stroke, as shown quantitatively in Fig. 5B for all frequencies.^21,24,39,45 However, the instantaneous maximal local Re during the elastic stroke is around 900 (details are available in ESI† 7), which is much larger than 1, thus inertial effects dominate the flow locally during the elastic stroke. This inertial effect at least partially explains the observed net flow generation in the elastic stroke direction at all frequencies, overruling the effect of the net swept area. In addition to the inertial effect, the propagating metachronal wave very likely contributes to the transportation of the liquid as well, since the observed net flow also has the same direction as the wave propagation. However, at this point the contributions of both these mechanisms (inertia and metachrony) to the net flow cannot be distinguished. This will become clearer when we consider the glycerol results, below.

Fig. 5 Quantitative analyses of the μMAC motion. (A) Tip speed in water during one beating cycle when the μMAC are actuated by the magnet–belt exhibiting metachronal 2D motion, as a function of time normalized by cilia cycle period. (B) Swept area by the μMAC during different strokes when the μMAC are actuated by the magnet–belt. (C) Opening angle of the μMAC motion as a function of the actuation frequency. The definition of the opening angle (OA) is indicated in Fig. 3. (D) Tip speed in one beating cycle when the μMAC are actuated by the rotating magnet to perform the tilted conical motion. The tip speed is calculated according to the simulated data in Fig. 2D. (E and F) Snapshots of the metachronal 2D motion of one row of μMAC in glycerol at an actuation frequency of (E) 50 Hz, and (F) 100 Hz showing a weakened metachronal wave. See also Movie ESI† 4. All error bars are standard deviations of the obtained data of at least five measurements.

The linear increase of water flow velocity with frequency in the metachrony experiments can be explained as follows. Note from Fig. 5A that the maximum tip speed has the same order of magnitude for all actuation frequencies. This is because the tip speed derives from the release of the accumulated elastic energy (which is almost constant since the cilia motion is almost the same at all frequencies in water) in combination with viscous drag. Moreover, the cilium is not driven by the applied magnetic field during the elastic stroke, which means the long axis of the cilium does not align with the applied magnetic field. Combined with the observation that the μMAC perform almost the same 2D motion at all actuation frequencies as evidenced by the barely changing opening angle of the μMAC motion in Fig. 3B and 5C, this leads us to conclude that the μMAC array transports almost the same amount of water during each cycle of metachronal wave, and therefore the flow speed scales linearly with the actuation frequency. It is expected that the water flow speed will increase further at higher frequencies than 100 Hz.

Turning to the glycerol results for the metachrony experiments (observation two), it is important to stress first that the glycerol flow is governed by viscous effects since Re in glycerol is much smaller than 1 at all frequencies (see Fig. S5B†), so inertial effects will not play a role and we have Stokes flow. This is completely different than for water, because of the high viscosity of the glycerol and consequently the lower cilia tip speed during the elastic stroke due to increased viscous drag, see Fig. S5A.† Hence, a single cilium is expected to generate a net fluid flow in the direction of the stroke that has the largest swept area, i.e. the magnetic stroke as can be seen in Fig. 3B and quantitatively in Fig. 5B. This behavior is indeed seen at low frequencies, and also for the single column of cilia actuated in glycerol by the magnet–belt when the metachrony is absent (observation three). In case the cilia array exhibits metachronal behavior however, the flow velocity changes direction with frequency, and becomes positive around 10 Hz, now directed along with the metachronal wave. Since inertia remains unimportant, this must be the effect of metachrony, which counteracts the effect of asymmetric cilia motion. From 10 Hz, the flow speed continues to increase linearly with actuation frequency which indicates that the metachronal wave transports the same amount of glycerol in each wave cycle. The μMAC motion, however, is clearly diminished with increasing frequency, due to the increasing viscous drag acting on the cilia (Fig. 3B and 5C), but this reduces the effect of the metachronal wave as well as that of the counteracting effect of swept area (see Fig. 5B). The metachronal wave remains in operation, though (see Movie ESI† 4), and the net balance of the two effects results in the observed linear velocity increase with frequency. However, when the actuation frequency goes beyond 50 Hz the μMAC motion is dramatically diminished (Fig. 3B and 5C), resulting in a weakened metachronal wave (Fig. 5E and F; see also Movie ESI† 4). As a result, the metachronal wave becomes less efficient for pumping glycerol, leading to a less-than-linear relationship between the flow speed and the actuation frequency.

The metachrony experiments with glycerol in combination with the single column experiments convincingly show that the metachronal wave has an important contribution to the net flow generation. Hence, the wave must also play a role in the flow generation in the metachrony experiments with water, discussed above. In that case, the effects of metachrony and inertia act together, leading to the much higher flow speeds in water than in glycerol, since inertia is absent in the latter.

Moving to the results we obtained for the synchronous 3D tilted conical motion in Fig. 4A (observations four and five), we observe that these are largely consistent with earlier reports,^{22,23,25,38,46} but the current results shed more light on the mechanism of the flow generation and form a good benchmark for the metachronal 2D results. Regarding the fourth observation, about the water flow generated by the synchronous 3D motion, the possible explanations are as follows. First, in contrast to the metachronally driven water flow, Re is small at actuation frequencies lower than 10 Hz (Re < 10 as shown in Fig. S5B†) so inertial effects are less important and the Stokes flow regime prevails; hence we see a net (positive) flow in the effective stroke direction. Moreover, as shown in Fig. 5C, the opening angle is constant at low actuation frequencies so that the μMAC largely follow the magnetic field in all cases; hence, in each revolution cycle the μMAC transport the same amount of liquid,³⁸ and therefore the flow speed scales linearly with frequency. For higher frequencies, however, the local Reynolds number increases (Fig. S5B†) up to 50 at 50 Hz, and inertial effects will begin to play an increasing role.⁴⁷ As shown in Fig. 5D, during the tilted conical motion the cilia on average move faster during the recovery stroke than during the effective stroke, which counteracts the induced net flow in the effective stroke direction, causing the generated net flow to decrease by inertial effects when the actuation frequency goes higher than 20 Hz. It is expected that the net flow will decrease further at higher frequencies than 50 Hz, and the net flow may even be in the opposite direction to the effective stroke at much higher frequencies than 50 Hz. A second factor that could play a role in decreasing the generated flow at higher frequencies, is the diminished μMAC motion as shown in Fig. 5C as a decrease in opening angle. Hence the μMAC transport a decreased amount of water per rotating cycle. Note that the decreased μMAC motion is mainly due to the fact that the μMAC are not able to fully follow the fast rotating magnet, and only slightly because of the increased hydrodynamic drag at higher frequencies since the opening angle is only slightly smaller in glycerol (Fig. 5C) where the viscous drag is around 1000 times larger. Another aspect that had an influence on the net flow in the microchannel is that complex 3D flow patterns are actually induced by the rotating μMAC in and around the ciliated area, resulting in local backflow and recirculation (see Movie ESI† 5), diminishing the net flow generation. These secondary flows become more and more vigorous at frequencies beyond 20 Hz since then the inertial effects already play an important role.

The flow generation of glycerol by the synchronous tilted conical motion (observation five) is fully dominated by viscosity because inertial effects are negligible since Re is much lower than 1 (Fig. S5B†). Hence, Stokes flow prevails, and the flow generation is caused by the (3D) asymmetry of the cilia motion, in the direction of the effective stroke. The opening and tilting angle of the cone traced by the μMAC determine the displaced fluid per rotation cycle. Since these remain constant up to 30 Hz (Fig. 5C), the velocity is proportional to the frequency in that range. At higher frequencies, the opening angle decreases (Fig. 5C) since the cilia cannot fully follow the magnetic field, and consequently the velocity increases less-than-linearly with frequency.

At low frequencies, Fig. 5C shows that the opening angle of the conical motion in water is slightly larger than in glycerol presumably due to lower viscous drag in water, so the generated velocity is larger in water (Fig. 4A, observation six). When inertia starts to dominate in water at higher frequencies, the generated water velocity drops below that of glycerol in which inertia remains absent as we have argued.

To explain the difference between the metachronal-2D and the synchronous-3D velocity data in Fig. 4A (final observation), we need to take into account that these experiments are different in two ways: first, the individual motion of the cilia is completely different (2D whip-like motion versus 3D tilted conical motion), and second the metachrony itself is either present or absent. As a consequence, depending on the viscosity of the fluid, the balance between the influence of spatial asymmetry, inertia (in combination with temporal asymmetry), and metachronal behavior was different depending on actuation mode and frequency. In the absence of inertia, such as in glycerol, the spatial asymmetry of the motion is important and a comparison between the 2D whip-like motion and the 3D tilted conical motion (Fig. 3) suggests that this mechanism is stronger for the tilted cone than for the whip-like shape in our experiments, since the net swept area is smaller for the latter. This is confirmed by the fact that the synchronous-3D actuation gives a higher fluid velocity than the metachronal-2D actuation in glycerol. However, the metachronal wave, here counteracting the spatial asymmetry effect, still enables to produce substantial fluid flow in glycerol even though the spatial asymmetry is small. Therefore, a collaborative instead of counteracting combination of asymmetric motion and metachronal motion (i.e. symplectic metachrony) would most likely enhance the fluid pumping in high viscous liquids. In water, the combined effects of inertia and metachronal wave lead to the very strong flow generation for the metachronal-2D actuation that is much higher than for the synchronous-3D actuated flow that is only driven by spatial asymmetry and in which the other effects are smaller (inertia) or absent (metachrony).

Finally, an important feature of the metachronal motion of the μMAC array, is that it is capable of generation versatile flows such as direction-reversible flow, oscillating flow and pulsatile flow, by reversing the translation direction of the magnet–belt, periodically altering its translation direction, and periodically changing its translation speed, respectively, through the control of the motor driving the belt. This is because the cilia motion is perfectly mirrored when the direction of the magnet–belt is reversed, and the cilia respond to the applied magnetic field immediately. Such versatility has already been demonstrated for the synchronous 3D motion.²⁵ Movies ESI† 6–8 show examples of the versatility of flow generation by the metachronal motion of the μMAC in water.

3 Conclusions

We have demonstrated the strong microfluidic pumping properties of the unique metachronal motion of microscopic magnetic artificial cilia (μMAC) by using a facile magnetic setup. The custom-made setup consists of a translating belt with an array of rod-shaped magnets in which adjacent magnets have opposite magnetic dipole orientations. This generates a non-uniform but periodic magnetic field, which causes adjacent cilia to move out-of-phase so that a metachronal wave is created. The individual cilia exhibit a two-dimensional whip-like motion with several phases, where especially the magnetic stroke and the elastic stroke play an important role. The magnetic stroke has a larger swept area and is primarily determined by the μMAC rotating with the magnetic field; the elastic stroke is determined by elastic recovery of the cilia combined with viscous drag and is faster but has a smaller swept area. The generated fluid flow is determined by the combined effects of motion asymmetry due to the difference in swept area, inertia due to temporal asymmetry, and metachrony. In glycerol, inertial effects are negligible (since Re < 0.03) and the fluid flow is due to the combination of motion asymmetry and metachrony, where the latter is dominant at higher frequencies, which proves that the metachronal motion has a substantial contribution to flow generation. The metachronal 2D μMAC actuation in glycerol is capable of generating a flow speed of up to 60 μm s⁻¹ at a beating frequency of 100 Hz (corresponding to a volumetric flow rate of 8 μL min⁻¹ and a pressure drop of 45 Pa in our microfluidic device). In water, however, inertia plays a dominant role (since the maximal Re during the elastic stroke is larger than 600 at all frequencies), and the flow generation by the metachronal 2D μMAC actuation is determined by the combined effect of temporal asymmetry and metachrony. This results in a water flow speed of up to 3000 μm s⁻¹ at 100 Hz, which corresponds to a volumetric flow rate and a pressure drop of 350 μL min⁻¹ and 1.5 Pa, respectively, in our microfluidic device. The flow speed can be tuned by adjusting the frequency.

Although the metachronal 2D actuation of the artificial cilia is inspired by biological cilia systems, and indeed at first sight is similar to what is observed in nature, our results show that its working principle, especially in water, is different since in biological cilia systems inertia is always negligible. For applications in microfluidic pumping, however, the strong effect of inertia in our μMAC system offers great opportunities. The importance of inertia is also clear from the comparison of the metachronal-2D results with results from commonly used synchronous 3D tilted conical motion actuation of the μMAC. The water flow generated by the metachronal-2D motion is more than 30 times higher than that generated by the synchronous-3D motion, while the glycerol flow generated by the metachronal-2D motion is only 1/3 of that generated by a synchronous-3D motion, partially due to the counteracting effect of the motion asymmetry against the metachrony although the asymmetry is small. This also indicates that a collaborative combination of asymmetric motion and metachronal motion would most likely enhance the flow pumping; this mode of operation is however out of reach using our current actuation method. Note that our actuation setup has a limited working distance from the μMAC, but still the moving belt is a relatively bulky setup compared to the microfluidic chip, especially for portable applications. In addition to miniaturizing the size of the belt by reducing the amount of the rod magnets and using smaller rod magnets than used here, this may be addressed by the integration of mushroom-shaped soft magnetic micro structures in the substrate of the cilia array, which can create a local non-uniform magnetic field traveling along the substrate surface when exposed to a uniform rotating magnetic field generated by e.g. an electromagnetic setup, quite similar to the time-dependent field caused by the magnet–belt.⁴⁸ This topic is currently under investigation. Another solution is to create a cilia array with different orientations in magnetic anisotropy in neighboring cilia so that they can perform metachronal motion under the actuation of a uniform magnetic field.^9,35

Our metachronal-2D actuation of μMAC in water outperforms all previously reported microscopic artificial cilia in terms of fluid pumping (see Table S2†). Moreover, the pumping performance of the μMAC is competitive with that of most of the existing microfluidic pumping methods,^42–44 while the proposed platform requires no physical connections to peripheral equipment, reduces the usage of reagents by minimizing “dead volumes”, avoids undesirable electrical effects, and accommodates a wide range of different fluids. These findings provide a novel way to create on-chip integrated versatile micropumps. In addition, the propagating metachronal wave may find other potential applications, including walking and swimming microrobots, particle manipulation, self-cleaning and antifouling surfaces, and signal transmission.

4 Experimental section

4.1 Fabrication of μMAC

The μMAC used in this article are the so-called LAP MAC (MAC with linearly aligned magnetic particles along the cilia's long axis) reported in our previous study.²⁵ In summary, the fabrication consisted of six steps as shown in Fig. 1A: (1) A 350 μm thick SU-8 mold, featured with an array of microwells of 10 × 10 + 9 × 9 = 181, was fabricated using standard photolithography. (2) A uniform magnetic precursor mixture of polydimethylsiloxane (PDMS, Sylgard 184, Dow Corning, base to curing agent weight ratio is 10 : 1) and magnetic microparticles (carbonyl iron powder, CIP, 99.5%, SIGMA-ALDRICH) was casted onto the mold, followed by a degassing procedure. The weight ratio between PDMS and CIP was 1 : 2. (3) The excess magnetic mixture outside the micro-wells was removed. (4) Pure PDMS (base to curing agent weight ratio = 10 : 1) was poured onto the mold. After degassing the pure PDMS layer was defined to a thickness of 100 μm by spin-coating at a rotating speed of 500 rpm for 50 s. (5) The sample was left in an oven at 80 °C for 3 hours to cure the mixture, during which a permanent magnet with a size of 15 × 15 × 8 mm³ and a remnant flux density of 1.2 T was put underneath the mold in order to align the magnetic particles within the mold. (6) The cured pure PDMS layer with PDMS–CIP micropillars was peeled off the mold. Finally, the μMAC with the same geometry as the mold, namely a diameter, a height and a pitch of 50 μm, 350 μm and 450 μm, respectively, were obtained (Fig. 1A), “standing” on a transparent PDMS base substrate.

4.2 Characterization of the metachronal motion

The metachronal motion of one row of μMAC was recorded using a high-speed camera (Phantom V9) connected to a stereo microscope (Olympus SZ61) from both the side and the top. This row of μMAC consisting of 10 cilia (i.e., one row of cilia) was cut off from the μMAC array in order to see the metachronal motion clearly. We chose an array of 10 cilia because 10 cilia make up exactly one row of cilia in our design. Moreover, as the cilia have a pitch of 450 μm, the total length of this cilia array is 4.1 mm, which is just a bit more than one metachronal wavelength (i.e., 4 mm, determined by the diameter of the rod magnets). This is a minimal but sufficient configuration to study the metachronal behavior. In future applications, naturally, larger cilia arrays can be used. The motion of a single cilium in water and glycerol was also captured using the high-speed camera at a frame rate of 50 000 fps and 1000 fps, respectively. The captured motion was analyzed with ImageJ to study the trajectory of the cilia, the opening angle of the motion, the swept area of the motion, and the speed of the cilia tip.

4.3 Rotating magnetic setup

The homebuilt rotating magnetic setup (shown in Fig. 2B) was comprised of a manual linear XYZ translational stage at the bottom, an electric motor in the middle, a magnet mounted off-axis on the motor, and a safety box containing the supporting plane on top of which the chip containing the μMAC could be placed. The magnet, which had a geometry of 20 × 20 × 10 mm³ with a remnant flux density of 1.3 T, was positioned at an offset of r = 6.5 mm with respect to its rotation axis. The center of the ciliated surface was vertically aligned with the center of the magnet (when the magnet is in its rightmost position as in Fig. 2B), i.e. d = r = 6.5 mm. The supporting plane was a transparent glass plate of thickness of 1.5 mm, coated with a layer of PDMS (100 μm, base to curing agent weight ratio = 10 : 1, cured at 80 °C for 3 hours). The high-speed camera (Phantom V9) mounted on the stereo microscope (Olympus SZ61) was used to capture the movement of the μMAC from right above by taking image sequences at a frame rate of 25f fps, where f is the revolution frequency of the μMAC.

4.4 Characterization of the flow generated by the μMAC

The flow generated by the μMAC was characterized at specific flow observation areas, indicated in Fig. 2A. The used liquids were deionized water and pure glycerol, and the flow speeds were visualized by seeding the fluids with 12 μm polystyrene tracer particles (micromod Partikeltechnologie GmbH). The high-speed camera (Phantom V9) connected to the stereo microscope (Olympus SZ61) was used to record the movement of the tracer particles by taking image sequences at a specific frame rate of 200 fps. The speed of the tracer particles in the geometrical center of the microfluidic channel (i.e. at a height of 330 μm above the channel substrate where the flow speeds are the highest) was measured by a manual tracking analysis using ImageJ. To obtain the data shown in Fig. 4, at least five independent measurements were done of which the mean and standard deviation were determined.

Author contributions

S. Z. Z. conceived and designed research; S. Z. Z. and Z. W. C. performed experiments and analyzed data; S. Z. Z. drafted the manuscript, Z. W. C., Y. W. and J. M. J. D. T. revised the manuscript, and J. M. J. D. T. supervised the project.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The research leading to these results has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme under grant agreement no. 833214. We thank Erwin Dekkers and Remco Felten of the TU/e Equipment & Prototyping Center for constructing the magnetic actuation setups. Zhiwei Cui is financially supported by the China Scholarship Council under grant no. 201706400061.

References

1. J. M. J. den Toonder and P. R. Onck, Artificial Cilia, RSC Publishing, Cambridge, 2013.
2. J. R. Blake and M. A. Sleigh, Biol. Rev., 1974, 49, 85–125.
3. L. J. Fauci and R. Dillon, Annu. Rev. Fluid Mech., 2005, 38, 371–394.
4. Y. Enuka, I. Hanukoglu, O. Edelheit, H. Vaknine and A. Hanukoglu, Histochem. Cell Biol., 2012, 137, 339–353.
5. H. U. Riisgard and P. S. Larsen, Limnol. Oceanogr., 2001, 46, 882–891.
6. M. G. Stafford-Smith and R. F. G. Ormond, Mar. Freshwater Res., 1992, 43, 683–705.
7. H. Machemer, J. Exp. Biol., 1972, 57, 239–259.
8. H. Lu, M. Zhang, Y. Yang, Q. Huang, T. Fukuda, Z. Wang and Y. Shen, Nat. Commun., 2018, 9, 3944.
9. H. Gu, Q. Boehler, H. Cui, E. Secchi, G. Savorana, C. De Marco, S. Gervasoni, Q. Peyron, T. Y. Huang, S. Pane, A. M. Hirt, D. Ahmed and B. J. Nelson, Nat. Commun., 2020, 11, 1–10.
10. N. J. Sniadecki, A. Anguelouch, M. T. Yang, C. M. Lamb, Z. Liu, S. B. Kirschner, Y. Liu, D. H. Reich and C. S. Chen, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 14553–14558.
11. N. J. Sniadecki, C. M. Lamb, Y. Liu, C. S. Chen and D. H. Reich, Rev. Sci. Instrum., 2008, 79, 1–8.
12. Y. Zhu, D. S. Antao, R. Xiao and E. N. Wang, Adv. Mater., 2014, 26, 6442–6446.
13. S. Zhang, Y. Wang, P. Onck and J. den Toonder, Microfluid. Nanofluid., 2020, 24, 1–20.
14. A. C. Balazs, A. Bhattacharya, A. Tripathi and H. Shum, J. Phys. Chem. Lett., 2014, 5, 1691–1700.
15. S. Zhang, Y. Wang, P. R. Onck and J. M. J. den Toonder, Adv. Funct. Mater., 2019, 29, 1806434.
16. S. Zhang, P. Zuo, Y. Wang, P. Onck and J. M. J. den Toonder, ACS Appl. Mater. Interfaces, 2020, 12, 27726–27736.
17. J. Den Toonder, F. Bos, D. Broer, L. Filippini, M. Gillies, J. De Goede, T. Mol, M. Reijme, W. Talen, H. Wilderbeek, V. Khatavkar and P. Anderson, Lab Chip, 2008, 8, 533–541.
18. J. M. J. den Toonder and P. R. Onck, Trends Biotechnol., 2013, 31, 85–91.
19. M. Vilfan, A. Potocnik, B. Kavcic, N. Osterman, I. Poberaj, A. Vilfan and D. Babic, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 1844–1847.
20. A. R. Shields, B. L. Fiser, B. A. Evans, M. R. Falvo, S. Washburn and R. Superfine, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 15670–15675.
21. S. N. Khaderi, C. B. Craus, J. Hussong, N. Schorr, J. Belardi, J. Westerweel, O. Prucker, J. Rühe, J. M. J. den Toonder and P. R. Onck, Lab Chip, 2011, 11, 2002–2010.
22. Y. Wang, Y. Gao, H. M. Wyss, P. D. Anderson and J. M. J. den Toonder, Microfluid. Nanofluid., 2014, 18, 167–174.
23. Y. Wang, J. Den Toonder, R. Cardinaels and P. Anderson, Lab Chip, 2016, 16, 2277–2286.
24. S. Hanasoge, P. J. Hesketh and A. Alexeev, Microsyst. Nanoeng., 2018, 4, 11.
25. S. Zhang, Y. Wang, R. Lavrijsen, P. R. Onck and J. M. J. den Toonder, Sens. Actuators, B, 2018, 263, 614–624.
26. N. Hirokawa, Y. Okada and Y. Tanaka, Annu. Rev. Fluid Mech., 2009, 41, 53–72.
27. J. Blake, J. Biomech., 1975, 8, 179–190.
28. M. A. Sleigh, Comp. Biochem. Physiol., Part A: Mol. Integr. Physiol., 1989, 94, 359–364.
29. S. M. Mitran, Comput. Struct., 2007, 85, 763–774.
30. N. Osterman and A. Vilfan, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 15727–15732.
31. S. N. Khaderi, J. M. J. den Toonder and P. R. Onck, Biomicrofluidics, 2012, 6, 014106.
32. S. N. Khaderi, J. M. J. Den Toonder and P. R. Onck, J. Fluid Mech., 2011, 688, 44–65.
33. J. Elgeti and G. Gompper, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4470–4475.
34. B. Gorissen, M. De Volder and D. Reynaerts, Lab Chip, 2015, 15, 4348–4355.
35. F. Tsumori, K. Kudo, T. Osada, H. Miura, R. Marume and A. Saijou, Jpn. J. Appl. Phys., 2016, 55, 06GP19.
36. S. Hanasoge, P. J. Hesketh and A. Alexeev, Soft Matter, 2018, 14, 3689–3693.
37. S. Zhang, R. Zhang, Y. Wang, P. R. Onck and J. M. J. Den Toonder, ACS Nano DOI:10.1021/acsnano.0c03801.
38. M. T. Downton and H. Stark, Epl, 2009, 85, 44002.
39. E. Milana, B. Gorissen, S. Peerlinck, M. De Volder and D. Reynaerts, Adv. Funct. Mater., 2019, 29.
40. A. Bhattacharya, G. A. Buxton, O. B. Usta and A. C. Balazs, Langmuir, 2012, 28, 3217–3226.
41. I. D. Johnston, D. K. McCluskey, C. K. L. Tan and M. C. Tracey, J. Micromech. Microeng., 2014, 24, 035017.
42. D. J. Laser and J. G. Santiago, J. Micromech. Microeng., 2004, 14, R35–R64.
43. Y. N. Wang and L. M. Fu, Microelectron. Eng., 2018, 195, 121–138.
44. S. Mohith, P. N. Karanth and S. M. Kulkarni, Mechatronics, 2019, 60, 34–55.
45. S. N. Khaderi, M. G. H. M. Baltussen, P. D. Anderson, D. Ioan, J. M. J. den Toonder and P. R. Onck, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 1–4.
46. Y. Wang, Y. Gao, H. Wyss, P. Anderson and J. M. J. den Toonder, Lab Chip, 2013, 13, 3360–3366.
47. M. Baltussen, P. Anderson, F. Bos and J. den Toonder, Lab Chip, 2009, 9, 2326–2331.
48. S. Van Pelt, A. Frijns and J. M. J. den Toonder, Lab Chip, 2017, 17, 3826–3840.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0lc00610f

---