 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A microfluidic strategy for the detection of membrane protein interactions†
Yuewen
Zhang‡§
 a,
Therese W.
Herling‡
a,
Therese W.
Herling‡
 a,
Stefan
Kreida
b,
Quentin A. E.
Peter¶
a,
Stefan
Kreida
b,
Quentin A. E.
Peter¶
 a,
Tadas
Kartanas
a,
Susanna
Törnroth-Horsefield
a,
Tadas
Kartanas
a,
Susanna
Törnroth-Horsefield
 b,
Sara
Linse
b,
Sara
Linse
 *b and
Tuomas P. J.
Knowles
*b and
Tuomas P. J.
Knowles
 *ac
*ac
aDepartment of Chemistry, University of Cambridge, Lensfield Road, Cambridge, CB2 1EW, UK. E-mail: tpjk2@cam.ac.uk
bDepartment of Biochemistry and Structural Biology, Lund University, Lund, 221 00, Sweden. E-mail: sara.linse@biochemistry.lu.se
cCavendish Laboratory, University of Cambridge, J J Thomson Avenue, Cambridge, CB3 0HE, UK
First published on 3rd August 2020
Abstract
Membrane proteins perform a vast range of vital biological functions and are the gatekeepers for exchange of information and matter between the intracellular and extracellular environment. However, membrane protein interactions can be challenging to characterise in a quantitative manner due to the low solubility and large size of the membrane protein complex with associated lipid or detergent molecules. Here, we show that measurements of the changes in charge and diffusivity on the micron scale allow for non-disruptive studies of membrane protein interactions in solution. The approach presented here uses measurements of key physical properties of membrane proteins and their ligands to characterise the binding equilibrium parameters. We demonstrate this approach for human aquaporins (AQPs), key membrane proteins in the regulation of water homeostasis in cells. We perform quantitative measurements to characterise the interactions between two full-length AQP isoforms and the regulatory protein, calmodulin (CaM), and show that CaM selectively binds AQP0. Through direct measurements of the diffusivity and mobility in an external electric field, the diffusion coefficients and electrophoretic mobilities are determined for the individual components and the resulting AQP0–CaM complex. Furthermore, we obtain directly the binding equilibrium parameters and effective charge of each component. These results open up a route towards the use of microfluidics as a general platform in protein science and open up new possibilities for the characterisation of membrane protein interactions in solution.
Introduction
Membrane proteins play many critical roles in living cells by controlling signalling, transport and molecular recognition. Membrane proteins represent approximately 25% of the human proteome, and they constitute more than 60% of current drug targets, due to their accessibility to extracellular molecules and roles in disease.1–4 Strategies for the study of membrane protein interactions, and indeed interactions between proteins and membranes,5 are therefore increasingly important to further our understanding of biomolecular function, both in fundamental research and drug discovery applications. However, membrane proteins are particularly challenging to study because they have large hydrophobic surfaces that can lead to misfolding or aggregation in aqueous solutions, as well as the low yield, solubility and stability of sample preparations.6 Detergents or lipids are therefore widely used to solubilise membrane proteins for many applications.6 This approach can in turn lead to obstacles arising from the large size of the stabilised protein.Microfluidic strategies for the characterisation and analysis of biomolecules and their complexes can readily accommodate sample species with a wide range of dimensions, from small molecules or even single ions, to lipid vesicles or cells.10–13 Microfluidic approaches can further be applied in the generation and manipulation of vesicles, particles and entire cells within microdroplets.14–17 The low sample volumes (microlitres) and fast measurement times (seconds) of microfluidic assays render them attractive for studies of biological systems, where the sample amount is limited, in particular as microfluidic measurements can be combined with single-molecule detection.18 Biomolecules can be analysed under native solution conditions without the need for surface-attachment or a matrix to aid separation. Due to the combination of these features, microfluidic technologies have great potential for applications in the study of membrane proteins. Physical properties, such as the size and charge of biomolecules are excellent reporters of interactions, for example, the apparent size of a small protein increases considerably upon binding to a membrane protein in a micelle or vesicle, (Fig. 1). Moreover, the change in the effective charge of a stabilised membrane protein can report on the binding of ligands that result in a relatively small size increase upon complex formation.
 | ||
| Fig. 1 (a) In the presence of Ca2+, CaM binds to AQP0, reducing the water permeability of the transmembrane AQP tetramer.7–9 (b) Schematic of the microfluidic device design used in this study. The channel passes through the detection region four times in order to collect data for diffusion at multiple time points within a single image. (c) Fluorescence images (top) for 1 μM fluorophore-labelled CaM (left) and AQP0 (right) with the corresponding fluorescence intensity profiles in blue and the fit to the data in orange (bottom). The sample diffuses into the flanking buffer as a function of the residence time in the channel and the sample diffusion coefficient. | ||
All cells depend on their ability to maintain water homeostasis, which is achieved via regulation of the permeability of AQPs. AQPs are a family of membrane proteins that conduct water and other small solutes across cell membranes.8 Structurally, AQPs are homo-tetramers, each monomer comprising six transmembrane α-helices surrounding a narrow water-conducting channel (Fig. 1a).19 There are multiple AQP isoforms and these can be found in most species, from bacteria to higher eukaryotes.20 Thirteen AQPs (AQP0–AQP12) have been identified in the human proteome, these are expressed and regulated in a tissue-dependent manner. AQPs are responsible for a diverse range of bioactivities, including urine concentration, cell migration, and adipocyte metabolism. Furthermore, AQPs are believed to play prominent roles in brain oedemas and cancer, and dysregulation of AQP directly leads to human diseases, such as nephrogenic diabetes insipidus, Sjögren's syndrome and cataract.21,22
AQP0, also known as the major intrinsic protein (MIP), is expressed in the eye lens, where it constitutes more than 60% of the total membrane protein content in the fiber cells.9,23 AQP0 permeability is regulated by diverse molecular mechanisms including pH, proteolytic cleavage, and the binding of a regulatory protein, CaM.6–8,24 CaM is central to calcium-mediated signalling.25,26 CaM binds Ca2+via four EF-hands, thus exposing hydrophobic patches, that can be used to bind a variety of target proteins and peptides.25,26 Previous studies have shown that CaM interacts with AQP0 in a Ca2+ dependent manner to decrease the water permeability by channel gating.7–9 In one study of mouse AQP0, CaM was found to increase the water permeability of one cell type, but decrease it in another, suggesting the effect may be cell specific.9
The size of solubilised AQP0 and technical difficulties in working with samples in detergent have limited the investigation of full-length AQP0. For these reasons, previous reports on the interaction between AQP0 and CaM have been carried out using the water-soluble C-terminal fragment of AQP0. Such an approach provides useful information concerning binding locations and specific interacting residues, but does not provide the complete biological context and may lack some factors that affect binding affinity.7,8,22,27 Recent methodological developments such as microscale thermophoresis have enabled studies of the interaction between full-length AQP0 and CaM, providing novel insights into the interaction mode.28 Nevertheless, our understanding of the biophysical properties of the AQP0–CaM complex is still limited, due to the lack of strategies to determine key physicochemical parameters such as the charge and size of such integral membrane protein complexes. Determination of the equilibrium parameters for CaM binding to full-length AQP0 and characterisation of the physicochemical properties defining the complex are therefore important for a full understanding of how CaM interacts with AQP0.
Although CaM is a ubiquitous mediator of Ca2+ signals, not all AQPs are regulated by interactions with CaM. AQP2 is a case in point and used in this study to demonstrate the selectivity of the binding assays. This AQP isoform is located in the kidney collecting duct. Its regulation by trafficking in response to the pituitary hormone vasopressin is essential for the ability to control urine volume.29 Several diseases, such as preeclampsia, nephrogenic diabetes insipidus, and liver cirrhosis, are related to AQP2 malfunction.30,31
In this study, we apply a multidimensional strategy to characterise the interactions between full-length AQPs and CaM using microfluidic free flow assays. These assays are combined with fluorescence microscopy using both intrinsic protein fluorescence and selective fluorophore labelling (Fig. 1b). Fig. 1c shows images acquired for 1 μM AlexaFluor488 labelled CaM and AQP0 respectively. This approach allows us to measure key physical parameters for the individual components and the resulting complex. Specifically, we determine their diffusion coefficients and electrophoretic mobilities,12,32 providing us with insight into the size, effective charge, and equilibrium parameters in free solution. The results show that CaM binds to full-length AQP0 with high nanomolar affinity, whereas no interaction was detected for AQP2, highlighting the tissue-specific nature of the regulation of water permeability.
Results and discussion
Microfluidic strategies enable us to study mixtures of sample components with a wide range of molecular dimensions. We can therefore probe the interaction between small proteins and large membrane protein complexes stabilised by lipids or detergent molecules, such as CaM and the full-length AQP0 tetramer. In addition to the large range of sample dimensions that can be accommodated within microfluidic channels, measurements can be readily performed in the presence of lipids or detergent molecules, rendering microfluidic methods very well suited for experiments with membrane proteins. Here, we apply two laminar flow based microfluidic assays, diffusional sizing and free flow electrophoresis, and show that these approaches enable us to monitor the non-covalent binding of the calcium dependent messenger protein CaM to the integral membrane protein AQP0.Diffusional sizing reveals CaM binding to full-length AQPs
First, we investigated the interaction between CaM and AQP0 tetramers embedded in detergent micelles by exploiting microfluidic diffusional sizing, (Fig. 1). In this experiment, the molecular diffusivity was monitored to determine the diffusion coefficient (D) and the corresponding hydrodynamic radius (RH). These parameters were monitored to determine the extent of complex formation (Fig. 2). The average sample diffusion coefficient was determined from the mass transport of sample molecules into parallel buffer streams, (Fig. 1c). In this experiment, a sample stream is introduced at the centre of the measurement channel, (Fig. 1b).12 We have designed the channel geometry so that four diffusion time points are captured in one field of view, thereby allowing a set of diffusion profiles for a sizing measurement to be acquired in a single image, (Fig. 1b and c). The spacing between read points and sample residence time in the measurement channel can be adapted to suit sample dimensions ranging from small molecules to vesicles or even entire cells. Here, we have chosen the experimental parameters to suit analytes with radii in the low nanometre range.The diffusion coefficients and corresponding RH were determined for AlexaFluor488 labelled CaM and AQP0 individually, (Fig. 1c). All experiments with CaM were performed using 1 μM CaM in the presence of excess calcium (100 μM Ca2+).33 The detergent concentration was kept constant in all samples at 0.03% w/v N-dodecyl β-D-maltoside (DDM) to stabilise the AQP micelles. The RH of CaM and fluorophore-labelled AQP0 were found to be 2.6 ± 0.2 nm and 6.5 ± 0.3 nm respectively.
AQP0 has a number of aromatic amino acid side chains and thus considerable intrinsic fluorescence when excited by UV light at 280 nm.34 We exploited this feature to perform diffusional sizing measurements for unlabelled AQP0 using a microscope equipped with a high-power UV LED, see the Methods section.35 We were thus able to compare AlexaFluor488-tagged and unlabelled AQP0, and we found the RH of the unlabelled tetramer to be unaltered at 6.5 ± 0.2 nm.
CaM is the smaller binding partner in the interaction, so we expect the observed D for CaM to exhibit a larger relative change upon binding than that of the micelle-embedded AQP0 tetramer. Indeed, when mixing with AQP0, the observed D of CaM decreases strongly as a function of AQP0 concentration and reaches a plateau value similar to the size of the AQP0 tetramer in a micelle. A fit to the data reveals an equilibrium dissociation constant (Kd) of 1.3 μM (Fig. 2a), see the ESI† for further details. The size measured at the end of the titration curve corresponds to the size of the AQP0 tetramer in complex with CaM.
To determine the size of the complex formed in the presence of excess CaM, we measured the diffusion coefficient for 1.25 μM AQP0 tetramer in the presence of 20 μM CaM (corresponding to saturating conditions), exploiting the intrinsic fluorescence of AQP0 for sample detection. The increase in the apparent AQP0 size upon complex formation is small, we measured the RH to be 6.7 ± 1 nm, which is within the error of the size measurements for the AQP0 tetramer alone, 6.5 ± 0.3 nm. For the diffusional sizing device configuration used in this study the resolution is typically 2–3 Ångström, with a larger standard deviation for intrinsic fluorescence measurements due to the reduced signal to noise ratio.
Deep UV (280 nm) illumination is able to excite the intrinsic fluorophores within proteins, including tryptophan (Trp) and tyrosine (Tyr) residues, which enables the detection of proteins without any extrinsic labelling. The effective brightness of Trp is higher than that of Tyr.34 Unlike AQP0, which has five Trp per monomer, CaM does not contain any Trp residues. We therefore used optical filters optimised for Trp fluorescence (emission at 357 ± 22 nm) to selectively monitor AQP0.
To allow for a differentiated response to calcium-mediated signalling in different tissues and cell types, the affinity for Ca2+–CaM varies between AQP isoforms. One of the AQPs that have not been reported to interact with CaM is AQP2. This isoform was therefore investigated to test whether our microfluidic approach accurately and selectively reports on non-covalent complex formation between membrane proteins and their ligands in solution. For this purpose, we monitored the average D for CaM as a function of the concentration of AQP2 under the same solution conditions as the experiments with AQP0. Indeed, the observed D for CaM remained constant against AQP2 concentration, (Fig. 2b).
Microfluidic free flow electrophoresis
Microfluidic free flow electrophoresis enables us to gather further insight into the interaction between CaM and AQP0. We use a microfluidic technique for quantitative free flow electrophoresis, which has been developed and demonstrated in earlier reports, (Fig. 3a).32 We have demonstrated that this approach can be applied to measure the effective charges of analytes and to characterise interaction equilibria between globular proteins in free solution.10,11The sample is introduced as a central stream in the main channel, and moves towards the anode or cathode according to its electrophoretic mobility when an electric field is applied perpendicularly to the direction of flow (Fig. 3), see the Methods section for further details. The sample position, deflection (δ), and current (I) are recorded as a function of the applied voltage. By combining the buffer conductance in a given device and I, the electric field value is calculated. In addition, drift velocities (vd), are calculated from δ and the residence time. The electrophoretic mobility (μ) is obtained through a linear fit to the slope of vd against the electric field across the solution.32
By measuring the change in the observed electrophoretic mobility (μobs) of labelled CaM as a function of AQP0 concentration, the binding equilibrium can be characterised (Fig. 4). First, the value of μobs for CaM alone was measured to yield −3.18 ± 0.03 × 10−8 m2 V−1 s−1, a value which is consistent with previous findings.11
 | ||
Fig. 4 (a), The intrinsic fluorescence of 1.25 μM AQP0 tetramer is monitored as a function of CaM concentration. (b), In the reverse experiment, the electrophoretic mobility of 1 μM CaM is monitored as a function of AQP0 concentration, as the fraction bound to the large positively charged membrane protein increases, the average mobility of CaM decreases. Fitting the binding curves with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding model results in Kd values of 0.3 μM for both datasets. (c), Expanded view of the data for 1.25 μM AQP0 tetramer in the presence of 0–5 μM CaM. (d), The measured and sequence charges for CaM, AQP0 and CaM–AQP0. The sign of the charges correlates with the predicted charges, the effective charge includes screening within the 3-dimensional protein structure and from interactions with solvent ions.10 1 binding model results in Kd values of 0.3 μM for both datasets. (c), Expanded view of the data for 1.25 μM AQP0 tetramer in the presence of 0–5 μM CaM. (d), The measured and sequence charges for CaM, AQP0 and CaM–AQP0. The sign of the charges correlates with the predicted charges, the effective charge includes screening within the 3-dimensional protein structure and from interactions with solvent ions.10 | ||
The electrophoretic mobility of CaM–Alexa488 was measured against an increasing concentration of AQP0 (Fig. 4). The observed mobility of CaM increased from −3.18 ± 0.03 × 10−8 to a plateau value of −0.20 ± 0.11 × 10−8 m2 V−1 s−1 at 7.5 μM AQP0 tetramer. The Kd (0.3 μM) is found based on one CaM binding to each tetramer (Fig. 4) and ESI.† Free flow electrophoresis measurements for μobs of CaM as a function of AQP2 concentration did not change at −3.17 ± 0.12 × 10−8 m2 V−1 s−1, see ESI† Fig. S2.
We next turned to detection through intrinsic protein fluorescence to selectively monitor μobs for AQP0 as a function of CaM concentration, (Fig. 4a and c). The electrophoretic mobility of AQP0 on its own was measured as 0.21 ± 0.02 × 10−8 m2 V−1 s−1. The result is consistent with the small positive sequence charge of human AQP0.36 When CaM (0–25 μM) was titrated against 1.25 μM AQP0 tetramer, μobs became negative upon complex formation and reached a plateau at −0.34 ± 0.08 × 10−8 m2 V−1 s−1 for 10–25 μM CaM (Fig. 4a), which is in good agreement with the result above for the electrophoretic mobility of full-length AQP0 and labelled CaM complex (Fig. 4b). The Kd was found to be 0.3 μM.
Both experimental results show that the electrophoretic mobility of the AQP0 and CaM complex reach to a plateau at approximately −0.3 × 10−8 m2 V−1 s−1, indicating that the complex formed in the presence of an excess of either binding partner has the same stoichiometry. This implies strong positive cooperativity of CaM binding to AQP0 in line with previous findings.28 In the absence of strong positive cooperativity, one CaM per AQP0 tetramer would dominate if AQP0 is in excess relative to CaM (Fig. 4b).
The interaction between CaM and AQP0 has been studied for a range of organisms and sometimes between homologs from different species.7–9,22,28,37 Interestingly, a wide range of Kd values have been reported for the interaction from below 100 nM to 40 μM, with most values in the low micromolar range,8,22,37 with micromolar affinities and strong positive cooperativity measured for the interaction between CaM and full-length AQP0 by thermophoresis.28 We have determined the Kd for the interaction through three direct measurements of the physical properties of the interaction partners (the electrophoretic mobilities of CaM and AQP0, and the diffusion coefficient of CaM), these all report on a Kd of 0.3–1.3 μM. In most reports of CaM–ligand interactions, CaM interacts with a single copy of the target sequence.8 Depending on the technique, CaM has been reported to interact with one or two C-termini of the AQP0 subunits,8,22,28,37 and it has been suggested that the specifics of the CaM–AQP0 interaction vary between species.9 In addition to the use of truncated versus full length AQP0, the spread in the reported Kd values for the interaction may further arise from differences solution conditions used for each study, including composition, pH, ionic strength, and protein concentration, NMR for instance employs CaM concentrations in the hundreds of μM.8 The microfluidic methods employed in this study report absolute values for the electrophoretic mobility and diffusion coefficient, enabling these parameters and membrane protein interactions to be compared directly between solution conditions.10,11
In this study, we effectively observe two states for bound and unbound CaM, consistent with either strong positive cooperativity, as previously shown for the full length AQP0–CaM complex or a single binding event per AQP0 tetramer. We measure the same values for the diffusion coefficient and electrophoretic mobility of the complex formed when either binding partner is in excess, suggesting that the stoichiometry is conserved in both scenarios.
Analysis of protein charge
Biomolecular charge is one of the key physical parameters that regulate protein interactions. The effective charges of proteins in solution arise from ionised amino acid side chains, the polypeptide termini, any post-translational modifications, and ligand binding. Unlike small molecules, the effective charge of a protein in solution often varies from the dry sequence charge,10 potentially due to a wide range of factors, including pKa perturbation, inter- and intramolecular charge screening. Thus, the effective charge of proteins in the solution phase is difficult to predict.38 The 17 kDa CaM is a ubiquitous calcium-sensitive signalling protein with a conserved amino acid sequence between the bovine and human form. CaM has 38 acidic residues (aspartic acid and glutamic acid), 14 basic residues (arginine and lysine), just one histidine, and the terminal titratable groups, and a net charge model predicts the overall charge to be −23 for apo-CaM.39,40 CaM remains negatively charged even when bound to four Ca2+ ions.38,41 In addition, CaM is labelled with AlexaFluor488, which carries two negative charges.26In order to calculate effective protein charges, we combined measurements of the diffusion coefficients and electrophoretic mobilities of CaM and AQP0. Based on these two parameters, the effective charge of molecules can be calculated.10 The relation between μobs, D, and effective charge (q) is described by the Nernst–Einstein equation (eqn (1)),
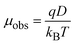 | (1) |
We found the sequence and measured charges to have the same sign, but differ in magnitude. The observed difference can be attributed to the fact that, the predicted charge does not take the three-dimensional structure into account and does thus not necessarily correlate with the solvated charge of the native protein structure. Many of the charged residues of AQP0 are located in the C-terminus,6 where CaM binds and are therefore likely to be screened by the interaction.
Conclusions
In conclusion, we have demonstrated a microfluidic platform for determination of the size and charge of membrane proteins, in addition to equilibrium studies. Here, we have shown that a multidimensional approach enables us to characterise the interaction between human CaM and AQPs, gaining insight into the physical properties of each species, including their effective charges in solution. The diffusion coefficient of CaM and electrophoretic mobilities for both AQP0 and CaM were monitored to characterise the binding equilibrium, resulting in an average Kd value of 0.6 μM. Furthermore, we showed that the microfluidic measurements detect specific interactions by verifying that there are no binding-related signals observed between CaM and AQP2. The results presented here illustrate how cellular water permeability is regulated in an AQP isoform specific manner. Furthermore, the methodology introduced in this work provides a general platform for non-disruptive studies of membrane protein interactions in free solution, which does not rely on specific analyte properties and has the potential to be widely applied in fundamental biological research and drug development.Methods
Preparation of AQP0/AQP2 and CaM
Full-length human AQP0 and AQP2 were expressed in Pichia pastoris as previous described.43 AQP0 and AQP2 were purified as described previously.28 Human CaM was expressed in Escherichia coli and purified as previously described.26 As human CaM does not contain any native cysteines, Ser 17 of CaM was replaced by cysteine, which allowed for labelling with cysteine-reactive dyes.26 This position is predicted to be surface exposed in the CaM–target complex structure and therefore not to interfere with complex formation.44 When a fluorophore was used for sample detection, the proteins were labelled with cysteine-reactive dye C5 maleimide-Alexa 488 (Thermo Fisher, UK) following the manufacturer's instructions and excess dye was removed by desalting on a PD-10 column (GE Healthcare).26,44 Samples were buffer exchanged into 10 mM Tris–HCl, 10 mM NaCl, 0.03% DDM, pH 7.5, with 0.1 mM CaCl2, these buffer conditions were used for all microfluidic measurements. Unless otherwise specified all chemicals were purchased from Sigma Aldrich UK.Fabrication of microfluidic devices
Microfluidic devices were fabricated in polydimethyl siloxane (PDMS) using standard UV light photolithography and soft lithography methods.45 In brief, the device height was set by spin coating negative epoxy photoresist (MicroChem SU-8 3025 or 3050, A-Gas, UK) onto a silicon wafer. Channels for use with AlexaFluor-labelled protein had a height of 25 μm, and those used for intrinsic fluorescence measurements were 50 μm. All the device heights were measured by scanning the soft-lithography master with a profilometer (DektakXT, Bruker). Height variations between devices were taken into account in the data analysis.PDMS devices where prepared using standard soft lithography methods.45 To minimise background signal, black PDMS was prepared by mixing 1 mg ml−1 black carbon nanopowder into the elastomer.32 Device were covalently bonded to a 76 × 26 mm glass slide (Thermo Scientific) or quartz slide (Advalue Technology, 76.2 × 25.4 × 1.0 mm) using an oxygen plasma oven (Diener Electronics, Germany). The devices and slides were exposed to an oxygen plasma for 10 s, bonded, incubated for 10 minutes at 65 °C. If applicable, electrodes were inserted as described previously,32 before exposure to a high-power oxygen plasma for 500 s to make the devices hydrophilic, to preserve the hydrophilic surfaces, channels were then filled with mQ water.46
Microfluidic diffusion experiments
Different flow rates of the experiment were set by withdrawal through the outlet using a glass syringe (Hamilton, Switzerland) and controlled by a neMESYS syringe pumps (Cetoni GmbH, Germany). For the AlexaFluor488-labelled samples, diffusion profiles were acquired by a fluorescence microscope (Zeiss Axio Observer) fitted with a white LED (Cairn Research, UK) and a fluorescence filter set with excitation at 470 ± 20 nm, dichroic mirror for 495 nm, and emission at 525 ± 25 nm (49002, Chroma Technology, Vermont, USA). The fluorescent diffusion profiles along the channel were imaged at the detection position using an Evolve 512 CCD camera (Photometrics, Arizona, USA) with a 5× objective and exposure times ranging from 0.5 s to 2 s depending on the sample concentration. Intrinsic protein fluorescence measurements were performed using a custom built microscope equipped with a 280 nm LED (M280L3, Thorlabs), using the Semrock TRP-A-000 filter set (Laser2000, UK) as described previously.35 Images were acquired using an EMCCD camera (Rolera EM-C2, Photometrics, UK). Each diffusion experiment consumed around 5 μL of sample. Three independent repeats were acquired for each sample concentration.In order to study the interactions between AQPs and CaM, the diffusion coefficients of the individual components and the complex were measured using the microfluidic diffusion device shown in Fig. 1a. The flow rate, device height, and temperature were taken into account for the data analysis. To determine the spatial sample distribution as a function of time, fluorescence profiles were extracted from the images, fluorescence data shown in blue in Fig. 1c. As the distance diffused by sample molecules across the channel scales with 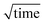 , the distances between read points were designed to increase the time interval between read points, thereby enhancing the changes between fluorescence profiles between time points to enable more precise sizing of sample molecules. Diffusion profiles corresponding to the diffusion coefficients of RH of particles between 0.5 nm and 10 nm were selected for simulation based on laminar Poiseuille flow through the diffusion channel.47 The best fit to the observed sample distribution at four time points was used to determine the average RH for each measurement, orange profiles in Fig. 1c.
, the distances between read points were designed to increase the time interval between read points, thereby enhancing the changes between fluorescence profiles between time points to enable more precise sizing of sample molecules. Diffusion profiles corresponding to the diffusion coefficients of RH of particles between 0.5 nm and 10 nm were selected for simulation based on laminar Poiseuille flow through the diffusion channel.47 The best fit to the observed sample distribution at four time points was used to determine the average RH for each measurement, orange profiles in Fig. 1c.
Microfluidic electrophoresis experiments
Microfluidic free flow electrophoresis measurements were performed using the same microscopes as above.Buffers and samples were loaded in their respective inlets, and a negative pressure applied at the outlet withdrawal with glass syringe (Hamilton, Switzerland) using neMESYS syringe pumps (Cetoni GmbH, Germany) to control flow rate at 500 μl h−1. As a result of the applied voltage, the sample stream migrated perpendicularly to the direction of flow according to the analyte electrophoretic mobility. Four repeats of a voltage range (0–2 V) with 0.2 V steps were applied for each sample, and at each voltage three images were acquired (Fig. 2a). Each electrophoretic mobility measurement consumed around 10 μL of sample. The cell constants for individual electrode devices and buffer conductivities were measured using a lock-in amplifier as previously described.32 The electrophoresis data was analysed using software written in Python.10 Linear fits to the slope of the plots of velocity against electric field, which were then performed to determine μobs for each sample.
Model for studying protein binding equilibria
The Kd values for CaM binding to AQP were determined for a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 interaction. The inclusion of additional free parameters to describe two binding sites did not improve the fit to the data (ESI† Fig. S1, S3 and S4), we therefore used the simplest model that would describe the data in this study. For each binding curve, the concentration of the observed protein (Pobs, CaM–AlexaFluor488 or AQP0) was kept constant and the concentration of binding partner varied. The measured RH or μobs were the result of the fractional contributions from the populations of free and bound Pobs. We fitted the data by solving the equilibrium equation for the concentration of free Pobs as described in the ESI† and previously.11
1 interaction. The inclusion of additional free parameters to describe two binding sites did not improve the fit to the data (ESI† Fig. S1, S3 and S4), we therefore used the simplest model that would describe the data in this study. For each binding curve, the concentration of the observed protein (Pobs, CaM–AlexaFluor488 or AQP0) was kept constant and the concentration of binding partner varied. The measured RH or μobs were the result of the fractional contributions from the populations of free and bound Pobs. We fitted the data by solving the equilibrium equation for the concentration of free Pobs as described in the ESI† and previously.11
Author contributions
YZ, TWH, SK, ST-H, SL and TPJK conceptualised and designed the work. TWH, QAEP, TK and TPJK developed methodology. TWH, QAEP and TK wrote software for the project. YZ, TWH, SK, ST-H, SL and TJPK provided resources. YZ and TWH performed the investigation. YZ, TWH, QAEP, SL, and TJPK analysed the data. YZ, TWH, SL and TPJK wrote the original manuscript draft. All authors reviewed and edited the manuscript.Conflicts of interest
The authors do not declare any conflicts of interest.Acknowledgements
The research leading to these results has received funding from the ERC under the European Union's Seventh Framework Programme (FP7/2007-2013) through the ERC grant PhysProt (agreement No. 337969) (TPJK), Svenska Vetenskapsrådet (SL), Oppenheimer Foundation (TWH), and BBSRC (TPJK, TWH).References
- C.-Y. Hsia, M. J. Richards and S. Daniel, Anal. Methods, 2015, 7, 7076–7094 RSC.
- K. Lundstrom, Comb. Chem. High Throughput Screening, 2004, 7, 431–439 CrossRef CAS PubMed.
- J. P. Overington, B. Al-Lazikani and A. L. Hopkins, Nat. Rev. Drug Discovery, 2006, 5, 993–996 CrossRef CAS PubMed.
- A. Engel and H. E. Gaub, Annu. Rev. Biochem., 2008, 77, 127–148 CrossRef CAS PubMed.
- C. Galvagnion, J. W. P. Brown, M. M. Ouberai, P. Flagmeier and M. Vendruscolo, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 7065–7070 CrossRef CAS PubMed.
- T. Gonen, P. Sliz, J. Kistler, Y. Cheng and T. Walz, Nature, 2004, 429, 193–197 CrossRef CAS PubMed.
- K. L. Németh-Cahalan, K. Kalman and J. E. Hall, J. Gen. Physiol., 2004, 123, 573–580 CrossRef PubMed.
- S. L. Reichow and T. Gonen, Structure, 2008, 16, 1389–1398 CrossRef CAS PubMed.
- K. Varadaraj, S. Kumari, A. Shiels and R. T. Mathias, Invest. Ophthalmol. Vis. Sci., 2005, 46, 1393–1402 CrossRef PubMed.
- T. W. Herling, P. Arosio, T. Muller, S. Linse and T. P. J. Knowles, Phys. Chem. Chem. Phys., 2015, 17, 12161–12167 RSC.
- T. W. Herling, D. J. O'Connell, M. C. Bauer, J. Persson, U. Weininger, T. P. J. Knowles and S. Linse, Biophys. J., 2016, 110, 1957–1966 CrossRef CAS.
- P. Arosio, T. Muller, L. Rajah, E. V. Yates, F. A. Aprile, Y. Zhang, S. I. A. Cohen, D. A. White, T. W. Herling, E. J. De Genst, S. Linse, M. Vendruscolo, C. M. Dobson and T. P. J. Knowles, ACS Nano, 2016, 10, 333–341 CrossRef CAS PubMed.
- H. Gang, G. Meisl, T. Muller, M. Pfammatter and T. P. J. Knowles, Anal. Chem., 2018, 90, 3284–3290 CrossRef CAS PubMed.
- H. C. Shum, D. Lee, I. Yoon, T. Kodger and D. A. Weitz, Langmuir, 2008, 24, 7651–7653 CrossRef CAS.
- A. R. Abate, C.-H. Chen, J. Agresti and D. A. Weitz, Lab Chip, 2009, 9, 2628–2631 RSC.
- J. J. Agresti, E. Antipov, A. R. Abate, K. Ahn, A. C. Rowat, J.-C. Baret, M. Marquez, A. M. Klibanov, A. D. Griffiths and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 4004–4009 CrossRef CAS PubMed.
- K. Karamdad, R. V. Law, J. M. Seddon, N. J. Brooks and O. Ces, Lab Chip, 2015, 15, 557–562 RSC.
- M. H. Horrocks, L. Tosatto, A. J. Dear, G. A. Garcia, M. Iljina, N. Cremades, M. Dalla Serra, T. P. J. Knowles, C. M. Dobson and D. Klenerman, Anal. Chem., 2015, 87, 8818–8826 CrossRef CAS PubMed.
- S. Törnroth-Horsefield, K. Hedfalk, G. Fischer, K. Lindkvist-Petersson and R. Neutze, FEBS Lett., 2010, 584, 2580–2588 CrossRef PubMed.
- L. S. King, D. Kozono and P. Agre, Nat. Rev. Mol. Cell Biol., 2004, 5, 687–698 CrossRef CAS PubMed.
- S. Kreida and S. Törnroth-Horsefield, Curr. Opin. Struct. Biol., 2015, 33, 126–134 CrossRef CAS PubMed.
- S. L. Reichow, D. M. Clemens, J. A. Freites, K. L. Németh-Cahalan, M. Heyden, D. J. Tobias, J. E. Hall and T. Gonen, Nat. Struct. Mol. Biol., 2013, 20, 1085–1092 CrossRef CAS PubMed.
- H. Bloemendal, A. Zweers, F. Vermorken, F. Dunia and E. Benedetti, Cell Differ., 1972, 1, 91–106 CrossRef CAS.
- K. L. Ne and J. E. Hall, J. Biol. Chem., 2000, 275, 6777–6782 CrossRef PubMed.
- Y. S. Babu, C. E. Bugg and W. J. Cook, J. Mol. Biol., 1988, 204, 191–204 CrossRef CAS PubMed.
- D. J. O'Connell, M. C. Bauer, J. O'Brien, W. M. Johnson, C. A. Divizio, S. L. O'Kane, T. Berggård, A. Merino, K. S. Akerfeldt, S. Linse and D. J. Cahill, Mol. Cell. Proteomics, 2010, 9, 1118–1132 CrossRef PubMed.
- K. Fetter, V. V. Wilder, M. Moshelion and F. Chaumont, Plant Cell, 2004, 16, 215–228 CrossRef CAS PubMed.
- S. Kreida, J. V. Roche, C. Olsson, S. Linse and S. Törnroth-Horsefield, Faraday Discuss., 2018, 209, 35–54 RSC.
- D. Pearce, R. Soundararajan, C. Trimpert, O. B. Kashlan, P. M. T. Deen and D. E. Kohan, Renal Physiology, 2015, 10, 135–146 CAS.
- R. W. Schrier, R. G. Fassett, M. Ohara and P. Y. Martin, Proc. Assoc. Am. Physicians, 1998, 110, 407–411 RSC.
- P. M. Murphy, H. L. Tiffany, J. B. Chem, P. M. T. Deen, M. A. J. Verdijk and N. V. A. M. Knoers, Science, 1994, 264, 92–95 CrossRef PubMed.
- T. W. Herling, T. Müller, L. Rajah, J. N. Skepper, M. Vendruscolo and T. P. J. Knowles, Appl. Phys. Lett., 2013, 102, 184102 CrossRef.
- S. Linse, C. Johansson, P. Brodin, T. Grundström, T. Drakenberg and S. Forsén, Biochemistry, 1991, 30, 154–162 CrossRef CAS PubMed.
- J. A. Ross, D. M. Jameson, J. A. Ross and D. M. Jameson, Photochem. Photobiol. Sci., 2008, 7, 1301–1312 RSC.
- P. K. Challa, Q. Peter, M. A. Wright, Y. Zhang, K. L. Saar, J. A. Carozza, J. L. Benesch and T. P. Knowles, Anal. Chem., 2018, 90, 3849–3855 CrossRef CAS PubMed.
- E. Gasteiger, C. Hoogland, A. Gattiker, S. Duvaud, M. R. Wilkins, R. D. Appel and A. Bairoch, The Proteomics Protocols Handbook, 2005, ch. 52, pp. 571–607 Search PubMed.
- K. M. L. Rose, Z. Wang, G. N. Magrath, E. S. Hazard, J. D. Hildebrandt and K. L. Schey, Biochemistry, 2008, 47, 339–347 CrossRef CAS PubMed.
- M. Lund and B. Jönsson, Biochemistry, 2005, 44, 5722–5727 CrossRef CAS PubMed.
- B. Svensson, B. Jonsson and E. Thulin, Biochemistry, 1993, 32, 2828–2834 CrossRef CAS PubMed.
- Y. Waltersson, S. Linse, P. Brodin and T. Grundström, Biochemistry, 1993, 32, 7866–7871 CrossRef CAS PubMed.
- I. Andre, T. Kesvatera, B. Jönsson, K. S. Åkerfeldt and S. Linse, Biophys. J., 2004, 87, 1929–1938 CrossRef CAS PubMed.
- J. Antosiewicz, A. J. McCammon and M. K. Gilson, J. Mol. Biol., 1994, 5, 415–436 CrossRef PubMed.
- F. Öberg, M. Ekvall, M. Nyblom, A. Backmark, R. Neutze and K. Hedfalk, Mol. Membr. Biol., 2009, 26, 215–227 CrossRef PubMed.
- E. Hellstrand, S. Kukora, C. F. Shuman, S. Steenbergen, E. Thulin, A. Kohli, B. Krouse, S. Linse and K. S. Åkerfeldt, FEBS J., 2013, 280, 2675–2687 CrossRef CAS PubMed.
- J. C. McDonald, D. C. Duffy, J. R. Anderson and D. T. Chiu, Electrophoresis, 2000, 21, 27–40 CrossRef CAS PubMed.
- S. H. Tan, N.-T. Nguyen and C. Chua, Biomicrofluidics, 2010, 4, 032204 CrossRef PubMed.
- T. Muller, P. Arosio, L. Rajah, S. I. Cohen, E. V. Yates, M. Vendruscolo, C. M. Dobson and T. P. J. Knowles, Int. J. Nonlinear Sci. Numer. Simul., 2016, 17, 175–183 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0lc00205d |
| ‡ These authors contributed equally to this work. |
| § Current address: Department of Chemistry, Lanzhou University, Lanzhou, Gansu, 730000, P.R. China. |
| ¶ Current address: Fluidic Analytics AG, Technopark, Wagistrasse 25, 8952 Schlieren, Switzerland. |
| This journal is © The Royal Society of Chemistry 2020 |


