Open Access Article
Open Access ArticleMonolithically-integrated cytometer for measuring particle diameter in the extracellular vesicle size range using multi-angle scattering†
Jonathan T.
Butement
 *ab,
Paul M.
Holloway‡
*ab,
Paul M.
Holloway‡
 bc,
Joshua A.
Welsh
bc,
Joshua A.
Welsh
 b,
Judith A.
Holloway
b,
Judith A.
Holloway
 bd,
Nicola A.
Englyst
bd,
Nicola A.
Englyst
 b,
Peter
Horak
b,
Peter
Horak
 a,
Jonathan
West
a,
Jonathan
West
 bcd and
James S.
Wilkinson
bcd and
James S.
Wilkinson
 ad
ad
aOptoelectronics Research Centre, University of Southampton, UK. E-mail: jb3006@soton.ac.uk
bFaculty of Medicine, University of Southampton, UK
cCentre for Hybrid Biodevices, University of Southampton, UK
dInstitute for Life Sciences, University of Southampton, UK
First published on 2nd March 2020
Abstract
Size measurement of extracellular vesicles is hampered by the high cost and measurement uncertainty of conventional flow cytometers which is mainly due to the use of non-specialised free space optics. Integrated cytometry, where the optics and fluidics are embedded in a monolithic chip shows promise for the production of low cost, micro-flow cytometers dedicated for extracellular vesicle (EV) analysis with improved size measurement accuracy and precision. This research demonstrates a unique integrated cytometer for sub-micron particle size measurement using multi-angle scattering analysis. A combination of three technologies is used: (i) Dean-based hydrodynamic focussing to deliver a tight sample core stream to the analysis region, (ii) integrated waveguides with multimode interference devices to focus a narrow excitation beam onto the sample stream, and (iii) an angular array of collection waveguides to measure particle scattering distribution and calculate diameter. Low index 200 nm liposomes could be detected and polystyrene size standards as small as 400 nm diameter could be measured with an uncertainty of ±21 nm (1/2 IQR) demonstrating a first step on the path to high performance integrated cytometry of EVs.
Introduction
Extracellular vesicles (EVs) are cell-derived membranous vesicles ranging in diameter from 30–1000 nm (ref. 1) and comprise subgroups including exosomes and microvesicles. The release of EVs of defined size distribution and cellular origin has been associated with a range of pathologies2–5 and there is currently a growing need for technology which can accurately measure EV size in combination with phenotypic signatures to fully exploit their potential as biomarkers.The small size of EVs presents a challenge for sensitive, precise and accurate size measurement. A variety of approaches are currently in use, each with various advantages and limitations which are discussed in detail in recent reviews.6,7 Two widely used techniques are nanoparticle tracking analysis (NTA) and conventional flow cytometry. NTA involves imaging EVs in suspension under dark-field illumination and digitally tracking the Brownian motion of individual particles to calculate size using the Stokes–Einstein equation. The technique can detect particles down to 50 nm in diameter and can be combined with fluorescence to indicate EV phenotype.8 The technique has a relatively low throughput however at around 16 particles per second9 compared to flow cytometry and concentration determination requires careful calibration and can be inaccurate with broad EV size distributions.10 Conventional flow cytometry has a higher limit of detection than NTA at 200 nm but is proving to be highly practical for EV analysis as it can measure the size and concentration of polydisperse samples at kHz rates11,12 along with detecting multiple molecular markers by antibody-based fluorescent labelling. The internal apparatus of a conventional flow cytometer has remained largely unchanged since its original inception and consists of a free space optical system of lenses, mirrors and filters aligned with a fluidic flow cell as well as photodetectors and data acquisition electronics. EVs are delivered as a tight core surrounded by sheath flow into one or more laser beams which excite scattering and fluorescence from antibody labels.13 The scattering signal is used to measure particle size and the fluorescence signal from antibody labels is used to detect phenotype.
The use of conventional cytometers for EV analysis has two primary drawbacks however. Firstly, the machines have substantial costs due to their complexity which limits their widespread use. Secondly and significantly, sizing accuracy and precision is limited due to the effects of Mie resonances which are prominent at the EV size range. To measure particle size on a conventional cytometer the magnitude of the optical power scattered into the side scatter channel (SSC) is typically used as a metric. The arbitrary SSC values are obtained for a range of diameters of size standards of known refractive index (usually polystyrene or silica) and these measurements are used to normalise the arbitrary scattered power calculated from a Mie scattering model onto the same scale. Literature refractive index values for EVs can then be used with the normalised Mie scattering model to calculate EV diameter from SSC values from samples of unknown diameter.12,14 Sizing inaccuracy and imprecision arise as the relationship between particle diameter and SSC value is non-monotonic, exhibiting plateaus and local minima at specific diameter ranges leading to ambiguity in sizing in these regions. An accurate model also requires knowledge of the system collection geometry which is often proprietary and can vary with optical alignment.
Multi-angle scattering approaches have been developed to improve sizing performance. These use the relative angular scattering distribution produced by a particle to calculate diameter as opposed to the magnitude of scattered power. Here the relative scattering distribution of a particle is obtained and an analytical model is fitted to calculate particle diameter. High accuracy and precision can be achieved because there are large form changes in scattering distribution for small incremental changes in particle diameter. There is also no need to take calibration measurements from size standards to normalise a scattering model. High performance multi-angle scattering approaches have been developed using cytometers with free space optics15–18 but have not been demonstrated in an integrated cytometer. Such optofluidic technology which combines microfluidics and integrated optical waveguides19–22 offers an ideal platform with which to develop cost effective and high performance flow cytometers dedicated for EV analysis using multi-angle scattering. For example, as will be demonstrated in this paper, an angular array of collection waveguides23 can be used to measure the light scattered at multiple discrete angles providing a relative scattering distribution for model fitting to calculate diameter. Further advantages are conferred by the intrinsic and permanent alignment of the monolithic platform, which effectively removes signal drift and background noise that would be caused by the vibration of independent optical and fluidic components. In addition, chips can be mass produced with conventional microfabrication techniques greatly lowering cost per device. In this contribution, we present the design, fabrication and characterisation of an integrated cytometer for measuring particle diameter in the extracellular vesicle size range using multi-angle scattering analysis.
Integrated cytometer design
The key challenge for developing an integrated cytometer is combining both optical and fluidic focussing within the constraints of planar fabrication techniques compatible with mass production. This section describes the development of the optical and fluidic focussing design of the integrated cytometer and presents the final chip design used for multi-angle scattering measurements of size standard particles in the EV size range.Optical design
A silica-based optical waveguide system was chosen as it offers better optical performance than polymer systems, having lower absorption24 and autofluorescence background, as well as allowing the refractive index contrast to be matched to commercial single mode optical fibres enabling efficient optical coupling. In addition, glass has greater rigidity and a lower thermal expansion coefficient than polymer systems which ensures stable performance of on-chip lenses which have tight dimensional tolerances. Basic fibre-compatible waveguides were required to connect the chip inputs to waveguide lenses and the microfluidic channel and to collect the light from the microfluidic channel and guide it to the chip outputs. The basic waveguide design chosen was that used previously25,26 with the waveguide cross sectional dimensions and refractive index shown in Fig. 1(a). The waveguide film thickness of 1.4 μm ensured single mode operation orthogonal to the optical film plane. The design of interconnecting waveguides was simply a matter of geometrical layout shown in Fig. 2(a) with a minimum bend radius of 6 mm to ensure low loss.Carefully designed on chip lenses were required to shape the excitation beam for intersection with the particles flowing along the centre of the fluidic channel, in order to optimise the performance of the integrated cytometer. The excitation beam dimensions orthogonal to the particle flow, here referred to as beam height, ideally had to exceed the height of the particle flow stream in order to ensure all flowing particles are illuminated. For this reason a beam launched into a microfluidic channel that diverged due to diffraction orthogonally to the waveguide plane was used. This also avoided the need for complex multilayer optical structures for vertical beam shaping. The vertical divergence of the beam crossing the microfluidic channel is shown in Fig. 2(c) and was estimated with an analytical approximation for a diverging Gaussian beam with the initial dimensions of the waveguide fundamental mode.27 The theoretical beam height of ≈3.5 μm in the centre of the channel dictates the largest detectable particle and is well outside the size range of EVs.
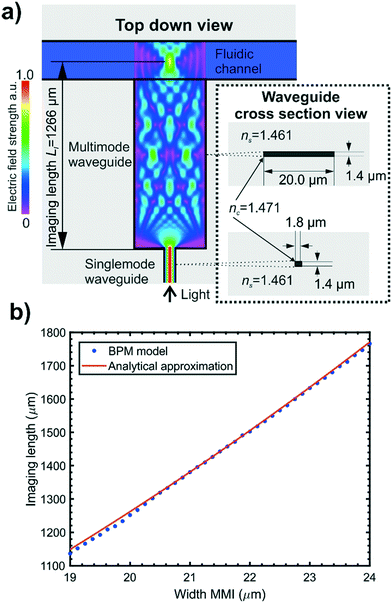
The excitation beam dimensions parallel to the particle flow and waveguide plane, here referred to as beam width, was required to be narrow in order to reduce the possibility of signals resulting from multiple particles simultaneously occurring within the beam14 and to minimise the amount of background light leaking into the collection waveguides. Previous work has demonstrated that multimode interference devices (MMIs) are well suited for use as on chip lenses25 and suggested their use in flow cytometry. We have implemented an MMI in our integrated cytometer design: the concept is shown schematically in Fig. 1(a). MMIs consist of a multimode waveguide with a narrow single mode input. Multiple modes are excited in the multimode waveguide and interfere with each other to produce a self-imaging phenomenon whereby the narrow single mode input is reimaged at a defined distance, known as the imaging length, from the start of the MMI.28 The MMI can be positioned relative to a microfluidic channel to focus light in the horizontal plane mid-way across the microfluidic channel.
A numerical simulation package (Beamprop, RSoft Synopsys) which uses the beam propagation method (BPM) was used to calculate imaging length for a range of MMI widths and compared to an analytical approximation as detailed in Hunt et al.25 The MMIs were designed to produce a single focal spot located mid-height and at the lateral midpoint of the fluidic channel. A restricted self-imaging configuration was chosen where the input light field from the single mode waveguide is symmetrical about the longitudinal axis of the multimode waveguide and excites only symmetrical modes. This allows self-imaging over a shorter MMI length and therefore a smaller device footprint. As the imaging length of an MMI is proportional to the square of its width, a narrower MMI was desirable to again offer a smaller device footprint and reduce the effect of fabrication tolerances on focal position. The numerical and analytical calculations presented in Fig. 1(b) show that an MMI width of 20.0 μm produced an imaging length at 1266 μm for a wavelength of 532 nm, enabling compact chip designs.25,28
The effects of the fluidic system on the performance of the waveguide circuit were considered. The inclusion of strip waveguide layers on a chip creates ridges in the top surface of the chip, which would make sealing a flat enclosing manifold against the top surface difficult. In order to remove these ridges and create a flat surface for bonding to a PDMS (polydimethylsiloxane) manifold, a fluidic border region was included in the optical layer design in a method similar to that used by Friis et al.29 This is shown in the schematic of the final design in Fig. 2(b), between the fluidic channel and waveguides. At the optical analysis region the fluidic border consists of a 10 μm deep border surrounding the fluidic channel. Light leaving the MMI must propagate through the fluidic border region which, having no lateral optical bounds, acts as a slab waveguide. A fluidic border region of too great a depth will therefore alter the imaging length of an MMI and so must be kept to the minimum depth required for effective fluidic sealing. Based on experimental experience a border depth of 10 μm was found to be acceptable for sealing against a PDMS manifold, and BPM simulations showed that a 10 μm deep fluidic border did not significantly affect the imaging length of a 20.0 μm wide MMI.
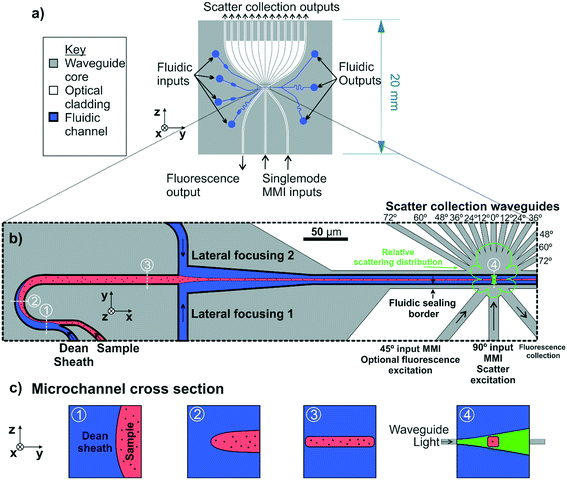
The final device design is shown as an overview in Fig. 2(a). Two MMIs are positioned to provide incident beams at 45° and 90° to the particle flow as shown in Fig. 2(b). The placement angles of the input MMIs are adjusted using Snell's law to account for refraction at the microfluidic channel walls. In this work only the 90° MMI was used for scattering excitation experiments. Importantly, having the additional optional input channel at 45° to particle flow allows the possibility of simultaneous fluorescence excitation for phenotyping EVs labelled with fluorescent antibodies. A wide multimode waveguide without an MMI is positioned to collect fluorescently emitted light at 90° to the fluorescence excitation beam for this future inclusion.
To collect the light scattered from particles at discrete angles in order to measure scattering distribution, 13 waveguides, 12 μm wide, are positioned at 12° intervals over a range of 0–72° relative to the excitation beam to create an angular array, as shown in Fig. 2(a) and in expanded detail in Fig. 2(b). The 12° angular interval of the waveguide placement was designed to be close to the waveguide full acceptance angle of 16.1° providing a balance between collecting sufficient optical power for a strong signal and providing 6 collection channels, an adequate number for least squares fitting of the theoretical scattering distribution to calculate particle diameter. Again, the placement angle of the collection waveguides is adjusted to account for refraction at the microfluidic channel wall. The output facets of the scatter collection waveguides at the chip edge are evenly spaced with a pitch of 1 mm to allow butt coupling to a fibre array or directly to a photomultiplier array of matching pitch.
Fluidic design
Confinement of the sample stream into a tight core in the centre of the fluidic channel was required to ensure all of the sample passed through the excitation beam. The microfluidic drifting strategy developed by Mao et al.30 was used for fluidic focussing of the sample as the fluidic designs required can be easily fabricated as a single layer. In this approach, which is shown schematically in Fig. 2(b) and (c), vertical focussing is performed by introducing the sample stream into a curved channel in parallel with a sheath flow at a higher flow rate. As both flows progress around the channel curve, secondary lateral flows are induced, known as Dean flows, which compress the sample stream vertically, while stretching it laterally resulting in a thin sheet of sample flowing at mid height in the channel. The magnitude of the secondary flows can be quantified using the Dean number, a dimensionless quantifier defined as De = Re(H/2R)0.5 where Re is the channel Reynolds number, H is the channel hydraulic diameter and R is the radius of curvature.31 Following vertical compression in the curved channel section, the sample stream progresses to a T junction where sheath flows from either side compress it laterally, resulting in a focussed core sample stream.The microchannel height in the integrated cytometer was constrained to 20 μm, as this was the maximum channel height which could be economically fabricated using the processes available in an academic setting. Channels of greater depth would require deposition of a thicker cladding and deeper etching greatly increasing fabrication time and cost. The microchannel width at the optical analysis region was chosen to be 20 μm in order to avoid disruption to MMI focussing. These dimensions substantially exceed the channel width![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) particle diameter maxima of 7, thereby avoiding inertial focussing of particles towards the channel walls, that would otherwise vertically migrate half of the particulate sample outside the excitation beam.31,32
particle diameter maxima of 7, thereby avoiding inertial focussing of particles towards the channel walls, that would otherwise vertically migrate half of the particulate sample outside the excitation beam.31,32
Materials and methods
Integrated cytometer fabrication
The fabrication process was based on one used for a first generation monolithically-integrated cytometer (without either fluidic Dean focussing or optical MMI focussing) and is described in detail in previous work by Butement et al.26 The process was designed to use techniques commonly used in the microelectronics industry to enable mass production. Silica substrates (Spectrosil2000, Heraeus, Germany) 4 inches in diameter and 1 mm thick, were cleaned and a 1.4 μm thick germania-silica waveguide layer (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75% wt% GeO2
75% wt% GeO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2) was deposited by RF magnetron sputtering (Plasmalab 300, OIPT, UK). The waveguide layer was then annealed at 950 °C for 6 h with a ramp up and down rate of 5 °C min−1, under an oxygen atmosphere in a tube furnace. Annealing was required to replace oxygen deficiencies in the waveguide layer and produce the correct refractive index. The refractive indices of the optical layers, measured by ellipsometry (MD2000D ellipsometer J.A. Woollam Co., USA), were 1.461 ± 0.001, 1.4671 ± 0.001 and 1.460 ± 0.001 for substrate, core and cladding respectively at λ = 532 nm. Lift-off photolithography and e-beam deposition were used to define a 150 nm thick chromium hard mask on the waveguide film. The waveguide structures were produced by inductively coupled plasma (ICP) etching (Plasmalab 100 ICP380, OIPT, UK) through the entire waveguide film, plus an additional 0.5 μm, to a total depth of 1.9 μm, to ensure a strip waveguide cross section. The remaining chrome hard mask was removed by wet etching. The waveguides were then clad with a 9.3 μm thick layer of silica by plasma enhanced chemical vapour deposition (PECVD) using a Plasmalab 100 LDS-PECVD system (OIPT, UK). To prevent stress-induced cracking and ensure correct stoichiometry, the cladding was deposited in steps of no more than 5 μm at a time, followed by annealing using the same process used for the waveguide core layer. The same photolithographic and e-beam protocols used to define the waveguide layer, with adjustment for increased mask thickness, were used to define the pattern for the microfluidic circuit in a 1.3 μm-thick chromium hard mask. The microfluidic channels were then etched through all the layers with ICP etching to a depth of 20 μm using the same protocol as used for the waveguide layer. This results in a microfluidic channel with the optical waveguide layer positioned at mid-height within the channel. The remaining chrome hard mask was removed by wet etching. Wafers were diced into individual chips and the input and output end facets were polished to an optical finish. To seal the microfluidic channels a PDMS (Sylgard 184, Dow, USA) manifold measuring 15 × 18 × 6 mm was moulded using PMMA frames and inlet/outlet holes corresponding with the inlet/outlet reservoir positions in the microfluidic circuitry were punched using a 1 mm diameter biopsy punch aided by an alignment jig. The PDMS manifolds were exposed to oxygen plasma (Tepla 300) at a pressure of 1.2 mbar and an RF power of 30 W for 30 s and then sealed within 30 s of exposure against the top surface of the optofluidic chip, again using an alignment jig. Assembled devices were baked for 24 h at 90 °C to strengthen the bond. The microfluidic connections were made with polyethylene tubing with an inner diameter of 0.38 mm and an outer diameter of 1.09 mm, which was inserted into the inlet/outlet holes in the PDMS manifold. Should a blockage occur, the chips can be recycled by immersion in ethanol at room temperature for 24 hours. The PDMS to glass bond then becomes sufficiently weak to allow the manifold to be peeled away by hand. Any remaining PDMS residue is removed by a 1 hour immersion in Piranha solution, washed in water and swabbed with a cotton bud followed by sonication in ethanol. This technique allowed devices to be recycled after blockages at least 5 times.
SiO2) was deposited by RF magnetron sputtering (Plasmalab 300, OIPT, UK). The waveguide layer was then annealed at 950 °C for 6 h with a ramp up and down rate of 5 °C min−1, under an oxygen atmosphere in a tube furnace. Annealing was required to replace oxygen deficiencies in the waveguide layer and produce the correct refractive index. The refractive indices of the optical layers, measured by ellipsometry (MD2000D ellipsometer J.A. Woollam Co., USA), were 1.461 ± 0.001, 1.4671 ± 0.001 and 1.460 ± 0.001 for substrate, core and cladding respectively at λ = 532 nm. Lift-off photolithography and e-beam deposition were used to define a 150 nm thick chromium hard mask on the waveguide film. The waveguide structures were produced by inductively coupled plasma (ICP) etching (Plasmalab 100 ICP380, OIPT, UK) through the entire waveguide film, plus an additional 0.5 μm, to a total depth of 1.9 μm, to ensure a strip waveguide cross section. The remaining chrome hard mask was removed by wet etching. The waveguides were then clad with a 9.3 μm thick layer of silica by plasma enhanced chemical vapour deposition (PECVD) using a Plasmalab 100 LDS-PECVD system (OIPT, UK). To prevent stress-induced cracking and ensure correct stoichiometry, the cladding was deposited in steps of no more than 5 μm at a time, followed by annealing using the same process used for the waveguide core layer. The same photolithographic and e-beam protocols used to define the waveguide layer, with adjustment for increased mask thickness, were used to define the pattern for the microfluidic circuit in a 1.3 μm-thick chromium hard mask. The microfluidic channels were then etched through all the layers with ICP etching to a depth of 20 μm using the same protocol as used for the waveguide layer. This results in a microfluidic channel with the optical waveguide layer positioned at mid-height within the channel. The remaining chrome hard mask was removed by wet etching. Wafers were diced into individual chips and the input and output end facets were polished to an optical finish. To seal the microfluidic channels a PDMS (Sylgard 184, Dow, USA) manifold measuring 15 × 18 × 6 mm was moulded using PMMA frames and inlet/outlet holes corresponding with the inlet/outlet reservoir positions in the microfluidic circuitry were punched using a 1 mm diameter biopsy punch aided by an alignment jig. The PDMS manifolds were exposed to oxygen plasma (Tepla 300) at a pressure of 1.2 mbar and an RF power of 30 W for 30 s and then sealed within 30 s of exposure against the top surface of the optofluidic chip, again using an alignment jig. Assembled devices were baked for 24 h at 90 °C to strengthen the bond. The microfluidic connections were made with polyethylene tubing with an inner diameter of 0.38 mm and an outer diameter of 1.09 mm, which was inserted into the inlet/outlet holes in the PDMS manifold. Should a blockage occur, the chips can be recycled by immersion in ethanol at room temperature for 24 hours. The PDMS to glass bond then becomes sufficiently weak to allow the manifold to be peeled away by hand. Any remaining PDMS residue is removed by a 1 hour immersion in Piranha solution, washed in water and swabbed with a cotton bud followed by sonication in ethanol. This technique allowed devices to be recycled after blockages at least 5 times.
Microfluidic focussing control and optimisation
To determine the optimal microfluidic geometry, an experimental matrix of curved microfluidic channel geometries were tested to ascertain which produced optimal vertical compression of the sample stream. The radii of curvature used were 25 μm, 50 μm and 100 μm, the curve arc angles used were 90° and 180° and the channel widths used were 10 μm and 20 μm. These microfluidic designs were fabricated in polydimethylsiloxane (PDMS) for rapid experimental iteration. Inlet and outlet ports were punched in the PDMS flow cells, which were then sealed to a glass slide after oxygen plasma exposure. Each fluidic input was interfaced to an independent syringe pump to enable independent flow rate control. This allowed for control of vertical compression by adjusting the sample to sheath flow ratio and the lateral position of the sample stream by adjusting the lateral sheath flow ratio. For curved channel geometry optimisation experiments an average flow velocity of 0.33 m s−1 in the curved channel was used with a flow rate ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 of sample to sheath fluid. Lateral compression was achieved with a flow rate ratio of lateral sheath 1: sample: Dean sheath
7 of sample to sheath fluid. Lateral compression was achieved with a flow rate ratio of lateral sheath 1: sample: Dean sheath![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lateral sheath 2 of 8
lateral sheath 2 of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7
7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8.
8.
A solution of 10 μM fluorescein sodium salt in phosphate buffered saline was used to image the sample stream in the Dean focussing element. Flow performance was assessed with standard fluorescence microscopy to straightforwardly infer the vertical compression by measuring the lateral stretching of the sample stream as a percentage of the channel width. Confocal microscopy was used to measure the lateral and vertical dimensions of the sample stream in the optical detection region of the microchannel. The sidewalls of the channels were visualised by staining the device for 30 minutes with 100 μg mL−1 of the co-polymer poly-L-lysine grafted to poly(ethylene glycol) and labelled with tetramethylrhodamine (PLL-g-PEG TRITC, SuSoS AG) immediately after plasma bonding. A Leica SP8 confocal microscope with a 20× objective and pinhole set to 1 airy unit was used to obtain confocal Z stack images with a 0.5 μm step. Image deconvolution was performed using the Huygens Essential software with a theoretical point spread function.
Optical apparatus
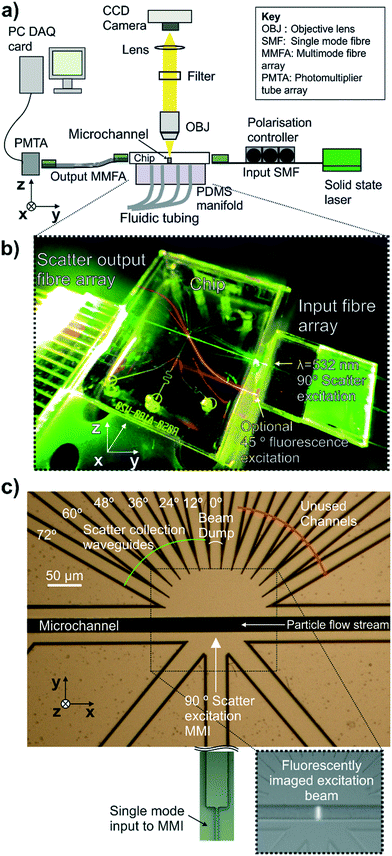
The apparatus shown in Fig. 3(a) was used for coupling light into and out of the integrated cytometer and to fluorescently image the shape of the excitation beam in the microfluidic channel. The apparatus consisted of a microscope with a 20×, 0.46 NA microscope objective lens focussed on the region of the microfluidic channel illuminated by the waveguide, a 542 nm long pass filter to cut out excitation light and a CCD camera (ORCA-R2, Hamamatsu, Japan). Input and output optical coupling are shown photographically in Fig. 3(b). Light from a 20 mW fibre-coupled diode-pumped solid-state 532 nm laser (OZ-2000-532, OZ Optics, Canada) was coupled into the input waveguide via a butt-coupled single mode fibre (S405-XP, Nufern, USA) mounted on a v-groove block with the fibre under polarisation control.For the scattering measurements of size standard particles, the waveguides set at 12–72° to the excitation beam axes were used as shown in Fig. 3(c). The 0° waveguide functioned as a beam dump. The mirrored set of scattered collection waveguides at equivalent angles were not used, due to a limited number of DAQ card input channels. The scatter collection array outputs were butt-coupled into an array of multimode fibres (GR-S50/125-20P, Nufern, USA) of matching pitch mounted on a v-groove block under 5 axis positional control. The v-groove block had a total of 16 fibres available but only 6 fibres were used by offsetting the v-groove block from the chip. This was to prevent collection of light from the beam dump waveguide at 0° which could damage the PMT and could be avoided in future with adjustment of the fibre array configuration. In this case, the output end of the multimode fibre array was also mounted on a v-groove block of identical layout to the input end. This output v-groove block was butt-coupled to a photomultiplier tube linear array module (H11459-20, Hamamatsu, Japan) with each fibre aligned with an individual photocathode element on the PMT array.
To characterise the shape of the beam focussed in the fluidic channel by the MMI, the beam was imaged by pumping a 0.4 μM solution of the fluorescent dye R-phycoerythrin through the channel at 0.1 m s−1 and imaging from above as shown in the inset fluorescence micrograph in Fig. 3(c) and false colour images in Fig. 4.
Measurement of scattering from particles
The apparatus shown in Fig. 3(a) was used to make scattering measurements of polystyrene particle size standards and also 200 nm liposomes. The polystyrene size standards consisted of a range of NIST (National Institutes of Standards and Technology, USA) traceable particle suspensions (Duke Standards, ThermoFisher) of diameter 400 nm, 700 nm, 1000 nm and 1600 nm with a maximum diameter CV of ±1.5%. Particles were made of solid polystyrene with a refractive index of 1.598 at 532 nm. 1% v/v particle suspensions were diluted to produce a count rate in the region of 200–1000 Hz. Unilamellar liposomes were made by extrusion through a polycarbonate track etched membrane with a 200 nm pore size using a manual extruder (Avanti Polar Lipids, US). Lyophilized 1,2-dilauroyl-sn-glycero-3-phosphocholine (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 PC DLPC) (Avanti Polar Lipids, US). Was rehydrated in PBS for 30 minutes at a concentration of 5 mM and extruded with 15 passes through the membrane. The liposome suspension was then diluted to 2.5 × 106 liposomes per mL in PBS for analysis on the integrated cytometer.
0 PC DLPC) (Avanti Polar Lipids, US). Was rehydrated in PBS for 30 minutes at a concentration of 5 mM and extruded with 15 passes through the membrane. The liposome suspension was then diluted to 2.5 × 106 liposomes per mL in PBS for analysis on the integrated cytometer.
Refractive index values for the liposome components at a wavelength of 532 nm were obtained from the literature and were 1.44 for the DPLC outer layer33 and 1.3367 for the PBS core.34 The refractive index of an entire liposome was estimated using the volumetric ratio of its components assuming a membrane thickness of 4 nm (ref. 33) and was calculated to be 1.3486. For acquisition of the scattering signals from a particle suspension, 3D fluidic focussing conditions were established at an average flow velocity of 0.75 m s−1 in the Dean curve channel, accelerating after lateral focussing to an average flow rate of 2.25 m s−1 within the analysis microchannel. The flow rate was held for 1 minute to ensure flow stabilisation before data acquisition commenced. Light was coupled into the excitation waveguide in the TM polarisation. Data from the six channels of the PMT were acquired on a 14 bit PCIE DAQ card (TPCE-2016-8S DAQ Module, Elsys, Switzerland). The data channels recorded a voltage proportional to the optical power incident on each of six individual PMT elements coupled to the scatter collection array waveguide outputs.
The DAQ card was set to AC coupling to remove constant background. A particle signal from the 12° scatter collection waveguide channel was used to trigger data acquisition of signal pulses on all channels. To set the trigger threshold, a background measurement of the 12° PMT voltage, 8 MS (Mega Samples) in length, was acquired at 20 MHz with fluid flowing under 3D focussing conditions without particles in order to acquire the noise on the detector when no particles are passing which was represented as the standard deviation of the detector voltage during this acquisition period. The trigger threshold voltage was then set at three standard deviations of this background signal above zero with a hysteresis of one standard deviation on a positive slope. A voltage above this threshold on the 12° channel was deemed to be due to particle-induced scattering and was used to trigger simultaneous acquisition of the pulse on all scatter collection waveguide channels at 20 MHz with a 1 KS acquisition length. A minimum of 1500 pulses were recorded for suspensions of each particle size.
Results and discussion
Optical focussing characterisation
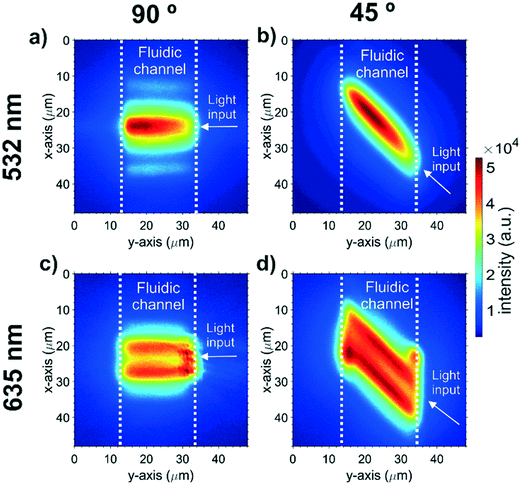
The intensity distribution of the MMI-focussed excitation beam crossing the microfluidic channel was imaged with fluorescence microscopy. Fig. 4 shows the intensity distributions for all the beam configurations available in the integrated cytometer device. The intensity distribution is only observed within the microfluidic channel as the dye is contained within the channel. Light at 532 nm produced a beam with a single focus and an approximately Gaussian cross section, which could be launched at either 45° (Fig. 4(a)) or 90° (Fig. 4(b)). The focus for the 532 nm wavelength beam at 90° to the particle flow, which was subsequently used for scattering excitation, was located 16 μm from the beam launching side, and thus 6 μm from the centre of the channel where the particle stream would flow. This offset from centre is attributed to fabrication tolerance, for example an increase in the MMI width of 60 nm can add 6 μm to the focal length. The focussed beam width, defined as full width at 1/e2 intensity was 14 μm and the beam shape was a near-Gaussian image of the single mode input with some additional side-lobes caused by light leaking into the cladding. Whilst the beam focus is not central in the channel, the width in the centre of the beam is still sufficiently narrow at 15 μm. This beam width is comparable to that used with benchtop flow cytometers used for EV analysis but critically it is in a monolithically-integrated format with intrinsic and permanent alignment. Further optimisation of the MMI design and fabrication process is expected to produce narrower beams. The ability of MMIs to produce multiple foci is shown in Fig. 4(c) and (d) where using light at a wavelength of 635 nm produces a double focus in the channel. Multiple foci could have many possible future applications, for example for particle velocity measurements by exciting a double pulse.Microfluidic focussing optimisation
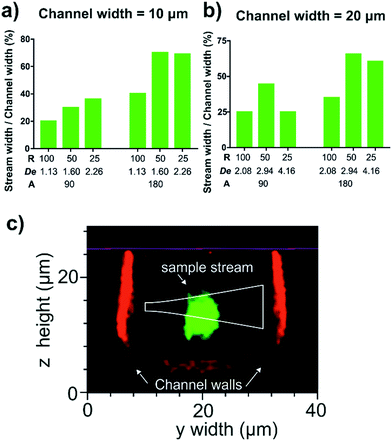
A range of Dean curve channel geometries with variations in radius of curvature (25, 50 and 100 μm), curve arc angle (90° and 180°) and channel width (10 and 20 μm) were tested to ascertain which combination provided the greatest vertical compression of the sample stream. The vertical compression of a fluorescent sample stream was inferred by measuring the width of the stream exiting the curve, represented as percentage channel width. For these experiments an average flow velocity of 0.33 m s−1 in the Dean curve channel, with a sample to sheath flow rate ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, were used.
7, were used.
The results from the experimental matrix to determine the optimum Dean flow geometry are presented in Fig. 5. Increasing the arc angle from 90° to 180° doubles the transport time and focussing duration to further the lateral stretch of the sample stream across the channel.35 Although the magnitude of the Dean secondary flows scales with (H/2R)0.5, larger bend radii also have extended travel and therefore focussing times. In our experiments a 50 μm radius of curvature produced marginally improved focussing than the 25 μm radius of curvature and was chosen with the further benefit of more available area to create a pressure-tolerant bond at this critical feature. The 10 μm-wide channel produced slightly greater proportional lateral stretching, albeit at the risk of increased local pressure and problems of clogging during prolonged operation. Based on the above observations the optimum geometry for reliable Dean focussing to a tight sample core involved a radius of curvature of 50 μm, a 180° arc angle and a channel width of 20 μm, and was implemented in the final integrated cytometer design.
The vertical compression of the sample stream in this optimised curved channel geometry was measured with confocal microscopy. It was found that increasing the average fluid flow velocity from 0.33 m s−1 (De = 2.94) to 0.66 m s−1 (De = 5.88), compressed the sample stream from a height of 8 μm to 6 μm. In addition, it was found that using a sample flow to sheath flow rate ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 was too unstable for long-term use as sheath fluid would occasionally back-flow into the sample channel. Reducing the sample to sheath flow ratio to 1
7 was too unstable for long-term use as sheath fluid would occasionally back-flow into the sample channel. Reducing the sample to sheath flow ratio to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 prevented these back-flows and still maintained a tight sample core with a height of 6 μm and a width of 4 μm which is shown in the confocal micrograph in Fig. 5(c) with an overlaid beam profile approximated using the equation for a propagating Gaussian beam launched from the waveguide.27 Here the sample stream passes below the excitation beam and is also slightly taller than the beam height of 3.9 μm and so some sample is expected to pass outside of the beam. Whilst this was expected to increase signal variability in absolute scattered power between individual particles, the effect on the shape of the relative scattering distribution was expected to be minimal and so would not critically effect the calculation of particle diameter. The flow focussing was sufficiently compact to ensure at least half the particles encountered the beam which would provide a sufficient number of measurements from a sample. Faster flow rates would be expected to further vertically compress the sample stream but were beyond the pressure tolerance limits of the PDMS microfluidic circuit used in the matrix study. The silica channel of the integrated cytometer, which was sealed with a flat PDMS manifold, showed a greater pressure tolerance and so here the average flow velocity in the Dean focussing channel could be increased to 0.75 m s−1 to achieve even greater vertical compression. This average flow velocity in the Dean focussing channel was used for the subsequent scattering measurements of size standard particles.
3 prevented these back-flows and still maintained a tight sample core with a height of 6 μm and a width of 4 μm which is shown in the confocal micrograph in Fig. 5(c) with an overlaid beam profile approximated using the equation for a propagating Gaussian beam launched from the waveguide.27 Here the sample stream passes below the excitation beam and is also slightly taller than the beam height of 3.9 μm and so some sample is expected to pass outside of the beam. Whilst this was expected to increase signal variability in absolute scattered power between individual particles, the effect on the shape of the relative scattering distribution was expected to be minimal and so would not critically effect the calculation of particle diameter. The flow focussing was sufficiently compact to ensure at least half the particles encountered the beam which would provide a sufficient number of measurements from a sample. Faster flow rates would be expected to further vertically compress the sample stream but were beyond the pressure tolerance limits of the PDMS microfluidic circuit used in the matrix study. The silica channel of the integrated cytometer, which was sealed with a flat PDMS manifold, showed a greater pressure tolerance and so here the average flow velocity in the Dean focussing channel could be increased to 0.75 m s−1 to achieve even greater vertical compression. This average flow velocity in the Dean focussing channel was used for the subsequent scattering measurements of size standard particles.
Diameter measurement of particles in the EV size range
In order to demonstrate particle size measurement on the integrated cytometer, a series of polystyrene particle size standards in the EV size range were analysed. These NIST traceable particles have a small diameter CV of ±1.5% and a reproducible refractive index. Whilst the refractive index of polystyrene is higher than the reported refractive index of EVs, resulting in an effectively larger scattering cross section, the particles would still give an initial measure of the device performance within the EV size range for refinement in future work.Fig. 6(a) shows an example of synchronised voltage pulses from the PMT array recorded from scattering from one individual 700 nm diameter particle into 6 collection waveguides set from 12–72° at 12° increments. ESI† Fig. S1 shows example voltage pulses for the other nominal particle diameters measured. In all cases as the collection angle increases, both the peak amplitude of the pulse and the pulse area decrease as less light is scattered into collection waveguides at greater angles to the excitation beam, as expected from scattering in the Mie regime. The pulse shapes exhibit multiple sub-peaks, which we propose are caused by optical interference between a fraction of the excitation beam light directly entering the collection waveguides and the phase-shifted light scattered by the particle. Specifically, if Pp(t) is the optical power scattered from the particle into one of the waveguides as a function of time and Pb is the power of background scattering e.g. from the fluid and from optical interfaces, then the total detected power is
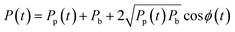 | (1) |
| E(t) = ∫Pp(t)dt + ∫Pbdt = ∫Pp(t)dt + const | (2) |
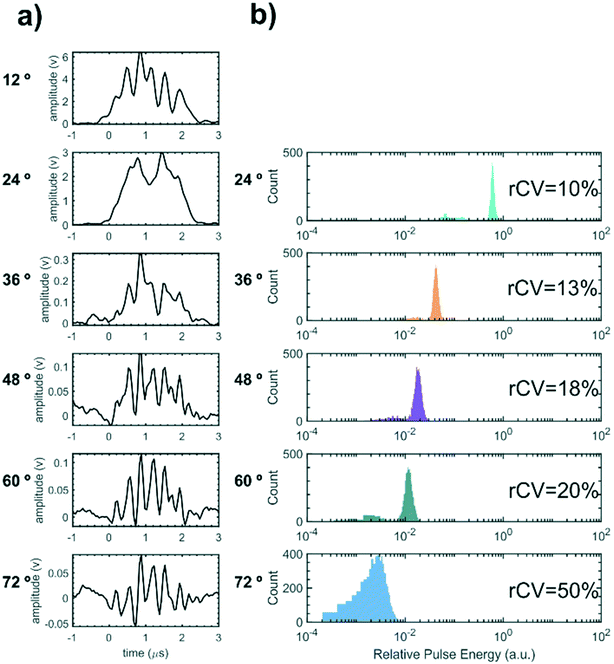
The scattering distributions of thousands of flowing particles for each nominal diameter of size standard were measured using the device. For each individual particle, the pulse energies for each angular scattering channel were converted to a relative scale with the 12° channel corresponding to unity. Fig. 6(b) visualises the particle scattering measurements as histograms of relative pulse energy for each angular collection channel for a sample of 700 nm nominal diameter particles. The robust coefficient of variation (rCV = 100 × 0.75 × sample interquartile range/median relative pulse energy)13 is displayed inset for each angular channel as a metric for variation about the median pulse energy. Pulse energy histograms for other nominal diameters are shown in ESI† Fig. S2 and sample statistics are shown in ESI† Table S1. For all particle samples measurement variation increases with angle because less light is scattered into the wider-angle channels whilst random noise remains constant.
Data were collected in the same way with monodisperse samples ranging in diameter from 400 nm to 1600 nm. Particle size was calculated from each individual particle scattering distribution by fitting a model using MATLAB® (MathWorks, US) based on Mie scattering theory.2,12,14 This model predicts the angular scattering of light from a spherical particle, such as EVs36 and the relative optical energy collected by each collection waveguide in the integrated cytometer. An optimal fit was achieved for each particle by minimizing the weighted sum of squared residuals
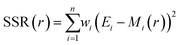 | (3) |
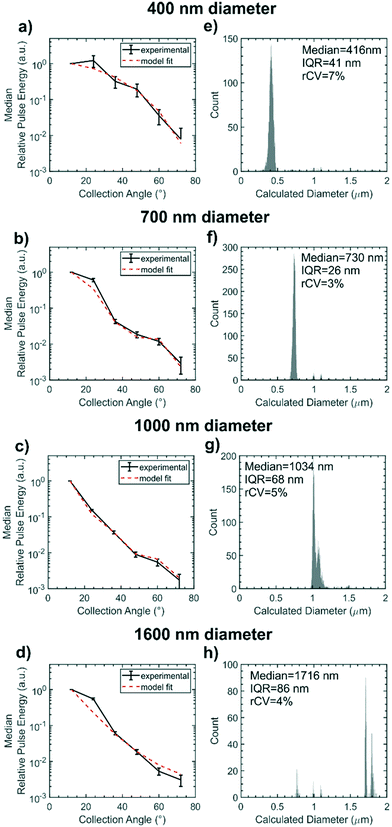
Fig. 7(a–d) represents the scattering distributions recorded for each sample of size standards as median relative pulse energies. To visualise the goodness of fit of the Mie scattering model, the scattering distribution of the median particle size calculated by the model is overlaid on the experimental data. The distribution of the calculated particle diameters for each size standard sample are shown in histograms in Fig. 7(e–h) with the sizing statistics for the sample inset. Particles as small as 400 nm nominal diameter could be detected. Sizing accuracy is comparable for the 400 nm, 700 nm and 1000 nm nominal diameter samples to within 34 nm of true size whilst the 1600 nm nominal diameter particles are within 116 nm. Sizing precision for all samples is between 3–7% rCV and is within the same order as the manufacturer stated CV of 1.5%. Absolute precision in diameter measurement, represented by the IQR, is highest for the 700 nm diameter sample because the waveguide configuration is most sensitive to scatter distribution form changes in this region. The scattering distribution for a ≈700 nm diameter particle is shown in Fig. 2(b), and exhibits a single local minimum in relative scattered energy around 46° which falls within the collection aperture of the 48° collection waveguide. Thus there is a large change in scattering distribution form for small changes in particle size whilst noise remains constant. Conversely, accuracy and precision are lowest for the 1600 nm nominal diameter particles, which are larger than typical EVs, because the number of local minima in the scattering distribution for particles at this size range approaches the number of waveguides and so local minima cannot be resolved. The change in scattering distribution form with diameter is therefore very small for particles ≈1600 nm in diameter and so there is an increased effect of random noise on the diameter calculation. Whilst this device was designed for sub-micron particles, future designs could tailor the number of waveguides or the excitation wavelength to a different size range of interest in order to ensure waveguide spacing is most sensitive to Mie resonance positioning. Overall the sensitivity accuracy and precision of the integrated cytometer for sizing polystyrene particles is comparable to the high performance achieved by free-space, multi-angle flow cytometers but crucially it has been demonstrated in a fully integrated chip.15
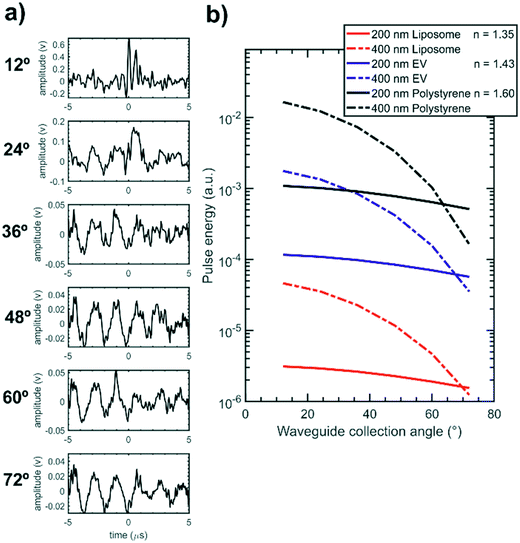
The integrated cytometer was also used to analyse samples of 200 nm diameter liposomes (n ≈ 1.35) in order to test the device performance with particles that more closely match the scattering response of EVs (n ≈ 1.43), which were not available. Fig. 8(a) presents an example detector pulse set recorded for an individual liposome showing that the 12° degree channel displays a clear pulse while the wider angle channels pulses are hidden within the background noise and so the full scattering distribution is not measurable. Without the full scattering distribution the least squares fitting process shown in ESI† Fig. S6 could not determine an accurate liposome diameter. The additional sensing challenge posed by EVs and liposomes is presented in Fig. 8(b) which compares the model-calculated scattering distributions for liposomes, EVs and polystyrene particles on an absolute scale and shows that EVs and liposomes scatter 1–2 orders of magnitude less light than polystyrene particles and thus require further improvements to the system in order to be measured. While these results do not show size determination they do demonstrate detection of a very low index particle in an integrated format and show promise that the integrated cytometer can be optimised for EV measurements.
The size measurement performance for low index particles can be improved by increasing the device signal to noise ratio. The scattering signal magnitude can be increased by using a greater excitation power and by individually increasing the gain on each PMT anode in the array. Background noise can be reduced by eliminating vibration from the system by gluing all optical connections and by using a laser source with improved power stability. Greater fluidic confinement of flowing particles in a tighter core would also reduce any effects of positional variation on the scattering distribution shape. Further improvements can also be made to the fitting process to improve size determination accuracy and precision. Characterising the individual optical losses in each optical channel including the propagation and coupling losses in the waveguides and fibre optics would reduce the effect of any systematic error on model fitting. In addition using a greater number of collection channels would improve fitting performance. Providing sufficient light is still collected, this could be achieved by using a new design with more waveguides with a smaller collection angle increment or by using the 45° excitation MMI in the existing design to collect light over 5–137°.
Conclusions and outlook
An integrated cytometer has been realised for multi-angle scattering-based size measurements in the EV size range using a unique combination of enabling technologies. Dean coupled hydrodynamic focussing provides a confined sample stream which intersects with a narrow optical beam focused with MMI-based on-chip lenses. An angular collection array enables measurement of particle scattering distribution showing high sizing accuracy and precision for sub-micron polystyrene particles comparable to other high performance but free space multi-angle cytometers. The cytometer was also used to detect 200 nm liposomes indicating a development path towards size determination of EVs. The integration of the different components paves the way for the monolithic manufacture of dedicated EV cytometers which can have tailored designs to the size range of interest and at greatly lower cost. Future work will use the device for simultaneous fluorescence measurements using the optics already included in the design and will move towards sizing and phenotyping of EVs from clinical samples to test the capabilities of the device and contribute to research into the role of EVs in health and disease.The data used in this publication can be accessed at DOI: https://doi.org/10.5258/SOTON/D1173.
Author contributions
Conceptualisation: J. T. B., J. W., J. S. W.; formal analysis: J. T. B., P. H.; investigation: J. T. B., P. M. H.; methodology: J. T. B. P. M. H., J. A. W., J. A. H., N. A. E., P. H., J. W., J. S. W.; resources: J. A. H., N. A. E., J. W., J. S. W.; software: J. T. B., J. A. W., P. H.; visualization: J. T. B.; writing – original draft: J. T. B.; writing – review and editing: all authors; supervision: J. W., J. S. W.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors would like to thank the European Research Council for funding this work under the European Union's Seventh Framework Programme (FP7/2007–2013) ERC grant agreement no. 291216 ‘Wideband Integrated Photonics for Accessible Biomedical Diagnostics’ and the Medical Research Council for a Discovery Grant (JTB, MC_PC_15078). The authors also thank Neil Sessions for advice in the cleanroom and Victor Calero-Martin for advice on reversible PDMS–glass bonding.References
- E. van der Pol, A. N. Böing, E. L. Gool and R. Nieuwland, Recent developments in the nomenclature, presence, isolation, detection and clinical impact of extracellular vesicles, J. Thromb. Haemostasis, 2016, 14(1), 48–56 CrossRef CAS PubMed.
- E. van der Pol, et al., Standardization of extracellular vesicle measurements by flow cytometry through vesicle diameter approximation, J. Thromb. Haemostasis, 2018, 16(6), 1236–1245 CrossRef CAS PubMed.
- C. Lawson, J. M. Vicencio, D. M. Yellon and S. M. Davidson, Microvesicles and exosomes: new players in metabolic and cardiovascular disease, J. Endocrinol., 2016, 228(2), R57–R71 Search PubMed.
- J. A. Welsh, E. Scorletti, G. F. Clough, N. A. Englyst and C. D. Byrne, Leukocyte extracellular vesicle concentration is inversely associated with liver fibrosis severity in NAFLD, J. Leukocyte Biol., 2018, 104(3), 631–639 CrossRef CAS PubMed.
- E. I. Buzas, B. György, G. Nagy, A. Falus and S. Gay, Emerging role of extracellular vesicles in inflammatory diseases, Nat. Rev. Rheumatol., 2014, 10, 356 CrossRef CAS PubMed.
- D. L. M. Rupert, V. Claudio, C. Lässer and M. Bally, Methods for the physical characterization and quantification of extracellular vesicles in biological samples, Biochim. Biophys. Acta, Gen. Subj., 2017, 1861(1), 3164–3179 CrossRef CAS PubMed.
- H. Shao, H. Im, C. M. Castro, X. Breakefield, R. Weissleder and H. Lee, New Technologies for Analysis of Extracellular Vesicles, Chem. Rev., 2018, 118(4), 1917–1950 CrossRef CAS PubMed.
- R. A. Dragovic, et al., Sizing and phenotyping of cellular vesicles using Nanoparticle Tracking Analysis, Nanotechnology, Biology and Medicine, 2011, 7(6), 780–788 CrossRef CAS PubMed.
- Malvern Panalytical, NanoSight NS300 features and benefits, 2019, [Online], Available: https://www.malvernpanalytical.com/en/products/product-range/nanosight-range/nanosight-ns300.
- E. van der Pol, et al., Particle size distribution of exosomes and microvesicles determined by transmission electron microscopy, flow cytometry, nanoparticle tracking analysis, and resistive pulse sensing, J. Thromb. Haemostasis, 2014, 12(7), 1182–1192 CrossRef CAS PubMed.
- J. A. Welsh, J. A. Holloway, J. S. Wilkinson and N. A. Englyst, Extracellular Vesicle Flow Cytometry Analysis and Standardization, Front. Cell Dev. Biol., 2017, 5, 1–7 Search PubMed.
- J. A. Welsh, et al., FCMPASS Software Aids Extracellular Vesicle Light Scatter Standardization, Cytometry, Part A, 2019 DOI:10.1002/cyto.a.23782.
- H. M. Shapiro, Practical Flow Cytometry, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2003 Search PubMed.
- E. Van Der Pol, M. J. C. Van Gemert, A. Sturk, R. Nieuwland and T. G. Van Leeuwen, Single vs. swarm detection of microparticles and exosomes by flow cytometry, J. Thromb. Haemostasis, 2012, 10(5), 919–930 CrossRef CAS PubMed.
- A. I. Konokhova, et al., Super-resolved calibration-free flow cytometric characterization of platelets and cell-derived microparticles in platelet-rich plasma, Cytometry, Part A, 2016, 89(2), 159–168 CrossRef CAS PubMed.
- P. J. Wyatt, Differential light scattering: a physical method for identidying living bacterial cells, Appl. Opt., 1968, 7(10), 1879–1896 CrossRef CAS PubMed.
- G. C. Salzman, et al., A flow system multiangle light scattering instrument for cell characterization, Clin. Chem., 1975, 21(9), 1297–1304 CrossRef CAS.
- M. Bartholdi, G. C. Salzman, R. D. Hiebert and M. Kerker, Differential light scattering photometer for rapid analysis of single particles in flow, Appl. Opt., 1980, 19(10), 1573–1581 CrossRef CAS PubMed.
- R. J. Yang, L. M. Fu and H. H. Hou, Review and perspectives on microfluidic flow cytometers, Sens. Actuators, B, 2018, 266, 26–45 CrossRef CAS.
- D. Barat, G. Benazzi, M. C. Mowlem, J. M. Ruano and H. Morgan, Design, simulation and characterisation of integrated optics for a microfabricated flow cytometer, Opt. Commun., 2010, 283(9), 1987–1992 CrossRef CAS.
- G. Zhuang, T. G. Jensen and J. P. Kutter, Detection of unlabeled particles in the low micrometer size range using light scattering and hydrodynamic 3D focusing in a microfluidic system, Electrophoresis, 2012, 33(12), 1715–1722 CrossRef CAS PubMed.
- B. R. Watts, Z. Zhang, C. Q. Xu, X. Cao and M. Lin, Scattering detection using a photonic-microfluidic integrated device with on-chip collection capabilities, Electrophoresis, 2014, 35(2–3), 271–281 CrossRef CAS PubMed.
- A. Ma, G. Matmon, D. Holmes and G. Aeppli, Monolithic Waveguide Array Platform for Photonic Characterisation of Biological Sample, in 16th international conference on miniaturized systems for chemistry and life sciences, 2012, pp. 1339–1341 Search PubMed.
- R. Kitamura, L. Pilon and M. Jonasz, Optical constants of silica glass from extreme ultraviolet to far infrared at near room temperature, Appl. Opt., 2007, 46(33), 8118 CrossRef CAS PubMed.
- H. C. Hunt and J. S. Wilkinson, Multimode interference devices for focusing in microfluidic channels, Opt. Lett., 2011, 36(16), 3067–3069 CrossRef CAS PubMed.
- J. T. Butement, et al., Integrated optical waveguides and inertial focussing microfluidics in silica for microflow cytometry applications, J. Micromech. Microeng., 2016, 26(10), 105004 CrossRef.
- A. Ghatak and K. Thyagarajan, Introduction to fiber optics, 1st edn, Cambridge university press, 1998 Search PubMed.
- L. B. Soldano and E. C. M. Pennings, Optical multi-mode interference devices based on self-imaging: principles and applications, J. Lightwave Technol., 1995, 13(4), 615–627 CrossRef.
- P. Friis, K. Hoppe, O. Leistiko, K. B. Mogensen, J. Hübner and J. P. Kutter, Monolithic integration of microfluidic channels and optical waveguides in silica on silicon, Appl. Opt., 2001, 40(34), 6246–6251 CrossRef CAS PubMed.
- X. Mao, J. R. Waldeisen and T. J. Huang, Microfluidic drifting’--implementing three-dimensional hydrodynamic focusing with a single-layer planar microfluidic device, Lab Chip, 2007, 7(10), 1260–1262 RSC.
- H. Amini, W. Lee and D. Di Carlo, Inertial microfluidic physics, Lab Chip, 2014, 14(15), 2739–2761 RSC.
- P. M. Holloway, J. Butement, M. Hegde and J. West, Serial integration of Dean-structured sample cores with linear inertial focussing for enhanced particle and cell sorting, Biomicrofluidics, 2018, 12(4), 1–12 CrossRef PubMed.
- M. C. Howland, A. W. Szmodis, B. Sanii and A. N. Parikh, Characterization of physical properties of supported phospholipid membranes using imaging ellipsometry at optical wavelengths, Biophys. J., 2007, 92(4), 1306–1317 CrossRef CAS PubMed.
- V. T. Hoang, et al., Optical properties of buffers and cell culture media for optofluidic and sensing applications, Appl. Sci., 2019, 9(6), 1–11 CAS.
- A. A. Nawaz, et al., Sub-micrometer-precision, three-dimensional (3D) hydrodynamic focusing via ‘microfluidic drifting, Lab Chip, 2014, 14(2), 415–423 RSC.
- N. Arraud, et al., Extracellular vesicles from blood plasma: determination of their morphology, size, phenotype and concentration, J. Thromb. Haemostasis, 2014, 12(5), 614–627 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI:10.1039/c9lc01182j |
| ‡ Now with: Investigative Medicine Division, Radcliffe Department of Medicine, University of Oxford, UK. |
| This journal is © The Royal Society of Chemistry 2020 |