Open Access Article
Open Access ArticleStretching DNA to twice the normal length with single-molecule hydrodynamic trapping†
Yan
Jiang
 ab,
Theodore
Feldman‡
a,
Julia A. M.
Bakx
c,
Darren
Yang
ab,
Theodore
Feldman‡
a,
Julia A. M.
Bakx
c,
Darren
Yang
 ad and
Wesley P.
Wong
ad and
Wesley P.
Wong
 *abde
*abde
aProgram in Cellular and Molecular Medicine, Boston Children's Hospital, Boston, MA 02115, USA
bDepartment of Pediatrics, Harvard Medical School, Boston, MA 02115, USA
cDepartment of Physics and Astronomy and LaserLaB, Vrije Universiteit Amsterdam, Amsterdam, The Netherlands
dWyss Institute for Biologically Inspired Engineering, Harvard University, Boston, MA 02115, USA
eDepartment of Biological Chemistry and Molecular Pharmacology, Blavatnik Institute, Harvard Medical School, Boston, MA 02115, USA. E-mail: wesley.wong@childrens.harvard.edu; Fax: +1 617 713 8393; Tel: +1 617 713 8383
First published on 17th April 2020
Abstract
Single-molecule force spectroscopy has brought many new insights into nanoscale biology, from the functioning of molecular motors to the mechanical response of soft materials within the cell. To expand the single-molecule toolbox, we have developed a surface-free force spectroscopy assay based on a high-speed hydrodynamic trap capable of applying extremely high tensions for long periods of time. High-speed single-molecule trapping is enabled by a rigid and gas-impermeable microfluidic chip, rapidly and inexpensively fabricated out of glass, double-sided tape and UV-curable adhesive. Our approach does not require difficult covalent attachment chemistries, and enables simultaneous force application and single-molecule fluorescence. Using this approach, we have induced a highly extended state with twice the contour length of B-DNA in regions of partially intercalated double-stranded (dsDNA) by applying forces up to 250 pN. This highly extended state resembles the hyperstretched state of dsDNA, which was initially discovered as a structure fully intercalated by dyes under high tension. It has been hypothesized that hyperstretched DNA could also be induced without the aid of intercalators if high-enough forces were applied, which matches our observation. Combining force application with single-molecule fluorescence imaging is critical for distinguishing hyperstretched DNA from single-stranded DNA that can result from peeling. High-speed hydrodynamic trapping is a powerful yet accessible force spectroscopy method that enables the mechanics of biomolecules to be probed in previously difficult to access regimes.
Introduction
Single-molecule force spectroscopy has greatly advanced our understanding of macromolecules, illuminating the mechanical properties of nucleic acids, the dynamics of motor proteins, and the kinetics of receptor–ligand binding.1 Although current approaches for force spectroscopy are powerful and relatively mature, the surface attachments required by most force spectroscopy methods1–8 often impose challenges. In particular, high force single-molecule measurements, for example in the range above 150 pN, can be difficult to perform in the equilibrium regime, because many common surface attachment strategies (e.g. biotin–streptavidin or digoxigenin–antidigoxigenin) have limited lifetimes and are rapidly ruptured at constant high forces.9–13 Even with multiple biotin–streptavidin bonds, the maximum force reported for near equilibrium conditions on a time scale of 1–10 minutes is ∼ 180 pN.14,15 In some cases, parts of the molecule can strongly adsorb onto gold surfaces and AFM tips, allowing constant application of hundreds of pN.16 When physical adsorption is unavailable or undesirable, more involved covalent conjugation chemistries are needed for high force application.13,17–23 Furthermore, the high force regime is outside the practical range of many standard approaches—for example, optical tweezers can run into problems with available laser power, local heating, or free radical generation, and magnetic tweezers typically do not have strong enough field gradients to generate these forces with standard magnetic microspheres.1,24,25 These problems limit investigations in the high force regime under conditions of constant force or loading rates slow enough to explore near-equilibrium behaviour. In addition, specific and homogeneous surface attachment can often be challenging to carry out, and can potentially lead to artifacts due to denaturation or distortion of molecules at the surface, or the addition of colloidal forces (e.g. van der Waals) that may be undesirable.26–28Here, we present a surface-free force spectroscopy approach that is not only inexpensive and accessible, but also able to probe tensions in the very high force regime without the need for challenging attachment chemistries. This method is based on an active-feedback hydrodynamic trap for particles and cells, pioneered by Schroeder et al.29–31 using a cross-slot flow channel.32 Flow gradients, such as shear and elongational flow,31–36 have been used to induce tension in untethered polymers, but single-molecule observation and force application is usually limited to a low level or a short amount of time as the molecule can simply flow away from the region of interest. Tanyeri et al.29,37,38 tackled this problem by combining elongational flow with automated active feedback of the outlet pressure using dual layer PDMS microfluidics. The hydrodynamic trap has been further developed to enable two-dimensional trapping, tighter trapping, and trapping of multiple particles by implementing multiple feedback channels, single-layer device design, and model predictive control (MPC) algorithms.37,39–42 The hydrodynamic trap and the newer Stokes trap have been used to measure the properties of complex fluids and to study the dynamics of single polymers, including DNA, under elongational flow.43–47 We have developed a simple and rapid approach to fabricate microfluidic devices for fluorescence-based hydrodynamic trapping, optimal for single-molecule force spectroscopy applications. Using this device, we have trapped single DNA molecules under high elongation rates and have induced extremely high tensions in them. The flow elongation rate is defined as the gradient of flow velocity along the direction of flow. Our microfluidic chip is rapidly and inexpensively fabricated out of glass, die cut double-sided tape and UV-cured adhesive. It is rigid and gas impermeable, ideal for high-pressure and fluorescence imaging applications. Our high-speed hydrodynamic trap can trap and apply high forces to single polymers or filaments under elongational flow, enabling us to perform force spectroscopy over a wide range of forces in solution without tethering. We have demonstrated the application of controlled tensions up to 250 pN on a single T4 DNA molecule without requiring the attachment of any beads or surfaces. High-speed hydrodynamic trapping can serve as a powerful yet accessible force spectroscopy method, particularly in the high force regime. Furthermore, our approach enables simultaneous monitoring of the sample with single-molecule fluorescence, which can provide essential information about the conformations and functions of biomolecules.
Mechanical studies of DNA have served as a cornerstone for single-molecule measurements, and have led to new insights into a range of biological processes.48–57 DNA has served not only as a subject of study, but also as a tool for the creation of handles and linkages with mechanical signatures, enabling the characterization of a variety of molecular structures and functions.58–62 More generally, the field of structural DNA nanotechnology has established DNA as a versatile programmable material for the creation of complex nanoscale structures and molecular devices.63,64 Therefore, a more comprehensive understanding of DNA mechanics would be of great value to both mechanobiology and DNA nanotechnology.
dsDNA exhibits complex elastic properties due to its characteristic base stacking and double-helical structure.65 For example, B-DNA, the structure most commonly found in nature, can transition to different structures under mechanical force. It has been known for over two decades that above a critical overstretching force of around 65 pN, B-DNA undergoes a transition to reach a contour length of 0.58 nm bp−1, 70% longer than the 0.34 nm bp−1 of B-DNA,5,66 and it has been established that this can occur in the absence of peeling.67–69 Recently, a new state of dsDNA with an even longer contour length of 0.7 nm bp−1—close to the maximum length allowed by the standard bond lengths within the backbone of DNA—was discovered under high force in the presence of intercalating dyes.14 Accordingly, they called this conformation hyperstretched DNA. Using fluorescently stained single DNA molecules, they were able to confirm that the DNA remained hybridized, and peeling did not occur, and also noted that it was fully intercalated by dyes, with the next-neighbour exclusion rule70 overcome by force. The authors proposed that hyperstretched DNA may be induced on naked DNA without intercalators in the extremely high force regime; yet testing this hypothesis is extremely challenging with standard experimental approaches. Using our approach, we have stretched regions of partially dye intercalated double-stranded DNA (dsDNA) to twice its normal length by applying forces up to 250 pN. The preserved intercalating dye fluorescence suggests that the two DNA strands remained hybridized. Our result supports the hypothesis that force alone is capable of inducing this hyperstretched state of DNA.
Experimental
Microfluidic cross-slot chip
To construct the microfluidic flow channel, a detergent cleaned #1.5 cover glass (Gold Seal, Thermo Scientific, Waltham, MA, USA) was overlaid with a central piece of 40 μm thick, double-sided polyester tape (ARcare 92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 712, Adhesive Research, Glen Rock, PA, USA) with a cut-out pattern shown in Fig. S1† and topped with a 1.1 mm thick glass slide (VWR, USA) with two access holes for each channel. To clean the #1.5 cover glasses, they were immersed in 1% (v/v) Hellmanex III solution (Hellma, Müllheim, Germany), heated to about 80 °C, sonicated for 1 min, and rinsed with Millipore water before being assembled for flow channels. The pattern was cut out from the tape using a die cutter (CE3000, Graphtec America, Irvine, CA, USA) fitted with a 60° angle blade (AGTK-60, Clean Cut Blade, Waterloo, IA, USA), following the sequence shown in Fig. S1.† The pattern can also be cut with an excimer laser, which produces more accurate lines. But the equipment is more expensive and the procedure is time-consuming. The performance of the die cutter is sufficient for this application. After the glass-tape-glass sandwich was assembled, the adhesive channels were filled with optical adhesive (NOA81, Norland Products, Cranbury, NJ, USA) using vacuum suction. The optical adhesive was cured by 365 nm UV illumination. The chip was then baked in a 100 °C oven for 1 hour or autoclaved to strengthen the bonding and smoothen the edges of the channels. A ∼3 mm thick polydimethylsiloxane slab with 0.75 mm diameter holes was aligned with the access holes and clamped onto the glass sandwich. To avoid trapping air bubbles in the PDMS holes, the PDMS surface was made hydrophilic via oxygen plasma activation prior to assembly. The holes on each end of the flow channel were connected through 1/32′′ outer diameter PEEK tubing to buffer or sample. The buffer inlets and the feedback outlet were connected via 0.01′′ and 0.02′′ inner diameter PEEK tubing (1569, IDEX Health & Science, Middleborough, MA, USA) to buffer in 4 ml gas tight vials containing nitrogen gas. The pressures of the nitrogen gas in the two bottles were controlled by a high-precision electronic pressure regulator (DQPV1TFEE010CXL, Proportion-Air, McCordsville, IN, USA) connected to a compressed nitrogen cylinder (>99% pure, Lifegas, Marlborough, MA, USA) to control the flow rate and to provide feedback, respectively. The other outlet was connected to buffer in an open container placed ∼20 cm above the chip to provide a constant pressure. The sample inlets were connected to two 25 μl glass syringes via 0.02′′ inner diameter PEEK tubing.
712, Adhesive Research, Glen Rock, PA, USA) with a cut-out pattern shown in Fig. S1† and topped with a 1.1 mm thick glass slide (VWR, USA) with two access holes for each channel. To clean the #1.5 cover glasses, they were immersed in 1% (v/v) Hellmanex III solution (Hellma, Müllheim, Germany), heated to about 80 °C, sonicated for 1 min, and rinsed with Millipore water before being assembled for flow channels. The pattern was cut out from the tape using a die cutter (CE3000, Graphtec America, Irvine, CA, USA) fitted with a 60° angle blade (AGTK-60, Clean Cut Blade, Waterloo, IA, USA), following the sequence shown in Fig. S1.† The pattern can also be cut with an excimer laser, which produces more accurate lines. But the equipment is more expensive and the procedure is time-consuming. The performance of the die cutter is sufficient for this application. After the glass-tape-glass sandwich was assembled, the adhesive channels were filled with optical adhesive (NOA81, Norland Products, Cranbury, NJ, USA) using vacuum suction. The optical adhesive was cured by 365 nm UV illumination. The chip was then baked in a 100 °C oven for 1 hour or autoclaved to strengthen the bonding and smoothen the edges of the channels. A ∼3 mm thick polydimethylsiloxane slab with 0.75 mm diameter holes was aligned with the access holes and clamped onto the glass sandwich. To avoid trapping air bubbles in the PDMS holes, the PDMS surface was made hydrophilic via oxygen plasma activation prior to assembly. The holes on each end of the flow channel were connected through 1/32′′ outer diameter PEEK tubing to buffer or sample. The buffer inlets and the feedback outlet were connected via 0.01′′ and 0.02′′ inner diameter PEEK tubing (1569, IDEX Health & Science, Middleborough, MA, USA) to buffer in 4 ml gas tight vials containing nitrogen gas. The pressures of the nitrogen gas in the two bottles were controlled by a high-precision electronic pressure regulator (DQPV1TFEE010CXL, Proportion-Air, McCordsville, IN, USA) connected to a compressed nitrogen cylinder (>99% pure, Lifegas, Marlborough, MA, USA) to control the flow rate and to provide feedback, respectively. The other outlet was connected to buffer in an open container placed ∼20 cm above the chip to provide a constant pressure. The sample inlets were connected to two 25 μl glass syringes via 0.02′′ inner diameter PEEK tubing.
Fluorescence imaging and active feedback
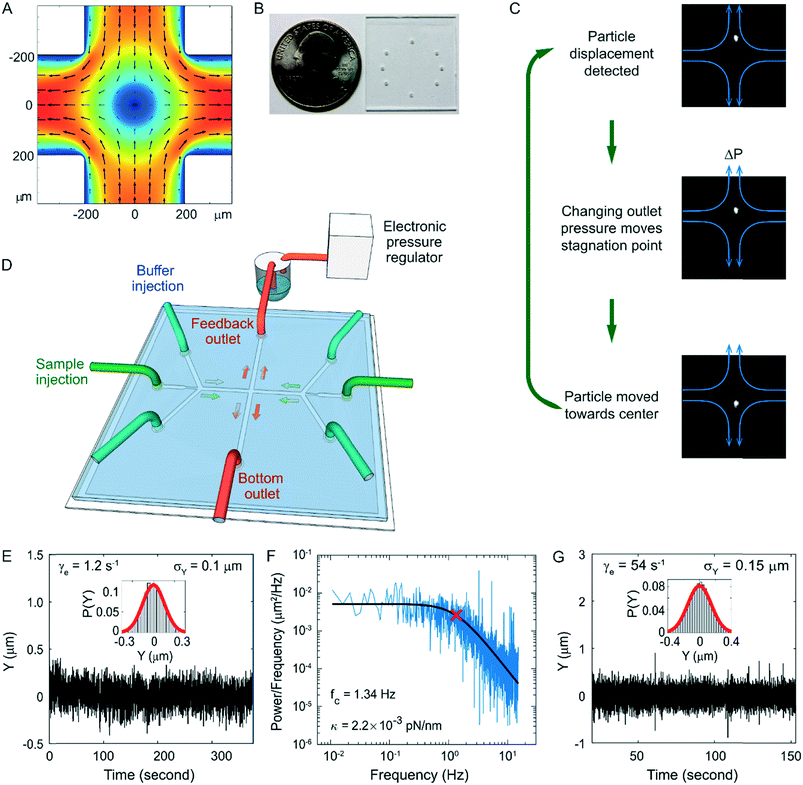
The fluorescence microscopy system was custom built on a vibration damping optical table (Thorlabs) with a 60× oil immersion objective (NA 1.49, CFI Apo TIRF 60× H, Nikon, Japan), 485 nm laser (CUBE 485-30C, Coherent, Santa Clara, CA, USA), with an oscillating diffuser (laser speckle reducer; Optotune, Switzerland), and an EMCCD camera (C9100, Hamamatsu, Japan). Synchronized image recording and flow was controlled with custom software (LabView, National Instruments, Austin, TX, USA).When a fluorescent molecule flowed into the cross slot, each image frame was analysed in real-time by the custom LabView code to determine the centre of the molecule. Briefly, each image was converted to a binary image using a threshold intensity. The binary image was then eroded and dilated to remove noise pixels. The center of mass for the brightest particle found in the binary image was calculated, and was used as the location of the particle. A feedback voltage was calculated based on the vertical position of the molecule using a PID controller with empirically selected parameters to optimize the trapping performance. The feedback voltage was then applied to the electronic pressure regulator. We optimized the PID controller in the pressure regulator for better performance at small step sizes, ∼0.25% of the current value. Occasionally, when larger steps were needed, the custom LabView code broke down the large step into smaller steps to avoid oscillations.
The fluorescent beads used for characterizing trap performance were FluoSpheres microspheres (F8827, ThermoFisher, Waltham, MA, USA). They were trapped in a 12.6 centipoise (cP) pH 7.4 1 × PBS buffer containing 137 mM NaCl, 10 mM Phosphate, 2.7 mM KCl and 48% weight/weight sucrose. When trapping these beads at 208 fps (Fig. 1G), it typically took 0.8–1.1 ms to process the region of interest, ∼100 × 100 pixels, in each image frame to localize the bead. It then took less than 0.3 ms to calculate the feedback voltage using a PID controller, and 0.6–1.1 ms to update the feedback voltage. Finally, it took less than 1 ms for the feedback pressure to reach the new setting, which usually involved a change less than 0.005 psi. The beads were initially trapped at low flow elongation rates ∼1 s−1 and remained trapped as the elongation rate ramped up to 54 s−1 over a 12 second period.
Labelling of DNA
2 μl of 5 ng μl−1 T4 GT7 DNA (318-03971, Nippon Gene, Tokyo, Japan) was slowly added to 298 μl diluted YOYO-1 solution to reach a final concentration of 52 nM DNA base pairs and 26 or 10.4 nM YOYO-1, for a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 5
1 or 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 base pair to dye ratio. Wide bore pipet tips were used to handle T4 DNA to avoid damaging them by shear flow. DNA and dye solution were mixed by slowly stirring with a pipet tip. The 298 μl YOYO-1 solution was prepared by diluting 0.98 or 0.39 μL 1 mM YOYO-1 (Y3601, ThermoFisher, Waltham, MA, USA) into 297.0 or 297.6 μl TE buffer. The intercalation of each YOYO-1 molecule increases the contour length of DNA by 0.34 nm but does not change the persistent length of DNA.71,72 For 2
1 base pair to dye ratio. Wide bore pipet tips were used to handle T4 DNA to avoid damaging them by shear flow. DNA and dye solution were mixed by slowly stirring with a pipet tip. The 298 μl YOYO-1 solution was prepared by diluting 0.98 or 0.39 μL 1 mM YOYO-1 (Y3601, ThermoFisher, Waltham, MA, USA) into 297.0 or 297.6 μl TE buffer. The intercalation of each YOYO-1 molecule increases the contour length of DNA by 0.34 nm but does not change the persistent length of DNA.71,72 For 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stained T4 DNA, the contour length was ∼0.43 nm bp−1 when in the partially intercalated B-DNA form. This means 26% of the spaces between base pairs were intercalated since intercalated base pairs result in a contour length of 0.68 nm bp−1, corresponding to a nucleic acid base pair to dye monomer ratio (N
1 stained T4 DNA, the contour length was ∼0.43 nm bp−1 when in the partially intercalated B-DNA form. This means 26% of the spaces between base pairs were intercalated since intercalated base pairs result in a contour length of 0.68 nm bp−1, corresponding to a nucleic acid base pair to dye monomer ratio (N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D) of about 4
D) of about 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. For 5
1. For 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stained DNA, the contour length was ∼0.38 nm bp−1 when in the partially intercalated B-DNA form. Given that each intercalated monomer increases the contour length by 0.34 nm, ∼12% of the spaces between base pairs were intercalated, corresponding to a nucleic acid base pair to dye monomer ratio (N
1 stained DNA, the contour length was ∼0.38 nm bp−1 when in the partially intercalated B-DNA form. Given that each intercalated monomer increases the contour length by 0.34 nm, ∼12% of the spaces between base pairs were intercalated, corresponding to a nucleic acid base pair to dye monomer ratio (N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D) of about 8
D) of about 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The DNA/dye mixtures were then incubated at 50 °C for 2 hours73 and stored at 4 °C until use.
1. The DNA/dye mixtures were then incubated at 50 °C for 2 hours73 and stored at 4 °C until use.
Trapping and stretching of DNA
The buffer used for the trapping experiments (trapping buffer) contained 60% weight/weight sucrose, 10 mM Tris-HCL pH 7.5, 140 mM 2-mercaptoethanol (BME), 3.5 mM protocatechuic acid (PCA, Santa Cruz Biotechnology, Dallas, Texas, USA), and 20 nM protocatechuate-3,4-dioxygenase (PCD, P87279, Sigma-Aldrich, St. Louis, Missouri, USA). The combination of the gas-impermeable microfluidic chip and the oxygen scavenger system greatly reduced the photobleaching of the dyes and photo-induced damage to DNA. To reduce shear damage to the DNA, the DNA sample was slowly loaded (0.5 μl min−1) into the PEEK tubing connected to the left syringe before the PEEK tubing was connected to the chip. To start the experiments, DNA was injected into the cross-slot from the left sample injection port at 0.5–1 μl h−1 (main text Fig. 1D) and the buffer was injected into the buffer inlets at flow rates that induced 0–5 s−1 elongational flow in the cross-slot. Upon the capture of a DNA molecule, the sample injection was turned off to prevent more molecules from entering the cross-slot. Meanwhile, the buffer injection rate was adjusted to achieve the specified flow elongation rate.To measure the flow elongation rate, we flowed fluorescent beads or DNA molecules into the cross-slot with active feedback turned off. The vertical position (y) trajectory of each particle was fit to the following equation to get the flow elongation rate γe.
| y = b·(exp(γet) − 1) + y0 | (1) |
Drag force on DNA under elongational flow
Assuming that dsDNA is a 2 nm diameter cylinder with length L, the drag force per unit length on a circular cylinder placed in a stream of uniform laminar flow along its long axis is74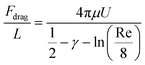 | (2) |
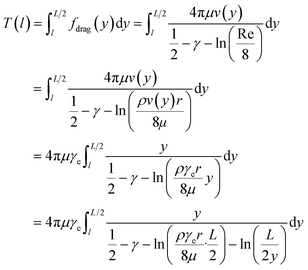 | (3) |
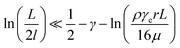 , we can take the following approximation:
, we can take the following approximation: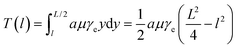 | (4) |
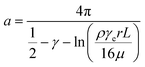 .
.
For the 60% w/w sucrose buffer used in our experiment, ρ = 1.289 g ml−1 and μ = 58 mPa s. For γe > 3 and L ≅ 70 μm , a = 0.6. 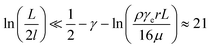 . This means that the above approximation holds valid for the majority of the range of l. For the lowest values of l, the fluid velocity is so low that the drag force on this segment can be neglected relative to the drag force on the rest of the filament. Therefore, eqn (4) is a good approximation for any l.
. This means that the above approximation holds valid for the majority of the range of l. For the lowest values of l, the fluid velocity is so low that the drag force on this segment can be neglected relative to the drag force on the rest of the filament. Therefore, eqn (4) is a good approximation for any l.
We note that when dsDNA stretches, the effective diameter of the filament may change—however eqn (4) suggests that this will have a negligible effect on the resulting tension. For example, let us assume that the volume of the cylinder is conserved as it is stretched. Then, the radius r of the cylinder would decrease by a factor of 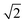 if the length were to double. According to the above calculation, such a change in r would have a negligible impact on the value of a, changing it by less than 2% for the range of parameters used in our experiments. Therefore, we can reasonably neglect the change in r when calculating the tension in DNA during structural transitions. This calculation also implies that small errors in our initial estimate of r will have very little quantitative effect on the calculated tension.
if the length were to double. According to the above calculation, such a change in r would have a negligible impact on the value of a, changing it by less than 2% for the range of parameters used in our experiments. Therefore, we can reasonably neglect the change in r when calculating the tension in DNA during structural transitions. This calculation also implies that small errors in our initial estimate of r will have very little quantitative effect on the calculated tension.
Image analysis
An intensity threshold was manually selected during experiments. The threshold was selected as low as possible while ensuring no fluorescent particle would be identified when sample injection was off. When fluorescent molecules flowed into the field of view, thresholding and particle analysis were used to determine the contours of individual molecules. In order to follow the same molecule, the code looked for a molecule that was similar in position, size and brightness to the molecule identified in the previous frame.Code availability
Custom-written Matlab scripts for data analysis are available from the corresponding author upon request, for non-profit research uses.Results and discussion
High-speed active-feedback hydrodynamic trap
To apply high forces to single DNA molecules, we have developed a rigid and gas-impermeable cross-slot microfluidic chip for fluorescence-based high-speed hydrodynamic trapping. The device can trap particles under elongational flow using active feedback with direct pressure control.44 In a cross-slot, the fluid flows in from the two inlets (the horizontal channels in Fig. 1a) and exits via the two outlets orthogonal to the inlets. This creates a pure elongational field in the cross region. For a filamentous object centred in an elongational flow field, the fluid exerts drag forces against the two halves of the filament in opposite directions, inducing tension in the filament. The centre of the cross slot has zero flow velocity and is called a stagnation point. The flow elongation rate is defined as the gradient of flow velocity along the direction of flow, which in this case is the rate of velocity increase as the fluid moves away from the stagnation point. Along the inlet axis, particles are always trapped in the centre by the converging flow fields in a stable manner, but in the perpendicular outlet direction, small positional deviations from the stagnation point cause the particles to flow away with increasing velocity. Thus, the stagnation point is an unstable saddle point. However, with the addition of active-feedback, particles can be stably trapped at the stagnation point in both dimensions. As illustrated in Fig. 1C, first, the position of the particle is detected by a video camera. Next, depending on the current position of the particle, the stagnation point of the flow field is moved by changing the back pressure in one of the outlets, in order to move the particle in the desired direction. The back pressure can be changed through a PDMS membrane valve in a dual-layer device,29 or direct pressure control in a single-layer device.41 Finally, the particle flows towards the desired trapping position (e.g. centre of the field of view) as a result of the shifted flow field. This cycle is rapidly repeated to keep the particle trapped.To date, hydrodynamic traps have been demonstrated to trap and stretch single polymers at flow elongation rates up to 1.5 s−1.43–46 In order to trap and fluorescently image single molecules under high elongational flow rates, we improved feedback performance by using a rigid single-layer glass microfluidic chip (Fig. 1B and D). One of the outlets is connected to a buffer reservoir filled with pressurized gas, which is controlled by an electronic pressure regulator. The other outlet is connected to a constant pressure source. Buffer injection was also driven by electronically regulated pressurized gas. This allows fast and linear control of the stagnation point position. The microfluidic chip consists of 40 μm thick double-sided tape with channels cut-out sandwiched between a glass cover glass and a glass slide.75,76 The tape was patterned using a die cutter.77 Because the adhesive on the tape is deformable and the bonding between the tape and glass weakens upon exposure to aqueous solution, the glass-tape-glass sandwich chip is not rigid enough for high-pressure applications. To improve the rigidity, we reinforced the chip using UV-cured optical adhesive near the channel region. We then heated up the chip to ∼100 °C, which not only further improved the strength of the bonding but also smoothened the edge of the channel. This rigid chip design ensures fast and stable response of the flow to pressure changes. In addition, this chip is impermeable to gas, reducing the oxygen related photobleaching and photodamage, and very durable, with no degradation in performance over a period of at least a month. These properties are desirable for not only the hydrodynamic trap but also other high-pressure and fluorescence imaging applications. Moreover, the fabrication is fast and inexpensive, requires no cleanroom equipment or special training, and therefore is accessible to almost any laboratory. Our high-speed trap allows us to trap 2 μm diameter fluorescent particles with about twice the trapping stiffness of the-state-of-art under similar conditions41 (Fig. 1E and F). We have also demonstrated stable trapping of the 2 μm fluorescent beads at flow elongation rates up to 54 s−1 with a moderate decrease in positional confinement (Fig. 1G).
Trapping and stretching DNA at high flow elongation rates
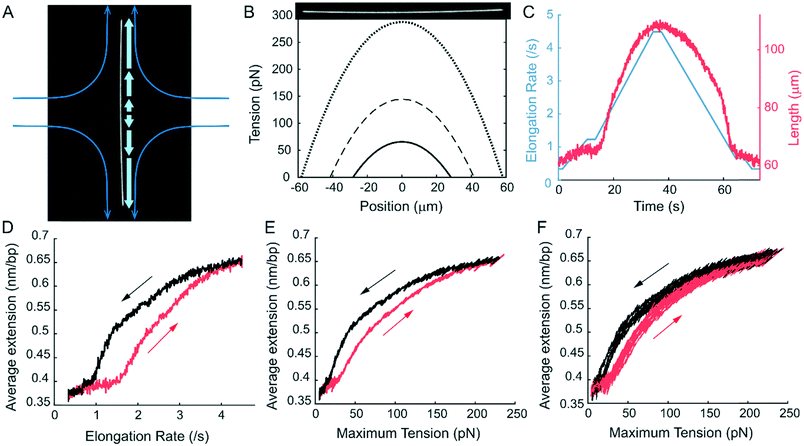
Using the hydrodynamic trap, we trapped and stretched YOYO-1 labelled T4 DNA to over 190% of its normal contour length in a high viscosity buffer. While DNA can be trapped and stretched in 1 cP buffer (Fig. S3†), we used a high viscosity buffer, ∼52 cP, to maximize the drag force on the DNA. As shown in Methods, for long filaments, the drag force on each segment is proportional to the flow velocity and therefore the distance from the stagnation point (Fig. 2A). As a result, the tension profile along the length of the filament is parabolic. Eqn (5) shows the tension in a filament with length L, at a point l distance from the centre.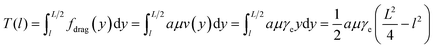 | (5) |
The maximum tension is at the centre of the filament and proportional to the square of the filament length (Fig. 2B). The tension is also proportional to the flow elongation rate and the viscosity. With a combination of a high flow elongation rate, a high viscosity buffer and long DNA, we were able to induce a maximum of 250 pN tension in DNA. We used bacteriophage T4 GT7 genome DNA with a length of 166 kbps and a contour length of 56.4 μm. We prepared DNA with two different labelling ratios, with nucleic acid base pair to dye monomer ratios (N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D) of 4
D) of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 8
1 and 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Methods). The DNA was stained and trapped in buffer with no salt to prevent the YOYO-1 dye from dissociating. Similar results were observed in buffers with up to 20 mM NaCl. With even higher salt concentrations, the dyes dissociate too fast to allow high-speed trapping. Even though low salt conditions usually shift the equilibrium of stretched dsDNA towards melting,78 the intercalated dyes likely protected the dsDNA from melting.15,72 We ramped tension in the trapped DNA up and down by ramping the flow elongation rate up and down (Fig. 2C, Movie S1†). The maximum tension in the DNA at each time point was calculated using the flow elongation rate and the measured length of the DNA filament (Fig. 2D), and the length of DNA was plotted as a function of the maximum tension (Fig. 2E). Because each intercalated dye monomer increases the contour length of dsDNA by 0.34 nm, the average extension of the intercalated B-form T4 DNA in our experiment was 0.37 nm bp−1, when the maximum tension was held at ∼10pN. The end-to-end distance of T4 DNA increased rapidly when the maximum tension exceeded 25 pN. The slope decreased for tensions above 100 pN. At the maximum flow elongation rate we applied, the total length of the 4
1 (Methods). The DNA was stained and trapped in buffer with no salt to prevent the YOYO-1 dye from dissociating. Similar results were observed in buffers with up to 20 mM NaCl. With even higher salt concentrations, the dyes dissociate too fast to allow high-speed trapping. Even though low salt conditions usually shift the equilibrium of stretched dsDNA towards melting,78 the intercalated dyes likely protected the dsDNA from melting.15,72 We ramped tension in the trapped DNA up and down by ramping the flow elongation rate up and down (Fig. 2C, Movie S1†). The maximum tension in the DNA at each time point was calculated using the flow elongation rate and the measured length of the DNA filament (Fig. 2D), and the length of DNA was plotted as a function of the maximum tension (Fig. 2E). Because each intercalated dye monomer increases the contour length of dsDNA by 0.34 nm, the average extension of the intercalated B-form T4 DNA in our experiment was 0.37 nm bp−1, when the maximum tension was held at ∼10pN. The end-to-end distance of T4 DNA increased rapidly when the maximum tension exceeded 25 pN. The slope decreased for tensions above 100 pN. At the maximum flow elongation rate we applied, the total length of the 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 labelled DNA was 0.65 nm bp−1, over 90% longer than regular B-DNA. The extreme length indicated a DNA structure more extended than overstretched DNA and resembling the newly discovered hyperstretched DNA. Because the total end-to-end distance is the sum of many segments, each under different force, the central region of the DNA will be extended longer than the average. From the large average extension, the maximum extension in the central region likely approached the length of the sugar-phosphate backbone, which is twice the contour length of B-DNA. As described in the next section, we confirmed this by analysing the fluorescence intensity profile. During elongation–relaxation cycles, we observed a significant hysteresis that could be reduced by lowering the flow ramping rates. But the hysteresis existed even at the slowest flow ramping rates we could achieve without incurring photodamage during the experiment (Fig. 2E and F). Based on the current experiment, we could not distinguish whether this hysteresis was dynamic, meaning that the structural transition was slow, or static, meaning that the B and the putative hyperstretched states were bistable under our experimental conditions. A similar hysteresis was previously reported for dsDNA stretching and relaxation in the presence of intercalating molecules.79–81 The hysteresis in those cases was attributed to the slow binding/dissociation of the intercalators. However, this cannot explain our observation because there was no free YOYO-1 dye in our experiment.
1 labelled DNA was 0.65 nm bp−1, over 90% longer than regular B-DNA. The extreme length indicated a DNA structure more extended than overstretched DNA and resembling the newly discovered hyperstretched DNA. Because the total end-to-end distance is the sum of many segments, each under different force, the central region of the DNA will be extended longer than the average. From the large average extension, the maximum extension in the central region likely approached the length of the sugar-phosphate backbone, which is twice the contour length of B-DNA. As described in the next section, we confirmed this by analysing the fluorescence intensity profile. During elongation–relaxation cycles, we observed a significant hysteresis that could be reduced by lowering the flow ramping rates. But the hysteresis existed even at the slowest flow ramping rates we could achieve without incurring photodamage during the experiment (Fig. 2E and F). Based on the current experiment, we could not distinguish whether this hysteresis was dynamic, meaning that the structural transition was slow, or static, meaning that the B and the putative hyperstretched states were bistable under our experimental conditions. A similar hysteresis was previously reported for dsDNA stretching and relaxation in the presence of intercalating molecules.79–81 The hysteresis in those cases was attributed to the slow binding/dissociation of the intercalators. However, this cannot explain our observation because there was no free YOYO-1 dye in our experiment.
We also note that it is important to distinguish the putative hyperstretched state from DNA peeling or bubble formation, which can also dramatically increase the length of DNA by converting regions of dsDNA to single-stranded DNA (ssDNA). As discussed by Schakenraad et al.,14 combining force application with single-molecule fluorescence is key, as DNA peeling can be observed by a sudden reduction in fluorescence intensity in regions of emergent ssDNA. These were not observed under our experimental conditions, as further discussed in the next section. Additionally, within DNA force-extension curves, melting transitions and peeling transitions are typically marked by sharp increases in length during stretching and more significant hysteresis during relaxation—features that were not observed during our experiments.68,69 It is possible that small bubbles of melted DNA occurred in the short DNA segments (about 5–14 base pairs depending on the labelling ratio) between intercalated dyes. However, as detailed in the next section, two melted ssDNA strands loaded in parallel typically require much more force than what we applied to the DNA filament to be extended to the same maximum extension. Therefore, the highly extended state we observed most closely resembles the hyperstretched DNA from ref. 14. We will refer to this putative hyperstretched state as HS† DNA from now on for brevity.
Fluorescence intensity profile indicates the force-dependent extension of DNA
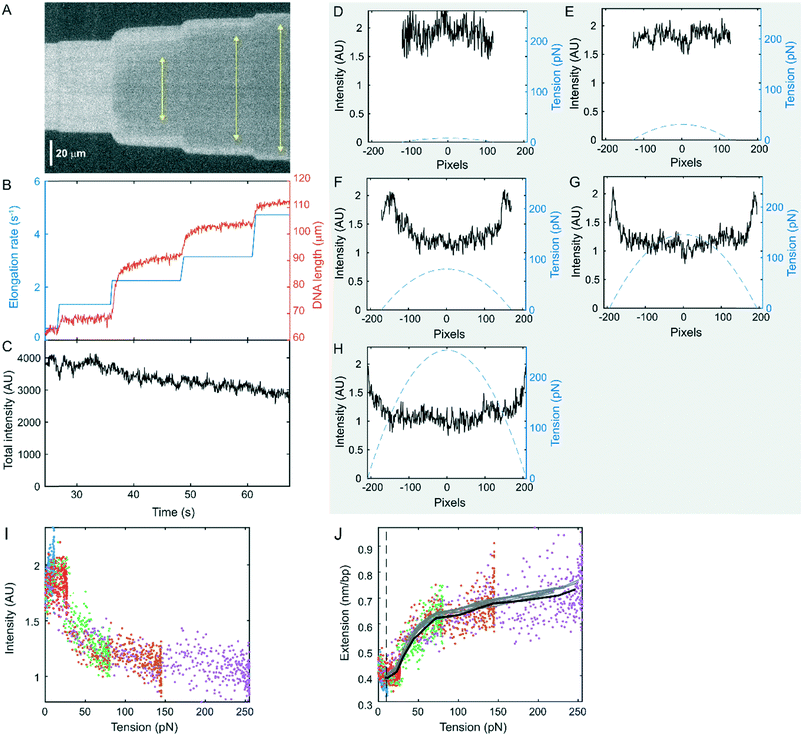
In addition to measuring the length of the DNA filament as a function of the flow-rate, we can also study the force-dependent properties of DNA by analysing the single-molecule fluorescence intensity profile. Because of the unique parabolic tension profile that we impose along each DNA molecule, we can sample a wide range of forces on a single DNA molecule under a single flow elongation rate. For example, the kymograph in Fig. 3A shows the evolution of the intensity profile of a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 labelled DNA molecule at 5 different flow elongation rates (Fig. 3B, Movie S2†). At low flow elongation rates, the fluorescence intensity profile is uniform, independent of the tension (Fig. 3A and D). At high flow elongation rates, the intensity remains the same in the lowest tension regions and decreases in the high-tension region (Fig. 3E–H). The intensity as a function of tension is consistent across different flow elongation rates (Fig. 3I). The intensity approaches a minimum for forces above 100 pN. Over the course of the experiment, the total intensity of the entire DNA molecule showed slow dissociation of the YOYO-1 dye but no clear changes correlated with changes in the length of the DNA (Fig. 3C, Fig. S4†). This suggests that the YOYO-1 dye did not dissociate, the intensity of each YOYO-1 did not change, and the dsDNA did not peel during the experiment, consistent with a direct transition into the hyperstretched state.14,15 Therefore, the change in intensity profile is mostly due to the change in dye distribution that results from local stretching of the molecule. At low flow elongation rates, the average extension was 0.42 nm bp−1 (Fig. 3B). As the tension increased, the length of DNA increased and so did the space between bound YOYO-1 molecules. Assuming the extension is proportional to the reciprocal of the intensity, we plotted the DNA extension as a function of the tension (Fig. 3J). The results from all 5 flow elongation rates are plotted together to show the overlap between them. The black curve is the average of all the data. At low forces, around 10 pN or lower, the DNA could diffuse in and out of the focal plane, making the measured intensity lower than the actual value. Therefore, this region, to the left of the dashed line in Fig. 3I, is not analysed. The extension first slightly increased from 10 to ∼25 pN, consistent with the high force region of a worm-like-chain force-extension curve.82 This suggests that the non-intercalated segments of DNA remained in the B-form in this regime. The local extension started to increase above 25 pN, consistent with the end-to-end distance measurements (Fig. 2F). This increase in length indicated a gradual transition from B-DNA into HS† DNA. The local extension of DNA rapidly increased to ∼0.65 nm bp−1 until ∼100 pN, and then the increase slowed down for even higher force, suggesting that most of the non-intercalated base pairs of DNA had transitioned to the HS† state above 100 pN. As the maximum tension increased, the region containing HS†-DNA expanded (Fig. 3A, yellow arrows). Above 200 pN, the local extension of DNA reached ∼0.7 nm bp−1, close to the contour length of the sugar-phosphate backbone. In comparison, two melted ssDNA strands loaded in parallel would require ∼500 pN in total to be extended to the same length under similar no salt conditions,83 which does not match our observation. On the other hand, our curve (Fig. 3J) matches well with the DNA hyperstretching curve measured by optical tweezer experiments in the presence of the fast equilibrating dye YO-PRO-1 (Fig. S1 in ref. 15). Both curves feature a slow increase in extension in the low-force regime, a rapid increase until ∼100 pN, and a slow increase above 100pN. The lower force regimes of both curves deviate from the usual dsDNA force-extension curves that can be described by the WLC model due to dye intercalation and hyperstretching. This suggests that our estimation of drag force on DNA is reasonably accurate. In their experiment, the gradual transition of DNA from the B form to the hyperstretched form was achieved through the combination of stretching and the intercalation of more dye molecules. In our experiment, as there was no free dye in solution during the stretching experiment, the non-intercalated DNA segments were transitioned to the HS† form just by force.
1 labelled DNA molecule at 5 different flow elongation rates (Fig. 3B, Movie S2†). At low flow elongation rates, the fluorescence intensity profile is uniform, independent of the tension (Fig. 3A and D). At high flow elongation rates, the intensity remains the same in the lowest tension regions and decreases in the high-tension region (Fig. 3E–H). The intensity as a function of tension is consistent across different flow elongation rates (Fig. 3I). The intensity approaches a minimum for forces above 100 pN. Over the course of the experiment, the total intensity of the entire DNA molecule showed slow dissociation of the YOYO-1 dye but no clear changes correlated with changes in the length of the DNA (Fig. 3C, Fig. S4†). This suggests that the YOYO-1 dye did not dissociate, the intensity of each YOYO-1 did not change, and the dsDNA did not peel during the experiment, consistent with a direct transition into the hyperstretched state.14,15 Therefore, the change in intensity profile is mostly due to the change in dye distribution that results from local stretching of the molecule. At low flow elongation rates, the average extension was 0.42 nm bp−1 (Fig. 3B). As the tension increased, the length of DNA increased and so did the space between bound YOYO-1 molecules. Assuming the extension is proportional to the reciprocal of the intensity, we plotted the DNA extension as a function of the tension (Fig. 3J). The results from all 5 flow elongation rates are plotted together to show the overlap between them. The black curve is the average of all the data. At low forces, around 10 pN or lower, the DNA could diffuse in and out of the focal plane, making the measured intensity lower than the actual value. Therefore, this region, to the left of the dashed line in Fig. 3I, is not analysed. The extension first slightly increased from 10 to ∼25 pN, consistent with the high force region of a worm-like-chain force-extension curve.82 This suggests that the non-intercalated segments of DNA remained in the B-form in this regime. The local extension started to increase above 25 pN, consistent with the end-to-end distance measurements (Fig. 2F). This increase in length indicated a gradual transition from B-DNA into HS† DNA. The local extension of DNA rapidly increased to ∼0.65 nm bp−1 until ∼100 pN, and then the increase slowed down for even higher force, suggesting that most of the non-intercalated base pairs of DNA had transitioned to the HS† state above 100 pN. As the maximum tension increased, the region containing HS†-DNA expanded (Fig. 3A, yellow arrows). Above 200 pN, the local extension of DNA reached ∼0.7 nm bp−1, close to the contour length of the sugar-phosphate backbone. In comparison, two melted ssDNA strands loaded in parallel would require ∼500 pN in total to be extended to the same length under similar no salt conditions,83 which does not match our observation. On the other hand, our curve (Fig. 3J) matches well with the DNA hyperstretching curve measured by optical tweezer experiments in the presence of the fast equilibrating dye YO-PRO-1 (Fig. S1 in ref. 15). Both curves feature a slow increase in extension in the low-force regime, a rapid increase until ∼100 pN, and a slow increase above 100pN. The lower force regimes of both curves deviate from the usual dsDNA force-extension curves that can be described by the WLC model due to dye intercalation and hyperstretching. This suggests that our estimation of drag force on DNA is reasonably accurate. In their experiment, the gradual transition of DNA from the B form to the hyperstretched form was achieved through the combination of stretching and the intercalation of more dye molecules. In our experiment, as there was no free dye in solution during the stretching experiment, the non-intercalated DNA segments were transitioned to the HS† form just by force.
Force-induced transitions to HS† DNA also occur in more sparsely-labelled DNA
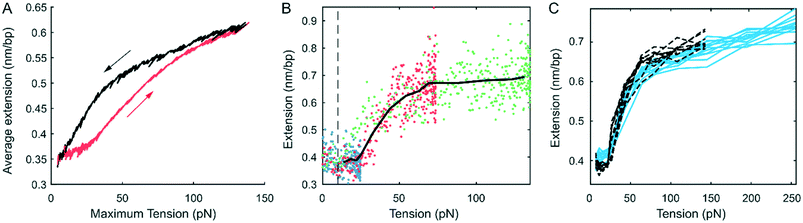
The transition to a state with a 0.7 nm bp−1 contour length was also observed in DNA with a lower staining ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Fig. 4), where non-intercalated regions were longer. At this staining ratio, only approximately 12% of the DNA was intercalated. Because YOYO-1 is a dimer that intercalates into the spaces between four consecutive base pairs,84 this corresponded to an average of 14 non-intercalated DNA base pairs between neighbouring pairs of intercalating dimers. Therefore, the majority of the DNA was not intercalated. With this lower staining ratio, the fluorescence signal was weaker, limiting the trapping to lower flow elongation rates. As a result, the maximum tension we could apply to these DNA molecules in this case was limited to approximately ∼150 pN. Nevertheless, the entire DNA filament could be stretched to an average distance per base pair ∼0.62 nm bp−1, longer than the contour length of S-DNA. The force-dependent intensity profile of the 8
1 (Fig. 4), where non-intercalated regions were longer. At this staining ratio, only approximately 12% of the DNA was intercalated. Because YOYO-1 is a dimer that intercalates into the spaces between four consecutive base pairs,84 this corresponded to an average of 14 non-intercalated DNA base pairs between neighbouring pairs of intercalating dimers. Therefore, the majority of the DNA was not intercalated. With this lower staining ratio, the fluorescence signal was weaker, limiting the trapping to lower flow elongation rates. As a result, the maximum tension we could apply to these DNA molecules in this case was limited to approximately ∼150 pN. Nevertheless, the entire DNA filament could be stretched to an average distance per base pair ∼0.62 nm bp−1, longer than the contour length of S-DNA. The force-dependent intensity profile of the 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 labelled DNA showed a similar behaviour to the 4
1 labelled DNA showed a similar behaviour to the 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 labelled DNA (Fig. 3). The calculated extension as a function of tension from the 8
1 labelled DNA (Fig. 3). The calculated extension as a function of tension from the 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 labelled DNA is shown in Fig. 4B, demonstrating high similarity to the results for the 4
1 labelled DNA is shown in Fig. 4B, demonstrating high similarity to the results for the 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 labelled DNA. A direct comparison between these two conditions is presented in Fig. 4C, showing an overlay of the results from the two staining ratios, with 10 replicas each. The results are very similar, though we note that the 8
1 labelled DNA. A direct comparison between these two conditions is presented in Fig. 4C, showing an overlay of the results from the two staining ratios, with 10 replicas each. The results are very similar, though we note that the 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 labelled DNA molecules have a shorter extension at low force because of their shorter contour length in the partially intercalated B-DNA form.71
1 labelled DNA molecules have a shorter extension at low force because of their shorter contour length in the partially intercalated B-DNA form.71
In the previous report of hyperstretched DNA, more and more dyes intercalated in the dsDNA as the force increased. According to the model, this helped stabilizing the hyperstretched conformation through the negative binding free energy. Our observation of dsDNA reaching an extension of ∼0.7 nm bp−1 under tension with significantly fewer intercalated dyes supports the hypothesis that force alone is capable of converting dsDNA from the B-form to the hyperstretched form in regions up to ∼14 base pair long. We cannot completely rule out the possibility that the intercalated dyes at the ends of these segments aided the structural transition, perhaps by disfavouring melting and overstretching transitions in the DNA segments between them.15,72 However, it was observed that dye intercalation does not change the persistent length of B-DNA or the orientation of the neighbouring base pairs,15,71,72,85 which suggests that intercalated dyes do not have a long range impact on the DNA structure.
The application of these extremely high forces to a single DNA molecule is enabled by our newly developed high-speed hydrodynamic trap with a gas-impermeable microfluidic chip. The maximum tension we induced in DNA was ∼250 pN, perhaps the highest constant stretching force applied to dsDNA in the literature. In principle, high forces can also be induced under lower flow elongation rates using even longer DNAs, which are not commonly commercially available. However, the ability to trap single polymers at higher flow elongation rates than before allows a wider range of DNA to be studied in a wider range of forces using hydrodynamic traps. For example, as shown in Fig. S3,† the end-to-end distance of λ DNA can be measured under ramping flow elongation rates in a buffer with no added viscosity.
Our surface-free approach allows simultaneous fluorescence detection and force spectroscopy, especially in force regimes that are traditionally difficult to study. In addition, the system can be less expensive and easier to set up than many commonly used force probes, particularly for users who already have microscopes capable of fluorescence imaging. Additionally, because no bead or surface attachments are needed for this method, sample preparation can also be simplified. While traditional force spectroscopy methods, such as AFM, optical tweezers and magnetic tweezers, have advantages that include improved spatial precision and the independence of force from the polymer length and buffer viscosity, the unique benefits of the hydrodynamic trapping method make it a good and complementary alternative to existing methods for certain applications.
Conclusions
We have demonstrated force-induced stretching of dsDNA to the length of the sugar-phosphate backbone, a state that matches the newly discovered hyperstretched DNA, with a high-speed hydrodynamic trap. This experiment not only has implications for understanding the mechanics and structure of DNA under stress, but also demonstrates the potential of the hydrodynamic trap as a powerful yet accessible force spectroscopy method, able to probe molecular mechanics in previously difficult to access regimes. Not only does it enable the application of extreme forces, but it also allows biomaterials, such as cytoskeletal filaments and chromatin, to be stretched without the distortions that can be induced by surface interactions, or the need to optimize surface attachment chemistries. Furthermore, the rapid and inexpensive fabrication techniques that we have developed to produce rigid and gas impermeable microfluidic devices will be useful for a wide range of applications, especially those that require high pressure or fluorescence imaging, and will be accessible to laboratories not specialized in microfabrication.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge help from the microfluidic prototyping facilities in Wyss Institute for Biologically Inspired Engineering on fabricating the microfluidic chip. We are also grateful to James Pelletier, the MIT Media Lab, and the Microfluidics Core Facility at Harvard Medical for their help in fabricating early versions of the microfluidic chip. This work was supported by the National Science Foundation Graduate Research Fellowship DGE-1144152 (D. Y.), NIH NIGMS R35 GM119537 (W. P. W.), and internal support from the Wyss Institute at Harvard.References
- K. C. Neuman and A. Nagy, Nat. Methods, 2008, 5, 491–505 CrossRef CAS PubMed.
- S. Smith, L. Finzi and C. Bustamante, Science, 1992, 258, 1122–1126 CrossRef CAS PubMed.
- B. Ladoux and P. S. Doyle, Europhys. Lett., 2000, 52, 511–517 CrossRef CAS.
- A. Kishino and T. Yanagida, Nature, 1988, 334, 74–76 CrossRef CAS PubMed.
- P. Cluzel, A. Lebrun, C. Heller, R. Lavery, J. L. Viovy, D. Chatenay and F. Caron, Science, 1996, 271, 792–794 CrossRef CAS PubMed.
- A. Ashkin, J. M. Dziedzic, J. E. Bjorkholm and S. Chu, Opt. Lett., 1986, 11, 288 CrossRef CAS PubMed.
- T. R. Strick, J. F. Allemand, D. Bensimon, A. Bensimon and V. Croquette, Science, 1996, 271, 1835–1837 CrossRef CAS PubMed.
- J. H. Hoh, J. P. Cleveland, C. B. Prater, J. P. Revel and P. K. Hansma, J. Am. Chem. Soc., 1992, 114, 4917–4918 CrossRef CAS.
- R. Merkel, P. Nassoy, A. Leung, K. Ritchie and E. Evans, Nature, 1999, 397, 50–53 CrossRef CAS PubMed.
- G. Neuert, C. Albrecht, E. Pamir and H. E. Gaub, FEBS Lett., 2006, 580, 505–509 CrossRef CAS PubMed.
- J. Lipfert, J. W. J. Kerssemakers, T. Jager and N. H. Dekker, Nat. Methods, 2010, 7, 977–980 CrossRef CAS PubMed.
- R. W. Friddle, A. Noy and J. J. De Yoreo, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 13573–13578 CrossRef CAS PubMed.
- R. Janissen, B. A. Berghuis, D. Dulin, M. Wink, T. van Laar and N. H. Dekker, Nucleic Acids Res., 2014, 42, e137 CrossRef PubMed.
- K. Schakenraad, A. S. Biebricher, M. Sebregts, B. ten Bensel, E. J. G. Peterman, G. J. L. Wuite, I. Heller, C. Storm and P. van der Schoot, Nat. Commun., 2017, 8, 2197 CrossRef PubMed.
- A. S. Backer, A. S. Biebricher, G. A. King, G. J. L. Wuite, I. Heller and E. J. G. Peterman, Sci. Adv., 2019, 5, eaav1083 CrossRef CAS PubMed.
- M. Rief, M. Gautel, F. Oesterhelt, J. M. Fernandez and H. E. Gaub, Science, 1997, 276, 1109–1112 CrossRef CAS PubMed.
- I. Popa, R. Berkovich, J. Alegre-Cebollada, C. L. Badilla, J. A. Rivas-Pardo, Y. Taniguchi, M. Kawakami and J. M. Fernandez, J. Am. Chem. Soc., 2013, 135, 12762–12771 CrossRef CAS PubMed.
- S. K. Kufer, H. Dietz, C. Albrecht, K. Blank, A. Kardinal, M. Rief and H. E. Gaub, Eur. Biophys. J., 2005, 35, 72–78 CrossRef CAS PubMed.
- B. Zakeri, J. O. Fierer, E. Celik, E. C. Chittock, U. Schwarz-Linek, V. T. Moy and M. Howarth, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, E690–E697 CrossRef CAS PubMed.
- D. A. Pippig, F. Baumann, M. Strackharn, D. Aschenbrenner and H. E. Gaub, ACS Nano, 2014, 8, 6551–6555 CrossRef CAS PubMed.
- J. L. Zimmermann, T. Nicolaus, G. Neuert and K. Blank, Nat. Protoc., 2010, 5, 975–985 CrossRef CAS PubMed.
- M. A. Koussa, M. Sotomayor and W. P. Wong, Methods, 2014, 67, 134–141 CrossRef CAS PubMed.
- K. N. Lovendahl, A. N. Hayward and W. R. Gordon, J. Am. Chem. Soc., 2017, 139, 7030–7035 CrossRef CAS PubMed.
- M. Tanase, N. Biais and M. Sheetz, Methods Cell Biol., 2007, 83, 473–493 CAS.
- K. C. Neuman and S. M. Block, Rev. Sci. Instrum., 2004, 75, 2787–2809 CrossRef CAS PubMed.
- L. Goldstein, Methods Enzymol., 1976, 44, 397–443 CAS.
- M. Friedel, A. Baumketner and J.-E. Shea, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 8396–8401 CrossRef CAS PubMed.
- Y. Shin, J. H. Davis, R. R. Brau, A. Martin, J. A. Kenniston, T. A. Baker, R. T. Sauer and M. J. Lang, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 19340–19345 CrossRef CAS PubMed.
- M. Tanyeri, E. M. Johnson-chavarria and C. M. Schroeder, Appl. Phys. Lett., 2010, 96, 224101 CrossRef PubMed.
- C. M. Schroeder, A. Eric, S. G. Shaqfeh and S. Chu, Macromolecules, 2004, 37, 9242–9256 CrossRef CAS.
- C. M. Schroeder, H. P. Babcock, E. S. G. Shaqfeh and S. Chu, Science, 2003, 301, 1515–1519 CrossRef CAS PubMed.
- T. T. Perkins, D. E. Smith and S. Chu, Science, 1997, 276, 2016–2021 CrossRef CAS PubMed.
- P. G. De Gennes, J. Chem. Phys., 1974, 60, 5030–5042 CrossRef CAS.
- D. E. Smith, H. P. Babcock and S. Chu, Science, 1999, 283, 1724–1727 CrossRef CAS PubMed.
- A. R. Klotz, B. W. Soh and P. S. Doyle, Phys. Rev. Lett., 2018, 120, 188003 CrossRef CAS PubMed.
- W. Xu and S. J. Muller, Lab Chip, 2012, 12, 647–651 RSC.
- M. Tanyeri and C. Schroeder, Nano Lett., 2013, 13, 2357–2364 CrossRef CAS PubMed.
- M. Tanyeri, M. Ranka, N. Sittipolkul and C. M. Schroeder, Lab Chip, 2011, 11, 1786–1794 RSC.
- Y. Zhou and C. M. Schroeder, Phys. Rev. Lett., 2018, 120, 267801 CrossRef CAS PubMed.
- Y. Zhou, K.-W. Hsiao, K. E. Regan, D. Kong, G. B. McKenna, R. M. Robertson-Anderson and C. M. Schroeder, Nat. Commun., 2019, 10, 1753 CrossRef PubMed.
- A. Shenoy, C. V. Rao and C. M. Schroeder, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 3976–3981 CrossRef CAS PubMed.
- A. Shenoy, D. Kumar, S. Hilgenfeldt and C. M. Schroeder, Phys. Rev. Appl., 2019, 12, 054010 CrossRef CAS.
- C. M. Schroeder, J. Rheol., 2018, 62, 371–403 CrossRef CAS.
- Y. Zhou and C. M. Schroeder, Macromolecules, 2016, 49, 8018–8030 CrossRef CAS.
- Y. Zhou and C. M. Schroeder, Phys. Rev. Fluids, 2016, 1, 053301 CrossRef.
- D. J. Mai, A. Saadat, B. Khomami and C. M. Schroeder, Macromolecules, 2018, 51, 1507–1517 CrossRef CAS.
- K.-W. Hsiao, J. Dinic, Y. Ren, V. Sharma and C. M. Schroeder, Phys. Fluids, 2017, 29, 121603 CrossRef.
- C. Bustamante, Z. Bryant and S. B. Smith, Nature, 2003, 421, 423–427 CrossRef PubMed.
- E. A. Abbondanzieri, W. J. Greenleaf, J. W. Shaevitz, R. Landick and S. M. Block, Nature, 2005, 438, 460–465 CrossRef CAS PubMed.
- M. D. Wang, M. J. Schnitzer, H. Yin, R. Landick, J. Gelles and S. M. Block, Science, 1998, 282, 902–907 CrossRef CAS PubMed.
- D. E. Smith, S. J. Tans, S. B. Smith, S. Grimes, D. L. Anderson and C. Bustamante, Nature, 2001, 413, 748–752 CrossRef CAS PubMed.
- R. T. Dame, M. C. Noom and G. J. L. Wuite, Nature, 2006, 444, 387–390 CrossRef CAS PubMed.
- S. Dumont, W. Cheng, V. Serebrov, R. K. Beran, I. Tinoco, A. M. Pyle and C. Bustamante, Nature, 2006, 439, 105–108 CrossRef CAS PubMed.
- T. R. Strick, V. Croquette and D. Bensimon, Nature, 2000, 404, 901–904 CrossRef CAS PubMed.
- D. A. Koster, V. Croquette, C. Dekker, S. Shuman and N. H. Dekker, Nature, 2005, 434, 671–674 CrossRef CAS PubMed.
- J. F. Leger, J. Robert, L. Bourdieu, D. Chatenay and J. F. Marko, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 12295–12299 CrossRef CAS PubMed.
- A. L. Forget and S. C. Kowalczykowski, Nature, 2012, 482, 423–427 CrossRef CAS PubMed.
- X. H. Zhang, K. Halvorsen, C.-Z. Z. Zhang, W. P. Wong and T. A. Springer, Science, 2009, 324, 1330–1334 CrossRef CAS PubMed.
- K. Halvorsen, D. Schaak and W. P. Wong, Nanotechnology, 2011, 22, 494005 CrossRef PubMed.
- J. Liphardt, B. Onoa, S. B. Smith, I. Tinoco and C. Bustamante, Science, 2001, 292, 733–737 CrossRef CAS PubMed.
- J. Kim, C.-Z. Zhang, X. Zhang and T. A. Springer, Nature, 2010, 466, 992–995 CrossRef CAS PubMed.
- C. M. Kaiser, D. H. Goldman, J. D. Chodera, I. Tinoco and C. Bustamante, Science, 2011, 334, 1723–1727 CrossRef CAS PubMed.
- N. C. Seeman, Mol. Biotechnol., 2007, 37, 246–257 CrossRef CAS PubMed.
- A. V. Pinheiro, D. Han, W. M. Shih and H. Yan, Nat. Nanotechnol., 2011, 6, 763–772 CrossRef CAS PubMed.
- J. D. Watson and F. H. C. Crick, Nature, 1953, 171, 737–738 CrossRef CAS PubMed.
- S. B. Smith, Y. Cui and C. Bustamante, Science, 1996, 271, 795–799 CrossRef CAS PubMed.
- D. H. Paik and T. T. Perkins, J. Am. Chem. Soc., 2011, 133, 3219–3221 CrossRef CAS PubMed.
- G. A. King, P. Gross, U. Bockelmann, M. Modesti, G. J. L. Wuite and E. J. G. Peterman, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3859–3864 CrossRef CAS PubMed.
- X. Zhang, H. Chen, S. Le, I. Rouzina, P. S. Doyle and J. Yan, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3865–3870 CrossRef CAS PubMed.
- S. N. Rao and P. A. Kollman, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 5735–5739 CrossRef CAS PubMed.
- K. Günther, M. Mertig and R. Seidel, Nucleic Acids Res., 2010, 38, 6526–6532 CrossRef PubMed.
- A. S. Biebricher, I. Heller, R. F. H. Roijmans, T. P. Hoekstra, E. J. G. Peterman and G. J. L. Wuite, Nat. Commun., 2015, 6, 7304 CrossRef CAS PubMed.
- B. Akerman and E. Tuite, Nucleic Acids Res., 1996, 24, 1080–9100 CrossRef CAS PubMed.
- H. Lamb, Hydrodynamics, Dover Publications, New York, 6th edn, 1932 Search PubMed.
- D. Patko, Z. Mártonfalvi, B. Kovacs, F. Vonderviszt, M. Kellermayer and R. Horvath, Sens. Actuators, B, 2014, 196, 352–356 CrossRef CAS.
- P. Nath, D. Fung, Y. A. Kunde, A. Zeytun, B. Branch and G. Goddard, Lab Chip, 2010, 10, 2286 RSC.
- P. K. Yuen and V. N. Goral, Lab Chip, 2010, 10, 384–387 RSC.
- N. Bosaeus, A. H. El-Sagheer, T. Brown, S. B. Smith, B. Akerman, C. Bustamante and B. Nordén, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15179–15184 CrossRef CAS PubMed.
- A. A. Almaqwashi, T. Paramanathan, I. Rouzina and M. C. Williams, Nucleic Acids Res., 2016, 44, 3971–3988 CrossRef CAS PubMed.
- C. U. Murade, V. Subramaniam, C. Otto and M. L. Bennink, Biophys. J., 2009, 97, 835–843 CrossRef CAS PubMed.
- C. Kleimann, A. Sischka, A. Spiering, K. Tönsing, N. Sewald, U. Diederichsen and D. Anselmetti, Biophys. J., 2009, 97, 2780–2784 CrossRef CAS PubMed.
- C. Bustamante, J. F. Marko, E. D. Siggia and S. Smith, Science, 1994, 265, 1599–1600 CrossRef CAS PubMed.
- Z. N. Scholl, M. Rabbi, D. Lee, L. Manson, H. S-Gracz and P. E. Marszalek, Phys. Rev. Lett., 2013, 111, 188302 CrossRef PubMed.
- H. P. Spielmann, D. E. Wemmer and J. P. Jacobsen, Biochemistry, 1995, 34, 8542–8553 CrossRef CAS PubMed.
- F. Johansen and J. P. Jacobsen, J. Biomol. Struct. Dyn., 1998, 16, 205–222 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9lc01028a |
| ‡ Present address: VA Boston Healthcare System, Boston, MA 02130, USA. |
| This journal is © The Royal Society of Chemistry 2020 |