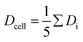Open Access Article
Open Access ArticleAcoustic erythrocytometer for mechanically probing cell viscoelasticity†
A.
Link
 and
T.
Franke
and
T.
Franke
 *
*
Division of Biomedical Engineering, School of Engineering, University of Glasgow, Oakfield Avenue, G12 8LT, Glasgow, UK. E-mail: thomas.franke@glasgow.ac.uk
First published on 21st April 2020
Abstract
We demonstrate an acoustic device to mechanically probe a population of red blood cells at the single cell level. The device operates by exciting a surface acoustic wave in a microfluidic channel creating a stationary acoustic wave field of nodes and antinodes. Erythrocytes are attracted to the nodes and are deformed. Using a stepwise increasing and periodically oscillating acoustic field we study the static and dynamic deformation of individual red blood cells one by one. We quantify the deformation by the Taylor deformation index D and relaxation times τ1 and τ2 that reveal both the viscous and elastic properties of the cells. The precision of the measurement allows us to distinguish between individual cells in the suspension and provides a quantitative viscoelastic fingerprint of the blood sample at single cell resolution. The method overcomes limitations of other techniques that provide averaged values and has the potential for high-throughput.
Introduction
The mechanical properties of cells provide key insights into the type,1,2 state,3,4 differentiation2,5,6 and/or pathology7–9 of a cell. The mechanical analysis of a cell population, such as a blood sample, enables meaningful biological and medical interpretation for diagnosis and monitoring of diseases. Malaria,10–12 diabetes,13,14 hypercholesterolemia14,15 and many others are examples of widespread blood diseases that alter the mechanics of human erythrocytes also called red blood cells (RBCs).16,17 Most methods for mechanical analysis provide number averaged values such as the blood's viscosity. However, cell populations are heterogeneous and even cells of the same type differ from each other. The importance of a comparison of individual cells in a heterogeneous population has been increasingly recognized and techniques with a resolution at the single cell level are required to pinpoint these differences.Single cells can be mechanically probed using a variety of forces18 and some techniques have been used to assay the mechanical properties of erythrocytes. Erythrocyte mechanics has been examined dielectrically,19 mechanically, magnetically,18 optically,13,20 in shear or extensional flow21,22 and acoustically.23
Micropipette aspiration has been used to measure the viscoelastic properties of single RBCs.24–26 However, precise alignment of glass capillaries to each cell before the measurement limits this technique to small cell numbers. Similarly, atomic force microscopy, though providing high spatial resolution, suffers from low throughput and a time-consuming cell selection procedure.27,28 Dielectric forces excited by inhomogeneous electric fields have been applied to characterize immobilized erythrocytes. In these experiments cells are attached to an electrode and subjected to high frequency and high voltage electric fields (several 100 V cm−1) to measure the shear elastic modulus and viscosity of the plasma membrane.19,29,30 Magnetic and optical tweezers use microbeads attached to erythrocyte membranes to transfer magnetic and electric forces to the cell. Magnetic tweezers and magnetic twisting cytometry use ferromagnetic beads attached to the cell membrane. Optical tweezers have also been used without attached beads in multiple beam mode in more complex optical setups31 that need precise optical alignment of lasers. However, exposure to the high intensity of the electric field of the laser beam causes local heating, which affects the measurement and may cause optical damage to the cell. Other optical methods to assess RBC properties are ektacytometry,32,33 which combines a bulk rheometer setup with diffraction analysis of cells. Diffraction patterns have also been used in diffraction phase microscopy34 – a label-free method that analyses shape fluctuations of the cell contour. Bulk acoustic waves have been used to deform osmotically swollen erythrocytes in glass capillaries by acoustic radiation forces. However, only elastic effects were considered, and the cell number was low (n = 8).23 Many of these techniques suffer from complex experimental setups or low cell numbers.
Microfluidic channels enable simple and controlled dispensing of cells in a single file, allowing for continuous measurement, and have the potential for high-throughput. Several methods have been integrated into microfluidic channels in the context of erythrocyte measurements including deformation in flow,35–37 dielectrophoresis,30 optical stretching,38 and flow methods analysing cell transit through microchannels and pores.39–41 However, such methods probe cells at constant deformation and only yield the elastic parameters.3
The combination of surface acoustic waves with planar microfluidic design has been proven to be a powerful tool for cell manipulation.42 Recently, traveling surface acoustic waves (T-SAWs) in microfluidics have been used to create time averaged, stationary wave fields that have been used to custom-made pattern acoustic fields to trap particles.43–45
In this paper, we introduce an acoustic method to probe for the first time both the viscous and elastic mechanics of single RBCs, in a microfluidic device. We use a travelling surface acoustic wave (T-SAW) to generate a tuneable, standing acoustic wave field to capture and deform RBCs. Individual cells are dispensed in a single file to the nodes of the standing acoustic wave field through a microchannel and are repeatedly deformed by changing the amplitude of the acoustic field. We determine the shape deformation and the shape relaxation by comparing two independent methods of analysis. From the spatio-temporal observation of deformation of a RBC we can derive each cell's individual viscoelastic properties. We screen a blood sample of healthy RBCs and demonstrate its cell heterogeneity by quantifying the viscous and elastic properties of individual erythrocytes in this population. The method allows us to differentiate between individual members of the cell population and provides characterization of the blood sample based on its viscoelastic fingerprint.
Experimental
Operation principle
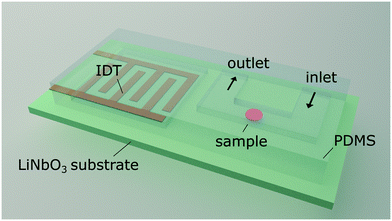
We excite an acoustic field in a microfluidic channel device as shown in Fig. 1. The acoustic field is generated by a single IDT deposited on a piezoelectric LiNbO3 substrate containing 60 finger pairs of electrodes and an aperture of 500 μm in width, operating at a frequency of 162.2 MHz. A polydimethylsiloxane (PDMS) replica containing the channel features is placed on the substrate. The microfluidic design contains a U-shaped channel geometry. The bottom of the U is the section where cells are probed, and the left and right arms are the inlet and outlet, respectively. The probing section has a length of l = 200 μm, a width of w = 22.5 μm and a height of h = 10 μm. In addition, the PDMS mould contains a cavity above the IDT to prevent damping and is separated by a wall of 60 μm to the fluid filled channel. The measurement section of the channel is aligned parallel to the direction of the travelling SAW as shown in Fig. 2. The geometric configuration and alignment of the acoustic path and the channel give rise to a standing acoustic wave field in the probing section. The incoming traveling SAW interacts with the channel wall and produces a knife-edge effect that excites a cylindrical wave at the edge where the SAW enters the fluid according to the Huygens–Fresnel principle.43 Interference of the cylindrical wave and the SAW propagating on the substrate leads to an acoustic pattern with spacing λnf. This pattern is superposed by a standing acoustic wave field that is perpendicular to the previous field and occurs because the wall bound channel acts as an acoustic waveguide.45 Therefore, despite the low impedance mismatch between PDMS and the fluid46 an acoustic field parallel to the propagation of the TSAW develops in the channel with width w = λSAW. Cells are dispensed through the inlet by carefully adjusting the pressure difference between the inlet and outlet using a displaceable height reservoir. As soon as a single cell is captured in the first intersection of nodes the pressure is reduced to stop the flow. The immobilized cell is then probed by variation of the acoustic power by amplitude modulation at a constant operating frequency (carrier frequency). For all measurements, a phosphate buffered RBC suspension of a haematocrit Hct. = 0.5% is used.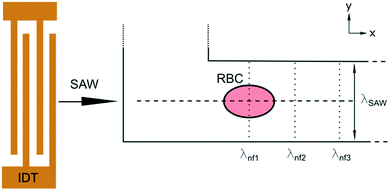 | ||
Fig. 2 Schematic sketch of the acoustic erythrocytometer device showing the probing section of the device. Single RBCs enter the inlet flow into the measurement region and are aligned to the centreline of the microchannel which is the position of the acoustic nodal line (dashed horizontal line). The other two horizontal nodal lines at the side walls of the channel very rarely attract cells since most cells enter the proximity of the centre. Focused cells then flow along the centreline and are captured as soon as they reach the first intersection with the vertical λnf1. Further vertical nodes exist at different positions on the substrate given by the periodic spacing condition 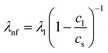 as shown where λl is the wavelength in the liquid and cl and cs are the speed of sound in the liquid and on the substrate, respectively. In the experiments we only use the first intersection to probe cells. The vertical nodes are caused by the interference of the traveling SAW excited by the IDT and its diffracted cylindrical wave excited at the edge of the PDMS wall at the fluidic channel. The superposition of these fields results in a grid-like pattern of intersecting and perpendicular nodal lines (dotted and dashed lines).43–45 as shown where λl is the wavelength in the liquid and cl and cs are the speed of sound in the liquid and on the substrate, respectively. In the experiments we only use the first intersection to probe cells. The vertical nodes are caused by the interference of the traveling SAW excited by the IDT and its diffracted cylindrical wave excited at the edge of the PDMS wall at the fluidic channel. The superposition of these fields results in a grid-like pattern of intersecting and perpendicular nodal lines (dotted and dashed lines).43–45 | ||
Mechanism
RBCs in the microchannel experience a radiation force in the standing surface acoustic wave field. The acoustic radiation force on a spherical object with volume Vc can be calculated by:47–49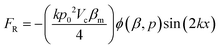 | (1) |
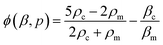 | (2) |
This force attracts an RBC to the node in order to maximise the cell volume close to the node. The acoustic force is opposed by elastic forces that occur as soon as the RBC gets deformed. Eventually, the balance of acoustic and elastic forces determines the overall stationary deformed shape of the RBC. However, when the acoustic field rapidly changes with time as compared to the typical response time of the cell deformation, the viscous properties of the cell and its environment have to be considered. These additional viscous forces slow down the transient process of relaxation in the final stationary shape.
Results
Static deformation D
We observe an increasing deformation of the cell with increasing acoustic power as shown in Fig. 3a and b. We quantify the deformation by finding the contour of the cell and fitting it with an ellipse using an image analysis software (ImageJ). From the elliptical fit, we determine the semi-major and semi–minor axes a and b, respectively, and calculate the Taylor deformation D according to: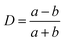 | (3) |
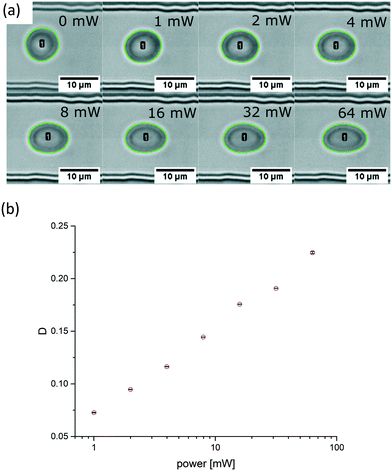 | ||
| Fig. 3 Micrographs and analysis of a RBC in the probing section. (a) Without application of an acoustic field the fitted contour (green line) is nearly circular and becomes progressively elliptical by increasing the acoustic amplitudes from 1 mW to 64 mW (0 dBm to 18 dBm) in doubling steps. The green contour around the cell was automatically analysed using image analysis software ImageJ and the built-in function “Analyse Particles”. The erythrocyte is labelled with a number, here cell #1. The black scale bar is 10 μm. (b) Plot of the Taylor deformation D as a function of applied power. With no applied SAW the deformation index of the RBC is D = 0.019 and for the power sweep D = 0.073, D = 0.095, D = 0.116, D = 0.144, D = 0.176, D = 0.191 and D = 0.225, accordingly. The error bars for each measure point are derived from the scattering from a single elongation around the saturation plateau for each power step. Data points are indicated by red circles and error bars by horizontal lines. Refer to ESI† Movie 1 which shows the deformation of the red blood cell with a stepwise increasing acoustic field. | ||
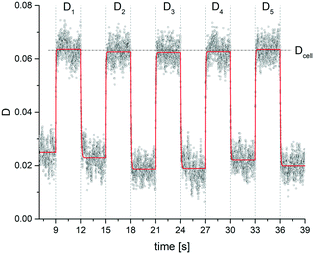
The curve progression of the Taylor deformation D follows a typical stress–strain relation of a relaxation curve with an increasing flank, a saturation at high deformation Di, a decreasing flank and again a saturation at minimal deformation. In total, we analysed 65 different RBCs in separate measurements, as shown in the scatter and box plots of Fig. 5a. The box plot displays a rather broad and slightly asymmetric distribution centred at around an average value of Dsample = 0.0729 ± 0.01896, where 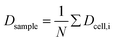 is the average value over all individual cells and cycles. Hence, the values for D scattering between different cells can be expressed by its relative error ΔDsample/Dsample = 0.01896/0.0729 = 26.0%. To demonstrate the significance of the distribution of the population, we plot Dcell for each cell as shown in Fig. 5a. The standard deviation for a single cell experiment is calculated from the scattering of the saturation value Di over all elongations. The plot in Fig. 5a shows that the absolute value of Dcell is much larger than the error of the repeated measurement on a single cell. For each cell we calculate the relative error ΔDcell/Dcell. On average the relative errors over all cells yield 2.6%, which is significantly smaller than the relative width of the population (26.0%). Therefore, our measurement can distinguish between single RBCs in the cell suspension and hence, has the potential to identify subpopulations of RBCs within a heterogeneous sample of RBCs. To effectively decouple the effect of cell deformation and size, we present the results in a scatter plot of D against an effective cell radius
is the average value over all individual cells and cycles. Hence, the values for D scattering between different cells can be expressed by its relative error ΔDsample/Dsample = 0.01896/0.0729 = 26.0%. To demonstrate the significance of the distribution of the population, we plot Dcell for each cell as shown in Fig. 5a. The standard deviation for a single cell experiment is calculated from the scattering of the saturation value Di over all elongations. The plot in Fig. 5a shows that the absolute value of Dcell is much larger than the error of the repeated measurement on a single cell. For each cell we calculate the relative error ΔDcell/Dcell. On average the relative errors over all cells yield 2.6%, which is significantly smaller than the relative width of the population (26.0%). Therefore, our measurement can distinguish between single RBCs in the cell suspension and hence, has the potential to identify subpopulations of RBCs within a heterogeneous sample of RBCs. To effectively decouple the effect of cell deformation and size, we present the results in a scatter plot of D against an effective cell radius 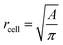 , with the projected area A as obtained at no deformation. The result as shown in Fig. 5b again underpins that the method allows individual erythrocytes to be resolved in the scatter plot and provides an elastic fingerprint of the sample.
, with the projected area A as obtained at no deformation. The result as shown in Fig. 5b again underpins that the method allows individual erythrocytes to be resolved in the scatter plot and provides an elastic fingerprint of the sample.
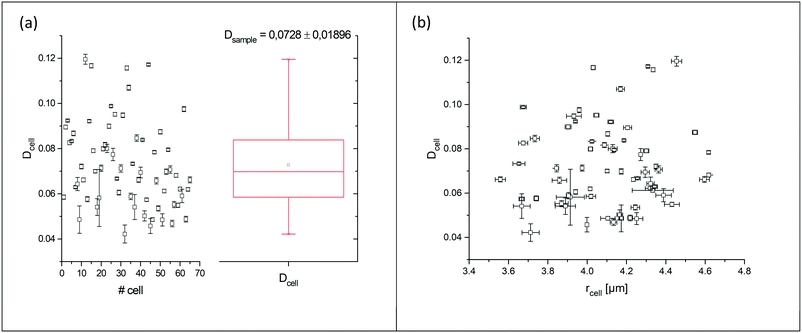 | ||
Fig. 5 (a) Summarized results of measurements for the deformation index as obtained from single cell experiments in Fig. 4. Cells were probed at a constant acoustic amplitude of 8 mW (9 dBm) for five elongations for the Taylor deformation index Dcell and represented in scatter and box plots. The heterogeneity of the RBC population for the deformation has a mean value Dsample = 0.0728 ± 0.01896, where 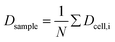 is the average value over all individual cells and cycles i. The standard deviation of the deformation index Dcell is much smaller than the differences of values among different cells. (b) Cell deformation and size results in a scatter plot of D against the effective cell radius is the average value over all individual cells and cycles i. The standard deviation of the deformation index Dcell is much smaller than the differences of values among different cells. (b) Cell deformation and size results in a scatter plot of D against the effective cell radius 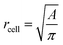 . The projected area A is obtained from the area enclosed by the contour without deformation. . The projected area A is obtained from the area enclosed by the contour without deformation. | ||
Relaxation times τ1 and τ2
So far, the analysis considered the stationary, equilibrium values of Dcell, which were obtained from analysing the stationary plateaus. These values reflect the balance of applied acoustic forces and restoring elastic forces of the cell. To gain information on the viscous forces, temporal changes of the deformation need to be accounted for and the time dependent dynamics needs to be analysed by D(t), indicating the dependence of the deformation parameter on time t. Viscous effects can be accounted for by analysing D at both flanks when switching the acoustics on and off. To quantify the response of the cell to stepwise changes of the acoustic power, we fit the rising and sloping curves with a simple exponential function and determine the response time τ from the fits. For comparison, we use separate fits for increasing and decreasing power steps, yielding τ1 and τ2, respectively, as shown in Fig. 6.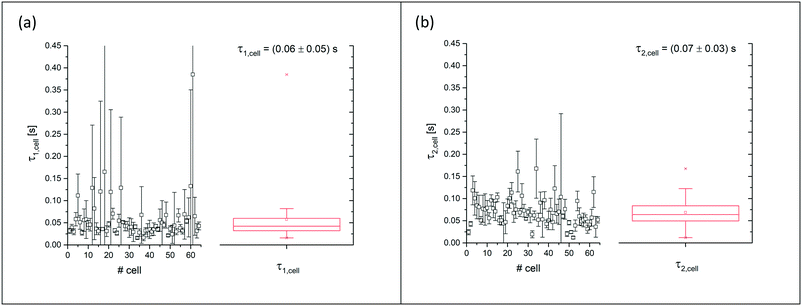 | ||
Fig. 6 Summarised results of measurements of the relaxation times as obtained from single cell experiments and simple exponential fits in Fig. 4. Cells were probed at a constant acoustic amplitude of 8 mW (9 dBm) for five elongations for the relaxation times τ1 and τ2 and represented in scatter and box plots (a) for the rising deformation followed by an increase to 8 mW and (b) for the falling deformation back to the trapping amplitude of 0.8 mW. The heterogeneity of the RBC population for the relaxation time τ1 has a mean value of τ1,sample = 0.06 ± 0.05 s for the rising deformation and that for the relaxation time τ2 has a mean value of τ2,sample = 0.07 ± 0.03 s for the falling deformation, where 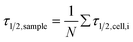 is the average value over all individual cells and cycles i. The values for cell #18 and cell #61 exceed the range of the plot. The corresponding values are τ1,#18 = 0.165 ± 0.329 s and τ1,#61 = 0.385 ± 0.794 s. is the average value over all individual cells and cycles i. The values for cell #18 and cell #61 exceed the range of the plot. The corresponding values are τ1,#18 = 0.165 ± 0.329 s and τ1,#61 = 0.385 ± 0.794 s. | ||
Discussion
We have presented a method to acoustically investigate the mechanical properties of erythrocytes in a microfluidic device using surface acoustic waves. We find that the Taylor deformation D increases with the stepwise increase of the acoustic amplitude. This deformation was reversible as can be seen from the small error bars in Fig. 3b, which were obtained from repeated measurements of the same erythrocyte. When applying very high acoustic fields >3.2 W (35 dBm), we observed a decreasing optical contrast of the cell and the deformation was no longer reversible. We suspect that at these high-power levels, transient pores may be formed in the plasma membrane and cytosol may be released. We limited the applied power to maximally 64 mW (18 dBm) for the power measurement and used an amplitude of 8 mW (9 dBm) for all subsequent deformation measurements. In previous studies, the viability of cells exposed to an acoustic field has been confirmed for acoustic power amplitudes in this range.50–54Using a square wave function for the acoustic amplitude of 8 mW (9 dBm), we have probed a sample of human erythrocytes. The oscillation period was chosen as T = 6 s to allow the cell deformation to relax and approach its saturation value. We analysed the cell response to the square wave excitation by fitting the data points between the square wave plateaus with a single exponential function as shown in Fig. 4. This fit assumes a simple model with the time constant, representing the ratio of viscous to elastic forces. From the analysis of the increasing and decreasing power jumps, we obtain average response times of τ1 = 0.06 ± 0.05 s and τ2 = 0.07 ± 0.03 s, respectively. These values are on the low side of previously measured time constants using different methods. However, the obtained mean values are in agreement with values from the literature using different methods, e.g., micropipette aspiration55 (∼0.3 s), microfluidic device21 (0.11 s < τ1 < 0.52 s), rheometer56 (light reflection 0.119 ± 0.017 s, ektacytometry 0.097 ± 0.015 s) and optical tweezers.57 It is apparent that the error bars for the sample average in our experiments are much higher than the ones given in the literature. This may be an indication that the scattering of viscoelastic values of a heterogeneous cell population is much larger than that previously assumed in studies where only a few cells have been probed and only represent a subpopulation. In this context, it is important to note that the error bars in our measurement mainly represent the variation of τ values between cells of the probed heterogeneous population and are not measurement errors.
The heterogeneity of response times may be an indication of the heterogeneity of the cell age. The average lifetime of erythrocytes is about 120 days and hence, a blood sample contains cells of very different cell ages. It is well known that erythrocytes are subjected to several changes upon aging, including morphological changes that are caused by the loss of the membrane material, and this has been argued to cause increased cell stiffness. Moreover, it has been reported that the viscosity of the erythrocyte cytosol increases with age.58 Density gradient isolated ‘young’ cells have been found to exhibit shorter (0.162 s) relaxation times as compared to ‘old’ cells (0.353 s) or the average of the whole cell population (0.271 s).59 In addition, measurements of response times depend on the surrounding fluid, since the shape changes are coupled to the viscous environment the cell is embedded in. For measurements in blood plasma, the response times are longer (∼0.3 s)59 than in phosphate-buffered saline solution in the literature (0.114 s),59 as well as in our experiments presented in Fig. 6.
It still remains challenging to link the cell response and the temporal progression of the shape deformation to the simple biomaterial properties of the cell, as given by its constituents. The RBC membrane is a complex composite envelope composed of a plasma membrane and macromolecular network, the cytoskeleton, attached to the cytoplasmic face of the plasma membrane.60 The mechanics of these two coupled shells contribute to the viscoelastic response of the erythrocyte. There are two restoring elastic moduli, the elastic bending stiffness κ and the shear elasticity μ, as given by the properties of the plasma membrane and the cytoskeleton, respectively. During the relaxation process, this elastic energy is opposed by dissipation in the membrane and the bulk fluid. These two contributions depend on the membrane shear viscosity ηmem and effective bulk viscosity of the fluid, which represent both the cytosol and the surrounding fluid. From these moduli, characteristic times for bending and shear can be estimated by τb and τs.21,24
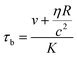 | (4) |
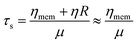 | (5) |
The transient erythrocyte deformation in our experiment contains both shear and bending deformations and it is difficult to estimate the relative contribution of each without having analysed the exact 3D shape of the cell. Moreover, even if a full 3D-contour is known, simulations are still required to model the temporal rearrangement of the cytoskeleton network that dominates the shear effects.62 Therefore, in our simple model using a one exponential fit for the relaxation, we cannot resolve all the complex mechanical aspects of the cell. A more refined model using multiple exponentials based on Kelvin–Voigt-like models has been used in the past.63 However, a more thorough theoretical analysis in three dimensions, which includes both the erythrocyte morphology and the three-dimensional acoustic field of our device, will be necessary, and that can only be provided by simulations.64,65
The scatter plot in Fig. 5a shows the time-independent deformation of the erythrocyte sample and only depends on the elastic parameters. This comparatively simpler situation disregarding viscous effects has been analysed for cells using iso-elasticity lines.3 Yet, for erythrocytes, this still remains challenging since multiple elastic moduli, such as bending and shear elasticity, are involved. In contrast to spherical cells, the analysis is further complicated by the non-spherical discoid shape of RBCs. The erythrocytes in our experiments align with their axis of symmetry perpendicular to the substrate so that the non-deformed contour is circular and simple to analyse. However, in the deformed state, also components of deformation out of this projection may occur which have not been taken into account. Again, a full 3D-analysis would be necessary to provide a more detailed analysis and provide lines of constant elastic moduli.
Here, we have demonstrated that a simple phenomenological model is useful to analyse the experiments of our acoustofluidic device and to determine elastic and viscous experimental parameters. The results indicate that the error of a repeated measurement of a single cell is significantly smaller than the scattering of experimental values between different cells in the population. Hence, the resolution of our device allows the analysis of an erythrocyte sample at the single cell level.
In recent publications,23,66 it was shown that ultrasonic manipulation provides precision and speed and can potentially work with thousands of cells whereas micropipette aspiration and optical tweezers are limited to a small number of cells. There are techniques available to probe the mechanics of cells at a high-throughput of a few hundred cells per second, for example using deformation in flow.3,67 However, these techniques exploit the static deformation such as the ellipticity of cells allowing only to derive the elastic parameters. Determination of viscous parameters requires an extended observation of temporal shape changes. Generally, the throughput of our device is therefore inherently limited by the response time of the cells. The cell sample rate has to be larger than the inverse of the response time to allow observation of the transient states of relaxation. For typical response times of 0.1 s this limits the throughput to 10 cells per second. However, exploiting multiple nodes of the acoustic wave field is a way to increase the sampling rate. This can be done for example by using the nodes in the channel shown in Fig. 2. In conclusion, combining microfluidics and acoustics allows the non-invasive, repeatable, electrically tuneable manipulation of living cells.
Conclusions
We have presented a microfluidic device using standing surface acoustic waves to analyse a cell population of erythrocytes mechanically. Our method allows us to simultaneously determine both the elastic and viscous parameters of single erythrocytes and provides a viscoelastic fingerprint of the erythrocyte sample at single cell resolution. The technique has high potential for automation and will be useful for high-throughput screening of blood samples, for example, to monitor or detect disease, particularly in early stages when small numbers of diseased cells form a subpopulation. This can be used to characterize a cell population by its viscoelastic fingerprint for example to identify or monitor disease. Comparison with detailed simulations of both the acoustic field and the erythrocyte shape should be used in the future, to refine the simple two parameter model presented here, and allow more specific interpretation of the transient shape deformations.Conflicts of interest
There are no conflicts to declare.Acknowledgements
AL and TF acknowledge support from the UK Engineering and Physical Sciences Research Council (EPSRC) via grant EP/P018882/1. The authors thank John McGrath for proofreading the manuscript.Notes and references
- E. Moeendarbary and A. R. Harris, Wiley Interdiscip. Rev.: Syst. Biol. Med., 2014, 6, 371–388 Search PubMed.
- J. Lin, D. Kim, H. T. Tse, P. Tseng, L. Peng, M. Dhar, S. Karumbayaram and D. Di Carlo, Microsyst. Nanoeng., 2017, 3, 17013 CrossRef CAS PubMed.
- O. Otto, P. Rosendahl, A. Mietke, S. Golfier, C. Herold, D. Klaue, S. Girardo, S. Pagliara, A. Ekpenyong, A. Jacobi, M. Wobus, N. Töpfner, U. F. Keyser, J. Mansfeld, E. Fischer-Friedrich and J. Guck, Nat. Methods, 2015, 12, 199–202 CrossRef CAS PubMed.
- M. N. Starodubtseva, Ageing Res. Rev., 2011, 10, 16–25 CrossRef PubMed.
- R. D. Gonzalez-Cruz, V. C. Fonseca and E. M. Darling, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, E1523–E1529 CrossRef CAS PubMed.
- M. M. Khani, M. Tafazzoli-Shadpour, M. Rostami, H. Peirovi and M. Janmaleki, Ann. Biomed. Eng., 2014, 42, 1373–1380 CrossRef PubMed.
- C. T. Mierke, Rep. Prog. Phys., 2019, 82, 064602 CrossRef CAS PubMed.
- M. Starodubtseva, S. Chizhik, N. Yegorenkov, I. Nikitina and E. Drozd, Microscopy: Science, Technology, Applications and Education, 2010, pp. 470–477 Search PubMed.
- P.-H. Wu, D. R.-B. Aroush, A. Asnacios, W.-C. Chen, M. E. Dokukin, B. L. Doss, P. Durand-Smet, A. Ekpenyong, J. Guck, N. V. Guz, P. A. Janmey, J. S. H. Lee, N. M. Moore, A. Ott, Y.-C. Poh, R. Ros, M. Sander, I. Sokolov, J. R. Staunton, N. Wang, G. Whyte and D. Wirtz, Nat. Methods, 2018, 15, 491–498 CrossRef CAS PubMed.
- H. A. Cranston, C. W. Boylan, G. L. Carroll, S. P. Sutera, J. R. Williamson, I. Y. Gluzman and D. J. Krogstad, Science, 1984, 223, 400–403 CrossRef CAS PubMed.
- T. M. Geislinger, S. Chan, K. Moll, A. Wixforth, M. Wahlgren and T. Franke, Malar. J., 2014, 13, 375 CrossRef PubMed.
- S. M. Hosseini and J. J. Feng, Biophys. J., 2012, 103, 1–10 CrossRef CAS PubMed.
- R. Agrawal, T. Smart, J. Nobre-Cardoso, C. Richards, R. Bhatnagar, A. Tufail, D. Shima, P. H. Jones and C. Pavesio, Sci. Rep., 2016, 6, 15873 CrossRef CAS PubMed.
- J. Radosinska and N. Vrbjar, Physiol. Res., 2016, 1, S43–54 Search PubMed.
- M. Kohno, K. Murakawa, K. Yasunari, K. Yokokawa, T. Horio, H. Kano, M. Minami and J. Yoshikawa, Metabolism, 1997, 46, 287–291 CrossRef CAS PubMed.
- G. Y. H. Lee and C. T. Lim, Trends Biotechnol., 2007, 25, 111–118 CrossRef CAS PubMed.
- M. Diez-Silva, M. Dao, J. Han, C. Lim and S. Suresh, MRS Bull., 2010, 35, 382–388 CrossRef CAS PubMed.
- M. L. Rodriguez, P. J. McGarry and N. J. Sniadecki, Appl. Mech. Rev., 2013, 65, 060801 CrossRef.
- H. Engelhardt and E. Sackmann, Biophys. J., 1988, 54, 495–508 CrossRef CAS PubMed.
- G. Lenormand, S. Hénon, A. Richert, J. Siméon and F. Gallet, Biophys. J., 2001, 81, 43–56 CrossRef CAS PubMed.
- S. Braunmüller, L. Schmid, E. Sackmann and T. Franke, Soft Matter, 2012, 8, 11240 RSC.
- P. M. Vlahovska, T. Podgorski and C. Misbah, C. R. Phys., 2009, 10, 775–789 CrossRef CAS.
- P. Mishra, M. Hill and P. Glynne-Jones, Biomicrofluidics, 2014, 8, 034109 CrossRef PubMed.
- E. A. Evans, Methods Enzymol., 1989, 173, 3–35 CAS.
- E. A. Evans, N. Mohandas and A. Leung, J. Clin. Invest., 1984, 73, 477–488 CrossRef CAS PubMed.
- D. Discher, N. Mohandas and E. A. Evans, Science, 1994, 266, 1032–1035 CrossRef CAS PubMed.
- V. Lulevich, T. Zink, H. Chen, F.-T. Liu and G. Liu, Langmuir, 2006, 22, 8151–8155 CrossRef CAS PubMed.
- P. A. Carvalho, M. Diez-Silva, H. Chen, M. Dao and S. Suresh, Acta Biomater., 2013, 9, 6349–6359 CrossRef CAS PubMed.
- H. Engelhardt, H. Gaub and E. Sackmann, Nature, 1984, 307, 378–380 CrossRef CAS PubMed.
- E. Du, M. Dao and S. Suresh, Extreme Mech. Lett., 2014, 1, 35–41 CrossRef CAS PubMed.
- X. Liu, J. Huang, Y. Li, Y. Zhang and B. Li, Nanophotonics, 2017, 6, 309–316 CAS.
- W. Groner, N. Mohandas and M. Bessis, Clin. Chem., 1980, 26, 1435–1442 CrossRef CAS.
- L. Da Costa, L. Suner, J. Galimand, A. Bonnel, T. Pascreau, N. Couque, O. Fenneteau and N. Mohandas, Blood Cells, Mol., Dis., 2016, 56, 9–22 CrossRef PubMed.
- R. Wang, H. Ding, M. Mir, K. Tangella and G. Popescu, Biomed. Opt. Express, 2011, 2, 485 CrossRef PubMed.
- S. Braunmüller, L. Schmid and T. Franke, J. Phys.: Condens. Matter, 2011, 23, 184116 CrossRef PubMed.
- A. M. Forsyth, S. Braunmüller, J. Wan, T. Franke and H. A. Stone, Microvasc. Res., 2012, 83, 347–351 CrossRef CAS PubMed.
- M. Abkarian, M. Faivre and A. Viallat, Phys. Rev. Lett., 2007, 98, 188302 CrossRef PubMed.
- I. Sraj, C. D. Eggleton, R. Jimenez, E. Hoover, J. Squier, J. Chichester and D. W. M. Marr, J. Biomed. Opt., 2010, 15, 047010 CrossRef PubMed.
- H. Bow, I. V. Pivkin, M. Diez-Silva, S. J. Goldfless, M. Dao, J. C. Niles, S. Suresh and J. Han, Lab Chip, 2011, 11, 1065 RSC.
- M. Abkarian, M. Faivre and H. A. Stone, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 538–542 CrossRef CAS PubMed.
- M. J. Rosenbluth, W. A. Lam and D. A. Fletcher, Lab Chip, 2008, 8, 1062 RSC.
- S. Li, X. Ding, Z. Mao, Y. Chen, N. Nama, F. Guo, P. Li, L. Wang, C. E. Cameron and T. J. Huang, Lab Chip, 2015, 15, 331–338 RSC.
- C. Devendran, D. J. Collins, Y. Ai and A. Neild, Phys. Rev. Lett., 2017, 118, 154501 CrossRef PubMed.
- A. Fakhfouri, C. Devendran, A. Ahmed, J. Soria and A. Neild, Lab Chip, 2018, 18, 3926–3938 RSC.
- D. J. Collins, R. O'Rorke, C. Devendran, Z. Ma, J. Han, A. Neild and Y. Ai, Phys. Rev. Lett., 2018, 120, 074502 CrossRef CAS PubMed.
- I. Leibacher, S. Schatzer and J. Dual, Lab Chip, 2014, 14, 463–470 RSC.
- X. Ding, S.-C. S. Lin, B. Kiraly, H. Yue, S. Li, I.-K. Chiang, J. Shi, S. J. Benkovic and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11105–11109 CrossRef CAS PubMed.
- M. Wiklund and H. M. Hertz, Lab Chip, 2006, 6, 1279 RSC.
- H. Bruus, Lab Chip, 2012, 12, 1014 RSC.
- D. J. Collins, B. Morahan, J. Garcia-Bustos, C. Doerig, M. Plebanski and A. Neild, Nat. Commun., 2015, 6, 8686 CrossRef CAS PubMed.
- T. Franke, S. Braunmüller, L. Schmid, A. Wixforth and D. A. Weitz, Lab Chip, 2010, 10, 789 RSC.
- I. Leibacher, P. Hahn and J. Dual, Microfluid. Nanofluid., 2015, 19, 923–933 CrossRef CAS.
- D. Bazou, W. T. Coakley, A. J. Hayes and S. K. Jackson, Toxicol. In Vitro, 2008, 22, 1321–1331 CrossRef CAS PubMed.
- M. Evander, L. Johansson, T. Lilliehorn, J. Piskur, M. Lindvall, S. Johansson, M. Almqvist, T. Laurell and J. Nilsson, Anal. Chem., 2007, 79, 2984–2991 CrossRef CAS PubMed.
- R. M. Hochmuth, K. L. Buxbaum and E. A. Evans, Biophys. J., 1980, 29, 177–182 CrossRef CAS PubMed.
- O. BASKURT and H. Meiselman, Biorheology, 1996, 33, 489–503 CAS.
- P. J. Bronkhorst, G. J. Streekstra, J. Grimbergen, E. J. Nijhof, J. J. J. Sixma, G. J. J. Brakenhoff, P. J. Bronkhorst, G. J. Streekstra, J. Grimbergen, E. J. Nijhof, J. J. J. Sixma and G. J. J. Brakenhoff, Biophys. J., 1995, 69, 1666–1673 CrossRef CAS PubMed.
- M. J. Simmonds, H. J. Meiselman and O. K. Baskurt, J. Geriatr. Cardiol., 2013, 10, 291–301 Search PubMed.
- J. Cao, W. Beisker, M. Nüsse and I.-D. Adler, Mutagenesis, 1993, 8, 533–541 CrossRef CAS PubMed.
- E. Sackmann, J. Phys.: Condens. Matter, 2006, 18, R785–R825 CrossRef CAS.
- R. M. Hochmuth and R. E. Waugh, Annu. Rev. Physiol., 1987, 49, 209–219 CrossRef CAS PubMed.
- P. J. Bronkhorst, G. J. Streekstra, J. Grimbergen, E. J. Nijhof, J. J. Sixma and G. J. Brakenhoff, Biophys. J., 1995, 69, 1666–1673 CrossRef CAS PubMed.
- R. M. Hochmuth, P. R. Worthy and E. A. Evans, Biophys. J., 1979, 26, 101–114 CrossRef CAS PubMed.
- B. Kaoui, G. Biros and C. Misbah, Phys. Rev. Lett., 2009, 103, 188101 CrossRef PubMed.
- J. Mauer, S. Mendez, L. Lanotte, F. Nicoud, M. Abkarian, G. Gompper and D. A. Fedosov, Phys. Rev. Lett., 2018, 121, 118103 CrossRef CAS PubMed.
- A. L. Bernassau, P. Glynne-Jones, F. Gesellchen, M. Riehle, M. Hill and D. R. S. Cumming, Ultrasonics, 2014, 54, 268–274 CrossRef CAS PubMed.
- D. R. Gossett, H. T. K. Tse, S. A. Lee, Y. Ying, A. G. Lindgren, O. O. Yang, J. Rao, A. T. Clark and D. Di Carlo, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 7630–7635 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Movie showing the surface acoustic wave actuated deformation of a red blood cell for stepwise increasing power amplitudes. See DOI: 10.1039/c9lc00999j |
| This journal is © The Royal Society of Chemistry 2020 |