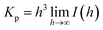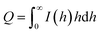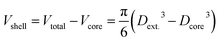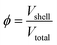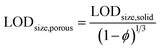Porosity determination of nano- and sub-micron particles by single particle inductively coupled plasma mass spectrometry

Abstract

A new porosity determination method for nano- and sub-micron particles is proposed, which is based on single particle inductively coupled plasma mass spectrometry (spICP-MS) measurements. The performance of the new method was tested on core–shell Ag–Au, hollow Au and mesoporous SiO₂ nanoparticles of different sizes and porosities and it was found that its accuracy and precision (e.g. 1–2 rel.%) are comparable to those of reference methods, such as small angle X-ray scattering (SAXS), gas adsorption or transmission electron microscopy imaging (TEM). It can be applied to nano- and submicron particles in the complete mesoporous pore (2–50 nm) range. The application to macroporous particles is also possible, but it is limited in size to particles that can be fully decomposed by the plasma. The proposed new spICP-MS method provides an advantageous set of features that is unparalleled among the porosity determination methods, namely (i) it only requires a very small amount of particulate sample (micrograms or even less) in the form of a dilute dispersion (e.g. in a 10⁵ mL⁻¹ particle concentration), so there is not even a need for a dry sample; (ii) it works for open and closed pores equally well; (iii) the measurement and calculation are quick and simple, and only need the external diameter of the particle (from e.g. electron microscopy or dynamic light scattering (DLS) measurements) as input. The overall porosity determined can also be used to calculate the density of the particles, a feat which is not easy to achieve from such a small amount of sample.

---

1. Introduction

These days the significance of nanotechnology can hardly be overemphasized. Numerous scientific and industrial fields (e.g. medicine, pharmaceutical, chemical, electronic, vehicle industries, etc.) exploit the unique properties of nanomaterials. Design, synthesis and testing of engineered nanoparticles (NPs) and submicron particles are highly active research areas in materials science, which therefore require the continuous development of analytical NP characterization techniques.^1,2 Main NP properties include morphology, size, structure, composition, density and porosity.

The overall porosity (ϕ) is typically defined as a ratio of pore (void) volume (V_p) to the total volume (V_t) of a material: ϕ = V_p/V_t. The word porosity is also used as a generic term, implicitly incorporating other related characteristics such as pore morphology (e.g. pore volume, pore size) or specific surface area.^3–6 Porosity has a profound impact on particle chemistry, due to the facts that (i) it can make the particles permeable, and (ii) an increase in the specific surface area boosts the activity of the surface and the adsorption of molecular species,^7,8 thereby promoting various industrial and environmental science applications.⁵ For example, porous silica particles find wide-scale application as catalyst supports (also in nanocomposite catalysts), adsorbents, molecular sieves, chemical sensors, etc.^9–13 Recent research also found mesoporous silica particles to be very promising medical drug carriers.¹⁴ Mesoporous TiO₂ is widely recognized as a photocatalyst, and it is also utilized in solar cells, lithium-ion batteries, biosensors and cancer therapy.^15,16 Mesoporous Co₃O₄ particles are exploited in the fields of energy storage, the semiconductor industry and catalysis.^17,18

Due to their above outlined importance, the determination of the porosity of nanoparticles, especially mesoporous particles with pore sizes in the 2–50 nm range, is crucial. Although well-established techniques (e.g. Brunauer–Emmett–Teller (BET) gas adsorption, gas expansion, small angle X-ray scattering (SAXS) and electron microscopy imaging (SEM, TEM), etc.) are available for porosity determination, they all have limitations in terms of pore size range, accuracy, required sample amount and sample preparation.^19,20 Also, many techniques can only determine the accessible (connected) pore volume, leaving closed pores out of calculations. Some of the techniques are used only comparatively, e.g. they allow the comparison of the porosity of particles through the determination of some related particle characteristics, such as specific surface area. There are only two, truly NP-dedicated techniques: TEM and focused ion beam SEM (FIB-SEM). Related reviews^19,20 and Table 1 give an overview of the commonly used techniques.

Table 1 An overview of some characteristics of porosity determination techniques

Method	Pore size range	Pore types	Sample amount	Comments
Saturation (gravimetry)	Macropores (>50 nm)	Open	Min. 1 g	Dry sample
Buoyancy (gravimetry)	Macropores (>50 nm)	Open	Min. 1 g	Dry sample
Gas expansion (He, Boyle)	All pore sizes (1 nm to 100 μm)	Open	Min. 1 g	Dry sample
Gas adsorption (N2, BET)	All pore sizes (2 nm to 100 μm)	Open	Min. 1 g	Dry sample
Hg intrusion	All pore sizes (3 nm to 350 μm)	Open	Min. 1 g	Dry sample, compressible structures cannot be measured
SAXS/SANS	All pore sizes (1 nm to 100 μm)	Open and closed	Min. mg	Dry sample, pelletized or cut to a thin slice
X-ray nano tomography	Macropores (>50 nm)	Open and closed	μm to mm particles	Dry sample
TEM	Meso- and micropores (e.g. 1 nm to 100 nm)	Open and closed	Many NPs	Dry sample, only for particles smaller than ca. 100 nm
FIB-SEM	Meso- and micropores (e.g. 1 nm to 100 nm)	Open and closed	Single NP	10–15 nm depth/slicing resolution

---

Single particle inductively coupled plasma mass spectrometry (spICP-MS) is a novel technique for the rapid characterization of the dilute dispersions of nano- and submicron particles. This technique is based on the recording of the time-resolved ICP-MS signal, where the intensity (area) of the signal peaks generated by individual NPs is proportional to the number of analyte atoms in the detected NPs, which is also proportional to the size (diameter) or mass of particles. In case of compact, single component, spherical NPs, the measured intensity is in a cubic relation with the particle diameter. Through the evaluation of the signal histograms, the technique can provide information about the presence, size distribution, number concentration, elemental or isotopic composition of nanoparticles.^21–24 In our previous studies, we demonstrated that not only single component or homogeneous (random) alloy spherical NPs can be analyzed, but additional information, such as the structure and aspect ratio, can also be obtained by the spICP-MS method.^25,26 The spICP-MS analysis is fast (takes only a couple of minutes) and the required sample volume is small (a few mL). For most monometallic NPs, typical size detection limits range from ca. 10 to 40 nm.²⁷ Kálomista et al.²⁴ and later Bolea-Fernandez et al.²⁸ showed that the collision/reaction cell technology can be used advantageously in spICP-MS measurements as well for diminishing spectral interferences without sacrificing much of the size detection limits or precision of the obtained data.

Our concept in the present study was that by comparing the spICP-MS signal peak intensities (areas) from solid, fully compact spherical particles to the signal intensities from porous particles of the same composition and size, one can potentially determine the “relative compactness” of particles. This information can then be combined with particle diameter or volume data from other NP characterization techniques, such as electron microscopy or dynamic light scattering, towards the calculation of the total pore (void) volume, porosity and density of nanoparticles. Of course, practical execution of the analysis is made possible via spICP-MS size calibration, thereby eliminating the need to use particles of the same size. If it proves to be accurate, our new method can make spICP-MS a very useful addition to the toolset of NP porosity characterization methods, as it potentially has a unique combination of exceptional features including that (i) it only requires a very small amount of nanoparticles (e.g. micrograms), (ii) it works for almost any nm-sized pore structure (as opposed to e.g. the immersion techniques) (iii) it works directly in dispersion form, so there is no need to evacuate adsorbates from the pores prior to the measurement (as opposed to e.g. gas adsorption techniques), (iv) the analysis and data evaluation are simple and quick.

In the present study, we tested the performance of our new spICP-MS concept on several NPs with different porosities and compositions (Au, Au–Ag and SiO₂) that we either purchased commercially or synthesized in our laboratory. The spICP-MS porosity, pore volume and density results were compared to values determined by reference methods (e.g. transmission electron microscopy, small angle X-ray scattering (SAXS) and BET gas adsorption measurements).

2. Experimental

2.1 Instrumentation and data evaluation

An Agilent 7700x quadrupole ICP-MS instrument (Agilent Technologies, California, USA) was used in all spICP-MS experiments. Sample introduction was performed by using an Agilent I-AS autosampler and a Micro Mist pneumatic nebulizer equipped with a Peltier-cooled Scott-type spray chamber. Data acquisition was performed in the time-resolved analysis (TRA) mode. Tuning of the ICP-MS was performed daily using tuning solutions supplied by Agilent (no. G1820-60410). Experimental parameters relevant to spICP-MS were optimized prior to the measurements. Plasma sampling depth was optimized using the signal-to-noise ratio as an objective function.²⁵ Dwell time (called integration time in the Agilent nomenclature) was decreased for ²⁸Si in order to lower the contribution of background to the measured signal. NP dispersions measured were diluted to a 2.5–5 × 10⁴ mL⁻¹ concentration in order to avoid signal peak overlaps, while the acquisition time was increased to ensure the detection of a sufficient number of particles that allows for statistically reliable results. The used experimental parameters are summarized in Table 2 for all three elements (Si, Ag, and Au) analyzed.

Table 2 Summary of the ICP-MS instrumental and data acquisition settings applied

Experimental parameters	Silicon	Silver	Gold
Monitored isotope	^28Si	^107Ag	^197Au
RF forward power (W)	1550	1550	1550
Plasma gas flow rate (L min^−1)	15	15	15
Carrier (nebulizer) gas flow rate (L min^−1)	1.05	1.05	1.05
Sampling depth (mm)	6.0	10.0	10.0
Sample uptake rate (μL min^−1)	600	600	600
Dwell time (ms)	3	6	6
Data acquisition time in TRA mode (s)	120	60	60

---

Single particle ICP-MS data evaluation is based on signal histograms (counts vs. detection frequency diagrams).^22,29 Background correction was carried out by subtracting the mode of the background peak (fittable by a Poisson function) from the mode of the particle peak (fittable by a lognormal function) resulting in the characteristic intensity (proportional to analyte mass). Details of the spICP-MS particle size calibration and data evaluation were described in our previous studies (e.g.ref. 23, 25 and 26). Data processing was performed using Agilent MassHunter (Santa Clara, California, USA) and OriginLab Origin 8.5 (Northampton, Massachusetts, USA) software.

SAXS was used to investigate the structure, porosity and specific surface area of silica NPs. SAXS curves were recorded with a slit-collimated Kratky compact small-angle system (KCEC/3 Anton-Paar KG, Graz, Austria) equipped with a position-sensitive detector (PSD 50 M from M. Braun AG Münich, Germany) containing 1024 channels, all 55 μm in width. Cu K_α radiation (1.5406 Å) was generated by using a Philips PW1830 X-ray generator run at 40 kV and 30 mA.

The surface area per unit volume (S/V) and the specific surface area (a^s) values were determined as:

S/V = 4w₁w₂K_p/Q

and

a^s = 10³ × ρ⁻¹ × S/V

where K_p is the Porod constant, Q is the invariant and ρ is the apparent density, while w₁ and w₂ are the volume fractions of the solid phase and pores, respectively. K_p and Q were determined as:

The scattering vector (h) was defined as h = (4πsin θ)/λ, where θ is one-half of the scattering angle, and λ is the measurement wavelength.^30–32

TEM images were captured by a Jeol JEM-1400plus instrument (JEOL Ltd., Tokyo, Japan) using 120 keV acceleration voltage. The samples were dropped on a carbon film-coated copper grid with 200 mesh (Agar Scientific, Essex, UK). SEM images of the synthesized silica NPs were recorded using a Hitachi S-4700 instrument operated at 20 kV acceleration voltage. Electron micrographs were analyzed by using ImageJ open-source software.

BET specific surface area and the average pore diameter of the investigated porous particles were determined by the Barrett–Joyner–Halenda (BJH) method³³ using a Quantachrome NOVA 2200 gas sorption analyzer (Anton Paar GmbH, Graz, Austria) by N₂ gas adsorption/desorption at 77 K. Before the measurements, the samples were pre-treated in a vacuum (<0.1 mbar) at 473 K for 2 h.

2.2 Synthesis and general characterization of nanoparticles

Based on the work of Wang et al.,³⁴ the synthesis of hollow Au NPs was optimized as follows. 2 mL of the tannin-stabilized Ag NPs were cleaned using centrifugation at 12 000 rpm for 20 min. Then, the particles were dispersed by using an ultrasonic bath (37 kHz, 15 min) into the same volume 80 mM CTAC solution, which was left undisturbed for 24 h at 35 °C. To synthesize gold shells on the surface of Ag NPs, 32 μL 0.34 mM HAuCl₄ solution was added into the suspension and the reaction mixture was thermostatted at 80 °C for 2 h. The colloids were then allowed to cool to room temperature. Purification was carried out by ultracentrifugation at 7000 rpm for 1 h. The obtained particles had 77.9 nm external and 65.3 nm internal (pore) average diameters with standard deviations of 5.9 nm and 5.9 nm, respectively (Fig. 1).

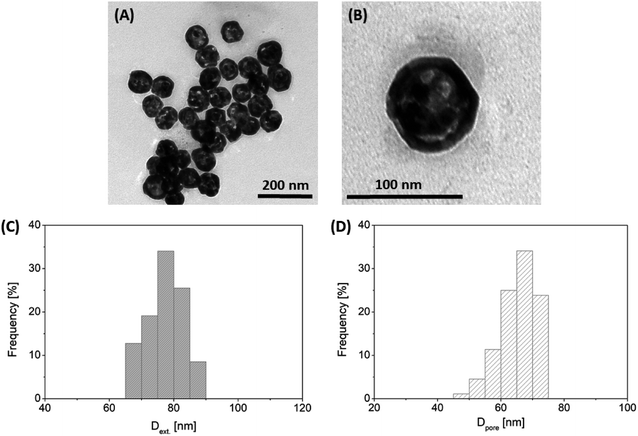Fig. 1 Representative TEM images of the synthesized hollow Au NPs at two magnifications (panels A and B) with their external and pore diameter distributions (panels C and D).

Porous silica particles were prepared by a process based on the Stöber method,³⁵ using a tetraethoxysilane (TEOS) precursor. The synthesis of the 373 nm particles was carried out by adding an ethanolic TEOS solution (containing 6.5 mL TEOS and 100 mL ethanol) in a dropwise manner to an ethanolic ammonia solution (prepared by mixing 50 mL 25 w% ammonia, 35 mL distilled water and 55 mL ethanol) under constant stirring at room temperature. The thus obtained, white coloured dispersion was further stirred, and then it was centrifuged at 4000 rpm and the supernatant was discarded. The precipitate was washed with an ethanol–distilled water mixture and collected via two-fold centrifugation. Finally, the particles were dried at 80 °C overnight. Other size particles were obtained by modifying the composition and mixing ratio of the TEOS and ammonia solutions. The SEM micrographs and size distribution diagrams of the synthesized silica particles are shown in Fig. 2.

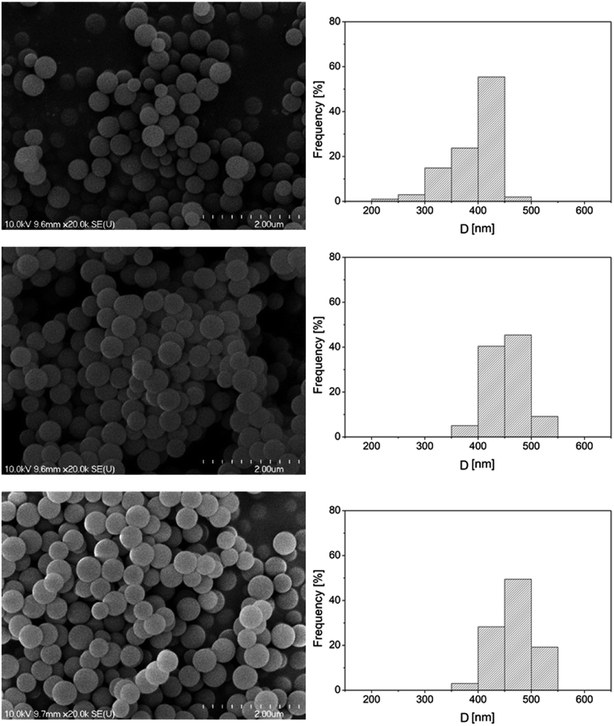Fig. 2 Typical SEM micrographs of the synthesized porous silica particles and their size distributions.

A SAXS-based reference method was used to determine the porosity of the silica particles. This method is based on density data measured by gravimetry corrected for the interparticle volume, according to Masalov et al.³⁶

The correctness of the porosity data was tested by the comparison of the specific surface area values determined by SAXS and BET, and they were found to be in good agreement (Table 3).

Table 3 Characterization results of the synthesized mesoporous Stöber silica particles

Average particle diameter [nm]	Specific surface area [m^2 g^−1]		Average pore diameter [nm]
	BET	SAXS
373	335	330	2.36
447	333	322	2.28
464	323	318	2.32

---

2.3 Materials and sample preparation

For spICP-MS size calibration purposes, a series of gold, silver and silica standard dispersions, specified in Table 4, were obtained from Ted Pella (Redding, California, USA) and NanoComposix (San Diego, California USA) companies. These particles were used for spICP-MS size calibration purposes, as they are solid and spherical. Sodium citrate stabilized, silver-shelled gold nanospheres with 61 nm external and 31 nm core diameters (standard deviations: 6 and 3 nm, respectively) as well as 79 nm external and 51 nm core diameters (standard deviations: 9 and 6 nm, respectively) were also obtained from NanoComposix.

Table 4 Characteristics of the standard (nano)dispersions used during spICP-MS size calibration. Data in brackets indicate the standard deviation of the particle size according to the certificates

Particle type	Average diameter [nm]	Capping agent	Distributor
Gold NanoXact	28.8 (3.6); 39.3 (3.2); 61.3 (8.7); 75.4 (9.5)	Tannic acid	Ted Pella
Gold Ultra Uniform	47.8 (1.8); 99.4 (3.0)	Polyethylene glycol	NanoComposix
Silver NanoXact	43.4 (3.2); 59.0 (5.0); 82.1 (5.5); 95.7 (10.2)	Tannic acid	Ted Pella
Silica NanoXact	277 (12); 386 (11); 518 (20)	—	NanoComposix

---

Before dilution and also directly before aspiration into the ICP-MS, the dispersions were sonicated in an ultrasonic bath for 10 min (Bransonic 300, Ney, Danbury, Connecticut, USA) in order to minimize particle aggregation. Dispersions were diluted with trace-quality de-ionized labwater from a MilliPore Elix 10 device equipped with a Synergy polishing unit (Merck GmbH, Darmstadt, Germany) prior to analysis. The 99.996% purity argon gas used in the ICP-MS experiments was purchased from Messer Hungarogáz.

For the synthesis of hollow Au NPs, solid, 82.1 nm NanoXact Ag particles were used as templates. Hexadecyltrimethylammonium chloride (C₁₉H₄₂ClN, 50% solution in a 3 : 2 mixture of 2-propanol and water), gold(III) chloride trihydrate (HAuCl₄·3H₂O, ≥99.9%), as well as all analytical grade chemicals used for the synthesis of Stöber SiO₂ particles were obtained from Sigma Aldrich (Merck GmbH, Darmstadt, Germany). For synthesis, all chemicals were used without any further purification and the stock solutions were freshly prepared using trace-quality de-ionized labwater.

3. Results and discussion

3.1 Analysis of core–shell NPs

As initial test samples, core–shell NPs were used. Taking advantage of the elemental selectivity of ICP-MS analysis, NPs can be considered as hollow objects, if only the material in the shell is analyzed. This way, a virtual porosity can be assigned to them for the sake of this test. Using the certification data of the analyzed core–shell particles, the volume of the shell (Ag content) can be calculated by subtracting the volume of the core from the total volume of the nanoparticle:

The porosity can then be determined by dividing the calculated V_shell by the V_total volume devised from the certified diameter of the particles:

In our study, silver shelled gold NPs in two sizes were analyzed by spICP-MS. To quantify the amount of silver (shell) contained in the particles, spICP-MS size calibration was carried out using standard NP dispersions according to the method described earlier.²⁶ The volume of the shell can be thus calculated from the calibration plot, and hence, ϕ_spICP-MS can be determined by dividing the measured V_shell by the certified V_total. The comparison of theoretical (based on diameter data taken from the certificate of the commercial NPs) and measured formal porosity values is presented in Table 5. As can be seen, the formal porosity results determined by spICP-MS are in good agreement with theoretical values and the precision is also very good (<1RSD%). We would also like to add that by taking advantage of the selectivity of ICP-MS measurements, the porosity of different structural parts of complex NPs, made up of different elements, can also be separately investigated.

Table 5 Comparison of theoretical and experimental (sp-ICP-MS) porosity data for Au–Ag core–shell (virtually porous) test NPs. RSD% data are calculated by also considering the propagation of uncertainty from the particle size

D ext. [nm]	ϕ theor. [%]	spICP-MS
		ϕ [%]	RSD [%]
61	11.9	14.6	0.4
79	26.9	24.7	0.8

---

3.2 Analysis of hollow NPs

As opposed to core–shell NPs, hollow particles are actually porous nanoobjects with one large closed pore. For the purpose of our investigation, hollow Au NPs were synthesized by the galvanic replacement method (detailed in Section 2.2). After performing size calibration, the Au content of the shell of the hollow NPs can be obtained by spICP-MS. ICP-MS is not capable of determining the external diameter of a hollow NP (since it only detects the mass of the analyte shell), but the pore volume and ϕ_spICP-MS can be calculated by taking external diameter data from e.g. electron microscopy measurements. A reference TEM-based value for the porosity (ϕ_TEM) was obtained by using the external and pore diameter data taken from electron micrographs (see Section 2.2). The results of porosity analyses are summarized in Table 6. As it can be seen, the accuracy and precision of the spICP-MS result is decent again; however, the spICP-MS porosity is ca. 8% lower than its TEM counterpart. Here, it can be assumed that the purely imaging-based TEM result carries a positive error. The reason for this lies in the fact that TEM porosity determination assumes a fully compact (non-porous) Au shell, whereas it is known that the galvanic replacement process loosens the packing of the shell. This is because the synthesis sacrifices the material of the core (here: Ag) via oxidation and the silver ions diffuse out from the core into the liquid matrix through the Au shell.³⁴ In other words, ϕ_TEM for hollow particles does not take into account the void volumes in the shell (e.g. intrawall pores) and so it tends to underestimate the overall particle porosity. The porosity of the shell of hollow NPs alone was found in some studies to be as high as 30%.²⁰ At the same time, the spICP-MS signal is proportional to the actual number of Au atoms in the shell, thus ϕ_spICP-MS is much closer to the true value.

Table 6 Comparison of the results of porosity determination of hollow and porous NPs. RSD% data for the TEM and spICP-MS methods are calculated by also considering the propagation of uncertainty from the particle size

Sample	D ext. [nm]	Reference method			spICP-MS
		Method	ϕ [%]	RSD [%]	ϕ [%]	RSD [%]
Hollow Au	77.9	TEM	58.9	3.0	66.7	1.5
Stöber SiO2	373	SAXS	53.2	0.4	54.5	3.8
Stöber SiO2	447	SAXS	46.6	0.5	47.5	2.9
Stöber SiO2	464	SAXS	51.8	0.4	53.0	2.5

---

At this point we would like to emphasize that there are added benefits of using ICP-MS measurements for porosity determination in spite of the fact that the calculation requires the knowledge of the external particle diameter to be taken from electron microscopy images. One could even argue that the availability of TEM imaging data makes the spICP-MS measurements redundant for spherical, hollow particles. Apart from the above outlined reasons explaining the better accuracy of spICP-MS porosity determination for such particles, it can also be added that characteristic external diameter data of NPs can also be obtained from scanning electron microscopy (also useful for larger, submicron particles, as opposed to TEM) or dynamic light scattering (DLS) measurements. The latter also has the benefit of working directly in dispersion, as does spICP-MS.

3.3 Analysis of mesoporous particles

Mesoporous particles have an extensive pore structure, that is why they are often utilized as medical drug carriers and catalyst supports. In the present study, Stöber silica particles were synthesized in three sizes and investigated as representative samples for mesoporous NPs. spICP-MS porosity analysis was carried out on these particles in a similar manner to that on the other particles, whereas reference porosity data were obtained by a SAXS-based method (see Section 2.2). As can be seen in Table 6, the determined ϕ values were between 45 and 55% and there is a decent agreement (only <2% difference) between the spICP-MS and SAXS values. Please note that spICP-MS precision data also includes the standard deviation from SEM particle diameter determination. The SAXS technique has better precision owing to the much larger required amount of sample material (tens of milligrams as opposed to sub-micrograms), which provides better averaging. However, the limitation of the SAXS method is that it requires a dry powder sample and the knowledge of the particle density, which may not be known for newly synthesized complex NPs.

3.4 Estimation of the porosity working range

In spICP-MS, size detection limits (LOD_size) for NPs play a similar role as LOD values in ICP-MS for solutions. As it was alluded to earlier, the minimum detectable particle size values for spICP-MS are typically in the range of 10–40 nm (ref. 27) for pure metallic particles, depending on the abundance of the analyte isotope monitored. When working with alloy, oxide or other compound particles, the size detection limit values will substantially increase since the analyte only makes up a fraction of the particle mass. We postulate that the situation is similar in the case of porous particles, where the presence of pores decreases the mass of the analyte in a particle. Thus, if LOD_size and the overall porosity are known for a solid particle, the size detection limit can be applied to the porous particle as

For example, with our ICP-MS instrument we found a 232 nm LOD_size for solid commercial SiO₂ particles, whereas for our mesoporous Stöber silica particles, the calculation gives a 292 nm minimum detectable particle size (using an average, 50% porosity value, c.f.Table 6). A similar measurement and calculation also shows that the minimum detectable particle size for the hollow Au NPs increases to 22.8 nm from 18.1 nm for the solid Au NPs. As an example, Fig. 3 shows our experimentally recorded spICP-MS size calibration curves for solid and porous SiO₂ particles, and their slope is indeed in a nearly 2 : 1 ratio, as predicted. The slight deviation (1.92 : 1) is caused by the fact that the porosity of the silica particles was not exactly the same 50% in all cases, but varied slightly between 46.6 and 53.2%.

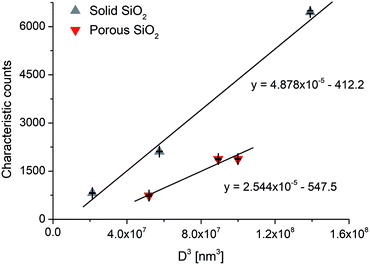Fig. 3 Single particle ICP-MS calibration curves for solid and porous SiO₂ particles. Error bars indicate the standard deviation from three parallel measurements.

In terms of percent porosity, the lower LOD is definitely determined by the precision of the measurements (1–2 absolute%), while the upper LOD basically depends on the overall mass of single nanoparticles. The mass detection limit can be simply calculated by multiplying the bulk density and the particle volume obtained from the LOD_size for solid particles. For silica it is 12.99 fg which, for example, enables the determination of porosity up to 80.5% for a 400 nm spherical particle. As the mass detection limit for Au NPs is 44.92 ag, the porosity of a gold NP with a size of 80 nm can be theoretically measured up to 98.8%.

The maximum accurately measurable particle size is limited in spICP-MS by the ability of the plasma to fully atomize and ionize the particle during the transition (residence) time in the plasma. In addition to the above factors, this limit is also influenced by the dynamic capabilities of the ICP-MS detection electronics, as well as the density and boiling point of the compound,³⁷ but generally it can be expected to shift upwards for porous NPs in a proportion similar to the shift of LOD_size. Upper particle limits in the literature range from ca. 1 to 1.5 μm for solid silica³⁸ and ca. 200 to 250 nm for solid Au particles^37,39 – depending on the RF power and plasma sampling depth settings, of course. In view of these and other data, it seems safe to state that spICP-MS porosity determination up to ca. 1–2 μm is possible. We would also like to add that the above estimations for LOD_size can also be used to obtain an upper limit value for porosity that can be measured in a given size of particle.

Since an important aspect of porosity determination is the pore size range in which the given method is capable of delivering porosity values, it is also relevant to assess the capabilities of the spICP-MS method in this regard. Obviously, spICP-MS is not capable of providing pore size distribution data as it only gives a single scalar value (signal response) for each NP, but the successful porosity determination of our Stöber silica particles and the Barrett–Joyner–Halenda³³ evaluation of their BET gas adsorption data can give us an indication about the pore size at which or above spICP-MS porosity measurement is possible. In the case of these particles, the average pore size was found to be ca. 2.3 nm (see Table 3), which suggests that spICP-MS porosity determination of NPs can be used in the whole mesoporous range (2–50 nm). Although pore detectability clearly also depends on the total pore volume, this minimum pore size definition is as valid as the next one in the world of porosity determination methods.^19,20 A further related benefit of our method is that not only open (connected and permeable) pores, but also closed ones are automatically included in the calculation.

3.6 Density determination

The simplest way to determine the density of materials is the Archimedes method. In the case of meso- or microporous particles, results from this method can easily carry error, as the applied wetting liquid may not be able to enter the pores due to their small size. It is also difficult to correct for interparticle (interstitial) voids in this classical method. At the same time, spICP-MS measurements can easily provide density values in these cases as well, directly in dispersion form, thus circumventing the need to dry the sample, as was described by Tadjiki et al.⁴⁰

Here, we would like to point out to that spICP-MS porosity data obtained by our method can be easily converted to density, if the bulk density is known,

ρ_particle = (1 − ϕ)ρ_bulk

As examples, we calculated the density of the hollow Au and SiO₂ NPs used in the present study, using a bulk density of 19.30 g cm⁻³ and 2.65 g cm⁻³ of Au and SiO₂, respectively.⁴¹ The results, which can be seen in Table 7, reveal that the spICP-MS density values determined this way agree quite well with the densities obtained by reference (TEM and SAXS) methods. Due to reasons already discussed, the porosity and hence density results for the hollow Au particles can be more accurately determined by spICP-MS than by TEM.

Table 7 Comparison of the results of porosity-based spICP-MS density determination of hollow and porous NPs

Sample	D ext. [nm]	Reference method		spICP-MS
		Method	ρ [g cm^−3]	ρ [g cm^−3]
Hollow Au	77.9	TEM	7.93	6.43
Stöber SiO2	373	SAXS	1.24	1.21
Stöber SiO2	447	SAXS	1.28	1.39
Stöber SiO2	464	SAXS	1.42	1.25

---

4. Conclusions

Porosity (and density) determination is of central importance for the characterization of nanoparticles. There are several established characterization techniques available for this task, but they all have limitations in terms of pore size range, accuracy, required sample amount and sample preparation, complexity of measurement, or their ability to account for closed pores, too. According to our results obtained with three different types of NPs of varying composition, size and porosity, our new, spICP-MS based porosity determination method was found to be quick, straightforward to use and to have accuracy and precision (e.g. 1–2 rel.%) comparable to those of the reference methods. It can be applied to nano- and sub-micron particles in the complete mesoporous pore range. The application to macroporous particles is also possible, but it is limited in size to particles that can be fully decomposed by the plasma (ca. 1–2 μm). The proposed new spICP-MS method provides an advantageous set of features that is unparalleled among the porosity determination methods. The overall porosity determined can also be used to calculate the density of the particles, a feat which is not easy to achieve from such a small amount of sample. It also has to be added that although we used particle standards for size calibration of the spICP-MS signal, which is the way we consider to be the most accurate, the spICP-MS literature also provides other calibration approaches based on standard solutions,^42,43 and thus not even the availability of suitable particle standards can hinder the application of this new method. Finally, we would also like to draw attention to the fact that our method is potentially also capable of measuring the porosity of non-spherical particles, considering e.g. the equivalent behaviour of spherical and rod-shaped nanoparticles during the size calibration process found earlier.²⁵ In addition, via capitalizing on the selectivity of ICP-MS measurements, the porosity of different structural parts of complex, nanocomposite NPs can also be investigated.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge the financial support received from the Ministry of Innovation and Technology (through project No. TUDFO/47138-1/2019-ITM FIKP) and the National Research, Development and Innovation Office (through projects No. FK_131446, PD_134282, PD_120877, K_120115, GINOP-2.3.2-15-2016-00013 “Intelligent materials based on functional surfaces – from syntheses to applications” and EFOP-3.6.2-16-2017-00005 “Ultrafast physical processes in atoms, molecules, nanostructures and biological systems”) of Hungary. A. Kéri also wishes to acknowledge the financial support from the ÚNKP-18-3 New National Excellence Program of the Ministry of Human Capacities project (Hungary).

References

1. R. Tantra, Nanomaterial characterization: An introduction, Wiley, 2016.
2. S. Mourdikoudis, R. M. Pallares and N. T. K. Thanh, Nanoscale, 2018, 10, 12871–12934.
3. M. Szekeres, J. Tóth and I. Dékány, Langmuir, 2002, 18, 2678–2685.
4. M. Kaasalainen, V. Aseyev, E. von Haartman, D. Ş. Karaman, E. Mäkilä and H. Tenhu, Nanoscale Res. Lett., 2017, 12, 74.
5. X. Jiao, S. V. Sokolov, E. E. L. Tanner, N. P. Young and R. G. Compton, Phys. Chem. Chem. Phys., 2017, 19, 64–68.
6. W. Yu, C. Batchelor-McAuley, Y.-C. Wang, S. Shao, S. M. Fairclough, S. J. Haigh, N. P. Young and R. G. Compton, Nanoscale, 2019, 11, 17791–17799.
7. N. C. Bell, C. Minelli, J. Tompkins, M. M. Stevens and A. G. Shard, Langmuir, 2012, 28, 10860–10872.
8. Y. Cai, Y. Chen, X. Hong, Z. Liu and W. Yuan, Int. J. Nanomed., 2013, 8, 1111–1120.
9. D. A. Kurdyukov, D. A. Eurov, D. A. Kirilenko, V. V. Sokolov and V. G. Golubev, Microporous Mesoporous Mater., 2018, 258, 205–210.
10. N. Yan, C. Xiao and Y. Kou, Coord. Chem. Rev., 2010, 254, 1179–1218.
11. T. S. Rodrigues, A. G. M. da Silva and P. H. C. Camargo, J. Mater. Chem. A, 2019, 7, 5857–5874.
12. J. E. Mondloch, E. Bayram and R. G. Finke, J. Mol. Catal. A: Chem., 2012, 355, 1–38.
13. A. Sápi, D. G. Dobó, D. Sebők, Gy. Halasi, K. L. Juhász, Á. Szamosvölgyi, P. Pusztai, E. Varga, I. Kálomista, G. Galbács, Á. Kukovecz and Z. Kónya, J. Phys. Chem. C, 2017, 121, 5130–5136.
14. R. Narayan, U. Y. Nayak, A. M. Raichur and S. Garg, Pharmaceutics, 2018, 10, 118.
15. R. Zhang, A. A. Elzatahry, S. S. Al-Deyab and D. Zhao, Nano Today, 2012, 7, 344–366.
16. B. Niu, X. Wang, K. Wu, X. He and R. Zhang, Materials, 2018, 11, 1910.
17. N. Dahal, I. A. Ibarra and S. M. Humphrey, J. Mater. Chem., 2012, 22, 12675–12681.
18. A. Sápi, Gy. Halasi, A. Grósz, J. Kiss, A. Kéri, G. Ballai, G. Galbács, Á. Kukovecz and Z. Kónya, J. Nanosci. Nanotechnol., 2019, 19, 436–441.
19. L. M. Anovitz and D. R. Cole, Rev. Mineral. Geochem., 2015, 80, 61–164.
20. Z. H. Chen, C. Kim, X.-B. Zeng, S. H. Hwang, J. Jang and G. Ungar, Langmuir, 2012, 28, 15350–15361.
21. C. Degueldre and P.-Y. Favarger, Colloids Surf., 2003, 217, 137–142.
22. M. D. Montaño, J. W. Olesik, A. G. Barber, K. Challis and J. F. Ranville, Anal. Bioanal. Chem., 2016, 408, 5053–5074.
23. A. Sápi, A. Kéri, I. Kálomista, D. G. Dobó, Á. Szamosvölgyi, K. L. Juhász, Á. Kukovecz and Z. Kónya, J. Anal. At. Spectrom., 2017, 32, 996–1003.
24. I. Kálomista, A. Kéri and G. Galbács, J. Anal. At. Spectrom., 2016, 31, 1112–1122.
25. I. Kálomista, A. Kéri, D. Ungor, E. Csapó, I. Dékány, T. Prohaska and G. Galbács, J. Anal. At. Spectrom., 2017, 32, 2455–2462.
26. A. Kéri, I. Kálomista, D. Ungor, Á. Bélteki, E. Csapó, I. Dékány, T. Prohaska and G. Galbács, Talanta, 2018, 179, 193–199.
27. S. Lee, X. Bi, R. B. Reed, J. F. Ranville, P. Herckes and P. Westerhoff, Environ. Sci. Technol., 2014, 48, 10291–10300.
28. E. Bolea-Fernandez, D. Leite, A. Rua-Ibarz, T. Liu, G. Woods, M. Aramendia, M. Resano and F. Vanhaecke, Anal. Chim. Acta, 2019, 1077, 95–106.
29. F. Laborda, E. Bolea and J. Jiménez-Lamana, Anal. Chem., 2014, 86, 2270–2278.
30. G. Porod, Kolloid-Z., 1951, 124, 83–114.
31. O. Glatter and O. Kratky, Small-Angle X-ray Scattering, Academic Press, 1982.
32. A. Jánosi, Z. Phys. B: Condens. Matter, 1986, 63, 375–381.
33. E. P. Barrett, L. G. Joyner and P. P. Halenda, J. Am. Chem. Soc., 1951, 61, 373–380.
34. J. Wang, L. Zhang, Y. Huang, A. Dandapat, L. Dai, G. Zhang, X. Lu, J. Zhang, W. Lai and T. Chen, Sci. Rep., 2017, 7, 1–9.
35. W. Stöber and A. Fink, J. Colloid Interface Sci., 1968, 26, 62–69.
36. V. M. Masalov, N. S. Sukhinina, E. A. Kudrenko and G. A. Emelchenko, Nanotechnol, 2011, 22, 275718.
37. W.-W. Lee and W.-T. Chan, J. Anal. At. Spectrom., 2015, 30, 1245–1254.
38. J. W. Olesik and P. J. Gray, J. Anal. At. Spectrom., 2012, 27, 1143–1155.
39. L. A. Rush, M. C. Endres, M. Liezers, J. D. Ward, G. C. Eiden and A. M. Duffin, Talanta, 2018, 189, 268–273.
40. S. Tadjiki, M. D. Montano, S. Assemi, A. Barber, J. F. Ranville and R. Beckett, Anal. Chem., 2017, 89, 6056–6064.
41. D. R. Lide, Handbook of Chemistry and Physics, CRC Press, 88th edn, 2008.
42. H. E. Pace, N. J. Rogers, C. Jarolimek, V. A. Coleman, C. P. Higgins and J. F. Ranville, Anal. Chem., 2011, 83, 9361–9369.
43. R. P. Lamsal, G. Jerkiewicz and D. Beauchemin, Microchem. J., 2018, 137, 485–489.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ja00020e

---