Open Access Article
Open Access ArticleThe accurate determination of number concentration of inorganic nanoparticles using spICP-MS with the dynamic mass flow approach†
Susana
Cuello-Nuñez
 a,
Isabel
Abad-Álvaro
a,
Isabel
Abad-Álvaro
 a,
Dorota
Bartczak
a,
Dorota
Bartczak
 a,
M. Estela
del Castillo Busto
a,
M. Estela
del Castillo Busto
 a,
David Alexander
Ramsay
a,
Francesco
Pellegrino
a,
David Alexander
Ramsay
a,
Francesco
Pellegrino
 b and
Heidi
Goenaga-Infante
b and
Heidi
Goenaga-Infante
 *a
*a
aLGC, Queens Road, Teddington, London, TW110LY, UK. E-mail: Heidi.Goenaga-Infante@LGCGroup.com
bChemistry Department, NIS Centre of Excellence, University of Torino, via P. Giuria 5, Torino, 10125, Italy
First published on 14th January 2020
Abstract
Methodology for the accurate determination of number concentration of inorganic nanoparticles (NP) by single particle inductively coupled plasma mass spectrometry (spICP-MS) using the novel dynamic mass flow (DMF) approach is systematically described. Using this method the determination of transport efficiency (TE) is achieved without the need for a reference nanomaterial. The impact of key parameters on the accuracy and uncertainty of the number concentration data obtained with this approach was evaluated. In particular the number of detected NP in the time scan is the major contributing factor to the overall measurement uncertainty. For Au NP of spherical shape with number based concentration in the range of 4.0 × 1012 to 2.0 × 1014 kg−1 (depending on the particle size) a relative expanded uncertainty (k = 2) of less than 10% was achieved. This reference methodology was also evaluated for the accurate determination of number concentration of more complex NP namely triethanolamine (TEA)-stabilised TiO2 NP, for which like-for-like NP reference materials are not available. Using a sample mass flow of 0.3578 g min−1 (with an associated uncertainty of 0.0002 g min−1, k = 1) the average transport efficiencies for Au NP (in trisodium citrate) and TiO2 NP (in TEA/NaOH) were very similar (7.57 ± 0.13% and 7.77 ± 0.22%, k = 1, respectively). Finally the number concentration values for both NP types agreed well with those obtained using particle tracking analysis (PTA), providing evidence for the good agreement between mass-based TE of the sample and NP-based TE with the newly proposed method.
Introduction
Nanotechnology is a rapidly growing science of producing and utilising objects within the size range of 1–100 nm.1 Nanomaterials (NM) are increasingly being used in innovative products manufactured by advanced industries and provide enhanced, unique properties of great commercial and societal value. The demand for high performance materials places increasingly stringent tolerances on the properties of NM.The EU recommendation for the definition of NM (2011/696/EU)2,3 for regulatory purposes states that the size distribution of a material should be presented as size distribution based on the number concentration (i.e. the number of objects within a given size range divided by the number of objects in total) rather than the mass fraction of nanoscale objects, since a small mass fraction may contain the largest number of particles. A number of methods capable of measuring particle number concentration in colloidal suspensions have been proposed,4,5 but neither SI traceable approaches, nor reference materials certified for NP number concentration have been made available so far. Such methods will help industry to ensure the quality and efficacy of products and compliance with legislation (e.g. cosmetics 1223/2009; novel food 2015/2283).
Since the introduction of spICP-MS by Degueldre,6 the technique has increasingly gained popularity due to its high sensitivity, elemental specificity and the development of much improved hardware with fast detectors and software able to handle large amount of data produced during spICP-MS experiments, even when using microsecond detection.7–9 In spICP-MS a very dilute suspension is introduced into the instrument, thus minimizing the possibility of more than one particle reaching the plasma at the same time. The plasma atomises and ionises the constituents of the particle, which are then quantified using the mass spectrometer. The characteristics of particles that can be measured include particle number concentration and mass concentration, as well as the mass of individual particles. For objects of known geometries the latter can be converted to particle diameter, also providing information about the number-based size distribution of particles in the sample. SpICP-MS, unlike other particle counting techniques,10 is also capable of measuring the dissolved fraction of the element within the same run provided that a fair distinction between the background and/or dissolved fraction and the nanoparticle fraction is achieved.7–9
In spICP-MS analysis, in order to establish a relationship between the number of particle events detected over a defined analysis window (time scan) and the number of nanoparticles in solution, the NP TE must be determined. The most popular methods used in the literature for calculation of the TE are the particle frequency and the particle size methods.11 However, both of these approaches rely on the use of nanoparticle reference materials (RM), which are very scarce and the few existing ones are neither like-for-like with NM used in real sample matrices, nor certified for the number concentration. Alternatively, efforts have been made to significantly increase the amount of sample entering the plasma by means of total consumption introduction systems12 with the purpose of avoiding the use of RM for TE estimation. Using such devices, Miyashita et al.12 achieved a TE of approximately 93%. Despite this relatively high TE value, the accurate determination of the correlation between the number of NP in a volume or mass solution and that detected by spICP-MS analysis is still a requirement. Another method which has been used for TE estimation purposes is the waste collection method,11 which has the advantage of not relying on NP RM. However, this method has been largely dismissed by the community due to reported biased results.7,11 The waste collection method is based on the collection and weighing of the waste separately and attempts to completely flush the system with air once the sample uptake pump is stopped to ensure that all liquid is collected. The sample vessel/liquid and waste vessel/liquid are weighed separately at the start and end. The bias is believed to be introduced by the high sensitivity of this indirect method to small recovery losses e.g. such driven by failure to completely flush the system.11
This work describes for the first time the development and validation of methodology for the accurate determination of number concentration of inorganic NP using spICP-MS without a nanoparticle RM. To achieve this a newly developed DMF approach is used for the TE determination. This method is based on the direct continuous measurement of the sample mass flow reaching the plasma and the mass flow of the sample uptake by the ICP-MS nebulisation system. Spherical Au NP were initially selected to demonstrate the proof of concept. The impact of critical parameters such as the number of NP detected in a time scan, TE, the sample uptake rate, sample dilution and the batch-to-batch variability on the accuracy and uncertainty of the number concentration data were systematically evaluated and a full measurement uncertainty budget was calculated. This reference methodology was further evaluated for the accurate determination of number concentration of TEA-stabilised TiO2 NP with non-spherical shape. For both Au NP and TiO2 NP, confirmation of the number concentration data obtained with the newly proposed method was achieved by comparison with alternative methodology, including PTA. For Au NP, such confirmation was also achieved by comparison with spICP-MS using the frequency method (against NIST RM 8013 Au NP) for TE estimation.
Experimental section
Reagents, solutions and materials
Au NP with nominal size of 30 nm and 100 nm were purchased from BBI International (Cardiff, UK). The particle manufacturer declared mean diameter of the particles of 30.2 nm and 100.6 nm, respectively, measured by transmission electron microscopy (TEM) and a concentration of 1.82 × 1011 mL−1 and 4.14 × 109 mL−1, respectively (estimated from UV-vis absorption). Ultrapure water (18.2 MΩ, 25 °C) was obtained from an Elga water purification unit (Elga, Marlow, Buckinghamshire, UK). A dissolved Au standard (with a mass fraction of 976 μg g−1 Au) from LGC Standards (VHG, Manchester, USA) and RM 8013 Au citrate NP (with nominal diameter of 60 nm and Au mass fraction of 51.86 μg g−1) and RM 8012 Au citrate NP (with nominal diameter of 30 nm and Au mass fraction of 48.17 μg g−1), both from NIST, Gaithersburg, USA were used. Further dilutions for dissolved and nanoparticulate Au were prepared in 1 mM trisodium citrate (Sigma-Aldrich, Gillingham, UK).TiO2 NP were obtained from the University of Torino (Italy) under the frame of the EMPIR nPSize project (improved traceability chain of nanoparticle size measurements).13 These particles with bipyramidal shape (Fig. S1†), had TEA as surface ligand.13 According to the manufacturer, they had an approximate size of 60 nm (lateral) × 40 nm (width), which leads to a theoretical equivalent sphere diameter of 39 nm. The stock suspension was in 1.2% (m/m) TEA (Sigma-Aldrich) and 0.2 g L−1 NaOH (Sigma-Aldrich). Stock standard solutions of 1000 mg kg−1 Ti and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mg kg−1 Ca (Romil Ltd., Cambridge, UK) were used. Further dilutions for dissolved Ti and Ca and nanoparticulate Ti were prepared in 0.012% (m/m) TEA and 2 mg L−1 NaOH.
000 mg kg−1 Ca (Romil Ltd., Cambridge, UK) were used. Further dilutions for dissolved Ti and Ca and nanoparticulate Ti were prepared in 0.012% (m/m) TEA and 2 mg L−1 NaOH.
Instrumentation
Number concentration measurements of inorganic particles using spICP-MS were performed with an Agilent 8900 ICP-MS/MS instrument with a conventional MicroMist nebulizer and cooled (2 °C) spray chamber. The instrument was tuned daily for optimum signal intensity and stability with typical operating parameters provided in Table S1.† The instrument was equipped with the MassHunter 4.3 (version: G72dC C.01.03) software and microsecond detection capability, enabling analysis in sp mode. Measurements in fast transient analysis (TRA) mode were carried out using a dwell time of 100 μs per point, with no settling time between the measurements and using the newly developed Single Particle Application Module of the ICP-MS MassHunter software (G5714A). Total acquisition time was fixed at 60 s for all analyses.Gold (197Au) was measured in no gas mode. The ICP-MS conditions were optimised to obtain maximum 197Au sensitivity with a minimum background contribution using 1 μg kg−1 ionic gold solution.
The most abundant Ti isotope, 48Ti was measured in MS/MS mass shift mode, using a reaction cell containing oxygen (O2) and hydrogen (H2) to resolve the polyatomic and isobaric interferences. The first quadrupole (Q1) was set to m/z 48, while the second quadrupole (Q2), separated from Q1 by the octopole reaction cell, was set to m/z 64 (reaction product ion 48Ti16O+). The cell gas conditions and the axial acceleration function were carefully optimised based on the detector response factor to 1 μg kg−1 of ionic Ti in order to get the best sensitivity with a minimum background contribution.
PTA was used as an alternative technique for the analysis of the number concentration of Au NP and TiO2 NP. For this, measurements and analysis of the recorded videos were performed with a NanoSight instrument (NS500, Malvern Panalytical) equipped with a light source (violet diode laser, 405 nm, power < 60 mW), electron multiplying charge coupled device (EMCCD) camera and NTA3.2 software.
Procedures
Measurement of NP by spICP-MS
Vials containing Au NP or TiO2 NP solutions were gently inverted several times to ensure homogeneity of the suspension. Prior to analysis, NIST RM 8013, 30 nm and 100 nm Au NP solutions were gravimetrically diluted using an analytical balance (4-decimal places) approximately 1.1 × 106, 4.5 × 106 and 1.5 × 105 times, respectively so that the working solutions had a final concentration of 2.65 × 107 kg−1, 4.04 × 107 kg−1 and 2.76 × 107 kg−1. The aforementioned final solutions were thoroughly shaken manually prior to analysis.For Au NP measurements, the instrument was cleaned with 1% (v/v) aqua regia solution followed by ultrapure water after each sample. 2.5 × 108-fold diluted suspensions of TiO2 NP were prepared in 0.012% (m/m) TEA containing 2 mg L−1 NaOH by accurately weighing (4-decimal places) aliquots of the stock suspension to achieve a final concentration of approximately 4.32 × 107 kg−1. After dilution, TiO2 suspensions were bath sonicated for 3 min. Within a measurement batch, three independent sample preparations were measured 5 times under repeatability conditions. Ionic Au and Ti solutions were prepared to matrix match the NP suspensions.
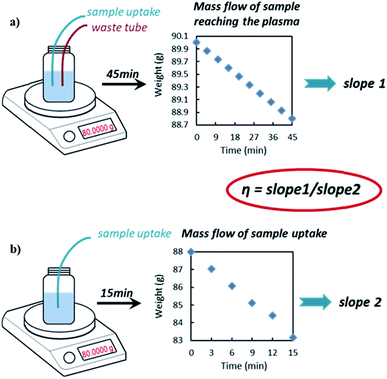
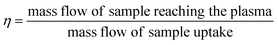 | (1) |
This procedure was performed at the beginning and at the end of each analysis day. Once the TE was determined samples were measured. Due to possible fluctuations in the uptake pump rate during the session, and in order to improve the accuracy of the results, the mass of real sample uptake was also monitored for each measurement, placing the sample vials on top of the balance and recording the real time weighting during the sample acquisition time. Nanoparticle number concentration (CNP) was derived from eqn (2), reported elsewhere:14
| NNP = ηnebQsamtiCNP | (2) |
Measurements of NP by PTA
NP suspensions for PTA analysis were prepared following the protocol previously described for spICP-MS. Prior to analysis, 30 nm and 100 nm Au NP samples were diluted 500 and 23 times, respectively. In the case of TiO2 NP, a 5 × 104-fold dilution was carried out. For all samples, three independent preparations were measured on three separate days, giving a total of 9 independent preparations. Performance of the instrument was checked daily with Au NP (NIST RM 8013) diluted approximately 50 times with 1 mM trisodium citrate.The instrument was switched on at least 30 min before the measurements. Before loading the sample, the gasket was cleaned with 0.1 μm filtered 10% (v/v) MicroSol (Anachem), whilst the top plate and prism holder were cleaned with 0.1 μm filtered 10% (v/v) Microsol followed by 0.1 μm filtered 70% (v/v) ethanol (Sigma-Aldrich) in water. All parts were rinsed with 0.1 μm filtered ultrapure water and dried with compressed air. The temperature was set and maintained at 25 °C throughout the measurements. In PTA, the particles are visualised in a confined and illuminated volume. Counting the particles in this volume translates directly to particle number-concentration. The PTA makes use of a fixed field of view (approximately 100 μm by 80 μm) illuminated by a beam approximately 10 μm in depth. By knowing the measurement volume, which is instrument specific, the number concentration is determined by counting all objects in the field of view. Movies were recorded over 60 s, with 15 s equilibration time prior to each measurement. For all samples 5 videos were recorded per sample under repeatability conditions. Camera settings were optimised manually. For the analysis of the recorded videos the detection threshold was selected manually, whilst other parameters were set to automatic. A minimum of 2000 completed tracks were recorded per video. The obtained data were collated and further processed with Excel. The values shown are the average of n = 45 measurements with the corresponding measurement uncertainty. More details on the PTA measurements are summarised elsewhere.10
Results and discussion
Optimisation of the spICP-MS parameters for number concentration determination of Au NP
Different parameters that can affect the accuracy of the number concentration data (as per eqn (2)) and its associated uncertainty were carefully optimised.Special attention was paid to the choice of sample diluent. Diluting the particles in a citrate solution was reported15 to achieve better recoveries of the expected nanoparticle number concentration than those obtained for 60 nm Ag NP using water as the diluent. The same paper15 reported that the citrate-based suspensions for the 80 and 100 nm NP showed lower recoveries. This paper, however, does not provide further evidence for NP destabilisation (e.g. size distribution histograms) in support of their recovery data. In the present work, the use of 1 mM trisodium citrate was found to keep the particles stable (no particle agglomeration was observed) with particle number concentration recoveries in the range of 93% to 100%. Such recoveries are calculated by comparison with the expected number concentration of the NIST RM 8013 Au NP, calculated using its Au mass fraction, size (TEM value) and density.
In support of this, Fig. 2 shows the particle size distribution histogram, obtained by PTA, of NIST RM 8013 Au NP suspended in 1 mM trisodium citrate in comparison to that obtained for particles diluted in water. PTA was used for this purpose since the sample dilution factor required for this technique is smaller than that for spICP-MS, offering higher potential for agglomerate detection. It can be seen from the histogram in Fig. 2, that diluting the Au NP in water may help destabilise them and promote agglomeration. This led to recoveries in terms of NP concentration of around 60% by PTA.
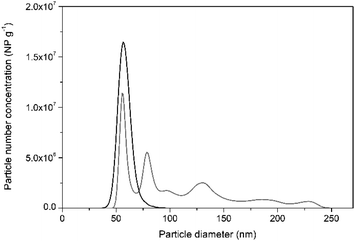 | ||
| Fig. 2 Representative PTA particle size distribution histograms of NIST RM 8013 prepared in water (grey line) and in 1 mM trisodium citrate (black line) after 50-fold dilution. | ||
Under high dilution factors, as required by the spICP-MS technique, citrate ions which are bound to the particle surface only electrostatically might dissociate, favouring a constant equilibrium between the citrate ions bound to the particles and those free in solution.
There are parameters such as the acquisition time and the uptaken sample mass flow in eqn (2) that can be measured with high accuracy. For these reasons, next steps focused on the optimisation of the number of detected particles and the TE.
In order to optimise the number of particles detected in time scan (particle counting), several parameters have to be taken into account, including instrument dwell time, threshold set up between the background signal and the particle events, and the sample dilution factor. Since the occurrence of multiple NP events depends on the particle number concentration and the dwell time (with pulse events working at millisecond dwell times, and transient signals when working at microsecond dwell times), the concentration should always be carefully optimised, regarding the instrument and the experimental conditions used, in order to minimise the occurrence of such multiple events.14
Following the approach recommended by Laborda's group,14 the optimal dilution factors for 30 nm and NIST RM 8013 60 nm Au NP (4.5 × 106 and 1.1 × 106, respectively) were selected to achieve an optimal NP flux and therefore, reduce impact of NP counting on the overall uncertainty with minimal formation of NP double and triple events. Theoretical and experimental number concentration calibration curves are represented in Fig. S2† by plotting the number of pulses versus the particle number concentration of NIST RM 8012. In the case of the theoretical calibration curve, the number of pulses was derived from eqn (2). In this graph, an evident curvature related to the occurrence of two or more nanoparticle events can be observed experimentally at high particle number concentrations. By using a dwell time of 100 μs and under the experimental conditions used along this work, the linear range was up to 6 × 107 kg−1. The final concentrations of NP in the working solutions (after dilution) were 4.04 × 107 kg−1 and 2.65 × 107 kg−1 for 30 nm and NIST RM 8013, respectively. For these concentrations, which are within the optimal concentration or linear range, the recoveries in terms of particle number concentration were between 97% and 102%. In the case of 100 nm particles the optimal dilution factor was found to be ∼1.5 × 105, resulting in a final concentration of NP in the working solution of 2.76 × 107 kg−1.
Two different dwell times (one shorter and one longer than the particle event of around 0.5 ms)12 were investigated. Results of the comparison of 100 μs and 3 ms dwell times for the detection of 30 nm Au NP are shown in Fig. S3.† This figure demonstrates that much better separation of NP from the background signal is achieved with the shortest dwell time. This agrees with the results reported by Abad-Álvaro et al.,14 showing that dwell times in the microsecond range help reduce significantly the contribution of the background and/or the presence of dissolved species in comparison with those in the millisecond range. With shorter dwell times smaller background equivalent diameters (BED) can be achieved.
The other parameter considered for the optimization was the particle detection threshold, which is defined by the cut-off between background counts and counts arising from particle events.16 For NP with size closer to the background the position of the detection threshold will have higher impact on the overall measurement uncertainty, therefore this parameter needs to be carefully considered for the accurate determination of the number concentration of NP. With the instrumental set-up used in this study, the background signal was well separated from the particle events (even for the smallest particles of around 30 nm diameter, see Fig. S3a†), nonetheless the impact of this parameter on the overall measurement uncertainty was evaluated.
A basic approach for the discrimination of the NP events over the baseline produced by the presence of the background/dissolved analyte is the application of n-sigma (n-σ) criteria, where σ is the standard deviation of the baseline. Commonly, coefficients of 3 (ref. 17) and 5 (ref. 18) are applied, although 7σ (ref. 19) and 8σ (ref. 20) criteria have also been used by some authors. Depending on the criterion adopted, the number of false positives can be more or less significant.16 In the current work, the effect of threshold selection using different sigma criteria (3σ, 5σ, 7σ, 8σ and 10σ) on the threshold selection contribution to the measurement uncertainty was investigated and no significant contribution (<0.1%) was observed. As discussed above, this is likely due to the significant gap between ionic and NP obtained when using 100 μs dwell time with our ICP-MS instrumentation.
Dynamic mass flow method for the determination of TE
The NP TE was estimated by using the newly developed DMF method as described earlier in this paper. Using this approach, the sample waste is continuously returned to the sample vessel (i.e. no separate waste collection) and the difference in the weight of the vessel due to simultaneous sample uptake and waste addition is recorded (as weight of sample reaching the plasma) by continuous weighing during the experiment over a time period while the system is in equilibrium (dynamic approach). Hence, we have a continuous and direct measurement of such difference with multiple data points over time. This is expected to greatly improve the precision and reduce bias by obviating the need to flush the system before collecting and weighing the waste separately as per waste collection method.11 Also the weight of sample uptake (sample pumped into the ICP) is determined on-line by weight in real time with this new method.The results of the DMF method, described in detail here for the first time, were compared with those of the frequency method, which is commonly used in spICP-MS analysis and can be found in ISO standards.21–23 Commercially available citrate capped Au spherical particles, with different sizes, were chosen as ‘model samples’ due to the availability of like-for-like Au NP reference materials, which are also spherical (NIST RM series). The summary of the obtained particle concentration values is shown in Table 1. The obtained values, with the DMF method, were in a very good agreement with the values obtained using the frequency method against NIST RM 8013.
| Au NP sample | Particle number-based concentration; mean ± U, k = 2 (kg−1) | ||
|---|---|---|---|
| spICP-MS: dynamic mass flow method | spICP-MS: particle frequency method | PTA | |
| 30 nm | (1.80 ± 0.18) × 1014 (10.0%) | (1.90 ± 0.31) × 1014 (16.4%) | (1.78 ± 0.16) × 1014 (8.9%) |
| 100 nm | (4.10 ± 0.39) × 1012 (9.5%) | (4.35 ± 0.68) × 1012 (15.6%) | (4.31 ± 0.47) × 1012 (10.9%) |
The main advantage of the DMF method over the frequency method is that it does not require a RM to determine the TE, which makes this approach quite promising due to the fact that NP RM certified for the number concentration are not currently available. Moreover, number concentration data obtained with methodology based on the DMF approach are traceable to the SI through gravimetric determination of the sample mass flow, gravimetric preparation of NP sample dilutions and gravimetric determination of the NP TE. Weighing operations are traceable to the SI through the use of calibrated weights traceable to the National Primary Standard of mass via the UK National Physical Laboratory (NPL). They are also traceable to the unit 1.24
In order to investigate whether or not the mass-based TE determined with this approach agrees well with the NP-based TE, the methodology proposed by Tuoriniemi et al.25 was revisited. These authors proposed to measure both the concentration in the input sample and the sample collected in the waste to check for possible analyte partitioning between the sample fraction reaching the plasma and the fraction removed through the waste. The likely to occur contamination of the waste solution and the large errors associated with the use of dissolved ion intensities to investigate NP behaviour made the verification of analyte partitioning with this indirect method a very difficult task. Therefore, comparison of the number concentration data obtained with the DMF approach with that of other methods including PTA and spICP-MS with the frequency approach was alternatively used for this purpose. The results of this comparison are summarised in Table 1. As shown in this table, the number concentration value agreed well with those obtained using PTA and spICP-MS with the frequency approach, providing evidence for the good agreement between mass-based TE of the sample and NP-based TE. It is important to note that in this work, a cooled spray chamber (2 °C) was used. This helps to reduce the amount of water vapor (produced from evaporation of water from aerosol in the spray chamber) entering the plasma, thus minimising the contribution of this source of error to the uncertainty of the mass-based TE.
Using a sample mass flow of 0.3578 g min−1 (with an uncertainty of 0.0002 g min−1, k = 1) the average TE for Au NP (in 1 mM trisodium citrate) was found to be 7.57% (with an uncertainty of 0.13% k = 1) using the DMF method. This agreed well with that obtained for the same Au NP using the frequency method (7.32% with an uncertainty of 0.51%, k = 1) against NIST RM 8013.
It is important to note that under the frame of the EU EMPIR project Innanopart, the number concentration data obtained for Au NP of very similar characteristics with spICP-MS and the DMF was demonstrated to agree well with that of reference techniques like Small Angle X-ray Scattering (SAXS).10 This paper,10 does not provide details on the systematic development and characterisation of the methodology discussed in the present work but describes a comprehensive comparison of a large set of data from several techniques developed by the EU consortium.
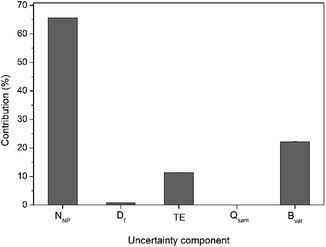
For calculation of the overall measurement uncertainty, on the particle number concentration, three independent batches each including five independent subsample replicates were run on three different days and the Eurachem CITAC guidelines were followed.26 The uncertainty budget was calculated considering different parameters that can affect the accuracy of the number concentration data. They include the number of NP detected in the time scan, sample dilution, TE, sample mass flow in time scan and the batch-to-batch variability. A detailed breakdown of the measurement uncertainty budget is given in Table S2,† with an example for 30 nm Au NP shown in Fig. 3. Also, for 30 nm Au NP a further breakdown of uncertainty contribution for both the number of particles detected and the TE is shown in Table S3.† The main factor contributing to the overall measurement uncertainty in case of the DMF method is the number of particles detected in time scan (65% of the overall uncertainty), followed by the batch-to-batch variability (22%) and the transport efficiency (12%).
ANOVA analysis and t test of the nine independent slope sets used to calculate the TE showed no significance difference. Two slopes (slope 1 and slope 2) were determined each day at the beginning and the end of a sample batch as per Fig. 1 and eqn (1), whilst three additional slope sets come from an independent day, on which only the variability in the slopes measurement was investigated. The average values for slope 1 (mass flow of sample reaching the plasma) and slope 2 (mass flow of sample uptake) were 0.0269 g min−1 (with an uncertainty of 0.0003 g min−1, k = 1) and 0.3554 g min−1 (with an uncertainty of 0.0003 g min−1, k = 1), respectively. The within day variability of slope 1 accounted for approximately 98% of the TE contribution to the overall measurement uncertainty (see Table S3†).
As also shown in Table S3,† the main contributing factor to the uncertainty associated with the number of particles detected was the between day variability in particle counts (accounted for approx. 99.9% of the NNP contribution to the overall measurement uncertainty). Conversely, using the particle frequency method (Table S2†), the main contribution factor was found to be the TE determination (approximately 64% of the overall uncertainty). The latter is in agreement with the report by Murphy et al.23 on the characterisation of Ag NP by spICP-MS following the particle size and the particle frequency methods for the TE determination. This is likely due to the fact that TE calculation using the particle size and frequency methods relies on the use of a RM for which the uncertainty associated to its characteristics such as size, mass concentration and density have to be accounted for in the calculation of the measurement uncertainty associated with the number concentration data produced by spICP-MS.
Application to the dynamic mass flow method to the determination of number concentration of non-spherical TiO2 NP
In order to evaluate the feasibility of the methodology based on the DMF approach for the accurate determination of number concentration of more complex NP for which like-for-like NP RM are not available, TEA-stabilised TiO2 NP were selected. Instrumental parameters and cell gas conditions were firstly optimised using as starting conditions those reported elsewhere.27 Two reaction gases were studied, oxygen (O2) and ammonia (data not shown). Finally, a cell gas containing 20% O2 and 4.5 mL min−1 H2 was selected to achieve maximum selectivity whilst fit for purpose signal-to-noise ratio for the most abundant Ti isotope (m/z 48). Q1 was set to m/z 48, only allowing 48Ti+ and any other on-mass interferences to enter the cell. Then, Q2 (placed after the collision/reaction cell) was set to m/z 64, allowing the product ion 48Ti16O+ to reach the detector. In order to check the possible interference of 48Ca with the product ion 48Ti16O+ at m/z 64 when it reacts with O2 to form 48Ca16O+, different concentrations of dissolved Ca (from 0 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μg kg−1) were added to 1 μg kg−1 of dissolved Ti; a recovery of 110% was obtained for a Ca/Ti ratio of 10
000 μg kg−1) were added to 1 μg kg−1 of dissolved Ti; a recovery of 110% was obtained for a Ca/Ti ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300. As TiO+ does not react with H2 in the same way as CaO+ (which is transformed to CaOH+), the addition of H2 to the O2 reaction gas allowed elimination of the Ca interference.27 The axial acceleration feature of the 8900 ICP-MS/MS instrument was also investigated for the selective detection of TiO2 NP. This feature accelerates the product ions generated in the collision/reaction cell, leading to an increase in the sensitivity of the product ions. This parameter was key to achieving resolution of the TiO2 NP from the background and, therefore, their selective detection (Fig. S5a and b†). An axial acceleration voltage of 1.5 V was selected as optimal for the analysis of TiO2 NP using mass-shift mode with 20% O2 and 4.5 mL min−1 H2 cell gas. Signal distribution histograms obtained for TiO2 NP under these conditions and dwell times of 100 μs and 3 ms are shown in Fig. S5.† Again, as previously shown for Au NP, the use of shorter dwell times led to a better discrimination between the background and the nanoparticle distributions (Fig. S5b and c†). It is worth noting that the equivalent diameter of the bipyramidal TiO2 NPs used in this paper is significantly smaller than that of the TiO2 NPs investigated elsewhere27 and therefore, achieving selectivity in NP detection required a systematic optimisation of the ICP-MS conditions as described above.
300. As TiO+ does not react with H2 in the same way as CaO+ (which is transformed to CaOH+), the addition of H2 to the O2 reaction gas allowed elimination of the Ca interference.27 The axial acceleration feature of the 8900 ICP-MS/MS instrument was also investigated for the selective detection of TiO2 NP. This feature accelerates the product ions generated in the collision/reaction cell, leading to an increase in the sensitivity of the product ions. This parameter was key to achieving resolution of the TiO2 NP from the background and, therefore, their selective detection (Fig. S5a and b†). An axial acceleration voltage of 1.5 V was selected as optimal for the analysis of TiO2 NP using mass-shift mode with 20% O2 and 4.5 mL min−1 H2 cell gas. Signal distribution histograms obtained for TiO2 NP under these conditions and dwell times of 100 μs and 3 ms are shown in Fig. S5.† Again, as previously shown for Au NP, the use of shorter dwell times led to a better discrimination between the background and the nanoparticle distributions (Fig. S5b and c†). It is worth noting that the equivalent diameter of the bipyramidal TiO2 NPs used in this paper is significantly smaller than that of the TiO2 NPs investigated elsewhere27 and therefore, achieving selectivity in NP detection required a systematic optimisation of the ICP-MS conditions as described above.
The TE of TiO2 NP was determined using the novel DMF method as described in this paper. Using a sample mass flow of 0.3578 g min−1 (with an associated uncertainty of 0.0002 g min−1, k = 1) the average TE obtained was 7.77% with an associated uncertainty of 0.22% (k = 1). This agrees well with the TE reported above for Au NP using the same sample mass flow. The number concentration data obtained with this method was compared with that obtained using PTA. The results of this comparison are summarised in Table 2. As can be seen, there is a good agreement between the number concentration values obtained by both methodologies, providing evidence for the good agreement between mass-based TE of the sample and NP-based TE with the DMF approach. Again, the number of NP detected in time scan (followed by the TE and batch-to-batch variability) was found to be the main contributing factor to the overall measurement uncertainty.
| Particle number-based concentration; mean ± U, k = 2 (kg−1) | ||
|---|---|---|
| spICP-MS: dynamic mass flow method | PTA | |
| TiO2 NP | (1.08 ± 0.11) × 1016 (10.1%) | (1.24 ± 0.19) × 1016 (15.6%) |
Conclusions
Methodology for SI traceable determination of particle number concentration by reference NM-free spICP-MS has been developed and characterised for the first time. It is based on a newly described DMF approach for the determination of TE. Such reference methodology although somewhat laborious (due to the consecutive measurements of mass flows), it is invaluable for validation of other laboratory methods for NP number concentration.10 It is also invaluable for the characterisation of quality control nanomaterials that can be used with the frequency method in a more targeted manner for a range of applications. Applicability to not only highly stable, spherical/nearly spherical and monodisperse/narrowly dispersed Au NP suspensions (for which NP RM have become available) but also more complex TiO2 NP (for which like-for-like NP RM are unavailable) has been demonstrated. The impact of key parameters on the accuracy and uncertainty of the number concentration data by the newly proposed approach was systematically evaluated. The number of detected NP in the time scan was the major contributing factor to the overall measurement uncertainty. The results obtained by spICP-MS using the methodology proposed in the present study were in good agreement with the number based concentration data obtained by confirmatory methods based on PTA as an independent technique and spICP-MS using the particle frequency approach, the latter only for Au NP.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work described in this manuscript was supported by EURAMET as part of the European Metrology Research Programme for Innovation and Research (EMPiR) projects 14IND12 Innanopart “Metrology for innovative nanoparticles” and 17NRM04 nPSize “Improved traceability chain of nanoparticle size measurements”. The authors thank Panayot Petrov from LGC for useful advice with regards to the TE determination using the DMF approach. Alexander G. Shard from NPL and Mike Sargent are gratefully acknowledged for providing very useful comments on the manuscript. Valter Maurino from the University of Torino (Italy) is acknowledged for his contribution to the synthesis and characterization of the TiO2 NP. Nicholas Dixon from Smith and Nephew, UK is acknowledged for liquid TEM measurements of TiO2 NP. This piece of science is dedicated to Gary, who has been an inspirational leader to several generations of scientists across the globe.References
- C ISO/TS 80004-2:2015.
- EU, Commission recommendation of 18 October 2011 on the definition of nanomaterial (2011/696/EU), Off. J. Eur. Communities: Legis., 2011a, 275, 38–40 Search PubMed.
- An overview of concepts and terms used in the European Commission's definition of nanomaterial (JRC Science for policy report), available at: https://publications.jrc.ec.europa.eu/repository/bitstream/JRC113469/kjna29647enn.pdf, accessed 3 December 2019.
- J. A. Gallego-Urrea, J. Tuoriniemi and M. Hassellöv, TrAC, Trends Anal. Chem., 2011, 30, 473–483 CrossRef CAS.
- E. Weatherall and G. R. Willmott, Analyst, 2015, 140, 3318–3334 RSC.
- C. Degueldre and P. Y. Favarger, Colloids Surf., 2003, 217, 137–142 CrossRef CAS.
- A. R. Montoro Bustos and M. R. Winchester, Anal. Bioanal. Chem., 2016, 408, 5051–5052 CrossRef PubMed.
- D. Mozhayeva and C. Engelhard, J. Anal. At. Spectrom., 2020 10.1039/c9ja00206e.
- F. Laborda, E. Bolea and J. Jimenez-Lamana, J. Anal. Chem., 2014, 86, 2270–2278 CAS.
- A. Schavkan, C. Gollwitzer, R. Garcia-Diez, M. Krumrey, C. Minelli, D. Bartczak, S. Cuello-Nuñez, H. Goenaga-Infante, J. Rissler, E. Sjöström, G. B. Baur, K. Vasilatou and A. G. Shard, Nanomaterials, 2019, 9, 502–522 CrossRef PubMed.
- H. E. Pace, N. J. Rogers, C. Jarolimek, V. A. Coleman, C. P. Higgins and J. F. Ranville, Anal. Chem., 2011, 83, 9361–9369 CrossRef CAS PubMed.
- S. Miyashita, H. Mitsuhashi, S. Fujii, A. Takatsu, K. Inagaki and T. Fujimoto, Anal. Bioanal. Chem., 2017, 409, 1531–1545 CrossRef CAS PubMed.
- L. Mino, F. Pellegrino, S. Rades, J. Radnik, V. D. Hodoroaba, G. Spoto, V. Maurino and G. Martra, ACS Appl. Nano Mater., 2018, 1, 5355–5365 CrossRef CAS.
- I. Abad-Álvaro, E. Peña-Vázquez, E. Bolea, P. Bermejo-Barrera, J. R. Castillo and F. Laborda, Anal. Bioanal. Chem., 2016, 408, 5089–5097 CrossRef PubMed.
- S. Gschwind, M. L. Aja Montes and D. Gunther, Anal. Bioanal. Chem., 2015, 407, 4035–4044 CrossRef CAS PubMed.
- F. Laborda, A. C. Gimenez-Ingalaturre, E. Bolea and J. R. Castillo, Spectrochim. Acta, Part B, 2019, 159, 105654–105666 CrossRef CAS.
- F. Laborda, J. Jimenez-Lamana and E. Bolea, J. Anal. At. Spectrom., 2013, 28, 1220–1232 RSC.
- J. Tuoriniemi, G. Cornelis and M. Hassellöv, Anal. Chem., 2012, 84(9), 3965–3972 CrossRef CAS PubMed.
- J. Navratilova, A. Praetorius, A. Gondikas, W. Fabienke, F. Kammer and T. Hofmann, Int. J. Environ. Res. Public Health, 2015, 12, 15756–15768 CrossRef CAS PubMed.
- J. Tuoriniemi, G. Cornelis and M. Hassellöv, Anal. Chem., 2012, 84, 3965–3972 CrossRef CAS PubMed.
- M. D. Montaño, H. R. Badiei, S. Bazargan and J. F. Ranville, Environ. Sci.: Nano, 2014, 1, 338–346 RSC.
- ISO/TS 19590:2017.
- K. E. Murphy, J. Liu, A. R. Montoro Bustos, M. E. Johnson and M. R. Winchester, Characterization of nanoparticle suspensions using single particle inductively coupled plasma mass spectrometry, available at: http://dx.doi.org/10.6028/NIST.SP.1200-21, accessed 16 August 2018.
- The International System of Units (SI), 8th edn, available at: https://www.bipm.org/utils/common/pdf/si_brochure_8_en.pdf, accessed 16 August 2018 Search PubMed.
- J. Tuoriniemi, G. Cornelis and M. J. Hassellöv, J. Anal. At. Spectrom., 2014, 29, 743–752 RSC.
- EURACHEM, Quantifying Uncertainty in Analytical Measurement, London, UK, 3rd edn, 2012, ISBN 978-0-948926-30-3 Search PubMed.
- Accurate Determination of TiO2 Nanoparticles in Complex Matrices using the Agilent 8900 ICP-QQQ, available at: https://www.agilent.com/cs/library/applications/Copy%20of%208900_ICP-MS_5991-<?pdb_no 8358?>8358<?pdb END?>_TiO2_nanoparticles.pdf, accessed 2 December 2019.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ja00415g |
| This journal is © The Royal Society of Chemistry 2020 |