Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Soft X-ray laser ablation for nano-scale chemical mapping microanalysis
Davide
Bleiner
 *ab,
Libor
Juha
*ab,
Libor
Juha
 cd and
Di
Qu
cd and
Di
Qu
 ab
ab
aSwiss Federal Laboratories for Materials & Technology (Empa), Überlandstrasse 129, CH 8600 Dübendorf, Switzerland. E-mail: davide.bleiner@empa.ch
bUniversity of Zurich, Dept. of Chemistry, Winterthurerstrasse 190, CH 8057 Zurich, Switzerland
cInstitute of Physics of the Czech Academy of Sciences, Dept. of Radiation and Chemical Physics, Na Slovance 2, 182 21 Prague, Czech Republic
dInstitute of Plasma Physics of the Czech Academy of Sciences, Laser Plasma Dept., Za Slovankou 3, 182 00 Prague, Czech Republic
First published on 8th April 2020
Abstract
Laser-assisted microanalysis offers the advantage of determining the spatially resolved compositions in 3D. Scanning a material with a sequence of sampling laser pulses and acquiring online the related spectra allow one to map the lateral and depth distribution of elements and molecules. However, the requirement to analyse smaller and smaller length-scales is challenged by focal diffraction as well as reduction of sensitivity at the nano-scale. Electron-based microprobes still offer unmatched spatial resolution. Disruptive improvements in laser technology are however demonstrated utilizing recently self-developed extreme ultraviolet or soft X-ray lasers. Firstly, a significant enhancement of the resolution is accomplished thanks to a much shorter wavelength, with respect to state-of-the-art commercial lasers. Furthermore, as the most innovative aspect, the sampling efficiency is enhanced using “ionizing radiation”, i.e. directly activating the target material. The high photon-energy (20–100 eV) makes the sampling process essentially single-photon, whatever bond or ionization energy. Furthermore, the analytical setup is simplified to a sampling source and detector, i.e. without the need for a secondary ionization or excitation source as in some state-of-the-art analytical systems. In this review, fundamental aspects of X-ray laser desorption and ablation are discussed, and a survey of the available literature is presented. The main objective is to convince the reader that desorption or ablation in this spectral domain is a significantly cleaner sampling process, with large potential, still requiring investigation for a complete fundamental understanding. Applications of laser microanalysis are thus entering the nano-scale era, which shrinks the gap with electron-based microprobes.
1. Introduction
Lasers have brought a dramatic advantage to the microanalysis, thanks to their flexibility in spatial resolution and selectivity. Indeed, microanalysis covers a wide range of application fields, ranging from chemical analysis of geomaterials to biomaterials, functional materials, and environmental samples. Lasers have indeed permitted 3D-resolved determination of the composition, which is essential for diffusion, heterogeneity, or contamination insights. Laser microanalysis generates large datasets, which poses challenges for hyperspectral processing.1–3 The combination of spectra from individual spots can visualize the pattern distribution of a set of analytes, such as elements, molecules, etc. Lasers have also enabled rapidity for an analysis to happen in seconds, not over hours or days, as for classical wet chemistry methods with time-consuming sample preparation. Indeed, lasers have enabled the universal application to any kind of matrix, even hard ceramics, non-conductive materials, or soft gels, with negligible sample preparation.Still, what laser microanalysis cannot do as good as contending charged particle techniques is accessing the nano-scale domain. Combining the latter with robust detection power is a fundamental analytical challenge. Firstly, while using optical lasers (i.e. the commercially available laser range from IR to UV), diffraction prevents spots smaller than a few microns. Shorter wavelengths, so far from spontaneous emission sources mainly used for calibration purposes of spectrometers, are not capable of ablation or desorption.
In fact, although spectroscopy instrumentation was already operated at wavelengths around 100 nm more than 100 years ago by Schumann,4–6 intense sources of radiation with wavelengths shorter than 100 nm appeared only recently in the laboratory.7–9 Three spectral regions have been established in spectroscopy,10i.e., extreme-ultraviolet radiation (XUV; typically 10 nm < λ < 100 nm, depending on the absorption edge), soft X-rays (SXR; typically 0.1 nm < λ < 10 nm) and hard X-rays (λ < 0.1 nm). For the extreme ultraviolet radiation, the acronym XUV was proposed by Tousey.11,12 In the literature, one will often found the synonym EUV which is now usually attributed to wavelengths adopted in lithography, i.e., wavelengths around the industry standard of λ = 13.5 nm.13
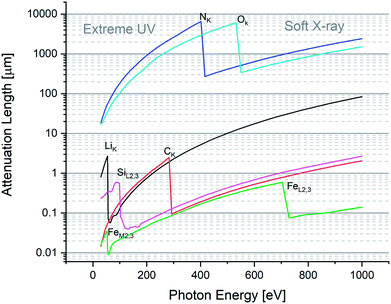
Fig. 1 highlights a few absorption edges for a selection of important elements, such as Li, C, N, O, Si, and Fe. On the low-energy (long wavelength) side of a given edge, one observes a so-called normal dispersion that is characteristic of (extreme) ultraviolet radiation. Otherwise on the high-energy (short wavelength) side of the shown absorption edges, one observes an anomalous dispersion with also the peculiar characteristic that the index of refraction is less than 1. Normal is the dispersion in relation to the historical fact that the first observations indicated that the index increased as a function of photon energy. The later discovery that close to the edges the dispersion curve drops as a function of energy was considered anomalous.
The region between 282 eV and 533 eV is known as the water window. In fact, the attenuation length for O is large (i.e. oxygen is transmissive) while for C it is short (i.e. carbon is opaque). Since optically O is the main component of water, while H is notoriously weakly absorbing, the domain is considered a water window. The fact is of remarkable interest: water is the natural environment for many bio-samples,14,15 whose main component is clearly carbon. Hence, in the water window region, one can optically image bio-materials in their natural water environment, i.e. without sample preparation procedures such as staining, obtaining a high chemical contrast between C and O.
For the purpose of microanalysis, e.g. using laser ablation, XUV is the “promised land” because it dramatically enhances the energy coupling across length-scales of approx. 10–100 nm (Fig. 1). Techniques to focus hard X-rays for fluorescence analysis to achieve spot sizes of a few microns, have been well established using polycapillary optics.16 However, penetration of hard X-rays by several microns is far from nano-scale resolution. On the other hand, a strong absorption coefficient at XUV/SXR favors the occurrence of sampling at scales as low as λ/2, i.e. fully nano-scale.
It is worth mentioning that unique XUV/SXR optics designs17–20 made it possible to create nano-spots, which now will become more and more popular. For a long time, XUV/SXR lasers have not been available. Such photons were so far “monopoly” of synchrotron beamlines though the peak power of such beams was usually not high enough to induce ablation. Nevertheless, erosion of solids was reported, due to desorption-like high photon energy phenomena,21 as discussed below. Fourth generation beamlines, i.e. so-called X-ray free-electron lasers (XFEL), have achieved remarkable peak powers, as high as seven orders of magnitude above top synchrotrons, and exacerbated damage effects, meanwhile making it a problem. Beamlines are not accessible on a 24/7 basis.
On the other hand, plasma-based short-wavelength laboratory sources9 can be used to perform tabletop ablation experiments in the own laboratory. Tabletop plasma-based XUV lasers give a chance for routine application of advanced microanalysis and nano-scale “imaging”, i.e. the subject of this review.
The structure of this paper is as follows: Section 1 is an introduction to spatially resolved chemical microanalysis, discussing the popular concept of “imaging” as well as the fundamental limit to make laser microanalysis nano-sensitive; Section 2 summarizes the main aspects of the rationale of using lasers for microanalysis; Section 3 introduces the rationale of XUV lasers for ablation/desorption, discussing general concepts and then more specific advantages of such spectral domains; Section 4 reviews short-wavelength laser microanalysis, based on the limited literature; finally Section 5 provides main conclusions and an outlook.
1.1. Chemical visualization: imaging versus mapping
In the common jargon, one speaks of “chemical imaging” to indicate the determination of the spatial distribution of compounds, and highlight a chemical pattern. It should be however pointed out that the term imaging has a specific technical meaning, well distinguished from that of mapping, which mostly applies to laser ablation methods. Three important characteristics are very different in the two modalities (see Table 1), i.e. (spatial) resolution, region-of-interest (ROI), and filling ratio. The resolution is the least length-scale that can be distinguished from neighboring elements. The ROI is the visualized scope or “field”. The filling ratio is the proportion or the actual space covered by the measurement sampling with respect to the spread of data space. For a scattered sampling across the material, the filling ratio can depart from 100%. In the latter case, interpolation is used to fill the data gaps.| Imaging (full field) | Mapping (scanning field) | |
|---|---|---|
| Process | Simultaneous projection of an object with full field storage | Sequential acquisition of objects with later data stitching |
| Region of interest (ROI) | Given by the detector size | Given by the span of spot distribution |
| Filling ratio | Full (100%) | Depends on the spot to spot interval |
| Resolution | Given by the detector pixel | Given by the spot size |
| Range | Limited to the collection aperture | Virtually unlimited (sample stage range) |
| Temporal skew | None (all points are coetaneous) | Sampling speed vs. object stability |
| Example | Optical microscopy, photography | Laser ablation spectrometries, SEM |
Regarding these two chemical visualization modalities, imaging indicates the (conjugate) visualization of a real object, with a simultaneous (full-field) projection of its parts, to have a (bandwidth-limited) representation, stored full-block on a detector. The collection occurs without mixing the information of the parts, which are stored across pixels over a 2D array detector. In imaging, the actual resolution is binned by the pixel size, although the “aerial” image has virtually infinitesimal resolution. This means that detection (not the sampling) is the quality-limiting factor in imaging. The ROI is given by the number of pixels of the array detector (detector size), while the filling-ratio is 100%, since the pixels are densely mounted next to each other. Imaging is routinely possible with photons, i.e. optical microscopy. For obvious reasons the information on each pixel cannot be of a full spectrum (hyperspectral microanalysis), but it is pre-filtered to collect the signal of a specific analyte of interest. Multiple analytes on the same array detector can be determined in sequential measurements with specific pre-filtering.
On the other hand, mapping indicates the sequential (field-scanning) acquisition of individual spectra (hyperspectral visualization) at specific spots across the sample surface. The resolution is given by the spot size. This means that the sampling (not the detection) is the quality-limiting parameter in mapping. The ROI is given by the span of the spots across the material as well as the sampling scheme, e.g. folded, straight, line-by-line, pushbroom, etc. The filling-ratio is obviously less than 100%, which depends on the strategy of spot-to-spot distribution across the sample, and on the shape of the spot. In fact, circular spots cannot fully tile a surface. Individual data are then “built together” during the data processing. This is important in the data visualization22 procedures, to prevent artifacts by inaccurate positioning of the individual measurements.
1.2. Nano-scale mapping and sensitivity
The spatially resolved chemical analysis of surfaces and/or buried interfaces (depth profiling) is a major insight for materials science, geochemistry, environmental science, life science, etc.23–25 The utilization of pulses to probe a restricted surface region, or “spot”, is the standard approach for the rapid and direct data extraction. Classical time-consuming alternatives implied a mechanical extraction with “post mortem” analysis. The utilization of photons proved advantageous in terms of flexibility to any kind of sample matrix as well as the minimization of sample preparation procedures. On the other hand, electron-based methods are more powerful in terms of spatial resolution, since the focusing of light is limited by the diffraction. Furthermore, electron methods can rapidly scan a surface to provide chemical patterns, while photon methods require a sequential mapping of the object, with subsequent (hyperspectral) data analysis.Signals from the sample matrix may overlay those from the analyte of interest, which would require a selective deconvolution method. In chemically structured samples, i.e. characterized by interfaces or heterogeneous assemblages, intermixing processes can self-contaminate the pristine components. During material synthesis, the apparatus or the ambient can contaminate the specimen and cause a systematic bias. The “purity” of a sample is pragmatically a function of the analytical detection capabilities, since heterogeneities or contaminants below the blank remain undistinguishable. The drastic enhancement of the detection power or the spatial resolution may thus highlight a more frequent occurrence of contaminants, which makes the interpretation of the data more complex. The accurate and precise determination of the local chemistry is the ultimate task of laser mapping. Clearly, no single analytical method works as a “Swiss Army knife” because a large degree of flexibility means the lack of specificity. The complementarity of the various microanalytical techniques is an essential element to realize. Technique-emphatic credos are inherently short reaching.
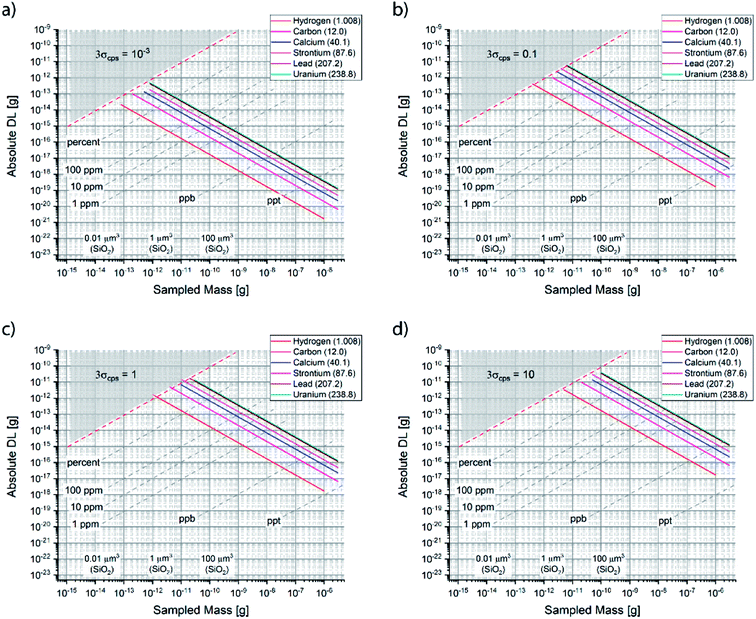
Fig. 2 summarizes the detection limit (DL) as a function of lateral (spot) and depth (ablation yield) resolution for different nominal sensitivities in counts/second (cps). One could plot the nominal specification of a number of microanalytical techniques, as done previously,26 and observe the complementarity of the methods. The theoretical limit given by counting statistics is shown as a tradeoff between the spatial resolution and detection limit,27 as discussed below in detail. It is noteworthy that the experimental DLs are indeed far from the theoretical limits, i.e. the sampling utilization efficiency28 (SUE) is poor. The latter implies that a large fraction of ablated and/or desorbed sample is not detected (analytical waste), and that there is in principle room for dramatic improvement in sensitivity. The utilization of XUV lasers29–31 with the enhancement in spot size and SUE is promising for the disruptive improvement (not incremental) of the laser microanalysis capabilities towards the nano length-scale.
 | ||
Fig. 2 Theoretical detection limit (DL, i.e. 10−2 = 1% or 10−6 = ppm) as a function of sampled volume (spot and depth resolution) for various sensitivities (in counts per second), namely: (a) 0.001 cps, (b) 0.01 cps, (c)1 cps, (d) 10 cps, (e) 100 cps, (f)1000 cps, (g) 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cps, and (h) 100 000 cps, and (h) 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cps. Based on eqn (3.c). 000 cps. Based on eqn (3.c). | ||
For instance, Laser-induced Breakdown Spectroscopy (LIBS)32 flexibility and rapidity have been proven crucial for application in industry, as well as for environmental studies. Furthermore, LIBS is a portable technique, which makes it advantageous even compared to a more established technique such as X-ray fluorescence spectrometry. Different from LIBS, laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) is a “transient technique” (prone to the risk of aerosol particle separation), as the laser-ablated aerosol is transported prior to atomization/ionization in the plasma and detection. The hyphenation provides depth-wise chemical information with documented mixing effects.33
While presenting the benefit of short-wavelength-lasers for plasma emission spectrometry, two crucial aspects need to be addressed in more detail, i.e. (i) the drastic change of ablation characteristics, and (ii) the special features of the XUV plasma and interaction with the drive pulse. With this technique being yet unexplored (to the best of our knowledge), the literature pivots around fundamental studies that are not strictly related to a microanalytical application. In this respect, the contribution of the present paper is to review and assemble the large body of available fundamental knowledge, to indicate the suitability of X-ray lasers for advancing the current capabilities of laser microanalysis.
2. Laser ablation for microchemical analysis
Two tradeoff parameters emerged in the literature as indicative of the capabilities of various micro-analytical techniques: the spatial resolution (Δx Δz, e.g. each dimension in nm) and the relative detection limit (DL, e.g. in mg kg−1). Further analytical parameters, such as precision or sensitivity, are contained in the definition of the metrics above, and indirectly considered. The spatial resolution is clearly related to the sampled mass yield (Δm) multiplying the ablated volume by the material's density. A minimization of the product T = Δm × DL can be a combined metrics (T for the Technique indicator, which has the unit of mass being the absolute detection limit) for the analytical impact of a technique.2.1. Spatial resolution for laser ablation and desorption
An important distinction to begin with is between the nominal (spot size) and the actual (crater size) spatial resolution in laser mapping. Nominal values are given by the beam delivery specifications. The interaction with the target material may develop the “optical size” and produce signals from a broader (e.g. melt rim, spallation) or tighter (e.g. refractory) domain. For instance, thermal diffusion can cause a sample spot to get larger than the focal spot. On the other hand, an absorption length may ensure that only the core above the threshold contributes to the sampling.The effective spatial resolution is thus a function of the crater size (or later resolution) and ablation yield (or depth resolution). Different operating conditions can cause different aspect ratios of the probed volume. The following relation gives the nominal spot size:
| s = 1.22M2f/#λ | (1) |
| l = λ/(4πβ) | (2) |
2.2. Chemical resolution
The definition of the detection limit (DL) stems from the theory of uncertainty and error, based on the sensitivity Si (i.e. intensity per unit analyte concentration) for the i-th analyte, and is defined as follows:34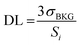 | (3) |
The expression indicates the threshold concentration sufficient to distinguish an analyte from noise with a 3σ confidence interval of 99.7%, i.e. using a “signal-to-noise scale”, as it is evident recasting the equation as follows:
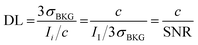 | (3.b) |
The use of concentration (c) instead of an absolute number of detected analytes in counts (N) has its justification. Indeed, the signal of a detector responds to the number of analyte hits. However, one has to consider the likelihood that N sampled particles in a probed volume V, i.e. with number concentration c = N/V (expression used below in eqn (3.c)), will at all reach the detector. Assuming a dispersive signal transfer model, the likelihood scales with the sample concentration. Henceforth, one apportions the signal “dilutively” indicating that the detection limit is a relative abundance, i.e. ppm (kg mg−1), ppb (ng g−1), etc.
The 3σ criterion is a practice, i.e. such to be very safely above noise level, and have robust chemical resolution. The precision of the detection is limited by fluctuations of the blank. Henceforth, to be able to suppress stray signals has dramatic benefits on the detection limit. The sensitivity, on the other hand, is related to the SUE, as defined above. However, when the measurement grows in sensitivity, it needs a dynamic range to exploit the full potential.
Finally, since the ultimate (absolute) detection limit is the single atom or molecule-fragment, one should also consider that the enhancement of DL requires larger volume samplings, as shown previously.35
2.3. Tradeoff between spatial and chemical resolution
An expression of the detection limit, which is an explicit function of the sample volume, shows how a reduction of sampled volume (i.e. enhancement of the spatial resolution) implies a degradation of the detection power (ceteris paribus, i.e. at comparable sensitivity). If one considers the detector efficiency (qε), i.e. the yield of the measured signal per specific count of analyte, i.e. qε = Icts/N, then one obtains an expression as follows: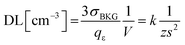 | (3.c) |
Therefore, in order to be able to expand the current laser microanalysis capabilities from the micro- down to the nano-scale, one has to accomplish higher sensitivity, and/or, lower background noise. The rest of the paper will show that the use of X-ray lasers is addressing this challenge.
The theoretical limit is a fundamental limit to pay attention to, and the following analysis will show that the state-of-the-art is still far from such a limit. The number of detected counts per second (ND), e.g. atoms, is given by the following expression
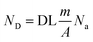 | (4) |
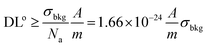 | (4.b) |
Fig. 3 shows how the theoretical absolute DL scales as a function of sampled mass (for reference, the corresponding sampled volume is given using the density of SiO2), for various noise levels and a selection of elements. One observes that the drastic degradation of DL is an issue that becomes evident only approaching the nano-scale (note that the scale is logarithmic).
One cannot have an absolute DL that is larger than the entire sampled mass (gray area), which represents a theoretical limit for quantitative analysis. In that range of ultralow mass sampling, the analysis has only a qualitative value, if any. Clearly, since the DL is defined per mass of sample, lighter elements plot along “better” absolute theoretical limits. The theoretical curves plotted in Fig. 3 consider that the nominal sampled mass is equal to the actual one, i.e. SUE = 100%. A more accurate form of eqn (4.b) would consider the experimental utilized mass as m times SUE. As shown in Fig. 3, any degradation of the DL implies that the experimentally processed mass is smaller. Henceforth, Fig. 3 offers a pragmatic way to determine graphically the SUE, which is the ratio between experimental and nominal sampled mass.
2.4. Strengths of XUV laser sampling and facing challenges
Darke et al.36 provided one of the milestone reviews on laser ablation microanalysis, which for many years was the state-of-the-art, showing that laser ablation (LA) is a rapid and universal sampling method. More recently, Aubriet et al.37 reviewed laser mass spectrometry for the analysis of environmental aerosols. The many techniques and instrumental architectures are discussed, with emphasis on the complementarity of online and offline analysis. It is impossible to do the laser-irradiation on particle by particle, and thus the data needs to be interpreted due to signal mixing. Clearly, one of the main issues is the ability to focus a laser for the ablation of a single 10–1′000 nm aerosol particle, which may become possible using a short-wavelength laser.Considering the fast transient nature of laser-assisted sample introduction, time-of-flight (TOF) mass spectrometry (MS) in different architectures38 has been widely preferred, especially in direct detection of the primary ion bunch. Many authors have however adopted a two-stage sampling/ionization such as in combination with ICP-MS, even if not with TOFMS, which should permit more robust quantitation. Recently, Lin et al.39 and Huang et al.38,40,41 reported an elemental “imaging” method using an optical laser (λ = 532 nm) for direct ionization, coupled to orthogonal time-of-flight mass spectrometry, for the simultaneous detection of elements. Such a system was capable of providing data at a spatial resolution of 50 μm, with detection limits of 3 × 10−7 g g−1 (Li), and in a dynamic range of 7 orders of magnitude. Elemental mapping on surfaces of several mm provided quantitative results in agreement with ICP-MS data.
Unfortunately, the generation of ions is orders of magnitude lower than neutrals and solid particulates, which limits the SUE. For that, Laser Ionization Mass Spectrometry42 (LIMS) is currently superseded by other techniques that use a secondary atomization and ionization source, such as the inductively coupled plasma (ICP). LA-ICPs with either optical emission spectrometry (OES) or MS have achieved the highest detection capabilities with limits in the low ppm range. Lately, a strong interest in bio-medical studies has driven the attention to “imaging” (rather mapping, as discussed above) techniques. The obtainment of full spectral information from a 2D or 3D array of laser spots permits reconstructing the pattern of distribution of chemicals in specific important bio-samples, such as tissues or organs. Although the technique is potentially of impact also in materials science, it is really the life sciences that are driving the progress of laser-assisted micro-visualization.
For instance, Halbach et al.43 discussed critical aspects of protein labeling with heteroatoms (i.e. any elements except C and H) for performing laser ablation ICP-MS hyperspectral microanalysis. They pointed out two main challenges: (i) a robust labeling scheme while using polyclone immunoglobulins; (ii) the obtainment of molecular information. A further critical aspect is the obtainment of (absolute) quantitative information, for which the authors discuss a decalogue of requirements. Halbach et al.43 used LA-ICP-MS for studying the analyte distribution, following Br-labeled organophosphate uptake, in the zebrafish embryo, which is an important model in ecotoxicology.
As mentioned above, materials science is another domain potentially benefitting from laser ablation for chemical pattern reconstruction. Harte et al.44 utilized laser ablation ICP-MS for the characterization of transition metal patterns in Li-ion batteries and carry out a parametric study of the optimum measurement conditions. A higher scanning speed has an observable influence on the resolution of the obtained image and an overall saving of 60% with regard to time and gas consumption can be achieved.
3. XUV laser ablation and desorption
The process of laser-assisted mass removal is traditionally distinguished into desorption or ablation. Historically, the former is more typical in the organic microanalysis, e.g. MALDI, while the latter in the elemental analysis, e.g. LA-ICP-MS. The two processes, traditionally distinguished based on the input laser energy and the sputtering effects left behind, are much more blurred in the case of X-ray laser irradiation. Haglund & Miller45 provided a definition for the two laser–matter processes, and showed that laser-induced desorption and ablation are commonly energy conversion processes, i.e. initial electronic or vibrational photoexcitation leading to ejection of atoms, ions, molecules, and even clusters from a surface. Laser-induced desorption is distinguished in that, as a particle ejection process, it operates without any mesoscopic modification of composition or structure, and with a linear yield. Laser ablation, in contrast, is a massive sputtering process in which material removal rates typically exceed one-tenth of a monolayer per pulse,45 and the surface is mesoscopically modified, structurally or compositionally, with non-linear yields. Laser-induced desorption and laser ablation are however not always fully distinct phenomena. Desorption initiation by a low-fluence “monolayer activation” may lead to “massive disrupture” at the onset of ablation. As the X-ray laser ablation is however a linear scaling process even in the ablation regime, it makes it hard to distinguish two processes. In the rest of the paper, to be consistent, we will use the term (micro/nano)sampling, in place of ablation or desorption.3.1. General mechanisms of laser sampling
The interaction of a laser pulse with a target material is a complex physical process. In particular, depending on laser and/or material characteristics, the ablation process assumes substantially different characteristics. Important laser parameters are the wavelength (or photon energy, considering that EeV = 1239.8/λnm), the pulse duration, and the irradiance (or power density). The fluence (energy per spot surface) is important when comparing lasers of different pulse durations. Important material parameters are• The optical properties, i.e. the complex index of refraction, i.e. with the absorption and dispersion components;
• The thermal properties;
• The mechanical properties.
A previous publication46 discusses these materials properties in full detail with respect to laser micro/nano-sampling. The primary interaction is always between the (laser's) photons and (material's) electrons. Secondary interactions imply electron energy transfer (and momentum) to the material's lattice (collisional processes) or radiative transfer into the surroundings. Two main classes of interaction mechanisms can be then distinguished: (i) photo-physical and (ii) photo-chemical.
The former is a thermo-mechanical process, e.g. melting, vaporization, phase explosion,47etc. that happens by energy transport over macroscopic durations (longer than nanoseconds), at low photon energies (IR to visible), and high repetition rates. Photo-chemical ablation, on the other hand, implies direct (quasi-resonant) absorption of photons to eject electrons, and thus break lattice bonds. Electrons may thus emit (so-called photoemission): the process is highly localized and chemically selective.
Both processes are accompanied by the phase change, i.e. melting and vaporization, or ionization. Plasma-breakdown is the sudden flow of a current, which is the consequence of an above-surface bias (electrically or optically induced) exceeding the dielectric limit.48 The acceleration and transport of electrons in the generated plasma causes massive collisions with the heavier and sluggish background species. This partially leads to excitation, and the subsequent relaxation of atomic and molecular radiators, with a microanalytically useful spectrum.
In LIBS the laser pulse, whose peak irradiance (power per spot area) determines the response, optically drives the bias. The electric amplitude (E, in V cm−1) of a laser pulse, noting the intensity as I, has been indicated in the early literature as follows:49
| E = (4πI/c)1/2 | (5) |
Since the plasma must initiate from a neutral dielectric medium, e.g. ambient gas, vaporized solid material, etc. either multi-photon ionization or cascade ionization has been indicated as responsible for the seed electrons.50 Lin et al.51 studied the plasma plume expansion and ion formation in Ar and He ambient gases in detail.
3.2. Optical mechanisms specific to XUV/SXR pulses
Fig. 1 indirectly shows the index of refraction as a function of the spectral domain, by means of the optical penetration depth. It is noteworthy that the occurrence of atomic resonances scopes the spectral ranges, e.g. XUV (characterized by normal dispersion) versus SXR (characterized by anomalous dispersion), as discussed above. It is customary, at short-wavelength, to indicate the index of refraction as a complex number close to unity, as follows:| ñ = 1 − δ +iβ | (6) |
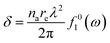 | (7.a) |
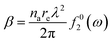 | (7.b) |
Inogamov et al.53,54 investigated experimentally and computationally the ablation of short wavelength pulses (from a tabletop plasma-laser as well as from a synchrotron beamline) of non-conductive materials (LiF) as well as metals, and compared it to that of commercially available optical lasers. Their study indicates a transition, from near-threshold to well above it, between a spallative mechanism and an evaporative one. Results from tabletop vs. beamline XUV sources converged toward a photochemical behavior, while results from optical lasers indicated thermo-mechanical processes and a preservation of the material elasticity, i.e. chemical bonding. Benware et al.55 showed that despite a low pulse energy of a few μJ, and relatively long pulse duration of ns, irradiation with a soft X-ray is very effective in inducing ablation, such that single-photon ablation is accomplished. Krzywinski et al.56 investigated the different ablation characteristics of conductors, insulators and semiconductors while using soft X-rays. They proposed a scaling law to explain the ablation threshold in the few mJ cm−2 range, which considers the threshold fluence, as follows:
| Fth = Ecn/α | (8) |
Toufarová et al.57 have also shown dramatic sample-specific differences, i.e. for carbon ablation when it is in covalent or molecular bonding. A non-thermal mechanism via intermolecular Coulomb explosion without phase transformation is presented for the ablation of C60. The ablation of amorphous carbon is characterized by the occurrence of graphitization. Juha et al.58 determined the ablation yield as a function of fluence well above the threshold, in the range of a few J cm−2, obtaining 100–200 nm per shot in PMMA. The comparison between ns and fs pulses (at λ = 86 nm) indicated an approx. factor of 2.5 thinner ablation yield for the ultrashort pulses. The ablation yield of PMMA got even thicker when incoherent plasma radiation was used. This was explained as due to the larger attenuation lengths of (incoherent) X-ray radiation in PMMA, which is approx. 1 μm, compared to approx. 10 nm for XUV. The etching rate for sub-100 ps pulses of XUV laser radiation is also slightly reduced with respect to the values calculated for nanosecond pulses. Ablation of PMMA was shown to be less efficient than that of PTFE (Teflon). In general, a non-thermal mechanism of radiation-induced mass removal was invoked, with an essentially “pure” radiolytic polymer scission.
3.3. Advantages of XUV/SXR for laser mapping
The utilization of short wavelengths for laser ablation and/or desorption has some unique benefits. The concept of “short wavelength” refers to any spectral domain of photon energy higher than the optical range, for which the discussed domain is also known as “ionizing radiation”. The following section addresses crucial advantages of XUV/SXR lasers for microanalysis.Vaschenko et al.29 reported ablation with pits as small as 82 nm and very clean walls in PMMA, focusing pulses from an Ar8+ (Ne-line shell) capillary-discharge plasma lasing at λ = 46.9 nm. The focusing was accomplished with a freestanding Fresnel zone plate diffracting into third order. These results demonstrated that focused soft X-ray laser beams are apt for the direct nanoscale ablation of materials, although they are not fully at the limit of the λ/2 criterion, due to a poor beam profile.
Ishino et al.59 investigated the surface modification and pulse impact (λ = 13.9 nm) on metallic samples, and concluded that the obtained crater structure, for a given nominal spot, was a function of elemental composition. In contrast to the conical structures induced on the Al surface, the formation of ripple-like structures was confirmed on the Au and Cu surfaces. Ablation thresholds of several tens of mJ cm−2 were reported. Chalupský et al.60–63 studied in detail the non-thermal ablation and desorption induced by single as well as multiple XUV/SXR laser shots on PMMA, comparing data obtained at beamlines (FLASH in Hamburg) as well as tabletop setups64 (High Order Harmonics). It was shown61 that even a single shot can produce a part of the damage pattern clearly assigned to the desorption which can be discerned from the ablated center of the crater. The procedure was utilized to characterize the energy profile of the irradiating pulse.
Table 2 summarizes milestone literature data, and highlights that the damage threshold of both organic and inorganic materials strongly depends on the wavelength of the XUV/SXR radiation. In general, going towards shorter wavelengths, the penetration depth becomes longer. Thus, the energy density drops in the near-surface region of the material and the damage thresholds increase. It is also clearly visible that interfaces play a key role. The threshold is much lower for thin films and multilayers in comparison with a bulk sample of the same or similar material. This could influence the depth profile analysis because the sampling yield should increase when the micro-beam reaches an interface in a layered material. Last, but not least, it seems that XUV/SXR ablation thresholds do not depend on the pulse duration (or peak intensity) so dramatically as revealed for optical lasers. This is consistent with a radically different mechanism of absorption and ablation in these spectral regions.
| Material | Wavelength/pulse duration | Threshold (mJ cm−2) | Note/ref. |
|---|---|---|---|
| Organic materials | |||
| PMMA | 32.5 nm/25 fs | 2 | Ablation, ref. 60 |
| PMMA | 13.5 nm/25 fs | 30 | Ablation, ref. 65 |
| PMMA | 4.6 nm/80–150 fs | 250 | Ablation, ref. 66 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Inorganic materials | |||
| Si (monocryst.) | 32.5 nm/25 fs | 100 | Melting, ref. 67 |
| Si (monocryst.) | 32.5 nm/25 fs | 380 | Ablation, ref. 67 |
| Si/Mo multilayer | 13.5 nm/25 fs | 45 | Melting, ref. 68 |
| a-C (thin film) | 32.5 nm/25 fs | 60 | Graphitization, ref. 69 |
| CVD diamond | 32.5 nm/25 fs | 140 | Melting, ref. 69 |
| SiC (bulk) | 32.5 nm/25 fs | 140 | Melting, ref. 69 and 70 |
| SiC (bulk) | 21.7 nm/25 fs | 298 | Melting, ref. 70 |
| SiC (bulk) | 13.5 nm/25 fs | 685 | Melting, ref. 70 |
| SiC (thin film) | 32.5 nm/25 fs | 35 | Melting, ref. 70 |
| SiC (thin film) | 21.7 nm/25 fs | 178 | Melting, ref. 70 |
| SiC (thin film) | 13.5 nm/25 fs | 326 | Melting, ref. 70 |
| B4C (bulk) | 32.5 nm/25 fs | 200 | Melting, ref. 69 |
| B4C (thin film) | 32.5 nm/25 fs | 18 | Melting, ref. 70 |
| B4C (thin film) | 21.7 nm/25 fs | 83 | Melting, ref. 70 |
| B4C (thin film) | 13.5 nm/25 fs | 348 | Melting, ref. 70 |
| PbWO4 | 4.6 nm/80–150 fs | 63 | Ablation, ref. 66 |
| PbWO4 | 1.55 nm/100 fs | 100 | Ablation, ref. 71 |
| Ce:YAG | 86 nm/30–150 fs | 20 | Ablation, ref. 66 |
| Ce:YAG | 4.6 nm/80–150 fs | 661 | Ablation, ref. 66 |
| ZnO | 4.6 nm/80–150 fs | 168 | Ablation, ref. 66 |
| LiF | 46.9 nm/1.7 ns | 100 | Ablation, ref. 72 |
| LiF | 13.9 nm/7 ps | 10 | Ablation, ref. 53 |
| CaF2 | 46.9 nm/1.7 ns | 60 | Ablation, ref. 72 |
| Ru (thin film) | 13.5 nm/100 fs | 200 | Spallation, ref. 73 |
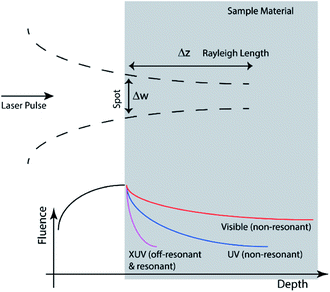
The vertical (depth) length-scale of energy deposition depends on beam delivery conditions (Fig. 4) as well as optical characteristics of the sample (see eqn (2)). The depth of focus is the “defocusing” that introduces λ/4 wavefront absolute error (i.e. a clearly unfocused image), as follows:
| Δz = 2λf/#2 | (9) |
The quadratic dependence shows how critical is the focusing, in order to take advantage of the linear downscaling thanks to the shorter wavelength. As discussed above, the refractive index of the material is important because it determines the pulse propagation characteristics and its absorption. Eqn (2) has given the characteristic length-scale of penetration. The mass absorption coefficient (μ) is the exponential coefficient that in a Lambert–Beer absorption model determines the decrease of penetrating intensity.
Depending which term between Δz (eqn (9)) or l (eqn (2)) is smaller, one can distinguish between photo-physical and photo-chemical processes. In general, as shown in Fig. 4, far from resonances (transparent material), the former is controlling the deposition, while close to material resonances (opaque) the latter characteristics are more important. Cross-sections of the XUV absorption, for various elements and materials, listed as a function of photon energy (or radiation wavelengths), are reported in several tables. The most popular ones are the tables originally compiled by Henke, Gullikson and Davis.52,74 There is an on-line calculator of XUV/X-ray optical properties of materials based on “Henke's tables” which is operated on the website of Lawrence Berkeley National Laboratory.
The efficiency of bond breaking of XUV/SXR is exemplary in the interaction with DNA. Vyšín et al.75 investigated the radiolytic action on DNA strands using extreme-ultraviolet laser pulses in a vacuum, with all the range of structural and functional damage. Using an Ar-plasma laser they could perform the study in a compact tabletop setup.
Barkusky et al.76 studied the ablation thresholds for a number of optical materials used with XUV. They have indicated thresholds in the range of 0.8–5 J cm−2. They have identified a smooth ablation profile in fused silica, which is possibly the indication of a direct photon-induced bond breaking process. The obtained values seem very large if compared with what reported by other authors. For instance, Steeg et al.77 determined an ablation threshold for amorphous carbon as low as 70 mJ cm−2. Faenov et al.54 also determined thresholds of 5–10 mJ cm−2, for various dielectric materials, which was explained with a shallow absorption thickness caused by a strong energy coupling.
The plasma electron frequency is obtained from the electron density. The critical electron density for plasma shielding is expressed as a function of the laser wavelength (here in μm), as follows:
| nc [cm−3] = 1.1 × 1021/λμm2 | (10) |
The quadratic dependence on cutting-down the wavelength indicates that at wavelengths of tens of 10–50 nm (XUV), a factor of 25–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 higher plasma penetration is accomplished with respect to lasers at 266–1064 nm. This means that the “plasma shielding” process is virtually eliminated using a XUV/SXR pulse. Frolov et al.78 imaged the plume for an ablation experiment with 46.9 nm laser pulses. They have observed a dependence on the pulse energy, in a number of metallic targets, such as Al, Si, Cu and Au. Pira et al.79 studied the soft X-ray laser-produced plasma with a Langmuir probe. Temperatures of a few eV, i.e. comparable to those known in plumes produced by optical lasers, were observed. This was attributed to relatively short attenuation lengths. A remarkable difference, however, is the much lower density, i.e. 107–108 cm−3. This finding indicates that desorption-like phenomena are responsible for the plume formation rather than bulky ablation processes.
000 higher plasma penetration is accomplished with respect to lasers at 266–1064 nm. This means that the “plasma shielding” process is virtually eliminated using a XUV/SXR pulse. Frolov et al.78 imaged the plume for an ablation experiment with 46.9 nm laser pulses. They have observed a dependence on the pulse energy, in a number of metallic targets, such as Al, Si, Cu and Au. Pira et al.79 studied the soft X-ray laser-produced plasma with a Langmuir probe. Temperatures of a few eV, i.e. comparable to those known in plumes produced by optical lasers, were observed. This was attributed to relatively short attenuation lengths. A remarkable difference, however, is the much lower density, i.e. 107–108 cm−3. This finding indicates that desorption-like phenomena are responsible for the plume formation rather than bulky ablation processes.
| σe = 8π/3re2 | (11) |
The density gradient of the plasma, denser at the core, and increasingly more rarefied towards the corona, has an impact on the optical properties. The index of refraction for free electrons in the plasma can be obtained from its electron density (ne) as follows:
| n = (1 − ne/nc)1/2 | (12) |
On the other hand, the utilization of high energy photons (short-wavelength pulses) increases the efficiency of the direct excitation process. The cross-section for excitation or ionization is given as a particular case of the scattering cross-section for a bound electron. In this case one can safely adopt a semi-classical treatment where an oscillating field (laser) exerts a force on an electron bound with a specific restoring force depending on the chemistry involved. Crucial is the spectral offset between the laser frequency (ωL) and the atomic resonances (ωs), or detuning Δ = ωL − ωs. The expression for the cross-section is thus a modification of the Thomson scattering (see above), which considers detuning and electron relaxation (γ), as follows (mathematical derivation can be found in Attwood20):
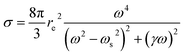 | (13) |
It is noteworthy that the scattering cross-section for bound electrons has a power of four frequency dependence, close to a resonance. This is a specific feature of short-wavelength laser LIBS and is an irrelevant fact in ordinary LIBS (optical area). Therefore, the high photon energy enhances the excitation and ionization efficiency, as long as the operating laser is close to an absorption edge of the target analytes.
| Iopt [W cm−2] = 3 × 1012TeV/λμm2 | (14) |
It is noteworthy that for shorter wavelengths, the optimum intensity increases quadratically. This is a major advantage for long wavelength pulses to generate optimum conditions efficiently, i.e. IR lasers can heat-up the plasma even with modest intensities. The situation at XUV, however, has its benefit, i.e. the Bremsstrahlung continuum, which covers the characteristic LIBS spectrum, is suppressed. Since excitation and ionization are anyway achieved by direct photo-mechanisms, there is no substantial drawback. In the end, operation at short wavelengths versus long wavelengths implies high electron density instead of high collisional energy.
3.4. XUV/SXR laser in the progress of laser microanalysis
Laser microanalysis has evolved dramatically in its 50–60 years lifetime. LIBS, for instance, was the very first microanalytical technique attempted with lasers, right after the demonstration of the first laser in the 1960s.82 This implied irradiating unknown materials to identify them by means of spectral fingerprinting. In more recent times, the progress of laser microanalysis has been mainly driven by the reduction of the pulse duration. Alternative approaches remained less explored, e.g. the use of short-wavelength pulses, for various reasons. Firstly, these are related to the lack of suitable laboratory instrumentation for the purpose. Secondly, an ingenious ablation scheme with the available systems did not force the community to look for alternatives. For instance, dual pulse techniques have shown satisfactory improvement. Lately, the discovery of signal enhancement by sample preparation with nano-particles83 also promises progress.There is a consensus on the fact that the thermal load was largely responsible for incongruent vaporization. Henceforth, many workers have looked for creative strategies to minimize the photo-thermal effects. Obviously, one straightforward approach has been to perform ablation in a time-scale significantly faster than the thermalization, which is in the range of nanoseconds (ns). Such “cool ablation” is accomplished with very intense pulses of >10 GW cm−2, which are possible with femtosecond (fs) lasers.85 In the latter case, even weak photon energies (long wavelengths) can efficiently produce ablation since the short delivery time-scale leads to multi-photon processes.
It is questionable whether the ultrafast energy delivery does strictly imply heat quenching in the material. In fact, the time scale of the lattice excitation kinetics is the real limiting factor in the ablation process. Indeed, the material-dependent parameters are more important, such as heat delocalization and lattice kinetics. In the case of extremely high energy delivery rates, e.g. 1011 K s−1 (ref. 86) (here one considers the pulse rise time) one expects superheating, which leads to spinodal phase explosion.47 For pulses that do not achieve the “phase explosion” regime, one may expect a behavior of fractional ablation, as a function of the lattice or bond energies. In this respect, femto-pulses do not systematically induce “heat-free ablation” rather “overpressure ablation” to trigger a sudden disrupture. With this, the often reported clean ablation craters87 are better explained as a steep lateral transition from the ultrahigh-pressure ablation region to the sub-threshold region, with no intermediate desorption region (moderate pressure and melt mobilization) at the crater rim.
The ultrafast pulse delivery also leads to the short-lived laser pulse being extinguished before the plasma initiation time (no plasma shielding is explained as there is no temporal overlapping). It remains debatable whether the pulse duration or the pulse rise-time is the key parameter to determine such a peculiar ablation regime. In fact, both the pulse rise-time and duration are, in all commercial femtolaser systems, strictly connected and a scientific investigation of one parameter at a time is not possible.
Such single-photon activation of materials is scalable in terms of pulse energy, because there is no time-duration requirement as in the case of multi-photons, when photons must be delivered in a short temporal window. Some authors have speculated that XUV sampling is threshold-free since even a single photon (least pulse amplitude) is sufficient to perform irreversible changes in solids. The term “single photon damage” was in that sense first used when possible non-thermal damage to short-wavelength free-electron laser (FEL) optics was anticipated and discussed by Deacon.88 Due to the strong absorption cross-section in the extreme ultraviolet and soft X-ray, these spectral domains are more studied. The field is relatively new since in the past only beamtime-limited facilities permitted these kinds of experiments. Experiments with excimer lasers have focused on showing the generation of a finer aerosol and higher ionization.
Kolacek et al.89 studied the XUV photon–matter interaction in an attempt to distinguish between desorption (less than a tenth of a monolayer, as discussed above) and ablation (otherwise) mass removal per shot. As mentioned above, the desorption induced by short XUV pulses can be so efficient that it is hard to discern it from the ablation, meanwhile for ultra-short pulses it is easy to distinguish areas formed by desorption and ablation. Direct nano-structuring was observed only in the desorption regime, which is in agreement with data from Norman et al.90 for the case of soft X-ray ablation of gold (ca. 20 mJ cm−2 while the ablation threshold is at 50 mJ cm−2). For femtosecond pulses the desorption process is insignificant with a steep transition into the ablation regime. For nanosecond pulses, a gradual transition between desorption and ablation makes the use of “crater geometry” as a metrics for fluency mapping misleading. The combination of coherent and incoherent radiation is also stressed to enhance the mass removal process.
Also Ritucci et al.91 reported the ablation yield of a few tens of nm for fluences in the range of 0.1–1 J cm−2, in combination with wide bandgap materials, i.e. LiF and CaF2 where ablation by optical laser radiation is hard. In Juha et al.,92 three polymers, i.e., PMMA, PI and PTFE, with different thermal and radiation resistances were ablated with focused pulses of 46.9 nm laser radiation. At fluences well above the ablation threshold one does not see so much difference in ablation rates among the three polymers. This is surprising because if the ablation is controlled just by non-thermal processes, materials sensitive to ionizing radiation (the most sensitive was PTFE and slightly less than PMMA) should be ablated more effectively than polyimide (PI), which is well known as a highly radiation-resistant polymer. If the ablation would be dominated by thermal processes, then PMMA should be more prone to decomposition and ablation in a vacuum because both PI and PTFE exhibit a high thermal resistance. It could indicate that although the XUV ablation of organic polymers is dominated by non-thermal (photolytic) processes, thermalized portions of absorbed energy play a certain role in the ablation process. Another factor is likely represented by nano-scale attenuation lengths of 46.9 nm radiation in the three polymers, which does not leave much space for zoning of thermal versus non-thermal processes in the ablation yield. An ablation rate was determined from the depths of craters created by a single pulse and then by 4 and 34 pulses accumulated. The ablation yield decreases with an increasing number of pulses. It could be a limiting factor in using the XUV ablation for the depth profiling. However, the focusing conditions were quite special (on axis irradiation, the target holder shadowed the center of the damage patten). So, further systematic research is needed.
Irradiation of amorphous carbon with multiple XUV laser pulses at a fluence below the single-shot damage threshold still showed an erosion of the material.93 This is an unexpected behavior because above the single-shot threshold the authors first observed expansion, then ablation and then α-C film delamination from the silicon substrate. Henceforth, the character of the process changed dramatically in the vicinity of the single-shot damage threshold, i.e., erosion turns into expansion. Interestingly, this behavior was registered just with short pulses from the plasma-based laser, and ultrashort pulses expand the material at any fluence. There may be two alternative explanations why nanosecond pulses induce the erosion of α-C. The first is based on how elevated temperature may stimulate the radiation induced desorption.94 The dangling bonds created by energetic XUV photons would be enforced to create a small volatile fragment, e.g., C2, by the thermalized part of the short pulse. An elevated temperature would also help to liberate such fragments into a vacuum. However, the temperature should not be elevated enough to transform diamond-like carbon into graphite. This would lead to expansion not to the erosion of α-C. The second explanation can be a synergy of the XUV action with effects of the long-wavelength radiation emitted by the plasma source simultaneously with the XUV laser pulse: the effects are termed as dual action in the literature.66,95 In addition to the dual action itself, the long-wavelength radiation would heat the sample more effectively because almost all energy is thermalized. Further studies are thus needed to resolve between the two alternatives.
Combined effects of short-pulse and short-wavelength have been studied by Juha et al.58 reporting ablation of molecular and covalent solids by ultra-short pulses of an X-ray FEL at λ < 100 nm. The study proved a predominantly non-thermal character in the XUV ablation, with very smooth residual surface structures and a low ablation threshold.
4. Benefits for state-of-the-art microanalytical techniques
A central question to be addressed is what concrete benefits will XUV/SXR lasers bring to the microanalysis, which is discussed in this section. In particular, we review the limited literature on emission spectrometry and mass spectrometry to highlight a few points to strengthen the fundamental considerations made above.4.1. Laser-plasma emission spectrometry
The plasma induced by XUV/SXR pulses is mainly generated as a consequence of the photoeffect (electron–hole or excitonic “plasma”) and in less proportion by the collisional absorption, i.e., inverse Bremsstrahlung.96 Emission spectra from plasmas produced by short97 as well as ultra-short98,99 pulses of short-wavelength lasers have been explored in not so many studies. Peculiar observations have been reported, which require more extensive studies in the future. Thanks to a very high electron density, and relatively low electron temperature in XUV/SXR laser-plasmas, recombination dominates, especially on the surface of the expanding plume, with some consequences. A sample spectrum is shown in Fig. 5, which shows that the intensity at λ = 13.5 nm radiation is remarkable. Further, only Cu atoms contribute to the line spectrum but not ions (also because of the domination of recombination). Hence, significantly simplified atomic spectroscopy is realized with XUV/SXR lasers as compared to the traditional LIBS analysis, which is one remarkable advantage. Further, due to the weak Bremsstrahlung, the signal-to-noise ratio is maximized. On the other hand, plasma absorption is faint, such that a second optical pulse may be needed to reignite the plume.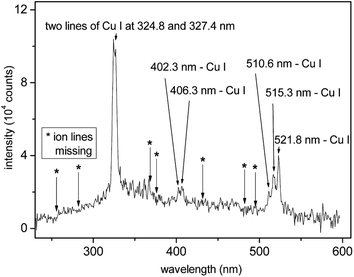 | ||
| Fig. 5 The time-integrated optical emission spectrum of the Cu plume formed in the micro-focus of the FLASH beam (BL3, a wavelength of 13.5 nm). Because of micro-focusing the irradiance was well above 1016 W cm−2. Positions of expected spectral lines of copper ions, e.g., Cu II and Cu III, are indicated by asterisks. There is no signal arising from the noise in the vicinity of these points. From Cihelka et al.100 | ||
4.2. Laser mass spectrometry
Lasers are used in MS with two purposes: (i) photoionization and (ii) micro-sampling. Hillenkamp et al.101 developed the first laser microprobe mass analyzer in 1975, which also promoted the use of the time-of-flight (TOF) analyzer for laser mass spectrometry. The setup was limited to irradiances below 108 W cm−2, and thus faced limitations for elemental quantification, e.g. for higher irradiance values, the large kinetic energy distribution of the ions affected the resolution of the mass spectra. The tremendous progress achieved so far did not really translate into the exploitation of short wavelengths, due to the lack of access to XUV lasers. Most of the MS studies using short wavelength photoionization have been done at synchrotron beamlines, as a proof-of-principle. It is clearly impractical to move MS equipment for a few beamtime shifts, since only a few worldwide beamlines offer access to permanent MS stations. This explains why, besides proof-of-principle studies, the large number of MS users has not considered XUV photons for routine applications. Mass spectra have also been taken from solid targets ablated by focused XUV and SXR from free-electron lasers.66,97 Li et al.102 took advantage of the synchrotron VUV tunability to characterize combustion intermediates in premixed flames and those from other systems in combustion research, such as hydrocarbon flames, diffusion flames, plasma and catalytic reactions. Giuliani and colleagues103,104 studied the application of synchrotron radiation for the photoactivation of ions in the short wavelength region, which is a rapidly growing field. In particular, the two-color scheme used to prepare and probe the spectra of radical anions is very interesting. It should be mentioned that Masoudnia et al.105 have shown two-color soft X-ray lasing on a tabletop laser setup.Mass spectrometry directly coupled to laser ionization37,106–108 (laser ionization mass spectrometry or LIMS), even though still without XUV, has been established as a technique for both elemental41,51,109 and molecular characterization.101,110 Since the early seminal paper of Woodin et al.111 for laser sample-ionization, two approaches have been reported, i.e. resonance-enhanced multiphoton ionization112 (REMPI) or single-photon ionization113,114 (SPI) using DUV lamps. The drastic enhancement of dissociation efficiency while using short-wavelength pulses may “relax” the need for a laser source, with the promise of being able to perform MS with a simple lamp. In general, SPI overcomes the performance of REMPI in terms of fragmentation, spatial resolution and chemical sensitivity. Demonstration of the benefit of deep and vacuum UV wavelengths (ArF* and F2 laser) was pioneered by the Kim and/or the Reilly group115,116 on the photodissociation of peptides.
Photoactivation is indeed significantly different from collisional absorption in several respects, most notably its independence on the translational excitation of ions.117 The utilization of IR lasers is popular as most organic molecules, oligonucleotides and nucleic acids have good absorption cross sections at 0.1 eV (CO2 laser), due to their phosphate backbone. Utilization of IR indeed benefits from short laser pulses, for multiphoton deposition, as well as ion trapping MS, for good temporal overlapping between photo-pulses and target analytes. IR multiphoton photodissociation has proved to be effective for DNA adducts.118 Typically, in stepwise processes, labile fragments are massively induced, which limits the access to high activation energy pathways for fragmentation. A further benefit of photodissociation is the mitigation of the low mass cutoff issue.119 Photodissociation efficiencies have been reported to be above 20%, and as high as 98%.120
Yu et al.109 developed a compact LIMS setup that included an orthogonal TOF analyzer and enabled the decrease of the kinetic energy of ions thus enhancing the resolution. The setup included a Nd:YAG laser operating at 355 nm (third harmonic), providing a spot size of 20 μm and irradiance of 1011 W cm−2, and it was used to investigate the elemental composition in metal samples. In that study, the matrix effects were observed to decrease upon increment of the laser energy, and detection limits of 10−8 mol g−1 were reported. In a more recent study,121 the same group performed LIMS orthogonal TOF at a laser irradiance of 1010 W cm−2 to analyze iron oxides. At that laser irradiance and using different laser wavelengths (i.e. 1064, 532 and 266 nm), a similar ion abundance/intensity in the mass spectra was observed. The latter was reported to be opposite to that observed for LIMS at laser irradiance ≤108 W cm−2, i.e. for low irradiance the spectra were reported to be wavelength-dependent. The same group also reported LIMS in a helium and argon environment to characterize metal targets.51 It was highlighted that at specific He and Ar pressures it was possible to moderate the energy of the ions as well as the number of multiply charged ions. Similarly, the temporal distributions of the ions were investigated for different laser-fluences and were essentially explained due to elastic-scattering and thermodynamic processes. LIMS coupling ion-storage and a TOF as a mass analyzer has been carried out for characterizing trace-elements. The setup was reported to use the storage ability of the ion trap to decrease background interference from sample-matrices, while allowing a resolution of 1500 and limits of detection of 10 pg.
Ignatova et al.122 used Fourier transform LIMS to investigate the molecular composition of inorganic mixtures based on the ratio of peak intensities. The experiments were carried out at laser irradiation <108 W cm−2 and desorption-ionization was highlighted as the main laser-sample interaction mechanism. Similarly, Posthumus et al.123 carried out LIMS for investigating nonvolatile organic molecules. A thin layer of sample was coated on a metal surface to be irradiated with a CO2 laser at 106 W cm−2. The ions generated were analyzed using a magnetic sector analyzer which included double focusing capabilities. It was highlighted that the applied method enabled the analysis of digitonin, a digitalis pentaglycoside, with a mass of 1228 Da. Hardin et al.124 developed an ingenious LIMS, which employed a moving stainless-steel belt where the sample was electro-sprayed for analysis. The system integrated a tunable dye laser and a quadrupole analyzer used to investigate nonvolatile biomolecules, e.g. saccharides, amino acids, peptides, nucleosides, and nucleotides. Limitations due to spectra reproducibility were highlighted. Similarly, it was reported that the ions generated upon desorption–ionization had a broad kinetic energy distribution, centered at about 6 eV and extending up to 25 eV. Voumard et al.112 developed a LIMS system including a reflectron TOF mass analyzer and a pulsed IR laser for desorption of neutral molecules, followed by a pulsed tunable UV laser for REMPI. The use of IR laser-induced thermal desorption followed by UV REMPI was reported to alleviate photochemical effects on the surface during desorption. In this study, spatial resolution in the μm range coupled with attomole sensitivity and a resolution of 2000 were reported. The targeted applications included spatially resolved organic-trace analysis as well as the detection of selected chemical compounds in complex mixtures.
Matrix-enhanced LIMS for the analysis of large ion-molecules has also been widely applied and many studies have been reported. Indeed, the crystallization of organic matrices together with the sample has been reported to allow the generation of large ion-molecules during the laser irradiation. Frankevich et al.125 reported matrix-assisted LIMS for the analysis of nonmetallic samples, e.g. bovine serum albumin, bradykinin and 2,5-dihydroxybenzoic acid (DHB). In that work, the samples were characterized using two different LIMS systems using nitrogen lasers emitting at 337 nm combined with reflectron TOF analyzers. Complementary experiments were also carried out using a FT-ICR mass analyzer which included a MALDI source. The measured spectra showed masses up to 66 kDa, and further highlighted a strong dependency between ion signal intensity and sample substrates. The effect of the sample substrate was related to the emission of photoelectrons under laser irradiation. The latter was reported to decrease the yield of positive ions in the MALDI plume and to perturb the ion velocity distribution. Pallix et al.113 compared mass spectra from organic polymers acquired through LIMS using REMPI and SPI. It was highlighted that the absorption of several photons through REMPI induced non-specific and massive fragmentation, which decreased the signal intensity for high mass fragments, e.g. the monomer peak was not detected. In contrast, through SPI it was possible to efficiently detect most of the species in the sample. Similarly, it was highlighted that while SPI provided a clear spectrum, SIMS generated many mass peaks of comparable intensity in the spectra, which complicated the peak assignment. The setup used 118 nm (10.5 eV) radiation for SPI, generated by frequency tripling of the third harmonic (355 nm) of an oscillator-only Nd:YAG laser, and 248 nm radiation generated by a KrF excimer laser for REMPI. Dong et al.126 further expanded the analytical capabilities of LIMS based on SPI, by using a capillary discharge XUV-laser operated at 46.9 nm (or 26.5 eV) combined with a reflectron TOF analyzer. In this study, metal-oxides having IP > 10.5 eV were characterized by using 26.5 eV and 10.5 eV laser excitation. Although, the agreement of the mass spectra acquired using the 26.5 eV and 10.5 eV lasers was highlighted, it was pointed out that the XUV-ionization approach allows measuring all the species in the sample, non-accessible otherwise with the 10.5 eV laser.
In a more recent study,31 the same XUV-SPI TOF system was used to generate 3D molecular mappings from biological samples. It was highlighted that the use of XUV-SPI enabled a sensitivity of 0.01 amol in the mass range up to 400 Da, combined with lateral and depth resolutions of about 80 nm and 20 nm respectively. Thus, XUV-SPI provided a superior performance in terms of sensitivity and spatial resolution than the VUV sources discussed in this review. Ly et al.127 discussed thoroughly the advantages of UV laser dissociation for proteomics MS, i.e. exciting the peptide backbone directly without the need of a chromophore, such as in the case of optical lasers. In particular short-wavelength laser photodissociation does not lead to fragmentation typical of collision-induced dissociation, i.e. by exciting vibrational modes in the ground electronic state. The utilization of femtosecond lasers, even when at λ = 800 nm, provided fragmentation patterns similar to those of UV lasers.
Besides the VUV lasers operating at 118 nm, Mühlberger et al.114 proposed a novel excimer VUV light source for SPI TOF mass spectrometry, which used electron beams for gas excitation. The VUV source was reported to allow wavelength tunability in the range of 100 to 200 nm by changing the working gases. The system was used to characterize organic trace species in complex gas mixtures. Similarly, other groups have reported SPI MS studies using synchrotron radiation sources, even though these sources are limited in accessibility. Devakumar et al.128 studied the 157 nm photo-fragmentation of native and derivatized oligosaccharides in a linear ion trap and in a home-built matrix-assisted laser desorption/ionization (MALDI) tandem time-of flight (TOF/TOF) mass spectrometer, and the results were compared with collision-induced dissociation (CID) experiments. VUV photo-dissociation produced product ions corresponding to high-energy fragmentation pathways; for cation-derivatized oligosaccharides, and it yielded strong cross-ring fragment ions and provided better sequence coverage than low- and high-energy CID experiments.
5. Conclusions & outlook
Increasing availability of XUV/SXR laser beams is likely to be triggering development and use in chemical analysis and mapping in the near future, benefiting from some original features of short-wavelength radiation and its interaction with matter, such as:(1) Nano-scale spot size because of a short wavelength, which brings higher spatial resolution and higher intensity in the focused beam to overcome an ablation threshold.
(2) Strong absorption of any sample, primarily controlled by an elemental composition and density of the material. The fine chemical structure plays a minor role, which may mitigate matrix effects.
(3) Single photon process: direct break of any chemical bond, since the photon energy exceeds the cohesive energy of even an ionic crystal or unsaturated bonds. The sample material can easily be ablated in a non-thermal way. In principle, the ratio of ionization and fragmentation could be shifted towards ionization choosing appropriate irradiation conditions, which should reduce the complexity of the mass spectra measured under these circumstances.
(4) Absence of non-linear optical processes. The interaction of high-power laser radiation with solids is often complicated by numerous non-linear optical processes due to the large photon number, while XUV/SXR radiation interacts mainly linearly with a few active photons.
(5) Very high plasma critical densities for XUV/SXR laser radiation. Practically, a critical density is never achieved which eliminates shielding effects by the plasma plume. The pulse energy can be deposited uniformly and deeply in the solid sample, and almost no radiation is back-reflected. The XUV/SXR ablation plume is formed from a very dense plasma, so that optical emission spectra (short-wavelength LIBS) coming from its surface are not flooded by a high number of lines assigned to higher ionization states but they are often dominated by atomic lines.
On the flip side, there are still some drawbacks hindering the prospective routine utilization of SXR/XUV laser beams in analytical spectroscopy:
(1) Limited availability of sources. While some tabletop plasma-based XUV/SXR sources are ready for applications, compact short-wavelength beamlines are still under development.
(2) Need of sophisticated techniques, i.e., radiometry at high dose rates, focused beam characterization, beamline transmission measurements, beamline and focusing optics alignment, and so on, as well as advanced, quite expensive, optical elements required for manipulation with XUV/SXR laser beams. Experienced staff is needed; while a large number of students and young investigators are educated, trained and skilled in the work with optical laser beams, just a few of them have an experience with intense XUV/SXR radiation.
(3) Lack of fundamental understanding. Interaction of optical laser radiation with matter has been studied and utilized in analytical spectroscopy for more than five decades. There is a large knowledge of various processes taking place in such an interaction summarized in many papers. A contrasting situation is in the study of interaction of XUV/SXR laser radiation with solids and molecular systems. As of today, there are around less than 200 papers published in the research area. Most of them appeared in the last decade. More fundamental and application-motivated research is needed for proper and effective applications.
(4) Limited reliability of lab systems. A few groups, including ours, have pioneered the development of tabletop systems, for fundamental studies and applications. However, an honest assessment has to mention the lack of “engineering robustness”. As mentioned at point 2, such setups require intense servicing and monitoring, which for the moment keep them away from the most of the users. It is a target goal for the next decade to make them market-ready.
The presented results may pave the way towards a promising alternative to the XUV/SXR-laser ablation spectrometry which could be the XUV/SXR-laser desorption spectrometry. The desorption mode should help to increase the sensitivity of the depth profiling because the desorption rate is smaller than the ablation rate. Thus the analyte would evaporate/ionize thin layer by thin layer. It could result in much higher depth resolution than in state-of-the-art ablation, which is interesting as long as this will not induce fractionation effects.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Ms Lydia Bradley (University of Bristol) is acknowledged for proof-reading the manuscript. Dr Yunieski Arbelo (Paul Scherrer Institute) is acknowledged for providing help during the very preliminary stages of manuscript preparation. Financial support by the Empa board of directors (PhD thesis DQ) is acknowledged. JH is supported by the Czech Science Foundation and the Czech Ministry of Education, Youth and Sports by grants 19-03314S and CZ.02.1.01/0.0/0.0/16 013/0001552 (EF16 013/0001552).References
- R. Salzer and H. W. Siesler, Infrared and Raman Spectroscopic Imaging, 2009 Search PubMed.
- C. Cheng-I, Hyperspectral Remote Sensing: Techniques for Spectral Detection and Classification, 2003 Search PubMed.
- D. Manolakis, G. S.-I. Signal Processing Magazine and undefined 2002, https://www.ieeexplore.ieee.org Search PubMed.
- J.-G. Hagmann, Ann. Phys., 2014, 526, A11–A15 CrossRef.
- T. Lyman, The Spectroscopy of the Extreme Ultra-Violet, Longmans, Green and Co., London-New York-Toronto, 1928 Search PubMed.
- J. A. R. Samson, Techniques of Vacuum Ultraviolet Spectroscopy, J. Wiley and Sons, New York-London-Sydney, 1967 Search PubMed.
- M. Ruiz-Lopez and D. Bleiner, Appl. Phys. B: Lasers Opt., 2014, 115, 311–324 CrossRef CAS.
- D. Bleiner, Y. Arbelo-Pena, L. Masoudnia and M. Ruiz-Lopez, Phys. Scr., 2014, T162, 014050 CrossRef.
- D. Bleiner, J. Costello, F. de Dortan, G. O'Sullivan and A. Michette, Short Wavelength Laboratory Sources, 2015 Search PubMed.
- Strahlungsphysik im optischen Bereich und Lichttechnik, Benennung der Wellenlängenbereiche.
- R. Tousey, J. Opt. Soc. Am., 1962, 52, 1186 CrossRef.
- R. Tousey, Appl. Opt., 1962, 1, 679–694 CrossRef CAS.
- O. Wood and H. Kinoshita, in EUV Lithography, ed. V. Bakshi, SPIE Press-Wiley Interscience, Bellingham-New York, 2009, pp. 1–54 Search PubMed.
- H. M. Hertz, M. Bertilson, E. Chubarova, J. Ewald, S. C. Gleber, O. Hemberg, M. Henriksson, O. V. Hofsten, A. Holmberg, M. Lindblom, E. Mudry, M. Otendal, J. Reinspach, M. Schlie, P. Skoglund, P. Takman, J. Thieme, J. Sedlmair, R. Tjörnhammar, T. Tuohimaa, M. Vita and U. Vogt, J. Phys.: Conf. Ser., 2009, 186 CrossRef.
- M. Berglund, L. Rymell, M. Peuker, T. Wilhein and H. M. Hertz, J. Microsc., 2000, 197, 268–273 CrossRef CAS PubMed.
- C. A. Macdonald, J. X-Ray Sci. Technol., 1996, 6, 32–47 CAS.
- A. G. Michette, Optical Systems for Soft X Rays, Springer US, Boston, MA, 1986 Search PubMed.
- E. Spiller, Soft X-Ray Optics, 1994 Search PubMed.
- S. Hau-Riege, High-Intensity X-Rays-Interaction with Matter: Processes in Plasmas, Clusters, Molecules and Solids, 2012 Search PubMed.
- D. Attwood, Soft X-Rays and Extreme Ultraviolet Radiation, Cambridge University Press, 1999 Search PubMed.
- Y. Zhang, Polym. Light, 2004, 168, 291–340 CAS.
- D. Bleiner, L. Rush, J. J. Rocca and C. S. Menoni, in X-Ray Lasers and Coherent X-Ray Sources: Development and Applications XIII, ed. A.Klisnick and C. S. Menoni, SPIE, 2019, vol. 11111, p. 6 Search PubMed.
- C. A. Heinrich, T. Pettke, W. E. Halter, M. Aigner-Torres, A. Audétat, D. Günther, B. Hattendorf, D. Bleiner, M. Guillong and I. Horn, Geochim. Cosmochim. Acta, 2003, 67, 3473–3496 CrossRef CAS.
- D. Günther and B. Hattendorf, TrAC, Trends Anal. Chem., 2005, 24, 255–265 CrossRef.
- D. Günther, D. Bleiner, M. Guillong, B. Hattendorf and I. Horn, Chimia, 2001, 55, 778–782 Search PubMed.
- D. Bleiner, M. Trottmann, A. Cabas-Vidani, A. Wichser, Y. E. Romanyuk and A. N. Tiwari, Appl. Phys. A: Mater. Sci. Process., 2020, 126, 230 CrossRef CAS.
- D. Bleiner, P. Lienemann, A. Ulrich, H. Vonmont and A. Wichser, 2003, 1146–1153.
- T. Green, I. Kuznetsov, D. Willingham, B. E. Naes, G. C. Eiden, Z. Zhu, W. Chao, J. J. Rocca, C. S. Menoni and A. M. Duffin, J. Anal. At. Spectrom., 2017, 32, 1092–1100 RSC.
- G. Vaschenko, A. G. Etxarri, C. S. Menoni, J. J. Rocca, O. Hemberg, S. Bloom, W. Chao, E. H. Anderson, D. T. Attwood, Y. Lu and B. Parkinson, Opt. Lett., 2006, 31, 3615 CrossRef CAS PubMed.
- R. Müller, I. Kuznetsov, Y. Arbelo, M. Trottmann, C. S. Menoni, J. J. Rocca, G. R. Patzke and D. Bleiner, Anal. Chem., 2018, 90, 9234–9240 CrossRef PubMed.
- I. Kuznetsov, J. Filevich, F. Dong, M. Woolston, W. Chao, E. H. Anderson, E. R. Bernstein, D. C. Crick, J. J. Rocca and C. S. Menoni, Nat. Commun., 2015, 6, 6944 CrossRef CAS PubMed.
- W. D. Hahn and N. Omenetto, Appl. Spectrosc., 2010, 64, 335A–366A CrossRef PubMed.
- D. Bleiner, F. Belloni, D. Doria, A. Lorusso and V. Nassisi, J. Anal. At. Spectrom., 2005, 20, 1337 RSC.
- H. P. Longerich, S. E. Jackson and D. Günther, J. Anal. At. Spectrom., 1996, 11, 899–904 RSC.
- D. Bleiner, P. Lienemann, A. Ulrich, H. Vonmont and A. Wichser, J. Anal. At. Spectrom., 2003, 18, 1146 RSC.
- S. A. Darke, S. E. Long, C. J. Pickford and J. F. Tyson, J. Anal. At. Spectrom., 1989, 4, 715–719 RSC.
- F. Aubriet and V. Carré, Anal. Chim. Acta, 2010, 659, 34–54 CrossRef CAS PubMed.
- Q. Yu, L. Chen, R. Huang, W. Hang, B. Huang, W. Hang and J. He, TrAC, Trends Anal. Chem., 2009, 28, 1174–1185 CrossRef CAS.
- Y. Lin, Q. Yu, W. Hang and B. Huang, Spectrochim. Acta, Part B, 2010, 65, 871–883 CrossRef.
- N. Li, B. Zhang, R. Huango, W. Hang, J. He and B. Huang, Anal. Chem., 2010, 82, 1949–1953 CrossRef PubMed.
- R. Huang, B. Zhang, D. Zou, W. Hang, J. He and B. Huang, Anal. Chem., 2011, 83, 1102–1107 CrossRef CAS PubMed.
- A. Riedo, V. Grimaudo, P. Moreno-García, M. B. Neuland, M. Tulej, P. Broekmann and P. Wurz, Chim. Int. J. Chem., 2016, 70, 268–273 CrossRef CAS PubMed.
- K. Halbach, S. Wagner, S. Scholz, T. Luckenbach and T. Reemtsma, Anal. Bioanal. Chem., 2019, 411, 617–627 CrossRef CAS PubMed.
- P. Harte, M. Evertz, T. Schwieters, M. Diehl, M. Winter and S. Nowak, 2019, 581–589.
- R. F. Haglund Jr, Appl. Surf. Sci., 1996, 96–98, 1 CrossRef.
- D. Bleiner and A. Bogaerts, Spectrochim. Acta, Part B, 2006, 61, 421–432 CrossRef.
- A. Miotello and R. Kelly, Appl. Phys. A: Mater. Sci. Process., 1999, 69, S67–S73 CrossRef CAS.
- M. A. Lieberman and A. J. Lichtenberg, Principles of Plasma Discharges and Materials Processing, John Wiley and Sons, 2nd edn, 2005 Search PubMed.
- C. De Michelis, IEEE J. Quantum Electron., 1969, 5, 188–202 CrossRef CAS.
- D. A. Cremers, L. J. Radziemski and L. J. Radziemski, in Laser Spectroscopy and its Applications, Routledge, 2017, pp. 351–415 Search PubMed.
- Y. Lin, Q. Yu, R. Huang, W. Hang, J. He and B. Huang, Spectrochim. Acta, Part B, 2009, 64, 1204–1211 CrossRef.
- B. L. Henke, E. M. Gullikson and J. C. Davis, At. Data Nucl. Data Tables, 1993, 54, 181–342 CrossRef CAS.
- N. A. Inogamov, V. V. Zhakhovsky, A. Y. Faenov, V. A. Khokhlov, V. V. Shepelev, I. Y. Skobelev, Y. Kato, M. Tanaka, T. A. Pikuz, M. Kishimoto, M. Ishino, M. Nishikino, Y. Fukuda, S. V. Bulanov, T. Kawachi, Y. V. Petrov, S. I. Anisimov and V. E. Fortov, Appl. Phys. A: Mater. Sci. Process., 2010, 101, 87–96 CrossRef.
- A. Y. Faenov, N. A. Inogamov, V. V. Zhakhovskii, V. A. Khokhlov, K. Nishihara, Y. Kato, M. Tanaka, T. A. Pikuz, M. Kishimoto, M. Ishino, M. Nishikino, T. Nakamura, Y. Fukuda, S. V. Bulanov and T. Kawachi, Appl. Phys. Lett., 2009, 94, 2–4 CrossRef.
- B. R. Benware, C. D. Macchietto, C. H. Moreno and J. J. Rocca, Phys. Rev. Lett., 1998, 81, 5804–5807 CrossRef CAS.
- J. Krzywinski, R. Sobierajski, M. Jurek, R. Nietubyc, J. B. Pelka, L. Juha, M. Bittner, V. Ĺtal, V. Vorlíček, A. Andrejczuk, J. Feldhaus, B. Keitel, E. L. Saldin, E. A. Schneidmiller, R. Treusch and M. V. Yurkov, J. Appl. Phys., 2007, 101, 2–5 CrossRef.
- M. Toufarová, V. Hájková, J. Chalupský, T. Burian, J. Vacík, V. Vorlíček, L. Vyšín, J. Gaudin, N. Medvedev, B. Ziaja, M. Nagasono, M. Yabashi, R. Sobierajski, J. Krzywinski, H. Sinn, M. Störmer, K. Koláček, K. Tiedtke, S. Toleikis and L. Juha, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 1–11 CrossRef.
- L. Juha, M. Bittner, D. Chvostova, J. Krasa, M. Kozlova, M. Pfeifer, J. Polan, A. R. Präg, B. Rus, M. Stupka, J. Feldhaus, V. Letal, Z. Otcenasek, J. Krzywinski, R. Nietubyc, J. B. Pelka, A. Andrejczuk, R. Sobierajski, L. Ryc, F. P. Boody, H. Fiedorowicz, A. Bartnik, J. Mikolajczyk, R. Rakowski, P. Kubat, L. Pina, M. Horvath, M. E. Grisham, G. O. Vaschenko, C. S. Menoni and J. J. Rocca, J. Microlithogr., Microfabr., Microsyst., 2005, 4, 033007 Search PubMed.
- M. Ishino, A. Y. Faenov, M. Tanaka, S. Tamotsu, N. Hasegawa, M. Nishikino, T. A. Pikuz, T. Kaihori and T. Kawachi, Appl. Phys. A, 2013, 110, 179–188 CrossRef CAS.
- J. Chalupský, L. Juha, J. Kuba, J. Cihelka, V. Hájková, S. Koptyaev, J. Krása, A. Velyhan, M. Bergh, C. Caleman, J. Hajdu, R. M. Bionta, H. Chapman, S. P. Hau-Riege, R. A. London, M. Jurek, J. Krzywinski, R. Nietubyc, J. B. Pelka, R. Sobierajski, J. Meyer-ter-Vehn, A. Tronnier, K. Sokolowski-Tinten, N. Stojanovic, K. Tiedtke, S. Toleikis, T. Tschentscher, H. Wabnitz and U. Zastrau, Opt. Express, 2007, 15, 6036 CrossRef PubMed.
- J. Chalupský, L. Juha, V. Hájková, J. Cihelka, L. Vyšín, J. Gautier, J. Hajdu, M. Jurek, J. Krzywinski, R. A. London, E. Papalazarou, J. B. Pelka, G. Rey, S. Sebban, R. Sobierajski, N. Stojanovic, K. Tiedtke, S. Toleikis, T. Tschentscher, C. Valentin, H. Wabnitz and P. Zeitoun, Opt. Express, 2009, 17(1), 208–217 CrossRef PubMed.
- J. Chalupský, P. Boháček, T. Burian, V. Hájková, S. P. Hau-Riege, P. A. Heimann, L. Juha, M. Messerschmidt, S. P. Moeller, B. Nagler, M. Rowen, W. F. Schlotter, M. L. Swiggers, J. J. Turner and J. Krzywinski, Phys. Rev. Appl., 2015, 4, 1–11 CrossRef.
- J. Chalupský, P. Bohacek, V. Hajkova, S. P. Hau-Riege, P. A. Heimann, L. Juha, J. Krzywinski, M. Messerschmidt, S. P. Moeller, B. Nagler, M. Rowen, W. F. Schlotter, M. L. Swiggers and J. J. Turner, Nucl. Instrum. Methods Phys. Res., Sect. A, 2011, 631, 130–133 CrossRef.
- M. Fuchs, R. Weingartner, A. Popp, Z. Major, S. Becker, J. Osterhoff, I. Cortrie, B. Zeitler, R. Hörlein, G. D. Tsakiris, U. Schramm, T. P. Rowlands-Rees, S. M. Hooker, D. Habs, F. Krausz, S. Karsch and F. Grüner, Nat. Phys., 2009, 5, 826–829 Search PubMed.
- J. Chalupský, J. Krzywinski, L. Juha, V. Hájková, J. Cihelka, T. Burian, J. Gaudin, A. Gleeson, M. Jurek, A. R. Khorsand, D. Klinger, H. Wabnitz, R. Sobierajski, M. Störmer, K. Tiedtke and S. Toleikis, Opt. Express, 2010, 18, 18271–18278 CrossRef PubMed.
- T. Burian, V. Hájková, J. Chalupský, L. Vyšín, P. Boháček, M. Přeček, J. Wild, C. Özkan, N. Coppola, S. D. Farahani, J. Schulz, H. Sinn, T. Tschentscher, J. Gaudin, S. Bajt, S. Toleikis, H. N. Chapman, R. A. Loch and M. Jurek, Opt. Mater. Express, 2015, 5(2), 254–264 CrossRef.
- N. Stojanovic, D. Von Der Linde, K. Sokolowski-Tinten, U. Zastrau, F. Perner, E. Förster, R. Sobierajski, R. Nietubyc, M. Jurek, D. Klinger, J. Pelka, J. Krzywinski, L. Juha, J. Cihelka, A. Velyhan, S. Koptyaev, V. Hajkova, J. Chalupsky, J. Kuba, T. Tschentscher, S. Toleikis, S. Düsterer and H. Redlin, Appl. Phys. Lett., 2006, 89, 1–3 CrossRef.
- A. Khorsand, R. Sobierajski, E. Louis and S. Bruijn, Opt. Express, 2010, 18(2), 700–712 CrossRef CAS PubMed.
- S. P. Hau-Riege, R. A. London, R. M. Bionta, M. A. McKernan, S. L. Baker, J. Krzywinski, R. Sobierajski, R. Nietubyc, J. B. Pelka, M. Jurek, L. Juha, J. Chalupský, J. Cihelka, V. Hájková, A. Velyhan, J. Krása, J. Kuba, K. Tiedtke, S. Toleikis, T. Tschentscher, H. Wabnitz, M. Bergh, C. Caleman, K. Sokolowski-Tinten, N. Stojanovic and U. Zastrau, Appl. Phys. Lett., 2007, 90, 46–48 CrossRef.
- S. P. Hau-Riege, R. A. London, R. M. Bionta, D. Ryutov, R. Soufli, S. Bajt, M. A. McKernan, S. L. Baker, J. Krzywinski, R. Sobierajski, R. Nietubyc, D. Klinger, J. B. Pelka, M. Jurek, L. Juha, J. Chalupský, J. Cihelka, V. Hájková, A. Velyhan, J. Krása, K. Tiedtke, S. Toleikis, H. Wabnitz, M. Bergh, C. Caleman and N. Timneanu, Appl. Phys. Lett., 2009, 95, 111104 CrossRef.
- V. Hájková, L. Juha, P. Boháček, T. Burian, J. Chalupský, L. Vyšín, J. Gaudin, P. A. Heimann, S. P. Hau-Riege, M. Jurek, D. Klinger, J. Pelka, R. Sobierajski, J. Krzywinski, M. Messerschmidt, S. P. Moeller, B. Nagler, M. Rowen, W. F. Schlotter, M. L. Swiggers, J. J. Turner, S. M. Vinko, T. Whitcher, J. Wark, M. Matuchová, S. Bajt, H. Chapman, T. Dzelzainis, D. Riley, J. Andreasson, J. Hajdu, B. Iwan, N. Timneanu, K. Saksl, R. Fäustlin, A. Singer, K. Tiedtke, S. Toleikis, I. Vartaniants and H. Wabnitz, in Damage to VUV, EUV, and X-Ray Optics III, ed. L. Juha, S. Bajt and R. A. London, SPIE, 2011, vol. 8077, p. 807718 Search PubMed.
- A. Ritucci, G. Tomassetti, A. Reale, L. Arrizza, P. Zuppella, L. Reale, L. Palladino, F. Flora, F. Bonfigli, A. Faenov, T. Pikuz, J. Kaiser, J. Nilsen and A. F. Jankowski, Opt. Lett., 2006, 31, 68 CrossRef CAS PubMed.
- I. Milov, I. A. Makhotkin, R. Sobierajski, N. Medvedev, V. Lipp, J. Chalupský, J. M. Sturm, K. Tiedtke, G. de Vries, M. Störmer, F. Siewert, R. van de Kruijs, E. Louis, I. Jacyna, M. Jurek, L. Juha, V. Hájková, V. Vozda, T. Burian, K. Saksl, B. Faatz, B. Keitel, E. Plönjes, S. Schreiber, S. Toleikis, R. Loch, M. Hermann, S. Strobel, H.-K. Nienhuys, G. Gwalt, T. Mey, H. Enkisch and F. Bijkerk, Opt. Express, 2018, 26, 19665 CrossRef CAS PubMed.
- B. L. Henke, P. Lee, T. J. Tanaka, R. L. Shimabukuro and B. K. Fujikawa, At. Data Nucl. Data Tables, 1982, 27, 1–144 CrossRef CAS.
- L. Vyšín, T. Burian, E. Ukraintsev, M. Davídková, M. E. Grisham, S. Heinbuch, J. J. Rocca and L. Juha, Radiat. Res., 2018, 189, 466–476 CrossRef PubMed.
- F. Barkusky, A. Bayer, S. Döring, P. Grossmann and K. Mann, Opt. Express, 2010, 18, 4346 CrossRef CAS PubMed.
- B. Steeg, L. Juha, J. Feldhaus, S. Jacobi, R. Sobierajski, C. Michaelsen, A. Andrejczuk and J. Krzywinski, Appl. Phys. Lett., 2004, 84, 657–659 CrossRef CAS.
- O. Frolov, K. Kolacek, J. Schmidt and J. Straus, Springer Proc. Phys., 2016, 169, 397–403 CAS.
- P. Pira, J. Wild, L. Vyšín, T. Burian, M. Toufarová, J. Chalupský and L. Juha, J. Phys. D: Appl. Phys., 2014, 47(40), 405205 CrossRef.
- D. Bleiner, Z. Chen, D. Autrique and A. Bogaerts, J. Anal. At. Spectrom., 2006, 21, 910 RSC.
- T. P. Hughes, Plasmas and Laser Light, John Wiley & Sons, New York, 1975 Search PubMed.
- F. Brech and L. Cross, Appl. Spectrosc., 1962, 16, 59 CrossRef.
- A. De Giacomo, R. Gaudiuso, C. Koral, M. Dell'Aglio and O. De Pascale, Spectrochim. Acta, Part B, 2014, 98, 19–27 CrossRef CAS.
- B. Kozlov, A. Saint and A. Skroce, J. Anal. At. Spectrom., 2003, 18, 1069–1075 RSC.
- C. Liu, X. L. Mao, S. S. Mao, X. Zeng, R. Greif and R. E. Russo, Anal. Chem., 2004, 76, 379–383 CrossRef CAS PubMed.
- D. Bleiner, Spectrochim. Acta, Part B, 2005, 60, 49–64 CrossRef.
- B. N. Chichkov, C. Momma, S. Nolte, F. von Alvensleben and A. Tiinnermann, Appl. Phys., 1996, 63, 109–115 Search PubMed.
- D. A. G. Deacon, Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip., 1986, 250(1–2), 283–288 CrossRef.
- K. Kolacek, J. Schmidt, J. Straus, O. Frolov, L. Juha and J. Chalupsky, in XX International Symposium on High-Power Laser Systems and Applications 2014, 2015, vol. 9255, p. 92553U Search PubMed.
- G. Norman, S. Starikov, V. Stegailov, V. Fortov, I. Skobelev, T. Pikuz, A. Faenov, S. Tamotsu, Y. Kato, M. Ishino, M. Tanaka, N. Hasegawa, M. Nishikino, T. Ohba, T. Kaihori, Y. Ochi, T. Imazono, Y. Fukuda, M. Kando and T. Kawachi, J. Appl. Phys., 2012, 112(1), 013104 CrossRef.
- A. Ritucci, G. Tomassetti, A. Reale, L. Arrizza, P. Zuppella, L. Reale, L. Palladino, F. Flora, F. Bonfigli, A. Faenov, T. Pikuz, J. Kaiser, J. Nilsen and A. F. Jankowski, Opt. Lett., 2006, 31, 68 CrossRef CAS PubMed.
- L. Juha, M. Bittner, D. Chvostova, J. Krasa, Z. Otcenasek, A. R. Präg, J. Ullschmied, Z. Pientka, J. Krzywinski, J. B. Pelka, A. Wawro, M. E. Grisham, G. Vaschenko, C. S. Menoni and J. J. Rocca, Appl. Phys. Lett., 2005, 86, 1–3 CrossRef.
- L. Juha, V. Hájková, J. Chalupsk, V. Vorlíček, A. Ritucci, A. Reale, P. Zuppella and M. Störmer, J. Appl. Phys., 2009, 105, 1–6 CrossRef.
- A. Bartnik, Opto-Electron. Rev., 2015, 23, 172–186 CAS.
- S. M. Vinko, U. Zastrau, S. Mazevet, J. Andreasson, S. Bajt, T. Burian, J. Chalupsky, H. N. Chapman, J. Cihelka, D. Doria, T. Döppner, S. Düsterer, T. Dzelzainis, R. R. Fäustlin, C. Fortmann, E. Förster, E. Galtier, S. H. Glenzer, S. Göde, G. Gregori, J. Hajdu, V. Hajkova, P. A. Heimann, R. Irsig, L. Juha, M. Jurek, J. Krzywinski, T. Laarmann, H. J. Lee, R. W. Lee, B. Li, K. H. Meiwes-Broer, J. P. Mithen, B. Nagler, A. J. Nelson, A. Przystawik, R. Redmer, D. Riley, F. Rosmej, R. Sobierajski, F. Tavella, R. Thiele, J. Tiggesbäumker, S. Toleikis, T. Tschentscher, L. Vysin, T. J. Whitcher, S. White and J. S. Wark, Phys. Rev. Lett., 2010, 104, 2–5 CrossRef PubMed.
- G. J. Tallents, S. Wilson, A. West, V. Aslanyan, J. Lolley and A. K. Rossall, High Energy Density Phys., 2017, 23, 129–132 CrossRef CAS.
- B. Iwan, J. Andreasson, A. Andrejczuk, E. Abreu, M. Bergh, C. Caleman, A. J. Nelson, S. Bajt, J. Chalupsky, H. N. Chapman, R. R. Fäustlin, V. Hajkova, P. A. Heimann, B. Hjörvarsson, L. Juha, D. Klinger, J. Krzywinski, B. Nagler, G. K. Pálsson, W. Singer, M. M. Seibert, R. Sobierajski, S. Toleikis, T. Tschentscher, S. M. Vinko, R. W. Lee, J. Hajdu and N. Tîmneanu, High Energy Density Phys., 2011, 7, 336–342 CrossRef CAS.
- M. Berrill, F. Brizuela, B. Langdon, H. Bravo, C. S. Menoni and J. J. Rocca, J. Opt. Soc. Am. B, 2008, 25(7), B32–B38 CrossRef CAS.
- U. Zastrau, S. M. Vinko, J. S. Wark, R. R. Fäustlin, N. Medvedev, S. Toleikis, T. Tschentscher, T. Burian, J. U. Zastrau, S. M. Vinko, J. S. Wark, R. R. Fäustlin, N. Medvedev, S. Toleikis, T. Tschentscher, T. Burian, J. Chalupsky, L. Juha, C. Fortmann, S. H. Glenzer, R. W. Lee, A. J. Nelson, T. W. J. Dzelzainis, D. Riley, B. Nagler, E. Galtier, F. B. Rosmej and E. Förster, Laser Part. Beams, 2012, 30, 45 CrossRef CAS.
- J. Cihelka, L. Juha, J. Chalupský, F. B. Rosmej, O. Renner, K. Saksl, V. Hájková, L. Vyšin, E. Galtier, R. Schott, A. R. Khorsand, D. Riley, T. Dzelzainis, A. Nelson, R. W. Lee, P. Heimann, B. Nagler, S. Vinko, J. Wark, T. Whitcher, S. Toleikis, T. Tschentscher, R. Faustlin, H. Wabnitz, S. Bajt, H. Chapman, J. Krzywinski, R. Sobierajski, D. Klinger, M. Jurek, J. Pelka, S. Hau-Riege, R. A. London, J. Kuba, N. Stojanovic, K. Sokolowski-Tinten, A. J. Gleeson, M. Störmer, J. Andreasson, J. Hajdu and N. Timneanu, Optical emission spectroscopy of various materials irradiated by soft x-ray free-electron laser, ed. L. Juha, S. Bajt and R. Sobierajski, 2009, p. 73610P Search PubMed.
- M. Karas and F. Hillenkamp, Anal. Chem., 1988, 60, 2299–2301 CrossRef CAS PubMed.
- Y. Y. Liu and F. Qi, National Synchrotron Radiation Labboratory, University of Science and Technology, Heifei, Acc. Chem. Res., 2010, 43, 68–78 CrossRef PubMed.
- A. Giuliani, J. P. Williams and M. R. Green, Anal. Chem., 2018, 90, 7176–7180 CrossRef CAS PubMed.
- F. Canon, A. R. Milosavljevi
![[c with combining umlaut]](https://www.rsc.org/images/entities/char_0063_0308.gif) , G. Van Der Rest, M. Réfrégiers, L. Nahon, P. Sarni-Manchado, V. Cheynier and A. Giuliani, Angew. Chem., Int. Ed., 2013, 52, 8377–8381 CrossRef CAS PubMed.
, G. Van Der Rest, M. Réfrégiers, L. Nahon, P. Sarni-Manchado, V. Cheynier and A. Giuliani, Angew. Chem., Int. Ed., 2013, 52, 8377–8381 CrossRef CAS PubMed. - L. Masoudnia, M. Ruiz-Lopez and D. Bleiner, Phys. Plasmas, 2016, 23, 1–14 CrossRef.
- J. Cai, M. Zheng, C. Q. Yan, H. Y. Fu, Y. J. Zhang, M. Li, Z. Zhou and Y. H. Zhang, Chin. J. Anal. Chem., 2015, 43, 765–774 CAS.
- R. J. Perchalski, R. A. Yost and B. J. Wilder, Anal. Chem., 1983, 55, 2002–2005 CrossRef CAS.
- V. Carré, L. Vernex-Loset, G. Krier, P. Manuelli and J. F. Muller, Anal. Chem., 2004, 76, 3979–3987 CrossRef PubMed.
- Q. Yu, L. Chen, R. Huang, W. Hang, J. He and B. Huang, Trends Anal. Chem., 2009, 28, 1174–1185 CrossRef CAS.
- M. A. Posthumus, P. G. Kistemaker and H. L. C. Meuzelaar, Anal. Chem., 1978, 50, 985–991 CrossRef CAS.
- R. L. Woodin, D. S. Bomse and J. L. Beauchamp, J. Am. Chem. Soc., 1978, 100, 3248–3250 CrossRef CAS.
- P. Voumard, Q. Zhan and R. Zenobi, Rev. Sci. Instrum., 1993, 64, 2215–2220 CrossRef CAS.
- J. B. Pallix, U. Schühle, C. H. Becker and D. L. Huestis, Anal. Chem., 1989, 61, 805–811 CrossRef CAS.
- F. Mühlberger, T. Streibel, J. Wieser, A. Ulrich and R. Zimmermann, Anal. Chem., 2005, 77, 7408–7414 CrossRef PubMed.
- T. Y. Kim, M. S. Thompson and J. P. Reilly, Rapid Commun. Mass Spectrom., 2005, 19, 1657–1665 CrossRef CAS PubMed.
- T. Y. Kim, J. C. Schwartz and J. P. Reilly, Anal. Chem., 2009, 81, 8809–8817 CrossRef CAS PubMed.
- J. S. Brodbelt, Chem. Soc. Rev., 2014, 43, 2757–2783 RSC.
- J. J. Wilson and J. S. Brodbelt, Anal. Chem., 2008, 80, 5186–5196 CrossRef CAS PubMed.
- J. L. Stephenson, M. M. Booth, J. A. Shalosky, J. R. Eyler and R. A. Yost, J. Am. Soc. Mass Spectrom., 1994, 5, 886–893 CrossRef CAS PubMed.
- J. A. Madsen, D. R. Boutz and J. S. Brodbelt, J. Proteome Res., 2010, 9, 4205–4214 CrossRef CAS PubMed.
- R. Huang, Q. Yu, L. Li, Y. Lin, W. Hang, J. He and B. Huang, Mass Spectrom. Rev., 2011, 30, 1256–1268 CrossRef CAS PubMed.
- V. Ignatova, L. Van Vaeck, R. Gijbels and F. Adams, Int. J. Mass Spectrom., 2003, 225, 213–224 CrossRef CAS.
- M. A. Posthumus, P. G. Kistemaker, H. L. C. Meuzelaar, M. A. Posthumus, M. C. Ten and N. de Brauw, Anal. Chem., 1978, 50, 985–991 CrossRef CAS.
- E. D. Hardin and M. L. Vestal, Anal. Chem., 1981, 53, 1492–1497 CrossRef CAS.
- V. E. Frankevich, J. Zhang, S. D. Friess, M. Dashtiev and R. Zenobi, Anal. Chem., 2003, 75, 6063–6067 CrossRef CAS PubMed.
- F. Dong, S. Heinbuch, S. G. He, Y. Xie, J. J. Rocca and E. R. Bernstein, J. Chem. Phys., 2006, 125, 164318 CrossRef CAS PubMed.
- T. Ly and R. R. Julian, Angew. Chem., Int. Ed., 2009, 48, 7130–7137 CrossRef CAS PubMed.
- A. Devakumar, M. S. Thompson and J. P. Reilly, Rapid Commun. Mass Spectrom., 2005, 19, 2313–2320 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2020 |