Open Access Article
Open Access ArticleZirconium stable isotope analysis of zircon by MC-ICP-MS: methods and application to evaluating intra-crystalline zonation in a zircon megacryst
Hannah G. D.
Tompkins
 *ab,
Lisa J.
Zieman
*ab,
Lisa J.
Zieman
 a,
Mauricio
Ibañez-Mejia
a,
Mauricio
Ibañez-Mejia
 a and
François L. H.
Tissot
a and
François L. H.
Tissot
 b
b
aDepartment of Earth and Environmental Sciences, University of Rochester, Rochester, NY 14627, USA. E-mail: htompkin@ur.rochester.edu
bThe Isotoparium, Division of Geological and Planetary Sciences, California Institute of Technology, Pasadena, CA 91125, USA
First published on 7th May 2020
Abstract
Zirconium (Zr) plays a key role in the development of phases like zircon (ZrSiO4) and baddeleyite (ZrO2) in magmatic systems. These minerals are crucial for the study of geologic time and crustal evolution, and their high resistivity to weathering and erosion results in their preservation on timescales of billions of years. Although zircon and baddeleyite may also preserve a robust record of Zr isotope behavior in high-temperature terrestrial environments, little is known about the factors that control Zr isotope partitioning in magmatic systems, the petrogenetic significance of fractionated compositions, or how these variations are recorded in Zr-rich accessory phases. Here, we describe a new analytical protocol for accurately determining the Zr stable isotope composition of zircon by multicollector-inductively coupled plasma-mass spectrometry (MC-ICP-MS), using the double-spike method to correct for procedural and instrumental mass bias. We apply this technique to test whether zircon crystallization in carbonatite magmatic systems is a driver of Zr isotope fractionation by interrogating the internal zonation of a zircon megacryst from the Mud Tank carbonatite (MTUR1). We find the MTUR1 megacryst to lack internal zoning within analytical uncertainties with a mean μ94/90ZrNIST = −55 ± 28 ppm (2 SD, n = 151), which suggests that zircon crystallization is not a driver of Zr isotope fractionation in carbonatite magmas. This observation is in stark contrast with those made in silicate magmatic systems, raising the possibility that the bonding environment of Zr4+ ions may be fundamentally different in carbonatite vs. silicate melts. Because of its remarkable homogeneity, the MTUR1 megacryst is an ideal natural reference material for Zr isotopic analysis of zircon using both solution and spatially resolved methods. The reproducibility of a pure Zr solution and our chemically purified zircon fractions indicate that the external reproducibility of our method is on the order of ±28 ppm for μ94/90Zr, or ±7 ppm per amu, at 95% confidence.
Introduction
Zirconium is geochemically classified as a High Field Strength Element (HFSE), a group of transition metals that play a fundamental role in studying the differentiation of magmatic systems and understanding the co-evolution of Earth's mantle and crust (e.g., (ref. 1–8)). Although mass-independent (e.g., nucleosynthetic and radiogenic) variations in Zr isotopic composition have been extensively studied in extra-terrestrial and some terrestrial materials (e.g., (ref. 9–19)), mass-dependent variations remain comparatively poorly studied and understood.20–24 Therefore, elucidating the mechanisms responsible for the partitioning of Zr isotopes amongst minerals and liquids in magmatic environments will be fundamental for interpreting the petrogenetic significance of fractionated isotopic compositions.According to first principles of stable isotope fractionation theory, heavy isotopes tend to preferentially occupy configurations with shorter bond lengths and lowest coordination state at thermodynamic equilibrium.25,26 Therefore, when Zr-rich phases like zircon and baddeleyite crystallize from a silicate melt, shifts in the coordination state of Zr4+ ions from 6-fold in the liquid27,28 to 8- and 7-fold in zircon29 and baddeleyite,30 respectively, have the potential to result in stable isotope fractionation. The expectation is that due to the higher coordination of Zr ions and longer Zr–O bond lengths in zircon29 and baddeleyite30 relative to the melt,27,28 these phases are likely to preferentially incorporate lighter Zr isotopes as they crystallize from a liquid.
Initial investigations of Zr stable isotope fractionation in magmatic systems, however, have resulted in conflicting observations. Studies of bulk igneous rocks20,21 interpreted a positive correlation between increasingly ‘heavy’ Zr isotopic composition and SiO2 wt% as being due to the removal of isotopically light zircon21 during magma differentiation. In contrast, a detailed study of single zircon and baddeleyite crystals from a closed igneous system has shown that these Zr-rich phases are isotopically heavy relative to the co-existing melt.23 These results not only point to opposite directions of isotope fractionation, but also show that the very hypothesis that Zr isotope variability in magmas can be driven by zircon crystallization is yet to be fully tested and understood. One approach to resolve this discrepancy is to determine the intra-crystalline zonation of zircon: if this phase is indeed driving Zr isotopic fractionation in a crystallizing magma via a Rayleigh-type mechanism,21,23 then zircon crystals should develop an internal zonation that records the compositional change of the melt as concurrent crystallization and fractionation take place.
Here, we describe a new analytical technique for the high-precision and accuracy analysis of mass-dependent Zr isotope variability in zircon using the double-spike MC-ICP-MS technique, and apply it to evaluate the intra-crystalline zoning of a zircon megacryst from the Mud Tank carbonatite.31,32 We also present results for the widely used 91500 zircon geostandard.33 In addition to testing the hypothesis that zircon crystallization may be a driver of Zr isotope fractionation in carbonatite magmatic systems, we show that: (i) our method is capable of determining Zr isotope compositions in zircon that are accurate and precise to within ±7 ppm per amu at the single measurement level, and (ii) that the megacryst studied here (MTUR1) is a valuable primary reference material for Zr isotope analyses of zircon, both by solution and spatially-resolved (e.g., SIMS and LA-ICP-MS) analytical methods.
Materials and methods
Preparation of a 91Zr–96Zr double spike
For elements with four isotopes or more, the double-spike (DS) technique is the method of choice for performing high-accuracy measurements of mass-dependent isotopic variations (e.g., (ref. 34–38)), as it allows for correction of instrumental mass-bias and fractionation during sample preparation. Three main criteria influence the choice of the two isotopes to spike and the four isotopes to use for inversion of the non-linear system of equations of the DS method: (i) the composition of the sample-spike mixture should minimize the uncertainty on α, the fractionation factor between the standard and the sample; (ii) slight variations in the sample-to-spike ratio should not lead to significant loss of precision and/or accuracy (i.e., robustness of the spike); (iii) isotopes whose abundance are affected by mass-independent effects should be avoided, as the DS method assumes that the relative abundances of all isotopes used for inversion are exclusively related to each other mass-dependently.The ‘double-spike toolbox’39 indicates that the most precise measurements of Zr isotopes are obtained using a 91Zr–96Zr DS along with 90Zr and 94Zr for inversion (see supplementary materials of Rudge et al.39). Although a 92Zr–96Zr DS can in theory be comparably robust, it is not ideal due to the potential of radiogenic 92Zr anomalies from decay of short-lived 92Nb (e.g., (ref. 13, 14 and 19)). Enriched isotopic materials were obtained from TRACE Sciences International (www.tracesciences.com) in oxide form for 91Zr (>90% purity) and 96Zr (>86%). Using the approximate isotopic composition of the primary single spikes (certified by the vendor) as input, we utilized the ‘double spike toolbox’39 MATLAB® package to estimate the DS composition that would minimize the uncertainty of α. This preliminary modelling indicated that a 0.43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.57 DS
0.57 DS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sample mixture, using a 91Zr–96Zr spike prepared in 0.49
sample mixture, using a 91Zr–96Zr spike prepared in 0.49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.51 proportions, would be optimal (blue curve in Fig. 1a).
0.51 proportions, would be optimal (blue curve in Fig. 1a).
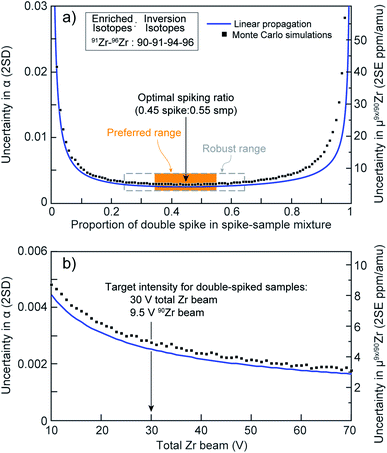 | ||
| Fig. 1 (a) Uncertainty in the sample-standard fractionation factor, α, as a function of the spike-to-sample ratio for the double spike used in this work. Orange box represents the preferred spiking range (±10%) and gray dashed box the ‘robust’ spiking range (±20%). (b) Expected uncertainty on Zr stable-isotope analyses using the optimum 91Zr–96Zr double spike as a function of the total Zr beam intensity (in V). Blue curves: calculations performed using single spike compositions as input and the code of Rudge et al.39 Black squares: Monte Carlo simulations performed using our calibrated double-spike composition and our data processing algorithm. | ||
Isotopically enriched oxides were loaded into pre-cleaned perfluoroalkoxy alkane (PFA) beakers, submerged in 5 ml of a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of ultra-pure concentrated HF and HNO3 and placed on a hot plate at 150 °C for one week to ensure complete digestion. The concentrated single spikes were then diluted to ∼120 ml of 3 M HNO3 + 0.5 M HF in pre-cleaned fluorinated ethylene propylene (FEP) bottles. Concentrations of 91Zr and 96Zr in the single spikes were determined using the standard addition method relative to a gravimetric solution prepared at the University of Rochester Laboratory for Isotope Geochemistry (UR-LIG) from high-purity Zr metal. Once the concentrations of the single spikes were known, these were mixed in the proportions needed to produce a DS of optimal composition.
1 mixture of ultra-pure concentrated HF and HNO3 and placed on a hot plate at 150 °C for one week to ensure complete digestion. The concentrated single spikes were then diluted to ∼120 ml of 3 M HNO3 + 0.5 M HF in pre-cleaned fluorinated ethylene propylene (FEP) bottles. Concentrations of 91Zr and 96Zr in the single spikes were determined using the standard addition method relative to a gravimetric solution prepared at the University of Rochester Laboratory for Isotope Geochemistry (UR-LIG) from high-purity Zr metal. Once the concentrations of the single spikes were known, these were mixed in the proportions needed to produce a DS of optimal composition.
Calibration of the DS was performed against the ZrNIST standard (see details below), by measuring the pure spike and pure standard as well as 9 standard-DS mixtures spaced every 10% in proportion (e.g., (ref. 34, 39–42)). The calculated isotopic composition of the DS is shown in Table 1. Once calibrated for its isotopic composition, the concentration of the DS was determined by reverse isotope dilution using the same gravimetric solution used for establishing the concentration of the single spikes.
| 91Zr/90Zr | 92Zr/90Zr | 94Zr/90Zr | 96Zr/90Zr | |
|---|---|---|---|---|
| Double spike | 8.169497 | 0.535834 | 0.430748 | 8.355763 |
| ±2se (abs) | 0.000017 | 0.000008 | 0.000006 | 0.000102 |
| ±2se (ppm) | 2 | 15 | 13 | 12 |
Spike optimization
After DS calibration, further optimization was performed to determine the best sample![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) spike proportion that would minimize the uncertainty on α, evaluate the potential impact of variable spiking ratios, and determine the beam intensity needed to achieve the desired measurement precision. Optimizations were performed numerically on MATLAB® using Monte Carlo simulations, such that our calibrated DS and data inversion code could be compared to the expectations from the linear error propagation modelling done using the ‘double spike toolbox’39 prior to spike mixing.
spike proportion that would minimize the uncertainty on α, evaluate the potential impact of variable spiking ratios, and determine the beam intensity needed to achieve the desired measurement precision. Optimizations were performed numerically on MATLAB® using Monte Carlo simulations, such that our calibrated DS and data inversion code could be compared to the expectations from the linear error propagation modelling done using the ‘double spike toolbox’39 prior to spike mixing.
Synthetic spike![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) standard mixtures ranging from 1% to 99% spike in 1% increments were computed numerically, using the composition of our standard and DS. Relative abundances of each isotope in the mixtures were converted to mean beam intensities by setting the total Zr beam to 30 V in each case, and standard deviations for each beam were calculated as the quadratic sum of the Johnson–Nyquist (i.e., thermal) noise and counting statistics39,41 using the following expression:
standard mixtures ranging from 1% to 99% spike in 1% increments were computed numerically, using the composition of our standard and DS. Relative abundances of each isotope in the mixtures were converted to mean beam intensities by setting the total Zr beam to 30 V in each case, and standard deviations for each beam were calculated as the quadratic sum of the Johnson–Nyquist (i.e., thermal) noise and counting statistics39,41 using the following expression:
σbeam2 = (4kTR + ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) eR)/Δt eR)/Δt | (1) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) is the mean voltage measured on the collector (in V), e is the elementary charge (1.602176634 × 10−19 C), and Δt is the integration time of our acquisition method (set to 4.192 s). Once the mean intensities and standard deviations of each beam in each mixture were calculated, 3000 synthetic integrations were simulated for each mixture as a normal random distribution and then processed using the same double spike inversion code we developed to reduce our data.
is the mean voltage measured on the collector (in V), e is the elementary charge (1.602176634 × 10−19 C), and Δt is the integration time of our acquisition method (set to 4.192 s). Once the mean intensities and standard deviations of each beam in each mixture were calculated, 3000 synthetic integrations were simulated for each mixture as a normal random distribution and then processed using the same double spike inversion code we developed to reduce our data.
Results of this numerical optimization are shown in Fig. 1a (black squares), where they are compared with expectations from the linear uncertainty propagations performed using the ‘double-spike toolbox’39 (blue curve). The agreement between both approaches is excellent, showing that our DS composition is optimal. Close inspection of the Monte Carlo simulations indicates that: (i) the optimal spike to sample ratio for minimizing the uncertainty on α is 0.45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.55, which is within 2% agreement of the linear propagation model; and (ii) there is only minimal uncertainty amplification for inaccurate spiking proportions within a ±20% range (≤1 ppm per amu), and completely negligible effects within ±10% (ca. 0.2 ppm per amu). Thus, our DS should remain highly robust when spiking ratios are within ±20% of the targeted proportion (dashed box, Fig. 1a), while the effects of a ±10% spiking inaccuracy would be negligible (orange box, Fig. 1a).
0.55, which is within 2% agreement of the linear propagation model; and (ii) there is only minimal uncertainty amplification for inaccurate spiking proportions within a ±20% range (≤1 ppm per amu), and completely negligible effects within ±10% (ca. 0.2 ppm per amu). Thus, our DS should remain highly robust when spiking ratios are within ±20% of the targeted proportion (dashed box, Fig. 1a), while the effects of a ±10% spiking inaccuracy would be negligible (orange box, Fig. 1a).
Lastly, in order to determine the total beam intensity at which samples need to be analyzed to achieve optimal precision, additional uncertainty propagation simulations were performed by varying the total Zr beam intensity at a constant (optimal) spike![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sample ratio. The results are shown in Fig. 1b. Calculations performed with the ‘double-spike toolbox’39 and our own Monte Carlo and inversion codes are in excellent agreement, and indicate that uncertainty on α decreases rapidly as the total Zr beam increases from 10 V to ca. 30 V. Above 30 V, large increases in intensity are only accompanied by moderate improvements in precision. Therefore, to minimize Zr concentrations in the measured solutions, wash-out times and the likelihood of memory effects in the sample introduction system, a total beam intensity of ca. 30 V was used in this study. This translates to approximately 9.5 V of 90Zr, which at ∼32% is the most abundant isotope in our DS–sample mixtures.
sample ratio. The results are shown in Fig. 1b. Calculations performed with the ‘double-spike toolbox’39 and our own Monte Carlo and inversion codes are in excellent agreement, and indicate that uncertainty on α decreases rapidly as the total Zr beam increases from 10 V to ca. 30 V. Above 30 V, large increases in intensity are only accompanied by moderate improvements in precision. Therefore, to minimize Zr concentrations in the measured solutions, wash-out times and the likelihood of memory effects in the sample introduction system, a total beam intensity of ca. 30 V was used in this study. This translates to approximately 9.5 V of 90Zr, which at ∼32% is the most abundant isotope in our DS–sample mixtures.
Zircon samples studied
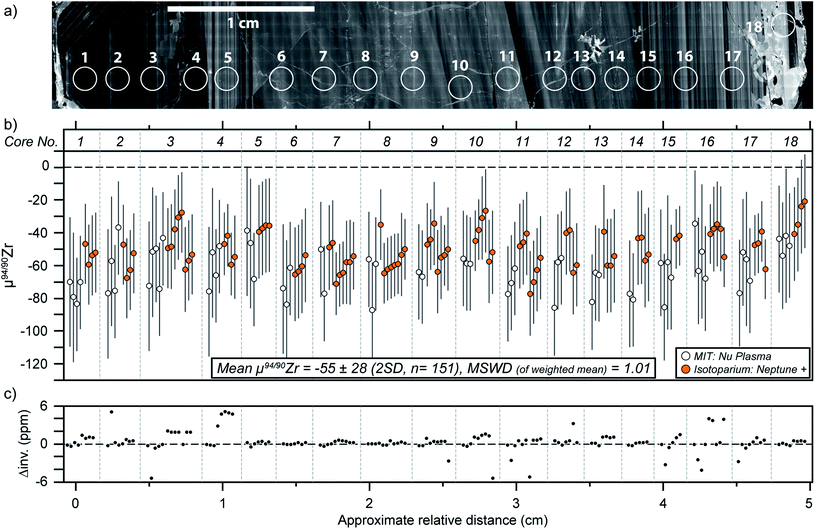
A single zircon (tetragonal ZrSiO4) megacryst from the ∼732 Ma Mud Tank carbonatite of Australia,31,32,43 hereafter referred as MTUR1, was obtained commercially, cast in epoxy resin, and sliced in half parallel to the c-axis using a low-speed saw to expose an internal section. One face of the sliced crystal was polished to a high-quality finish using 0.25 μm diamond paste and imaged by cathodoluminescence (CL; Fig. 2) using a Deben panchromatic detector mounted on a JEOL 7100FT Field Emission Scanning Electron Microscope in the Mackay Microbeam Laboratory at University of Nevada, Reno. Using the CL mosaic as a guide, 18 fragments of the crystal were carefully micro-drilled along a rim-core-rim transect (Fig. 2), using a hollow diamond drill-bit of 0.5 mm internal diameter that was custom manufactured by UKAM industrial superhard tools. Individual cores extracted from this megacryst were ∼500 μm in diameter by 500 μm in depth.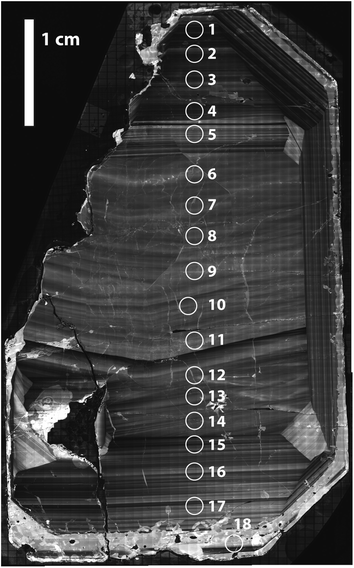 | ||
| Fig. 2 Cathodoluminescence mosaic of a sliced face of the Mud Tank zircon megacryst MTUR1, showing internal oscillatory zoning and approximate location of micro-drilled samples. | ||
Several small fragments of the 91500 zircon,33 a widely-used geostandard in the isotope geochemistry literature, were also individually picked for analysis. All samples were processed in a clean laboratory environment at the UR-LIG, as described below.
Zircon cleaning, chemical abrasion and dissolution
Each zircon fragment was rinsed twice in Milli-Q water and acetone before being transferred to individual fused quartz crucibles and placed in a muffle furnace at 900 °C for 60 hours. This thermal annealing step heals the short-range order of low to moderately radiation damaged zircon domains while leaving high-dose domains unhealed.44,45Thermally annealed fragments were carefully pipetted into 200 μl PFA microcapsules along with ca. 10 μl of MQ–H2O and submerged in ca. 100 μl of 29 M HF. Microcapsules were then placed inside a large-capacity Parr® acid digestion vessel and zircon leaching (i.e., ‘chemical abrasion’) was performed at 215 °C for 12 hours. This chemical attack preferentially removes inclusions and zircon domains with moderate to high radiation damage that may have behaved as chemically open systems after zircon crystallization,45 in addition to removing any ‘blank’ contributions from handling and micro-coring. The remaining solids (i.e., chemically abraded residues) were transferred into pre-cleaned 7 ml vials and thoroughly rinsed twice in MQ H2O, fluxed on a hot plate at 90 °C using ultrapure 6.2 M HCl, and rinsed again thrice in MQ H2O. The cleaned chemically abraded residues were loaded back into pre-cleaned microcapsules and fully dissolved using ca. 100 μl of ultra-pure 29 M HF and trace HNO3 at 215 °C for 48 hours in a high-capacity Parr® acid digestion vessel.
Concentration measurements and spiking
After complete zircon dissolution was achieved, the sample solutions (ca. 100 μl of 29 M HF) were transferred into pre-cleaned 7 ml PFA beakers containing 1 ml of 0.59 M HNO3 + 0.28 M HF. The solution was allowed to mix thoroughly on a hot plate at 120 °C for 48 hours prior to aliquoting for concentration measurements. Aliquots of 50 μl (5% of sample) were taken from each solution and diluted with 950 μl of 0.48 M HNO3 + 0.25 M HF + 2 ppb In. Concentration measurements were performed on an Agilent 7900 quadrupole ICP-MS at the University of Rochester using In as an internal standard for drift correction.After Zr concentration measurements, aliquots containing approximately 340 ng of natural Zr were pipetted from each sample, transferred into pre-cleaned 7 ml PFA beakers, and mixed with 260 ng Zr from the 91Zr–96Zr DS to achieve optimal spike![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sample proportions of 0.45
sample proportions of 0.45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.55 (Fig. 1). Spiked aliquots were fluxed at 140 °C on a hotplate overnight, dried down to a salt, re-digested in 1 ml of 12 M HCl, dried down one more time, and re-digested in 1 ml of 6 M HCl + 0.06 M HF for chromatographic purification. Complete spike-sample equilibration prior to chemical purification is vital for obtaining accurate isotopic results (e.g., (ref. 46)). Mixing the spike and sample using the same solution matrix, followed by consecutive drying steps during acid conversion before ion-exchange chemistry, ensures that spike-sample equilibration is achieved.
0.55 (Fig. 1). Spiked aliquots were fluxed at 140 °C on a hotplate overnight, dried down to a salt, re-digested in 1 ml of 12 M HCl, dried down one more time, and re-digested in 1 ml of 6 M HCl + 0.06 M HF for chromatographic purification. Complete spike-sample equilibration prior to chemical purification is vital for obtaining accurate isotopic results (e.g., (ref. 46)). Mixing the spike and sample using the same solution matrix, followed by consecutive drying steps during acid conversion before ion-exchange chemistry, ensures that spike-sample equilibration is achieved.
Chromatographic purification of Zr
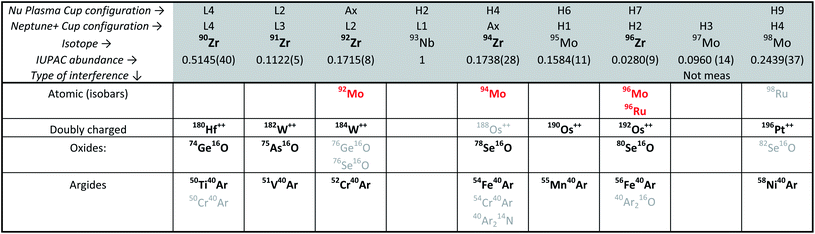
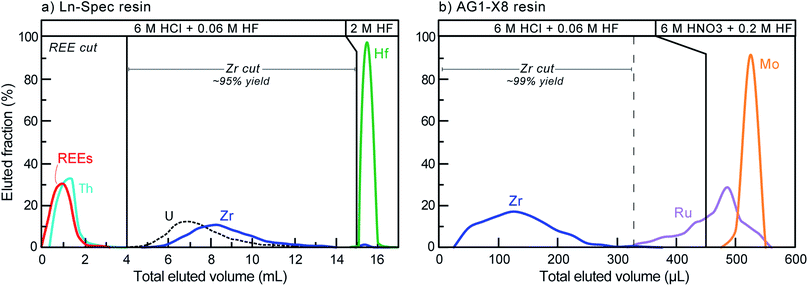
Although Zr represents ca. 50 wt% in the zircon structure, the variable yet non-negligible trace element contents that are typical in natural crystals (e.g., Hf, U, Th, REE, Ti, Mo) may be problematic for high-accuracy Zr stable isotope measurements due to spectral interferences (Table 2) and/or matrix effects during mass spectrometry. Of these, Hf and Mo are of particular concern. With typical HfO2 contents on the order of 1 to 2 wt%,5,23,47 Hf is by far the most abundant trace element in natural zircon. If not removed prior to analysis, the production of 180Hf++ species may introduce non-systematic interferences on 90Zr+. Molybdenum, although only present in low concentrations in the zircon structure, has in some Proterozoic zircon been shown to have isotopic compositions that deviate significantly from ‘normal’.48,49 This is particularly problematic because Mo isobaric interference corrections, which rely on the assumption of a ‘normal’ Mo composition (e.g., IUPAC50), would be unlikely to be accurate. Therefore, to ensure both precise and accurate Zr isotope determinations, trace elements, particularly Hf and Mo, must be removed from the sample solutions prior to MC-ICP-MS measurement.Zirconium purification was achieved using a two-column procedure, modified after Münker et al.51 and optimized at the UR-LIG to improve purity, yields, and separation of Zr from Mo, Ru and Hf (Table 3; Fig. 3). The first column step used ∼190 μl of Eichrom Ln–Spec resin (25 to 50 μm mesh) in custom-made FEP columns (L = 6 cm, ϕ = 2 mm). Elution curves were calibrated and samples were processed using an Eichrom vacuum box to enhance liquid flow and decrease elution times. Flow rates were kept below ∼50 μl per minute to avoid sample-resin disequilibrium effects. The second step utilized gravity driven flow and 50 μl of Bio-Rad AG1-X8 resin (100 to 200 μm mesh), using custom-made FEP ‘micro-columns’ (L = 1.6 cm, ϕ = 2 mm). For all separations, new (pre-cleaned) resin was loaded onto the columns and samples were processed following the steps shown in Table 3. This two-column procedure resulted in final purified fractions with >92% Zr yields, undetectable Th, U, Ru and REEs, <2% of the initial Hf, and <0.04% Mo.
| Step | Reagent volume | Reagent |
|---|---|---|
| Column 1: Eichrom Ln–Spec, 20–50 μm mesh ∼ 190 μl resin volume (ca. 6.0 × 0.2 cm) | ||
| Clean | 2 ml | 2 M HF |
| Clean | 2 ml | MQ–H2O |
| Condition | 1.5 ml | 6 M HCl − 0.06 M HF |
| Load | 1.0 ml | 6 M HCl − 0.06 M HF |
| Rinse REE | 3.0 ml | 6 M HCl − 0.06 M HF |
| Zr | 11 ml | 6 M HCl − 0.06 M HF |
| Hf | 2.0 ml | 2 M HF |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Column 2: Bio-Rad AG1-X8, 100-200 μm mesh ∼ 50 μl stem volume (ca. 1.6 × 0.2 cm) | ||
| Clean | 1.0 ml | 6 M HNO3 − 0.2 M HF |
| Clean | 1.0 ml | 6 M HCl − 0.06 M HF |
| Clean | 1.0 ml | MQ–H2O |
| Condition | 0.5 ml | 6 M HCl − 0.06 M HF |
| Load | 0.23 ml | 6 M HCl − 0.06 M HF |
| Zr | 0.1 ml | 6 M HCl − 0.06 M HF |
| Mo | 0.25 ml | 6 M HNO3 − 0.2 M HF |
The purified Zr cuts were evaporated to dryness on a hot plate at 130 °C, fluxed overnight in 2 ml of 8 M HNO3 + 15 wt% H2O2 mixture to decompose organic residues from the resin, dried down again, taken up in 1 ml of 8 M HNO3 + 14 M HF to ensure complete re-digestion, slowly evaporated to near dryness, and diluted into 2 ml of 0.59 M HNO3 + 0.28 M HF. A 2.5% (50 μl) aliquot from this solution was taken for Zr concentration measurement on the MC-ICP-MS and to verify optimal Mo removal. Samples were then diluted to a final Zr concentration of 60 ng g−1 in 0.59 M HNO3 + 0.28 M HF for MC-ICP-MS measurements.
Reagent and procedural blanks
Reagents used in this study were prepared at UR-LIG using sub-boiling distillation in dedicated Savillex® DST-1000 units. Reagent blanks determined by isotope dilution were between 2.5 and 3.6 pg g−1 Zr for the batches of concentrated HCl, HF and HNO3 used for this study.Several total procedural blanks were also measured to determine the level of laboratory contamination introduced by our dissolution and chemical purification methods. Pre-cleaned beakers were loaded with the same volumes of clean acid used for digesting our samples and spiked with ca. 50 ng of total Zr from our calibrated DS tracer. These blank loads underwent the complete chemical procedure alongside ‘unknown’ double-spiked zircons, and measurements were performed using the methods outlined below. Procedural blanks were found to be between ca. 0.2 and 0.5 ng of Zr, which are three orders of magnitude smaller than the typical Zr loads of our double-spiked samples (∼600 ng) and thus negligible.
Mass spectrometry
Zr isotopic measurements were performed using two instruments: (i) a Nu Plasma II MC-ICP-MS using an Aridus II desolvating nebulizer at the Massachusetts Institute of Technology, and (ii) a Thermo Scientific Neptune Plus using an Aridus 3 at the Isotoparium, California Institute of Technology. Measurements were performed in low mass resolution on both instruments. Static configurations were used to monitor masses 90 through 98 (Table 2). All Faraday cups in the Nu Plasma II were fitted with 1011 Ω feedback resistors. On the Neptune Plus, all Faraday cups were assigned 1011 Ω feedback resistors with the exception of H1 (95Mo) and H4 (98Mo), which were assigned 1012 Ω feedback resistors to improve measurement accuracy for Mo isobaric interference monitoring and corrections. Cup gains are calibrated daily on both instruments.Solutions were aspired using nebulizers with nominal flow rates of 100 μl min−1 in both laboratories. The average sensitivities were ∼450 V per ppm Zr on the Nu Plasma II using enhanced sensitivity cones, and ∼520 V per ppm Zr on the Neptune Plus using regular cones. This resulted in average beam intensities of 8.5 V (Nu Plasma II) and 9.2 V (Neptune Plus) on 90Zr, the most abundant isotope (∼32%) in our DS–sample mixtures when analyzing 60 ng g−1 (total Zr) solutions.
For wet-plasma measurements performed on the Nu Plasma II, sample introduction of 1 μg g−1 Zr solutions using a 100 μl min−1 nebulizer resulted in total beam intensities of ∼30 V, or a sensitivity of ∼30 V per ppm.
Each unknown measurement was bracketed by measurements of the NIST RM8299 Zr iRM, a new Zr isotopic reference material recently prepared in a collaboration between the UR-LIG, the Isotoparium, and the U.S. National Institute of Standards and Technology (NIST). Bracketing standards were spiked at the same level as the samples. Before each measurement, a 60 s baseline integration was performed while deflecting the ion beam using the ESA. On-peak-zeros (OPZ) were measured using a 50 s uptake and 20 s on-peak measurement of clean acid solution from the same batch used to dilute the samples, allowing monitoring of memory effects of the sample introduction system. Sample and bracketing standard measurements consisted of 50 s of sample uptake, followed by 50 cycles of 4.192 s (Neptune) or 5 s (Nu Plasma) integration time each, for a total of ca. 210–250 s of static on-peak sample measurement. The sample introduction system was rinsed for 360 s between samples using 0.59 M HNO3 + 0.56 M HF, before repeating the cycle for the next standard/unknown. Each measurement consumed approximately 750 mg of solution (i.e., ∼680 μl), equivalent to ∼45 ng of Zr (∼25 ng from the sample and ∼20 ng from the spike).
Within each sequence, a secondary reference material was measured to monitor mass spectrometer performance and ensure inter-session data accuracy (see details below). The 18 micro-cores from MTUR1 were analyzed three to six times each on both mass spectrometers, in a non-sequential fashion to evaluate the reproducibility of individual measurements and thus accuracy of the isotopic composition determined for each micro-core.
Double-spike data reduction
After OPZ correction, data reduction of double-spiked data was performed by simultaneously solving a system of non-linear equations of the form:| Ri/nMeas = [pRi/nSpike + (1 − p)Ri/nStd(Mi/Mn)α](Mi/Mn)β | (2) |
A key assumption of the double spike approach, which is built into eqn (2), is that the composition of the sample and the standard are mass-dependently related by a fractionation factor α:
| Ri/nsample = Ri/nStd(Mi/Mn)α | (3) |
By rearranging eqn (2) and (3), the sample ratios can also be calculated explicitly as the measured ratios stripped from the spike composition and corrected for instrumental mass bias, β:
| Ri/nsample = (Ri/nMeas/(Mi/Mn)β − pRi/nSpike)/(1 − p) | (4) |
When only 3 ratios are used to solve for α, β, and p, an exact solution always exists, and eqn (3) and (4) will, by construction, yield the exact same results. In such cases, mass-dependency amongst the three ratios used for inversion after DS processing is an outcome imposed by the data treatment assumptions.
Zirconium, however, has 5 stable isotopes, providing 4 ratios that can be used to reduce the data in at least two general ways: (i) using different combinations of 4 isotopes (e.g., 90/91/92/96Zr or 90/91/94/96Zr) for exactly solving the system as described above, or (ii) with a minimization approach that uses all 5 isotopes (i.e., 4 ratios). Unlike the exact solving method, when using a 4-ratio minimization approach, eqn (3) and (4) do not necessarily return the same result. The values of α, β, and p found by the minimization algorithm will return a sample composition, as calculated with eqn (4), that is mass-dependently related to the standard for all four ratios only if the measured ratios are free of mass-independent artifacts: e.g., isotope anomalies, interferences, and/or other systematic biases. The 4-ratio minimization approach therefore comes with a built-in data quality control, which we leverage here.
Data was reduced using a minimization approach implemented in Mathematica®, taking into account all ratios (i.e., 91/90Zr, 92/90Zr, 94/90Zr and 96/90Zr) with different weights being assigned to each based on their associated measurement uncertainty. All reported Zr isotope ratios are calculated explicitly using eqn (4) to allow any deviations from mass-dependency to be readily identified. For completeness, ‘exact’ solutions to the system using only 3 isotope ratios were also performed using the 91/90Zr, 94/90Zr and 96/90Zr ratios (i.e., optimal data reduction recommended by the double spike toolbox39). This procedure was done as an internal consistency check and in all instances the exact solving and 4-ratio minimization approaches yielded identical results within uncertainty (see discussion in Results section). The data reported throughout this study correspond to values obtained using the 4-ratio minimization approach for DS inversion.
Primary isotopic reference material and data reporting
Due to the dearth of previous Zr stable isotopic investigations, no standards of certified isotopic composition are available. In order to remediate this, a new isotopic standard for Zr was prepared in collaboration between our group and NIST. A large batch of a concentrated gravimetric Zr solution was prepared at NIST using an ultra-high purity Zr metal rod as starting material, and an aliquot of that solution was used for this investigation (henceforth referred to as ZrNIST). An exhaustive inter-laboratory calibration of the NIST solution (NIST RM8299 Zr iRM) is currently underway and will be reported in a future contribution. Therefore, no values for this standard are reported here to avoid future confusion. It should be noted, however, that the absolute isotopic composition of the ZrNIST standard is immaterial for the conclusions of this study as all data reported here are expressed as offsets relative to ZrNIST. Our results will thus be readily comparable to all future Zr isotopic investigations using the ZrNIST standard once it becomes commercially available.The isotopic compositions reported here use the mu (μ) notation,53 which represents part-per-million deviations in the Zr isotopic composition of our samples relative to the ZrNIST isotopic standard according to eqn (5):
| μ9x/90Zr = [(9x/90Zrsample/9x/90ZrNIST) − 1] × 106 | (5) |
| μ91/90Zr | Zr stable isotope compositionsa | Mo interference | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (±2σ) | μ92/90Zr | (±2σ) | μ94/90Zr | (±2σ) | μ96/90Zr | (±2σ) | 98Mo/90Zrb | Mo/Zrc | ||
| a Reported values are individual measurements, expressed as part per million deviations relative to the Zr-NIST standard according to: μ9x/90Zr = ([9x/90Zr]sample/[9x/90Zr]NIST − 1) × 106. Uncertainties reported for each ratio/measurement are daily 2SD reproducibilities of the bracketing NIST standard. b Ratio of measured ion beam intensities. c Percent Mo/Zr, expressed as atomic ratio. | ||||||||||
| Wet Plasma reference value, [Zr] = 1 μg g −1 | ||||||||||
| SPEX-Wet | −81 | (2) | −156 | (29) | −318 | (20) | −479 | (46) | 2.00 × 10−5 | 0.003% |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| MIT Nu Plasma II, Dry Plasma (Aridus II), [Zr] = 60 ng g −1 | ||||||||||
| SPEX 1 | −79 | (10) | −173 | (21) | −304 | (40) | −462 | (56) | 2.18 × 10−5 | 0.003% |
| SPEX 2 | −80 | (10) | −178 | (21) | −308 | (40) | −469 | (56) | 2.16 × 10−5 | 0.003% |
| SPEX 3 | −85 | (10) | −170 | (21) | −333 | (40) | −496 | (56) | 2.17 × 10−5 | 0.003% |
| SPEX 4 | −82 | (10) | −161 | (21) | −323 | (40) | −479 | (56) | 2.02 × 10−5 | 0.003% |
| SPEX 5 | −81 | (10) | −160 | (21) | −318 | (40) | −472 | (56) | 1.98 × 10−5 | 0.002% |
| SPEX 6 | −83 | (7) | −165 | (26) | −328 | (29) | −486 | (43) | 1.58 × 10−5 | 0.002% |
| SPEX 7 | −80 | (7) | −159 | (26) | −314 | (29) | −465 | (43) | 2.00 × 10−5 | 0.002% |
| SPEX 8 | −80 | (7) | −164 | (26) | −313 | (29) | −467 | (43) | 2.15 × 10−5 | 0.003% |
| SPEX 9 | −85 | (7) | −172 | (26) | −334 | (29) | −497 | (43) | 1.90 × 10−5 | 0.002% |
| SPEX 10 | −81 | (7) | −163 | (26) | −318 | (29) | −474 | (43) | 1.72 × 10−5 | 0.002% |
| SPEX 11 | −82 | (8) | −169 | (20) | −324 | (33) | −482 | (48) | 2.11 × 10−5 | 0.003% |
| SPEX 12 | −89 | (8) | −185 | (20) | −348 | (33) | −520 | (48) | 1.74 × 10−5 | 0.002% |
| SPEX 13 | −80 | (8) | −168 | (20) | −310 | (33) | −466 | (48) | 2.12 × 10−5 | 0.003% |
| SPEX 14 | −83 | (8) | −165 | (20) | −325 | (33) | −483 | (48) | 2.05 × 10−5 | 0.003% |
| SPEX 15 | −73 | (8) | −162 | (20) | −282 | (33) | −429 | (48) | 2.14 × 10−5 | 0.003% |
| SPEX 16 | −81 | (7) | −163 | (26) | −318 | (29) | −474 | (43) | 1.72 × 10−5 | 0.002% |
| SPEX 17 | −83 | (7) | −159 | (26) | −329 | (29) | −485 | (44) | 1.58 × 10−5 | 0.002% |
| SPEX 18 | −88 | (7) | −167 | (26) | −349 | (29) | −515 | (44) | 1.55 × 10−5 | 0.002% |
| SPEX 19 | −78 | (7) | −150 | (26) | −308 | (29) | −454 | (44) | 1.69 × 10−5 | 0.002% |
| SPEX 20 | −83 | (7) | −159 | (26) | −330 | (29) | −487 | (44) | 1.76 × 10−5 | 0.002% |
| SPEX 21 | −86 | (7) | −174 | (26) | −339 | (29) | −505 | (44) | 1.92 × 10−5 | 0.002% |
| SPEX 22 | −76 | (11) | −150 | (34) | −300 | (41) | −445 | (64) | 1.91 × 10−5 | 0.002% |
| SPEX 23 | −79 | (11) | −172 | (34) | −307 | (41) | −464 | (64) | 2.05 × 10−5 | 0.003% |
| SPEX 24 | −83 | (11) | −160 | (34) | −327 | (41) | −483 | (64) | 2.02 × 10−5 | 0.003% |
| SPEX 25 | −80 | (11) | −161 | (34) | −314 | (41) | −467 | (64) | 2.29 × 10−5 | 0.003% |
| SPEX 26 | −79 | (11) | −161 | (34) | −311 | (41) | −463 | (64) | 1.96 × 10−5 | 0.002% |
| SPEX 27 | −76 | (8) | −148 | (17) | −298 | (32) | −441 | (45) | 1.68 × 10−5 | 0.002% |
| SPEX 28 | −80 | (8) | −144 | (17) | −321 | (32) | −466 | (45) | 1.91 × 10−5 | 0.002% |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Isotoparium Neptune Plus, Dry Plasma (Aridus 3), [Zr] = 60 ng g −1 | ||||||||||
| SPEX 1 | −86 | (7) | −169 | (17) | −339 | (29) | −502 | (41) | 2.26 × 10−5 | 0.003% |
| SPEX 2 | −84 | (7) | −177 | (17) | −328 | (29) | −493 | (41) | 2.15 × 10−5 | 0.003% |
| SPEX 3 | −82 | (7) | −168 | (17) | −319 | (29) | −477 | (41) | 2.30 × 10−5 | 0.003% |
| SPEX 4 | −79 | (7) | −148 | (17) | −313 | (29) | −459 | (41) | 2.28 × 10−5 | 0.003% |
| SPEX 5 | −79 | (7) | −159 | (17) | −311 | (29) | −464 | (41) | 2.26 × 10−5 | 0.003% |
| SPEX 6 | −85 | (6) | −172 | (15) | −334 | (24) | −498 | (35) | 2.60 × 10−5 | 0.003% |
| SPEX 7 | −80 | (6) | −156 | (15) | −317 | (24) | −468 | (35) | 2.55 × 10−5 | 0.003% |
| SPEX 8 | −80 | (6) | −168 | (15) | −312 | (24) | −469 | (35) | 2.59 × 10−5 | 0.003% |
| SPEX 9 | −84 | (4) | −159 | (27) | −334 | (19) | −490 | (26) | 2.67 × 10−5 | 0.003% |
| SPEX 10 | −86 | (4) | −181 | (27) | −333 | (19) | −502 | (26) | 2.63 × 10−5 | 0.003% |
| SPEX 11 | −85 | (7) | −163 | (21) | −337 | (25) | −496 | (40) | 2.65 × 10−5 | 0.003% |
| SPEX 12 | −84 | (7) | −170 | (21) | −329 | (25) | −491 | (40) | 2.66 × 10−5 | 0.003% |
| SPEX 13 | −83 | (7) | −163 | (21) | −325 | (25) | −482 | (40) | 2.72 × 10−5 | 0.003% |
| SPEX 14 | −85 | (4) | −153 | (21) | −339 | (18) | −493 | (24) | 2.79 × 10−5 | 0.004% |
| SPEX 15 | −81 | (4) | −153 | (21) | −322 | (18) | −474 | (24) | 2.73 × 10−5 | 0.003% |
| SPEX 16 | −83 | (3) | −166 | (10) | −328 | (12) | −487 | (19) | 2.49 × 10−5 | 0.003% |
| SPEX 17 | −80 | (4) | −154 | (17) | −315 | (19) | −466 | (25) | 2.47 × 10−5 | 0.003% |
| SPEX 18 | −79 | (4) | −169 | (17) | −309 | (19) | −466 | (25) | 2.48 × 10−5 | 0.003% |
| SPEX 19 | −83 | (6) | −162 | (18) | −326 | (26) | −482 | (37) | 2.58 × 10−5 | 0.003% |
| SPEX 20 | −87 | (7) | −178 | (16) | −340 | (30) | −508 | (43) | 2.60 × 10−5 | 0.003% |
| SPEX 21 | −80 | (7) | −166 | (16) | −313 | (30) | −469 | (43) | 2.28 × 10−5 | 0.003% |
| SPEX 22 | −82 | (5) | −158 | (20) | −326 | (21) | −480 | (26) | 2.49 × 10−5 | 0.003% |
| SPEX 23 | −83 | (5) | −166 | (20) | −325 | (21) | −483 | (26) | 2.30 × 10−5 | 0.003% |
| SPEX 24 | −81 | (5) | −155 | (20) | −320 | (21) | −471 | (26) | 2.65 × 10−5 | 0.003% |
| SPEX 25 | −83 | (4) | −171 | (24) | −324 | (25) | −486 | (24) | 2.15 × 10−5 | 0.003% |
| SPEX 26 | −82 | (4) | −157 | (24) | −323 | (25) | −477 | (24) | 2.67 × 10−5 | 0.003% |
| SPEX 27 | −86 | (4) | −173 | (24) | −337 | (25) | −502 | (24) | 2.48 × 10−5 | 0.003% |
| Zr stable isotope compositionsb | Mo interference | |||||||
|---|---|---|---|---|---|---|---|---|
| ZrSpk/ZrTota | μ91/90Zr (±2σ) | μ92/90Zr (±2σ) | μ94/90Zr (±2σ) | μ96/90Zr (±2σ) | 98Mo/90Zrc | Mo/Zrd | Lab | |
| a Fraction of Zr (by mass) from double spike in the spike-sample mixture, calculated by isotope dilution. b Reported values are individual measurements for each fraction, expressed as part per million deviations relative to the Zr-NIST standard according to: μ9x/90Zr = ([9x/90Zr]sample/[9x/90Zr]NIST − 1) × 106. Uncertainties reported for each ratio/measurement are daily 2SD reproducibilities of the bracketing NIST standard. c Ratio of measured ion beam intensities. d Percent Mo/Zr, expressed as atomic ratio. Lab: 1 = Nu Plasma II at MIT; 2 = Neptune Plus at Caltech's Isotoparium. | ||||||||
| MTUR1-c1 | 52% | −18 (10) | −34 (21) | −70 (40) | −103 (56) | 5.15 × 10−5 | 0.006% | 1 |
| −21 (10) | −54 (21) | −79 (40) | −125 (56) | 5.09 × 10−5 | 0.006% | 1 | ||
| −20 (7) | −27 (26) | −84 (29) | −116 (44) | 5.02 × 10−5 | 0.006% | 1 | ||
| −18 (7) | −43 (26) | −70 (29) | −108 (44) | 4.78 × 10−5 | 0.005% | 1 | ||
| −9 (6) | −12 (15) | −47 (24) | −50 (35) | 5.85 × 10−5 | 0.007% | 2 | ||
| −15 (6) | −27 (15) | −59 (24) | −87 (35) | 5.87 × 10−5 | 0.007% | 2 | ||
| −13 (6) | −12 (15) | −54 (24) | −72 (35) | 5.86 × 10−5 | 0.007% | 2 | ||
| −13 (6) | −17 (15) | −52 (24) | −72 (35) | 5.89 × 10−5 | 0.007% | 2 | ||
| MTUR1-c2 | 48% | −20 (10) | −47 (21) | −77 (40) | −119 (56) | 4.70 × 10−5 | 0.006% | 1 |
| −15 (10) | −31 (21) | −57 (40) | −87 (56) | 4.57 × 10−5 | 0.005% | 1 | ||
| −18 (7) | −22 (26) | −76(29) | −103 (44) | 4.44 × 10−5 | 0.005% | 1 | ||
| −10 (7) | −22 (26) | −37 (29) | −57 (44) | 4.26 × 10−5 | 0.005% | 1 | ||
| −13 (6) | −45 (15) | −47 (24) | −81 (35) | 5.26 × 10−5 | 0.006% | 2 | ||
| −16 (6) | −24 (15) | −68 (24) | −90 (35) | 5.31 × 10−5 | 0.006% | 2 | ||
| −16 (6) | −28 (15) | −63 (24) | −91 (35) | 5.24 × 10−5 | 0.006% | 2 | ||
| −13 (6) | −20 (15) | −52 (24) | −74 (35) | 5.28 × 10−5 | 0.006% | 2 | ||
| MTUR1-c3 | 49% | −19 (10) | −46 (21) | −73 (40) | −112 (56) | 5.37 × 10−5 | 0.006% | 1 |
| −14 (10) | −40 (21) | −52 (40) | −84 (56) | 5.69 × 10−5 | 0.007% | 1 | ||
| −15 (8) | −55 (20) | −50 (33) | −90 (48) | 5.49 × 10−5 | 0.007% | 1 | ||
| −20 (7) | −54 (26) | −74 (29) | −119 (44) | 5.49 × 10−5 | 0.007% | 1 | ||
| −11 (7) | −19 (26) | −44 (29) | −63 (44) | 5.11 × 10−5 | 0.006% | 1 | ||
| −12 (6) | −15 (15) | −49 (24) | −68 (35) | 1.39 × 10−4 | 0.017% | 2 | ||
| −13 (6) | −28 (18) | −48 (26) | −74 (37) | 1.26 × 10−4 | 0.015% | 2 | ||
| −10 (6) | −21 (15) | −38 (24) | −57 (35) | 1.39 × 10−4 | 0.017% | 2 | ||
| −8 (6) | −16 (18) | −31 (26) | −46 (37) | 1.28 × 10−4 | 0.015% | 2 | ||
| −7 (6) | −20 (15) | −27 (25) | −44 (35) | 1.26 × 10−4 | 0.015% | 2 | ||
| −16 (6) | −36 (18) | −62 (26) | −95 (37) | 1.27 × 10−4 | 0.015% | 2 | ||
| −15 (6) | −33 (15) | −57 (24) | −87 (35) | 1.39 × 10−4 | 0.017% | 2 | ||
| −14 (6) | −29 (15) | −53 (24) | −80 (35) | 1.39 × 10−4 | 0.017% | 2 | ||
| MTUR1-c4 | 47% | −19 (10) | −35 (21) | −76 (40) | −111 (56) | 3.50 × 10−5 | 0.004% | 1 |
| −13 (10) | −29 (21) | −52 (40) | −79 (56) | 3.45 × 10−5 | 0.004% | 1 | ||
| −17 (7) | −42 (26) | −66 (29) | −103 (44) | 3.18 × 10−5 | 0.004% | 1 | ||
| −12 (7) | −18 (26) | −48 (29) | −68 (44) | 3.22 × 10−5 | 0.004% | 1 | ||
| −11 (4) | −17 (27) | −47 (19) | −60 (26) | 3.20 × 10−4 | 0.040% | 2 | ||
| −8 (4) | −14 (27) | −41 (19) | −41 (26) | 3.26 × 10−4 | 0.040% | 2 | ||
| −13 (4) | −12 (27) | −59 (19) | −71 (26) | 3.23 × 10−4 | 0.040% | 2 | ||
| −13 (7) | −13 (21) | −55 (25) | −73 (40) | 3.26 × 10−4 | 0.040% | 2 | ||
| MTUR1-c5 | 47% | −9 (10) | −1 (21) | −39 (40) | −47 (56) | 4.09 × 10−5 | 0.005% | 1 |
| −13 (10) | −40 (21) | −46 (40) | −78 (56) | 3.82 × 10−5 | 0.005% | 1 | ||
| −17 (7) | −31 (26) | −68 (29) | −97 (44) | 3.56 × 10−5 | 0.004% | 1 | ||
| −9 (7) | −11 (17) | −39 (29) | −54 (41) | 4.61 × 10−5 | 0.006% | 2 | ||
| −8 (7) | −13 (17) | −37 (29) | −46 (41) | 4.63 × 10−5 | 0.006% | 2 | ||
| −7 (7) | −22 (17) | −36 (29) | −43 (41) | 4.54 × 10−5 | 0.006% | 2 | ||
| −6 (7) | −13 (17) | −35 (29) | −32 (41) | 4.59 × 10−5 | 0.006% | 2 | ||
| MTUR1-c6 | 46% | −18 (10) | −28 (21) | −74 (40) | −105 (56) | 4.39 × 10−5 | 0.005% | 1 |
| −21 (10) | −42 (21) | −84 (40) | −124 (56) | 4.20 × 10−5 | 0.005% | 1 | ||
| −16 (7) | −30 (26) | −62 (29) | −91 (44) | 3.96 × 10−5 | 0.005% | 1 | ||
| −17 (7) | −40 (17) | −65 (29) | −101 (41) | 5.09 × 10−5 | 0.006% | 2 | ||
| −16 (7) | −31 (17) | −64 (29) | −94 (41) | 5.10 × 10−5 | 0.006% | 2 | ||
| −16 (7) | −43 (17) | −60 (29) | −97 (41) | 5.08 × 10−5 | 0.006% | 2 | ||
| −13 (7) | −25 (17) | −54 (29) | −78 (41) | 5.06 × 10−5 | 0.006% | 2 | ||
| MTUR1-c7 | 45% | −13 (7) | −29 (26) | −50 (29) | −76 (43) | 4.44 × 10−5 | 0.006% | 1 |
| −20 (7) | −48 (26) | −77 (29) | −119 (43) | 3.95 × 10−5 | 0.005% | 1 | ||
| −11 (6) | −11 (18) | −49 (26) | −65 (37) | 4.93 × 10−5 | 0.006% | 2 | ||
| −12 (6) | −25 (18) | −46 (26) | −69 (37) | 4.96 × 10−5 | 0.006% | 2 | ||
| −17 (4) | −20 (27) | −71 (19) | −96 (26) | 5.25 × 10−5 | 0.007% | 2 | ||
| −15 (4) | −8 (27) | −66 (19) | −84 (26) | 5.33 × 10−5 | 0.007% | 2 | ||
| −15 (4) | −12 (27) | −64 (19) | −84 (26) | 5.28 × 10−5 | 0.007% | 2 | ||
| −13 (7) | −11 (21) | −58 (25) | −76 (40) | 5.36 × 10−5 | 0.007% | 2 | ||
| −14 (6) | −20 (18) | −58 (26) | −81 (37) | 4.88 × 10−5 | 0.006% | 2 | ||
| −13 (6) | −19 (18) | −54 (21) | −76 (30) | 4.89 × 10−5 | 0.006% | 2 | ||
| MTUR1-c8 | 45% | −14 (7) | −21 (26) | −56 (29) | −79 (43) | 3.60 × 10−5 | 0.005% | 1 |
| −22 (7) | −38 (26) | −87 (29) | −126 (43) | 4.20 × 10−5 | 0.005% | 1 | ||
| −14 (7) | −21 (26) | −59 (29) | −83 (44) | 3.33 × 10−5 | 0.004% | 1 | ||
| −8 (7) | −13 (17) | −35 (22) | −44 (37) | 4.13 × 10−5 | 0.005% | 2 | ||
| −17 (4) | −36 (17) | −65 (19) | −98 (25) | 4.18 × 10−5 | 0.005% | 2 | ||
| −16 (4) | −34 (27) | −62 (19) | −94 (26) | 4.43 × 10−5 | 0.006% | 2 | ||
| −13 (4) | −14 (27) | −61 (19) | −72 (26) | 4.43 × 10−5 | 0.006% | 2 | ||
| −15 (4) | −23 (27) | −60 (19) | −86 (26) | 4.47 × 10−5 | 0.006% | 2 | ||
| −14 (4) | −17 (17) | −59 (19) | −80 (25) | 4.26 × 10−5 | 0.005% | 2 | ||
| −12 (7) | −15 (21) | −53 (25) | −67 (40) | 4.55 × 10−5 | 0.006% | 2 | ||
| −12 (4) | −12 (17) | −50 (19) | −66 (25) | 4.24 × 10−5 | 0.005% | 2 | ||
| MTUR1-c9 | 46% | −17 (7) | −38 (26) | −64 (29) | −97 (43) | 4.11 × 10−5 | 0.005% | 1 |
| −17 (7) | −40 (26) | −67 (29) | −103 (44) | 3.90 × 10−5 | 0.005% | 1 | ||
| −9 (7) | −24 (21) | −47 (25) | −49 (40) | 5.22 × 10−5 | 0.007% | 2 | ||
| −12 (4) | −27 (17) | −44 (19) | −69 (25) | 4.83 × 10−5 | 0.006% | 2 | ||
| −5 (7) | −11 (21) | −34 (25) | −69 (40) | 4.79 × 10−5 | 0.006% | 2 | ||
| −16 (7) | −28 (21) | −64 (25) | −92 (40) | 5.21 × 10−5 | 0.006% | 2 | ||
| −13 (7) | −13 (21) | −55 (25) | −74 (40) | 5.21 × 10−5 | 0.006% | 2 | ||
| −13 (4) | −14 (17) | −54 (19) | −73 (25) | 4.90 × 10−5 | 0.006% | 2 | ||
| −11 (7) | −10 (21) | −50 (25) | −60 (40) | 5.28 × 10−5 | 0.007% | 2 | ||
| MTUR1-c10 | 55% | −14 (7) | −32 (26) | −56 (29) | −85 (43) | 5.44 × 10−5 | 0.006% | 1 |
| −16 (7) | −49 (26) | −58 (29) | −98 (43) | 5.53 × 10−5 | 0.006% | 1 | ||
| −15 (7) | −30 (26) | −59 (29) | −87 (44) | 5.49 × 10−5 | 0.006% | 1 | ||
| −12 (4) | −33 (17) | −45 (19) | −72 (25) | 6.13 × 10−5 | 0.007% | 2 | ||
| −11 (4) | −42 (17) | −38 (19) | −69 (25) | 6.11 × 10−5 | 0.007% | 2 | ||
| −7 (7) | −15 (21) | −31 (25) | −41 (40) | 6.58 × 10−5 | 0.007% | 2 | ||
| −6 (7) | −13 (21) | −27 (25) | −34 (40) | 6.66 × 10−5 | 0.007% | 2 | ||
| −15 (7) | −30 (21) | −57 (25) | −86 (40) | 6.57 × 10−5 | 0.007% | 2 | ||
| −13 (7) | −28 (21) | −52 (25) | −78 (40) | 6.57 × 10−5 | 0.007% | 2 | ||
| MTUR1-c11 | 49% | −20 (7) | −45 (26) | −77 (29) | −118 (43) | 4.78 × 10−5 | 0.006% | 1 |
| −19 (7) | −45 (26) | −70 (29) | −110 (43) | 4.83 × 10−5 | 0.006% | 1 | ||
| −17 (7) | −46 (26) | −62 (29) | −100 (44) | 4.53 × 10−5 | 0.005% | 1 | ||
| −12 (6) | −23 (18) | −48 (26) | −71 (37) | 5.13 × 10−5 | 0.006% | 2 | ||
| −12 (6) | −24 (18) | −46 (26) | −68 (37) | 5.14 × 10−5 | 0.006% | 2 | ||
| −10 (7) | −20 (21) | −40 (25) | −60 (40) | 5.56 × 10−5 | 0.007% | 2 | ||
| −19 (6) | −32 (18) | −77 (26) | −110 (37) | 5.09 × 10−5 | 0.006% | 2 | ||
| −18 (7) | −31 (21) | −70 (25) | −102 (40) | 5.56 × 10−5 | 0.007% | 2 | ||
| −16 (7) | −32 (21) | −62 (25) | −93 (40) | 5.58 × 10−5 | 0.007% | 2 | ||
| −13 (7) | −17 (21) | −55 (25) | −76 (40) | 5.61 × 10−5 | 0.007% | 2 | ||
| MTUR1-c12 | 48% | −20 (7) | −11 (26) | −86 (29) | −110 (43) | 4.36 × 10−5 | 0.005% | 1 |
| −15 (7) | −34 (26) | −58 (29) | −89 (43) | 4.08 × 10−5 | 0.005% | 1 | ||
| −14 (7) | −31 (26) | −55 (29) | −83 (44) | 3.92 × 10−5 | 0.005% | 1 | ||
| −10 (7) | −18 (21) | −40 (25) | −58 (40) | 4.89 × 10−5 | 0.006% | 2 | ||
| −9 (7) | −11 (21) | −38 (25) | −51 (40) | 4.89 × 10−5 | 0.006% | 2 | ||
| −15 (7) | −15 (21) | −64 (25) | −86 (40) | 4.85 × 10−5 | 0.006% | 2 | ||
| −15 (7) | −32 (21) | −59 (25) | −89 (40) | 4.86 × 10−5 | 0.006% | 2 | ||
| MTUR1-c13 | 55% | −20 (7) | −34 (26) | −82 (29) | −118 (43) | 5.33 × 10−5 | 0.006% | 1 |
| −16 (7) | −23 (26) | −64 (29) | −90 (43) | 5.74 × 10−5 | 0.006% | 1 | ||
| −18 (7) | −53 (26) | −66 (29) | −109 (44) | 5.24 × 10−5 | 0.006% | 1 | ||
| −10 (7) | −23 (17) | −39 (29) | −60 (41) | 6.46 × 10−5 | 0.007% | 2 | ||
| −15 (7) | −23 (17) | −60 (29) | −85 (41) | 6.52 × 10−5 | 0.007% | 2 | ||
| −16 (7) | −38 (17) | −60 (29) | −93 (41) | 6.44 × 10−5 | 0.007% | 2 | ||
| −14 (7) | −31 (17) | −54 (29) | −82 (41) | 6.50 × 10−5 | 0.007% | 2 | ||
| MTUR1-c14 | 47% | −20 (8) | −42 (20) | −77 (33) | −118 (48) | 3.88 × 10−5 | 0.005% | 1 |
| −21 (7) | −51 (26) | −81 (29) | −125 (44) | 4.03 × 10−5 | 0.005% | 1 | ||
| −11 (7) | −27 (17) | −43 (29) | −66 (41) | 4.74 × 10−5 | 0.006% | 2 | ||
| −11 (7) | −21 (17) | −43 (29) | −62 (41) | 4.76 × 10−5 | 0.006% | 2 | ||
| −14 (7) | −27 (17) | −57 (29) | −83 (41) | 4.76 × 10−5 | 0.006% | 2 | ||
| −13 (7) | −18 (17) | −53 (29) | −75 (41) | 4.78 × 10−5 | 0.006% | 2 | ||
| MTUR1-c15 | 48% | −15 (8) | −29 (20) | −58 (33) | −87 (48) | 4.92 × 10−5 | 0.006% | 1 |
| −21 (8) | −28 (20) | −85 (33) | −118 (48) | 4.68 × 10−5 | 0.006% | 1 | ||
| −16 (11) | −50 (34) | −58 (41) | −98 (64) | 5.42 × 10−5 | 0.007% | 1 | ||
| −16 (8) | −15 (17) | −67 (32) | −89 (45) | 5.00 × 10−5 | 0.006% | 1 | ||
| −9 (4) | −15 (21) | −44 (18) | −50 (24) | 6.37 × 10−5 | 0.008% | 2 | ||
| −7 (4) | −13 (21) | −42 (18) | −32 (24) | 6.30 × 10−5 | 0.008% | 2 | ||
| MTUR1-c16 | 53% | −9 (8) | −22 (20) | −34 (33) | −53 (48) | 1.84 × 10−4 | 0.020% | 1 |
| −16 (8) | −35 (20) | −63 (33) | −95 (48) | 1.86 × 10−4 | 0.020% | 1 | ||
| −14 (11) | −38 (34) | −51 (41) | −83 (64) | 1.84 × 10−4 | 0.020% | 1 | ||
| −18 (8) | −39 (17) | −68 (32) | −103 (45) | 1.84 × 10−4 | 0.020% | 1 | ||
| −10 (4) | −15 (21) | −41 (18) | −58 (24) | 2.20 × 10−4 | 0.024% | 2 | ||
| −11 (6) | −34 (18) | −38 (26) | −64 (37) | 1.98 × 10−4 | 0.022% | 2 | ||
| −8 (6) | −33 (18) | −34 (26) | −48 (37) | 1.99 × 10−4 | 0.022% | 2 | ||
| −4 (6) | −10 (18) | −37 (26) | −26 (37) | 1.98 × 10−4 | 0.022% | 2 | ||
| −14 (4) | −25 (21) | −55 (18) | −80 (24) | 2.18 × 10−4 | 0.024% | 2 | ||
| MTUR1-c17 | 48% | −20 (8) | −45 (20) | −77 (33) | −117 (48) | 4.56 × 10−5 | 0.005% | 1 |
| −13 (8) | −24 (20) | −52 (33) | −76 (48) | 4.42 × 10−5 | 0.005% | 1 | ||
| −16 (11) | −59 (34) | −56 (41) | −100 (64) | 4.24 × 10−5 | 0.005% | 1 | ||
| −17 (8) | −31 (17) | −69 (32) | −101 (45) | 4.15 × 10−5 | 0.005% | 1 | ||
| −12 (4) | −28 (17) | −48 (19) | −73 (25) | 4.85 × 10−5 | 0.006% | 2 | ||
| −9 (4) | −17 (21) | −46 (18) | −46 (24) | 5.29 × 10−5 | 0.006% | 2 | ||
| −10 (4) | −29 (17) | −39 (19) | −62 (25) | 4.88 × 10−5 | 0.006% | 2 | ||
| −15 (4) | −18 (21) | −62 (18) | −85 (24) | 5.33 × 10−5 | 0.006% | 2 | ||
| MTUR1-c18 | 47% | −11 (8) | −26 (20) | −44 (33) | −67 (48) | 4.27 × 10−5 | 0.005% | 1 |
| −13 (8) | −17 (20) | −54 (33) | −75 (48) | 4.19 × 10−5 | 0.005% | 1 | ||
| −10 (11) | −18 (34) | −42 (41) | −60 (64) | 4.23 × 10−5 | 0.005% | 1 | ||
| −13 (8) | −32 (17) | −48 (32) | −75 (45) | 4.66 × 10−5 | 0.006% | 1 | ||
| −10 (7) | −12 (17) | −41 (29) | −56 (41) | 5.44 × 10−5 | 0.007% | 2 | ||
| −9 (7) | −17 (17) | −35 (29) | −51(41) | 5.48 × 10−5 | 0.007% | 2 | ||
| −5(7) | −12 (17) | −24 (29) | −30 (41) | 5.45 × 10−5 | 0.007% | 2 | ||
| −5 (7) | −12 (17) | −21 (29) | −27 (41) | 5.46 × 10−5 | 0.007% | 2 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| 91500 z1 | 47% | −34 (11) | −45 (34) | −140 (41) | −194 (64) | 2.13 × 10−4 | 0.026% | 1 |
| 91500 z2 | 46% | −36 (11) | −65 (34) | −145 (41) | −211 (64) | 2.38 × 10−4 | 0.030% | 1 |
| 91500 z3 | 46% | −34 (8) | −69 (17) | −132 (32) | −198 (45) | 2.39 × 10−4 | 0.030% | 1 |
| 91500 z4 | 46% | −34 (11) | −48 (34) | −139 (41) | −194 (64) | 1.99 × 10−4 | 0.025% | 1 |
| 91500 z5 | 46% | −38 (8) | −64 (17) | −153 (32) | −220 (45) | 1.98 × 10−4 | 0.025% | 1 |
| 91500 z6 | 46% | −24 (11) | −42 (34) | −98 (41) | −142 (64) | 1.89 × 10−4 | 0.024% | 1 |
| 91500 z7 | 46% | −39 (8) | −70 (17) | −154 (32) | −225 (45) | 1.87 × 10−4 | 0.023% | 1 |
| 91500 z8 | 46% | −30 (11) | −48 (34) | −120 (41) | −171 (64) | 2.25 × 10−4 | 0.028% | 1 |
While stable isotope studies traditionally report sample compositions in delta (δ) notation (i.e., isotope-ratio offsets relative to the standard in parts-per-mil), we use here the μ notation because of: (i) the small degree of variability observed, and (ii) the high level of analytical precision. Conversion to traditional δ values can be simply done by dividing our reported μ offsets by 103.
For each day of analyses, the dispersion of the standard-bracketed standard (2SD) for each isotope ratio was calculated using linear interpolation. Uncertainties for individual sample measurements are reported as the 2SD daily external reproducibility of the standard, rather than the internal precision (i.e., from counting statistics) of each measurement.
Monitoring data accuracy: the need for secondary isotopic reference materials
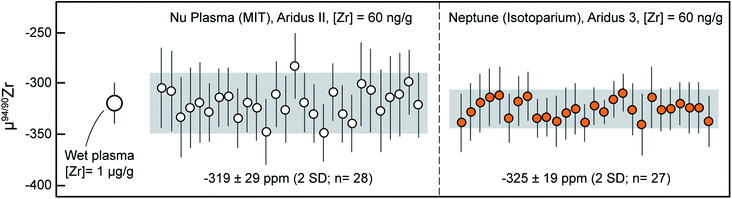
Because Zr stable isotope analyses are still in their infancy, no reference materials with ‘known’ isotopic composition relative to ZrNIST are available. To alleviate this, and to monitor data accuracy during and in-between measurement sessions and instruments, we used an ICP-MS Zr calibration solution obtained from SPEX CertiPrep (Lot# 21-168ZRM; ‘Assurance’ grade) that was measured systematically during our sessions. This solution consistently yielded values fractionated by ca. −80 ppm per amu relative to ZrNIST, and can thus become a useful secondary reference material for Zr stable isotope analysis. A reference μ94/90Zr value of −320 ± 20 ppm (2SD) was determined using ‘wet plasma’ measurements of a 1 μg g−1 solution. Measurements in ‘wet plasma’ mode were performed to evaluate consistency relative to those obtained subsequent by ‘dry plasma’ using the Aridus II and 3 desolvating nebulizer inlet systems.During the analytical sessions in which MUTR1 zircon was analyzed, this SPEX solution was measured approximately 28 times in each laboratory: ∼10 times daily, once every 2 to 3 hours. The results of all individual measurement are reported in Table 4 and μ94/90Zr values summarized in Fig. 4. Results obtained using the Nu Plasma II yield a mean μ94/90Zr = −319 ± 29 ppm (2SD) and measurements made on the Neptune Plus yield a mean μ94/90Zr = −325 ± 19 ppm (2SD). Mean values obtained using both instruments are in excellent agreement with each other and with the wet plasma value, demonstrating accuracy of all routines and the lack of inter-laboratory bias in our measurements.
Industrial secondary reference materials such as the high-purity SPEX solution introduced here are different from natural secondary reference materials (known as ‘geostandards’) in that they need no additional chemical purification prior to analysis. Measurements of such solutions provide a direct assessment of mass-spectrometer performance, free from potential biases introduced by the chromatographic purification required by natural samples.
Natural ‘geostandard’ results, on the other hand, provide an assessment for the reproducibility of the complete analytical protocol, being sensitive to biases in sample preparation, chemical purification and mass spectrometry. Industrial secondary reference materials are thus not a replacement for natural ‘geostandards’, but rather a complement that can be used to isolate mass spectrometry (and/or data acquisition and processing) bias, and to monitor mass spectrometer performance within and in-between analytical sessions.
Aliquots of the SPEX stock solution used in this study can be obtained from M. Ibañez-Mejia and/or F. L. H. Tissot upon request.
Mo isobaric interferences
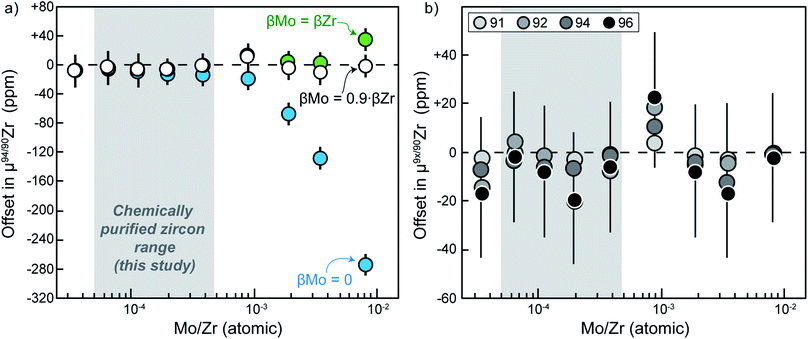
Due to the multiple isobaric interferences that Mo isotopes have on Zr (Table 2), evaluating the effects that residual Mo in purified sample solutions have on the accuracy of the results is paramount. To address this, a doping test was performed in which variable amounts of natural Mo ranging from ca. 3 × 10−5 (0.003% atomic Mo/Zr) to ca. 1 × 10−2 (1%) were added to aliquots of a double-spiked ZrNIST standard solution. Doped solutions were analyzed using the Neptune Plus at Caltech, bracketed by measurements of the Mo-free standard batch from which all doped solutions were derived.Results of Mo doping tests are shown in Fig. 5. Isobaric interferences on the 92Zr, 94Zr and 96Zr beams were corrected according to the general relationship:
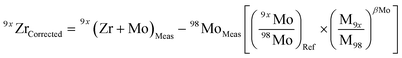 | (6) |
Due to the low beam intensities measured for the un-interfered 95Mo, 97Mo and 98Mo masses in doping experiments and chemically purified solutions, accurate determination of within-run βMo is not possible. Three potential ways for addressing this issue are illustrated in Fig. 5a, namely: (i) no correction for Mo instrumental mass fractionation is applied for isobaric interference corrections (i.e., βMo = 0; blue symbols); (ii) Mo instrumental mass fractionation is approximated from the mean Zr mass fractionation determined from bracketing standards (i.e., βMo = βZr; green symbols); (iii) Mo instrumental mass fractionation is approximated by optimization, using the mean Zr fractionation determined from bracketing standards multiplied by a conversion factor (x) that minimizes the offset between the Mo-doped solutions and the Mo-free bracketing standards (i.e., βMo = x × βZr; white symbols).
The first approach, βMo = 0, clearly makes an unsatisfactory assumption, because Mo will in fact be affected by instrumental mass fractionation. The inaccuracy of this is confirmed by the large negative offsets in μ94/90Zr that arise when Mo/Zr ratios are near or above 2 × 10−4 (Fig. 5a). Assuming βMo = βZr results in more accurate corrections, and resolvable deviations only occur when Mo/Zr ratios exceed ca. 5 × 10−3. Nevertheless, at large interference ratios this approach over-corrects Mo interference (i.e., μ94/90Zr offsets becomes resolvably positive), indicating that the effective βMo during measurements is smaller than βZr. Lastly, using the optimization approach (βMo = x × βZr), we find that a conversion factor x = 0.9 results in isobaric interference corrections that are accurate even for our highest doping ratio of ca. 1% Mo/Zr. We note that such percent-level differences in the magnitude of β even for elements of similar mass are common, as are, for example, typically observed when correcting Hf isotopic ratios for Yb and/or Lu isobaric interference (e.g., (ref. 54–57)).
Fig. 5b shows the offset of all ratios (i.e., 91/90Zr, 92/90Zr, 94/90Zr, 96/90Zr) as obtained after correction using our optimization approach (i.e., βMo = 0.9 × βZr). This demonstrates that the optimization method could potentially be used to accurately correct large offsets caused by Mo isobaric interference in all Zr masses, even when within-run Mo beams are too low for allowing direct determination of βMo. Nevertheless, even the simplest βMo = βZr model yields indistinguishable results from the optimization model within the Mo/Zr range measured in our chemically purified zircon solutions (grey shaded range in Fig. 5). Therefore, selection of one correction method over the other has no impact on the accuracy of our results. For simplicity, the data reported here were calculated assuming βMo = βZr.
Results
The 18 micro-cores from MTUR1 were analyzed three to six times each on both mass spectrometers, and the results (Table 5) indicate that this megacryst is isotopically homogeneous within the uncertainties of our method (Fig. 6). All MTUR1 replicates yield a mean μ94/90Zr = −55 ± 28 ppm (2 SD, n = 151). As mentioned previously, data reduction was performed in two ways for all measurements: (i) by exactly constraining the system described in eqn (2) using only the 91/90Zr, 94/90Zr and 96/90Zr ratios; and (ii) by over-constraining the system using a minimization approach that takes into account all measured ratios (i.e., 91/90Zr, 92/90Zr, 94/90Zr and 96/90Zr). Fig. 6c illustrates a comparison of these two reduction approaches, where “Δinv.” represents the difference in μ94/90Zr for all replicates between the two data reduction methods. Differences are always smaller than ±6 ppm, or ±1.5 ppm per amu, and thus negligible compared to our average uncertainties (∼±7 ppm per amu). Values shown in all figures and Tables 4 and 5 correspond to results obtained using the 4-ratio minimization approach.Results from all 91500 fragments analyzed here (Table 5) are also identical within uncertainty (Fig. 7) and yield a mean μ94/90Zr = −135 ± 37 ppm (2 SD, n = 8). Although we have no spatial control of where within the 91500 zircon megacryst the fragments analyzed here were derived, the fact that all results agree within uncertainty suggests that this megacryst is likely compositionally homogeneous for Zr isotopes.
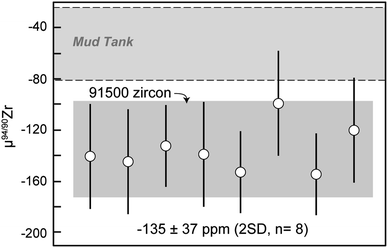 | ||
| Fig. 7 91500 zircon μ94/90Zr results. Data point uncertainties are the 2SD of bracketing standards and gray shaded regions represent the 2SD of the data. | ||
Discussion
Accuracy of Zr stable isotope results
In order to assess the accuracy of the MTUR1 Zr isotope results described above, two key aspects were carefully evaluated: (1) the effect of residual isobaric interferences, and (2) the mass dependency of the determined variations after DS inversion.Potential offsets due to residual Mo isobaric interferences can be assessed using the doping experiment shown in Fig. 5 and the Mo/Zr ratios determined in our samples during MC-ICP-MS measurement (Table 5). The Mo/Zr ratios of our chemically purified solutions are all below 4 × 10−4, within the range where no resolvable offsets are observed in our doping test. Furthermore, the lack of a systematic dependence between μ94/90Zr and Mo/Zr in the MTUR1 dataset (Fig. 8) bolsters the conclusion that the low residual Mo present in our samples after chemical purification do not impact the accuracy of our results outside the reported uncertainties.
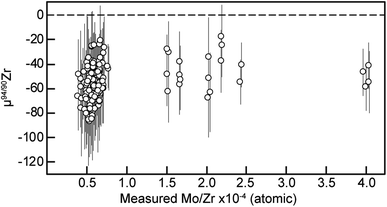 | ||
| Fig. 8 μ94/90Zr vs. Mo/Zr (atom%) of all replicates measured from the 18 MTUR1 zircon micro-cores. Data point uncertainties are the 2SD of bracketing standards. | ||
Determining stable isotope variations in natural samples using a DS relies on a key assumption: the differences in composition between a sample and the standard must be mass-dependent in nature, at least for the masses being used for DS inversion34,38,39,58 (see eqn (2)). If after performing the DS inversion with more than 3 isotope ratios the relative offsets of the spike-stripped ratios used to solve the system do not scale proportionally with mass difference, then this could indicate that: (i) the measurements may be affected by residual spectral interferences; (ii) there may be mass-independent (e.g., radiogenic) sources of variability in at least one of the isotopes used for inversion; or (iii) the mass fractionation law used for inversion is not correct.
The means and 2SD of all Zr isotopic ratios (n = 151) determined in the MTUR1 micro-cores are μ91/90Zr = −14 ± 8 ppm, μ92/90Zr = −27 ± 24 ppm, μ94/90Zr = −55 ± 28 ppm and μ96/90Zr = −80 ± 46 ppm. When scaled relative to mass difference, these translate to offsets of −14 ± 8, −13 ± 12, −14 ± 7 and −13 ± 8 ppm per amu, respectively, indicating mass dependency within uncertainty. In the case of 91500, the means and 2SD of all ratios (n = 8) are μ91/90Zr = −34 ± 9 ppm, μ92/90Zr = −56 ± 23 ppm, μ94/90Zr = −135 ± 37 ppm and μ96/90Zr = −194 ± 54 ppm, which translate to −34 ± 9, −28 ± 12, −34 ± 9 and −32 ± 9 ppm per amu offsets, respectively. The fact that all ratios are mass-dependently related to the standard, clearly demonstrates that: (1) the measured variations are indeed mass-dependent in nature and can be accurately resolved using our method; (2) the use of the double spike technique is warranted, and (3) no unidentified interferences are causing systematic biases to the reported ratios.
Precision of Zr stable isotope analysis of zircon
Multiple factors are known to contribute to the uncertainty of isotopic measurements conducted by MC-ICP-MS, such as counting statistics, thermal (i.e., Johnson–Nyquist) noise, instrumental mass-bias instability and isobaric interferences, amongst others.38,41,59,60 In the case where samples are accurately spiked, the mass spectrometer is stable, and instrumental mass bias and isobaric interferences are properly accounted for, measurement uncertainties should closely approach theoretical expectations. Fig. 9a shows the proportion of Zr DS in the spike-sample mixture (calculated by isotope dilution) for all measured MTUR1 micro-cores. A comparison with the optimal spike![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sample ratio (see Fig. 1a) demonstrates that all solutions were appropriately spiked: i.e., within ±10% of the optimal spiking value where negligible uncertainty amplification (ca. 0.2 ppm per amu) is introduced.
sample ratio (see Fig. 1a) demonstrates that all solutions were appropriately spiked: i.e., within ±10% of the optimal spiking value where negligible uncertainty amplification (ca. 0.2 ppm per amu) is introduced.
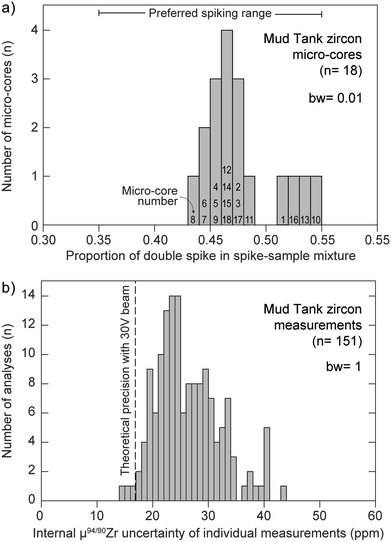 | ||
| Fig. 9 (a) Proportion of double-spike in the spike-sample mix for all measured MTUR1 micro-cores, determined by isotope dilution. See Fig. 1a for definition of ‘preferred spiking range’. Bin width (bw) = 0.01. (b) Histogram of internal measurement uncertainty, expressed as 2 standard error, of all MTUR1 measurements. Vertical dashed line represents the theoretical precision limit from our spike optimization (see Fig. 1b). Bin width (bw) = 1. | ||
Fig. 9b compares the theoretically predicted uncertainty (expressed as standard error) of individual μ94/90Zr determinations (see Fig. 1b) with the internal precision of all MTUR1 measurements. Although the single-measurement precision approaches theoretical expectations from detector thermal-noise modelling, the distribution of uncertainty indicates that there must be additional sources of instability contributing to the final uncertainties (e.g., sample introduction instabilities or small secular deviations from exponential mass bias). Therefore, the precision of individual μ94/90Zr determinations may be better approximated using the reproducibility (standard deviation) of standard-bracketed-standards, herein called σMassSpec, rather than from internal counting statistics alone.
Dauphas et al.59 proposed a scheme for determining the precision of stable Fe isotope measurements, by combining the reproducibility of the primary reference material within a given analytical session with the reproducibility of a secondary reference material that has undergone chemical purification. Using their approach, the total uncertainty of the analytical protocol (σData) for an initially homogeneous material can be estimated from the sum of the variance associated with mass spectrometer instability (σMassSpec2) and other sources of variance associated with the procedure (σUnknown2) according to the relationship: σData2 = σMassSpec2 + σUnknown2. Beginning with the σMassSpec term only, if the MSWD for a weighted mean of replicate measurements of a standard material is sufficiently close to unity (i.e., within the 95% confidence interval at a given number of degrees of freedom61,62), this indicates that analytical uncertainties are properly estimated and are well explained by mass spectrometer instability. On the other hand, if the calculated MSWD is significantly above 1 (i.e., outside 95% confidence), then the results call for a non-zero σUnknown that can be empirically estimated by adjusting this parameter until the MSWD statistic is brought down to unity.
Using the uncertainties reported for all dry-plasma measurements of the SPEX solution (Table 4), the calculated MSWD of the μ94/90Zr weighted mean is 0.85 for measurements made with the Nu Plasma II, and 0.64 for measurements performed on the Neptune Plus. In both cases, the MSWD falls within the 95% confidence interval when the number of degrees of freedom (ν) equals 27 (i.e., MSWD between 0.48 and 1.62). These results indicate that the analytical uncertainties assigned to each replicate (σMassSpec) are adequate for explaining the scatter observed in repeated measurement of a pure secondary reference material that has not undergone chemical purification after DS addition and equilibration.
To assess whether the assigned analytical uncertainties can adequately explain the scatter of a natural material analyzed multiple times after undergoing chemical purification, we use the MTUR1 zircon results. In the Results section, we argued that the MTUR1 zircon crystal is homogeneous within uncertainty of our measurements. Indeed, the MSWD of a weighted mean μ94/90Zr using all MTUR1 data yields a value of 1.01, which is within the 95% confidence interval for ν = 150 (i.e., from ca. 0.78 to 1.27). This observation again indicates that the uncertainties assigned to each replicate adequately explain their scatter around the mean, and therefore that σUnknown for the Zr isotope analysis of zircon using our method is statistically insignificant. This result shows that our double-spike method effectively accounts for mass fractionation during chemical purification and drifts in instrumental mass-bias, which can be significant when determining stable isotope compositions of unspiked solutions relying solely on standard-sample bracketing.59
In summary, the reproducibility of the n = 151 MTUR1 zircon measurements reported here is in excellent agreement with the reproducibility of the SPEX reference solution, and both are well explained by the external reproducibility (2SD) of standard-bracketed-standards. This indicates that short-term fluctuations in the linearity of instrumental drift appear to be the dominant source of uncertainty for the Zr isotopic measurements (i.e., σMassSpec ≫ σUnknown). Therefore, no propagation of uncertainties beyond those determined from the external reproducibility of the standard (σMassSpec) within each run are necessary. The method described here hence yields Zr isotope results that are both accurate and precise to within ca. ±7 ppm per amu, or ±28 ppm for μ94/90Zr (at 95% confidence), at the individual measurement level.
Influence of sample preparation on Zr isotope analysis
Mass-dependent Zr isotope variability was first reported by Akram and Schönbächler18 (see their supplementary materials), who found pure (synthetic) solutions and three natural samples to yield 91Zr/90Zr offsets between −0.4‰ and +0.3‰ relative to an in-house standard. Because these results plot along a mass-dependent fractionation line in 91Zr/90Zr vs.96Zr/90Zr space it is clear the variations are mass-dependent in origin. Nevertheless, the natural sample data were obtained from unspiked solutions that had undergone chemical purification with variable yields, and thus the authors were unable to ascertain whether the observed mass-dependent variations were in fact natural in origin or an artifact of chemical separation.18 Although the effects that different chemical purification schemes have in fractionating Zr isotopes remain to be explored in greater detail, the potential of sample preparation for introducing biases in Zr isotope data is non-negligible.Potential biases introduced by different analytical protocols can be better evaluated by comparing results obtained using a DS. While this work is the first to report an in-depth examination of Mud Tank and 91500 zircon, a recent study by Zhang et al.22 quoted unpublished Zr isotope data for these two localities. Both our data and that of Zhang et al.22 were produced using a 91Zr–96Zr DS (independently prepared and calibrated), and state-of-the-art MC-ICPMS instruments. In contrast to our method, however, Zhang et al. used the method of Inglis et al.20 in which zircon samples are analyzed without any chemical purification. Furthermore, because normalization was done relative to in-house standards (i.e., IPGP-Zr and GJ-1 zircon), comparison of absolute values is not yet possible.
Taken at face value, the μ94/90Zr offset between Mud Tank and 91500 (μ94/90Zr(MudTank) − μ94/90Zr(91500)) obtained in this study, 80 ± 65 ppm (2SD), is in good agreement with the value of 100 ± 110 ppm (2SD) reported by Zhang et al.22 To first-order, this suggests that the lack of chemical purification did not result in significant biases in the Zhang et al.22 results. We note, however, that the limited Zr isotope data from zircon available to date and the twice lower precision of the Zhang et al.22 data, is insufficient to completely rule out the presence of systematic biases between methods that analyze chemically purified vs. non-purified zircon solutions.
No Zr isotope fractionation in carbonatite systems by zircon crystallization
Zircon crystallization from a melt has been posited as a driver of Zr isotope fractionation in silicate magmatic systems,21,23 but discrepancies remain both in the magnitude and direction of the induced variability. While a study in bulk-rock samples from the Hekla volcano inferred zircon to be isotopically light relative to co-existing melt,21 a detailed study of zircon and baddeleyite from a closed igneous system in the Duluth Complex concluded that these solids are isotopically heavy relative to the melt from which they precipitated.23 In carbonatite systems, the question of whether Zr isotope fractionation occurs at all remains entirely unconstrained.If zircon crystallization indeed drives Zr isotope fractionation via a Rayleigh-type mechanism as previously suggested,21,23 then individual zircon crystals growing from a magma would record the changing composition of the liquid as concurrent crystallization and isotopic fractionation take place. To illustrate this, Fig. 10a shows the melt and solid compositional evolution that would be expected from closed-system Rayleigh fractionation of a liquid as a function of the Zr fraction removed (f),63 using the αsol–liq = 1.00106 (or Δ94/90Zrsol–liq ≈ +1.06‰) inferred by Ibañez-Mejia and Tissot23 as an example. As f increases, the removal of isotopically ‘heavy’ zircon would drive the liquid towards a complementary ‘light’ composition, and this change would be recorded by the instantaneous solid composition forming from the liquid at each subsequent step.
 | ||
| Fig. 10 Illustration of how Rayleigh-type Zr isotopic fractionation of a magma, as driven by zircon crystallization, would result in intra-crystalline isotopic zonation of the solid. (a) Example Rayleigh fractionation diagram showing how the Zr isotopic composition (μ94/90Zr) of the liquid and instantaneous solid change as a function of the fraction of Zr removed from the liquid (f). Plot was calculated using an αsolid–liquid = 1.00106 (or Δ94/90Zr ≈ +1.06‰; after Ibañez-Mejia and Tissot23) for illustration. (b) Diagram showing how different magnitudes of αsolid–liquid (expressed as Δ94/90Zr, for simplicity) translate into different intra-crystalline μ94/90Zr zonation topologies. Calculations were made assuming a spherical geometry of 5 cm in diameter (i.e., long-axis dimensions of the MTUR1 megacryst) growing from f ≈ 0 at the core to f ≈ 1 at the rim. | ||
Fig. 10b shows a transformation of the instantaneous solid composition of a Rayleigh fractionation model to radial coordinates, assuming: (i) a spherical geometry of 5 cm diameter (i.e., long-axis dimension of MTUR1); and (ii) that the internal zoning represents growth-integration from f ≈ 0 at the core, to f ≈ 1 at the rim. The different curves shown in Fig. 10b represent the different intra-crystalline μ94/90Zr zonation patterns that would result from various fractionation coefficients between solid and liquid (expressed as Δ94/90Zr). As shown in Fig. 6, the MTUR1 megacryst exhibits no resolvable internal variability, which suggests a Δ94/90Zr ≈ 0 (within uncertainty) given the calculations shown in Fig. 10b.
An alternative possibility to explain the lack of internal isotopic zonation in the MTUR1 megacryst is sub-solidus re-equilibration after crystallization. Under this scenario, initial zonation in the megacryst could have been subsequently erased by thermally activated diffusion. Although no experimental or empirical data for Zr diffusion in zircon are currently available, the relationship between pre-exponential factor for diffusion (D0) and ionic radius of tetravalent species in zircon64 can be used to approximate Zr4+ diffusivity to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D0 ≈ 2.67 m2 s−1. Assuming a 190 kcal mol−1 activation energy for diffusion, which is typical of tetravalent cations in zircon,64 the effective diffusion distance (2√Dt) for Zr in zircon can be estimated as a function of time and temperature.65 At 650 °C, which is the maximum estimated temperature of emplacement for the Mud Tank carbonatite,43 the effective diffusion distance of Zr for a heating event of 10 Myr duration is estimated to be on the order of 2 × 10−8 μm (i.e., twelve orders of magnitude shorter than the long axis of the studied megacryst). Even if this crystal was held at 1500 °C for 10 Myr, the effective diffusion distance estimated for Zr would be ca. 1.5 mm, which is still negligible relative to the length of the profile shown in Fig. 6. Therefore, the possibility that the isotopic homogeneity observed in MTUR1 reflects a sub-solidus re-equilibration feature is highly unlikely.
D0 ≈ 2.67 m2 s−1. Assuming a 190 kcal mol−1 activation energy for diffusion, which is typical of tetravalent cations in zircon,64 the effective diffusion distance (2√Dt) for Zr in zircon can be estimated as a function of time and temperature.65 At 650 °C, which is the maximum estimated temperature of emplacement for the Mud Tank carbonatite,43 the effective diffusion distance of Zr for a heating event of 10 Myr duration is estimated to be on the order of 2 × 10−8 μm (i.e., twelve orders of magnitude shorter than the long axis of the studied megacryst). Even if this crystal was held at 1500 °C for 10 Myr, the effective diffusion distance estimated for Zr would be ca. 1.5 mm, which is still negligible relative to the length of the profile shown in Fig. 6. Therefore, the possibility that the isotopic homogeneity observed in MTUR1 reflects a sub-solidus re-equilibration feature is highly unlikely.
The observations made above indicate that the exceedingly slow diffusivity of tetravalent species in zircon likely prevent efficient diffusive re-equilibration of Zr within this mineral (and with the surrounding melt) over typical magmatic temperatures and timescales. Thus, the lack of resolvable isotopic zonation at the ±7 ppm per amu level in the MTUR1 megacryst is most compatible with the conclusion that zircon crystallization in carbonatite magmas is not a main driver of Zr stable isotope fractionation.
MTUR1, a natural zircon reference material for Zr isotope analysis
Zircon megacrysts from the Mud Tank locality are widely used as a natural ‘geostandards’ for U–Pb geochronology, trace element analyses and Lu–Hf isotope geochemistry by spatially resolved methods32 (e.g., SIMS and LA-ICP-MS). Our results demonstrate that the MTUR1 megacryst studied here is isotopically homogenous for Zr isotopes, therefore providing an opportunity to use it as a natural reference material for Zr isotopic analyses. Small aliquots of this crystal can be requested by other laboratories interested in conducting Zr stable isotope measurements in zircon by solution (±double spike) methods, and rigorously evaluate potential inter-laboratory biases at high precision.Recent studies have also explored the potential of obtaining moderate-precision Zr stable isotope compositions of zircon via micro-beam methods such as LA-MC-ICP-MS22 and Hyperion-SIMS.66 Because the accuracy of isotopic compositions determined by micro-beam methods is, in general, significantly improved by the use of matrix-matched reference materials,56,67 a demonstrably homogeneous zircon for Zr stable isotopes is a valuable resource for these approaches. Furthermore, because Mud Tank zircon crystals are well-known for having low accumulated radiation damage68,69 due to their generally low U concentrations,32 a homogeneous megacryst from this locality is particularly well suited as a primary reference material for micro-beam Zr isotope analysis as it will minimize potential matrix effects introduced by sampling of a radiation-damaged structure.
Fragments of the MTUR1 megacryst are available for distribution to interested laboratories and can be obtained by contacting M. Ibañez-Mejia and/or F. L. H. Tissot.
Recommendations for reporting Zr stable isotope data
Although Zr stable isotope analyses are still in their infancy, it is clear that the production of highly precise and accurate data requires careful considerations of the impact of interferences and other analytical artifacts stemming from sample processing. To enhance data transparency and evaluation of data accuracy, we propose that future Zr studies adopt some simple recommendations:(1) Given the large impact of even small amounts of Mo and isobaric interference correction strategies (see Fig. 5), Mo/Zr ratios for each sample fraction should be measured, reported (e.g., Tables 4 and 5) and isobaric interference corrections performed. Because MC-ICP-MS instruments allow simultaneous monitoring of at least 95Mo, 97Mo, and/or 98Mo along with all Zr masses of interest, this critical measurement is easy to perform and does not add additional time or difficulty to the process.
(2) Because of the potential that isobaric and/or molecular interferences and matrix effects have for introducing non-systematic offsets to stable isotope results,41,52,59,60 particularly when multiple isotopic ratios must be considered simultaneously in DS inversions, the mass-dependency of the data should be documented. For example, in the case of Zr this can be done by reporting the δ (or ε, μ, etc.) values of all Zr isotopic ratios (e.g., Tables 4 and 5) and/or by using a 4-ratio minimization as described here. When measurements are performed using a double-spike, a lack of mass-dependency, if present, would be indicative of an inaccurate result. Reporting all isotope ratios will thus allow verification of the mass-dependent nature of the isotopic effects, which is a requirement for accurate double-spike inversion and data reduction (e.g., (ref. 34, 35, 38, 39, 41 and 70)).
(3) Inter-comparisons of Zr isotope data would be significantly enhanced by the use of a common standard. The ZrNIST standard described here is currently undergoing rigorous inter-laboratory calibration as a community-wide effort. This standard was designed and produced using NIST and community53 guidelines to meet the stringent needs of a system where single-digit ppm precisions need to be achieved. We note that this is the first effort of its kind for Zr isotopes, and suggest this standard be adopted by all laboratories performing Zr isotopic measurement (mass-dependent and -independent) once it becomes commercially available. In the meantime, aliquots of the standard solution can be obtained upon request to the authors.
(4) Results for at least one secondary reference material should be reported, to further support the accuracy of the results. These can be results from either a pure (industrial) reference material, a ‘geostandard’ that has undergone chemical purification, or ideally both. Consistent reporting of secondary reference material data will provide the means to continuously re-assess the accuracy and reproducibility of Zr stable isotope measurements as the technique matures, and will enable robust inter-laboratory comparisons needed to evaluate/resolve bias.
Conclusions
We have shown that: (1) the Mud Tank zircon megacryst studied here, MTUR1, has a homogenous Zr stable isotope composition (μ94/90Zr = −55 ± 28 ppm), indicating that zircon crystallization is unlikely to be a driver of Zr stable isotopic fractionation in carbonatitic magmas; (2) our analytical method for Zr isotope analysis of zircon is precise and accurate to within ±7 ppm per amu (at 2SD) for individual measurements consuming only ∼25 ng of sample Zr, which opens new avenues for probing the isotopic composition of zircon and other minerals at high analytical and volume resolution (e.g., single-silicate-crystal scale); and (3) the MTUR1 zircon megacryst provides a demonstrably homogenous reference material for Zr isotopic determinations in zircon. This new natural reference material directly bridges the gap between micro-beam and solution-based (±double spike) methods, by allowing results obtained using both approaches to be directly linked to the new ZrNIST isotopic standard currently under development.The contrast between the results presented here and studies of silicate igneous systems21,23 suggests that differences in Zr speciation may result in contrasting Zr isotope fractionation during crystallization of zircon from carbonatite vs. silicate liquids. Therefore, additional ab initio, experimental and spectroscopic investigations of Zr speciation in magmas of variable compositions will be key to further understand the drivers of Zr stable isotope fractionation during magmatic fractional crystallization.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
David McGee is thanked for access to the MIT Nu Plasma II, and Joel DesOrmeau for the careful and time-consuming SEM-CL imaging of MTUR1 at U. Nevada in Reno. Matthew Bown, Chaofeng Li and an anonymous reviewer are thanked for constructive comments that helped improve the final version of this manuscript. This research was supported by a Stephen Pollock Undergraduate Research Grant awarded by the NE section of the Geological Society of America (to HT), NSF-EAR grants 1823748 (to MIM) and 1824002 (to FT) and start-up funds to MIM provided by University of Rochester and to FT provided by Caltech.Notes and references
- S. Weyer, C. Münker, M. Rehkämper and K. Mezger, Chem. Geol., 2002, 187, 295–313 CrossRef CAS.
- C. Münker, G. Wörner, G. Yogodzinski and T. Churikova, Earth Planet. Sci. Lett., 2004, 224, 275–293 CrossRef.
- J. A. Pfänder, C. Münker, A. Stracke and K. Mezger, Earth Planet. Sci. Lett., 2007, 254, 158–172 CrossRef.
- P. B. Kelemen, K. Johnson, R. J. Kinzler and A. J. Irving, Nature, 1990, 345, 521–524 CrossRef CAS.
- L. Lowery Claiborne, C. F. Miller, B. A. Walker, J. L. Wooden, F. K. Mazdab and F. Bea, Mineral. Mag., 2006, 70, 517–543 CrossRef.
- A. R. Chakhmouradian, Chem. Geol., 2006, 235, 138–160 CrossRef CAS.
- Q. Xie, R. Kerrich and J. Fan, Geochim. Cosmochim. Acta, 1993, 57, 4111–4118 CrossRef.
- K. David, P. Schiano and C. J. Allègre, Earth Planet. Sci. Lett., 2000, 178, 285–301 CrossRef CAS.
- J. F. Minster and L. Ricard, Int. J. Mass Spectrom. Ion Phys., 1981, 37, 259–272 CrossRef CAS.
- J. F. Minster and C. J. Allègre, Geochim. Cosmochim. Acta, 1982, 46, 565–573 CrossRef CAS.
- C. Sanloup, J. Blichert-Toft, P. Télouk, P. Gillet and F. Albarède, Earth Planet. Sci. Lett., 2000, 184, 75–81 CrossRef CAS.
- C. Münker, S. Weyer, K. Mezger, M. Rehkämper, F. Wombacher and A. Bischoff, Science, 2000, 289, 1538–1542 CrossRef PubMed.
- Q. Z. Yin, S. B. Jacobsen, W. F. McDonough, I. Horn, M. I. Petaev and J. Zipfel, Astrophys. J., 2000, 536, L49–L53 CrossRef CAS PubMed.
- M. Schönbächler, M. Rehkämper, A. N. Halliday, D.-C. Lee, M. Bourot-Denise, B. Zanda, B. Hattendorf and D. Günther, Science, 2002, 295, 1705–1708 CrossRef PubMed.
- M. Schönbächler, M. Rehkämper, M. A. Fehr, A. N. Halliday, B. Hattendorf and D. Günther, Geochim. Cosmochim. Acta, 2005, 69, 5113–5122 CrossRef.
- M. Schönbächler, D.-C. Lee, M. Rehkämper, A. N. Halliday, B. Hattendorf and D. Günther, Geochim. Cosmochim. Acta, 2005, 69, 775–785 CrossRef.
- W. Akram, M. Schönbächler, S. Bisterzo and R. Gallino, Geochim. Cosmochim. Acta, 2015, 1–46 Search PubMed.
- W. Akram and M. Schönbächler, Earth Planet. Sci. Lett., 2016, 449, 302–310 CrossRef CAS.
- T. Iizuka, Y.-J. Lai, W. Akram, Y. Amelin and M. Schönbächler, Earth Planet. Sci. Lett., 2016, 439, 172–181 CrossRef CAS.
- E. C. Inglis, J. B. Creech, Z. Deng and F. Moynier, Chem. Geol., 2018, 493, 544–552 CrossRef CAS.
- E. C. Inglis, F. Moynier, J. Creech, Z. Deng, J. M. D. Day, F.-Z. Teng, M. Bizzarro, M. Jackson and P. Savage, Geochim. Cosmochim. Acta, 2019, 250, 311–323 CrossRef CAS.
- W. Zhang, Z. Wang, F. Moynier, E. Inglis, S. Tian, M. Li, Y. Liu and Z. Hu, J. Anal. At. Spectrom., 2019, 34, 1800–1809 RSC.
- M. Ibañez-Mejia and F. L. H. Tissot, Sci. Adv., 2019, 5, eaax8648 CrossRef PubMed.
- L. Feng, W. Hu, Y. Jiao, L. Zhou, W. Zhang, Z. Hu and Y. Liu, J. Anal. At. Spectrom., 2020, 88, 293–310 Search PubMed.
- E. D. Young, C. E. Manning, E. A. Schauble, A. Shahar, C. A. Macris, C. Lazar and M. Jordan, Chem. Geol., 2015, 395, 176–195 CrossRef CAS.
- M. Blanchard, E. Balan and E. A. Schauble, Rev. Mineral. Geochem., 2017, 82, 27–63 CrossRef CAS.
- F. Farges, Geochim. Cosmochim. Acta, 1991, 55, 3303–3319 CrossRef CAS.
- M. Louvel, C. Sanchez-Valle, W. J. Malfait, D. Testemale and J.-L. Hazemann, Geochim. Cosmochim. Acta, 2013, 104, 281–299 CrossRef CAS.
- K. Robinson, G. V. Gibbs and P. H. Ribbe, Am. Mineral., 1971, 56, 782–790 CAS.
- D. K. Smith and W. Newkirk, Acta Crystallogr., 1965, 18, 983–991 CrossRef CAS.
- P. W. Crohn and D. H. Moore, BMR J. Aust. Geol. Geophys., 1984, 9, 13–18 CAS.
- S. E. M. Gain, Y. Gréau, H. Henry, E. Belousova, I. Dainis, W. L. Griffin and S. Y. O'Reilly, Geostand. Geoanal. Res., 2019, 3, 227–316 Search PubMed.
- M. Wiedenbeck, J. M. Hanchar, W. H. Peck, P. Sylvester, J. W. Valley, M. Whitehouse, A. Kronz, Y. Morishita, L. Nasdala, J. Fiebig, I. Franchi, J. P. Girard, R. C. Greenwood, R. Hinton, N. Kita, P. Mason, M. Norman, M. Ogasawara, R. Piccoli, D. Rhede, H. Satoh, B. Schulz-Dobrick, O. Skar, M. J. Spicuzza, K. Terada, A. Tindle, S. Togashi, T. Vennemann, Q. Xie and Y. F. Zheng, Geostand. Geoanal. Res., 2004, 28, 9–39 CrossRef CAS.
- M. H. Dodson, J. Sci. Instrum., 1963, 40, 289–295 CrossRef.
- M. H. Dodson, J. Phys. E: Sci. Instrum., 1969, 2, 490–498 CrossRef.
- S. J. G. Galer, Chem. Geol., 1999, 157, 255–274 CrossRef CAS.
- C. M. Johnson and B. L. Beard, Int. J. Mass Spectrom. Ion Phys., 1999, 193, 87–99 CrossRef CAS.
- F. Albarede and B. L. Beard, in Geochemistry of Non-Traditional Stable Isotopes, ed. C. M. Johnson, B. L. Beard and F. Albarede, 2004, vol. 55, pp. 113–152 Search PubMed.
- J. F. Rudge, B. C. Reynolds and B. Bourdon, Chem. Geol., 2009, 265, 420–431 CrossRef CAS.
- A. J. Mayer and M. E. Wieser, J. Anal. At. Spectrom., 2014, 29, 85–94 RSC.
- M.-A. Millet and N. Dauphas, J. Anal. At. Spectrom., 2014, 29, 1444 RSC.
- F. Kurzweil, C. Münker, J. Tusch and R. Schoenberg, Chem. Geol., 2018, 476, 407–417 CrossRef CAS.
- K. L. Currie, J. Knutson and P. A. Temby, Contrib. Mineral. Petrol., 1992, 109, 326–339 CrossRef CAS.
- J. Mattinson, Chem. Geol., 2005, 220, 47–66 CrossRef CAS.
- P. Widmann, J. H. F. L. Davies and U. Schaltegger, Chem. Geol., 2019, 511, 1–10 CrossRef CAS.
- T. Meisel, J. Moser, N. Fellner, W. Wegscheider and R. Schoenberg, Analyst, 2001, 126, 322–328 RSC.
- K. M. Samperton, B. Schoene, J. M. Cottle, C. Brenhin Keller, J. L. Crowley and M. D. Schmitz, Chem. Geol., 2015, 417, 322–340 CrossRef CAS.
- A. Kawashima, K. Takahashi and A. Masuda, Phys. Rev. C: Nucl. Phys., 1993, 47, R2452–R2456 CrossRef CAS PubMed.
- M. E. Wieser and J. R. De Laeter, Phys. Rev. C: Nucl. Phys., 2001, 64, 7 CrossRef.
- J. Meija, T. B. Coplen, M. Berglund, W. A. Brand, P. De Bièvre, M. Gröning, N. E. Holden, J. Irrgeher, R. D. Loss, T. Walczyk and T. Prohaska, Pure Appl. Chem., 2016, 88, 252–314 Search PubMed.
- C. Münker, S. Weyer, E. Scherer and K. Mezger, Geochem., Geophys., Geosyst., 2001, 2, 19 CrossRef.
- F. L. H. Tissot and N. Dauphas, Geochim. Cosmochim. Acta, 2015, 167, 113–143 CrossRef CAS.
- F.-Z. Teng, N. Dauphas and J. M. Watkins, Rev. Mineral. Geochem., 2017, 82, 1–26 CrossRef CAS.
- J. Vervoort, P. Patchett, U. Söderlund and M. Baker, Geochem., Geophys., Geosyst., 2004, 5, Q11002 CrossRef.
- C. M. Fisher, J. M. Hanchar, S. D. Samson, B. Dhuime, J. Blichert-Toft, J. D. Vervoort and R. Lam, Chem. Geol., 2011, 286, 32–47 CrossRef CAS.
- M. Ibañez-Mejia, G. E. Gehrels, J. Ruiz, J. D. Vervoort, M. E. Eddy and C. Li, Chem. Geol., 2014, 384, 149–167 CrossRef.
- M. Ibañez-Mejia, A. Pullen, J. Arenstein, G. E. Gehrels, J. Valley, M. N. Ducea, A. R. Mora, M. Pecha and J. Ruiz, Precambrian Res., 2015, 267, 285–310 CrossRef.
- N. Dauphas and E. A. Schauble, Annu. Rev. Earth Planet. Sci., 2016, 44, 709–783 CrossRef CAS.
- N. Dauphas, A. Pourmand and F.-Z. Teng, Chem. Geol., 2009, 267, 175–184 CrossRef CAS.
- F. L. H. Tissot, M. Ibañez-Mejia, P. Boehnke, N. Dauphas, D. McGee, T. L. Grove and T. M. Harrison, J. Anal. At. Spectrom., 2019, 1–18 Search PubMed.
- I. Wendt and C. Carl, Chem. Geol., 1991, 86, 275–285 Search PubMed.
- K. Mahon, Int. Geol. Rev., 1996, 38, 293–303 CrossRef.
- R. E. Criss, Principles of Stable Isotope Distribution, Oxford University Press, New York, 1999 Search PubMed.
- D. J. Cherniak, J. M. Hanchar and E. B. Watson, Contrib. Mineral. Petrol., 1997, 127, 383–390 CrossRef CAS.
- J. Crank, The Mathematics of Diffusion, Oxford University Press, 2nd edn, 1975 Search PubMed.
- H. M. Kirkpatrick, T. M. Harrison, M.-C. Liu, E. A. Bell, F. L. H. Tissot and M. Ibañez-Mejia, In situ δ94/90Zr variations in zircon as an indicator of magmatic differentiation, AGU Fall Meeting, San Francisco, December 2019 Search PubMed.
- J. Valley and N. Kita, Mineral. Assoc. Can., Short Course Ser., 2009, 41, 19–63 CAS.
- L. Nasdala, M. Zhang, U. Kempe, G. Panczer, M. Gaft, M. Andrut and M. Plötze, in Zircon, ed. J. M. Hanchar and P. W. O. Hoskin, Mineralogical Society of America, 2003, vol. 53, pp. 427–467 Search PubMed.
- W. R. Guenthner, P. W. Reiners, R. A. Ketcham, L. Nasdala and G. Giester, Am. J. Sci., 2013, 313, 145–198 CrossRef CAS.
- M. H. Dodson, Geochim. Cosmochim. Acta, 1970, 34, 1241–1244 CrossRef CAS.
- M. Schönbächler, M. Rehkämper, D.-C. Lee and A. N. Halliday, Analyst, 2004, 129, 32 RSC.
| This journal is © The Royal Society of Chemistry 2020 |