Open Access Article
Open Access ArticleMeasurements of rhenium isotopic composition in low-abundance samples†
Mathieu
Dellinger
 *a,
Robert G.
Hilton
a and
Geoffrey M.
Nowell
*a,
Robert G.
Hilton
a and
Geoffrey M.
Nowell
 b
b
aDepartment of Geography, Durham University, DH1 3LE Durham, UK. E-mail: mathieu.dellinger@durham.ac.uk
bDepartment of Earth Sciences, Durham University, DH1 3LE Durham, UK
First published on 7th January 2020
Abstract
Rhenium (Re) is a trace element whose redox chemistry makes it an ideal candidate to trace a range of geochemical processes. In particular, fractionation of its isotopes 187Re (62.6% abundance) and 185Re (37.4%) may be used to improve our understanding of redox reactions during weathering, both in the modern day and in geological archives. Published methods for measurement of Re isotopic composition are limited by the requirements of Re mass to reach a desirable precision, making the analysis of many geological materials unfeasible at present. Here we develop new methods which allow us to measure Re isotope ratios (reported as δ187Re) with improved precision: ±0.10‰ (2σ) for a mass of Re of ∼1 ng to ±0.03‰ (2σ) for a mass of Re of >10 ng. This is possible due to the combination of a modified column chemistry procedure and the use of 1013 Ω amplifiers for measurement via multicollector inductively coupled plasma mass spectrometry (MC-ICP-MS). For river water samples (with Re concentrations typically ∼10−12 g g−1) we design a field-based pre-concentration of Re that can be used with large volumes of filtered water (5–20 L) shortly after sample collection to provide abundant Re for isotope analysis. As a result of these developments we provide new measurements of δ187Re in standards reference materials (δ187Re values range from −0.06 ± 0.07‰ to +0.19 ± 0.05‰) and a seawater standard (δ187Re = +0.10 ± 0.04‰), providing impetus for further exploration of the Re isotope system.
Introduction
Rhenium (Re, atomic mass 186.207) is one of the least abundant chemical elements present on Earth, with concentrations in most materials ranging from 10−12 g g−1 (ppt) to 10−9 g g−1 (ppb),1–3 with 10−6 g g−1 (ppm) only in found in specific phases.4 Several characteristics make Re a useful element for tracking geochemical processes. Notably, its redox-dependent solubility makes it a target for tracking oxidation reactions during chemical weathering1,5–7 and reconstructing redox cycling in lake and oceanic sediments.8Rhenium oxidation states range from −1 to +7, with the most abundant being +7, +6 and +4.9 Rhenium is a soluble element in oxic conditions and mostly present in surface waters in the form of the oxyanion ReVIIO4−.1,2,10 In seawater, Re has a conservative behaviour with an average present-day concentration around 7.5 ppt.2,3 Under anoxic conditions, ReVII is reduced to ReIV, becomes insoluble and is removed from water either through complexation of ReIV with organic matter and/or incorporated into sulphides.11–13 Among the redox sensitive metals, Re has the largest enrichment factor in authigenic phases of anoxic sediments relative to the detrital background.8 As such, high concentrations of Re are observed in Phanerozoic sedimentary rocks formed under reducing conditions, such as black shales (average 150 ppb), relative to the upper continental crust (∼0.3 ppb) and most Precambrian sedimentary rocks (10–30 ppb).8,14 Earth's core represents the main Re reservoir on Earth (230 ppb) and the abundance of Re in Bulk Silicate Earth (BSE, 0.35 ppb) is about two orders of magnitude lower than in carbonaceous chondrite (about 40 ppb).15,16 During magmatic processes, Re behaves as a moderately incompatible element during melting and differentiation processes.15,17,18
Rhenium is composed of two naturally abundant isotopes 187Re (62.6%) and 185Re (37.4%). The 187Re isotope is radioactive and undergoes β-decay to 187Os with a half-life of 4.35 × 1010 years. Following the pioneering work of Miller et al., (2009),19 two studies have measured the Re isotopic composition expressed as δ187Re, where δ187Re = ((187Re/185Re)/(187Re/185Re)std − 1) × 1000, in shales and weathered sedimentary rocks9 and iron meteorites.20 These studies have documented a total of ∼0.80‰ variability in δ187Re values, including ∼0.30‰ across a chemical weathering profile in soil developed on a Devonian black shale9 and 0.40‰ between iron meteorites.20 In addition, an ab initio calculation9 shows that oxidized ReVII species are usually enriched in 187Re relative to more reduced ReIV. The fractionation factor between ReIV and ReVII (103 × log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e(αReIV–ReVII)) could potentially vary between −0.80‰ and +0.50‰, depending on the degree of thiolation of the ReVII species.9 Overall, the existing measurements and calculations suggest that Re isotope ratios have strong potential to help track redox processes.
e(αReIV–ReVII)) could potentially vary between −0.80‰ and +0.50‰, depending on the degree of thiolation of the ReVII species.9 Overall, the existing measurements and calculations suggest that Re isotope ratios have strong potential to help track redox processes.
The previous measurements of the Re isotopic composition of materials19,20 were made by multicollector inductively coupled plasma mass spectrometry (MC-ICP-MS – Thermo Fisher Scientific Neptune, fitted with 1011 Ω amplifiers) with the combination of tungsten (W) doping and standard-sample bracketing to correct for instrumental mass bias. With that set-up, a precision of ±0.10‰ (2σ) was achieved for a concentration of 10 ppb Re. Based on that pioneering work, many sample types were thus considered too low in Re concentration (e.g. river water, felsic rocks) to permit δ187Re measurement. Here, we revisit the Re isotopic analysis by MC-ICP-MS with the aim to establish a method to measure Re isotopic composition in low abundance samples which are relevant to understanding crucial redox processes on Earth. These include grey shales with lower organic carbon contents than black shales (and Re < 1 ppb),6,7 felsic igneous rocks (Re < 2 ppb),17,21 weathered rocks and soils (Re ∼ ppt–ppb range),6,7,22 river waters and seawater (Re ∼ ppt).1,2 To do this we: (i) make use of recent mass spectrometry hardware advances (notably the development of 1013 Ω amplifiers23) and very low uptake rate nebulizer (CF 35) which allows us to run smaller volumes at higher concentrations; (ii) explore and refine sample preparation and purification by column chemistry for solids; (iii) propose a new field pre-concentration method for river water samples; and (iv) measure and report a range of natural low Re abundance standard reference materials. We recommend repeated column chemistry procedures (loading and elution) to purify samples. The methods allow for the measurement of δ187Re values to a precision of better than ±0.05‰ (2σ) for Re mass > 3 ng, unlocking the vast majority of natural samples for the analysis of Re isotopic composition.
Experimental methods
Reference materials and samples
In this study, we used a wide range of SRM (Standard Reference Materials), including basalts (BCR-2, BCR-1, BHVO-2, BIR-1), sediments (MAG-1, SCO-1, NIST 1646a), granites (JG-2), peridotite (GP13), serpentinite (UB-N), andesite (AGV-1), diabase (TBD-1) and dolerite (DNC-1). We also used river samples from different locations (UK, Canada, France), a black shale and a carbonaceous chondrite sample (see ESI†).Dissolution of solid samples
The low Re concentration of most rock and sediment samples mean that a mass of at least ∼0.5 g is necessary for a precise δ187Re. To ensure complete re-dissolution of fluorides, a maximum aliquot mass of 0.5 g per beaker was dissolved for each sample. A volume of 3 mL 29 M HF and 3 mL of 16 M HNO3 was added to each sample in PFA Teflon beakers and heated at 120 °C for at least 24 h. Following initial digestion, samples were evaporated to dryness at 80 °C and then re-dissolved in aqua regia to destroy fluorides, heated at 120 °C for 24 h before being evaporated. Finally, samples were re-dissolved in 1 M HCl. Care was taken to ensure complete dissolution and a volume of about 20 to 40 mL of 1 M HCl was required to achieve this. For samples containing refractory organic matter, a black residue was treated in 16 M HNO3 and aqua regia for several days at 160 °C. Ultimately, only the most refractory organic matter (e.g. graphite) was left un-dissolved and removed from the solution by centrifugation and pipetting of the supernatant.We tested for the potential loss of Re during heating and evaporation for 16 M HNO3, 10 M HCl, H2O, aqua regia and HClO4, at temperatures of 80, 120, 150 and 190 °C. We found no loss of Re and recovery of 100% for all reagents except for HClO4, for which there are significant evaporative losses of Re (>85%) at temperatures higher than 150 °C.
Chemical separation for solid samples
The chemical separation procedure is modified from those previously described.19,24 Polypropylene columns (inner diameter of 7.1 mm) are filled with 1 mL of AG1-X8 resin (200–400 mesh). A frit was added to the top of the resin-bed to avoid remobilization of the resin during addition of reagents. The resin is cleaned with 30 mL of 8 M HNO3, and conditioned with 5 mL of 1 M HCl. Samples are loaded on the column in 1 M HCl. At low acid concentration, Re is strongly bounded to this resin,25 with the partition coefficient of Re with the AG1-X8 resin (Kd Re = [Re]resin/[Re]solution) > 100 for HCl and HNO3 concentrations < 1 mol L−1. Before collecting the Re fraction, elution of the sample matrix is achieved in 3 steps: (i) addition of 10 mL of 1 M HCl, (ii) addition of 15 mL of 0.5 M HNO3 and (iii) 1.5 mL of 4 M HNO3 (Table 1). The Re fraction is eluted with 12.5 mL of 4 M HNO3 (Kd Re ∼ 8–10). The Re fraction is then evaporated at temperature of 100 to 120 °C to complete dryness and refluxed in 16 M HNO3 at 120 to 150 °C for at least 24 h. This full procedure is repeated two more times (i.e. three identical column chemistry steps) to purify the Re fraction from the residual matrix. Samples are refluxed in 16 M HNO3 after each column step to destroy resin-derived organic residues. A small aliquot (2% of the sample Re mass) is taken after 1 column pass to measure the Re concentration and after 3 column passes to check the total yield of the separation.| Step | Acid | Volume (mL) | Elements eluted |
|---|---|---|---|
| a Bulk elements are elements for which more than 85% of the elements is not fixed to the resin. It includes Li, Be, Na, Mg, Al, K, Ca, V, Cr, Mn, Fe, Co, Ni, Cu, Se, Sr, Y | |||
| Resin AG1-X8; 1 mL | |||
| Precleaning | HNO3 8 N (twice) | 15 | |
| Precleaning | H2O | 5 | |
| Equilibration | HCl 1 N | 5 | |
| Introduction | HCl 1 N | 2–50 | Bulk elements |
| Cleaning step 1 | HCl 1 N | 10 | Residual bulk elements + Mo, Nb, Ti, Ta, Pb, Ag, W |
| Cleaning step 2 | HNO3 0.5 N | 15 | Zn, Cd and Residual Pb, Ta, Nb |
| Cleaning step 3 | HNO3 4 N | 1.5 | Residual Ta, Nb, Ag |
| Elution of Re | HNO3 4 N | 12.5 | Re |
Chemical separation for dissolved samples
For dissolved Re samples (e.g. filtered river water and seawater), a volume of 1 to 20 L is usually necessary to recover enough Re for accurate δ187Re (>0.4 ng of Re). Such volumes present significant handling and shipping issues. To overcome this, we developed a method for pre-concentrating Re in the field. River water samples are filtered at 0.2 μm (through PES Millipore filters) and collected in 20 L sterile double-lined beverage bags that are commercially available. The sample mass is measured and the bags are then connected (using a custom fitting) to a BioRad Econo-Pac® 20 mL column filled with 2 to 4 mL of AG1-X8 resin, and passed through the column in a field laboratory (typically over a 6–10 h period). The Re-loaded columns are then capped, packaged and returned to Durham. Upon return to the laboratory, 50 mL of 1 M HCl is passed through the resin to remove some of the matrix (and if required, to collect the SO4 fraction for sulfur isotope analysis26). Finally, the Re is collected with 30 to 40 mL of 8 M HNO3. Using a higher HNO3 molarity allows better recovery of the proportion of Re bound to the resin. Organic molecules from dissolved organic carbon also have strong affinity with this resin (the resin colour becomes darker for water samples with high dissolved organic carbon) and are partly eluted with Re. Therefore, to destroy these organics, the Re residue is re-dissolved in 16 M HNO3 and refluxed for 5–7 days at 150 °C. These samples are then passed through the three steps of column chemistry separation as described for solid samples.Mass spectrometry
Following the method developed by Miller et al., (2009),19 rhenium isotopic ratios were measured by MC-ICP MS (ThermoFisher Scientific NetunePlus without jet interface) at the Arthur Holmes Isotope Geology Laboratory, Dept. Earth Sciences, University of Durham. We use a combination of standard-sample bracketing and external normalization to tungsten (W). Following separation of Re, samples were re-dissolved in 0.5 M HNO3 and a small aliquot (2% of the sample mass) was taken to measure the Re concentration by MC-ICP MS. Once the mass of Re in the remaining sample aliquot is determined, a known amount of pure W solution (ROMIL PrimAg Mono-Component Reference Solution) was added to each sample, so that the ratio (in g g−1) between W and Re in the sample is 20. Samples were run in 0.5 M HNO3 and introduced using a either PFA-50 or CF 35 nebuliser together with a micro-cyclonic spray chamber. For the CF 35 nebuliser, the measured uptake rate was ∼37 μL min−1, giving a sensitivity of 0.26 V (187Re) for a 10 ppb Re solution. In this study, we have not tested whether the use of other introduction systems (Aridus, Apex) could improve the sensitivity of the measurement. The standard NEPTUNE sample and H skimmer cones were used. Solution uptake time is 50 to 60 seconds with a 70 second wash time. Complete measurement of a sample (2 sample replicate analysis and 3 standards) takes ∼50 minutes, consuming ∼0.65 mL. The cup configuration allows simultaneous measurement of Re (185Re and 187Re), W (182W, 184W and 186W) and monitoring of Os (188Os, 189Os and 190Os) isotopes for possible isobaric interference (see ESI†).Analysis were performed in low mass resolution mode (MR ∼400) and consisted, like previous methods,19 of 25 cycles with an integration time of 16.77 s each. Whether this method is optimal for accuracy has not been fully assessed here and remains to be investigated. Hereafter, the term “analysis” is used to refer only to the 25 cycles measured on a given sample aliquot solution (one or several analysis) whereas the term “measurement” refers to the complete procedure (including digestion for solids, preparation and dilution). As Re concentrations are low in geological materials, our study used 1013 Ω amplifiers for detectors measuring 187Re and 185Re isotopes and 1011 Ω amplifiers for other detectors. The 1013 Ω amplifiers allow improved precision over 1011 Ω amplifiers on ion beams less than 0.52 V (ref. 23) (see section “Result and discussion”). Samples were typically measured at least twice (“replicate analysis” of the same purified Re solution) or more, depending upon the mass of Re available, with a bracketing standard in between (e.g. standard–sample–standard–sample–standard). All analytical sessions were carried out automatically using an SC-μ DX autosampler to ensure that the measurements and washouts followed a strict time sequence; necessary for interpolating and correcting for instrumental mass bias (IMB) using a standard–sample bracketing analysis method (see below).
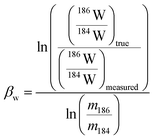
In plasma mass spectrometry IMB is the tendency of measured isotope ratios to be biased in favour of the heavier isotope.27 To a first approximation IMB is only mass dependant in MC-ICP-MS, although in reality IMB can drift slightly over time or can change as a result of instabilities in the plasma or of non-spectral interferences/matrix load on the plasma (due to residual elements).27 Rhenium has only two isotopes so IMB cannot be corrected for internally. There are two alternative approaches to correct for Re mass bias, both of which we employ in this study. It can be corrected for by doping the Re with an element of similar mass but with no isobaric masses (e.g. Ir or W)20,28 and normalizing to a known ratio of that element (a method referred to as “external normalization”, EN). Similar to previous studies,19,20,29 we doped the Re with tungsten and corrected for Re mass bias using an exponential law using the measured 186W/184W. The related equations are:
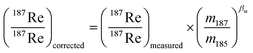 | (1) |
 | (2) |
The measured delta value expressed as below:
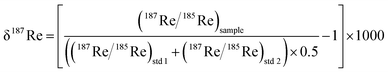 | (3) |
Results and discussion
Yield of the column chemistry separation and Re concentration measurements
We evaluate the yield of our column chemistry procedure by measuring the Re concentration of standard reference materials (SRMs) and a pure Re solution after a single pass of the column chemistry. In general, we find a good agreement (within ±10%) between our measured Re concentration values and those from the literature measured by isotope dilution30–32 (Table 2). Measured yields range from 92% to 124% with a median value of 96% (N = 44 digestions on 10 different SRM) with no systematic differences between rock types. This shows that HF–HNO3 digestion and column chemistry can be used to determine Re concentration in solid material with only slightly less precision than by isotope dilution techniques. For the pure Re solution, we find yields ranging between 85% and 105%, with an average value of 98.9% (N = 10). This indicates that additional matrix in rock samples does not detrimentally lower the Re yield.| SRM name | This study | Literature | ||||||
|---|---|---|---|---|---|---|---|---|
| Mass digested per sample (mg) | [Re] (ppb) | ±2SD (in %) | N measurements | [Re] (ppb) | Uncertainty (in %, 2σ) | N | Reference | |
| BCR-2 | 60 to 514 | 11.56 | 6.4 | 8 | 12.60 | 15.9 | 4 | Jochum et al., (2016)32 |
| BCR-1 | 480 to 653 | 0.81 | 9.6 | 9 | 0.84 | 30 | Jochum et al., (2016)32 | |
| UB-N | 466 to 698 | 0.20 | 14.3 | 9 | 0.21 | 4.8 | 14 | Meisel and Moser (2004)30 |
| MAG-1 | 172 to 559 | 3.65 | 7.3 | 6 | 3.91 | 1 | Meisel and Moser (2004)30 | |
| BHVO-2 | 498 to 617 | 0.61 | 12.8 | 5 | 0.54 | 5.3 | 6 | Jochum et al., (2016)32 |
| BIR-1 | 208 | 0.70 | 1 | 0.65 | 2 | Jochum et al., (2016)32 | ||
| JG-2 | 379 | 0.015 | 1 | 0.016 | 1 | Imai et al., (1995)33 | ||
| GP-13 | 200 | 0.30 | 1 | 0.32 | 14.2 | 4 | Meisel and Moser (2004)30 | |
| AGV-1 | 197 | 0.38 | 1 | 0.38 | 3 | Jochum et al., (2016)32 | ||
| TDB-1 | 497 | 0.99 | 1 | 0.79 | 6.0 | 7 | Meisel and Moser (2004)30 | |
| DNC-1 | 197 | 0.85 | 1 | 0.91 | 1 | Meisel and Moser (2004)30 | ||
| SCO-1 | 130 | 0.97 | 1 | 1.01 | 12.4 | 5 | Meisel and Moser (2004)30 | |
| SCO-1 | 591 | 0.04 | 1 | |||||
| NIST 1646a | 515 | 1.99 | 1 | |||||
Efficiency of the separation
Our column chemistry procedure aims to remove inorganic and organic matrices that can create spectral and non-spectral effects and impact the accuracy of the Re isotope measurement. A large number of elements (Li, Be, Na, Mg, Al, K, Ca, V, Cr, Mn, Fe, Co, Ni, Cu, Se, Sr, Y, Cs, Nd, Hf, Th, U) are not retained by the resin (Fig. 1) and are eluted almost immediately following the initial loading step (>85%). Some elements are partly eluted during the loading step and during the initial 1 M HCl elution step (Ti, As, Zr, Mo, Sb, W). Zinc is fully retained by the resin until the 0.5 M HNO3 step (Fig. 1) at which point it is quantitatively removed along with most of the remaining Cd (70%). About 60 to 80% of the Nb is eluted during the sample loading and 1 M HCl steps, with the remainder eluted during the 0.5 M and 4 M HNO3 steps. Thallium is the element with the highest proportion eluted during the Re elution step (about 30% of the original thallium). Importantly for Re isotope measurement protocol, where samples are spiked with a W solution that is isotopically homogenous, W originating in the sample is almost quantitatively removed prior to the Re elution peak (Fig. 1). Compared to previous methods,19,20 the use of the 1 M HCl step prior to the 0.5 M HNO3 allows for a more efficient removal of most chemical elements. The Re blank of the whole method (including digestion) range from 0 to 14 pg with a mean value of 3 ± 4 pg (n = 9, 1σ).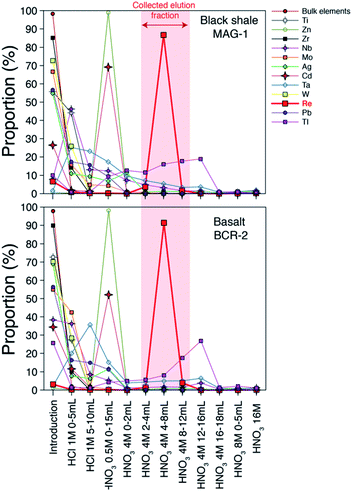 | ||
| Fig. 1 Elution curves of chemical elements and Re for two standard materials. Element concentrations were measured by quadrupole ICP-MS. Bulk elements are shown in Table 1. | ||
Fractionation of Re isotopes during the elution
Previous studies19,20 have shown that Re isotopes are fractionated during column chemistry and that a minimum yield of 80% is required for preventing resolvable fractionation of Re isotopes on the column. We measure δ187Re as a function of the yield of the procedure for a pure Re solution (Fig. 2) and find a similar behaviour as previous work.19,20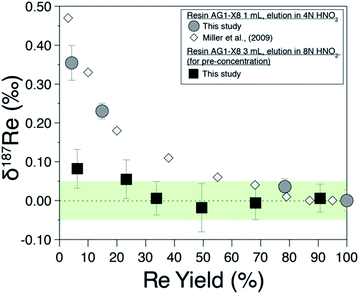 | ||
| Fig. 2 Rhenium isotope composition of pure Re solution (NIST-SRM989) as a function of the proportion of recovery from (i) field-based columns (black squares) and (ii) laboratory columns (grey circles). White diamonds are from Miller et al., (2009).19 The green area is the ±0.05‰ long-term external reproducibility of pure Re solution at 5 ppb Re concentration. | ||
Field pre-concentration of Re from water samples
The Re recovery of field pre-concentration columns were checked for all water samples. For a sample set of 55 water samples, we find recovery yields ranging from 43% to 118% with a median value of 95.7%, with 48 of 55 samples having recovery yield between 75 and 120% (considering an uncertainty of ±15%). Possible fractionation of Re isotopes due to incomplete recovery of the Re pre-concentrated on the resin has been investigated by recovering various amount of pure Re solution on the 3 mL of BioRad resin used for pre-concentration (Fig. 2; filled squares). For Re recovery >30%, no Re isotopic fractionation is observed. This decreased sensitivity to fractionation compared to the 1 mL column is probably due to the different aspect ratio of the column used for the field and/or the different eluent concentration (here 8 M HNO3).Evaluation of analytical errors
Here we discuss the different sources of error34,35 during Re isotopic measurement by MC ICP-MS. We refer to the “internal error” as the standard error (SE, in 2σ) of the 25 cycles of 16.77 second-integration periods (corresponding to one “analysis”). The “intermediate error” is the standard deviation (SD, in 2σ) of repeated analysis of the same solution, (here 2 sample analysis and 3 bracketing standards, giving 3 measured δ187Re). This within-run-precision will be influenced by mass bias instability over tens of minutes to an hour. Finally, the “external error” corresponds to the standard deviation (SD, in 2σ) of several measurements of a given solid or dissolved material (including digestion for solids, preparation and dilution) over an extended period of time. This between-run-precision will be influenced by day-to-day differences in instrumental plasma conditions and by sample preparation steps for samples.There are two major sources of noise that influence the internal error: counting statistics and the Johnson–Nyquist noise.27,34,36 The internal error for a given signal intensity corresponds to the sum of these two sources of error. The counting statistics can be predicted following the Poisson distribution.27,34,35 The relative standard error (RSE) in the isotope ratio due to counting statistics (σcounting statistics) is:
 | (4) |
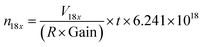 | (5) |
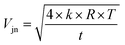 | (6) |
 | (7) |
We can see from eqn (7) that an increase of the resistor amplifier from 1011 to 1013 Ω results into an increase of the Johnson–Nyquist noise by a factor of 10, whereas at the same time the gain increases by a factor 100, which implies that the signal/noise ratio is improved by a factor of 10 using 1013 Ω amplifiers.23 Finally, the total internal error, corresponding to the sum of the counting statistics noise and the Johnson noise is calculated34,35 as:
 | (8) |
These theoretical calculations show that for a signal intensity higher than 0.5 V, the only significant source of uncertainty is the counting statistics. In this case, the SE is the same for the 1011 Ω and 1013 Ω amplifiers (Fig. 3). Below 0.5 V, the role of Johnson–Nyquist noise increases for the 1011 Ω amplifier but remains negligible for the 1013 Ω amplifier (Fig. 3). The difference between the SE (2σ) of 1011 Ω and 1013 Ω amplifier is small (<0.01‰) for 187Re intensity > 0.3 V, but significant (0.04‰) for 187Re intensity of 0.1 V, and very high (>0.10‰) for intensity < 0.1 V. Our measurements of pure Re solutions agree well with theoretical predictions and confirm the lower SE at a given intensity for 1013 Ω relative to 1011 Ω amplifiers. No difference in the measured internal error was observed between pure Re solutions and samples processed through column chemistry. Hence, the use of 1013 Ω amplifiers acts to significantly improve the internal error for small beam intensities, i.e. < 0.2 V. The internal error for 1 ng of Re, is less than 0.10‰ for 1013 Ω amplifiers but higher than 0.20‰ for 1011 Ω amplifiers.
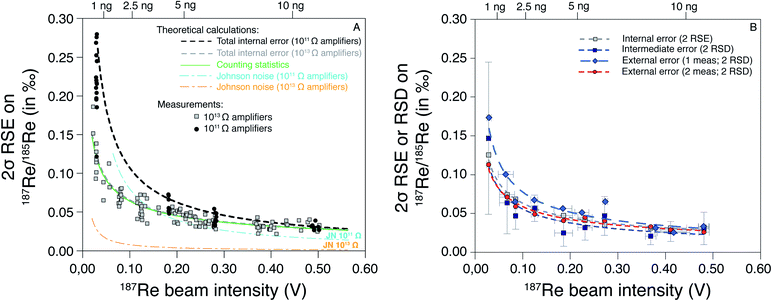 | ||
| Fig. 3 Standard error and deviation on 187Re/185Re ratio (as 2σ) as a function of the 187Re beam intensity (in V). In (A) are the predicted trends (see main text) and data measured with 1011 and 1013 Ω amplifiers on both Re isotopes. (B) Average intermediate and external error calculated every 0.05 V for a HReO4 solution measured over the course of three years (see Table 3). The relationship between the beam intensity (I187Re) and the mass of Re required (mRe, in ng) for two repeated analysis of each sample is mRe = 24.866 × I187Re. | ||
We also evaluated the variability of the intermediate error as a function of the 187Re beam intensity (Fig. 3B). We observe no significant difference between pure Re solutions and samples (which include column chemistry). The average values of intermediate errors increase with decreasing 187Re beam intensity. The average intermediate errors for a given 187Re beam intensity are similar to internal errors, showing that the internal errors can explain the variability between consecutive replicate analysis. To evaluate the long-term reproducibility (i.e. external error) associated to our Re isotope measurements, we repeatedly measured a pure Re solution (HReO4) at various 187Re beam intensity over the course of three years (Table 3). We calculated the external error as 2 SD of: (i) of individual analysis of HReO4; and (ii) averages of consecutive replicate analysis of HReO4 solutions. No significant difference is observed between the internal, intermediate and external error for replicate analysis (Fig. 3B). However, the external error is higher than the internal error on individual analysis. This shows that, on average, the internal errors can explain the variability between consecutive replicates, and between long-term repeated measurements. There is a tradeoff between running a sample once (1 analysis) at higher concentration (with issues to consider, e.g. potential for short-term blockage or instability) and running a sample multiple times (several analysis) at lower concentration. Here we choose to analyse each sample twice consecutively and use the relationship between the external error and the 187Re beam intensity (red curve on the Fig. 3B) to determine the “overall uncertainty” for each sample.
| Standard solution | Range of 187Re intensity (V) | 2 replicate analysis | 1 analysis | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Average 187Re intensity (V) | δ187ReSRM989 (‰) | Internal error (±2 SE) | Intermediate error (±2 SD) | External error (±2 SD) | Number of measurements | Average 187Re intensity (V) | δ187ReSRM989 (‰) | External error (±2 SD) | Number of measurements | ||
| HReO4 | 0.45–0.50 | 0.48 | 0.22 | 0.03 | 0.03 | 0.03 | 4 | 0.48 | 0.21 | 0.03 | 6 |
| 0.40–0.45 | 0.41 | 0.23 | 0.03 | 0.03 | 0.03 | 5 | 0.42 | 0.23 | 0.03 | 7 | |
| 0.35–0.40 | 0.37 | 0.22 | 0.03 | 0.02 | 0.03 | 5 | 0.38 | 0.23 | 0.03 | 14 | |
| 0.25–0.30 | 0.27 | 0.23 | 0.04 | 0.05 | 0.04 | 8 | 0.27 | 0.23 | 0.07 | 17 | |
| 0.20–0.25 | 0.23 | 0.22 | 0.04 | 0.03 | 0.05 | 11 | 0.22 | 0.21 | 0.05 | 23 | |
| 0.15–0.20 | 0.19 | 0.20 | 0.05 | 0.03 | 0.04 | 4 | 0.18 | 0.20 | 0.06 | 7 | |
| 0.10–0.15 | 0.12 | 0.23 | 0.06 | 0.06 | 0.05 | 7 | 0.12 | 0.23 | 0.07 | 16 | |
| 0.08–0.10 | 0.09 | 0.21 | 0.07 | 0.05 | 0.06 | 5 | 0.08 | 0.21 | 0.07 | 12 | |
| 0.04–0.08 | 0.07 | 0.23 | 0.08 | 0.06 | 0.07 | 5 | 0.06 | 0.22 | 0.10 | 8 | |
| 0.02–0.04 | 0.03 | 0.21 | 0.13 | 0.15 | 0.11 | 8 | 0.03 | 0.18 | 0.17 | 14 | |
| SRM 3141 | 0.48–0.52 | 0.49 | 0.28 | 0.03 | 0.03 | 0.03 | 13 | 0.49 | 0.28 | 0.04 | 26 |
| DURH-Re-1 | 1.08–1.10 | 1.09 | 0.44 | 0.02 | 0.02 | 0.02 | 5 | 1.09 | 0.44 | 0.03 | 10 |
Influence of W/Re ratio and intensity matching
Previous study19 doped samples to W/Re ratio of 2. However, in our case, since we measured Re isotopes at lower Re concentration with 1013 Ω amplifiers on Re isotope cups and 1011 Ω amplifiers on W isotope cups, we required a higher W/Re ratio. A W/Re ratio of 2 would result in an internal error on the 186W/184W higher than that for the 187Re/185Re ratio and this would be propagated onto the latter through the mass bias correction. Instead, we used a W/Re ratio of 20, so that even at very low Re concentration, the internal error on the 186W/184W is at least three times lower than the internal error on the 187Re/185Re. In addition, having a high W/Re ratio means that the contribution of residual W from the sample is lower. To ensure that this W/Re ratio does not create problems (in terms of abundance sensitivity or hydrides), we tested different W/Re ratios (1, 5, 10, 20 and 40) for two different Re concentrations (1 ppb and 5 ppb) and found no differences in precision and accuracy for W/Re ratios ranging from 5 to 40 (see ESI†).Differences in the concentrations between the sample and bracketing standard can potentially influence isotopic measurements. To test this, we measured pure rhenium solutions prepared with distinct Re/W ratio relative to the Re/W of the bracketing standard. We observe that δ187Re values are offset by more than 0.05‰ for a ratio mismatch of more than 40% (Fig. 4). This shows that is crucial to match within 10% the Re/W of the measured sample with that of the bracketing standard. The reasons for this effect may be due to different contributions of hydrides or W backgrounds.
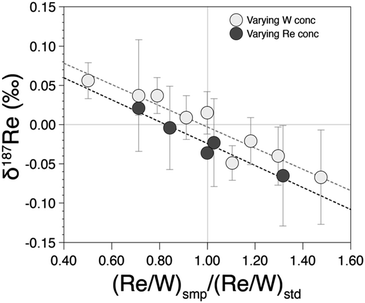 | ||
| Fig. 4 δ187Re as a function of the ratio between the (Re/W) ratio of the measured test standard relative to the (Re/W) ratio of the bracketing standard. | ||
Matrix effects and accuracy of the measurements
Residual inorganic and/or organic matrices following column separation can impact the accuracy of isotope measurement.27,29 We compared the measured δ187Re after one, two, three and four repeated column separations (Fig. 5). This test illustrates that the measured δ187Re can change as a function of number of column passes but how it does so is somewhat dependent on sample type. For BCR-2 (basalt), the δ187Re values are lower for two column passes relative to one, but similar for two and three column passes. For a chondrite (Allende), we also observe no difference in δ187Re between the second and fourth column passes on the same aliquot. For a seawater reference material (OSIL Atlantic seawater standard), the δ187Re for three and four column passes are identical, but lower than for two columns passes. For one river water (River 2 Canada), the δ187Re is significantly higher for 1 column pass relative to the value measured after 2 or more passes. For others (River 1 and 2 Canada), there is a small decrease of the δ187Re value after three passes relative to two, although this is not observed for every river sample (e.g. River UK and River 3 Canada).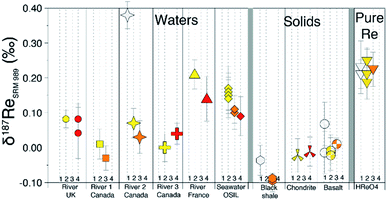 | ||
| Fig. 5 δ187Re (relative to NIST-SRM989) measured for different samples after repeated column separations (1 column pass = white, 2 = yellow, 3 = orange, 4 = red). | ||
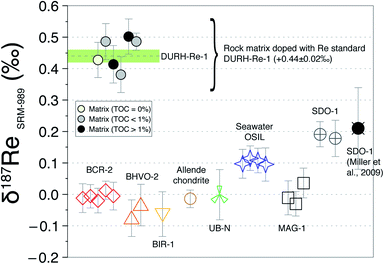
Overall, these tests reveal two things: (i) in general, the δ187Re values are unchanged after three column chemistry separations; (ii) the materials which continue to show a change in δ187Re after more than two repeated separations are materials that originally contain organic matter (river water and shales). To test whether the amount of remaining inorganic matrix can affect the accuracy of δ187Re measurement, we performed a series of tests where a Re standard solution, doped with various elements (Al, Fe, Mg, Nb, Zr, Ta, Mo, Zn, U, Hf) at different concentrations, covering a range of value of X/Re (where X is the doped element), was measured. We observe that over the range of concentrations of dopant tested, there is no effect, within uncertainty, on the accuracy of the δ187Re value (see ESI†). In addition, we used a granite SRM (USGS “G-2”) with a very low Re concentration (11 ppt) that we doped with a known mass of 187Re-rich standard solution DURH-1 (+0.44 ± 0.02‰, Table 3) so that the contribution of Re from the sample is negligible (<0.6%, see ESI†). This modified granite SRM was passed through column chemistry (3 times) and measured as a normal sample and returned the same value as pure DURH-1 (Fig. 6). These tests show that our column procedure is optimal for removing effects caused by an inorganic matrix.
Organics that influence isotopic measurement can originate from: (i) the resin or (ii) the sample. Matrix effects caused by resin degradation have been documented for other isotope systems.37,38 In this study, we systematically treat the column residue with concentrated HNO3 at 130–150 °C for 24 h before isotope measurement. Measurements of pure Re solutions processed and non-processed through column chemistry return identical δ187Re values (Table S4, ESI†) suggesting that any residual organic molecules derived from the resin do not affect the measurement. We note though that for some of these tests, abrupt changes in the 186W/184W mass bias are observed, leading to inaccurate δ187ReSSB and (δ187ReSSB–δ187Re) values up to +0.35‰ but correct δ187Re. This shows that matrix effects caused by residual resin-derived organics are adequately corrected for using W normalization.
Resin AG1-X8 is a cationic resin for which organic molecules (negatively charged) have a high affinity. Adsorption of organic molecules to the resin is evidenced by a change in the colour (orange to dark) of the resin. Some of the organics are eluted in 4 M HNO3, at the same time as Re, observed as a yellowish colour of the solution and the size/colour of the residue. These organics could potentially create interferences on the Re isotopic measurement and influence the elution volume of Re (e.g. competition for binding sites on the resin). To assess the role of organic matter we used two samples (New Zealand soils with 1 and 6% organic carbon) that have a very low Re concentration (<35 ppt)7 and several shale-type Re-free matrix (by mixing volume cuts before and after Re elution peak, see ESI†) and doped them with Re solution DURH-Re-1. Following three column chemistry separations, we measured δ187Re respectively which are in agreement within uncertainty with the value of the DURH-Re-1 standard (Fig. 6). Collectively, this shows that our column procedure successfully remove effects caused by sample-derived organic matrix.
Application to reference materials and assessment of data quality
The δ187Re values of several reference materials (BCR-2, BHVO-2, UB-N, BIR-1, MAG-1, SDO-1, OSIL Atlantic Seawater) have been determined (Table 4). The variability in δ187Re values defined by these standards is about 0.28‰ (Fig. 6). The intermediate and external error of the SRM are comparable to those of pure Re solutions, indicating that digestion and column chemistry does not introduce additional uncertainty on the δ187Re measurement relative to pure Re solution. Since there are very few reference materials that have been measured for δ187Re, it is of prime importance to assess the accuracy of the measurements. Our analysis of NIST 3141 and HReO4 return δ187Re values respectively of 0.28 ± 0.03‰ and 0.22 ± 0.03‰, in agreement with published values.19 The δ187Re value we obtain for the SDO-1 standard, δ187Re = 0.19 ± 0.03‰, also matches previously published value.19 These results are encouraging for accurate analysis, however in future a wider range of materials will need to be cross-calibrated between laboratories for a more thorough assessment.| Reference material | δ187Re SRM989 (‰) | Overall uncertainty (±2 SD) | External error (±2 SD) | Number of measurements | Intermediate error (±2 SD) | Internal error (±2 SE) | Mass Re per analysis (ng) |
|---|---|---|---|---|---|---|---|
| OSIL (Atlantic seawater) | 0.10 | 0.04 | 0.02 | 4 | 0.05 | 0.05 | 3.9 |
| MAG-1 (marine mud) | 0.00 | 0.05 | 0.07 | 3 | 0.05 | 0.05 | 4.2–5.5 |
| BHVO-2 (basalt) | −0.06 | 0.06 | 0.07 | 2 | 0.06 | 2–2.5 | |
| BIR-1(basalt) | −0.06 | 0.07 | 1 | 0.06 | 0.9 | ||
| BCR-2 (basalt) | −0.01 | 0.04 | 0.02 | 5 | 0.05 | 0.04 | 4.9–12.2 |
| CV3 Allende (chondrite) | −0.01 | 0.03 | 1 | 0.01 | 0.04 | 21 | |
| SDO-1 (black shale) | 0.19 | 0.05 | 0.03 | 2 | 0.01 | 3–12 | |
| UB-N (serpetinite) | 0.00 | 0.08 | 1 | 0.04 | 0.08 | 1.3 |
Perspectives for the measurement of δ187Re in geological samples
The first Re isotope study19 achieved precision of ±0.10‰ for 10 ng of Re. From this, the authors concluded that Re isotope measurements would be limited only to Re-rich samples (such as black shales or sulfide ores). Here, our external reproducibility is ±0.04‰ for 5 ng of Re (Fig. 3) based on the use of 1013 Ω amplifiers in wet plasma conditions (micro-cyclonic chamber). There are potential alternative methods that could be used to deliver this improvement, or further refine it. A desolvator (Aridus, Apex) combined with a jet sample cone and X-skimmer cone could lead to a further significant increase of the sensitivity for Re. However, there are concerns regarding the Re beam stability in dry plasma conditions and the possibility of Re isotope fractionation on the desolvator membrane.39 Future studies should assess whether these additional changes to the sample introduction and/or interface could allow further reduction in the volume of sample required for making precise Re isotopic measurements.Irrespective of any refinements to the sample introduction and interface, the modified column chemistry and analytical advances we have made allow a large range of geological materials to be measured at high precision (Fig. 7). For instance, for most organic rich shales, we estimate that only ∼0.1 g of sample is required for a precision of ±0.04‰. For igneous rock samples (e.g. Mid-Ocean Ridge Basalts, MORB), we estimate that ∼1–5 g would be required for a precision of ±0.04‰. For river waters, a large volume of sample (∼1 to 20 L) is still required because most rivers have dissolved Re concentrations in the ppt range (Fig. 7). Our field pre-concentration method addresses this. Instead of transporting many kilograms of filtered water, we are able to concentrate ∼5–10 ng of Re onto a few mL of resin and subsequently recover Re for precise isotopic analysis. The required precision for any isotopic analysis will depend on the range of δ187Re values expected in the samples undergoing analysis. So far, the range of measured δ187Re in geological materials is ∼0.80‰,9 a range much larger than the analytical precision. Along with the method developments described here which make the vast majority of natural samples available for analysis (Fig. 7), these calculations provide impetus for further exploration of the Re isotope system.
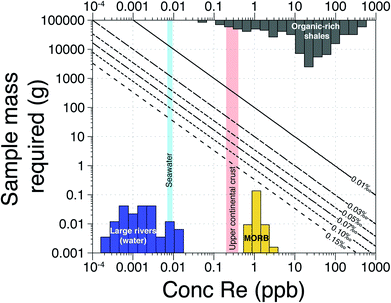 | ||
| Fig. 7 Sample mass required (in g) as a function of the Re concentration of geological materials for different measurement precisions. Rhenium concentration data from published work.1,2,14,21 | ||
Conclusions
Here we provide new methods to measure the isotopic composition of Re in a wide range of solid and liquid samples. The main points are:- An improved precision via MC-ICP-MS afforded by the use of 1013 Ω amplifiers on 185Re and 187Re.
- The use of W doping, matching W/Re ratios of samples and standards, and standard-sample bracketing allows for the correction of instrumental mass bias and some matrix affects.
- The importance of column chemistry separation, and here we provide evidence that three repeated separations are necessary.
- The use of a field-based pre-concentration of Re for river water samples, which makes the analyses of river waters feasible.
Combining these approaches, we are able to report an improved precision on δ187Re measurements for a lower required mass of Re (±0.10‰ for a mass of Re of ∼1 ng to ±0.03‰ for a mass of Re of >10 ng) compared to previous studies.19,20 We have analysed a range of solid geological reference materials, and a seawater standard, and observe variability of 0.28‰. The approaches here open up studies of Re isotopic fractionation, in particular opening up the potential of Re isotopes as a proxy for oxidative weathering, and for reconstruction of past redox cycling.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded by the European Research Council (ERC) Starting Grant “ROC-CO2” (project 678779) awarded to Robert Hilton and a COFUND Junior Research Fellowship supported by the European Union's Seventh Framework Programme to Mathieu Dellinger. We thank: Bernard Peucker-Ehrenbrink and Alex Dickson for sharing Re isotope standards; Martin West for laboratory assistance; Josh West, Kevin Burton, Julie Prytulak, Ambre Luguet for discussions prior to submission.Notes and references
- C. A. Miller, B. Peucker-Ehrenbrink, B. D. Walker and F. Marcantonio, Geochim. Cosmochim. Acta, 2011, 75, 7146–7179 CrossRef CAS.
- D. Colodner, J. Sachs, G. Ravizza, K. Turekian, J. Edmond and E. Boyle, Earth Planet. Sci. Lett., 1993, 117, 205–221 CrossRef CAS.
- A. D. Anbar, R. A. Creaser, D. A. Papanastassiou and G. J. Wasserburg, Geochim. Cosmochim. Acta, 1992, 56, 4099–4103 CrossRef CAS.
- J. Golden, M. McMillan, R. T. Downs, G. Hystad, I. Goldstein, H. J. Stein, A. Zimmerman, D. A. Sverjensky, J. T. Armstrong and R. M. Hazen, Earth Planet. Sci. Lett., 2013, 366, 1–5 CrossRef CAS.
- T. K. Dalai, S. K. Singh, J. R. Trivedi and S. Krishnaswami, Geochim. Cosmochim. Acta, 2002, 66, 29–43 CrossRef CAS.
- R. G. Hilton, J. Gaillardet, D. Calmels and J.-L. Birck, Earth Planet. Sci. Lett., 2014, 403, 27–36 CrossRef CAS.
- K. Horan, R. G. Hilton, D. Selby, C. J. Ottley, D. R. Gröcke, M. Hicks and K. W. Burton, Sci. Adv., 2017, 3, e1701107 CrossRef PubMed.
- A. I. Sheen, B. Kendall, C. T. Reinhard, R. A. Creaser, T. W. Lyons, A. Bekker, S. W. Poulton and A. D. Anbar, Geochim. Cosmochim. Acta, 2018, 227, 75–95 CrossRef CAS.
- C. A. Miller, B. Peucker-Ehrenbrink and E. A. Schauble, Earth Planet. Sci. Lett., 2015, 430, 339–348 CrossRef CAS.
- J. Crusius, S. Calvert, T. Pedersen and D. Sage, Earth Planet. Sci. Lett., 1996, 145, 65–78 CrossRef CAS.
- J. L. Morford, W. R. Martin and C. M. Carney, Chem. Geol., 2012, 324–325, 73–86 CrossRef CAS.
- D. Selby, R. A. Creaser and M. G. Fowler, Geochim. Cosmochim. Acta, 2007, 71, 378–386 CrossRef CAS.
- F. Mahdaoui, L. Reisberg, R. Michels, Y. Hautevelle, Y. Poirier and J.-P. Girard, Chem. Geol., 2013, 358, 90–100 CrossRef CAS.
- A. Dubin and B. Peucker-Ehrenbrink, Chem. Geol., 2015, 403, 111–120 CrossRef CAS.
- R. J. Walker, Geochemical Perspectives, 2016, 5, 1–2 CrossRef PubMed.
- K. Lodders, Astrophys. J., 2003, 591, 1220 CrossRef CAS.
- E. H. Hauri and S. R. Hart, Chem. Geol., 1997, 139, 185–205 CrossRef CAS.
- J. W. Morgan, J. Geophys. Res.: Solid Earth, 1986, 91, 12375–12387 CrossRef.
- C. A. Miller, B. Peucker-Ehrenbrink and L. Ball, J. Anal. At. Spectrom., 2009, 24, 1069–1078 RSC.
- R. Liu, L. Hu and M. Humayun, Meteorit. Planet. Sci., 2017, 52, 479–492 CrossRef CAS.
- A. Gannoun, K. W. Burton, I. J. Parkinson, O. Alard, P. Schiano and L. E. Thomas, Earth Planet. Sci. Lett., 2007, 259, 541–556 CrossRef CAS.
- L. A. Jaffe, B. Peucker-Ehrenbrink and S. T. Petsch, Earth Planet. Sci. Lett., 2002, 198, 339–353 CrossRef CAS.
- T. Breton, N. S. Lloyd, A. Trinquier, C. Bouman and J. B. Schwieters, Procedia Earth Planet. Sci., 2015, 13, 240–243 CrossRef CAS.
- Z. Chu, Y. Yan, Z. Chen, J. Guo, Y. Yang, C. Li and Y. Zhang, Geostand. Geoanal. Res., 2015, 39, 151–169 CrossRef CAS.
- J. P. Faris and R. F. Buchanan, Anal. Chem., 1964, 36, 1157–1158 CrossRef CAS.
- E. L. Gendre, E. Martin, B. Villemant, P. Cartigny and N. Assayag, Rapid Commun. Mass Spectrom., 2017, 31, 137–144 CrossRef PubMed.
- F. Albarède and B. Beard, Rev. Mineral. Geochem., 2004, 55, 113–152 CrossRef.
- J. Day, D. G. Pearson and G. M. Nowell, in Plasma Source Mass Spectrometry: applications and emerging technologies, 2003, pp. 374–390 Search PubMed.
- A. Poirier and R. Doucelance, Geostand. Geoanal. Res., 2009, 33, 195–204 CrossRef CAS.
- T. Meisel and J. Moser, Geostand. Geoanal. Res., 2004, 28, 233–250 CrossRef CAS.
- T. Meisel and M. F. Horan, Rev. Mineral. Geochem., 2016, 81, 89–106 CrossRef.
- K. P. Jochum, U. Weis, B. Schwager, B. Stoll, S. A. Wilson, G. H. Haug, M. O. Andreae and J. Enzweiler, Geostand. Geoanal. Res., 2016, 40, 333–350 CrossRef CAS.
- N. Imai, S. Terashima, S. Itoh and A. Ando, Geostand. Newsl., 1995, 19(2), 135–213 CrossRef CAS.
- S. G. John and J. F. Adkins, Mar. Chem., 2010, 119, 65–76 CrossRef CAS.
- G. Paris, A. L. Sessions, A. V. Subhas and J. F. Adkins, Chem. Geol., 2013, 345, 50–61 CrossRef CAS.
- J. Liu and D. G. Pearson, Chem. Geol., 2014, 363, 301–311 CrossRef CAS.
- A. J. Pietruszka and A. D. Reznik, Int. J. Mass Spectrom., 2008, 270, 23–30 CrossRef CAS.
- F. Kurzweil, C. Münker, J. Tusch and R. Schoenberg, Chem. Geol., 2018, 476, 407–417 CrossRef CAS.
- M. Pfeifer, N. S. Lloyd, S. T. M. Peters, F. Wombacher, B. M. Elfers, T. Schulz and C. Münker, J. Anal. At. Spectrom., 2017, 32, 130–143 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ja00288j |
| This journal is © The Royal Society of Chemistry 2020 |