Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Martini coarse-grained models of imidazolium-based ionic liquids: from nanostructural organization to liquid–liquid extraction†
Luis Itza
Vazquez-Salazar‡
 ,
Michele
Selle§‡
,
Alex H.
de Vries
,
Michele
Selle§‡
,
Alex H.
de Vries
 ,
Siewert J.
Marrink
,
Siewert J.
Marrink
 * and
Paulo C. T.
Souza
* and
Paulo C. T.
Souza
 *
*
Groningen Biomolecular Sciences and Biotechnology Institute and Zernike Institute for Advanced Materials, University of Groningen, Nijenborgh 7, 9747 AG Groningen, The Netherlands. E-mail: p.c.telles.de.souza@rug.nl; s.j.marrink@rug.nl
First published on 24th August 2020
Abstract
Ionic liquids (ILs) are remarkable green solvents, which find applications in many areas of nano- and biotechnology including extraction and purification of value-added compounds or fine chemicals. These liquid salts possess versatile solvation properties that can be tuned by modifications in the cation or anion structure. So far, in contrast to the great success of theoretical and computational methodologies applied to other fields, only a few IL models have been able to bring insights towards the rational design of such solvents. In this work, we develop coarse-grained (CG) models for imidazolium-based ILs using a new version of the Martini force field. The model is able to reproduce the main structural properties of pure ILs, including spatial heterogeneity and global densities over a wide range of temperatures. More importantly, given the high intermolecular compatibility of the Martini force field, this new IL CG model opens the possibility of large-scale simulations of liquid–liquid extraction experiments. As examples, we show two applications, namely the extraction of aromatic molecules from a petroleum oil model and the extraction of omega-3 polyunsaturated fatty acids from a fish oil model. In semi-quantitative agreement with the experiments, we show how the extraction capacity and selectivity of the IL could be affected by the cation chain length or addition of co-solvents.
1 Introduction
Ionic liquids (ILs) have been gaining importance during the last few years because of the many possible applications in different areas of chemistry like electrochemistry, chemical synthesis, catalysis, pharmaceutics and medicine, separation and extraction of fine chemicals and nanotechnology.1–7 These unusual substances are a special class of liquids composed entirely of ions with melting points below 100 °C. Generally, an IL consists of one large organic cation and an organic or inorganic anion. Among the existing ILs, the most commonly used are the ones based on non-symmetrically substituted dialkylimidazolium cations and bulky anions.8,9 ILs are also known as “designer solvents” because one can modify their physical properties by changing the anionic and cationic components.8One of the most prominent applications of ILs is in separation science, as ILs have characteristics such as unusual selectivities, high extraction efficiencies, durability and resistance to thermal degradation which makes them ideal for performing extractions.10 ILs have found a major application field in the extraction and separation of bioactive compounds.10,11 One of the most widely investigated IL for extractions is the cation 1-alkyl-3-methylimidazolium [Cnmim]+ in combination with [BF4]−, [PF6]−, Cl−, or Br− as anions.10
Understanding the structure of ILs is one of the cornerstones for the development and improvement of applications of ILs.2,8,9,12 In this direction, computational modelling, in particular through the use of molecular dynamics (MD) simulations, has proven to be a powerful technique to obtain insights into the nanostructure and dynamics of ILs.13–18 However, the use of full atomistic simulations of ILs is computationally intensive.13,18–20 Consequently, there is a need to develop coarse-grain (CG) models11,14 that can address the problem by simulating ILs at a low computational cost while still capturing the details of the structure and properties of these polar solvents. A number of bottom-up CG approaches have been developed for ILs that are capable of accurately reproducing reference data obtained from all-atom simulations.21–27 However, most of these CG force fields are specific for certain ILs or are not compatible with other molecules,16 such that these models cannot be easily extended or adapted to describe complex mixtures with other compounds. Alternatively, top-down CG force fields such as Martini are more amenable to ‘mixing-and-matching’ several classes of compounds.
The Martini CG force field developed by Marrink and co-workers29,30 is one of the most popular CG force fields for simulations of biomolecules31,32 and nowadays is extending its applications to soft materials science.31–34 This force field is constructed in a top-down approach by extensive calibration of the non-bonded interactions by comparison against thermodynamic data.31 Because of the way it is constructed, Martini can be used in a broader range of applications without the necessity of reparametrize the model for every specific application. Currently, only three classes of ILs models were developed for Martini 2.2, with the studies focused on pure IL, aqueous biphasic mixtures35,36 and interactions with membranes.37 Recently a number of limitations of the current version 2.2 of the Martini model have been reviewed,31,38 which paved the way for developing a new version, Martini 3.0.
In this paper, we elaborate and test a new CG model for imidazolium-based ILs in the framework of the Martini 3.0 force field, and we investigate applications of our model on the extraction of fine chemicals. The rest of the paper is structured as follows. The next section describes the concept of our CG model and methods used for the construction and simulation of pure IL and biphasic systems used for extractions. Thereafter, the results are presented, with the first part mainly devoted to description of the structure of the studied ILs in relation to experimental data, while the second part is focused on two extraction simulations: (i) extraction of aromatic compounds from a petroleum oil model system; (ii) extraction of omega-3 polyunsaturated fatty acids from a fish oil model. The final section draws some conclusions and presents future perspectives for the simulation of these systems.
2 Materials and methods
2.1 Simulation details
All simulations described were performed using the GROMACS 5.139 simulation package and the open beta version of the Martini 3.0 CG force field.40 We tested long-range coulombic interactions by using both a particle mesh Ewald method (PME)41 and a reaction field (RF) method.42 The cutoff distance was defined as 1.1 nm for coulombic and Lennard-Jones interactions as suggested by de Jong et al.43 The Verlet neighbour search algorithm44 was used in combination with the neighbour list, which was updated every 20 steps. We use the LINCS algorithm45 to constrain the bonds and the leapfrog integration algorithm for the solution of the equations of motion. The temperature was controlled using the v-rescale thermostat46 with a coupling time of 1 ps. For pressure coupling, the Parrinello–Rahman47 barostat was used (compressibility 3 × 10−4 bar−1). All initial configurations were built using GROMACS tools and the PACKMOL software.482.2 CG models
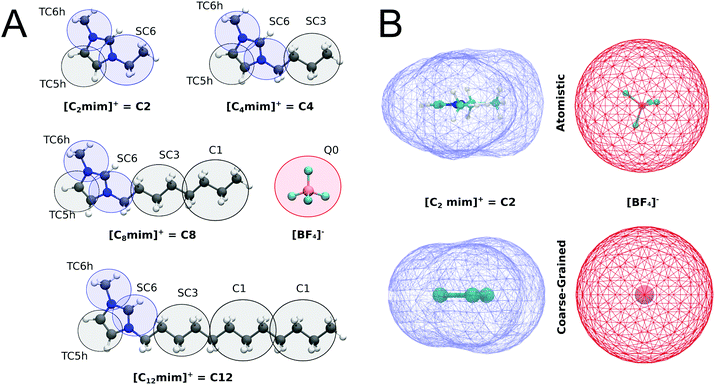
For the imidazolium IL type [Cnmim]+[BF4]−, henceforth called Cn, the CG models described in Fig. 1A were constructed. The substituted imidazolium rings were initially modelled with three beads, using the bead type TC6 for the nitrogen-containing aromatic fragments while the rest of the carbon-based aromatic ring is represented by a TC5 bead. Tiny bead sizes were used to better mimic the overall shape and packing of the molecule, which is important for the stacking of the imidazolium cation with other aromatic compounds. From this template, that represents the C1 cation, the different tail lengths were modelled. For C2, the size of one of the TC6 beads was increased to its small “S” version (SC6), which includes an ethyl group attached to one of the nitrogen atoms. For C4, an SC3 bead was added to represent the additional n-propyl fragment while the subsequent tail lengths in C8 and C12 were obtained adding a regular size C1 bead for each additional n-butyl fragment (which is analogous to the strategy used to build different lipid tail lengths in Martini49). A representation of the coarse-grained models of imidazolium cations is shown in Fig. 1A.In contrast to most Martini models, partial (instead of integer) charges are used to describe the Cn cations. The values of the charges in the imidazolium ring (+0.5 on each nitrogen-based bead) were computed according to a variant of the Dipole Preserving Charge50 method described in the ESI.† Based on the open-beta release of Martini 3.0, the Lennard-Jones interactions of beads in the imidazolium ring are slightly increased with themselves (in one interaction level) and with the rest of the neutral beads (two interaction levels) compared to neutral versions of the same bead type. At the moment, this is implemented by introducing bead-types carrying the label “h”, which will be updated in the final release of Martini 3. The bonded parameters for the tails are inspired by the lipid CG model.49 The bond lengths of the imidazolium ring were tuned to get the best compromise in terms of bulk density and molecular surface area. A comparison of the molecular surfaces of atomistic and coarse-grained structures of C2 cation and [BF4]− anion are shown in Fig. 1B. The molecular surfaces (also called Connolly surfaces) were estimated with the GROMACS tool gmx sasa.39 For these calculations, we used a probe of 0.185 nm and assigned correct sizes for the CG beads (as they are not defined in the van der Waals radius file of GROMACS). All structural parameters are described in the ESI (Table S1†).
The benzene molecule used is constructed with three TC4 beads with a constrained bond between them of 0.291 nm. For octane and the fatty acids of the fish oil, we use the same bonded parameters and mapping from the previous version of Martini,29,30 adapting some bead types to the new ones of the beta version of Martini 3.0. For the neutral carboxylic heads of the fatty acids, we use a P2 bead. All the parameters are available on our web portal cgmartini.nl.
2.3 System setup
For simulations of pure ionic liquids, a cubic box of approx. 6.4 × 6.4 × 6.4 nm3 was used. ILs of C2, C4, C8, and C12 (Fig. 1A) were each simulated over a temperature range of 293–393 K. The number of molecules for each system is described in Table S2 in the ESI.† The energy of the system was minimized for 500 steps using the steepest descent algorithm. The system was then equilibrated in two steps: 500 ps at 298 K and 100 ns at the target temperature. The length of the production simulation was 400 ns. For the simulations used to study the temperature-driven phase transition in C12, a bigger and rectangular box (12.7 × 12.7 × 6.4 nm3) was also used, avoiding possible artefacts induced by periodic boundary conditions. For these simulations, the initial configuration was built in a lamellar form, resembling a smectic A phase. For comparison of structural properties, atomistic simulations of pure C2, C4, and C8 ILs were performed according to the procedure described in the ESI.†Biphasic systems containing two liquid phases, namely an oil and an IL, were simulated at 300 K and 1 bar in the NPzT ensemble, with X and Y dimensions fixed and pressure applied in z-direction (normal to the liquid/liquid interface). The energy of the system was first minimized using 5000 steps. Equilibration of the system was performed using a time step of 5 fs during 1 ns. Production was generated using a time step of 20 ps during 6 μs. The ILs considered are C2, C4, C8, and C12 (Fig. 1). For the extraction simulation of aromatic compounds from a model of petroleum oil, the system was built as a mixture of octane and benzene at a weight ratio of 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10.51 Subsequently, this model system was mixed with IL, adding the same number of cation and anion pairs as the number of octane molecules. For the construction of the system with fish oil, we follow an approximate composition of a model fish oil from Chinook Salmon according to the data reported by Stansby et al.52 The composition of the fish oil is 48% of Oleic Acid (OLE), 48% of Palmitic Acid (PAL) and 4% of Docosahexaenoic Acid (DHA) in weight percentage. The biphasic systems were constructed in a proportion of 2
10.51 Subsequently, this model system was mixed with IL, adding the same number of cation and anion pairs as the number of octane molecules. For the construction of the system with fish oil, we follow an approximate composition of a model fish oil from Chinook Salmon according to the data reported by Stansby et al.52 The composition of the fish oil is 48% of Oleic Acid (OLE), 48% of Palmitic Acid (PAL) and 4% of Docosahexaenoic Acid (DHA) in weight percentage. The biphasic systems were constructed in a proportion of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 IL/fish oil in volume percentage. To test the stability of the biphasic system through the addition of co-solvents, we add octane in the same volume percentage of IL as suggested in experimental tests.53 The number of particles and the size of the boxes used for all systems modelated are described in the ESI (Table S2†).
1 IL/fish oil in volume percentage. To test the stability of the biphasic system through the addition of co-solvents, we add octane in the same volume percentage of IL as suggested in experimental tests.53 The number of particles and the size of the boxes used for all systems modelated are described in the ESI (Table S2†).
2.4 Analysis for pure ionic liquids
Radial distribution functions (RDFs) were computed using GROMACS tool gmx rdf.39 Snapshots of the simulations were generated using the VMD (Visual Molecular Dynamics) suite.54 The size of the nanodomains for C4, C8 and C12 were estimated by determining the average cluster size formed by the anions, using a cutoff of 0.55, 0.60 and 0.65 nm, respectively, using the GROMACS tool gmx clustsize.39 Different choices of cutoff were used to reflect the fact that the size of the nanodomains depends on the length of the alkyl tail of the cation. This strategy is in line with the approach used in the recent work of Bresme et al. 2020.27 In our case, we select the cutoff that better estimates the aggregate sizes (in terms of number of anions) visually observed in the trajectories. To characterize long range order in the C12 system, we computed the order parameter of the alkyl tail defined as: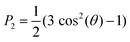 | (1) |
Heat capacity was computed as the derivative of the energy with respect of the temperature as:
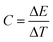 | (2) |
2.5 Viscosity calculations
Following the recommendations given by Maginn,57 specific MD simulations were performed in the NVT ensemble to estimate viscosities. Only C2, C4 and C8 were considered, as experimental data for comparison is available for them.58–60 Estimates were performed over a temperature range of 293–353 K. For each temperature, 100 replicates were used to ensure an adequate sampling and convergence. Each system was equilibrated for 1.5 ns in the NPT ensemble followed by production for 2.5 ns in the NVT ensemble. Shear viscosity was computed using the Einstein relationship (eqn (3)) as implemented on the GROMACS tool gmx energy:39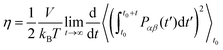 | (3) |
2.6 Oil/IL transfer free energy and selectivity calculations
For those biphasic systems for which conventional MD simulations showed enough sampling of the all the relevant components in both phases, the oil/IL transfer free energy (ΔGtrans) was simply computed as:ΔGtrans = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Dx) ln(Dx) | (4) |
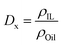 | (5) |
For systems where more sampling was required, the ΔGtrans was obtained from umbrella sampling (US) simulations,62 extracting the free energies with the weighted histogram analysis method (WHAM),63 as implemented in the GROMACS tool gmx wham.39 In this case, errors were estimated using bootstrapping. The reaction coordinate was the distance between the center of mass of one molecule of component x and the IL phase; 56 windows spaced 0.1 nm apart were used, with a simple harmonic umbrella potential with a force constant of 2000 kJ mol−1 nm−2. The sampling time for each window was 100 to 200 ns, depending on the convergence. The same biphasic systems (in terms of box size and composition) used for the conventional MD simulations were also used for the US. To quantify the selectivity of the extraction (Sx), we use the following expression:53,64
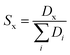 | (6) |
3 Results and discussion
3.1 Pure ionic liquids
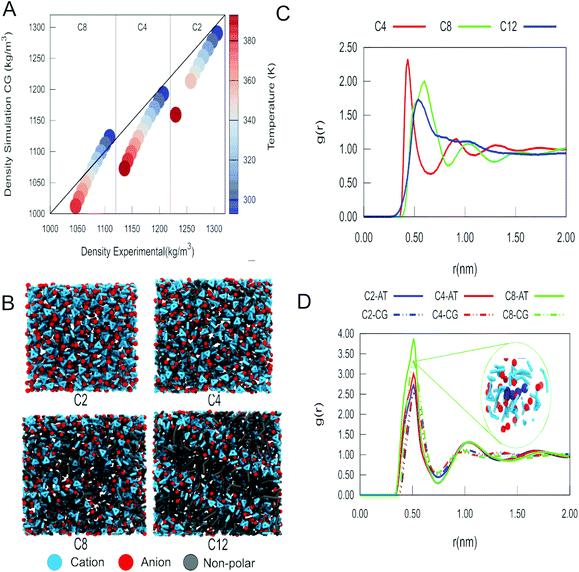
Experimentally, it has been documented that the density of imidazolium-based ILs decreases as the temperature rises.65,66 Density is also affected by the length of the alkyl tail of the imidazolium cation, with long alkyl tail cations showing lower density than the counterparts with shorter alkyl tails.65,66 The results of our MD simulations with the pure ILs indicate that the densities of the ILs studied (Fig. 2A and Fig. S1, S2†) follow these experimental trends. In all cases, we observe that as the temperature decreases, the agreement of the densities obtained with our model and the experimental values improves. The use of PME or reaction-field electrostatics does not lead to notable differences in the density (see Fig. S3–S5 and Tables S3, S4†). This was also observed for all the other systems simulated in this work. So, from this point on, we will only describe the results using PME.One crucial aspect that is well described by our model is the formation of nanodomains in the ILs. We can see in Fig. 2B that as we increase the length of the tail of the alkyl fragment, the organization of the liquid becomes more heterogeneous. Estimates of the size of the nanodomains are presented in Fig. S9.† For C12, we observe the formation of a smectic phase. The formation of domains as a function of the length of the alkyl tail of the imidazolium cation was further quantified using the radial distribution function (RDF). In the RDF profiles between the centre of mass of the alkyl tails and itself (Fig. 2C), we observe that the size of the domain increases from C4 to C8 and has a maximum for C12. Despite the changes in long range organization, the short range structure of the IL charged groups is conserved for different cations, as evidenced by the RDFs between the charged groups (Fig. S6–S8†). The RDFs between the imidazolium ring and the anion are also in close agreement with those obtained from our reference atomistic simulations (Fig. 2D), as well as with those obtained with another CG model by Wang et al.22 However, it is also evident that the aggregation of nonpolar tails affects the local structure to some extent, in particular a closer approach of the anions to the imidazolium ring as the tail length increases (Fig. 2D). These features clearly imply that our model can describe the spatial heterogeneity of the ILs.
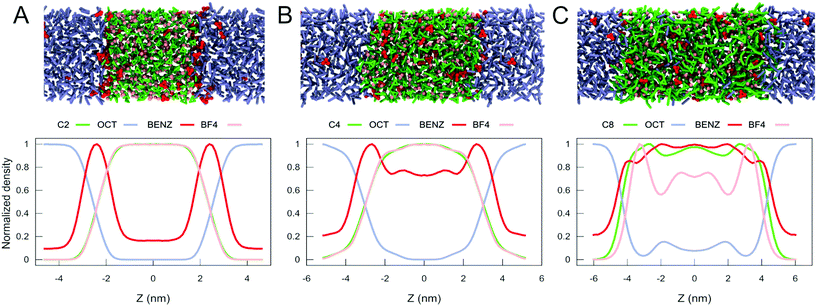
It is known from the literature that the range of temperatures simulated in this work includes a phase transition for C12.67,68 To study this phase transition in more detail, additional simulations of the C12 system were performed with a bigger simulation box (see Methods). Upon analysis of the RDFs of the cation C12 IL at different temperatures, we observed a change in the long-range structure of the IL (Fig. 3A and S10†). In particular, we observe a change of the intensity of the second peak (around 1.05 nm) of the RDFs between the alkyl tails, which is lower at a higher temperature (see insert, Fig. 3A). A plot of the intensity of the second peak of the RDF with respect to temperature (Fig. 3B) clearly shows a transition occurring around 330 K. The phase transition was further quantified by measuring the order parameter of the alkyl tail with respect to the system's z-axis (Fig. 3C). From this data, it is clear that the phase transition of C12 is accompanied by a change in the orientation of the alkyl tails of the C12 cation, passing from a smectic (order parameter around 0.3) to a completely isotropic orientation (order parameter close to zero). Finally, in order to obtain a more accurate estimate of the temperature at which this phase transition occurs, we analyze the derivative of the energy with respect to the temperature, which corresponds to the heat capacity of the system (Fig. 3D). From this figure, it is immediately clear that the phase transition from the smectic phase to the isotropic phase occurs at 325 K, a value that is in very good agreement with the experimental reported value for C12 of 324.75 K.68 Snapshots from the simulation box at different temperatures (Fig. 3E) also provide visual evidence for the phase transition.
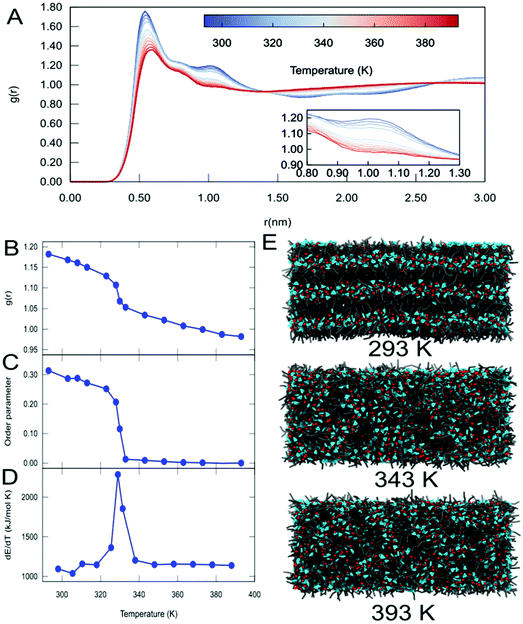 | ||
| Fig. 3 Temperature-driven phase transition in C12. (A) Radial distribution functions between the centers of mass of the alkyl tails as a function of temperature. The insert highlights the changes in the 2nd peak (around 1.05 nm) indicative of the long-range structure. (B) Plot of the intensity of the peak of the RDF at 1.05 nm as a function of temperature. (C) Plot of the order parameter of the alkyl tails with respect to temperature. (D) Plot of the derivative of total energy (heat capacity) with respect to temperature. (E) Representative snapshots for the different phases of C12 at different temperatures. Representations and colours are the same as used in Fig. 2B. | ||
Next to the structure and phase behavior, we analyzed another commonly studied property of ILs, namely the diffusion coefficient. This dynamical property gives us an insight into the mobility of cations and anions in the ionic liquid. The existing coarse-grain models used to study ILs,28,69 usually overestimate the value of the diffusion coefficients by several orders of magnitude. This is a natural consequence of the reduction of the degrees of freedom of the system. In the cases studied in this work the obtained diffusion coefficients are of the order 10−5 cm2 s−1 (Fig. S11 and S12†), between 2 to 3 orders of magnitude bigger than the values obtained from atomistic simulations.20,70 As expected, the diffusivity of the ions increases with temperature, and decreases with the length of the alkyl tails. For short tail ILs (C2–C4), the cations and anions diffuse at roughly the same speed (Fig. S11 and S12†) reproducing the experimental trend19 and results obtained at the atomistic level19 and reflecting the behavior that the anion prefers to stay close to the positively charged imidazolium ring. For the longer tailed ILs, however, the anion is diffusing relatively fast compared to the cation, presumably because the larger mass of the long tail cation. In addition, the anion becomes increasingly trapped inside the nanodomains (or lamellae in case of C12) as can be observed in Fig. 2B. Viscosity estimates (Fig. S13†) are in line with the diffusion coefficients, showing results between two and three orders of magnitude smaller than the experimental ones.58–60 More importantly, the results show the same trend regarding chain length and temperature as observed experimentally.
3.2 Petroleum oil extraction
ILs have been proposed as an alternative to conventional solvents for the extraction of aromatic compounds from mixtures of them with aliphatic species.71,72 This proposal is based on the fact that the solubility of aliphatic compounds in ILs can be modulated by making changes to the structure of the cation or anion; meanwhile, the solubility of aromatic substances in ILs is always considerable.73 Additionally to these advantages, it has been proven that the use of IL in the extraction of aromatic compounds is economically feasible.72 Selectivity and the distribution ratio of the aromatic molecules between the IL and the aliphatic solvent are the main criteria for the economic sustainability of the extraction process73 of aromatic compounds. These parameters depend on many factors such as the type of hydrocarbon compounds in the mixture, the type of IL used for the extraction, the length of the alkyl tail on the cation, the temperature of the process, among other considerations.74 For instance, an increase in the length of the alkyl tail on the cation results in an increased solubility of aliphatic molecules, but a reduced selectivity.73 Furthermore, ILs can be used for the extraction of aromatic molecules from mixtures in which those compounds are present at low concentration with a good selectivity.74In order to test our model in the simulation of the extraction of molecules from complex mixtures, we build a simple system analogous to petroleum oil to analyze the extraction of aromatic molecules, following a methodology which was previously used experimentally.51 Our petroleum oil model consists of octane with 10% (weight) of benzene. The oil phase was put into contact with a specific IL phase (either C2, C4, C8, or C12), creating a biphasic system as shown in Fig. 4 and Fig. S14, S15.† From this system, we evaluate the efficiency of the extraction of benzene molecules to the IL and the contamination by the migration of octane to the IL. We did not consider the effect of increased temperature as it is known that an increase in the temperature of the mixture reduces the selectivity on the extraction of aromatic molecules.71
To analyze the extraction efficiency of the various ILs considered, we computed the normalized partial density profiles of the IL/oil mixtures, as shown in Fig. 4A, B and C for C2, C4 and C8, respectively. Additional results for C12 are shown in Fig. S14.† Except for C12, all IL/oil systems remain clearly biphasic. In case of C12, the solubility of octane in the IL is considerable and the phase separation becomes less clear (see Fig. S14 and S15†). In terms of benzene extraction, comparison of the normalized densities (Fig. 4) as well as the transfer free energy of benzene between the oil phase and the IL (Table 1), indicates that the longer tail ILs extract the largest fraction of benzene. However, also the fraction of octane that is extracted increases with the size of the alkyl tail (Fig. 4), making the long tail ILs less selective for the extraction of benzene. The selectivity is quantified by computing the ratio of the distribution coefficients of benzene over octane in the IL (Table 1). From this data it appears that C4 would be the optimal choice for extraction of benzene, with both a high extraction capacity and high selectivity for benzene.
| IL cation | ΔGBENZ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a (kJ mol−1) a (kJ mol−1) |
ΔGOCT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a (kJ mol−1) a (kJ mol−1) |
Selectivity |
|---|---|---|---|
| a Free sampling obtained by conventional MD simulation was used to estimate the ΔGtrans for all octane/IL biphasic systems. Convergence analysis of the free energy calculations are displayed in Fig. S16.† | |||
| C2 | −1.4 ± 0.1 | 30.2 ± 1.5 | 310 × 103 |
| C4 | −3.2 ± 0.1 | 18.2 ± 0.2 | 5.2 × 103 |
| C8 | −3.9 ± 0.1 | 6.3 ± 0.1 | 59 |
In summary, with the growth of the hydrocarbon tail, our CG simulations show that more benzene can migrate to the bulk of the IL. At the same time, the selectivity starts to be reduced, and part of the octane migrates to the IL phase. This is exactly the behaviour experimentally shown for C4, C6 and C10 IL/octane mixtures containing 10% of benzene.51 Consequently, the extraction efficiency and selectivity of benzene can be accurately captured by our new Martini IL model. Except for C12, we also noticed that the molecules of benzene have the highest concentration at the oil/IL interface. In our view, this behaviour suggests that the full separation of benzene from octane using imidazolium-based IL may need experimental protocols using multiple extraction steps.
3.3 Fish oil extraction
Encouraged by the results obtained for the extraction of benzene from the model petroleum oil, we study a more complex system: a model fish oil, which consists of a mixture of saturated and polyunsaturated fatty acids. The saturated ones were represented by palmitic (PAL) and oleic (OLE) acids, while the docosahexaenoic acid (DHA) was used as a model of typical omega-3 fatty acids present in salmon oil. DHA has many recognized human health benefits for cardiovascular diseases, diabetes, cancer, depression and various mental illnesses, age-related cognitive decline, periodontal disease, and rheumatoid arthritis.75,76 Unfortunately, DHA cannot be produced by the human body because of an absence of desaturase enzymes77 and consequently, DHA needs to be ingested from the food. Therefore, the extraction of DHA from different sources has won interest.Extraction of polyunsaturated compounds with the aid of imidazolium-based ionic liquids has been previously studied experimentally.53,78,79 These studies tested the extraction of omega-3 fatty acids (PUFAs) or ester derivatives from fish oil in the presence of silver salts.53,78,79 However, silver salts are toxic and corrosive making its use in food application not suitable.53 As an alternative for the use of silver salts, the addition of solvents has been proposed or the use of sorbents.79 Some of the experimental findings from these studies are (i) the extraction of omega-3 compounds is governed by the π–π stacking between the aromatic ring of the imidazolium cation and the double bonds of the omega-3 fatty acids, (ii) the increase in the size of the alkyl length with its concomitant increase in hydrophobicity of the compound aids in the extraction of the PUFAs, and (iii) the use of alkanes as co-solvents is recommended to enhance the extraction because ILs are highly miscible in polar solvents but immiscible in non-polar solvents.
To investigate to what extent we can reproduce these experimental findings, we simulated the extraction efficiency of DHA from fish oil by the imidazolium-based ILs, both in the presence of a non-polar co-solvent (octane) and without it. It is observed in Fig. 5 and S17† that when the length of the alkyl tail grows, also the miscibility with the OLE and PAL increases. The final configurations of the systems C2 and C4 and the normalized partial density profiles are shown in Fig. 5 and S18, S19.† Cations C8 and C12 are mixed with the fish oil, losing the biphasic nature of the system (Fig. S17†). In case of C4, mixing is also observed (Fig. 5C) but only in the absence of the co-solvent octane. Apparently octane can stabilize the fish oil with respect to the IL (Fig. 5D), probably by making it more hydrophobic.
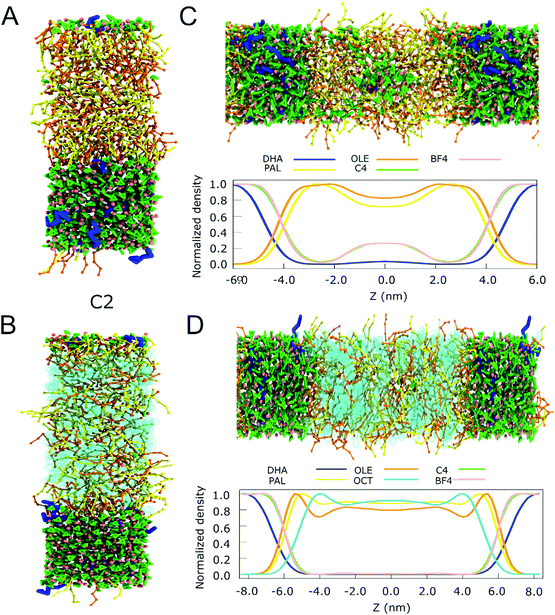 | ||
| Fig. 5 Extraction of DHA from fish oil. (A) Snapshots of the final simulation box of the IL and the fish oil without octane for C2 systems (B) Snapshots of the final simulation box of the IL and the fish oil with octane for C2 systems. (C) Snapshot of the final state of the biphasic system C4 and the fish oil without octane and its normalized density profile. (D) Snapshot of the final state of the biphasic system C4 and the fish oil with octane and its normalized density profile. For the IL, the colour code is the same one as used in Fig. 4. For the fatty acids, DHA is shown in blue, OLE and PAL in yellow and orange, respectively. Octane is depicted in cyan. | ||
To quantify the level of DHA extraction as well as selectivity, we computed the transfer free energy of the fish oil components between the two phases in the cases of C2 and C4 (see Methods for more details). The results, presented in Table 2, show that the free energy of transfer of DHA from fish oil to IL is favorable in all cases. The most efficient extraction (i.e. lowest free energy) for mixtures without octane is observed for C2. Upon addition of octane to the mixture, the transfer of DHA becomes even more favorable, with the largest effect observed for C4. For the other components of our fish oil model, OLE and PAL, transfer to the IL is unfavorable. The differences between OLE and PAL are small in mixtures without octane (around 4 kJ mol−1), which is to be expected given their comparable chemical nature. With octane added, transfer of these compounds to the IL becomes even less favorable. As a consequence, the addition of the co-solvent decreases the miscibility of the short tail ILs with fish oil, implying that less OLE and PAL can migrate to the IL phase. An example of DHA extraction with C4 and octane is provided in the ESI Movie.†
| IL | ΔGDHA (kJ mol−1) | ΔGOLE (kJ mol−1) | ΔGPAL (kJ mol−1) | Selectivity |
|---|---|---|---|---|
| −octane/+octane | −octane/+octane | −octane/+octane | −octane/+octane | |
| a Free sampling obtained by convention MD simulation was used to estimate the ΔGtrans in the case of C4 without octane. Convergence analysis of these free energy calculations are displayed in Fig. S20.† For all the other systems, ΔGtrans was obtained by US simulations. | ||||
| C2 | −10.2 ± 1.8/−11.8 ± 0.2 | 24.2 ± 2.1/27.4 ± 0.3 | 34.1 ± 2.0/35.2 ± 0.2 | 931 × 103/6011 × 103 |
| C4 | −8.3 ± 0.2a/−16.8 ± 2.8 | 12.9 ± 0.3a/16.0 ± 3.4 | 15.2 ± 1.0a/20.4 ± 1.7 | 5 × 103/418 × 103 |
The consequence of this behavior on the extraction selectivity is shown in Table 2. The selectivity is computed as the ratio between the distribution coefficients of DHA and OLE + PAL in the IL (see Methods). The selectivity for the extraction has its maximum for C2. We can understand the trend in selectivity considering the interactions between the components of the mixture. In experimental studies,53,78 it was found that π interactions between the double bonds of DHA and the imidazole aromatic ring are one of the leading forces for the extraction of this compound. These interactions are parameterized explicitly in the current Martini model. An opposing force is also present, as the nonpolar character of DHA gives rise to a repulsive interaction with the polar IL. Progressive addition of methyl groups to the IL could reduce that repulsive interaction and increase extraction of DHA, but this structural change on the imidazolium cation also results in more mixing with the other non-polar components of fish oil. Then, the selectivity of extraction is modulated by a compromise between the π interactions of DHA and the IL and hydrophobic interactions between the IL and the other molecules in the mixture. In the presence of octane, the balance is shifted and C4 becomes the IL with the highest extraction capacity (i.e. lowest free energy, see Table 2), with also an increase of selectivity of two orders of magnitude.
Taken together, our data show that we can capture the experimental trends on the extraction of PUFAs from fish oil with our IL Martini model. In particular, we show the migration of the PUFA DHA from the oil to the IL phase, driven by favorable π interactions between the unsaturated DHA bonds and the imidazolium rings. We also showed a favorable effect on the extraction efficiency and selectivity by addition of co-solvents. Consequently the proper selection of co-solvents and chain length of the cation is a critical point for the extraction of a desired compound. However, the overall efficiency is also governed by the stability of the biphasic system. As the hydrophobicity of the IL increases (i.e., longer tailed cations), or the hydrophobicity of the oil phase is reduced (in the absence of co-solvent), the biphasic system becomes less stable.
4 Conclusions and further considerations
We presented a new Martini CG model for imidazolium-based ionic liquids. We showed that the model can describe the macroscopic density of the ILs studied in good agreement with the experimental values. The model can also accurately describe their nanostructure, comparable to atomistic models. Additionally, our model is able to capture collective behavior of the IL, such as the temperature induced phase transition of C12, a process that can not be easily simulated using full-atomistic simulations.A significant advantage of our new model in comparison with other CG models is that it can be used in combination with other Martini 3 CG molecules, which allows simulations of extraction experiments. To exemplify such features, two extraction studies were performed: benzene extraction from a petroleum oil model and omega-3 extraction from a fish oil model. In both cases, we find that the length of the alkyl tail of the IL was fundamental for the extraction and the selectivity. Concerning the fish oil, we also tested the effect of co-solvents in our extraction predictions. We show that the addition of octane can be a useful resource to increase the IL extraction capacity, selectivity for omega-3 fatty acids extraction, and the stability of the phase separation in the IL/oil biphasic mixtures.
Our results largely agree with previous experiments reported, indicating that the new Martini 3 CG model could be useful for the computational design of extraction experiments using ionic liquids. Addition of cosolvents, polarity modulation of tails attached to the charged groups or mixture of different IL cations could be straightforwardly employed, enabling the virtual screening of thousands of IL combinations. In the future, further development of the model should allow its usage in aqueous biphasic extraction of other biomolecules of interest like amino acids, peptides or proteins.
Abbreviations
| C2 | 1-Ethyl-3-methylimidazolium tetrafluoroborate |
| C4 | 1-Butyl-3-methylimidazolium tetrafluoroborate |
| C8 | 1-Octyl-3-methylimidazolium tetraflouroborate |
| C12 | 1-Dodecyl-3-methylimidazolium tetrafluoroborate |
| CG | Coarse-grain |
| DHA | Docosahexaenoic acid |
| IL | Ionic liquid |
| OLE | Oleic acid |
| PAL | Palmitic acid |
| RDF | Radial distribution function |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is in loving memory of Michele Selle, deceased on July 29th, 2018. L. I. Vazquez-Salazar acknowledges financial support by the EACEA in the form of an Erasmus+ scholarship (Project 159680-EPP-1-2015-ES-EPPKA1-EPQR). All the authors thank the Center for Information Technology of the University of Groningen for providing access to the Peregrine high-performance computing cluster.References
- M. Freemantle, An Introduction to Ionic Liquids, Royal Society of Chemistry, 2010 Search PubMed.
- R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426 CrossRef CAS.
- P. Wasserscheid and T. Welton, Ionic Liquids in Synthesis, John Wiley & Sons, 2008 Search PubMed.
- H.-P. Steinrück and P. Wasserscheid, Catal. Lett., 2015, 145, 380–397 CrossRef.
- K. S. Egorova, E. G. Gordeev and V. P. Ananikov, Chem. Rev., 2017, 117, 7132–7189 CrossRef CAS.
- H. Rodríguez, Ionic Liquids for Better Separation Processes, Springer, 2015 Search PubMed.
- V. Arumugam, G. Redhi and R. M. Gengan, in Fundamentals of Nanoparticles Classifications, Synthesis Methods, Properties and Characterization, ed. A. Barhoum and A. S. H. Makhlouf, Elsevier, 2018, pp. 371–400 Search PubMed.
- C. Chiappe, Monatsh. Chem. – Chem. Mon., 2007, 138, 1035–1043 CrossRef CAS.
- H. Weingärtner, Angew. Chem., Int. Ed., 2008, 47, 654–670 CrossRef.
- X. Han and D. W. Armstrong, Acc. Chem. Res., 2007, 40, 1079–1086 CrossRef CAS.
- S. P. M. Ventura, F. A. E. Silva, M. V. Quental, D. Mondal, M. G. Freire and J. A. P. Coutinho, Chem. Rev., 2017, 117, 6984–7052 CrossRef CAS.
- S. Chen, S. Zhang, X. Liu, J. Wang, J. Wang, K. Dong, J. Sun and B. Xu, Phys. Chem. Chem. Phys., 2014, 16, 5893–5906 RSC.
- Y. Wang, W. Jiang, T. Yan and G. A. Voth, Acc. Chem. Res., 2007, 40, 1193–1199 CrossRef CAS.
- K. Dong, X. Liu, H. Dong, X. Zhang and S. Zhang, Chem. Rev., 2017, 117, 6636–6695 CrossRef CAS.
- E. J. Maginn, J. Phys.: Condens. Matter, 2009, 21, 373101 CrossRef CAS.
- M. Salanne, Phys. Chem. Chem. Phys., 2015, 17, 14270–14279 RSC.
- P. A. Hunt, Mol. Simul., 2006, 32, 1–10 CrossRef CAS.
- J. N. A. Canongia Lopes and A. A. H. Pádua, J. Phys. Chem. B, 2006, 110, 3330–3335 CrossRef CAS.
- J. de Andrade, E. S. Böes and H. Stassen, J. Phys. Chem. B, 2002, 106, 13344–13351 CrossRef CAS.
- O. Borodin, J. Phys. Chem. B, 2009, 113, 11463–11478 CrossRef CAS.
- Y. Wang and G. A. Voth, J. Am. Chem. Soc., 2005, 127, 12192–12193 CrossRef CAS.
- Y. Wang, S. Feng and G. A. Voth, J. Chem. Theory Comput., 2009, 5, 1091–1098 CrossRef CAS.
- D. Roy and M. Maroncelli, J. Phys. Chem. B, 2010, 114, 12629–12631 CrossRef CAS.
- H. A. Karimi-Varzaneh, F. Müller-Plathe, S. Balasubramanian and P. Carbone, Phys. Chem. Chem. Phys., 2010, 12, 4714–4724 RSC.
- C. Merlet, M. Salanne and B. Rotenberg, J. Phys. Chem. C, 2012, 116, 7687–7693 CrossRef CAS.
- J. Zeman, F. Uhlig, J. Smiatek and C. Holm, J. Phys.: Condens. Matter, 2017, 29, 504004 CrossRef.
- O. Y. Fajardo, S. Di Lecce and F. Bresme, Phys. Chem. Chem. Phys., 2020, 22, 1682–1692 RSC.
- A. Moradzadeh, M. H. Motevaselian, S. Y. Mashayak and N. R. Aluru, J. Chem. Theory Comput., 2018, 14, 3252–3261 CrossRef CAS.
- S. J. Marrink, A. H. de Vries and A. E. Mark, J. Phys. Chem. B, 2004, 108, 750–760 CrossRef CAS.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS.
- S. J. Marrink and D. P. Tieleman, Chem. Soc. Rev., 2013, 42, 6801–6822 RSC.
- R. Alessandri, J. J. Uusitalo, A. H. de Vries, R. W. A. Havenith and S. J. Marrink, J. Am. Chem. Soc., 2017, 139, 3697–3705 CrossRef CAS.
- F. Grunewald, G. Rossi, A. H. de Vries, S. J. Marrink and L. Monticelli, J. Phys. Chem. B, 2018, 122, 7436–7449 CrossRef CAS.
- J. Liu, L. Qiu, R. Alessandri, X. Qiu, G. Portale, J. Dong, W. Talsma, G. Ye, A. A. Sengrian, P. C. T. Souza, M. A. Loi, R. C. Chiechi, S. J. Marrink, J. C. Hummelen and L. J. A. Koster, Adv. Mater., 2018, 30, 1704630 CrossRef.
- E. A. Crespo, N. Schaeffer, J. A. P. Coutinho and G. Perez-Sanchez, J. Colloid Interface Sci., 2020, 574, 324–336 CrossRef CAS.
- N. Schaeffer, G. Pérez-Sánchez, H. Passos, J. R. B. Gomes, N. Papaiconomou and J. A. P. Coutinho, Phys. Chem. Chem. Phys., 2019, 21, 7462–7473 RSC.
- G. Huet, M. Araya-Farias, R. Alayoubi, S. Laclef, B. Bouvier, I. Gosselin, C. Cézard, R. Roulard, M. Courty, C. Hadad, E. Husson, C. Sarazin and A. N. Van Nhien, Green Chem., 2020, 22, 2935–2946 RSC.
- R. Alessandri, P. C. T. Souza, S. Thallmair, M. N. Melo, A. H. de Vries and S. J. Marrink, J. Chem. Theory Comput., 2019, 15, 5448–5460 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- Martini 3.0 open beta, http://www.cgmartini.nl/index.php/martini3beta (accessed 20 November 2019).
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- I. G. Tironi, R. Sperb, P. E. Smith and W. F. van Gunsteren, J. Chem. Phys., 1995, 102, 5451–5459 CrossRef CAS.
- D. H. de Jong, S. Baoukina, H. I. Ingólfsson and S. J. Marrink, Comput. Phys. Commun., 2016, 199, 1–7 CrossRef CAS.
- L. Verlet, Phys. Rev., 1967, 159, 98–103 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and G. E. Johannes, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef.
- T. A. Wassenaar, H. I. Ingólfsson, R. A. Böckmann, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2015, 11, 2144–2155 CrossRef CAS.
- B. T. Thole and P. T. Duijnen, Theor. Chim. Acta, 1983, 63, 209–221 CrossRef CAS.
- C. Cassol, A. Umpierre, G. Ebeling, B. Ferrera, S. Chiaro and J. Dupont, Int. J. Mol. Sci., 2007, 8, 593–605 CrossRef CAS.
- E. H. Gruger, R. W. Nelson and M. E. Stansby, J. Am. Oil Chem. Soc., 1964, 41, 662–667 CrossRef CAS.
- L.-Z. Cheong, Z. Guo, Z. Yang, S.-C. Chua and X. Xu, J. Agric. Food Chem., 2011, 59, 8961–8967 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- Martini force field - Other tools, http://cgmartini.nl/index.php/tools2/other-tools (accessed 20 November 2019).
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- E. J. Maginn, R. A. Messerly, D. J. Carlson, D. R. Roe and J. R. Elliot, Living J. Comput. Mol. Sci., 2019, 1, 6324 Search PubMed.
- O. Ciocirlan, O. Croitoru and O. Iulian, J. Chem. Thermodyn., 2016, 101, 285–292 CrossRef CAS.
- H. F. D. Almeida, J. N. A. Canongia Lopes, L. P. N. Rebelo, J. A. P. Coutinho, M. G. Freire and I. M. Marrucho, J. Chem. Eng. Data, 2016, 61, 2828–2843 CrossRef CAS.
- L. G. Sánchez, J. R. Espel, F. Onink, G. W. Meindersma and A. B. de Haan, J. Chem. Eng. Data, 2009, 54, 2803–2812 CrossRef.
- B. Hess, J. Chem. Phys., 2002, 116, 209 CrossRef CAS.
- G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1995, 16, 1339–1350 CrossRef CAS.
- E. Núñez-Rojas, H. M. Flores-Ruiz and J. Alejandre, J. Mol. Liq., 2018, 249, 591–599 CrossRef.
- R. L. Gardas, M. G. Freire, P. J. Carvalho, I. M. Marrucho, I. M. A. Fonseca, A. G. M. Ferreira and J. A. P. Coutinho, J. Chem. Eng. Data, 2007, 52, 80–88 CrossRef CAS.
- R. L. Gardas, M. G. Freire, P. J. Carvalho, I. M. Marrucho, I. M. A. Fonseca, A. G. M. Ferreira and J. A. P. Coutinho, J. Chem. Eng. Data, 2007, 52, 1881–1888 CrossRef CAS.
- J. D. Holbrey and K. R. Seddon, J. Chem. Soc., Dalton Trans., 1999, 2133–2140 RSC.
- Y. Nozaki, K. Yamaguchi, K. Tomida, N. Taniguchi, H. Hara, Y. Takikawa, K. Sadakane, K. Nakamura, T. Konishi and K. Fukao, J. Phys. Chem. B, 2016, 120, 5291–5300 CrossRef CAS.
- Y. Wang, S. Izvekov, T. Yan and G. A. Voth, J. Phys. Chem. B, 2006, 110, 3564–3575 CrossRef CAS.
- A. Bagno, F. D'Amico and G. Saielli, J. Mol. Liq., 2007, 131–132, 17–23 CrossRef CAS.
- G. W. Meindersma and A. B. de Haan, in Ionic Liquids: From Knowledge to Application, ed. N. V. Plechkova, R. D. Rogers and K. R. Seddon, American Chemical Society, 2010, vol. 1030, pp. 255–272 Search PubMed.
- G. W. Meindersma and A. B. De Haan, in Ionic Liquids Uncoiled: Critical Expert Overviews, ed. N. V. Plechkova and K. R. Seddon, Jonh Wiley and Sons, 2012, pp. 119–179 Search PubMed.
- R. I. Canales and J. F. Brennecke, J. Chem. Eng. Data, 2016, 61, 1685–1699 CrossRef CAS.
- A. R. Ferreira, M. G. Freire, J. C. Ribeiro, F. M. Lopes, J. G. Crespo and J. A. P. Coutinho, Ind. Eng. Chem. Res., 2012, 51, 3483–3507 CrossRef CAS.
- F. Shahidi and P. Ambigaipalan, Annu. Rev. Food Sci. Technol., 2018, 9, 345–381 CrossRef CAS.
- C. H. S. Ruxton, S. C. Reed, M. J. A. Simpson and K. J. Millington, J. Hum. Nutr. Diet., 2004, 20, 275–285 Search PubMed.
- H. Sprecher, D. L. Luthria, B. S. Mohammed and S. P. Baykousheva, J. Lipid Res., 1995, 36, 2471–2477 CAS.
- M. Li and T. Li, Sep. Sci. Technol., 2008, 43, 2072–2089 CrossRef CAS.
- M. Li, P. J. Pham, T. Wang, C. U. Pittman and T. Li, Sep. Purif. Technol., 2009, 66, 1–8 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0gc01823f |
| ‡ These authors made equal contributions to this work. |
| § Deceased on July 29th, 2018. |
| This journal is © The Royal Society of Chemistry 2020 |