Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mechanism of selective gold extraction from multi-metal chloride solutions by electrodeposition-redox replacement†
Ivan
Korolev
 ab,
Stylianos
Spathariotis
ab,
Stylianos
Spathariotis
 c,
Kirsi
Yliniemi
c,
Kirsi
Yliniemi
 d,
Benjamin P.
Wilson
d,
Benjamin P.
Wilson
 a,
Andrew P.
Abbott
a,
Andrew P.
Abbott
 c and
Mari
Lundström
c and
Mari
Lundström
 *a
*a
aHydrometallurgy and Corrosion, Department of Chemical and Metallurgical Engineering, Aalto University, 02150 Espoo, Finland. E-mail: mari.lundstrom@aalto.fi
bOutotec Research Center, 28101 Pori, Finland
cMaterials Centre, Department of Chemistry, University of Leicester, LE1 7RH, UK
dDepartment of Chemistry and Material Science, Aalto University, 02150 Espoo, Finland
First published on 19th May 2020
Abstract
The electrodeposition-redox replacement (EDRR) process is a promising method for a selective extraction of minor metals from complex mixtures. When it is performed in a benign medium (such as sodium chloride solution or deep eutectic solvent), the EDRR method provides a non-toxic alternative for a conventional cyanide-based process. The detailed reaction mechanisms of the EDRR in Cu–Au systems, as well as the effect of the reaction medium are elucidated in this article. Electrogravimetric studies show that the EDRR process comprises three distinct stages: (1) deposition of Cu at a constant applied potential; (2) dissolution of deposited Cu at open circuit conditions in reaction with dissolved species in solution; (3) reduction of Au to elemental form in reaction with various Cu species. It is discovered that the recovery of Au takes place surprisingly via both the redox replacement between Cu and Au at the surface and the homogeneous Au reduction by Cu(I) species in solution. Both of these reaction pathways are facilitated by open circuit conditions (redox replacement step) between electrodeposition cycles and the utilization of other sacrificial elements in the solution is crucial. The use of aqueous chloride solution is advantageous over 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG for the increased Au recovery (94.4%) and the purity of the product (93.7%), although it consumes slightly more electricity. Therefore, the EDRR enables energy and resource efficient selective extraction of Au from multi-metal industrial solutions even when it is present at low concentrations.
EG for the increased Au recovery (94.4%) and the purity of the product (93.7%), although it consumes slightly more electricity. Therefore, the EDRR enables energy and resource efficient selective extraction of Au from multi-metal industrial solutions even when it is present at low concentrations.
Introduction
The global focus on the sustainable use of Earth's natural resources, especially non-renewables like metals and minerals, demands that the concepts of circular economy be realized on an industrial scale.1,2 The use of raw materials – both primary and secondary – must be performed with low energy and chemical consumption, and with minimum waste accumulation.3,4 At the same time, the renewable energy has become more affordable and easily available making electrochemical metal recovery methods a feasible option to reduce the carbon footprint of extractive industry.5,6 With this framework in mind, the electrodeposition-redox replacement (EDRR) method has been introduced for selective recovery of gold,7,8 silver,9,10 and platinum11 from complex industrial effluents. It has also been studied for its versatility and ability to create functional surfaces directly from industrial process solutions.12,13 Nevertheless, the process mechanism is currently only understood on a phenomenological level and more detailed investigations into the reactions involved has not been carried out yet. In this paper, the underlying mechanism of the gold recovery from copper containing solutions – including both aqueous and deep eutectic solvents – by EDRR is explored for the first time. Such an in-depth understanding is essential when it comes to the exploitation of EDRR's full potential, the main goal being the sustainable recovery of gold from solutions which contain precious metals only in trace amounts and other base metals (e.g., copper) as major elements.Following the principles of green engineering,14 sustainable gold production also encourages the development of eco-friendly, non-toxic extractants to replace commonly used cyanide.15,16 Chloride-based processes of gold leaching have proven their efficiency and are considered a viable alternative to conventional hydrometallurgical technologies.17,18 The efficient extraction of gold in aqueous chloride solutions is possible even with minor reagent addition.19 However, in some regions of the world, water is viewed as a critical resource, and reducing its consumption is one of key requirements for a sustainable development.20,21 Among non-aqueous lixiviants, the environmentally benign deep eutectic solvents (DESs) are the subject of significant research from a metallurgical perspective.22–24 Their wide electrochemical window makes DESs especially advantageous in deposition and plating applications for metals with low reduction potential, such as aluminum, chromium, zinc and nickel.25–27 In addition, DESs enable precious metals to be oxidized at lower overpotentials,28 and are thus preferred in leaching applications.29–32
In this paper, the effects of solvent's physicochemical properties, such as metal speciation and mass transport, on the efficiency of the EDRR method were investigated in aqueous chloride solution and in deep eutectic mixture of choline chloride with ethylene glycol in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio (1
2 molar ratio (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG). Moreover, the concentration of chloride ions in this DES is ca. 4.8 M, which is similar to commonly used in hydrometallurgical gold recovery processes,33–36 and therefore it makes the comparative study of these two systems from the EDRR perspective justified.
EG). Moreover, the concentration of chloride ions in this DES is ca. 4.8 M, which is similar to commonly used in hydrometallurgical gold recovery processes,33–36 and therefore it makes the comparative study of these two systems from the EDRR perspective justified.
Experimental
Chemicals
The aqueous solution was prepared by mixing AuCl, CuCl2·2H2O and NaCl in deionized water to obtain the following concentrations: 5 × 10−4 M Au, 6 × 10−2 M Cu and 4.5 M Cl−. HCl was added to maintain pH below 3. This Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au ratio of 120
Au ratio of 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was selected based on previous investigations that simulated gold chloride leaching solutions.7 DES solution was made by mixing choline chloride (CH3)3NC2H4OHCl (ChCl) with 1,2-ethanediol HOCH2CH2OH (EG) in a molar ratio of 1
1 was selected based on previous investigations that simulated gold chloride leaching solutions.7 DES solution was made by mixing choline chloride (CH3)3NC2H4OHCl (ChCl) with 1,2-ethanediol HOCH2CH2OH (EG) in a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and then gold and copper chloride salts were added in order to obtain the same concentrations as present in the aqueous solution. All chemicals were of reagent grade (Sigma Aldrich, USA). The concentration of dissolved oxygen was measured in both chloride-containing solutions prior to experiments with a Clark-type polarographic sensor and it was 1.56 mg l−1 in aqueous 4.5 M NaCl solution and 1.32 mg l−1 in 1
2 and then gold and copper chloride salts were added in order to obtain the same concentrations as present in the aqueous solution. All chemicals were of reagent grade (Sigma Aldrich, USA). The concentration of dissolved oxygen was measured in both chloride-containing solutions prior to experiments with a Clark-type polarographic sensor and it was 1.56 mg l−1 in aqueous 4.5 M NaCl solution and 1.32 mg l−1 in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG.
EG.
Electrodeposition-redox replacement method
The EDRR method – previously described in more detail7 – includes two consecutive stages that are repeated N times:• electrodeposition (ED) stage – the potentiostatic deposition of copper at potential Edep for a short time tED;
• redox replacement (RR) stage – when the system is switched to open circuit conditions for a time tRR to allow redox replacement between gold and copper.
Actual values of the EDRR process parameters Edep, tED, tRR are dependent on the solution composition and for aqueous solution, the parameters were based on previous research.7 For 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG solution, the Edep value can be identified from the copper deposition range in cyclic voltammetry (CV), while tED and tRR are kept the same as for the aqueous solution (Table 1).
EG solution, the Edep value can be identified from the copper deposition range in cyclic voltammetry (CV), while tED and tRR are kept the same as for the aqueous solution (Table 1).
| Solution | E dep (V vs. Ag/AgCl) | t ED (s) | t RR (s) | N |
|---|---|---|---|---|
| Aqueous 4.5 M NaCl | −0.35 | 10 | 600 | 50 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl 2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG EG |
−0.45 |
Electrochemical quartz-crystal microbalance experiments
EQCM experiments were performed in a three-electrode cell with the Gamry eQCM 10 MHz resonator controlled by a Reference 600 potentiostat (Gamry Instruments, USA). A 10 MHz platinum coated AT-cut quartz crystal (surface area: 0.21 cm2) was used as a working electrode and platinum foil as a counter electrode (area: 3 cm2). The measurements in aqueous solutions were conducted with the standard Ag/AgCl (sat. KCl) reference electrode (0.197 V vs. SHE, SI Analytics, Germany), whereas in non-aqueous the reference electrode consisted of a silver wire immersed in a 0.1 M solution of AgCl in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG and separated from the electrochemical cell by a Vycor glass frit to allow for the mobility of the ions. For the consistency of reporting, all the potential values in the figures and text are brought to the same basis following the procedure described by Frenzel et al.37 and referred vs. Ag/AgCl.
EG and separated from the electrochemical cell by a Vycor glass frit to allow for the mobility of the ions. For the consistency of reporting, all the potential values in the figures and text are brought to the same basis following the procedure described by Frenzel et al.37 and referred vs. Ag/AgCl.
According to the Sauerbrey equation,38 a frequency shift Δf of the quartz crystal is proportional to the mass change Δm on the electrode:
| Δf = −Cf·Δm | (1) |
For an AT-cut 10 MHz quartz crystal with an active surface area of 0.21 cm2, the constant equals Cf = 1.1 Hz ng−1. On the other hand, assuming that only faradaic processes occur during the deposition, the mass recovered on the electrode can be related to the amount of charge Q passed during deposition time tED through Faraday's law:
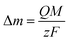 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1 is the Faraday constant. Combining eqn (1) and (2), the ratio M/z can be calculated:
485 C mol−1 is the Faraday constant. Combining eqn (1) and (2), the ratio M/z can be calculated: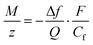 | (3) |
Rotating ring-disk electrode measurements
Rotating ring-disk electrode (RRDE) measurements were performed with a variable speed set-up (MSR, Pine Research, US): the platinum disk (area: 16.4 mm2) mounted in Teflon was surrounded by a platinum ring (3.6 mm2) with a 180 μm gap between them, resulting in the set-up of two working electrodes, hereafter referred to as a disk electrode and a ring electrode. The counter electrode was a platinum mesh and reference electrode Ag/AgCl (0.197 V vs. SHE, SI Analytics, Germany). The disk electrode was held at −0.35 V vs. Ag/AgCl for 1 min before the potential was set to ED = 0.1 V vs. Ag/AgCl. At the same time the amperometric measurement was started at the ring electrode with constant oxidizing potential ER = 0.65 V vs. Ag/AgCl. Apparent collection efficiency Napp of the RRDE is the ratio of the current at the ring iR to the current at the disk electrode iD: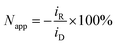 | (4) |
Process efficiency evaluation
The composition and morphology of the surface were analyzed with a Zeiss Sigma 300 scanning electron microscope (SEM) equipped with an EDX detector (Carl Zeiss Ltd, UK). The applied acceleration voltage and the beam intensity were 5 kV and 0.2 nA, respectively. Metal recoveries were calculated from the inductively coupled plasma mass-spectroscopy (iCAP Q, Thermo Scientific, USA) assays of the solutions before and after the EDRR experiments. As the potential was applied to the cell only during the deposition step, the specific energy consumption w, kW h kg−1, can be calculated as follows: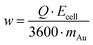 | (5) |
Results and discussion
Speciation of gold and copper in chloride solutions
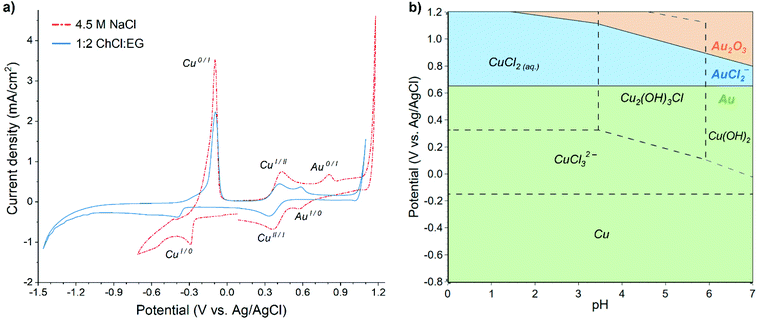
Cyclic voltammograms (CV) recorded in both aqueous 4.5 M NaCl and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG solutions containing 60 mM Cu and 0.5 mM Au display similar features (Fig. 1a), i.e. reduction and oxidation peaks of copper and gold, although their positions are slightly shifted. Lower cathodic limit of stability exists in the 1
EG solutions containing 60 mM Cu and 0.5 mM Au display similar features (Fig. 1a), i.e. reduction and oxidation peaks of copper and gold, although their positions are slightly shifted. Lower cathodic limit of stability exists in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG solution around −1.2 V vs. Ag/AgCl, while hydrogen evolution onset in the aqueous solution occurs already at −0.6 V vs. Ag/AgCl, providing the stability limit of this solution.
EG solution around −1.2 V vs. Ag/AgCl, while hydrogen evolution onset in the aqueous solution occurs already at −0.6 V vs. Ag/AgCl, providing the stability limit of this solution.
In the case of EDRR, the difference between the reduction potentials of the sacrificial metal, e.g. copper, and the metal being recovered, i.e. gold is an important parameter, affecting the overall efficiency of the process.7 In theory, the further apart these two potentials are (and assuming no other steps or species), the bigger the driving force is for the redox replacement reaction.39 However, the lower the reduction potential of the sacrificial metal, the higher are the cell voltage and energy consumption for the deposition. Therefore, all of these potentials affect greatly the efficiency of EDRR. Fig. 1a shows that in both solutions the potential difference between copper and gold reduction peaks is nearly the same, about 0.85 V vs. Ag/AgCl, albeit their positions in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG have moved in a cathodic direction, and the cupric/cuprous reaction is partially overlapping with the gold reduction peak. The absolute values of open circuit potential (OCP) are different in two systems (0.51 V vs. Ag/AgCl in 1
EG have moved in a cathodic direction, and the cupric/cuprous reaction is partially overlapping with the gold reduction peak. The absolute values of open circuit potential (OCP) are different in two systems (0.51 V vs. Ag/AgCl in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG against 0.69 V vs. Ag/AgCl in aqueous solution), but in both cases it falls in the region where copper(II) and gold(I) species are the dominant species in the solution.
EG against 0.69 V vs. Ag/AgCl in aqueous solution), but in both cases it falls in the region where copper(II) and gold(I) species are the dominant species in the solution.
The speciation of copper and gold in aqueous chloride solutions has been extensively researched in past decades,40–42 and it was found that the prevailing copper chlorocomplexes in 4.5 M NaCl brine are CuCl20 and CuCl32−, whereas gold is mostly present as AuCl2−. The predominance regions of these species are illustrated in the Pourbaix diagram (Fig. 1b) and it corroborates the assignment of electrochemical processes to the peaks seen in the voltammogram, which could thus be expressed by following half-reactions:
| AuCl2− + e− ⇄ Au + 2Cl− | (6) |
| CuCl2(aq.) + Cl− + e− ⇄ CuCl32− | (7) |
| CuCl32− + e− ⇄ Cu + 3Cl− | (8) |
Although the chloride content in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG is similar to that of aqueous 4.5 M NaCl solution, the speciation of metals differs due to lower concentration of available water ligands.43 The dominant species in this case are CuCl42− and AuCl2−, along with CuCl2− for monovalent copper.44–46 Therefore, the reactions according to eqn (6) as well as eqn (9) and (10) can be associated to the corresponding peaks in 1
EG is similar to that of aqueous 4.5 M NaCl solution, the speciation of metals differs due to lower concentration of available water ligands.43 The dominant species in this case are CuCl42− and AuCl2−, along with CuCl2− for monovalent copper.44–46 Therefore, the reactions according to eqn (6) as well as eqn (9) and (10) can be associated to the corresponding peaks in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG solution:
EG solution:
| CuCl42− + e− ⇄ CuCl2− + 2Cl− | (9) |
| CuCl2− + e− ⇄ Cu + 2Cl− | (10) |
Electrogravimetric study
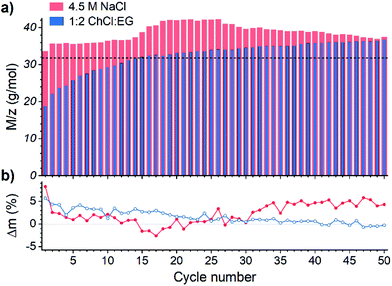
The electrochemical quartz crystal microbalance (EQCM) is a powerful tool to study both faradaic and gravimetric aspects of electrochemical reactions simultaneously, and it is often used to study metal deposition and dissolution processes.47–49 Theoretical background of the method is comprehensively described in the literature50–52 that makes it a technique of choice for studying the recovery of gold by the EDRR process.In total, 50 cycles of EDRR were carried in both solutions (Fig. 2) and it shows a clear pattern of the EDRR process. During ED there was a rapid increase in the deposited mass. This was followed by a RR step, showing first a sharp decline and then a moderate growth of the mass. During 50 cycles the trend shows a clearly increasing change in mass with an average rate around 9.7 μg cm−2 h−1 in the aqueous solution. A smaller total mass change was observed in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG, with two different rates for mass increase; the average deposition rate dropped from 5.4 μg cm−2 h−1 at the start of the measurement to 2.4 μg cm−2 h−1 by the end of the experiment. This is most likely due to the higher viscosity and lower ionic conductivity of the DES that causes slower mass transport.53 Despite this difference, during the RR stage, a mass increase was observed in both systems, retarding only slightly with the number of cycles.
EG, with two different rates for mass increase; the average deposition rate dropped from 5.4 μg cm−2 h−1 at the start of the measurement to 2.4 μg cm−2 h−1 by the end of the experiment. This is most likely due to the higher viscosity and lower ionic conductivity of the DES that causes slower mass transport.53 Despite this difference, during the RR stage, a mass increase was observed in both systems, retarding only slightly with the number of cycles.
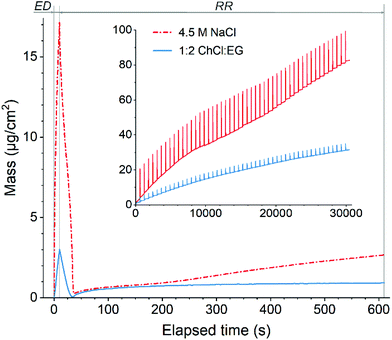 | ||
Fig. 2 Variation of mass during one EDRR cycle (10 s ED + 600 s RR) in aqueous 4.5 M NaCl solution and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl 2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG (60 mM Cu, 0.5 mM Au, T = 25 °C). Inset: mass change throughout 50 EDRR cycles. EG (60 mM Cu, 0.5 mM Au, T = 25 °C). Inset: mass change throughout 50 EDRR cycles. | ||
Magnification of one EDRR cycle in Fig. 2 shows that it consists of three consecutive electrochemical processes:
• metal deposition during the ED stage resulting in a significant surge in mass over a short period of time;
• rapid stripping of metal from the electrode surface as soon as the potential is switched off and the cell is at open circuit potential conditions (start of RR step);
• gradual mass buildup on the electrode via different redox reactions during the rest of RR stage.
In order to understand this behavior, each of these events was examined to get the full picture of the reaction mechanism of the EDRR process.
The M/z values obtained for ED from aqueous solution (Fig. 3a) in all cycles exceed the theoretical value for copper deposition – denoted with a dotted line – according to eqn (11), suggesting that more than one reaction take place simultaneously. The most likely parallel reaction in absence of other metals is a co-deposition of gold according to eqn (12):
| CuCl2(aq.) + 2e− → Cu + 2Cl−, M/z = 31.8 g mol−1 | (11) |
| AuCl2− + e− → Au + 2Cl−, M/z = 197.0 g mol−1 | (12) |
Because the OCP of both solutions lay below the oxidation potential of gold and hence cannot cause its dissolution, the extent of gold co-deposition could be approximated from the difference between mass deposited during ED and mass dissolved in the RR step (Fig. 3b), assuming complete copper dissolution during the RR step. In both systems the average amount of co-deposited gold is about 2 wt%, which correlates well with the composition of the initial solution.
In aqueous solution, the gold co-deposition rate is roughly constant through the first 10–15 cycles as is the M/z ratio with an exception for the very first cycle, when the deposition occurs on the pristine Pt surface. Negative mass change observed in some cycles implies that more material was dissolved than deposited during that cycle, presumably due to “refining” of the gold accumulated on the electrode surface, i.e. dissolution of the residual copper that was entrained in the previous cycles. As the EDRR proceeds over 20 cycles, the difference between mass deposited and mass dissolved tends to increase (Fig. 3b), whereas the M/z shows the opposite trend; this is an indication of a declining faradaic efficiency of the electrodeposition caused by additional, undetermined side process(es), for example, nanoparticles adsorption onto the electrode surface and their further growth via nucleation or Ostwald ripening.59,60
While in the aqueous solution the M/z ratio is constantly above the theoretical line, in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG it evolves from 18.7 g mol−1 in the 1st cycle up to 36.7 g mol−1 in 50th cycle. In the early cycles rather low values are detected, due to decreased deposition efficiency as also non-faradaic processes occur at the solution–electrode interface, like double layer rearrangement and displacement of solvent molecules,61,62 along with reactions according to eqn (12) and (13):
EG it evolves from 18.7 g mol−1 in the 1st cycle up to 36.7 g mol−1 in 50th cycle. In the early cycles rather low values are detected, due to decreased deposition efficiency as also non-faradaic processes occur at the solution–electrode interface, like double layer rearrangement and displacement of solvent molecules,61,62 along with reactions according to eqn (12) and (13):
| CuCl42− + 2e− → Cu + 4Cl−, M/z = 31.8 g mol−1 | (13) |
As the EDRR cycling continues, the local concentration of copper species in the proximity of the electrode rises due to a slow diffusion rate in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG. This leads to a lower gold co-deposition rate (Fig. 3b), but the concurrent increase of M/z suggests that reduction of cuprous species at the electrode (eqn (10), M/z = 63.5 g mol−1) starts playing a bigger role in the ED.
EG. This leads to a lower gold co-deposition rate (Fig. 3b), but the concurrent increase of M/z suggests that reduction of cuprous species at the electrode (eqn (10), M/z = 63.5 g mol−1) starts playing a bigger role in the ED.
• redox replacement by dissolved gold;
• reaction with dissolved oxygen in the solution;
• oxidation to copper(I) by dissolved cupric ions.
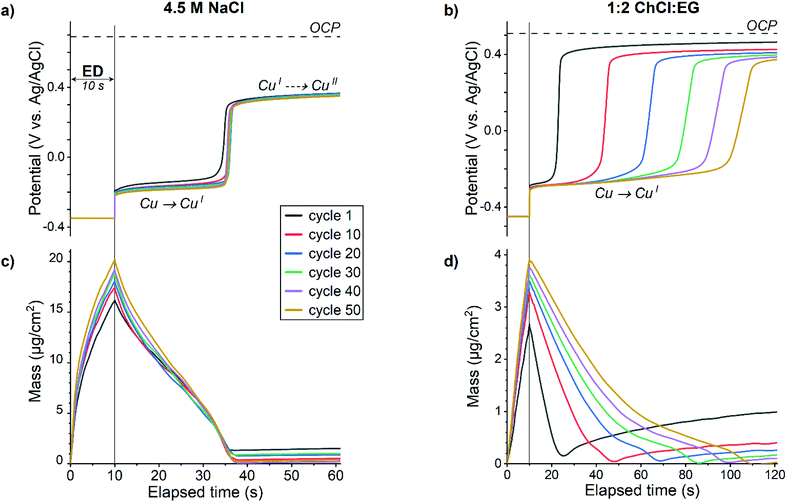 | ||
Fig. 4 Measured potential (a, b) and mass change (c, d) during first minutes of EDRR cycles in aqueous 4.5 M NaCl solution (left) and in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl 2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG (right). EG (right). | ||
Although the redox replacement reaction (eqn (14)) is thermodynamically favored, this reaction is surface limited and therefore, only copper in the top-most surface layer will be replaced by gold:
| Cu + AuCl2− + Cl− → Au + CuCl32− | (14) |
Moreover, redox replacement will not only dissolve copper from the surface but also deposit gold on the surface, thus the net mass change should be positive as gold is heavier than copper. However, the mass increase at the beginning of RR stage (Fig. 4c and d) is marginal, hence another mechanism of copper dissolution is prevailing.
The presence of Cl− ions in the solution alters the speciation of copper and makes possible its dissolution by cupric species. This can be deduced from the mass decrease of a copper-coated QCM crystal placed in different chloride containing media (Table 2). Minor amount of dissolved oxygen present in the solution under atmospheric conditions facilitates the oxidation of metallic copper,63 further promoted by complexation with chloride ions.
| Solution | Dissolution rate (μg cm−2 h−1) |
|---|---|
60 mM CuCl2 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl 2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG) EG) |
2.5 |
| 60 mM CuCl2 (aqueous) | 119.9 |
| 10 mM HCl (aqueous) | 201.2 |
| 60 mM CuCl2 + 10 mM HCl (aqueous) | 954.4 |
| 60 mM CuCl2 + 10 mM HCl + 4.5 M NaCl (aqueous) | 3289.0 |
The copper dissolution rate in the EDRR experiments (on average ca. 2700 μg cm−2 h−1) was close to that observed in acidic copper-bearing aqueous 4.5 M NaCl solution (Table 2). Therefore, it can be concluded that the mass drop occurring in the aqueous solution in the beginning of the RR stage is caused by the oxidation of copper:
| 2Cu + CuCl2(aq.) + 4Cl− → 2CuCl32− | (15) |
The redox potential of the aqueous solution measured during the RR (Fig. 4a) indicates a two-step electrochemical process. First, a dissolution of elemental copper according to eqn (15) happens at the potential around −0.2 V. This reaction is limited by the amount of copper on the electrode surface, which is corroborated by the mass change of the QCM crystal (Fig. 4c) – as soon as almost all of copper is stripped, the potential instantly shifts to a more positive direction. Thanks to a rapid mass transfer in aqueous solution, the dissolution time is rather constant in all 50 cycles and it takes about 25 s before the redox potential of the solution rises to ca. 0.3 V vs. Ag/AgCl. According to a CV (Fig. 1a), this potential corresponds to the cuprous/cupric redox reaction (eqn (7)) and implies that concentration of the copper(II) species increases in the vicinity of the electrode. Possible cathodic half-reactions are discussed below. The diffusion of oxidized species towards the electrode surface leads to a gradual rise of measured potential with time; however, due to changing with every EDRR cycle both the electrode surface and the composition of the solution, the initial OCP of 0.69 V vs. Ag/AgCl will not be reached.
In the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG solution, comproportionation reaction (eqn (16)) provides a plausible explanation for the oxidation of copper at the early RR stage in 1
EG solution, comproportionation reaction (eqn (16)) provides a plausible explanation for the oxidation of copper at the early RR stage in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG:64,65
EG:64,65
| Cu + CuCl42− → 2CuCl2− | (16) |
The stability of the copper(I) complex in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG together with a slightly lower dissolved oxygen concentration and hindered mass transport leads to a gradual depletion of copper(II) species near the electrode with every cycle. As a result, the copper dissolution is slowed down by an order of magnitude (from 10 s to 100 s) as the EDRR progresses (Fig. 4d).
EG together with a slightly lower dissolved oxygen concentration and hindered mass transport leads to a gradual depletion of copper(II) species near the electrode with every cycle. As a result, the copper dissolution is slowed down by an order of magnitude (from 10 s to 100 s) as the EDRR progresses (Fig. 4d).
The potential used in the EDRR (−0.35 V vs. Ag/AgCl) is by design7 selected such that hydrogen evolution does not occur, so the reduction of gold by hydrogen is prevented. This was also verified by an additional EDRR experiment which was performed without copper in solution but using the same ED potential. The mass change during the EDRR cycles is shown in Fig. S1 in the ESI.† In RR step no mass gain were observed, which means that copper plays a crucial role in mass accumulation. It was previously reported66,67 that under certain conditions cuprous ions may cause homogenous reduction of dissolved gold to its metallic state (eqn (17)), which provides a conceivable reason for such constant increase of mass on the electrode in addition to cementation:
| AuCl2− + CuCl32− → Au + CuCl2(aq.) + 3Cl− | (17) |
It is worth noting that if copper in aqueous solution is present only as its monovalent chlorocomplex, steady gold mass buildup begins even without any potential applied to the electrode.67 This was experimentally demonstrated in a measurement, where copper(I) chloride was added to solution instead of copper(II) chloride salt (Fig. S2†). Also, the mass increase is observed at the deposition rate of 19.6 μg cm−2 h−1, which is more than double of the rate measured in a copper(II) solution due to increased amount of cuprous ions available. This finding emphasizes the essential function of copper(I) ions for the recovery of gold from the aqueous solution, and the fact that in EDRR copper(I) can be generated electrochemically – rather than through chemical addition – highlights the versatility of this method. Moreover, previous research has shown that cuprous species are more stable in concentrated chloride media when compared to dilute solutions, both in aqueous systems68,69 and in deep eutectic solvents,70,71 which can further promote the role of copper(I) in gold recovery.
Electrogravimetric measurements alone, however, cannot conclusively interpret the mechanism in details, and RRDE amperometry is often used to define the reaction paths and determine the rates of competing chemical reactions.72,73 Additional generator–collector experiments with RRDE were performed in aqueous chloride solution for definitive verification of the role of copper(I) complexes in the gold recovery process (Fig. S3†).
The disk electrode, after a short copper deposition period, was set to the copper dissolution potential (0.1 V vs. Ag/AgCl) while the ring was constantly maintained at the copper(I)/copper(II) oxidation potential (0.65 V vs. Ag/AgCl), so that anodic current observed on the ring electrode indicates the cuprous/cupric reaction. Apparent collection efficiency (Fig. 5) of the ring electrode is smaller than the theoretical efficiency (N = 21.8%) either with or without gold in solution, and this suggests that a parallel chemical reaction, which does not involve gold, is consuming copper(I) species. In copper chloride solution, this could be due to oxidation of copper(I) to copper(II):
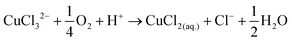 | (18) |
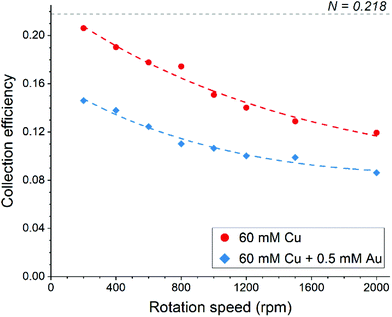 | ||
| Fig. 5 Apparent collection efficiency of the ring-disk electrode as a function of rotation speed in aqueous 4.5 M NaCl solution. | ||
In the presence of gold in the solution, the apparent collection efficiency is approximately 30% lower, showing that cuprous ions are also consumed for the homogenous reduction of gold (eqn (17)). Further decrease in collection efficiency at faster rotation speed is related to a better aeration of the solution and much improved mass transfer of oxygen; more cuprous species are oxidized according to eqn (18) and hence are not detected at the ring electrode. Therefore, it can be concluded that both redox replacement at the electrode surface and reduction of gold by copper(I) species in solution volume are the reasons for the mass increase on the electrode during the RR step with the latter one being prevalent.
Process efficiency
The efficiency of the overall EDRR process was estimated through the amount of gold recovered from either the aqueous chloride solution or 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG after 50 cycles of EDRR. The quality of the obtained product is also shown in the Table 3. A particularly high selectivity is achieved for gold recovery from the aqueous solution with the purity of the cathode product close to 95%. A small amount of oxygen was detected on the surface, which is most likely because of its oxidation in contact with air. The SEM micrographs (Fig. 6) highlight the difference in the quality of the obtained deposit. The EDRR process carried out in aqueous solution resulted in a granular morphology with fine gold particles (ca. 10 nm) distributed over the surface. These particles also appear to aggregate into larger clusters up to a few μm in size. Irregular surface coverage could be partly a result of the nanoparticle growth through coalescence and recrystallization of neighboring nuclei particles.74,75
EG after 50 cycles of EDRR. The quality of the obtained product is also shown in the Table 3. A particularly high selectivity is achieved for gold recovery from the aqueous solution with the purity of the cathode product close to 95%. A small amount of oxygen was detected on the surface, which is most likely because of its oxidation in contact with air. The SEM micrographs (Fig. 6) highlight the difference in the quality of the obtained deposit. The EDRR process carried out in aqueous solution resulted in a granular morphology with fine gold particles (ca. 10 nm) distributed over the surface. These particles also appear to aggregate into larger clusters up to a few μm in size. Irregular surface coverage could be partly a result of the nanoparticle growth through coalescence and recrystallization of neighboring nuclei particles.74,75
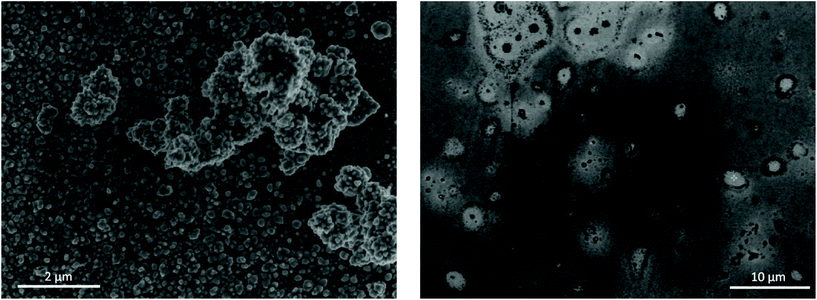 | ||
Fig. 6 SEM images of electrode surface after 50 cycles of EDRR in aqueous 4.5 NaCl solution (left) and in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl 2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG (right). EG (right). | ||
In 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG, on the other hand, the coating was smoother, though very uneven in chemical composition. The surface was covered with a thin film composed mostly of gold, but occasionally incorporating some amount of copper. Also, the EDX analysis of the deposit (Fig. S4†) showed significant levels for carbon as a result of solvent being trapped inside the deposit. Few micron-size gold particles occur sparingly across the surface as well, often surrounded by a halo of organic substances. Poor gold recovery from the 1
EG, on the other hand, the coating was smoother, though very uneven in chemical composition. The surface was covered with a thin film composed mostly of gold, but occasionally incorporating some amount of copper. Also, the EDX analysis of the deposit (Fig. S4†) showed significant levels for carbon as a result of solvent being trapped inside the deposit. Few micron-size gold particles occur sparingly across the surface as well, often surrounded by a halo of organic substances. Poor gold recovery from the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG in comparison to aqueous solution is due to the mass transport limitations. The effect of restricted mass transport could be overcome by mixing or heating the solution. Nevertheless, the copper content in the final product obtained from both solutions is rather low at about 2 at%, implying effective gold enrichment and selective dissolution of copper during the RR step.
EG in comparison to aqueous solution is due to the mass transport limitations. The effect of restricted mass transport could be overcome by mixing or heating the solution. Nevertheless, the copper content in the final product obtained from both solutions is rather low at about 2 at%, implying effective gold enrichment and selective dissolution of copper during the RR step.
In conventional gold recovery processes, the purity of gold cathodes exceeds 99% with traces of other elements found only at a ppm level.76,77 This is achieved by passing the leaching solution through a sophisticated process flowsheet that includes several concentration and purification operations, such as carbon adsorption/ion exchange and elution prior to electrochemical recovery by electrowinning.78 By using EDRR instead, gold can be recovered in one stage directly from complex impure process solutions, with remarkable selectivity and acceptable purity for further refining to the bullion grade. The energy consumption is nearly the same in both cases, 11.6 kW h kg−1 in aqueous solution and 9.7 kW h kg−1 in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG, which falls in the range of the values achieved in the state-of-the-art industrial processes.79,80 However, the higher gold recovery and purity of the product make the aqueous chloride solution preferable medium for the selective recovery of gold by EDRR process.
EG, which falls in the range of the values achieved in the state-of-the-art industrial processes.79,80 However, the higher gold recovery and purity of the product make the aqueous chloride solution preferable medium for the selective recovery of gold by EDRR process.
Discussion
Based on the results of EQCM study and RRDE measurements, the reaction mechanism of the EDRR process in aqueous chloride solution is outlined as follows:• during the ED stage, copper is deposited at constant potential on the electrode together with a minor amount of co-deposited gold – eqn (11) and (12);
• when the current is switched off (early RR stage), the deposited copper starts to dissolve through the reaction with copper(II) species in the solution (eqn (15)), facilitated by low pH, dissolved oxygen and high concentration of chlorides; also, the redox replacement reaction according to eqn (14) occurs on the surface to a certain extent;
• at the same time, gold is continuously reduced throughout the RR stage by the reaction with cuprous species (generated from the dissolution of deposited copper) in the vicinity of the electrode surface (eqn (17)) and precipitated onto the working electrode.
In 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG, the process follows a similar route, although some of the reactions are different due to the distinct physicochemical properties of the solvent; for instance, the driving force of copper stripping (the presence of cupric ions in the vicinity of the electrode surface) and the hindered kinetics due to the poor ionic conductivity in 1
EG, the process follows a similar route, although some of the reactions are different due to the distinct physicochemical properties of the solvent; for instance, the driving force of copper stripping (the presence of cupric ions in the vicinity of the electrode surface) and the hindered kinetics due to the poor ionic conductivity in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG. Therefore, gold recovery takes place via both the homogenous reduction in solution followed by precipitation and the redox replacement at the surface, and the open circuit conditions (RR stage) between electrodeposition steps is a necessity for both reaction pathways.
EG. Therefore, gold recovery takes place via both the homogenous reduction in solution followed by precipitation and the redox replacement at the surface, and the open circuit conditions (RR stage) between electrodeposition steps is a necessity for both reaction pathways.
The role of fairly stable intermediate copper(I) species in the process investigated makes the copper–gold chloride system rather atypical from the EDRR perspective, and it is debatable as to whether such reaction processes should be referred to as EDRR rather than pulse electrodeposition followed by an open circuit potential step (ED-tOCP). Indeed, the pure redox replacement action was reported for metal couples like platinum/lead,81 platinum/nickel82 or silver/zinc.83 The common feature of these systems is that the sacrificial metal (either nickel, lead or zinc) can be present in the solution only in one oxidation state, i.e. “+2”. As a consequence, when the sacrificial metal dissolves from the electrode surface, it does not form intermediate species, and therefore no reduction of valuable metal (silver or platinum) occurs in the solution volume. Other elements with similar behavior, such as tin, arsenic or bismuth were also shown suitable as sacrificial metals in EDRR process for recovery of valuable metals from hydrometallurgical process solutions.84
The copper(I) species involved in the homogenous reduction of dissolved gold are produced almost exclusively through dissolution of previously electrodeposited copper with a tiny fraction of cuprous chlorocomplexes also formed during short ED step by a one-electron reduction of copper(II) species (eqn (7)). The excessive charge applied to the system to reduce copper to its elemental state therefore seems to be “wasted”, and the energy consumption of the overall gold recovery process is high. The energy efficiency might be improved by producing copper(I) at lower overpotential, i.e. without actual copper deposition. Also, the optimization of the RR time may further minimize the diffusion of copper(I) species out of the reaction layer, although consequently decreasing the local concentration of dissolved gold species. Nevertheless, the copper layer deposited on the electrode surface during the ED step is shown to make a contribution (however small it is) to ensuring the adhesion of gold nanoparticles to the substrate. In the studied copper–gold chloride system, the redox replacement cannot be totally excluded even if the major contribution of gold recovery arises from the dissolution of the electrodeposited copper as cuprous chlorocomplexes, followed by homogenous gold reduction in the liquid phase by the same copper(I) species. These results clearly highlight that the process, which involves a short deposition step followed by an extended time at OCP, results in a dramatic increase in the rate of gold extraction.
If there were no species in the intermediate oxidation state formed in the process, the homogenous reduction of gold in the solution would not occur, and thus only redox replacement at the solid/liquid interface would contribute to the gold recovery. This was observed in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ChCl
2 ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG solution, in which the copper(I) species are fairly stable and do not tend to oxidize further to cupric chlorocomplexes, hence the extent of homogenous reaction of dissolved gold with copper was minimal. Another way to ensure that redox replacement reaction prevails over precipitation is to use an alternative sacrificial metal that exists only in one oxidized state in the solution like silver, tin or bismuth. Unfortunately, in a majority of industrial applications it is not always possible to tailor the solution composition prior to the metal recovery since this is governed by the upstream processes.
EG solution, in which the copper(I) species are fairly stable and do not tend to oxidize further to cupric chlorocomplexes, hence the extent of homogenous reaction of dissolved gold with copper was minimal. Another way to ensure that redox replacement reaction prevails over precipitation is to use an alternative sacrificial metal that exists only in one oxidized state in the solution like silver, tin or bismuth. Unfortunately, in a majority of industrial applications it is not always possible to tailor the solution composition prior to the metal recovery since this is governed by the upstream processes.
From an industrial perspective, the EDRR process could be applied to recover gold from process streams that contain gold in minor amounts with respect to a base metal, like copper. Usually, such solutions result from the hydrometallurgical treatment of gold ores and concentrates,85,86 recycling of electronic scrap,87,88 leaching of anode slimes,89,90 or refining of platinum group metals (PGM).91,92 Depending on the origin, the solution will have various impurities that can influence the EDRR process. For example, effluents from PGM refineries contain residual amounts of dissolved platinum and palladium, which would reduce together with gold because of close values of standard electrode potential (0.755 V and 0.591 V for platinum(IV) and palladium(IV) chlorocomplexes, respectively).93 Similar behavior is expected for other metals with standard reduction potentials that fall in the range between those of gold and copper, e.g. silver, antimony, arsenic. These metals will end up in the cathode product and potentially lower its purity. On the other hand, with skillful tailoring of the electrochemical parameters, these metals can act as the sacrificial elements for further recovery of the most noble element. This was previously suggested to occur in nickel-rich sulfate solution, as copper and nickel replacement was dominated by silver, but with increasing number of EDRR cycles platinum further replaced silver on the electrode surface.11 Any elements that reduce at potentials more negative than copper do not have any detrimental impact on the EDRR process of gold recovery. However, special attention needs to be paid to iron, which is a typical impurity in ore leaching. In aqueous chloride solutions, iron – like copper – can be present in two oxidation states, either as di- or trivalent species. During the ED step of the EDRR process, iron(III) is reduced to iron(II), thus consuming some electric charge and decreasing the current efficiency.83 In the RR step, the effect of iron is two-fold: ferric ions acting as an oxidant would enhance dissolution of the deposited copper and improve the purity of the gold deposit;12 at the same time, ferrous ions may reduce dissolved gold in chloride media by a homogenous reaction, which increases overall recovery of gold from solution.94
Conclusions
Although the reaction pathway outlined is specific for the copper–gold chloride system investigated, this study reveals the crucial, beneficial roles of both the open circuit steps and other elements present in industrial solutions when it comes to metal recovery. Also, gold reduction in a solution does not exclude redox replacement reaction at the surface, but instead the possibility of both reaction routes increases the overall efficiency and can thus lead to a sustainable gold production from solutions containing only minor concentrations of a valuable metal. Both of these factors could – and should – be fully exploited in the extraction of other metals as they increase the efficiency without any additional chemical or energy consumption, which is in line with the green engineering principles. Overall, the EDRR process from aqueous solution appeared to be advantageous over deep eutectic solvent due to enhanced mass transfer and better-quality deposit. On the downside, a too rapid dissolution of copper at the start of the RR step may result in poor current efficiency and higher energy consumption. The power consumption of gold recovery achieved in this study was of the order of 10 kW h kg−1 from a solution containing only 0.5 mM Au, with the recovery efficiency of 95%, and this result is indeed a solid proof of the EDRR method's potential as an industrial gold extraction technology.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This research has received funding from the European Union Framework Program for Research and Innovation Horizon 2020 under Grant Agreement No. 721385 (EU MSCA-ETN SOCRATES; project website: https://www.etn-socrates.eu). GoldTail (Grant 319691, ML) and NoWASTE (Grant 297962, KY) projects funded by the Academy of Finland are greatly acknowledged.References
- E. A. Olivetti and J. M. Cullen, Science, 2018, 360, 1396–1398 CrossRef CAS PubMed.
- R. Bleischwitz, C. Spataru, S. D. VanDeveer, M. Obersteiner, E. van der Voet, C. Johnson, P. Andrews-Speed, T. Boersma, H. Hoff and D. P. van Vuuren, Nat. Sustainability, 2018, 1, 737–743 CrossRef.
- T. Keijer, V. Bakker and J. C. Slootweg, Nat. Chem., 2019, 11, 190–195 CrossRef CAS PubMed.
- M. A. Reuter, A. van Schaik, J. Gutzmer, N. Bartie and A. Abadías Llamas, Annu. Rev. Mater. Res., 2019, 49, 253–274 CrossRef CAS.
- B. C. McLellan, G. D. Corder, D. P. Giurco and K. N. Ishihara, J. Cleaner Prod., 2012, 32, 32–44 CrossRef.
- O. Vidal, F. Rostom, C. François and G. Giraud, Elements, 2017, 13, 319–324 CrossRef CAS.
- I. Korolev, P. Altinkaya, P. Halli, P.-M. Hannula, K. Yliniemi and M. Lundström, J. Cleaner Prod., 2018, 186, 840–850 CrossRef CAS.
- I. Korolev, E. Kolehmainen, M. Haapalainen, K. Yliniemi and M. Lundström, in 10th European Metallurgical Conference (EMC 2019), ed. U. Waschki, GDMB Verlag GmbH, Düsseldorf, Germany, 2019, vol. 2, pp. 623–630 Search PubMed.
- P. Halli, H. Elomaa, B. P. Wilson, K. Yliniemi and M. Lundström, ACS Sustainable Chem. Eng., 2017, 5, 10996–11004 CrossRef CAS.
- H. Elomaa, P. Halli, T. Sirviö, K. Yliniemi and M. Lundström, Trans. IMF, 2018, 96, 253–257 CrossRef CAS.
- P. Halli, J. J. Heikkinen, H. Elomaa, B. P. Wilson, V. Jokinen, K. Yliniemi, S. Franssila and M. Lundström, ACS Sustainable Chem. Eng., 2018, 6, 14631–14640 CrossRef CAS PubMed.
- K. Yliniemi, Z. Wang, I. Korolev, P.-M. Hannula, P. Halli and M. Lundström, ECS Trans., 2018, 85, 59–67 CrossRef CAS.
- P.-M. Hannula, S. Pletincx, D. Janas, K. Yliniemi, A. Hubin and M. Lundström, Surf. Coat. Technol., 2019, 374, 305–316 CrossRef CAS.
- P. T. Anastas and J. B. Zimmerman, Environ. Sci. Technol., 2003, 37, 94A–101A CrossRef PubMed.
- G. Hilson and A. Monhemius, J. Cleaner Prod., 2006, 14, 1158 CrossRef.
- J. Wang, Y. Lu and Z. Xu, ACS Sustainable Chem. Eng., 2019, 7, 7260–7267 CrossRef CAS.
- J. Viñals, E. Juan, M. C. Ruiz, E. Ferrando, M. Cruells, A. Roca and J. Casado, Hydrometallurgy, 2006, 81, 142–151 CrossRef.
- P. Altinkaya, J. Liipo, E. Kolehmainen, M. Haapalainen, M. Leikola and M. Lundström, Min., Metall., Explor., 2019, 36, 335–342 Search PubMed.
- R. Ahtiainen and M. Lundström, J. Cleaner Prod., 2019, 234, 9 CrossRef CAS.
- A. J. Gunson, B. Klein, M. Veiga and S. Dunbar, J. Cleaner Prod., 2012, 21, 71–82 CrossRef.
- T. Sonderegger, S. Pfister and S. Hellweg, Environ. Sci. Technol., 2015, 49, 12315–12323 CrossRef CAS PubMed.
- Q. Zhang, K. de Oliveira Vigier, S. Royer and F. Jérôme, Chem. Soc. Rev., 2012, 41, 7108–7146 RSC.
- E. L. Smith, A. P. Abbott and K. S. Ryder, Chem. Rev., 2014, 114, 11060–11082 CrossRef CAS PubMed.
- A. P. Abbott, R. C. Harris, F. Holyoak, G. Frisch, J. M. Hartley and G. R. T. Jenkin, Green Chem., 2015, 17, 2172–2179 RSC.
- A. P. Abbott, G. Capper, K. J. McKenzie and K. S. Ryder, J. Electroanal. Chem., 2007, 599, 288–294 CrossRef CAS.
- A. P. Abbott, K. S. Ryder and U. König, Trans. IMF, 2008, 86, 196–204 CrossRef CAS.
- V. S. Protsenko, L. S. Bobrova, D. E. Golubtsov, S. A. Korniy and F. I. Danilov, Russ. J. Appl. Chem., 2018, 91, 1106–1111 CrossRef CAS.
- A. P. Abbott, G. Frisch, S. Gurman, A. R. Hillman, J. Hartley, F. Holyoak and K. Ryder, Chem. Commun., 2011, 47, 10031–10033 RSC.
- G. R. T. Jenkin, A. Z. M. Al-Bassam, R. C. Harris, A. P. Abbott, D. J. Smith, D. A. Holwell, R. J. Chapman and C. J. Stanley, Miner. Eng., 2016, 87, 18–24 CrossRef CAS.
- S. Anggara, F. Bevan, R. C. Harris, J. M. Hartley, G. Frisch, G. R. T. Jenkin and A. P. Abbott, Green Chem., 2019, 21, 6502–6512 RSC.
- H. Elomaa, S. Seisko, J. Lehtola and M. Lundström, J. Mater. Cycles Waste Manage., 2019, 21, 1004–1013 CrossRef CAS.
- X. Li, W. Monnens, Z. Li, J. Fransaer and K. Binnemans, Green Chem., 2020, 22, 417–426 RSC.
- D. Lu, L. Shi and Z. Jin, Adv. Mater. Res., 2011, 391, 1138–1142 Search PubMed.
- E. S. Kshumaneva, A. G. Kasikov, V. Y. Kuznetsov, Y. N. Neradovskii, R. G. Kushlyaev and V. V. Semushin, Russ. J. Appl. Chem., 2015, 88, 724–732 CrossRef CAS.
- S. Seisko, M. Lampinen, J. Aromaa, A. Laari, T. Koiranen and M. Lundström, Miner. Eng., 2018, 115, 131–141 CrossRef CAS.
- P. Altinkaya, I. Korolev, E. Kolehmainen, M. Haapalainen and M. Lundström, in 10th European Metallurgical Conference (EMC 2019), ed. U. Waschki, GDMB Verlag GmbH, Düsseldorf, Germany, 2019, vol. 2, pp. 821–829 Search PubMed.
- N. Frenzel, J. M. Hartley and G. Frisch, Phys. Chem. Chem. Phys., 2017, 19, 28841–28852 RSC.
- G. H. Sauerbrey, Z. Phys., 1959, 155, 206–222 CrossRef CAS.
- C. K. Gupta and T. K. Mukherjee, Hydrometallurgy in Extraction Processes, Routledge, New York, USA, 1990, vol. 2 Search PubMed.
- J. J. Fritz, J. Phys. Chem., 1980, 84, 2241–2246 CrossRef CAS.
- M. Uchikoshi, J. Solution Chem., 2017, 46, 704–719 CrossRef CAS.
- M. Lampinen, S. Seisko, O. Forsström, A. Laari, J. Aromaa, M. Lundström and T. Koiranen, Hydrometallurgy, 2017, 169, 103–111 CrossRef CAS.
- A. Y. M. Al-Murshedi, J. M. Hartley, A. P. Abbott and K. S. Ryder, Trans. Inst. Met. Finish., 2019, 97, 321–329 CrossRef CAS.
- D. Lloyd, T. Vainikka, L. Murtomäki, K. Kontturi and E. Ahlberg, Electrochim. Acta, 2011, 56, 4942–4948 CrossRef CAS.
- J. Hartley, C.-M. Ip, G. Forrest, K. Singh, S. Gurman, K. S. Ryder, A. P. Abbott and G. Frisch, Inorg. Chem., 2014, 53, 6280–6288 CrossRef CAS PubMed.
- A. D. Ballantyne, G. C. H. Forrest, G. Frisch, J. M. Hartley and K. S. Ryder, Phys. Chem. Chem. Phys., 2015, 17, 30540–30550 RSC.
- A. R. Hillman, J. Solid State Electrochem., 2011, 15, 1647–1660 CrossRef CAS.
- S. Kologo, M. Eyraud, L. Bonou, F. Vacandio and Y. Massiani, Electrochim. Acta, 2007, 52, 3105–3113 CrossRef CAS.
- A. Collazo, R. Figueroa, X. R. Nóvoa and C. Pérez, Surf. Coat. Technol., 2015, 280, 8–15 CrossRef CAS.
- S. Bruckenstein and M. Shay, Electrochim. Acta, 1985, 30, 1295–1300 CrossRef CAS.
- K. K. Kanazawa and O. R. Melroy, IBM J. Res. Dev., 1993, 37, 157–171 CAS.
- A. R. Hillman, A. Jackson and S. J. Martin, Anal. Chem., 2001, 73, 540–549 CrossRef CAS PubMed.
- S. Ghosh, K. S. Ryder and S. Roy, Trans. IMF, 2014, 92, 41–46 CrossRef CAS.
- J. G. N. Matias, J. F. Julião, D. M. Soares and A. Gorenstein, J. Electroanal. Chem., 1997, 431, 163–169 CrossRef CAS.
- J. T. Matsushima, F. Trivinho-Strixino and E. C. Pereira, Electrochim. Acta, 2006, 51, 1960–1966 CrossRef CAS.
- E. Rudnik and J. Kozłowski, Electrochim. Acta, 2013, 107, 103 CrossRef CAS.
- R. Schumacher, G. Borges and K. K. Kanazawa, Surf. Sci., 1985, 163, L621–L626 CrossRef CAS.
- M. Kemell, H. Saloniemi, M. Ritala and M. Leskelä, J. Electrochem. Soc., 2001, 148, C110–C118 CrossRef CAS.
- P. Redmond, A. Hallock and L. Brus, Nano Lett., 2005, 5, 131 CrossRef CAS PubMed.
- T. W. Hansen, A. T. Delariva, S. R. Challa and A. K. Datye, Acc. Chem. Res., 2013, 46, 1720–1730 CrossRef CAS PubMed.
- O. S. Hammond, H. Li, C. Westermann, A. Y. M. Al-Murshedi, F. Endres, A. P. Abbott, G. G. Warr, K. J. Edler and R. Atkin, Nanoscale Horiz., 2019, 4, 158–168 RSC.
- J. D. Gamarra, K. Marcoen, A. Hubin and T. Hauffman, Electrochim. Acta, 2019, 312, 303–312 CrossRef CAS.
- M. Iwai, H. Majima and Y. Awakura, Hydrometallurgy, 1988, 20, 87–95 CrossRef CAS.
- Y. Su, J. Liu, R. Wang, S. Aisa, X. Cao, S. Li, B. Wang and Q. Zhou, J. Electrochem. Soc., 2018, 165, H78–H83 CrossRef CAS.
- T. A. Green, P. E. Valverde Armas and S. Roy, J. Electrochem. Soc., 2018, 165, D313–D320 CrossRef CAS.
- S. Dong and X. Yang, Talanta, 1996, 43, 1109–1115 CrossRef CAS PubMed.
- J. J. Lingane, Anal. Chim. Acta, 1958, 19, 394–401 CrossRef CAS.
- H. K. Lin, X. J. Wu and P. D. Rao, JOM, 1991, 43, 60–65 CrossRef CAS.
- L. M. Abrantes, L. V. Araújo and M. D. Levi, Miner. Eng., 1995, 8, 1467–1475 CrossRef CAS.
- A. P. Abbott, K. El Ttaib, G. Frisch, K. J. McKenzie and K. S. Ryder, Phys. Chem. Chem. Phys., 2009, 11, 4269 RSC.
- S. Ghosh and S. Roy, Surf. Coat. Technol., 2014, 238, 165–173 CrossRef CAS.
- L. N. Nekrasov, Faraday Discuss., 1973, 56, 308–316 RSC.
- E. O. Barnes, G. E. M. Lewis, S. E. C. Dale, F. Marken and R. G. Compton, Analyst, 2012, 137, 1068–1081 RSC.
- E. Fratini, A. Girella, I. Saldan, C. Milanese, O. Dobrovetska, L. Sus, Y. Okhremchuk, O. Kuntyi and O. Reshetnyak, Mater. Lett., 2015, 161, 263–266 CrossRef CAS.
- H. E. M. Hussein, R. J. Maurer, H. Amari, J. J. P. Peters, L. Meng, R. Beanland, M. E. Newton and J. V. Macpherson, ACS Nano, 2018, 12, 7388–7396 CrossRef CAS PubMed.
- E. Schalch and M. J. Nicol, Gold Bull., 1978, 11, 117–123 CrossRef CAS.
- D. J. Kinneberg, S. R. Williams and D. P. Agarwal, Gold Bull., 1998, 31, 58–67 CrossRef CAS.
- P. J. Conradie, M. W. Johns and R. J. Fowles, Hydrometallurgy, 1995, 37, 349–366 CrossRef CAS.
- J. O. Marsden, Min., Metall., Explor., 2006, 23, 121–125 CAS.
- M. Costello, in Gold Ore Processing, ed. M. D. Adams, Elsevier, Amsterdam, The Netherlands, 2nd edn, 2016, pp. 585–594 Search PubMed.
- K. Yliniemi, D. Wragg, B. P. Wilson, H. N. McMurray, D. A. Worsley, P. Schmuki and K. Kontturi, Electrochim. Acta, 2013, 88, 278–286 CrossRef CAS.
- K. Yliniemi, N. T. Nguyen, S. Mohajernia, N. Liu, B. P. Wilson, P. Schmuki and M. Lundström, J. Cleaner Prod., 2018, 201, 39–48 CrossRef CAS.
- Z. Wang, P. Halli, P. Hannula, F. Liu, B. Wilson, K. Yliniemi and M. Lundström, J. Electrochem. Soc., 2019, 166, E266–E274 CrossRef CAS.
- P. Halli, B. Wilson, T. Hailemariam, P. Latostenmaa, K. Yliniemi and M. Lundström, J. Appl. Electrochem., 2020, 50, 1–14 CrossRef CAS.
- V. Miettinen, M. Haapalainen, R. Ahtiainen and J. Karonen, in ALTA 2013 Gold Conference, ed. A. Taylor, Perth, WA, Australia, 2013, pp. 187–202 Search PubMed.
- D. Lemieux, J.-M. Lalancette and B. Dubreuil, in 23rd World Mining Congress, Canadian Institute of Mining, Metallurgy and Petroleum, Montréal, QC, Canada, 2013, p. 364 Search PubMed.
- E. Yazici and H. Deveci, Int. J. Miner. Process., 2015, 134, 89–96 CrossRef CAS.
- H. Elomaa, S. Seisko, T. Junnila, T. Sirviö, B. P. Wilson, J. Aromaa and M. Lundström, Recycling, 2017, 2, 14 CrossRef.
- Y. Ding, S. Zhang, B. Liu and B. Li, J. Cleaner Prod., 2017, 165, 48 CrossRef CAS.
- W. D. Xing, M. S. Lee and G. Senanayake, Hydrometallurgy, 2018, 180, 58–64 CrossRef CAS.
- L. A. Cramer, JOM, 2001, 53, 14–18 CrossRef CAS.
- F. K. Crundwell, M. S. Moats, V. Ramachandran, T. G. Robinson and W. G. Davenport, in Extractive Metallurgy of Nickel, Cobalt and Platinum Group Metals, Elsevier Ltd., Oxford, UK, 1st edn, 2011, pp. 489–534 Search PubMed.
- CRC Handbook of Chemistry and Physics, ed. J. R. Rumble, CRC Press, Boca Raton, FL, United States, 100th edn, 2019 Search PubMed.
- M. Wojnicki, K. Fitzner and M. Luty-Błocho, Trans. Nonferrous Met. Soc. China, 2015, 25, 2027–2036 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Mass change during EDRR with Cu(I) and in absence of Cu in the solution; RRDE measurements with and without gold in cupric chloride solution; EDX spectra of final gold product after 50 cycles of EDRR. See DOI: 10.1039/d0gc00985g |
| This journal is © The Royal Society of Chemistry 2020 |