On the multifunctionality of butterfly scales: a scaling law for the ridges of cover scales

Abstract

The bright colors found on the wings of some butterflies have been widely examined during recent decades because they are frequently caused by nano-structures and not by pigments or dyes. Sometimes it is puzzling to discover the physical origin of these structural colors because the color-causing nano-structures are integrated into a complex structure of scales that densely covers the butterfly wings. While the color of the wings serves purposes ranging from mating to camouflage and thermoregulation, the overall structure of the scales is commonly believed to assist with aerodynamics, self-cleaning, and easy release from spider webs. This multi-functionality of butterfly scales causes various constraints for their evolutionary design. Here, we present a structural analysis of the height and distance of the ridges in cover scales of butterfly species from different families. The subsequent analysis reveals a linear scaling law. The height of the ridges is always less than half of the distance between them. Finally, we discuss possible reasons for this geometrical scaling law.

---

1 Introduction

The bright and shiny appearance of several butterflies is caused by so-called ‘structural colours’ originating from the smart combination of nano- and microstructures. Colours produced in this way are of special interest because they do not bleach like some pigments or dyes. This feature together with their attractive and colourful appearance has generated significant attention during recent decades.^1–4

Interestingly, some principles of structural colours in butterflies were already discovered in the 1920s when high-resolution microscopy was limited to optical methods.^5–7 However, with the advent of advanced microscopy and simulation techniques during recent decades, imaging nano-scale structures has become a standard procedure. This progress helped to explain the physical origin of structural colours in butterflies as well as in other animals, and plants.^1–4

Nonetheless, sometimes it is tricky to identify the optical effective components in these nano-structures because they can be hidden in a complex design which might not only be responsible for colour effects, i.e., the overall structure is multifunctional and serves several purposes at the same time. These multi-dimensional constraints prevent a nano-structure embedded in the butterfly scales from being optimized solely for colour production. The optical effective part has to be integrated into a structure which has to fulfil mechanical constraints and serves purposes including self-cleaning,⁸ aerodynamics,^9,10 and thermoregulation.^11,12 Furthermore, there are evolutionary constraints, i.e., the phylogenetic constraint prevents butterfly scales from developing into a fully arbitrary shape.¹³

Here, we report on the result of such a constraint observed in the ‘generic’ shape of butterfly scales. Analysing the geometry of ridges, we observe a scaling law which seems to be caused by this multifunctionality. Analysing ten different butterfly species, we observe that the ridges in the scales of butterflies follow a common scaling law. The distance between two ridges is roughly twice their height, i.e., the ratio between these two parameters is roughly constant. As shown and discussed in the following, the presented scaling law has most likely evolved as a result of the multiple constraints butterfly scales have to fulfil at the same time. Beside the easily visible task of colouring the wing of butterflies, they assist in ‘dry’ self-cleaning and improve aerodynamics. We hypothesise that this multifunctionality causes the observed scaling law.

2 Experimental

2.1 Examined butterflies

Altogether, we analysed 10 different butterfly species from 7 sub-families and 3 families of Lepidoptera. Fig. 1 displays photos of the dorsal sides of all examined butterflies roughly positioned on a world map in accordance with their natural habitats. They originate from all five continents and differ in colour appearance and habitat.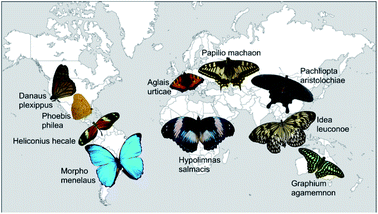

Fig. 1 Photos of all butterflies examined in this study. They are arranged on a map of the world in order to indicate their natural habitat.

Table 1 summarizes the examined species together with their respective sub-families and families. All butterflies were purchased from or kindly provided by butterfly greenhouses. As we analyse the microstructure of the scales in our study, we also give the respective size of each individual examined butterfly.

Table 1 List of the examined butterfly species with their respective families and sub-families. For comparison the body sizes (wingspans) of examined butterflies are given in the second column

Species	Size (mm)	Sub-family	Family
Aglais urticae	49	Nymphalinae	Nymphalidae
Danaus plexippus	47	Danainae	Nymphalidae
Idea leuconoe	139	Danainae	Nymphalidae
Hypolimnas salmacis	113	Junoniini	Nymphalidae
Morpho menelaus	110	Morphinae	Nymphalidae
Graphium agamemnon	96	Papilioninae	Papilionidae
Papilio machaon	75	Papilioninae	Papilionidae
Pachliopta aristolochiae	95	Papilioninae	Papilionidae
Heliconius hecale	73	Heliconiinae	Papilionidae
Phoebis philea	48	Coliadinae	Pieridae

---

2.2 Analysis of the butterfly scales

Before analysing the dimensions of the ridges, all butterfly wings and the overall structure of their scales were imaged by scanning electron microscopy (SEM). Some scales were also examined by transmission electron microscopy (TEM). Fig. 2 displays examples of such images for the Eurasian butterfly Aglais urticae commonly known as ‘small tortoiseshell’. Its dorsal wings are mostly covered with orange/brownish and black areas but also contain blue and white spots (see Fig. 1). Imaging the wing by scanning electron microscopy reveals that the scales lie on one another like roof tiles all over the wing (Fig. 2a). Zooming into single scales shows that the scales of A. urticae exhibit a hollow structure (Fig. 2b). Ridges, ribs, and trabeculae can be easily distinguished.¹⁴ The ridges and ribs belong to the upper lamina. The trabeculae connect these to the flat lower lamina. As described by Ghiradella et al.,^14–16 this structure can be seen as ‘typical’ or ‘generic’ for many – but not all – butterfly scales.

Fig. 2 (a) Scales of A. urticae imaged by scanning electron microscopy. The scales are arranged in a shingle-like structure. (b) Zooming into a single scale shows the ridges and ribs of the upper lamina as well as trabeculae which connect the upper and lower laminae. (c) A side view of the same structure recorded by transmission electron microscopy. The height h and distance d of the ridges as defined in this study are indicated by arrows. Please note that the overall structure is partly distorted due to the embedding of the sample in an epoxy resin.

As briefly mentioned in the introduction, we are mostly interested in the height of the ridges and the distance between them. Measuring the distance between the ridges is straightforward by SEM. Height measurements, however, are possible with subsequent software analysis considering the tilt angle of the sample but this subsequent analysis step is comparably elaborate. Measuring both parameters from TEM images seems more straightforward at first sight but has other obstacles. The samples have to be embedded into an epoxy resin before thin slices are prepared for imaging with transmission electron microscopy. This sample preparation is comparatively elaborate, too. In addition, the scale structure might be slightly distorted during this process. Furthermore, it is not possible to perfectly control the orientation of a single scale relative to the cut. We therefore analysed the topography of the upper lamina of the scales by atomic force microscopy (AFM) which allows for the direct imaging of biological surfaces without elaborate sample preparation. Nonetheless, SEM is the perfect tool to confirm that the cover scales on the wings feature the common, ‘typical’ structure.

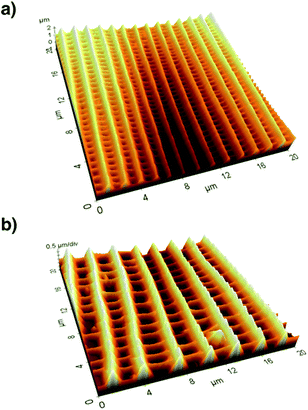
After recording electron microscopy images of all specifiable areas, we validated the respective structures of the scales in these areas. Subsequently, we recorded atomic force microscopy (Multimode SPM, Veeco Inc.) images of suitable single scales. For this we applied the so-called tapping mode with micro-machined silicon cantilevers (All-In-One Al, BudgetSensors). Fig. 3 compares the three-dimensional representations of the measured topographies for two butterfly species.

Fig. 3 (a) The topography of an area (10 μm × 10 μm) of a single scale of A. urticae imaged by atomic force microscopy. There are about 13 ridges per 10 μm. (b) The topography of I. leuconoe shows the same type of structure but the overall size of the ridges is scaled. The distance and height of the ridges are nearly twice as much compared to A. urticae (approx. 7 ridges per 10 μm).

We analysed the height h and distance d of the ridges from this topography data by averaging over several periods of ridges. We determined these two parameters for several parts of the wing and calculated their respective ratio

Table 2 summarizes the resulting ratios obtained at differently coloured positions of the wing of A. urticae. All AFM measurements were conducted at several wing positions and we averaged the height and distance for each AFM image. The error bars correspond to the respective statistical errors. A comparison of the values shows that the ratio r obtained for different coloured areas has an average of 0.425.

Table 2 List of the distances and heights measured for different areas of the scales of the butterfly A. urticae. The error is about 15%. All ratios calculated from these two parameters are between 0.39 and 0.47. The average value is 0.425

Area	Colour	Height (nm)	Distance (nm)	Ratio
Dorsal side	Yellow	770	1810	0.43
Dorsal side	Orange	680	1700	0.40
Dorsal side	Black	830	1780	0.47
Ventral side	Yellow	900	2080	0.43
Ventral side	White	900	2340	0.39
Ventral side	Black	840	1970	0.43

---

2.3 Height of the ridges and the distance between them

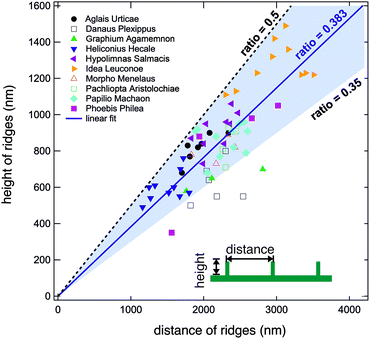
We conducted the above described analysis on all ten of the above listed butterflies considering especially the most prominent distinguishable parts of their wings. For every butterfly, we measured at least three different areas. For some butterflies we recorded data for up to ten areas including dorsal and ventral sides. At every position, we took several AFM images and averaged the height and width of at least three different positions.

In this way, we obtained between one and ten averaged pairs of height and distance data for each of the ten examined butterflies. Fig. 4 displays a plot of the complete set of data pairs we recorded in this study.¹⁷ Each data point is the outcome of the above described procedure. The distance between the ridges is shown on the horizontal axis and their corresponding height is shown on the vertical axis. There is some scatter in the data and one can observe that some butterflies have smaller ridge heights and distances. Fitting all data points to a straight line, however, we obtain a ratio of 0.383 (solid blue line). Interestingly, we did not observe ratios larger than 0.5. The black dashed line corresponds to a ratio of r = 0.5 and marks an upper limit for all experimental data. There are no data points above this line, indicating that the distance between ridges of cover scales is never larger than double their height. The majority of data points have ratios between 0.35 and 0.5 as marked by the light blue background. 63 out of 68 data points lie in this range. The lowest values are found for the butterfly D. plexippus.

Fig. 4 Height and distance data of all examined butterfly scales. The black dashed line corresponds to a ratio of 0.5. No data points are found above this line. Fitting all data to a straight line gives a ratio of 0.383 (solid blue line). The light blue background indicates the ratios between 0.35 and 0.5. Most values lie in this range. The inset indicates the definition of the distance and height of the ridges.

Here, it is important to mention that this ratio between the height and distance of ridges holds only for cover scales. There are several butterflies with ground scales with very dense ridges. As shown in Fig. 5a and b (and also in other studies), the densities of the ridges in ground and cover scales of Morpho butterflies differ significantly. The ridges of the ground scales of M. menelaus are much more densely packed than the ridges of the cover scales. This reduced density of ridges in the cover scales is surprising because the ‘Christmas tree’ like shape of the ridges is known to cause the famous blue colour of Morpho butterflies and denser ribs will increase the reflection of blue light. So, it seems that Morpho butterflies have fewer ridges on their cover scales even though this reduces the famous blue appearance of their dorsal wings.

Fig. 5 (a) Scanning electron microscopy image of a dorsal wing of M. menelaus allowing a direct comparison of cover and base scales. (b) A zoomed image displaying the ridges of cover and base scales. The base scales have a much higher density of ridges and these are much closer together than on the cover scales. The analysis of ridges presented in this study deals only with cover scales. (c) An example of a butterfly where the scales do not have the ‘typical’ structure displayed in Fig. 2. This SEM image shows the border between the green and black areas of G. agamemnon. The green areas are covered with ‘hair-like’ scales which do not allow a proper determination of ridges and ribs. In the lower left corner are some scales found in the black areas.

Furthermore, there are several butterflies where the scales have adapted to specialized functions like ‘scent scales’¹⁸ or they are reduced to elongated ‘hair-like’ structures. Fig. 5c shows the border between the black and green areas of a G. agamemnon butterfly. The green areas of this butterfly are covered with ‘hair-like’ scales. Other prominent examples of butterflies with such scales include species with nearly transparent wings, like the glasswing butterfly Greta oto.¹⁹ Here, all transparent areas of the wings are covered with these ‘hair-like’ scales, too. Other cases where it makes no sense to define a ratio between height and distance between ridges include butterflies where the upper lamina is a closed membrane with dimples, like Papilio palinurus.²⁰ While this type of structure is known to cause interesting structural colour effects, it is less meaningful to include it in statistics for the geometry of cover scale ridges.

3 Discussion

The data presented in the previous section gives strong evidence that the height and distance of ridges of butterfly cover scales with the ‘typical’ structure follow a linear scaling law. The height h and distance d of the ridges in the upper lamina correlate with a linear law h = 0.383 × d. The ratio between the parameters varies between 0.35 and 0.5. Interestingly, we observed an upper limit of 0.5 for the ratio, i.e., the ridges of cover scales are restricted in their height and density.

Some studies have already reported on other correlations for butterfly scales. Simonsen and Kristensen²¹ examined 120 Lepidoptera species and found a positive correlation between wing and scale length which is best fitted with a nonlinear power law. Kusaba and Otaki²² observed a positional dependence of scale size and shape for the butterfly Junonia orithya. In most studies, butterfly scales are seen as colouring elements causing the tremendous variety of colours observed in the 157 000 species described in the order of Lepidoptera.²³ Following this route, Janssen et al.²⁴ analysed the correlation between pigmentation and density of ribs for the butterflies Bicyclus anynana and Heliconius melpomene. These above-mentioned studies have in common that they discuss whether morphogenesis leads to these correlations, i.e., whether the scaling law is caused by genetic constraints.

Since we observe the scaling law only for cover scales and not for ground scales, we assume that simple morphogenesis is not the cause of our observation. Considering that butterfly scales can be found with a tremendous variety of shapes, it seems unlikely that the scaling of the ridges observed on cover scales with the typical geometry is a result of genetic constraints. However, so far, we cannot identify a monocausal advantage of the morphological scaling law. Nonetheless, it is reasonable to conclude that the scaling of the ridges has some significant benefit for butterflies. In the following we discuss possible advantages of the observed geometry in the upper lamina.

In general, it is reported that butterfly scales, in addition to colouring, assist in thermoregulation,^11,12,25 escape from spider webs,²⁶ aerodynamics,^10,27,28 and wet self-cleaning.^8,29 Among these, aerodynamics and wet self-cleaning are the only features which rely mainly on the microstructure of the surface, i.e., the geometry of the upper lamina. Escape from spider webs is explained by the easy release of scales from butterfly wings.²⁶ The scales are only loosely bound to the wing membrane and can be easily released (for comparative experiments for example).^10,19,28 The microstructure of the upper lamina has practically no effect on this. Thermoregulation in butterfly wings, however, is in most cases a complex phenomenon where the combination of pigmentation as well as the micro- and nanostructure in the scales is important. In some black butterflies, for example, the disordered arrangement of nanoholes formed by the ribs increases the absorption of light in addition to black pigmentation.^25,30 Consequently, in the following we focus on the possible influence of the scaling law of the ridges on the aerodynamics and the self-cleaning of butterfly wings.

There are several reports indicating that wing scales are beneficial for the aerodynamics of butterfly flight.²⁷ Nachtigall^9,10 measured the aerodynamic properties of butterfly wings with and without wing scales. He reported an improvement in lift of about 15% for wings with scales. Slegers et al.²⁸ analysed the flight of living butterflies utilizing high-speed cameras. Comparing the flight performance of butterflies with and without scales, they observed that scales improve the climbing efficiency of butterflies. Additionally, it is interesting to note that Kovalev^31–33 designed an artificial ‘butterfly skin’ inspired by the open and hollow structure of butterflies. His experiments with this artificial surface demonstrated a significant advantage in aerodynamics and he suggested applying it to helicopters³¹ and wind turbines.³³ Although the above mentioned studies strongly suggest that butterfly scales support the flight of butterflies, it is an often reported observation that butterflies can still fly without scales.²⁸ Nonetheless, the overall structure of the ridges and the observed ratio limit of 0.5 remind us of the famous study of Bechert et al.³⁴ who studied the drag of a ribbed surface inspired by shark scales. Searching for an optimized design for these ‘riblets’, the authors found that a ratio of 0.5 between height and distance is optimal. Summing up all these experimental observations, it seems very likely that the ridge design is beneficial for butterfly flight although the detailed mechanism has to be explained.

The scaling law also has some advantages in the cleaning of butterfly wings. Butterfly wings self-clean to remove dirt particles if they are sprayed with liquids like water.⁸ Here, the cleaning effect is comparable to the cleaning observed on several superhydrophobic plant leaves like the famous lotus leaf.³⁵ Small water droplets collect small dirt particles and roll off superhydrophobic surfaces. For this effect, however, the scaling of the ridges is of limited help. The water droplets only touch the top edges of the ridges, and the height influences the superhydrophobicity only indirectly (at most). Furthermore, one might ask what evolutionary advantage wet self-cleaning might have for butterflies? It is common knowledge that butterflies avoid rain because they are very lightweight.³⁶ Furthermore, most butterflies live only for a short time or they might live in a dry environment, so that it might not rain at all during their full lifetime. Consequently, we can exclude that the ridge scaling law is of importance for a wet self-cleaning effect. Nonetheless, during our experiments we observed that butterfly wings easily self-clean by air strokes and this ‘dry’ self-cleaning clearly benefits from the scaling law of the ridges.

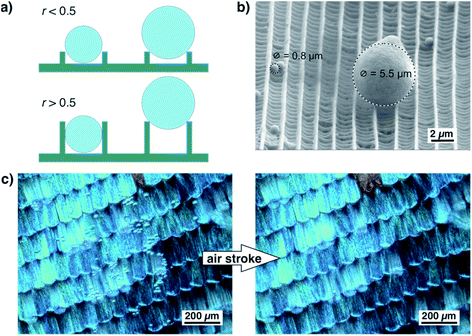
As shown in Fig. 6a, the ratio of ridge height and distance greatly influences the adherence of small particles. If the ratio of ridge height and distance is well below 0.5, a spherical dirt particle cannot get stuck between two ridges. If the ratio is higher, particles might get stuck between ridges. Their release might be difficult and seems unrealistic for wet self-cleaning. Such a particle will not be released by a rolling water droplet. For larger particles, however, the height of the ridges is less important. They touch only the top edges of the ridges and can be easily released. This situation is shown by the example in Fig. 6b. In this SEM image, one larger particle and several smaller ones rest on top of a scale of A. urticae.³⁷ The smaller particles lie between the ridges but do not become stuck while the larger particle touches only the edges of two ridges and might be easily detached. Fig. 6c shows an optical image of a wing of M. menelaus covered with several small glass particles. They are easily blown off by a simple air stroke which is comparable to the situation of a butterfly flapping its wings. We observed this dry self-cleaning on all examined butterfly wings³⁸ as well as on artificial surfaces covered with ‘butterfly ridges’.³⁹ So, the scaling law seems beneficial for the ‘dry’ self-cleaning of butterfly wings.

Fig. 6 (a) Schematic illustrating the influence of the ratio between ridge distance and height on dry self-cleaning. If the ratio is well below 0.5, small dirt particles cannot get stuck between ridges. For higher ridges leading to ratios above 0.5, small dirt particles might get stuck between ridges. Dirt particles with a size larger than the distance between the ridges are only in contact with the top edges of the ridges. Consequently, they adhere only loosely to the scale. (b) SEM image of small glass spheres on top of the scales of A. urticae. Smaller particles with a diameter of 0.8 μm are much smaller than the distance between the ridges and stick to the sides of the ridges while larger particles stay on top of the ridges. The latter are only in contact with the edges of the ridges and adhere only loosely. (c) Demonstration of dry self-cleaning on the scales of the butterfly M. menelaus. Small glass spheres distributed on top of the wing do not adhere to the scales and can be easily blown off.

4 Conclusions

In conclusion, we have shown that the height and distance of ridges in cover scales of many butterflies follow a linear scaling law. The height of the ridges increases linearly with the distance between them. In all examined cases the height of the ridges is less than half the distance between them. This seems to be independent of the actual colour of the scales, the respective species, and the butterfly family. Considering also the quite different habitats of the examined species, it is astonishing how well this scaling law holds. There is no obvious monocausal advantage of this design of the ridges in the upper lamina. Most likely, it is a result of the multiple requirements butterfly scales have to fulfil because butterfly wings have to serve several purposes at the same time.

We have presented and discussed several reasons why the scaling law of the ridge structure might result in an advantage for the butterfly’s survival. None of them can be identified as causative up to now. Most likely, the scaling law is a result of multifunctional optimization. The fact that several butterflies follow the presented scaling law for their cover scales, but not for their ground scales, suggests that this structural constraint is most important at the surface of the thin wings. Here, the structure of the upper lamina can potentially influence drag for the improvement of aerodynamics and ‘dry’ self-cleaning properties.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Martin Börner (nanoAnalytics GmbH, Münster) and Paul Abbafy (Karlsruhe Institute of Technology) for the recording of the SEM images. Furthermore, we thank Jan-Erik Schmutz (University of Münster), André Schirmeisen (University of Gießen), and Volker Saile (Karlsruhe Institute of Technology) for support and helpful discussions. Some of the examined butterfly species were kindly provided by Stefan Reisch (Mainau GmbH) and the ‘Schmetterlingshaus’ of EGA Park Erfurt.

References

1. A. R. Parker, J. Opt. A: Pure Appl. Opt., 2000, 2, R15–R28.
2. Biomimetics in Photonics, ed. O. Karthaus, CRC Press, 2013.
3. M. Kolle, Photonic Structures Inspired by Nature, Springer, Berlin, Heidelberg, 2011.
4. S. Vignolini, E. Moyroud, B. J. Glover and U. Steiner, J. R. Soc., Interface, 2013, 10, 20130394.
5. C. W. Mason, J. Phys. Chem., 1926, 30, 383–395.
6. C. W. Mason, J. Phys. Chem., 1927, 31, 1856–1872.
7. C. W. Mason, J. Phys. Chem., 1927, 31, 321–354.
8. T. Wagner, C. Neinhuis and W. Barthlott, Acta Zool., 1996, 77, 213–225.
9. W. Nachtigall, Naturwissenschaften, 1965, 52, 216–217.
10. W. Nachtigall, J. Comp. Physiol., A, 1966, 54, 210–231.
11. L. T. Wasserthal, J. Insect Physiol., 1975, 21, 1921–1930.
12. H. Schmitz, J. Therm. Biol., 1994, 19, 403–412.
13. D. Adriaens, Proc. SPIE, 2019, 10965, 1096509.
14. H. Ghiradella and W. Radigan, J. Morphol., 1976, 150, 279–297.
15. H. Ghiradella, Appl. Opt., 1991, 30, 3492–3499.
16. H. Ghiradella, Microscopic Anatomy of Invertebrates, ed. F. W. Harrison and M. Locke, Wiley-Liss, Inc., 1998, vol. 11A: Insecta, pp. 257–287.
17. A. Niebel, Bachelor thesis, Hochschule Offenburg, 2009.
18. F. Müller, Kosmos, 1877, 2, 38–41.
19. R. H. Siddique, G. Gomard and H. Hölscher, Nat. Commun., 2015, 6, 6909.
20. P. Vukusic, J. R. Sambles and C. R. Lawrence, Nature, 2000, 404, 457.
21. T. J. Simonsen and N. P. Kristensen, J. Nat. Hist., 2003, 37, 673–679.
22. K. Kusaba and J. M. Otaki, J. Insect Physiol., 2009, 55, 175–183.
23. E. J. v. Nieukerken, L. Kaila, I. J. Kitching, N. P. Kristensen, D. C. Lees, J. Minet, C. Mitter, M. Mutanen, J. C. Regier, T. J. Simonsen, N. Wahlberg, S.-H. Yen, R. Zahiri, D. Adamski, J. Baixeras, D. Bartsch, B. Å. Bengtsson, J. W. Brown, S. R. Bucheli, D. R. Davis, J. D. Prins, W. D. Prins, M. E. Epstein, P. Gentili-Poole, C. Gielis, P. Hättenschwiler, A. Hausmann, J. D. Holloway, A. Kallies, O. Karsholt, A. Y. Kawahara, S. J. C. Koster, M. V. Kozlov, J. D. Lafontaine, G. Lamas, J.-F. Landry, S. Lee, M. Nuss, K.-T. Park, C. Penz, J. Rota, A. Schintlmeister, B. C. Schmidt, J.-C. Sohn, M. A. Solis, G. M. Tarmann, A. D. Warren, S. Weller, R. V. Yakovlev, V. V. Zolotuhin and A. Zwick, Zootaxa, 2001, 3148, 212–221.
24. J. M. Janssen, A. Monteiro and P. M. Brakefield, Evol. Dev., 2001, 3, 415–423.
25. Q. Zhao, X. Guo, T. Fan, J. Ding, D. Zhang and Q. Guo, Soft Matter, 2011, 7, 11433.
26. T. Eisner, R. Alsop and G. Ettershank, Science, 1964, 146, 1058–1061.
27. R. Dudley, The Biomechanics of Insect Flight, Princeton University Press, Princeton, 2000.
28. N. Slegers, M. Heilman, J. Cranford, A. Lang, J. Yoder and M. L. Habegger, Bioinspiration Biomimetics, 2017, 12, 016013.
29. Y. Zheng, X. Gao and L. Jiang, Soft Matter, 2007, 3, 178.
30. R. H. Siddique, Y. J. Donie, G. Gomard, S. Yalamanchili, T. Merdzhanova, U. Lemmer and H. Holscher, Sci. Adv., 2017, 3, e1700232.
31. I. Kovalev, Bulletin Entomological Society of Canada, 2005, 37, 140–142.
32. I. Kovalev, J. Bionic Eng., 2008, 5, 224–230.
33. I. Kovalev, Wind Eng., 2010, 34, 351–360.
34. D. W. Bechert, M. Bruse, W. Hage, J. T. Van der Hoeven and G. Hoppe, J. Fluid Mech., 1997, 338, 59–87.
35. W. Barthlott, M. Mail and C. Neinhuis, Philos. Trans. R. Soc., A, 2016, 374, 20160191.
36. M. Raupp, What do butterflies do when it rains?, https://www.scientificamerican.com/article/what-do-butterflies-do-wh/, accessed 2020-04-05.
37. P. Köchling, Diploma thesis, Westfälische Wilhelms-Universität Münster, 2007.
38. K. Hurka, Bachelor thesis, Fachhochschule Münster, 2009.
39. F. Vorholt, Bachelor thesis, Fachhochschule Münster, 2009.

---