Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
An experimental and computational study of the effect of aqueous solution on the multiphoton ionisation photoelectron spectrum of phenol†
Alice
Henley‡
 ,
Jamie W.
Riley‡
,
Jamie W.
Riley‡
 ,
Bingxing
Wang§
,
Bingxing
Wang§
 and
Helen H.
Fielding
and
Helen H.
Fielding
 *
*
Department of Chemistry, University College London, 20 Gordon Street, London WC1H 0AJ, UK. E-mail: h.h.fielding@ucl.ac.uk
First published on 15th July 2019
Abstract
We revisit the photoelectron spectroscopy of aqueous phenol in an effort to improve our understanding of the impact of inhomogeneous broadening and inelastic scattering on solution-phase photoelectron spectra. Following resonance-enhanced multiphoton ionisation via the 11ππ* and 11πσ* states of phenol, we observe 11ππ*–D0/D1 ionisation and competing direct S0–D0/D1 ionisation. Following resonance-enhanced multiphoton ionisation via the 21ππ* state, we observe the signature of solvated electrons. By comparing the photoelectron spectra of aqueous phenol with those of gas-phase phenol, we find that inelastic scattering results in peak shifts with similar values to those that have been observed in photoelectron spectra of solvated electrons, highlighting the need for a robust way of deconvoluting the effect of inelastic scattering from liquid-phase photoelectron spectra. We also present a computational strategy for calculating vertical ionisation energies using a quantum-mechanics/effective fragmentation potential (QM/EFP) approach, in which we find that optimising the configurations obtained from molecular dynamics simulations and using the [phenol·(H2O)5]QM[(H2O)n≥250]EFP (B3LYP/aug-cc-pvdz) method gives good agreement with experiment.
1 Introduction
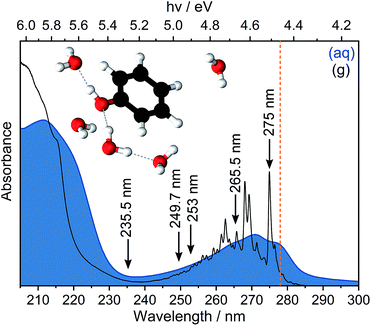
Ionisation is the most fundamental photophysical process accompanying the interaction of ionising radiation with biologically important molecules and plays a central role in radiation chemistry and biology. The formation of an electron and a radical is the first step in a chain of chemical reactions that results in DNA damage. The most direct way to probe ionisation experimentally is to use photoelectron spectroscopy (PES), which measures the electron kinetic energies (eKEs) of electrons emitted following ionisation. The eKE distribution encodes the role of each vibrational mode of the radical in its subsequent structural relaxation and, in the case of solution-phase photoelectron spectra, also contains information about solvent relaxation. However, the interpretation of solution-phase photoelectron spectra is complicated by the inhomogeneous environment of the solution causing spectral broadening and inelastic scattering of photoelectrons in the solution before emission causing the measured electron kinetic energies to be lower than their true values.1,2 Disentangling the various contributions to solution-phase photoelectron spectra requires gas-phase PES as an essential reference and synergistic contributions from experiment and theory. Here, we revisit the PES of aqueous phenol in an effort to improve our understanding of the impact of inhomogeneous broadening and inelastic scattering on the photoelectron spectra.Phenol is a ubiquitous molecular motif in many biologically relevant chromophores. It is the chromophore in the amino acid tyrosine, which plays an important role in photosynthesis,3 and it is a building block of the chromophore in green fluorescent protein, the most widely used fluorescent probe for in vivo monitoring of biological and biochemical processes.4,5 The UV absorption spectrum of phenol is dominated by two bands centered around 270 nm (4.6 eV) and 210 nm (5.9 eV), corresponding to transitions from the electronic ground state, S0, to the first two 1ππ* states, labelled 11ππ* and 21ππ* (Fig. 1). Between these two 1ππ* states lies a 1πσ* state, labelled 11πσ*. The 11πσ* state is composed of O-centered π 3s and πσ* configurations and is dissociative along the O–H stretch coordinate. The 11πσ* state forms conical intersections (CIs) with the 11ππ* and S0 states at modest O–H bond lengths and, therefore, plays an important role in the photostability of chromophores containing the phenol motif.6,7
There have been numerous experimental and computational studies of the photochemistry and photophysics of isolated phenol molecules in vacuo and in solution.6,8–34 Gas-phase studies have revealed that following photoexcitation above the 11ππ*/11πσ* CI, the dissociative 11πσ* potential energy surface is accessed directly and O–H bond fission occurs, forming phenoxyl radical and hydrogen atom products (PhO˙ + H) on a femtosecond timescale.20 Following photoexcitation just below the 11ππ*/11πσ* CI, the dissociative 11πσ* potential energy surface is accessed by tunnelling through the barrier under the CI, forming PhO˙ + H on a nanosecond timescale.14,22,23 In hexane, an aprotic solvent, the initial bond fission processes and timescales have been found to be very similar to those in the gas phase.35 However, in aqueous solution, new relaxation pathways are possible. Following photoexcitation of the 21ππ* state at 200 nm and the 11ππ* state below the 11ππ*/11πσ* CI, solvated electrons and PhO˙ radicals were observed to be formed on timescales of 200 fs and 2 ns, respectively, using transient absorption spectroscopy.28 In both cases, autoionisation was proposed as a mechanism for the formation of solvated electrons. A recent liquid-microjet PES study by our group found that following photoexcitation of the 11πσ* state at 235 nm, just above the 11ππ*/11πσ* CI, IC to the 11ππ* state occurred on a 150 fs timescale.31 It was also suggested that solvated electrons were formed on the same ultrafast timescale by a sequential mechanism, involving O–H bond fission to form PhO˙ + H followed by proton-coupled electron transfer (PCET).
Although the electronic relaxation dynamics of photoexcited neutral phenol molecules has been studied extensively, there has been less interest in the photoionisation of phenol. PES36–40 and multiphoton ionisation (MPI) mass-spectrometry41 measurements of gas-phase phenol have determined the first two adiabatic ionisation energies (AIEs) to be 8.508 eV (ref. 41) and 9.36 eV,36 for the ground and first electronically excited states of the radical ion, D0 and D1, respectively. A resonance-enhanced MPI (REMPI) PES study of gas-phase phenol revealed the vertical ionisation energy (VIE) from the 11ππ* state to D0 to be around 0.3 eV higher than the AIE.42 Recent quantum dynamics calculations have identified the key vibrational modes contributing to the subsequent electronic relaxation of the radical ion following photoionisation.33 In aqueous solution, an X-ray PES study of aqueous phenol using a liquid-microjet revealed the VIEs for D0 and D1 to be lowered to 7.8 ± 0.1 eV and 8.6 ± 0.1 eV, respectively.43 Two independent liquid-microjet MPI PES studies of phenol in aqueous solution gave VIEs of 7.6 ± 0.1 eV, 8.5 ± 0.1 eV (ref. 31) and 8.0 ± 0.1 eV, 8.5 ± 0.1 eV.44 Despite both studies yielding VIEs within experimental error of the X-ray PES data, the two experiments did not yield values that were in good agreement with each other. The photoelectron spectra recorded by us were analysed by fitting the data to a single photoionisation process from 11ππ*, to D0.31 The photoelectron spectra recorded by Roy et al. were analysed by fitting the data to two ionisation processes from 11ππ*, to D0 and D1, and by including a shift to account for inelastic scattering, estimated from photoelectron spectra of solvated electrons in aqueous solution.44 Calculations of phenol·(H2O)4 clusters, in which the VIEs were determined using the equation-of-motion coupled-cluster method with single and double excitations for ionisation potentials (EOM-IP-CCSD)45 method for phenol perturbed by the electrostatic field of a 35 Å spherical box of water molecules modelled using the effective fragment potential (EFP) method, have given VIEs to D0 and D1 of 7.9 eV and 8.6 eV, respectively,43 in agreement with the experimental measurements.
The different approaches to the analysis of liquid-microjet MPI photoelectron spectra31,44 motivated us to revisit the MPI PES of aqueous phenol. In this paper, we compare the results of new liquid-microjet MPI PES experiments with gas-phase MPI PES measurements31 and liquid-microjet X-ray PES measurements.43 We also compare photoionisation calculations of phenol in the gas phase with those in aqueous solution using density functional theory (DFT) and EOM-IP-CCSD methods for phenol·(H2O)5 clusters perturbed by the electrostatic field of water molecules modelled using the EFP method.
2 Methods
2.1 Experimental
Photoelectron spectra were recorded using our recirculating liquid-microjet magnetic-bottle time-of-flight (TOF) photoelectron spectrometer that has been described in detail elsewhere.46 Briefly, a 100 mM aqueous phenol solution, with 30 mM sodium fluoride added to minimise charging effects and increase the conductivity, was introduced through a 20 μm diameter quartz nozzle into the spectrometer. The liquid-microjet was intersected with femtosecond laser pulses approximately 1 mm below the nozzle, in the region of laminar flow. The femtosecond laser pulses were generated by frequency upconverting the output of an optical parametric amplifier pumped by an amplified Ti:sapphire femtosecond laser system operating at 1 kHz; the electric field vectors of the laser pulses were parallel to the TOF axis and the 1/e2 pulse duration of the 235.5 nm pulses was measured to be ∼150 fs. Photoelectrons were detected at the end of the TOF tube and the photoelectron current was recorded together with the arrival time relative to the trigger of the laser pulse. The photoelectron count-rate was kept at around 500 Hz to avoid space-charge effects and saturation of the detector. eKE spectra were determined by calibrating the TOF against the MPI photoelectron spectrum of NO47 and multiplying the photoelectron counts by the Jacobian mes2/(t − t0)3, where me is the mass of an electron, t is the TOF and s and t0 are calibration constants. Photoelectron spectra of Xe were recorded to determine the energy resolution and streaming potential, which were ΔE/E ∼ 1% and ϕstr = 0,† respectively.Compared with our previous work,31 we have employed a recirculating system instead of a liquid nitrogen cold-trap, which improves the quality of the photoelectron spectra at low eKE. We have also rewritten the data analysis software and corrected an error in the way the Jacobian was implemented, which results in higher photoelectron counts at low eKE (see ref. 46).
2.2 Computational
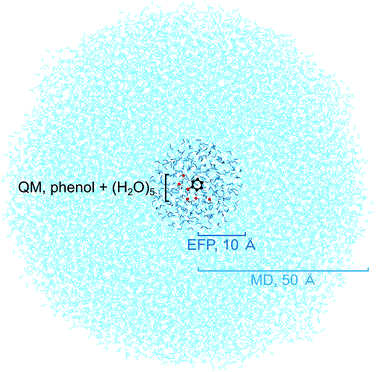
To benchmark the quantum mechanical (QM) computational methods used to calculate the VIEs and vertical excitation energies (VEEs) of aqueous phenol, calculations of isolated phenol molecules in the gas phase were performed at the same levels of theory. The structure of gas-phase phenol was optimised using the B3LYP48–51/6-311++G(3df,3pd)52–54 method and frequency-calculations were performed to ensure that a minimum on the potential energy surface was reached. The VIE was determined using two methods: B3LYP/aug-cc-pvdz to determine the energy difference between neutral phenol and its corresponding cation, at the minimum energy geometry of neutral phenol, and the EOM-IP-CCSD/6-31+G* method. VEEs were calculated using the equation-of-motion coupled-cluster method with single and double excitations for excitation energies (EOM-EE-CCSD)45 and the algebraic diagrammatic construction method to second order (ADC(2)),55,56 both with the 6-31+G* basis set. All gas-phase calculations were performed using the QChem software package57 apart from the optimisation and frequency calculations which were performed using Gaussian 09.58Several steps were involved in the calculation of VIEs and VEEs of phenol in aqueous solution. First, a classical molecular dynamics (MD) simulation (NAMD,59 developed by the Theoretical and Computational Biophysics Group in the Beckman Institute for Advanced Science and Technology at the University of Illinois at Urbana-Champaign) was used to sample an ensemble of conformations of phenol in bulk water (Fig. 2). In the MD simulation, phenol was soaked in a sphere of water with radius 50 Å (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 877 water molecules) and the CHARMM force field was used to model the system.60–62 The system was minimised for 2 ps and then allowed to equilibrate at 300 K for a further 20 ps before running a trajectory for 150 ps. Frames from the trajectory were saved every 500 fs (300 frames in total) for subsequent quantum mechanical/EFP (QM/EFP) calculations. Hybrid QM/EFP methods provide a rigorous yet computationally affordable way to include solute–solvent interactions.63 In the EFP region, solvent molecules are modelled as discrete entities using non-empirical model potentials that perturb the QM region by their electrostatic potentials. The EFP also includes polarisation, dispersion and exchange interaction energies at the QM/EFP interface and between the individual EFP fragments.
877 water molecules) and the CHARMM force field was used to model the system.60–62 The system was minimised for 2 ps and then allowed to equilibrate at 300 K for a further 20 ps before running a trajectory for 150 ps. Frames from the trajectory were saved every 500 fs (300 frames in total) for subsequent quantum mechanical/EFP (QM/EFP) calculations. Hybrid QM/EFP methods provide a rigorous yet computationally affordable way to include solute–solvent interactions.63 In the EFP region, solvent molecules are modelled as discrete entities using non-empirical model potentials that perturb the QM region by their electrostatic potentials. The EFP also includes polarisation, dispersion and exchange interaction energies at the QM/EFP interface and between the individual EFP fragments.
For the QM/EFP calculations, the QM region was selected to be phenol plus the five water molecules closest to any atom within phenol. Although fewer water molecules have been employed for other calculations of phenol in aqueous solution,34,43 we used five because we found this was enough to ensure that all the water molecules that are hydrogen-bonded to phenol (donor–acceptor distance < 3 Å, donor–H–acceptor bond angle 180 ± 20°) were included in the QM region. The EFP region was selected to be all other water molecules within 10 Å of any atom in the phenol molecule (250–300 water molecules). A radius of 10 Å was selected because it has been shown to work well for similar calculations for the green fluorescent protein chromophore in bulk water.64 The water molecules outside the EFP region were then discarded. The EFP parameters used to represent water were the standard parameters in the Q-Chem65 or Firefly66 libraries.
The QM and EFP selections were made independently for each of the 300 frames saved from the MD simulation and therefore each frame has a different phenol conformation as well as different configurations of water molecules, in both the QM and EFP regions. The energies of each of the 300 configurations were calculated using QM/EFP at the B3LYP/aug-cc-pvdz level of theory for both S0 (Fig. S7†) and D0 using the QChem software package. VIEs were then calculated as the difference between these S0 and D0 energies. Higher level calculations were then performed using a selection of the 300 frames. To make these calculations computationally affordable, we selected a relatively small set of frames and a smaller basis set. The ten configurations with S0 energies closest to the mean S0 energy at the QM/EFP (B3LYP/aug-cc-pvdz) level were selected (Fig. S7†) for QM/EFP calculations using EOM-IP-CCSD, EOM-EE-CCSD and ADC(2), with the 6-31+G* basis set. These calculations were performed using the QChem software package.
To investigate whether optimisation with QM/EFP improved the calculations, additional QM/EFP calculations of VIEs and VEEs, using B3LYP/aug-cc-pvdz, EOM-IP-CCSD/6-31+G*, EOM-EE-CCSD/6-31+G* and ADC(2)/6-31+G*, were performed for the same ten frames following optimisation at the PBE0 (ref. 67–69)/aug-cc-pvdz level of theory. The geometry optimisation was carried out using the Firefly quantum chemistry package,70 which is partially based on the GAMESS (US) source code;71 it adjusts the positions of all atoms within the QM region at the PBE0/aug-cc-pvdz level and the 250–300 explicit water molecules modelled by EFP are also reorientated (rotational and translational degrees of freedom).
3 Results and discussion
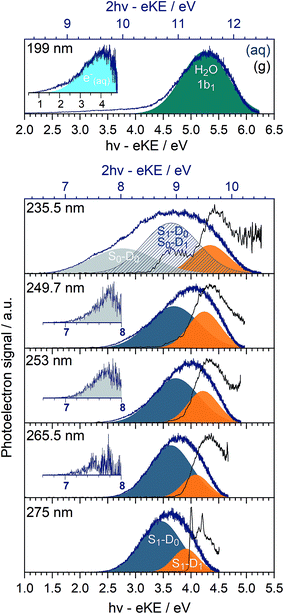
In Fig. 3, we present 1 + 1 MPI photoelectron spectra of phenol in aqueous solution as a function of one-photon electron binding energy, eBE = hν − eKE where hν is photon energy, together with the equivalent gas-phase photoelectron spectra.31 The photoelectron spectra of phenol in aqueous solution are shifted to lower eBEs by around 0.8 eV compared to the gas phase and are similar to those reported in our earlier work;31 however, as a result of the improved quality of data obtained using a recirculator compared to a liquid nitrogen cold-trap (Section 2.1) we are able to identify additional features. The 275–249.7 nm photoelectron spectra recorded following resonance-enhanced MPI via the 11ππ* state are now best fit with two Gaussians, corresponding to 11ππ*–D0/D1 ionisation processes. At 275 nm, the area of the peak corresponding to ionisation to D0 is around three times larger than that of the peak corresponding to ionisation to D1, in agreement with our earlier calculations of photoionisation cross-sections from the 11ππ* state.31 This contrasts with the 267 nm MPI photoelectron spectrum reported by Roy et al. in which the area of the peak corresponding to ionisation to D0 was substantially less than the area of the peak corresponding to ionisation to D1.44 The ratios of the areas of the two peaks corresponding to ionisation from 11ππ* to D0 and D1 are observed to decrease with increasing photon energy (Fig. 3), unlike the calculations;31 this could be attributed to increased solute and solvent reorganisation during ionisation to D1 compared to ionisation to D0. The residuals of the fits at the low eBE edges of the 265.5–249.7 nm spectra are plotted as insets in Fig. 3 and can be attributed to non-resonant S0–D0 MPI that competes with resonance-enhanced MPI. The contribution from non-resonant MPI increases with decreasing S0–11ππ* absorption cross-section, as we would expect. This feature was not observed in either of the previous MPI studies of aqueous phenol but is observed in the MPI gas-phase PES.31,44The 235.5 nm (5.26 eV) MPI photoelectron spectrum is very broad and can be fit with either three or four Gaussians; however, we believe that fitting to three Gaussians is more appropriate (see below). There are four processes contributing to the photoelectron spectrum fit to three Gaussians: resonant 11ππ*–D0/D1 MPI and non-resonant S0–D0/D1 MPI. At this photon energy, the photoelectron spectra corresponding to 11ππ*–D0 and S0–D1 lie on top of one another and it is not possible to distinguish between them by fitting an additional Gaussian. The peak centered at 8.0 ± 0.1 eV two-photon eBE corresponds to S0–D0 ionisation and is close to the X-ray PES measurement.43 At 235.5 nm, the 11ππ* state is not populated directly (Fig. 1) but our observation of 11ππ*–D0/D1 ionisation is consistent with photoexcitation of the 11πσ* state followed by rapid relaxation to the 11ππ*/11πσ* CI, after which some population will undergo IC to the 11ππ* state before photoionisation, on the timescale of the measurement (∼150 fs).
In our earlier work, the 235.5 nm MPI photoelectron spectrum was fit to four Gaussians. The additional Gaussian was attributed to the photoelectron spectrum of the solvated electron that we proposed was formed following relaxation through the 11ππ*/11πσ* CI after which, in addition to IC to the 11ππ* state, O–H dissociation could occur to form PhO˙ + H, followed by proton-coupled electron transfer, H(aq) + H2O → H2O+(aq) + e−(aq). It is possible that there is a contribution from solvated electrons to the peak we have assigned as S1–D1.
The 199 nm (6.23 eV) MPI photoelectron spectrum, which has not been reported before, is dominated by a peak centred around 5.25 ± 0.1 eV eBE with a long tail at low eBE. The peak centred around 5.25 ± 0.1 eV eBE can be fit with a single Gaussian and corresponds to 11.5 ± 0.1 eV two-photon eBE, which we attribute to ionisation from the 1b1 molecular orbital of water.72 The residual of this fit is plotted as an inset and it can be fit with a Gaussian centred around 4.0 ± 0.1 eV (one-photon eBE) which we attribute to the photoelectron spectrum of the solvated electron. This value of eBE lies between the values of 4.5 eV and 3.7 eV obtained from careful measurements of the photoelectron spectra of solvated electrons at 5.8 eV and 13.6 eV, respectively,2 and its observation is consistent with transient absorption measurements of solvated electrons being formed on a 200 fs timescale following 200 nm excitation.28 The residual on the low eBE edge of the solvated electron photoelectron spectrum can be attributed to S0–D0 ionisation (Fig. S4†).
Now we consider the effect of inelastic scattering on our photoelectron spectra. Recent careful measurements of UV photoelectron spectra of solvated electrons revealed that the measured eBE gradually increased with photon energy, indicating that the photoelectron energy diminished as a result of electron-solvent molecule inelastic scattering before emission from the surface of the liquid.1 Subsequent scattering simulations quantified the role of inelastic scattering on the photoelectron spectra.2 In order to investigate the impact of inelastic scattering on the peak positions and widths of our liquid-microjet photoelectron spectra, we plotted the eKEs of the maxima and full-width half-maxima (FWHM) of the Gaussians fitted to the 11ππ*–D0/D1 processes, as a function of photon energy, alongside those for the 11ππ*–D0 process for gas-phase phenol (Fig. 4). The peak widths do not seem to vary substantially with photon energy. The overall shapes of the three sets of data are very similar, with the peak eKEs remaining the same for both 275 nm and 265.5 nm spectra but then increasing approximately linearly. The gradient of the line fitted to the linearly increasing component of the plot for the gas-phase data is 1.02 ± 0.02, indicating that the propensity for conserving vibrational energy during the 11ππ*–D0 photoionisation process holds extremely well over this energy range. In contrast, the gradients of the lines fit to the peak positions corresponding to 11ππ*–D0/D1 processes in aqueous phenol are less than unity. Moreover, these lines are shifted from the positions estimated using S0–D0/D1 VIEs obtained from X-ray PES43 and the S0–11ππ* AEE determined from the UV-vis absorption spectrum (4.46 eV, Fig. 1), assuming that vibrational energy is conserved during photoionisation (dashed lines in Fig. 4). We used VIEs from X-ray PES measurements rather than our own measurement at 235.5 nm because we have not deconvoluted inelastic scattering from our 235.5 nm spectrum. Although it is possible that the propensity for conserving vibrational energy does not hold for aqueous phenol, we believe this is unlikely because it holds so well for gas-phase phenol, the UV-vis spectra of gas-phase and aqueous phenol are remarkably similar (Fig. 1) and the overall trends of the lines plotted in Fig. 4 are similar for aqueous phenol and gas-phase phenol. Thus, we believe the differences between the estimated peak positions and the actual peak positions can be attributed to inelastic electron scattering and note that our peak shifts are similar to those reported in ref. 2 over the same energy range.
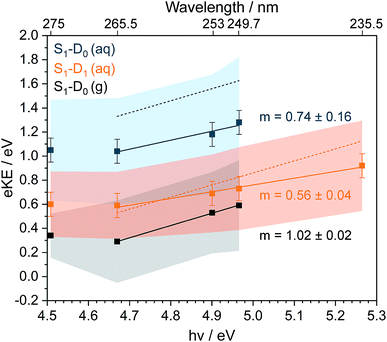 | ||
| Fig. 4 Plots of fitted Gaussian peak maxima (data points) and full-width half maxima (shaded areas) corresponding to S1(11ππ*)–D0 in the gas phase (g) and S1(11ππ*)–D0/D1 in aqueous solution (aq), as a function of photon energy (bottom axis) and wavelength (top axis). Solid straight lines are fits to the higher photon energy data points, with gradients m indicated. Dashed lines are peak maxima estimated using S0–D0/D1 VIEs obtained from X-ray PES43 and the S0–S1(11ππ*) AEE determined from the UV-vis absorption spectrum (Fig. 1, orange dashed line), assuming that vibrational energy is conserved during photoionisation. | ||
It is this consideration of inelastic scattering that suggests the 235.5 nm photoelectron spectrum should be fit to three Gaussians rather than four. In the fit to four Gaussians (Fig. S5†), the S1–D0 peak is shifted to lower eBE than the X-ray data whereas in the fit to three Gaussians (Fig. 3), it is shifted to higher eBE than the X-ray data. Although both fitted eBEs can be considered to be equivalent to the X-ray data within the experimental errors of both measurements, inelastic scattering would shift the measured peak to higher eBE, which suggests that the fit to three Gaussians is more appropriate. The wavelength dependence of inelastic scattering poses a particular problem for photoelectron spectra that span a wide range of eKEs, such as the 235.5 nm photoelectron spectrum. Although it is reasonable to fit Gaussians to a true photoelectron spectrum, Gaussians will be distorted by a wavelength-dependent inelastic scattering shift. Therefore, it is desirable to deconvolute inelastic scattering from a measured photoelectron spectrum to obtain a true photoelectron spectrum before fitting Gaussians. Unfortunately, this is not possible without detailed modelling of inelastic scattering across the relevant range of eKEs.
In Table 1, we present our measured S0–D0/D1 peak maxima together with our calculated VIEs and experimental and calculated values from the literature. For gas-phase phenol, our B3LYP/aug-cc-pvdz and EOM-IP-CCSD/6-31+G* methods both give VIEs that are within 0.2 eV of the experimental AIEs36,41 and are as good as other calculated VIEs reported in the literature.31,33,43 This gives us confidence that these are appropriate methods to investigate for the solution phase calculations.
| D0 | D1 | ||
|---|---|---|---|
| a Average of 300 unoptimised configurations from the MD sampling trajectory. b Average of 10 configurations with S0 energy close to the average S0 energy (see text). Values in parentheses relate to configurations that have not been optimised using QM/EFP methods. | |||
| Gas-phase | |||
| B3LYP/aug-cc-pvdz | 8.49 | ||
| EOM-IP-CCSD/6-31+G* | 8.34 | 9.22 | |
| Experimental AIE (ref. 41) | 8.51 | ||
| Experimental AIE (ref. 36) | 8.52 | 9.36 | |
| EOM-IP-CCSD/aug-cc-pvdz (ref. 31) | 8.46 | 9.29 | |
| EOM-IP-CCSD/cc-pvtz (ref. 43) | 8.55 | ||
| CAS(7,8)/6-31+G* (ref. 33) | 7.99 | 8.67 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Aqueous solution | |||
| [Phenol·(H2O)5]QM[(H2O)n≥250]EFP | B3LYP/aug-cc-pvdza | 8.17 | |
| [Phenol·(H2O)5]QM[(H2O)n≥250]EFP | B3LYP/aug-cc-pvdzb | 7.93 (8.24) | |
| [Phenol·(H2O)5]QM[(H2O)n≥250]EFP | B3LYP/6-31+G*b | 7.94 (8.25) | |
| [Phenol·(H2O)5]QM[(H2O)n≥250]EFP | EOM-IP-CCSD/6-31+G*b | 8.29 (8.64) | 9.19 (9.23) |
| Fitted peak maxima (Fig. 3) | 8.0 ± 0.1 | 8.9 ± 0.1 | |
| X-ray PES (ref. 43) | 7.8 ± 0.1 | 8.6 ± 0.1 | |
| [phenol]QM[(H2O)bulk]EFP (ref. 43) | EOM-IP-CCSD/6-31+G* | 7.9 | 8.6 |
For aqueous phenol, Ghosh et al. employed a [phenol]QM[(H2O)bulk]EFP (EOM-IP-CCSD/6-31+G*) method to calculate VIEs which were in very good agreement with X-ray PES measurements.43 However, we chose to include water molecules that were hydrogen-bonded to phenol in the QM region as well. For our aqueous phenol calculations, the VIE averaged over the 300 configurations saved from the MD calculations, using the [phenol·(H2O)5]QM[(H2O)n≥250]EFP (B3LYP/aug-cc-pvdz) method, is almost 0.4 eV higher than the value obtained from X-ray PES measurements.43 The average VIE for the ten probable configurations (Section 2.2) calculated using the same method is slightly higher. Interestingly, using the smaller 6-31+G* basis set does not make much difference. The average VIE calculated using the EOM-IP-CCSD/6-31+G* method is around 0.3 eV higher than that calculated using the B3LYP/6-31+G*.
We found that optimisation of the ten probable [phenol·(H2O)5]QM[(H2O)n≥250]EFP configurations lowered the calculated VIE values by around 0.1–0.3 eV. The average VIE calculated for the ten probable configurations following optimisation and using the B3LYP/aug-cc-pvdz method was 7.93 eV, which is in good agreement with the X-ray PES measurement. Again, using the smaller 6-31+G* basis set made little difference. The average VIEs calculated for the optimised ten probable configurations using the EOM-IP-CCSD/6-31+G* method are around 0.4 eV higher than the experimental values, although the difference between the S0–D0 and S0–D1 values (0.9 eV) is reasonably close to the difference measured using X-ray PES. These calculations suggest that optimisation of configurations obtained from MD simulations could be important for determining accurate VIEs and that the simple DFT approach seems to work particularly well. It will be interesting to test this procedure for calculating VIEs on other molecules in aqueous solution to see if it is general rather than specific to phenol. Curiously, our EOM-IP-CCSD/EFP method, which includes water molecules that are hydrogen-bonded to phenol in the QM region, does not agree as well with the experimental measurements as the EOM-IP-CCSD/EFP method employed by Ghosh et al., which only included phenol in the QM region.43 However, it is worth noting that Ghosh et al. applied a correction to account for the effect of increasing basis set from 6-31+G(d) to cc-pVTZ.
Fig. 5 shows a simulated S0–D0 photoelectron spectrum obtained by plotting the distribution of VIEs calculated using the [phenol·(H2O)5]QM[(H2O)n≥250]EFP (B3LYP/aug-cc-pvdz) method as a histogram with bin size 0.12 eV. The full-width half-maximum (FWHM) of the Gaussian fitted to the histogram is 0.86 eV. The FWHM of the S0–D0 photoelectron spectrum obtained from the fit to the 235.5 nm spectrum (Fig. 3) is significantly larger (1.34 eV, similar to the X-ray PES FWHM43). The difference could be attributed to solute and solvent reorganisation, which is not accounted for in the simulation. The eKE dependence of inelastic scattering can also affect the widths of measured photoelectron spectra but to account for this properly requires detailed modelling of the electron scattering process.2
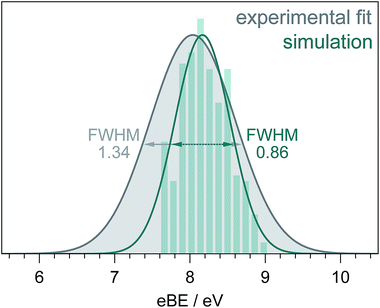 | ||
| Fig. 5 S0–D0 photoelectron spectra obtained from the fit to the 235.5 nm experimental data (Fig. 3) and simulation (see text). The full-width-half-maxima are shown for both Gaussian fits. | ||
4 Conclusion
We have reported new MPI PES measurements of phenol in aqueous solution recorded using our recirculating liquid-microjet apparatus. Following resonant MPI via the 11ππ* state, the improved quality of these photoelectron spectra of phenol compared to those reported previously has allowed us to identify 11ππ*–D0 and 11ππ*–D1 ionisation processes and competing direct S0–D0 ionisation. Following resonant MPI via the 21ππ* state, we have observed the signature of solvated electrons. Following resonant MPI via the 11πσ* state, we observed 11ππ*–D0/D1 and S0–D0/D1 processes and, although we no longer find evidence for the formation of solvated electrons, we cannot rule out the possibility that solvated electrons are formed. Time-resolved PES measurements will be able to identify whether or not solvated electrons are formed following photoexcitation of the 11πσ* state and such measurements are planned in our laboratory. The VIEs of photoexcited states of biologically relevant molecules in aqueous solution underpin ionisation and charge transfer processes and are thus important in radiation chemistry and biology. Solvated electrons, or more precisely pre-solvated electrons, are also known to play a role in inducing damage to DNA in aqueous solution.By comparing the MPI photoelectron spectra of aqueous phenol and gas-phase phenol, we found that inelastic scattering resulted in peak shifts similar to those reported for photoelectron spectra of the solvated electron.1,2 The wavelength dependence of inelastic scattering poses a particular problem for interpreting broad photoelectron spectra and highlights a need for a robust way of deconvoluting the effect of inelastic scattering from liquid-phase photoelectron spectra. Quantifying the inelastic scattering of low energy electrons in aqueous solution is also crucially important for improving our understanding of the role of (pre-)solvated electrons in inducing damage in DNA in aqueous solution.
We have developed a QM/EFP protocol for calculating the VIEs of aqueous phenol. We found that DFT with a reasonably large basis set performed well. We also found that optimising the configurations obtained from MD simulations improved the value for the VIE. It will be interesting to investigate whether optimising greater numbers of configurations improves the agreement with experiment and to test the protocol on other molecules. The FWHM of our simulated S0–D0 photoelectron spectrum was less than that obtained from our fit to experimental data, which we attribute to solute and solvent reorganisation. Calculating solute and solvent reorganisation energies during ionisation is challenging, but we believe that high quality liquid-microjet photoelectron spectra together with analogous measurements in the gas-phase provide ideal benchmarks for theory.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the EPSRC (EP/L005646/1), the Diamond Light Source (STU0157) and the Royal Society and Leverhulme Trust (SRF/R1/180079). We are grateful to Dr Anastasia Bochenkova (Moscow State University) for advice on the computational chemistry methods, to Professors Graham Worth (UCL) and Michael Robb (Imperial) for useful discussions and Dr Frank Otto for computational support.Notes and references
- Y. I. Yamamoto, S. Karashima, S. Adachi and T. Suzuki, J. Phys. Chem. A, 2016, 120, 1153–1159 CrossRef CAS PubMed.
- D. Luckhaus, Y.-i. Yamamoto, T. Suzuki and R. Signorell, Sci. Adv., 2017, 3, e1603224 CrossRef PubMed.
- B. A. Barry, Photochem. Photobiol., 1993, 57, 179–188 CrossRef CAS.
- A. Acharya, A. M. Bogdanov, B. L. Grigorenko, K. B. Bravaya, A. V. Nemukhin, K. A. Lukyanov and A. I. Krylov, Chem. Rev., 2017, 117, 758–795 CrossRef CAS.
- A. Henley and H. Fielding, Int. Rev. Phys. Chem., 2019, 38, 1–34 Search PubMed.
- A. L. Sobolewski, W. Domcke, C. Dedonder-Lardeux and C. Jouvet, Phys. Chem. Chem. Phys., 2002, 4, 1093–1100 RSC.
- M. N. R. Ashfold, G. A. King, D. Murdock, M. G. D. Nix, T. A. A. Oliver and A. G. Sage, Phys. Chem. Chem. Phys., 2010, 12, 1218–1238 RSC.
- A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2001, 105, 9275–9283 CrossRef CAS.
- W. Domcke and A. L. Sobolewski, Science, 2003, 302, 1693–1694 CrossRef CAS PubMed.
- K. Daigoku, S.-I. Ishiuchi, M. Sakai, M. Fujii and K. Hashimoto, J. Chem. Phys., 2003, 119, 5149–5158 CrossRef CAS.
- C. M. Tseng, Y. T. Lee and C. K. Ni, J. Chem. Phys., 2004, 121, 2459–2461 CrossRef CAS PubMed.
- Z. Lan, W. Domcke, V. Vallet, A. L. Sobolewski and S. Mahapatra, J. Chem. Phys., 2005, 122, 224315 CrossRef PubMed.
- M. N. R. Ashfold, B. Cronin, A. L. Devine, R. N. Dixon and M. G. D. Nix, Science, 2006, 312, 1637–1640 CrossRef CAS PubMed.
- M. G. Nix, A. L. Devine, B. Cronin, R. N. Dixon and M. N. R. Ashfold, J. Chem. Phys., 2006, 125, 133318 CrossRef.
- C.-M. Tseng, Y. T. Lee, M.-F. Lin, C.-K. Ni, S.-Y. Liu, Y.-P. Lee, Z. F. Xu and M. C. Lin, J. Phys. Chem. A, 2007, 111, 9463–9470 CrossRef CAS.
- M. N. R. Ashfold, A. L. Devine, R. N. Dixon, G. A. King, M. G. D. Nix and T. A. A. Oliver, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12701–12706 CrossRef CAS.
- O. P. Vieuxmaire, Z. Lan, A. L. Sobolewski and W. Domcke, J. Chem. Phys., 2008, 129, 224307 CrossRef PubMed.
- G. A. King, T. A. A. Oliver, M. G. D. Nix and M. N. R. Ashfold, J. Phys. Chem. A, 2009, 113, 7984–7993 CrossRef CAS PubMed.
- A. Iqbal, L. J. Pegg and V. G. Stavros, J. Phys. Chem. A, 2008, 112, 9531–9534 CrossRef CAS PubMed.
- A. Iqbal, M. S. Y. Cheung, M. G. D. Nix and V. G. Stavros, J. Phys. Chem. A, 2009, 113, 8157–8163 CrossRef CAS PubMed.
- R. N. Dixon, T. A. A. Oliver and M. N. R. Ashfold, J. Chem. Phys., 2011, 134, 194303 CrossRef.
- G. M. Roberts, A. S. Chatterley, J. D. Young and V. G. Stavros, J. Phys. Chem. Lett., 2012, 3, 348–352 CrossRef CAS PubMed.
- R. A. Livingstone, J. O. F. Thompson, M. Iljina, R. J. Donaldson, B. J. Sussman, M. J. Paterson and D. Townsend, J. Chem. Phys., 2012, 137, 184304 CrossRef PubMed.
- S. G. Ramesh and W. Domcke, Faraday Discuss., 2013, 163, 73–94 RSC.
- X. Xu, K. R. Yang and D. G. Truhlar, J. Chem. Theory Comput., 2013, 9, 3612–3625 CrossRef CAS.
- X. Xu, J. Zheng, K. R. Yang and D. G. Truhlar, J. Am. Chem. Soc., 2014, 136, 16378–16386 CrossRef CAS.
- K. R. Yang, X. Xu, J. Zheng and D. G. Truhlar, Chem. Sci., 2014, 5, 4661–4680 RSC.
- T. A. A. Oliver, Y. Zhang, A. Roy, M. N. R. Ashfold and S. E. Bradforth, J. Phys. Chem. Lett., 2015, 6, 4159–4164 CrossRef CAS.
- C. Xie, J. Ma, X. Zhu, D. R. Yarkony, D. Xie and H. Guo, J. Am. Chem. Soc., 2016, 138, 7828–7831 CrossRef CAS PubMed.
- W. Xie and W. Domcke, J. Chem. Phys., 2017, 147, 184114 CrossRef.
- J. W. Riley, B. Wang, J. L. Woodhouse, M. Assmann, G. A. Worth and H. H. Fielding, J. Phys. Chem. Lett., 2018, 9, 678–682 CrossRef CAS.
- G. Kumar, A. Roy, R. S. McMullen, S. Kutagulla and S. E. Bradforth, Faraday Discuss., 2018, 212, 359–381 RSC.
- M. P. Taylor and G. A. Worth, Chem. Phys., 2018, 515, 719–727 CrossRef CAS.
- I. Sandler, J. J. Nogueira and L. González, Phys. Chem. Chem. Phys., 2019, 21, 14261–14269 RSC.
- S. J. Harris, D. Murdock, Y. Zhang, T. A. A. Oliver, M. P. Grubb, A. J. Orr-Ewing, G. M. Greetham, I. P. Clark, M. Towrie, S. E. Bradforth and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2013, 15, 6567–6582 RSC.
- M. J. S. Dewar and S. D. Worley, J. Chem. Phys., 1969, 50, 654 CrossRef CAS.
- T. P. Debies and J. W. Rabalais, J. Chem. Soc., Faraday Trans., 1972, 1, 355–370 Search PubMed.
- J. P. Maier and D. W. Turner, J. Chem. Soc., Faraday Trans., 1973, 2, 521–531 RSC.
- T. Kobayashi and S. Nagakura, Bull. Chem. Soc. Jpn., 1974, 47, 2563–2572 CrossRef CAS.
- M. H. Palmer, W. Moyes, M. Speirs and J. N. A. Ridyard, J. Mol. Struct., 1979, 52, 293–307 CrossRef CAS.
- R. J. Lipert and S. D. Colson, J. Chem. Phys., 1990, 92, 3240–3241 CrossRef CAS.
- S. L. Anderson, L. Goodman, K. Krogh-Jespersen, A. G. Ozkabak, R. N. Zare and C.-f. Zheng, J. Chem. Phys., 1985, 82, 5329–5339 CrossRef CAS.
- D. Ghosh, A. Roy, R. Seidel, B. Winter, S. Bradforth and A. I. Krylov, J. Phys. Chem. B, 2012, 116, 7269–7280 CrossRef CAS.
- A. Roy, R. Seidel, G. Kumar and S. E. Bradforth, J. Phys. Chem. B, 2018, 122, 3723–3733 CrossRef CAS.
- A. I. Krylov, Annu. Rev. Phys. Chem., 2008, 59, 433–462 CrossRef CAS.
- J. W. Riley, B. Wang, M. A. Parkes and H. H. Fielding, Rev. Sci. Instrum., 2019, 90, 083104 CrossRef.
- G. K. Jarvis, M. Evans, C. Y. Ng and K. Mitsuke, J. Chem. Phys., 1999, 111, 3058 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 2395–2416 CrossRef CAS.
- A. B. Trofimov and J. Schirmer, J. Phys. B: At., Mol. Opt. Phys., 1995, 28, 2299–2324 CrossRef CAS.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. Hanson-Heine, P. H. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O’Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. CrossV. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2013 Search PubMed.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kalé and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS.
- R. B. Best, X. Zhu, J. Shim, P. E. M. Lopes, J. Mittal, M. Feig and A. D. Mackerell, J. Chem. Theory Comput., 2012, 3257–3273 CrossRef CAS.
- A. D. Mackerell, M. Feig and C. L. Brooks, J. Am. Chem. Soc., 2004, 126, 698–699 CrossRef CAS.
- A. D. Mackerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-Mccarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 3586–3616 CrossRef CAS PubMed.
- M. S. Gordon, D. G. Fedorov, S. R. Pruitt and L. V. Slipchenko, Chem. Rev., 2012, 112, 632–672 CrossRef CAS PubMed.
- S. Bose, S. Chakrabarty and D. Ghosh, J. Phys. Chem. B, 2016, 120, 4410–4420 CrossRef CAS PubMed.
- D. Ghosh, D. Kosenkov, V. Vanovschi, J. Flick, I. Kaliman, Y. Shao, A. T. Gilbert, A. I. Krylov and L. V. Slipchenko, J. Comput. Chem., 2013, 34, 1060–1070 CrossRef CAS PubMed.
- P. N. Day, J. H. Jensen, M. S. Gordon, S. P. Webb, W. J. Stevens, M. Krauss, D. Garmer, H. Basch and D. Cohen, J. Chem. Phys., 1996, 105, 1968–1986 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- A. A. Granovsky, Firefly version 8.2.0, http://classic.chem.msu.su/gran/firefly/index.html Search PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery Jr, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- B. Winter and M. Faubel, Chem. Rev., 2006, 106, 1176–1211 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Streaming potential measurement; photoelectron spectra plotted as a function of eKE; details of fitting procedures; convergence of VIE; tables of calculated and experimental VIEs and VEEs; selection of probable configurations; consistencies between software packages; molecular orbitals; coordinates of QM region. See DOI: 10.1039/c9fd00079h |
| ‡ These authors contributed equally to this work. |
| § Present address: College of Chemistry and Chemical Engineering, Henan Institute of Science and Technology, Eastern Hualan Avenue, Xinxiang, 453003, China. |
| This journal is © The Royal Society of Chemistry 2020 |