Open Access Article
Open Access ArticleLimits of exciton delocalization in molecular aggregates
Gregory D.
Scholes

Department of Chemistry, Princeton University, Princeton, New Jersey 08544, USA. E-mail: gscholes@princeton.edu
First published on 12th August 2019
Abstract
Exciton states of molecular aggregates, with a particular focus on delocalization length, are discussed. Despite the huge number of studies of molecular excitons, it is argued that there remain interesting open questions. It is hypothesized that limits for equilibrium delocalization length are generally in the range of tens of molecules, even at very low temperatures. Effects that limit delocalization include: phase disorder from wave-zone electronic coupling, polarization fluctuations, and the extreme sensitivity of perfect delocalization to disorder as the size of the molecular aggregate increases. To gain physical insight, the inverse participation ratio is compared to the order parameter for a classical system of coupled, and hence entrained, oscillators—the Kuramoto model. The main result of the paper is that the inverse participation ratio obtained from the quantum mechanical exciton model and the Kuramoto order parameter obtained from coupled classical oscillators estimate the same coherence length. Conclusions suggest discussion topics that touch on limits of delocalization, quantum-to-classical transitions in molecular exciton systems, and whether excitons are good prospects for exploring and exploiting quantum information resources from coherence.
Introduction
Molecules can be assembled so that, despite weak interactions among them in the ground electronic state, photoexcitation yields states remarkably different from those of the molecules in isolation. These ‘collective’, delocalized electronic excited states arise from coherent superpositions of excitations of molecules in the assembly—molecular exciton states. Despite the importance of molecular excitons, the many detailed investigations reported to date, and thorough reviews,1–8 there remain interesting questions to explore in this field.In this report I will discuss two questions: (a) Is there a limit to how large a molecular exciton state can be? and (b) Are excitons good prospects for exploring and exploiting quantum information resources from coherence?
When electronic coupling is large compared to absorption line widths, coherence (delocalization) causes splitting of bands in absorption spectra (Fig. 1). Equilibrium delocalization lengths can often be estimated, even when splitting of absorption bands is obscured, from superradiant enhancement of fluorescence radiative rates9,10 (Fig. 1). Superradiance is the collective fluorescence emission from two or more interacting chromophores, which leads to shorter radiative rates. Superradiant enhancement of fluorescence reveals the robustness of exciton delocalization.10 The exciton coherence (or delocalization) length implied by splitting of absorption bands is often quite different from that inferred by measurements of superradiance because excitons can localize or partially localize after photoexcitation owing to the interplay of averaging over disorder, decoherence, and population relaxation and thermalization.11–13
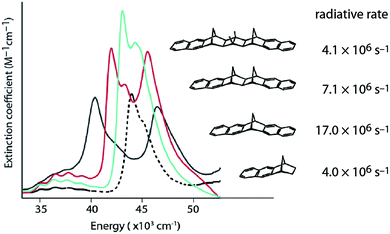 | ||
| Fig. 1 Coherences revealed by experiment. Absorption spectra of rigidly-linked dinaphthyl molecules DN-2 (black line), DN-4 (red line) and DN-6 (aqua line), where n in DN-n indicates the number of bonds spanning the norbornane bridge, compared to the model chromophore N-2 (black dotted line). Radiative decay rates measured for this series of rigidly-bridged dinaphthyl molecules are indicated.9 | ||
Spano and co-workers have shown that for J-aggregates and conjugated polymers the mean delocalization length of excitons can be quantified by the ratio of the electronic photoluminescence band intensity (I0–0) and that of the first vibronic band (I0–1).14–16 Specifically, I0–0/I0–1 = κNcoh/S, where Ncoh is the number of chromophores (repeat units) over which the exciton is coherently delocalized, S is the vibronic Huang–Rhys factor and κ is a dimensionless parameter which is exactly unity in the Frenkel exciton limit for J-aggregates and deviates from unity when charge-transfer configurations between subunits couple significantly into the exciton wavefunction. In the limit of low temperature and no disorder, Ncoh reduces to N, the total number of chromophores (repeat units) comprising the J-aggregate (polymer). In one interesting application, analysis of the photoluminescence ratio analysis revealed an extraordinary coherent delocalization of the exciton along disorder-free polydiacetylene chains,15,17 estimated to be ∼30–50 nm at 15 K. Other work has shown how and why exciton delocalization depends on conjugated polymer molecular weight.18,19
The elegant relationship between the exciton coherence size and I0–0/I0–1 can also be employed to track temporal changes in the coherence length.20 Kim and co-workers have used time-resolved fluorescence spectroscopy to follow the I0–0/I0–1 ratio in time, thereby discovering the dynamics of exciton localization in perylene tetracarboxylic acid bisimide aggregates.21 The dynamics of delocalization competing with localization are seen in experimental data and well-illustrated by recent studies of various supramolecular systems21–23 as well as in natural ring-shaped light harvesting complexes from purple bacteria.24 Pump–probe spectroscopy has been used with reasonable success in past studies.25–28 The concept is that the ground state to exciton transition, seen in the bleach and stimulated emission contributions to the signal, is shifted and has a different oscillator strength from the exciton to two-exciton excited state absorption contribution to the pump–probe transient spectrum. When line broadening is entirely from static energetic disorder and the electronic coupling J is known, then coherence length Ncoh is indicated by the shift of the bleach and excited state absorption bands Δ according to ref. 28: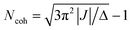 .
.
The quantum mechanical model for excitons
Quantum information science provides ways of speeding up computations, encoding and transmitting information, and enabling quantum sensing. Implementations of quantum information are often based on qubits—‘switches’ that can be entangled. Entanglement is a property of correlation between two or more quantum systems. The key point is that these correlations defy classical description.29,30 Consider the exciton state for a dimer comprising the molecules 1 and 2: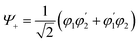 | (1) |
Are exciton states a potential resource for quantum information? That question was highlighted after the 2007 report by Fleming and co-workers31 that revealed unusual coherence in a photosynthetic protein. The work sparked intense interest in the possibility that quantum effects underlie light-harvesting function.32,33 Since that time our understanding of these data is more deeply developed,34 but calculations predicting entanglement of excitons in such large and complex systems remain intriguing.32,33,35–37 It seems that a shift in thinking might be interesting, from considering whether entanglement enhances function to asking what kind of quantum information is encoded in complex systems and how could we exploit it?
Entanglement is a focus of quantum information, but it is difficult to employ as a resource for function in complex, multimolecular systems. Recently a promising alternative—coherence as a resource—has been proposed and axiomatically formulated.38 Hence it is important to assess some properties and limits of coherence in large-scale molecular aggregates as a first step to working out practical demonstrations of quantum information based on coherence. To that end, the present report focuses on estimates for the size (coherence length) of exciton states, vide infra, but does not attempt to quantify entanglement. Nevertheless, our prior studies of multipartite entanglement in excitonic systems39 raise interesting questions. For instance, we discovered how under decoherence, n-partite entanglement of an exciton is lost faster than (n − 1)-partite entanglement (see Fig. 3 of ref. 39). This makes sense: it is easier to keep two particles perfectly in step than three (or more) particles. This result, in part, motivates the studies below of limits for coherence length of excitons in many-molecule systems. The concept is related to the interplay of site disorder and entropic effects discussed in the next section.
To discuss the size-limits of molecular exciton states below, one element we can think more deeply about is the electronic coupling. Our focus is on electronic interactions that dominate in the intermolecular separation regime where orbital overlap effects are negligible. This means we neglect the leading orbital-overlap dependent coupling that involves charge-transfer configurations in our basis.40–42 We only consider, therefore, the coulombic interactions. One relatively long-range Coulomb interaction—related to London dispersion forces—lowers the exciton transition energy.43 I will not discuss that interaction here. Instead we focus on the interaction, J, that exchanges excitation between two molecules.
The electronic coupling J arises from the way a molecule interacts with the Maxwell fields produced by another, nearby, molecule—the displacement vector field.44 Thinking in such general terms as the quantum electrodynamical (QED) theory might sound abstract, but it has important advantages that include accounting properly for how the coupling propagates at the speed of light—in accord with special relativity—and is mediated by real photons in the limit of large intermolecular separations compared to the wavelength of the optical absorption band.45
For identical donor and acceptor molecules with transition energy of wavevector k and positioned at Ri and Rj respectively, such that R = |Rj − Ri|, the coupling matrix element is (ref. 46)
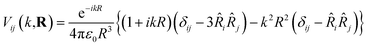 | (2) |
Interactions that propagate at the speed of light may introduce phase disorder in the Hamiltonian of large aggregates by adding a phase term to J, i.e. a distribution of interaction times. This concept has some analogy to the phase-dependent coupling in the Kuramoto model described below. Previous studies have shown that a satisfactory resolution of causality in long-range energy transfer is challenging,47 in part because of the choices of contours for the complex integrations.48 Further, Power and Thirunamachandran have shown that analysis should be specific to the measurements.49
While in principle these phase delays should be insignificant in nearest-neighbour coupling models, where J is instantaneous, an open question is how to think about phase delays for Coulomb interactions mediated over long length scales by a series of intermediate chromophores. For example, imagine a linear molecular aggregate comprising 100 molecules, where each molecule is separated from its neighbour by 1 nm. Since each nearest-neighbour interaction falls well within the limits of near-zone (instantaneous) coupling, it appears that the relayed coupling from one end of the aggregate to the other is predicted to be instantaneous. On the other hand, the speed of 500 nm light suggests that the interaction—relayed or not—from a molecule at one end of the aggregate to the other end should be delayed by 0.3 fs, corresponding to a phase delay of 0.375π. The instantaneous Coulomb interaction is required in quantum mechanics to produce perfect eigenstates of the aggregate, where phases of all molecules are locked together. This issue is not the same as the “EPR paradox” of quantum information, but it is related to the difficult question of causality in the QED formulation and careful formulation of the theory with respect to the chosen gauge transformation.50
Another speculative element neglected in this model is random fluctuations of transition densities. Such fluctuations, for example, give rise to dispersion forces.51,52 Do these fluctuations cause off-diagonal disorder (disorder in J) by modulating transition moments, or are the transition densities entrained by locking to J? We will see below the contrast of the classical model of entrained oscillators, where the phase-locking is established over time.
Excitons and the extent of quantum delocalization
The studies of coherence length and its time-dependence described above show that exciton delocalization is sensitive to the balance between the magnitude of electronic coupling—that de-excites one molecule and synchronously excites another—and the energy and time scales of spectral line broadening.53 When electronic coupling is very weak, excitation is localized, but can hop stochastically from one molecule to another. That process is known as Förster energy transfer or electronic energy transfer.54 Coherent energy transfer has been of interest recently.34,55 It is energy transfer in an intermediate regime, where there is a balance between interference among electronic resonances to give coherence and coupling to the environment causing decoherence.Understanding the balance between disorder (static or dynamic) and electronic coupling is a difficult issue, and is fundamental for explaining decoherence and the quantum to classical transition.56–58 In cavity quantum electrodynamics, measurements of the polariton states as a function of temperature have been reported.59 In such studies an oscillator response in the quantum regime is indicated by the characteristic ladder of states according to the Jaynes–Cummings model.60 The classical regime is the high temperature limit, where many quanta are populated.
The exciton problem is different because we study how the quantum-mechanical delocalization across many coupled molecules changes as a function of coupling strength and disorder. Therefore we do not expect to observe a quantum to classical transition, but instead characterize the degrees of delocalization within the ensemble system. The question of main interest for this discussion is how large can an exciton really be? The question is motivated by the hypothesis that as the size of the molecular aggregate increases, the delocalization will be increasingly limited by small disorder. At very low temperature it is anticipated that even very small effects, like the phase delays in long-range Coulomb interactions, may start to become important for very large aggregates, and contribute to exciton localization. At large exciton sizes there may also be localizing effects derived from mixing of spin eigenstates. The exchange splitting between singlet and triplet excitons diminishes with increasing delocalization.1 Therefore these states can become close in energy compared to kT, facilitating intersystem crossing. At finite temperature, disorder will enable distributions of localization that mean entropic effects will play a role of exponential significance as the aggregate size grows.
The Inverse Participation Ratio (IPR)61 is frequently and conveniently employed as a measure of delocalization.62–64 This measure looks at the variance of probabilities within a wavefunction delocalized among N sites. The exciton wavefunction Ψj, with a basis of N single-molecule excitation states 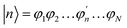 (where the primed molecular wavefunction denotes the electronic excited state), is:
(where the primed molecular wavefunction denotes the electronic excited state), is:
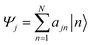 | (3) |
Then, the IPR for exciton state j is defined as:
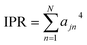 | (4) |
Macroscopic quantum-mechanical superpositions have been well-studied, and the results point to remarkable length scales over which superpositions or quantum interferences can be demonstrated.65 Exciton states are complex quantum systems owing to the large number of molecules involved. How delocalized can molecular aggregates be at very low temperature and what limits delocalization? Some small effects have been discussed above, but it is worth thinking more about entropic effects and the diminishing return of delocalization.
When two identical molecules couple by electronic coupling J to form dimer exciton states, like the states indicated by the absorption spectra of the dinaphthyl molecules shown in Fig. 1, the splitting between the absorption bands is 2J. Assuming the bands shift symmetrically up and down in energy, then the lowest energy exciton state of the dimer is J lower in energy than the monomer. The dimer contains N = 2 molecules and I denote it by the index p = 0, defined by the number of molecules in the aggregate according to N/2 = 2(p+1). If we take a dimer of dimers (p = 1, N = 4), then the energy of this lowest exciton state is further reduced by J/2. Combining two tetramers (p = 2, N = 8) further reduces the energy by J/4, and so on. In other words, the energy lowering (half the exciton bandwidth) is given by the series
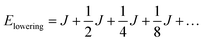 | (5) |
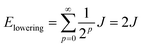 | (6) |
To model the effects of temperature, we construct density matrix operators in the molecular site basis from eqn (3),
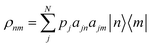 | (7) |
The delocalization is estimated by using the purity, a quantity closely related to the IPR. Recall that Tr(ρ2) = 1 for a pure state. By multiplying the purity by N, a size of delocalization, in units of the number of molecules, is estimated:
| Deloc = N × Tr(ρ2) | (8) |
To keep the model simple, phonons and dynamic energy fluctuations are not included, so the thermal effects simply reflect population of a density of eigenstates for each system in the ensemble. The effects of temperature are most important when the standard deviation of the site energy distribution is less than J.
The Kuramoto model as a classical analog
Coordinated and controlled oscillations are ubiquitous in biology,66,67 where cycles range from lockstep breathing and heart beating that involves choreography of every heart muscle cell, to annual foliage changes in trees. Sophisticated clocks for these rhythms are locked together—entrained—by coupling among oscillators. These entrained systems can be understood through simple mathematical models for phase oscillators, for example by the van der Pol model (ref. 68),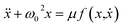 | (9) |
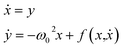 | (10) |
When μ = 0 the system reduces to the harmonic oscillator, where we can easily map the motion of the oscillator onto a point rotating around a circle of radius ρ (interpreted as the oscillator amplitude) on the (x,y) plane,
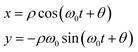 | (11) |
The angle θ defines the oscillator phase in the rotating frame. A similar, approximate, solution can be written for the van der Pol oscillator. Solving for a damped oscillator shows that the point mapped by ρ and total phase (ω0t + θ)—rather than rotating around a circle—spirals into the origin.
Kuramoto considered a model for many oscillators (N), with respective phases θj (in the rotating frame) all weakly coupled to each other by a uniform coupling K. The mean-field solution turns out to be remarkably simple.69 For all-to-all coupling:
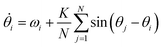 | (12) |
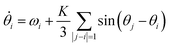 | (13) |
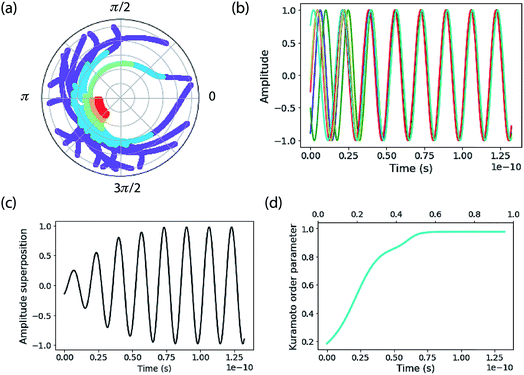
This ensemble of oscillators shows rich nonlinear dynamics as a function of parameters and has been well studied.72,73 When K is larger than the oscillator phase distribution a remarkable self-synchronization of the oscillators is found (Fig. 2). The phase distribution of a small ensemble of 20 oscillators as a function of time is plotted on polar axes in Fig. 2a. The points are plotted at different radii, where time starts on the outside of the plot and increases as the radius diminishes. The purple points show that the initial phases span a large fraction of the range [0,2π]. That initial phase distribution comes from a random phase assigned to the oscillators in the ensemble from a normal distribution (typically with a standard deviation of 3.0 radians).
After a time delay of about two periods, the oscillators abruptly lock together—see the way the red points at long time are clustered on the phase plot. That same information is shown by the amplitude versus time plots in Fig. 2b. This plot emphasizes the frequency distribution of each oscillator, assigned as a random frequency off-set from ω0 (the mean). The normal distribution of frequencies has a standard deviation of the order of 10% of ω0. Note that the natural frequency of each oscillator is constant, so that phase-locking is achieved by speeding up and slowing down oscillators—by nonlinear feedback—during the course of their periodic motion. Fig. 2c shows the sum of all the amplitude oscillators, highlighting the “rephasing” as the ensemble becomes entrained.
By taking the sum of the complex exponential of each phase, Kuramoto defined a complex order parameter, where r(t) indicates the coherence of the phases:
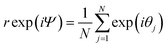 | (14) |
The synchronization of the ensemble is clearly shown by the plot of r(t) in Fig. 2d. Nr(t) gives an estimate of the number of synchronized oscillators and in the simulations below we compare it to the quantum-mechanical delocalization length, 1/IPR.
The coupled oscillators model is clearly a good analogy for coupled molecules and their exciton states, and a formal mapping of the energy eigenstates of coupled classical oscillators onto the exciton problem has been described.74 A difference between the Kuramoto (classical) model for coupled oscillators and the quantum mechanical model is that the quantum model predicts energy eigenstates for perfectly phased oscillators, whereas the oscillators in the classical nonlinear model become phased with time. As seen below, there is often surprising agreement between the number of synchronized oscillators after several periods of oscillation and the delocalization length.
Results
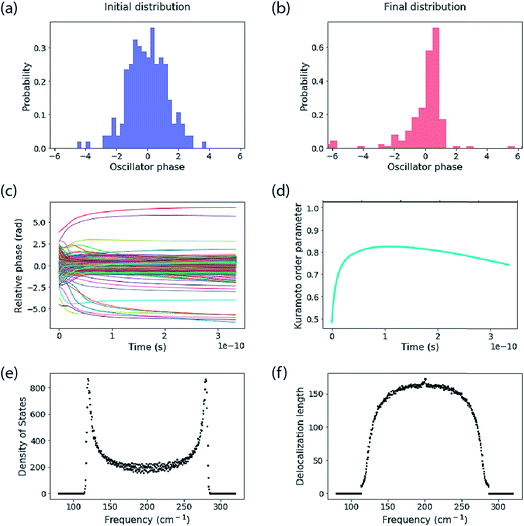
The calculations reported here do not include dynamic energy fluctuations, so they formally correspond to the limit of T = 0. The same Hamiltonian matrix is used for input to the Kuramoto calculation and to construct the Hamiltonian matrix that is diagonalized to yield the exciton eigenstates and energies. The diagonal elements are the oscillator frequency (200 cm−1, but note this is arbitrary because we report results in the rotating frame). An offset is added to each oscillator’s frequency, randomly taken from a normal distribution with standard deviation specified below. The coupling parameter is specified also. A key difference between the Kuramoto model and the exciton model is that the Kuramoto coupling depends on phase difference. We use the nearest-neighbour coupling model, J = K/3.An example of calculations for an ensemble of 200 molecules is reported in Fig. 3. The top panels show the initial distribution of oscillator phases, which include the distribution of frequency inputs for the diagonal elements of the Hamiltonian as well as a random oscillator phase. This is compared to the final distribution of phases decided by the Kuramoto model. The middle panels report the time evolution of phases and the corresponding Kuramoto order parameter. The bottom panels show the spectra of the exciton density of states and delocalization lengths (1/IPR) for an ensemble of 500 molecular aggregates. The Kuramoto order parameter estimates a coherence size of 149 molecules. The delocalization length estimated from the mean of 1/IPR is 95 molecules, while the delocalization across the middle of the band of states is ∼150, in close agreement with that predicted by the order parameter. The mean delocalization from the quantum mechanical model comes from the low delocalization in the tails of the density of states, which is indicative of an Urbach tail—that is, low (or high) lying localized states owing to the tail of the distribution of disorder.
A study of the effect of temperature on delocalization length for the 200-molecule system is reported in Table 1. I report two analyses: band edge (dominated by the Urbach tail) and mid-band (lowest energy cutoff state at 80% ω0). As expected, temperature has a significant effect to localize exciton states by generating a superposition of eigenstates. The von Neumann entropy, S = −Tr(ρ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ), is also reported. It is an indicator of how mixed the state is.
ρ), is also reported. It is an indicator of how mixed the state is.
| Temperature (K) | Band edge | Mid-band | ||||
|---|---|---|---|---|---|---|
| Tr(ρ2) | Delocalization | Entropy | Tr(ρ2) | Delocalization | Entropy | |
| 0.1 | 0.066 | 13 | 3.0 | 0.33 | 65 | 1.6 |
| 1.0 | 0.062 | 12 | 3.0 | 0.27 | 54 | 1.8 |
| 10 | 0.029 | 6 | 3.5 | 0.066 | 13 | 2.9 |
| 20 | 0.020 | 4 | 3.7 | 0.037 | 7 | 3.3 |
In Table 2 the results from a study of a 1000-molecule aggregate are reported. The results should be treated with care since the Kuramoto model converges quite slowly, taking 50 periods of oscillation or more. The initial phase distribution was chosen, by testing various parameters, to optimize convergence. For most entries in the table multiple calculations were carried out and a representative, converged result is reported. The Kuramoto order parameter is closely consistent with the average exciton delocalization number. When the ratio σ/K is very small—meaning the exciton is closer to perfect—both models predict close to perfect order, but clearly the delocalization is strongly attenuated by disorder.
| Standard deviation (cm−1) | Order length | Average delocalization |
|---|---|---|
| 0.2 | 882 | 962 |
| 1.0 | 841 | 798 |
| 2.0 | 695 | 614 |
| 2.5 | 537 | 548 |
| 3.0 | 268 | 464 |
| 4.0 | 139 | 375 |
| 10 | 145 | 218 |
In Fig. 4 the results of calculations for a temperature of 5 K are shown, highlighting the size-dependence of delocalization (purity) and the van Neumann entropy. Note that the coupling is very large compared to the disorder, so the (zero-temperature) IPR measure and the Kuramoto model predict almost perfect delocalization for every blue point plotted (i.e. K = 120 cm−1, σ = 0.1 cm−1). The delocalization saturates with N because the density-of-states increases proportional to N, making the density matrix more mixed in character. That is reflected in the plot of entropy versus N.
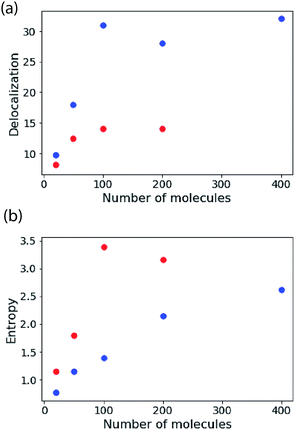 | ||
| Fig. 4 The stability of large excitons. Delocalization estimated from eqn (8) and the von Neumann entropy as a function of the number of molecules in the aggregate. These simulations are for the nearest-neighbour coupling model and an ensemble average of 500 copies of the system. For the blue points K = 120 cm−1, σ = 0.1 cm−1. For the red points K = 120 cm−1, σ = 10 cm−1. | ||
Questions raised and conclusions
To gain physical insight in to the size-limits for molecular exciton states, the inverse participation ratio was compared to the order parameter for a classical system of coupled, and hence entrained, oscillators—the Kuramoto model. The Kuramoto model gives physical insight into coherence and decoherence and highlights properties of the quantum mechanical model—in particular how the phases of basis functions (molecular excitations) must be locked perfectly together in the construction of eigenstates. Simulations using the same parameters in the Kuramoto model and a quantum mechanical model for predicting exciton eigenstates showed that the Kuramoto order parameter makes very similar predictions of coherence lengths to the inverse participation ratio (IPR).The Kuramoto model is known to show a transition from order to disorder as a function of parameters, and I speculate that this might inspire how to think about a quantum to classical transition in large molecular aggregates. In considering factors that limit exciton delocalization length, I suggested that entropy should be the major limiting factor, and therefore it is unlikely that delocalization lengths greater than the wavelength of the excitation light are possible. That, in turn, means it is challenging for experiments to be devised to demonstrate superpositions of macroscopically distinguishable states (“cat” states) in molecular aggregates.
A series of key questions emerge for discussion:
• Can molecular excitons be used as a resource for quantum information38 or as models for studying quantum phenomena,75 and if so, how?
• What are the size limits for molecular excitons? What chemical strategies could increase delocalization lengths?
• Can exciton delocalization be enhanced by entraining transition densities by a driving field? That field might be excitation light or it could be a cavity mode.
• Is there a way to produce a quantum to classical transition for exciton states of large molecular aggregates, in analogy to nonlinear oscillator models?
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by the Gordon and Betty Moore Foundation through Grant GBMF7114.References
- G. D. Scholes and G. Rumbles, Nat. Mater., 2006, 5, 683–696 CrossRef CAS PubMed.
- C. J. Bardeen, Annu. Rev. Phys. Chem., 2014, 65, 127–148 CrossRef CAS PubMed.
- M. Kasha, Radiat. Res., 1963, 20, 55 CrossRef CAS PubMed.
- J. Singh, Solid State Phys., 1984, 38, 295–370 CAS.
- H. Fidder, J. Knoester and D. A. Wiersma, J. Chem. Phys., 1991, 95, 7880–7890 CrossRef CAS.
- Photosynthetic Excitons, ed. H. van Amerongen, L. Valkunas and R. van Grondelle, World Scientific, Singapore, 2000 Search PubMed.
- J. L. Brédas, E. H. Sargent and G. D. Scholes, Nat. Mater., 2016, 16, 35–44 CrossRef PubMed.
- D. P. Craig and S. H. Walmsley, Excitons in Molecular Crystals, Benjamin, New York, 1968 Search PubMed.
- G. Scholes, G. Turner, K. Ghiggino, M. N. Paddon-Row, W. Schuddeboom, J. Piet and J. Waman, Chem. Phys. Lett., 1998, 292, 601–606 CrossRef CAS.
- R. Monshouwer, M. Abrahamsson, F. van Mourik and R. van Grondelle, J. Phys. Chem. B, 1997, 101, 7241–7248 CrossRef CAS.
- F. Fassioli, A. Olaya-Castro and G. D. Scholes, J. Phys. Chem. Lett., 2012, 3, 3136–3142 CrossRef CAS PubMed.
- D. Yarkony and R. Silbey, J. Chem. Phys., 1976, 65, 1042–1052 CrossRef CAS.
- D. R. Yarkony and R. Silbey, J. Chem. Phys., 1977, 67, 5818–5827 CrossRef CAS.
- H. Yamagata and F. C. Spano, J. Phys. Chem. Lett., 2014, 5, 622–632 CrossRef CAS PubMed.
- H. Yamagata and F. Spano, J. Chem. Phys., 2011, 135, 054906 CrossRef CAS PubMed.
- F. C. Spano and H. Yamagata, J. Phys. Chem. B, 2011, 115, 5133–5143 CrossRef CAS.
- F. Dubin, R. Melet, T. Barisien, R. Grousson, L. Legrand, M. Schott and V. Voliotis, Nat. Phys., 2006, 2, 32–35 Search PubMed.
- J. Clark, J. Chang, F. C. Spano, R. H. Friend and C. Silva, Appl. Phys. Lett., 2009, 94, 163306 CrossRef.
- F. C. Spano and C. Silva, Annu. Rev. Phys. Chem., 2014, 65, 477–500 CrossRef CAS PubMed.
- R. Tempelaar, F. C. Spano, J. Knoester and T. Jansen, J. Phys. Chem. Lett., 2014, 5, 1505–1510 CrossRef CAS.
- J. Sung, P. Kim, F. Würthner and D. Kim, Nat. Commun., 2015, 6, 8646 CrossRef CAS.
- C. Yong, P. Parkinson, D. Kondratuk, W. Chen, A. Stannard, A. Summerfield, J. Sprafke, M. O’Sullivan, P. Beton, H. Anderson and L. Herz, Chem. Sci., 2015, 6, 181–189 RSC.
- A. Aggarwal, A. Thiessen, A. Idelson, D. Kalle, D. Würsch, T. Stangl, F. Steiner, S. Jester, J. Vogelsang, S. Höger and J. Lupton, Nat. Chem., 2013, 5, 964–969 CrossRef CAS.
- A. M. van Oijen, M. Ketelaars, J. Köhler, T. J. Aartsma and J. Schmidt, Science, 1999, 285, 400–402 CrossRef CAS.
- T. Pullerits, M. Chachisvilis and V. Sundström, J. Phys. Chem., 1996, 100, 10787–10792 CrossRef CAS.
- M. Chachisvilis, O. Kühn, T. Pullerits and V. Sundström, J. Phys. Chem. B, 1997, 101, 7275–7283 CrossRef CAS.
- T. Meier, V. Chernyak and S. Mukamel, J. Phys. Chem. B, 1997, 101, 7332–7342 CrossRef CAS.
- L. Bakalis and J. Knoester, J. Phys. Chem. B, 1999, 103, 6620–6628 CrossRef CAS.
- C. Bennett and D. DiVencenzo, Nature, 2000, 404, 247–255 CrossRef CAS PubMed.
- S. Barnett, Quantum Information, Oxford University Press, Oxford, 2009 Search PubMed.
- G. S. Engel, T. R. Calhoun, E. L. Read, T.-K. Ahn, T. Mancal, Y.-C. Cheng, R. E. Blankenship and G. R. Fleming, Nature, 2007, 446, 782–786 CrossRef CAS PubMed.
- A. W. Chin, J. Prior, R. Rosenbach, F. Caycedo-Soler, S. F. Huelga and M. B. Plenio, Nat. Phys., 2012, 9, 113–118 Search PubMed.
- E. J. O’Reilly and A. Olaya-Castro, Nat. Commun., 2014, 5, 3012 Search PubMed.
- C. Jumper, S. Rafiq, S. Wang and G. D. Scholes, Curr. Opin. Chem. Biol., 2018, 47, 39–46 CrossRef CAS PubMed.
- P. Rebentrost, M. Mohseni, I. Kassal, S. Lloyd and A. Aspuru-Guzik, New J. Phys., 2009, 11, 033003 CrossRef.
- S. Lloyd, M. Mohseni, A. Shabani and H. Rabitz, arXiv:1111.4982, 2011.
- M. Mohseni, A. Shabani, S. Lloyd and H. Rabitz, arXiv:1104.4812, 2011.
- A. Streltsov, G. Adesso and M. Plenio, Rev. Mod. Phys., 2017, 89, 041003 CrossRef.
- C. Smyth and G. D. Scholes, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 90, 032312 CrossRef.
- T. Mirkovic, E. E. Ostroumov, J. M. Anna, R. van Grondelle, Govindjee and G. D. Scholes, Chem. Rev., 2017, 117, 249–293 CrossRef CAS PubMed.
- R. D. Harcourt, G. D. Scholes and K. P. Ghiggino, J. Chem. Phys., 1994, 101, 10521–10525 CrossRef CAS.
- G. Scholes, ACS Nano, 2008, 2, 523–537 CrossRef CAS PubMed.
- E. Power and T. Thirunamachandran, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 51, 3660–3666 CrossRef CAS PubMed.
- E. Power and T. Thirunamachandran, Phys. Rev. A: At., Mol., Opt. Phys., 1983, 28, 2663–2670 CrossRef CAS.
- D. L. Andrews, Can. J. Chem., 2008, 86, 855–870 CrossRef CAS.
- G. Daniels, R. Jenkins, D. S. Bradshaw and D. L. Andrews, J. Chem. Phys., 2003, 119, 2264–2274 CrossRef CAS.
- D. P. Craig and T. Thirunamachandran, Chem. Phys., 1992, 167, 229–240 CrossRef CAS.
- D. L. Andrews and B. Sherborne, J. Chem. Phys., 1987, 86, 4011–4017 CrossRef CAS.
- E. Power and T. Thirunamachandran, Phys. Rev. A: At., Mol., Opt. Phys., 1997, 56, 3395–3408 CrossRef CAS.
- J. Jackson, Am. J. Phys., 2002, 70, 917 CrossRef.
- M. Hawton, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 6846–6850 CrossRef PubMed.
- R. McWeeny, Croat. Chem. Acta, 1984, 57, 865–878 CAS.
- G. D. Scholes, J. Phys. Chem. Lett., 2010, 1, 2–8 CrossRef CAS.
- G. D. Scholes, Annu. Rev. Phys. Chem., 2003, 54, 57–87 CrossRef CAS.
- A. Chenu and G. D. Scholes, Annu. Rev. Phys. Chem., 2015, 66, 69–96 CrossRef CAS.
- W. H. Zurek, Rev. Mod. Phys., 2003, 75, 715 CrossRef.
- W. H. Zurek, Phys. Today, 1991, 44, 36–44 CrossRef.
- Quantum Decoherence. Poincaré Seminar 2005, ed. B. Duplantier, J. Raimond and V. Rivasseau, Birkhäuser Verlag, Basel, 2007 Search PubMed.
- J. Fink, L. Steffen, P. Studer, L. Bishop, M. Baur, R. Bianchetti, D. Bozyigit, C. Lang, S. Filipp, P. Leek and A. Wallraff, Phys. Rev. Lett., 2010, 105, 163601 CrossRef CAS.
- B. Garraway, Philos. Trans. R. Soc., A, 2011, 369, 1137–1155 CrossRef.
- D. Thouless, Phys. Rep., 1974, 13, 93 CrossRef.
- R. Jimenez, S. N. Dikshit, S. E. Bradforth and G. R. Fleming, J. Phys. Chem., 1996, 100, 6825–6834 CrossRef CAS.
- V. Novoderezhkin, R. Monshouwer and R. van Grondelle, J. Phys. Chem. B, 1999, 103, 10540–10548 CrossRef CAS.
- T. Meier, V. Chernyak and S. Mukamel, J. Phys. Chem. B, 1997, 101, 7332–7342 CrossRef CAS.
- M. Arndt and K. Hornberger, Nat. Phys., 2014, 10, 271–277 Search PubMed.
- L. Glass and M. Mackey, From Clocks to Chaos, Princeton University Press, 1988 Search PubMed.
- S. H. Strogatz and I. Stewart, Sci. Am., 1993, 102–109 CrossRef CAS.
- V. Nekorkin, Introduction to Nonlinear Oscillations, Wiley-VCH, Weinheim, 2015 Search PubMed.
- S. Strogatz, Phys. D, 2000, 143, 1–20 CrossRef.
- H. Hong, H. Park and M. Choi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 036217 CrossRef CAS.
- H. El-Nashar, Y.-Z. Zhang, H. Cerdeira and F. Ibiyinka A., Chaos, 2003, 13, 1216–1225 CrossRef.
- A. Pikovsky and M. Rosenblum, Chaos, 2015, 25, 097616 CrossRef.
- J. Acebrón, L. Bonilla, C. Pérez Vicente, F. Ritort and R. Spigler, Rev. Mod. Phys., 2005, 77, 137–185 CrossRef.
- J. Briggs and A. Eisfeld, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 052111 CrossRef.
- E. Carnio, H. i. Breuer and A. Buchleitner, J. Phys. Chem. Lett., 2019, 10, 2121–2129 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |