 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Improved population operators for multi-state nonadiabatic dynamics with the mixed quantum-classical mapping approach
Maximilian A. C.
Saller
 a,
Aaron
Kelly
a,
Aaron
Kelly
 b and
Jeremy O.
Richardson
b and
Jeremy O.
Richardson
 a
a
aLaboratory of Physical Chemistry, ETH Zurich, Switzerland. E-mail: maximilian.saller@phys.chem.ethz.ch; jeremy.richardson@phys.chem.ethz.ch
bDepartment of Chemistry, Dalhousie University, Halifax, Canada. E-mail: aaron.kelly@dal.ca
First published on 24th September 2019
Abstract
The mapping approach addresses the mismatch between the continuous nuclear phase space and discrete electronic states by creating an extended, fully continuous phase space using a set of harmonic oscillators to encode the populations and coherences of the electronic states. Existing quasiclassical dynamics methods based on mapping, such as the linearised semiclassical initial value representation (LSC-IVR) and Poisson bracket mapping equation (PBME) approaches, have been shown to fail in predicting the correct relaxation of electronic-state populations following an initial excitation. Here we generalise our recently published modification to the standard quasiclassical approximation for simulating quantum correlation functions. We show that the electronic-state population operator in any system can be exactly rewritten as a sum of a traceless operator and the identity operator. We show that by treating the latter at a quantum level instead of using the mapping approach, the accuracy of traditional quasiclassical dynamics methods can be drastically improved, without changes to their underlying equations of motion. We demonstrate this approach for the seven-state Frenkel-exciton model of the Fenna–Matthews–Olson light harvesting complex, showing that our modification significantly improves the accuracy of traditional mapping approaches when compared to numerically exact quantum results.
1 Introduction
Simulating nonadiabatic effects in quantum dynamics continues to pose a considerable challenge in theoretical chemistry and physics, especially in the condensed phase. Arising when the energies of two or more electronic states approach each other, resulting in the breakdown of the Born–Oppenheimer approximation, these effects have been found to have a profound impact on a wide range of systems spanning physics, chemistry and biology.1–3The development of simulation methods for nonadiabatic effects has thus continued to be the focus of considerable research efforts. Methods relying on an explicit expansion and propagation of the wavefunction, often on a grid, have yielded highly accurate results.4–6 However, many models inspired by condensed-phase systems still prove too computationally expensive to treat with these methods, due to their unfavourable exponential scaling with system size. Despite recent efforts to overcome this scaling hurdle,7,8 many systems from the fields of chemistry and biology, especially those in a condensed-phase environment, are simply too large to treat using a wavefunction-based approach. Mixed quantum-classical methods,9–29 though inherently more approximate, are often the only choice when seeking to simulate nonadiabatic dynamics in the condensed phase. As many of these scale linearly with system size, they can readily be applied to large and complex realistic systems, yielding highly valuable insights at reasonable computational costs.
The representation typically chosen for a nonadiabatic process consists of a continuous nuclear phase space and a set of discrete electronic states. The resulting Hamiltonian is given by
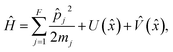 | (1) |
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) j and mj are the momentum operator and mass of nuclear degree of freedom (DoF) j respectively, and
j and mj are the momentum operator and mass of nuclear degree of freedom (DoF) j respectively, and ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) is a vector of length F consisting of the position operators for each nuclear DoF. U(
is a vector of length F consisting of the position operators for each nuclear DoF. U(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ) is the state-independent potential, and the state-dependent potential is given by
) is the state-independent potential, and the state-dependent potential is given by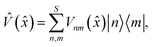 | (2) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (
(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ) are the diabatic potential energy surfaces, while its off-diagonal elements are the couplings between the electronic states. Everything that follows does not rely on a particular choice of potential, i.e. we are not limited to simple harmonic models. Note that we will use reduced units throughout, such that ħ = 1.
) are the diabatic potential energy surfaces, while its off-diagonal elements are the couplings between the electronic states. Everything that follows does not rely on a particular choice of potential, i.e. we are not limited to simple harmonic models. Note that we will use reduced units throughout, such that ħ = 1.
The mismatch between the continuous nuclear phase space and the discrete space of electronic states constitutes a recurring challenge in mixed quantum-classical dynamics. The mapping approach solves this problem by projecting the electronic degrees of freedom into a space of singly-excited harmonic oscillators (SEOs).12,30,31 In the space of the SEO wavefunctions, the representation of state |n〉 is given by
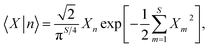 | (3) |
 given by
given by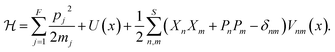 | (4) |
In addition to the relative simplicity of the mapping approach, the extended phase space grows linearly with the number of electronic states. Furthermore, given the favourable scaling of classical trajectories with respect to the nuclear DoFs, a number of mixed quantum-classical dynamics approaches, aimed specifically at large, realistic systems in the condensed phase, have been developed based on this formalism.10–12,14,24,26 Note that in this work we will use the term quasiclassical to refer to mixed quantum-classical approaches which employ a single set of mapping variables per electronic state as well as a single set of positions and momenta for each nuclear degree of freedom.
Quasiclassical methods yield accurate results for most observables at short times. In the long time limit however, they are well known to degrade in accuracy, especially for the relaxation to thermal equilibrium following an initial electronic excitation. Attempts to address this shortcoming with the use of master equations have shown considerable promise.32,33 Other approaches to improve quasiclassical dynamics have led to the development of related dynamics approaches. For instance, the symmetrical quasiclassical windowing method uses a windowing function to “bin” the electronic populations, ensuring that they have integer values at the beginning and end of each trajectory. This approach has been applied to the benchmark we study below, achieving accuracy comparable to that reported here.34–38 A number of methods which depart from the equations of motion underlying quasiclassical dynamics, but remain close to its overall motivation, have also shown considerable promise in treating multi-state systems. Prominent examples, which have been very successfully applied to the benchmark studied here, include the forward-backward trajectory solution19,20 (FBTS) and the partially linearised density matrix (PLDM) method.16,17
In a recent publication, we have however shown that a simple modification, with a similar motivation as that underlying the use of master equations, can drastically improve the performance of quasiclassical methods, without changing the equations of motion.39 We split the population operator into two parts, one of which is the identity.18 We can then use our understanding of the exact behaviour of this operator to drastically improve traditional quasiclassical methods. The resulting approach has the benefit of retaining all the advantages of these methods, as the underlying equations of motion are unchanged.
Here we extend this approach, which was originally presented for only two electronic states, to an arbitrarily large electronic space. We use the fact that the electronic population, like any Hermitian operator, can be expanded exactly into the identity and a purely traceless component.18 Given that the behaviour of its quantum operator is well understood, we treat the identity exactly, resulting in a simpler phase-space representation of the population operator, involving only the traceless part. Population dynamics calculated using these modified operators are of drastically higher quality than those obtained from the traditional quasiclassical definition.
We apply this general formulation to the challenging benchmark model for the Fenna–Matthews–Olson (FMO) light harvesting complex.40–44 Our results are significantly more accurate than those obtained using the standard operator definitions and in excellent agreement with numerically exact quantum dynamics methods.
2 Theory
Here we extend our previous work39 by presenting a general formalism, which can be applied to any system of multiple electronic states.2.1 Quasiclassical population operators
In the mapping formalism, the operator |n〉〈n|, which measures the population of electronic state |n〉 can be written as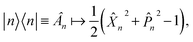 | (5) |
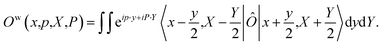 | (6) |
When considering the population operator, there are two representations one can choose to Wigner transform, corresponding to either the left- or right-hand side of eqn (5). Using the left-hand side is equivalent to including a projection on the SEO subspace, which yields an expression in terms of the harmonic oscillator wavefunctions as in eqn (3).18 The resulting phase-space representations, identified as Awn and ASEOn respectively, are
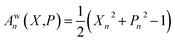 | (7a) |
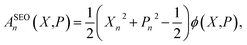 | (7b) |
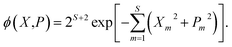 | (8) |
Note that crucially, Awn ≠ ASEOn × ϕ. Each of these phase-space representations is derived via the Wigner transform of a formally exact mapping form of the |n〉〈n| operator. Therefore, a clear choice of which to use when calculating observables is not obvious a priori. A more detailed discussion of the possible combinations of phase-space representations and electronic initial conditions can be found in our recent work.39
An observable commonly computed using quasiclassical methods is the population of a given electronic state, |n〉, given that the system was initially in a pure state, |m〉. In quantum mechanics this is defined by
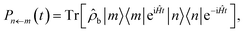 | (9) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) b is a density matrix which defines the initial state of the nuclei, normalised such that the trace over nuclear DoFs only is Trb[
b is a density matrix which defines the initial state of the nuclei, normalised such that the trace over nuclear DoFs only is Trb[![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) b] = 1.
b] = 1.
2.2 Traceless projection operators
There are two differences between the phase-space representations given in eqn (7a) and (7b): the factor of ϕ(X,P), which is only present in ASEOn, and the differing constant terms, which are related to zero-point energy (ZPE) of the mapping DoFs.45 The origin of the latter is that both the projected and unprojected forms of |n〉〈n| have a non-zero trace. We propose a form of the quantum population operator in which the trace is shifted to the identity operator, which in turn is treated exactly using quantum mechanics.39 The result is a phase-space representation of the quantum population operator which is traceless.There is a unique expansion of the population operator |n〉〈n|, such that:
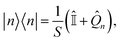 | (10) |
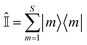 is the identity operator, and
is the identity operator, and ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) n is, by design, traceless,
n is, by design, traceless,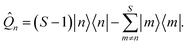 | (11) |
Note that in a two-level system, this operator is the Pauli spin matrix, i.e. ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) 1 =
1 = ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) z, such that |1〉〈1|=(
z, such that |1〉〈1|=( +
+ ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) z)/2, which was used in our previous work.39 Substituting this definition for the quantum population operator into eqn (9) and expanding yields
z)/2, which was used in our previous work.39 Substituting this definition for the quantum population operator into eqn (9) and expanding yields
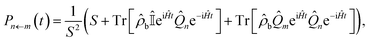 | (12) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) b
b![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) m] = 0 and Tr[
m] = 0 and Tr[![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) b
b ] = S. The final two terms in this expression are quantum correlation functions which can be approximated by well-known quasiclassical dynamics methods.
] = S. The final two terms in this expression are quantum correlation functions which can be approximated by well-known quasiclassical dynamics methods.
Following the standard quasiclassical procedure, in order to calculate the value of the population operator given in eqn (12), we Wigner transform the operators in these two constituent correlation functions. The phase-space representation of the traceless operator ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) n is
n is
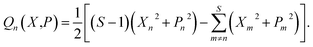 | (13) |
If we had performed the Wigner transform on the projected operator, the phase-space representation would simply be Qn(X,P)ϕ(X,P). Note that neither expression contains constant terms which play the role of ZPE-parameters.
It would be possible to arrive at a phase-space representation of the identity operator via similar Wigner transforms. However, we suggested in our previous work39 that we can instead use our understanding of its behaviour in quantum mechanics, which is to leave its operand unchanged. We therefore simply avoid directly computing the identity altogether.
Starting from the exact expression for 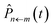 in eqn (12), we thus arrive at our final quasiclassical expression for the population of electronic state |n〉, assuming the system was initially in state |m〉,
in eqn (12), we thus arrive at our final quasiclassical expression for the population of electronic state |n〉, assuming the system was initially in state |m〉,
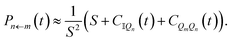 | (14) |
The constituent correlation functions C![[Doublestruck I]](https://www.rsc.org/images/entities/char_e16c.gif) Qn and CQmQn are given by
Qn and CQmQn are given by
C![[Doublestruck I]](https://www.rsc.org/images/entities/char_e16c.gif) Qn(t) = 〈ϕa(X,P)Qn(X(t),P(t))〉 Qn(t) = 〈ϕa(X,P)Qn(X(t),P(t))〉 | (15a) |
| CQmQn(t) = 〈ϕa(X,P)Qm(X,P)Qn(X(t),P(t))〉, | (15b) |
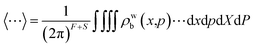 and ρwb(x,p) is the Wigner transformed density matrix of the nuclear DOFs. In practice the values of these correlation functions are averaged over an ensemble of trajectories, with initial conditions for the mapping variables being drawn from either ϕ(X,P) or ϕ2(X,P), depending on whether the projected forms of one or both of
and ρwb(x,p) is the Wigner transformed density matrix of the nuclear DOFs. In practice the values of these correlation functions are averaged over an ensemble of trajectories, with initial conditions for the mapping variables being drawn from either ϕ(X,P) or ϕ2(X,P), depending on whether the projected forms of one or both of ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) m and
m and ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) n were Wigner transformed. This corresponds to a = 1 and a = 2 respectively.
n were Wigner transformed. This corresponds to a = 1 and a = 2 respectively.
Note that we can include the factors of ϕ(X,P) at time zero, because this function is constant over the course of any trajectory evolving under the Hamiltonian 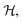 given in eqn (4). Also the two constituent correlation functions can be calculated for all values of m and n in a single simulation. Just as in traditional quasiclassical methods,11,14 the values of these constituent correlation functions, and therefore
given in eqn (4). Also the two constituent correlation functions can be calculated for all values of m and n in a single simulation. Just as in traditional quasiclassical methods,11,14 the values of these constituent correlation functions, and therefore 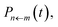 are exact in the limit of t = 0.
are exact in the limit of t = 0.
2.3 Traditional quasiclassical dynamics methods
The traditional quasiclassical approach does not involve treating the identity quantum mechanically as we have done above. There are two standard approaches which differ in whether both population operators are projected onto the subspace, or just one. These methods were derived in different ways11,14 and are called the Poisson bracket mapping equation14,18 (PBME) and the linearised semiclassical initial value representation10,11 (LSC-IVR) methods. LSC-IVR commonly involves projecting both operators prior to Wigner transforming them, i.e. using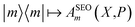 and
and 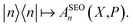 The Wigner transform of each operator yields, as per eqn (7b), a factor of ϕ(X,P). Initial conditions for the mapping variables are therefore sampled from ϕ2(X,P). In PBME on the other hand, traditionally only the operator for the initial population is Wigner transformed in its projected form. The operators are therefore
The Wigner transform of each operator yields, as per eqn (7b), a factor of ϕ(X,P). Initial conditions for the mapping variables are therefore sampled from ϕ2(X,P). In PBME on the other hand, traditionally only the operator for the initial population is Wigner transformed in its projected form. The operators are therefore 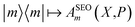 and
and 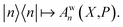 Only the transform of |m〉〈m| yields a factor of ϕ(X,P). Consequently, electronic initial conditions are sampled from ϕ(X,P). Using these definitions, the electronic population can be calculated from
Only the transform of |m〉〈m| yields a factor of ϕ(X,P). Consequently, electronic initial conditions are sampled from ϕ(X,P). Using these definitions, the electronic population can be calculated from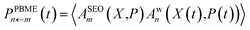 | (16a) |
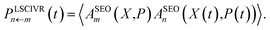 | (16b) |
We note that the differences between these two methods do not actually stem from the derivations, but are mere convention. It would in principle be possible to derive a PBME method using two projections. However for convenience, we will use eqn (16) as the definition of PBME and LSC-IVR throughout this work. Finally, it is important to note that at least one of the operators has to be Wigner transformed in its projected form in order to ensure that the dynamics are initialised to the physical subspace.
While both LSC-IVR and PBME, as well as other mixed quantum-classical methods, have been applied to challenging systems with considerable success, their failure to accurately reproduce population dynamics in the long time limit has been well documented.18,39,46,47 As mentioned above, a number of modifications to quasiclassical methods which aim to address this issue have been proposed.34–39,48
In practice, both eqn (16) and (15) are evaluated by averaging over an ensemble of trajectories, propagated with Hamilton’s equations of motion defined by 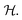 Initial conditions for each trajectory are sampled from ρwb(x,p) for the nuclei and ϕa(X,P) for the mapping variables.
Initial conditions for each trajectory are sampled from ρwb(x,p) for the nuclei and ϕa(X,P) for the mapping variables.
3 Results and discussion
3.1 The Fenna–Matthews–Olson Hamiltonian
The Fenna–Matthews–Olson complex is a pigment protein biomolecule found in green sulfur bacteria adapted for low-light environments. It consists of three identical trimers, each containing seven bacteriochlorophyll (BChl) pigments supported by a protein backbone. In photosynthesis the task of FMO is to transport the excitation gained from absorbing sunlight to the reaction centre where it is converted into electrochemical energy.40–42,44,49The Frenkel-exciton model for the energy transfer in FMO is a challenging benchmark for quantum dynamics methods. In comparison to the Spin–Boson systems studied in our previous work,39 the FMO Hamiltonian presents a different kind of challenge to quasiclassical dynamics methods: the electronic subsystem is comprised of more electronic states and the system-bath coupling is different. We note that the key challenge resulting from a larger electronic state space is the possibility of reaction chains involving more than two states. As a result this benchmark and the FMO system in general has been extensively studied using a considerable number of approaches.16,20,36–38,48,50–60 In addition, though computationally challenging, numerically exact results are available, e.g. from hierarchical equations of motion (HEOM).42–44,61,62
In the seven-site model (S = 7), the full FMO Hamiltonian is given by
| ĤFMO = Ĥs + Ĥsb + Ĥb, | (17) |
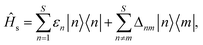 | (18) |
 | (19) |
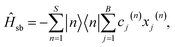 | (20) |
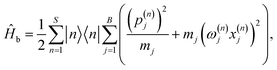 | (21) |
The frequencies, ωj(n), and coupling coefficients, cj(n), which are identical for each bath, are drawn from a spectral density of the Debye form, given by
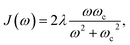 | (22) |
We define the initial nuclear density matrix ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) b = e−βĤb/Zb, where the partition function Zb is defined such that the trace over bath modes only is Trb[
b = e−βĤb/Zb, where the partition function Zb is defined such that the trace over bath modes only is Trb[![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0b7.gif) b] = 1. Nuclear positions and momenta were sampled from the thermal Wigner distribution of the uncorrelated bath, given, for any bath, by
b] = 1. Nuclear positions and momenta were sampled from the thermal Wigner distribution of the uncorrelated bath, given, for any bath, by
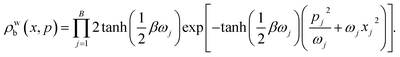 | (23) |
3.2 Simulation parameters
In order to test our alternative definition of the quasiclassical population in eqn (15), we investigated three parameter regimes of the FMO Hamiltonian, which have been studied extensively, including using the numerically exact HEOM approach.42–44,61,62 All our simulations used a timestep of δt = 1 fs, which was found to be numerically converged. The results presented here are averaged over an ensemble of 106 trajectories in order to demonstrate the converged performance of our approach. We found however that using as few as 103 trajectories was enough to qualitatively capture all significant features of the population dynamics and already exhibits a clear improvement over a fully converged traditional quasiclassical result. We note that in all our simulations, we used the traceless form of the![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (x) matrix to propagate our trajectories, absorbing the remainder into U(x). Finally, while the results presented here were obtained using the integrator presented in ref. 23, we have also tested the integrators discussed in ref. 65 and found our approach to be insensitive to the choice of integration scheme.
(x) matrix to propagate our trajectories, absorbing the remainder into U(x). Finally, while the results presented here were obtained using the integrator presented in ref. 23, we have also tested the integrators discussed in ref. 65 and found our approach to be insensitive to the choice of integration scheme.
3.3 Constituent correlation functions
Fig. 1 shows the constituent correlation functions, C![[Doublestruck I]](https://www.rsc.org/images/entities/char_e16c.gif) Qn(t) and CQmQn(t), calculated with electronic initial conditions having been sampled from both ϕ(X,P) and ϕ2(X,P).
Qn(t) and CQmQn(t), calculated with electronic initial conditions having been sampled from both ϕ(X,P) and ϕ2(X,P).
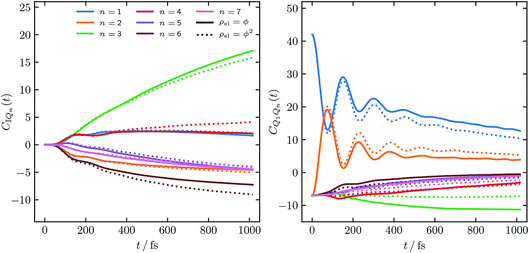 | ||
| Fig. 1 Constituent correlation functions of the FMO population, with T = 77 K, and τc = 50 fs and an initial excitation of site |1〉. The solid and dotted lines correspond to the electronic initial conditions having been sampled either from ϕ(X,P) or ϕ2(X,P). In eqn (15) this corresponds to a = 1 and a = 2 respectively. | ||
Considering the overall expression for the population given in eqn (14), the magnitudes of the constituent correlation functions are as one might expect. Notably the negative values observed for both C![[Doublestruck I]](https://www.rsc.org/images/entities/char_e16c.gif) Qn(t) and CQmQn(t) are not unphysical, as exact quantum mechanics would yield similar magnitudes for both correlation functions. We note that there is a noticeable difference between the correlation functions obtained from the two different initial distributions of the mapping variables we investigated. In order to assess their comparative accuracy however they must be combined, using eqn (14), into a population and compared to exact results.
Qn(t) and CQmQn(t) are not unphysical, as exact quantum mechanics would yield similar magnitudes for both correlation functions. We note that there is a noticeable difference between the correlation functions obtained from the two different initial distributions of the mapping variables we investigated. In order to assess their comparative accuracy however they must be combined, using eqn (14), into a population and compared to exact results.
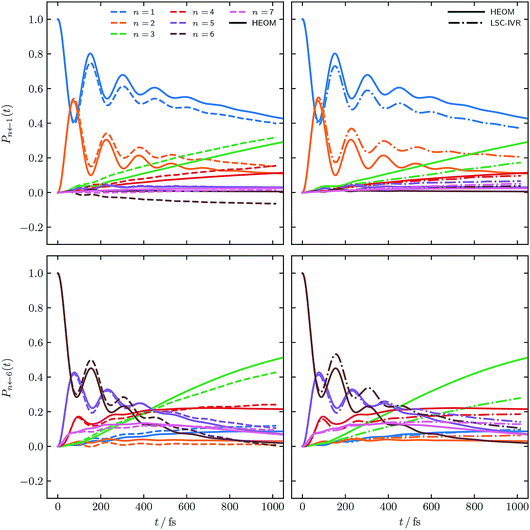
3.4 Population dynamics
Fig. 2 shows the population dynamics resulting from combining the constituent correlation functions using initial conditions sampled from ϕ(X,P), i.e. the solid lines in Fig. 1. In addition to results obtained for an initial excitation of the |1〉 site, populations starting in site |6〉 are also shown. In both cases the traditional PBME populations, calculated as per eqn (16a), are shown for comparison, along with numerically exact HEOM results.42–44,61,62 The comparison to PBME is a natural one here, as, in practice, the electronic initial conditions of PBME are also sampled from ϕ(X,P), i.e. a = 1. It is worth noting that this parameter regime of the FMO Hamiltonian is the most challenging for quasiclassical methods, due to the significant impact of quantum effects at low temperatures.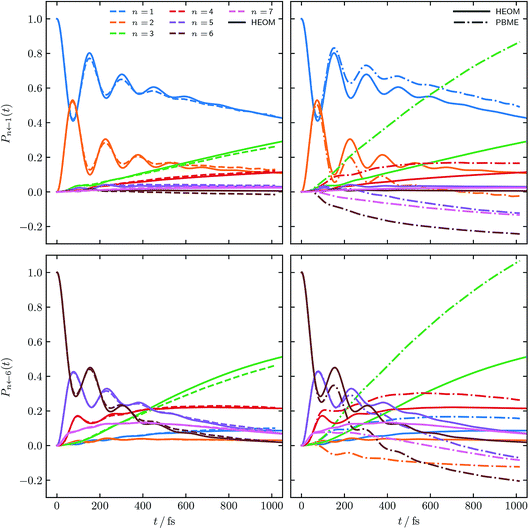 | ||
| Fig. 2 FMO site populations, with T = 77 K, and τc = 50 fs. Initial excitations of the |1〉 and |6〉 site are shown in the upper and lower panels respectively. Initial conditions for both constituent correlation functions sampled from ϕ(X,P). Results using our alternative population operator are shown as dashed lines, traditional PBME are dash-dotted while solid lines are the numerical HEOM benchmark.44 | ||
Our alternative definition of the population operators results in dynamics strikingly close in accuracy to the HEOM benchmark. We reproduce not only the correct ordering of states, even in the long time limit, but also capture all features present in the benchmark. We note that while we do observe negative populations for 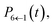 their magnitude is almost negligible. In addition, our values for
their magnitude is almost negligible. In addition, our values for 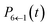 are within the same margin of error of the exact HEOM result as every other population. This is especially encouraging when comparing the accuracy of our approach to that achieved with traditional PBME. The latter, while capturing the population dynamics at short times rather well, completely fails to reproduce the long time behaviour. Notably the distribution and ordering of states beyond the short time limit degrades drastically with this approach. Considering that the low-temperature parameter regime of the FMO Hamiltonian poses a considerable challenge to quasiclassical methods, the accuracy of our results is highly encouraging.
are within the same margin of error of the exact HEOM result as every other population. This is especially encouraging when comparing the accuracy of our approach to that achieved with traditional PBME. The latter, while capturing the population dynamics at short times rather well, completely fails to reproduce the long time behaviour. Notably the distribution and ordering of states beyond the short time limit degrades drastically with this approach. Considering that the low-temperature parameter regime of the FMO Hamiltonian poses a considerable challenge to quasiclassical methods, the accuracy of our results is highly encouraging.
Fig. 3 shows populations for the same parameter regime of the FMO Hamiltonian as Fig. 2 however with electronic initial conditions now having been sampled from ϕ2(X,P). This corresponds to adding the dotted lines of Fig. 1 as per eqn (14). Also shown are standard LSC-IVR results, which again are a natural source of comparison as they use the same electronic initial conditions.
 | ||
| Fig. 3 FMO site populations, with T = 77 K, and τc = 50 fs. Initial conditions for both constituent correlation functions sampled from ϕ2(X,P). As in Fig. 2, results using our approach are shown as dashed lines and the numerical HEOM benchmark44 as solid lines. The dash-dotted results are the traditional LSC-IVR approach. | ||
Comparing to Fig. 2, LSC-IVR is seen to perform better than PBME for this particular parameter regime. Interestingly, the results achieved with our approach, using initial conditions sampled from ϕ2(X,P), do not give a considerable improvement over LSC-IVR. We thus conclude that the most consistently accurate method is that shown in Fig. 2 using our improved population operators and sampling from ϕ(X,P). This is the approach which we shall continue to employ for the remaining calculations.
Fig. 4 and 5 show the population dynamics of the FMO Hamiltonian, calculated with our alternative definition of the population operators and, as in Fig. 2, with electronic initial conditions sampled from ϕ(X,P), for two additional parameter regimes at T = 300 K. Traditional PBME is again shown for comparison along with numerically exact HEOM benchmark results.42–44,61,62 We note that the dynamics in the parameter regimes shown in these two figures are, owing to the higher temperature, less likely to be affected by nuclear quantum effects. Nevertheless it is clear that in the long-time limit, PBME diverges significantly from the HEOM benchmark and yields an incorrect distribution of states.
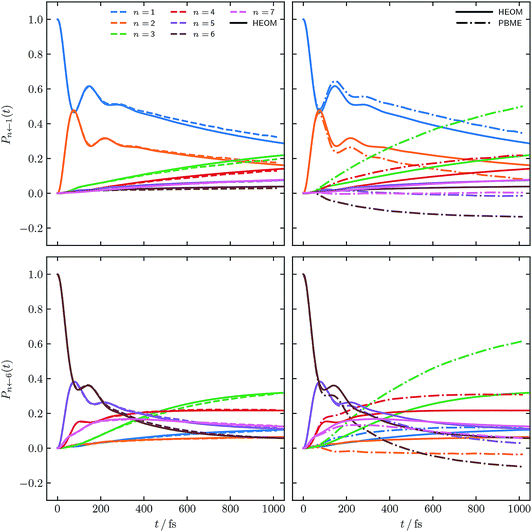 | ||
| Fig. 4 FMO site populations, with T = 300 K, and a slower bath, τc = 166 fs. Initial conditions for both constituent correlation functions sampled from ϕ(X,P). Results are presented as in Fig. 2 and compared to numerical HEOM benchmark results.44 | ||
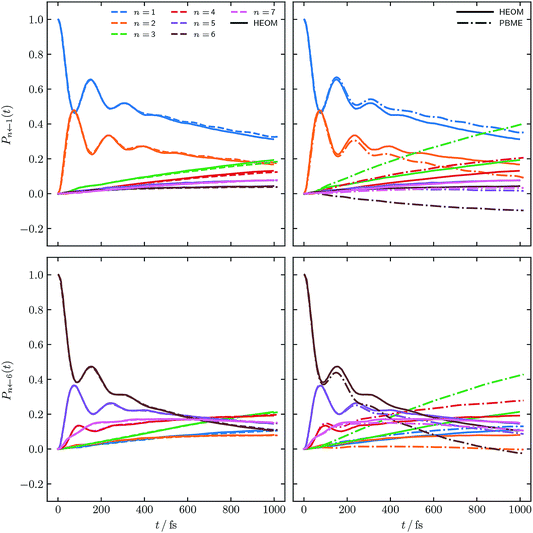 | ||
| Fig. 5 FMO site populations, with T = 300 K, and a faster bath, τc = 166 fs. Initial conditions for both constituent correlation functions sampled from ϕ(X,P). Numerical HEOM benchmark results are taken from ref. 42. | ||
Using our alternative definition of the population operator again drastically improves the traditional quasiclassical result in both cases. Our approach in fact yields dynamics which now approach quantitative accuracy with respect to the exact HEOM benchmark. We furthermore note that the issue of small negative populations observed for our approach observed in Fig. 2 has now disappeared. This is not surprising, given that low temperature systems are well known to constitute a more considerable challenge for quasiclassical approaches. We recognise that quasiclassical approaches are well known not to capture nuclear effects, owing to the fact that the trajectories underlying them are driven by classical equations of motion. We note however that our alternative definition of the population operator is in fact not limited to quasiclassical methods, but may be applicable to other approaches based on mapping, which can capture nuclear quantum effects, such as nonadiabatic ring polymer molecular dynamics.21–23,27–29
3.5 Populations in the long time limit
One of the well known failings of quasiclassical dynamics methods is that they do not preserve detailed balance of the populations and are therefore inaccurate at long times. In order to investigate whether our alternative definition of the population operator can improve on this, we have carried out a longer simulation of the parameter regime shown in Fig. 2 and 3. We used the same timestep, δt = 1 fs, as in the simulations above and averaged over the same number of trajectories (106). Fig. 6 shows the FMO site populations, following an initial excitation of either the |1〉 or the |6〉 site, up to 10 ps, calculated with our definition of the population operator. Electronic initial conditions for both were sampled from ϕ(X,P).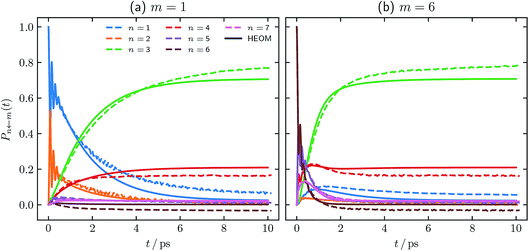 | ||
| Fig. 6 Long time FMO site populations, with T = 77 K, and τc = 50 fs. Initial conditions for both constituent correlation functions sampled from ϕ(X,P). Numerical HEOM benchmark results are taken from ref. 44. | ||
Comparing our results to the long-time limit of the HEOM benchmark,44 it is clear that our method does not rigorously preserve detailed balance. In addition, one of the populations is unphysically predicted to be slightly negative. We note however that as in Fig. 2 and 3, our negative result is within the same margin of error of the exact result as every other state population. It is well known that the long-time limits of the populations obtained from traditional quasiclassical approaches such as PBME and LSC-IVR can be much worse, predicting more strongly negative populations, and some greater than 1.50
We are therefore encouraged that the equilibrium distribution predicted using our approach is qualitatively similar to the HEOM benchmark. We note furthermore that our approach predicts identical equilibrium distributions, whether site |1〉 or site |6〉 is initially excited. We have not computed the long-time dynamics of the other two parameter regimes we studied above. We do however expect that, owing to their higher temperature and the lower impact nuclear quantum effects are therefore likely to have on them, our approach would perform even better than in the T = 77 K system. The fact that we do not observe negative populations in Fig. 4 and 5 further supports this hypothesis.
Overall we consider these population results, along with the others shown above, to be highly encouraging. They clearly demonstrate that our definition of the population operator can drastically improve the accuracy of traditional quasiclassical approaches11,14 at both intermediate and long times.
4 Conclusion
We have outlined an extension of our previous work,39 presenting an alternative definition of the electronic population operator for any system of multiple electronic states. We rely on the fact that any Hermitian operator can be split into two terms, one of which is the identity, the other being traceless.18 We then use our understanding of the exact behaviour of the quantum identity instead of a quasiclassical treatment. The combination of this splitting and exact treatment of the identity results in a new form of the electronic population operator. Our approach retains the excellent scaling with respect to system size of traditional quasiclassical methods as well as their underlying equations of motion. Notably, as the constituent correlation functions into which our new operator is split can be calculated for all states in a single simulation, our approach is no more computationally expensive than the traditional methods it seeks to improve.We have applied our approach to the challenging seven-state Frenkel-exciton model of the FMO light harvesting complex.40–44 In addition to having been studied extensively with traditional quasiclassical methods,50–52 the fact that numerically exact quantum results are available42–44,61,62 makes this system an ideal benchmark for our modification of the traditional quasiclassical population operators.
Overall we find that using our alternative definition of the electronic population operator drastically improves on the results obtainable with other quasiclassical methods. In addition, our results actually approach the exact quantum benchmark in accuracy for the three parameter regimes we study. Finally, we find that rather encouragingly, our method reproduces the long-time distribution of the electronic states with far higher accuracy than existing quasiclassical approaches.
We recognise that there have been other efforts to fix the well documented shortcomings of traditional quasiclassical dynamics methods. For instance, the symmetrical quasiclassical windowing approach uses “binning” to convert the population into an integer, using a windowing function applied symmetrically at the beginning and end of each classical trajectory.34–38 This approach has been applied to the FMO Hamiltonian we study here with considerable success, yielding results comparable in accuracy to those presented here.36–38
In recent work a post-processing method for the traditional LSC-IVR quasiclassical method has been proposed.48 The dynamics resulting from the traditional approach are shifted by a function which imposes the long-time Boltzmann distribution of the FMO subsystem Hamiltonian. We note that while the results obtained from this long-time correction do constitute an improvement over the traditional approach, they fail to address any inaccuracies at short to medium times. In addition, this approach relies on either having prior knowledge of the correct long-time distribution of states or approximating it.
Other mixed quantum-classical dynamics methods have also been applied to the FMO Hamiltonian with considerable success. In recent work both the forward-backward trajectory solution19,20 and the partially linearised density matrix16,17 approaches have yielded accurate results for the FMO systems studied here. We note however that these methods use a different set of equations of motion to propagate the classical trajectories from the quasiclassical approaches used here. This does however not disqualify them from also benefiting from our alternative definition of the population operator, as the latter is independent of the equations of motion.
While we have shown that our alternative definition of the electronic population operator can drastically improve on the dynamics obtained from traditional quasiclassical methods, it cannot address all their shortcomings. Notably, it cannot capture nuclear quantum effects, which are fundamentally inaccessible to an approach relying on purely classical trajectories to calculate operators. Due to its simplicity and generality however, our approach could be combined with methods which can capture some nuclear quantum effects such as tunnelling. The nonadiabatic ring polymer molecular dynamics21–23,27–29 method would seem to be a logical candidate for benefiting from our definition of the population operator, given that it is also based on the mapping formalism. We anticipate that the low temperature regime of the FMO Hamiltonian studied here may particularly benefit from such a combination, as nuclear quantum effects are likely to have a greater impact in this system.
Overall we have shown that using our alternative definition of the population operator results in a considerable improvement over traditional quasiclassical approaches. Our results in fact approach the accuracy of the numerically exact benchmark for the systems we have studied. This is highly encouraging, given that the traditional methods we compare to have previously been considered inadequate for the simulation of long-time nonadiabatic dynamics. Our modification does not involve changing the equations of motion underlying quasiclassical methods and in fact also scales identically. We therefore hope that this work will further the development of dynamics methods based on the quasiclassical approach, and the progress of mixed quantum-classical dynamics as a whole.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. A. C. S. and J. O. R. also acknowledge financial support via the ETH postdoctoral fellowship. The authors also acknowledge the support from the Swiss National Science Foundation through the NCCR MUST (Molecular Ultrafast Science and Technology) Network. The authors would also like to thank David Wilkins and Nike Dattani for providing their benchmark data.References
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599 CrossRef CAS.
- D. Chandler, Classical and Quantum Dynamics in Condensed Phase Simulations, World Scientific, Singapore, 1998, ch. 2, pp. 25–49 Search PubMed.
- J. C. Tully, J. Chem. Phys., 2012, 137, 22A301 CrossRef.
- H.-D. Meyer, U. Manthe and L. S. Cederbaum, Chem. Phys. Lett., 1990, 165, 73–78 CrossRef CAS.
- Multidimensional Quantum Dynamics: MCTDH Theory and Applications, ed. H.-D. Meyer, F. Gatti and G. W. Worth, Wiley-VCH, Weinheim, 2009 Search PubMed.
- G. W. Richings, I. Polyak, K. E. Spinlove, G. A. Worth, I. Burghardt and B. Lasorne, Int. Rev. Phys. Chem., 2015, 34, 269–308 Search PubMed.
- M. Ben-Nun and T. J. Martínez, J. Chem. Phys., 1998, 108, 7244 CrossRef CAS.
- M. A. C. Saller and S. Habershon, J. Chem. Theory Comput., 2017, 13, 3085–3096 CrossRef CAS PubMed.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- X. Sun and W. H. Miller, J. Chem. Phys., 1997, 106, 6346–6353 CrossRef CAS.
- X. Sun, H. Wang and W. H. Miller, J. Chem. Phys., 1998, 109, 7064–7074 CrossRef CAS.
- G. Stock and M. Thoss, Adv. Chem. Phys., 2005, 131, 243–376 CrossRef CAS.
- S. Bonella and D. F. Coker, J. Chem. Phys., 2005, 122, 194102 CrossRef CAS.
- H. Kim, A. Nassimi and R. Kapral, J. Chem. Phys., 2008, 129, 084102 CrossRef PubMed.
- N. Ananth and T. F. Miller III, J. Chem. Phys., 2010, 133, 234103 CrossRef.
- P. Huo and D. F. Coker, J. Chem. Phys., 2011, 135, 201101 CrossRef.
- P. Huo and D. F. Coker, Mol. Phys., 2012, 110, 1035–1052 CrossRef CAS.
- A. Kelly, R. van Zon, J. Schofield and R. Kapral, J. Chem. Phys., 2012, 136, 084101 CrossRef.
- C.-Y. Hsieh and R. Kapral, J. Chem. Phys., 2012, 137, 22A507 CrossRef PubMed.
- C.-Y. Hsieh and R. Kapral, J. Chem. Phys., 2013, 138, 134110 CrossRef PubMed.
- N. Ananth, J. Chem. Phys., 2013, 139, 124102 CrossRef.
- J. O. Richardson and M. Thoss, J. Chem. Phys., 2013, 139, 031102 CrossRef.
- J. O. Richardson, P. Meyer, M.-O. Pleinert and M. Thoss, Chem. Phys., 2017, 482, 124–134 CrossRef CAS.
- F. Agostini, A. Abedi and E. K. U. Gross, J. Chem. Phys., 2014, 141, 214101 CrossRef.
- N. Makri, Int. J. Quantum Chem., 2015, 115, 1209–1214 CrossRef CAS.
- R. Kapral, J. Phys.: Condens. Matter, 2015, 27, 073201 CrossRef.
- J. R. Duke and N. Ananth, J. Phys. Chem. Lett., 2015, 6, 4219–4223 CrossRef CAS.
- T. J. H. Hele and N. Ananth, Faraday Discuss., 2016, 195, 269–289 RSC.
- S. N. Chowdhury and P. Huo, J. Chem. Phys., 2017, 147, 214109 CrossRef.
- H.-D. Meyer and W. H. Miller, J. Chem. Phys., 1979, 70, 3214–3223 CrossRef CAS.
- G. Stock and M. Thoss, Phys. Rev. Lett., 1997, 78, 578–581 CrossRef CAS.
- A. Kelly, N. Brackbill and T. E. Markland, J. Chem. Phys., 2015, 142, 094110 CrossRef.
- A. Kelly, A. Montoya-Castillo, L. Wang and T. E. Markland, J. Chem. Phys., 2016, 144, 184105 CrossRef.
- S. J. Cotton and W. H. Miller, J. Phys. Chem. A, 2013, 117, 7190–7194 CrossRef CAS.
- S. J. Cotton and W. H. Miller, J. Chem. Phys., 2013, 139, 234112 CrossRef.
- W. H. Miller and S. J. Cotton, Faraday Discuss., 2016, 195, 9–30 RSC.
- S. J. Cotton and W. H. Miller, J. Chem. Theory Comput., 2016, 12, 983–991 CrossRef CAS.
- S. J. Cotton and W. H. Miller, J. Chem. Phys., 2019, 150, 104101 CrossRef.
- M. A. C. Saller, A. Kelly and J. O. Richardson, J. Chem. Phys., 2019, 150, 071101 CrossRef.
- R. E. Fenna and B. W. Matthews, Nature, 1975, 258, 573–577 CrossRef CAS.
- J. Adolphs and T. Renger, Biophys. J., 2006, 91, 2778–2797 CrossRef CAS PubMed.
- A. Ishizaki and G. R. Fleming, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 17255–17260 CrossRef PubMed.
- M. Sarovar, A. Ishizaki, G. R. Fleming and K. B. Whaley, Nat. Phys., 2010, 6, 462 Search PubMed.
- D. M. Wilkins and N. S. Dattani, J. Chem. Theory Comput., 2015, 11, 3411–3419 CrossRef CAS PubMed.
- U. Müller and G. Stock, J. Chem. Phys., 1999, 111, 77 CrossRef.
- U. Müller and G. Stock, J. Chem. Phys., 1998, 108, 7516–7526 CrossRef.
- S. Bonella and D. F. Coker, J. Chem. Phys., 2003, 118, 4370–4385 CrossRef CAS.
- H.-H. Teh and Y.-C. Cheng, J. Chem. Phys., 2017, 146, 144105 CrossRef PubMed.
- Y.-F. Li, W. Zhou, R. E. Blankenship and J. P. Allen, J. Mol. Biol., 1997, 271, 456–471 CrossRef CAS PubMed.
- G. Tao and W. H. Miller, J. Phys. Chem. Lett., 2010, 1, 891–894 CrossRef CAS.
- A. Kelly and Y. M. Rhee, J. Phys. Chem. Lett., 2011, 2, 808–812 CrossRef CAS.
- H. W. Kim, A. Kelly, J. W. Park and Y. M. Rhee, J. Am. Chem. Soc., 2012, 134, 11640–11651 CrossRef CAS PubMed.
- G. D. Scholes, C. Curutchet, B. Mennucci, R. Cammi and J. Tomasi, J. Phys. Chem. B, 2007, 111, 6978–6982 CrossRef CAS PubMed.
- J. Adolphs, F. Müh, M. E.-A. Madjet and T. Renger, Photosynth. Res., 2007, 95, 197 CrossRef PubMed.
- M. B. Plenio and S. F. Huelga, New J. Phys., 2008, 10, 113019 CrossRef.
- F. Caruso, A. W. Chin, A. Datta, S. F. Huelga and M. B. Plenio, Phys. Rev. A, 2010, 81, 062346 CrossRef.
- F. Fassioli and A. Olaya-Castro, New J. Phys., 2010, 12, 085006 CrossRef.
- A. Kolli, A. Nazir and A. Olaya-Castro, J. Chem. Phys., 2011, 135, 154112 CrossRef.
- A. Olaya-Castro and G. D. Scholes, Int. Rev. Phys. Chem., 2011, 30, 49–77 Search PubMed.
- A. W. Chin, J. Prior, R. Rosenbach, F. Caycedo-Soler, S. F. Huelga and M. B. Plenio, Nat. Phys., 2013, 9, 113 Search PubMed.
- A. Ishizaki, T. R. Calhoun, G. S. Schlau-Cohen and G. R. Fleming, Phys. Chem. Chem. Phys., 2010, 12, 7319–7337 RSC.
- J. Zhu, S. Kais, P. Rebentrost and A. Aspuru-Guzik, J. Phys. Chem. B, 2011, 115, 1531–1537 CrossRef CAS PubMed.
- H. Wang, M. Thoss and W. H. Miller, J. Chem. Phys., 2001, 115, 2979 CrossRef CAS.
- I. R. Craig, M. Thoss and H. Wang, J. Chem. Phys., 2007, 127, 144503 CrossRef PubMed.
- F. Martinez and G. Hanna, Mol. Simul., 2015, 41, 107–122 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |
