Open Access Article
Open Access ArticleHow quantum is radical pair magnetoreception?
Thomas P.
Fay†
,
Lachlan P.
Lindoy†
,
David E.
Manolopoulos
and
P. J.
Hore
 *
*
Department of Chemistry, Physical & Theoretical Chemistry Laboratory, University of Oxford, South Parks Road, Oxford OX1 3QZ, UK. E-mail: peter.hore@chem.ox.ac.uk
First published on 21st June 2019
Abstract
Currently the most likely mechanism of the magnetic compass sense in migratory songbirds relies on the coherent spin dynamics of pairs of photochemically formed radicals in the retina. Spin-conserving electron transfer reactions are thought to result in radical pairs whose near-degenerate electronic singlet and triplet states interconvert coherently as a result of hyperfine, exchange, and dipolar couplings and, crucially for a compass sensor, Zeeman interactions with the geomagnetic field. In this way, the yields of the reaction products can be influenced by magnetic interactions a million times smaller than kBT. The question we ask here is whether one can only account for the coherent spin dynamics using quantum mechanics. We find that semiclassical approximations to the spin dynamics of radical pairs only provide a satisfactory description of the anisotropic product yields when there is no electron spin–spin coupling, a situation unlikely to be consistent with a magnetic sensing function. Although these methods perform reasonably well for shorter-lived radical pairs with stronger electron-spin coupling, the accurate simulation of anisotropic magnetic field effects relevant to magnetoreception seems to require full quantum mechanical calculations.
Introduction
The biophysical mechanism by which migratory songbirds extract directional information from the Earth’s magnetic field is something of a mystery.1 The most promising hypothesis involves light-induced, magnetically sensitive chemical reactions in the birds’ retinas.2 Photo-excitation of the flavin adenine dinucleotide (FAD) chromophore in cryptochrome proteins is thought to trigger a sequence of intra-protein electron transfers along a chain of three or four tryptophan (Trp) residues, producing a FAD–Trp radical pair in a highly non-equilibrium (initially singlet) electron spin state.3 Electron-nuclear hyperfine interactions within the radicals break the symmetry of the two electron spins and drive coherent interconversion of the singlet and triplet states at MHz frequencies. These oscillations are sensitive to the strength and the direction of an external magnetic field via the electron Zeeman interaction and the anisotropic components of the hyperfine and dipolar interactions. If the singlet and triplet states of the radical pair react to give distinct products, the direction of the geomagnetic field vector with respect to the bird’s head direction could be encoded in the quantum yield of one of the products acting as a signaling state.2The radical pair mechanism is an established phenomenon supported by hundreds of laboratory-based studies of organic radical reactions and has a well-developed theoretical basis.4 That it provides birds with a magnetic compass bearing is less clear. Blue-light irradiation of purified cryptochromes produces magnetically sensitive FAD–Trp radical pairs which appear to be fit for purpose as magnetoreceptors.2,3 A cryptochrome-based radical pair sensor would be compatible with the observations that the avian compass is light-dependent,5,6 detects the inclination rather than the polarity of the Earth’s field,7,8 and can be disrupted by radiofrequency electromagnetic fields.9–11
The spin dynamics of radical pairs are fundamentally quantum mechanical. Unless the electron spins are strongly exchange-coupled, the initial singlet state is a coherent superposition of the spin eigenstates of the pair resulting in oscillatory time-dependence at frequencies corresponding to eigenvalue differences (Fig. 1). The main requirement for a magnetic field as weak as the Earth’s (∼50 μT) to affect the spin dynamics is that the coherence persists for at least one period (∼700 ns) of the electron Larmor frequency (∼1.4 MHz). This condition is not particularly restrictive: electron spin relaxation times of radicals in cryptochromes could be as long as ∼1 μs.12–14 Field-induced changes in the instantaneous probability that the radical pair is singlet or triplet determine the probability of the pair reacting along spin-selective pathways and translate into reaction product yields that depend on the intensity and direction of the magnetic field. Because the electron spins are not at thermal equilibrium, it is irrelevant that all the magnetic interactions are orders of magnitude weaker than kBT.
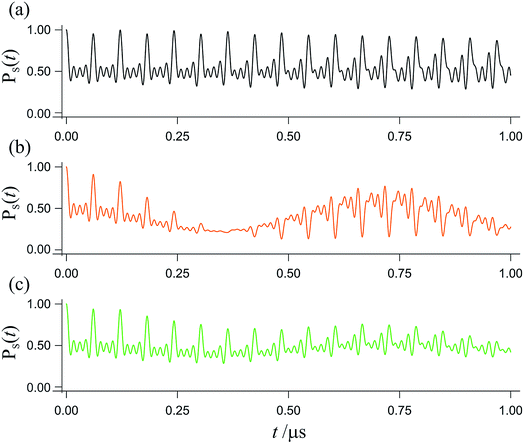 | ||
| Fig. 1 Interconversion of the singlet and triplet states of a model radical pair. The fraction of radical pairs in the singlet state, PS(t), has been calculated as a function of time (0 ≤ t ≤ 1 μs) starting in a singlet state at t = 0. (a) In the absence of an external magnetic field. (b) In the presence of a 50 μT external magnetic field. (c) As in panel (b) but with the magnetic field rotated by 90°. This model radical pair contains two nuclear spins in one radical (with hyperfine tensors appropriate for N5 and N10 in FAD˙−, ref. 35) and no nuclei in the other radical. For (b), the magnetic field is at an angle of 60° to the symmetry axis of the hyperfine interactions. Chemical reactions and spin relaxation were not included. | ||
The potential involvement of coherent spin dynamics in the “warm, wet and noisy” environment of a living cell has led to the inclusion of avian magnetic sensing in the currently fashionable field of “quantum biology”.15–19 Radical pair magnetoreception has proved popular amongst those interested in quantum information and quantum computation,20–24 and has prompted speculations about magnetic sensing devices inspired by the quantum physics of migratory birds.
But how “quantum” is this mechanism? The photochemical formation of the radical pair in a non-equilibrium electronic spin state is undeniably important. If the electron spins were always at thermal equilibrium (25% singlet, 75% triplet), weak Zeeman interactions would never be detectable in the reaction product yields. The question is whether one can only quantitatively account for the effects of coherent singlet-triplet interconversion using quantum mechanics. In the 1970s, Schulten and Wolynes (SW) proposed a semiclassical approximation in which the electron spin in each radical precesses around a hyperfine-weighted sum of classical nuclear spin vectors, assumed to be fixed in space.25 The approach was shown to be in excellent agreement with exact quantum simulations for a sufficiently large number, N, of nuclear spins. A few years ago, we presented an extension to the SW approach in which each individual nuclear spin is allowed to precess around the electron spin to which it is coupled.26 This method also approaches quantitative agreement with quantum mechanics for large numbers of coupled nuclear spins, and, unlike the SW theory, accurately captures the effects of weak external magnetic fields on long-lived radical pairs with isotropic hyperfine couplings. It has also been tested against exact quantum mechanical calculations for systems with anisotropic hyperfine interactions.27 It has not however been tested for systems in which both anisotropic interactions and electron-spin coupling are present.
Comparison of quantum and (semi)classical calculations is a standard way of assessing “quantumness” in other contexts.28 If classical motions of classical spin vectors could adequately describe the operation of a radical pair compass sensor, then avian magnetoreception would not be a quantum biological phenomenon. In this report we evaluate the accuracy with which three semiclassical methods reproduce quantum mechanical calculations of the reaction product yields of cryptochrome-based radical pairs.
Theoretical methods
In this section we outline the theory used in describing the radical pair spin dynamics, including the quantum master equation and effective spin Hamiltonian under which the spin density operator evolves. We also describe the methods employed here to perform the exact quantum mechanical and approximate semiclassical calculations of the product quantum yields of the radical pair reactions and their dependence on the direction of the applied magnetic field.Spin Hamiltonian and dynamical equations
Anisotropic magnetic field effects on the radical pair dynamics can be described by the following quantum master equation for the spin density operator for the radical pair,![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t):4,29–31
(t):4,29–31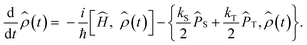 | (1) |
Here [·,·] is a commutator, {·,·} is an anticommutator, kS and kT are the first order recombination rate constants for the singlet and triplet pairs, and ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) S and
S and ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) T are projection operators onto the singlet and triplet electronic subspaces. Ĥ is the effective spin Hamiltonian for the radical pair, which is given by
T are projection operators onto the singlet and triplet electronic subspaces. Ĥ is the effective spin Hamiltonian for the radical pair, which is given by
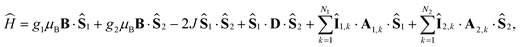 | (2) |
We will always take the radical pair to be initially in a singlet state, corresponding to the following initial condition,
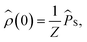 | (3) |
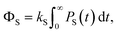 | (4) |
PS(t) = Tr[![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) S S![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t)]. (t)]. | (5) |
Model systems
We consider two model radical pairs based on the photochemistry of cryptochromes. One is [FAD˙− TrpH˙+], the magnetically sensitive state of the protein formed by electron transfer from the Trp-triad or tetrad to the photo-excited flavin chromophore (Fig. 2).3,32,33 The other is [FAD˙− Z˙], a hypothetical magnetic sensing state of cryptochrome,10,34 in which Z˙ is a radical with no hyperfine-coupled nuclear spins. Henceforth we refer to them as FAD–Trp and FAD–Z respectively. As the lifetimes, spin-coupling tensors and other properties of the radicals are not known in vivo, we consider simplified models of these species. Our prime interest is the ability of semiclassical approximations to capture the anisotropy of the singlet yield, ΦS. We ignore spin relaxation which generally diminishes the role of quantum mechanical coherences in the spin dynamics. As such, these models are likely to pose the largest challenge for semiclassical methods.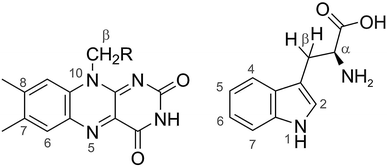 | ||
| Fig. 2 Structures of FAD (left) and Trp (right). The calculations with 7 hyperfine interactions in each radical used the following nuclei (chosen to be roughly in order of decreasing magnitude): N5, N10, H6, 3 × H8, 1 × Hβ in FAD˙− and N1, H1, H2, H4, H5, H7, Hβ1 in TrpH˙+. The following hyperfine interactions were added for the calculations with 11 nuclear spins in each radical: 1 × Hβ, 3 × H7 in FAD˙− and H6, Hα, Hβ2, and the NH2 nitrogen in TrpH˙+. The hyperfine tensors of all 22 nuclei are listed in ref. 35. | ||
We first consider models of FAD–Trp and FAD–Z in the absence of electron-spin coupling, with the number of hyperfine-coupled nuclear spins in each radical truncated at 7 or 11 (Fig. 2). The hyperfine coupling tensors were taken from ref. 35. We also consider models with non-zero electron-spin coupling. The dipolar interaction parameters36 (D = −0.38 mT, E = 0) were calculated for the FAD–TrpC radical pair in Drosophila cryptochrome, and the exchange interaction was taken to be J = 0.224 mT.37 The resulting total coupling tensor, C = D − 2J1, is
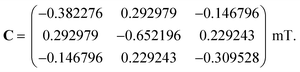 | (6) |
For comparison, we use the same C for the hypothetical FAD–Z pair for which J and D are unknown.
In all models, we only consider symmetric recombination, where kS = kT = k = 106 s−1, and take the g-values of both electron spins to be the free-electron g-value, g1 = g2 = ge. For each model, we calculate the singlet quantum yield as a function of the angle, θ, between the applied magnetic field and the normal to the plane of the tricyclic aromatic ring system of the FAD radical,
B(θ) = B(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, 0, cos θ, 0, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)⊤, θ)⊤, | (7) |
Quantum dynamics
For FAD–Z, eqn (4) and (5) can be evaluated exactly after numerical diagonalization of the Hamiltonian. The singlet quantum yield is then given by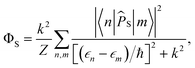 | (8) |
For the FAD–Trp radical pair when no electron-spin coupling is present, the Hamiltonian is separable into two lower-dimensional single-radical terms, Ĥ = Ĥ1 + Ĥ2. In this case the single-radical spin correlation tensors R(i)α,β(t) can be evaluated directly,
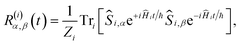 | (9) |
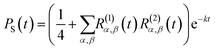 | (10) |
For the largest model system considered, FAD–Trp with electron-spin coupling and 7 nuclear spins in each radical, we employ a coherent state sampling method to evaluate PS(t). Using the resolution of the identity operator in terms of coherent spin states, PS(t) can be written as39,40
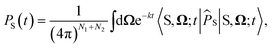 | (11) |
Semiclassical dynamics
We employ three different semiclassical methods for calculating the singlet quantum yields.Schulten–Wolynes theory
Within the Schulten–Wolynes (SW) approximation we replace the quantum mechanical spin operators Îi,k with static classical spin vectors Ii,k of length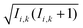 , and the trace over the nuclear spins is replaced with an integral over all orientations of the nuclear spin vectors,
, and the trace over the nuclear spins is replaced with an integral over all orientations of the nuclear spin vectors, 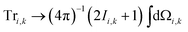 .25 The resulting approximation to the electron spin density operator,
.25 The resulting approximation to the electron spin density operator, ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (t) = TrN[
(t) = TrN[![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t)], is given by
(t)], is given by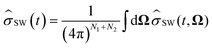 | (12) |
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) SW(t, Ω) is the electron spin density operator that evolves in the presence of the static nuclear spin vectors in given orientation Ω,
SW(t, Ω) is the electron spin density operator that evolves in the presence of the static nuclear spin vectors in given orientation Ω,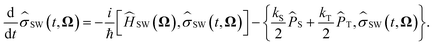 | (13) |
Here ĤSW(Ω) is the spin Hamiltonian Ĥ with all nuclear spin operators Îi,k replaced with static vectors Ii,k in a given orientation Ωi,k. This gives the Schulten–Wolynes approximation to the singlet probability PSWS(t). This approximation is exact when there are no hyperfine-coupled nuclei in either radical, and also in the limit of a very large number of hyperfine-coupled nuclei.
Improved semiclassical theory 1
An alternative approach is to note that the singlet projection operator is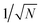 | (14) |
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) S autocorrelation function,
S autocorrelation function,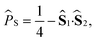 | (15) |
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) S(t) = e+iĤt/ℏ
S(t) = e+iĤt/ℏ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) Se−iĤt/ℏ. The semiclassical approximation to this in terms of one-spin variables (which we will call SC1) is obtained by replacing all operators with classical vectors, Îi,k(t) → Ii,k(t) and Ŝi(t) → Si(t), of length
Se−iĤt/ℏ. The semiclassical approximation to this in terms of one-spin variables (which we will call SC1) is obtained by replacing all operators with classical vectors, Îi,k(t) → Ii,k(t) and Ŝi(t) → Si(t), of length 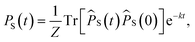 and
and 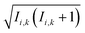 , and replacing
, and replacing ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) S(t) → PS(t,Ω) = 1/4 − S1(t)·S2(t). The trace is replaced with an integral over the orientations of all spin vectors, and the vectors evolve according to the Heisenberg equations of motion, again replacing all quantum mechanical operators with classical vectors,26
S(t) → PS(t,Ω) = 1/4 − S1(t)·S2(t). The trace is replaced with an integral over the orientations of all spin vectors, and the vectors evolve according to the Heisenberg equations of motion, again replacing all quantum mechanical operators with classical vectors,26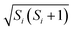 | (16) |
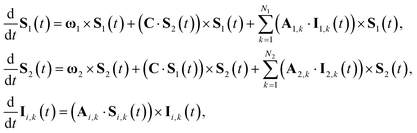 | (17) |
Improved semiclassical theory 2
As stated above, the SC1 approximation is not exact when electron-spin coupling is present, even when there are no hyperfine-coupled nuclei in either radical. To remedy this, we explicitly include two-electron spin variables, to give the SC2 approximation. As well as replacing single-spin quantum mechanical operators with classical variables, we also replace the set of nine two-electron spin operators with classical variables, Ŝ1(t)⊗Ŝ2(t) → T12(t). The singlet projection operator is replaced with![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) S(t) → 1/4 − Tr[T12(t)], and the equations of motion of the semiclassical variables are again obtained by taking the Heisenberg equations of motion and replacing time-dependent operators with their corresponding classical variables,42
S(t) → 1/4 − Tr[T12(t)], and the equations of motion of the semiclassical variables are again obtained by taking the Heisenberg equations of motion and replacing time-dependent operators with their corresponding classical variables,42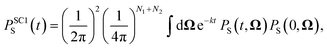 | (18) |
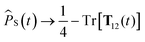 | (19) |
The initial value of T12(t) is set as T12(0) = S1(0)⊗S2(0) and the initial values of Si(t) and Ii,k(t) are sampled as in the SC1 approximation. The SC1 and SC2 approximations agree exactly when the electron-spin coupling tensor is zero, C = 0, but predict different dynamics in the presence of electron-spin coupling, the SC2 approximation being exact in the absence of hyperfine-coupled nuclei when C ≠ 0.
Results
FAD–Z radical pair
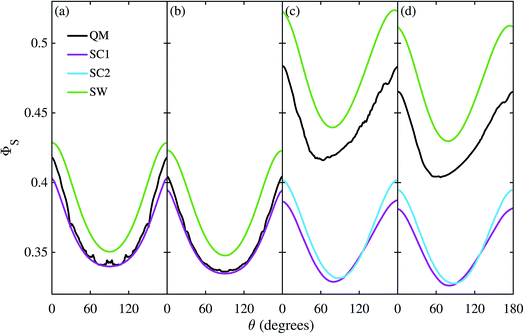
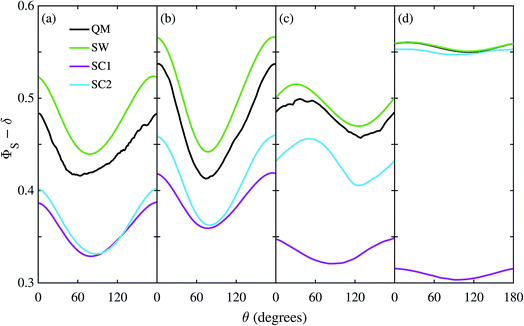
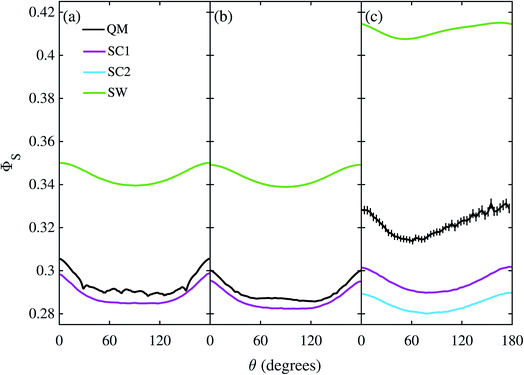
Fig. 3 shows the singlet yield, ΦS, as a function of the (1 mT) magnetic field direction for FAD–Z, the simpler of the two model radical pairs. When the electron spins are not coupled (a, b), the two SC approaches are identical and agree almost quantitatively with quantum mechanics apart from the weak fine structure arising from avoided energy-level crossings. As the number of nuclear spins increases, the fine structure is washed out and the accuracy of the SC method improves. As expected,26 the SW method is less accurate (although it correctly predicts the shape of ΦS). When electron exchange and dipolar interactions are included (c, d), all three semiclassical methods fail, getting the minimum of ΦS wrong by 15–30°. The situation is not improved by including 11 rather than 7 nuclear spins in FAD˙−, probably because the 4 extra nuclei have small anisotropic hyperfine interactions.The reason the SC methods fail in this case is that the electron–electron coupling is similar in strength to the hyperfine interactions. This point is demonstrated by Fig. 4 which shows the calculation of Fig. 3(c) repeated (a) with the coupling tensor, C, multiplied by 2, 5 and 10 (b–d). As the exchange and dipolar couplings increase, the SW and SC2 methods agree more closely with quantum mechanics, while the accuracy of the SC1 method (which does not allow for any quantum coherence between the two electron spins in the dynamics) degrades.
For this problem, the remarkable accuracy of the SW method for large C can be explained by a fortuitous cancellation of errors. The SC methods capture the effect of the motion of the nuclear spins, which drives singlet-triplet interconversion, however they ignore the effects of electron-nuclear quantum coherences, which reduce net singlet-triplet interconversion. The SW method on the other hand ignores both of these effects, which approximately cancel in this problem. This also explains why the SC1 and SC2 methods do not perform considerably better for the model when the number of nuclear spins is increased from 7 to 11. When the two electron spins interact, the electron spin in the Z radical couples indirectly to the nuclear spins, enhancing the effect of electron-nuclear spin coherences in the exact (QM) calculation, especially in this intermediate coupling regime.
FAD–Trp radical pair
The corresponding calculations for FAD–Trp are shown in Fig. 5 with the exception of the model with 22 nuclei and electron-spin coupling, for which the quantum calculation was impractical. The same pattern is found: SC1 and SC2 agree well, especially for the 22 nuclear spin model (b), and SW poorly, with quantum mechanics in the absence of electron coupling (a, b), and all three approximate methods do badly when the electrons are coupled (c). The poorer performance of the SC methods when no electron-spin coupling is present (a, b) is because these methods are all exact for the Z radical subsystem, but only approximate for the Trp radical. In the coupled case (c) the SC1 and SC2 methods perform better than the SW method for the average singlet yield, although they still do not quantitatively agree with the QM simulation. The relatively poor performance of the SW approximation in this case suggests that the motion of the nuclear spins is more important than the development of electron-nuclear coherences, in contrast to the situation for the FAD–Z radical pair (see Fig. 4).Discussion
When the two radicals do not interact, the SC1 and SC2 semiclassical methods agree well with quantum mechanics for both cryptochrome-based radical pairs. The question posed in the title of this paper therefore becomes: could a radical pair with negligible electron-spin coupling feasibly form the basis of a geomagnetic compass sensor? If the answer is yes, then radical pair magnetoreception arguably has no place in quantum biology.Both the exchange and dipolar interactions depend on the distance, R, between the radicals, the former approximately exponentially (e−βR), the latter as R−3. In Drosophila cryptochrome, R for FAD–Trp is either 1.91 nm or 2.21 nm depending on whether the third or the fourth tryptophan of the electron transfer chain is involved. We have used the former here, for which the dipolar coupling parameter D ≈ −400 μT (using a point-dipole approximation).37 When R = 2.21 nm, D ≈ −260 μT. The exchange interaction has a much shorter range and is probably negligible for R ≳ 2.2 nm.37 We expect that the semiclassical approaches would adequately reproduce the quantum spin dynamics only when D and J are smaller than the strength of the Earth’s magnetic field (i.e. ≲50 μT) which, for the dipolar coupling, requires R ≳ 3.82 nm. In principle, such a large distance between spin-correlated radicals in cryptochromes could be achieved if the electron transfer chain could be extended to include a binding-partner protein. However, the rate of back electron transfer from the singlet state of the radical pair varies approximately as e−βR and is almost certainly slower than 105 s−1 for R ≳ 2 nm.45 As spin relaxation in the radicals is unlikely to be much slower than 1 μs,12 all spin coherence in a radical pair with R ≳ 2 nm would be lost before significant recombination could take place and no magnetic field effects would arise. It therefore seems highly improbable that significant magnetic sensitivity is compatible with sufficiently weak electron-spin coupling. The only way we know of that this restriction could be circumvented is if Kattnig’s paramagnetic scavenging proposal turns out to be right.46,47
We anticipate that the semiclassical approximations may provide unsatisfactory descriptions of the spin dynamics in three other situations: (a) when the two spin-selective rate constants, kS and kT, differ significantly; (b) when pronounced avoided level-crossing effects are present in ΦS; and (c) when the radical that partners FAD˙− contains only a few (e.g. 2 or 3) hyperfine-coupled nuclear spins.
(a) When kS = kT, the sum of the two spin-selective recombination operators (eqn (1)) is proportional to the identity operator which uncouples the coherent spin dynamics from the incoherent kinetics. This is not the case when kS ≠ kT because the recombination operators (like the exchange and dipolar terms in the spin Hamiltonian) are bilinear in the two electron spins. Symmetric recombination of FAD–Trp in cryptochrome is unlikely. There is no triplet product energetically accessible from the radical pair state, meaning that spin-selective singlet recombination must compete with non-spin-selective (de)protonation of one or both radicals to generate a magnetic field effect.3 Even if the rate constants for these competing processes are equal, the fact that singlet and triplet both undergo the (de)protonation step, while only the singlet recombines, means that the kinetics are once again coupled to the coherent spin dynamics. Similar arguments would apply to FAD–Z and other putative FAD˙−-containing radical pairs.34
(b) Previous simulations of the FAD–Trp models without electron-spin coupling show that when the spin coherence lasts longer than a few microseconds, the rather shallow and broad minimum in ΦS (Fig. 5) acquires a sharp and pronounced “spike” that perhaps could provide birds with a more precise compass bearing.35 This “quantum needle” arises from avoided level-crossings associated with the hyperfine tensors for the two nitrogen atoms (N5 and N10) in FAD˙−. Fundamentally quantum effects such as this would not be captured by semiclassical methods35 and are anyway destroyed by electron-spin coupling.11
(c) As shown in ref. 26, the semiclassical approximations do not perform well when one of the radicals contains a small number of hyperfine interactions. An example would be [FAD˙− Asc˙−] in which Asc˙− is a radical derived from ascorbic acid.34 It is only when there are enough nuclear spins that the coherent oscillations are largely damped by destructive interference that the semiclassical methods approach quantitative agreement with quantum mechanics.
On the other hand, in these models we have not included the effects of spin relaxation, which results from the coupling of the spins to their environment. Relaxation leads to decay of quantum mechanical coherences between the electron and nuclear spins, which may lead to better performance of the semiclassical methods. The extent of spin relaxation depends on the details of nuclear motions which modulate spin interactions in the radical pairs, and is hard to predict quantitatively. A detailed analysis of semiclassical methods and relaxation effects is beyond the scope of this work.
Conclusion
We find that semiclassical approximations to the spin dynamics of radical pairs only provide a satisfactory description of the anisotropic reaction product yields when there is no electron-spin coupling, a situation unlikely to be consistent with a magnetic sensing function. Although semiclassical methods perform reasonably well for shorter-lived radical pairs with stronger electron-spin coupling,48 for which it is valid to treat the hyperfine interactions as a perturbation, the accurate simulation of anisotropic magnetic field effects relevant to magnetoreception seems to require full quantum mechanical calculations. We therefore conclude that radical pair avian magnetoreception may indeed have a place in “quantum biology”.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to the following for financial support: the Air Force Office of Scientific Research (Air Force Materiel Command, USAF award no. FA9550-14-1-0095) and the European Research Council (under the European Union’s Horizon 2020 research and innovation programme, grant agreement no. 810002). TPF is supported by a Clarendon Scholarship from Oxford University, an E.A. Haigh Scholarship from Corpus Christi College, Oxford, and by the EPSRC Centre for Doctoral Training in Theory and Modelling in the Chemical Sciences, EPSRC Grant No. EP/L015722/1. LPL is supported by a Perkin Research Studentship from Magdalen College, Oxford; an Eleanor Sophia Wood Postgraduate Research Travelling Scholarship from the University of Sydney; and a James Fairfax Oxford Australia Scholarship.References
- H. Mouritsen, Nature, 2018, 558, 50–59 CrossRef CAS.
- P. J. Hore and H. Mouritsen, Annu. Rev. Biophys., 2016, 45, 299–344 CrossRef CAS.
- K. Maeda, A. J. Robinson, K. B. Henbest, H. J. Hogben, T. Biskup, M. Ahmad, E. Schleicher, S. Weber, C. R. Timmel and P. J. Hore, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4774–4779 CrossRef CAS.
- U. E. Steiner and T. Ulrich, Chem. Rev., 1989, 89, 51–147 CrossRef CAS.
- W. Wiltschko and R. Wiltschko, J. Exp. Biol., 2001, 204, 3295–3302 CAS.
- R. Wiltschko, K. Stapput, P. Thalau and W. Wiltschko, J. R. Soc., Interface, 2010, 7, S163–S177 CrossRef PubMed.
- R. Wiltschko and W. Wiltschko, Magnetic orientation in animals, Springer Verlag, Berlin, 1995 Search PubMed.
- W. Wiltschko and R. Wiltschko, Science, 1972, 176, 62–64 CrossRef CAS PubMed.
- T. Ritz, P. Thalau, J. B. Phillips, R. Wiltschko and W. Wiltschko, Nature, 2004, 429, 177–180 CrossRef CAS PubMed.
- T. Ritz, R. Wiltschko, P. J. Hore, C. T. Rodgers, K. Stapput, P. Thalau, C. R. Timmel and W. Wiltschko, Biophys. J., 2009, 96, 3451–3457 CrossRef CAS PubMed.
- H. G. Hiscock, H. Mouritsen, D. E. Manolopoulos and P. J. Hore, Biophys. J., 2017, 113, 1475–1484 CrossRef CAS PubMed.
- D. R. Kattnig, I. A. Solov’yov and P. J. Hore, Phys. Chem. Chem. Phys., 2016, 18, 12443–12456 RSC.
- D. R. Kattnig, J. K. Sowa, I. A. Solov’yov and P. J. Hore, New J. Phys., 2016, 18, 063007 CrossRef.
- S. Worster, D. R. Kattnig and P. J. Hore, J. Chem. Phys., 2016, 145, 035104 CrossRef.
- S. F. Huelga and M. B. Plenio, Contemp. Phys., 2013, 54, 181–207 CrossRef CAS.
- N. Lambert, Y. N. Chen, Y. C. Cheng, C. M. Li, G. Y. Chen and F. Nori, Nat. Phys., 2013, 9, 10–18 Search PubMed.
- Quantum effects in biology, ed. M. Mohseni, Y. Omar, G. S.Engel and M. B. Plenio, Cambridge University Press, Cambridge, 2014 Search PubMed.
- A. Marais, B. Adams, A. K. Ringsmuth, M. Ferretti, J. M. Gruber, R. Hendrikx, M. Schuld, S. L. Smith, I. Sinayskiy, T. P. J. Kruger, F. Petruccione and R. van Grondelle, J. R. Soc., Interface, 2018, 15, 20180640 CrossRef.
- J. Al-Khalili and J. McFadden, Life on the edge: the coming of age of quantum biology, Bantam Press, London, 2014 Search PubMed.
- J. Cai, G. G. Guerreschi and H. J. Briegel, Phys. Rev. Lett., 2010, 104, 220502 CrossRef PubMed.
- E. M. Gauger, E. Rieper, J. J. L. Morton, S. C. Benjamin and V. Vedral, Phys. Rev. Lett., 2011, 106, 040503 CrossRef PubMed.
- H. J. Hogben, T. Biskup and P. J. Hore, Phys. Rev. Lett., 2012, 109, 220501 CrossRef.
- M. Tiersch and H. J. Briegel, Philos. Trans. R. Soc., A, 2012, 370, 4517–4540 CrossRef.
- Y. T. Zhang, G. P. Berman and S. Kais, Phys.Rev. E, 2014, 90, 042707 CrossRef.
- K. Schulten and P. G. Wolynes, J. Chem. Phys., 1978, 68, 3292–3297 CrossRef CAS.
- D. E. Manolopoulos and P. J. Hore, J. Chem. Phys., 2013, 139, 124106 CrossRef CAS.
- A. Lewis, Spin Dynamics in Radical Pairs, Springer International Publishing, 2018 Search PubMed.
- W. H. Miller, J. Chem. Phys., 2012, 136, 210901 CrossRef.
- R. Haberkorn, Mol. Phys., 1976, 32, 1491–1493 CrossRef CAS.
- T. P. Fay, L. P. Lindoy and D. E. Manolopoulos, J. Chem. Phys., 2018, 149, 064107 CrossRef.
- K. L. Ivanov, M. V. Petrova, N. N. Lukzen and K. Maeda, J. Phys. Chem. A, 2010, 114, 9447–9455 CrossRef CAS PubMed.
- D. Nohr, S. Franz, R. Rodriguez, B. Paulus, L.-O. Essen, S. Weber and E. Schleicher, Biophys. J., 2016, 111, 301–311 CrossRef CAS PubMed.
- P. Müller, J. Yamamoto, R. Martin, S. Iwai and K. Brettel, Chem. Commun., 2015, 51, 15502–15505 RSC.
- A. A. Lee, J. C. S. Lau, H. J. Hogben, T. Biskup, D. R. Kattnig and P. J. Hore, J. R. Soc., Interface, 2014, 11, 20131063 CrossRef.
- H. G. Hiscock, S. Worster, D. R. Kattnig, C. Steers, Y. Jin, D. E. Manolopoulos, H. Mouritsen and P. J. Hore, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 4634–4639 CrossRef CAS.
- A. Schweiger and G. Jeschke, Principles of pulse electron paramagnetic resonance, Oxford University Press, New York, 2001 Search PubMed.
- O. Efimova and P. J. Hore, Biophys. J., 2008, 94, 1565–1574 CrossRef CAS.
- C. R. Timmel, U. Till, B. Brocklehurst, K. A. McLauchlan and P. J. Hore, Mol. Phys., 1998, 95, 71–89 CrossRef CAS.
- A. M. Lewis, T. P. Fay and D. E. Manolopoulos, J. Chem. Phys., 2016, 145, 244101 CrossRef.
- T. P. Fay, A. M. Lewis and D. E. Manolopoulos, J. Chem. Phys., 2017, 147, 064107 CrossRef PubMed.
- J. M. Radcliffe, J. Phys. A: Gen. Phys., 1971, 4, 313–323 CrossRef.
- A. M. Lewis, D. E. Manolopoulos and P. J. Hore, J. Chem. Phys., 2014, 141, 044111 CrossRef.
- J. C. Varilly and J. M. Gracia-Bondia, Ann. Phys., 1989, 190, 107–148 Search PubMed.
- F. Li, C. Braun and A. Garg, Europhys. Lett., 2013, 102, 60006 CrossRef CAS.
- C. C. Moser, J. L. R. Anderson and P. L. Dutton, Biochim. Biophys. Acta, Bioenerg., 2010, 1797, 1573–1586 CrossRef CAS PubMed.
- D. R. Kattnig and P. J. Hore, Sci. Rep., 2017, 7, 11640 CrossRef.
- D. R. Kattnig, J. Phys. Chem. B, 2017, 121, 10215–10227 CrossRef CAS.
- T. Miura, A. M. Scott and M. R. Wasielewski, J. Phys. Chem. C, 2010, 114, 20370–20379 CrossRef CAS.
Footnote |
| † TPF and LPL contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |