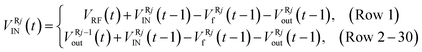Open Access Article
Open Access ArticleModelling the clogging of a field filtration system used for stormwater harvesting
Harpreet
Kandra
 a,
David T.
McCarthy
a,
David T.
McCarthy
 b,
Ana
Deletic
b,
Ana
Deletic
 c and
Kefeng
Zhang
c and
Kefeng
Zhang
 *c
*c
aSchool of Science, Engineering and IT, Federation University Australia, Churchill, Victoria 3842, Australia
bEnvironmental and Public Health Microbiology Laboratory (EPHM Lab), Department of Civil Engineering, Monash University, Wellington Road, Clayton, VIC 3800, Australia
cWater Research Centre, School of Civil and Environmental Engineering, UNSW Sydney, NSW 2052, Australia. E-mail: Kefeng.zhang@unsw.edu.au; Tel: +61 2 9385 5072
First published on 31st January 2020
Abstract
Non-vegetated high-flow stormwater filters have had widespread implementation in urban areas for stormwater management due to their small footprints. Relevant studies on investigation and modelling of the clogging of these systems, however, are quite limited, especially where they are based on real field observations. In this study, the infiltration rates (IR) of a field stormwater harvesting system, consisting of individual high-flow modules for water filtration, were monitored over a 2.5-year time period. A simple conceptual model, comprising a rainfall runoff model and a water balance model (that includes a water distribution model and a linear/exponential regression model), was developed to simulate the evolution of the IR of each filter module. The field observations show that the IR of the entire system dropped from 2000 mm h−1 to an average of 711 mm h−1 after 2.5 years of operation, with the filters closer to the inlet having the lowest IR at the end of testing (i.e., only 167 mm h−1). The models were calibrated highly satisfactorily against a different number of field observation events, with an average Nash–Sutcliffe coefficient (E) value of 0.64 and mean absolute error (MAE) value of 11.8. The validation results show that the linear regression model had better performance, with E mostly being positive (0.03–0.60) and MAE values (15.0–18.9) smaller than the exponential regression model (E < 0 in many cases, and MAE = 14.5–20.7). Compared to the results of previous laboratory experiments, data from this study indicate a slower decline rate of IR in field conditions, showing the importance of natural wetting/drying regimes for the longevity of such filters. The model could be very useful for optimisation of the design and long-term maintenance (e.g., replacement of clogged filter modular components) of modular filtration systems.
Water impactNon-vegetated stormwater filters are widely implemented in urban areas due to their small footprints. This study examines, at the field scale, the evolution of infiltration rate of a stormwater filtration system over 2.5 years. A simple conceptual model, developed and validated successfully against the field observations, can be used to optimise the design and long-term maintenance of such stormwater filters. |
1. Introduction
Urban stormwater can be treated and harvested for a range of non-potable urban water uses, reducing the pressure on the existing potable water supply.1 Often this can be done through Water Sensitive Urban Design (WSUD) technologies (e.g., raingardens, porous pavements, and wetlands) that have been traditionally developed for runoff volume control and stormwater pollution mitigation.2,3 WSUD are multifunctional systems that provide various other benefits, such as frequent flood mitigation under changing climates, flow regime restoration, as well as amenity improvements.4–6 However, their relatively large size and low reliability are often seen as key barriers in their implementation for stormwater harvesting, especially in space-limited urban areas.Despite the implementation of non-vegetated high-flow stormwater filters (infiltration rate – IR often >800 mm h−1) in urban areas due to their smaller footprints,7,8 studies on these systems are still limited, especially in comparison to studies on vegetated systems such as bioretentions that have much lower IR (usually <300 mm h−1, and up to 600 mm h−1 in tropical conditions).9,10 Clogging of the high-flow filters is an operational issue that can lead to diminishing of their performance and ultimately failure of the system.11 Therefore, the longevity of these stormwater systems is a limiting factor for acceptance of these technologies.
Current studies to understand clogging processes in the context of high-flow stormwater filters are mainly limited to laboratory environments. These studies have been undertaken under controlled conditions using synthetic stormwater.12,13 Due to logistical reasons, they have often been done in compressed time periods, simulating years or over a decade of a system's operational life over only a few weeks to months.8,14 For example, Kandra et al. (2014)15 tested the impact of stormwater characteristics on the clogging of stormwater filters in the laboratory within a year to mimic over 10 years of system operation, and found clogging is specific to the type of water treated (e.g., sediment levels and sizes) and loading rates. Although stormwater loading regime was found to be less influential to the clogging in their compressed study, it was suggested that further studies were needed to understand the impact of drying and wetting regimes and/or higher pollution concentrations, which is very likely to occur in field conditions. Biological clogging (i.e., the pore of media space is clogged by microbes), which does not usually occur in accelerated laboratory experiments, was also found to impact upon the clogging.16 Given the unfortunate scarcity of relevant field studies, it is therefore pertinent to study clogging processes in the context of non-vegetated stormwater filters with high IRs in field conditions.
In addition, stormwater models have largely focused on vegetated filtration systems, such as grass swales and bioretentions,17,18 where extensive laboratory and field investigations are available. Siriwardene et al. (2007)19 used the results of laboratory experiments to test two models to predict the sediment transport through a stormwater gravel filter and found the models were able to reliably predict sediment behavior in clean filters but failed once the filter accumulated sediment. There are also models developed in similar stormwater systems specifically on the clogging process, such as infiltration trenches20 and porous pavements.21 A four-parameter black-box regression model was proposed by Yong et al. (2013)21 to predict physical clogging of porous pavements as a function of cumulative volume and climatic conditions, using the data from accelerated laboratory experiments. Relevant studies on simulating the clogging of stormwater filters with high infiltration rates are however quite limited, especially those based on real field observations.
The aim of his study, therefore, are two folded: (1) understanding the long-term hydraulic performance of a field stormwater harvesting system consisting of individual high-flow filter modules located in Melbourne, Australia; (2) developing a simple conceptual model that is generally applicable to high flow filter systems for predicting their clogging (i.e., evolution of infiltration rate (IR)) over time, using the results from this field infiltration systems. The results of the study can then be used to optimise the design and long-term maintenance of high flow modular filtration systems. Specific objectives of this study include the following:
• monitor the change of IR for the field system over 2.5 years;
• develop and test a simple conceptual model to estimate the changes in IR over time; and
• compare the results from the field site to the laboratory findings collected previously.
2. Methods
2.1 Description of site and treatment systems
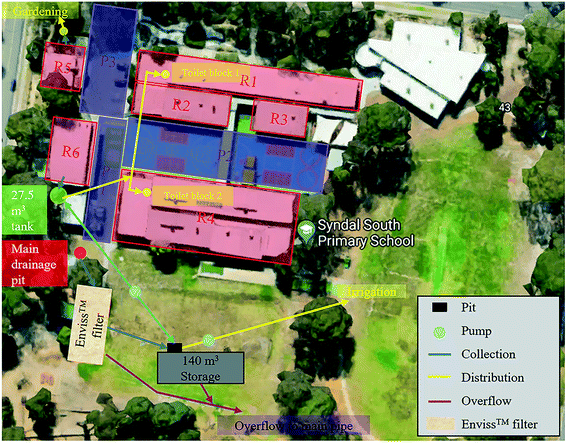
Fig. 1 shows the stormwater harvesting system located in Melbourne, Australia, where Enviss™ filters have been installed for treatment of stormwater from the 5000 m2 catchment consisting of roofs (R1–R6) and paved areas (P1–P3). The Enviss™ filter has been developed to remove key pollutants (nutrients, microbes, metals and hydrocarbons) from stormwater.22 Although Enviss™ filter is a proprietary system, it represents a group of high flow infiltration systems, with an initial IR of about 2000–2500 mm h−1, and is among the systems with the highest flow rate in Australian practice,23 and thus has an advantage over other WSUD measures when stormwater needs to be treated within space-constrained urban environments.24The Enviss™ filter system has a size of 20 m × 1.12 m (length × width), with a maximum ponding of 0.15 m, and a total effective filter area of only 8 m2 (i.e., 0.16% of the impervious catchment area), which is able to treat 80% of flows expected from the catchment at a design IR of 2000 mm h−1. Treated water from the filter is conveyed to the storage tank and then used for irrigation of the sports grounds and toilet flushing of the school's main buildings. It is made of 60 treatment modules (in two rows of 30 pits) with an inlet at one end (Fig. 2a). Two overflow chambers draining into the public stormwater system were set along the system, with one shown in Fig. 2a and another at the end of the system next to cells in row 30.
 | ||
| Fig. 2 The Enviss™ filter system installed at Syndal South Primary School (a), the configuration of each filter module (b), and the schematic of the system for testing (c). | ||
The filters are modular (Fig. 2b), consisting of: (1) a trafficable porous pavement grate that removes gross pollutants; (2) a replaceable sediment trap (layered filtration media) that protects the underlying filter from premature clogging; (3) a sand-based, fine filter media layer that removes finer sediments and dissolved pollutants (e.g., nutrients and metals);22 and (4) a drainage layer to prevent filter media migration and outlet clogging.
2.2 Monitoring of IR in the field system
The field measurements of IRs were undertaken for 13 of the 60 modules at various distances from the inlet (Fig. 2c) six times over a 2.5-year period, namely event 1 (17 April 2010), event 2 (19 April 2011), event 3 (10 May 2011), event 4 (31 May 2011), event 5 (14 May 2012), and event 6 (07 June 2012). Days have been selected to allow comparisons both over long-term and short-term intervals. Before the measurements, the lids of porous pavement (PP) were removed from all the cells, as the intent was to study the underlying filter media. Previous laboratory work for layered systems also suggests that it is the hydraulic performance of the finest media that controls the overall performance of a layered filtration system.8 Poly-ethylene sheets were then placed on the top of the cell to facilitate even water distribution. Each filter cell was filled with tap water and kept saturated for two hours before taking field measurements. A constant ponding depth was maintained during the measurements, and the inflow rate was measured three times using a 9 L bucket and stopwatch to estimate the average IR.2.3 Model development
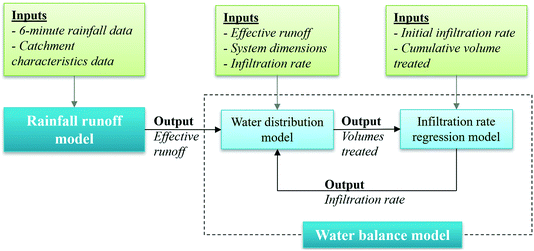
A model with two main components was developed to allow continuous simulation of IR decline of these filters over time: (Fig. 3): (1) the rainfall-runoff model, which simulates inflow into the system, and (2) the water balancing model, which includes: water distribution model to assess how much water is treated within a given time step, the distribution of inflow across different rows of the entire filter system, and the cumulative treated volume over time; and IR regression model that predicts decline of IR in each row as a simple function of cumulative treated volume. The model inputs are: time series rainfall data, system dimensions and initial value of IR (i.e., 2000 mm h−1).| (1) | RF(t) = Loss(t) − IL if Loss(t) > IL, else equals to 0 |
| (2) | Loss(t) = Rain(t) + Loss (t − 1) − RF(t − 1) − ILR(t) |
| (3) | ILR(t) = IL/(24 × 60) × 6 if Rain(t) = 0, else equals to 0 |
| (4) | Rout(t) = RF(t) + Rout(t − 1) − Rout(t − 1) |
| (5) | R out(t) = Rout(t) × Crout |
| (6) | V RF(t) = Rout(t) × Catchment impervious area |
| Wherein | |
| RF(t) | Effective runoff at time t, mm |
| Loss(t) | Initial loss bucket at time t, mm |
| IL | Initial infiltration loss of the catchment, equals to 1.0 mm |
| Rain(t) | Rainfall at time t, mm, collected from Melbourne Water's Notting Hill rain gauge station (2.8 km south-east of the site), 6 min resolution |
| ILR(t) | Accounts for initial infiltration loss recovery if no rain occurs over the 6 min timestep |
| Rout(t) | Routing bucket at time t, mm |
| R out(t) | Routed outflow at time t, mm |
| C out | Routing coefficient, 0.05 |
| V RF(t) | Runoff created at time t, L |
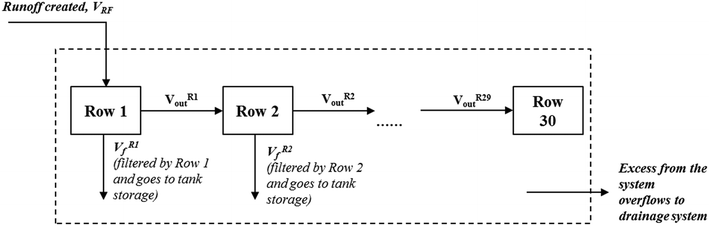
Component 1 – water distribution model. The concept of this model and the equations are shown in Table 2. Effective runoff first reaches row 1 (consisting of cells L1 and R1, Fig. 2c) and infiltrates vertically to fill in the cells comprising voids in the filter bed, sediment trap, and the free space in each of the cells. Any excess volume of untreated flow from row 1 (i.e., the volume of inflow minus volume filtered for a given time step) flows into the cells in row 2, and so on. Once all rows are in operation and effective runoff is greater than the capacity of the system (equal to volume of water held by all cells minus outflow), water starts ponding on top of the permeable pavement and then overflow occurs when the ponding depth exceeds 0.15 m. Therefore, there is a continuous process of filling, infiltrating, emptying, and overflowing. As the cells clog overtime, their IR drops and therefore the volume of water treated also drops.
In the water distribution model, the following assumptions were made:
• Any flow resistance by the porous pavement of the filter (the top 50 mm of the filter) was ignored. This assumption is in line with findings from our previous laboratory work for layered systems, where it was found that hydraulic performance of the finest media (the fine filter media, in this case) controls overall performance of the layered system.8
• It was also assumed that all modular units perform similarly and have a design initial IR of 2000 mm h−1. This means that any effect of a longer drying period on the modules located at the end of the filtration system is neglected and all modules perform with comparable treatment efficiency. Thus, we can group two cells to form one row.
• As water overflows through to the downstream cells, no treatment occurs in the upstream cells (i.e., sediment concentration in stormwater entering the different cells across all rainfall events is similar/comparable).
• The sandpit in the school play area next to the system (Fig. 2a) was assumed to have negligible impact on the system.
Component 2 – IR regression model. The decline in IR is related to the mass of sediment retained by the filter bed, as observed from laboratory experiments.8 The amount of sediment trapped is in turn a function of the amount of water treated by the system and its treatment efficiency. Since the treatment efficiency of a modular system is rather constant with time, the main assumption for this component of the model is that decline in IR of each filter is a simple function of the total volume treated by the cell, assuming inflow water quality and treatment performance are consistent. Preliminary laboratory results suggest that the decline in IR for the similar filtration systems follow either linear or exponential trends,8,15 hence these two different regression approaches were tested for the field system in the current study (Table 3).
| Linear regression model | Exponential regression model |
|---|---|
| K(t) = K0 − a × ∑V(t) | K(t) = K0 × e−b∑V(t) |
| Wherein | |
| K t = IR of cell at t (mm h−1) | |
| K 0, initial IR, 2000 mm h−1 | |
| ∑V(t) = total accumulated volume of stormwater treated till time t (mm – normalised based on effective treatment area of each row) | |
| a/b = rate of linear/exponential decline, mm h−1 per millimetre of stormwater treated | |
2.4 Model testing
To estimate the IR of each row over time, the model was run with 6-minute rainfall intervals from 08 December 2009 (shortly after the system started operation) to 07 June 2012. During this 2.5-year period, the catchment received 2590 mm of rainfall. Since field data were available on only six monitoring events, model calibration and validation were performed using the protocol following the methodology from past stormwater studies that also had small field data sets:26(i) ‘1–5’: calibration on the first event, validation using the remaining five events;
(ii) ‘2–4’: calibration on the first two events, validation on the remaining four events;
(iii) ‘3–3’: calibration on the first three events, validation on the remaining three events;
(iv) ‘4–2’: calibration on the first four events, validation on the last two events;
(v) ‘5–1’: calibration on the first five events, validation on the last event; and
(vi) ‘6–0’: calibration on all the events (i.e., calibration only).
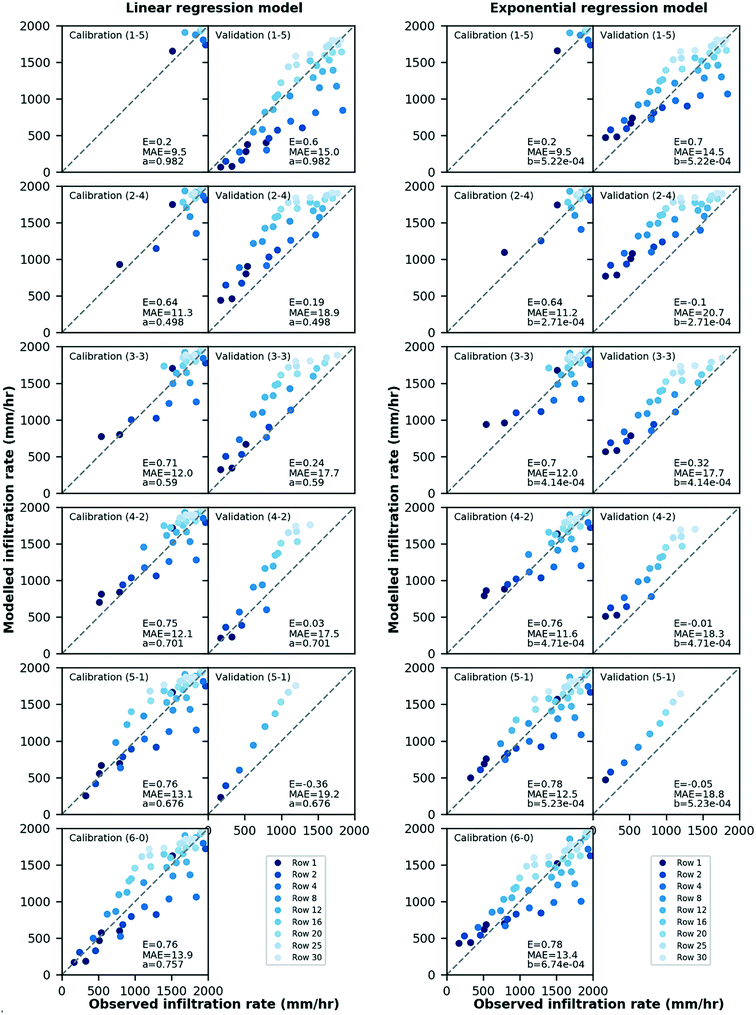
A simple Monte Carlo-based calibration process was used to obtain the best fit parameters: 1000 model runs were conducted for calibration with parameter from uniform distributions (range informed by preliminary model run practice of 200 times). As the model has only one parameter (i.e., the decline rate a/b), 1000 model runs were regarded as sufficient. The Nash–Sutcliffe coefficient (E) as well as the mean absolute error (MAE) between observed and modelled IRs were used to evaluate the model efficiency. Here the performance of the model was classified into four levels based on E values: excellent/very good (E ≥ 0.9), good (E ≥ 0.5), moderate (E ≥ 0.2) and poor/weak (E < 0.2).
2.5 Comparison against laboratory results
The rates of linear and exponential decline coefficients estimated from the model based on field observations were compared to the values estimated from two past laboratory column studies that were done in compressed time to simulate system performance over a long period: (1) one study by Bratières et al. (2012)22 in which the same Enviss™ filter was used, and (2) another study done by Kandra et al. (2014)8 who tested the clogging behaviour of a wider range of high-flow stormwater filters with various designs (e.g., depths, particle sizes, layers).The data of IR evolution with time (and volume of water treated) from these two studies were simply fitted to the regressions in Table 3 to estimate the linear and exponential decline coefficients. It should be noted that for the laboratory studies, only the IR evolution data from the start of the column operations until they reached 20% of their initial infiltration capacity were used, due to two reasons: (i) there were huge variations of IR observed in the last 20% of the lifetime of the tested systems, and measurement errors and uncertainties in measuring low IR values were high; (ii) 80% of the lifetime for the tested filter systems had already exceeded the age of the field systems (i.e., ∼2 years).
2.6 Optimising the maintenance of the system
To showcase how the model can help to inform the maintenance timing in practical cases for asset owners or operational staff, the best performing model was used to estimate the change of IR for an individual module of the system over time, which was then plotted against total volume treated by the module. Maintenance timing can then be determined directly when the IR of the module drops to a certain level (e.g., 500 mm h−1) if the flows of the system are fully monitored. In addition, the change of IR was also plotted against the total cumulative runoff from the catchment and total cumulative rainfall (since the system was installed); therefore, in circumstances where the treated runoff volume is not monitored, the operators can use these alternative plots to estimate the IR, according to either the total accumulative rainfall (easily acquired from a nearby rain gauge), or the total runoff volume (from the catchment, using a simple modelling exercise or level measurements of the rain tanks used for harvesting).3. Results and discussion
3.1 Observations from field measurements
Field results clearly indicate that IR of the entire system declined over time from event 1 (average 1840 mm h−1 across all rows) to event 6 (average 711 mm h−1), as shown in Fig. 4a. Interestingly, the decrease in IR is not uniform, a matter that has also been observed in laboratory studies.8 For example, with a further look into a shorter time period, i.e., from event 3 to event 4, which were conducted within a one-month time period, increased IR was even observed in row 16 and row 30 (Fig. 4b). Uneven drying and wetting due to varying levels of saturation in different rows is expected to be the main cause, and other possible explanations include uncertainties in the data collected and irregular rainfall. The findings indicate the importance of investigating the system performance over a longer time period for these high-flow filters.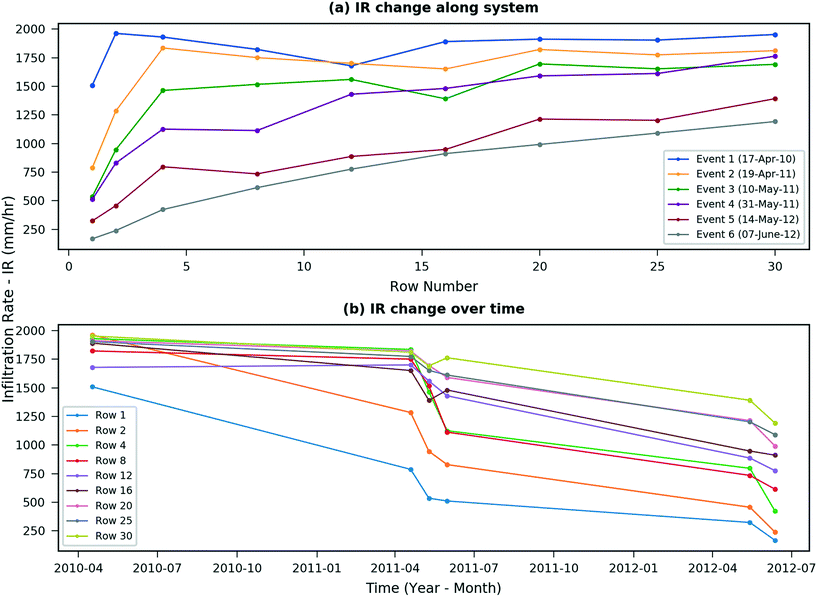 | ||
| Fig. 4 Change of IR (a) along the system for different events, and (b) over time for different rows as observed in the field. | ||
Fig. 4b shows differences in the IR of all the rows over time. After 2.5 years of operation, IR of Row 1 dropped from 2000 mm h−1 to only 167.4 mm h−1, while row 30 still had IR of 1192 mm h−1. This directly reflects that rows closer to the inlet received comparatively more stormwater and hence clogged earlier than their counterparts located further from the inlet, even though they had comparable IR at the start.
3.2 Model performance
| Model testing schemea | Linear regression model | Exponential regression model | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Calibration | Validation | Calibration | Validation | |||||||
| a value | E | MAE | E | MAE | b value | E | MAE | E | MAE | |
| a The testing scheme “i–j” indicates that the first i events were used for model calibration and last j events were used for model validation (see methods above). | ||||||||||
| 1–5 | 0.014 | 0.20 | 9.5 | 0.6 | 15.0 | 7.45 × 10−6 | 0.20 | 9.5 | 0.70 | 14.5 |
| 2–4 | 0.007 | 0.64 | 11.3 | 0.19 | 18.9 | 3.86 × 10−6 | 0.64 | 11.2 | −0.10 | 20.7 |
| 3–3 | 0.008 | 0.71 | 12.0 | 0.24 | 17.7 | 5.91 × 10−6 | 0.70 | 12.0 | 0.32 | 17.7 |
| 4–2 | 0.010 | 0.75 | 12.1 | 0.03 | 17.5 | 6.72 × 10−6 | 0.76 | 11.6 | −0.01 | 18.3 |
| 5–1 | 0.010 | 0.76 | 13.1 | −0.36 | 19.2 | 7.47 × 10−6 | 0.78 | 12.5 | −0.05 | 18.8 |
| 6–0 | 0.011 | 0.76 | 13.9 | N.A. | N.A. | 9.62 × 10−6 | 0.78 | 13.4 | N.A. | N.A. |
The exponential regression model, however, did not perform as effectively as the linear regression model did, with only two calibration–validation schemes (‘1–5’ and ‘3–3’) showing a positive E value (0.70 and 0.32, respectively), and a relative higher MAE value for all the testing schemes (18.3–20.7). It is therefore recommended that a linear regression model should be used for prediction of the performance of such systems over time and in relation to the volume of water treated.
With further investigation into the prediction results during model validation, it was found that the models often result in over-predictions of the IR, e.g., on average the predicted IR by linear regression model were 35% than the observed IR values. This is more obvious with regards to the cells that are further away from the inlet and towards the end of the system (e.g., row 20, 25 and 30). This could be because that these rows experienced extreme drying regimes as compared to other rows (e.g., less water reached these rows for low rainfall events). This was however not taken into account by the model despite the fact that it was found to have a significant impact on similar systems, like porous pavement.21 Moreover, these rows are also likely to receive less sediment load for every event as compared to rows located upstream in the system because some sediment will be trapped in these upstream rows. In this case, the IR of upstream rows will decline quicker, and thus more water is distributed into downstream rows. Therefore, the assumption made earlier regarding ignoring the sediment treatment in the upstream rows is just an ideal case. The model could have been improved further by taking into consideration the sediment accumulation in different rows along the system. This finding also provides advice for asset management, i.e., that the asset life could be extended more cheaply by just replacing or refurbishing filter modules in the upstream section of the system.
3.3 Comparison of results from field and laboratory
Table 5 presents the decline rates estimated from previous laboratory column experiments for different high-flow filter designs using both the linear and exponential regression model. As shown, comparing to the field results of this study, the estimated a and b coefficients were considerably higher in laboratory studies. This could be due to many reasons. Firstly, the majority of laboratory filters used coarser media (2 mm) than the field system (<1 mm) which led to much higher initial IR. As such, the base case scenario of the laboratory testing by Kandra et al. (2014) had 43 times higher initial IR than the field systems,8 consequently leading to a much quicker decline of IR in their study (a = 5123 and b = 0.100) than was evidenced by the current field study (a = 0.498–0.982 and b = 0.00027–0.00067). Bratières et al. (2012) tested the same Enviss™ filter as for this field system in the laboratory, also obtaining similar initial IRs of 2525 mm h−1.22 The estimated a (= 48) and b values (= 0.030), however, are still higher than this study (Table 5). This is likely due to the fact that the laboratory experiments were conducted in accelerated testing regimes while the field system was subjected to natural wetting and drying conditions over a 2.5-year period that is beneficial to the system's longevity. This again suggests that the natural wetting and drying cycles present an important factor affecting the performance of these filters, and therefore field investigations are necessary to estimate the decline rates accurately. Moreover, the monitored sediment concentrations in the field was found to be much lower (3.3–178 mg L−1 with a median of only 10 mg L−1) than the concentrations used in laboratory experiments (150 mg L−1). As was previously found, TSS concentrations in the inflow can affect the longevity and the rate of decline of IR in granular filters.15| Source | Configuration | Initial infiltration rate, K0 (mm h−1) | Linear | Exponential |
|---|---|---|---|---|
| a | b | |||
| a ‘Base case’ indicates zeolite media, 2 mm media size, single layer, 300 mm deep filter bed, while the others just indicate the difference from this base case. For more details, please refer to Kandra et al. (2014).8 | ||||
| Kandra et al. (2014)8 | Base casea | 87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 689 689 |
5123 | 0.100 |
| 100 mm deep filter bed | 68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 225 225 |
4458 | 0.110 | |
| 500 mm deep filter bed | 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 645 645 |
3837 | 0.070 | |
| 0.5 mm media size | 1227 | 425 | 0.730 | |
| 5 mm media size | 170![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 434 434 |
667 | 0.006 | |
| 2-Layered (0.5 and 2 mm) | 2195 | 267 | 0.230 | |
| 2-Layered (2 and 5 mm) | 118![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 265 265 |
2939 | 0.046 | |
| 3-Layered (0.5, 2 and 5 mm) | 2256 | 393 | 0.320 | |
| Mixed media (0.5, 2 and 5 mm) | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 395 395 |
1998 | 0.390 | |
| Bratières et al. (2012)22 | Enviss™ systems (lab) | 2525 | 48 | 0.030 |
| This study | Enviss™ systems (field) | 2000 | 0.498–0.982 | 0.00027–0.00067 |
3.4 Practical application of the model
Fig. 6 plots the decline of IR for each row against total cumulative rainfall amount, total catchment runoff, and total volume of runoff treated by the system, predicted using the linear regression model (where decline rate is taken from the ‘3–3’ testing scheme, which has the best validation results, i.e., a = 0.59). This gives a good indication for asset owners or operational staff of how to maintain such a filter system. For example, if a particular module needs to be replaced once the IR of this module drops to below 500 mm h−1, for row 1, it could be done after 2540 m of runoff (normalised by the effective treatment area of each row, Table 3) treated by this row. Alternatively, if only rainfall data is available, it can be estimated that row 1 needs to be replaced after a total of 2000 mm rainfall on this catchment since the start date of the system's operation (Fig. 6); this is equivalent to approximately 24 months of system operation. Although this method is less accurate, e.g., the field monitoring data showed that IR of row 1 dropped to below 500 mm h−1 shortly after event 4 (i.e., 19 months since the system started operation, as per Fig. 4b), it could be the most practical approach since rainfall data is often readily available.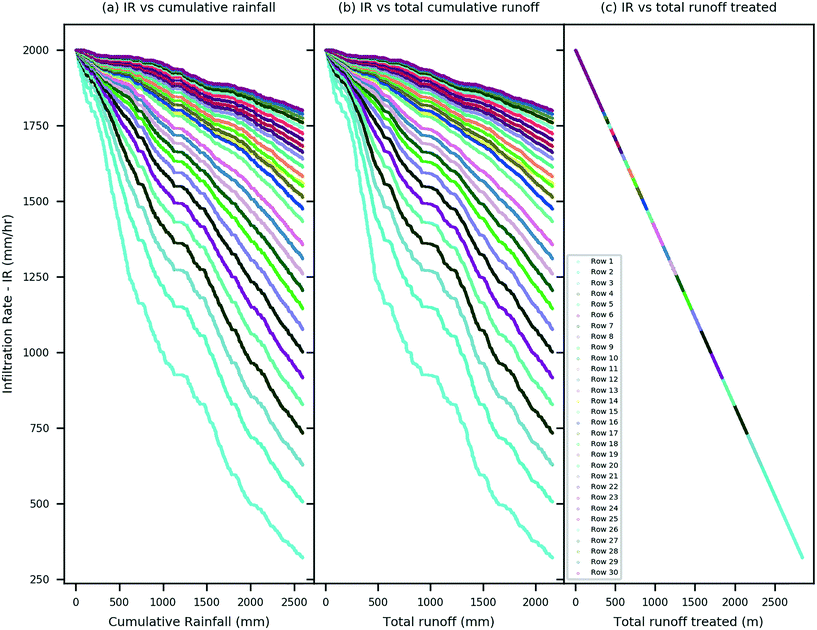 | ||
| Fig. 6 Change in average IR of the entire system versus (a) cumulative rainfall, (b) total cumulative runoff of the catchment, and (c) total runoff treated (normalised based on effective treatment area of each row, per Table 3). The points of different rows overlap but are following the best linear regression model, i.e., K(t) = 2000 − 0.59 × ∑V(t). | ||
The above results are applicable to the current systems, or similar field systems with high flow filters that receive stormwater from similar type of urban catchments. Nevertheless, the developed conceptual model can have broader applications. For example, the water distribution model, although simplified with many assumptions to suit this current field system, has potential to be revised to suit a variety of infiltration systems with modular treatment filter, that could be either high flow filters as this study or relatively low flow filters. Further studies are thus recommended to test and improve the model through multiple field-scale case studies with different type of these infiltration systems (and across various catchments – with new data collected for model testing). A suit of plots similar to the ones in Fig. 6 that suit different environmental conditions, as well as catchment characteristics, could then be developed to guide the practical maintenance of such systems.
4. Conclusions
This study tested a field filtration system used for stormwater harvesting over 2.5 years of its operation. Simple conceptual models were developed to simulate the decline of the infiltration rate (IR) of this system.The field monitoring results indicate that the IR of the entire system declined over time from 2000 mm h−1 to an average of 711 mm h−1. The filters closer to the inlet had the lowest IR at the completion of the field testing (i.e., only 167.4 mm h−1) compared to the filters towards the end of the system (IR = 1192 mm h−1). Both models were calibrated satisfactorily against a different number of field observation events, with calculated MAE values lower than 13.9 (average 11.8), and E values larger than 0.64, except for the ‘1–5’ testing scheme (E = 0.20). The linear regression model had better performance, with E values being positive (0.03–0.60) and MAE values (15.0–18.9) smaller than the exponential regression model (E < 0 in many cases, and MAE = 14.5–20.7) in the majority of the testing schemes during model validation. Results from this study indicate a slower decline rate of IR in the field conditions than occurred in the laboratory experiments, showing the impact of the natural wetting and drying cycle on the longevity of such filters, and the importance of conducting field experiments to understand the system's performance.
The modelling results from this study can be readily used to help to better design and maintain stormwater filters in similar urban catchments. The model could also be applicable to catchments that are different from this study with further calibration and validation ideally using field data. Future studies thus are recommended to account for a range of environmental variables across multiple field-scale case studies.
Conflicts of interest
There are no conflicts to declare.References
- L. Fisher-Jeffes, K. Carden, N. P. Armitage and K. Winter, Stormwater harvesting: Improving water security in South Africa's urban areas, S. Afr. J. Sci., 2017, 113, 1–4 CrossRef.
- J. Steffen, M. Jensen, C. A. Pomeroy and S. J. Burian, Water Supply and Stormwater Management Benefits of Residential Rainwater Harvesting in U.S. Cities, J. Am. Water Resour. Assoc., 2013, 49, 810–824 CrossRef.
- E. G. I. Payne, D. T. McCarthy, A. Deletic and K. Zhang, Biotreatment technologies for stormwater harvesting: critical perspectives, Curr. Opin. Biotechnol., 2019, 57, 191–196 CrossRef.
- H. E. Tavakol-Davani, H. Tavakol-Davani, S. J. Burian, B. J. McPherson and M. E. Barber, Green infrastructure optimization to achieve pre-development conditions of a semiarid urban catchment, Environ. Sci.: Water Res. Technol., 2019, 5, 1157–1171 RSC.
- K. Zhang, D. Manuelpillai, B. Raut, A. Deletic and P. M. Bach, Evaluating the reliability of stormwater treatment systems under various future climate conditions, J. Hydrol., 2019, 568, 57–66 CrossRef.
- M. Polyakov, S. Iftekhar, F. Zhang and J. Fogarty, The amenity value of water sensitive urban infrastructure: A case study on rain gardens. , presented in part at the 59th Annual Conference of the Australian Agricultural and Resource Economics Society, Rotorua, N.Z., 2015 Search PubMed.
- S.-A. Tan, T.-F. Fwa and C.-T. Han, Clogging Evaluation of Permeable Bases, J. Transp. Eng., 2003, 129, 309–315 CrossRef.
- H. S. Kandra, A. Deletic and D. McCarthy, Assessment of Impact of Filter Design Variables on Clogging in Stormwater Filters, Water Resour. Manage., 2014, 28, 1873–1885 CrossRef.
- G. H. LeFevre, K. H. Paus, P. Natarajan, J. S. Gulliver, P. J. Novak and R. M. Hozalski, Review of Dissolved Pollutants in Urban Storm Water and Their Removal and Fate in Bioretention Cells, J. Environ. Eng., 2015, 141, 04014050 CrossRef.
- C. P. Muerdter, C. K. Wong and G. H. LeFevre, Emerging investigator series: the role of vegetation in bioretention for stormwater treatment in the built environment: pollutant removal, hydrologic function, and ancillary benefits, Environ. Sci.: Water Res. Technol., 2018, 4, 592–612 RSC.
- P. Knowles, G. Dotro, J. Nivala and J. García, Clogging in subsurface-flow treatment wetlands: Occurrence and contributing factors, Ecol. Eng., 2011, 37, 99–112 CrossRef.
- J. M. R. Mercado, M. C. Maniquiz-Redillas and L. H. Kim, Laboratory study on the clogging potential of a hybrid best management practice, Desalin. Water Treat., 2015, 53, 3126–3133 CrossRef.
- B. Myers, S. Beecham and J. A. van Leeuwen, Water quality with storage in permeable pavement base course, Proceedings of the Institution of Civil Engineers: Water Management, 2011, 164, 361–372 Search PubMed.
- C. F. Yong, A. Deletic, T. D. Fletcher and M. R. Grace, Hydraulic and treatment performance of pervious pavements under variable drying and wetting regimes, Water Sci. Technol., 2011, 64, 1692–1699 CrossRef.
- H. Kandra, D. McCarthy and A. Deletic, Assessment of the Impact of Stormwater Characteristics on Clogging in Stormwater Filters, Water Resour. Manage., 2015, 29, 1031–1048 CrossRef.
- H. S. Kandra, J. Callaghan, A. Deletic and D. T. McCarthy, Biological clogging in storm water filters, J. Environ. Eng., 2015, 141, 04014057 CrossRef.
- M. Masi, A SWMM-5 Model of a Denitrifying Bioretention System to Estimate Nitrogen Removal From Stormwater Runoff, Dissertations & Theses - Gradworks, MPhil, 2011, 69, 133–148 Search PubMed.
- V. M. Jayasooriya and A. W. M. Ng, Tools for Modeling of Stormwater Management and Economics of Green Infrastructure Practices: a Review, Water, Air, Soil Pollut., 2014, 225, 2055 CrossRef.
- N. R. Siriwardene, A. Deletic and T. D. Fletcher, Modeling of sediment transport through stormwater gravel filters over their lifespan, Environ. Sci. Technol., 2007, 41, 8099–8103 CrossRef.
- P. Cannavo, A. Coulon, S. Charpentier, B. Béchet and L. Vidal-Beaudet, Water balance prediction in stormwater infiltration basins using 2-D modeling: An application to evaluate the clogging process, Int. J. Sediment Res., 2018, 33, 371–384 CrossRef.
- C. F. Yong, D. T. McCarthy and A. Deletic, Predicting physical clogging of porous and permeable pavements, J. Hydrol., 2013, 481, 48–55 CrossRef.
- K. Bratières, C. Schang, A. Deletić and D. T. McCarthy, Performance of enviss™ stormwater filters: results of a laboratory trial, Water Sci. Technol., 2012, 66, 719–727 CrossRef.
- P. J. Poelsma, D. T. McCarthy and A. Deletic, Changes in the filtration rate of a novel stormwater harvesting system: impacts of clogging and moisture content, presented in part at the 7th Novatech conference, Lyon, France, 2010 Search PubMed.
- K. Zhang, F. Yong, D. T. McCarthy and A. Deletic, Predicting long term removal of heavy metals from porous pavements for stormwater treatment, Water Res., 2018, 142, 236–245 CrossRef.
- eWater, Model for urban stormwater improvement conceptualisation (MUSIC Version 6), 2014.
- M. Mourad, J. L. Bertrand-Krajewski and G. Chebbo, Calibration and validation of multiple regression models for stormwater quality prediction: data partitioning, effect of dataset size and characteristics, Water Sci. Technol., 2005, 52, 45–52 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |