Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Strategies for determining heteroaggregation attachment efficiencies of engineered nanoparticles in aquatic environments
Antonia
Praetorius†
 *a,
Elena
Badetti
b,
Andrea
Brunelli
ab,
Arnaud
Clavier
c,
Julián Alberto
Gallego-Urrea
*a,
Elena
Badetti
b,
Andrea
Brunelli
ab,
Arnaud
Clavier
c,
Julián Alberto
Gallego-Urrea
 d,
Andreas
Gondikas
de,
Martin
Hassellöv
d,
Thilo
Hofmann
d,
Andreas
Gondikas
de,
Martin
Hassellöv
d,
Thilo
Hofmann
 a,
Aiga
Mackevica
a,
Antonio
Marcomini
b,
Willie
Peijnenburg
a,
Aiga
Mackevica
a,
Antonio
Marcomini
b,
Willie
Peijnenburg
 fg,
Joris T. K.
Quik
fg,
Joris T. K.
Quik
 h,
Marianne
Seijo
c,
Serge
Stoll
h,
Marianne
Seijo
c,
Serge
Stoll
 c,
Nathalie
Tepe
a,
Helene
Walch
a and
Frank
von der Kammer
a
c,
Nathalie
Tepe
a,
Helene
Walch
a and
Frank
von der Kammer
a
aDepartment of Environmental Geosciences, Centre for Microbiology and Environmental Systems Science, University of Vienna, Althanstr. 14, UZA II, 1090 Vienna, Austria. E-mail: antonia.praetorius@univie.ac.at
bDAIS – Department of Environmental Sciences, Informatics and Statistics, University Ca' Foscari of Venice, Via Torino 155, 30172 Venice, Italy
cDepartment F.-A. Forel for Environmental and Aquatic Sciences, University of Geneva, Switzerland
dUniversity of Gothenburg, Department of Marine Sciences, Kristineberg Marine Research Station, Fiskebäckskil, Sweden
eFaculty of Geology and Geo-environment, National and Kapodistrian University of Athens, Panepistimioupoli Zographou, 15784, Athens, Greece
fCentre for Safety of Substances and Products, National Institute of Public Health and the Environment (RIVM), Bilthoven, The Netherlands
gInstitute of Environmental Sciences (CML), Leiden University, Leiden, The Netherlands
hCentre for Sustainability, Environment and Health, National Institute of Public Health and the Environment (RIVM), Bilthoven, The Netherlands
First published on 8th January 2020
Abstract
Heteroaggregation of engineered nanoparticles (ENPs) with suspended particulate matter (SPM) ubiquitous in natural waters often dominates the transport behaviour and overall fate of ENPs in aquatic environments. In order to provide meaningful exposure predictions and support risk assessment for ENPs, environmental fate and transport models require quantitative information about this process, typically in the form of the so-called attachment efficiency for heteroaggregation αhetero. The inherent complexity of heteroaggregation—encompassing at least two different particle populations, various aggregation pathways and several possible attachment efficiencies (α values)—makes its theoretical and experimental determination challenging. In this frontier review we assess the current state of knowledge on heteroaggregation of ENPs with a focus on natural surface waters. A theoretical analysis presents relevant equations, outlines the possible aggregation pathways and highlights different types of α. In a second part, experimental approaches to study heteroaggregation and derive α values are reviewed and three possible strategies are identified: i) monitoring changes in size, ii) monitoring number or mass distribution and iii) studying indirect effects, such as sedimentation. It becomes apparent that the complexity of heteroaggregation creates various challenges and no single best method for its assessment has been developed yet. Nevertheless, many promising strategies have been identified and meaningful data can be derived from carefully designed experiments when accounting for the different concurrent aggregation pathways and clearly stating the type of α reported. For future method development a closer connection between experiments and models is encouraged.
Environmental significanceHeteroaggregation has been identified as a key process for the fate of engineered nanoparticles (ENPs) in aquatic environments. However, experimental approaches to determine attachment efficiencies for heteroaggregation (αhetero) remain comparatively limited and often lack specification of the type of attachment efficiency (α) that is reported. Here we provide a thorough review of both the theoretical background and current state of experimental approaches for studying heteroaggregation. By clarifying the possible heteroaggregation pathways and types of α values as well as critically assessing the strengths and weaknesses of different experimental strategies, we provide a strong basis for the future development of approaches to study heteroaggregation and to generate reliable data to predict exposure and enable a stronger risk assessment of ENPs. |
Introduction
Upon release to natural surface waters, engineered nanoparticles (ENPs) will undergo a variety of transformation and transport processes, affecting their ultimate fate and hazard potential.1 Natural waters already contain a multitude of natural particles in the nano- and micrometre size range, which can be composed of aggregates of minerals and organic substances of various origins and can be loosely referred to as suspended particulate matter (SPM). A new generation of ENP-specific multimedia fate and transport models2–7 has demonstrated that heteroaggregation, the attachment of ENPs with naturally occurring SPM, is one of the most important processes driving the overall fate of ENPs in natural waters. Once the ENPs are attached to SPM, their transport (floating, sedimentation, resuspension etc.) is dominated by the transport behaviour of the SPM itself, commonly resulting in sediments being final or transient sinks for waterborne ENPs.6,8 SPM-bound ENPs are also likely to display differences in bioavailability and toxicity compared to free ENPs.2,9,10 Additionally, other fate processes, such as dissolution, might be altered by heteroaggregation.11 It is therefore crucial for ENP exposure and risk assessment to understand and quantify heteroaggregation processes.The attachment efficiency (α) is a common fate descriptor for aggregation processes.12 It has been employed as an input parameter to describe ENP heteroaggregation in spatially explicit regional-scale fate and transport models6,7,13,14 as well as in unit-world type multimedia models.3–5 These models operate at very different temporal and spatial scales, at levels of detail ranging from modelling individual particle collisions to predicting fate at a systems scale, and often address different scientific and or regulatory questions. Nevertheless, implications of model scale towards input parameter needs for heteroaggregation are rarely discussed. It is important to be aware that ENPs heteroaggregating with SPM in natural waters represent a system of two or more different particle populations interacting with one another. This can result in a complex combination of different aggregation processes and attachment efficiencies (α values) and the formation of various homo- and heteroaggregates. Consequently, different types of α values may be required for different applications. In order to ensure that selected α values are adequately describing the system at hand, it is critical to improve our theoretical understanding of the complexities of heteroaggregation.
A better mechanistic understanding of heteroaggregation is also needed to develop adequate experimental protocols for its assessment and generate solid data to parameterize environmental fate models and inform risk assessment. Currently, most experimental studies on the aggregation behaviour of ENPs have focused on homoaggregation, i.e. aggregation between ENPs of the same nature.15–18 However, this process is likely less relevant in most natural waters than heteroaggregation, due to the relatively low expected ENP concentrations, generally in the ng L−1 or μg L−1 range,19,20 and the large available SPM surface area. Often, experimental approaches used to study homoaggregation cannot be directly applied to heteroaggregation due to the inherently higher system complexity and studies on heteroaggregation are still comparatively scarce.
In this contribution we carefully review the underlying theory relevant to describe heteroaggregation together with existing experimental approaches to measure aggregation processes. A focus is placed on heteroaggregation of ENPs with SPM in natural surface waters, e.g. rivers, lakes, estuaries, oceans; systems that are most relevant for exposure and risk assessment. We identify the most promising strategies for determining different types of α values and discuss their application in different fate and transport models.
Theoretical background
Aggregation theory
Particle aggregation has been well-described in colloid theory (e.g. Elimelech et al.,21 Li & Logan22 or Lyklema23). The formation of aggregates from two colliding entities i and j can be broken down into two steps: collision and attachment, which are described by the collision rate constant, ki,jcoll, and the attachment efficiency, αij, respectively (eqn (1)). A quantitative measure of the aggregation process is the aggregation rate constant, ki,jagg:| ki,jagg = αijki,jcoll | (1) |
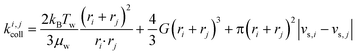 | (2) |
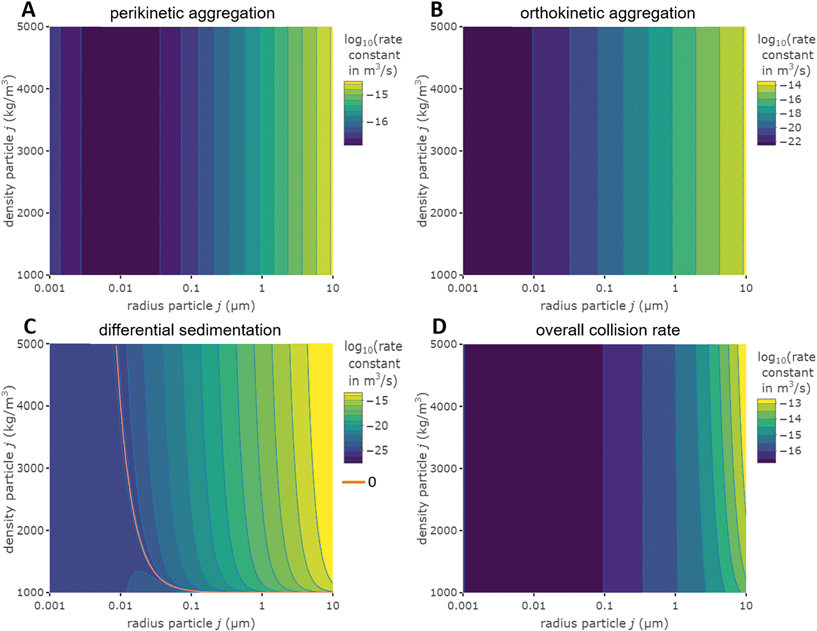 | ||
Fig. 1 Effect of relative size and density on collision rate constants of two heteroaggregating particles assuming the simplest case of a rectilinear collision model. The size and density of one particle i is fixed at 10 nm and 4000 kg m−3, respectively (representative e.g. of a TiO2 ENP), while size and density of particle j are varied from 1 nm to 10 μm and from 1000 to 5000 kg m−3, respectively. A temperature of 293 K and a shear rate G of 10 s−1 were assumed for the calculations. The influence of relative size and density between two colliding particles on the individual terms in eqn (2), namely perikinetic (A) and orthokinetic (B) collisions and differential sedimentation (C), as well as on the collision frequency as the sum of all three contributions (D), is shown. Settling velocities vs,i and vs,j are calculated from Stoke's law: 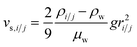 , where ρi/j and ρw are the density of particle i (or j) and of water, respectively, and g is the gravitational acceleration on earth.‡ , where ρi/j and ρw are the density of particle i (or j) and of water, respectively, and g is the gravitational acceleration on earth.‡ | ||
Structural effects and short-range forces
As defined in eqn (2), the collision rate constant considers two spherical particles i and j in a rectilinear collision mode.26,27 However, this ignores short-range forces and changes in fluid motion as particles (solid spheres) approach one another. To account for short-range effects, such as hydrodynamic forces and particle attraction (van der Waals and electrical double layer forces), in particle collisions, corrections to the rectilinear collision frequency function for each mechanism have been proposed via a curvilinear approach.26–30 For example, Lawler and co-workers28,29 have numerically developed a set of corrections for solid spheres, which have been recently updated to include nanoparticle interactions.31In the case of aggregates, their internal structure can strongly affect hydrodynamics around colliding entities and lead to non-linear collision trajectories requiring different corrections than single (spherical) particles.27,30 The fractal concept32 is widely accepted to provide insights into the influence of aggregation mechanisms on aggregate structure by giving a simple mathematical and quantitative measure of the aggregate mass distribution in space. In simple terms, the fractal dimension, df, provides a measure of aggregate structure: aggregates of low df have a loose, rather open structure, whereas a df closer to the maximum value of 3 represent more dense aggregates (a solid sphere has a df value of 3). Experiments and computer simulations of irreversible diffusion limited aggregation (DLA), i.e. αi,j = 1, typically yield a fractal dimension close to 1.8 whereas for reaction limited aggregation (RLA), i.e. αi,j < 1, a fractal dimension of around 2.1 is generally obtained.33,34
To account for the influence of aggregate structure on the hydrodynamics of collisions, different equations were proposed in the literature.30 For example, when the particle motion is purely Brownian, it was found that the analytical expression for the collision rate constant between two aggregates composed of identical primary monomers is given by:
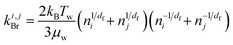 | (3) |
Attachment efficiency (α)
The attachment efficiency, α, which is sometimes also referred to as sticking probability or collision efficiency, has a value between zero and unity describing the probability of a collision between particles or aggregates to result in attachment. The value of α is related to the presence of an energy barrier, which can decrease the number of effective collisions as the barrier height becomes higher than the energy of the attractive forces between particles and their kinetic energies.35,36 This net result of the interplay of attraction and repulsion is mainly dependent on the van der Waals, electrostatic and steric interactions, which affect particles in suspension.23The interaction of van der Waals and electrostatic forces was first described by Derjaguin, Landau, Verwey, and Overbeek37,38 in the well-known DLVO theory. The DLVO theory includes properties of the particles and the medium, e.g. the Hamaker constant, surface charge density and Debye length, which depend on parameters like ionic strength, pH, temperature and particle diameter.18 The DLVO theory has been extended to include additional interactions,39,40e.g. hydrogen bonding, hydration pressure, Lewis acid base interactions, charge regulations, image charge effects41 or steric effects, which can be particularly relevant for particles in the nano-range.
The attachment efficiency α can also be expressed as the inverse of the Fuchs stability ratio W (α = 1/W). W is defined as the ratio between the aggregation rate of primary particles in the absence of any repulsive or attractive force as derived theoretically by Smoluchowski and the aggregation rate in case of repulsions between particles. If the interparticle interaction potential is known, W can be calculated by considering particle diffusion in a force field. However, in practice, the estimation of the total interaction energy requires a good knowledge of particle properties (surface charge density, Hamaker constants, possible charge regulation processes, etc.) in specific media conditions (pH, ionic strength, temperature, dielectric constants). In addition, interactions of natural or synthetic coatings, e.g. polymers or surfactants attached to the particle surface, can complicate such calculations.18 Therefore, effects of particle (or aggregate) properties, possible surface coatings and medium characteristics on particle interactions need to be considered on a more detailed scale.42
Challenges in predicting α
Despite the theoretical basis described above, calculating α ab initio remains very challenging. The extended DLVO theory can be used as a starting point, but it is very difficult to predict α for environmentally relevant scenarios. The required input parameters for the models developed to date are not available for many, even relatively simple, systems of homoaggregating particles. A more detailed description of the system is necessary to get an insight into possible competitive effects in multi-component systems. For natural waters, the situation therefore becomes particularly challenging. Several complexities related to natural particles, such as non-spherical shapes, heterogeneous surface properties, or natural polyelectrolyte coatings (e.g. from NOM) are not considered by known quantitative theories.Nevertheless, few attempts to predict α values in multi-component systems have been reported. For example, the behaviour of fulvic acids in the presence of hematite particles was modelled by Brownian dynamics simulations to investigate the competition between fulvic acids homoaggregation and their adsorption onto the hematite particles as a function of solution ionic strength.43 Attachment efficiency values were calculated to illustrate the complex interplay between electro-attractive and repulsive forces. In another recent study, adsorption of different natural organic matter (NOM) on different shapes of Ag ENPs was investigated44 using various in silico techniques (density functional theory, classical lattice dynamics, and quantum mechanical calculations). It was found that adsorption energies increased as the molecular weight of NOM increased and preferred adsorption sites were defined. However, such calculations can still only be applied to relatively well-defined systems, not representative of natural environments. Furthermore, they would be too computationally intensive to run alongside larger scale fate and transport models and currently do not replace the need for experimentally determined α values.
Heteroaggregation and increasing system complexity
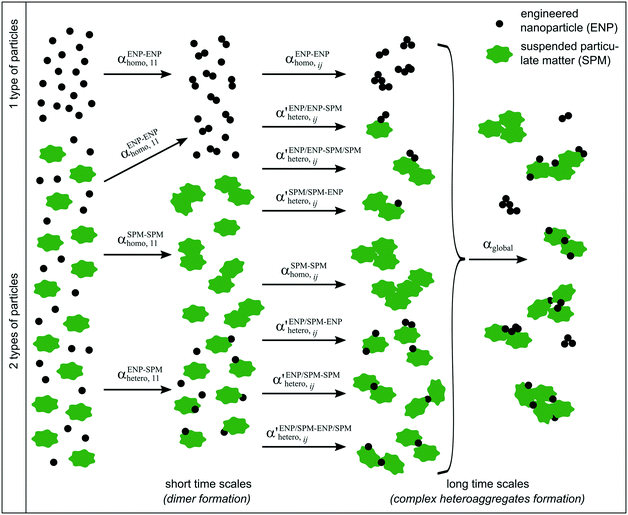
Simple systems containing only one type of particles (homoaggregation) have been studied experimentally and described theoretically in great detail.18 However various particle types are the norm in natural waters and heteroaggregation of ENPs with SPM generally dominates. In principle, homo- and heteroaggregation follow the same theoretical basis, with homoaggregation essentially representing a special, simpler case of heteroaggregation (particles i and j are of the same nature, which simplifies the equations above). During heteroaggregation, two or more distinct particle populations are interacting and various aggregation processes are taking place simultaneously.45 For example, in a system with one ENP and one SPM population several different aggregation pathways occur at the same time (Fig. 2).As can be seen in Fig. 2 the aggregation process initiates with dimer formation at short time scales, described by αENP–ENPhomo,11 or αSPM–SPMhomo,11 in the case of homoaggregation and by αENP–SPMhetero,11 when ENPs and SPM are forming ENP–SPM heteroaggregates. Immediately after the dimer formation step, a multitude of more complex aggregation processes occur, where different combinations of monomers, dimers and bigger aggregates form larger structures. Each aggregation step can, in theory, be described by a specific attachment efficiency value. In the case of homoaggregation, the α values describing the aggregation between same particle types, consisting of different amounts of monomers i and j, are described by αENP–ENPhomo,ij or αSPM–SPMhomo,ij. Although aggregate size and structure can affect the attachment efficiency, in the case of homoaggregation the surface chemistry of the aggregating particles is often assumed to remain unchanged and the αhomo,11 and αhomo,ij will in most cases not vary substantially if the aggregate size remains limited.46 For the heteroaggregation process, however, the relative amounts of ENPs and SPM in a heteroaggregate will strongly affect the heteroaggregate's surface characteristics47 and consequently the subsequent heteroaggregation steps.48,49 For example, at low ENP to SPM volume ratios, the surface properties of the heteroaggregates will resemble those of the bare SPM, whereas high volume ratios of ENP to SPM may lead to an almost full coverage of the SPM surface with ENPs and the surface properties will be largely dominated by the ENP characteristics. 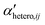 values are therefore expected to vary based on different combinations of i and j. In real environmental systems the situation will often be even more complex than depicted in Fig. 2, for example when the presence of additional aquatic components such as NOM affects the various α values.50
values are therefore expected to vary based on different combinations of i and j. In real environmental systems the situation will often be even more complex than depicted in Fig. 2, for example when the presence of additional aquatic components such as NOM affects the various α values.50
Modelling the impact of α
Assessing the impact of α on the aggregation kinetics is not trivial and straightforward, in particular for collisions beyond initial dimer formation and/or for particles with heterogeneous surface properties. To illustrate the complexity of aggregation processes, a theoretical model for describing the initial stages of the aggregation of spherical and partially coated particles was developed.51 To capture the model complexity, three types of attachment efficiencies, related to collisions between bare particle surfaces, between coated and bare parts and between two coated surface patches, were introduced. Finally, the model enabled an exact analytical expression for the dimer formation rate constant as a function of the degree of surface coverage. More recently, a cluster–cluster Monte Carlo model was developed for heteroaggregation and tested on a two-component system of ENPs and fulvic acid monomers.48 Different combinations of α values for dimer formation for ENP and fulvic acid homo- and heteroaggregation were used as input into the model, demonstrating a significant effect on predicted αhetero values.Expanding upon the Smoluchowski model, Therezien et al.52 proposed a computer model describing the heterogeneous aggregation between ENPs and natural SPM particles over a range of sizes and concentrations to explore the effects of α values on heteroaggregation. As heteroaggregation progresses, this model accounts for changes in heteroaggregate density and porosity, as well as in collision frequency and attachment efficiency. The model was tested with different attachment efficiency values. It was shown that αENP–ENPhomo,ij, αSPM–SPMhomo,ij and αENP–SPMhetero,ij affect the complexity of ENP behaviour in aqueous systems and influence the persistence of free ENPs in the water column.
Experimental approaches
Based on the underlying heteroaggregation theory described above, we review existing experimental approaches to study heteroaggregation of ENPs with SPM. Measuring heteroaggregation and extracting individual αhetero,ij values, related to dimers formed by one ENP and one SPM, from experiments is very challenging due to the large number of simultaneously occurring competing processes (Fig. 2). Additionally, it is possible that the heteroaggregate dimers further aggregate to rapidly form larger, more complex, heteroaggregates.53 At longer time scales, it therefore often makes more sense to describe the overall heteroaggregation behaviour of the system with a global attachment efficiency value αglobal.48 The value of αglobal is very system-specific compared to individual αhetero,ij values and will depend on the relative properties and concentrations of ENPs and SPM.For natural environments, a simplified but realistic assumption is that most ENP–SPM interactions will not go beyond the dimer formation step. Even if ENPs encountered ENP–SPM dimers, the larger surface area of the SPM would result in a high probability of the ENPs colliding with bare SPM surfaces and the interaction could be considered almost equivalent to that of true dimer formation. Consequently, αENP–SPMhetero,11 is most relevant input parameter for most environmental fate models. However, when experimentally determining heteroaggregation, ENP concentrations will typically be orders of magnitude higher than expected in the environment, to remain above instrument detection limits. As a result, concurrent homoaggregation of ENPs cannot be excluded and may often need to be accounted for when analysing and interpreting experimental results. Additionally, necessary increased concentrations in laboratory experiments likely lead to heteroaggregation much further than dimer formation towards more complex heteroaggregates composed of several ENPs and SPM at intermediate time scales (Fig. 2).49,53,54 This has implications for the types of α values that can be derived experimentally. It is often challenging to determine concentration-independent αENP–SPMhetero,11 and reported attachment efficiencies commonly correspond to the more system specific αglobal. It is therefore important to be aware of the types of heteroaggregation processes occurring in a given system and to be coherent about the meaning of the α values reported.
In the following we present and discuss different approaches applied to or suggested for studying ENP–SPM heteroaggregation. Special emphasis is placed on the ability to determine αENP–SPMhetero,11 and/or αglobal. Additionally, where applicable, the following criteria are examined: i) applicability to fast and slowly aggregating systems; ii) ability to perform under low (i.e. environmentally relevant) ENP concentrations; iii) possibility to distinguish and assess both homo- and heteroaggregation; iv) suitability for studying complex SPM and heteroaggregates in the micrometre size range; and v) minimisation of experimental artefacts.
Strategy 1: monitor size increase
The most common approach for studying aggregation kinetics is to measure changes in the average size of the aggregating particles, which has been widely applied to investigate homoaggregation.18 The attachment efficiency αhomo,11 can be determined by considering early aggregation, where dimer formation of initially monodisperse particles is dominant. Aggregation rates of the monomers are measured under diffusion limited aggregation (DLA) conditions (khomo,11,DLA), where there is no significant energy barrier as defined by the DLVO theory and aggregation runs at its maximum rate. This condition is typically achieved by increasing the ionic strength above the critical coagulation concentration (CCC).18 After repeating the experiment under reaction limited aggregation (RLA) conditions to obtain khomo,11,RLA, αhomo,11 can be obtained from the ratio of khomo,11,RLA and khomo,11,DLA, which is related to the changes in size (normally hydrodynamic radius, rH) during the initial aggregation stage.18,55 For dynamic light scattering (DLS) measurements the following relation is generally accepted:56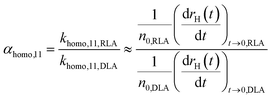 | (4) |
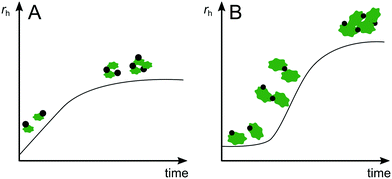
For heteroaggregation, monitoring the increase of average size of a system can provide valuable insights into the progression of heteroaggregation. However, the increased complexity of a heteroaggregating system (Fig. 2) requires consideration of several limitations and challenges for deriving quantitative information from experiments. For example, since size determination techniques typically operate in a specific size range, the relative initial sizes of the aggregation partners will affect the applicable measurement method and the information that can be obtained. If ENPs heteroaggregate with SPM of similar initial size, the aggregation curves will look similar as they would for ENP homoaggregation (Fig. 3A). In the absence of ENP–ENP and SPM–SPM homoaggregation, the initial linear portion of the rH increase corresponds to ENP–SPM dimer formation and may be used to derive αENP–SPMhetero,11. However, if SPM are orders of magnitude larger than ENPs (e.g. μm-range versus nm-range), the formation of ENP–SPM dimers will likely not result in a measurable increase in average size (Fig. 3B). Only the subsequent formation of more complex heteroaggregates consisting of two or more SPM and several ENPs would lead to a significant increase in size. Consequently, insights into the initial heteroaggregation step are limited and αENP–SPMhetero,11 cannot be determined directly.53 In either case, concurrent homoaggregation of ENPs and/or SPM is a very likely source of measurement artefacts and needs to be carefully verified. Furthermore, heteroaggregation kinetics are highly dependent on relative ENP and SPM concentrations in the system.45 It is therefore recommended to perform experiments at several concentration combinations to ensure the reported α values are concentration independent.
Typical size determination methods based on light scattering or laser diffraction are ensemble techniques providing size averages of the system studied. Measurements are strongly biased towards larger particles, especially in the Raleigh range (particles are much smaller than the incident light wavelength), where the light scattering intensity is proportional to the 6th power of the diameter. The transformation of light scattering intensities to volume or mass distributions requires detailed information on optical and physical material properties; which are not available in most cases.57 While this might be feasible for homoaggregation studies, heteroaggregation studies and non-homogeneous optical properties are limited in using this approach. Further research is needed to improve sizing techniques of complex (hetero-)aggregates. Additionally, differences in material properties between ENPs and SPM, such as different refractive indices, can affect the sensitivity of the analytical method towards one or the other particle population and thus impact the relative “visibility” of certain particle fractions.
Various analytical methods exist to measure particles sizes at sufficiently high time resolution to study aggregation processes. The most commonly applied and most suited methods are discussed below. Criteria for the selection of an adequate method include the type of materials that can be detected by a given method and the size range that can be resolved.
The main advantages of DLS are its relative ease of use and the wide availability of the instrument. However, DLS relies on particle motion being solely driven by diffusion. Consequently, size records are biased by settling, which occurs as aggregates grow or simply due to heterogeneous particle sizes and densities in multiple component systems. This results in a serious limitation of DLS for heteroaggregation studies: its practical upper size limit of ∼1 μm for many low-density materials, or even smaller for materials with a higher density. This is too low for investigating heteroaggregation with much of environmentally relevant SPM, typically present in the μm size range. Additionally, heterogeneity in particle size and in material properties (e.g. refractive index) influences the light scattering intensity and thus affects the relative “visibility” of certain particle fractions. For example, small numbers of large particles greatly influence the derived z-averaged diameter masking the smaller particles due to the very strong dependency of light intensity with size. Therefore, DLS is more appropriate for monodisperse suspensions and polydispersity should always be reported. Finally, complex aggregate morphology can cause multiple scattering of a single photon (inducing a bias towards smaller sizes).69
Determination of khetero,11 with DLS would require similarly sized spherical ENPs and SPM and a high resolution of the initial rH increase owed to dimer formation (Fig. 3A). Besides deviations of experimental conditions from these ideals, achieving DLA conditions appears to be problematic sometimes: in a heteroaggregation study on Au-ENPs and carbon nanotubes (CNTs), the diffusion limited regime was not reached even at high ionic strength, probably due to physical hindrance by CNTs.60 Gallego-Urrea et al.63 used khomo,11,DLA determined for Au-ENPs in NaCl solution as a baseline, to which aggregation rate constants of more complex systems (Au-ENPs, illite, NOM combinations in different water chemistries) were related to determine α. However, being obtained by comparing two different systems, these α values only reveal relative information.
Zhou et al.67 reported attachment efficiencies for a two-component system (montmorillonite + Ag or TiO2 ENPs), but the values probably do not reflect αhetero,11, as the ENPs (∼20–30 nm) were much smaller than montmorillonite (100–500 nm) and the increase of rH likely reflected aggregation stages beyond dimer formation. Additionally, the particle number concentrations of ENPs and montmorillonite were in the same order of magnitude, which suggests that homoaggregation cannot be excluded and deduced attachment efficiency values are more likely to represent αglobal. Furthermore, the experiments were performed at only one ENP/SPM concentration ratio and the determined α is most likely not concentration-independent, which makes it not directly useful as an input parameter for fate models.
Summing-up, time-resolved DLS does not seem suitable for most heteroaggregation studies under environmentally relevant settings, but it can be employed to separately determine αhomo,11, often needed for the determination of αENP–SPMhetero,11 in combination with other techniques (e.g. laser diffraction) and model calculations.53,54 Moreover, the determination of αglobal may be feasible65 when the limitations of DLS are taken into account.
Determining αENP–SPMhetero,11 from the laser diffraction experiments therefore requires indirect approaches, which represents one of the main limitations of this method. In the work by Praetorius et al.53 and Labille et al.54 a Smoluchowski-based aggregation model, including more complex descriptions of the particle collisions based on the fractal dimension, was used to first derive attachment efficiencies for the formation of larger heteroaggregates (αglobal). Calculation of αENP–SPMhetero,11 from a series of assumptions followed. More specifically, it was assumed that i) the dimer formation step is very fast due to higher particle concentrations than expected in the environment, ii) the individual attachment efficiencies are not altered by aggregation state (i.e. αENP–ENPhomo,11 = αENP–ENPhomo,ij, αSPM–SPMhomo,11 = αSPM–SPMhomo,ij and αENP–SPMhetero,11 = αENPx–SPMyhetero,ij), iii) the ENPs are distributed homogeneously on the SPM surface, and iv) homoaggregation is negligible.
As soon as the system deviates from the model SPM (e.g. spherical SiO2 particles in Praetorius et al.53) to more complex shapes (e.g. clay platelets in Labille et al.54), the determination of αENP–SPMhetero,11 becomes increasingly challenging and the assumptions listed above are less likely to be acceptable. For more environmentally relevant experimental conditions, including more complex SPM and SPM mixtures, experiments combined with advanced modelling tools will be required to determine αENP–SPMhetero,11 from laser diffraction measurements. An additional limitation of the laser diffraction method as described above is the difficulty to determine low αENP–SPMhetero,11 values. These would result in very slow heteroaggregation kinetics, requiring extensive measurement times and possibly the formation of more complex heteroaggregates needed for the analysis would not be achieved.
An interesting feature of NTA is that for each particle the scattering intensity is recorded along with its size, enabling the discrimination between particles with significantly different scattering intensities, such as, for example, gold and clay particles.63 Additionally, the detection threshold can be adjusted so that only particles with high scattering intensity are measured.75 A fluorescence optical filter can be used for measuring fluorescence in parallel to scattering intensity, and using the extended dynamic range mode two parallel videos can be analyzed with different optical settings.70 The simultaneous measurement of particle trajectories with scattering intensity and/or fluorescence could be utilized for determining heteroaggregation rates between particles with different scattering intensities and/or fluorescence properties. For example, if a suspension containing small ENPs with high scattering intensity is mixed with a suspension of large SPM with low scattering intensity, then as aggregation proceeds, heteroaggregates with a particle size close to the SPM size and a scattering intensity close that of the ENPs will dominate the signal. However, this combination of strongly scattering ENPs and weakly scattering SPM in the appropriate size ranges may not be available for many relevant ENP and SPM combinations in practice.
The overall measurement uncertainty in relation to size, composition, shape, and position in the laser volume etc. needs to be considered for the determination of α values using NTA. Other effects from light scattered from odd-shaped or poorly scattering particles on the measurement of particle size using NTA have to be carefully addressed.57 Finally, the similar upper size limit as for DLS, represents a serious limitation for employing NTA to study heteroaggregation in environmentally relevant systems.
Strategy 2: monitor distribution of free versus SPM-bound ENPs
Rather than measuring size increase, it is also possible to study heteroaggregation by monitoring the relative amounts of freely dispersed ENPs versus ENPs attached to SPM as a function of time (Fig. 4). As heteroaggregation proceeds the number or mass of ENPs freely dispersed in suspension decreases and the fraction of ENPs attached to SPM increases. However, also with this approach concurrent ENP homoaggregation can interfere with the analysis, since a decrease in the number concentration of ENPs can be a result of either homo- or heteroaggregation. Furthermore, losses, e.g. by attachment to vessel walls or tubing, might be mistaken for losses via heteroaggregation. Ideally, changes in both number and mass concentrations are monitored to account for homo- and heteroaggregation and close the overall mass balance. Alternatively, control experiments without SPM can be performed to rule out or confirm the degree of homoaggregation under equivalent conditions.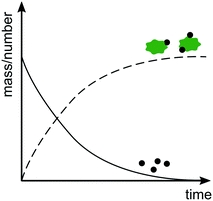 | ||
| Fig. 4 Evolution of number or mass of free ENPs (solid line) versus ENPs bound to SPM (dashed line) as a function of time. | ||
Similar to the size monitoring approach, α values can be derived by studying aggregation under DLA and RLA conditions employing the following relation:77,78
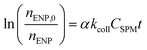 | (5) |
 for the early stages of aggregation is expected to yield a linear slope that is proportional to α. Keeping CSPM constant, α can be derived from the observed value of αkcollCSPM by normalizing it with the αkcollCSPM obtained under conditions of favorable attachment (i.e. DLA where α = 1). This eliminates the need to determine kcoll separately.78 To obtain true αENP–SPMhetero,11 is often challenging since it is difficult to clearly assign changes in mass or number to a single aggregation pathway (Fig. 2). In most experimental set-ups using this approach the obtained α values are more likely equivalent to αglobal.
for the early stages of aggregation is expected to yield a linear slope that is proportional to α. Keeping CSPM constant, α can be derived from the observed value of αkcollCSPM by normalizing it with the αkcollCSPM obtained under conditions of favorable attachment (i.e. DLA where α = 1). This eliminates the need to determine kcoll separately.78 To obtain true αENP–SPMhetero,11 is often challenging since it is difficult to clearly assign changes in mass or number to a single aggregation pathway (Fig. 2). In most experimental set-ups using this approach the obtained α values are more likely equivalent to αglobal.
A main challenge when studying heteroaggregation by monitoring ENP distribution between the dispersed and SPM-bound phase is its sensitivity to the efficient separation of the SPM phase. Phase separation can be achieved by taking advantage of the differences in ENP and SPM size and settling velocities, e.g. via centrifugation. This is challenging in cases where there is an overlap between (some) ENPs and the SPM phase, such as a small and light fraction of the SPM distribution, which would behave similarly to the ENPs or in cases where homoaggregated ENPs settle at a similar speed as larger SPM or ENP–SPM heteroaggregates. Some approaches are able to avoid a separation step by employing analytical methods able to simultaneously monitor free and SPM-bound ENPs.
NTA, described in more detail under Strategy 1, offers the possibility to count each particle individually. Combined with size monitoring, conducting a series of experiments varying the number concentration ratios between two dissimilar suspensions (size and/or other scattering properties) could potentially provide information about the different aggregation pathways and attachment efficiencies presented in Fig. 2 by counting the number of homo- and heteroaggregates as a function of time. By using the appropriate detector, the fluorescence signal would shift from particles with small size to aggregates of larger size. However, this is limited by the measurable size range and typical μm-size heteroaggregates cannot be followed. Another obstacle for NTA, as with any particle counting technique, is the fact that the data collected are dependent on the number abundance of each particle type in the sample, so multiple and longer measurements need to be made for heterogeneous samples, which increases the duration of measurements. The measurement error thus increases, due to the fact that the aggregation process (and possibly settling) continues during the measurements.
A Coulter Counter Multisizer instrument has been applied to study heteroaggregation of TiO2 NPs and micron-sized latex particles.47 The influence of TiO2 adsorption and concentration on the aggregation kinetics of latex suspensions was investigated by monitoring the decrease of the number of non-aggregated latex monomer particles as a function of time. No α values were reported but if the system is well-known and -controlled in terms of medium properties and particle concentrations, 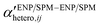 or even αENP–SPMhetero,11 might be derived with this approach. However, this technique only operates in a defined size range and does not detect particles below 1 μm. Therefore, its applicability to study the details of heteroaggregation processes involving ENPs is limited.
or even αENP–SPMhetero,11 might be derived with this approach. However, this technique only operates in a defined size range and does not detect particles below 1 μm. Therefore, its applicability to study the details of heteroaggregation processes involving ENPs is limited.
Single-particle inductively-coupled plasma mass spectrometry (spICP-MS) 80 might be considered as another useful tool for studying heteroaggregation and determining α values. In addition to deriving particle size from conversion of measured element mass, spICP-MS can act as a particle counting technique. Currently spICP-MS can be used as routine analysis for measuring only one element at a time, so distinguishing between ENP and ENP–SPM signals is of utmost importance. Multi-element single particle measurements, as possible with a more specialised inductively-coupled plasma time-of-flight mass spectrometer (ICP-TOFMS)81–84 have the potential to further improve the differentiation between free and SPM-bound ENPs. This enables monitoring multiple elements simultaneously, making it possible to distinguish between ENP-specific and SPM-specific element signals. As an emerging technique for ENP analysis spICP-TOFMS has been successfully applied for distinguishing between naturally occurring particles and ENPs83,84 and analysing colloids in environmental samples, demonstrating its promise for heteroaggregation investigations. However, spICP-MS and spICP-TOFMS analysis requires low concentrations (in sub-ppb range), which complicates the use of this technique directly for environmentally relevant set-ups with high SPM contents. Another disadvantage of this approach is that dissolved metal species adsorbed on SPM may be mistakenly identified as nanoparticles attached on the SPM.
One of the most straightforward reaction techniques is the batch reaction, where all components are mixed and left to react in one reaction vessel with small aliquots removed for sampling at set time intervals. To minimise artefacts from loss in reaction volume through sampling, parallel identical batches are often prepared, each serving for sampling at one time point. Some of the measurement techniques for following size or number distributions over time mentioned above are a form of batch reactors (e.g. DLS, NTA), since the suspension as a whole is left in the cuvettes or cells and then measured continuously in situ. A more general approach for quantifying heteroaggregation in a batch method was introduced by Barton et al.77 and further developed by Geitner et al.78,79 In this so-called functional assay85 ENPs are mixed with SPM (referred to as “background particles”) in water. Aliquots are taken at different time points and after separation of the SPM phase the residual concentration of ENPs in the supernatant, nENP, is determined (Fig. 5)77–79 to derive α values according to eqn (5). Depending on the density of the SPM (which have included activated sludge, algae, glass beads, kaolinite) phase separation is achieved either by gravitational settling77,78 or centrifugation.79 Since the individual aggregation steps cannot be separated in the set-up presented here, the α values derived with the batch mixing method are equivalent to αglobal (Fig. 2).
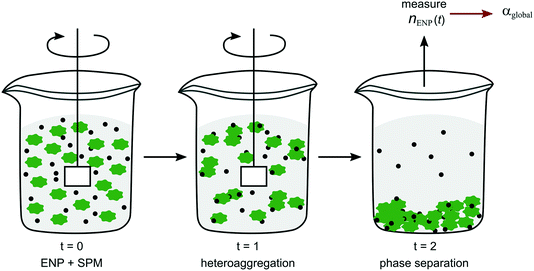 | ||
| Fig. 5 Schematic representation of the experimental set-up of the batch method as described in Barton et al.77 and Geitner et al.78,79 | ||
The Barton et al.77 and Geitner et al.78,79 method is sensitive to the efficient separation of the SPM phase. In the case of gravitational settling, aggregation might continue during the settling period required for separation of free and heteroaggregated ENPs. Furthermore, settling SPM may “trap” free ENPs (differential settling) leading to increased removal of free ENPs and consequently to an overestimation of αglobal. Very fast aggregation is difficult to study reliably with this set-up since the need to take aliquots and separate the phases limits the possible time resolution. Important challenges have been identified when applying the method to real freshwaters and lower ENP concentrations.50 Nevertheless, the relative simplicity of the batch method in terms of experimental set-up makes it appealing and it has already been applied to determine αglobal equivalents also for nano- and microplastics.13
In addition to batch reactors as those mentioned above, other approaches can include i) semi-batch reactors, when a significant fraction compared to the total volume is removed for analysis, ii) plug flow reactors where components are perfectly mixed in a T-junction (usually specially designed for this, e.g. stopped-flow devices) and the reaction time is determined by the length of tubing before measurement and iii) completely stirred tank reactors (CSTR) which are containers with a fixed volume for reaction with permanent inputs and outputs.
Strategy 3: indirect assessment of heteroaggregation via sedimentation
Another strategy is to monitor effects resulting from heteroaggregation instead of measuring the heteroaggregation processes directly. As ENPs aggregate to larger and larger particles, the gravitational force on the aggregates increases compared to the kinetic energy of the system. This leads to increased settling of aggregates. This settling or sedimentation can be measured using different techniques and has been used to quantify the rate of ENP homo- and heteroaggregation. To follow the sedimentation of ENPs one can either take a sample from the supernatant at specific time points and measure the residual ENP concentration63,86,87 or follow the sedimentation dynamics in situ using, for example, a UV-vis spectrophotometer.17,61,88–90In situ measurements are superior for measuring fast aggregation due to a better time resolution of measurements.The approach of following sedimentation of ENPs was first used to assess stability of ENP suspensions against homoaggregation under different conditions, ranging from simple to more complex aquatic conditions, including NOM in artificial media and natural waters.17,86,88 Several studies have reported sedimentation rates of ENPs in natural waters that include natural colloids,17,63,88,91,92 which means that the observed settling was at least partially due to heteroaggregation of ENPs with natural colloids. However, heteroaggregation was not explicitly indicated or measured, neither were α values derived. Mesocosm experiments were used to correlate field-observed ENP sedimentation rates to α values obtained for heteroaggregation using a batch method in the laboratory.93,94 These studies indicated a strong influence of heteroaggregation on ENP removal from the water column, but also highlighted the importance of other processes, such as homoaggregation or deposition on plant surfaces.
Only a few studies explicitly reported heteroaggregation rates.87,95 Deriving heteroaggregation rates of ENPs with natural colloids based on the measurements of sedimentation rates in filtered and unfiltered natural waters (i.e. in absence or presence of SPM) helps separating settling solely due to heteroaggregation from settling due to homoaggregation. To obtain αglobal values from sedimentation experiments the possibility of further aggregation during settling and effects of differential settling need to be accounted for. Furthermore, measuring sedimentation rates instead of free and SPM-bound ENP concentrations may add additional uncertainties to the system as several assumptions, e.g. related to SPM versus heteroaggregate settling velocities, are required to infer heteroaggregation behaviour from sedimentation.
SPM analogues for heteroaggregation experiments
An important aspect to consider when designing heteroaggregation experiments is the selection of adequate SPM analogues. Natural SPM is complex: concentrations, sizes and compositions are dynamic and depend on water flow regime (e.g. storm or base flow), season (e.g. snowmelt, primary production), catchment geology and vegetation, photo- and hydro-chemistry (e.g. pH, electrolyte/DOM concentrations and compositions, organic and inorganic redox couples) and human impact (e.g. dams, pollution). Not all these factors can be considered when selecting SPM analogues for studying heteroaggregation. To date, most heteroaggregation studies have been performed either in very simple systems, with single mineral compounds (e.g. SiO2 or clays) as SPM analogues53,54,62,66,78 or using unfiltered natural waters.50,95 For heteroaggregation experiments aiming at providing relevant input data for environmental fate models, selected SPM analogues would ideally fall between these two extremes and be of sufficient complexity to represent the characteristics of SPM that drive the heteroaggregation processes, while being simple enough to be reproducible under controlled laboratory conditions.The composition of natural riverine SPM appears to be most relevant for SPM analogue selection to derive data for fate models and exposure assessment, since rivers are the most likely receiving waters of ENPs and rivers transport large amounts of SPM over long distances. Imaging of SPM usually reveals floc-like structures (Fig. 6), consisting of mineral and organic components.96–100 Studies on the mineral and molecular composition of SPM are rather rare and mainly qualitative or semi-quantitative in nature, as sampling and analytical techniques are not straightforward101,102 and great variation can be expected depending on the water chemistry.103
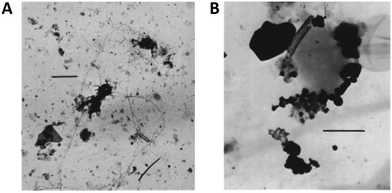 | ||
| Fig. 6 Natural SPM from (A) the river Rhine (Germany), scale bar 1 μm; and (B) Lake Bret (Switzerland), scale bar 250 nm. Reprinted with permission from Buffle et al.96 Copyright (1998) American Chemical Society. | ||
The major mineral fractions found in riverine SPM are phyllosilicates (clay minerals, chlorite & micas), feldspars, quartz, carbonates (calcite, dolomite) and oxides. The dominant clay minerals are illite, kaolinite and smectite, and identified micas include muscovite and biotite.98,100,104–108 Except for the iron oxyhydroxides most inorganic colloids will be negatively charged around neutral pH.96 Organic matter in SPM ranges from the molecular up to the organism level, including microorganisms, soil- or aquagenic refractory material and labile large organic polymers. It can be autochthonous (bioproduction-based carbohydrates, proteins and refractory aquagenic organics) or allochthonous (mainly soil-derived fulvics or humics).96,109 Organics in the particulate fraction have been found to be mainly microbial in nature and the importance of extracellular polymeric substances (large organic fibrils and networks) in SPM was underlined.99,107
Since the attachment of ENPs to SPM (and between SPM inner components) is governed by surface physiochemistry, the composition and surface properties of SPM are of major interest. Geitner et al.93 therefore chose to employ glass beads previously homogenized with water from a mesocosm, to obtain a surface coated with components from this system. Slomberg et al.108 tried to generate SPM analogues on the basis of the mineralogical composition of SPM in the Rhône river catchment. However, they did not include organic components (despite dissolved organics, <20 nm, present in the river water) and the mineral fractions used were all negatively charged under the given conditions. The composition of riverine SPM described above indicates that organic macromolecules of microbial origin as well as positively charged oxyhydroxide minerals play an important role in the SPM formation.110 Consequently, they may be crucial constituents coining SPM surface characteristics relevant for heteroaggregation processes.
In seawater systems, aggregation and settling are favored by the high salinity. Consequently, riverine particles are removed from the water column in the estuarine mixing zone and inorganic particles are less frequently observed in marine systems. However, oceans and seas play a major role in the global carbon cycle111 and the particulate fraction of abiotic carbon in these waters comprises a significant fraction of the global carbon and is dominated by polysaccharide fibrils and microgels.112,113 Ranging from small particles, such as transparent exopolymeric particles (TEP) and their precursors, to micron-sized aggregates, e.g. marine snow, these particles, together with the high salinity, favor aggregation and are likely to play an important role in the fate of ENPs in marine waters.114
Overall, it is challenging to identify SPM characteristics relevant for heteroaggregation and to choose SPM analogue constituents representing those major features. Additionally, the dynamics of the composition of the organic and inorganic components of SPM along its transport pathways need to be accounted for when selecting the components of a heteroaggregation experiment. Some of these dynamic processes can lead to a restricted range of combinations being relevant for a specific water type and this should be considered in the selection process in the case of using artificial test media or to interpret results when using natural waters.
Conclusions and outlook
Heteroaggregation between ENPs and SPM in natural waters is inherently complex. The selection of adequate methods to assess heteroaggregation therefore requires a careful balance of environmental relevance with practicality and reproducibility. It is essential that especially the selected SPM analogues used in laboratory experiments are sufficiently complex to represent relevant driving forces of the processes studied whilst being reproducible in common laboratory settings and enabling systematic assessments and comparisons. A particular challenge for the quantification of heteroaggregation is the complexity of concurrent homo- and heteroaggregation pathways and the resulting variance of the corresponding rate constants and α values. Most laboratory studies reporting α values fail to acknowledge this and do not specify whether αhetero or αglobal is derived.Clearly, there is no single best method for measuring heteroaggregation in environmentally relevant scenarios. Ideally, a combination of different methods, including sizing and counting techniques, is employed to provide most detailed insights and enable the effective differentiation of concurrent homo- and heteroaggregation processes. For any chosen approach it is crucial to be conscious of a given method's limitations and to be aware of which type of α can be derived with the chosen set-up.
Combining experiments with modelling approaches represents an important strategy in the development of methods to study heteroaggregation. In particular fast aggregation processes, such as the initial dimer formation steps or adsorption of smaller organic molecules on the surface of ENPs or SPM, could be elucidated in more depth with the help of models. For example Monte Carlo cluster–cluster aggregation models48 can support the interpretation of experimental data by assessing the effect of different initial αhomo and αhetero values on the observed aggregation rates and on experimentally derived αglobal values. Furthermore, improving our ability to calculate interaction forces between heteroaggregating particles would help assess the validity of experimentally derived α values.
Improving the quantitative assessment of heteroaggregation will help shed light on one of the most important fate processes of ENPs in natural aquatic systems. As a crucial fate descriptor, reliable α values are needed to refine exposure predictions of ENP transport and fate models and thereby support risk assessment. The type of α required will depend on the type of model employed as well as the research or risk assessment question that is being addressed. For example, detailed αhetero values will be required for mechanistic fate and transport models of high spatial and temporal resolution, whereas αglobal will be more adequate as an input parameter into unit-world type models predicting ENP fate at a more global, less detailed scale.
Finally, heteroaggregation also plays an important role in the fate of other particulate contaminants, such as for example nano- and microplastics.115–118 Efforts to improve the study of heteroaggregation will therefore benefit other fields as well.
Author contributions
AP coordinated the writing process. AP, AC, WP, JTKQ, MS, SS wrote the theory section. AP, EB, AB, JAGU, AG, TH, AM, AM, JTKQ, NT, HW, FvdK wrote the experimental sections. JAGU, AG, MH, HW wrote the SPM section. AP & AC made Fig. 1, AP made Fig. 2–4, AP & AB made Fig. 5. All authors edited the text and commented on all parts of the manuscript, revised and approved the final version.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work received support from European Union's Horizon 2020 research and innovation programme under grant agreement No. 646002 (NanoFASE). AG was also supported by the Mistra Environmental Nanosafety program financed by the Swedish Foundation for Strategic Environmental Research (grant no. DIA 2013/48), the Hellenic Foundation for Research and Innovation (HFRI) and the General Secretariat for Research and Technology (GSRT) (grant no. 1317).References
- G. V. Lowry, E. M. Hotze, E. S. Bernhardt, D. D. Dionysiou, J. A. Pedersen, M. R. Wiesner and B. Xing, Environmental occurrences, behavior, fate, and ecological effects of nanomaterials: an introduction to the special series, J. Environ. Qual., 2010, 39, 1867–1874 CrossRef CAS PubMed.
- K. L. Garner, S. Suh and A. A. Keller, Assessing the Risk of Engineered Nanomaterials in the Environment: Development and Application of the nanoFate Model, Environ. Sci. Technol., 2017, 51, 5541–5551 CrossRef CAS PubMed.
- J. Meesters, W. Peijnenburg, J. Hendriks, D. van de Meent and J. Quik, A Model Sensitivity Analysis to Determine the Most Important Physicochemical Properties Driving Environmental Fate and Exposure of Engineered Nanoparticles, Environ. Sci.: Nano, 2019, 6, 2049–2060 RSC.
- J. A. J. Meesters, A. A. Koelmans, J. T. K. Quik, A. J. Hendriks and D. van de Meent, Multimedia Modeling of Engineered Nanoparticles with SimpleBox4nano: Model Definition and Evaluation, Environ. Sci. Technol., 2014, 48, 5726–5736 CrossRef CAS PubMed.
- J. A. J. Meesters, J. T. K. Quik, A. A. Koelmans, A. J. Hendriks and D. van de Meent, Multimedia environmental fate and speciation of engineered nanoparticles: a probabilistic modeling approach, Environ. Sci.: Nano, 2016, 3, 715–727 RSC.
- A. Praetorius, M. Scheringer and K. Hungerbühler, Development of Environmental Fate Models for Engineered Nanoparticles - A Case Study of TiO2 Nanoparticles in the Rhine River, Environ. Sci. Technol., 2012, 46, 6705–6713 CrossRef CAS PubMed.
- N. Sani-Kast, M. Scheringer, D. Slomberg, J. Labille, A. Praetorius, P. Ollivier and K. Hungerbühler, Addressing the complexity of water chemistry in environmental fate modeling for engineered nanoparticles, Sci. Total Environ., 2015, 535, 150–159 CrossRef CAS.
- H. H. Liu and Y. Cohen, Multimedia Environmental Distribution of Engineered Nanomaterials, Environ. Sci. Technol., 2014, 48, 3281–3292 CrossRef CAS.
- K. A. Huynh, J. M. McCaffery and K. L. Chen, Heteroaggregation Reduces Antimicrobial Activity of Silver Nanoparticles: Evidence for Nanoparticle–Cell Proximity Effects, Environ. Sci. Technol. Lett., 2014, 1, 361–366 CrossRef CAS.
- J. Zhao, Y. Dai, Z. Wang, W. Ren, Y. Wei, X. Cao and B. Xing, Toxicity of GO to Freshwater Algae in the Presence of Al2O3 Particles with Different Morphologies: Importance of Heteroaggregation, Environ. Sci. Technol., 2018, 52, 13448–13456 CrossRef CAS PubMed.
- R. Wang, F. Dang, C. Liu, D. Wang, P. Cui, H. Yan and D. Zhou, Heteroaggregation and dissolution of silver nanoparticles by iron oxide colloids under environmentally relevant conditions, Environ. Sci.: Nano, 2019, 6, 195–206 RSC.
- A. Praetorius, N. Tufenkji, K.-U. Goss, M. Scheringer, F. von der Kammer and M. Elimelech, The road to nowhere: equilibrium partition coefficients for nanoparticles, Environ. Sci.: Nano, 2014, 1, 317–323 RSC.
- E. Besseling, J. T. K. Quik, M. Sun and A. A. Koelmans, Fate of nano- and microplastic in freshwater systems: A modeling study, Environ. Pollut., 2017, 220, 540–548 CrossRef CAS PubMed.
- J. T. K. Quik, J. J. M. de Klein and A. A. Koelmans, Spatially explicit fate modelling of nanomaterials in natural waters, Water Res., 2015, 80, 200–208 CrossRef CAS PubMed.
- F. Abdolahpur Monikh, A. Praetorius, A. Schmid, P. Kozin, B. Meisterjahn, E. Makarova, T. Hofmann and F. von der Kammer, Scientific rationale for the development of an OECD test guideline on engineered nanomaterial stability, NanoImpact, 2018, 11, 42–50 CrossRef.
- J. Hammes, J. A. Gallego-Urrea and M. Hassellöv, Geographically distributed classification of surface water chemical parameters influencing fate and behavior of nanoparticles and colloid facilitated contaminant transport, Water Res., 2013, 47, 5350–5361 CrossRef CAS PubMed.
- A. A. Keller, H. Wang, D. Zhou, H. S. Lenihan, G. Cherr, B. J. Cardinale, R. Miller and Z. Ji, Stability and Aggregation of Metal Oxide Nanoparticles in Natural Aqueous Matrices, Environ. Sci. Technol., 2010, 44, 1962–1967 CrossRef CAS PubMed.
- A. R. Petosa, D. P. Jaisi, I. R. Quevedo, M. Elimelech and N. Tufenkji, Aggregation and Deposition of Engineered Nanomaterials in Aquatic Environments: Role of Physicochemical Interactions, Environ. Sci. Technol., 2010, 44, 6532–6549 CrossRef CAS PubMed.
- B. Giese, F. Klaessig, B. Park, R. Kaegi, M. Steinfeldt, H. Wigger, A. von Gleich and F. Gottschalk, Risks, Release and Concentrations of Engineered Nanomaterial in the Environment, Sci. Rep., 2018, 8, 1565 CrossRef PubMed.
- N. Parker and A. A. Keller, Variation in regional risk of engineered nanoparticles: nanoTiO2 as a case study, Environ. Sci.: Nano, 2019, 6, 444–455 RSC.
- M. Elimelech, J. Gregory, X. Jia and R. A. Williams, Particle Deposition & Aggregation: Measurement, Modelling and Simulation, Butterworth-Heinemann, Woburn, 1998 Search PubMed.
- X.-Y. Li and B. E. Logan, Settling and coagulating behaviour of fractal aggregates, Water Sci. Technol., 2000, 42, 253–258 CrossRef CAS.
- J. Lyklema, Particulate Colloids, Fundamentals of Interface and Colloid Science, Academic Press, Elsevier Academic Press, Amsterdam, 2005, vol. 4 Search PubMed.
- G. G. Stokes, On the effect of the internal friction of fluids on the motion of pendulums, Trans. Cambridge Philos. Soc., 1850, 9, 8 Search PubMed.
- W. E. Dietrich, Settling velocity of natural particles, Water Resour. Res., 1982, 18, 1615–1626 CrossRef.
- P. M. Adler, Heterocoagulation in shear flow, J. Colloid Interface Sci., 1981, 83, 106–115 CrossRef CAS.
- A. Thill, S. Moustier, J. Aziz, M. R. Wiesner and J. Y. Bottero, Flocs Restructuring during Aggregation: Experimental Evidence and Numerical Simulation, J. Colloid Interface Sci., 2001, 243, 171–182 CrossRef CAS.
- M. Han and D. F. Lawler, Interactions of Two Settling Spheres: Settling Rates and Collision Efficiency, J. Hydraul. Eng., 1991, 117, 1269–1289 CrossRef.
- M. Han and D. F. Lawler, The (Relative) Insignificance of G in Flocculation, J. AWWA, 1992, 84, 79–91 CrossRef CAS.
- S. Veerapaneni and M. R. Wiesner, Hydrodynamics of Fractal Aggregates with Radially Varying Permeability, J. Colloid Interface Sci., 1996, 177, 45–57 CrossRef CAS PubMed.
- S. Youn and D. F. Lawler, The (relative) insignificance of G revisited to include nanoparticles, AWWA Water Science, 2019, 1, e1138 CrossRef.
- B. B. Mandelbrot, The Fractal Geometry of Nature, W. H. Freeman and Company, New York, 1982 Search PubMed.
- R. Jullien, R. Botet and P. M. Mors, Computer simulations of cluster-cluster aggregation, Faraday Discuss. Chem. Soc., 1987, 83, 125–137 RSC.
- M. Y. Lin, H. M. Lindsay, D. A. Weitz, R. C. Ball, R. Klein and P. Meakin, Universality in colloid aggregation, Nature, 1989, 339, 360–362 CrossRef CAS.
- M. Elimelech, J. Gregory, X. Jia and R. A. Williams, in Particle Deposition & Aggregation, ed. M. Elimelech, J. Gregory, X. Jia and R. A. Williams, Butterworth-Heinemann, Woburn, 1995, pp. 157–202 Search PubMed.
- W. Zhang, J. Crittenden, K. Li and Y. Chen, Attachment Efficiency of Nanoparticle Aggregation in Aqueous Dispersions: Modeling and Experimental Validation, Environ. Sci. Technol., 2012, 46, 7054–7062 CrossRef CAS PubMed.
- B. Derjaguin and L. Landau, Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes, Acta Physicochim. URSS, 1941, 14, 633 Search PubMed.
- E. J. W. Verwey and J. T. H. G. Overbeek, Theory of the Stability of Lyophobic Colloids, Elsevier Publishing Company, Inc., New York, Amsterdam, London, Brussels, 1948 Search PubMed.
- D. Grasso, K. Subramaniam, M. Butkus, K. Strevett and J. Bergendahl, A review of non-DLVO interactions in environmental colloidal systems, Rev. Environ. Sci. Bio/Technol., 2002, 1, 17–38 CrossRef CAS.
- C. J. van Oss, in Interface Science and Technology, ed. C. J. van Oss, Elsevier, 2008, vol. 16, pp. 31–48 Search PubMed.
- M. Seijo, M. Pohl, S. Ulrich and S. Stoll, Dielectric discontinuity effects on the adsorption of a linear polyelectrolyte at the surface of a neutral nanoparticle, J. Chem. Phys., 2009, 131, 174704 CrossRef PubMed.
- A. Clavier, F. Carnal and S. Stoll, Effect of Surface and Salt Properties on the Ion Distribution around Spherical Nanoparticles: Monte Carlo Simulations, J. Phys. Chem. B, 2016, 120, 7988–7997 CrossRef CAS PubMed.
- M. Seijo, S. Ulrich, M. Filella, J. Buffle and S. Stoll, Modeling the Adsorption and Coagulation of Fulvic Acids on Colloids by Brownian Dynamics Simulations, Environ. Sci. Technol., 2009, 43, 7265–7269 CrossRef CAS PubMed.
- N. N. Nyangiwe, C. N. Ouma and N. Musee, Study on the interactions of Ag nanoparticles with low molecular weight organic matter using first principles calculations, Mater. Chem. Phys., 2017, 200, 270–279 CrossRef CAS.
- R. Hogg, T. W. Healy and D. W. Fuerstenau, Mutual coagulation of colloidal dispersions, Trans. Faraday Soc., 1966, 62, 1638–1651 RSC.
- S. Lin and M. R. Wiesner, Deposition of Aggregated Nanoparticles — A Theoretical and Experimental Study on the Effect of Aggregation State on the Affinity between Nanoparticles and a Collector Surface, Environ. Sci. Technol., 2012, 46, 13270–13277 CrossRef CAS PubMed.
- F. Loosli and S. Stoll, Adsorption of TiO2 Nanoparticles at the Surface of Micron-Sized Latex Particles. pH and Concentration Effects on Suspension Stability, J. Colloid Sci. Biotechnol., 2012, 1, 113–121 CrossRef CAS.
- A. Clavier, A. Praetorius and S. Stoll, Determination of nanoparticle heteroaggregation attachment efficiencies and rates in presence of natural organic matter monomers. Monte Carlo modelling, Sci. Total Environ., 2019, 650, 530–540 CrossRef CAS PubMed.
- B. M. Smith, D. J. Pike, M. O. Kelly and J. A. Nason, Quantification of Heteroaggregation between Citrate-Stabilized Gold Nanoparticles and Hematite Colloids, Environ. Sci. Technol., 2015, 49, 12789–12797 CrossRef CAS PubMed.
- M. C. Surette and J. A. Nason, Nanoparticle aggregation in a freshwater river: the role of engineered surface coatings, Environ. Sci.: Nano, 2019, 6, 540–553 RSC.
- A. Moncho-Jordá, G. Odriozola, M. Tirado-Miranda, A. Schmitt and R. Hidalgo-Álvarez, Modeling the aggregation of partially covered particles: Theory and simulation, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 011404 CrossRef PubMed.
- M. Therezien, A. Thill and M. R. Wiesner, Importance of heterogeneous aggregation for NP fate in natural and engineered systems, Sci. Total Environ., 2014, 485–486, 309–318 CrossRef CAS PubMed.
- A. Praetorius, J. Labille, M. Scheringer, A. Thill, K. Hungerbühler and J.-Y. Bottero, Heteroaggregation of titanium dioxide nanoparticles with model natural colloids under environmentally relevant conditions, Environ. Sci. Technol., 2014, 48, 10690–10698 CrossRef CAS PubMed.
- J. Labille, C. Harns, J.-Y. Bottero and J. Brant, Heteroaggregation of Titanium Dioxide Nanoparticles with Natural Clay Colloids, Environ. Sci. Technol., 2015, 49, 6608–6616 CrossRef CAS PubMed.
- K. L. Chen and M. Elimelech, Aggregation and Deposition Kinetics of Fullerene (C60) Nanoparticles, Langmuir, 2006, 22, 10994–11001 CrossRef CAS PubMed.
- H. Holthoff, S. U. Egelhaaf, M. Borkovec, P. Schurtenberger and H. Sticher, Coagulation Rate Measurements of Colloidal Particles by Simultaneous Static and Dynamic Light Scattering, Langmuir, 1996, 12, 5541–5549 CrossRef CAS.
- J. A. Gallego-Urrea, J. Hammes, G. Cornelis and M. Hassellöv, Multimethod 3D characterization of natural plate-like nanoparticles: shape effects on equivalent size measurements, J. Nanopart. Res., 2014, 16, 2383 CrossRef.
- R. Pecora, Dynamic Light Scattering Measurement of Nanometer Particles in Liquids, J. Nanopart. Res., 2000, 2, 123–131 CrossRef CAS.
- B. B. Weiner, in Particle Size Analysis, The Royal Society of Chemistry, 1992, pp. 173–185 Search PubMed.
- A. R. M. N. Afrooz, I. A. Khan, S. M. Hussain and N. B. Saleh, Mechanistic Heteroaggregation of Gold Nanoparticles in a Wide Range of Solution Chemistry, Environ. Sci. Technol., 2013, 47, 1853–1860 CrossRef CAS PubMed.
- Y. Feng, X. Liu, K. A. Huynh, J. M. McCaffery, L. Mao, S. Gao and K. L. Chen, Heteroaggregation of Graphene Oxide with Nanometer- and Micrometer-Sized Hematite Colloids: Influence on Nanohybrid Aggregation and Microparticle Sedimentation, Environ. Sci. Technol., 2017, 51, 6821–6828 CrossRef CAS PubMed.
- Y. Feng, K. A. Huynh, Z. Xie, G. Liu and S. Gao, Heteroaggregation and sedimentation of graphene oxide with hematite colloids: Influence of water constituents and impact on tetracycline adsorption, Sci. Total Environ., 2019, 647, 708–715 CrossRef CAS PubMed.
- J. A. Gallego-Urrea, J. Hammes, G. Cornelis and M. Hassellöv, Coagulation and sedimentation of gold nanoparticles and illite in model natural waters: Influence of initial particle concentration, NanoImpact, 2016, 3, 67–74 CrossRef.
- K. A. Huynh, J. M. McCaffery and K. L. Chen, Heteroaggregation of Multiwalled Carbon Nanotubes and Hematite Nanoparticles: Rates and Mechanisms, Environ. Sci. Technol., 2012, 46, 5912–5920 CrossRef CAS PubMed.
- O. Oriekhova and S. Stoll, Heteroaggregation of CeO2 nanoparticles in presence of alginate and iron (III) oxide, Sci. Total Environ., 2019, 648, 1171–1178 CrossRef CAS PubMed.
- Y. Wang, K. Yang, B. Chefetz, B. Xing and D. Lin, The pH and Concentration Dependent Interfacial Interaction and Heteroaggregation between Nanoparticulate Zero-valent Iron and Clay Mineral Particles, Environ. Sci.: Nano, 2019, 6, 2129–2140 RSC.
- D. Zhou, A. I. Abdel-Fattah and A. A. Keller, Clay Particles Destabilize Engineered Nanoparticles in Aqueous Environments, Environ. Sci. Technol., 2012, 46, 7520–7526 CrossRef CAS PubMed.
- R. Kretzschmar, H. Holthoff and H. Sticher, Influence of pH and Humic Acid on Coagulation Kinetics of Kaolinite: A Dynamic Light Scattering Study, J. Colloid Interface Sci., 1998, 202, 95–103 CrossRef CAS.
- F. Gambinossi, S. E. Mylon and J. K. Ferri, Aggregation kinetics and colloidal stability of functionalized nanoparticles, Adv. Colloid Interface Sci., 2015, 222, 332–349 CrossRef CAS PubMed.
- J. A. Gallego-Urrea, J. Tuoriniemi, T. Pallander and M. Hassellöv, Measurements of nanoparticle number concentrations and size distributions in contrasting aquatic environments using nanoparticle tracking analysis, Environ. Chem., 2010, 7, 67–81 CrossRef CAS.
- J. A. Gallego-Urrea, J. Tuoriniemi and M. Hassellöv, Applications of particle-tracking analysis to the determination of size distributions and concentrations of nanoparticles in environmental, biological and food samples, TrAC, Trends Anal. Chem., 2011, 30, 473–483 CrossRef CAS.
- T. Raychoudhury, N. Tufenkji and S. Ghoshal, Aggregation and deposition kinetics of carboxymethyl cellulose-modified zero-valent iron nanoparticles in porous media, Water Res., 2012, 46, 1735–1744 CrossRef CAS PubMed.
- D. L. Slomberg, P. Ollivier, H. Miche, B. Angeletti, A. Bruchet, M. Philibert, J. Brant and J. Labille, Nanoparticle stability in lake water shaped by natural organic matter properties and presence of particulate matter, Sci. Total Environ., 2019, 656, 338–346 CrossRef CAS PubMed.
- V. Filipe, A. Hawe and W. Jiskoot, Critical Evaluation of Nanoparticle Tracking Analysis (NTA) by NanoSight for the Measurement of Nanoparticles and Protein Aggregates, Pharm. Res., 2010, 27, 796–810 CrossRef CAS PubMed.
- K. Mehrabi, B. Nowack, Y. Arroyo Rojas Dasilva and D. M. Mitrano, Improvements in Nanoparticle Tracking Analysis To Measure Particle Aggregation and Mass Distribution: A Case Study on Engineered Nanomaterial Stability in Incineration Landfill Leachates, Environ. Sci. Technol., 2017, 51, 5611–5621 CrossRef CAS PubMed.
- S. Maillette, C. Peyrot, T. Purkait, M. Iqbal, J. G. C. Veinot and K. J. Wilkinson, Heteroagglomeration of nanosilver with colloidal SiO2 and clay, Environ. Chem., 2016, 14, 1–8 CrossRef.
- L. E. Barton, M. Therezien, M. Auffan, J.-Y. Bottero and M. R. Wiesner, Theory and Methodology for Determining Nanoparticle Affinity for Heteroaggregation in Environmental Matrices Using Batch Measurements, Environ. Eng. Sci., 2014, 31, 421–427 CrossRef CAS.
- N. K. Geitner, N. J. O'Brien, A. A. Turner, E. J. Cummins and M. R. Wiesner, Measuring Nanoparticle Attachment Efficiency in Complex Systems, Environ. Sci. Technol., 2017, 51, 13288–13294 CrossRef CAS PubMed.
- N. K. Geitner, S. M. Marinakos, C. Guo, N. O'Brien and M. R. Wiesner, Nanoparticle Surface Affinity as a Predictor of Trophic Transfer, Environ. Sci. Technol., 2016, 50, 6663–6669 CrossRef CAS PubMed.
- M. D. Montaño, J. W. Olesik, A. G. Barber, K. Challis and J. F. Ranville, Single Particle ICP-MS: Advances toward routine analysis of nanomaterials, Anal. Bioanal. Chem., 2016, 408, 5053–5074 CrossRef PubMed.
- O. Borovinskaya, S. Gschwind, B. Hattendorf, M. Tanner and D. Günther, Simultaneous Mass Quantification of Nanoparticles of Different Composition in a Mixture by Microdroplet Generator-ICPTOFMS, Anal. Chem., 2014, 86, 8142–8148 CrossRef CAS PubMed.
- L. Hendriks, B. Ramkorun-Schmidt, A. Gundlach-Graham, J. Koch, R. N. Grass, N. Jakubowski and D. Günther, Single-particle ICP-MS with online microdroplet calibration: toward matrix independent nanoparticle sizing, J. Anal. At. Spectrom., 2019, 34, 716–728 RSC.
- F. Loosli, J. Wang, S. Rothenberg, M. Bizimis, C. Winkler, O. Borovinskaya, L. Flamigni and M. Baalousha, Sewage spills are a major source of titanium dioxide engineered (nano)-particle release into the environment, Environ. Sci.: Nano, 2019, 6, 763–777 RSC.
- A. Praetorius, A. Gundlach-Graham, E. Goldberg, W. Fabienke, J. Navratilova, A. Gondikas, R. Kaegi, D. Günther, T. Hofmann and F. von der Kammer, Single-particle multi-element fingerprinting (spMEF) using inductively-coupled plasma time-of-flight mass spectrometry (ICP-TOFMS) to identify engineered nanoparticles against the elevated natural background in soils, Environ. Sci.: Nano, 2017, 4, 307–314 RSC.
- C. O. Hendren, G. V. Lowry, J. M. Unrine and M. R. Wiesner, A functional assay-based strategy for nanomaterial risk forecasting, Sci. Total Environ., 2015, 536, 1029–1037 CrossRef CAS PubMed.
- J. T. K. Quik, I. Lynch, K. V. Hoecke, C. J. H. Miermans, K. A. C. D. Schamphelaere, C. R. Janssen, K. A. Dawson, M. A. C. Stuart and D. V. D. Meent, Effect of natural organic matter on cerium dioxide nanoparticles settling in model fresh water, Chemosphere, 2010, 81, 711–715 CrossRef CAS PubMed.
- I. Velzeboer, J. T. K. Quik, D. van de Meent and A. A. Koelmans, Rapid settling of nanoparticles due to heteroaggregation with suspended sediment, Environ. Toxicol. Chem., 2014, 33, 1766–1773 CrossRef CAS PubMed.
- J. R. Conway, A. S. Adeleye, J. Gardea-Torresdey and A. A. Keller, Aggregation, Dissolution, and Transformation of Copper Nanoparticles in Natural Waters, Environ. Sci. Technol., 2015, 49, 2749–2756 CrossRef CAS PubMed.
- A. J. Kennedy, M. S. Hull, J. A. Steevens, K. M. Dontsova, M. A. Chappell, J. C. Gunter and C. A. Weiss, Factors influencing the partitioning and toxicity of nanotubes in the aquatic environment, Environ. Toxicol. Chem., 2008, 27, 1932–1941 CrossRef CAS PubMed.
- T. Phenrat, N. Saleh, K. Sirk, H.-J. Kim, R. D. Tilton and G. V. Lowry, Stabilization of aqueous nanoscale zerovalent iron dispersions by anionic polyelectrolytes: adsorbed anionic polyelectrolyte layer properties and their effect on aggregation and sedimentation, J. Nanopart. Res., 2008, 10, 795–814 CrossRef CAS.
- A. Brunelli, G. Pojana, S. Callegaro and A. Marcomini, Agglomeration and sedimentation of titanium dioxide nanoparticles (n-TiO2) in synthetic and real waters, J. Nanopart. Res., 2013, 15, 1–10 CrossRef.
- J. T. K. Quik, M. C. Stuart, M. Wouterse, W. Peijnenburg, A. J. Hendriks and D. van de Meent, Natural colloids are the dominant factor in the sedimentation of nanoparticles, Environ. Toxicol. Chem., 2012, 31, 1019–1022 CrossRef CAS PubMed.
- N. K. Geitner, N. Bossa and M. R. Wiesner, Formulation and Validation of a Functional Assay-Driven Model of Nanoparticle Aquatic Transport, Environ. Sci. Technol., 2019, 53, 3104–3109 CrossRef CAS PubMed.
- B. P. Espinasse, N. K. Geitner, A. Schierz, M. Therezien, C. J. Richardson, G. V. Lowry, L. Ferguson and M. R. Wiesner, Comparative Persistence of Engineered Nanoparticles in a Complex Aquatic Ecosystem, Environ. Sci. Technol., 2018, 52, 4072–4078 CrossRef CAS PubMed.
- J. T. K. Quik, I. Velzeboer, M. Wouterse, A. A. Koelmans and D. van de Meent, Heteroaggregation and Sedimentation Rates for Nanomaterials in Natural Waters, Water Res., 2014, 48, 269–279 CrossRef CAS PubMed.
- J. Buffle, K. J. Wilkinson, S. Stoll, M. Filella and J. Zhang, A Generalized Description of Aquatic Colloidal Interactions: The Three-colloidal Component Approach, Environ. Sci. Technol., 1998, 32, 2887–2899 CrossRef CAS.
- V. Chanudet and M. Filella, Submicron organic matter in a peri-alpine, ultra-oligotrophic lake, Org. Geochem., 2007, 38, 1146–1160 CrossRef CAS.
- K.-H. Henning, H. Damke, J. Kasbohm, T. Puff, E. Breitenbach, O. Theel and A. Kießling, Schwebstoffbeschaffenheit im Odersystem, Ernst-Moritz-Arndt-Universität Greifswald, Greifswald, 2001 Search PubMed.
- B. S. Lartiges, S. Deneux-Mustin, G. Villemin, C. Mustin, O. Barrès, M. Chamerois, B. Gerard and M. Babut, Composition, structure and size distribution of suspended particulates from the Rhine River, Water Res., 2001, 35, 808–816 CrossRef CAS PubMed.
- M. Le Meur, E. Montargès-Pelletier, A. Bauer, R. Gley, S. Migot, O. Barres, C. Delus and F. Villiéras, Characterization of suspended particulate matter in the Moselle River (Lorraine, France): evolution along the course of the river and in different hydrologic regimes, J. Soils Sediments, 2016, 16, 1625–1642 CrossRef CAS.
- V. Chanudet and M. Filella, A Non-Perturbing Scheme for the Mineralogical Characterization and Quantification of Inorganic Colloids in Natural Waters, Environ. Sci. Technol., 2006, 40, 5045–5051 CrossRef CAS PubMed.
- J. R. Lead, W. Davison, J. Hamilton-Taylor and J. Buffle, Characterizing Colloidal Material in Natural Waters, Aquat. Geochem., 1997, 3, 213–232 CrossRef CAS.
- R. Salminen, M. J. Batista, M. Bidovec, A. Demetriades, B. De Vivo, W. De Vos, M. Duris, A. Gilucis, V. Gregorauskiene, J. Halamic, P. Heitzmann, A. Lima, G. Jordan, G. Klaver, P. Klein, J. Lis, J. Locutura, K. Marsina, A. Mazreku, P. J. O'Connor, S. Å. Olsson, R.-T. Ottesen, V. Petersell, J. A. Plant, S. Reeder, I. Salpeteur, H. Sandström, U. Siewers, A. Steenfelt and T. Tarvainen, Geochemical Atlas of Europe. Part 1 - Background Information, Methodology and Maps, 2005 Search PubMed.
- V. Chanudet and M. Filella, Size and composition of inorganic colloids in a peri-alpine, glacial flour-rich lake, Geochim. Cosmochim. Acta, 2008, 72, 1466–1479 CrossRef CAS.
- S. Hillier, Particulate composition and origin of suspended sediment in the R. Don, Aberdeenshire, UK, Sci. Total Environ., 2001, 265, 281–293 CrossRef CAS PubMed.
- C. P. Mao, J. Chen, X. Y. Yuan, Z. F. Yang, W. Balsam and J. F. Ji, Seasonal variation in the mineralogy of the suspended particulate matter of the lower Changjiang River at Nanjing, China, Clays Clay Miner., 2010, 58, 691–706 CrossRef CAS.
- D. Perret, M. E. Newman, J. C. Negre, Y. W. Chen and J. Buffle, Submicron Particles in the Rhine River .1. Physicochemical Characterization, Water Res., 1994, 28, 91–106 CrossRef CAS.
- D. L. Slomberg, P. Ollivier, O. Radakovitch, N. Baran, N. Sani-Kast, H. Miche, D. Borschneck, O. Grauby, A. Bruchet, M. Scheringer and J. Labille, Characterisation of suspended particulate matter in the Rhone River: insights into analogue selection, Environ. Chem., 2016, 13, 804–815 CrossRef CAS.
- V. Ittekkot and R. Laane, in Biogeochemistry of major world rivers, John Wiley, 1991, vol. 42, pp. 233–242 Search PubMed.
- A. P. Gondikas, A. Masion, M. Auffan, B. L. T. Lau and H. Hsu-Kim, Early-stage precipitation kinetics of zinc sulfide nanoclusters forming in the presence of cysteine, Chem. Geol., 2012, 329, 10–17 CrossRef CAS.
- J. I. Hedges, Global biogeochemical cycles: progress and problems, Mar. Chem., 1992, 39, 67–93 CrossRef CAS.
- J. J. Boon, V. A. Klap and T. I. Eglinton, Molecular characterization of microgram amounts of oceanic colloidal organic matter by direct temperature-resolved ammonia chemical ionization mass spectrometry, Org. Geochem., 1998, 29, 1051–1061 CrossRef CAS.
- P. H. Santschi, E. Balnois, K. J. Wilkinson, J. Zhang, J. Buffle and L. Guo, Fibrillar polysaccharides in marine macromolecular organic matter as imaged by atomic force microscopy and transmission electron microscopy, Limnol. Oceanogr., 1998, 43, 896–908 CrossRef CAS.
- E.-M. Zetsche and H. Ploug, Marine chemistry special issue: Particles in aquatic environments: From invisible exopolymers to sinking aggregates, Mar. Chem., 2015, 175, 1–4 CrossRef CAS.
- F. Lagarde, O. Olivier, M. Zanella, P. Daniel, S. Hiard and A. Caruso, Microplastic interactions with freshwater microalgae: Hetero-aggregation and changes in plastic density appear strongly dependent on polymer type, Environ. Pollut., 2016, 215, 331–339 CrossRef CAS PubMed.
- M. Long, I. Paul-Pont, H. Hégaret, B. Moriceau, C. Lambert, A. Huvet and P. Soudant, Interactions between polystyrene microplastics and marine phytoplankton lead to species-specific hetero-aggregation, Environ. Pollut., 2017, 228, 454–463 CrossRef CAS PubMed.
- J. Michels, A. Stippkugel, M. Lenz, K. Wirtz and A. Engel, Rapid aggregation of biofilm-covered microplastics with marine biogenic particles, Proc. R. Soc. B, 2018, 285, 20181203 CrossRef PubMed.
- O. Oriekhova and S. Stoll, Heteroaggregation of nanoplastic particles in the presence of inorganic colloids and natural organic matter, Environ. Sci.: Nano, 2018, 5, 792–799 RSC.
Footnotes |
| † Current address: Institute for Biodiversity and Ecosystem Dynamics, University of Amsterdam, Amsterdam, The Netherlands. E-mail: a.praetorius@uva.nl. |
| ‡ The code to create Fig. 1 is available online: https://github.com/apraetorius/collision_mechanisms. |
| This journal is © The Royal Society of Chemistry 2020 |