Open Access Article
Open Access ArticleSynchrotron X-ray quantitative evaluation of transient deformation and damage phenomena in a single nickel-rich cathode particle†
León
Romano Brandt
 *a,
John-Joseph
Marie
b,
Thomas
Moxham
a,
Dominic P.
Förstermann
b,
Enrico
Salvati
*a,
John-Joseph
Marie
b,
Thomas
Moxham
a,
Dominic P.
Förstermann
b,
Enrico
Salvati
 ac,
Cyril
Besnard
a,
Chrysanthi
Papadaki
a,
Zifan
Wang
ac,
Cyril
Besnard
a,
Chrysanthi
Papadaki
a,
Zifan
Wang
 a,
Peter G.
Bruce
a,
Peter G.
Bruce
 bdef and
Alexander M.
Korsunsky
bdef and
Alexander M.
Korsunsky
 a
a
aKorsunsky group, Multi-Beam Laboratory for Engineering Microscopy (MBLEM), Department of Engineering Science, University of Oxford, Parks Road, Oxford OX1 3PJ, UK. E-mail: leon.romanobrandt@eng.ox.ac.uk
bDepartment of Materials, University of Oxford, Parks Road, Oxford, OX1 3PH, UK
cPolytechnic Department of Engineering and Architecture (DPIA), University of Udine, Via delle Scienze 206, Udine, 33100, Italy
dDepartment of Chemistry, University of Oxford, South Parks Road, Oxford OX1 3QZ, UK
eThe Henry Royce Institute, Parks Road, Oxford, OX1 3PH, UK
fThe Faraday Institution, Quad One, Becquerel Avenue, Harwell Campus, Didcot, OX11 0RA, UK
First published on 27th August 2020
Abstract
The performance and durability of Ni-rich cathode materials are controlled in no small part by their mechanical durability, as chemomechanical breakdown at the nano-scale leads to increased internal resistance and decreased storage capacity. The mechanical degradation is caused by the transient lithium diffusion processes during charge and discharge of layered oxide spherical cathode micro-particles, leading to highly anisotropic incompatible strain fields. Experimental characterisation of the transient mechanisms underlying crack and void formation requires the combination of very high resolution in space (sub-micron) and time (sub-second) domains without charge interruption. The present study is focused on sub-micron focused operando synchrotron X-ray diffraction and in situ Ptycho-Tomographic nano-scale imaging of a single nano-structured LiNi0.8Co0.1Mn0.1O2 core–shell particle during charge to obtain a thorough understanding of the anisotropic deformation and damage phenomena at a particle level. Preferential grain orientation within the shell of a spherical secondary cathode particle provides improved lithium transport but is also associated with spatially varying anisotropic expansion of the hexagonal unit cell in the c-axis and contraction in the a-axis. These effects were resolved in relation to the grain orientation, and the link established with the nucleation and growth of intergranular cracks and voids that causes electrical isolation of active cathode material. Coupled multi-physics Finite Element Modelling of diffusion and deformation inside a single cathode particle during charge and discharge was validated by comparison with experimental evidence and allowed unequivocal identification of key mechanical drivers underlying Li-ion battery degradation.
Broader contextIn order to support the growth of electrochemical energy storage applications in applications such as electric vehicles and grid scale storage, improved cathode, anode and electrolyte materials are required to unlock higher attainable charge rates in combination with enhanced energy density. The main bottleneck in high performance Li-ion battery cells is the cathode material, as novel Ni-rich stoichiometries with promising electrochemical properties suffer from significant degradation during the first charge and discharge cycles, which can be linked to a complex interplay of multiple transient phenomena. The overall performance of the cell can therefore only be enhanced by in-depth understanding of processes at the micro- and nano scale, due to the carefully designed microstructure of particles that are forming the cathode. In addition, the complex micro-scale phenomena underlying degradation are highly time-dependent, which complicates experimental analysis further. Isolating the behaviour of cathode material at the relevant single particle scale is therefore a crucial step towards improving battery cells as a whole. In the following study we present operando data at the micron scale, thus revealing the mechanical mechanisms underlying the degradation of novel high-performance Ni-rich cathodes. |
Introduction
Li-ion batteries are seen as the technology of choice for many energy storage applications, including electronics, grid storage, electric vehicles (EV). As the need for higher energy density batteries continues, research is focused on the development of cathode materials with higher useable capacities. The so called NMC compositions (LiNixMnyCozO2, where x + y + z = 1) have proven successful in this endeavour. These materials have been synthesised in a variety of compositions (NMC111, NMC622, NMC811), with higher nickel contents providing higher energy densities, despite reducing electrochemical and mechanical cathode stability, leading to loss of capacity retention over cell life.1,2 The present study focuses LiNi0.8Mn0.1Co0.1O2 (NMC811), which is widely regarded as the state of the art cathode material. Capacity loss in NMC811 is evident from the first charge, with losses of up to 10% as a consequence of the first ‘formation’ cycle.3–5 Over extended cycling complex chemomechanical interactions linking lithium diffusion, anisotropic lattice strain, surface oxygen depletion and cathode particle degradation have been identified as other reasons for performance fading over cycling.6–9 At the crystal lattice scale, the cycling-induced mechanical degradation is caused by the anisotropic lattice expansion during lithium (de-)intercalation. Depending on the crystal lattice orientation within primary crystallites,10 large stresses exceeding the material cohesive strength can arise at grain boundaries, resulting in crack nucleation and propagation.7,11,12 An example for fracture and void formation is shown in Appendix A.1. At particle level, cracking exposes more surface area to the electrolyte, causing further degradation of the active cathode material through multiple mechanisms: phase transformation,13 cathode-electrolyte parasitic reactions,14–18 and transition metal dissolution.19,20 Cracking and debonding of primary particles further contribute to the capacity fade phenomenon by interrupting electron conduction from detached fragments to the cathode conductive matrix,9,21 thus preventing further contribution to charging and discharging.19 Recent efforts aimed at optimising the charging behaviour of NMC811 include the use of coatings,22 the design of core–shell particles with a Ni-rich core,23 and secondary particles with optimised lithium diffusion pathways between particle boundary and core.24,25The key aspect of diffusion and degradation processes is their transient nature at particle scale. Pristine spheroidal NMC particles rely on intra- and intergranular Li+ and electron conduction from the particle–electrolyte interface into the particle core. Interrupting electrochemical processes for diffraction measurements initiates charge re-balancing, thus masking lithiation and lattice parameter anisotropy along the radial particle direction. To understand underlying breakdown mechanisms, experimental techniques must be able to probe undisturbed charging/discharging processes at high resolution in both time and space. Characterising the electromechanical behaviour of NMC particles operando at the micron-scale poses a significant experimental challenge. As a result, direct experimental operando evidence for the evolution of both stress state and structural integrity in single secondary Li-ion cathode particles has remained lacking. Previously published operando experiments on single particles were limited to qualitative, averaged analysis of the degradation phenomena26,27 and electrochemical processes.3,28–33 Detailed post mortem characterisation of microstructural changes within secondary NMC particles or full cathodes provided insights into the consequences of degradation.8,34–36 However, the dynamic phenomena driving degradation cannot be captured using this approach. We report direct evidence obtained using synchrotron science techniques for operando sub-micron X-ray diffraction and in situ lensless coherent ptycho-tomography. Combined with Finite Element (FE) modelling and additional ex situ material characterisation, we develop deep model-based understanding of the mechanisms that underlie particle degradation, which can ultimately improve the design and fabrication of Ni-rich cathode materials.
Results and discussion
Diffusion pathways in core–shell particles
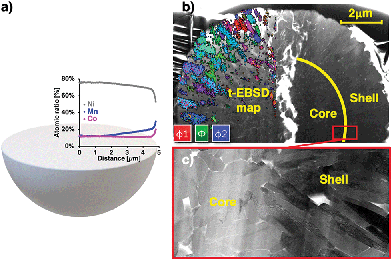
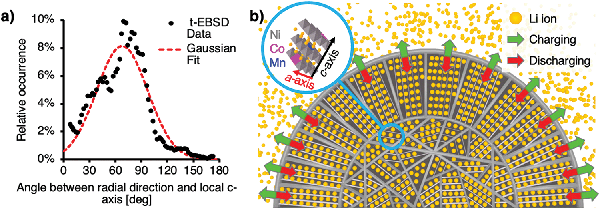
LiNi0.8Mn0.1Co0.1O2 cathodes were charged to 4.2 V and discharged to 3.0 V from pristine state at a rate of C/10. Subsequently, they were charged to 100% State of Charge (SoC) at a rate of C/3. Stoichiometric ratios were obtained from transmission Energy-Dispersive X-Ray Spectroscopy (t-EDX) performed on a thin, electron-transparent lamella containing half of a fractured particle at the electron energy of 20 keV, thus reducing the sample–beam interaction volume and increasing the resolution as compared to bulk sample measurements. The lamella was produced and fine-polished using FIB milling and revealed the grain orientation of primary particles in the shell. The data in Fig. 1a shows the progressive concentration gradients for Ni, Mn and Co along the radial particle direction. A Mn-rich surface with composition of LiNi0.5Mn0.3Co0.2O2 (NMC532) was found, while a bulk material composition of NMC811 was confirmed. To determine the crystal orientation of primary particles and the orientation of the local c-axis, Transmission Electron Back-Scattered Diffraction (t-EBSD) mapping was performed alongside the t-EDX analysis at the electron energy of 20 keV. For this purpose, back-scattered electron diffraction patterns showing Kikuchi bands37 were acquired in transmission mode and indexed, revealing local phase and grain orientation information. A more detailed description of the t-EBSD acquisition process is provided in the ESI.† The obtained t-EBSD map with colour-coded Euler angles is shown in Fig. 1b, alongside a Scanning Transmission Electron Microscopy (STEM) micrograph of the lamella and an illustration of primary particles in the core and shell. Elongated, radially oriented particles are visible in the particle shell, while smaller, randomly shaped particles were found in the particle core.Subsequently, the obtained Euler angles were converted from Cartesian coordinate base to the angles between the radial direction (from particle centre to t-EBSD measurement point) and the c-axis of the hexagonal particle lattice. The findings were normalised with respect to the statistical frequency of angle occurrence within a sphere. Further details are provided in the ESI.† The angle distribution shown in Fig. 2a confirmed a carefully designed grain orientation distribution within the secondary particle shell, resulting in radially aligned Li diffusion layers with respect to the particle centre, as illustrated in Fig. 2b.
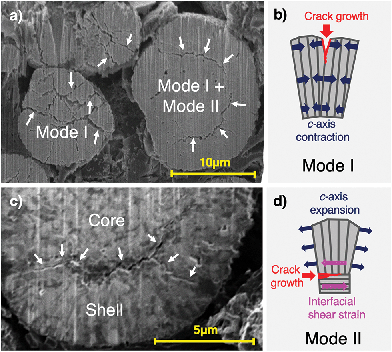
The experimentally confirmed diffusion pathway optimisation by design enables higher Li diffusion rates, however, it may also have a detrimental impact on the mechanical stability of spherical secondary particles. Preferential expansion and contraction directions of the hexagonal NMC811 lattice perpendicular to the lithium diffusion direction can cause large stresses between grains and within the microsphere overall, and lead to Mode I (opening), II (in-plane shear) and III (out-of-plane shear) fracture,38 as depicted in Fig. 3. A close relationship between microstructure and cracking mode can be seen in Fig. 3c: while radial Mode I cracks travel along the elongated grains in the shell, crack deflection resulting in Mode II cracking along the core–shell interface is visible. This ultimately leads to electrical isolation of active material.
High local deformation upon first charge onset
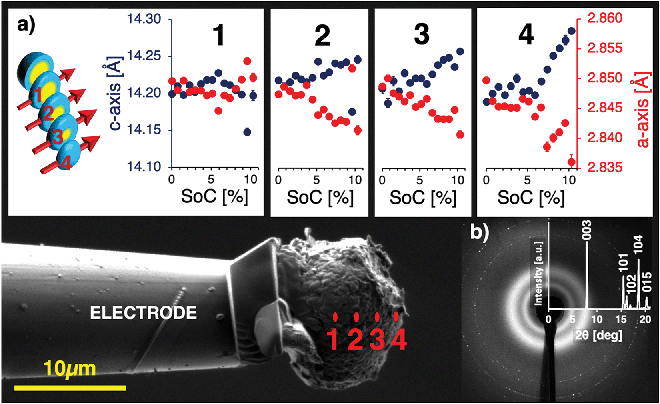
To measure the lattice parameter distortion within a single core–shell particle during operando charging, a sub-micron focus wide-angle X-ray scattering (WAXS) experiment was performed at the B16 Test beamline at Diamond Light Source, to collect local probes of the lattice parameter variations within a single particle. A pristine single NMC811 particle with the mass of 4.69 × 10−9 g was attached to an Al-coated nano-manipulator tungsten needle using an in-SEM Pt gas injection system. The particle was immersed in a LiTFSI:PYR13 ionic liquid droplet to substitute the more volatile and air-sensitive electrolyte.39 A lithium disc served as anode and a Kapton container, as well as a Faraday cage with X-ray inlet and outlet windows, were built around the setup. The volume was continuously flushed with Argon, ensuring an inert gas sheath atmosphere and minimal electromagnetic disturbances. Further details of the setup are described in the ‘Methods’ section. A photon energy of 19 keV was selected using a multilayer monochromator and focused onto the particle using Kirkpatrick-Baez (KB) mirrors, resulting in a beam size of around 380 nm on the sample. A low current potentiostat was connected to the tungsten needle with attached particle (cathode) and the Li disc (anode). The particle was charged up to a SoC of 10.3%, while a line scan across the particle was repeatedly acquired. The implications of the large overpotential introduced by the use of ionic liquid with high internal resistance meant that the experimental data were limited to the SoC range of 0% to 10.3%, as determined by current readings and the specific capacity of NMC811.Debye–Scherrer diffraction rings of the 003 and 104 reflections representing the c- and a-axis, were collected using an Image Star 9000 detector (Photonic Science Ltd, UK) and integrated azimuthally. The results presented in Fig. 4, showing the local c- and a-lattice parameter evolution during charge from 0% to 10.3% SoC along the particle radius, reveal the rise of significant local strain gradients during the early stages of the formation cycle, which would have been masked by averaging techniques. The free secondary particle surface closest to the lithium anode (location 4, Fig. 4) experiences an expansion of the hoop-oriented c-axis from 14.20 Å at 0% SoC to 14.30 Å at 10.3% SoC, as well as a contraction of the radially oriented a-axis from 2.850 Å at 0% SoC to 2.835 Å at 10.3% SoC. c-Axis expansion in hoop direction leads to the formation of compressive residual hoop stress in the particle shell, while contraction of the a-axis lattice parameter in radial direction leads to tensile residual stress in radial direction. As the illuminated material volume in locations 2 and 3 increasingly contains contributions from inactive primary particles under tension in the core, the resulting lattice parameter distributions represent a superposition of increasing and decreasing lattice parameters, which ultimately cancel each other out along the beam path through the particle centre in location 1.
Averaging operando strain measurements of a full NMC811 cathode were carried out for lattice strain comparison under identical beam conditions, but without the use of focusing KB mirrors to ensure sufficient averaging for reliable probing statistics. The cathode was charged from 3.4 to 4.4 V at a C-rate of 0.5. Further experimental details can be found in the supplementary information. Average lattice strains at 10.3% SoC were found to be 0.18% for the c-axis and −0.19% for the a-axis, as compared the observed inter-particle strain at single particle level of 0.71% at 10.3% SoC for the c-axis and −0.53% for the a-axis. Due to the anisotropic lithium intercalation and de-intercalation and resulting uneven lattice parameter distribution within a single particle, averaging measurements mask local peak strains during charge and discharge. The above-presented comparison of single particle results with averaging measurements reflect the unique insights gained by local probing by operando diffraction.
Stress analysis of the particle deformation obtained from operando XRD revealed the stress distribution in hoop and radial direction along the particle radius, as shown in Fig. 5. Assuming a stress free reference state before charging, pronounced compressive stresses of up to −1 GPa were found in the particle shell at a SoC of 10.3%, while tension of around 0.4 GPa was present in radial direction. As the lattice parameters in locations 1 and 2 were probed and averaged along the diameter of the particle, local stresses were masked by averaging and thus resulted in near zero stress values.
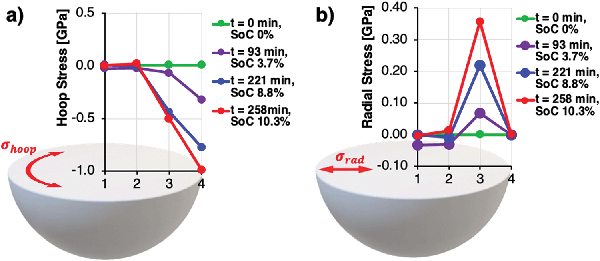 | ||
| Fig. 5 Reconstructed stress state along the particle radius vs. time and SoC, based on the lattice parameter data shown in Fig. 4. Assumption: Stress-free pristine particle. (a) Hoop stress. (b) Radial stress. | ||
Considering the designed radial grain orientation of the shell particles, the observed high stresses at low SoC appear to provide a reasonable explanation for the high incidence of void formation and intergranular fracture observed using FIB-SEM cross-sectional imaging shown in Fig. 3 and Appendix A.1 (Fig. 10). A significantly reduced deterioration rate of maximum capacity observed across literature in subsequent cycles can be explained by the significant amount of distributed micro-cracking and pseudo-plastic deformation during the first charging cycle, during which cracks and voids are formed initially.
First charge degradation observed by nano-resolution ptycho-tomography
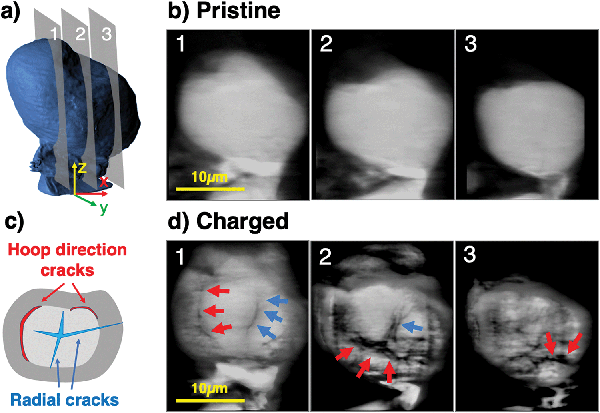
Ptychographic imaging was performed at the I13-1 beamline at Diamond Light source and combined with in situ particle charging, permitting the comparison of 3D tomographic data of one and the same single particle before and after charge with a voxel size of 43 × 43 × 43 nm3. This approach overcomes the well-known challenge of comparing different particles in ex situ and post mortem experiments, in which the prior damage state of different particles being compared cannot be known. The present operando approach ensures that the observed particle degradation can be compared to the pristine state of the same particle, and can be unequivocally ascribed to charging-related damage, as opposed to pre-existing particle damage inherited from particle manufacturing. A similar setup described above for the single particle diffraction experiment was employed, allowing to charge a single pristine NMC811 particle of mass 5.23 × 10−9 g to a SoC of 17.8%, thus demonstrating the effect of high-rate charging on the structural integrity of NMC811. A higher SoC was reached than in the previous experiment to ensure the capture of mechanical fracture within the particle. The reconstructed particle Ptycho-Tomography slices in Fig. 6 show significant microstructural degradation after one single charge to 17.8% SoC. Two types of cracks can be identified and show agreement with those observed in Fig. 3, namely, radial cracks reaching from the particle centre to the particle boundary (represented by blue arrows), and cracks in hoop direction along the core–shell interface (red arrows) – both of which limit lithium diffusion significantly.Modelling and simulation
A coupled diffusion-strain simulation was implemented in COMSOL Multiphysics®, which combined the solution of a generalised diffusion equation with sequentially coupled strain and stress analysis. More precisely, the model consisted of solving the diffusion equation for a Li-concentration gradient within the particle using a prescribed boundary concentration. In a second step, the calculated concentration was related to strain in prescribed expansion directions based on the t-EBSD results presented above and finally converted into stress. A lithium concentration of 20% was assumed for a fully charged particle, while a lithium saturation of 100% was assumed for the fully discharged state. Further model details are described in the ‘Methods’ section.
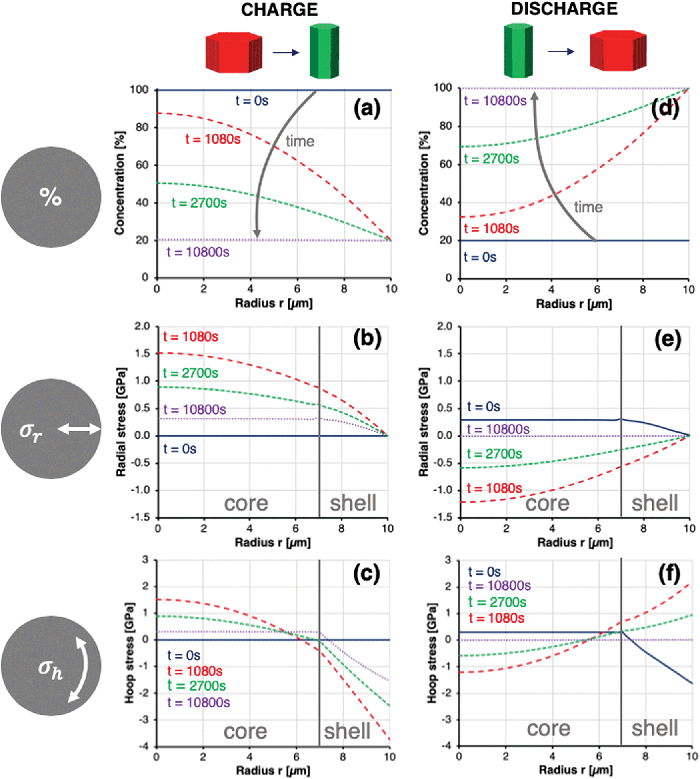
Fig. 7 shows the distribution of concentration, radial stress and hoop stress along the particle radius as a function of time during charge and discharge. Fig. 7a and b represent the full de-lithiation evolution from 100% to 20% and vice versa within 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 s or 3 hours. The prescribed diffusion coefficient DLi obtained from literature30,40 thus results in an effective charge rate of C/3, showing good agreement with real-world Li-NMC battery testing and applications.
800 s or 3 hours. The prescribed diffusion coefficient DLi obtained from literature30,40 thus results in an effective charge rate of C/3, showing good agreement with real-world Li-NMC battery testing and applications.
The time-dependent hoop stresses at the particle core and shell during charge and discharge, which are shown in Fig. 8, reveal peak stresses at time t = 1080 s. Stresses ranging from −4 GPa compression at the particle boundary to 1.5 GPa tension at the particle core can be expected to exceed the cohesive strength between particles by far, resulting in void formation, crack nucleation and growth. Lithium deintercalation from the particle boundary leads to an abrupt increase in c-axis lattice parameter, resulting in compressive boundary hoop stresses, which are balanced by tensile hoop stresses in the particle core. This simulated behaviour showed good agreement with operando diffraction data shown in Fig. 4, as well as the radial cracking pattern observed by Ptycho-Tomography shown in Fig. 6. Radial stresses remained tensile across the particle during charge, thus providing a good explanation for the observed cracks in hoop orientation at the core–shell interface in Fig. 6. This also agrees with the reduction in a-axis lattice parameter in radial direction observed by XRD in Fig. 4. After time t = 1080 s the stresses reduce without returning to a stress-free state. Upon discharge, the sense of stresses within the particle is invert between compressive and tensile, and vice versa, before returning to zero stress. All calculated stresses were obtained based on the assumption of a residual stress-free sample before the initial charge. As this assumption is difficult to verify experimentally, real stresses might be shifted by the amount of prevailing residual stress before first charge. Furthermore, inelastic processes that modify the material properties and response and lead to strain accumulation have also been ignored in this simulation.
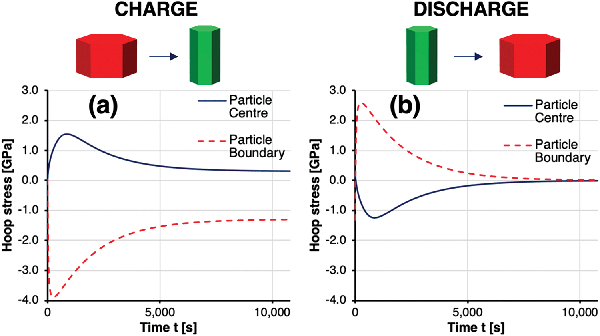 | ||
| Fig. 8 Simulated hoop stress evolution versus time during (a) charge and (b) discharge in the core and shell of a secondary particle. | ||
The graphs in Fig. 7 and 8 clearly show why averaging experimental techniques fail to determine the real stress state within NMC cathodes during charge, as the integral of hoop stresses along the radius lie significantly below the locally observed stresses. Clearly, the realistic mechanisms that underly Li intercalation and de-intercalation are significantly more intricate. However, the overall mechanical implications and some quantitative insights obtained by the combination of experimental and modelling studies presented here are representative and in good agreement with previous studies.12 The simulation described here provides reliable insights into the mechanical processes underlying fracture, although attendant chemical processes such as the formation of additional solid–electrolyte interfaces or oxygen depletion of surface layers are ignored. Excellent agreement between the simulated and observed radial and hoop stress profiles shown in Fig. 5 was confirmed. Given the high magnitudes and gradients of stresses within the particles during the initial charge, the greatest proportion of plastic deformation and primary particle de-bonding (micro-cracking) are likely to occur immediately during the first charge and discharge (‘formation’) cycle, with tensile stresses during discharge being the main driver for particle-level damage. During subsequent cycles, the accommodation of unit cell volume changes of up to 4% does not require similar magnitudes of additional plastic deformation and micro-fracture. The degradation therefore proceeds at a significantly reduced rate, with cyclic fatigue being the main mechanical driver, alongside electrochemical degradation processes. Optimising diffusion pathways in the core–shell secondary particles by orienting the lithium conduction pathways in the radial direction permits a faster transport of lithium ions from the electrolyte towards the centre of the particle, and results in higher achievable charge rates. In terms of the mechanical consequences for the durability of the cathode material, however, these appear to be somewhat detrimental to the long term performance.
Discussion
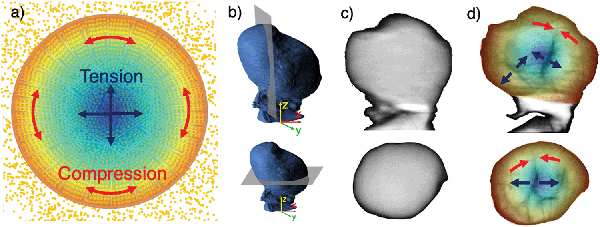
Combining the results of operando X-ray diffraction with in situ tomographic imaging demonstrates that a large proportion of the damage observed during the first charge stems from the electrochemical and mechanical phenomena triggered by lithium de-intercalation, especially at high charging rates. Tensile stress in the particle core balancing the compressive hoop stress caused by an expansion of the c-axis in the shell leads to void formation in the core, followed by radial crack growth towards the particle shell, as summarised in Fig. 9. Red arrows in Fig. 9d highlight that crack growth is impeded when reaching the particle shell, which further supports a change in stress along the radial direction from tensile to compressive. In addition, a decrease in the radially oriented a-axis lattice parameter leads to tensile residual stress in radial direction, resulting in hoop-oriented cracks between shell core and shell, which are shown in Fig. 9d and indicate a reduced core–shell interfacial strength. This permits further crack propagation along the core–shell interface and partial electrochemical isolation of the Ni-rich NMC811 particle core. FEM simulation results showing the simultaneous formation of peak tensile stresses in the particle core and peak compressive hoop stresses in the particle shell (Fig. 8a) shortly after the onset of charging confirm the described mechanisms underlying the experimental observations. Tensile radial stresses along the radial direction were also confirmed by FEM simulations (Fig. 7b) and support the assumptions made regarding the formation of core–shell interface cracks. Finally, the FEM results predict inverted stress values during particle discharge, which gives rise to further fracturing upon first discharge. We note that stresses in subsequent cycles are unlikely to reach identical peak stresses due to the “particle training” associated with distributed micro-cracking and pseudo-plastic deformation, which enable the particle to accommodate stresses with a smaller amount of further fragmentation.The experimental evidence presented in this work additionally points at a diffusion limit induced phase separation during the intercalation wave, resulting in a ‘shrinking core’ scenario, as first described by Fraggedakis et al.:41 while XRD tomography and SEM imaging techniques revealed crack growth along the core–shell interface, diffraction data confirmed the presence of high tensile stresses in radial direction. This mechanism can contribute to increased internal resistance in two different ways, depending on whether or not electrolyte is present in the newly formed void: (1) lacking the conducting properties of electrolyte, Li-ions can no longer be transported across the fractured part of the core–shell interface, resulting in a reduced Li-ion diffusion rate from boundary to core. (2) Crack channels connecting the void with the particle boundary are present and enable the transport of electrolyte into the newly formed void. This promotes chemical side reactions due to the exposed additional surface area, such as the formation of a Solid–Electrolyte Interface (SEI) and surface oxygen depletion, which are likely contributors to further degradation.
Conclusion
A novel experimental multi-technique approach for the quantitative evaluation of NMC811 particle degradation upon first charge was presented in this work. The combination of nanoscale synchrotron X-ray analysis with locally resolved structural insights obtained from t-EBSD mapping revealed the presence of a complex stress state upon de-lithiation during charge, which was shown to be strongly correlated with the designed microstructure of core–shell type particles. The locally measured strains, particularly in the particle shell, exceeded the averaged data obtained from conventional full cathode diffraction by far and highlight the drawbacks that diffusion rate optimisation of Ni-rich particles can have on their structural integrity. Based on the observed degradation mechanisms, two main fracture modes were found to underlie primary particle decohesion. To expand on the insights gained from the experimental data, a multiphysics model of the interlinked Li diffusion and strain state within a single particle was created. Excellent agreement between the experimental XRD data obtained during the onset of single particle charge as well as the structural degradation observed by in situ ptycho-tomographic imaging and the simulation data was found. The presence of peak strains in radial and hoop direction during the early stages of charge was confirmed experimentally, while an inversion of stresses predicted by FEM suggests further significant particle degradation during the first discharge.Conflicts of interest
There are no conflicts of interest to declare.Appendix
A.1 Void formation upon first charge
LiNi0.8Mn0.1Co0.1O2 cathodes were obtained from an industrial supplier, charged to 4.2 V and discharged to 3.0 V from pristine state at a rate of C/10. Subsequently, they were charged to levels of 50% and 100% SoC at a rate of C/3, respectively. Initial post mortem characterisation of the void evolution versus SoC was performed by creating FIB cross-sections through the bulk cathodes, revealing microstructural details in the centre of the spherical NMC811 particles. Sectioning of the cathode was carried out using Ga FIB at a voltage of 30 kV and a beam current of 11 nA, followed by fine polishing at 0.2 nA. The observed fragmentation is shown in Fig. 10, with voids highlighted in orange. The electron-conductive PVDF matrix can be seen in between particles. Combining the formation cycle with one single charge was thus sufficient to drive strong fragmentation and void formation, causing significant and irreversible loss in maximum capacity of around 10% after first charge. Intergranular voids result in reduced internal Li and electron conductivity, a significantly increased charge-transfer kinetic resistance and therefore lower attainable charging rates. In addition, fragmentation of secondary particles leads to de-bonding and electrical isolation of primary particles, which stop contributing to electrochemical processes due to a lack of electron conductivity through the enclosing electrolyte.19 | ||
| Fig. 10 Intergranular void evolution vs. SOC in NMC811 material observed by FIB-SEM cross-sectional imaging. Cracks and voids highlighted in orange. | ||
Acknowledgements
The authors would like to acknowledge Diamond Light Source for providing the beamtime under experiment MM22503 and MG22217-1 as well as the helping support of Igor Dolbnya, Oliver Fox, Darren Batey and Silvia Cipiccia. A. M. K. would like to acknowledge funding received from the Engineering and Physical Sciences Research Council (EPSRC) [EP/P005381/1]. P. G. B. is indebted to the Engineering and Physical Sciences Research Council (EPSRC), including Enabling Next Generation Lithium Batteries [EP/M009521/1], Henry Royce Institute for Advanced Materials [EP/R00661X/1, EP/S019367/1, EP/R010145/1] and the Faraday Institution All-Solid-State Batteries with Li and Na Anodes [FIRG007, FIRG008] for financial support.References
- M. D. Radin, S. Hy, M. Sina, C. Fang, H. Liu, J. Vinckeviciute, M. Zhang, M. S. Whittingham, Y. S. Meng and A. Van der Ven, Narrowing the Gap between Theoretical and Practical Capacities in Li-Ion Layered Oxide Cathode Materials, Adv. Energy Mater., 2017, 7, 1–33, DOI:10.1002/aenm.201602888.
- F. Schipper, E. M. Erickson, C. Erk, J.-Y. Shin, F. F. Chesneau and D. Aurbach, Review—Recent Advances and Remaining Challenges for Lithium Ion Battery Cathodes, J. Electrochem. Soc., 2017, 164, A6220–A6228, DOI:10.1149/2.0351701jes.
- F. Friedrich, B. Strehle, A. T. S. Freiberg, K. Kleiner, S. J. Day, C. Erk, M. Piana and H. A. Gasteiger, Capacity fading mechanisms of NCM-811 cathodes in lithium-ion batteries studied by X-ray diffraction and other diagnostics, J. Electrochem. Soc., 2019, 166, A3760–A3774, DOI:10.1149/2.0821915jes.
- J. V. Laveda, J. E. Low, F. Pagani, E. Stilp, S. Dilger, V. Baran, M. Heere and C. Battaglia, Stabilizing Capacity Retention in NMC811/Graphite Full Cells via TMSPi Electrolyte Additives, ACS Appl. Energy Mater., 2019, 2, 7036–7044, DOI:10.1021/acsaem.9b00727.
- H. Zhou, F. Xin, B. Pei and M. S. Whittingham, What Limits the Capacity of Layered Oxide Cathodes in Lithium Batteries?, ACS Energy Lett., 2019, 4, 1902–1906, DOI:10.1021/acsenergylett.9b01236.
- S. Xia, L. Mu, Z. Xu, J. Wang, C. Wei, L. Liu, P. Pianetta, K. Zhao, X. Yu, F. Lin and Y. Liu, Chemomechanical Interplay of Layered Cathode Materials undergoing Fast Charging in Lithium Batteries, Nano Energy, 2018, 53, 753–762, DOI:10.1016/j.nanoen.2018.09.051.
- L. Mu, R. Lin, R. Xu, L. Han, S. Xia, D. Sokaras, J. D. Steiner, T. C. Weng, D. Nordlund, M. M. Doeff, Y. Liu, K. Zhao, H. L. Xin and F. Lin, Oxygen Release Induced Chemomechanical Breakdown of Layered Cathode Materials, Nano Lett., 2018, 18, 3241–3249, DOI:10.1021/acs.nanolett.8b01036.
- Y. Yang, R. Xu, K. Zhang, S. Lee, L. Mu, P. Liu, C. K. Waters, S. Spence, Z. Xu, C. Wei, D. J. Kautz, Q. Yuan, Y. Dong, Y. Yu, X. Xiao, H. Lee, P. Pianetta, P. Cloetens, J. Lee, K. Zhao, F. Lin and Y. Liu, Quantification of Heterogeneous Degradation in Li-Ion Batteries, Adv. Energy Mater., 2019, 9, 1900674, DOI:10.1002/aenm.201900674.
- B. Song, T. Sui, S. Ying, L. Li, L. Lu and A. M. Korsunsky, Nano-structural changes in Li-ion battery cathodes during cycling revealed by FIB-SEM serial sectioning tomography, J. Mater. Chem. A, 2015, 3, 18171–18179, 10.1039/C5TA04151A.
- J. Li, A. R. Cameron, H. Li, S. Glazier, D. Xiong, M. Chatzidakis, J. Allen, G. A. Botton and J. R. Dahn, Comparison of Single Crystal and Polycrystalline LiNi0.5Mn0.3Co0.2O2 Positive Electrode Materials for High Voltage Li-Ion Cells, J. Electrochem. Soc., 2017, 164, A1534–A1544, DOI:10.1149/2.0991707jes.
- G. Sun, T. Sui, B. Song, H. Zheng, L. Lu and A. M. Korsunsky, On the fragmentation of active material secondary particles in lithium ion battery cathodes induced by charge cycling, Extrem. Mech. Lett., 2016, 9, 449–458, DOI:10.1016/J.EML.2016.03.018.
- A. M. Korsunsky, T. Sui and B. Song, Explicit formulae for the internal stress in spherical particles of active material within lithium ion battery cathodes during charging and discharging, Mater. Des., 2015, 69, 247–252, DOI:10.1016/j.matdes.2014.12.058.
- J. Li, R. Shunmugasundaram, R. Doig and J. R. Dahn, In Situ X-ray Diffraction Study of Layered Li–Ni–Mn–Co Oxides: Effect of Particle Size and Structural Stability of Core-Shell Materials, Chem. Mater., 2016, 28, 162–171, DOI:10.1021/acs.chemmater.5b03500.
- S. M. Bak, E. Hu, Y. Zhou, X. Yu, S. D. Senanayake, S. J. Cho, K. B. Kim, K. Y. Chung, X. Q. Yang and K. W. Nam, Structural changes and thermal stability of charged LiNixMnyCozO2 cathode materials studied by combined in situ time-resolved XRD and mass spectroscopy, ACS Appl. Mater. Interfaces, 2014, 6, 22594–22601, DOI:10.1021/am506712c.
- R. Jung, M. Metzger, F. Maglia, C. Stinner and H. A. Gasteiger, Oxygen Release and Its Effect on the Cycling Stability of LiNixMnyCozO2 (NMC) Cathode Materials for Li-Ion Batteries, J. Electrochem. Soc., 2017, 164, A1361–A1377, DOI:10.1149/2.0021707jes.
- J. Li, L. E. Downie, L. Ma, W. Qiu and J. R. Dahn, Study of the Failure Mechanisms of LiNi0.8Mn0.1Co0.1O2 Cathode Material for Lithium Ion Batteries, J. Electrochem. Soc., 2015, 162, A1401–A1408, DOI:10.1149/2.1011507jes.
- R. Jung, M. Metzger, F. Maglia, C. Stinner and H. A. Gasteiger, Chemical versus electrochemical electrolyte oxidation on NMC111, NMC622, NMC811, LNMO, and conductive carbon, J. Phys. Chem. Lett., 2017, 8, 4820–4825, DOI:10.1021/acs.jpclett.7b01927.
- T. Hatsukade, A. Schiele, P. Hartmann, T. Brezesinski and J. Janek, Origin of Carbon Dioxide Evolved during Cycling of Nickel-Rich Layered NCM Cathodes, ACS Appl. Mater. Interfaces, 2018, 10, 38892–38899, DOI:10.1021/acsami.8b13158.
- Z. Xu, M. M. Rahman, L. Mu, Y. Liu and F. Lin, Chemomechanical behaviors of layered cathode materials in alkali metal ion batteries, J. Mater. Chem. A, 2018, 6, 21859–21884, 10.1039/C8TA06875E.
- H. H. Ryu, K. J. Park, C. S. Yoon and Y. K. Sun, Capacity fading of Ni-rich Li[NixCoy Mn1−x−y]O2 (0.6 ≤ x ≤ 0.95) Cathodes for High-Energy-Density Lithium-Ion Batteries: Bulk or Surface Degradation?, Chem. Mater., 2018, 30, 1155–1163, DOI:10.1021/acs.chemmater.7b05269.
- W. H. Woodford, Y.-M. Chiang and W. C. Carter, “Electrochemical Shock” of Intercalation Electrodes: A Fracture Mechanics Analysis, J. Electrochem. Soc., 2010, 157, A1052, DOI:10.1149/1.3464773.
- F. Xin, H. Zhou, X. Chen, M. Zuba, N. Chernova, G. Zhou and M. S. Whittingham, Li-Nb-O Coating/Substitution Enhances the Electrochemical Performance of the LiNi0.8Mn0.1Co0.1O2 (NMC 811) Cathode, ACS Appl. Mater. Interfaces, 2019, 11, 34889–34894, DOI:10.1021/acsami.9b09696.
- X. Xu, L. Xiang, L. Wang, J. Jian, C. Du, X. He, H. Huo, X. Cheng and G. Yin, Progressive concentration gradient nickel-rich oxide cathode material for high-energy and long-life lithium-ion batteries, J. Mater. Chem. A, 2019, 7, 7728–7735, 10.1039/C9TA00224C.
- R. Chen, T. Zhao, X. Zhang, L. Li and F. Wu, Advanced cathode materials for lithium-ion batteries using nanoarchitectonics, Nanoscale Horiz., 2016, 1, 423–444, 10.1039/c6nh00016a.
- X. Xu, H. Huo, J. Jian, L. Wang, H. Zhu, S. Xu, X. He, G. Yin, C. Du and X. Sun, Radially Oriented Single-Crystal Primary Nanosheets Enable Ultrahigh Rate and Cycling Properties of LiNi0.8Co0.1 Mn0.1O2 Cathode Material for Lithium-Ion Batteries, Adv. Energy Mater. 9, 2019, 1803963, DOI:10.1002/aenm.201803963.
- D. J. Miller, C. Proff, J. G. Wen, D. P. Abraham and J. Bareño, Observation of microstructural evolution in li battery cathode oxide particles by in situ electron microscopy, Adv. Energy Mater., 2013, 3, 1098–1103, DOI:10.1002/aenm.201300015.
- J. Y. Huang, L. Zhong, C. M. Wang, J. P. Sullivan, W. Xu, L. Q. Zhang, S. X. Mao, N. S. Hudak, X. H. Liu, A. Subramanian, H. Fan, L. Qi, A. Kushima and J. Li, In situ observation of the electrochemical lithiation of a single SnO2 nanowire electrode, Science, 2010, 330, 1515–1520, DOI:10.1126/science.1195628.
- A. Demortiere, J. Ando, M. Bettge, V. De Andrade, K. Amine and D. Miller, Monitoring morphological evolution of Li-ion cathode secondary particles through In situ FIB/SEM electrochemical experiment, in Eur. Microsc. Congr. 2016 Proc., Wiley-VCH Verlag GmbH & Co. KGaA, 2016, pp. 293–295. DOI:10.1002/9783527808465.emc2016.6960.
- C. Heubner, U. Langklotz, C. Lämmel, M. Schneider and A. Michaelis, Electrochemical single-particle measurements of electrode materials for Li-ion batteries: Possibilities, insights and implications for future development, Electrochim. Acta, 2020, 330, 135160, DOI:10.1016/j.electacta.2019.135160.
- P.-C. Tsai, B. Wen, M. Wolfman, M.-J. Choe, M. S. Pan, L. Su, K. Thornton, J. Cabana and Y.-M. Chiang, Single-particle measurements of electrochemical kinetics in NMC and NCA cathodes for Li-ion batteries, Energy Environ. Sci., 2018, 11, 860–871, 10.1039/C8EE00001H.
- H. Munakata, B. Takemura, T. Saito and K. Kanamura, Evaluation of real performance of LiFePO4 by using single particle technique, J. Power Sources, 2012, 217, 444–448, DOI:10.1016/j.jpowsour.2012.06.037.
- I. Uchida, H. Fujiyoshi and S. Waki, Microvoltammetric studies on single particles of battery active materials, J. Power Sources, 1997, 68, 139–144 CrossRef CAS.
- K. Dokko, M. Mohamedi, Y. Fujita, T. Itoh, M. Nishizawa, M. Umeda and I. Uchida, Kinetic Characterization of Single Particles of LiCoO2 by AC Impedance and Potential Step Methods, J. Electrochem. Soc., 2001, 148, A422, DOI:10.1149/1.1359197.
- E. H. R. Tsai, J. Billaud, D. F. Sanchez, J. Ihli, M. Odstrčil, M. Holler, D. Grolimund, C. Villevieille and M. Guizar-Sicairos, Correlated X-Ray 3D Ptychography and Diffraction Microscopy Visualize Links between Morphology and Crystal Structure of Lithium-Rich Cathode Materials, iScience, 2019, 11, 356–365, DOI:10.1016/j.isci.2018.12.028.
- R. F. Ziesche, T. Arlt, D. P. Finegan, T. M. M. Heenan, A. Tengattini, D. Baum, N. Kardjilov, H. Markötter, I. Manke, W. Kockelmann, D. J. L. Brett and P. R. Shearing, 4D imaging of lithium-batteries using correlative neutron and X-ray tomography with a virtual unrolling technique, Nat. Commun., 2020, 11, 1–11, DOI:10.1038/s41467-019-13943-3.
- R. Xu, Y. Yang, F. Yin, P. Liu, P. Cloetens, Y. Liu, F. Lin and K. Zhao, Heterogeneous damage in Li-ion batteries: Experimental analysis and theoretical modeling, J. Mech. Phys. Solids, 2019, 129, 160–183, DOI:10.1016/j.jmps.2019.05.003.
- R. R. Keller and R. H. Geiss, Transmission EBSD from 10 nm domains in a scanning electron microscope, J. Microsc., 2012, 245, 245–251, DOI:10.1111/j.1365-2818.2011.03566.x.
- T. L. Anderson, Fracture Mechanics: Fundamentals and Applications, CRC Press, 4th edn, 2017 Search PubMed.
- Q. Huang, Y. Y. Lee and B. Gurkan, Pyrrolidinium Ionic Liquid Electrolyte with Bis(trifluoromethylsulfonyl)imide and Bis(fluorosulfonyl)imide Anions: Lithium Solvation and Mobility, and Performance in Lithium Metal-Lithium Iron Phosphate Batteries, Ind. Eng. Chem. Res., 2019, 58, 22587–22597, DOI:10.1021/acs.iecr.9b03202.
- E. Zhao, L. Fang, M. Chen, D. Chen, Q. Huang, Z. Hu, Q. B. Yan, M. Wu and X. Xiao, New insight into Li/Ni disorder in layered cathode materials for lithium ion batteries: A joint study of neutron diffraction, electrochemical kinetic analysis and first-principles calculations, J. Mater. Chem. A, 2017, 5, 1679–1686, 10.1039/c6ta08448f.
- D. Fraggedakis, N. Nadkarni, T. Gao, T. Zhou, Y. Zhang, Y. Han, R. M. Stephens, Y. Shao-Horn and M. Z. Bazant, A scaling law to determine phase morphologies during ion intercalation, Energy Environ. Sci., 2020, 13, 2142, 10.1039/d0ee00653j.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ee02290j |
| This journal is © The Royal Society of Chemistry 2020 |