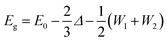Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mg3(Bi,Sb)2 single crystals towards high thermoelectric performance†
Yu
Pan‡
 *a,
Mengyu
Yao‡
a,
Xiaochen
Hong
b,
Yifan
Zhu
cd,
Fengren
Fan
a,
Kazuki
Imasato
*a,
Mengyu
Yao‡
a,
Xiaochen
Hong
b,
Yifan
Zhu
cd,
Fengren
Fan
a,
Kazuki
Imasato
 e,
Yangkun
He
a,
Christian
Hess
b,
Jörg
Fink
abf,
Jiong
Yang
e,
Yangkun
He
a,
Christian
Hess
b,
Jörg
Fink
abf,
Jiong
Yang
 c,
Bernd
Büchner
bf,
Chenguang
Fu
c,
Bernd
Büchner
bf,
Chenguang
Fu
 *a,
G. Jeffrey
Snyder
*a,
G. Jeffrey
Snyder
 e and
Claudia
Felser
a
e and
Claudia
Felser
a
aMax Planck Institute for Chemical Physics of Solids, Nöthnitzer Str. 40, 01187, Dresden, Germany. E-mail: yu.pan@cpfs.mpg.de; chenguang.fu@cpfs.mpg.de
bLeibniz-Institute for Solid State and Materials Research (IFW-Dresden), Helmholtzstraße 20, 01069, Dresden, Germany
cMaterials Genome Institute, Shanghai University, 99 Shangda Road, Shanghai 200444, China
dState Key Laboratory of High Performance Ceramics and Superfine Microstructure, Shanghai Institute of Ceramics, Chinese Academy of Sciences, Shanghai 200050, China
eDepartment of Materials Science and Engineering, Northwestern University, Evanston, IL 60208, USA
fInstitute for Solid-State and Materials Physics, Technical University Dresden, 01062 Dresden, Germany
First published on 4th May 2020
Abstract
The rapid growth of the thermoelectric cooler market makes the development of novel room temperature thermoelectric materials of great importance. Ternary n-type Mg3(Bi,Sb)2 alloys are promising alternatives to the state-of-the-art Bi2(Te,Se)3 alloys but grain boundary resistance is the most important limitation. n-type Mg3(Bi,Sb)2 single crystals with negligible grain boundaries are expected to have particularly high zT but have rarely been realized due to the demanding Mg-rich growth conditions required. Here, we report, for the first time, the thermoelectric properties of n-type Mg3(Bi,Sb)2 alloyed single crystals grown by a one-step Mg-flux method using sealed tantalum tubes. High weighted mobility ∼140 cm2 V−1 s−1 and a high zT of 0.82 at 315 K are achieved in Y-doped Mg3Bi1.25Sb0.75 single crystals. Through both experimental angle-resolved photoemission spectroscopy and theoretical calculations, we denote the origin of the high thermoelectric performance from a point of view of band widening effect and electronegativity, as well as the necessity to form high Bi/Sb ratio ternary Mg3(Bi,Sb)2 alloys. The present work paves the way for further development of Mg3(Bi,Sb)2 for near room temperature thermoelectric applications.
Broader contextThere are only few thermoelectric materials show high performance in the temperature range of 300–500 K, especially for the n-type. Bi2Te3-based alloys have been the only commercialized thermoelectric alloys for more than 50 years. Searching for thermoelectric materials with high figure of merit at 300–500 K has great significance for low-grade waste-heat recovery and solid-state cooling. In recent years, n-type Mg3(Bi,Sb)2 ternary alloys are found to be promising as an alternative for the n-type Bi2(Te,Se)3 thermoelectric alloys. Successful growth of the single crystals of n-type Mg3(Bi,Sb)2 alloys can enable the investigation of band structure analysis by ARPES, as well as the grain boundary effect on the transport of charge carriers and phonons which greatly affect the room temperature thermoelectric figure of merit. These insights into the fundamental physics of Mg3(Bi,Sb)2 alloys could shed light on further strategies for enhancing the thermoelectric performance, and thus promote their application in waste-heat recovery and solid-state cooling. |
Introduction
Thermoelectric materials possess great potential in waste heat recovery and as static state Peltier coolers, since they are able to convert heat into electricity and vice versa.1,2 Application of thermoelectric technology near room temperature offers a great opportunity for energy saving and solid-state cooling.3 Wide application of thermoelectric technology is constrained by the energy conversion efficiency, which is closely related to the material's dimensionless figure of merit zT, defined as zT = α2σT/(κL + κe), where α, σ, κL, κe, and T are Seebeck coefficient, electrical conductivity, lattice thermal conductivity, electronic thermal conductivity, and absolute temperature, respectively.4,5 To date, most good thermoelectric materials achieve peak zT values at middle-to-high temperatures.6–11 Only a few materials exhibit high zT at or near room temperature, for example, the conventional (Bi,Sb)2(Te,Se)3 alloys,12,13 MgAgSb,14,15 and the very recently reported n-type Mg3(Bi,Sb)2 compounds.16,17The high zT in n-type Mg3(Bi,Sb)2 alloys stems from the high degeneracy of the conduction band, and the intrinsic low thermal conductivity due to soft and highly anharmonic transverse phonons.18,19 However, only until recently n-type ternary polycrystalline samples are achieved due to the lack of understanding of the Mg vacancies acting as “electron killers”20 as well as the importance of Bi alloying which advantages electron doping. The remarkable zT, which is greater than 1.5 at high temperatures (700 K),20,21 has led to extensive studies on Mg3(Bi,Sb)2, in which excess Mg is commonly added to compensate for evaporation.22–26 Then notably in 2018 grain size was found to significantly limit the room temperature mobility as well as the zT.27 Thereafter, room temperature zT values have been considerably enhanced in coarse-grained samples by either increasing the sintering temperature or high temperature annealing.16,17,28,29 Nevertheless, few n-type single crystals have been reported, and none for ternary solid solutions exhibiting high zT.30,31
Previously reported Mg3Bi2 or Mg3Sb2 single crystals are binary compounds that cannot result in high zT. First, they exhibit p-type transport properties as grown under Mg-poor conditions,32 and must later be annealed under Mg-atmosphere to become n-type.33 Second, even with annealing, it is difficult to obtain ternary Mg3(Bi,Sb)2 by starting with Bi or Sb as the flux, as it is difficult to control the Bi/Sb ratio; this results in binary compounds with maximum zT limited to 0.4 at 300 K.33 Therefore, it would be of great significance to grow n-type ternary Mg3(Bi,Sb)2 single crystals for both the understanding of the thermoelectric transport and also further enhancement in the thermoelectric performance. This would enable the experimental investigations of the grain boundary effect (which was proved to inhibit charge carrier mobility at room temperature34) in ternary Mg3(Bi,Sb)2 by directly removing the grain boundaries, according to which higher zT is expected for ternary Mg3(Bi,Sb)2 single crystals. Furthermore, the successful growth of single crystals provides an opportunity to unravel the band structure of Mg3(Bi,Sb)2 by angle-resolved photoemission spectroscopy (ARPES), which can give a deeper understanding of the origin of the excellent thermoelectric performance of Mg3(Bi,Sb)2.
In this work, we report the successful growth of n-type ternary Mg3Bi1.25Sb0.75 and binary Mg3Bi2 and Mg3Sb2 single crystals using a Mg-flux method. A zT of 0.82 is achieved at 315 K in Y-doped Mg3Bi1.25Sb0.75 single crystals, which is much higher than values seen for fine-grained polycrystalline samples. Moreover, the present n-type single crystals grown under the Mg-flux condition avoid adding uncontrollable Mg as in polycrystals, which would be advantageous for the stability of the single crystals. Furthermore, we investigate for the first time the band structure of this material with ARPES. The high thermoelectric performance of Mg3(Bi,Sb)2 can be attributed to the large band degeneracy since the lowest conduction band shifts off the high symmetry point. Notably, the alloying of Mg3Bi2 and Mg3Sb2 is essential for the high thermoelectric performance, not only because of the commonly known alloying effect in reducing thermal conductivity, but more importantly, because Mg3Bi2 contributes to higher mobility and Mg3Sb2 can enlarge the band gap to suppress the bipolar effect. The present work advances the understanding and development of the important Mg3(Bi,Sb)2 thermoelectric alloys in several significant respects, including the evolution of band structure with alloying, the effect of grain boundary on both charge carriers and phonons, as well as a time-saving one-step synthesis of n-type ternary single crystals with high zT at room temperature for cooling applications.
Experimental
Mg3Bi2, Mg3Sb2, and Mg3Bi1.25Sb0.75 single crystals were grown using a flux method, employing Mg as the flux. Starting elements Mg (pieces, 99.8%), Bi (ingot, 99.9999%) and Sb (shot, 99.9999%) were weighed and mixed with molar ratios of Mg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Bi = 5
Bi = 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, Mg
2, Mg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sb = 8
Sb = 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and Mg
2 and Mg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Bi
Bi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sb = 11
Sb = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively. Approximately 0.2 mol% of yttrium is added as an efficient n-type dopant (to occupy Mg sites) for optimizing electron concentration.35,36 The mixtures were then sealed in tantalum tubes under a partial pressure of argon in a glove box, where a specially designed tantalum filter is used for the separation of grown crystals and the liquid flux during centrifugation. The tantalum tubes were then sealed in quartz tubes under partial argon pressure. Excess Mg melts prevent the reaction between Sb and Ta, and thus protect the Ta tube and filter. Temperature procedures are as follows: for Mg3Bi2, the sample was first heated up to 750 °C for over 30 h, kept for 48 h, then slowly cooled to 600 °C at the rate of 2 °C h−1; for Mg3Sb2 and Mg3Bi2–Mg3Sb2 alloys, samples were first heated up to 900 °C for 30 h, kept for 48 h, then slowly cooled to 700 °C with a rate of 2 °C h−1. Subsequently, single crystals were obtained by removing the liquid flux in a centrifugation process.
1, respectively. Approximately 0.2 mol% of yttrium is added as an efficient n-type dopant (to occupy Mg sites) for optimizing electron concentration.35,36 The mixtures were then sealed in tantalum tubes under a partial pressure of argon in a glove box, where a specially designed tantalum filter is used for the separation of grown crystals and the liquid flux during centrifugation. The tantalum tubes were then sealed in quartz tubes under partial argon pressure. Excess Mg melts prevent the reaction between Sb and Ta, and thus protect the Ta tube and filter. Temperature procedures are as follows: for Mg3Bi2, the sample was first heated up to 750 °C for over 30 h, kept for 48 h, then slowly cooled to 600 °C at the rate of 2 °C h−1; for Mg3Sb2 and Mg3Bi2–Mg3Sb2 alloys, samples were first heated up to 900 °C for 30 h, kept for 48 h, then slowly cooled to 700 °C with a rate of 2 °C h−1. Subsequently, single crystals were obtained by removing the liquid flux in a centrifugation process.
The orientation of the single crystals was determined by the backscattering Laue X-ray diffraction method. Chemical compositions were examined by scanning electron microscope (SEM) with an attached energy-dispersive X-ray spectrometer, and results agreed with the nominal compositions. Resistivity and Hall resistivity were measured simultaneously using a physical property measurement system (PPMS, Quantum Design) in the AC transport option. Seebeck coefficient was measured with PPMS, using the thermal transport option with one-heater and two-thermometer configurations. Thermal conductivity was measured in a home-built high vacuum cryostat using the standard four-contact steady-state method. The sample was glued onto the thermal bath with DeltaBond™ 152 adhesive, which is electrically insulating. Temperature gradient was measured with differential AuFe/Chromel thermocouples (Fig. S1, ESI†). All the transport properties were measured in the ab plane. Different samples are measured to check the consistency of the sample quality (Fig. S2, ESI†), since Seebeck coefficient is measured on a sample different from the piece used for resistivity and thermal conductivity measurements. ARPES experiments were carried out at the Berliner Elektronenspeicherring für Synchrotronstrahlung (BESSY) (beamline UE112-PGM-1) with a Scienta Omicron R8000 analyzer, and at beam line 13U of the National Synchrotron Radiation Laboratory with a Scienta Omicron DA30 analyzer. The single crystals were cleaved in situ below 15 K, under a pressure of ∼1 × 10−10 mbar.
The density functional theory (DFT) calculations were performed using projector-augmented wave method as implemented in the Vienna ab initio Simulation Package.37,38 The exchange and correlation functional was treated by the Perdew–Burke–Ernzerhof (PBE)-generalized gradient approximation.39 The Mg3Bi1.25Sb0.75 was obtained by Special Quasirandom Structure method40 in a supercell with 160 atoms (4 × 4 × 2 unit cell). The band structure calculations for Mg3Bi2, Mg3Bi1.25Sb0.75 and Mg3Sb2 were conducted using the modified Becke–Johnson (mBJ) potential41 to get more accurate band gaps. Spin–orbit coupling was considered throughout this study. The energy and Hellmann–Feynman force convergences were less than 10−4 eV and 0.01 eV Å−1, respectively. The Brillouin zones were sampled by an 11 × 11 × 7 Γ-centred k-mesh for the relaxations of Mg3Bi2 and Mg3Sb2 unit cells. The Fermi surface of Mg3Bi2 was calculated with a dense 40 × 40 × 25 k-mesh and plotted with XCrySDen.42 The band structure of Mg3Bi1.25Sb0.75 was determined by adopting the band unfolding method.43
Results and discussion
High zT in Mg3Bi1.25Sb0.75 single crystal
n-Type ternary Mg3(Bi,Sb)2 single crystals are highly desired for achieving optimal thermoelectric performance at around room temperature. Firstly, only ternary Mg3(Bi,Sb)2 compounds show exceptional zT values, instead of binary Mg3Bi2 or Mg3Sb2. Secondly, zT of this system is found to be strongly affected by the grain size.27Fig. 1(a) summarizes the grain size dependence of electron mobility (μH) and lattice thermal conductivity (κL) for n-type Mg3(Bi2,Sb)2 polycrystalline samples reported in the literature.17,20,27,28,44–46 It is obvious that κL is nearly independent of grain size, whereas μH exhibits a significant increase with larger grain size. Therefore, the ratio of μH/κL exhibits a positive correlation with grain size. Along with the independence of Seebeck coefficient on grain boundaries, indicate that single crystals show great potential to exhibit higher zT values.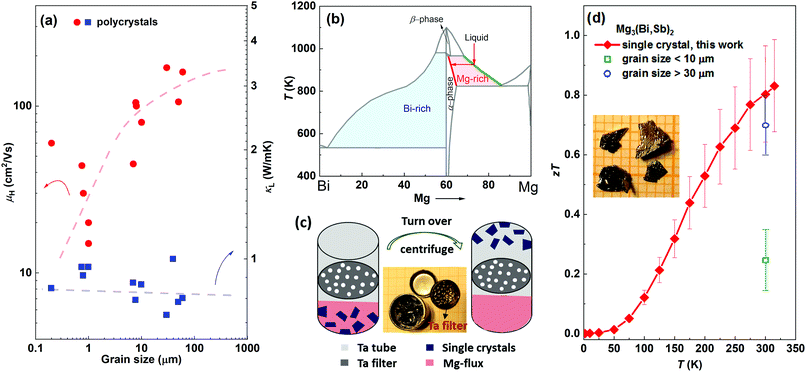 | ||
| Fig. 1 (a) Charge carrier mobility and lattice thermal conductivity versus grain size for polycrystalline Mg3(Bi,Sb)2 samples, the data are collected from the literature.17,20,27,28,44–46 Although the data points are scattered, which can be due to different charge carrier concentration and Bi/Sb ratios, or the effects of differing amounts of excess Mg on the sample quality, the trends as guided by the dashed lines are clear. Schematics of (b) Mg–Bi phase diagram, (c) Mg-flux method using a Ta tube with self-designed Ta filter made from a Ta cap. (d) zT of Y-doped Mg3Bi1.25Sb0.75 single crystal (an error bar of 20% is added), with a comparison to the Mg3(Bi,Sb)2 polycrystalline samples whose grain sizes are larger than 30 μm (blue) and below 10 μm (green).17,20,27,28,44–46 The inset image shows the single crystals. | ||
The difficulties in growing n-type Mg3(Bi2,Sb)2 single crystals lie in the complexity of the phase diagram and the high chemical reactivity of Mg. Taking Mg3Bi2 as an example (Mg3Sb2 is similar (Fig. S3, ESI†)), it is not a line compound and undergoes a phase transition from a high-temperature β-phase (cubic) to a low-temperature α-phase (trigonal) (Fig. 1(b)).47 Hence, it would be difficult to grow high-quality α-phase single crystals (desired for thermoelectrics) using high-temperature methods, as the structural transition during cooling would lead to a multi-domain α-phase polycrystalline sample. Instead, a low-temperature flux method can avoid structural change by maintaining the growth temperature below the phase transition point. Previous studies using Bi- or Sb-flux methods only result in p-type (and only binary) single crystals because of the Mg-deficient environment.32,48 A probable solution for growing n-type (both binary and ternary) single crystals involves using the Mg-flux method. However, this is extremely challenging since Mg is highly reactive with most conventional crucibles, including quartz, graphite, and the Al2O3 crucibles which are commonly used for flux growth. Tantalum metal, however, is stable in the presence of Mg melts, but there is no commercially available Ta filter for use with the molten flux method. To solve this problem, a self-designed tantalum filter was employed to separate the single crystals from the Mg-flux, as illustrated in Fig. 1(c).
The Ta filter setup and the use of Mg as the flux allowed the preparation of ternary alloyed Mg3(Bi,Sb)2 single crystals which should possess high zT. n-Type Mg3Bi2 and Mg3Sb2 single crystals were also successfully grown. The single crystals show a typical layered structure with widths ranging from a few millimeters to one centimeter and a thickness of ∼0.2 mm (Fig. 1(d)). The backscattering Laue XRD diffraction patterns show clear diffraction spots, indicating the high quality and crystallinity of the as-grown single crystals (Fig. S4, ESI†). Further SEM and EDX analysis demonstrate that the chemical compositions of Mg3Bi2 and Mg3Sb2 agree well with the stoichiometric compositions (Fig. S5, ESI†). The actual composition of the ternary compound is determined to be Mg3Bi1.25Sb0.75 by the EDX analysis. It is worth noting that the compositions of the single crystals are very close to the Mg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X = 3
X = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 relationship (X = Bi, Sb), without the uncontrollable large excess of Mg seen in polycrystalline samples. Excess Mg impurities would reduce the stability due to its high reactivity, and also impair the thermoelectric performance.49 Consequently, the high-quality n-type single crystal results in a high zT over 0.82 at 315 K for Y-doped Mg3Bi1.25Sb0.75, as shown in Fig. 1(e). This zT value is much higher than that of the fine-grained polycrystalline samples and surpasses most coarse-grained samples, demonstrating that zT is closely related to the density of grain boundaries. Further zT enhancement is possible by tuning the Bi/Sb ratio and Fermi level. Moreover, the high thermoelectric performance of n-type Mg3(Bi,Sb)2 rivals that of n-type Bi2(Te,Se)3 samples,50–53 which is of great significance since Bi2(Te,Se)3 is the only commercial n-type thermoelectric material used near room temperature.
2 relationship (X = Bi, Sb), without the uncontrollable large excess of Mg seen in polycrystalline samples. Excess Mg impurities would reduce the stability due to its high reactivity, and also impair the thermoelectric performance.49 Consequently, the high-quality n-type single crystal results in a high zT over 0.82 at 315 K for Y-doped Mg3Bi1.25Sb0.75, as shown in Fig. 1(e). This zT value is much higher than that of the fine-grained polycrystalline samples and surpasses most coarse-grained samples, demonstrating that zT is closely related to the density of grain boundaries. Further zT enhancement is possible by tuning the Bi/Sb ratio and Fermi level. Moreover, the high thermoelectric performance of n-type Mg3(Bi,Sb)2 rivals that of n-type Bi2(Te,Se)3 samples,50–53 which is of great significance since Bi2(Te,Se)3 is the only commercial n-type thermoelectric material used near room temperature.
Thermoelectric transport properties
The Y-doped Mg3Bi1.25Sb0.75 and Mg3Sb2 crystals are n-type and show metallic transport behaviour down to the lowest temperatures measured (Fig. 2(a)). The Y-doped Mg3Bi2 displays a mixed conduction character of two types of charge carriers, in which the major carrier changes from hole to electron at temperatures above ∼200 K. Hence, only the carrier concentration above 200 K is given for Y-doped Mg3Bi2. All samples show a Hall electron concentration of ∼1019 cm−3 (Fig. 2(b)). In contrast, pure Mg3Sb2 (without Y doping) displays p-type semiconducting behavior (Fig. S6, ESI†), clarifying that Mg-excess growth condition cannot directly lead to n-type conduction but can only guarantee effective n-type doping, which is instructive for further research on this system.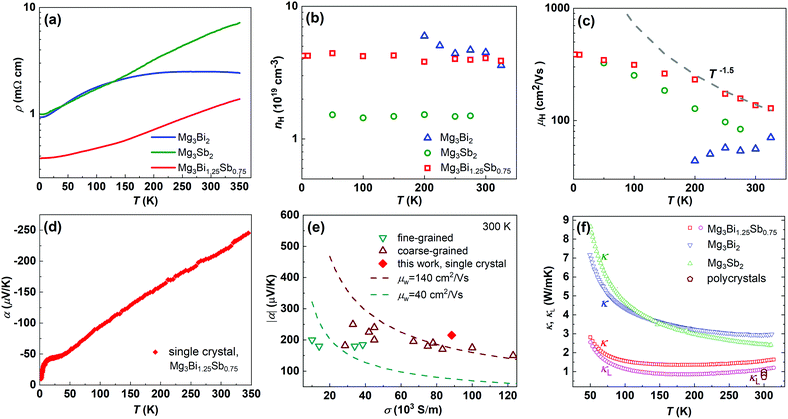 | ||
| Fig. 2 Temperature dependence of (a) resistivity, (b) Hall charge carrier concentration, (c) Hall charge carrier mobility, (d) Seebeck coefficient, (e) conductivity dependence of Seebeck coefficient of Y-doped Mg3Bi1.25Sb0.75 single crystal at 300 K, with a comparison to polycrystalline samples,16,17,20,23,26–28,44,46 and (f) temperature dependence of total and lattice thermal conductivity, with a comparison to the lattice thermal conductivity of polycrystalline samples.17,20,27,28,44–46 | ||
The single crystal outperforms traditional polycrystals because of the higher mobility with comparable thermal conductivity. As shown in Fig. 2(c), the charge carrier mobility of Mg3Bi1.25Sb0.75 and Mg3Sb2 single crystals exhibit a T−1.5 dependence, indicating a phonon-dominated scattering mechanism. Notably, previously reported fine-grained (<10 μm) samples usually show lower mobility with decreasing temperature under 400 K,20,27,44,45 which has been initially and widely attributed to the ionized impurity scattering mechanism. The present results demonstrate the absence of ionized impurity scattering in limiting low temperature charge carrier mobility for ternary Mg3(Bi,Sb)2 alloys. Nevertheless, the Seebeck coefficient (Fig. 2(d)) would be nearly independent on the grain size. As a result, the single crystal shows more than three times higher weighted mobility than that of the fine-grained samples, and also better than the coarse-grained samples, as shown in Fig. 2(e). Conversely, the thermal conductivity of the Mg3Bi1.25Sb0.75 single crystal is still low, and is only slightly increased compared to the polycrystalline samples (Fig. 2(f)),17,20,27,28,44–46 directly demonstrating that grain boundaries have very small effect on the phonon transport. The higher weighted mobility, together with the comparably low thermal conductivity, leading to the excellent thermoelectric performance in single crystals.
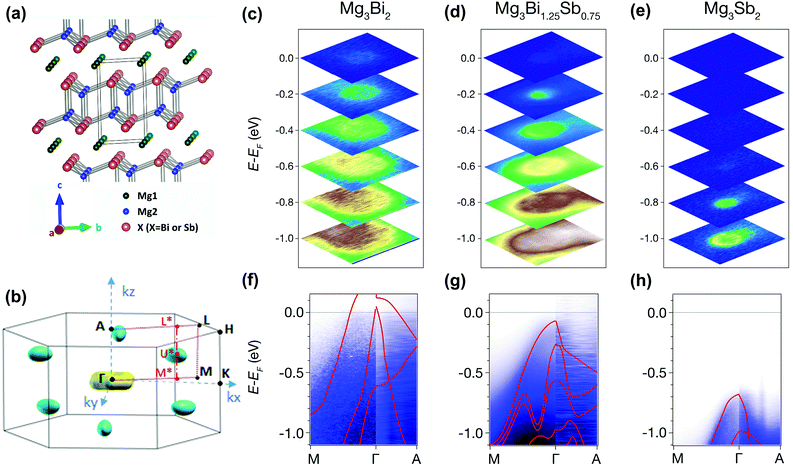
Band structure analysis by ARPES and DFT
The origin of the exceptional thermoelectric performance is further investigated by analyzing the electronic band structure. In addition to DFT calculations, the high-quality single crystals enable experimental investigation of the electronic structure by ARPES.54 The crystal structure and corresponding Brillouin zone of Mg3X2 (X = Bi and Sb) are illustrated in Fig. 3(a) and (b). For ARPES experiments, the crystals were cleaved in situ along ab plane, corresponding to the kx–ky plane in the reciprocal space. For each sample, ARPES spectra were first measured along the Γ–M–K plane. As shown in Fig. 3(c)–(e), all three compounds show an obvious increase in the electron states with rising binding energy (absolute value of E − EF), indicating the hole pockets at around the Γ point. From Mg3Bi2 to Mg3Sb2, the electron states near EF disappear and the top of the valence band shifts dramatically to higher binding energy, leading to a significant expansion in the band gap. No obvious electron states were observed at lower binding energy, which may be due to the shift of the conduction band from the Γ–M–K plane. To further probe the conduction band, we changed the photon energy to acquire the ARPES spectra in the entire Γ–M–A–L plane; while no electron pockets were found (Fig. S7, ESI†), although all of the crystals have an electron density larger than 1019 cm−3.The observation of conduction bands is very challenging. First, DFT calculations indicate that the lowest conduction band is located at U* (in the Γ*–M* direction), not at the high-symmetry points of the Brillouin zone. This, to some extent, makes it difficult to observe the conduction bands. Second, the EF of the single crystals might not be high enough to guarantee that there are sufficient electron states to be observed by ARPES, suggesting the necessity of further n-type doping to elevate the EF. Therefore, potassium deposition, generally employed to raise the EF of samples during the ARPES experiments, was attempted for Mg3(Bi,Sb)2. Nonetheless, there was no obvious improvement of the EF after several minutes of potassium deposition (Fig. S8, ESI†). These attempts demonstrate the difficulties in observing the electron pockets of the Mg3Bi2–Mg3Sb2 system with ARPES. Future ARPES experiments may require heavily-doped single crystals with higher EF and larger electron density of states, with, for example, an electron density of ∼1020 cm−3.
Nevertheless, the valence bands of all three compounds have been clearly observed along different directions. As shown in Fig. 3(f)–(h), the ARPES intensities along the Γ–M and Γ–A directions are resolved. The band dispersion in ARPES spectra along Γ–A is steeper than that along Γ–M, indicating a smaller effective mass (Fig. S9, ESI†) and higher hole velocity along the kz direction, corresponding to the c-axis in real space. Moreover, the ARPES spectra observed for all three compounds are consistent with the calculated valence bands (red lines in Fig. 3(f)–(h)), corroborating the reliability of our DFT calculations.
A molecular orbital analysis was performed to develop an intuitive understanding of the enlargement of the band gap (as observed in ARPES) from the bonding interactions,55 as depicted in Fig. 4(a) and (b). This schematic illustration sheds light on two important aspects. First, the band gap can be described as in the following equation:
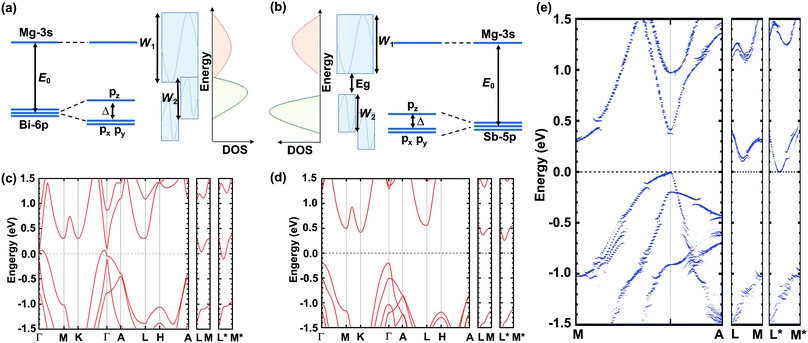 | ||
| Fig. 4 (a) and (b) Schematic illustration of band widening effect and (c)–(e) DFT-calculated band structures of Mg3Bi2, Mg3Sb2, and Mg3Bi1.25Sb0.75, respectively. | ||
Further DFT calculations resolve more details of the band evolution from Mg3Bi2 to Mg3Sb2, and therefore explain how the high thermoelectric performance of Mg3(Bi,Sb)2 is rooted in the band structure. The DFT-calculated band structures of Mg3Bi2, Mg3Sb2, and Mg3Bi1.25Sb0.75 are shown in Fig. 4(c)–(e), respectively. The band gap values are slightly lower than that observed by ARPES, due to the typical underestimation of band gaps in DFT calculations. But the trend in band gap variation is identical, ranging from a negative band gap for Mg3Bi2, to a near-zero gap for Mg3Bi1.25Sb0.75 and ∼0.45 eV for Mg3Sb2. More important, the conduction band minimum is located at U* (along L*–M*) for all of the compounds investigated, since it is mainly dominated by Mg–Mg bonding interactions56,57 and is relatively independent of Bi or Sb composition. The shift of the conduction band bottom off a high symmetry point contributes to a large band degeneracy, favoring a large quality factor and also zT. Although the large band degeneracy that favors the high thermoelectric performance of Mg3(Bi,Sb)2 stems from the Mg–Mg interaction introduced off-high-symmetry-point conduction band, it is worth noting that the Bi/Sb ratio is also of great significance. This is because Mg3Bi2 can exhibit higher mobility, and Mg3Sb2 is needed to enlarge the band gap and suppress the detrimental bipolar effect. Therefore, at near room temperatures, we emphasize that larger Mg3Bi2 content is needed to achieve higher zT in Mg3(Bi,Sb)2, as long as the band gap is large enough to avoid intrinsic excitation. This ensures the high zT observed in the Y-doped Mg3Bi1.25Sb0.75 single crystals studied here and also suggests future paths to better thermoelectric performance.
Conclusions
High-quality n-type ternary Mg3(Bi,Sb)2 single crystals are synthesized using a facile Mg-flux method. The single crystals show higher mobility and low lattice thermal conductivity comparable to that of polycrystalline samples, indicating the unfavourable nature of grain boundaries. A high zT over 0.82 at 315 K is achieved in a Y-doped Mg3Bi1.25Sb0.75 single crystal, demonstrating its great potential in application of low-grade waste heat recovery and room temperature Peltier coolers. Moreover, ARPES combined with DFT calculations denote the band evolution from Mg3Bi2 to Mg3Sb2, and consequently indicate the need for a large Bi/Sb ratio for high thermoelectric performance of Mg3(Bi,Sb)2. These findings provide future avenues to higher thermoelectric performance.Author contributions
Y. P. designed the experiment, synthesized the samples, measured the electrical transport properties; Y. M. conducted the ARPES; X. H. and C. H. measured the thermal conductivity; Y. Z., F. F. and J. Y. completed the DFT calculations; K. I. confirmed the Hall data; Y. P. and C. Fu wrote and edited the manuscript; G. J. S. analysed the experimental data and all authors edited the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation – 392228380) and the ERC Advanced “TOP-MAT” (742068). YP acknowledges the support from the Alexander von Humboldt Foundation. CH and XH acknowledge support from the European Research Council (ERC) under the European Unions’ Horizon 2020 research and innovation programme (647276-MARS-ERC-2014-CoG). JY acknowledges the support from National Natural Science Foundation of China (51761135127). GJS, KI acknowledge the support of award 70NANB19H005 from U.S. Department of Commerce, National Institute of Standards and Technology as part of the Center for Hierarchical Materials Design (CHiMaD). Open Access funding provided by the Max Planck Society.References
- F. J. DiSalvo, Science, 1999, 285, 703 CrossRef CAS PubMed.
- G. Snyder and E. Toberer, Nat. Mater., 2008, 7, 105–114 CrossRef CAS PubMed.
- M. Zebarjadi, K. Esfarjani, M. S. Dresselhaus, Z. F. Ren and G. Chen, Energy Environ. Sci., 2012, 5, 5147–5162 RSC.
- D. M. Rowe, Thermoelectrics Handbook: Macro to Nano, CRC Press, 2006 Search PubMed.
- J.-F. Li, W.-S. Liu, L.-D. Zhao and M. Zhou, NPG Asia Mater., 2010, 2, 152–158 CrossRef.
- Y. Pei, X. Shi, A. LaLonde, H. Wang, L. Chen and G. J. Snyder, Nature, 2011, 473, 66–69 CrossRef CAS PubMed.
- H. Liu, X. Shi, F. Xu, L. Zhang, W. Zhang, L. Chen, Q. Li, C. Uher, T. Day and G. J. Snyder, Nat. Mater., 2012, 11, 422–425 CrossRef CAS PubMed.
- C. Fu, S. Bai, Y. Liu, Y. Tang, L. Chen, X. Zhao and T. Zhu, Nat. Commun., 2015, 6, 8144 CrossRef PubMed.
- L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373–377 CrossRef CAS PubMed.
- W. Zhao, Z. Liu, Z. Sun, Q. Zhang, P. Wei, X. Mu, H. Zhou, C. Li, S. Ma, D. He, P. Ji, W. Zhu, X. Nie, X. Su, X. Tang, B. Shen, X. Dong, J. Yang, Y. Liu and J. Shi, Nature, 2017, 549, 247–251 CrossRef CAS PubMed.
- W. He, D. Wang, H. Wu, Y. Xiao, Y. Zhang, D. He, Y. Feng, Y.-J. Hao, J.-F. Dong, R. Chetty, L. Hao, D. Chen, J. Qin, Q. Yang, X. Li, J.-M. Song, Y. Zhu, W. Xu, C. Niu, X. Li, G. Wang, C. Liu, M. Ohta, S. J. Pennycook, J. He, J.-F. Li and L.-D. Zhao, Science, 2019, 365, 1418–1424 CrossRef CAS PubMed.
- B. Poudel, Q. Hao, Y. Ma, Y. Lan, A. Minnich, B. Yu, X. Yan, D. Wang, A. Muto, D. Vashaee, X. Chen, J. Liu, M. S. Dresselhaus, G. Chen and Z. Ren, Science, 2008, 320, 634–638 CrossRef CAS.
- Y. Pan, Y. Qiu, I. Witting, L. Zhang, C. Fu, J.-W. Li, Y. Huang, F.-H. Sun, J. He, G. J. Snyder, C. Felser and J.-F. Li, Energy Environ. Sci., 2019, 12, 624–630 RSC.
- H. Zhao, J. Sui, Z. Tang, Y. Lan, Q. Jie, D. Kraemer, K. McEnaney, A. Guloy, G. Chen and Z. Ren, Nano Energy, 2014, 7, 97–103 CrossRef CAS.
- D. Kraemer, J. Sui, K. McEnaney, H. Zhao, Q. Jie, Z. F. Ren and G. Chen, Energy Environ. Sci., 2015, 8, 1299–1308 RSC.
- J. Mao, H. Zhu, Z. Ding, Z. Liu, G. A. Gamage, G. Chen and Z. Ren, Science, 2019, 365, 495–498 CrossRef CAS PubMed.
- K. Imasato, S. D. Kang and G. J. Snyder, Energy Environ. Sci., 2019, 12, 965 RSC.
- W. Peng, G. Petretto, G.-M. Rignanese, G. Hautier and A. Zevalkink, Joule, 2018, 2, 1879–1893 CrossRef CAS.
- J. Zhang, L. Song and B. B. Iversen, npj Comput. Mater., 2019, 5, 76 CrossRef.
- H. Tamaki, H. K. Sato and T. Kanno, Adv. Mater., 2016, 28, 10182–10187 CrossRef CAS PubMed.
- J. Zhang, L. Song, S. H. Pedersen, H. Yin, L. T. Hung and B. B. Iversen, Nat. Commun., 2017, 8, 13901 CrossRef CAS PubMed.
- J. Zhang, L. Song, A. Mamakhel, M. R. V. Jørgensen and B. B. Iversen, Chem. Mater., 2017, 29, 5371–5383 CrossRef CAS.
- J. Shuai, J. Mao, S. Song, Q. Zhu, J. Sun, Y. Wang, R. He, J. Zhou, G. Chen, D. J. Singh and Z. Ren, Energy Environ. Sci., 2017, 10, 799–807 RSC.
- S. Ohno, K. Imasato, S. Anand, H. Tamaki, S. D. Kang, P. Gorai, H. K. Sato, E. S. Toberer, T. Kanno and G. J. Snyder, Joule, 2018, 2, 141–154 CrossRef CAS.
- J. Mao, J. Shuai, S. Song, Y. Wu, R. Dally, J. Zhou, Z. Liu, J. Sun, Q. Zhang, C. dela Cruz, S. Wilson, Y. Pei, D. J. Singh, G. Chen, C.-W. Chu and Z. Ren, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10548–10553 CrossRef CAS PubMed.
- K. Imasato, S. D. Kang, S. Ohno and G. J. Snyder, Mater. Horiz., 2018, 5, 59–64 RSC.
- T. Kanno, H. Tamaki, H. K. Sato, S. D. Kang, S. Ohno, K. Imasato, J. J. Kuo, G. J. Snyder and Y. Miyazaki, Appl. Phys. Lett., 2018, 112, 033903 CrossRef.
- M. Wood, J. J. Kuo, K. Imasato and G. J. Snyder, Adv. Mater., 2019, 31, 1902337 CrossRef PubMed.
- X. Chen, S. Chang, J. Chen, P. Nan, X. Li, X. Chen, X. Zhu, B. Ge, W. Cai, J. Sui, S. Zheng, F. Wang, X. Chen and H. Zhao, 2018, arXiv preprint arXiv:1810.03356.
- S. Kim, C. Kim, Y.-K. Hong, T. Onimaru, K. Suekuni, T. Takabatake and M.-H. Jung, J. Mater. Chem. A, 2014, 2, 12311–12316 RSC.
- S. H. Kim, C. M. Kim, Y.-K. Hong, K. I. Sim, J. H. Kim, T. Onimaru, T. Takabatake and M.-H. Jung, Mater. Res. Express, 2015, 2, 055903 CrossRef.
- J. Xin, G. Li, G. Auffermann, H. Borrmann, W. Schnelle, J. Gooth, X. Zhao, T. Zhu, C. Felser and C. Fu, Mater. Today Phys., 2018, 7, 61–68 CrossRef.
- K. Imasato, C. Fu, Y. Pan, M. Wood, J. J. Kuo, C. Felser and G. J. Snyder, Adv. Mater., 2020, 32, 1908218 CrossRef CAS PubMed.
- J. J. Kuo, S. D. Kang, K. Imasato, H. Tamaki, S. Ohno, T. Kanno and G. J. Snyder, Energy Environ. Sci., 2018, 11, 429–434 RSC.
- P. Gorai, E. S. Toberer and V. Stevanovic, J. Appl. Phys., 2019, 125, 025105 CrossRef.
- X. Shi, T. Zhao, X. Zhang, C. Sun, Z. Chen, S. Lin, W. Li, H. Gu and Y. Pei, Adv. Mater., 2019, 31, 1903387 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 77, 3865 CrossRef PubMed.
- A. van de Walle, P. Tiwary, M. de Jong, D. L. Olmsted, M. Asta, A. Dick, D. Shin, Y. Wang, L. Q. Chen and Z.-K. Liu, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2013, 42, 13 CrossRef CAS.
- F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401 CrossRef PubMed.
- A. Kokalj, J. Mol. Graphics Modell., 1999, 17, 215 CrossRef.
- P. V. C. Medeiros, S. Stafström and J. Björk, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 041407 CrossRef.
- J. Shuai, B. Ge, J. Mao, S. Song, Y. Wang and Z. Ren, J. Am. Chem. Soc., 2018, 140, 1910–1915 CrossRef CAS PubMed.
- X. Chen, H. Wu, J. Cui, Y. Xiao, Y. Zhang, J. He, Y. Chen, J. Cao, W. Cai, S. J. Pennycook, Z. Liu, L.-D. Zhao and J. Sui, Nano Energy, 2018, 52, 246–255 CrossRef CAS.
- X. Shi, C. Sun, Z. Bu, X. Zhang, Y. Wu, S. Lin, W. Li, A. Faghaninia, A. Jain and Y. Pei, Adv. Sci., 2019, 6, 1802286 CrossRef PubMed.
- A. A. Nayeb-Hashemi and J. B. Clark, Bull. Alloy Phase Diagrams, 1985, 6, 528–533 CrossRef CAS.
- T.-R. Chang, I. Pletikosic, T. Kong, G. Bian, A. Huang, J. Denlinger, S. K. Kushwaha, B. Sinkovic, H.-T. Jeng, T. Valla, W. Xie and R. J. Cava, Adv. Sci., 2019, 6, 1800897 CrossRef PubMed.
- K. Imasato, S. Ohno, S. D. Kang and G. J. Snyder, Appl. Phys. Lett. Mater., 2018, 6, 016106 Search PubMed.
- Y. Pan, T.-R. Wei, C.-F. Wu and J.-F. Li, J. Mater. Chem. C, 2015, 3, 10583 RSC.
- L. Hu, T. Zhu, X. Liu and X. Zhao, Adv. Funct. Mater., 2014, 24, 5211–5218 CrossRef CAS.
- Y. Pan and J.-F. Li, NPG Asia Mater., 2016, 8, e275 CrossRef CAS.
- G. S. Nolas, J. Sharp and J. Goldsmid, Thermoelectrics: Basic Principles and New Materials Developments, Springer Science & Business Media, 2013 Search PubMed.
- C. Fu, M. Yao, X. Chen, L. Z. Maulana, X. Li, J. Yang, K. Imasato, F. Zhu, G. Li, G. Auffermann, U. Burkhardt, W. Schnelle, J. Zhou, T. Zhu, X. Zhao, M. Shi, M. Dressel, A. V. Pronin, G. J. Snyder and C. Felser, Adv. Sci., 2020, 7, 1902409 CrossRef CAS PubMed.
- W. G. Zeier, A. Zevalkink, Z. M. Gibbs, G. Hautier, M. G. Kanatzidis and G. J. Snyder, Angew. Chem., Int. Ed., 2016, 55, 6826 CrossRef CAS PubMed.
- X. Sun, X. Li, J. Yang, J. Xi, R. Nelson, C. Ertural, R. Dronskowski, W. Liu, G. J. Snyder, D. J. Singh and W. Zhang, J. Comput. Chem., 2019, 9999, 1–8 Search PubMed.
- M. Wood, K. Imasato, S. Anand, J. Yang and G. J. Snyder, J. Mater. Chem. A, 2020, 4, 2033 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ee00838a |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2020 |