Open Access Article
Open Access ArticleA scaling law to determine phase morphologies during ion intercalation†
Dimitrios
Fraggedakis‡
 a,
Neel
Nadkarni‡
a,
Tao
Gao‡
a,
Tingtao
Zhou
b,
Yirui
Zhang
a,
Neel
Nadkarni‡
a,
Tao
Gao‡
a,
Tingtao
Zhou
b,
Yirui
Zhang
 c,
Yu
Han
a,
Ryan M.
Stephens
d,
Yang
Shao-Horn
c,
Yu
Han
a,
Ryan M.
Stephens
d,
Yang
Shao-Horn
 ce and
Martin Z.
Bazant
ce and
Martin Z.
Bazant
 *af
*af
aDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: dimfraged@gmail.com
bDepartment of Physics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
cDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
dShell International Exploration & Production Inc., Houston, Texas 77082, USA
eDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
fDepartment of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: bazant@mit.edu
First published on 22nd May 2020
Abstract
Driven phase separation in ion intercalation materials is known to result in different non-equilibrium phase morphologies, such as intercalation waves and shrinking-core structures, but the mechanisms of pattern selection are poorly understood. Here, based on the idea that the coarsening of the slowest phase is the rate limiting step, we introduce a scaling law that quantifies the transition from quasi-equilibrium intercalation-wave to diffusion-limited shrinking-core behavior. The scaling law is validated by phase-field simulations of single LixCoO2 particles, in situ optical imaging of single LixC6 particles undergoing transitions between stage 1 (x = 1) and 2 (x = 0.5) at different rates, and all the available literature data for single-particle imaging of LixCoO2, LixC6 and LixFePO4. The results are summarized in operational phase diagrams to guide simulations, experiments, and engineering applications of phase-separating active materials. Implications for Li-ion battery performance and degradation are discussed.
Broader contextPhase separation is ubiquitous in most commercial Li-ion battery materials, e.g. LiFePO4, LiC6, LiCoO2, and affects the (dis)charging dynamics on both single-and multi-particle levels. Based on the (dis)charge rate, different phase morphologies – intercalation wave or core–shell structures – within single particles can be observed. These morphologies are intimately linked to the performance and lifetime of Li-ion batteries. Therefore, it is important to understand the conditions for intra-particle phase separation, not only for its scientific interest, but also for battery engineering. When intercalation waves arise, the active area within the battery is reduced as intercalation reactions concentrate on the exposed phase boundaries, leaving a large area of the electrode inert during cycling. Additionally, core–shell morphologies are undesirable since they are associated with large concentration overpotentials and reduce the utilization of the available stored energy. Also, phase separation is responsible for mechanical deformation that can lead to battery degradation via microstructure fracture and damage. In this work, we provide a simple way to classify the observed phase morphologies during battery operation through a simple scaling law that combines the (dis)charge current, the size of the particles, and the diffusivity of the slowest phase. |
Introduction
Ion intercalation materials have proven paramount in the field of energy storage.1 Their best known application is the Li-ion battery,2 where the process of lithium intercalation in solid active particles enables portable storage devices that exhibit high power and energy densities.1,3 Traditional engineering models assume purely diffusive transport of intercalated ions,4–6 but many common electrode materials undergo phase separation during cycling into thermodynamically stable phases at specific filling fractions (x ∈ [0,1]). Important examples include most commercialized Li-ion battery materials, such as iron phosphate (LixFePO4, LFP)7 and cobalt oxide (LixCoO2, LCO)8 for the cathode and graphite (LixC6)9–12 and titanate (Li4+3xTi5O12, LTO)13,14 for the anode, as well as some emerging materials, such as Ni-rich oxides15 and anatase (LixTiO2).16,17 Phase separation results in spatial heterogeneity, which complicates the interpretation of experimental data and often defies the common assumption of spherical shrinking-core phase morphology, e.g. for LFP18–20 or graphite.21 A more consistent and accurate approach is to use phase-field models,22–27 generalized for electrochemical thermodynamics28 of single particles23,29–39 and porous electrodes,40–45 but a clear classification of the possible non-equilibrium phase morphologies has not yet emerged.Phase-separation dynamics are intimately linked to the performance and degradation of Li-ion batteries.7,12,24,29,40,46–48 In porous electrodes, the so-called “mosaic phase separation” between different nearly homogeneous, stress-free particles30,49,50 affects performance through the rate-dependent active population,12,42–44,47 but this collective phenomenon competes with the more fundamental process of coherent phase separation within individual particles. In particular, the formation of intra-particle interfaces between high-and low-concentration phases has been shown to: (i) affect the local intercalation current, where the largest electrochemical driving force results in the vicinity of the formed interfaces;23,29,35,51 (ii) lead to accumulation of elastic,30–32,35,37,39 and consequently inelastic stresses, resulting in the formation of dislocations,52,53 fatigue and cracking of battery particles;54–56 (iii) cause abrupt changes of the local electronic conductivity,14,48,57 which suppresses electron transfer reactions associated with ion intercalation. The morphology of phase boundaries within single particles is thus directly connected to the rate capability and degradation of the battery.
Electrochemical phase separation differs from other types of phase transformations in that it occurs in a driven open system:58 the applied current or voltage modulates the availability of electrons for faradaic reactions and thus controls the pattern formation.59 In the case of ion intercalation, reaction limitations can lead to intercalation waves23,29,35,60 that propagate across the reacting surface until the insertion or extraction of ions is completed, as shown in Fig. 1(a). In contrast, when bulk diffusion cannot keep up with ion insertion/extraction, the phase boundary assumes a non-equilibrium shrinking-core morphology,40,42,51,54,61 as assumed in traditional battery models,4,6,62 even for phase separating materials,18,19,21 as shown in Fig. 1(d). In this case, the reactive boundaries attain the extreme stable ion concentration, highest during insertion61 and lowest during extraction,51 resulting in poor utilization of the bulk material and potentially damaging stresses. The rate-dependent transition between the different morphologies thus has a direct impact on battery performance and begs a quantitative description.
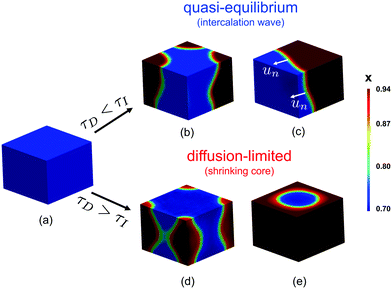
 | ||
| Fig. 1 Ion intercalation of single particles. Here, we show the representative case of LiCoO2,37 where Li ions are inserted from the sides of the particle (reactive boundaries), while the top and bottom ones are impermeable to any ion. Both the quasi-equilibrium (a–c) and diffusion-limited cases are shown (d–f). In the quasi-equilibrium case the interface between the Li-rich and -poor phases has a 3D orientation and form an intercalation wave, while the diffusion-limited regime is governed by a shrinking-core structure that can be described effectively by 1D axisymmetric profiles. (a and d) show the Li-ion concentration, c ∈ [0,cmax], in full 3D view, (b and e) a cartoon of the inserted ions along a 2D plane, and (c and f) the concentration profile along an 1D slice. cs,1 and cs,2 correspond to the representative equilibrium concentrations. | ||
Although many battery materials exhibit phase separation, both in situ experimental imaging7,46,52,63,64 and computational studies23,29–32,35,36,39,65,66 of non-equilibrium phase morphologies have focused on LFP,67 despite its highly anisotropic properties,68 which strongly affect the dynamics.23,37,69 In contrast, very few studies have been conducted to understand single-particle phase separation in other common battery materials, such as LCO70 or graphite,11 which exhibit far less anisotropy. Recently, we developed a phase-field model for LCO to describe its phase separation and metal–insulator transition for x ∈ [0.75, 0.94],48 which predicts two distinct dynamical regimes. For particle sizes around ∼100 nm and under realistic lithiation rates, three-dimensional intercalation waves are observed, as shown in Fig. 1(b and c). For very large particles (>10 μm), there is a transition to shrinking core behavior with approximately one-dimensional axisymmetric profiles, as shown in Fig. 1(e and f). In the latter case, the high concentration of Li-ions at the boundaries shuts down the intercalation reaction prior to full lithiation of the system. Similar observations have been reported for LFP,51,53 but as yet, there have been no attempts to unify the description of this morphological transition across different intercalation materials and applied currents.
We thus arrive at our central question: what are the conditions that control the morphology of phase separation in single particles undergoing ion intercalation? The answer lies in a universal scaling law, based only upon the reactive surface area, bulk volume, dimensionality of transport, diffusivity of the slowest phase, and the applied current, which determines whether subsurface phase separation can maintain quasi-equilibrium patterns or must form a diffusion-limited shrinking core. Reaction kinetics play only a secondary role in controlling phase patterns, unless the bulk and surface concentrations are strongly coupled,58 as in the special case of LFP nanoparticles.7,31,32,37 The scaling analysis is supported by 3D phase-field simulations of LCO, as well as in situ optical imaging of lithiated graphite. The results are summarized in operational phase diagrams that may be used to guide the design of both simulations and experiments.
Theory
During battery operation, there are conditions where the Li average concentration enters the phase-separating regime, leading to the formation of Li-rich and -poor regions. The dynamics of the formed interfaces, however, are coupled through surface reactions and bulk diffusion.37,48 In this section, we describe the theoretical framework for reaction-driven phase separation and then derive the scaling law quantifying the transition between intercalation wave (quasi-equilibrium) and shrinking-core (diffusion-limited) morphologies.Model for reaction-driven phase separation
We begin by describing the general mathematical structure of phase-field models of intercalation driven by faradaic reactions.28,40,58 We consider the insertion of a chemical species in a system of volume V (in m3) through reactive boundaries of total surface area, A (in m2). The concentration c (in mol m−3) of the species evolves according to mass conservation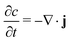 | (1) |
| −n·j = R | (2) |
A unique characteristic of electrochemical systems is the ability to control the overall reaction rate by applying a constant current i, which implies the following integral constraint,
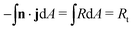 | (3) |
The model is completed by specifying the thermodynamics of the bulk material through the free energy functional,
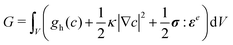 | (4) |
| ∇·σ = 0 | (5) |
In this work, we use the above framework to simulate the evolution of driven phase morphologies in LCO, using our recently published chemo-mechanical model.48 The functional form of the mobility/diffusivity as a function of concentration is determined through ab initio calculations,73 while ion intercalation is described through generalized Butler–Volmer kinetics.28 The complete functional forms of the homogeneous chemical free energy gh, the mobility M and the reaction model R are given in the ESI.† Finally, we discretize the model equations using the finite element method74 by expressing the unknown functions with linear basis functions.
Scaling law for phase morphologies
The scaling relation can be derived by comparing the timescales of ion insertion and the coarsening process during phase separation. In a single electrode particle that undergoes (de)lithiation, there are three important timescales. Two are material timescales, related to intercalation reactions, τR ∼ Q/i0A, and solid diffusion, τD ∼ L2/Dch, and the third is the process timescale, τI ∼ Q/IA, specified by the time required to (dis)charge the particle, where Q = FVcmax corresponds to the maximum ion storage capacity of the particle; i0 = Fk0 is the characteristic (e.g. mean) exchange current density and k0 the reaction rate constant; L ∼ V/A is the characteristic size of the particle; and Dch is a characteristic value of the diffusivity, to be specified below.When phase separation occurs under constant current, there is a competition between ion insertion over the active surfaces and the re-distribution of the inserted ions in bulk, as shown in Fig. 2(b–e), which can be quantified by the following dimensionless ratio, τD/τI ∼ iL/DFcmax. For τD/τI > 1, the diffusion of ions in the phase-separated domain is the slow process, while for τD/τI < 1, bulk diffusion is fast enough to maintain a quasi-equilibrium, meta-stable state. By rescaling each time scale to the reaction time, τR, this criterion can be restated as
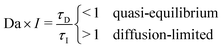 | (6) |
In chemical engineering, it is well known that the ratio of the diffusion time τD to an imposed “process time” τp generally controls the transition from pseudo-steady (τp > τD) to diffusion-limited (τp < τD) transient concentration profiles.75 Applications of the pseudo-steady approximation range from driven transport in fixed membranes to moving free boundaries of combustion, dissolution, drying, or melting, including the transition to 1D radial shrinking-core morphologies in spherical particles.76–79 In the context of Li-ion batteries with τp = τI, Doyle, Fuller and Newman first noted that τD/τp similarly controls the onset of 1D diffusion limitation for spherical solid-solution particles. Here, we demonstrate the role of eqn (6) for heterogeneous phase-separating particles, where the pseudo-steady regime corresponds to 3D quasi-equilibrium phase separation, strongly influenced by boundary conditions and surface reactions, and we identify the relevant diffusivity controlling the transition.
In phase-separating materials, the co-existing phases often have vastly different ionic diffusivities,73,80 which must be taken into account. In LCO for example, ab initio calculations predict that the diffusivity ratio between the Li-poor (x = 0.75) and Li-rich (x = 0.94) phases is D0.75/D0.94 ≃ 300, which implies that ion transport in the ‘dilute’ phase is over two orders of magnitude faster than the ‘concentrated’ one.73 When comparing the rates of ion insertion and phase separation, it is reasonable to focus on the phase with the smaller diffusivity, i.e. the Li-rich one in the case of LixCoO2, so the definition of Da should be based on the diffusivity of slowest phase, Dch ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Dslow.
Dslow.
At first, it may seem surprising that the intrinsic reaction timescale τR ∼ i0−1 does not affect the transition in phase morphologies described by eqn (6), but this is because we consider an externally driven reaction at constant overall rate Rt. Therefore, the resulting phase morphologies will be determined mainly by the competition between the equilibration timescale (bulk diffusion) and the imposed insertion rate. On the other hand, when ion insertion proceeds under constant voltage conditions, τR will also be a critical timescale, as described elsewhere.23,58
Results
In order to test the proposed scaling law for phase-separating intercalation materials, we perform simulations of LCO and in situ optical microscopy experiments on graphite single particles. In both cases, we visualize the non-equilibrium phase morphologies over a range of operational conditions and observe when the transition between the quasi-equilibrium and diffusion-limited regimes occurs.Simulations of rate-dependent phase morphologies
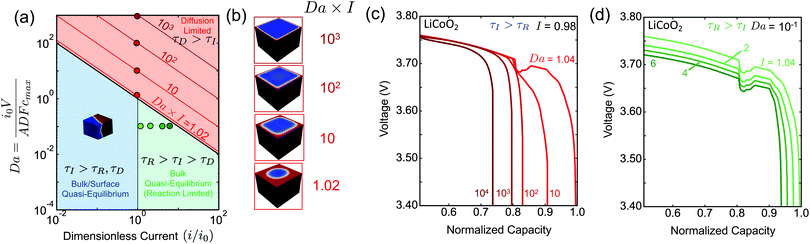
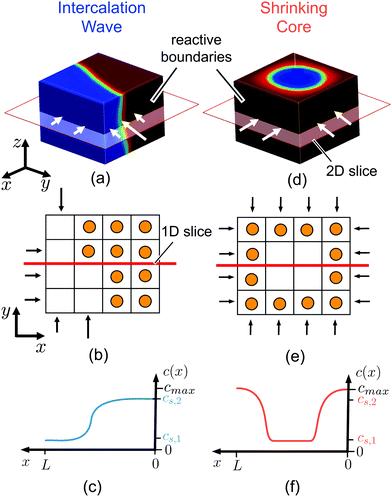
The spatial dependence of the predicted concentration profile varies with the rate-limiting conditions. For τI > τD intercalation waves are formed, while for τI < τD shrinking-core structures are observed. In the former case, the insertion process is slow compared to the diffusive flux to allow the collapse of the nucleated phases, Fig. 2(b), into a single region due to coarsening, Fig. 2(c). As Li insertion continues, the intercalation wave propagates across the solid until the particle is fully lithiated. This corresponds to the quasi-equilibrium regime, where solid diffusion is fast compared to ion insertion and bulk equilibrium is achieved. In the opposite limit, where τD > τI, the applied current is larger than the diffusional flux of the Li-rich phase (slowest phase). In this case, there is no time for the formed nuclei to coarsen into a single domain as before, Fig. 2(d). At later times, Li ions pile up at the sides of the domain forming a core–shell structure, Fig. 2(e), which eventually shuts down the reaction because there is no space for more lithium ions to be inserted.In the quasi-equilibrium case, the nucleated phases, Fig. 2(b), as well as the advancing intercalation wave, Fig. 2(c), do not result in simple one-dimensional structures. On the contrary, when the diffusion of Li-rich phase is the limiting step, the concentration profile can be considered as symmetric, both during the nucleation, Fig. 2(d), and the time at which the sides of the particle are fully lithiated, Fig. 2(e). After the reaction stops, the profile is radially symmetric, Fig. 2(e). To conclude, quasi-equilibrium conditions give rise to full 3D interface morphologies, Fig. 2(c), while diffusion limitations can be approximated by 1D axisymmetric models, Fig. 2(e). More details on the implications of these findings on modeling the insertion in phase-separating materials is presented in the Discussion section.
To summarize our findings related to eqn (6), we construct the phase morphology diagram based on the Da of the system and the applied current i scaled to the intrinsic reaction rate i0, Fig. 3(a). The light red region corresponds to the diffusion-limited (τD > τI) regime, while the light blue and green ones to the quasi-equilibrium bulk regime (τD < τI). In the latter regime, all the combinations of Da and I produce qualitatively similar concentration profiles, viz. intercalation wave patterns. In the diffusion-limited regime, however, the lithiated regions have qualitatively different concentration profiles, namely shrinking-core structure, Fig. 3(b). For example, under constant I and increasing Da the penetration depth of the Li-rich region decreases because solid-state transport cannot keep up with the imposed ion insertion rate. From Fig. 3(b) in the diffusion-limited regime, it is apparent that the Li-rich region transforms from a radially symmetric to a purely planar one.
Although the intrinsic reaction timescale τR does not affect the observed phase morphologies, we show in Fig. 3(a) that there are two distinct regions for τI > τD that affect the dependence of the battery voltage V as a function of the stored capacity, Fig. 3(c and d). When the morphology attains its quasi-equilibrium state (intercalation wave), the two regimes separate at I = 1(τI = τR). For I < 1(τI < τR), the surface reactions equilibrate equally fast with the diffusion and no reaction overpotential is built up allowing the voltage to attain its open-circuit value (dark blue line). When the system is under diffusion-limited conditions, τD > τI, the inserted ions pile up on the sides of the domain, effectively shutting down the reaction and causing a large diffusion overpotential, which limits the maximum attainable capacity, Fig. 3(c). For I > 1(τI < τR), however, the intrinsic kinetic capability of the system cannot balance the imposed insertion rate, leading in the development of reaction overpotential. Therefore, when neither solid nor liquid diffusion limit the dynamics, any decrease in the maximum capacity as a function of the applied current, Fig. 3(d), is due to slow kinetics of the intercalation reactions, especially at high concentration near lattice saturation.
Scaling of the critical rate with particle size
For practical considerations, we express eqn (6) in terms of experimentally accessible quantities. More specifically, given specific ion intercalation chemistry, the criterion related to τD/τI can be written in terms of the system size, V/A, and the applied C rate as| C rate < Dslow(A/V)2 quasi-equilibrium | (7a) |
| C rate > Dslow(A/V)2 diffusion-limited | (7b) |
This form of the criterion is demonstrated in Fig. 4(a) for three different phase-separating materials, which are widely used in commercial Li-ion batteries. The black lines correspond to LixCoO2 for x ∈ [0.5, 1.0], LixFePO4 for x ∈ [0.0, 1.0], and LixC6 with x ∈ [0.5, 0.95] (State 2 to Stage 1), respectively. The diffusivities of the slowest phase for these materials are taken from ab initio calculations.69,73,81
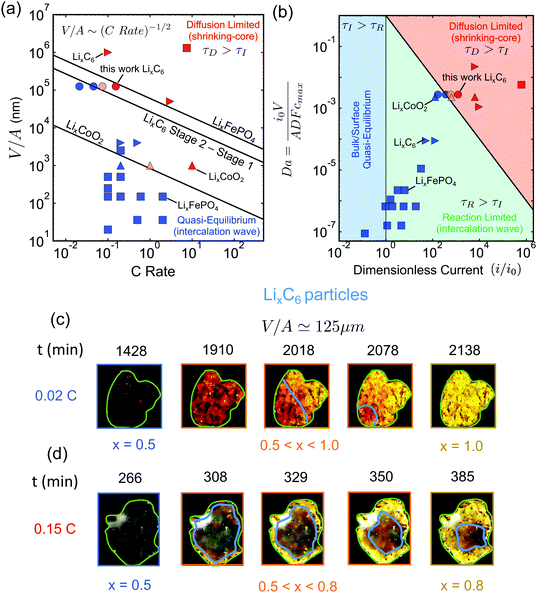 | ||
Fig. 4 Experimental validation of the scaling law. (a) Phase diagram classifying the quasi-equilibrium and diffusion-limited regimes given the volume to reactive surface area ratio V/A and the applied C rate, for three different materials, viz. LixCoO2 (LCO), LixFePO4 (LFP), and LixC6 (graphite). Here, the diffusivity of the slowest phase in the insertion direction is used (DLFPx=0.95 ∼ 10−12 m2 s−1,69DLCOx=0.9 ∼ 10−16 m2 s−1,73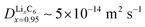 ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 81). Literature data for LCO83 are shown with △, for LFP7,51,64,84–86 with □, and for graphite11,12,82 with ▷. Our results on the lithiation of LixC6 particles based on in situ optical experiments are shown with ○. The blue color indicates the quasi-equilibrium regime, while the red the diffusion limited particles showing shrinking-core morphologies. The experimentally observed transition point for both LCO and graphite agree with the predictions by the simple scaling that is based on the predicted ab initio diffusivities.81,87 (b) Morphology classification map based on the data of (a), in terms of the dimensionless numbers Da and I = i/i0. The black line separates the diffusion limited from the quasi-equilibrium regime. (c and d) Dynamics of Li-ion intercalation of two representative single LixC6 polycrystalline particles for x ∈ [0.5, 1.0]. The images are obtained using in situ optical microscopy (see ESI† for experimental details). The particle size V/A is approximately 125 μm. The C rate is (c) 0.02 h−1 and (d) 0.15 h−1, respectively. The interface between the Li-rich (x = 0.95) and the Li-poor (x = 0.50) regions is shown with the blue line. The boundary of the particles is shown with light green line. At the smaller applied C rate, Li-ion insertion proceeds via the intercalation wave mechanism (c), while for applied C rates the particles form shrinking-core structures (d). 81). Literature data for LCO83 are shown with △, for LFP7,51,64,84–86 with □, and for graphite11,12,82 with ▷. Our results on the lithiation of LixC6 particles based on in situ optical experiments are shown with ○. The blue color indicates the quasi-equilibrium regime, while the red the diffusion limited particles showing shrinking-core morphologies. The experimentally observed transition point for both LCO and graphite agree with the predictions by the simple scaling that is based on the predicted ab initio diffusivities.81,87 (b) Morphology classification map based on the data of (a), in terms of the dimensionless numbers Da and I = i/i0. The black line separates the diffusion limited from the quasi-equilibrium regime. (c and d) Dynamics of Li-ion intercalation of two representative single LixC6 polycrystalline particles for x ∈ [0.5, 1.0]. The images are obtained using in situ optical microscopy (see ESI† for experimental details). The particle size V/A is approximately 125 μm. The C rate is (c) 0.02 h−1 and (d) 0.15 h−1, respectively. The interface between the Li-rich (x = 0.95) and the Li-poor (x = 0.50) regions is shown with the blue line. The boundary of the particles is shown with light green line. At the smaller applied C rate, Li-ion insertion proceeds via the intercalation wave mechanism (c), while for applied C rates the particles form shrinking-core structures (d). | ||
It is important to determine the upper bound of the quasi-equilibrium regime in terms of particle size for a given C rate in order to identify whether the maximum capacity is controlled by intercalation kinetics or solid-state diffusion. Fig. 4(a) can serve as a design guideline for battery electrodes. The main information that is contained in eqn (7) is the maximum particle size that should be used in order to fully utilize the active material under a given (dis)charge time, where the marginal stability curve scales as V/A ∼ C rate−1/2. For example, in order to discharge a Li-ion battery in 6 minutes (10C), we find from the diagram that the maximum particle size to avoid diffusion-limited shrinking core morphologies is ∼300 nm for LCO, ∼800 nm for LixC6 phase 2, ∼9 μm for LixC6 phase 3, and ∼35 μm for LFP. Larger particle sizes for each material would lead to incomplete capacity utilization at the desired current.
To validate the predictions of the scaling law, we first resort to reported literature data on graphite,11,12,82 LCO83 and LFP.7,51,64,84–86 The goal of the comparison is to test the universality of the scaling law and to validate the use of eqn (7) for the design of Li-ion batteries with phase-separating materials. Several experimental studies have been conducted trying to understand the impact of phase separation dynamics in LFP and graphite electrodes, as well as how different phase morphologies affect the performance of Li-ion batteries. All the symbols in Fig. 4(a) (except the circles) correspond to the reported phase morphologies data for specific C rates (exact values are given in the ESI†). The blue color symbols correspond to particles that undergo intercalation wave lithiation, and the red ones to shrinking-core structures due to diffusion limitations. With light red are mixed cases where either shrinking-core or intercalation waves are observed (Da × I ≃ 1). The different symbols denote the different materials used, i.e. □ for LFP, ▷ for graphite, and △ for LCO. From Fig. 4(a), it is clear that most of the LFP and graphite data are either deep in the quasi-equilibrium regime or in the diffusion-limited one, while only those of LCO show a clear transition behavior. In order to strengthen our conclusion regarding the proposed scaling law, we need to design controlled experiments that probe the transition between the two regimes.
Experimental validation for lithium intercalation in graphite
Next, we test the predictions of the proposed scaling by performing in situ optical microscopy of single graphite particles during lithium insertion. As in previous work,10–12,43 graphite is a convenient material for microscopy because its phases (stages) appear as different optical colors. Relatively large flake-like particles of average size 〈V/A〉 ≃ 125 μm were used, in order to visualize clearly the intra-particle phase morphologies. The experiment was done in a custom electrochemical visualization cell, in which a working electrode/separator/Li counter electrode sandwich were pushed against a spacer and washer by a quartz window. The working electrode consisted of graphite flakes loaded onto a stainless-steel mesh, and the electrolyte was 1 M LiPF6-EC–EMC. The particles were initially prepared at x = 0.5 in order to study the Stage 2 to State 1 transition due to the distinct color change from red to gold with increasing Li fraction. A digital camera was used to record images of the graphite electrode during charge/discharge cycles.Fig. 4(c) and (d) demonstrate two representative graphite particles undergoing Li intercalation under different applied C rates, 0.02C and 0.15C. The particle of Fig. 4(c) undergoes lithiation via the intercalation wave mechanism, while that of Fig. 4(d) shows a clear shrinking-core structure. According to the simulation results, Fig. 2, the first case corresponds to the quasi-equilibrium regime, the second to the diffusion-limited regime. Using the size of the particles, V/A ≃ 125 μm, the applied C rate, and the ab initio calculated diffusivity of the slowest graphite phase for x ∈ [0.5, 0.95]81 we predict the slowest charged particle to be in quasi-equilibrium, Fig. 4(c), and the fastest charged one to be diffusion-limited, Fig. 4(d), in qualitative agreement with the experimental observations.
For a more quantitative comparison that validates the critical C rate where the transition between the two regimes occurs, we perform statistical analysis for quantifying how many of the particles undergo shrinking-core lithiation for two intermediate values of C rate, i.e. 0.045C and 0.075C. In Fig. 4(a), the circle symbols show the results for 60 different LixC6 particles (with x ∈ [0.5, 0.95]) under four different applied C rates. The different shades of red indicate different percentage of particles that undergo core–shell structure during lithiation: (i) light red for around 20%, (ii) red for more than 60%. For applied current less than the critical value, Ic ∼ 0.055C, the majority of the particles are lithiated via intercalation wave mechanism as less than 5% of them undergo core–shell lithiation. When the applied current, however, increases slightly above Ic, then more than half of the particles start showing a core–shell structure at around 80% state-of-charge (see ESI,† Fig. S3). For the largest applied rate, i.e. 0.15C, more than 60% of the particles are core–shell, Fig. 4(c), and full lithiation of the active material is prevented due to diffusion limitations. The other 40% of the particles are not lithiated before the voltage of the cell approaches 0 V Li+vs. Li. Our observations are in very good agreement with the phase diagram predicted by eqn (7) and show that the ab initio calculated diffusivity for LixC6 (at x = 0.95)81 provides a good estimate for practical graphite electrodes.
Morphology classification map of literature data
We close the Results section by demonstrating the classification of all the available experimental data for in situ phase visualization in single particles of Li-ion battery materials (tabulated with references in the ESI†), along with our new results for graphite flakes, on a dimensionless map, Fig. 4(b), showing the observed phase morphology (shrinking core or intercalation wave) versus the Damköller number, Da and the applied dimensionless current I = i/i0. For the construction of the master plot, we used the following estimated values for the characteristic exchange current densities i0: i0,LCO ∼ 10−3 A m−2,48i0,LFP ∼ 10−2 A m−2,7 and i0,LiC6 ∼ 10−2 A m−2.11,82 While these values are only rough estimates, which are expected to vary between different systems, our conclusions on the classification of the data across orders of magnitude in the dimensionless variables will not change. More specifically, in all cases where intercalation waves are observed the collected data lie below the black line (τD = τI), while experiments with shrinking-core structures are always above the predicted boundary. The successful prediction of all of the observed morphologies for three different battery materials (one anode and two cathodes) over a wide range of currents and particle sizes shows the power of simple scaling arguments to reveal the underlying physics.Discussion
The proposed scaling law, eqn (6), is of both experimental and theoretical significance. Given the diffusivity of the slowest phase in a two-phase system and the applied reaction rate, the criterion can be used to provide an upper bound of system size below which the maximum capacity is governed only by the ion intercalation characteristics, eqn (7). For example, in LCO, we find that particles smaller than 100 nm can support up to 100C current before diffusion limitation arises, in agreement with previous experimental observations.88 Moreover, our simulations reveal that the quasi-equilibrium regime is described by 3D interface morphologies, while diffusion-limited systems can be approximated by axisymmetric or planar 1D models.Although we have focused on layered materials (LCO and graphite) where diffusion is restricted to two-dimensional planes, the analysis of our results, as well as the constructed phase diagrams, Fig. 3(a) and 4(a, b), should hold for any 3D diffusion mechanism, even anisotropic ones, given that the diffusivity of the slowest phase in the insertion direction is used in the developed scaling law. Whenever the dynamics are limited by insertion reactions, the formed phase boundaries will always have three-dimensional structure (see ESI,† Fig. S4(a)). The specific diffusion mechanism, however, will lead to different concentration profiles in the diffusion-limited case, as phase separation is only allowed in specific directions. For example, when diffusion occurs through 1D channels, as in LFP,69 the diffusion-limited case is expected to be characterized by a ‘sandwich’/layered structure, ESI,† Fig. S4(b), where the phase of the highest concentration is located at the insertion boundaries on the (010) facets. The 2D case is described in Fig. 2(e), and in (ESI†) Fig. S4(c), where a shrinking-core structure is observed. In the 3D case, the visualization becomes more complicated, but again a shrinking-core structure is expected, leading to all the boundaries to be surrounded by the phase of the higher concentration.
Regarding simulations, the use of 1D models for phase-separating particles under quasi-equilibrium conditions can inaccurately predict the battery voltage. For phase-separating mixtures, the ion concentration at the reactive boundary experiences sudden increase during phase separation. When electrochemical insertion is driven galvanostatically, the artificially increased concentration tends to shut-down the reaction,37,58,61 leading to abrupt decrease in the voltage. Therefore, in cases where we are interested in predicting when the voltage reaches a critical value, such as the Li plating on graphite at 0 V (Li/Li+), reduced-order models can lead to inaccurate predictions. Therefore, the criterion of eqn (6) and the morphology phase diagram of Fig. 3(a) can be used to inform computational studies for the conditions in which one-dimensional models40,42,61 could be applicable.
As noted above, various forms of eqn (6) and (7) have appeared in the chemical engineering literature75–79 to describe the transition from pseudo-steady to shrinking-core concentration profiles, including the case of solid-solution Li-ion battery particles.89 Here, we have shown their relevance for driven phase separation, whether by heterogeneous nucleation or spinodal decomposition. When the average concentration of the active material lies in the spinodal region,90 the concentration of the system is approximately fixed to the values of the binodal points, which are likely to have a very different diffusivities.80,87 Until the average concentration leaves the spinodal region, the onset of diffusion-limited phase morphologies is governed by diffusivity of the slowest phase. This observation, which has been overlooked in previous theoretical works,62,91 is clear from our simulations of LCO particles and experimental observations of graphite intercalation.
The parameters in the theory can be augmented to account for material and microstructural complexities. It is commonly observed that battery materials are polycrystalline in nature with the presence of a large number of grain boundaries. In such a case, the diffusivity required to evaluate the criterion will be the effective diffusivity that can be predicted by averaging techniques such as percolation or effective medium theories.92,93 However, our results for single LixC6 particles suggest this correction might not be necessary. Another example is when the system has a non-uniform coating at the reactive boundaries.7,94,95 This is expected to induce a spatially dependent reaction rate constant. Previous studies on LiFePO4 have shown that surface ‘wetting’ by competing phases of different surface tensions can influence pattern formation during ion insertion.31,37,61 In particular, when the surface is fully wetted by one phase (Young–Laplace contact angle of 0 or 180°), then shrinking-core patterns are observed, and intercalation waves are suppressed at the surface. Although this situation is expected for binary solids with large differences in surface energy, it has not been directly observed experimentally for Li-ion battery materials14,57 other than LFP.32,96
A surprising prediction of our theory is that the phase morphology is not affected by surface reactions, even in reaction-limited particles with Da ≪ 1 (τD ≪ τR), as long as phase separation proceeds by bulk diffusion. A characteristic example is shown in our previous work on LCO, where the intercalation wave structure (shown in Fig. 3B of ref. 48) that corresponds to Da × I ≃ 5 × 10−6 is almost identical to the result shown in Fig. 2(a–c) for Da × I = 0.98. Of course, slow reactions will alter transient phase morphologies close to the surface, and in some unusual situations where the formed interface thickness 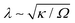 (where Ω is a characteristic free energy barrier, such as the regular solution parameter97) is comparable to the size of the system L,37 there can be reaction-limited phase separation in single particles controlled by nonlinearities in the reaction rate (‘electroautocatalysis’).58 In particular, depth-averaged models have predicted28–30 and experiments have confirmed7,32 this regime for thin platelets of anisotropic single-crystal LFP (L ≤ 22 nm or L/λ ≤ 431,98), consistent with suppressed bulk phase separation,37 fast b-axis (depth) bulk diffusion,23 and slow surface diffusion.94
(where Ω is a characteristic free energy barrier, such as the regular solution parameter97) is comparable to the size of the system L,37 there can be reaction-limited phase separation in single particles controlled by nonlinearities in the reaction rate (‘electroautocatalysis’).58 In particular, depth-averaged models have predicted28–30 and experiments have confirmed7,32 this regime for thin platelets of anisotropic single-crystal LFP (L ≤ 22 nm or L/λ ≤ 431,98), consistent with suppressed bulk phase separation,37 fast b-axis (depth) bulk diffusion,23 and slow surface diffusion.94
Another important dimensionless parameter is the ratio of the interfacial thickness λ to the system size, L, assumed here to be large (L/λ > 20), corresponding to ‘thin’ phase boundaries. For very small particles with L < λ, the predictions of our criterion may break down. In particular, it is known that for nano-sized particles phase separation can be suppressed due to the large energy penalty for forming interfaces inside the domain.37,98 Additionally, elastic effects due to the existence of misfit strains can also affect the phase separation behavior. An example is given in ref. 30 and 32, where coherent elasticity forces the formed interfaces to orient towards specific crystallographic directions such that to minimize the developed misfit stresses.48,99 While in our simulations we showed the formation of a single intercalation wave, in the case of constrained nanosized particles multiple interfaces can show up in the form of ‘stripes’. Their spacing has been shown30,32,99 to depend on the directional elastic modulus of the material and on the ratio L/λ.
It is also important to stress that slow reactions, which are typical for most battery materials in Fig. 4, can influence macroscopic patterns of phase separation across a collection of many interacting particles in a porous electrode, where diffusion of Li+ in the electrolyte also plays an important role.42,43,100 For thick Li-ion battery electrodes, electrolyte transport is often the rate-limiting step, in which case the capacity decrease at high currents can be attributed to concentration polarization in the liquid matrix, as opposite the solid particles. In phase separating materials, macroscopic reaction limitation can also lead to electro-autocatalytic suppression or enhancement of mosaic instability,43,44 while electrolyte diffusion limitation leads to macroscopic intercalation waves (or reaction fronts),42 as observed in both LFP46,47 and graphite.10,12 In non-phase-separating materials, such as LiNi1/3Co1/3Mn1/3O2, reaction limitation can also be observed, leading to fictitious ‘phase separation’ in porous electrodes driven by electro-autocatalysis.44,58 Nevertheless, in all of these cases, the concentration evolution within each individual particle will be governed by the scaling principles revealed here, based on the dimensionless ratio τD/τI = iV/ADslowFcmax.
The results of the present study are expected to apply not only in Li-ion batteries but also to other situations of chemical intercalation, such as hydrogen insertion in palladium (HxPd). As in the case of LixCoO2, HxPd co-exists in hydrogen-rich and -poor phases101,102 for a certain range of hydrogen fraction. Recent in situ imaging techniques were able to visualize the hydrogen distribution inside nanosized Pd particles102–104 where an insertion-limited hydrogen intercalation wave was directly observed for small (∼20 nm) nanoparticles. In addition, combined computational and experimental work105 demonstrated the importance of the morphology of the formed interfaces on the accumulation of dislocations inside nanosized Pd particles. Therefore, understanding the competition between insertion and diffusion limitations can also help engineer hydrogen storage systems.
Conclusion
In summary, we have introduced a scaling law to classify pattern formation for driven ion intercalation in phase-separating particles, analogous to the diffusion-to-process-time ratio which controls the onset of diffusion limitation in single-phase systems. The criterion requires only the knowledge of the solid-state diffusivity of the slowest phase, D, the size of the system, which is expressed as the ratio between the volume to the reactive surface area, V/A, and the applied reaction rate Rt (or current density i). We have tested the criterion by carrying out phase-field simulations and in situ optical experiments and demonstrating the classification of literature data for a wide range of particle sizes and C-rates in the most common Li-ion battery materials (LCO, graphite and LFP). The simulations and experiments reveal that under quasi-equilibrium conditions with fast diffusion, the formation of three-dimensional intercalation waves is favored, while under diffusion limitation, the phases form a shrinking core. Surface reaction limitation, which is common in most Li-ion battery materials, affects the voltage behavior through internal resistance but does not influence the phase morphology, which is typically controlled by bulk diffusion. The dimensionless criterion allows us to construct an operational diagram that determines when reduced-order models may be valid and, more importantly, how the detrimental effects of intra-particle phase separation may be avoided in the design of Li-ion batteries.Author contributions
D. F. (aka dfrag) proposed the classification, conceptualized the scaling law, designed and conducted the theoretical/computational study, and wrote the manuscript. T. G. and Y. H. conducted the experimental study. N. N. provided the chemomechanical model. D. F. and T. Z. performed the statistical analysis of the experimental results. Y. Z., R. M. S., Y. S.-H. provided comments on the text. M. Z. B. supervised the study and revised the manuscript. All authors contributed to the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge support from Shell International Exploration & Production Inc. (D. F., Y. Z., R. M. S., Y. S.-H., M. Z. B.) and the Toyota Research Institute through the D3BATT Center on Data-Driven-Design of Rechargeable Batteries (N. N., T. G., Y. H., M. Z. B.). Finally, D. F. is thankful to M. A. Alkhadra for insightful discussions.Notes and references
- N. Nitta, F. Wu, J. T. Lee and G. Yushin, Mater. Today, 2015, 18, 252–264 CrossRef CAS.
- J. B. Goodenough and K. S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176 CrossRef CAS PubMed.
- Y. Liu, Y. Zhu and Y. Cui, Nat. Energy, 2019, 4, 540–550 CrossRef.
- K. E. Thomas, J. Newman and R. M. Darling, Advances in Lithium-Ion Batteries, Springer, 2002, pp. 345–392 Search PubMed.
- J. Newman and K. E. Thomas-Alyea, Electrochemical Systems, John Wiley and Sons, Hoboken, New Jersey, 3rd edn, 2004 Search PubMed.
- V. Ramadesigan, P. W. C. Northrop, S. De, S. Santhanagopalan, R. D. Braatz and V. R. Subramanian, J. Electrochem. Soc., 2012, 159, R31–R45 CrossRef CAS.
- J. Lim, Y. Li, D. H. Alsem, H. So, S. C. Lee, P. Bai, D. A. Cogswell, X. Liu, N. Jin, Y.-S. Yu, N. J. Salmon, D. A. Shapiro, M. Z. Bazant, T. Tyliszczak and W. C. Chueh, Science, 2016, 353, 566–571 CrossRef CAS PubMed.
- K. Mizushima, P. C. Jones, P. J. Wiseman and J. B. Goodenough, Solid State Ionics, 1981, 3–4, 171–174 CrossRef CAS.
- T. Ohzuku, Y. Iwakoshi and K. Sawai, J. Electrochem. Soc., 1993, 140, 2490–2498 CrossRef CAS.
- S. J. Harris, A. Timmons, D. R. Baker and C. Monroe, Chem. Phys. Lett., 2010, 485, 265–274 CrossRef CAS.
- Y. Guo, R. B. Smith, Z. Yu, D. K. Efetov, J. Wang, P. Kim, M. Z. Bazant and L. E. Brus, J. Phys. Chem. Lett., 2016, 7, 2151–2156 CrossRef CAS PubMed.
- K. E. Thomas-Alyea, C. Jung, R. B. Smith and M. Z. Bazant, J. Electrochem. Soc., 2017, 164, E3063–E3072 CrossRef CAS.
- T. Ohzuku, A. Ueda and N. Yamamoto, J. Electrochem. Soc., 1995, 142, 1431–1435 CrossRef CAS.
- M. G. Verde, L. Baggetto, N. Balke, G. M. Veith, J. K. Seo, Z. Wang and Y. S. Meng, ACS Nano, 2016, 10, 4312–4321 CrossRef CAS PubMed.
- Y. Zhang, Y. Katayama, R. Tatara, L. Giordano, Y. Yu, D. Fraggedakis, J. G. Sun, F. Maglia, R. Jung, M. Z. Bazant and Y. Shao-Horn, Energy Environ. Sci., 2020, 13, 183–199 RSC.
- M. Wagemaker, W. J. H. Borghols and F. M. Mulder, J. Am. Chem. Soc., 2007, 129, 4323–4327 CrossRef CAS PubMed.
- N. J. J. de Klerk, A. Vasileiadis, R. B. Smith, M. Z. Bazant and M. Wagemaker, Phys. Rev. Mater., 2017, 1, 025404 CrossRef.
- V. Srinivasan and J. Newman, J. Electrochem. Soc., 2004, 151, A1517–A1529 CrossRef CAS.
- V. Srinivasan and J. Newman, J. Electrochem. Soc., 2004, 151, A1530 CrossRef CAS.
- V. Srinivasan and J. Newman, Electrochem. Solid-State Lett., 2006, 9, A110 CrossRef CAS.
- M. Heß and P. Novák, Electrochim. Acta, 2013, 106, 149–158 CrossRef.
- B. Han, A. Van der Ven, D. Morgan and G. Ceder, Electrochim. Acta, 2004, 49, 4691–4699 CrossRef CAS.
- G. K. Singh, G. Ceder and M. Z. Bazant, Electrochim. Acta, 2008, 53, 7599–7613 CrossRef CAS.
- M. Tang, W. C. Carter and Y.-M. Chiang, Annu. Rev. Mater. Res., 2010, 40, 501–529 CrossRef CAS.
- Y.-H. Kao, M. Tang, N. Meethong, J. Bai, W. C. Carter and Y.-M. Chiang, Chem. Mater., 2010, 22, 5845–5855 CrossRef CAS.
- N. Meethong, Y.-H. Kao, M. Tang, H.-Y. Huang, W. C. Carter and Y.-M. Chiang, Chem. Mater., 2008, 20, 6189–6198 CrossRef CAS.
- M. Tang, H.-Y. Huang, N. Meethong, Y.-H. Kao, W. C. Carter and Y.-M. Chiang, Chem. Mater., 2009, 21, 1557–1571 CrossRef CAS.
- M. Z. Bazant, Acc. Chem. Res., 2013, 46, 1144–1160 CrossRef CAS PubMed.
- P. Bai, D. A. Cogswell and M. Z. Bazant, Nano Lett., 2011, 11, 4890–4896 CrossRef CAS PubMed.
- D. A. Cogswell and M. Z. Bazant, ACS Nano, 2012, 6, 2215–2225 CrossRef CAS PubMed.
- D. A. Cogswell and M. Z. Bazant, Nano Lett., 2013, 13, 3036–3041 CrossRef CAS PubMed.
- D. A. Cogswell and M. Z. Bazant, Electrochem. Commun., 2018, 95, 33–37 CrossRef CAS.
- W. Lai and F. Ciucci, Electrochim. Acta, 2010, 56, 531–542 CrossRef CAS.
- W. Lai, J. Power Sources, 2011, 196, 6534–6553 CrossRef CAS.
- M. Tang, J. F. Belak and M. R. Dorr, J. Phys. Chem. C, 2011, 115, 4922–4926 CrossRef CAS.
- M. J. Welland, D. Karpeyev, D. T. OConnor and O. Heinonen, ACS Nano, 2015, 9, 9757 CrossRef CAS PubMed.
- N. Nadkarni, E. Rejovitsky, D. Fraggedakis, C. V. Di Leo, R. B. Smith, P. Bai and M. Z. Bazant, Phys. Rev. Mater., 2018, 2, 085406 CrossRef CAS.
- R. B. Smith, E. Khoo and M. Z. Bazant, J. Phys. Chem. C, 2017, 121, 12505–12523 CrossRef CAS.
- K. Yang and M. Tang, J. Mater. Chem. A, 2020, 8, 3060–3070 RSC.
- R. B. Smith and M. Z. Bazant, J. Electrochem. Soc., 2017, 164, E3291–E3310 CrossRef CAS.
- W. Lai and F. Ciucci, Electrochim. Acta, 2011, 56, 4369–4377 CrossRef CAS.
- T. R. Ferguson and M. Z. Bazant, J. Electrochem. Soc., 2012, 159, A1967–A1985 CrossRef CAS.
- T. R. Ferguson and M. Z. Bazant, Electrochim. Acta, 2014, 146, 89–97 CrossRef CAS.
- H. Zhao and M. Z. Bazant, Phys. Rev. E, 2019, 100, 012144 CrossRef CAS PubMed.
- A. Vasileiadis, N. J. de Klerk, R. B. Smith, S. Ganapathy, P. P. R. Harks, M. Z. Bazant and M. Wagemaker, Adv. Funct. Mater., 2018, 28, 1705992 CrossRef.
- W. C. Chueh, F. El Gabaly, J. D. Sugar, N. C. Bartelt, A. H. McDaniel, K. R. Fenton, K. R. Zavadil, T. Tyliszczak, W. Lai and K. F. McCarty, Nano Lett., 2013, 13, 866–872 CrossRef CAS PubMed.
- Y. Li, F. El Gabaly, T. R. Ferguson, R. B. Smith, N. C. Bartelt, J. D. Sugar, K. R. Fenton, D. A. Cogswell, A. L. D. Kilcoyne, T. Tyliszczak, M. Z. Bazant and W. C. Chueh, Nat. Mater., 2014, 13, 1149–1156 CrossRef CAS PubMed.
- N. Nadkarni, T. Zhou, D. Fraggedakis, T. Gao and M. Z. Bazant, Adv. Funct. Mater., 2019, 29, 1902821 CrossRef.
- W. Dreyer, J. Jamnik, C. Guhlke, R. Huth, J. Moškon and M. Gaberš, Nat. Mater., 2010, 9, 448–453 CrossRef CAS PubMed.
- D. Dreyer, C. Guhlke and R. Huth, Physica D, 2011, 240, 1008–1019 CrossRef.
- L. Hong, L. Li, Y.-K. Chen-Wiegart, J. Wang, K. Xiang, L. Gan, W. Li, F. Meng, F. Wang, J. Wang, Y.-M. Chiang, S. Jin and M. Tang, Nat. Commun., 2017, 8, 1194 CrossRef PubMed.
- Y. Zhu, J. W. Wang, Y. Liu, X. Liu, A. Kushima, Y. Liu, Y. Xu, S. X. Mao, J. Li and C. Wang, et al. , Adv. Mater., 2013, 25, 5461–5466 CrossRef CAS PubMed.
- L. Hong, K. Yang and M. Tang, npj Comput. Mater., 2019, 5, 1–9 CrossRef.
- C. V. Di Leo, E. Rejovitzky and L. Anand, J. Mech. Phys. Solids, 2014, 70, 1–29 CrossRef CAS.
- P. Zuo and Y.-P. Zhao, Extreme Mech. Lett., 2016, 9, 467–479 CrossRef.
- J.-M. Lim, T. Hwang, D. Kim, M.-S. Park, K. Cho and M. Cho, Sci. Rep., 2017, 7, 39669 CrossRef CAS PubMed.
- X. Zhu, C. S. Ong, X. Xu, B. Hu, J. Shang, H. Yang, S. Katlakunta, Y. Liu, X. Chen and L. Pan, et al. , Sci. Rep., 2013, 3, 1084 CrossRef PubMed.
- M. Z. Bazant, Faraday Discuss., 2017, 199, 423–463 RSC.
- D. Fraggedakis and M. Z. Bazant, 2020, arXiv preprint, arXiv:2003.03057.
- D. Burch, G. K. Singh, G. Ceder and M. Z. Bazant, Solid State Phenom., 2008, 139, 95–100 CAS.
- Y. Zeng and M. Z. Bazant, SIAM J. Appl. Math., 2014, 74, 980–1004 CrossRef.
- M. Doyle, T. F. Fuller and J. Newman, J. Electrochem. Soc., 1993, 140, 1526–1533 CrossRef CAS.
- J. Niu, A. Kushima, X. Qian, L. Qi, K. Xiang, Y.-M. Chiang and J. Li, Nano Lett., 2014, 14, 4005–4010 CrossRef CAS PubMed.
- X. Zhang, M. Van Hulzen, D. P. Singh, A. Brownrigg, J. P. Wright, N. H. Van Dijk and M. Wagemaker, Nat. Commun., 2015, 6, 8333 CrossRef CAS PubMed.
- R. Malik, F. Zhou and G. Ceder, Nat. Mater., 2011, 10, 587 CrossRef CAS PubMed.
- W. Zhang, H.-C. Yu, L. Wu, H. Liu, A. Abdellahi, B. Qiu, J. Bai, B. Orvananos, F. C. Strobridge and X. Zhou, et al. , Sci. Adv., 2018, 4, eaao2608 CrossRef PubMed.
- R. Malik, A. Abdellahi and G. Ceder, J. Electrochem. Soc., 2013, 160, A3179–A3197 CrossRef CAS.
- T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 174112 CrossRef.
- R. Malik, D. Burch, M. Bazant and G. Ceder, Nano Lett., 2010, 10, 4123–4127 CrossRef CAS PubMed.
- D. Jiang, Y. Jiang, Z. Li, T. Liu, X. Wo, Y. Fang, N. Tao, W. Wang and H.-Y. Chen, J. Am. Chem. Soc., 2016, 139, 186–192 CrossRef PubMed.
- S. R. De Groot and P. Mazur, Non-equilibrium thermodynamics, Courier Corporation, 2013 Search PubMed.
- J. Keizer, Statistical thermodynamics of nonequilibrium processes, Springer Science & Business Media, 2012 Search PubMed.
- A. Van der Ven and G. Ceder, Electrochem. Solid-State Lett., 2000, 3, 301–304 CrossRef CAS.
- D. Fraggedakis, J. Papaioannou, Y. Dimakopoulos and J. Tsamopoulos, J. Comput. Phys., 2017, 344, 127–150 CrossRef CAS.
- W. M. Deen, Analysis of transport phenomena, Oxford University Press, New York, 2nd edn, 2012 Search PubMed.
- M. Ishida and C. Wen, AIChE J., 1968, 14, 311–317 CrossRef CAS.
- N. Lindman and D. Simonsson, Chem. Eng. Sci., 1979, 34, 31–35 CrossRef CAS.
- P. K. Gbor and C. Q. Jia, Chem. Eng. Sci., 2004, 59, 1979–1987 CrossRef CAS.
- W.-L. Hsu, M.-J. Lin and J.-P. Hsu, Int. J. Chem. Biol. Eng., 2009, 2, 205–210 CAS.
- K. Persson, V. A. Sethuraman, L. J. Hardwick, Y. Hinuma, Y. S. Meng, A. van der Ven, V. Srinivasan, R. Kostecki and G. Ceder, J. Phys. Chem. Lett., 2010, 1, 1176–1180 CrossRef CAS.
- K. Persson, Y. Hinuma, Y. S. Meng, A. Van der Ven and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 125416 CrossRef.
- T. Gao, Y. Han, D. Fraggedakis, T. Zhou, S. Das, C.-N. Yeh, S. Xu, W. C. Chueh, J. Li and M. Z. Bazant, to be submitted.
- Y. Xu, E. Hu, K. Zhang, X. Wang, V. Borzenets, Z. Sun, P. Pianetta, X. Yu, Y. Liu and X.-Q. Yang, et al. , ACS Energy Lett., 2017, 2, 1240–1245 CrossRef CAS.
- J. Wang, Y.-C. K. Chen-Wiegart and J. Wang, Nat. Commun., 2014, 5, 1–10 CAS.
- Y.-S. Yu, C. Kim, D. A. Shapiro, M. Farmand, D. Qian, T. Tyliszczak, A. D. Kilcoyne, R. Celestre, S. Marchesini and J. Joseph, et al. , Nano Lett., 2015, 15, 4282–4288 CrossRef CAS PubMed.
- K. Weichert, W. Sigle, P. A. van Aken, J. Jamnik, C. Zhu, R. Amin, T. Acarturk, U. Starke and J. Maier, J. Am. Chem. Soc., 2012, 134, 2988–2992 CrossRef CAS PubMed.
- A. Van der Ven and G. Ceder, Electrochem. Solid-State Lett., 2000, 3, 301–304 CrossRef CAS.
- K. Dokko, N. Nakata and K. Kanamura, J. Power Sources, 2009, 189, 783–785 CrossRef CAS.
- T. F. Fuller, M. Doyle and J. Newman, J. Electrochem. Soc., 1994, 141, 1 CrossRef CAS.
- R. W. Balluffi, S. Allen and W. C. Carter, Kinetics of materials, John Wiley & Sons, 2005 Search PubMed.
- T. F. Fuller, M. Doyle and J. Newman, J. Electrochem. Soc., 1994, 141, 982–990 CrossRef CAS.
- Y. Chen and C. A. Schuh, Acta Mater., 2006, 54, 4709–4720 CrossRef CAS.
- S. Torquato, Random Heterogeneous Materials: Microstructure and Macroscopic Properties, Springer Science & Business Media, 2013, vol. 16 Search PubMed.
- Y. Li, H. Chen, K. Lim, H. D. Deng, J. Lim, D. Fraggedakis, P. M. Attia, S. C. Lee, N. Jin, J. Moškon, Z. Guan, W. E. Gent, J. Hong, Y. S. Yu, M. Gaberšček, M. S. Islam, M. Z. Bazant and W. C. Chueh, Nat. Mater., 2018, 17, 915–922 CrossRef CAS PubMed.
- K. A. Severson, P. M. Attia, N. Jin, N. Perkins, B. Jiang, Z. Yang, M. H. Chen, M. Aykol, P. K. Herring, D. Fraggedakis, M. Z. Bazant, S. J. Harris, W. C. Chueh and R. D. Braatz, Nat. Energy, 2019, 4, 383–391 CrossRef.
- I. Lucas, A. McLeod, J. Syzdek, D. S. Middlemiss, C. P. Grey, D. N. Basov and R. M. Kostecki, Nano Lett., 2014, 15, 1–7 CrossRef PubMed.
- J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1958, 28, 258 CrossRef CAS.
- D. Burch and M. Z. Bazant, Nano Lett., 2009, 9, 3795–3800 CrossRef CAS PubMed.
- A. G. Khachaturyan, Theory of Structural Transformations in Solids, Dover Publications, Inc., Mineola, New York, 1983 Search PubMed.
- J. Huang, Z. Li, J. Zhang, S. Song, Z. Lou and N. Wu, J. Electrochem. Soc., 2015, 162, A585–A595 CrossRef CAS.
- Y. Li and W. C. Chueh, Annu. Rev. Mater. Res., 2018, 48, 1–29 CrossRef.
- F. Hayee, T. C. Narayan, N. Nadkarni, A. Baldi, A. L. Koh, M. Z. Bazant, R. Sinclair and J. A. Dionne, Nat. Commun., 2018, 9, 1775 CrossRef PubMed.
- A. Baldi, T. C. Narayan, A. L. Koh and J. A. Dionne, Nat. Mater., 2014, 13, 1143 CrossRef CAS PubMed.
- T. C. Narayan, F. Hayee, A. Baldi, A. L. Koh, R. Sinclair and J. A. Dionne, Nat. Commun., 2017, 8, 14020 CrossRef CAS PubMed.
- A. Ulvestad, M. Welland, W. Cha, Y. Liu, J. Kim, R. Harder, E. Maxey, J. Clark, M. Highland and H. You, et al. , Nat. Mater., 2017, 16, 565–571 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ee00653j |
| ‡ Equal contributions. |
| This journal is © The Royal Society of Chemistry 2020 |