Open Access Article
Open Access ArticleCation-disordered rocksalt transition metal oxides and oxyfluorides for high energy lithium-ion cathodes
R. J.
Clément
 ab,
Z.
Lun
ab,
Z.
Lun
 ac and
G.
Ceder
*ac
ac and
G.
Ceder
*ac
aDepartment of Materials Science and Engineering, University of California, Berkeley, CA 94720, USA. E-mail: gceder@berkeley.edu
bMaterials Department, University of California, Santa Barbara, CA 93106, USA
cMaterials Science Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
First published on 13th January 2020
Abstract
For lithium-ion rechargeable batteries to meet society's ever-growing demands in electrical energy storage, e.g. for the electrification of transportation, for portable electronics and for grid storage applications, novel electrode materials with a large charge storage capacity and a high energy density are needed. Over the last five years, several experimental and theoretical studies have demonstrated the feasibility of disordered rocksalt (DRX) cathodes, that is, lithium transition metal oxide cathodes with a crystalline rocksalt structure but with a disordered arrangement of lithium and transition metal on the cation lattice. We provide here an overview of the current understanding of DRX materials, in terms of their structural and compositional characteristics, as well as their electrochemical properties. We also present important considerations for the design of high performance DRX cathodes and suggest future research directions. Because no specific order is needed, DRX compounds can be composed of a wide variety of transition metal species, which can create long-term benefits for the lithium battery industry by making it less reliant on scarce and expensive raw materials. While some DRX compositions can simply be synthesized at high temperature to induce thermal cation disorder, other compositions require mechanochemical methods to induce a disordered arrangement of cation species. Cation disorder leads to unique lithium transport properties, small volume changes during charge–discharge cycling and sloping electrochemical profiles. Fluorine substitution for oxygen and the incorporation of high-valent d0 transition metals in the bulk DRX structure are two strategies used to increase the lithium content in the material, improve lithium percolation and to keep the valence of redox-active metal species low so that high transition metal redox capacity can be obtained. Short-range cation order, which is affected by thermal treatment, metal composition and fluorine substitution, has a significant impact on electrochemical performance. Moreover, fluorine substitution for oxygen improves long-term capacity retention by significantly reducing anion-based charge compensation mechanisms during charge. Fluorinated DRXs have recently demonstrated reversible capacities >300 mA h g−1 and extremely high energy densities approaching 1000 W h kg−1, holding promise for a nearly two-fold increase in the energy density of commercial lithium-ion batteries.
Broader contextRechargeable batteries are still the limiting component of portable electronics, hybrid electric and electric vehicles, motivating research efforts to improve the energy density, power capability and safety of lithium-ion batteries, and specifically of the cathode material. Additionally, electrical energy storage plays a key role in the worldwide strategy to combat global warming. For grid storage applications, low-cost battery technologies requiring minimal maintenance and with a long charge–discharge cycle life are needed. Over the last few years, lithium transition metal oxides with a cation-disordered rocksalt-type structure have emerged as potential high energy density cathodes. These compounds can be reasonable ionic and electronic conductors when prepared with excess Li content, a realization which has led to the investigation of a large range of compositions in this structure space. Already, several cation-disordered rocksalt cathodes have demonstrated very high specific capacities and energy densities up to 1000 W h kg−1, well exceeding commercially-available layered lithium transition metal oxide cathodes. Cation-disordered rocksalt cathodes also hold promise for the integration of cheap and Earth-abundant transition metal species, enabling more sustainable battery chemistries for large-scale electric transportation and grid storage applications. |
Introduction
The transition to a more carbon-neutral society requires significant advances in electrical energy storage technologies, both for load leveling of the power grid, an important step towards replacing steady electric supplies from, e.g., coal and fossil fuels, by intermittent energy sources from renewables (wind, tide, solar, etc.), and for the electrification of transportation. A large research effort is targeted at improving the current rechargeable battery technology, which provides a means of storing energy electrochemically. Among the different battery chemistries, lithium(Li)-ion systems are closest to meeting gravimetric and volumetric energy density requirements for a variety of applications, ranging from portable electronics to electric and hybrid electric cars. Today, Li-ion batteries are even considered for the (partial) electrification of aviation and marine transportation.1,2 This tremendous growth of the Li-ion battery industry underscores the need for novel cathode materials. Not only does the current cathode technology create resource strains on the transition metal elements needed for cathode manufacturing,3 but further improvements in energy density will also require cathode materials that surpass the current Li(Ni,Co,Mn)O2 (NMC) layered cathodes.In 1976, Whittingham demonstrated that transition metal (M)-containing compounds, such as TiS2, can undergo reversible Li intercalation reactions at reasonably high voltages, paving the way to a new class of cathode materials.4 The development of high-voltage stable electrolytes quickly led to the replacement of sulfide cathodes by oxides, as the latter provide higher working voltages, and hence higher energy densities. Nowadays, the great majority of commercial Li-ion cathodes are high-voltage intercalation-type lithium transition metal oxides and phosphates. A commonality between these cathode materials is the ordered arrangement of Li and M species, which provides clear paths for Li+ transport during electrochemical cycling. Olivine-structured transition metal phosphates (LiMPO4) feature one-dimensional diffusion paths for Li with very low Li migration barriers,5 thus providing very high rate capability. Depending on the cation-to-anion ratio, lithium transition metal oxide (LMO) cathodes form either spinel (LiM2O4) structures featuring three-dimensional interconnected pathways for Li+ migration or layered (LiMO2) structures, where Li+ diffusion occurs within the two-dimensional Li slabs.6 LiMn2O4 spinels7 have been commercialized as cathodes but are steadily being replaced by NMC layered cathodes due to these materials’ higher energy density and good stability. While olivine LiFePO4 is employed in commercial Li-ion batteries, its use is mostly limited to low energy density applications, leaving most of the Li-ion market dominated by NMC cathodes.
For decades, cation disorder, whereby the Li and M metals mix on each other's position in the layered or spinel LMO structures, has been considered detrimental to Li+ transport, hence to the reversible capacity of intercalation-type electrodes. While this assumption has proven true in certain cases,8 several recent theoretical and experimental studies have demonstrated the feasibility of disordered rocksalt (DRX) cathodes, that is, LMO cathodes with a disordered arrangement of Li and M on the cation lattice as shown in Fig. 1a9–21 This finding is important as it broadens the chemical space in which cathode materials can be designed. In fact, the main reason why NMC layered cathodes (with the cation ordering shown in Fig. 1b) must use Ni, Co and Mn as majority elements is that these are among the very few transition metals that do not migrate to Li sites when a large amount of Li is removed from the structure upon charge,23 thereby setting the industry up for a Co/Ni resource problem. When the Li-ion battery industry grows to an annual production of 1 TW h, it will require more than a million tons of combined Co/Ni,3 which far surpasses the annual Co production, and makes up about half of the annual Ni production in the world (U.S. Geological Survey 201924).
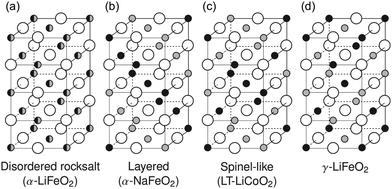 | ||
| Fig. 1 Common rocksalt-type lithium transition metal oxide crystal structures: (a) the disordered rocksalt α-LiFeO2 structure in which all cation sites are equivalent, (b) the layered α-NaFeO2 structure, (c) the spinel-like low-temperature LiCoO2 structure, (d) the γ-LiFeO2 structure. Large empty circles indicate oxygen sites, small gray and black filled circles stand for lithium and transition metal sites, respectively. Adapted with permission from Urban et al.22 Copyright Wiley-VCH. | ||
We note here that layered and DRX LiMO2 compounds crystallize in two variants of the rocksalt (NaCl) structure, where cations and anions occupy octahedral (Oh) sites on two interpenetrating face-centered cubic (FCC) lattices. With a common close-packed oxygen framework, these LiMO2 structures differ in the arrangement of the Li and M species on the cation sites, as shown in Fig. 1. DRX compounds exhibit, in theory, a random arrangement of Li and M, leading to the α-LiFeO2 structure shown in Fig. 1a, while layered compounds exhibit an ordered arrangement of Li and M in alternating planes along the (1 1 1) direction, leading to the α-NaFeO2 structure shown in Fig. 1b. The spinel-like low temperature structure of LiCoO2 and the γ-LiFeO2 structure are two other cation-ordered variants of the NaCl structure shown in Fig. 1c and d, respectively. Criteria for the stabilization of each NaCl variant will be discussed later.
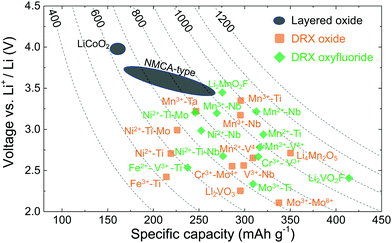
Rather than leading to performance degradation, intrinsic disorder on the cation lattice usually results in small and isotropic volume changes on charge and discharge and can remedy issues related to structural degradation upon cycling. A comparative plot showing the performance of selected cation-disordered and layered LMOs, in terms of average working potential, gravimetric capacity and energy density, is given in Fig. 2. Compared to commercial layered LMO systems, such as NCA-type (with a Li–Ni–Co–Al–O2 composition) and NMC-type (with a Li–Ni–Mn–Co–O2 composition) compounds, or the standard LCO (LiCoO2) cathode, the capacity and energy density of DRXs is at least as good or superior. However, DRXs are not nearly as well optimized as today's commercial cathode materials, and better insight into the relation between chemistry, structure and performance is required in order to create DRX cathodes that are competitive in all respects with (or even outperform) today's cathodes.
The aim of this review paper is to provide an overview of the current understanding of DRX materials, in terms of their structural and compositional characteristics and electrochemical properties. We first examine the characteristic features of DRX cathodes; these insights are used in the second part of the paper to discuss and compare the different classes of DRX compounds that have been synthesized and tested as Li-ion cathodes. Important considerations for the design of high performance DRX cathodes and future research directions are presented in a third part.
I. Cation disorder: impact on the structure and properties of rocksalt-type lithium transition metal oxides
a. What factors govern cation order/disorder in lithium transition metal oxides?
As mentioned earlier, many LiMO2 compounds crystallize in variants of the rocksalt-type crystal structure, as shown in Fig. 1. The optical, magnetic and electronic properties of LiMO2 materials are dictated by the type of Li–M bond formed, which in turn depends on the electronic configuration and size of the M3+ cation.25 Among first row LiMO2 compounds, partially-filled t2g orbitals and t2g–t2g orbital overlap result in d electron itinerancy in LiTiO2 and LixVO2, as revealed by the Pauli paramagnetic behavior of the former and the semiconducting-to-metallic transition within the V planes of the latter, while transition metals to the right of V are characterized by more contracted t2g orbitals, localized d electrons and a semiconducting behavior. LiScO2, with no d valence electrons, is insulating.25Hewston and Chamberland25 first organized LiMO2 structure types according to the size of the M3+ ion relative to that of Li+, which was later rationalized with modeling by Wu et al.26 The formation of a layered α-NaFeO2-type structure (see Fig. 1b) is favorable when the M3+ ion is significantly smaller than Li+ (r(Li+) = 0.76 Å), as in LiCoO2 (r(Co3+) = 0.545 Å),27 LiVO2 (r(V3+) = 0.64 Å),28 LiNiO2 (r(Ni3+) = 0.56 Å),29 and LiCrO2 (r(Cr3+) = 0.615 Å),28 as this structure type allows for independent relaxation of bond lengths in LiO6 and MO6 octahedra. When all cations are of similar size, e.g. in LiScO2 (r(Sc3+) = 0.745 Å), this relaxation effect is less significant and the structure type is governed instead by favorable electrostatics,26 resulting in the formation of the ordered γ-LiFeO2 structure30–32 (see Fig. 1d). Some unique cases in which other structure types form also exist. For instance, the presence of Jahn–Teller distorted Mn3+ ions in LiMnO2 results in the crystallization of a unique low-temperature orthorhombic form33–35 (the high temperature polymorph of LiMnO2 has the α-NaFeO2 layered structure). Another example is the spinel-like LiCoO2 structure (see Fig. 1c), with cations in the 16c and 16d Oh sites of the spinel structure, which does not appear to be an equilibrium structure under any conditions and has only been stabilized in rare cases, typically via low-temperature synthesis routes.36–38 While many metals and metal combinations can form the layered structure type, very few will remain layered when a substantial amount of Li is removed from the compound. Driven by lower electrostatics, many metal cations will migrate into the vacancies created in the Li layer by the charging process. Only metals with very high Oh site preference will have high enough kinetic barriers to prevent disordering of the layered structure upon cycling. Typically, these are metals with filled or half-filled t2g shells, such as Co3+ (low-spin d6), Mn4+ and Cr3+ (high spin d3).23,39 An important consideration for the stability of the layered structure is that the transition metals retain their high Oh site preference upon oxidation, which is true for Ni3+/Ni4+ (d7 to d6) and Co3+/Co4+ (d6 to d5). Hence, the practical compositional space of layered LMOs is by and large limited to Co, Ni and Mn (the latter when it does not undergo reduction from Mn4+). In contrast, one important advantage of making functional cathodes with cation disorder is that it opens up the possibility of using a larger range of transition metal species, and combinations of them.
The cation-disordered structure shown in Fig. 1a is never a ground state but a high-temperature form of the other structure types. The equilibrium temperature at which a structure disorders is controlled by the balance of entropy (TS) and energy change (E) associated with the disorder. While the entropy increase caused by a given level of disorder is chemistry-independent, the energy increase is not, and depends on the ability of the system to accommodate that disorder. Hence, disorder can be promoted by high temperature (which multiplies S), by low energy cost for disorder, or by both. This principle has been demonstrated in an earlier work by Wolverton et al.,40 who showed, for example, that the hypothetical disordering temperature for LiCoO2 is over 5000 K, because the energy cost for accommodating Co3+ in the deformed octahedra that arise from cation disorder is very high.
Two first principles studies by Urban et al.41 and Richards et al.42 evaluated the propensity of various LMO compositions to form a cation-disordered structure (Fig. 1a) and identified Ti-containing oxides as potential DRX candidates due to their low disordering energies. Experimentally, cation-disordered LiTiO2 has been synthesized8,25 and a large number of Ti4+-containing DRX oxides43–54 have been both successfully synthesized and electrochemically tested in Li-ion cells, with Li2−xVTiO4 exhibiting >300 mA h g−1 of reversible capacity.55 Urban's study was later extended to more broadly understand the elements that help stabilize cation disorder at low enough temperature to be synthetically accessible.56 In stark contrast to metallic alloys, which only form a solid-solution when the species of interest have similar electronegativities and atomic radii (<15% difference), DRX oxides composed of cations with large ionic radius and charge differences, e.g. Li+/Mo6+,9,14–17 Li+/Nb5+,13,18,19,57–59 or Li+/Ti4+,44–46,48,50,51,53–55 are commonly observed, suggesting that the physics of disorder is driven by considerations other than ionic size in rocksalt-based materials. Urban et al.56 suggested that the ability to accommodate disorder is controlled by the d-level orbital occupancy in transition metals. When cations are randomly distributed over the Oh sites of a rocksalt structure, their different sizes and valences create octahedral distortions. Because octahedra in rocksalts are edge sharing, these distortions must be accommodated in part by neighboring octahedra. Hence, the ability for a structure to cation disorder reflects the energy cost to distort the octahedra around the various cations. With no valence electrons, Li+ has no crystal field stabilization energy, and therefore no particular octahedral shape preference. The propensity of a given LMO to disorder can therefore be predicted solely from the d shell filling of the transition metals, as each filled orbital imposes a particular preferred octahedral distortion mode. Using density functional theory (DFT), Urban et al.56 evaluated the energy cost of all M3+O6 octahedral distortion modes in LiMO2 compounds and concluded that elements with no d electrons can accommodate octahedral variations at the lowest energy cost. Perhaps unsurprisingly, the band energy of d0 metals solely depends on lower-lying oxygen-dominated orbitals that are always occupied and is largely insensitive to site distortions. Hence, transition metals with no valence d electrons can best stabilize disordered rocksalt phases even when ionic radius differences between the cation species are relatively large.56 This finding relates the physics of DRX materials to that of ferroelectrics, where d0 elements (e.g. Ti4+ or Nb5+) are often the critical elements that create electric dipoles in a composition due to their ability to displace from the center of the octahedron at a low energy cost.
Simulations of disordered structures in mixed transition metal systems showed that the presence of at least one d0 species can help stabilize the disordered structure, as the d0 ions (M and Li+) occupy the distorted Oh sites, leaving the less distorted cation sites for species with d valence electrons.56 These electronic structure insights help rationalize why LMOs containing at least one redox-inactive d0 element account for the overwhelming majority of DRXs reported to date, with Ti4+, V5+, Nb5+, and Mo6+ being the most commonly encountered d0 species.9,10,13–19,44–46,48,50,53–55,57–62 This model, however, does not explain why certain DRX materials with no d0 M species are stable,8,63–65 a topic covered in the second part of this review.
While cation disorder can be created at reasonable synthesis temperatures in many DRX compounds, for some compositions, disorder cannot be accessed thermally and instead requires extensive ball-milling. While the relation between the mechanical forces that induce disorder in ball-milling and entropy are unclear, the high energy ball-milling process has been related to an “equivalent” synthesis temperature of ≈1750 °C on a purely empirical basis.66 To more systematically design DRX materials and their synthesis route, a better mechanistic understanding of the milling process is required.67,68
The discovery of DRXs as candidate Li-ion cathode materials enables the use of a large range of 3d and 4d metals, including those species which, in layered LMOs, are prone to migrate from the transition metal layers to octahedral (Oh) and tetrahedral (Td) sites in the interlayer space during electrochemical cycling and impede Li+ diffusion. The natural abundance and metal price of selected transition metal species present in DRX compounds reported to date is shown in Fig. 3. It is clear from this figure that rocksalt cathodes based on Earth-abundant Mn, Fe and Ti hold promise in terms of sustainability and cost.
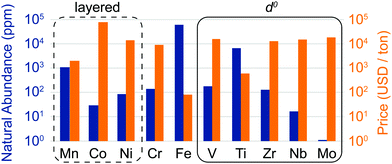 | ||
| Fig. 3 Natural abundance (blue bars) and price (orange bars) of selected 3d and 4d transition metal elements found in disordered lithium transition metal oxide cathodes (on a log scale). The metal prices for V, Ti, Nb and Mo were obtained from the prices of their metal oxides, by accounting for the weight fraction of the transition metal element. The oxide precursor cost is more relevant for cathode production, and for some metals, such as Ti, the oxide precursor price is considerably lower than the metal price due to the high cost of extracting the metal from the oxide. However, it is difficult to obtain consistent data for the relevant ores, which is why we have listed the metal price directly obtained from our sources for Mn, Co, Ni, Cr, Fe and Zr. The compositional space of layered oxides is enclosed in a dashed black rectangle, while d0 species favoring cation disorder (V5+, Ti4+, Zr4+, Nb5+ and Mo6+) are enclosed in a solid black rectangle. Sources: http://www.webelements.com; http://www.metalary.com (accessed Aug. 2019); U.S. Geological Survey 2019.24 | ||
Disordering cations results in properties that are radically different from those of ordered cathode compounds, representing both challenges and opportunities for their application in batteries. These typically include a modified diffusion process, smaller and isotropic lattice expansion, easier anion redox, a more sloped voltage profile, and the ability for large compositional variety, including oxygen to fluorine substitution. Each of these topics is discussed in turn.
b. Consequences of cation disorder on Li+ mobility and Li percolation
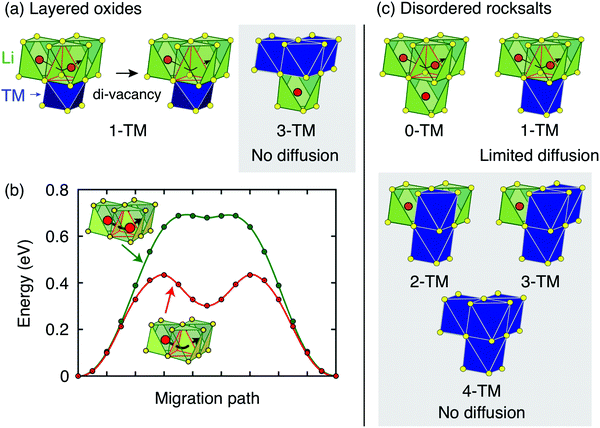 | ||
| Fig. 4 Li+ diffusion between neighboring Oh sites in rocksalt-type LixMO2 takes place via an intermediate Td site (o–t–o diffusion). (a) Layered LixMO2 compounds exhibit 1-TM and 3-TM Td sites, corresponding to Li3M and LiM3 clusters, respectively. 1-TM channels are responsible for Li+ diffusion. (b) Li migration barriers for hops between neighboring Oh sites in layered LixMO2 are very sensitive to the occupancy of sites adjacent to the intermediate Td site of the hop. The barrier for hops into isolated vacancies is significantly larger than for di-vacancy hops. Adapted with permission from Van der Ven et al.6 Copyright 2013 American Chemical Society. (c) Cation disorder results in the formation of all types of tetrahedral clusters (0-TM, 1-TM, 2-TM, 3-TM and 4-TM channels). In this case, 0-TM channels (and, to some extent, 1-TM channels) are responsible for Li+ conduction. | ||
i.i. Layered lithium transition metal oxides and other ordered structures. Cation ordering in stoichiometric layered LiMO2 and Li-rich layered Li1+xM1−xO2 results in the formation of LiM3 clusters (3-TM channels) in the transition metal slabs, which are not involved in Li+ diffusion, and Li3M clusters (1-TM channels) in the Li slabs, which support Li migration (see Fig. 4a). The size of the activated Td site is controlled by the layer spacing of the Li slab,72,73 which is primarily determined by the Li content in the layers,6 does not vary significantly with the nature of the M species, and typically lies in the range of 2.6–2.7 Å for LiMO2 compositions.22 When Li+ is extracted on charge, face-sharing octahedral sites initially occupied by Li in 1-TM channels are progressively emptied. Typical migration barriers computed for a 1-TM channel with a single Li vacancy and a di-vacancy are shown in Fig. 4b. The single vacancy hop results in strong Coulombic interactions between Li+ in the activated site and Li+ in the face-sharing octahedral site. On the other hand, the di-vacancy hop has no such repulsion and the Li+ diffusion barrier is lower than for hops into isolated vacancies.6 Upon charge, the activation energy for o–t–o diffusion is modified by two oppositely acting mechanisms. The increase in the oxidation state of transition metals in gate sites increases the electrostatic interaction with the migrating Li+ ion, but an increase in slab spacing at the beginning of charge counteracts this by allowing the distance between Li+ in the Td site and the gate metals to remain larger. Typically, for 0.5 ≲ x <1 in LixMO2, this leads to an increase in Li diffusivity with charge. For x ≲ 0.5 the layer spacing decreases with charge, causing an increase in the activation barrier. At very low Li content, the slab spacing contracts due to increased hybridization and van der Waals interactions between the oxygens across the slab, leading to an abrupt increase in the Li+ migration barriers.6 This geometric change is observed for all layered oxides, although the extent to which it influences Li diffusivity depends somewhat on the nature of the transition metal species and type of bonding to oxygen, which in turn determines how much the oxygen can hybridize across the empty slab. To a good approximation, Li+ diffusion is dominated by a di-vacancy mechanism at all practical Li concentrations in layered LixMO2 compounds.6 This results in a Li+ diffusion coefficient that depends on the overall concentration of Li in the material; this dependence is particularly pronounced at high Li concentrations, where the vacancy concentration is low.6 In fact, at x ≈ 1, the di-vacancy mechanism is activated by a finite number of intrinsic vacancy defects always present in these materials.69
The ability to diffuse Li in other ordered rocksalts can be analyzed in a similar way. For example, the reason that the low temperature γ-LiFeO2 structure shows no reversible Li deintercalation is because it only contains 2-TM tetrahedral environments making Li migration extremely high in energy. Spinel-type ordering leads to segregation into 0-TM, 2-TM and 4-TM environments, consistent with its good Li diffusivity.22
i.ii. Disordered rocksalts (DRX). If only the 1-TM diffusion mechanism typical of layered oxides were considered, Li+ mobility would be expected to be negligible in DRX compounds, due to the significant reduction of the slab spacing and size of the Td site upon cation mixing. Yet, this analysis does not account for other types of clusters forming on disordering, as shown in Fig. 4c. In 0-TM channels, for instance, the absence of transition metals in face-sharing octahedra leads to a reduction of the electrostatic repulsion in the activated Li site. As a result, while disordering causes Li+ diffusion via 1-TM channels to become poor, it also forms active 0-TM channels. 0-TM and 1-TM migration barriers computed from first principles in model disordered Li2MoO3 and LiCrO2 structures are shown in Fig. 5 and indicate that, while the 0-TM barrier does not exceed 300 meV even for a small average tetrahedron height (e.g., 2.35 Å), ca. 500 meV migration barriers are obtained for 1-TM jumps,9 much larger than the typical ca. 300 meV barriers in layered oxides.72 Furthermore, Li extraction from nearest-neighbor octahedral sites during charge leads to a progressive decrease in the 0-TM Td site energy, eventually stabilizing Td Li once all face-sharing octahedral Li sites are empty. The relatively low barrier for Li migration between two 0-TM Td sites, ca. 415 meV,9 indicates that Li can escape the Td sites created at the end of charge and Td Li formation has little impact on the overall Li+ diffusion rate.
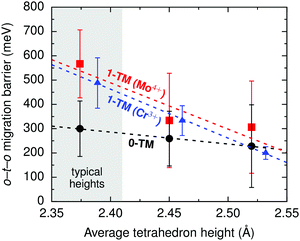 | ||
| Fig. 5 Calculated Li migration barriers along 1-TM channels (red squares: one Mo4+ neighbor; blue triangles: one Cr3+ neighbor), and along 0-TM channels (black circles) as a function of the average tetrahedron height in model disordered Li2MoO3 and LiCrO2 structures. Error bars represent standard deviations and the shaded area highlights the typical range of tetrahedron heights in disordered materials. From Lee et al.9 Reprinted with permission from AAAS. | ||
In summary, microscopic o–t–o Li+ diffusion in layered LixMO2 compounds proceeds via a Li di-vacancy mechanism and relies on 1-TM channels with a Li+ diffusion coefficient determined by the Li slab spacing and the oxidation state of the transition metal face-sharing with Li+ in the activated site. In contrast, Li+ migration in DRX compounds is primarily mediated by 0-TM channels with a diffusion barrier that is almost independent of the average tetrahedron height and the transition metal composition.22 We note that the Li+ diffusion mechanisms identified in bulk DRX cathodes can also provide insight into cation migration through the disordered surface phases that form on a number of layered LixMO2 compounds at high voltage and how this disorder impacts the electrochemical performance.
In summary, whether a given rocksalt-type LMO structure is percolating to Li depends on: (1) the distribution of Li4, Li3M, Li2M2, LiM3 and M4 tetrahedral clusters (equivalently, the distribution of 0-, 1-, 2-, 3- and 4-TM channels) in the structure, which depends on the degree of cation disorder, the type of (short-range) order present, if any, and the Li to M ratio, and (2) the connectivity of open (low Li+ migration barrier) diffusion channels.
In stoichiometric, layered LiMO2, for instance, all Li sites are connected via 1-TM channels with low Li+ migration barriers and form a percolating network enabling two-dimensional Li+ conduction within the Li slabs. Macroscopic Li+ diffusion paths are less obvious in a cation-disordered structure, which explains why DRXs have long been considered electrochemically inactive and were only recently found to be percolating under certain conditions.9,22
Using Monte Carlo simulations, Urban et al.22 investigated the impact of cation disorder and Li content x on Li percolation via only 0-TM channels in LixM2−xO2 (0 ≤ x ≤ 2) structures. Since the number of Li4 clusters increases with x, regardless of the degree of cation disorder, a percolating network of 0-TM channels is formed at a critical Li concentration xC. The graphs in Fig. 6 depict the level of Li excess corresponding to the threshold for (1) Li to percolate through the structure via the network of 0-TM channels, and (2) one Li per formula unit (1 Li per f.u.) to be accessible via 0-TM channels as a function of cation mixing in layered (α-NaFeO2), spinel-like (LT-LiCoO2) and γ-LiFeO2 structures. Fig. 6a and c clearly show that the spinel-like structure has the best 0-TM percolation properties, with low critical Li concentrations for percolation (xC = 0.77) and for access to 1 Li per f.u. (xC = 1.016); this can be explained by the segregation of 0-TM channels in the structure.22 A steady increase in the Li concentration thresholds is observed upon increasing cation disorder in the spinel-like structure, and the critical Li excess levels reach values of xC = 1.092 for 0-TM percolation and xC = 1.257 for access to 1 Li per f.u. in the fully random limit. For the layered structure, the critical lithium concentration for 0-TM percolation is maximal in the fully ordered structure, with a value xC,max = 1.14, and reaches a minimum at ca. 50% cation mixing, xC,min = 1.05, due to the formation of 0-TM channels, before increasing again slightly upon further disordering. The lithium concentration threshold required for access to 1 Li per f.u., xC = 1.233 in the ordered structure, reaches a minimum xC,min = 1.22 for 24% cation disorder.22 The γ-LiFeO2 structure only possesses 2-TM channels, leading to very poor percolation properties with Li concentration thresholds xC = 1.33 for 0-TM percolation and xC = 1.417 for access to 1 Li per f.u. With the formation of 0-TM channels, a steady decrease in the percolation thresholds is observed on cation disordering. As expected, the fully disordered limit is common to all three structure-types and corresponds to a normal distribution of Li4, Li3M, Li2M2, Li3M and M4 clusters based on the Li/M ratio in the material.
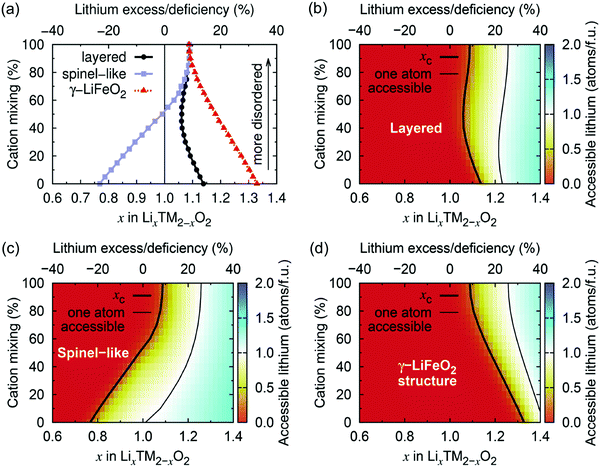 | ||
| Fig. 6 (a) Critical lithium concentrations (xC) for 0-TM Li percolation, and (b–d) for one Li per formula unit (1 Li per f.u.) to be accessible via 0-TM channels as a function of the overall lithium content and the degree of cation mixing in LixM2−xO2 compounds with the layered (α-NaFeO2), spinel-like (LT-LiCoO2) and γ-LiFeO2 structure. Structure-specific xC values are indicated by a thick black contour line. Compositions falling to the left of these contour lines are not 0-TM percolating. Thin lines indicate the compositions at which 1 Li per f.u. becomes 0-TM accessible. Adapted with permission from Urban et al.22 Copyright Wiley-VCH. | ||
Urban et al.'s study22 demonstrates that, even in the fully disordered limit, rocksalt-type LMOs can sustain long-range 0-TM Li+ diffusion as long as Li is present in excess (Li/M > 1). Only 10% Li excess is needed for Li percolation, and approximately 26% Li excess is required to extract 1 Li per f.u. It is important to maintain relatively low Li excess levels in these materials, as too high a Li/M ratio results in limited transition metal redox capacity, which negatively impacts the energy density of the cathode and the overall reversibility of the charge compensation mechanisms during cycling,22 as will be discussed in Section d. We note that, while the results reported here describe Li+ diffusion supported by 0-TM channels only, in reality, Li+ migration may occasionally involve 1-TM channels for which the tetrahedron height is sufficiently large (2-TM channels have very high migration barriers and are never involved in macroscopic Li+ diffusion), hence the percolation thresholds in Fig. 6 are likely overestimated.
Kan et al.75 showed that SRO in LixNb0.3Mn0.4O2, with the formation of thermodynamically favorable Nb-rich O sites (i.e. ONb6 and ONb5Mn configurations), perturbs the otherwise percolating Li+ diffusion network of the disordered structure. Jones et al.80 investigated cation SRO in a similar material, Li1.25Nb0.25Mn0.5O2, using a range of experimental techniques and comparing samples prepared via solid-state reactions at different cooling rates. For all samples, low intensity superstructure reflections present in the X-ray diffraction (XRD) patterns shown in Fig. 8a and b could be accounted for by short-range ordering of the Li, Nb and Mn species akin to the γ-LiFeO2 structure (see Fig. 1d), with a correlation length of ca. 125 Å for slow-cooled and 30 Å for rapidly-cooled samples. However, the appearance of superstructure reflections and the long correlation length in the slowly-cooled samples is more likely a reflection of small ordered domains. The presence of SRO was confirmed by pair distribution function analysis of neutron diffraction data collected on the slow-cooled sample, while both magnetic susceptibility and 7Li nuclear magnetic resonance (NMR) measurements on both samples indicated different distributions of Li, Nb, Mn among cation sites in the structure, with a more ordered arrangement forming on slow cooling. Compared to the broad, featureless 7Li NMR data obtained on the rapidly-cooled sample (the sharp signal at ca. 0 ppm is likely due to diamagnetic Li2O or Li2CO3), the reduced range of local Li environments in the more ordered, slow-cooled structure gives rise to distinct features around 240 and 70 ppm in the 7Li NMR data shown in Fig. 7c. Jones et al.80 rationalized the formation of small ordered domains within the disordered structure by a general tendency towards local electroneutrality, whereby OLi3Mn3 and OLi4NbMn clusters form preferentially, resulting in a local γ-LiFeO2-like local arrangement of cations. Unsurprisingly, the more ordered, slow-cooled sample suffers from greater voltage fade and poorer capacity retention than the more disordered, rapidly-cooled sample, consistent with the presence of only 2-TM channels in γ-LiFeO2-like domains, leading to higher average Li+ diffusion barriers in the former sample.80 In this study, the authors did not mention particle size effects, but slow cooling may presumably lead to the formation of larger particles than rapid cooling, increasing the diffusion length of Li+ and contributing to the more rapid performance degradation.
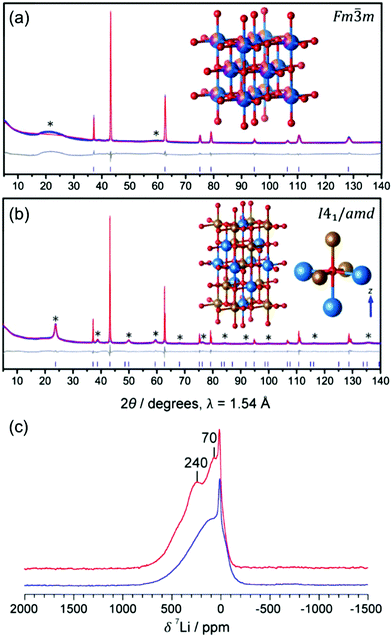 | ||
Fig. 7 Experimental evidence for small ordered domains in the Li1.25Nb0.25Mn0.5O2 DRX. Powder XRD patterns collected on (a) rapidly-cooled and (b) slow-cooled Li1.25Nb0.25Mn0.5O2. The Rietveld refinement for the rapidly-cooled sample (in (a)) yields a DRX Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m unit cell with a = 4.19551(7) Å, and a statistical distribution of Li (blue), Nb (orange) and Mn (purple) on the metal site. The Rietveld refinement for the slow-cooled sample (in (b)) yields a body centered tetragonal unit cell with a′ = b′ = ars, and c′ = 2ars, with space group I41/amd and ars = 4.18651(1) Å, the space group of γ-LiFeO2 (shown in the inset). (c) 7Li pj-MATPASS81 spectra of rapidly-cooled (blue) and slow-cooled (red) samples of Li1.25Nb0.25Mn0.5O2, scaled by sample mass and number of scans. The pj-MATPASS pulse sequence is used to separate the isotropic resonance from the sideband manifold. Figures adapted from Jones et al.80 with permission from the Royal Society of Chemistry. m unit cell with a = 4.19551(7) Å, and a statistical distribution of Li (blue), Nb (orange) and Mn (purple) on the metal site. The Rietveld refinement for the slow-cooled sample (in (b)) yields a body centered tetragonal unit cell with a′ = b′ = ars, and c′ = 2ars, with space group I41/amd and ars = 4.18651(1) Å, the space group of γ-LiFeO2 (shown in the inset). (c) 7Li pj-MATPASS81 spectra of rapidly-cooled (blue) and slow-cooled (red) samples of Li1.25Nb0.25Mn0.5O2, scaled by sample mass and number of scans. The pj-MATPASS pulse sequence is used to separate the isotropic resonance from the sideband manifold. Figures adapted from Jones et al.80 with permission from the Royal Society of Chemistry. | ||
Ji et al.21 were able to explain the very different performance of Li1.2Mn0.4Ti0.4O2 and Li1.2Mn0.4Zr0.4O2 by characterizing the different SRO in these cathodes. These two compounds have the same Li and Mn content and a similar concentration of high-valent d0 cations (Ti4+ and Zr4+). However, while 0.79 Li per formula unit can be reversibly extracted from/inserted into Li1.2Mn0.4Ti0.4O2 at room temperature, this value goes down to approximately 0.52 Li per formula unit for Li1.2Mn0.4Zr0.4O2 under similar conditions, as shown by the black electrochemical curves in the bottom and top panels of Fig. 8a, respectively. The 54% increase in reversible capacity observed for Li1.2Mn0.4Zr0.4O2 at 50 °C (red curve in Fig. 8a, top panel) clearly suggests that its room temperature capacity is limited by Li+ transport kinetics. On the other hand, Li1.2Mn0.4Ti0.4O2 is less affected by sluggish Li+ conduction, and a 27% increase in capacity is observed on cycling at 50 °C (red curve in Fig. 8a, bottom panel).21 As shown in Fig. 8b, electron diffraction patterns, together with neutron pair distribution function analysis and Monte Carlo simulations, indicate the presence of different levels and types of SRO in the two as-synthesized compounds, with SRO particularly pronounced in Li1.2Mn0.4Zr0.4O2.21,82 The distribution of tetrahedral clusters in Li1.2Mn0.4Ti0.4O2 and Li1.2Mn0.4Zr0.4O2, derived from Monte Carlo simulations at 1000 °C, is plotted in Fig. 8c. Both materials exhibit fewer 0-TM channels (Li4 clusters) than the fully disordered structure, with Li1.2Mn0.4Zr0.4O2 having the lowest number of Li4 clusters. Concurrently, there are more 1-TM channels (or Li3M clusters) in Li1.2Mn0.4Zr0.4O2 (31% of all cation tetrahedra) than in Li1.2Mn0.4Ti0.4O2 (22%) or in the random limit (17%), likely due to the large 1-TM/0-TM ratio in Li1.2Mn0.4Zr0.4O2. As a consequence, there are very few Li sites connected via 0-TM channels in Li1.2Mn0.4Zr0.4O2 compared to in Li1.2Mn0.4Ti0.4O2, and in both cases the Li connectivity is worse than in the random limit based on Monte Carlo structures representative of the two compounds (see Fig. 8d).21 The resulting low number of connected Li likely contribute to the poor Li transport kinetics in Li1.2Mn0.4Zr0.4O2. Overall, Ji et al.'s study21 indicates that, for Li1.2Mn0.4Zr0.4O2 and Li1.2Mn0.4Ti0.4O2, SRO has a clear impact on Li diffusivity which in turn impacts the rate capability. However, the influence of SRO on rate performance deserves to be investigated in more detail for a range of DRX cathodes.
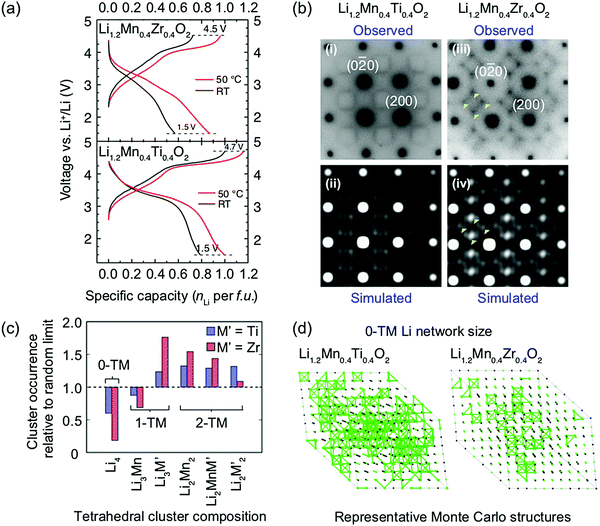 | ||
Fig. 8 (a) Comparison of room temperature and 50 °C galvanostatic cycling data for Li1.2Mn0.4Zr0.4O2 (top panel) and Li1.2Mn0.4Ti0.4O2 (bottom panel). (b) Electron diffraction patterns of (i) Li1.2Mn0.4Ti0.4O2 and (iii) Li1.2Mn0.4Zr0.4O2 along the [100] zone axis. The round spots are indexed to the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group, while the diffuse scattering patterns around the spots are attributed to SRO. Several intensity maxima in the diffuse scattering pattern of Li1.2Mn0.4Zr0.4O2 are highlighted with yellow arrows. Simulations of electron diffraction patterns for (ii) Li1.2Mn0.4Ti0.4O2 and (iv) Li1.2Mn0.4Zr0.4O2 along the same zone axis are consistent with experimental observations. (c) Occurrence of various tetrahedron clusters (0-TM, 1-TM, 2-TM) in Li1.2Mn0.4Ti0.4O2 (blue) and Li1.2Mn0.4Zr0.4O2 (red), as compared to the random limit (dotted line). The analysis is based on structures derived from Monte Carlo simulations at 1000 °C. (d) Representative Monte Carlo structures for Li1.2Mn0.4Ti0.4O2 and Li1.2Mn0.4Zr0.4O2. Li+ ions are labeled with green spheres and 0-TM connected Li sites are bridged with green bonds.21 Figures adapted from Ji et al.21 under the Creative Commons CC BY license. m space group, while the diffuse scattering patterns around the spots are attributed to SRO. Several intensity maxima in the diffuse scattering pattern of Li1.2Mn0.4Zr0.4O2 are highlighted with yellow arrows. Simulations of electron diffraction patterns for (ii) Li1.2Mn0.4Ti0.4O2 and (iv) Li1.2Mn0.4Zr0.4O2 along the same zone axis are consistent with experimental observations. (c) Occurrence of various tetrahedron clusters (0-TM, 1-TM, 2-TM) in Li1.2Mn0.4Ti0.4O2 (blue) and Li1.2Mn0.4Zr0.4O2 (red), as compared to the random limit (dotted line). The analysis is based on structures derived from Monte Carlo simulations at 1000 °C. (d) Representative Monte Carlo structures for Li1.2Mn0.4Ti0.4O2 and Li1.2Mn0.4Zr0.4O2. Li+ ions are labeled with green spheres and 0-TM connected Li sites are bridged with green bonds.21 Figures adapted from Ji et al.21 under the Creative Commons CC BY license. | ||
All studies discussed above reveal that, rather than exhibiting a purely random arrangement of cations, DRX structures may exhibit some degree of SRO, and this SRO can be manipulated to modify the transport properties. While it may seem that the random limit would be the ideal state of cation disorder, this is not necessarily the case, as SRO of the low temperature LiCoO2 spinel structure-type will actually increase the fraction of 0-TM channels as compared to a statistical distribution of cation species. To our knowledge, spinel-type SRO has not been observed yet in any DRX, which may be due to either the small number of investigations performed so far or the fact that the spinel structure is never really the lowest energy ground state for a compound with a 1–1 metal (Li+ and M) to anion ratio.
Just as the ground state ordered structure of a given LixMO2 compound is dictated by the nature of the transition metal species, SRO and Li site connectivity in DRXs depend on chemistry. Generally speaking, segregation of Li+ and M ions into separate tetrahedra (i.e., Li4 and M4) is ideal to create a high number of interconnected 0-TM channels. Ji et al.21 used DFT with a cluster expansion method to model SRO in a variety of Li1.2M′aM′′bO2 structures (where M′ = Mn2+, Mn3+, V3+, Co2+, Ni2+ and d0 M′′ = Ti4+, Zr4+, Nb5+ and Mo6+) and computed the fraction of Li accessible through a percolating network of active diffusion channels. The authors rationalized SRO on the basis of charge and size effects. For Li1.2M′aM′′bO2 with a trivalent M′ element and small M′′ ions (e.g. Li1.2Mn0.4Ti0.4O2), size effects dominate and lead to Li segregation and the formation of tetrahedral Li4 clusters supporting long-range Li+ diffusion. For Li1.2M′aM′′bO2 with a trivalent M′ element and large M′′ ions (e.g. Li1.2Mn0.4Zr0.4O2), electrostatic effects dominate, favoring maximal separation between the M′′ cations and mixing with Li, leading to poor Li percolation.21 Li1.2M′aM′′bO2 with a divalent M′ element form a unique class of compounds: divalent M′ ions have the proper metal valence to provide electroneutrality in the oxide framework without needing to mix with Li+.21 Consequently, compounds with a divalent M′ form more 0-TM channels and the accessible Li content is typically larger than Li1.2M′aM′′bO2 DRXs containing trivalent M′ ions.21 In summary, the average ionic radius of the high-valent d0 M′′ is important in determining the degree of Li segregation into percolating tetrahedral Li4 clusters, small M′′ metals (Ti4+, Nb5+, and Mo6+) leading to more favorable percolation properties than larger metals (Zr4+, Sc3+, In3+).21 For the choice of redox-active M′, divalent M′ ions favor Li4 formation and long-range Li+ diffusion to a greater extent than trivalent M′ ions.21
To illustrate the important points raised in this and the previous section, the factors determining whether a DRX Li1+xM′1−x−yM′′yO2 structure is stabilized and whether the structure is percolating to Li are summarized in Fig. 9.
c. Effect of cation disorder on the voltage profile
By changing the distribution of local environments of Li and redox active species, cation disorder has a direct effect on the average potential and the shape of the voltage vs. capacity curve, two important properties determining the energy density of the cathode. Few studies have investigated the effect of disorder on the average voltage. Using a simplified model, Saubanère et al.83 argued that the average voltage should increase upon disordering. While this was found to be mostly true in more accurate DFT calculations performed on the LiMO2 stoichiometry, a small decrease in the average potential upon disordering was observed for V and Cr systems.84 A detailed study on more realistic DRX compounds has not yet been performed.Experimentally, a decrease in the average voltage upon cation disordering has been observed in Cr-containing oxides such as LiCrO2,85 NaCrO286 and Li1.211Mo0.467Cr0.3O2.9 This can be leveraged to access more Cr-based capacity at moderate potentials: in disordered Li1.211Mo0.467Cr0.3O2, Cr3+/4+ oxidation dominates at high potentials, with little competing O redox and O loss.9 On the other hand, the increase in the average potential of Ni-containing compounds upon cation mixing is problematic because it prevents full oxidation to Ni4+ when combined with a lowered anion redox potential (discussed later). This phenomenon is evidenced by the strong overlap between Ni and O oxidation processes in, e.g., cation-disordered Li–Ni–Ti–Mo–O systems. This strong overlap between Ni and O processes results in O redox and some O loss at high voltage and in limited use of the Ni redox reservoir on cycling, with a maximum Ni oxidation state of only approximately 3.5+ at the end of charge.14,87
The slope of the electrochemical profile is another important feature of DRX materials, as it can control the accessible capacity. For ordered compounds, the voltage slope is controlled by the effective alkali–alkali interaction.88 For Li-containing layered oxides, strong screening of this Coulombic interaction by oxygen leads to only moderate slope,89 and for layered cathodes most of the capacity is delivered within a ≈1 V voltage window. In cation-disordered materials, variations in the Li+ and M site energies (due to the large number of Li and M local environments in the material) add to this interaction-determined effect to create larger voltage slopes. While theoretical work by Abdellahi et al.90 reveals that the voltage slope of first-row disordered LiMO2 is indeed much larger than that of their layered counterparts, as shown qualitatively in Fig. 10a, significant variations have been found with chemistry.90 While the origin of this variability has not been investigated in detail, it may be related to the difference in screening power of oxygen when bonded to different metals and to the sensitivity of a transition metal's redox voltage to Oh site distortions.
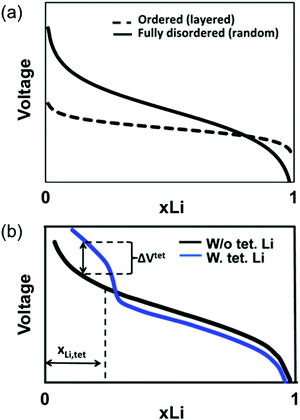 | ||
| Fig. 10 Qualitative diagrams illustrating the factors contributing to the increase in the voltage slope of lithium transition metal oxides on cation disordering. (a) The range of Li environments present in the material leads to a variety of Li extraction potentials at any given state of charge and hence to an increased voltage slope. (b) The possible migration of Li to stable Td sites in 0-TM channels on Li extraction (when all face-sharing Oh sites are vacant) leads to a voltage increase at the end of charge, also resulting in a steeper voltage slope. Adapted with permission from Abdellahi et al.90 Copyright 2016 American Chemical Society. | ||
One effect that is likely to contribute significantly to the voltage slope is the formation of Td Li near the end of charge. While Td Li site formation is not possible in layered LiMO2 (Td sites are destabilized by the presence of at least one M nearest neighbor), in disordered compounds, Li can migrate to 0-TM Td sites on charge. Increasing the Li excess level also increases the proportion of 0-TM channels in the as-synthesized material, leading to a greater number of available Td sites on Li deintercalation.90 As shown qualitatively in Fig. 10b, at the beginning of charge, Li migration from higher energy Oh to lower energy Td sites lowers the overall energy needed to extract Li and hence decreases the extraction voltage. At the end of charge, stabilized Td Li is extracted at a higher potential than Oh Li, leading to a high-voltage region in the electrochemical profile, as was observed for LiNi0.5Mn0.5O2 (with a small amount of Li/Ni mixing) above 4.6 V.91 The additional voltage increase due to Td site formation at the end of charge can render inaccessible up to 25% of the material's capacity if combined with late transition metals, requiring high potentials outside of the stability window of common electrolytes (>4.5 V).90
As discussed in the previous section, all DRXs exhibit some amount of SRO, resulting in an observed voltage profile lying somewhere between the limiting ordered and disordered cases. Hence, changes to the voltage profile of real DRXs are not as severe as Fig. 10a and b suggest. For high-voltage transition metals, for example, some of the inaccessible capacity (Li extraction > 4.5 V) predicted for the fully disordered structure can be recovered if SRO is present. Similarly, a reduced fraction of stable Td Li sites is expected at the end of charge in a short-range ordered structure compared to a fully disordered one.
Reducing the voltage slope of DRX materials is a key opportunity for these materials, as it will further increase their energy density by making high voltage capacity available and by raising the energy content of the capacity that is currently delivered at low voltage. While anion screening plays a role in reducing voltage slope, SRO is likely the most important factor governing the shape of the voltage curve, as well as the average potential of the cathode, and leads to electrochemical characteristics somewhere between those of the ordered and fully disordered structures. Thus, a thorough understanding of the tendency towards local cation ordering in DRX is crucial to understanding Li+ transport and the electrochemical properties of this class of materials.
Finally, because O redox (and O loss) mechanisms often show poor reversibility, M species with a relatively low potential in the disordered state, e.g. Cr, Mn, Co and Fe, are preferred.84
d. Oxygen-based charge compensation mechanisms
The traditional picture of charge compensation mechanisms in LMOs associates Li+ extraction with M oxidation during charge. Yet, in recent years, a number of theoretical and experimental studies have suggested that there are many instances where this picture is incomplete, and O species may also participate in the redox processes, particularly in Li-excess16,92–108 and/or cation-disordered13,14,18,54,57,63,65,87 compounds. A significant research effort is currently targeted at investigating the oxygen charge compensation mechanisms,109–117 motivated by the prospect of very high energy density cathodes with a capacity greatly exceeding the theoretical M redox capacity. However, anion redox, while creating high initial capacities, seems to lead to rapid capacity fade,14,19,57,118 and understanding how to either suppress it or stabilize it are important research directions.The sequence of redox processes taking place during electrochemical cycling of an LMO cathode depends on the relative energy of the M and O states (see Fig. 11e and f),119,120 which is determined by the nature of the M species and the chemical bonding environment of the redox-active elements.115,116,121,122 Since Li excess and cation disorder result in a distribution of local environments in the structure, both parameters can in theory be used to tune the accessibility of M- and O-based charge compensation processes at different stages of charge.
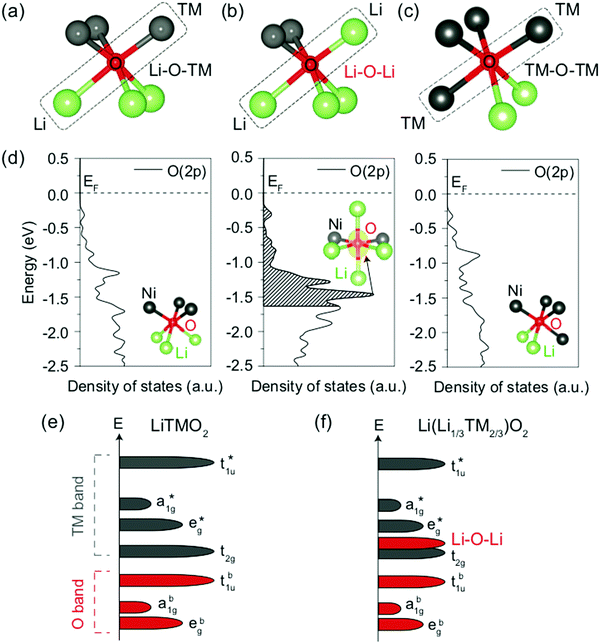 | ||
| Fig. 11 (a–c) Local atomic configuration around O in Li-excess layered or cation-disordered LMOs. The O coordinated to three Li and three M depicted in (a) is the single anion site observed in layered LiMO2 compounds. (d) Projected density of states (pDOS) of the O 2p orbitals for the three different types of O local environments depicted in (a–c), computed in cation-mixed layered LiNiO2. Specifically, O coordinated to three Li and three Ni (left panel), four Li and two Ni (middle panel) and two Li and four Ni (right panel). The insets show the local coordination of the O anion. The isosurface of the charge density (yellow) around the O coordinated to four Li and two Ni is shown in the energy range of 0 to −1.64 eV, corresponding to the extraction of one electron per formula unit. (e and f) Schematics of the band structures of layered LiMO2 compounds (e) and Li-excess layered or cation-disordered LMOs (f). Adapted by permission from Springer Nature: Seo et al.,122 copyright 2016. | ||
A first principles study by Seo et al.122 investigated the origin of O redox processes in Li-excess LMOs. In purely ionic compounds, such as Li2O, O oxidation takes place just above 3 V.123 In stoichiometric layered LiMO2 compounds, all O are bonded to three Li and three M such that each O 2p orbital hybridizes with a M orbital (see Fig. 11a). This hybridization lowers the filled O states and provides them with remarkable protection against oxidation. In contrast, several different O coordination environments are present in Li excess and/or DRX (see Fig. 11b and c), resulting in three types of O 2p orbitals along Li–O–M, Li–O–Li and M–O–M configurations. The projected DOS (pDOS) of O ions in the various types of local environments depicted in Fig. 11a–c, computed on layered LiNiO2 with a certain amount of Li/Ni mixing, are shown in Fig. 11d. For the O ion bonded to two Li in a 180° Li–O–Li configuration, a larger pDOS is observed in the energy range from which electrons are extracted when one Li is removed per formula unit (0 to −1.64 eV below the Fermi level), as compared to O ions not involved in Li–O–Li bonding. This upshift of the O DOS upon coordination by more Li is general and has been confirmed for other M species. The increase in pDOS below the Fermi level for O bonded to four Li and two Ni was identified by visualizing the charge density around the O anion for the energy range of interest. The isosurface plot, shown in the middle panel of Fig. 11d, reveals that a large charge density resembling the shape of an isolated O 2p orbital is present along the 180° Li–O–Li direction, indicating that the oxidizable electrons on O in this local Li-rich environment are located in the 2p orbital linearly bonded to the two Li. A qualitative model based on orbital overlap arguments helps to explain these results. The molecular orbital diagram of a typical stoichiometric 3d LiMO2 compound is shown in Fig. 11e. Overlap between the O 2p orbitals and the metal 4s, 4p, and 3dx2−y2 and 3dz2 orbitals leads to three sets of bonding a1g, t1u and eg molecular orbitals with dominantly O character, and three corresponding sets of antibonding a1g*, t1u* and eg* molecular orbitals with dominantly M character. The 3dxy, 3dyz and 3dxz metal orbitals do not overlap significantly with the O 2p orbitals and result in a non-bonding t2g set with dominantly M character. Since the Fermi level lies in between the non-bonding t2g set and the antibonding eg* set, oxidation proceeds by removing electrons from these M-dominated states. In Li-excess and/or cation-disordered transition metal oxides, O 2p orbitals along Li–O–M configurations hybridize with the 3d M orbitals to form the same molecular orbitals as in the stoichiometric layered LiMO2 case. However, O orbitals along Li–O–Li configurations do not hybridize with Li orbitals because of the large energy difference between the O 2p and Li 2s orbitals (see Fig. 11f), leading to essentially unhybridized O 2p states at an energy close to that of the isolated O 2p orbital with a DOS proportional to the number of Li–O–Li configurations in the crystal structure and determined by the Li content and degree of cation mixing.122 More recently, it was also shown that vacant sites near O have a similar effect in unhybridizing the oxygen and making its states more available for oxidation.108
The formation of unhybridized, oxidizable O 2p states is not restricted to rocksalt-type alkali transition metal oxide structures with an alkali/M ratio >1 but can also take place in other alkali transition metal oxide structure types and/or when the alkali/M ratio <1, provided that either vacancies or highly electropositive metals are present in the M layers. It has also been observed in several sodium transition metal oxide systems with a P2-type layered structure, namely Na2/3Mg0.28Mn0.72O2 with Mg2+ in the transition metal layers124 and Na0.78Ni0.23Mn0.69O2 with vacancies in the M layers,125 as well as in Na2Mn3O7 with a layered structure and vacancies in the Mn layers.126
While Li–O–Li (or equivalent) configurations are required to activate oxygen oxidation in LMOs, the position of the unhybridized O 2p orbital relative to the M-dominated t2g and eg* frontier orbitals dictates whether O oxidation occurs before, after or concurrently with M oxidation.122 In Ni-containing DRX systems, the Li–O–Li band overlaps with the Ni-dominated eg* band,122 leading to concurrent Ni and O redox processes and accounting for the incomplete Ni2+ to Ni4+ oxidation observed in Li1.2Ni1/3Ti1/3Mo2/15O214 and Li1.2Ni0.2Ti0.6O2.47 In contrast, there is no overlap between the Mn3+/4+ eg* and Li–O–Li states,122 in good agreement with the sequential oxidation of Mn and O on Li extraction from DRX Li1.3Nb0.3Mn0.4O2,13 Li1.25Nb0.25Mn0.5O257 and layered NaxMn3O7.126
Practical high energy density layered Li-excess and DRX cathodes rely on redox-active 3d M species and fall in the charge-transfer regime, where O redox is activated and poor stabilization of the oxidized O anions leads to O release on Li extraction,116 as reported for Ni,14 Ni/Mn,109 and NMC-type systems,102,114 as well as activated Li2MnO3.111,113 Oxygen redox and the creation of short O–O bonds and/or O vacancies in the lattice inevitably leads to M migration,105,107,127,128 with important consequences on the long-term performance such as voltage decay107 and capacity fade. Transition metal migration may also explain the end-of-charge hysteresis observed for almost all DRXs during the first cycle and to a lesser extent on subsequent cycles. Hence, strategies to stabilize the MO2 structure are essential to the potential commercialization of both Li-excess layered oxides and DRX cathodes. A promising approach is the incorporation of electrochemically-inactive elements in the framework. These d0 elements stabilize the oxidized O species created on charge, as noted, for instance, in the Mn/Nb systems.13,18
It should be pointed out that an alternative explanation to O oxidation was recently suggested,129 which emphasizes the need to analyze experimental data obtained on highly charged Li-excess and DRX cathodes in a critical manner and to consider several possible redox processes and changes in M–O bonding (M–O orbital hybridization) upon oxidation. Clearly, further studies that employ in situ/operando techniques to monitor redox processes are needed in order to avoid spontaneous decomposition of metastable ex situ cathode materials obtained at high states of charge, which hinders access to the true redox mechanism taking place during normal function.129
e. Fluorination
Fluorination is a common strategy to increase the thermal and electrochemical stability of secondary battery components. For example, the high voltage stability of organic electrolytes is improved on incorporation of highly electronegative F, lowering the highest occupied molecular orbital (HOMO) level and leading to an increase in the oxidation potential. In addition, fluorinated electrolyte salts (e.g. LiPF6) and solvents (e.g. fluoroethylene carbonate) are often used in the preparation of high voltage inorganic electrolyte solutions. Insulating fluorinated coatings are also an effective means of preventing exothermic reactions at the cathode/electrolyte interface on charge.74 The ability of DRX materials to substitute some of the O anions by F may ultimately become one of the most important factors in creating high capacity, stable novel cathode materials. We discuss what is currently understood about the effect of fluorine on capacity, voltage, percolation and high voltage stability.The reason for the remarkably different F solubility in layered and cation-disordered LMOs was elucidated by Richards et al.42 using first principles calculations. The authors found that the high M–F bond energy leads to unfavorable F incorporation into anion sites with three M nearest-neighbors, as in layered LMOs. By creating anion sites with fewer M neighbors in the DRX structure, both Li excess and cation disorder enable F incorporation into metal-poor, Li-rich sites in the DRX structure, a result confirmed by 19F NMR.74 Even then, the typical equilibrium solubility limit for LiF in the DRX lattice is around 10% (or a stoichiometry of Li1+xM1−xO1.8F0.2) under practical experimental conditions (<1100 °C) using a standard solid-state route, while DRXs with a higher F content (30%, or a stoichiometry of F0.6 or more) can only be synthesized using a mechanochemical route to form a metastable product.
The mechanism by which F changes the voltage curve is complex, as it modifies both the redox behavior of the transition metal as well as the Li site energy. First principles calculations exploring the redox mechanism in Li1.15Ni0.45Ti0.3Mo0.1O1.85F0.15 have shown that F doping leads to a transition from a direct Ni2+ → Ni4+ redox process, due to complete Ni3+ disproportionation in ‘pure oxide’ NiO6 environments, to a sequential Ni2+ → Ni3+ → Ni4+ redox process for Ni ions with at least one Ni–F bond.74 In a similar way, while there is no overlap between Mn and O states in DRX oxides,13,57,122,126 as discussed in the previous section, concurrent Mn and O redox processes have been identified in Li2Mn2/3Nb1/3O2F.20Ab initio simulations have suggested that the increased overlap between the Mn eg* and unhybridized Li–O–Li orbitals can be attributed to the presence of Mn-F bonds and to longer average Mn-anion distances.20 Finally, F doping was found to increase the M redox potential in Li2MO2F (M = V, Mo), as compared to their pure oxide Li2MO3 counterparts.10,133 F tends to attract Li in DRX structures, creating Li-rich F environments (e.g., F–Li6 or F–Li5M). The strong attraction between F and Li may render some Li+ ions bonded to F not electrochemically extractable. In fact, Kitchaev et al.66 introduced the concept of a “Li gettering effect” of the F ions, whereby F ions present in Li-rich environments in the pristine oxyfluoride cathode become undercoordinated on charge and bind more strongly to the remaining Li+ ions in the structure, making these Li+ ions unextractable within a reasonable voltage window. This gettering effect may be significant, with an average of 0.4–0.8 Li per F being inaccessible on charge to 4.6 V,66 and may act to stabilize the structure at high voltage. Despite having demonstrated effects on both the M redox and the Li binding energy, the average experimentally measured voltage of F-substituted compounds is similar to or slightly higher than that of the comparable oxides, indicating that there are potentially other physical mechanisms at work that buffer the voltage.
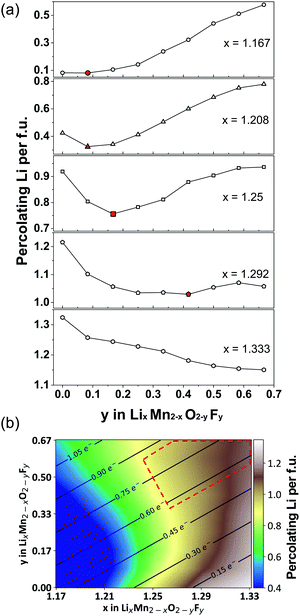 | ||
| Fig. 12 (a) Li percolation in LixMn2−xO2−yFy DRX cathodes as a function of F (y values) at various Li-excess levels (x values). For each Li excess level, the critical F content at which Li percolation encounters a minimum is highlighted in red. (b) Design map within the Li–Mn–O–F DRX space. The color scale represents the total amount of percolating Li per formula unit (f.u.) through the 0-TM percolation network at each composition, obtained from Monte Carlo simulations at 2573 K. The solid lines and numbers in this map indicate the theoretical Mn redox capacity. The region of compositional space where DRX Li–Mn–O–F cathodes with a high capacity and good cyclability are likely to be obtained is enclosed with a red dashed line. Adapted from Z. Lun, B. Ouyang, Z. Cai, R. J. Clément, D.-H. Kwon, J. Huang, J. K. Papp, M. Balasubramanian, Y. Tian, B. D. McCloskey, H. Ji, H. Kim, D. A. Kitchaev, G. Ceder, Design Principles for High-Capacity Mn-Based Cation-Disordered Rocksalt Cathodes, Chem, in press, Copyright 2020, with permission from Elsevier.140 | ||
Overall, the collection of theoretical and experimental studies discussed in the first part of this review reveal that cation disorder and Li excess have profound effects on the Li+ transport properties and electrochemical properties of LMOs. These insights facilitate the identification of common and distinctive features across different classes of Li-excess DRX cathodes synthesized and tested electrochemically and discussed in the second part of the review.
II. Electrochemical and structural studies of DRX cathodes
a. Early studies on disordered oxides
Although DRX oxide cathodes have only been in the spotlight of the battery research community for about five years, a few early observations on disordered cathodes were published in the 1990s. In 1991, Delmas et al.60 obtained disordered ω-Li3V2O5 by electrochemically lithiating LixV2O5 (0 < x < 1). This cathode exhibited a very high energy density of 800 W h kg−1 when cycled between 1.9 and 4.0 V and a sloping voltage profile.60 Based on the insights gained in the first part of this review, cation disordering on electrochemical Li insertion into LixV2O5 can be rationalized by the presence of a large amount of d0 V5+ in the pristine LiV2O5 material and in the initial stages of discharge. As mentioned earlier, these d0 metal ions stabilize the disordered structure by occupying the most distorted Oh sites. In addition, the good percolation properties of the Li3V2O5 cathode, or equivalently Li1.2V0.8O2, stems from the 20% Li-excess in the disordered structure.A study published in 1998 by Obrovac et al.8 investigated a number of disordered LixMO2 compounds (M = Ti, Mn, Fe, Co, Ni) prepared via a mechanochemical route. Loss of Li and O during ball milling resulted in a Li content x ≤ 1 and, apart from LixMnO2, all cathode materials exhibited very limited electrochemical activity (<10 mA h g−1 of reversible capacity, see Fig. 13). At the time, the poor performance was attributed to cation disorder, consistent with the previous belief that disorder prevents Li diffusion.8 Urban et al.'s recent work on Li percolation in DRXs22 suggests instead that the poor Li+ diffusion properties of this series of compounds result from low Li contents below the percolation threshold, and that cation disorder will no longer impede Li+ conduction once 5 to 15% excess Li (x = 1.05–1.15) is introduced in the material (see Fig. 6b). Interestingly, disordered LixMnO2 exhibited a first charge capacity of ca. 150 mA h g−1 and a remarkably high reversible capacity of 130 mA h g−1 (see Fig. 13), which was tentatively attributed to SRO in the structure, as revealed by broad superlattice peaks in the XRD pattern.8 As mentioned in the introduction, unique among the LiMO2 compounds, LiMnO2 forms an orthorhombic structure featuring corrugated Li and MnO2 layers. This distinct ground state structure strongly suggests that the superior electrochemical properties of disordered LiMnO2 result from the short-range ordered cation distribution in the material. We note that Obrovac et al.'s study is an early demonstration of mechanochemical synthesis of electrode materials. Ball milling of precursor powders is now routinely used to obtain metastable cathode compounds, such as DRX LMOs.
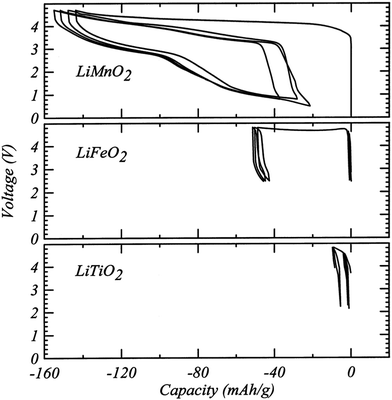 | ||
| Fig. 13 Electrochemical profiles from cathodes prepared from LiMnO2, LiFeO2 and LiTiO2 milled for 48 h. Reprinted from M. N. Obrovac, O. Mao, J. R. Dahn, Structure and electrochemistry of LiMO2 (M = Ti, Mn, Fe, Co, Ni) prepared by mechanochemical synthesis,8Solid State Ionics, vol. 112, pp. 9–19, copyright 1998, with permission from Elsevier. | ||
b. How complete is the theoretical framework established in part I?
Having demonstrated that the electrochemical properties of early disordered LixMO2 cathodes can be rationalized from a relatively small set of principles outlined in the first part of this review, we extend our analysis to a range of disordered LMO cathode materials reported in the last few years, with results presented in Table 1. We focus here on characteristic features of DRX cathodes which can easily be verified experimentally:| Cathode composition | Particle size and preparation | d0 species | Li excess level and electrochemical activity | Smooth/sloppy voltage curve | Oxygen redox/loss |
|---|---|---|---|---|---|
| Li0.24CoO2, Li0.23NiO28 | No d0 element | Li deficient. 10–20 mA h g−1 reversible capacity. | Yes | Not specified | |
| LixTiO2, LixFeO28 | No d0 element | Li deficient. <10 mA h g−1 reversible capacity. | Yes | Not specified | |
| LixMnO2 with SRO8 | No d0 element | Li deficient. 130 mA h g−1 reversible capacity. | No | Not specified | |
| w-Li3V2O5 formed electrochemically from V2O560 | V5+ in V2O5 precursor | 20% Li excess. Energy density of 800 W h kg−1 of V2O5. | Yes | Not specified | |
| Li2VO3 formed electrochemically from LiVO361 | V5+ in LiVO3 precursor | 33% Li excess. 253–295 mA h g−1 reversible capacity. | Yes (after first discharge) | No | |
| Li2VO310 | Nano particles (tens nm) synthesized by mechanochemi-cal method | V5+ (charge) | 33% Li excess. Around 290 mA h g−1 reversible capacity. | Yes | No |
| Li2V3+O2F11 | V5+ (charge) | 33% Li excess. Around 420 mA h g−1 initial capacity. | Yes | Yes | |
| Li1.171Mn0.3432+V0.4864+O1.8F0.266 | 100–200 nm primary particle size | V5+ (charge) | 17.1% Li excess. 317 mA h g−1 reversible capacity. | Yes | Limited |
| Li1.211Mo(IV)0.467Cr0.3O2, disorders after a few cycles9 | ∼100 nm after ball-milling with sucrose. | Mo6+ (charge) | 21.1% Li excess. 266 mA h g−1 reversible capacity. | Yes | Not specified |
| Li1.2Mo(IV)0.6Fe0.2O2, disorders during the first cycle62 | Mo6+ (charge) | 20% Li excess. 120 mA h g−1 reversible capacity from second cycle. | Yes, after first charge | No | |
| Li4NiMoO6, partially-disordered15 | Sub-micrometer particles after ball-milling with C black. | Mo6+ | 33% Li excess. >300 mA h g−1 reversible capacity. | No | Not reported (likely yes) |
| Li1.42Mo0.29Fe0.29O2, partially-disordered16 | Sub-micrometer particles after ball-milling with C black. | Mo6+ | 42% Li excess. >200 mA h g−1 reversible capacity. | No | Yes |
| Li1.2Ni1/3Ti1/3Mo2/15O214 | ∼100 nm particles after ball-milling with C black. | Mo6+/Ti4+ | 20% Li excess. 230 mA h g−1. | No | Yes |
| Li1.15Ni0.45Ti0.3Mo0.1 O1.85F0.1587 | ∼100 nm particles after shaker-milling with C black. | Mo6+/Ti4+ | 20% Li excess. 250 mA h g−1. | Yes | Yes |
| Li9/7Nb2/7Mo3/7O217 | Few 100 s of nm particles after ball-milling with C black. | Nb5+/Mo6+ (charge) | 28.6% Li excess. 280 mA h g−1 reversible capacity. | Yes | No (up to 4.3 V) |
| Li6/5Ti2/5Mo2/5O2136 | Ti4+/Mo6+ (charge) | 20% Li excess. 270 mA h g−1 reversible capacity. | Yes | No (up to 4.3 V) | |
| Li4/3Mo2/96+Mo4/93+O217 | Mo6+ (charge) | 33% Li excess. 320 mA h g−1 reversible capacity. | Yes | No (up to 4.3 V) | |
| Li2Mo3+O2F136 | Nano particles after ball-milling | Mo6+ (charge) | 33% Li excess. 320 mA h g−1 reversible capacity. | Yes | Limited |
| Li1.3Nb0.3Mn0.43+O213 | Sub-micrometer particles after ball-milling with C black. | Nb5+ | 30% Li excess. 300 mA h g−1 reversible capacity cycled at 60 °C. | No | Yes |
| Li1.25Nb0.25Mn0.53+O257 | <100 nm particles after ball-milling with C black. | Nb5+ | 25% Li excess. 287 mA h g−1 reversible capacity. | No | Yes |
| Li1.2Nb0.175Mn3+0.625 O1.95F0.05135 | 100–200 nm particles after shaker-milling with C black | Nb5+ | 20% Li excess. 275 mA h g−1 reversible capacity. | No | Yes |
| Li1.3Nb0.3Fe0.4O213 | Sub-micrometer particles after ball-milling with C black. | Nb5+ | 30% Li excess. 245 mA h g−1. | No | Yes |
| Li1.3Nb0.3V0.4O258 | Sub-micrometer particles after ball-milling with C black. | Nb5+ | 30% Li excess. 230 mA h g−1. | Yes | No |
| Li1.25Nb0.25V0.5O259 | Sub-micrometer particles after ball-milling with C black. | Nb5+ | 25% Li excess. 300 mA h g−1 at 50 °C (250 mA h g−1 room T). | Yes | Limited |
| Li1.19Ni0.59Nb0.22 O1.46F0.54138 | 100–200 nm with multiple crystallites | Nb5+ | 25% Li excess. 257 mA h g−1 | No (low voltage tail) | Yes |
| Li2Mn2+2/3Nb1/3O2F20 | 100–200 nm with multiple crystallites of about 15 nm in size | Nb5+ | 33% Li excess. 317 mA h g−1 | Yes | Yes |
| Li1.2Ni0.35Ti0.35Nb0.1 O1.8F0.2141 | 100–300 nm | Nb5+/Ti4+ | 20% Li excess. ∼280 mA h g−1 | No (low voltage tail) | Yes |
| Li1.2Ti0.4Fe0.4O245 | <50–100 nm particles. | Ti4+ | 20% Li excess. 150 mA h g−1 reversible capacity. | No | Yes |
| Li1.05Ni0.5Ti0.5O1.8946 | 50–100 nm particles. | Ti4+ | ∼5% Li excess. 96 mA h g−1 reversible capacity. | No | Yes |
| Li2CoTiO4 (with spinel LiTi2O4 impurity)48 | 100 nm C-coated particles | Ti4+ | No excess Li. 144 mA h g−1 reversible capacity. | No | Maybe some O loss |
| Li2FeTiO450 | 10–25 nm C-coated particles. | Ti4+ | No excess Li. 83 mA h g−1 reversible capacity. | Yes | No |
| Li2FeTiO4/graphene nanocomposite53 | 20–50 nm particles | Ti4+ | No excess Li. 219 mA h g−1 reversible capacity. | Yes (after first cycle) | No |
| Li2FeVyTi1−yO4 (y = 0, 0.2, 0.5) embedded in C matrix54 | ∼10 nm particles embedded in C matrix. | Ti4+ | No excess Li. 150, 190 and 240 mA h g−1 reversible capacity for y = 0.0, 0.2 and 0.5, respectively. | Yes | Yes |
| Li2−xVTiO4 embedded in C matrix55 | 40–60 nm particles. | Ti4+ | Slightly Li deficient. 350 mA h g−1 reversible capacity. | Yes (after first cycle) | No |
| Li1.2Ti0.4Mn0.4O218 | 2–3 μm primary particle size | Ti4+ | 20% Li excess. 320 mA h g−1 reversible capacity cycled at 50 °C. | No (high voltage plateau) | Yes |
| Li2Mn1/22+Ti1/2O2F20 | 50 nm primary particle size | Ti4+ | 33% Li excess. 321 mA h g−1 reversible capacity. | Yes | Yes |
| Li4Mn2O5–Li2O (nanocomposite)64 | <10 nm particles, ground with C black. | No d0 element | Large Li excess (LiMnO2 + Li2O). 355 mA h g−1 reversible capacity. | No | Yes |
| Li2MnO3 (nanostructured), disorders on first charge65 | 10 nm particles after ball-milling with C black. | No d0 element | 33% Li excess. 335–350 mA h g−1 reversible capacity. | Yes | Yes |
| Li1.9Mn0.95O2.05F0.95134 | 100–500 nm primary particle size | No d0 element | 26.7% Li excess. 280 mA h g−1 reversible capacity. | Yes | Yes |
(1) The presence of at least one d0 element is usually necessary for the formation and stabilization of the DRX structure.
(2) Li percolation and therefore electrochemical activity relies on 5–15% excess Li.
(3) Cation disorder results in smoother electrochemical profiles and steeper voltage slopes compared to layered systems, partly because of the greater range of Li site energies.
(4) Cation disorder and Li excess lead to Li–O–Li configurations, activating O redox/loss mechanisms.
The results presented in Table 1 clearly indicate that the great majority of DRXs reported to date contain at least one d0 transition metal species. We also find that DRXs with the best electrochemical performance (reversible capacity ≥300 mA h g−1) contain more than 25% Li excess (e.g. Li1.25Nb0.25V0.5O2 at 50 °C,59 Li1.3Nb0.3Mn0.43+O2,13,18,19 Li4/3Mo2/96+Mo4/93+O2,17 Li4NiMoO615) and that the electrochemical curves are generally smooth, with no major voltage step or plateau. Nevertheless, a number of experimental studies on Ti-containing DRXs report good electrochemical performance for materials with a Li content below the percolation threshold concentration predicted by Urban et al.,22 with reversible capacities exceeding 200 mA h g−1 in certain cases.53–55 In addition, several LMO compounds that do not contain a d0 transition metal species have been successfully synthesized and tested as cathode materials,64,65,134 suggesting that other factors are important to the stability and electrochemical behavior of this class of materials. In an attempt to identify more subtle composition-dependent factors and particle-size effects, the electrochemical and structural properties of several families of disordered compounds are discussed hereafter.
c. Survey of several families of disordered oxides and oxyfluorides
In general, average discharge potentials of DRX oxides that rely on V redox chemistry (both V3+/V5+ and V4+/V5+) are relatively low, around 2.5–2.6 V, as indicated in Fig. 2. This leads to very little overlap between V and O electronic states and is likely the reason for their highly reversible electrochemistry and good long-term performance. Fluorination both decreases the oxidation state of V in the as-prepared cathode, thereby increasing the available V redox capacity, and alters the V redox potential, resulting in more overlap between V and anion redox processes at high potentials. This, in turn, results in a higher initial capacity but can worsen long-term capacity retention.
A downside of the high potentials at which Ni redox processes occur is the incomplete oxidation of Ni2+ on charge because Ni oxidation competes with O redox. For most Ni redox-based DRXs, reports of hard XAS measurements on Li1.2Ni0.333Ti0.333Mo0.133O2,14 Li1.19Ni0.59Nb0.22O1.46F0.54,138 and Li1.2Ni0.35Ti0.35Nb0.1O1.8F0.2141 at the Ni K-edge have shown that Ni2+ is only oxidized to an average oxidation state of about Ni3+ on charge to 4.6 V. This is remarkably different from layered NCM-type cathodes and DRX Mn redox-based, for which Ni2+/Ni4+ and Mn3+/Mn4+ redox processes are almost complete. Fig. 14 shows qualitative electronic energy level diagrams for Ni2+/Ni4+ redox-based and Mn3+/Mn4+ redox-based DRX cathodes. Significant overlap between Ni eg* orbitals and Li–O–Li unhybridized orbitals causes incomplete oxidation of Ni2+ to Ni4+, while Mn electronic levels lie higher in energy, and the Mn3+/Mn4+ redox reservoir is mostly accessible on charge.
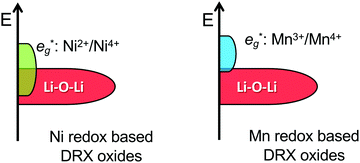 | ||
| Fig. 14 Qualitative diagrams of transition metal and oxygen electronic states in Ni2+/Ni4+ redox-based and Mn3+/Mn4+ redox-based DRXs. | ||
As a consequence of the strong overlap between Ni and Li–O–Li electronic bands, more O2 and CO2 gas is released upon electrochemical cycling of Ni redox-based DRX materials compared to, e.g., Mn redox based DRXs,20,66,134 which can lead to transition metal densification at the surface and to a large polarization of the discharge curve.87 Bulk fluorination87 and surface modification144,145 are two effective strategies to mitigate irreversible gas loss and to reduce polarization on discharge.
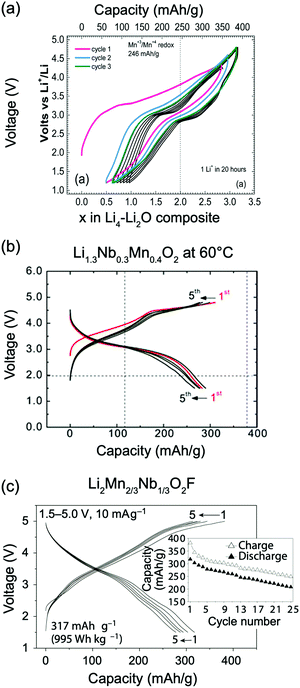 | ||
| Fig. 15 Electrochemical performance of selected Mn redox-based DRX cathodes. Room temperature electrochemical profiles of the nanostructured (a) 0.93Li3.6Mn2.4O5.4–0.07Li2O composite, when cycled between 1.2 and 4.8 V. Figure adapted from Freire et al.64 with permission from the Royal Society of Chemistry. (b) Electrochemical profile of Li1.3Nb0.3Mn0.4O2 at 60 °C, when cycled between 1.5 and 4.8 V. Figure adapted from Yabuuchi et al.13 with permission from PNAS. (c) Room temperature electrochemical profile of Li2Mn2/3Nb1/3O2F, when cycled between 1.5 and 5.0 V. Adapted by permission from Springer Nature: Lee et al.,20 copyright 2018. | ||
More recently, Kataoka et al.146 reported a series of DRX Li2MnO3 and spinel LiMn2O4 composites prepared via mechanochemical synthesis, with very high initial capacities of 400 mA h g−1 and 80% capacity retention after 15 cycles. Given that spinel and DRX LMOs share a common oxygen framework, the composite nature of this series of compounds is difficult to assess using scattering and microscopy techniques, and these compounds could also potentially be single-phased but metastable with respect to decomposition into the limiting DRX and spinel phases.
The Li1.3Nb0.3Mn0.43+O2 cathode was first reported by Yabuuchi et al.13 and exhibits a high initial discharge capacity of 300 mA h g−1 and energy density of 950 W h kg−1 over the range 1.5–4.8 V at 60 °C, as shown in Fig. 15b. Half of this capacity comes from Mn3+/Mn4+ redox processes, while the other half has been attributed to O charge compensation processes, resulting in significant capacity fade upon extended cycling. Several strategies have been devised to enhance the long-term cycling stability, which include reducing the Li content (e.g., Li1.25Nb0.25Mn0.53+O2)57 and fluorination.135 High-valent charge compensators other than Nb5+ have also been tested, including Ti4+ and Zr4+, as in Li1.2Mn0.4Ti0.4O2 and Li1.2Mn0.4Zr0.4O2.21 As discussed in part I.b, the electrochemical performance of Li1.2Mn0.4Ti0.4O2 is far superior to that of Li1.2Mn0.4Zr0.4O2 (see Fig. 8a) due to the presence of SRO more favorable to Li percolation in the former material.21
Fluorination has been employed as a strategy to improve the long-term performance of Li–Mn–O DRX cathodes. Li1.9Mn0.95O2.05F0.95, prepared by ball milling, exhibits a high initial capacity of 280 mA h g−1, with about 170 mA h g−1 of capacity retained after 50 cycles.134 Differential electrochemical mass spectrometry (DEMS) indicated negligible O2 loss during cycling, in contrast with layered Li2MnO3. Li2Mn2/3Nb1/3O2F and Li2Mn1/2Ti1/2O2F DRXs were stabilized by Lee et al.20 through a mechanochemical synthesis route. The combination of high-valent charge compensating cations (Nb5+ and Ti4+) and fluorination in these materials greatly increases the theoretical metal redox capacity (ca. 270 mA h g−1 for Li2Mn2/3Nb1/3O2F and ca. 230 mA h g−1 Li2Mn1/2Ti1/2O2F), providing a new strategy to achieve high capacities while keeping O redox processes minimal. Indeed, these two cathodes make use of the Mn2+/Mn4+ double redox chemistry to achieve extremely high capacities (>300 mA h g−1) and energy densities (ca. 1000 W h kg−1), as shown in Fig. 15c for Li2Mn2/3Nb1/3O2F, with negligible irreversible O loss detected with DEMS up to 5.0 V.20
Kitchaev et al. devised yet another strategy to reduce the participation of O-based charge compensation processes. Instead of using redox-inactive Ti4+ and Nb5+ charge compensators, the authors chose high-valent yet redox-active V4+ to provide addition electron capacity from V4+/V5+ redox in a series of Li–Mn–V–O–F DRX cathodes.66
When used as a redox species, Mo is usually found as Mo3+ or Mo4+ in the as-synthesized material. As mentioned earlier, Li1.211Mo4+0.467Cr0.3O2 forms as a layered rocksalt but disorders upon cycling,9 presumably due to the facile interchange of Li+ and d0 Mo6+ cations formed on charge. For this material, carbon-coating of the cathode particles leads to an initial reversible capacity of 257 mA h g−1, equivalent to the reversible extraction of 1 Li per f.u., and significantly reduces Mo dissolution, resulting in improved capacity retention.9 In a similar manner, Li1.2Mo0.6Fe0.2O2 reported by Liu et al.62 disorders during the first cycle. While only 0.7 Li is reversibly extracted and reinserted during cycling, leading to a moderate capacity of about 125 mA h g−1 after the first few cycles, this material exhibits a remarkable 92.7% capacity retention between the 5th and 105th cycle as well as negligible potential decay on extended cycling. The stable electrochemical properties of Li1.2Mo0.6Fe0.2O2 have been attributed to highly reversible Mo4+/6+ and Fe2+/3+ redox processes, with no involvement of lattice O.62 Hoshino et al.17 explored several solid-solutions composed of electrochemically-active LiMoO2 and an electrochemically-inactive component containing d0 Nb5+, Ti4+ or Mo6+, achieving impressive reversible capacities in the 270–320 mA h g−1 range. Unlike xLi4MoO5–(1 − x)LiFeO2,16xLi4MoO5–(1 − x)NiO,15 and xLiNi0.5Ti0.5O2–(1 − x)Li1.6Mo0.4O214 solid-solutions, these systems exhibit very low polarization and there is no evidence of O redox activity on charge to 4.3 V. In the LiMoO2–Li3NbO4 system, Mo6+ migration on cycling was proposed to account for the very small volume change observed in the material during electrochemical cycling.17
By comparing three different Nb5+-based systems, namely Li1.3Nb0.3V0.43+O2, Li1.3Nb0.3Fe0.43+O2, and Li1.3Nb0.3Mn0.43+O2, Yabuuchi et al.18 demonstrated that the reversibility of O-based charge compensation processes in this family of materials is highly dependent on the nature of the redox-active 3d M species. Consistent with previous work,10 no O redox was observed for the V system, which may be related to the low oxidation potential of V3+ and the high theoretical metal redox capacity (V3+/V4+/V5+).18 For the Fe system, O oxidation was found to be accompanied by irreversible O loss, which the authors attributed to the high Fe4+–O covalency, resulting in charge transfer from O to Fe via a reductive coupling mechanism (RCM) at the end of charge and the formation of Fe3+ and unstable superoxide species.18 The remarkable reversibility of O redox for the Mn system was rationalized by the absence of O to Mn charge transfer at high voltage, due to the weak covalency of the Mn4+–O bond, and the stabilization of isolated O holes in the material by neighboring Li+ and Nb5+ species.18 It is however possible that the higher stability of the Mn-containing system is simply because Mn4+ compound are fairly stable at normal conditions and are not nearly as over-oxidized as Fe4+.
A large number of mixed transition metal DRXs containing Ti4+ as a high-valent charge compensator have been synthesized and electrochemically tested over the past few years. Zhang et al.47 reported on the Li1+z/3Ni1/2−z/22+Ti1/2+z/6O2 (0 ≤ z ≤ 0.5) series and showed that LiNi1/2Ti1/2O2 displays only 30 mA h g−1 of reversible capacity at room temperature. Cycling at 50 °C increases this value to approximately 150 mA h g−1, indicating kinetic limitations due to poor Li percolation for this composition with no Li excess. Increasing the Li content helps to achieve higher reversible capacities at room temperature (85 mA h g−1 for x = 0.27), but no noticeable capacity improvement is observed at higher temperature (140 mA h g−1 at 50 °C). The authors suggest that particle size is crucial to achieve high electrochemical activity of Li in stoichiometric compositions, consistent with previous studies reporting considerable electrochemical capacity for nanosized LiNi1/2Ti1/2O2 (50–100 nm particles) prepared via a low temperature sol–gel route (600 °C)46 but no electrochemical activity up to 4.8 V when the same composition was obtained through high temperature sintering.147 More recently, Liu et al.148 found that, among the Li1+z/3Ni1/2−z/22+Ti1/2+z/6O2 (z = 0, 0.1, 0.2, 0.3, 0.4, 0.5) series prepared via a sol–gel method, primary particles tend to become larger and to agglomerate as the Li and Ti contents are increased. The LNTO (z = 0) to LNTO3 (z = 0.3) compositions have an average particle size around 100 nm, while LNTO4 and LNTO5 (z = 0.4 and 0.5, respectively) particles are larger, and LNTO5 particles are more agglomerated. Out of all Li1+z/3Ni1/2−z/2Ti1/2+z/6O2 compositions, LNTO3 was found to have the best electrochemical performance, with 116 mA h g−1 of first cycle reversible capacity, and the lowest charge-transfer resistance. Comparing the 0 ≤ z ≤ 0.3 samples with small particle size, it is clear that the Li+ kinetics improve with increasing Li excess. Increasing z also decreases the Ni content, thus increasing the amount of O redox necessary to obtain the same capacity. In the case of LNTO4 and LNTO5 electrodes, a high voltage plateau commonly observed with O redox occurs at 4.4 V during the initial charge, leading to high first charge capacities of 211 and 231 mA h g−1, respectively. These anion processes are poorly reversible, with only 75 and 61 mA h g−1 of reversible capacity on first discharge. While the larger particle size and particle agglomeration likely contribute to the sluggish Li+ transport in LNTO4 and LNTO5, as suggested by the authors, we note that O loss and structural degradation at the surface of the particles likely impedes Li+ transport further. Hence, for this series of cathodes, electrochemical performance depends on a combination of factors, including particle size, particle agglomeration, Li excess content and the size of the transition metal redox reservoir (Ni content), but performance clearly improves when the Li content is increased as long as the negative consequences of O redox can be kept under control.
Li–Ti–Fe–O2 compounds are attractive positive electrode materials containing only 3d M species with a high natural abundance and low toxicity, but it has so far been difficult to achieve high reversible capacity from Fe-containing materials. Similarly to the Li1+z/3Ni1/2−z/22+Ti1/2+z/6O2 systems discussed above, Glazier et al.43 observed that an increase in the Li and Ti contents in Li(1+x)Ti2xFe(1−3x)O2 leads to primary particles (around 1 micron in size) that tend to agglomerate into larger secondary particles. Starting from an almost fully disordered cation arrangement at x = 0, the authors found that the degree of cation ordering increases with x by comparing the c/3a lattice parameter ratio to the 1.6333 value expected for a fully cation-disordered rocksalt. Oxygen redox processes were observed for compositions x ≥ 0.13, possibly accompanied by O loss at the end of charge.43 All compounds exhibited moderate first cycle reversible capacities, with the highest discharge capacity, close to 145 mA h g−1, obtained for x = 0.21. Tabuchi et al.'s45 study on the related Li1.2Ti0.4Fe0.43+O2 obtained via a hydrothermal route revealed a strong decrease in reversible capacity, from approximately 160 mA h g−1 to 55 mA h g−1, as the post-synthesis calcination temperature was increased from 400 °C to 600 °C, strongly suggesting that grain growth after firing at 600 °C significantly impacts Li+ transport. Using data from 57Fe Mössbauer spectroscopy and XRD the authors argued for partial displacement of Fe and Ti species from Oh to Td sites with as much as 17.5% of M ions displaced to interstitial Td sites on charge to 4.5 V.45 The displacement of Ti4+ to tetrahedral sites would be surprising as this ion is not often found in 4-fold coordination. Transition metal migration was found to be only partially reversible on discharge, which likely impedes Li+ transport and contributes to the moderate capacities that are observed for Li1.2Ti0.4Fe0.43+O2.
Several studies50,51,53–55 have investigated the electrochemical performance of nanosized Li stoichiometric, Ti4+-containing oxides with a cubic rocksalt structure. Küzma et al.50 demonstrated that a small average particle size is crucial to the good electrochemical performance of Li2Fe2+TiO4, Li2Ni2+TiO4, and Li2Mn2+TiO4. In this respect, carbon coating was found to be important for preventing particle growth during the heat treatment and mitigating particle agglomeration.50 Dominko et al.55 showed that a highly porous composite composed of nanosized (40–60 nm) Li2−xVTiO4 embedded in a carbon matrix exhibits a reversible capacity close to the theoretical value of 165 mA h g−1 for the V3+/4+ redox reaction when cycled between 2.0 and 4.4 V. Yang et al.53 reported a Li2Fe2+TiO4/graphene nanocomposite electrode with a high reversible capacity of 219 mA h g−1, equivalent to the reversible extraction of 1.4 Li per formula unit, when cycled between 1.5 and 5.0 V. Chen et al.54 prepared a series of electrodes composed of 10-nm sized Li2FeVyTi1−yO4 embedded in a carbon matrix. When cycled between 1.5 and 4.8 V at 40 °C, Li2FeTiO4, Li2FeV0.2Ti0.8O4 and Li2FeV0.5Ti0.5O4 delivered a reversible capacity of about 150 mA h g−1 (exchange of 1 Li per f.u.), 190 mA h g−1 (1.3 Li per f.u.) and 240 mA h g−1 (1.6 Li per f.u.), respectively, indicating that the reversible capacity increases with the M redox reservoir.54 The good Li+ transport properties of these Li stoichiometric compounds is likely, at least in part, due to nanosizing, which increases the ionic conductivity by reducing Li+ diffusion path lengths, and carbon coating/embedding, which enhances the electronic conductivity. Another potential explanation for the high performance of Ti4+-containing disordered compounds, despite the lack of Li excess for the creation of a percolation network, is the favorable short-range order generated by Ti4+ ions, as observed by Ji et al.21
The experimental studies discussed in this section illustrate that DRX cathodes are a very active area of research. The insights obtained from these experimental studies, as well as the theoretical framework presented in the first part of the review are combined hereafter into a set of directions for the design of high performance DRX cathodes.
III. Design considerations and future prospects for high performance DRX cathodes
The electrochemical performance of secondary battery electrodes depends on high Li+ and electronic conductivity, a large charge storage capacity and highly reversible structural and redox processes on charge and discharge. These requirements, together with raw materials cost and sustainability considerations, lead to specific design criteria for DRX cathodes.a. Compositional considerations
By lifting the restriction that rocksalt-type cathodes have to be layered and remain layered upon cycling, DRX materials open up a wide compositional space for cathodes, comprising a large number of possible redox centers (Ni, Co, Mn, as in layered LMOs, but also V, Fe, Cr, Mo, Ti) often combined with d0 charge compensator metal ions (Ti4+, Zr4+, Nb5+, Mo6+). In addition, part of the oxygen content can be substituted by F. Most current studies have created prototypical materials using one each from the redox center and charge compensator categories, and limited work has been performed investigating possible synergies between multiple redox elements or charge compensators. Beyond these “functional” elements, one can imagine optimization of performance through other “non-active” elements, such as Al, Mg, etc., which are commonly used as structural stabilizers in the battery field and may establish an additional handle on the type and extent of SRO present in DRX compounds. This creates a very large possible compositional space over which to design DRX materials. Though this leaves much to be investigated, we summarize below some of the basic understanding on the role of each compositional element.Li excess is needed for percolation of 0-TM channel. While the original percolation theory indicated that >9% Li excess is needed for percolation of 0-TM channel, a higher Li content is generally found to lead to larger and more reversible capacities, as long as the amount of anion redox can be limited. In general, more anion-redox seems to lead to poor cyclability,87,118 even though it may promote high capacity in the first few cycles. Short-range cation order clearly modifies percolation, and both theoretical9,22 and experimental studies9,10,13–19,44,45,57–65 have shown that around 10–15% Li excess is usually required for long-range Li+ diffusion in DRX oxides, while about 25% Li excess enables 1 Li per f.u. to be extracted from the material during charge.
The d0 charge compensator is electrochemically inactive but plays an important role in the performance of DRX materials. Specifically, it helps stabilize the disordered structure by occupying the more distorted Oh sites, leaving the less distorted Oh sites for the redox-active M′ metal species. As evidenced by Ji et al.'s theoretical work,21 the high-valent d0 M′′ determines the degree and type of SRO in the material, with important consequences on the formation of a percolating network of Li sites throughout the disordered structure. The exceptional electrochemical activity of Li stoichiometric Ti4+-containing DRXs strongly suggests that the type of SRO induced by Ti4+ is particularly favorable to Li+ diffusion, in good agreement with theoretical predictions (see Fig. 8).21 Finally, it has been speculated that the d0 element may also play a role in protecting a material with anion redox against O loss, though the precise mechanism by which this occurs is not clear.118
The redox-active metal is a critical choice. Maximizing the theoretical metal redox capacity seems to almost always improve cyclability, probably by reducing O redox activity and the associated surface modification processes. While most metals mentioned earlier appear to be reasonable choices, multi-electron redox species such as Mn2+/Mn4+, Ni2+/Ni4+, V3+/V5+, Cr3+/Cr6+ or Mo3+/Mo6+, are particularly promising in this context, though full oxidation of Ni2+ to Ni4+ seems to be difficult in DRX materials.14,87,138,141 Possible Mo dissolution in the electrolyte has been observed and needs to be investigated further before Mo is extensively used as a redox active element in practical DRX materials. In addition, Mo redox reactions take place at voltages below 2.5 V17 (see Fig. 2) which, combined with a high molecular weight for Mo, results in only modest energy densities. The redox-active transition metal and its valence also influence SRO,21 with divalent metal ions favoring the formation of Li4 clusters (0-TM channels) and long-range Li+ diffusion more than trivalent metal ions do, though a more comprehensive understanding of SRO-directing factors is still required. In this context, it is worth nothing that the propensity for Mn3+ to stabilize a unique orthorhombic ground state structure, o-LiMnO2, may lead to a specific SRO favorable to Li+ diffusion in Mn3+-containing cation-disordered compounds. Finally, the choice of M′ and M′′ species should also be informed by their tendency to migrate from Oh to Td sites on cycling, resulting in reduced Li+ motion in the material. For instance, several studies have pointed out that transition metal migration can be an issue in Mo6+-14–16 and Fe3+-containing45 compounds.
Anion substitution by fluorine further enlarges the design space of DRX cathodes. Fluorine comes with important benefits: the substitution of O2− by F− lowers the average valence of the anion sublattice, which allows for a greater fraction of low-valent, redox-active transition metal (such as Mn2+ or Ni2+)20,87 on the cation sublattice. As a result, the M redox capacity is increased, resulting in energy densities as high as 1000 W h kg−1.20 While the larger fraction of transition metal redox capacity in fluorinated DRX materials improves cycling stability87 by reducing the amount of anion redox on cycling, the presence of fluorine in the structure may result in additional benefits, such as enhanced surface stability or modification of the cation configuration and its stability upon cycling. These effects are currently very poorly understood. It is notable that almost no oxygen is released from highly fluorinated DRX materials even up to 5 V charge.20 Since F and Li prefer to associate,42 F incorporation modifies the SRO in the DRX structure, impacting the distribution of Li+ diffusion channels and Li percolation. The creation of Li-rich F environments (e.g., F–Li6 or F–Li5M) can also cause a “Li locking” or “Li gettering” effect, whereby F ions in Li-rich environments in the as-prepared material become undercoordinated on charge and bind more strongly to the remaining Li+ ions in the structure, making them unextractable within a reasonable voltage window. While it was initially believed that the solubility limit of F at a typical synthesis temperature of 1000 °C is relatively independent of composition at about 7.5 to 10% F, a more nuanced picture is that short-range order and fluorine solubility limits are highly related, with fluorine strongly preferring certain cation arrangements. In this regard, Monte Carlo simulations have proven to be a powerful tool to guide the compositional design of DRX cathodes.66,138
b. Synthetic methods, compositional inhomogeneities and carbon embedding
Developing synthesis routes that optimize the performance of DRX materials is a field in its infancy. Most DRX materials are synthesized by classic solid-state synthesis methods around 700–1100 °C. Metastable materials, such as compounds with a high fluorine content or compositions that are not cation-disordered at typical firing temperatures, are made by extensive ball milling. DRX oxides prepared via a solid-state synthetic route generally consist of micron-sized particles, which are then reduced to sub-micrometer sizes by milling. In fact, most Mo6+-containing, Nb5+-containing and V5+-containing DRXs reported to date have average particle sizes ranging from 100 nm to 100 s of nm, as shown in Table 1, and generally require an excess of Li to be percolating. Hydrothermal synthesis,44,45 soft chemistry approaches,46 spray-drying methods47 and sol–gel techniques49,53,54 have been used to synthesize Ti4+-containing DRXs, resulting in smaller particles (<100 nm) and good Li percolation at stoichiometric or even sub-stoichiometric Li contents. A reduced Li content is advantageous as it enables more redox-active M species in the material, resulting in an increase in the transition metal redox reservoir, though the high surface area of nanomaterials is problematic in terms of surface reactivity and electrode energy density. The relative importance of Ti4+-induced SRO and particle size on the exceptional Li+ transport properties of Ti4+-containing DRX cathodes has not yet been elucidated, hence, further studies investigating nanosized Mo6+-, Nb5+- and V5+-containing DRXs will be useful to disentangle SRO and particle size factors.Fluorination can lead to additional compositional inhomogeneities and more complicated SRO, requiring advanced characterization techniques to unravel details of the complex crystal structure of the cathode. To date, DRX oxyfluorides with a high F content (more than 10% or a stoichiometry of F0.2) can only be synthesized via mechanochemical ball milling. While these cathodes generally exhibit excellent electrochemical performance, it can be very difficult to characterize them due to the small particle size, poor crystallinity and potential presence of amorphous phases or domains. Traditional solid-state synthesis for low fluorination levels (below 10% or F0.2) yields samples with a higher crystallinity and a lower fraction of amorphous impurities. It is worth noting that LiF is the only source of F currently used to synthesize DRX oxyfluorides and is a relatively stable precursor. Alternative F precursors and advanced fluorination techniques are needed to achieve higher fluorination levels while maintaining good crystallinity. In addition, more research is required to understand the fluorine solubility in DRX materials and to establish alternative and scalable paths for the synthesis of materials with high fluorine contents.
Finally, the standard procedure for making DRX cathode films involves the use of a carbonaceous material to increase the electronic conductivity of the electrode. In the majority of cases, the precursor oxide powders are ball-milled with carbon black (or an equivalent source of carbon) to decrease the average particle size and intimately mix the active material with conductive carbon. Rather than mixing in carbon, carbon embedding or the use of a carbonaceous template during synthesis has been suggested to prevent particle agglomeration50 and presumably contributes to the exceptional electrochemical performance of nanosized, Li stoichiometric Li2FeVyTi1−yO4 compounds.53–55 Hence, the exploration carbon-templated nanosized cathodes holds promise for the development of very high energy density DRX cathodes.
In summary, while the compositional and structural freedom in DRX cathodes holds tremendous promise for the Li-ion battery field, they also pose new challenges in terms of characterization and synthesis. While we have covered some of the important aspects of these materials, others, such as the low and isotropic volume expansion identified in early DRX9 have not been discussed as no information exists as to how general this low volume expansion is. In particular, for solid-state batteries, the low volume expansion may be a significant advantage.
c. Compatibility of DRX cathodes with electrolytes and anodes – full cell design
Electrolyte stability against DRX cathodes has not been at the focus of any study to date. Yet, DEMS measurements on half-cells containing a carbonate-based electrolyte and a DRX cathode hint to electrolyte decomposition at high potentials.19,20,135 In these studies, irreversible carbon dioxide gas release was observed above 4.4 V vs. Li+/Li, but the mechanisms underlying electrolyte decomposition remain unclear. Such irreversible processes are problematic as they can lead to growth of a cathode electrolyte interphase with poor Li+ conductivity and to impedance buildup. In DRX oxyfluorides, the cathode surface is expected to be partially passivated by the presence of F, but a fluorinated surface may also reduce the electronic conductivity, and the net impact of F doping on interfacial stability has yet to be elucidated. Since electrolyte stability is directly related to the Coulombic efficiency of the full cell, it will need to be evaluated more carefully in future work.Transition metal dissolution into the electrolyte can reduce long-term cyclability of full cells and cause impedance growth at the anode and should therefore be considered in full cell designs. In this regard, the use of a concentrated electrolyte136,149 and DRX cathode surface coatings9 are two promising approaches to mitigate transition metal dissolution.
Full cell studies are rare. So far, the great majority of studies on DRX cathodes have used half-cells, i.e., a Li metal anode. Amongst the few full cell studies of DRX cathodes, Chen et al. demonstrated that the Li2VO2F DRX cathode exhibits comparable capacity and reasonable cyclability in a Li2VO2F/graphite full cell compared to a Li2VO2F/Li half-cell.11 Similarly, the Li4Ti5O12 anode was found to be compatible with the Li2.1Ti0.2Mo0.7O2F DRX cathode.136 The demonstration of full cells containing DRX cathodes is crucial for their commercialization and requires that the compatibility between the DRX cathode, the electrolyte and the anode be considered.
Conclusions
Disordered lithium transition metal oxides with the rocksalt structure are an emerging class of high energy density Li-ion cathodes. These compounds exhibit a number of unique characteristics, including small volume changes during cycling and sloping voltage profiles. Most of these compounds require a d0 metal species to stabilize the disordered structure, as well as Li excess to ensure good Li+ transport. One of the main advantages of DRXs is the ability to use a wide range of transition metal species, as compared to layered oxides which are mainly based on a combination of Ni, Co and Mn species. Fe-, Ti-, and Mn-containing disordered oxides are particularly attractive in terms of sustainability and cost.The choice of d0 metal species determines the degree and type of short-range order in the material, strongly impacting Li+ conductivity. In this respect, Ti4+-containing disordered oxides have demonstrated superior Li percolation properties, even at stoichiometric or sub-stoichiometric Li contents. Particle size and compositional homogeneity are other important considerations. As compared to standard solid-state synthesis, soft chemistry, sol–gel and hydrothermal routes can result in smaller particles and fewer compositional inhomogeneities, enhancing both Li+ and electronic conduction.
As in layered Li-excess transition metal oxides, the presence of unhybridized O 2p states in the disordered structure activates O oxidation and/or O loss at the end of charge, leading to poorly reversible electrochemistry on discharge. F substitution for O can be used to increase the transition metal redox reservoir, thereby reducing O oxidation and/or O loss at high voltage, resulting in more reversible redox reactions. Fluorinated DRXs have recently demonstrated reversible capacities > 300 mA h g−1 and extremely high energy densities approaching 1000 W h kg−1 over the range 1.5–5.0 V vs. Li+/Li,20 holding promise for a nearly two-fold increase in the energy density of commercial Li-ion batteries.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partly supported by Umicore Specialty Oxides and Chemicals. Modeling work was supported by the Assistant Secretary for Energy Efficiency and Renewable Energy, Vehicle Technologies Office, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231, under the Advanced Battery Materials Research (BMR) Program. Recent work in this area also received support from the Assistant Secretary for Energy Efficiency and Renewable Energy, Vehicle Technologies Office, under the Applied Battery Materials Program, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. The authors would like to thank Prof. Elsa Olivetti (MIT) for help with obtaining metal prices and Ms Tina Chen for proofreading the final manuscript with great care.References
- M. Hepperle, presented at Energy Efficient Technologies and Concept of Operation, Lisbon, October, 2012.
- A. Misra, presented at SciTech Forum, Kissimmee, FL, January, 2018.
- E. A. Olivetti, G. Ceder, G. G. Gaustad and X. Fu, Joule, 2017, 1, 229–243 CrossRef.
- M. S. Whittingham, Science, 1976, 192, 1126–1127 CrossRef CAS PubMed.
- D. Morgan, A. Van der Ven and G. Ceder, Electrochem. Solid-State Lett., 2004, 7, A30–A32 CrossRef CAS.
- A. Van der Ven, J. Bhattacharya and A. A. Belak, Acc. Chem. Res., 2013, 46, 1216–1225 CrossRef CAS PubMed.
- M. M. Thackeray, P. J. Johnson, L. A. de Picciotto, P. G. Bruce and J. B. Goodenough, Mater. Res. Bull., 1984, 19, 179–187 CrossRef CAS.
- M. N. Obrovac, O. Mao and J. R. Dahn, Solid State Ionics, 1998, 112, 9–19 CrossRef CAS.
- J. Lee, A. Urban, X. Li, D. Su, G. Hautier and G. Ceder, Science, 2014, 343, 519–522 CrossRef CAS PubMed.
- R. Chen, S. Ren, M. Yavuz, A. A. Guda, V. Shapovalov, R. Witter, M. Fichtner and H. Hahn, Phys. Chem. Chem. Phys., 2015, 17, 17288–17295 RSC.
- R. Chen, S. Ren, M. Knapp, D. Wang, R. Witter, M. Fichtner and H. Hahn, Adv. Energy Mater., 2015, 5, 1401814 CrossRef.
- S. Ren, R. Chen, E. Maawad, O. Dolotko, A. A. Guda, V. Shapovalov, D. Wang, H. Hahn and M. Fichtner, Adv. Sci., 2015, 2, 1500128 CrossRef PubMed.
- N. Yabuuchi, M. Takeuchi, M. Nakayama, H. Shiiba, M. Ogawa, K. Nakayama, T. Ohta, D. Endo, T. Ozaki, T. Inamasu, K. Sato and S. Komaba, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7650–7655 CrossRef CAS PubMed.
- J. Lee, D.-H. Seo, M. Balasubramanian, N. Twu, X. Li and G. Ceder, Energy Environ. Sci., 2015, 8, 3255–3265 RSC.
- N. Yabuuchi, Y. Tahara, S. Komaba, S. Kitada and Y. Kajiya, Chem. Mater., 2016, 28, 416–419 CrossRef CAS.
- T. Matsuhara, Y. Tsuchiya, K. Yamanaka, K. Mitsuhara, T. Ohta and N. Yabuuchi, Electrochemistry, 2016, 84, 797–801 CrossRef CAS.
- S. Hoshino, A. M. Glushenkov, S. Ichikawa, T. Ozaki, T. Inamasu and N. Yabuuchi, ACS Energy Lett., 2017, 2, 733–738 CrossRef CAS.
- N. Yabuuchi, M. Nakayama, M. Takeuchi, S. Komaba, Y. Hashimoto, T. Mukai, H. Shiiba, K. Sato, Y. Kobayashi, A. Nakao, M. Yonemura, K. Yamanaka, K. Mitsuhara and T. Ohta, Nat. Commun., 2016, 7, 13814 CrossRef CAS PubMed.
- W. H. Kan, D. Chen, J. K. Papp, A. K. Shukla, A. Huq, C. M. Brown, B. D. McCloskey and G. Chen, Chem. Mater., 2018, 30, 1655–1666 CrossRef CAS.
- J. Lee, D. A. Kitchaev, D.-H. Kwon, C.-W. Lee, J. K. Papp, Y.-S. Liu, Z. Lun, R. J. Clément, T. Shi, B. D. McCloskey, J. Guo, M. Balasubramanian and G. Ceder, Nature, 2018, 556, 185–190 CrossRef CAS PubMed.
- H. Ji, A. Urban, D. A. Kitchaev, D.-H. Kwon, N. Artrith, C. Ophus, W. Huang, Z. Cai, T. Shi, J. C. Kim, H. Kim and G. Ceder, Nat. Commun., 2019, 10, 592 CrossRef PubMed.
- A. Urban, J. Lee and G. Ceder, Adv. Energy Mater., 2014, 4, 1400478 CrossRef.
- J. Reed and G. Ceder, Chem. Rev., 2004, 104, 4513–4534 CrossRef CAS PubMed.
- U.S. Geological Survey, 2019, Mineral commodity summaries 2019: U.S. Geological Survey, p. 200, https://doi.org/10.3133/70202434.
- T. A. Hewston and B. L. Chamberland, J. Phys. Chem. Solids, 1987, 48, 97–108 CrossRef CAS.
- E. J. Wu, P. D. Tepesch and G. Ceder, Philos. Mag. B, 1998, 77, 1039–1047 CrossRef CAS.
- H. J. Orman and P. J. Wiseman, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1984, 40, 12–14 CrossRef.
- W. Rüdorff and H. Becker, Z. Naturforsch. B, 1954, 9, 614–615 Search PubMed.
- L. D. Dyer, B. S. Borie Jr. and G. P. Smith, J. Am. Chem. Soc., 1954, 76, 1499–1503 CrossRef CAS.
- R. Hoppe, Angew. Chem., 1959, 71, 457 Search PubMed.
- C. J. M. Rooymans, Z. Anorg. Allg. Chem., 1961, 313, 234–235 CrossRef CAS.
- R. Hoppe, B. Schepers, H.-J. Rohrborn and E. Vielhaber, Z. Anorg. Allg. Chem., 1965, 339, 130–143 CrossRef CAS.
- W. D. Johnston and R. R. Heikes, J. Am. Chem. Soc., 1956, 78, 3255–3260 CrossRef CAS.
- J. B. Goodenough, J. Phys. Radium, 1959, 20, 155–159 CrossRef CAS.
- J. D. Dunitz and L. E. Orgel, J. Phys. Chem. Solids, 1957, 3, 20–29 CrossRef CAS.
- E. Rossen, J. N. Reimers and J. R. Dahn, Solid State Ionics, 1993, 62, 53–60 CrossRef CAS.
- E. Lee, J. Blauwkamp, F. C. Castro, J. Wu, V. P. Dravid, P. Yan, C. Wang, S. Kim, C. Wolverton, R. Benedek, F. Dogan, J. S. Park, J. R. Croy and M. M. Thackeray, ACS Appl. Mater. Interfaces, 2016, 8, 27720–27729 CrossRef CAS PubMed.
- R. J. Gummow and M. M. Thackeray, Solid State Ionics, 1992, 53–56, 681–687 CrossRef CAS.
- J. Reed and G. Ceder, Electrochem. Solid-State Lett., 2002, 5, A145–A148 CrossRef CAS.
- C. Wolverton and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 2242–2252 CrossRef CAS.
- A. Urban, I. Matts, A. Abdellahi and G. Ceder, Adv. Energy Mater., 2016, 6, 1600488 CrossRef.
- W. D. Richards, S. T. Dacek, D. A. Kitchaev and G. Ceder, Adv. Energy Mater., 2017, 1701533 Search PubMed.
- S. L. Glazier, J. Li, J. Zhou, T. Bond and J. R. Dahn, Chem. Mater., 2015, 27, 7751–7756 CrossRef CAS.
- H. Shigemura, M. Tabuchi, H. Sakaebe, H. Kobayashi and H. Kageyama, J. Electrochem. Soc., 2003, 150, A638–A644 CrossRef CAS.
- M. Tabuchi, A. Nakashima, H. Shigemura, K. Ado, H. Kobayashi, H. Sakaebe, K. Tatsumi, H. Kageyama, T. Nakamura and R. Kanno, J. Mater. Chem., 2003, 13, 1747–1757 RSC.
- S. Prabaharan, M. S. Michael, H. Ikuta, Y. Uchimoto and M. Wakihara, Solid State Ionics, 2004, 172, 39–45 CrossRef CAS.
- L. Zhang, H. Noguchi, D. Li, T. Muta, X. Wang, M. Yoshio and I. Taniguchi, J. Power Sources, 2008, 185, 534–541 CrossRef CAS.
- M. Yang, X. Zhao, Y. Bian, L. Ma, Y. Ding and X. Shen, J. Mater. Chem., 2012, 22, 6200–6205 RSC.
- X. Zhang, L. Yang, F. Hao, H. Chen, M. Yang and D. Fang, Nanomaterials, 2015, 5, 1985–1994 CrossRef CAS PubMed.
- M. Küzma, R. Dominko, A. Meden, D. Makovec, M. Bele, J. Jamnik and M. Gaberšček, J. Power Sources, 2009, 189, 81–88 CrossRef.
- M. Kuezma, R. Dominko, D. Hanžel, A. Kodre, I. Arčon, A. Meden and M. Gaberšček, J. Electrochem. Soc., 2009, 156, A809–A816 CrossRef CAS.
- A. Kitajou, K. Tanaka, H. Miki, H. Koga, T. Okajima and S. Okada, Electrochemistry, 2016, 84, 597–600 CrossRef CAS.
- M. Yang, X. Zhao, C. Yao, Y. Kong, L. Ma and X. Shen, Mater. Technol., 2016, 31, 537–543 CrossRef CAS.
- R. Chen, R. Witte, R. Heinzmann, S. Ren, S. Mangold, H. Hahn, R. Hempelmann, H. Ehrenberg and S. Indris, Phys. Chem. Chem. Phys., 2016, 18, 7695–7701 RSC.
- R. Dominko, C. V.-A. Garrido, M. Bele, M. Kuezma, I. Arcon and M. Gaberscek, J. Power Sources, 2011, 196, 6856–6862 CrossRef CAS.
- A. Urban, A. Abdellahi, S. Dacek, N. Artrith and G. Ceder, Phys. Rev. Lett., 2017, 119, 176402 CrossRef PubMed.
- R. Wang, X. Li, L. Liu, J. Lee, D.-H. Seo, S.-H. Bo, A. Urban and G. Ceder, Electrochem. Commun., 2015, 60, 70–73 CrossRef CAS.
- N. Yabuuchi, M. Takeuchi, S. Komaba, S. Ichikawa, T. Ozaki and T. Inamasu, Chem. Commun., 2016, 52, 2051–2054 RSC.
- M. Nakajima and N. Yabuuchi, Chem. Mater., 2017, 29, 6927–6935 CrossRef CAS.
- C. Delmas, S. Brèthes and M. Ménétrier, J. Power Sources, 1991, 34, 113–118 CrossRef CAS.
- V. Pralong, V. Gopal, V. Caignaert, V. Duffort and B. Raveau, Chem. Mater., 2011, 24, 12–14 CrossRef.
- S. Liu, X. Feng, X. Wang, X. Shen, E. Hu, R. Xiao, R. Yu, H. Yang, N. Song, Z. Wang, X. Yang and L. Chen, Adv. Energy Mater., 2018, 149, 1703092 CrossRef.
- M. Freire, N. V. Kosova, C. Jordy, D. Chateigner, O. I. Lebedev, A. Maignan and V. Pralong, Nat. Mater., 2016, 15, 173–177 CrossRef CAS PubMed.
- M. Freire, M. Diaz-Lopez, P. Bordet, C. V. Colin, O. I. Lebedev, N. V. Kosova, C. Jordy, D. Chateigner, A. L. Chuvilin, A. Maignan and V. Pralong, J. Mater. Chem. A, 2018, 6, 5156–5165 RSC.
- M. Freire, O. I. Lebedev, A. Maignan, C. Jordy and V. Pralong, J. Mater. Chem. A, 2017, 5, 21898–21902 RSC.
- D. A. Kitchaev, Z. Lun, W. D. Richards, H. Ji, R. J. Clément, M. Balasubramanian, D.-H. Kwon, K. Dai, J. K. Papp, T. Lei, B. D. McCloskey, W. Yang, J. Lee and G. Ceder, Energy Environ. Sci., 2018, 104, 4271 Search PubMed.
- E. M. Gutman, Mechanochemistry of Solid Surfaces, World Scientific Publishing Co. Inc., Singapore, 1994 Search PubMed.
- F. Dachille and R. Roy, J. Geol., 1964, 72, 243–247 CrossRef CAS.
- A. Van der Ven and G. Ceder, Electrochem. Solid-State Lett., 2000, 3, 301–304 CrossRef CAS.
- A. Van der Ven and G. Ceder, J. Power Sources, 2001, 97–98, 529–531 CrossRef CAS.
- M. Catti, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 1795–1803 CrossRef CAS.
- K. Kang and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 094105 CrossRef.
- K. Kang, Y. S. Meng, J. Breger, C. P. Grey and G. Ceder, Science, 2006, 311, 977–980 CrossRef CAS PubMed.
- R. J. Clément, D. Kitchaev, J. Lee and G. Ceder, Chem. Mater., 2018, 30, 6945–6956 CrossRef.
- W. H. Kan, B. Deng, Y. Xu, A. K. Shukla, T. Bo, S. Zhang, J. Liu, P. Pianetta, B.-T. Wang, Y. Liu and G. Chen, Chem, 2018, 4, 2108–2123 CAS.
- M. A. Jones, P. J. Reeves, I. D. Seymour, M. J. Cliffe, S. E. Dutton and C. P. Grey, Chem. Commun., 2019, 55, 9027–9030 RSC.
- D. D. Fontaine, J. Phys. Chem. Solids, 1973, 34, 1285–1304 CrossRef.
- F. Ducastelle, in Order and Phase Stability in Alloys, ed. K. Terakura and H. Akai, Springer Berlin Heidelberg, Berlin, Heidelberg, 1993, pp. 133–142 Search PubMed.
- L. Reinhard and S. C. Moss, Ultramicroscopy, 1993, 52, 223–232 CrossRef CAS.
- M. A. Jones, P. J. Reeves, I. D. Seymour, M. J. Cliffe, S. E. Dutton and C. P. Grey, Chem. Commun., 2019, 55, 9027–9030 RSC.
- I. Hung, L. Zhou, F. Pourpoint, C. P. Grey and Z. Gan, J. Am. Chem. Soc., 2012, 134, 1898–1901 CrossRef CAS PubMed.
- R. De Ridder, G. van Tendeloo and S. Amelinckx, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 216–224 CrossRef.
- M. Saubanère, M. Ben Yahia, S. Lebègue and M.-L. Doublet, Nat. Commun., 2014, 5, 5559 CrossRef PubMed.
- A. Abdellahi, A. Urban, S. Dacek and G. Ceder, Chem. Mater., 2016, 28, 3659–3665 CrossRef CAS.
- Y. Lyu, L. Ben, Y. Sun, D. Tang, K. Xu, L. Gu, R. Xiao, H. Li, L. Chen and X. Huang, J. Power Sources, 2015, 273, 1218–1225 CrossRef CAS.
- S.-H. Bo, X. Li, A. J. Toumar and G. Ceder, Chem. Mater., 2016, 28, 1419–1429 CrossRef CAS.
- J. Lee, J. K. Papp, R. J. Clément, S. Sallis, D.-H. Kwon, T. Shi, W. Yang, B. D. McCloskey and G. Ceder, Nat. Commun., 2017, 8, 981 CrossRef PubMed.
- H. Kim, J. C. Kim, M. Bianchini, D.-H. Seo, J. R. Garcia and G. Ceder, Adv. Energy Mater., 2018, 8, 1702384 CrossRef.
- A. Van der Ven, M. K. Aydinol, G. Ceder, G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 2975–2987 CrossRef CAS.
- A. Abdellahi, A. Urban, S. Dacek and G. Ceder, Chem. Mater., 2016, 28, 5373–5383 CrossRef CAS.
- J. Bréger, Y. S. Meng, Y. Hinuma, S. Kumar, K. Kang, Y. Shao-Horn, A. G. Ceder and C. P. Grey, Chem. Mater., 2006, 18, 4768–4781 CrossRef.
- W.-S. Yoon, K.-B. Kim, M.-G. Kim, M.-K. Lee, H.-J. Shin and J.-M. Lee, J. Electrochem. Soc., 2002, 149, A1305–A1309 CrossRef CAS.
- W.-S. Yoon, M. Balasubramanian, K.-Y. Chung, X.-Q. Yang, J. McBreen, C. P. Grey and D. A. Fischer, J. Am. Chem. Soc., 2005, 127, 17479–17487 CrossRef CAS PubMed.
- L. Dahéron, R. Dedryvère, H. Martinez, M. Ménétrier, C. Denage, C. Delmas and D. Gonbeau, Chem. Mater., 2007, 20, 583–590 CrossRef.
- N. Yabuuchi, K. Yoshii, S.-T. Myung, I. Nakai and S. Komaba, J. Am. Chem. Soc., 2011, 133, 4404–4419 CrossRef CAS PubMed.
- H. Koga, L. Croguennec, M. Ménétrier, K. Douhil, S. Belin, L. Bourgeois, E. Suard, F. Weill and C. Delmas, J. Electrochem. Soc., 2013, 160, A786–A792 CrossRef CAS.
- H. Koga, L. Croguennec, M. Ménétrier, P. Mannessiez, F. Weill and C. Delmas, J. Power Sources, 2013, 236, 250–258 CrossRef CAS.
- M. Sathiya, G. Rousse, K. Ramesha, C. P. Laisa, H. Vezin, M. T. Sougrati, M.-L. Doublet, D. Foix, D. Gonbeau, W. Walker, A. S. Prakash, M. Ben Hassine, L. Dupont and J.-M. Tarascon, Nat. Mater., 2013, 12, 827–835 CrossRef CAS PubMed.
- M. Sathiya, A. M. Abakumov, D. Foix, G. Rousse, K. Ramesha, M. Saubanère, M.-L. Doublet, H. Vezin, C. P. Laisa, A. S. Prakash, D. Gonbeau, G. VanTendeloo and J.-M. Tarascon, Nat. Mater., 2015, 14, 230–238 CrossRef CAS PubMed.
- E. McCalla, A. M. Abakumov, M. Saubanère, D. Foix, E. J. Berg, G. Rousse, M.-L. Doublet, D. Gonbeau, P. Novák, G. Van Tendeloo, R. Dominko and J.-M. Tarascon, Science, 2015, 350, 1516–1521 CrossRef CAS PubMed.
- G. Assat, C. Delacourt, D. A. D. Corte and J.-M. Tarascon, J. Electrochem. Soc., 2016, 163, A2965–A2976 CrossRef CAS.
- K. Luo, M. R. Roberts, R. Hao, N. Guerrini, D. M. Pickup, Y.-S. Liu, K. Edström, J. Guo, A. V. Chadwick, L. C. Duda and P. G. Bruce, Nat. Chem., 2016, 8, 684–691 CrossRef CAS PubMed.
- S. Hy, H. Liu, M. Zhang, D. Qian, B.-J. Hwang and Y. S. Meng, Energy Environ. Sci., 2016, 9, 1931–1954 RSC.
- G. Assat, D. Foix, C. Delacourt, A. Iadecola, R. Dedryvère and J.-M. Tarascon, Nat. Commun., 2017, 8, 2219 CrossRef PubMed.
- W. E. Gent, K. Lim, Y. Liang, Q. Li, T. Barnes, S.-J. Ahn, K. H. Stone, M. McIntire, J. Hong, J. H. Song, Y. Li, A. Mehta, S. Ermon, T. Tyliszczak, D. Kilcoyne, D. Vine, J.-H. Park, S.-K. Doo, M. F. Toney, W. Yang, D. Prendergast and W. C. Chueh, Nat. Commun., 2017, 8, 2091 CrossRef PubMed.
- B. Li and D. Xia, Adv. Mater., 2017, 29, 1701054 CrossRef PubMed.
- E. Lee and K. A. Persson, Adv. Energy Mater., 2014, 4, 1400498 CrossRef.
- J. Hong, W. E. Gent, P. Xiao, K. Lim, D.-H. Seo, J. Wu, P. M. Csernica, C. J. Takacs, D. Nordlund, C.-J. Sun, K. H. Stone, D. Passarello, W. Yang, D. Prendergast, G. Ceder, M. F. Toney and W. C. Chueh, Nat. Mater., 2019, 18, 256–265 CrossRef CAS PubMed.
- Z. Lu and J. R. Dahn, J. Electrochem. Soc., 2002, 149, A815–A822 CrossRef CAS.
- A. R. Armstrong, A. D. Robertson and P. G. Bruce, J. Power Sources, 2005, 146, 275–280 CrossRef CAS.
- S. F. Amalraj, B. Markovsky, D. Sharon, M. Talianker, E. Zinigrad, R. Persky, O. Haik, J. Grinblat, J. Lampert, M. Schulz-Dobrick, A. Garsuch, L. Burlaka and D. Aurbach, Electrochim. Acta, 2012, 78, 32–39 CrossRef.
- M. Gu, I. Belharouak, J. Zheng, H. Wu, J. Xiao, A. Genc, K. Amine, S. Thevuthasan, D. R. Baer, J.-G. Zhang, N. D. Browning, J. Liu and C. Wang, ACS Nano, 2012, 7, 760–767 CrossRef PubMed.
- J. Rana, M. Stan, R. Kloepsch, J. Li, G. Schumacher, E. Welter, I. Zizak, J. Banhart and M. Winter, Adv. Energy Mater., 2013, 4, 1300998 CrossRef.
- D. Mohanty, J. Li, D. P. Abraham, A. Huq, E. A. Payzant, D. L. Wood III and C. Daniel, Chem. Mater., 2014, 26, 6272–6280 CrossRef CAS.
- M. Saubanère, E. McCalla, J.-M. Tarascon and M.-L. Doublet, Energy Environ. Sci., 2016, 9, 984–991 RSC.
- Y. Xie, M. Saubanère and M.-L. Doublet, Energy Environ. Sci., 2017, 10, 266–274 RSC.
- M. Ben Yahia, J. Vergnet, M. Saubanère and M.-L. Doublet, Nat. Mater., 2019, 18, 496–502 CrossRef CAS PubMed.
- D. Chen, W. H. Kan and G. Chen, Adv. Energy Mater., 2019, 9, 1901255 CrossRef.
- J. B. Goodenough and K.-S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176 CrossRef CAS PubMed.
- J. B. Goodenough and Y. Kim, J. Power Sources, 2011, 196, 6688–6694 CrossRef CAS.
- M. K. Aydinol, A. F. Kohan, G. Ceder, K. Cho and J. Joannopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 1354–1365 CrossRef CAS.
- D.-H. Seo, J. Lee, A. Urban, R. Malik, S. Kang and G. Ceder, Nat. Chem., 2016, 8, 692–697 CrossRef CAS PubMed.
- S. Kang, Y. Mo, S. P. Ong and G. Ceder, Chem. Mater., 2013, 25, 3328–3336 CrossRef CAS.
- U. Maitra, R. A. House, J. W. Somerville, N. Tapia-Ruiz, J. G. Lozano, N. Guerrini, R. Hao, K. Luo, L. Jin, M. A. Pérez-Osorio, F. Massel, D. M. Pickup, S. Ramos, X. Lu, D. E. McNally, A. V. Chadwick, F. Giustino, T. Schmitt, L. C. Duda, M. R. Roberts and P. G. Bruce, Nat. Chem., 2018, 10, 288–295 CrossRef CAS PubMed.
- C. Ma, J. Alvarado, J. Xu, R. J. Clément, M. Kodur, W. Tong, C. P. Grey and Y. S. Meng, J. Am. Chem. Soc., 2017, 139, 4835–4845 CrossRef CAS PubMed.
- B. M. de Boisse, S.-I. Nishimura, E. Watanabe, L. Lander, A. Tsuchimoto, J. Kikkawa, E. Kobayashi, D. Asakura, M. Okubo and A. Yamada, Adv. Energy Mater., 2018, 8, 1800409 CrossRef.
- N. Tran, L. Croguennec, M. Ménétrier, F. Weill, P. Biensan, C. Jordy and C. Delmas, Chem. Mater., 2008, 20, 4815–4825 CrossRef CAS.
- A. R. Armstrong, M. Holzapfel, P. Novák, C. S. Johnson, S.-H. Kang, M. M. Thackeray and P. G. Bruce, J. Am. Chem. Soc., 2006, 128, 8694–8698 CrossRef CAS PubMed.
- M. D. Radin, J. Vinckevičiūtė, R. Seshadri and A. Van der Ven, Nat. Energy, 2019, 4, 639–646 CrossRef CAS.
- M. Ménétrier, J. Bains, L. Croguennec, A. Flambard, E. Bekaert, C. Jordy, P. Biensan and C. Delmas, J. Solid State Chem., 2008, 181, 3303–3307 CrossRef.
- L. Croguennec, J. Bains, M. Ménétrier, A. Flambard, E. Bekaert, C. Jordy, P. Biensan and C. Delmas, J. Electrochem. Soc., 2009, 156, A349–A355 CrossRef CAS.
- R. Chen, S. Ren, X. Mu, E. Maawad, S. Zander, R. Hempelmann and H. Hahn, ChemElectroChem, 2016, 3, 892–895 CrossRef CAS.
- N. Takeda, S. Hoshino, L. Xie, S. Chen, I. Ikeuchi, R. Natsui, K. Nakura and N. Yabuuchi, J. Power Sources, 2017, 367, 122–129 CrossRef CAS.
- R. A. House, L. Jin, U. Maitra, K. Tsuruta, J. W. Somerville, D. P. Förstermann, F. Massel, L. Duda, M. R. Roberts and P. G. Bruce, Energy Environ. Sci., 2018, 11, 926–932 RSC.
- Z. Lun, B. Ouyang, D. A. Kitchaev, R. J. Clément, J. K. Papp, M. Balasubramanian, Y. Tian, T. Lei, T. Shi, B. D. McCloskey, J. Lee and G. Ceder, Adv. Energy Mater., 2019, 9, 1802959 CrossRef.
- N. Takeda, I. Ikeuchi, R. Natsui, K. Nakura and N. Yabuuchi, ACS Appl. Energy Mater., 2019, 2, 1629–1633 CrossRef CAS.
- E. Zhao, Q. Li, F. Meng, J. Liu, J. Wang, L. He, Z. Jiang, Q. Zhang, X. Yu, L. Gu, W. Yang, H. Li, F. Wang and X. Huang, Angew. Chem., Int. Ed., 2019, 58, 4323–4327 CrossRef CAS PubMed.
- H. Ji, D. A. Kitchaev, Z. Lun, H. Kim, E. Foley, D.-H. Kwon, Y. Tian, M. Balasubramanian, M. Bianchini, Z. Cai, R. J. Clément, J. C. Kim and G. Ceder, Chem. Mater., 2019, 31, 2431–2442 CrossRef CAS.
- Q. Wang, A. Sarkar, Di Wang, L. Velasco, R. Azmi, S. S. Bhattacharya, T. Bergfeldt, A. Düvel, P. Heitjans, T. Brezesinski, H. Hahn and B. Breitung, Energy Environ. Sci., 2019, 6, 8485 Search PubMed.
- Z. Lun, B. Ouyang, Z. Cai, R. J. Clément, D.-H. Kwon, J. Huang, J. K. Papp, M. Balasubramanian, Y. Tian, B. D. McCloskey, H. Ji, H. Kim, D. A. Kitchaev and G. Ceder, Chem, 2020 DOI:10.1016/j.chempr.2019.10.001.
- E. Zhao, L. He, B. Wang, X. Li, J. Zhang, Y. Wu, J. Chen, S. Zhang, T. Liang, Y. Chen, X. Yu, H. Li, L. Chen, X. Huang, H. Chen and F. Wang, Energy Storage Mater., 2019, 16, 354–363 CrossRef.
- I. Källquist, A. J. Naylor, C. Baur, J. Chable, J. Kullgren, M. Fichtner, K. Edström, D. Brandell and M. Hahlin, Chem. Mater., 2019, 31, 6084–6096 CrossRef.
- S. Zheng, D. Liu, L. Tao, X. Fan, K. Liu, G. Liang, A. Dou, M. Su, Y. Liu and D. Chu, J. Alloys Compd., 2019, 773, 1–10 CrossRef CAS.
- M. A. Cambaz, B. P. Vinayan, H. Geßwein, A. Schiele, A. Sarapulova, T. Diemant, A. Mazilkin, T. Brezesinski, R. J. Behm, H. Ehrenberg and M. Fichtner, Chem. Mater., 2019, 31, 4330–4340 CrossRef CAS.
- Y. Shin, W. H. Kan, M. Aykol, J. K. Papp, B. D. McCloskey, G. Chen and K. A. Persson, Nat. Commun., 2018, 9, 4597 CrossRef PubMed.
- R. Kataoka, N. Taguchi, T. Kojima, N. Takeichi and T. Kiyobayashi, J. Mater. Chem. A, 2019, 7, 5381–5390 RSC.
- Y. Sun, Z. Wang, X. Huang and L. Chen, J. Power Sources, 2005, 146, 678–681 CrossRef CAS.
- Y. Liu, S. Zheng, H. Wan, A. Dou, D. Chu and M. Su, J. Alloys Compd., 2017, 728, 659–668 CrossRef CAS.
- M. A. Cambaz, B. P. Vinayan, H. Euchner, S. A. Pervez, H. Geßwein, T. Braun, A. Gross and M. Fichtner, ACS Appl. Mater. Interfaces, 2019, 11, 39848–39858 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2020 |