On the comparison of oxygen and sulfur transfer reactivities in phosphine and phosphorene: the case of R₃Sb(X) carriers (X = O or S)

Abstract

Functionalization is one of the most powerful tools in materials science for the development of new and innovative materials with tailored properties purposefully designed to enhance the overall stability of the system. This is particularly true for exfoliated black phosphorus, which suffers from easy decomposition by air and moisture, hampering its highly desirable applications, especially in electronics. The present work suggests an innovative approach to the functionalization process of this 2D-material based on the selective introduction of chalcogen atoms on the material surface through a reaction with suitable molecular precursors such as stibine chalcogenides (R₃Sb(X), X = O or S; R = organyl group). These molecules may readily act as chalcogen-transfer agents and, upon releasing the chalcogen atom atop the bP surface, leave stable stibines (R₃Sb) as byproducts, which may be easily removed from the functionalized bP surface. The work provides an overview of all the possible structural, electronic and energy aspects associated with the chalcogen-atom transfer from the stibine to phosphorus based compounds, exemplified by trialkyl phosphines and single layer exfoliated black phosphorus, i.e. phosphorene, P_n. In both cases the oxygen transfer is more exergonic than the sulfur transfer, with the associated free energy barrier for the phosphine process being higher. Although the sulfur transfer for the P_n is found to be endergonic (ca. +3.6 kcal mol⁻¹), the process may surely occur at high temperature. The evolution of the band structure upon the chalcogen transfer has been depicted in detail.

---

Introduction

Understanding the reactivity at the molecular level is essential in chemistry. In the blooming research area of 2D materials science, black phosphorus (bP) and its fully exfoliated form, phosphorene (P_n),¹ have acquired particular importance owing to their tunable direct band gap. The band gap of the latter, depending on the thickness of the material, ranges from 0.3 up to more than 2.0 eV on going from bulk bP to phosphorene, and it could also be modulated by different physical perturbations such as laser action.² The limited usage of exfoliated bP in the fabrication of devices for application in both electronics and optics is mostly due to the low stability of the material when exposed to oxygen and/or moisture.³ In principle, the great availability of P-based lone pairs at the 2D-material surface may indicate an easy functionalization, but, although in the last years a lot of effort has been made to achieve a genuine covalent functionalization, the results are still very scarce or not undoubted.⁴ On the other hand, in order to enhance the stability of the material, many results have been obtained by the encapsulation of exfoliated black phosphorus into different matrices through noncovalent interactions.⁵

The difficulty of achieving covalent functionalization has been associated with the reduced donor power of the surface lone pairs together with some degree of delocalization.⁶ The choice of suitable substrates for reaction with the P_n layer may not only enhance the stability but also impart peculiar electronic properties to the functionalized surface.⁶ In a recent study, a detailed in silico investigation allowed us to provide useful guidelines for proposing an efficient functionalization of the phosphorene P_n surface with Lewis acidic groups or transition metal based moieties (direct path a in Scheme 1).

Scheme 1 Alternative pathways for the direct (path a) and non-direct (path b) metal functionalization of 2D phosphorene.

A perfect σ interaction between the phosphorus lone pairs and suitable empty orbitals of the reagent fragments is fundamental to achieve a good degree of functionalization.⁶ In principle, three different plausible coordination modes were envisaged between the P_n surface and an acidic transition metal fragment, indicated as η¹, η² and η³-coordination modes, respectively, depending on the number of the involved P-lone pairs. In any case, the improper orientation of the P-lone pairs, which are bent by 30° rather than orthogonal to the surface, requires some degree of structural deformation, especially for accomplishing the more sterically demanding η² or η³ coordination mode.^6,7 Thus, in order to prevent any steric and electronic problems, a careful choice of both the metal fragment and suitable co-ligands is required.

An alternative approach, see path b in Scheme 1, for the successful functionalization of phosphorene could involve the decoration of the monolayer with suitable groups showing well defined donor capabilities. These could then be exploited for maximizing the interaction with transition metal fragments or nanoparticles decorating the reactive surface. This kind of functionalization would likely impart a higher stability to the functionalized material toward degradation, bypassing the otherwise required structural deformations, especially associated with η² or η³ coordination mode, and provide a modular electronic structure by changing the loading and the nature of the functionalizing group.

Among the potential fragments, oxygen and sulfur are the best candidates in view of the high inclination of phosphorus to react with them.^3,8 For example, through the reaction of a molecular phosphorus allotrope, white phosphorus, P₄, with oxygen, two different phosphorus oxides may be easily produced with P₄O₆ or P₄O₁₀ stoichiometry, depending on the reaction conditions.⁹ More extended is the series of the phosphorus sulfides; namely, molecular species from P₄S₃ up to P₄S₁₀ may be produced by stepwise breaking the P–P bonds of P₄ and bridging the broken bond with a sulfur atom or just decorating the polyphosphorus unit with terminal sulfur atoms.¹⁰

Concerning exfoliated bP, its reactivity with O₂ has been amply debated under different conditions governing the degradation toward the molecular species while the reaction with sulfur has been less investigated. Generally, the experimental synthetic protocols require harsh reaction conditions,¹¹ such as high temperature and pressure, and start from the phosphorus red allotrope that is reacted with elemental sulfur at about 1000 °C and 2 GPa. In any case, no useful insights have been provided to understand how the reactions proceed and give the obtained by-products.

Thus in order to overcome the possible problem of degradation or low selectivity, the choice of the chalcogenide educt from which the chalcogen atom may effectively be transferred to phosphorene is of great importance. Sulphur transfer reactions between trisubstituted pnictogens (R₃E) have been successfully addressed with phosphorus and arsenic with a large variety of organic groups.¹² More recently, Cummins et al.¹³ reported an efficient method for bringing about the selective sulfuration of a cyclic diphosphane using triphenylstibine sulfide as the S-transfer reagent. Remarkably, the stepwise formation of the P(E) bond (E = O or S) was achieved without affecting the original P–P bond. The present paper predicts and compares the employment of stibine oxide or sulfide as a suitable reagent to deliver chalcogen atoms to different phosphorus-based compounds such as phosphine and 2D black phosphorus sheets. A complete description of the electronic underpinnings, ruling such a process, is examined starting from the phosphine moiety in order to compare the molecular reactivity with that on a 2D surface. A detailed structural/electronic monitoring of the reaction of chalcogen transfer is also provided together with the analysis of the effects on the band gap of the 2D-material.

Results and discussion

Reactivity of the pnictogen–chalcogen system

The electronic nature of the pnictogen/chalcogen bonding is still particularly debated in spite of the large amount of computational and experimental efforts. The most representative examples are phosphine oxides, R₃P(O), whose electronic nature is still the subject of different interpretations described in detail in the review of Gilheany.¹⁴ In particular, there are two opposite viewpoints related to the relative contribution percentage of the electrostatic and covalent interactions to the overall bonding. Everyone now agrees that the strength of the P–O bonds is somewhat comparable to a double bond but with the electronic density polarized towards the oxygen atom. In this regard, Chesnut et al. described such a bond as a highly polar σ bond featuring a strong π back-donation from the oxygen with a final description resembling an ionic π R₃P⁺–O⁻ bond rather than a conventional double bond.¹⁵ Atoms in molecules theory calculations¹⁶ described the P–O bond as a single highly polarized sigma bond whose strength correlated with the electrostatic interactions. More recently, Frenking et al. provided¹⁷ a detailed analysis of the bond in a series of phosphine oxides R₃P(O) where R = H, F, Cl, Me or Ph. In particular, these authors focused on the electronic features of three different plausible interaction models of the phosphine oxides. The first one is the purely dative from a phosphine fragment closed shell into an oxygen center, while the second and the third models involve radical species: an electron sharing double bond between triplet fragments in the former and a single bond between doublets in the latter. The decomposition schemes of energy interactions highlight that in the phosphines the bonding pattern may be described as electron sharing single bonds between charged fragments R₃P⁺–O⁻ with a non-negligible contribution of π back-donation from the oxygen ranging between 22 and 32% depending on the nature of the R substituent. In this regard, we calculated the interaction energy between the radical species for the optimized structures of both the phosphine oxide and sulfide and their stibine analogues. The calculated interaction energy is maximum for the phosphine oxide (−292.5 kcal mol⁻¹) and becomes less efficient by varying both the chalcogen [−224.3 kcal mol⁻¹ for Me₃P(S)] and the pnictogen [−234.2 kcal mol⁻¹ for Me₃Sb(O)], reaching the lowest value for the Me₃Sb(S) (−197.9 kcal mol⁻¹).¹⁸

For the purpose of this article, the main frontier occupied molecular orbitals of the groups involved in the reactivity with the oxygen are drawn in Fig. 1. The situation is similar for the sulphur case. The HOMO of the stibine oxide species is mainly centered on the oxygen atom, while the HOMO−2 could be better described as a σ Sb–O bonding. In the case of the phosphine the HOMO is most purely the lone pair on the phosphorus atom.

Fig. 1 Molecular orbitals involved in the reaction between Me₃Sb(O) and Me₃P.

In conclusion, while the main picture of the electronic structure in the pnictogen/chalcogen system will remain the same, differences are in the different degree of charge separation between the two centers, in the bond strength and also in the reactivity. The analysis of the electronic structure, especially of the MOs or bands near to the frontier, helped us understand the chalcogen transfer both in molecular compounds like trimethyl phosphine and in materials such as single layer exfoliated black phosphorus, phosphorene.

Chalcogen source and mechanism

As said before, moving from phosphorus to antimony and changing the chalcogen from oxygen to sulfur significantly weaken the pnictogen–chalcogen bond. Thus, on the basis of the available information, attention was focused on trimethylstibine oxide or sulfide as a chalcogen transfer reagent. The analysis of the chalcogen transfer processes started from the description of oxygen and sulfur atom transfer from Me₃Sb to the corresponding phosphine, Me₃P. Such processes have been previously investigated and have been reported to be thermodynamically favored.¹²Chart 1 summarizes the energetic features of the reactions together with the energy barriers associated with the achievement of the transition states. Both oxygen and sulfur transfer between stibine abd phosphine are exergonic. The process for the oxygen is in any case more favorable compared to the one involving sulfur, being the free energy gain almost three times greater in the former process compared to the latter one. The situation is reverse for the free energy cost required to achieve the transition states, as shown in Fig. 2, with the barrier being smaller for sulfur than for oxygen.

Chart 1 Free energy parameters associated with the overall chalcogen transfer reaction and with the achievement of the transition state.

Fig. 2 Transition state associated with the oxygen (TS_O) and sulfur (TS_S) transfer from Me₃Sb(X) to Me₃P (X = O or S).

Fig. 2 shows the structure of the transition state of the reaction of Me₃Sb(O) (TS_O) and Me₃Sb(S) (TS_S) with Me₃P. Starting from the stibine oxide, the TS_O displays a linear Sb⋯O⋯P arrangement with the transferred oxygen lying in between the Sb and P centers, with the Sb–O and P–O distances of 2.03 and 2.08 Å, respectively. More importantly, the stibine and phosphine groupings are particularly rearranged compared to the starting reactants. First of all, the Sb–O bond is elongated by 0.16 Å compared to the stibine oxide and, more importantly, both antimony and phosphorus centers exhibit a geometry far from the starting tetrahedral or the trigonal pyramid. In particular, the geometry around the Sb assumes a butterfly conformation with a wider C–Sb–O angle of around 20° and an elongation by 0.05 Å of the trans Sb–C bond. A similar trend occurs also for the phosphine grouping; thus, at the transition state TS_O the transferring oxygen is in between two butterfly arrangements. In a similar structure, the phosphine and the stibine moieties are ready to host and lose the oxygen atom, respectively, by minimizing the repulsions between the lone pairs.

The analysis of the two structures shown in Fig. 2 revealed a substantial difference between the two transition states, although this discrepancy is only apparent. In this regard, in the transition state associated with the sulfur transfer an almost C₃ symmetry seems to be maintained. In any case, a detailed investigation on the transfer of the stibine sulfide to the phosphine revealed that the process occurs in quite the same way as the oxygen transfer, although the structural deformations are not so evident.

Two different mechanisms had already been proposed for the chalcogen exchange reaction between a phosphine (R₃P) and a phosphine chalcogenide, R₃P(X), with different electronic and structural features.^12,19 The former process implies a nucleophilic attack by the lone pair of the R₃P at the phosphorus of R₃P(X) through a three-membered cyclic transition state. Otherwise the latter one involves a R₃P⋯X⋯PR₃ linear arrangement, associated with the chalcophilic attack of the pnictide nucleophile. The latter mechanism has been preferred to the former, especially for the reaction involving heavier chalcogen transfer, while the situation remains quite unclear for the oxygen.¹⁹

A very intriguing view of the bonding in the transition state of the chalcogen transfer process has been suggested by a reviewer of the present manuscript, proposing some similarities to the electronic structure in trifluoride, trichloride or triiodide anions. These systems could be classified as three center-four electron species with the involvement of three molecular orbitals of the σ-system, two of which are filled, namely bonding and non-bonding, and the third is empty with an anti-bonding character.²⁰ On the basis of the isolobal analogy,²¹ the chalcogen transfer between the trimethyl stibine and the trimethyl phosphine could be related, with opportune differences, with the formation of the triiodide anion from iodide and the di-iodine molecule, with the I₂ being similar to the stibine–oxide as the acidic center and the phosphine as iodide. Obviously in contrast with the formation of the tri-halogen anion, in the present case after the TS the oxygen is transferred to the phosphine moiety, providing the stibine.

The suggested intriguing analogy is well highlighted by the HOMO of the transition state, shown in Fig. 3, as the Ψ₂ non-bonding filled combination of the σ system mainly localized on the peripheral phosphorus and antimony centers with a very low contribution from the transferred chalcogen atom.

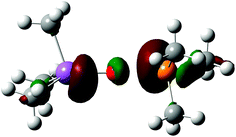Fig. 3 Plot of the HOMO of the transition state, TS_O, for the transfer of the oxygen. The situation is similar for the sulphur case.

In order to better understand the electronic features associated with the chalcogen transfer, a detailed analysis has therefore been carried out on how the reaction proceeds, in particular, by stepwise shortening the P⋯X distance up to the minimum value. The relaxed scan of the potential energy surface revealed that in both cases the transfer of the chalcogen to the phosphorus occurs with the elongation (0.03 Å) of only one of the P–C bond lengths in Me₃P and the distortion of the structure toward the butterfly geometry. Only beyond the transition states the antimony and phosphorus centers reacquire again a C₃ symmetry. Such a structural arrangement is not totally unknown for phosphorus compounds and at least fifteen X-ray structures are available at the Cambridge Crystallographic Database.²² For example, in a constrained system such as (8-dimethylamino-1-naphthyl)diphenylphosphane, the arrangement around the phosphorus atom is far from being trigonal pyramidal, but more close to a butterfly geometry with an intramolecular N → P coordination. The X-ray structure shows a N⋯P distance of 2.7 Å and the N–P–C(phen) angle very close to being linear (173.87°), while among the three C–P–C angles around the phosphorus two are 100° and one is larger showing 103°.²³ Other pertinent examples are the phosphorus compounds with phenylpirazole substituents, where the phosphorus interacts with the lone pair of a nitrogen with the attainment of a butterfly geometry.²⁴

Mulliken charge analysis was carried out at the TS and compared to the starting phosphine and stibine oxide or sulfide and the final phosphorus oxide or sulfide and stibine products. The obtained results are reported in Table 1 together with the optimized phosphorus or antimony distances with oxygen or sulfur.

Table 1 Calculated Mulliken charges and overlap for the reactants, transition states and products of the chalcogen transfer reactions

	Mulliken P/Sb	Mulliken O/S	d(P/Sb–O/S) (Å)	Overlap population (P–O or Sb–O)
Me3P	+0.32		—	—
Me3Sb	+0.24		—	—
Me3Sb(O)	+0.89	−0.82	1.86	0.45
Me3P(O)	+0.92	−0.77	1.52	0.51
Me3Sb(S)	+0.50	−0.48	2.26	0.51
Me3P(S)	+0.68	−0.55	1.98	0.50
TSO	+0.54(P)	−0.68	2.08 (P–O)	0.00
	+0.62 (Sb)		2.03 (Sb–O)	0.30
TSS	+0.41(P)	−0.42	2.59 (P–O)	0.04
	+0.35 (Sb)		2.46 (Sb–O)	0.23

---

As shown in Table 1, in the chalcogen transfer between phosphorus and antimony centers the oxygen or the sulfur atom changes only marginally their charge compared to the variations of the pnictogens, with the phosphorus becoming more positive and the antimony less positive. In this case, the transfer can be described as a redox reaction between phosphorus and antimony, which becomes oxidized and reduced, respectively, accompanied by the transfer of the oxygen or sulfur. The transition states may be described as reactant-like in view of the null or negligible overlap population between the phosphorus and the transferring chalcogen atom, while the variations are more evident in the case of antimony.

Extension of the chalcogen transfer to the phosphorene surface

On the basis of the results entailing the chalcogen transfer from a stibine to the phosphine, we wonder whether a similar approach could be extended also to the mono-layer exfoliated black phosphorus, P_n, allowing a robust and selective functionalization of this intriguing 2D-material. Remarkably, the structural arrangement in the phosphorene surface already features an inner asymmetry in the P–P distances and the P–P–P angles as shown by the optimized structure in Fig. 4. In the P_n sheets each phosphorus center is three-coordinated with two in-plane P–P distances shorter by 0.05 Å than the third (2.29 vs. 2.24 Å) and with two P–P–P angles ca. 8° wider than the third one (104.6° vs. 96.7°). The smallest value of two non-bonding P atoms facing in the ditch is 3.6 Å.

Fig. 4 Optimized structure of single layer exfoliated black phosphorus, P_n.

The lone pair associated with each phosphorus atom is far from being orthogonal to the surface but bent by 30°, suggesting that an efficient functionalization of the surface with acidic moieties requires serious steric and electronic rearrangements.⁶ As highlighted above for the case of the phosphine, also for the P_n surface the chalcogen transfer is improbable to directly involve the lone pair but a low lying acidic system, able to interact with a basic moiety such as an oxide or sulfide moiety. In contrast with the case of the phosphine, hardly the material surface is able to rearrange to achieve a perfect butterfly arrangement. One of the possible low lying energy levels, able to interact with the incoming nucleophilic oxygen or sulfur, is a P–P σ* system and in particular the out-of-plane system, which represents the bottom of the conduction band for the 2D-material. A recent article highlighted the pH influence on the degradation of the exfoliated bP in water and a related computational investigation revealed that under basic pH conditions, the hydroxide anion in solution may interact with the surface, allowing a significant P–P bond elongation in the 0.3–0.6 Å range. The authors suggested that a similar interaction may be considered as the initial step in the experimentally observed degradation of the phosphorene sheet to molecular compounds such as hypophosphite or phosphate.²⁵

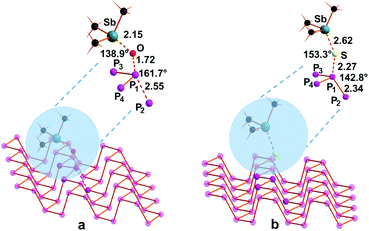
Fig. 5a and b show the optimized structures of the functionalized surface with oxygen and sulfur, respectively, obtained through solid state calculations by using the CRYSTAL17 package²⁶ using a supercell of 32 phosphorus atoms, namely P₃₂, and one chalcogen atom.

Fig. 5 Drawings of optimized molecular geometries of phosphorene–oxide (a) and –sulfide (b), namely P₃₂O and P₃₂S, respectively.

The insertion of the chalcogen atom on the naked P_n surface has some effects on the structural arrangement around the perturbed local cluster of P atoms as shown in Fig. 5. Although the asymmetry between both P–P distances and P–P–P angles is maintained, the width of the ditch is enlarged by 0.1 and 0.2 Å for the phosphorene oxide and sulfide, respectively, compared with the pristine material. Single point calculations revealed a comparable deformation energy of the surface of the naked P_n material to accommodate the oxygen or the sulfur atom (ca. 0.1 eV).⁶ This deformation is required in order to assure a less efficient repulsion between the introduced chalcogen lone pairs and the facing ones on the phosphorus atoms at the other side of the ditch. The free energy contribution associated with the functionalization of the material is shown in Chart 2, together with the energetic barriers for the corresponding transition states. As occurred in the case of the single phosphine molecule, also for phosphorene the functionalization with oxygen seems to be particularly efficient compared to the same process, encompassing the delivery of one sulfur atom onto the polyphosphorus platform. In particular, the latter seems to be slightly endergonic by only +3.6 kcal mol⁻¹, possibly due to somewhat more hindered transfer of the sulfur in view of a more pronounced deformation of the material surface due to the steric requirements to host the incoming chalcogen atom. This is testified by the wide opening of the channels in the case of sulfur, which doubles that occurrence when one oxygen atom is delivered onto the P₃₂ surface, mimicking the phosphorene layer.

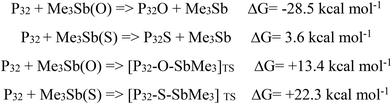Chart 2 Free energy parameters associated with the overall chalcogen transfer reaction and with the achievement of the transition state.

In order to better understand the mechanism of the chalcogen transfer from the stibine oxide or sulfide to the naked phosphorene layer, P_n, we focused our attention on searching for the possible transition state associated with such a process. Conversely in the case of the phosphine, the evaluated free energy barriers are quasi doubled in the case of sulfur, namely [P₃₂–S–SbMe₃]_TS, compared to those of the oxygen [P₃₂–O–SbMe₃]_TS, +22.3 vs. +13.4 kcal mol⁻¹, respectively. The optimized structures of the transition state are reported in Fig. 6.

Fig. 6 Optimized structure of transition states of (a) [P₃₂–O–SbMe₃]_TS and (b) [P₃₂–S–SbMe₃]_TS.

The structure of the transition state, shown in Fig. 6a, associated with the oxygen transfer features an arrangement near to a butterfly with a P₂P₁O angle of 161.7°. The chalcogen is far to interact with the lone pair but most likely it can actively intermingle with the σ* P₁P₂, which, as shown in Fig. 6, is 0.26 Å longer than the corresponding value in pristine phosphorene. A similar trend occurs also for the related Sb–O distance with a value of 2.15 Å. The Sb–O–P₁ angle is far from being close to 180° but it is smaller by ca. 40°, showing 138.9°. Remarkably, in the transition state, the interaction with the oxygen does not affect the width of the channels, with the lone pair on phosphorus not involved in such an interaction. The free energy barrier (see Chart 2) is estimated to be +13.4 kcal mol⁻¹, thus significantly smaller than the one obtained for the Me₃P case. The nature of the transition state of the optimized [P₃₂–O–SbMe₃]_TS structure is confirmed by the calculation of a single imaginary frequency at −292.3 cm⁻¹, associated with the combined transfer of the oxygen to the phosphorus centre together with the P₁–P₂ elongation. After that, the system gains as large as −41.8 kcal mol⁻¹ with the final formation of one P–O bond on the material surface.

When the sulfur atom has to be transferred, the transition state is somewhat different compared to the oxygen case, as shown in Fig. 6b. The process in this case appears somewhat more hindered than the oxygen transfer with a total free energy loss of +3.6 kcal mol⁻¹ with a calculated free energy barrier of ca. +22.3 kcal mol⁻¹ for the achievement of the [P₃₂–S–SbMe₃]_TS transition state. From a structural viewpoint, the Sb–S distance elongates by 0.36 Å, while the effect on the P₁–P₂ distance is less evident since the elongation is only by 0.05 Å compared to the naked material, as also mirrored by the significantly smaller (ca. 20°) S–P₁–P₂ angle. In any case, although the process seems somewhat hindered, the free energy barrier and the very small endergonic feature of the total reaction are not so prohibitive and surely a higher temperature may help the process. The nature of the transition state has also been testified by the presence of an imaginary frequency at −191.7 cm⁻¹ corresponding to the combined sulfur transfer between antimony and P₁ centers coupled with the P₁–P₂ elongation. A second imaginary frequency was obtained at −26.5 cm⁻¹ associated with the methyl rotation at the stibine group.

Band structure features

The structural and energetic analysis of the chalcogen transfer pointed out some fundamental differences in the two processes especially in the nature of the obtained transition states. In the [P₃₂–S–SbMe₃]_TS the process has already occurred; thus, the transition state is product like; otherwise, in the oxygen case, the situation is reverse. Aimed at better elucidating how the electronic structures could be influenced by the chalcogen transfer, a detailed band and density of states analysis has been carried out on the final products and the transition states. In both functionalized P_n, P_n(O) and P_n(S), band gaps of 2.33 and 2.31 eV have been predicted for the oxygen and sulfur cases, respectively, which are 0.13 and 0.11 eV larger than that shown by pristine phosphorene. A reasonable explanation has been recently provided,⁶ the lone pairs at the top of the valence band stabilized through the interaction with the chalcogen with a narrowing of the top of the valence band and a final effect of an enlargement of the resulting band gap. By the examination of the density of states, the main difference in the two cases is related to the great contribution of sulfur at the bands at the top of the valence band, which in contrast are particularly lower in the case of the oxygen.

Particularly interesting is the inspection of density of states for the two different transition states. Starting from the [P₃₂–O–SbMe₃]_TS, Fig. 7a, a significantly small band gap of 1.57 eV is predicted. The conduction band appears particularly changed in the bottom part with the formation of an isolated band with the main contribution from the oxygen and σ* P–P bond character. This is strictly correlated with the structural features found for the [P₃₂–O–SbMe₃]_TS with a strong elongation of the out-of-plane P–P. The involvement in the process of σ* P–P bonds, which are the main contribution to the conduction band in the phosphorene material, allows their energy stabilization and the reduction of the band gap between valence and conduction bands up to 1.57 eV. Only after the transition state, the phosphorus–oxygen bond forms and the band gap increases up to 2.33 eV.

Fig. 7 Density of states of the transition states before the attainment of the functionalized material: (a) [P₃₂–O–SbMe₃]_TS and (b) [P₃₂–S–SbMe₃]_TS. The contribution from the chalcogen has been highlighted in grey.

The trend is not so evident in the sulfur transfer, with the predicted band gap being 2.17 eV, i.e. only 0.14 eV smaller than that of the naked phosphorene as evident in the density of states in Fig. 7b. In that case, the chalcogen transfer has already occurred and the transition state is more product-like in contrast to the oxygen one, as confirmed by the energy and structural features pointed out before.

Conclusions

The present work suggests a promising route for the functionalization of the exfoliated black phosphorus, which suffers from easy decomposition by air and moisture. In particular, we suggest that the selective introduction of chalcogen atoms on the material surface may occur following the reaction with suitable chalcogen-atom transfer reagents, such as stibine oxide and sulfide. In this way many drawbacks related to the reactivity of the naked material with Lewis acids or transition metal fragments might be overcome. The study suggests the available features of this reactivity with a not so high energy barrier to be bypassed or, as occurs for the stibine sulfide case, with very low overall free energy costs. The work provides a complete overview of all the possible structural, electronic and energy aspects associated with the chalcogen transfer between a stibine chalcogenide and a phosphorus based compound, in particular trialkyl phosphine or single layer exfoliated black phosphorus, phosphorene, P_n. In view of the very similar features of the molecular and 2D material processes and computationally proved their feasibility, we strongly hope that such a reactivity will be addressed in laboratory, also being supported by precedent experimental investigations on diphosphane.¹³ The results of the present manuscript will represent the starting point for a more efficient functionalization.

bP-Based materials through the immobilization of metal complexes and/or nanoparticles take advantage of the strong interaction with the chalcogen centers without significantly affecting the structure of the P_n sheets.

Computational details

The optimized geometries and energetics of the all the molecular reactants and the naked and functionalized phosphorene surfaces have been studied at B3LYP-DFT²⁷ level of theory by using the CRYSTAL17 package.²⁶ The material structure has been studied by using a selected supercell of 32 phosphorus atoms, optimizing both the atomic positions and lattice parameters. The TZVP basis set²⁸ has been used for all the atomic species. The minima/transition state features were validated by performing the vibrational frequency calculation. Band and Crystal Overlap Orbital Population (COOP) analyses have been carried out with the available routines of the CRYSTAL17 package.²⁶ Lists of all the optimized structural and energy parameters are available in the ESI.‡

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (Grant Agreement No. 670173) for funding the project PHOSFUN “Phosphorene functionalization: a new platform for advanced multifunctional materials” through an ERC Advanced Grant to MP. Thanks are due also to ISCRA-CINECA HP Grants HP10C2QI78 and HP10CFMSCC for the computational resources. Thanks are expressed to Dr Carlo Mealli (CNR-ICCOM) for helpful and stimulating discussions.

References

1. (a) K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666; (b) K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, C. V. Dubonos and A. A. Frisov, Nature, 2005, 438, 197; (c) K. S. Novoselov, Z. Jiang, Y. Zhang, S. V. Morozov, H. L. Stormer, U. Zeitler, J. C. Maan, G. S. Boebinger, P. Kim and A. K. Geim, Science, 2007, 315, 1379; (d) M. Peruzzini, R. Bini, M. Bolognesi, M. Caporali, M. Ceppatelli, F. Cicogna, S. Coiai, S. Heun, A. Ienco, I. Iglesias Benito, A. Kumar, G. Manca, E. Passaglia, D. Scelta, M. Serrano-Ruiz, F. Telesio, S. Toffanin and M. Vanni, Eur. J. Inorg. Chem., 2019, 1476–1494; (e) J. Sturala, D. Sofer and M. Pumera, Angew. Chem., Int. Ed., 2019, 58, 7551–7557; A. Hirsch and F. Hauke, Angew. Chem., Int. Ed., 2018, 57, 2–19.
2. (a) A. Castellanos-Gomez, L. Vicarelli, E. Prada, J. O. Island, K. L. Narasimha-Acharya, S. I. Blanter, D. J. Groenendijk, M. Buscema, G. A. Steele, J. V. Alvarez, H. W. Zandbergen, J. J. Palacios and H. S. J. van der Zant, 2D Mater., 2014, 1, 025001; (b) J. Plutnar, Z. Sofer and M. Pumera, ACS Nano, 2018, 12, 8390–8396; (c) J. Pei, J. Yang, T. Yildirim, H. Zhang and Y. Lu, Adv. Mater., 2019, 31, 1706945; (d) J. He, L. Tao, H. Zhang, B. Zhou and J. Li, Nanoscale, 2019, 11, 2577–2259.
3. (a) J. D. Wood, S. A. Wells, D. Jariwala, K.-S. Chen, E. Cho, V. K. Sangwan, X. Liu, L. J. Lauhon, T. J. Marks and M. C. Hersam, Nano Lett., 2014, 14, 6964–6970; (b) A. Favron, E. Gaufrès, F. Fossard, A.-L. Phaneuf-L'Heureux, N. Y.-W. Tang, P. L. Lévesque, A. Loiseau, R. Leonelli, S. Francoeur and R. Martel, Nat. Mater., 2015, 14, 826–832.
4. (a) C. R. Ryder, S. A. Wells, Y. Yang, D. Jariwala, T. J. Marks, G. C. Schatz and M. C. Hersam, Nat. Chem., 2016, 8, 597–602; (b) Y. Zhao, L. Tong, Z. Li, N. Yang, H. Fu, L. Wu, H. Cui, W. Zhou, J. Wang, H. Wang and P. K. Chu, Chem. Mater., 2017, 29(17), 7131–7139; (c) Y. Cao, X. Tian, J. Gu, B. Liu, B. Zhang, S. Song, F. Fan and Y. Chen, Angew. Chem., Int. Ed., 2018, 57, 4543–4548; (d) M. Gu, B. Zhang, B. Liu, Q. Che, Z. Zhao and Y. Chen, J. Mater. Chem. C, 2020, 8, 1231–1238; (e) M. van Druenen, F. Davitt, T. Collins, C. Glynn, C. O'Dwyer, J. D. Holmes and G. Collins, Chem. Mater., 2018, 30, 4667–4674; (f) Y. Liu, P. Gao, T. Zhang, X. Zhu, M. Zhang, M. Chen, P. Du, G.-W. Wang, H. Ji, J. Yang and S. Yang, Angew. Chem., Int. Ed., 2019, 58, 1479–1483; (g) L. Shao, H. Sun, L. Miao, X. Chen, M. Han, J. Sun, S. Liu, L. Li, F. Cheng and J. Chen, J. Mater. Chem. A, 2018, 6, 2494–2499; (h) Z. Sofer, J. Luxa, D. Bousa, D. Sedmidubsky, P. Lazar, T. Hartman, H. Hardtdegen and M. Pumera, Angew. Chem., Int. Ed., 2017, 56, 9891–9896; (i) M. Vanni, M. Serrano Ruiz, F. Telesio, S. Heun, M. Banchelli, P. Matteini, A. M. Mio, G. Nicotra, C. Spinella, S. Caporali, A. Giaccherini, F. d'Acapito, M. Caporali and M. Peruzzini, Chem. Mater., 2019, 31, 5075–5080.
5. (a) G. Abellan, V. LLoret, U. Mundloch, M. Marcia, C. Neiss, A. Gorling, M. Varela, F. Hauke and A. Hirsch, Angew. Chem., Int. Ed., 2016, 55, 14557–14562; (b) M. Bolognesi, S. Moschetto, M. Trapani, F. Prescimone, C. Ferroni, G. Manca, A. Ienco, S. Borsacchi, M. Caporali, M. Muccini, M. Peruzzini, M. Serrano-Ruiz, L. Calucci, M. A. Castriciano and S. Toffanin, ACS Appl. Mater. Interfaces, 2019, 11, 22637–22647; (c) R. Gusmao, Z. Sofer and M. Pumera, ACS Nano, 2018, 12, 5666–5673; (d) E. Passaglia, F. Cicogna, G. Lorenzetti, S. Legnaioli, M. Caporali, M. Serrano-Ruiz, A. Ienco and M. Peruzzini, RSC Adv., 2016, 6, 53777–53783; (e) E. Passaglia, F. Cicogna, F. Costantino, S. Coiai, S. Legnaioli, G. Lorenzetti, S. Borsacchi, M. Geppi, F. Telesio, S. Heun, A. Ienco, M. Serrano-Ruiz and M. Peruzzini, Chem. Mater., 2018, 30, 2036–2048; (f) C. Jellett, J. Plutnar and M. Pumera, ACS Nano, 2020, 14, 7722–2233; (g) V. Artel, Q. Guo, H. Cohen, R. Gasper, A. Ramasubramaniam, F. Xia and D. Naveh, npj 2D Mater. Appl., 2017, 1, 6.
6. (a) A. Ienco, G. Manca, M. Peruzzini and C. Mealli, Dalton Trans., 2018, 47, 17243–17256; (b) C. Mealli, A. Ienco, M. Peruzzini and G. Manca, Dalton Trans., 2018, 47, 394–408.
7. V. V. Kulish, O. Malyi, C. Persson and P. Wu, Phys. Chem. Chem. Phys., 2015, 17, 992–1000.
8. S. Wu, F. He, G. Xie, Z. Bian, J. Luo and S. Wen, Nano Lett., 2018, 18, 5618–5627.
9. N. N. Greenwood and A. Earnshaw, Chemistry of the Elements, 2nd edn, Elsevier, Amsterdam, 2007.
10. D. E. C. Corbridge, Phosphorus: Chemistry, Biochemistry and Technology, 6th edn, CRC Press, 2013.
11. W. Lv, B. Yang, B. Wang, W. Wan, Y. Ge, R. Yang, C. Hao, J. Xiang, B. Zhang, Z. Zeng and Z. Liu, ACS Appl. Mater. Interfaces, 2018, 10, 9663–9668.
12. J. P. Donahue, Chem. Rev., 2006, 106, 4747–4783.
13. D. Tofan, M. Temprado, S. Majumdar, C. D. Hoff and C. Cummins, Inorg. Chem., 2013, 52, 8851–8864.
14. D. G. Gilheany, Chem. Rev., 1994, 94, 1339–1374.
15. (a) D. B. Chesnut, Chem. Phys., 2003, 291, 141–152; (b) D. B. Chesnut, J. Phys. Chem. A, 2003, 107, 4307–4313 and references within.
16. J. A. Dobado, H. Martínez-García, J. Molina Molina and M. R. Sundberg, J. Am. Chem. Soc., 1998, 120, 8461–8471.
17. T. Yang, D. M. Andrada and G. Frenking, Phys. Chem. Chem. Phys., 2018, 20, 11856–11866.
18. S. I. Gorelsky, AOMix: Program for Molecular Orbital Analysis, version 6.94b, http://www.sg-chem.net/, 2019.
19. M. Kullberg and J. Stawinski, J. Organomet. Chem., 2005, 690, 2571–2576.
20. (a) G. A. Landrum, N. Goldberg and R. Hoffmann, J. Chem. Soc., Dalton Trans., 1997, 3605–3613; (b) M. L. Munzarova and R. Hoffmann, J. Am. Chem. Soc., 2002, 124, 4787–4795; (c) M. L. H. Green and G. Parkin, Dalton Trans., 2016, 45, 18784–18795; (d) G. Manca, A. Ienco and C. Mealli, Cryst. Growth Des., 2012, 12, 1762–1771; (e) F. Bigoli, P. Deplano, A. Ienco, C. Mealli, M. L. Mercuri, M. A. Pellinghelli, G. Pintus, G. Saba and E. F. Trogu, Inorg. Chem., 1999, 38, 4626–4636; (f) M. E. G. Mosquera, P. Gomez-Sal, L. Diaz, L. M. Aguirre, A. Ienco, G. Manca and C. Mealli, Inorg. Chem., 2016, 55, 283–291.
21. R. Hoffmann, Angew. Chem., Int. Ed. Engl., 1982, 21, 711–724.
22. (a) C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, The Cambridge Structural Database, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179; (b) Cambridge Structural Database System 2020, Cambridge Crystallographic Data Centre, Cambridge, UK.
23. C. Chuit, R. J. P. Corriu, P. Monforte, C. Reye, J.-P. Declercq and A. Dubourg, J. Organomet. Chem., 1996, 511, 171–175.
24. A. N. Kornev, V. V. Sushev, N. V. Zolotareva, E. V. Baranov, G. K. Fukin and G. A. Abakumov, Eur. J. Inorg. Chem., 2015, 2057–2066.
25. S. Zhang, X. Zhang, L. Lei, X.-F. Yu, J. Chen, C. Ma, F. Wu, Q. Zhao and B. Xing, Angew. Chem., Int. Ed., 2019, 58, 467–471.
26. R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arco, M. Llunel, M. Caus'a, Y. Nöel, L. Maschio, A. Erba, M. R′erat and S. Casassa, CRYSTAL 17.
27. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
28. M. F. Peintinger, D. V. Oliveira and T. Bredow, J. Comput. Chem., 2013, 34, 451–459.

---

Footnotes

† This article is dedicated to our Friend and Colleague, Professor Pierre H. Dixneuf, for his outstanding career achievements in organometallic chemistry and homogeneous catalysis.

‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/d0dt02860f

---