Applications of electron paramagnetic resonance spectroscopy to heavy main-group radicals

Abstract

The exploration of heavy main-group radicals is rapidly expanding, for which electron paramagnetic resonance (EPR) spectroscopic characterisation plays a key role. EPR spectroscopy has the capacity to deliver information of the radical's electronic, geometric and bonding structure. Herein, foundations of electron-nuclear hyperfine analysis are detailed before reviewing more recent applications of EPR spectroscopy to As, Sb, and Bi centred radicals. Additional diverse examples of the application of EPR spectroscopy to other heavy main group radicals are highlighted.

---

George E. Cutsail

Born in Maryland, USA in 1988, George E. Cutsail III earned his B.Sc. of Chemistry (2010) at the University of Maryland, Baltimore County and his Ph.D. (2014) at Northwestern University. George then moved to Germany for a postdoctoral research position at the Max Planck Institute for Chemical Energy Conversion (MPI-CEC). Now, he is an independent Max Planck Research Group Leader at the MPI-CEC, working in collaboration with the University of Duisburg-Essen. His group employs advanced electronic paramagnetic spectroscopic techniques in additional to other inorganic spectroscopies to understand unique inorganic electronic structure questions.

---

Electron paramagnetic resonance (EPR) spectroscopy is an extremely valuable tool for the characterisation of unpaired electrons of both radicals and paramagnetic transition metal complexes. Although main-group compounds are less prone to form paramagnetic spin-states, numerous light-atom (e.g. C, N, O and P) centred radicals are known.¹ In fact, many of these persistent radicals, such as Frémy's salt (K₂[ON(SO₃)₂]) and the Gomberg radical (Ph₃C˙), pre-date the invention of EPR spectroscopy.^2,3 However, the isolation and subsequent EPR characterisation of stable heavy main-group radicals, periods 4 to 6, is much less common.¹ More recently, new synthetic approaches and efforts have dramatically increased the variety of isolated and characterized heavy main-group paramagnetic radical complexes. Alongside these new complexes, the application of EPR spectroscopy to heavy main-group radicals has expanded also, including recent characterization of heavy Group 13,^4–8 14^9–12 and 15 radicals.^13–26

EPR spectroscopy yields valuable coordination environment and electronic structure information. The main-group elements are diverse in their nuclear properties, Fig. 1, including a variety of nuclear spin-states at high abundances that will yield complex and rich electron-nuclear hyperfine interactions. EPR techniques are therefore able to elucidate ligand identity and determine radical(metal)–ligand covalencies and bonding structures.

Fig. 1 NMR active isotopes of the p block with relevant nucleotides, percent natural abundances, nuclear spin (I) and nuclear g-values (g_n). Data taken from ref. 27.

Diphenylpnictanyl radicals

Fundamental case studies of heavy main-group radicals in the 1970s serve as excellent examples and tutorials for the basis of our analysis of these radicals. Ultraviolet irradiation of single crystals of triphenylphosphine, -arsine and -antimony yields diphenylphosphinyl, -arsinyl, or -antimony radicals: Ph₂E˙, E = P, As and Sb.^23,24,28 Single crystal EPR analysis of the Ph₂E˙ radicals exhibit a S = 1/2 signal. In the basic EPR experiment,^27,29,30 the degeneracy of the unpaired electron spin, m_s = ±1/2, is split by the magnetic field. A constant microwave wavelength is used during the experiment and one sweeps the magnetic field so that when the Zeeman's splitting energy matches the microwave energy at given magnetic field, a transition occurs. Observed transitions, reported as individual g-values or a complete g-tensor, are the measurement of their deviation from the value for a free electron, g_e = 2.0023…, and depend on a variety of factors, but are not limited to, the electron's chemical and molecular environment, symmetry, ligand field, and spin–orbit coupling (SOC). The rhombic g-tensor (g₁ > g₂ > g₃) measured for the Ph₂E˙ radicals exhibit increased g-anisotropy as observed by larger spectral width (Δ = g₁–g₃) going from P → As → Sb, expected for the increased SOC of E. For these Ph₂E˙ radicals, the g_y value is aligned with the unpaired electron's p orbital, Fig. 2, and is near to the value of g_e. The g-values with the largest positive deviation from g_e lie in the C–E–C bonding plane, as expected for AB₂˙ type radical.^24,31

Fig. 2 Orbital diagram of the Ph₂E˙ radical centres (E = As and Sb) with corresponding g-tensor and dipolar, T, hyperfine coupling constants obtained from single crystal EPR experiments.^23,24 The figure is partially adapted from M. Geoffroy, L. Ginet and E. A. C. Lucken, J. Chem. Phys., 1976, 65, 729–732, with the permission of AIP Publishing.

The single crystal EPR spectrum's primary Zeeman interaction is further split by electron-nuclear hyperfine interaction of the radical's unpaired electron with its own nuclear centre and/or neighbouring nuclei. Analysis of the hyperfine tensor allows for detailed magnetic structure determinations. While both ³¹P and ⁷⁵As are present at 100% natural abundance allowing for simple analysis, Fig. 1, ¹²¹Sb and ¹²³Sb exist in close populations but have different nuclear spins (I = 7/2 and 5/2, respectively) producing 8- and 6-line splitting patterns respectively, scaled relative to one another by their g_n values.

To extract information from the hyperfine tensor (A), several interactions must be considered. The hyperfine tensor is generally comprised of both local and non-local interactions. The non-local interaction is a through-space dipolar coupling (T_nonloc) that follows a follows a ∼1/r³ distance relationship between the electron–spin and neighbouring nuclei (i.e. ligands).³² The local hyperfine components contain both isotropic and anisotropic hyperfine contributions. The isotropic hyperfine component (a_iso = (A₁ + A₂ + A₃)/3) is approximated to be proportional to s orbital spin density because only the s orbital wavefunction has electron probability at the nucleus.^32,33 An estimate of the s orbital spin density (or spin population)† is made by ρ(s) = a_iso/a₀, where a₀ is the isotropic hyperfine coupling constant for a given nucleotide.‡ The anisotropic component (T_loc) is an axial tensor, [−t, −t, 2t], and is traceless (sum of the three components is zero). T_loc is a measure of the p (and/or d) orbital spin density reflecting the zero probability of finding the electron at the nucleus.^32,33 The p orbital spin density is estimated by ρ(p) = t/b₀, where t is the anisotropic hyperfine coupling and b₀ is the anisotropic hyperfine coupling constant.³² Addition of the three components yields the observed hyperfine tensor, A = a_iso + T_loc + T_nonloc.

While absolute hyperfine signs are not directly measured in the EPR experiment, one may assign expected signs for the radical's hyperfine tensor based on a few simple logical cases. Following convention, the unpaired electron has positive spin density and the radical centre must have positive a_iso and/or t values. Take the diphenylantimony radical observed values of A(¹²¹Sb) = [|352|, |704|, |352|] MHz,²³ all positive values would yield a_iso = +469 MHz and t = +117 MHz (T = A − a_iso). Given a₀(¹²¹Sb) = +35 098 MHz and b₀(¹²¹Sb) = +629 MHz,²⁷ resultant spin density estimates would be ρ(Sb s) ∼ +0.013 and ρ(Sb p) ∼ +0.19. While it is expected that the two-coordinate antimony radical would be localized in a Sb p orbital, this low estimate of Sb p orbital density would require a majority of the unpaired electron spin delocalization onto the phenyl groups and large ¹H^Ar hyperfine couplings,²³ however, no resolved ¹H splittings are observed. Evaluation of the [−A₁, +A₂, −A₃] assigned hyperfine signs yields approximately zero Sb s orbital spin density and a dipolar coupling of t = +352 MHz corresponding to ρ(Sb p) ∼ +0.56. The latter is accepted as the correct sign assignment where the unpaired electron is in a nearly pure Sb p orbital perpendicular to the C–Sb–C plane with partial delocalization of the unpaired spin onto the phenyl ligands, Fig. 2. The Ph₂P˙ exhibits more localized p orbital radical character with ρ(P p) ∼ +0.94 and Ph₂As˙ has ρ(As p) ∼ +0.74 density (using a₀ values from ref. 27). A clear periodic trend is observed for the radical p orbital spin density (P > As > Sb) where the larger E centre allows for more delocalization of the radical electron onto the ligands. It was suggested that the phenyl rings may reorient to allow better unpaired spin delocalisation into its π orbitals.²³

Geoffroy et al. were able to resolve an additional quadrupole interaction of the I = 3/2 ⁷⁵As nuclei, yielding additional electronic insight from the measured electric field gradient.²⁴ The quadrupole interaction further corroborated the assignment of unpaired electron to a single p orbital and the asymmetry of the quadrupole tensor led to an C–As–C bond angle estimation of 96 to 99°, in excellent agreement with the triphenylarsane complex,³⁴ demonstrating that no significant rearrangement of the As centre occurs in the crystal upon irradiation.

EPR spectroscopy of heavy Group 15 radicals

Recently, I have had the privilege to study and characterise the stable neutral radicals [L(Cl)Ga]₂As˙,¹⁵ [L(Cl)Ga]₂Sb˙,^17,25 and [L(I)Ga]₂Bi˙ ²⁵ containing paramagnetic As, Sb and Bi centres, Fig. 3 (L = HC[C(Me)N(Dip)]₂, Dip = 2,6-i-Pr₂C₆H₃). The homoleptic [L(X)Ga] coordinated radicals all exhibit broad and complex multiline EPR spectra from the various ⁷⁵As, ^121,123Sb, and ²⁰³Bi centres and superhyperfine splitting from the equivalent ^69,71Ga ligands. The breadth of the EPR spectrum and g-anisotropy increases with the SOC of the main-group element. Refinement of the EPR parameters, including the g-tensor, and metal (As/Sb) and ligand Ga hyperfine tensors was only successfully achieved through multifrequency EPR analysis. Here, increased resolution of the g-tensor is gained with increased microwave frequency (and increased magnetic field strength), but the magnitude of hyperfine splittings is insensitive to the external magnetic field strength. This allows the g- and A-tensors to be more well refined than in a single microwave frequency experiment previously employed for other Group 15 radicals that present spectra of high complexity.^20,35

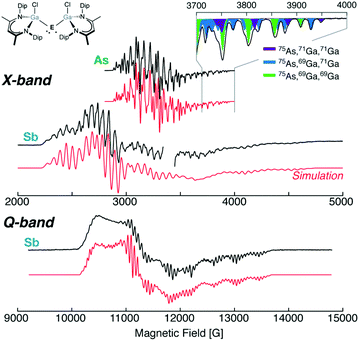Fig. 3 The homoleptic [L(Cl)Ga]₂E˙, X-band (9.6 GHz) EPR spectra of E = As and Sb, and Q-band (34 GHz) EPR spectrum of E = Sb with corresponding simulations. The figure inset details the superhyperfine splitting resulting from the equivalent [L(Cl)Ga] ligands and naturally abundant nuclear isotopes. As˙ data adapted with permission from C. Helling, C. Wölper, Y. Schulte, G. E. Cutsail and S. Schulz, Inorg. Chem., 2019, 58, 10323–10332. Copyright 2019 American Chemical Society. Sb˙ data reproduced from C. Ganesamoorthy et al.²⁵ under a CC BY 4.0 license (http://creativecommons.org/licenses/by/4.0/), Copyright 2018 The Authors.

The high-field features of the X-band spectrum of [L(Cl)Ga]₂E˙ radicals (E = As and Sb) present sharp superhyperfine features that allowed precise determination of the lowest g-value (g₃) and its corresponding hyperfine couplings, Fig. 3. The two approximately equivalent Ga ligands further split the As or Sb hyperfine in 2NI + 1 fashion, however this is complicated by the two different nuclear isotopes of Ga with slightly different g_n and differing natural abundances, Fig. 1 and 3. The complete mixture of natural abundance isotope interactions may be simulated through common EPR software packages such as EasySpin.³⁶ The highly anisotropic As or Sb A-tensors observed in these radicals have large dipolar components. Decomposition of their hyperfine tensors similar to the procedure described for Ph₂E˙ reveals that [L(Cl)Ga]₂E˙ are indeed E p centred radicals: ρ(E p > 0.80). Partial delocalization of the unpaired electron onto the Ga ligands (∼4%) is also estimated. No resolved hyperfine coupling to the halides or nitrogen atoms of the ligands have been observed in the EPR spectra. Recently, isolation of [L(X)Ga]₂Sb˙ varying X = Cl, Br and I shows that the coordinated halide to the Ga ligand does not influence the electronics of the Sb radical as these all have similar g- and A(Ga, Sb)-tensors.¹⁷

Despite the unique similar electronic character of the As and Sb radicals observed, the radicals are not produced through identical synthetic procedures.^18,25,37 The reactions require weak As/Sb–R bonds for homolytic bond cleavage and radical formation as previous mechanistic studies have shown and which are summarized in Fig. 4. Reactions of LGa with Cp*SbCl₂ yield the desired [L(Cl)Ga]₂Sb˙ radical and 0.5 equivalents of decamethylfulvalene (Cp*₂) as a by-product from the homolytic cleavage of one Cp* ligand. Attempts to react LGa with Cp*AsCl₂ yields complex LGa=AsCp* via LGaCl₂ elimination and no radical formation is observed.¹⁵ However, utilization of a bulkier aryl-substituted ligand, Cp^Ar, yields the desired [L(Cl)Ga]₂As˙ product and a new stable Cp^Ar˙ radical that may be separated and characterized by EPR spectroscopy,¹⁵Fig. 4. The aryl-substituents of the Cp^Ar˙ ligand have lower As–C bond strength than the Cp* ligand, helping force homolytic As–C bond cleavage and stable radical product formation. Furthermore, the aryl substituents further electronically stabilize the cyclopentadienyl's radical electron. The Sb–C bond of the Cp*SbCl₂ reactant appears as weak or weaker than the As–C(Cp^Ar) bond strength due its ability to form the Sb centred radical via homolytic bond cleavage. While Cp*₂ product formation is monitored by NMR spectroscopy during the generation of the [L(Cl)Ga]₂Sb˙ radical, the stability of the Cp^Ar˙ product makes it a potential target for in situ EPR spectroscopic reaction monitoring, a possibility that has yet to be explored.

Fig. 4 The E–C bond strength determines whether homolytic E–C bond cleavage occurs to form [L(Cl)Ga]₂E˙ radical (top and bottom reactions) or LGaCl₂ elimination to form E=Ga double-bond product (middle reaction). Figure is adapted with permission from C. Helling, C. Wölper, Y. Schulte, G. E. Cutsail and S. Schulz, Inorg. Chem., 2019, 58, 10323–10332. Copyright 2019 American Chemical Society.

The magnitude of the E centre's hyperfine coupling reflects its degree of delocalization. The hyperfine of the [BptE=EBpt]˙⁻ [Bpt = bis[bis(trimethylsilyl)methyl]-4-[tris(trimethylsilyl)methyl]phenyl] radicals³⁸ is approximately half that of the mononuclear E˙ radicals detailed above. This supports that the unpaired electron is delocalized in an E–E π* orbital and therefore, the measured unpaired spin density is split among the two equivalent E centres. In these examples, analysis of the hyperfine couplings demonstrate the delocalization of the radical's electron in a metal–metal bond/antibonding orbital.³⁸

Radical tuning

While the majority of heavy main-group radicals have been (semi-)symmetric and homoleptic in their coordination sphere, our characterization of the [L(Cl)Ga]₂Sb˙ radical inspired the design and isolation of heterolyptic Sb radicals to study the electronic influences of the ligands. Here, one Ga ligand is replaced by a B, C or N based ligand (R = B[N(Dip)CH]₂, 2,6-Mes₂C₆H₃, or N(SiMe₃)Dip, respectively), Fig. 5.¹⁸ The displacement of the electropositive Ga metal ligand with these light element-based ligands has immediately apparent electronic structure influences, observed in the EPR spectra, Fig. 5A. The amount of g-anisotropy, measured by the g₁ value, decreases with increased electronegativity of the ligand, Fig. 5B. Absorption spectroscopy also reveals transitions in the range of 605 to 875 nm, Fig. 5C, assigned to HOMO → SOMO transitions.

Fig. 5 (A) Frozen solution Q-band (34 GHz) EPR spectra of [L(Cl)Ga]RSb˙, black, overlaid with simulations, coloured lines. (B) Determined g₁ value vs. electronegativity of the R ligand of [L(Cl)Ga]RSb˙ radicals, where R = L(Cl)Ga, B[N(Dip)CH]₂, 2,6-Mes₂C₆H₃, or N(SiMe₃)Dip. (C) Room-temperature UV/Vis absorption spectra of [L(Cl)Ga]RSb˙ radicals with photograph (inset) of prepared solutions. (D) Variable-temperature X-band (∼9.5 GHz) EPR spectroscopy of [L(Cl)Ga]NSb˙. Data reproduced from C. Helling et al.¹⁸ under a CC BY 4.0 license (http://creativecommons.org/licenses/by/4.0/), Copyright 2020 The Authors.

It is reasoned that the more electronegative N donor destabilizes the SOMO due to its lone-pair and electron donation to the Sb centre. The less electronegative B ligand further stabilizes the SOMO through its empty π orbital. Absorption spectroscopy supports this assigned stabilization as [L(Cl)Ga]BSb˙ has the lowest energy absorption transition, Fig. 5C. The observed EPR trend complements the observed absorption spectroscopic trends as the g-shift (primarily g₁ in these complexes) is proportional to the energy gap of the ground-state electron and low-lying excited states, Fig. 5B. Ultimately, the combined spectroscopic characterization of the radical's electronic structure rationalizes the ability of [L(Cl)Ga]BSb˙ (Fig. 5) to form the Sb=B double-bonded complex by an one electron reduction process.¹⁸

Our characterization of As and Sb radicals has predominantly been performed at low temperatures with frozen solutions. In my experience, low temperatures are required to overcome the fast electron relaxation behaviour of these heavy radical centres, reflecting their metal-like character.^39,40 However, substantial amounts of main-group radical characterization have relied only on solution-phase EPR characterization and hyperfine analysis.^1,13,19,22 In room-temperature EPR spectroscopy, the rapid tumbling of the molecule averages the anisotropic contributions to the spectrum and directly measures g_iso and a_iso values. The minimal s orbital spin density estimated from measured a_iso couplings have been used to infer large p orbital localization of the electron.¹⁹ However, only through the measurement of the anisotropic hyperfine tensor in frozen solution, powder or crystal samples, may this assumption be confirmed.

Measurement of room-temperature spectra of heavy main-group radicals is not always feasible, as shown by variable-temperature EPR spectroscopy of [L(Cl)Ga]NSb˙, Fig. 5D. The room-temperature isotropic EPR spectrum is nearly 300 G wide (peak-to-peak) and offers no resolved Sb hyperfine couplings. The g_iso measured is in excellent agreement with that determined from the average of the frozen solution's g-tensor. These results highlight the importance of employing low-temperature EPR techniques for such heavy main-group radicals.

EPR spectroscopy of bismuth radicals

An emerging area of interest is the isolation and characterization of stable bismuth radicals which exhibit metal-like bevahior.⁴⁰ To date, only a few bismuth radicals have been characterized^19,22,25,26 and their EPR spectra recorded.^25,26 Isolation of low-valent bismuth centres is difficult to achieve as these complexes are prone to overreduction and disproportionation reactions. Due to the challenges, the isolation and characterization of stable Bi(II) radicals is of great curiosity.

Several examples of P–P and As–As bonded diamagnetic dimers exist at room temperatures but undergo homolytic cleavage of the E–E bond to form E-centred radicals at elevated temperatures (∼350 K) as monitored by EPR spectroscopy.^41,42

The R^H₂Sb˙ and R^H₂Bi˙ radicals (R^H₂ = 1,1,4,4-tetrakis(trimethylsilyl)butane-1,4-diyl), Fig. 6, stabilized in solution by Ishida et al. are also produced by the homolytic cleavage of the Sb–Sb or Bi–Bi bonds of their parent R^H₂EER^H₂ dimers.^19,22 The room-temperature EPR spectrum of R^H₂Sb˙ exhibits a broad signal with a g_iso value significantly shifted from g_e but no resolved Sb hyperfine is observed, Fig. 6. The detection of Bi centred radicals becomes more challenging because heavier Z atoms typically exhibit faster electron spin relaxation,²² necessitating that low temperature spectra are recorded. However, these R^H₂Sb˙ and R^H₂Bi˙ radicals exist in equilibrium with the dimeric distibane and dibismuthane complexes where the equilibrium shifts towards the diamagnetic dimers at lower temperatures as evidenced by UV-vis absorption spectroscopy. The thermodynamic behaviour of these heavier Sb and Bi radical/dimer complexes is opposite to other lighter P and As examples, making preparations of frozen EPR samples of the radical difficult.²²

Fig. 6 (Top) Schematic representation of R^H₂Sb˙ radical with X-band room-temperature solution EPR spectrum and schematic representation of the analogous R^H₂Bi˙ radical. (Bottom) Schematic representation of [O(SiMe₂NAr)₂]Bi˙ and frozen solution X- and Q-band pulsed-detected EPR spectra yielding an absorption line shape. EPR spectrum of R^H₂Sb˙ is reproduced from ref. 22, Copyright 2014 WILEY–VCH Verlag GmbH & Co. KGaA, Weinheim. EPR spectra of [O(SiMe₂NAr)₂]₂Bi˙ are reproduced from ref. 26, Copyright 2015 WILEY–VCH Verlag GmbH & Co. KGaA, Weinheim.

The potential employment of rapid-freeze quench techniques to trap a larger population of the radical at room-temperature (or elevated temperatures when the thermodynamics favours radical formation) by “instantaneously” freezing into a cryobath has yet to be reported or explored for heavy main-group radicals such as R^H₂Bi˙ and may be a valuable approach for the trapping and characterization of such samples. In fact, the reversibility of a Sn–Sn triple bond cleavage to form Sn˙ radicals was supported by the heating of samples to 80 °C and UV irradiation for 30 minutes before “flash-freezing”.¹⁰ The low-temperature EPR measurements revealed a pronounced Sn˙ signal allowing for further characterization.⁴³

Bismuth radicals also exhibit much greater hyperfine coupling than lighter Group 15 radicals.³³ For instance, the isotropic hyperfine coupling constant for Bi is more than five times greater than As, meaning that even the minutest s orbital contribution will significantly broaden the spectrum. The magnitude of the hyperfine coupling becomes an important consideration when analysing Bi radicals. For instance, X-band EPR analysis of [O(SiMe₂NAr)₂]Bi˙ revealed²⁶ that the large ²⁰⁹Bi hyperfine had so largely split the Zeeman interaction, that only the two lowest energy transitions of the 8 hyperfine transitions were observable in the X-band EPR spectrum (9.6 GHz; ∼0.3 cm⁻¹ excitation energy), Fig. 6.²⁶ Q-band EPR spectroscopy has a larger excitation energy (34 GHz; ∼1.1 cm⁻¹) and able to record all of the allowed hyperfine transitions, albeit the experiment was limited by the field strength of the magnet, Fig. 6.²⁶ We have reported the X- and Q-band EPR spectra of [L(I)Ga]₂Bi˙ that exhibits significantly less Bi hyperfine coupling in the Q-band spectrum²⁵ than [O(SiMe₂NAr)₂]Bi˙. The X-band EPR spectrum of [L(I)Ga]₂Bi˙ also spans approximately 8000 Gauss and has additional superhyperfine of the Ga ligands.²⁵ While the X- and Q-band spectra support the assignment of Bi centred radical, the current inability to fully refine the EPR parameters of low-symmetry [L(I)Ga]₂Bi˙ radical hinders full electronic structure analysis.

Other heavy main-group radicals

Similar explorations of Group 13 radicals^6,44–46 are of current interest and EPR spectroscopy has played a significant role in characterizing these novel complexes. Two-coordinate Ga, In, and Tl radicals coordinated by B(NDipCH)₂ ligands, were previously characterized by both low-temperature X- and W-band (94 GHz) EPR spectroscopies.⁵ The spectra have resolved Ga, In or Tl hyperfine couplings and exhibit an increase in the g-anisotropy with increased atomic number. Here, the multifrequency analysis appears to have significantly benefited the authors to well simulate the complex spectra. Interesting, very low g-values were observed for Tl (g = [0.6, 0.7, 1.23]) and the utilization of spin nutation experiments confirm their low nature. Advanced techniques such as electron nuclear double resonance (ENDOR) and hyperfine sublevel correlation (HYSCORE) spectroscopies reveal the small boron and nitrogen hyperfine couplings of the ligands, demonstrating that ∼20% of the unpaired spin is delocalized onto the ligand. The large Ga, In, and Tl hyperfine couplings observed affirm that the radical is overwhelmingly a metal centred radical.

Heavier Group 14 radical complexes^{9,10,12,47,48} are of particular interest for numerous analogues within carbon chemistry. Previously, several Group 14 radicals generated within solid matrixes through ⁶⁰Co γ-irradiation or other means such as E–X halogen abstraction have been characterized by EPR spectroscopy.⁴⁹ A stable genuine Ge(I) radical supported by the popular β-diketiminate ligand ([{N(Dip)C(^tBu)}₂CH]⁻) was extensively characterized by EPR and ENDOR spectroscopy.¹¹ This Ge(I)˙ radical has a g_iso = 1.988 close to g_e with a slightly rhombic split of the axial spectrum. The general shifts of the g-values, where a large shift below g_e is observed, consistent with an one electron π radical structure.¹¹ The supporting ligand exhibits ¹H and ¹⁴N hyperfine couplings measured by ENDOR spectroscopy, indicating some delocalisation of the radical's spin onto the ligand. While the percent delocalization is not experimentally estimated, the authors have calculated the spin density by DFT. The Ge(I)˙ centre has a spin density population of ∼85 to 91%, depending on the functional employed and its degree of Hartree–Fock exchange.¹¹

The Power group in collaboration with the EPR group of Britt, have characterized a Ge(III) hydride radical product formed from a Ge(I) radical intermediate's C–H bond insertion.⁹ The Ge(I) radical appears very reactive and has precluded trapping and characterization by EPR. The EPR spectrum of the Ge(III) hydride product exhibits large ¹H proton splittings and orientation-selective ENDOR spectroscopy⁵⁰ allowed for the complete refinement of the hydride's hyperfine tensor and orientation relative to the g-tensor. Despite the H atom having no p or d orbitals, it exhibits a large dipolar anisotropic coupling. Therefore, the dipolar contribution to the hyperfine is not local (p orbital) but the result of through-space dipolar couplings. This allowed the authors to estimate the anisotropic contribution to the hyperfine tensor through a point-dipole approximation^27,32 that suggests the Ge(III)˙ hydride is pseudoplanar. The high-resolution and precision of the data, paired with DFT predictions of the hyperfine tensor, support a locally trigonal planar Ge(III) radical with SOMO p orbital perpendicular to the plane, Fig. 7. Doming of the Ge centre out of the ligand plane as shown by DFT calculations dramatically increases the predicted a_iso¹H-hydride coupling and dipolar couplings in large disagreement with the experiment, Fig. 7. Not only does EPR spectroscopy characterise this product as a Ge(III) hydride, but advanced EPR techniques paired with DFT return fine structural insight.

Fig. 7 (A) DFT calculated SOMO of Ge(III) hydride exhibiting a p-orbital radical centre. (B) Predicted hyperfine parameters for distorted and planar Ge radical centres vs. experimental data. Reprinted with permission from T. Y. Lai, L. Tao, R. D. Britt and P. P. Power, J. Am. Chem. Soc., 2019, 141, 12527–12530. Copyright 2019 American Chemical Society.

Similar to Group 15, the field lacks isolated examples of stable period 6 radicals. One of the first stable stannyl radicals isolated featured a three-coordinate Sn(I) site with di-tert-butyl(methyl)silyl ligands.¹² Room-temperature solution EPR spectroscopy of this radical featured a g_iso = 2.0482 and ¹¹⁹Sn isotropic hyperfine couplings of 329 G (a₀(¹¹⁹Sn) = 15 671.8 G), a magnitude smaller than most previously reported Sn radicals.^12,49 The small isotropic coupling supports minimal s orbital spin density for the trigonal planar site that is maintained in the solution phase. This observed coupling is much larger than the 8 G Sn hyperfine coupling described for the [Ar^iPr4SnSnAr^iPr4]⁻ radical anion where the unpaired electron is delocalized in an out-of-plane π(Sn–Sn) orbital.^47,51

Heavy Group 16 radicals are very underexplored but are of growing interest as sulphur analogues.^1,52 An elegant series of E = S, Se, Te thermally unstable radical [(2,6-Mes₂C₆H₃E)₂]˙⁺ cations were studied and characterised by multifrequency (X and Q-band) EPR spectroscopy as frozen solutions.⁵³ For these radicals, interpretation of the g-values from the rhombic spectra is much simpler compared to previous examples because S, Se and Te all have low natural abundant nuclear active nucleotides, Fig. 1. Mirroring the trends discussed for Group 15 radicals, the g-anisotropy increases with atomic number and SOC. The [(2,6-Mes₂C₆H₃E)₂]˙⁺ complexes exhibit weak but resolved Se or Te hyperfine transitions. The ¹H couplings of the m-terphenyl substituents were measured by electron nuclear double resonance (ENDOR) spectroscopy and showed decreasing isotropic ¹H couplings for the S → Se → Te centred radicals. The ENDOR experiment here essentially measures the degree of electron delocalization onto the ligand showing that the sulphur radical cation has slightly more unpaired spin delocalization than its Te counterpart.⁵³ Ultimately, the hyperfine analysis and computational efforts support S/Se/Te centred radicals with greater than 70% of the unpaired electron centred on the chalcogen atom.

Future outlook

Multifrequency EPR spectroscopy has proven invaluable in resolving and refining complex superhyperfine patterns that in turn afford deep magnetic structure and bonding insight. It is evident that advanced techniques such as electron spin echo envelope modulation (ESEEM), ENDOR, and HYSCORE spectroscopies have great potential to resolve smaller hyperfine coupling not observed in the EPR spectrum. Employment of EPR spectroscopy has already proven valuable in determining the delocalization and covalency of supporting ligands and more advanced techniques can expand the information available.

Many of spectroscopic studies of main-group radicals have been paired with computational efforts to calculate absorption spectra and magnetic properties such as g- and hyperfine tensors. DFT methods has proven useful and fairly accurate for calculations of EPR parameters of lighter radicals.⁵⁴ Time-domain DFT approaches have had acceptable agreement with absorption spectroscopy and assignments of isolated transitions. However, much work is needed for the computation of heavy main-group radical EPR parameters. Larger disagreement between experiment and predicted hyperfine couplings are observed, including large a_iso errors.⁵⁴ As the hyperfine coupling is an electronic core property, it is critical that all-electron basis sets are used and the recent development of relativistic contracted basis sets for the employment with relativistic approximation of heavier elements has shown potential to improve the accuracy of calculated EPR properties.⁵⁵

In the future, as more stable heavy main-group radicals are isolated, both EPR and its advanced techniques will continue to shed light on the electronic structure of the radical centre. The techniques ability to probe both the electronic and magnetic structure through the g-tensor and hyperfine interactions, respectively, yields valuable insight for the electronic and geometric structure of the radical centre. New approaches in synthesis will allow for continued tuning of the electronic structure of these radicals and influence their reactivity, all to be probed by EPR spectroscopy.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The Max Planck Society is thanked for financial support. Open Access funding provided by the Max Planck Society. I would also like to thank Prof. Stephan Schulz and Christoph Helling for insightful discussions.

Notes and references

1. P. P. Power, Chem. Rev., 2003, 103, 789–809.
2. E. Divers and T. Haga, J. Chem. Soc., Trans., 1900, 77, 440–446.
3. M. Gomberg, J. Am. Chem. Soc., 1900, 22, 757–771.
4. N. Wiberg, K. Amelunxen, H. Nöth, H. Schwenk, W. Kaim, A. Klein and T. Scheiring, Angew. Chem., Int. Ed. Engl., 1997, 36, 1213–1215.
5. A. V. Protchenko, D. Dange, J. R. Harmer, C. Y. Tang, A. D. Schwarz, M. J. Kelly, N. Phillips, R. Tirfoin, K. H. Birjkumar, C. Jones, N. Kaltsoyannis, P. Mountford and S. Aldridge, Nat. Chem., 2014, 6, 315–319.
6. W. Uhl, L. Cuypers, W. Kaim, B. Schwederski and R. Koch, Angew. Chem., Int. Ed., 2003, 42, 2422–2423.
7. J. A. J. Pardoe and A. J. Downs, Chem. Rev., 2007, 107, 2–45.
8. M. M. Siddiqui, S. K. Sarkar, S. Sinhababu, P. N. Ruth, R. Herbst-Irmer, D. Stalke, M. Ghosh, M. Fu, L. Zhao, D. Casanova, G. Frenking, B. Schwederski, W. Kaim and H. W. Roesky, J. Am. Chem. Soc., 2019, 141, 1908–1912.
9. L. Tao, T. Y. Lai, P. P. Power and R. D. Britt, Inorg. Chem., 2019, 58, 15034–15038.
10. T. Y. Lai, L. Tao, R. D. Britt and P. P. Power, J. Am. Chem. Soc., 2019, 141, 12527–12530.
11. W. D. Woodul, E. Carter, R. Müller, A. F. Richards, A. Stasch, M. Kaupp, D. M. Murphy, M. Driess and C. Jones, J. Am. Chem. Soc., 2011, 133, 10074–10077.
12. A. Sekiguchi, T. Fukawa, V. Y. Lee and M. Nakamoto, J. Am. Chem. Soc., 2003, 125, 9250–9251.
13. A. Brueckner, A. Hinz, J. B. Priebe, A. Schulz and A. Villinger, Angew. Chem., Int. Ed., 2015, 54, 7426–7430.
14. Y. Fang, L. Zhang, C. Cheng, Y. Zhao, M. Abe, G. Tan and X. Wang, Chem. – Eur. J., 2018, 24, 3156–3160.
15. C. Helling, C. Wölper, Y. Schulte, G. E. Cutsail III and S. Schulz, Inorg. Chem., 2019, 58, 10323–10332.
16. M. Y. Abraham, Y. Wang, Y. Xie, R. J. Gilliard Jr., P. Wei, B. J. Vaccaro, M. K. Johnson, H. F. Schaefer III, P. V. R. Schleyer and G. H. Robinson, J. Am. Chem. Soc., 2013, 135, 2486–2488.
17. C. Helling, C. Wölper, G. E. Cutsail III, G. Haberhauer and S. Schulz, Chem. – Eur. J., 2020 DOI:10.1002/chem.202001739.
18. C. Helling, G. E. Cutsail III, H. Weinert, C. Wölper and S. Schulz, Angew. Chem., Int. Ed., 2020, 59, 7561–7568.
19. S. Ishida, F. Hirakawa and T. Iwamoto, Bull. Chem. Soc. Jpn., 2018, 91, 1168–1175.
20. T. Li, H. Wei, Y. Fang, L. Wang, S. Chen, Z. Zhang, Y. Zhao, G. Tan and X. Wang, Angew. Chem., Int. Ed., 2017, 56, 632–636.
21. R. Kretschmer, D. A. Ruiz, C. E. Moore, A. L. Rheingold and G. Bertrand, Angew. Chem., Int. Ed., 2014, 53, 8176–8179.
22. S. Ishida, F. Hirakawa, K. Furukawa, K. Yoza and T. Iwamoto, Angew. Chem., Int. Ed., 2014, 53, 11172–11176.
23. W. T. Cook and J. S. Vincent, J. Chem. Phys., 1977, 67, 5766–5769.
24. M. Geoffroy, L. Ginet and E. A. C. Lucken, J. Chem. Phys., 1976, 65, 729–732.
25. C. Ganesamoorthy, C. Helling, C. Wölper, W. Frank, E. Bill, G. E. Cutsail III and S. Schulz, Nat. Commun., 2018, 9, 87.
26. R. J. Schwamm, J. R. Harmer, M. Lein, C. M. Fitchett, S. Granville and M. P. Coles, Angew. Chem., Int. Ed., 2015, 54, 10630–10633.
27. J. A. Weil and J. R. Bolton, Electron paramagnetic resonance: elementary theory and practical applications, Wiley-Interscience, Hoboken, N.J., 2nd edn, 2007.
28. W. T. Cook, J. S. Vincent, I. Bernal and F. Ramirez, J. Chem. Phys., 1974, 61, 3479–3480.
29. M. M. Roessler and E. Salvadori, Chem. Soc. Rev., 2018, 47, 2534–2553.
30. A. Schweiger, Angew. Chem., Int. Ed. Engl., 1991, 30, 265–292.
31. P. W. Atkins and M. C. R. Symons, The structure of inorganic radicals; an application of electron spin resonance to the study of molecular structure, Elsevier Pub. Co., Amsterdam, 1967.
32. A. Carrington and A. D. McLachlan, Introduction to magnetic resonance with applications to chemistry and chemical physics, Harper & Row, New York, 1967.
33. J. R. Morton and K. F. Preston, J. Magn. Reson., 1978, 30, 577–582.
34. K. Lisac, F. Topić, M. Arhangelskis, S. Cepić, P. A. Julien, C. W. Nickels, A. J. Morris, T. Friščić and D. Cinčić, Nat. Commun., 2019, 10, 61.
35. M. K. Mondal, L. Zhang, Z. Feng, S. Tang, R. Feng, Y. Zhao, G. Tan, H. Ruan and X. Wang, Angew. Chem., Int. Ed., 2019, 58, 15829–15833.
36. S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55.
37. C. Helling and S. Schulz, Eur. J. Inorg. Chem., 2020 DOI:10.1002/ejic.20200057.
38. T. Sasamori, E. Mieda, N. Nagahora, K. Sato, D. Shiomi, T. Takui, Y. Hosoi, Y. Furukawa, N. Takagi, S. Nagase and N. Tokitoh, J. Am. Chem. Soc., 2006, 128, 12582–12588.
39. P. P. Power, Nature, 2010, 463, 171–177.
40. C. Lichtenberg, Angew. Chem., Int. Ed., 2016, 55, 484–486.
41. D. M. C. Ould, A. C. Rigby, L. C. Wilkins, S. J. Adams, J. A. Platts, S. J. A. Pope, E. Richards and R. L. Melen, Organometallics, 2018, 37, 712–719.
42. R. Edge, R. J. Less, E. J. L. McInnes, K. Müther, V. Naseri, J. M. Rawson and D. S. Wright, Chem. Commun., 2009, 13, 1691–1693.
43. T. Y. Lai, J. C. Fettinger and P. P. Power, J. Am. Chem. Soc., 2018, 140, 5674–5677.
44. W. Kaim and W. Matheis, J. Chem. Soc., Chem. Commun., 1991, 8, 597–598.
45. L. B. Knight, J. J. Banisaukas, R. Babb and E. R. Davidson, J. Chem. Phys., 1996, 105, 6607–6615.
46. M. Nakamoto, T. Yamasaki and A. Sekiguchi, J. Am. Chem. Soc., 2005, 127, 6954–6955.
47. M. M. Olmstead, R. S. Simons and P. P. Power, J. Am. Chem. Soc., 1997, 119, 11705–11706.
48. V. Y. Lee and A. Sekiguchi, Acc. Chem. Res., 2007, 40, 410–419.
49. J. Iley, in The Chemistry of Organic Germanium, Tin and Lead Compounds, 1995, pp. 267–289,  DOI:10.1002/0470857242.ch5.
50. B. M. Hoffman, J. Martinsen and R. A. Venters, J. Magn. Reson., 1984, 59, 110–123.
51. Y. Jung, M. Brynda, P. P. Power and M. Head-Gordon, J. Am. Chem. Soc., 2006, 128, 7185–7192.
52. P. Renaud, in Organoselenium Chemistry, ed. T. Wirth, Springer, Berlin, Heidelberg, 2000, vol. 208, pp. 81–112.
53. O. Mallow, M. A. Khanfar, M. Malischewski, P. Finke, M. Hesse, E. Lork, T. Augenstein, F. Breher, J. R. Harmer, N. V. Vasilieva, A. Zibarev, A. S. Bogomyakov, K. Seppelt and J. Beckmann, Chem. Sci., 2015, 6, 497–504.
54. F. Neese, eMagRes, 2007, 6, 1–22.
55. J. D. Rolfes, F. Neese and D. A. Pantazis, J. Comput. Chem., 2020, 41, 1842–1849.

---

Footnotes

† While the term “spin density” is used throughout this article, it is formally incorrect. Spin density is the 3D functional representation of the unpaired spin in space. “Spin population” better refers to the arbitrary partitioning of the unpaired spin onto individual atoms or orbitals. Historically and currently, these two terms are used interchangeably within the EPR community.

‡ Excellent resources of isotropic (a0) and anisotropic (b0) hyperfine coupling constants are Appendix H of ref. 27 and 33.

---