Visible-NIR absorption spectroscopy study of the formation of ternary plutonyl(VI) carbonate complexes

Abstract

We present the first experimental evidence for the ternary complexation of calcium and magnesium ions with plutonyl(VI)tricarbonate species in carbonate-containing aqueous solutions using visible-NIR spectrophotometric titration. Prior to studying the ternary plutonyl(VI) carbonate complexation, visible-NIR absorption spectral information of PuO₂(CO₃)₂²⁻ and PuO₂(CO₃)₃⁴⁻ was successfully obtained. PuO₂(CO₃)₂²⁻ has a prominent peak at 853 nm and its molar absorptivity was determined to be ε_{853, PuO2(CO3)2²⁻} = 49.0 ± 4.2 M⁻¹·cm⁻¹. The spectrophotometric titration results by adding calcium or magnesium to the plutonyl(VI) carbonate system consisting of PuO₂(CO₃)₂²⁻ and PuO₂(CO₃)₃⁴⁻ indicate the formation of CaPuO₂(CO₃)₃²⁻ and MgPuO₂(CO₃)₃²⁻ complexes and provide the formation constants at 0.1 M H/NaClO₄ for MPuO₂(CO₃)₃²⁻ from PuO₂(CO₃)₃⁴⁻, log K = 4.33 ± 0.50 and 2.58 ± 0.18 for M = Ca²⁺ and Mg²⁺, respectively. In addition, the formation constants of CaPuO₂(CO₃)₃²⁻ and MgPuO₂(CO₃)₃²⁻ from PuO₂(CO₃)₃⁴⁻ at infinite dilution (log K°) were proposed to be 6.05 ± 0.50 and 4.29 ± 0.18, respectively, based on the correction of ionic strength using the Davies equation. The absorption spectrum of the ternary plutonyl(VI) complexes of CaPuO₂(CO₃)₃²⁻ is similar to that of PuO₂(CO₃)₃⁴⁻ with the exception of a characteristic absorption peak at 808 nm (ε_{808, CaPuO2(CO3)3²⁻} = 42.9 ± 1.6 M⁻¹·cm⁻¹). According to the calculated aqueous plutonyl(VI) speciation including the ternary plutonyl(VI) complexes, CaPuO₂(CO₃)₃²⁻ is considered the dominant Pu(VI) species under environmental conditions, and plutonyl(VI) may be more mobile than expected in previous assessments.

---

1. Introduction

Plutonium is generally produced during nuclear power generation and by nuclear weapons programmes and is one of the most strictly regulated elements in the world because of national security, nuclear proliferation, and radiological hazard concerns. Anthropogenic activities such as nuclear weapons testing,¹ severe accidents in nuclear power plants, improper waste management, and disposal of legacy waste² can cause plutonium contamination in the environment. The fate and transport of plutonium in the environment must be assessed for the remediation of polluted sites and nuclear waste management.³ However, it is very difficult to predict the chemical behaviour of plutonium in the environment because plutonium can simultaneously exist in multiple oxidation states (+3, +4, +5, and +6) in a single aquatic system, and aquatic plutonium (bio)geochemistry is exclusively governed by the oxidation state.⁴ For instance, tetravalent plutonium, Pu(IV), is considered insoluble and readily adsorbed, but Pu(IV) transport can be facilitated by colloids. However, hexavalent plutonium, Pu(VI), is relatively soluble and behaves as an aqueous species due to its complexation with a variety of inorganic and organic ligands.⁵

Natural waters such as rainwater, groundwater, and seawater can not only leach plutonium from plutonium-bearing pollutants but also transport plutonium. The oxidation state and aqueous speciation of plutonium are of utmost importance for the understanding of plutonium transport and migration via natural fluids. In contact with atmospheric air, natural waters are oxidizing, and the higher oxidation states of plutonyl ions, namely, Pu(V) and Pu(VI), are widely observed in oxic rainwater, surface groundwater, seawater, and drinking water.^2,6–9 Radiolysis also plays an important role in the oxidation of plutonium and the stabilization of a high oxidation state.^9,10 In the weakly acidic to weakly alkaline pH range (pH 5–9) of natural water, carbonate ion (CO₃²⁻) is one of the most influential ligands in aquatic chemistry due to its high concentration and strong affinity for cations. In oxidizing natural waters of neutral to weakly alkaline pH, plutonyl(V,VI)carbonato species such as PuO₂CO₃⁻ and PuO₂(CO₃)₂²⁻ are expected to be the dominant aqueous plutonium species^5,11,12 based on a thermodynamic database¹³ and modelling.

Beyond the binary carbonato complexes, ternary complexes containing divalent alkaline earth ions were found for hexavalent uranium, U(VI),¹⁴ and are regarded as the major U(VI) complexes. Over the past two decades, the formation of ternary species (M_xUO₂(CO₃)₃^2x−4, M = Ca²⁺ and Mg²⁺) has been intensively studied and the M_xUO₂(CO₃)₃^2x−4 complexes are the dominant aqueous U(VI) species in the presence of naturally abundant Ca²⁺ and Mg²⁺ ions in groundwater and seawater.^15–25 In addition to their overwhelming predominance in aqueous U(VI) species in natural waters, the ternary complexes are U(VI) species with significantly increased mobility resulting from decreased U(VI) sorption^26–28 and hindered reduction to immobile tetravalent uranium.^29–32 In a field study, the occurrence of Ca₂UO₂(CO₃)₃(aq) was observed even in deep, reducing, Fe(II)-containing groundwater (E_h – 140 mV, ∼500 metres below sea level).³³ A study of uranium speciation in sea urchins identified the uptake of uranium in the form of ternary calcium carbonato species.³⁴ Although ternary complexation is very striking with respect to the common fate of uranium under various environmental conditions, it has not been reported for hexavalent actinides other than U(VI).

Here, we identify the ternary complexation of plutonyl(VI) tricarbonate with calcium and magnesium ions for the first time. Visible-near infrared (vis-NIR) absorption spectroscopy is employed to elucidate the chemical interaction of Ca²⁺ and Mg²⁺ with plutonyl(VI) carbonate species. Among the various chemical models, a chemical model involving the formation of CaPuO₂(CO₃)₃²⁻ confirms our spectrophotometric results. Finally, the noticeable impacts of the ternary complexation of Pu(VI) on its aqueous chemistry and mobility in the environment are discussed based on the obtained formation constants for CaPuO₂(CO₃)₃²⁻ and MgPuO₂(CO₃)₃²⁻.

2. Experimental section

2.1. Cautions

Plutonium is radioactive and toxic. For experiments with plutonium, a restricted area with appropriate safety equipment and authorization is required. In this work, the plutonium solutions were carefully handled in a chemical fume hood and negative pressure glove box.

2.2. Chemicals

Plutonium stock solution was prepared by the dissolution of PuO₂ (ORNL, ²⁴²Pu: 99.932% with trace levels of ²³⁸Pu, ²³⁹Pu, ²⁴⁰Pu, ²⁴¹Pu, and ²⁴⁴Pu) with concentrated HNO₃ and a small amount of HF. ²⁴¹Am generated from the β-decay of ²⁴¹Pu was separated from the plutonium stock solution by anion exchange (AG 1-X8, Bio-Rad). The background electrolyte (HNO₃ and HF) was converted to HClO₄ by fuming with concentrated HClO₄ solution before drying and re-dissolution. The absence of the oxidation states of plutonium other than +6 was confirmed by vis-NIR absorption spectroscopy. Ultrafiltration (10 kDa, Ultracel YM regenerated cellulose membrane, Centricon-10, Millipore) was employed to eliminate particulates and the breakdown probability obtained using laser-induced breakdown detection (LIBD) of the Pu(VI) stock solution was comparable to that of ultrapure water (Milli-Q, Merck Millipore), which indicates the absence of particulates in the solution. The concentration of the Pu(VI) stock solution was determined to be 6 mM by liquid scintillation counting (LSC). The detailed experimental setups for LIBD have been described elsewhere.^35,36 Aliquots of plutonium stock solution were taken to obtain the desired plutonium concentration.

Stock solutions of 0.5 M Na₂CO₃ and 1.5 M NaClO₄ were prepared by the dissolution of anhydrous Na₂CO₃ (99.999%, Aldrich) and hydrate NaClO₄ (99.99%, Aldrich), respectively, in Milli-Q water. Pu(VI) samples for vis-NIR spectrophotometric titration were prepared with a Pu concentration of 0.35–0.40 mM. The initial carbonate concentration was set to 18 mM. To minimize the reduction of Pu, NaOCl was spiked at a 0.2 mM concentration of hypochlorite in the samples. HClO₄ (99.999%, Aldrich) was used to adjust the pH of the Pu samples. The pH was measured using a combination glass Ross-type electrode (Thermo Scientific Orion) filled with 3 M KCl calibrated with pH buffers (pH 4.01, 7.00, and 10.01, Thermo Scientific Orion). The pH measurement was carried with a separated and duplicated sample solution in each titration step. The pH values mentioned throughout this manuscript are the measured values. The magnesium and calcium titrants were prepared by the dissolution of Mg(ClO₄)₂·4H₂O (99%, Aldrich) and Ca(ClO₄)₂·4H₂O (99%, Aldrich) in 0.1 M NaClO₄ to obtain 0.23 M Mg²⁺ and 0.14 M Ca²⁺. The ionic strength of the Pu(VI) sample was set to 0.1 M H/NaClO₄. All solutions were prepared with ultrapure Milli-Q water (18.2 MΩ cm⁻¹). The plutonium concentration was measured using LSC (Tri-Carb 3110TR, PerkinElmer) and the concentrations of magnesium and calcium were analysed by inductively coupled plasma-optical emission spectroscopy (ICP-OES).

2.3. Vis-NIR spectrophotometry and data processing

A 2.5 mL Pu sample was contained in a sealable quartz cell (Hellma Analytics) with an optical path length of 1 cm, and the cell was mounted in a temperature-controllable cuvette holder (Agilent Technologies) during the measurement. The vis-NIR absorption spectra were recorded by a spectrophotometer (Cary 5000, Agilent) at 25 °C. To increase the concentrations of H⁺, Mg²⁺, and Ca²⁺, aliquots of HClO₄ and titrants, Mg(ClO₄)₂ and Ca(ClO₄)₂ in 0.1 M NaClO₄, were added, and the sample was equilibrated for 10 min with magnetic stirring before the absorption measurements. The equilibrium constants and absorption spectra of each species were calculated from the recorded spectra using a minimization program (Hypspec2014).³⁷ For the fitting of the spectrophotometric results and the calculation of formation constants and absorption spectra of CaPuO₂(CO₃)₃²⁻, the aqueous species H₂CO₃, HCO₃⁻, NaHCO₃, NaCO₃⁻, CaHCO₃⁺, CaCO₃, PuO₂(CO₃)₂²⁻, PuO₂(CO₃)₃⁴⁻, H⁺, and OH⁻ were included in the model as the existing species in the system. The equilibrium constants were obtained from ref. 13 and 38 and corrected to those at 0.1 M H/NaClO₄ based on the specific ion interaction theory (SIT)³⁹ and the corresponding coefficients in ref. 40 and 41. The absorption spectrum in the range of 873 nm to 899 nm was excluded from data processing due to the meaningless signals with noisy fluctuation generated while exchanging the detectors of the spectrometer. All experiments were performed in triplicate. Errors of the data obtained in this work represent ±1σ. The formation constant of CaPuO₂(CO₃)₃²⁻ was calculated to inherently include the errors of the formation constants of PuO₂(CO₃)₂²⁻ and PuO₂(CO₃)₃⁴⁻ since the log K values of PuO₂(CO₃)₂²⁻ and PuO₂(CO₃)₃⁴⁻ were taken into account in the calculation with their errors (±0.50). On the other hand, the error for the log K of MgPuO₂(CO₃)₃²⁻ was obtained independent of the errors for PuO₂(CO₃)₂²⁻ and PuO₂(CO₃)₃⁴⁻.

The stepwise formation constants of MgPuO₂(CO₃)₃²⁻ and CaPuO₂(CO₃)₃²⁻ species (log K_{MPuO2(CO3)3²⁻}, M²⁺ + PuO₂(CO₃)₃⁴⁻ ↔ MPuO₂(CO₃)²⁻, M = Mg and Ca) at infinite dilution were determined using the Davies equation.⁴³

2.4. Geochemical modelling

PHREEQC (version 3)⁴⁴ was used to calculate the aqueous Pourbaix diagram (E_h-pH diagram) and Pu(VI) speciation with pH at 25 °C and infinite dilution. The thermodynamic data for Pu(VI) species were basically obtained from NEA-TDB in PHREEQC format (updated in November, 2018).⁴⁵ For the formation constants of MgPuO₂(CO₃)₃²⁻ and CaPuO₂(CO₃)₃²⁻, the data obtained in this work were used. For the aqueous and solid species for calcium, magnesium, and carbonate, the thermodynamic data of WATEQ4F³⁸ were used. In the calculations, calcite, magnesite, dolomite, PuO₂CO₃(cr), and PuO₂(OH)₂·H₂O(cr) were taken into account as solubility limiting phases. The Pourbaix diagram was illustrated using PhreePlot software.⁴⁶

3. Results and discussion

3.1. Vis-NIR absorption spectral properties of PuO₂(CO₃)₂²⁻ and PuO₂(CO₃)₃⁴⁻

Prior to the investigation of Ca²⁺ complexation with plutonyl(VI)carbonate species, the vis-NIR absorption characteristics of PuO₂(CO₃)₂²⁻ and PuO₂(CO₃)₃⁴⁻ species were identified. Fig. 1a and b show the results of a vis-NIR spectrophotometric titration with decreasing pH. At the starting point of the spectrophotometric titration (pH 9.78, Fig. 1a and b), the aqueous Pu(VI) speciation is calculated to be 100% PuO₂(CO₃)₃⁴⁻ by thermodynamic modelling based on the critically reviewed NEA-TDB (ESI, Fig. S1†), and the recorded spectrum at pH 9.78 is identical to the absorption spectrum of Pu(VI) observed under concentrated carbonate conditions at a strongly alkaline pH (2 M Na₂CO₃, pH 12.6) in a previous study.⁴⁷ It is therefore assumed that the spectrophotometric titration starts at 100% PuO₂(CO₃)₃⁴⁻, and the observed spectrum of Pu(VI) at the initial point (pH 9.78) is ascribed to the characteristic absorption spectrum of PuO₂(CO₃)₃⁴⁻. The characteristic sharp absorption peak of PuO₂²⁺ ions at 830 nm completely disappears due to carbonato complexation, and instead, broad absorption from 500 nm to 650 nm (molar absorptivity ε = 55.7 ± 2.8 M⁻¹ cm⁻¹ at the peak position of 569 nm) is observed. In addition, the observed absorption bands in the ranges of 840–870 nm, 900–960 nm, and 1000–1120 nm are comparable to the reported absorption bands of Pu(VI) carbonate species in previous work.^47,48

Fig. 1 Representative results of the spectrophotometric pH titration of the plutonyl(VI) carbonate system ([Pu(VI)] = 0.36 mM, [CO₃²⁻]_total = 18 mM, pH 9.78 (black line) to 7.73 (red line), and I = 0.1 M H/NaClO₄) with decreasing pH in the wavelength ranges of (a) 500–870 nm and (b) 900–1120 nm. The arrows indicate a gradual increase (up) and decrease (down) in absorbance due to acidification. (c) Vis-NIR absorption spectra (500–1120 nm) of PuO₂(CO₃)₃⁴⁻ (solid line, measured at pH 9.78) and PuO₂(CO₃)₂²⁻ (dotted line, determined from the equilibrium constant of the transition reaction, PuO₂(CO₃)₃⁴⁻ ↔ PuO₂(CO₃)₂²⁻ + CO₃²⁻).

As the pH decreased, the recorded absorption spectra gradually changed (Fig. 1a and b), indicating chemical changes in the aqueous Pu(VI) species. A decrease in absorbance with a continuous hypsochromic shift in the broad absorption between 500 nm and 650 nm and the appearance of isosbestic points at 540, 654, 823, 953, and 1054 nm representing a one-to-one transition of PuO₂(CO₃)₃⁴⁻ to PuO₂(CO₃)₂²⁻ are observed with decreasing pH. With acidification, absorption bands at 853 nm and 1010 nm appear and gradually grow, whereas the intensity of the double peaks in the 1000–1120 nm region decreases.

In addition to the characteristic changes in the absorption spectra, the calculated equilibrium constant also supports a change in aqueous Pu(VI) species from PuO₂(CO₃)₃⁴⁻ to PuO₂(CO₃)₂²⁻ after comparison with the reported thermodynamic data. The chemical reaction is as follows:

PuO₂(CO₃)₃⁴⁻ ↔ PuO₂(CO₃)₂²⁻ + CO₃²⁻ (1)

From the results of the spectrophotometric titration, the equilibrium constant (log K) of reaction (1) is calculated to be −4.02 ± 0.19 at 0.1 M H/NaClO₄ by the data processing software³⁷ and is corrected to −3.15 ± 0.20 at infinite dilution by SIT³⁹ using ion interaction coefficients from previous work.⁴¹ The corrected formation constant of −3.15 ± 0.20 is very comparable to the value of −3.30 ± 1.02, which resulted from the difference in the Gibb's free energies of formation for PuO₂(CO₃)₂²⁻ and PuO₂(CO₃)₃⁴⁻ species.¹³ These critically reviewed formation constants of reactions (2) and (3) are 14.7 ± 0.50 and 18.0 ± 0.50, respectively.

PuO₂²⁺ + 2CO₃²⁻ ↔ PuO₂(CO₃)₂²⁻ (2)

PuO₂²⁺ + 3CO₃²⁻ ↔ PuO₂(CO₃)₃⁴⁻ (3)

The stability constants and interaction coefficients of Pu(VI) carbonate species in 0.202 m NaClO₄ were recently revisited by coupling capillary electrophoresis and ICP-MS.⁴¹ The newly obtained stability constants at infinite dilution based on the reactions (2) and (3) were 14.99 ± 0.06 and 17.94 ± 0.30, respectively. This corresponds to −2.95 ± 0.31 for reaction (1), which is also comparable to our data (−3.15 ± 0.20).

The aqueous Pu(VI) speciation from the spectrophotometry in this study and from the thermodynamic modelling with NEA-TDB are in good agreement (ESI, Fig. S1†). Along with the equilibrium constant of reaction (1), the pure absorption spectrum of PuO₂(CO₃)₂²⁻ is obtained accordingly based on the results of the potentiometric titration (Fig. 1c). The molar absorptivity of the most prominent peak of PuO₂(CO₃)₂²⁻ at 853 nm is determined to be 49.0 ± 4.2 M⁻¹ cm⁻¹. Notably, a shoulder peak in the vicinity of the PuO₂(CO₃)₂²⁻ band at 853 nm arises at approximately 843 nm below pH 8.2. Thermodynamic modelling reveals the formation of plutonyl(VI) monocarbonate species in very low abundance, <5%. To avoid interference from Pu(VI) species other than PuO₂(CO₃)₂²⁻ and PuO₂(CO₃)₃⁴⁻, the equilibrium constant and the absorption spectrum of PuO₂(CO₃)₂²⁻ species are determined using the result obtained above pH 8.2.

3.2. Interaction of Ca²⁺ with Pu(VI) carbonate species

On the basis of the absorption spectral information of PuO₂(CO₃)₂²⁻ and PuO₂(CO₃)₃⁴⁻, the ternary complexation of plutonyl(VI)carbonate species with Ca²⁺ is investigated (Fig. 2). At 808 nm, a new sharp peak, which is not observed in the PuO₂(CO₃)₂²⁻/PuO₂(CO₃)₃⁴⁻ system, appears after adding Ca²⁺ and is thus a strong indication of the interaction of Ca²⁺ with Pu(VI) carbonate species. Together with the growth of this peak at 808 nm characteristic of the interaction with Ca²⁺, the broad absorption band between 500 nm and 650 nm, representing the equilibrium of PuO₂(CO₃)₂²⁻ and PuO₂(CO₃)₃⁴⁻, undergoes a bathochromic shift after addition of Ca²⁺ even at a constant pH of 7.9 during the titration. These spectral features are identical to other spectrophotometric Ca²⁺ titrations with varying starting pH values and different ratios of PuO₂(CO₃)₂²⁻/PuO₂(CO₃)₃⁴⁻ (ESI, Fig. S2†). This unambiguously indicates that a simultaneous interaction of Ca²⁺ with PuO₂(CO₃)₂²⁻ and PuO₂(CO₃)₃⁴⁻ is unlikely. In addition, the clear isosbestic points at 540 and 651 nm are independent of the pH of the Ca²⁺ titration, indicating that only one Ca–Pu(VI) carbonate species is formed: either Ca²⁺–PuO₂(CO₃)₂²⁻ or Ca²⁺–PuO₂(CO₃)₃⁴⁻. The redshift in the broad peak (500–650 nm) and the disappearance of absorbance at 853 nm correspond to the change in the aqueous Pu(VI) species from PuO₂(CO₃)₂²⁻ to PuO₂(CO₃)₃⁴⁻. The absorption spectrum of the newly formed Ca²⁺–Pu(VI) carbonate species is similar to that of PuO₂(CO₃)₃⁴⁻, except for a distinguishable absorption band at 808 nm. In addition, the characteristic peak of PuO₂(CO₃)₂²⁻ at 853 nm is attenuated by the addition of Ca²⁺ and nearly vanishes at the end of the Ca²⁺ titration ([Ca²⁺] = 0.72 mM), which reflects a significant decrease in the PuO₂(CO₃)₂²⁻ concentration with Ca²⁺ addition. Thus, Ca²⁺ likely interacts with PuO₂(CO₃)₃⁴⁻ rather than PuO₂(CO₃)₂²⁻. This interaction is also experimentally confirmed by the results of the spectrophotometric titration at pH 9.1, showing the appearance of the peak at 808 nm even in the absence of PuO₂(CO₃)₂²⁻ (Fig. 2b).

Fig. 2 Results of the spectrophotometric Ca²⁺ titration. (a) Representative results of the spectrophotometric Ca²⁺ titration of the plutonyl(VI)carbonate system ([Pu(VI)] = 0.39 mM, [CO₃²⁻]_total = 17 mM, [Ca²⁺] = 0 to 0.72 mM, pH 7.9, and I = 0.1 M H/NaClO₄) with increasing Ca²⁺ in the wavelength range of 500–870 nm. The arrows indicate a gradual increase (up) and decrease (down) in absorbance due to Ca²⁺ complexation. (b) Increase in the peak at 808 nm under PuO₂(CO₃)₃⁴⁻-dominant conditions ([Pu(VI)] = 0.39 mM, [CO₃²⁻]_total = 17 mM, [Ca²⁺] = 0 to 0.11 mM, pH 9.1, and I = 0.1 M H/NaClO₄). (c) Results of a triplicate slope analysis (log R vs. log [Ca²⁺]_total) with the slope (x) representing the stoichiometric number of complexed Ca²⁺ obtained from linear regression. (d) Deconvoluted vis-NIR absorption spectra of CaPuO₂(CO₃)₃²⁻ from the results of the spectrophotometric Ca²⁺ titrations.

Slope analysis (Fig. 2c) was conducted to determine the stoichiometric number (x) of Ca²⁺ complexing with PuO₂(CO₃)₃⁴⁻. The chemical reaction of Ca²⁺ with PuO₂(CO₃)₃⁴⁻ and its equilibrium constant of Ca_xPuO₂(CO₃)₃^2x−4 (log K) are described with the concentration ratio (R) of Ca²⁺-complexed and uncomplexed plutonyl(VI) species, i.e., [Ca_xPuO₂(CO₃)₃^2x−4]/[PuO₂(CO₃)₃⁴⁻], as follows:

xCa²⁺ + PuO₂(CO₃)₃⁴⁻ ↔ Ca_xPuO₂(CO₃)₃^2x−4

log K = log R − x·log [Ca²⁺] (4)

At the first measurement point, the total Pu(VI) concentration ([Pu]_total) is the sum of the concentrations of PuO₂(CO₃)₂²⁻ and PuO₂(CO₃)₃⁴⁻ in the absence of Ca²⁺. In each step of the titration, the concentration of PuO₂(CO₃)₂²⁻ is determined from the absorbance (A₈₅₃) and the molar absorptivity at 853 nm (ε_{853, PuO2(CO3)2²⁻}), where the characteristic peak of PuO₂(CO₃)₂²⁻ is located. The concentration ratio of PuO₂(CO₃)₃⁴⁻ to PuO₂(CO₃)₂²⁻ can be assumed to be constant (C) in all steps of the Ca²⁺ titration at a consistent pH and CO₃²⁻ concentration; thus, the concentration of Ca_xPuO₂(CO₃)₃^2x−4 is calculated from the Pu(VI) concentration balance. Accordingly, the concentration ratio (R) of Ca²⁺-complexed and uncomplexed Pu species is rearranged in terms of the absorption properties as follows:

As shown in Fig. 2c, the slope of log R vs. log [Ca²⁺]_total is 1.14 ± 0.21, indicating that the stoichiometric number of Ca²⁺ ions complexing with PuO₂(CO₃)₃⁴⁻ is close to 1 and CaPuO₂(CO₃)₃²⁻ species are formed. The positive deviation of the obtained slope from the ideal value of 1 may be attributed to an overestimation of the free Ca²⁺ ion concentration because the amount of Ca²⁺ actually consumed by complexation is neglected. Taking into account the consumed Ca²⁺ concentration based on the assumption of x = 1, the slope is determined to be 0.94 ± 0.26 (ESI, Fig. S3†).

The formation of the monocalcium plutonyl(VI)tricarbonate, CaPuO₂(CO₃)₃²⁻, was also confirmed by the examination of possible chemical models. A chemical model based on the formation of CaPuO₂(CO₃)₃²⁻ shows a very successful fitting result with the spectrophotometric titration, and the stepwise formation constant of CaPuO₂(CO₃)₃²⁻ (log K_{CaPuO2(CO3)3²⁻}, Ca²⁺ + PuO₂(CO₃)₃⁴⁻ ↔ CaPuO₂(CO₃)₃²⁻) corresponding to reaction (4) with x = 1 is calculated to be 4.33 ± 0.50 in 0.1 M H/NaClO₄. The absorption spectrum of CaPuO₂(CO₃)₃²⁻ calculated from the results of spectrophotometric titration is presented in Fig. 2d. The stepwise formation constant of the similar uranyl(VI) species, CaUO₂(CO₃)₃²⁻, in 0.1 M H/NaClO₄ medium (log K_{CaUO2(CO3)3²⁻}, Ca²⁺ + UO₂(CO₃)₃⁴⁻ ↔ CaUO₂(CO₃)₃²⁻) has been reported to be 3.13 ± 0.22²⁰ and 3.00 ± 0.25²³ in previous work. Other chemical models presuming the formation of neutral Ca₂PuO₂(CO₃)₃(aq) species show unsatisfactory spectrophotometric results with failures in the spectral fitting procedure (ESI, Fig. S4†) and implausible formation constants. Even though the ternary Ca²⁺ complexation of PuO₂(CO₃)₃⁴⁻ is more favourable than that of UO₂(CO₃)₃⁴⁻, the di-calcium species, which is frequently observed for U(VI) as Ca₂UO₂(CO₃)₃(aq), appears to be difficult to form for PuO₂(CO₃)₃⁴⁻. UO₂(CO₃)₃⁴⁻ can be dominant even at a low pH and carbonate concentration, where a millimolar concentration of Ca²⁺ is sufficient to form di-calcium species that can be dissolved. However, in the case of Pu(VI), the formation of a considerable amount of PuO₂(CO₃)₃⁴⁻ requires a relatively high pH and carbonate concentration, but the amount of Ca²⁺ ions needed to form di-calcium species is limited due to the solubility limit imposed by the formation of CaCO₃(s) under these conditions.

3.3. Mg²⁺–PuO₂(CO₃)₃⁴⁻ system

Similar to Ca²⁺ complexation, an identical trend in spectrophotometric changes is also observed for the titration with Mg²⁺ ions (ESI, Fig. S5†). However, the evolution of the absorbance is more insensitive to the Mg²⁺ concentration than to the Ca²⁺ system, which represents a stronger affinity of Ca²⁺ than that of Mg²⁺ for PuO₂(CO₃)₃⁴⁻. Because of this small spectral change in absorbance, even with a large variation in the Mg²⁺ concentrations compared to the Ca²⁺ system, data processing by the minimization software³⁷ and the convolution of the characteristic absorption spectrum of MgPuO₂(CO₃)₃²⁻ are problematic. Instead, the concentration balance used in the slope analysis (eqn (4) and (5)) is utilized to quantitatively determine the concentration of Mg²⁺-complexed PuO₂(CO₃)₃⁴⁻ in each step of the titration based on the assumed formation of MgPuO₂(CO₃)₃²⁻. The stepwise formation constant of MgPuO₂(CO₃)₃²⁻ at 0.1 M H/NaClO₄ (log K_{MgPuO2(CO3)3²⁻}) is calculated to be 2.58 ± 0.18, which is smaller than log K_{CaPuO2(CO3)3²⁻}. The favourability of Ca²⁺ over Mg²⁺ is widely observed in Mg²⁺/Ca²⁺–UO₂(CO₃)₃⁴⁻ complexations as well.^18,22,24

To make the formation constants applicable to thermodynamic modelling, the Davies equation⁴³ is applied to correct the ionic strength to infinite dilution. The stepwise formations of MgPuO₂(CO₃)₃²⁻ and CaPuO₂(CO₃)₃²⁻ at infinite dilution are determined to be log K°_{MgPuO2(CO3)3²⁻} = 4.29 ± 0.18 and log K°_{CaPuO2(CO3)3²⁻} = 6.05 ± 0.50. To the best of our knowledge, the formations of MgPuO₂(CO₃)₃²⁻ and CaPuO₂(CO₃)₃²⁻ are reported for the first time in this work. For that reason, the ion interaction coefficients of the ternary plutonyl(VI) species are still unknown. Nonetheless, it is worth noting that the use of the SIT approach³⁹ with the ion interaction coefficient of CaUO₂(CO₃)₃²⁻ with Na⁺ suggested from PSI/Nagra-TDB,⁴²ε(CaUO₂(CO₃)₃²⁻, Na⁺) = –(0.1 ± 0.1) kg·mol⁻¹, as a surrogate coefficient for MPuO₂(CO₃)₃²⁻ shows insignificant differences in log K° (4.27 ± 0.19 and 6.02 ± 0.50 for M = Mg²⁺ and Ca²⁺, respectively) with the values obtained using the Davies equation.⁴³Table 1 summarizes the formation constants of ternary plutonyl(VI) complexes in 0.1 M H/NaClO₄ and at infinite dilution (Davies equation⁴³).

Table 1 Equilibrium constants (log K) of Mg²⁺/Ca²⁺ complexation with PuO₂(CO₃)₃⁴⁻

log K
Reactions	I = 0.1 M H/NaClO4	I = 0 M infinite dilution	Ref.
a Present work. b Corrected by using the Davies equation.^43
PuO2^2+ + 3CO3^2− ↔ PuO2(CO3)3^4−	—	18.00 ± 0.50	13
Mg^2+ + PuO2(CO3)3^4− ↔ MgPuO2(CO3)3^2−	2.58 ± 0.18	4.29 ± 0.18^b	p.w.^a
Mg^2+ + PuO2^2+ + 3CO3^2− ↔ MgPuO2(CO3)3^2−	—	22.29 ± 0.53	p.w.^a
Ca^2+ + PuO2(CO3)3^4− ↔ CaPuO2(CO3)3^2−	4.33 ± 0.50	6.05 ± 0.50^b	p.w.^a
Ca^2+ + PuO2^2+ + 3CO3^2− ↔ CaPuO2(CO3)3^2−	—	24.05 ± 0.50	p.w.^a

---

3.4. Aqueous Pu speciation

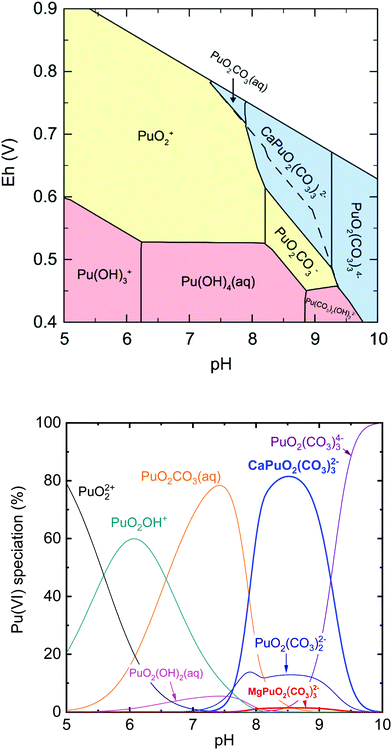
Fig. 3 presents the Pourbaix diagram (Eh–pH diagram) and the aqueous Pu(VI) species distribution based on the obtained thermodynamic data of CaPuO₂(CO₃)₃²⁻ and MgPuO₂(CO₃)₃²⁻ and the data from NEA-TDB.¹³ It is worth noting that the modelling was performed at considerably reduced Pu concentrations (10⁻⁹ M) and carbonate amount (atmospheric CO₂(g) equilibrium) as compared to those used in the experiments ([Pu(VI)] = 0.35–0.40 mM and [CO₃²⁻]_initial = 18 mM). At weakly alkaline pH under oxidizing conditions, CaPuO₂(CO₃)₃²⁻ is the dominant aqueous Pu(VI) species and the apparent Pu(VI/V) Nernstian potential is shifted toward a less positive value, which suggests a slight but further redox stabilization of Pu(VI). As a consequence of the formation of CaPuO₂(CO₃)₃²⁻, the effect of PuO₂(CO₃)₂²⁻, which was expected to be the major Pu(VI) species in previous work,^5,11,12 would be weakened in the presence of calcium at environmental (millimolar) concentrations. Based on the aqueous Pu(VI) speciation (Fig. 3b), the predominance of CaPuO₂(CO₃)₃²⁻ and a correspondingly decreased amount of PuO₂(CO₃)₂²⁻ are expected in natural waters such as rainwater, groundwater, and seawater. In addition, the strong ternary complexation could increase Pu(VI) solubility up to approximately six times at pH 7.5–9.0 (ESI, Fig. S7†).

Fig. 3 Environmental implications of the formation of CaPuO₂(CO₃)₃²⁻ and MgPuO₂(CO₃)₃²⁻ ([Pu] = 1 × 10⁻⁹ M, [Ca²⁺] = [Mg²⁺] = 1 mM, in equilibrium with p_CO2(g) = 10^−3.4 atm, at 25 °C and infinite dilution). (a) Calculated Pourbaix (E_h-pH) diagram of aqueous plutonium species. The dashed line represents the boundary of apparent Pu(VI/V) Nernstian potential in the absence of Ca²⁺ and Mg²⁺. (b) Calculated aqueous Pu(VI) species distribution. The abrupt change at pH 8.1 occurs due to the solubility of Ca²⁺ in the carbonate system. For the details of calculation, see section 2.4.

4. Conclusions

The complexations of aqueous plutonyl(VI) carbonate species with Ca²⁺ and Mg²⁺ were identified for the first time using vis-NIR absorption spectroscopy. In Ca²⁺ or Mg²⁺ titrations, a characteristic absorption signal at 808 nm, which was not observed in the plutonyl carbonate system, i.e. PuO₂(CO₃)₂²⁻ and PuO₂(CO₃)₃⁴⁻, appears and it is a clear indication of the ternary complexation of plutonyl(VI)carbonate with alkaline earth metals. The results of vis-NIR absorption spectroscopy evidently show that Ca²⁺ interacts with PuO₂(CO₃)₃⁴⁻ rather than with PuO₂(CO₃)₂²⁻, and the results of slope analysis provide the stoichiometric number of Ca²⁺ complexing with PuO₂(CO₃)₃⁴⁻ as 1, indicating the formation of MPuO₂(CO₃)₃²⁻ (M = Ca²⁺ and Mg²⁺). Based on the results of spectrophotometric titration and the correction of ionic strength using the Davies equation, the formation constants of CaPuO₂(CO₃)₃²⁻ and MgPuO₂(CO₃)₃²⁻ from PuO₂(CO₃)₃⁴⁻ are determined to be log K° = 6.05 ± 0.50 and 4.29 ± 0.18, respectively.

The prediction of the environmental behaviour of plutonium based on the geochemical calculation considering MPuO₂(CO₃)₃²⁻ suggests that CaPuO₂(CO₃)₃²⁻ would be the most predominant Pu(VI) species and increase Pu(VI) solubility in the natural waters. It may also affect the redox property of plutonium and stabilize Pu in the hexavalent state by strong complexation. Ternary Mg²⁺/Ca²⁺–PuO₂(CO₃)₃⁴⁻ complexes can enhance Pu migration in aqueous systems under oxidizing conditions such as groundwater and seawater containing abundant calcium, magnesium, and carbonate.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by a grant from the Nuclear R&D Program of the National Research Foundation of Korea funded by the Korean Ministry of Science and ICT (grant codes: 2016M2B2B1945252 and 2017M2A8A5014719).

Notes and references

1. E. P. Hardy, P. W. Krey and H. L. Volchok, Nature, 1973, 241, 444–445.
2. D. M. Nelson and M. B. Lovett, Nature, 1978, 276, 599–601.
3. K. J. Cantrell and A. R. Felmy, Plutonium and americium geochemistry at Hanford: a site wide review, Report PNNL-21651, Pacific Northwest National Lab. (PNNL), Richland, WA (United States), 2012.
4. D. L. Clark, The chemical complexities of plutonium, NM, 2000.
5. A. E. Hixon and B. A. Powell, Environ. Sci.: Processes Impacts, 2018, 20, 1306–1322.
6. R. Fukai, A. Yamato, M. Thein and H. Bilinski, Geochem. J., 1987, 21, 51–57.
7. G. R. Choppin and A. Morgenstern, in Radioactivity in the Environment, ed. A. Kudo, Elsevier, Amsterdam, 2001, vol. 1, pp. 91–105.
8. G. R. Choppin and P. J. Wong, Aquat. Geochem., 1998, 4, 77–101.
9. R. P. Larsen and R. D. Oldham, Science, 1978, 201, 1008–1009.
10. I. Pashalidis, J. I. Kim, C. Lierse and J. C. Sullivan, Radiochim. Acta, 1993, 60, 99.
11. K. Maher, J. R. Bargar and G. E. Brown, Inorg. Chem., 2013, 52, 3510–3532.
12. S. D. Reilly, W. Runde and M. P. Neu, Geochim. Cosmochim. Acta, 2007, 71, 2672–2679.
13. R. Guillaumont, T. Fanghänel, J. Fuger, I. Grenthe, V. Neck, D. A. Palmer and M. H. Rand, Chemical thermodynamics, in Update on the chemical thermodynamics of uranium, neptunium, plutonium, americium and technetium, Elsevier, Amsterdam, 2003, vol. 5.
14. G. Bernhard, G. Geipel, V. Brendler and H. Nitsche, Radiochim. Acta, 1996, 74, 87–91.
15. S. N. Kalmykov and G. R. Choppin, Radiochim. Acta, 2000, 88, 603–606.
16. G. Bernhard, G. Geipel, T. Reich, V. Brendler, S. Amayri and H. Nitsche, Radiochim. Acta, 2001, 89, 511–518.
17. W. Dong and S. C. Brooks, Environ. Sci. Technol., 2006, 40, 4689–4695.
18. W. Dong and S. C. Brooks, Environ. Sci. Technol., 2008, 42, 1979–1983.
19. G. Geipel, S. Amayri and G. Bernhard, Spectrochim. Acta, Part A, 2008, 71, 53–58.
20. J.-Y. Lee and J.-I. Yun, Dalton Trans., 2013, 42, 9862–9869.
21. F. Endrizzi and L. Rao, Chem. – Eur. J., 2014, 20, 14499–14506.
22. J.-Y. Lee, M. Vespa, X. Gaona, K. Dardenne, J. Rothe, T. Rabung, M. Altmaier and J.-I. Yun, Radiochim. Acta, 2017, 105, 171–185.
23. Y. Jo, A. Kirishima, S. Kimuro, H.-K. Kim and J.-I. Yun, Dalton Trans., 2019, 48, 6942–6950.
24. Y. Jo, H.-K. Kim and J.-I. Yun, Dalton Trans., 2019, 48, 14769–14776.
25. C. Shang and P. E. Reiller, Dalton Trans., 2020, 49, 466–481.
26. Z. Zheng, T. K. Tokunaga and J. Wan, Environ. Sci. Technol., 2003, 37, 5603–5608.
27. P. M. Fox, J. A. Davis and J. M. Zachara, Geochim. Cosmochim. Acta, 2006, 70, 1379–1387.
28. B. D. Stewart, M. A. Mayes and S. Fendorf, Environ. Sci. Technol., 2010, 44, 928–934.
29. S. C. Brooks, J. K. Fredrickson, S. L. Carroll, D. W. Kennedy, J. M. Zachara, A. E. Plymale, S. D. Kelly, K. M. Kemner and S. Fendorf, Environ. Sci. Technol., 2003, 37, 1850–1858.
30. J. Wan, T. K. Tokunaga, E. Brodie, Z. Wang, Z. Zheng, D. Herman, T. C. Hazen, M. K. Firestone and S. R. Sutton, Environ. Sci. Technol., 2005, 39, 6162–6169.
31. B. D. Stewart, P. S. Nico and S. Fendorf, Environ. Sci. Technol., 2009, 43, 4922–4927.
32. C. Liu, J. M. Zachara, L. Zhong, S. M. Heald, Z. Wang, B.-H. Jeon and J. K. Fredrickson, Environ. Sci. Technol., 2009, 43, 4928–4933.
33. E. L. Tullborg, J. Suksi, G. Geipel, L. Krall, L. Auqué, M. Gimeno and I. Puigdomenech, Procedia Earth Planet. Sci., 2017, 17, 440–443.
34. B. Reeves, M. R. Beccia, P. L. Solari, D. E. Smiles, D. K. Shuh, C. Berthomieu, D. Marcellin, N. Bremond, L. Mangialajo, S. Pagnotta, M. Monfort, C. Moulin and C. Den Auwer, Environ. Sci. Technol., 2019, 53, 7974–7983.
35. H.-R. Cho, Y.-S. Youn, E. C. Jung and W. Cha, Dalton Trans., 2016, 45, 19449–19457.
36. E. C. Jung and H.-R. Cho, in The delivery of nanoparticles, ed. A. A. Hashim, InTech, Rijeka, 2012.
37. P. Gans, A. Sabatini and A. Vacca, Talanta, 1996, 43, 1739–1753.
38. J. W. Ball and D. K. Nordstrom, WATEQ4F – User's manual with revised thermodynamic data base and test cases for calculating speciation of major, trace and redox elements in natural waters, U.S. Geological Survey, 1991.
39. L. Ciavatta, Ann. Chim., 1980, 70, 551–567.
40. I. Grenthe, F. Mompean, K. Spahiu and H. Wanner, TDB-2: guidelines for the extrapolation to zero ionic strength, OECD Nuclear Energy Agency, Issy-les-Moulineaux, 2013.
41. J.-C. Alexandre, N. Dacheux and J. Aupiais, Radiochim. Acta, 2018, 106, 801.
42. T. Thoenen, W. Hummel, U. Berner and E. Curti, The PSI/Nagra chemical thermodynamic database 12/07, Paul Scherrer Institut, Villigen PSI, Switzerland, 2014.
43. C. W. Davies, Ion association, Butterworths, Washington D.C., 1962.
44. D. L. Parkhurst and C. Appelo, Description of input and examples for PHREEQC version 3: a computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations, U.S. Geological Survey, 2013.
45. J. S. Martinez, E.-F. Santillan, M. Bossant, D. Costa and M.-E. Ragoussi, Appl. Geochem., 2019, 107, 159–170.
46. D. G. Kinniburgh and D. M. Cooper, PhreePlot-Creating graphical output with PHREEQC, http://www.phreeplot.org/, version updated 4 May 2020.
47. P. G. Varlashkin, G. M. Begun and J. R. Peterson, Radiochim. Acta, 1984, 35, 211.
48. D. T. Reed, Radiochim. Acta, 1994, 66–67, 95.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/D0DT01982H

---