Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Co(II)-Based single-ion magnets with 1,1′-ferrocenediyl-bis(diphenylphosphine) metalloligands†
J.
Hrubý
 a,
D.
Dvořák
b,
L.
Squillantini
c,
M.
Mannini
a,
D.
Dvořák
b,
L.
Squillantini
c,
M.
Mannini
 c,
J.
van Slageren
c,
J.
van Slageren
 d,
R.
Herchel
d,
R.
Herchel
 b,
I.
Nemec
b,
I.
Nemec
 *ab and
P.
Neugebauer
*ab and
P.
Neugebauer
 a
a
aCentral European Institute of Technology, CEITEC BUT, Purkyňova 656/123, 61200 Brno, Czech Republic. E-mail: ivan.nemec@ceitec.vutbr.cz
bDepartment of Inorganic Chemistry, Faculty of Science, Palacký University, 17. listopadu 12, 77147 Olomouc, Czech Republic
cDepartment of Chemistry “Ugo Schiff”, University of Florence and INSTM Research Unit of Florence, via Lastruccia 3-13, 50019 Sesto Fiorentino, Italy
dInstitute of Physical Chemistry, University of Stuttgart, Pfaffenwaldring 55, 70569 Stuttgart, Germany
First published on 13th August 2020
Abstract
Herein, we report on investigations of magnetic and spectroscopic properties of three heterobimetallic Fe(II)–Co(II) coordination compounds based on the tetracoordinate {CoP2X2} core encapsulated by dppf metalloligand, where X = Cl (1), Br (2), I (3), dppf = 1,1′-ferrocenediyl -bis(diphenylphosphine). The analysis of static magnetic data has revealed the presence of axial magnetic anisotropy in compounds (1) and (2) and this was further confirmed by high-frequency electron spin resonance (HF-ESR) spectroscopy. Dynamic magnetic data confirmed that (1) and (2) behave as field-induced Single-Ion Magnets (SIMs). Together with bulk studies, we have also tested the possibility of depositing (2) as thick films on Au(111), glass, and polymeric acetate by drop-casting as well as thermal sublimation, a key aspect for the development of future devices embedding these magnetic objects.
Introduction
Single-Molecule Magnets (SMMs) feature magnetic bistability at low temperature1 due to the intrinsic energy barrier (U), which is a function of the total spin in the ground state (S) and the axial parameter of the molecular anisotropy (D): U = |D| × S2 for integer spins and U = |D| × (S2 − 1/4) for non-integer spins, under the condition that the magnetic anisotropy is axial −D < 0. However, it has been reported that D is inversely dependent on S2 as can be extracted from the relationships describing spin–orbit contributions to D-tensor.2 Therefore, in parallel with a growing interest in the use of SMM archetypes for the exploration of innovative devices for spintronics3 and quantum computing,4 research efforts in recent decades have been concentrated on maximising the magnetic anisotropy in novel molecular systems, and thus the dynamic magnetic properties of transition metal-ion and rare-earth-based complexes.5 As a result, a plethora of 3d or 4f SMMs with one paramagnetic metal centre, called Single-Ion Magnets (SIMs), have been reported,6 including one with the highest blocking temperature, exceeding the temperature of liquid nitrogen.7 Among the group of 3d SIMs, the Co(II) compounds are the most abundant and the SMM phenomenon was reported for a great variety of the coordination numbers and geometries such as tetracoordinate,8 pentacoordinate,9 hexacoordinate,10 heptacoordinate11 or even octacoordinate.12 In these compounds, the ground spin state is split by strong spin–orbit coupling into two Kramers doublets (|3/2, ±1/2〉 and |3/2, ±3/2〉), which are separated by the energy equal to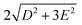 . In the case of tetracoordinate Co(II) compounds with the general formula [Co(LN/P)2(L1)2] or [Co(LN/P)(L1)2], where LN/P represents mono or bidentate N- or P-donor ligands and L1 is halido or pseudohalido ligands, a magneto-structural correlation was established by Boča and co-workers in 2013.13 It reads δ = 2αTd − (α), where αTd is the angle of the ideal tetrahedron (109.5°), α is the angle between the two Co–N/P bonds. Despite some limitations,14 this relationship has proved to be successful in the prediction of sign and magnitude of D, such that more negative/positive δ should lead to more negative/positive value of D. Therefore, our attention has focused on compounds with rather large and negative parameter δ and these were further investigated for their static and dynamic magnetic properties.14,15 Therefore, we opted to investigate the compound [CoCl2(dppf)] as a suitable SIM candidate, where dppf represents the 1,1′-ferrocenediyl-bis(diphenylphosphine). This complex can be prepared by the reaction between dppf and CoCl2 where both dppf and the resulting product [CoCl2(dppf)] are very well known, thoroughly studied (besides magnetic properties)16 and even commercially available coordination compounds.17 The crystal structure of [CoCl2(dppf)] was reported in 199918 and this compound has tetracoordinate {CoP2Cl2} arrangement with δ = −4.8°. Therefore, according to the magneto-structural correlation by Boča et al.,10 it should possess negative D. Furthermore, having in mind influence of the intermolecular interactions which often effectively decrease U,19 giving also the rise to other relaxation channels,20 another structural property of [CoCl2(dppf)] must be emphasised. The crystal structure of this compound is composed of the complex molecules connected only by weak C–H⋯π and C–H⋯Cl non-covalent interactions (Scheme 1).
. In the case of tetracoordinate Co(II) compounds with the general formula [Co(LN/P)2(L1)2] or [Co(LN/P)(L1)2], where LN/P represents mono or bidentate N- or P-donor ligands and L1 is halido or pseudohalido ligands, a magneto-structural correlation was established by Boča and co-workers in 2013.13 It reads δ = 2αTd − (α), where αTd is the angle of the ideal tetrahedron (109.5°), α is the angle between the two Co–N/P bonds. Despite some limitations,14 this relationship has proved to be successful in the prediction of sign and magnitude of D, such that more negative/positive δ should lead to more negative/positive value of D. Therefore, our attention has focused on compounds with rather large and negative parameter δ and these were further investigated for their static and dynamic magnetic properties.14,15 Therefore, we opted to investigate the compound [CoCl2(dppf)] as a suitable SIM candidate, where dppf represents the 1,1′-ferrocenediyl-bis(diphenylphosphine). This complex can be prepared by the reaction between dppf and CoCl2 where both dppf and the resulting product [CoCl2(dppf)] are very well known, thoroughly studied (besides magnetic properties)16 and even commercially available coordination compounds.17 The crystal structure of [CoCl2(dppf)] was reported in 199918 and this compound has tetracoordinate {CoP2Cl2} arrangement with δ = −4.8°. Therefore, according to the magneto-structural correlation by Boča et al.,10 it should possess negative D. Furthermore, having in mind influence of the intermolecular interactions which often effectively decrease U,19 giving also the rise to other relaxation channels,20 another structural property of [CoCl2(dppf)] must be emphasised. The crystal structure of this compound is composed of the complex molecules connected only by weak C–H⋯π and C–H⋯Cl non-covalent interactions (Scheme 1).
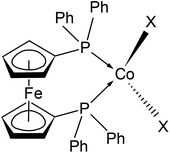 | ||
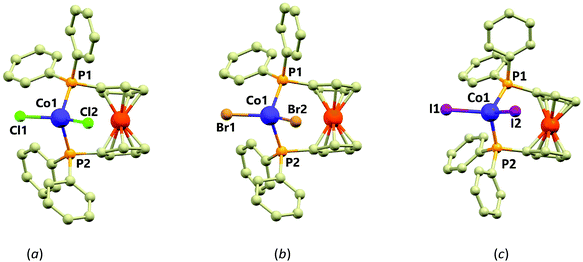
| Scheme 1 Drawing of the molecular structure of compounds 1–3, X stands for halido ligands (X = Cl in 1, Br in 2 and I in 3). Ph stands for the phenyl rings. | ||
Due to the bulkiness of the dppf metalloligand, these interactions are organised in a way (vide infra) that they cannot effectively transmit even very weak exchange interactions. The shortest Co⋯Co separations are longer than 9.6 Å assuring that also dipolar interactions between the Co(II) atoms are negligible. Therefore, we decided to study the static and dynamic magnetic properties of the compound [CoCl2(dppf)], (1), together with the bromido [CoBr2(dppf)], (2) and iodido [CoI2(dppf)], (3) analogues. The precise determination of the magnetic anisotropy parameters was performed by High-Frequency and -Field Electron Spin Resonance (HF-ESR) measurements. We also focused our synthetic strategy on the preparation of the single crystals of compounds 2 and 3 and the determination of their crystal structures by the X-ray diffraction. The analysis of the experimental data was supported by ab initio calculations (CASSCF/NEVPT2). Furthermore, we tested the deposition21 of thick films of these complexes on surfaces via both thermal sublimation and wet-chemistry-based protocols.
Results and discussion
Crystal structure
Crystal structure of the compound 1 was reported previously (T = 293 K),15 here we report on its re-determination at a lower temperature (T = 150 K) and determination of the new structures of the bromide (2) and iodide (3) analogues. Compounds 1 and 2 are isostructural, both crystallising in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (see ESI, Table S1†). Compound 3 crystallises in the monoclinic space group P21. All three complexes contain dinuclear [CoX2(dppf)] molecules in their crystal structures. In these, the Fe(II) centres are coordinated by two cyclopentadienyl rings (Cp) in the almost eclipsed geometry (Fig. 1) and they are rotated by only 9.3(2)° (1), 9.1(1)° (2) and 0.2(4)° (3) as based on the P–C⋯C–P torsion angle of two Cp–P moieties. The Cp rings are tilted by 6.3° (1), 6.3° (2) and 6° (3). The dppf metalloligand coordinates the Co(II) centre by two diphenylphosphine groups which together with coordination of two other halide ligands lead to the formation of the P2X2 coordination sphere.
(see ESI, Table S1†). Compound 3 crystallises in the monoclinic space group P21. All three complexes contain dinuclear [CoX2(dppf)] molecules in their crystal structures. In these, the Fe(II) centres are coordinated by two cyclopentadienyl rings (Cp) in the almost eclipsed geometry (Fig. 1) and they are rotated by only 9.3(2)° (1), 9.1(1)° (2) and 0.2(4)° (3) as based on the P–C⋯C–P torsion angle of two Cp–P moieties. The Cp rings are tilted by 6.3° (1), 6.3° (2) and 6° (3). The dppf metalloligand coordinates the Co(II) centre by two diphenylphosphine groups which together with coordination of two other halide ligands lead to the formation of the P2X2 coordination sphere.
The geometry around the Co(II) centres can be described as distorted tetrahedral (continuous shape measures indexes22 for Td: 0.356 in 1, 0.399 in 2 and 0.637 in 3) with the P–Co–P, P–Co–X and X–Co–X angles deviating significantly from the ideal tetrahedron with the largest deviation observed for the X–Co–X angles (in °): 116.14(4) in 1, 114.87(2) in 2 and 116.82(4) in 3. The P–Co–P angles are much closer to the ideal tetrahedral angle (109.5, all values in °): 108.17(4) in 1, 108.65(2) in 2 and 106.31(5) in 3. The distortion from ideal tetrahedron is not only of angular character, but also the bond lengths significantly differ. The Co–P bonds in 1–3 adopt lengths ranging from 2.35 to 2.37 Å, whereas the Co–X bond lengths vary within a series significantly (in Å): 2.2229(10) and 2.2353(9) in 1, 2.3874(6) and 2.3640(6) in 2 and 2.5596(6) and 2.5581(6) in 3. The non-covalent interactions in 1–3 are of very weak character represented only by the C–H⋯X and C–H⋯π contacts. Furthermore, the closest Co⋯Co distances are 9.609(1) Å in 1, 9.680(3) Å in 2 and 8.9206(8) Å in 3. Therefore, the presence of the magnetic exchange or dipolar interactions cannot be expected.
Electron spin resonance
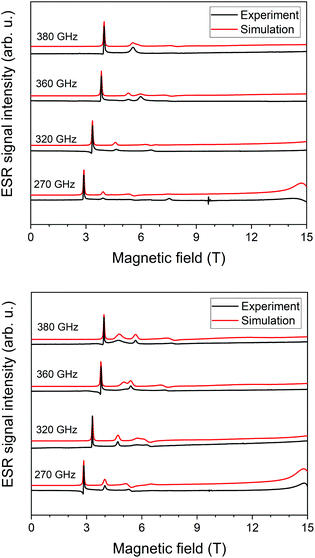
We acquired HF-ESR spectra at four frequencies: 270 GHz, 320 GHz, 360 GHz, and 380 GHz while sweeping the magnetic field from 0–15 T at temperature of 5 K. By these measurements we were able to correlate g-tensor values and zero-field splitting parameters from ab initio simulations with HF-ESR measurements. The best fit for 1 (Fig. 2 top) was found for D = −12.0 cm−1 with E/D = 0.106, and gx = 2.20, gy = 2.20, gz = 2.28; for 2 (Fig. 2 bottom) was found for D = −11.2 cm−1 with E/D = 0.090, and gx = 2.22, gy = 2.22, gz = 2.31. For 1 and 2 we have also acquired HF-ESR spectra at 10 K, 20 K, and 40 K (see ESI, Fig. S1 and S2†).Static magnetic properties
The temperature and field-dependent magnetic data were collected and analysed for compounds 1–2. We were not successful in obtaining the pure phase of compound 3 as was confirmed by measurements of elemental analysis, X-ray powder diffraction and magnetic data (vide infra). We believe that partial decomposition of 3 occurred, as can be judged from outward reddish-brown and inner green colours of obtained crystals. Therefore, we briefly describe and discuss magnetic data of 3 only to draw the attention to potential issues with surprisingly large D parameters of Co(II) tetracoordinate complexes with iodide ligands.The temperature dependencies of the effective magnetic moment (μeff/μB) are similar for 1–2, adopting values (4.4–4.5μB) larger than spin only value for Co(II) with e4 t23 configuration in tetrahedral symmetry of the coordination polyhedron (g = 2.0, S = 3/2, μeff/μB = 3.87). The μeff value was almost constant to ca. 20 K and then decrease to ca. 3.5 (1) and 3.7 (2) μB was observed. With respect to the crystal structures of 1–2 compounds as discussed above, we can conclude that there are no covalent or non-covalent magnetic exchange pathways, which could be responsible for mediation of weak antiferromagnetic interactions. Hence, the observed decreases of μeff can only be attributed to the occurrence of the zero-field splitting (ZFS), and thus magnetic anisotropy. Therefore, the magnetic data were fitted for spin Hamiltonian including axial and rhombic ZFS terms:
| Ĥ = D(Ŝz2 − Ŝ2/3) + E(Ŝx2 − Ŝy2) + μBBgŜa | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(φ), sin(θ)
cos(φ), sin(θ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(φ), cos(θ)) with the help of the polar coordinates.
sin(φ), cos(θ)) with the help of the polar coordinates.
Next, the molar magnetisation in a-direction of the magnetic field was numerically calculated as:
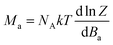 | (2) |
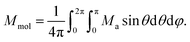 | (3) |
Taking into account the fitting procedure for both temperature and field-dependent magnetisation data, the best fits were found for 1 with g = 2.20, D = −11.0 cm−1, E/D = 0.00, χTIP = 10.1 × 10−9 m3 mol−1 and for 2 with g = 2.24, D = −8.7 cm−1, E/D = 0.24, χTIP = 6.1 × 10−9 m3 mol−1 – Fig. 3. These parameters confirm that an axial magnetic anisotropy is present in both compounds 1 and 2.
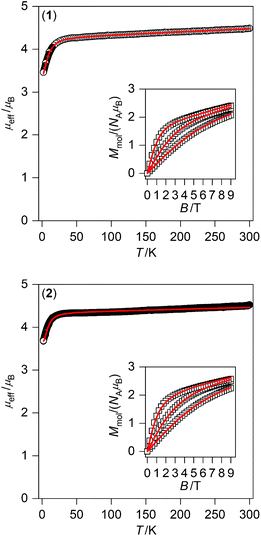 | ||
| Fig. 3 Magnetic data for 1 (top) and 2 (bottom) displayed as the temperature dependence of the effective magnetic moment, and the isothermal molar magnetisation measured at T = 2, 5, and 10 K is in the inset. The empty symbols represent the experimental data; red full lines represent the fitted data using eqn (1) and parameters listed in Table 1. | ||
Static and dynamic magnetic data were measured for two different batches of 3 (see ESI, Fig. S3†). The first batch was crystallised for longer than 3 weeks and the analysis of magnetic data using eqn (1)–(3) resulted in a rather unsatisfactory fit with a rather large value of D = −29.2 cm−1 (Fig. S3†). This can be explained by the occurrence of a decomposition process resulting in hexacoordinate Co(II) species and triiodide anion (deduced from the reddish-brown colour of contaminant). Hexacoordinate Co(II) complexes typically possess large and positive values of D (i.e. >30 cm−1),10 while the compound 3 is expected to have ca. 3-times smaller and negative D value. Simultaneous fitting of both temperature and magnetic dependencies of the magnetic moment is then very sensitive to the occurrence of hexacoordinate contaminant, which might be a plausible explanation for very low fit quality observed for this batch of 3.
The crystals of the second batch were collected immediately after the first crystals appeared and the surface of crystals was again reddish-brown coloured.
The magnetic data were analysed in the same manner as the first batch with a much better quality of fit and lower D value of −14.0 cm−1.
However, this value is inconsistent with expected lower |D| values for complexes with heavier halido ligands within this series as was corroborated by results from HF-ESR spectroscopy (comparison of 1 and 2), and also supported by CASSCF calculations (Table 1). Furthermore, the results of X-ray powder diffraction obtained for both batches of 3 indicate that they contain small amount of impurity (see ESI† for details) Therefore, we decided not to include a detailed discussion of its magnetic properties in the paper.
| 1 | 2 | 3 | |
|---|---|---|---|
| a U calc is the energy separation between the first two Kramers doublets arising from S = 3/2. | |||
| CASSCF/NEVPT2 with CAS(7,5) | |||
| D (cm−1) | −13.2 | −10.1 | −7.44 |
| E/D | 0.130 | 0.106 | 0.119 |
| g x | 2.215 | 2.233 | 2.256 |
| g y | 2.188 | 2.215 | 2.239 |
| g z | 2.331 | 2.321 | 2.318 |
| U calc (cm−1) | 27.1 | 20.6 | 15.2 |
| CASSCF/NEVPT2 with CAS(7,10) | |||
| D (cm−1) | −15.0 | −12.1 | −9.59 |
| E/D | 0.116 | 0.102 | 0.146 |
| g x | 2.238 | 2.264 | 2.296 |
| g y | 2.207 | 2.241 | 2.275 |
| g z | 2.374 | 2.373 | 2.382 |
| U calc (cm−1) | 30.6 | 24.7 | 19.8 |
| The best-fit of the experimental HF-ESR data | |||
| D (cm−1) | −12.0 | −11.2 | |
| E/D | 0.106 | 0.090 | |
| g x | 2.20 | 2.22 | |
| g y | 2.20 | 2.22 | |
| g z | 2.28 | 2.31 | |
| U calc (cm−1) | 24.0 | 22.4 | |
| The best-fit of the experimental magnetic data | |||
| D (cm−1) | −11.0 | −8.7 | |
| E/D | 0.00 | 0.24 | |
| g | 2.20 | 2.24 | |
| χ TIP (10−9 m3 mol−1) | 10.1 | 6.1 | |
| U calc (cm−1) | 22.0 | 18.7 | |
Dynamic magnetic properties
To further characterise compounds 1 and 2, AC susceptibility was measured for both compounds. Unfortunately, there were no out-of-phase signals in zero static magnetic field, but the small static magnetic field was enough to suppress fast relaxations and the imaginary susceptibility became non-zero for both compounds (see ESI, Fig. S4 and 5†). Therefore, the AC susceptibility was measured at BDC = 0.1 T and revealed frequency-dependent maxima of the imaginary susceptibility, and thus confirming the slow relaxation of the magnetisation in 1 and 2. Next, the one-component Debye's model was applied based on the equation: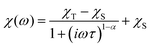 | (4) |
The Argand (Cole–Cole) plots are depicted above (Fig. 4). The extracted relaxation times follow the Arrhenius law and subsequent analysis yielded these parameters: τ0 = 5.17 × 10−9 s, Ueff = 33.3 K (23.2 cm−1) for 1, and τ0 = 1.80 × 10−9 s, Ueff = 28.8 K (20.0 cm−1) for 2. The values of Ueff are very close to Ucalc calculated with fitted parameters from the analysis of HF-ESR or experimental magnetic data – Table 1.
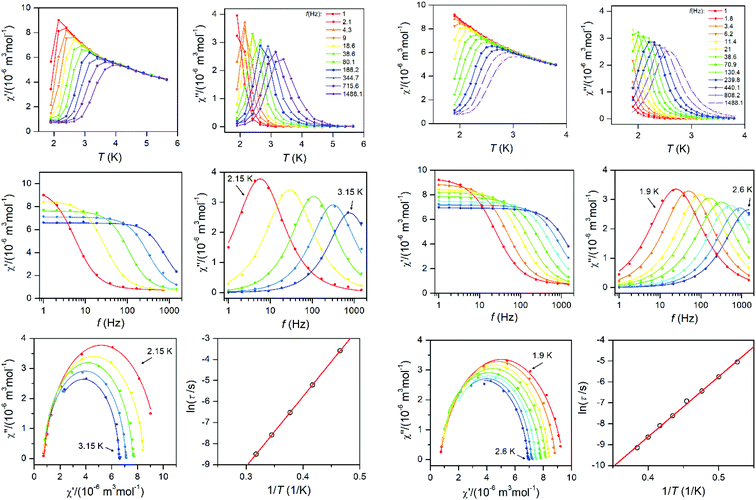 | ||
| Fig. 4 AC susceptibility data for 1 (left two columns) and 2 (right two columns). Top: In-phase χ′ and out-of-phase χ′′ molar susceptibilities at the applied external magnetic field BDC = 0.1 T (full lines are only guides for eyes). Middle: Frequency dependence of in-phase χ′ and out-of-phase χ′′ molar susceptibilities fitted with one-component Debye's model using eqn (4) (full lines). Bottom: The Argand (Cole–Cole) plot with full lines fitted with eqn (4) and the fit of resulting relaxation times τ with Arrhenius law (red line). | ||
Theoretical calculations
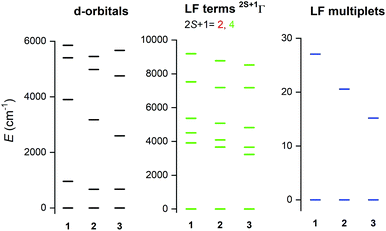
To support the analysis of the experimental magnetic and HF-ESR data, a multi-reference method based on the Spin-Averaged Complete Active Space Self Consistent Field (SA-CASSCF) was utilised to calculate all energy levels resulting from 3d7 electronic configuration with the ORCA 4.0 computational package. The active space was defined as seven electrons in five d-orbitals, CAS(7,5) and dynamic electronic correlation was treated with the NEVPT2 method. The ab initio ligand field theory (AILFT)24 was used to calculate the splitting of d-orbitals as shown in Fig. 5 (left). The overall pattern is similar to Td symmetry of the ligand field, but the degeneracy of e and t2 orbitals is removed due to lower symmetry of the complexes under study. Moreover, the size of the d-orbitals splitting is decreasing from 1 to 2 according to the decrease of the ligand field of halogenido ligands (Br− < Cl−), but in case of 3, the splitting pattern of d-orbitals is slightly different due to larger change of the ligand field geometry evidenced by continuous shape measures indexes22 (for Td: 0.356 in 1, 0.399 in 2 and 0.637 in 3). Next, CASSCF/NEVPT2 calculations provided the energies of the ligand-field (LF) terms – Fig. 5 (middle), in which lowering the energies of first excited quartet state is observed from 3914 cm−1 for 1 to 3227 cm−1 for 3. Next, due to the spin–orbit coupling, the ligand-field terms (LFT) are split into the ligand-field multiplets (LFM) showing the ZFS into two Kramers doublets arising from S = 3/2 ground spin state – Fig. 5 (right). The energy separation of these two doublets is decreasing from 1 to 3 which means that the axial ZFS parameter |D| is also decreasing in this order – Table 1. As the sign of D is negative for all complexes, they possess axial magnetic anisotropy. The spin-orbital interaction is responsible for the largest contribution of the first four excited states to the ZFS parameters as can be elucidated from Table S4.† Evidently, the size of the contributions of these excited states is varying across series 1–3 due to the changes of the ligand field strength and symmetry. Furthermore, the double-shell effect was encountered by enlarging the active space to ten d-orbitals, CAS(7,10). These calculations led to a small increase of |D| parameters preserving the rhombicity (E/D) – see Table 1. To summarise, the theoretical calculations are in good quantitative and qualitative agreement with the parameters extracted from the experiments, which is also reflected in the good agreement of the calculated magnetic data from CASCCF/NEVPT2 calculations compared to the experimental data themselves – Fig. S6.†Surface depositions
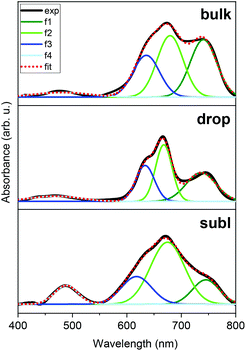
Deposition of 2 on surfaces was also investigated by two distinct techniques: by drop-casting under an inert nitrogen atmosphere (drop hereafter) and by thermal sublimation in high-vacuum (subl hereafter). Fig. 6 shows a comparison of UV-VIS spectra of 2 as a bulk powder, the deposit obtained from the drop-casting on glass, and the 30 nm thick film obtained by the sublimation onto acetate substrate. Spectra of all three solid samples exhibited two dominant absorptions in the visible part of the spectra: the peak around 480 nm, which corresponds to the e2–e1 transition in ferrocenyl moiety (in approximate D5h symmetry)25 and the cluster of peaks between ca. 600–800 nm, that can be assigned to d–d transitions of the tetracoordinate 3d7 central ion.26 Despite the same absorption bands in all three spectra, it is apparent that profile of each spectrum is slightly different, e.g. the subl spectra show broader bands and more intense e2–e1 transition band than in bulk and drop. Despite being aware of different samples’ nature requiring different approaches in acquiring the UV-VIS data, we attempted to fit all three spectra to quantify the observed differences. Each spectrum (400–800 nm) was fitted using four Gaussian primitives, three peaks (olive – f1, green – f2, blue – f3) sufficiently reconstructed the d–d band,27 while the fourth one (light blue – f4, Fig. 6) was used to fit the e2–e1 transition. Three rather well separated components of the d–d band arising from 4A2 → 4T1(P) transition (in ideal Td symmetry)28 reflect the lower symmetry of coordination polyhedron, because the parent term 4T1(P) splits into three terms {4A1 + 4B1 + 4B2}29 in more realistic C2v symmetry.30 The peak heights cannot be directly compared among the spectra, therefore we compared ratios of the peak heights derived for each spectrum.The f1/f2 ratios are similar for drop (0.49) and subl (0.39) samples, while in the bulk f1/f2 is rather larger (0.94). On the other hand, the f4/f2 ratios are similar for bulk (0.06) and drop (0.07) samples, while f4/f2 is significantly larger in subl (0.30). From the presented UV-VIS data it is hard to determine if any variations among the spectra, such as one described by f1/f2 ratio, originate from chemical changes or different spectral resolution due to different nature of the measured sample. However, it must be noted that an increase of f4/f2 in subl spectrum can be reasonably explained by partial decomposition of 2 to metalloligand dppf during sublimation process resulting in a larger abundance of dppf in the deposit.
We have also investigated the chemical composition of bulk 1 and 2 by means of XPS (see ESI, Fig. S8 and S9†) and a survey comparison for 2 as a bulk powder, drop and subl deposits (see ESI, Fig. S10†). Detailed XPS spectra for depositions are shown in Fig. 7 along with a semi-quantitative determination of the elemental composition in Table 2. Carbon and oxygen contributions were considered not relevant since they may be affected by adventitious contaminations due to the ex situ preparation procedures. The quantitative analysis for an as-synthesised powder of 2 and drop-cast in nitrogen atmosphere of 2 suggests preserved stoichiometric composition structure, whereas, in the case of sublimated 2, the amount of Co and Br was lower than expected, which could be attributed to partial chemical decomposition. In the case of Fe 2p and Co 2p, shake-up satellite features were present in all three investigated samples as expected. No significant shift in binding energies among the different samples has been detected.
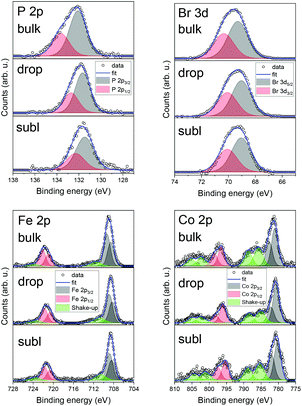 | ||
| Fig. 7 Detailed XPS spectra comparison of 2 for bulk powder, drop-cast, and sublimation for P 2p, Br 3d, Fe 2p, and Co 2p photoelectron peaks. | ||
Iron 2p3/2 peak positions were in good agreement with previous studies addressing the iron in ferrocene molecules (see ESI, Table S6†). This might be due to the intactness of ferrocene moiety on the surface, even after utilising high vacuum sublimation techniques. However, in the case of the film of 2 obtained by sublimation we observed a shift in binding energies of both elements which can be attributed to partial decomposition to the thermally stable dppf,31 which serves as a precursor for synthesis. This finding agrees with decomposition hypothesis deduced from UV-VIS spectroscopy. These findings suggest that films obtained via sublimation are affected by a partial decomposition. Therefore, we may conclude, that the future deposition attempts should adopt preferentially wet-chemistry based protocols under inert atmosphere,32 which have proven to provide chemically intact deposits of 2.
Conclusions
In this paper, we reported on the crystal structure, magnetic properties and field-induced single-molecule magnet behaviour of series of Co(II) tetracoordinate compounds with 1,1′-ferrocenediyl-bis(diphenylphosphine) metalloligand (dppf) and with the general formula [Co(dppf)X2], where X = Cl (1), Br (2), I (3). The static and dynamic magnetic properties were thoroughly studied only for complexes 1–2 because magnetic properties of 3 were found to be very sensitive to even slight decomposition of the sample. Investigations by magnetometry and HF-ESR revealed that 1–2 possess relatively large and axial magnetic anisotropy (D = −12.0 cm−1 in 1 and −11.2 cm−1 in 2) and significant rhombicity (E/D = 0.106 in 1 and 0.090 in 2), in good agreement with ab initio quantum chemical calculations. Measurements of dynamic AC susceptibility revealed that both compounds behave as field-induced single-ion magnets with predominant Orbach relaxation of magnetisation. Sublimation in high-vacuum and drop-casting were attempted in order to deposit 2 on selected surfaces (Au(111), glass, acetate). Despite the sensitivity to moisture, 2 was successfully deposited by drop-casting under inert nitrogen atmosphere, while attempting thermal sublimation, we observed a partial decomposition of the complex, and thus suggesting that nano-structuration of these systems should be operated by the introduction of functional groups allowing the chemisorption from diluted solution and promoting the formation of monolayers on surfaces.Experimental details
Synthesis
All used chemicals and solvents were purchased from commercial sources and were used without any further purification.Compounds 1–3 were synthesised similarly by adapting previously reported methods,33 however, during attempts to prepare phase pure compound 3, we modified the procedure as described below.
Synthesis of 1 and 2
0.5 mmol of CoCl2 (65 mg) or CoBr2 (108 mg) was dissolved in 10 mL of methanol and subsequently, solution of 0.5 mmol of dppf (277 mg) in 25 mL of CH2Cl2 was slowly added. The colour of the solution turned green and it was stirred under heating to boiling for 20 min. Heating together with a stream of nitrogen gas led to a significant reduction of solution volume followed by precipitation of green powder which was filtered off. The mother liquor was crystallised by slow diffusion of diethyl ether and this led to precipitation of hexagonally shaped green crystals, which were filtered off and dried in a desiccator.1: Anal. Calc. for C34H28Cl2CoFeP2Mw = 684.22 g mol−1, (in %): C, 59.45; H, 4.33. Observed: C, 59.68; H, 4.12.
2: Anal. Calc. for C34H28Br2CoFeP2Mw = 773.12 g mol−1, (in %): C, 52.89; H, 3.47. Observed: C, 52.82; H, 3.65. Thermal stability was investigated using DSC-TGA measurements and the compound is stable up to 260 °C.
Positions of peaks in powder diffraction patterns agree rather well with calculated patterns from the single-crystal structures (see ESI, Fig. S11†). Intensities of the diffraction peaks were strongly affected by texture with crystals preferentially oriented along (00l) crystal planes.
Synthesis of 3
The first batch of 3 was synthesised in the same way as compounds 1 and 2. 0.5 mmol of Col2 (156 mg) was dissolved in 10 mL of methanol and subsequently, solution of 0.5 mmol of dppf (277 mg) in 25 mL of CH2Cl2 was slowly added. The colour of the solution turned green brown and it was stirred under heating to boiling for 20 min. Heating together with a stream of nitrogen gas led to a significant reduction of solution volume followed by precipitation of brown powder which was filtered off. The mother liquor was crystallised by slow diffusion of diethyl ether and this led to precipitation of brown crystals, which were filtered off and dried in a desiccator.The second batch of 3 was prepared in the same way as the first batch, with the crystallisation performed by slow diffusion of diethyl ether but in presence of a drying medium (pellets of KOH).34 Brown crystals were isolated by filtration immediately after they appeared in a vial.
3: Anal. Calc. for C34H28l2CoFeP2Mw = 867.14 g mol−1, (in %): C, 44.89; H, 2.82. Observed: C, 47.68; H, 4.12.
Positions of peaks in diffraction patterns of both batches of 3 agree well with the calculated pattern (see ESI, Fig. S11 and 12†). However, peaks originating from the presence of the contaminant are visible in the diffraction pattern of the first batch (e.g. at 2θ = 6.7, 9.3, 11.7 deg.). Some of the contaminant peaks (e.g. at 2θ = 11.7 deg.) are still visible in diffraction pattern of the second batch (Fig. S12 and 13†).
Deposition techniques
For the preparation of thick films, we used a home-built high-vacuum sublimation chamber. For sublimations of 2, a cleaned quartz crucible was used. The base chamber pressure during the sublimation was 1 × 10−7 mbar. We prepared a 30 nm thick molecular film on Au(111) surface deposited on muscovite mica previously treated with a hydrogen flame annealing treatment and a 30 nm thick film on acetate for UV-VIS measurements. The sublimation was performed at 225 °C with a growth rate of 1 Å per 9 min. This was carefully monitored by calibrated quartz crystal microbalance (STM-2, Inficon) placed at the same height as samples inside the vacuum chamber.UV-VIS
Absorption spectra were acquired using a JASCO V670 UV–VIS-NIR spectrophotometer. The bulk powder of 2 was grafted onto filtration paper, the wet deposition sample was prepared by drop-casting of 1 mL of a 5 mM DCM solution onto a cover glass substrate inside inert nitrogen atmosphere, and the 30 nm thick film obtained by the sublimation onto acetate substrate. All samples were put into the light beam of the UV-VIS spectrometer filled with nitrogen (Fig. 6). UV-VIS spectra of 1 mM solutions of 1 and 2 in dichloromethane (SigmaAldrich, 99.8%) were obtained in quartz 10 mm path-length cuvettes (see ESI, Fig. S7 and Table S5†).X-ray photoelectron spectroscopy (XPS)
XPS measurements were carried out at room temperature in a UHV chamber equipped with X-ray source (non-monochromatic Mg-Kα source, 1253.6 eV) and hemispherical analyser by VSW mounting a 16-channel detector. The X-ray source mounted at 54.44° with respect to the analyser was operated at a power of 120 W (12 kV and 10 mA). Survey and detailed XPS spectra were acquired at normal emission with the fixed pass energy of 44 eV. All bulk powder spectra were referenced to the Cu 2p3/2 peak at 932.7 eV, because it served as a substrate for investigated molecules, therefore, no change in position for this peak was expected. Drop-cast and evaporated samples were referenced to the Au 4f7/2 peak at 84.0 eV. The inelastic backgrounds in spectra were subtracted according to Shirley method35 except for Fe peaks, where a linear background was used. Data analysis was based on a standard deconvolution method using mixed Gaussian (G) and Lorentzian (L) line shape (G = 70% and L = 30%, Gaussian–Lorentzian product) for each component in the spectra. Elemental composition of the samples was evaluated using a semi-empirical approach. The integrated intensity of each component was corrected with the photoionization cross-section calculated for each atom, neglecting the differences in photoelectron escape length as a function of the kinetic energy.36 Spectra were analysed using CasaXPS software (version 2.3.18).HF-ESR measurements
High-frequency ESR (HF-ESR) spectra at 5 K, 10 K, 20 K, and 40 K for four frequencies 270 GHz, 320 GHz, 360 GHz, and 380 GHz were recorded on a home-built spectrometer37 featuring a VDI signal generator, a VDI amplifier-multiplier chain, a Thomas Keating quasi-optical bridge, an Oxford Instruments 15/17 T solenoid cryogenic magnet and a QMC Instruments InSb hot-electron bolometer. Both 1 and 2 samples were studied as pressed Teflon®-wrapped powder pellets. All spectra were simulated using the EasySpin toolbox for Matlab.38Physical methods
Temperature dependence of the magnetisation at B = 0.1 T from 1.9 to 300 K and the isothermal magnetisations at T = 2.0, 5.0 and 10.0 K up to B = 9 T were measured using a PPMS Dynacool with a VSM option. The experimental data were corrected for diamagnetism and the signal of the sample holder. Measurements of AC susceptibility were carried out in a 3.8 Oe AC field oscillating at various frequencies from 1 to 1500 Hz and with various dc fields using a MPMS XL7 SQUID magnetometer. The DSC-TGA measurements were performed using a Thermal Analyzer SDT65.Crystallography
X-ray measurements on the selected crystal of 1 were performed on an Oxford Diffraction Xcalibur™2 equipped with a Sapphire2 CCD detector using Mo-Kα radiation. The CrysAlis program package (version 1.171.33.52, Oxford Diffraction) was used for data collection and reduction.39 X-ray measurements on the single-crystals of 2 and 3 were performed on a Bruker D8 Quest diffractometer equipped with a Photon 100 CMOS detector using the Mo-Kα radiation. Data collection, data reduction, and cell parameters refinements were performed using the Bruker Apex III software package.40 The molecular structures were solved by direct methods SHELXS-2014 and all non-hydrogen atoms were refined anisotropically on F2 using full-matrix least-squares procedure SHELXL-2014.41 All hydrogen atoms were found in differential Fourier maps and their parameters were refined using a riding model with Uiso(H) = 1.2(CH) or 1.5(CH3)Ueq.The X-ray powder diffraction patterns of all solid samples were recorded on an MiniFlex600 (Rigaku) instrument equipped with the Bragg–Brentano geometry, and with iron-filtered Cu Kα1,2 radiation.
Theoretical methods
All theoretical calculations were performed with the ORCA 4.0 computational package.42 All the calculations employed the triple-ζ def2-TZVP basis functions43 together with the auxiliary basis def2/JK44 and also utilising the chain-of-spheres (RIJCOSX) approximation to exact exchange.45 The ZFS and g tensors were calculated using self-consistent field (SA-CASSCF) wave functions46 complemented by N-electron valence second-order perturbation theory (NEVPT2).47 The active space of the CASSCF calculation was set to five d-orbitals of Co(II) (CAS(7,5)) or as a combination of 3d and 4d orbitals CAS(7,10). The ZFS parameters, based on dominant spin–orbit coupling contributions from excited states, were calculated through quasi-degenerate perturbation theory (QDPT),48 in which approximations to the Breit–Pauli form of the spin–orbit coupling operator (SOMF approximation)49 and the effective Hamiltonian theory50 were utilised.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank to Martina Kubíková for TGA/DSC measurements. The presented work has been funded by: the EU (COST Action CA15128 MOLSPIN); the Ministry of Education, Youth and Sports of the Czech Republic under the projects: CEITEC 2020 (LQ1601), LO1305, LTAUSA19060 in the INTER-EXCELLENCE programme and GAČR 19-01536S; DFG SPP1601 (SL104/3-2, NE1900/3-2), INST41/863-1 and the Italian MIUR through the “Progetto Dipartimenti di Eccellenza 2018–2022 ref. B96C1700020008” allocated to Department of Chemistry “Ugo Schiff”, by the Fondazione Cassa di Risparmio di Firenze for the support to the CETECS activities. J. H. acknowledges Dominik Bloos and Michal Kern for help with HF-ESR measurements. I. N. and R. H. gratefully acknowledge the support received from the Department of Inorganic Chemistry, Palacký University Olomouc. This project has received funding from the ERC under the European Union's Horizon 2020 research and innovation programme (GA No 714850). M. M., L. S., and J. H. acknowledge Brunetto Cortigiani for the technical support during XPS experiments.Notes and references
-
D. Gatteschi, R. Sessoli and J. Villain, Molecular nanomagnets, Oxford University Press on Demand, 2006, vol. 5 Search PubMed
.
- F. Neese and D. A. Pantazis, Faraday Discuss., 2011, 148, 229–238 RSC
.
-
(a) M. Cinchetti, V. A. Dediu and L. E. Hueso, Nat. Mater., 2017, 16, 507–515 CrossRef CAS PubMed
; (b) R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2012, 488, 357–360 CrossRef CAS PubMed
; (c) G. Cucinotta, L. Poggini, A. Pedrini, F. Bertani, N. Cristiani, M. Torelli, P. Graziosi, I. Cimatti, B. Cortigiani, E. Otero, P. Ohresser, P. Sainctavit, A. Dediu, E. Dalcanale, R. Sessoli and M. Mannini, Adv. Funct. Mater., 2017, 27, 1703600 CrossRef
.
-
(a) F. Meier, J. Levy and D. Loss, Phys. Rev. Lett., 2003, 90, 167204 CrossRef PubMed
; (b) M. D. Jenkins, D. Zueco, O. Roubeau, G. Aromí, J. Majer and F. Luis, Dalton Trans., 2016, 45, 16682–16693 RSC
; (c) E. Moreno-Pineda, C. Godfrin, F. Balestro, W. Wernsdorfer and M. Ruben, Chem. Soc. Rev., 2018, 47, 501–513 RSC
; (d) C. Godfrin, A. Ferhat, R. Ballou, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Phys. Rev. Lett., 2017, 119, 187702 CrossRef CAS PubMed
.
-
(a) S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC
; (b) J. M. Frost, K. L. M. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470–2491 RSC
; (c) J.-L. Liu, Y.-C. Chen and M.-L. Tong, Chem. Soc. Rev., 2018, 47, 2431–2453 RSC
; (d) E. Coronado, Nat. Rev. Mater., 2020, 5, 87–104 CrossRef
.
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed
.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403 CrossRef CAS PubMed
.
-
(a) Y.-Q. Zhai, Y.-F. Deng and Y.-Z. Zheng, Dalton Trans., 2018, 47, 8874–8878 RSC
; (b) D.-K. Cao, J.-Q. Feng, M. Ren, Y.-W. Gu, Y. Song and M. D. Ward, Chem. Commun., 2013, 49, 8863–8865 RSC
; (c) J. M. Zadrozny, J. Liu, N. A. Piro, C. J. Chang, S. Hill and J. R. Long, Chem. Commun., 2012, 48, 3927–3929 RSC
; (d) J. M. Zadrozny and J. R. Long, J. Am. Chem. Soc., 2011, 133, 20732–20734 CrossRef CAS PubMed
; (e) M. Böhme, S. Ziegenbalg, A. Aliabadi, A. Schnegg, H. Görls and W. Plass, Dalton Trans., 2018, 47, 10861–10873 RSC
; (f) T. Wu, Y.-Q. Zhai, Y.-F. Deng, W.-P. Chen, T. Zhang and Y.-Z. Zheng, Dalton Trans., 2019, 48, 15419–15426 RSC
; (g) M. S. Fataftah, J. M. Zadrozny, D. M. Rogers and D. E. Freedman, Inorg. Chem., 2014, 53, 10716–10721 CrossRef CAS PubMed
; (h) F. Yang, Q. Zhou, Y. Zhang, G. Zeng, G. Li, Z. Shi, B. Wang and S. Feng, Chem. Commun., 2013, 49, 5289–5291 RSC
; (i) S. Ziegenbalg, D. Hornig, H. Görls and W. Plass, Inorg. Chem., 2016, 55, 4047–4058 CrossRef CAS PubMed
; (j) Y. Rechkemmer, F. D. Breitgoff, M. van der Meer, M. Atanasov, M. Hakl, M. Orlita, P. Neugebauer, F. Neese, B. Sarkar and J. van Slageren, Nat. Commun., 2016, 7, 10467 CrossRef CAS PubMed
; (k) S. Vaidya, S. K. Singh, P. Shukla, K. Ansari, G. Rajaraman and M. Shanmugam, Chem. – Eur. J., 2017, 23, 9546–9559 CrossRef CAS PubMed
; (l) S. Vaidya, P. Shukla, S. Tripathi, E. Rivière, T. Mallah, G. Rajaraman and M. Shanmugam, Inorg. Chem., 2018, 57, 3371–3386 CrossRef CAS PubMed
; (m) S. Vaidya, S. Tewary, S. K. Singh, S. K. Langley, K. S. Murray, Y. Lan, W. Wernsdorfer, G. Rajaraman and M. Shanmugam, Inorg. Chem., 2016, 55, 9564–9578 CrossRef CAS PubMed
; (n) S. Vaidya, A. Upadhyay, S. K. Singh, T. Gupta, S. Tewary, S. K. Langley, J. P. S. Walsh, K. S. Murray, G. Rajaraman and M. Shanmugam, Chem. Commun., 2015, 51, 3739–3742 RSC
.
-
(a) F. Habib, O. R. Luca, V. Vieru, M. Shiddiq, I. Korobkov, S. I. Gorelsky, M. K. Takase, L. F. Chibotaru, S. Hill, R. H. Crabtree and M. Murugesu, Angew. Chem., Int. Ed., 2013, 52, 11290–11293 CrossRef CAS PubMed
; (b) T. J. Woods, M. F. Ballesteros-Rivas, S. Gómez-Coca, E. Ruiz and K. R. Dunbar, J. Am. Chem. Soc., 2016, 138, 16407–16416 CrossRef CAS PubMed
; (c) S. S. Massoud, R. C. Fischer, F. A. Mautner, M. M. Parfait, R. Herchel and Z. Trávníček, Inorg. Chim. Acta, 2018, 471, 630–639 CrossRef CAS
; (d) A. K. Mondal, J. Jover, E. Ruiz and S. Konar, Chem. Commun., 2017, 53, 5338–5341 RSC
.
-
(a) V. Chandrasekhar, A. Dey, A. J. Mota and E. Colacio, Inorg. Chem., 2013, 52, 4554–4561 CrossRef CAS PubMed
; (b) Y.-Y. Zhu, C. Cui, Y.-Q. Zhang, J.-H. Jia, X. Guo, C. Gao, K. Qian, S.-D. Jiang, B.-W. Wang, Z.-M. Wang and S. Gao, Chem. Sci., 2013, 4, 1802–1806 RSC
; (c) J. Vallejo, I. Castro, R. Ruiz-García, J. Cano, M. Julve, F. Lloret, G. De Munno, W. Wernsdorfer and E. Pardo, J. Am. Chem. Soc., 2012, 134, 15704–15707 CrossRef CAS PubMed
; (d) Y. Peng, V. Mereacre, C. E. Anson, Y. Zhang, T. Bodenstein, K. Fink and A. K. Powell, Inorg. Chem., 2017, 56, 6056–6066 CrossRef CAS PubMed
; (e) Y.-L. Wang, L. Chen, C.-M. Liu, Y.-Q. Zhang, S.-G. Yin and Q.-Y. Liu, Inorg. Chem., 2015, 54, 11362–11368 CrossRef CAS PubMed
; (f) A. Świtlicka-Olszewska, J. Palion-Gazda, T. Klemens, B. Machura, J. Vallejo, J. Cano, F. Lloret and M. Julve, Dalton Trans., 2016, 45, 10181–10193 RSC
; (g) S. Roy, I. Oyarzabal, J. Vallejo, J. Cano, E. Colacio, A. Bauza, A. Frontera, A. M. Kirillov, M. G. B. Drew and S. Das, Inorg. Chem., 2016, 55, 8502–8513 CrossRef CAS PubMed
; (h) A. A. Pavlov, Y. V. Nelyubina, S. V. Kats, L. V. Penkova, N. N. Efimov, A. O. Dmitrienko, A. V. Vologzhanina, A. S. Belov, Y. Z. Voloshin and V. V. Novikov, J. Phys. Chem. Lett., 2016, 7, 4111–4116 CrossRef CAS PubMed
; (i) C. Villa-Pérez, I. Oyarzabal, G. A. Echeverría, G. C. Valencia-Uribe, J. M. Seco and D. B. Soria, Eur. J. Inorg. Chem., 2016, 29, 4835–4841 CrossRef
; (j) M. A. Lemes, F. Magnan, B. Gabidullin and J. Brusso, Dalton Trans., 2018, 47, 4678–4684 RSC
; (k) C. M. Klug, T. J. Ozumerzifon, I. Bhowmick, B. N. Livesay, A. K. Rappé and M. P. Shores, Dalton Trans., 2019, 48, 9117–9126 RSC
.
-
(a) X.-C. Huang, C. Zhou, D. Shao and X.-Y. Wang, Inorg. Chem., 2014, 53, 12671–12673 CrossRef CAS PubMed
; (b) P. Antal, B. Drahoš, R. Herchel and Z. Trávníček, Inorg. Chem., 2016, 55, 5957–5972 CrossRef CAS PubMed
; (c) D. Shao, S.-L. Zhang, L. Shi, Y.-Q. Zhang and X.-Y. Wang, Inorg. Chem., 2016, 55, 10859–10869 CrossRef CAS PubMed
; (d) B. Drahoš, R. Herchel and Z. Trávníček, Inorg. Chem., 2017, 56, 5076–5088 CrossRef PubMed
; (e) P. Antal, B. Drahoš, R. Herchel and Z. Trávníček, Eur. J. Inorg. Chem., 2018, 38, 4286–4297 CrossRef
.
- L. Chen, J. Wang, J.-M. Wei, W. Wernsdorfer, X.-T. Chen, Y.-Q. Zhang, Y. Song and Z.-L. Xue, J. Am. Chem. Soc., 2014, 136, 12213–12216 CrossRef CAS PubMed
.
- J. Titiš, J. Miklovič and R. Boča, Inorg. Chem. Commun., 2013, 35, 72–75 CrossRef
.
- I. Nemec, R. Herchel, M. Kern, P. Neugebauer, J. van Slageren and Z. Trávníček, Materials, 2017, 10, 249 CrossRef PubMed
.
- I. Nemec, R. Herchel and Z. Trávníček, Sci. Rep., 2015, 5, 10761 CrossRef CAS PubMed
.
- B. Corain, B. Longato, G. Favero, D. Ajò, G. Pilloni, U. Russo and F. R. Kreissl, Inorg. Chim. Acta, 1989, 157, 259–266 CrossRef CAS
.
- CAS numbers: dppf, 12150-46-8; [CoCl2(dppf)], 67292-36-8.
- T.-J. Park, S. Huh, Y. Kim and M.-J. Jun, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1999, 55, 848–850 CrossRef
.
- K. R. Meihaus, J. D. Rinehart and J. R. Long, Inorg. Chem., 2011, 50, 8484–8489 CrossRef CAS PubMed
.
- I. Nemec, R. Herchel and Z. Travnicek, Dalton Trans., 2016, 45, 12479–12482 RSC
.
-
(a) F. Ciccullo, M. Glaser, M. S. Sättele, S. Lenz, P. Neugebauer, Y. Rechkemmer, J. van Slageren and M. B. Casu, J. Mater. Chem. C, 2018, 6, 8028–8034 RSC
; (b) F. Ciccullo, A. Calzolari, K. Bader, P. Neugebauer, N. M. Gallagher, A. Rajca, J. van Slageren and M. B. Casu, ACS Appl. Mater. Interfaces, 2019, 11, 1571–1578 CrossRef CAS PubMed
; (c) J. Rozbořil, Y. Rechkemmer, D. Bloos, F. Münz, C. N. Wang, P. Neugebauer, J. Čechal, J. Novák and J. van Slageren, Dalton Trans., 2016, 45, 7555–7558 RSC
; (d) J. Hrubý, V. T. Santana, D. Kostiuk, M. Bouček, S. Lenz, M. Kern, P. Šiffalovič, J. van Slageren and P. Neugebauer, RSC Adv., 2019, 9, 24066–24073 RSC
; (e) L. S. Marie, A. El Fatimy, J. Hrubý, I. Nemec, J. Hunt, R. Myers-Ward, D. K. Gaskill, M. Kruskopf, Y. Yang, R. Elmquist, R. Marx, J. van Slageren, P. Neugebauer and P. Barbara, J. Phys. Mater., 2020, 3, 014013 CrossRef
.
-
M. Llunell, D. Casanova, J. Cicera, P. Alemany and S. Alvarez, SHAPE, Version 2.1, Barcelona, Spain, 2013 Search PubMed
.
-
R. Boča and R. Herchel, Program Polymagnet, 2009–2019 Search PubMed
.
-
(a)
M. Atanasov, D. Ganyushin, K. Sivalingam and F. Neese, in Molecular Electronic Structures of Transition Metal Complexes II, ed. D. M. P. Mingos, P. Day and J. P. Dahl, Springer Berlin Heidelberg, Berlin, Heidelberg, 2012, pp. 149–220 Search PubMed
; (b) S. K. Singh, J. Eng, M. Atanasov and F. Neese, Coord. Chem. Rev., 2017, 344, 2–25 CrossRef CAS
.
-
(a) B. Corain, B. Longato, G. Favero, D. Ajò, G. Pilloni, U. Russo and F. R. Kreissl, Inorg. Chim. Acta, 1989, 157, 259–266 CrossRef CAS
; (b) U. Salzner, J. Chem. Theory Comput., 2013, 9, 4064–4073 CrossRef CAS PubMed
.
- M. M. Rohmer, A. Veillard and M. H. Wood, Chem. Phys. Lett., 1974, 29, 466–468 CrossRef CAS
.
- D. Lomjanský, F. Varga, C. Rajnák, J. Moncol, R. Boča and J. Titiš, Nova Biotechnol. Chim., 2016, 15–2, 200 Search PubMed
.
-
B. N. Figgis and M. A. Hitchman, Ligand Field Thery and Its Applications, Special Topics in Inorganic Chemistry, John Wiley, India, 2010 Search PubMed
.
- M. Idešicová, J. Titiš, J. Krzystek and R. Boča, Inorg. Chem., 2013, 52, 9409–9417 CrossRef PubMed
.
- L. Masaryk, J. Moncol, R. Herchel and I. Nemec, Crystals, 2020, 10, 354 CrossRef CAS
.
- C. M. Woodbridge, D. L. Pugmire, R. C. Johnson, N. M. Boag and M. A. Langell, J. Phys. Chem. B, 2000, 104, 3085–3093 CrossRef CAS
.
-
M. Mannini and L. Poggini, in Encyclopedia of Interfacial Chemistry, Elsevier, 2018, pp. 538–546 Search PubMed
.
- U. Casellato, D. Ajò, G. Valle, B. Corain, B. Longato and R. Graziani, J. Crystallogr. Spectrosc. Res., 1988, 18, 583–590 CrossRef CAS
.
- I. Nemec, R. Marx, R. Herchel, P. Neugebauer, J. Van Slageren and Z. Trávníček, Dalton Trans., 2015, 44, 15014–15021 RSC
.
- D. A. Shirley, Phys. Rev. B: Solid State, 1972, 5, 4709–4714 CrossRef
.
- J. J. Yeh and I. Lindau, At. Data Nucl. Data Tables, 1985, 32, 1–155 CrossRef CAS
.
- P. Neugebauer, D. Bloos, R. Marx, P. Lutz, M. Kern, D. Aguilà, J. Vaverka, O. Laguta, C. Dietrich, R. Clérac and J. van Slageren, Phys. Chem. Chem. Phys., 2018, 20, 15528–15534 RSC
.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed
.
-
CrysAlis CCD and CrysAlis RED, Version 1.171.33.52, Oxford Diffraction Ltd, England, 2009 Search PubMed
.
-
Bruker. Apex3, Bruker AXS Inc., Madison, Wisconsin, USA, 2015 Search PubMed
.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed
.
-
(a) F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS
; (b) F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
- F. Weigend, J. Comput. Chem., 2008, 29, 167–175 CrossRef CAS PubMed
.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS
.
- P. A. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189–194 CrossRef CAS
.
-
(a) C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J. P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS
; (b) C. Angeli, R. Cimiraglia and J. P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef CAS
; (c) C. Angeli, R. Cimiraglia and J. P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS
; (d) C. Angeli, S. Borini, M. Cestari and R. Cimiraglia, J. Chem. Phys., 2004, 121, 4043–4049 CrossRef CAS
; (e) C. Angeli, B. Bories, A. Cavallini and R. Cimiraglia, J. Chem. Phys., 2006, 124, 054108 CrossRef
.
- D. Ganyushin and F. Neese, J. Chem. Phys., 2006, 125, 024103 CrossRef
.
- F. Neese, J. Chem. Phys., 2005, 122, 034107 CrossRef PubMed
.
- R. Maurice, R. Bastardis, C. de Graaf, N. Suaud, T. Mallah and N. Guihéry, J. Chem. Theory Comput., 2009, 5, 2977–2984 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Crystallographic data, temperature dependence in HF-ESR spectra, static magnetic data measured for two batches of 3, dynamic magnetic properties at zero magnetic field, Debye's model parameters, CASSCF/NEVPT2 calculations comparison, individual contributions to D-tensor, UV-VIS solution spectra comparison, XPS spectra comparison, XRPD data. CCDC 1998989–1998991. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0dt01512a |
| This journal is © The Royal Society of Chemistry 2020 |