Y₄Be₃₃Pt₁₆ – a non-centrosymmetric cage superconductor with multi-centre bonding in the framework

Abstract

The new ternary compound Y₄Be₃₃Pt₁₆ was prepared from elements by arc melting, and its crystal structure was determined from single-crystal X-ray diffraction data (space group I4̄3d, a = 13.4849(3) Å). The material is the first representative of a new structure type of complex intermetallic compounds and reveals a cage-like crystal structure. Analysis of chemical bonding by means of the electron localizabilty approach indicates ionic interaction of yttrium with the rest of the crystal structure, characteristic for cage compounds, in particular for clathrates. In contrast to the mostly two-centre bonding in the framework of clathrates, the new compound is characterized by a multi-centre interaction within the framework, caused by the demand of the valence electrons in the system. The non-centrosymmetric material enters the superconducting state at T_C = 0.9 K.

---

Introduction

The diversity of intermetallic structures is fascinating. These compounds can have unit cells with one atom as in α-Po (Pearson symbol cP1) or with more than twenty thousand atoms as in Ta₉₀₆₃Al_12827.56Cu_1244.05 (Pearson symbol cF23134).^1–3 The reasons for such complex behaviour are still under discussion. The compounds with crystal structures containing more than ca. 100 atoms in the unit cell are notated as complex metallic alloys (CMA) or complex intermetallic compounds.⁴ One of the characteristic features for CMA (but not for all) is the presence of different types of crystallographic disorder in crystal structures, which de facto means the violation of the translational symmetry in the strict sense. Recently, this was shown on examples of o-Al₁₃Co₄ (oP102-x)⁵ and ternary clathrate Ba_7.81Ge_40.67Au_5.33 (cP54-x)⁶ by the combination of X-ray diffraction on single crystals with high-resolution transmission electron microscopy. One of the possible reasons for such complex behaviour may be the low valence electron concentration in these materials, which (i) does not allow to use traditional electron counting schemes for understanding the composition and the crystal structure, and (ii) leads to multi-centre atomic interactions in the structures, recently shown e.g. for Be₂₁Pt₅.⁷ Intermetallic compounds with complex crystal structures often show unusual physical behaviours. Physics and chemistry of CMA are discussed on the basis of the complexity of their crystal structures, whereby the latter is considered to be the origin of some specific behaviour of these substances. For instance, the intermetallic clathrates reveal unusual functionality in heat transport as a kind of phonon filters with the mean free path of phonons 10–100 nm.^6,8,9

From the position in the Periodic Table, beryllium contributes only two valence electrons for the formation of bonds, thus the compounds with high beryllium content should be a suitable field to search for new complex intermetallic materials. The recently described binary Be₂₁Pt₅ has a large unit cell with 416 atoms (cF416), but does not reveal any crystallographic disorder.⁷ The information about the ternary compounds of Be with other metals is rather scarce in the literature.¹⁰ Our initial phase diagram studies showed, that – despite the clear electronic demand – the R–Be–T systems are characterized by formation of several ternary compounds similar to the R–E–T systems with R being alkaline- or rare-earth metals, E – p-block elements, and T – late transition metals. In this work, we present crystal structure and bonding analysis of the new superconductor Y₄Be₃₃Pt₁₆.

Results and discussion

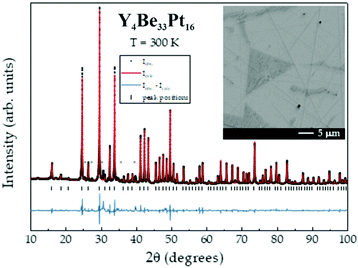
The powder X-ray diffraction pattern of Y₄Be₃₃Pt₁₆, shown in Fig. 1, was indexed using a cubic cell with a = 13.4849(3) Å. The structure was solved and refined from single-crystal diffraction data in the non-centrosymmetric space group I4̄3d. The main crystallographic information is presented in Table 1, the atomic coordinates and isotropic atomic displacement parameters are shown in Table 2, the anisotropic displacement parameters for Y and Pt atoms as well as the interatomic distances are listed in ESI (Tables S1 and S2,† respectively).

Fig. 1 X-ray powder diffraction pattern for Y₄Be₃₃Pt₁₆. Reflections of the minority phases (Be₂₁Pt₅, Y, and Pt) are marked by asterisks. Inset: Microstructure (material contrast image, SEM) shows the Y- and Pt-containing majority phase (light gray) and the Pt-poor minority phase (dark gray).

Table 1 Crystallographic data for Y₄Be₃₃Pt₁₆ (single-crystal diffraction experiment)

a Lattice parameter refined from the X-ray powder diffraction data (CuKα1 radiation).
Crystal system	Cubic
Composition	Y4Be33Pt16
Space group	I4̄3d
Pearson symbol	cI212
Formula units per u. c. Z	4
Unit cell parameter a	13.4849(3) Å^a
Unit cell volume V	2452.1(2) Å^3
Calculated density	10.22 g cm^−3
Radiation, wavelength	MoKa, 0.71073 Å
Absorption coefficient	105.2 mm^−1
Diffraction system	Rigaku AFC7
2θmax	86.2°
N(hkl) measured	27 218
N(hkl) unique	1477
N(hkl) observed	1446
R int; Rs	0.045; 0.032
Refined parameters	28
R F; wRF^2	0.044; 0.088
Weighting scheme	w i = [ln(Fobs,i^4)]^−1
Extinction coefficient^17	0.000062(9)
Flack parameter	−0.005(10)
Residual electron density max; min	+2.3; −1.9 e Å^−3

---

Table 2 Atomic coordinates and displacement parameters for Y₄Be₃₃Pt₁₆

Atom	Site	x/a	y/b	z/c	B eq/iso ^a (Å^−2)
a B eq = ⅓[B11 × a*^2 × a^2 + ⋯ + 2B23 × b* × c* × b × c × cos(α)].
Y	16c	0.8097(1)	x	x	0.66(2)
Pt1	16c	0.93652(4)	x	x	0.594(6)
Pt2	48e	0.48917(4)	0.89865(4)	0.77608(4)	0.607(8)
Be1	12a	⅝	0	¾	1.2(6)
Be2	24d	0.914(3)	0	¾	1.1(4)
Be3	48e	0.056(2)	0.989(2)	0.664(2)	1.1(3)
Be4	48e	0.620(2)	0.919(2)	0.893(2)	1.0(3)

---

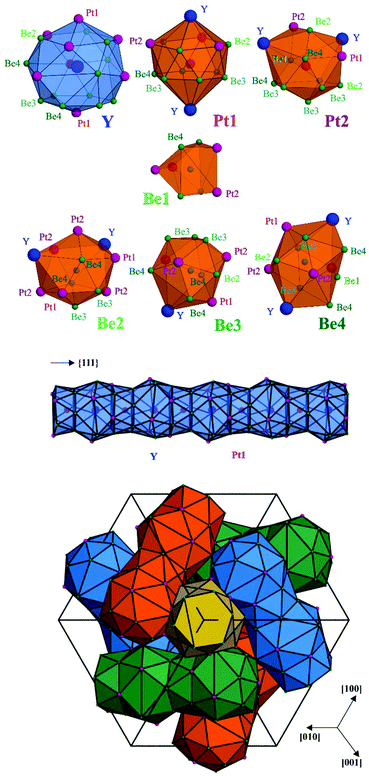
The atoms in the crystal structure of Y₄Be₃₃Pt₁₆ reveal coordination polyhedrons characteristic for intermetallic compounds in the ternary systems of rare-earth and related metals as R component with transition metals and p-block elements. The yttrium atoms are located within a spacious polyhedron with 20 vertices, being very similar to that of Ca in the CaCu₅ structure type and its several derivatives^11,12 (Fig. 2, top panel). Interestingly, there are three additional Be1 ligands at the distance of 3.666 Å, which is much longer than other yttrium contacts (Table S2†) and – from distance analysis – these three do not necessarily belong to the first coordination sphere (cf. analysis of chemical bonding below). While the platinum atoms have environments derived from the Frank–Kasper polyhedrons with coordination numbers of CN(Pt1) = 14 and CN(Pt2) = 13, Be1 has a bisdisphenoid-like environment with eight closer neighbours (and additional four yttrium species at a much longer distance), all remaining beryllium species have 12 or 13 ligands with their coordination environments derived from an icosahedron (Fig. 2, top panel).

Fig. 2 Crystal structure of Y₄Be₃₃Pt₁₆ with the Y, Pt, and Be atoms represented by blue, pink, and green spheres, respectively: (top) coordination polyhedrons of atoms as obtained from analysis of interatomic distances; (middle) interpenetrating polyhedrons of Y and Pt1 along the three-fold axes; (bottom) rod packing of the interpenetrating polyhedron arrangements in the unit cell, the different colours visualize rods on different three-fold axes.

The crystal structure of Y₄Be₃₃Pt₁₆ can be visualized by considering the coordination environment of yttrium. Adjacent coordination polyhedrons of Y are vertex-sharing via the Pt1 position. This results in the formation of a linear rod-like arrangement of interpenetrating Y and Pt1 polyhedrons, as shown in Fig. 2 (middle panel), along the three-fold axes of the cubic unit cell ({111} directions). The resultant rod packing is presented in Fig. 2 (bottom panel) and was first described as crystallographic object in ref. 13. The existence of voids between the rods is due to an incomplete space filling. These voids are located at (⅞ 0 ¼) (Wyckoff site 12b) and (⅜ 0 ¼) (Wyckoff site 12a). The former are empty in Y₄Be₃₃Pt₁₆, as they are too small to contain an atom. The voids located at (⅜ 0 ¼) having the shape of a bisdisphenoid are occupied by Be1.

Among the CaCu₅ derivatives, the crystal structure of Y₄Be₃₃Pt₁₆ is closely related to the ferromagnet Nd₂Fe₂₃B₃ (space group I4̄3d, a = 14.19 Å).^14–16 For a comparison, the compositions can be written as Nd₄Fe₃₀(B₂)₃Fe₁₆ and Y₄Be₃₀Be₃Pt₁₆. In the Nd₂Fe₂₃B₃ structure, the Y site is occupied by Nd, all other positions beside Be1 – by iron. While the bisdisphenoid in Y₄Be₃₃Pt₁₆ is occupied by a single Be1 atom (Wyckoff site 12a), the same coordination environment is occupied in Nd₂Fe₂₃B₃ by a B₂ pair with the centre at the 12a site (Fig. S1†). In this way, the B atoms belong to the coordination sphere of Nd with d(B1–Nd1) = 3.32 Å in Nd₂Fe₂₃B₃, in contrast to Be1 in Y₄Be₃₃Pt₁₆ which shows much longer distance of d(Be1–Y) = 3.666 Å.

The complex intermetallic structures with large cubic unit cell, in particular derivatives of the gamma-brass structural pattern, can often be interpreted from the crystallographic point of view as packings of nested polyhedrons.¹⁸ Recently, this was explained on example of Be₂₁Pt₅ by the formation of multi-atomic bonding interactions centred at the middle points of the nested polyhedrons.⁷ Interestingly, this approach does not work reasonably well for Y₄Be₃₃Pt₁₆. This observation was the starting point for the analysis of chemical bonding in Y₄Be₃₃Pt₁₆ employing the electron localizability approach.

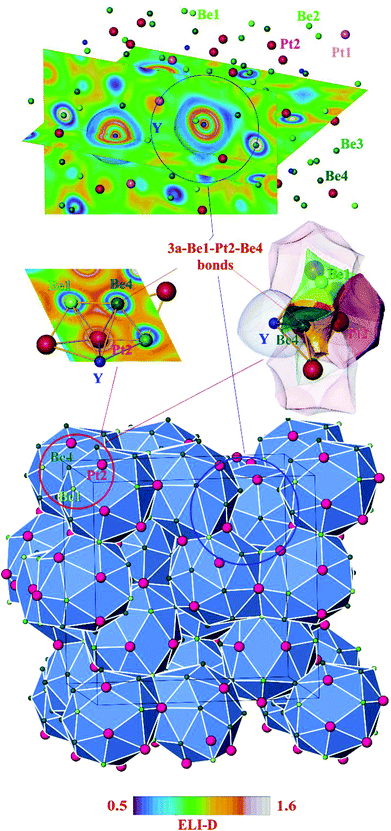
As for most intermetallic beryllium compounds, a characteristic feature of Y₄Be₃₃Pt₁₆ is the very low valence electron concentration (VEC) of ca. 1.4 e per atom, which is even lower than in the gamma-brass derivative Be₂₁Pt₅ (1.62 e per atom). An important factor stabilizing the latter structure was found to be the charge transfer from Be to Pt.⁷ In order to study the role of the ionic contributions to the bonding, the electron density in Y₄Be₃₃Pt₁₆ was investigated applying the QTAIM (Quantum Theory of Atoms In Molecules¹⁹) approach. The zero-flux surfaces in the distribution of electron density define the shape of the atoms in the QTAIM representation. Integration of electron density within the atomic shapes yields their electronic populations and effective charges (Fig. 3). The yttrium atoms in Y₄Be₃₃Pt₁₆ in the QTAIM representation have a shape close to a spherical one, which is characteristic for cage compounds, e.g. clathrates of Ba or Sr.^9,20 Their effective charge of +1.70 is also characteristic for the earth-alkaline and rare-earth atoms in intermetallic clathrates.^20,21 The shapes of the QTAIM atoms of platinum and beryllium are far from a sphere. They have closer to plane or even concave faces. While beryllium atoms – as expected from the electronegativity differences – reveal positive effective charges between +1.30 and +1.40, the platinum species have large negative charges of −2.72 and −3.31 for Pt1 and Pt2, respectively. This confirms strong charge transfer in the compound according to the scheme [Y^+1.70]₄[Be1^+1.36]₃[Be2^+1.30]₆[Be3^+1.36]₁₂[Be4^+1.31]₁₂[Pt1^–2.72]₄[Pt2^−3.31]₁₂.

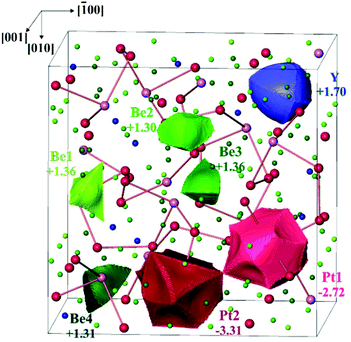Fig. 3 QTAIM atoms and their effective charges in Y₄Be₃₃Pt₁₆. The Pt–Pt contacts with 2.82 Å < d(Pt–Pt) < 2.91 Å are shown to emphasize the volume representation.

Further information about atomic interactions was obtained by applying the electron localizability approach. The distribution of the electron localizability indicator (ELI-D) in the vicinity of the yttrium nuclei is close to a spherical one, whereby the valence shell (4^th) is absent. The light structuring of the penultimate shell indicates the participation of the electrons from this shell in the bonding. The intersection with the QTAIM yttrium atom reveals that the latter bears only the inner shells, confirming the ionic interaction of yttrium with the Be–Pt framework (Fig. 4, top panel). In the cage wall, there are two bonds involving Be2, Be4 and Pt2. Populations are 1.63 and 1.36 electrons, respectively. The interesting aspect is that Pt1 also contributes to them. Its contribution is comparable to those of Be2 and Be4. Hence, each attractor describes a four-atomic bond, two Pt and two Be. This reflects the characteristic multi-atomic interaction in the whole Be–Pt framework. The distribution of ELI-D in the (Be1–Pt2–Be4) triangle reveals one maximum located within the triangle. The intersection of the ELI-D basin of this maximum with the QTAIM shapes of the neighbouring atoms (Fig. 4, middle panel) shows the Be1, Be4, and Pt2 atoms contributing 0.11, 0.15, and 1.45 of the total population of 1.84 electrons for this basin. This confirms the mainly three-atomic (3a) character of the interaction in this part of the structure. The remaining 0.13 electrons originate from two other Pt2, one Be3, and even one yttrium neighbours, suggesting that even more atoms are participating in this multi-atomic bonding. The Pt atoms contribute the majority of the population for the bonding basins, which makes the multi-centre interactions strongly polar. The bonding analysis reveals that the Be1 atoms should be included into the coordination sphere of yttrium despite a large interatomic distance (cf. distance-based considerations above and comparison of the Y-polyhedrons in Fig. S1(e)†). The Y-centred cages – as obtained from the bonding analysis – within the three-dimensional Be–Pt framework fill-up the large part of the unit cell of Y₄Be₃₃Pt₁₆ (Fig. 4, bottom panel). In summary, analysis of the chemical bonding classifies Y₄Be₃₃Pt₁₆ as a cage compound, e.g. a material with its crystal structure in the form of a 3D framework with large cages. Ionic interaction of cationic yttrium species in the cages of the anionic Be–Pt framework is the bonding characteristic of this cage structure. In contrast to other representatives of cage compounds, e.g. intermetallic clathrates with mainly two-centre (non-polar or polar) bonds in the framework, the framework in Y₈Be₆₆Pt₃₂ is formed by multi-atomic (polar) interaction. In agreement with the chemical bonding picture, the calculated electronic density of states of Y₄Be₃₃Pt₁₆ is characterized by the intermixing of Pt and Be states in the whole energy range and shows three main regions (Fig. 5). The low-energy range (E < −6.7 eV) is formed mainly by the s states of Be and Pt with small contributions of the s states of yttrium, reflecting the bonding in the Be–Pt framework. The middle-energy region (−6.7 eV < E < −2.3 eV) is dominated by d states of platinum atoms. The region below the Fermi level (E_F) contains contributions of all essential atomic states. Interestingly, a pseudo gap is found above the Fermi level (due to the band dispersion along Γ–H in the Brillouin zone, Fig. S2†), in contrast to the typical DOS distribution in cage compounds with two-centre bonds in the framework, where the pseudo gap appears typically close to E_F.⁹ The presence of non-filled states agrees with the electron-deficient situation in this material.

Fig. 4 Atomic interactions in Y₄Be₃₃Pt₁₆ by electron localizability approach: (top panel) distribution of the ELI-D in the plane crossing two neighbouring yttrium atoms; (middle left panel) distribution of ELI-D in one of the face planes of the coordination polyhedron of yttrium with the Pt2, Be1 and Be4 atoms; (middle right panel) bonding basin of the three-atomic interaction Pt2–Be1–Be4 (yellow bulk) intersected by the QTAIM atomic basins of the participating atoms (transparent), three main contributing atoms are labelled; (bottom panel) crystal structure of Y₄Be₃₃Pt₁₆ as a packing of the coordination polyhedrons of Y (blue) as obtained from the bonding analysis.

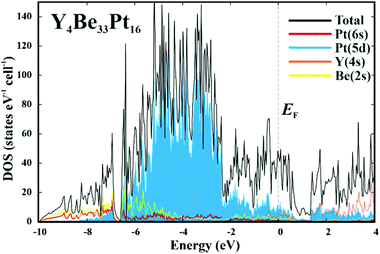Fig. 5 Calculated electronic density of states (DOS) for Y₄Be₃₃Pt₁₆. The total DOS (black line) is shown together with the contributions of essential atomic states.

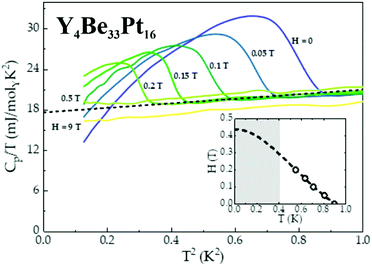
The non-centrosymmetric compound Y₄Be₃₃Pt₁₆ enters a superconducting state below T_C = 0.9 K, as evidenced by the BCS-like anomaly observed in specific heat data, shown in Fig. 6. A fit to the specific heat data above the superconducting transition (dashed line), can be used to estimate the value of the normal state electronic specific heat coefficient γ_n = 18 mJ mol_Y⁻¹ K⁻², as well as cubic term coefficient β = 4.5 mJ mol_Y⁻¹ K⁻³. Using the value of γ_n, it is then possible to estimate the effective mass m* from the following relation:²²m* = (γ_nħ²k_F²)/(π²nk_B²) ≈ m_e, indicating lack of electron mass enhancement (equivalently, the theoretically computed value of DOS at the Fermi energy yields γ_calc = 16.3 mJ mol_Y⁻¹ K⁻²). From the value of β, the Debye temperature θ_D can be calculated using θ_D = [(14π⁴N_Ark_B)/(5β)]^1/3 = 358 K.²² Consequently, the value of θ_D can then be used to estimate the strength of the electron–phonon coupling, employing the McMillan's formula.²³ Typically, materials with λ_e–p → 1 are classified as strongly-coupled superconductors, while λ_e–p → 0.5 indicates weak coupling.²³ For Y₄Be₃₃Pt₁₆, 0.38 ≤ λ_e–p ≤ 0.47, indicating weakly-coupled superconductivity. Once the phonon contribution to the specific heat (βT³) has been subtracted from the specific heat data, an entropy conserving construction (not shown) yields the ratio ΔC_e/γ_nT_C ≈ 1.80, which is comparable to the BCS value of ΔC_e/γ_nT_C = 1.44, consistent with Y₄Be₃₃Pt₁₆ being a weakly-coupled superconductor. As expected, the critical temperature T_C is gradually suppressed by the application of a magnetic field, consistent with type-II superconductivity, allowing to construct the H−T phase diagram (inset of Fig. 6). A relatively small value of the upper critical field H_c2 = 0.44 T, extracted from a Ginzburg–Landau fit²² (dashed line), further confirms weak coupling in Y₄Be₃₃Pt₁₆. The upper critical fields of non-centrosymmetric superconductors are often rather high (on the order of several or even dozens of Tesla), but Y₄Be₃₃Pt₁₆ belongs to the smaller family of non-centrosymmetric superconductors with the upper critical fields on the order of few hundred Oersted. The other examples are AuBe (H_c2 = 335 Oe),²⁴ Mo₂Al₃C (H_c2 = 50 Oe),²⁵ or LaRhSi₃ (H_c2 = 180 Oe).²⁶

Fig. 6 Superconducting properties of Y₄Be₃₃Pt₁₆: specific heat data, scaled by temperature T, C_P/T as a function of T² in applied magnetic fields 0 ≤ H ≤ 9 T. The dashed line represents a fit from which the value of γ_n was extracted. Inset: H–T phase diagram for Y₄Be₃₃Pt₁₆ with the values of H_c2(T) taken from specific heat data.

The fact, that – despite of absence of inversion symmetry – no distinct deviations from BCS theory are observed, points towards the lack of strong correlation effects.^27,28 However, a more comprehensive analysis of the superconducting state in Y₄Be₃₃Pt₁₆ is currently underway. In particular, because several in-depth muon spin-rotation, relaxation, and resonance experiments performed on another Be-containing non-centrosymmetric superconductor BeAu²⁴ revealed that not only type-I character,²⁹ but also a multi-gap nature of superconductivity³⁰ may exist in such unconventional systems.

Experimental

Synthetic procedures

All sample preparation was performed in a laboratory specialized for work with Be, inside a argon-atmosphere glove box system (MBraun, p(H₂O/O₂) < 0.1 ppm).

Caution! Beryllium is considered (according to UN GHS criteria) a health risk and experiments require appropriate infra structure.

Polycrystalline samples around the composition Y₄Be₃₃Pt₁₆ were synthesized by arc melting Y (pieces, Ames, >99.9%), Pt (foil, Chempur, >99.9%), and Be (sheet, Heraeus, >99.9%) in the 10 : 30 : 60 ratio. The samples did not exhibit any marked air or moisture sensitivity. Small amounts of impurities were found to be present in all samples. The minority phases are Be₂₁Pt₅ (superconductor with T_C = 2.06 K (ref. 7)), Be₅Pt (semiconductor³¹), as well as elemental Pt in the amount of <3%. Temperature treatment, as well as slight variation of the initial composition did not result in an improved sample quality.

Crystallography

Powder X-ray diffraction was performed on a Huber G670 Image plate Guinier camera with a Ge-monochromator (CuK_α1 radiation, λ = 1.54056 Å). Phase identification was done using the WinXPow software.³² All crystallographic calculations were done with the WinCSD software package³³ Single-crystal X-ray diffraction data have been collected on a Rigaku AFC7 diffractometer equipped with a Saturn 724 + CCD detector using MoK_α radiation (λ = 0.71073 Å).

Chemical analysis

Chemical composition of polished samples was studied using energy-dispersive X-ray spectroscopy (EDS) with an UltraDry EDS detector (ThermoFisher NSS7) attached to a Jeol JSM 6610 scanning electron microscope (SEM). The semi-quantitative analysis was performed with 25 keV acceleration voltage and ≈3 nA beam current.

Physical properties measurements

Heat capacity was measured in the temperature range from 0.4 K to 10 K, in magnetic fields up to H = 9 T using a QD Physical Property Measurement System.

Calculation procedures

Electronic structure calculations were performed by using the all-electron, full-potential local orbital (FPLO) method.³⁴ All main results were obtained within the local density approximation (LDA) to the density functional theory through the Perdew–Wang parametrization for the exchange–correlation effects.³⁵ Application of the generalized gradient approximation did not reveal essential differences in the electronic structure below and in vicinity of the Fermi level. Chemical bonding analysis in position space was performed within the approach of combined topological analysis of electron density (ED) and electron localizability indicator (ELI). The former type of analysis forms the basis of the quantum theory of atoms in molecules (QTAIM).¹⁹ ELI was calculated in the ELI-D representation^36–38 by a module implemented in the FPLO package.³⁹ Topological analysis of the ED and the ELI-D were carried out by the program DGrid.⁴⁰

Conclusions

The ternary compound Y₄Be₃₃Pt₁₆ is the first representative of a new prototype of intermetallic cage compounds with an unusual combination of structural and bonding features. The cubic crystal structure with 212 atoms in the unit cell is – in contrast to many other complex intermetallic structures – completely ordered and does not show violation of the translational symmetry, characteristic for CMA materials. Analysis of chemical bonding in position space reveals mainly ionic interaction of Y with the remaining parts of the structure, indicating an analogy to intermetallic clathrates and classifying the new atomic arrangement as a cage-like one. In contrast to other cage materials – clathrates – with mainly two-centre bonding in the framework, the framework atoms in Y₄Be₃₃Pt₁₆ participate only in multi-centre interactions. On top of the interesting structure-bonding relationship, the new compound is a non-centrosymmetric BCS-type superconductor with T_C = 0.9 K.

Conflicts of interest

There are no conflicts of interest.

Acknowledgements

The authors acknowledge W. Schnelle for valuable discussions, H. Borrmann and S. Hückmann for assistance in powder diffraction experiments, K. Vanatko and R. Gellrich for support of preparative work. Open Access funding provided by the Max Planck Society.

References

1. R. J. de Sando and R. C. Lange, J. Inorg. Nucl. Chem., 1966, 28, 1837.
2. T. Weber, J. Dshemuchadse, M. Kobas, M. Conrad, B. Harbrecht and W. Steurer, Acta Crystallogr., Sect. B: Struct. Sci., 2009, 65, 308.
3. Yu. Grin, in Comprehensive Inorganic Chemistry II, Elsevier, Oxford, 2013, vol. 2, p. 359.
4. Complex Metallic Alloys Fundamentals and Applications, ed. J.-M. Dubois and E. Belin-Ferré, Wiley-VCH, Weinheim, 2011.
5. P. Simon, I. Zelenina, R. Ramlau, W. Carrillo-Cabrera, U. Burkhardt, H. Borrmann, R. Cardoso Gil, M. Feuerbacher, P. Gille and Yu. Grin, J. Alloys Compd., 2020, 820, 153363.
6. P. F. Lory, S. Pailhès, V. M. Giordano, H. Euchner, H. D. Nguyen, R. Ramlau, H. Borrmann, M. Schmidt, M. Baitinger, M. Ikeda, P. Tomeš, M. Mihalkovič, C. Allio, M. R. Johnson, H. Schober, Y. Sidis, F. Boudarot, L. P. Regnault, J. Ollivier, S. Paschen, Yu. Grin and M. de Boissieu, Nat. Commun., 2017, 8, 1.
7. A. Amon, A. Ormeci, M. Bobnar, L. G. Akselrud, M. Avdeev, R. Gumeniuk, U. Burkhardt, Yu. Prots, C. Hennig, A. Leithe-Jasper and Yu. Grin, Acc. Chem. Res., 2018, 51, 214.
8. H. Euchner, S. Pailhès, L. T. Nguyen, W. Assmus, F. Ritter, A. Haghighirad, Yu. Grin, S. Paschen and M. de Boissieu, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 224303.
9. H. Zhang, H. Borrmann, N. Oeschler, C. Candolfi, W. Schnelle, M. Schmidt, U. Burkhardt, M. Baitinger, J.-T. Zhao and Yu. Grin, Inorg. Chem., 2011, 50, 1250.
10. O. Janka and R. Pöttgen, Z. Naturforsch., B: J. Chem. Sci., 2020, 75, 143.
11. W. B. Pearson, The crystal Chemistry and Physics of metals and Alloys, Wiley-Interscience, N.Y., 1972, p. 643.
12. P. I. Krypiakevich, Structure Types of Intermetallic Compounds, Nauka, Moscow, 1977 (in Russian).
13. M. O'Keeffe and S. Andersson, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1977, 33, 914.
14. K. H. Buschow, D. B. de Mooij and H. M. van Noort, J. Less-Common Met., 1986, 125, 135.
15. D. de Mooij and K. H. J. Buschow, Philips J. Res., 1986, 41, 400.
16. C. Gou, Z. X. Cheng, D. F. Chen, S. W. Niu, Q. W. Yan, P. L. Zhang, B. G. Shen and L. Y. Yang, J. Magn. Magn. Mater., 1993, 128, 26.
17. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112.
18. B. Chabot, K. Cenzual and E. Parthé, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1981, 37, 6.
19. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Clarendon Press, 1994.
20. J. Hübner, Yu. Prots, W. Schnelle, M. Bobnar, M. König, M. Baitinger, P. Simon, W. Carrillo-Cabrera, A. Ormeci, E. Svanidze, Yu. Grin and U. Schwarz, Chem. – Eur. J., 2020, 26, 756.
21. A. Ormeci and Yu. Grin, J. Thermoelectr., 2015, 6, 16.
22. M. Tinkham, Introduction to Superconductivity, McGraw-Hill, New York, 1996.
23. W. L. McMillan, Phys. Rev., 1968, 167, 331.
24. A. Amon, E. Svanidze, R. Cardoso-Gil, M. N. Wilson, H. Rosner, M. Bobnar, W. Schnelle, J. W. Lynn, R. Gumeniuk, C. Hennig, G. M. Luke, H. Borrmann, A. Leithe-Jasper and Yu. Grin, Phys. Rev. B, 2018, 97, 014501.
25. A. B. Karki, Y. M. Xiong, I. Vekhter, D. Browne, P. W. Adams, D. P. Young, K. R. Thomas, J. Y. Chan, H. Kim and R. Prozorow, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 064512.
26. N. Kimura, H. Ogi, K. Satoh, G. Ohsaki, K. Saitoh, H. Iida and H. Aoki, JPS Conf. Proc., 2014, 3, 015011.
27. Non-centrosymmetric superconductors, Lecture Notes in Physics, ed. E. Bauer and M. Sigrist, 2012, vol. 847, p. 3.
28. F. Kneidinger, E. Bauer, I. Zeiringer, P. Rogl, C. Blaas-Schenner, D. Reith and R. Podloucky, Phys. C, 2015, 514, 388.
29. J. Beare, M. Nugent, M. N. Wilson, Y. Cai, T. J. S. Munsie, A. Amon, A. Leithe-Jasper, Z. Gong, S. L. Guo, Z. Guguchia, Yu. Grin, Y. J. Uemura, E. Svanidze and G. M. Luke, Phys. Rev. B, 2019, 99, 134510.
30. R. Khasanov, R. Gupta, D. Das, A. Amon, A. Leithe-Jasper and E. Svanidze, Phys. Rev. Res., 2020, 2, 023142.
31. A. Amon, E. Svanidze, A. Ormeci, M. König, D. Kasinathan, D. Takegami, Yu. Prots, Y. F. Liao, K. D. Tsuei, L. H. Tjeng, A. Leithe-Jasper and Yu. Grin, Angew. Chem., Int. Ed., 2019, 58, 15928.
32. STOE Powder Diffraction Software WinXPow (version 2), STOE and Cie GmbH, Darmstadt, 2001.
33. L. Akselrud and Yu. Grin, J. Appl. Crystallogr., 2014, 47, 803.
34. K. Koepernik and H. Eschrig, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1743.
35. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244.
36. M. Kohout, Int. J. Quantum Chem., 2004, 97, 651.
37. M. Kohout, F. R. Wagner and Yu. Grin, Int. J. Quantum Chem., 2006, 106, 1499.
38. M. Kohout, Faraday Discuss., 2007, 135, 43.
39. A. Ormeci, H. Rosner, F. R. Wagner, M. Kohout and Yu. Grin, J. Phys. Chem. A, 2006, 110, 1100.
40. M. Kohout, DGrid, version 4.6, Radebeul, 2011.

---

Footnotes

† Electronic supplementary information (ESI) available. CCDC 1996617. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0dt01374a

‡ Current address: Department of Chemistry, University College London.

---