Multifunctional coordination polymers based on copper(I) and mercaptonicotinic ligands: synthesis, and structural, optical and electrical characterization

Abstract

Three new coordination polymers (CPs) named [Cu(6mna)]_n (CP1), [CuCl(H6mna)(H₂O)_0.33]_n (CP2), and {[(CuI)₂H₂dtdn].MeCN}_n (CP3), (H6mna = 6-mercaptonicotinic acid, and H₂dtdn = 6,6′-dithiodinicotinic acid) have been synthesized and their structures determined by single-crystal X-ray diffraction. Complexes 1 and 3 are 2D-CPs while complex 2 is a 1D-CP. The optical properties of these complexes have been evaluated in the solid state, at room temperature and at 77 K, and compared with those of the starting ligands. The electrical conductivity of CPs 1–3 has been evaluated and their thermal stabilities have been studied. CP2 shows an interesting crystal arrangement, where the connection between the ligand and the copper forms a channel-like structure characterized by an intrinsic disorder. Crystal data collected at low temperatures for this complex revealed minor structural changes in the Cu⋯Cu distances and Cu–S–Cu angles along the chain, excluding phase transition. In CP1, the N and S atoms are involved in metal coordination bonds giving rise to a 2D coordination polymer. In CP3, the Cu-I bonds compose double ladder-like structures, bridged by H₂dtdn ligands. The electrical conductivities of CPs 1–3 suggest their semiconductive behavior.

---

Introduction

Coordination polymers (CPs), which consist of infinite arrays of metal ions (or clusters) linked by coordinating organic ligands, have attracted considerable interest as functional materials that can display remarkable physical properties such as luminescence,¹ magnetism,² electrical conductivity,³ or a combination of them (multifunctional materials)⁴ as, for instance, optical and electrical features.⁵ The properties of CPs, basically, depend on the suitable selection of their main components, i.e. the metal ion or cluster and the multidentate organic ligand, and on how they arrange to form the final solid structure.

Copper(I) based CPs have attracted great attention as potential candidates for optical,⁶ electronic,⁷ and optoelectronic applications.⁸ Copper(I), with a d¹⁰ electronic configuration, is well known for its diverse coordination geometries, which afforded CPs with unprecedented structural motifs and physico–chemical properties.^8,9 Among copper(I) based CPs, copper(I) halides, particularly copper(I) iodide, have been widely employed as inorganic components in the construction of CPs due to their rich coordination ability and their excellent photophysical and electronic properties.¹⁰ The soft-acceptor nature of the copper(I) ion, which gives rise to a relatively flexible coordination sphere, together with the flexibility of halides as bridging ligands (e.g. μ₂, μ₃, or μ₄ bridging modes), play an important role in their structural diversity and physical properties.¹¹ On the other hand, copper(I) complexes with nitrogen–sulfur donor ligands have drawn much attention as suitable building units to construct new multifunctional materials with fascinating structures and properties, where they adopt a wide range of coordination modes.¹² The incorporation of thiolate (S-bridging) ligands between adjacent Cu(I) centers is a well-established strategy to produce CPs showing interesting electrical and luminescence properties.¹³ In this work, we have selected nitrogen−sulfur heterocyclic chelating ligands, known as 6-mercaptonicotinic acid (H6mna, 6mna in its deprotonated from) and 6,6′-dithionicotinic acid (H₂dtdn, Fig. 1). These ligands are multifunctional ligands containing a carboxylic acid group, a thiol, and a pyridinic nitrogen atom. Thus, they can exhibit different coordination sites for copper(I) giving rise to variable structures with different properties. It is well known that thiolate and disulfide ligands can display in situ S–S formation or cleavage, respectively, under specific reaction conditions.¹⁴ By the same way, the inter-conversion between H6mna and H₂dtdn has been observed (Fig. 1).¹⁵ In our study, the interaction of H6mna or H₂dtdn with copper(I) iodide gave rise to three copper(I) CPs. These new materials have been characterized by means of single crystal X-ray diffraction and their optical and electronic behaviors have been explored.

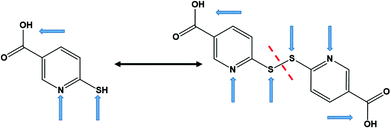Fig. 1 Chemical structures of H6mna (left) and H₂dtdn (right) ligands. The arrows indicate the usual metal binding sites.

Results and discussion

Synthesis and structural characterization

It is well-known that CuI reactions with organic thiol or disulfide derivatives under energetic conditions can give rise to a large variety of coordination compounds including coordination polymers in which direct coordination of the thiolate group or in situ reduction of the disulfide and thiolate coordination to the copper center take place, generating a large structural variety with interesting electronic properties.¹⁷

In our case, the direct reactions between CuI and H6mna or H₂dtdn at high temperature in MeCN/EtOH(MeOH) as solvents, lead to the formation of the coordination polymer [Cu(6mna)]_n (CP1), where the negatively charged ligand, due to the formation of the sulphide anion, directly coordinates the copper(I) atom and the iodide is not present in the structure. On the other hand, mild conditions using either H6mna or H₂dtdn lead to the formation of {[(CuI)₂H₂dtdn]·MeCN}_n (CP3), where the organic ligand is neutral and the charge of the copper(I) is neutralized by the iodide. However, the formation of CP3 from CuI and H6mna implies an oxidation process of the H6mna ligand to the disulfide form dtdn²⁻, a reaction that is known to proceed in the presence of oxygen under mild conditions.^14bc Finally, the solvothermal reaction in the presence of CH₂Cl₂ leads to an unexpected but very reproducible product: [CuCl(H6mna)(H₂O)_0.33]_n (CP2), where the ligand is zwitterionic, with the sulphide coordinating the copper(I) atoms and chloride instead of iodide as the counterion.

The different synthetic routes are summarized in Scheme 1. The crystal structures of the obtained CPs are discussed in detail below.

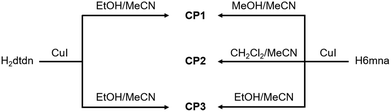Scheme 1 Synthetic routes for CPs 1–3. The reactions have been done using Cu : L stoichiometry 1 : 1 with H6mna and 2 : 1 with H₂dtdn (method A).

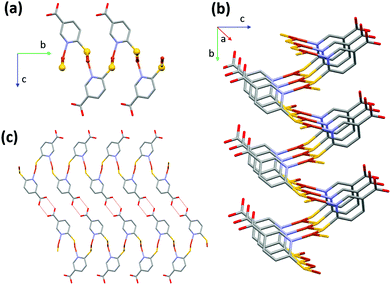
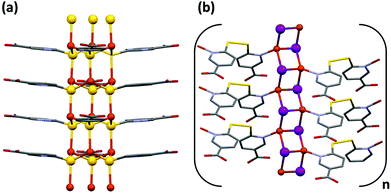
CP1 crystallizes in the monoclinic crystal system with P2₁/c space group and its asymmetric unit consists of one copper atom and one 6mna molecule (Fig. S7†), the positive charge of the copper is balanced by S⁻ present in the ligand. The packing is characterized by the presence of a 2D sheet structure, generated by the μ₂ coordination of the S atoms that form a zig-zag infinite chain of S and Cu along the a axis (Fig. 2b). The Cu(I) atom possesses a distorted trigonal coordination, with two positions occupied by the S atoms and the third one occupied by the N of 6mna⁽⁻⁾, so that the organic molecules allow extension of the expansion along the b axis (Fig. 2a). These infinite sheets are connected to each other through ring dimer H-bonds formed between the carboxylic acid groups of the 6mna⁽⁻⁾ ligands (Fig. 2c).

Fig. 2 Fragments of the polymeric chain (a), details of the bidimensional expansion (b), and the H-bonding between carboxylic acid groups (c) in CP1. The dashed lines indicate hydrogen bonding interactions. Hydrogen atoms have been omitted for clarity. Color legend: gray = carbon, red = oxygen, light-blue = nitrogen, yellow = sulphur, orange = copper.

To test the stability of the compound, a variable temperature X-ray powder diffraction (VT-XRPD) analysis was performed and the structure of CP1 does not show any modification upon heating up to 150 °C (Fig. S12 and S4† for thermogravimetric analysis (TGA)).

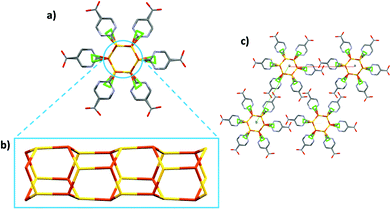
CP2 crystallizes in the hexagonal system, as P6₃, and the asymmetric unit consists of [CuCl(H6mna)]. The Cu(I) metal is characterized by a distorted tetrahedral geometry and is linked with three different sulphur atoms from three H6mna ligands and one chlorine atom which is disordered over four different positions (see Fig. S8† for more crystallographic details). The chloride is coming from the degradation of CH₂Cl₂ during the solvothermal synthesis.¹⁸ The disorder seems to be static and intrinsic of the crystal structure of the compound since it has been observed in several crystals from different batches, and as it persists also at 100 K. A detailed description of the disorder refinement is reported in the ESI (Fig. S10 and S11†).

Also part of the ligand is disordered; in fact, the sulphur atom and the aromatic ring occupy two distinct positions, while the carboxylic acid group is refined over only one position. It is worth noting that the C–O distances (1.19(2) and 1.31(1) Å) are consistent with that of a carboxyl group and the hydroxyl group points versus the chlorine atoms, with O–Cl distances characteristic of H-bonds (between 2.95(1) and 3.12(1) Å at RT, 2.92(1)–3.14(1) Å at 100 K). The oxidation state of copper is +1, and chloride atom is the counterion. Since sulphur is deprotonated in order to bind the Cu atoms, the neutrality of the structure is maintained by the protonation of the pyridine nitrogen. Again, some of the distances between the N atom and chloride suggest the presence of hydrogen bonds (N–Cl distances between 2.90(3) and 3.23(3) Å at RT, 2.93(3) and 3.16(2) Å at 100 K). The infinite hexagonal channel-like structure based on Cu–S is generated by the chiral 6₃ axis; however, the sulphur position disordered over two sites implies the presence of channels with opposite chirality (Fig. 3). The Cu⋯Cu distances of 3.749(1) Å and 3.932(6) Å are long compared to other Cu(I) thiolate polymeric structures, excluding any cuprophilic interactions.

Fig. 3 Polymeric chain of CP2 along the c axis (a). Fragment of Cu–S connectivity along the chain (b). The packing of CP2 (c). Hydrogen atoms have been omitted for clarity. Color legend: gray = carbon, red = oxygen, light-blue = nitrogen, yellow = sulphur, orange = copper, green = chlorine.

Around the three-fold axis, in the area surrounded by the organic ligands, some disordered electron density is present, which suggests the presence of residual solvent molecules. Elemental analysis is consistent with the presence of two water molecules for the unit cell.

In the VT-XRPD analysis, a phase transition was observed around 190 °C (Fig. S13†). This change occurs at the same temperature of the initials weight loss observed in the TGA analysis (Fig. S5†).

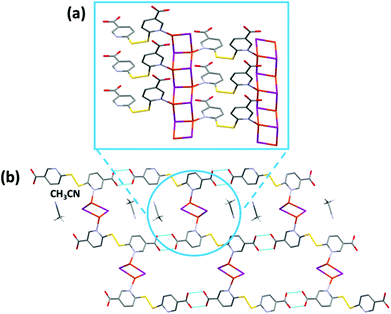
CP3 crystallizes in the P2₁/c space group and its asymmetric unit consists of [(CuI)₂(H₂dtdn)(MeCN)]. The structure is characterized by the presence of 1D ladder-like [Cu₂I₂]_n chains, interlinked by H₂dtdn bridges to form a 2D sheet (Fig. 4 and S9†). Each independent copper metal belongs to a different 1D ladder-like chain, one grows along the screw axis and is characterized by a long Cu⋯Cu distance (3.218(2) Å), while the second is generated by the inversion center and presents one short and one long distance (respectively 2.822(1) and 3.420(1) Å). Both Cu metal ions are characterized by a distorted tetrahedral geometry formed by three iodine anions and a nitrogen atom from the bridging H₂dtdn ligand. The resulting planar sheets are piled up by hydrogen bonds between carboxylic acid groups of adjacent layers. Table S3† gathers the coordination bond lengths.

Fig. 4 Fragment of the polymeric chain (a) and the H-bonding between carboxylic acid groups (b) in CP3. The dashed lines indicate hydrogen bonding interactions (O⋯O distances 2.587(9) and 2.795(9) Å). Hydrogen atoms have been omitted for clarity. Color legend: gray = carbon, red = oxygen, light-blue = nitrogen, yellow = sulphur, orange = copper, purple = iodine.

From the VT-XRPD analysis a solid-state transition around 180 °C was observed (Fig. S14†). This transition corresponds to the solvent loss, as observed in the TGA analysis (Fig. S6†).

Infrared (IR) spectroscopy allowed us to gain additional information on the different environments experienced by the functional groups of the ligands in the three structures. The analysis has been focused on selected bands, useful to define interactions within the crystal arrangements. The IR spectra of CP1–3 are compared in Fig. S15 and S16,† together with that of H6mna. The C=O stretching band of the bare ligand appears at 1680 cm⁻¹, indicative of the involvement of the carbonyl group in a hydrogen bond with the hydroxyl group of another H6mna molecule. In CP1 the C=O group of the ligand shows an intense stretching band at 1671 cm⁻¹ (close to the frequency observed for H6mna) and a characteristic band of a dimeric form at 925 cm⁻¹ (bending of the O–H bond). This is in good agreement with the formation of double H-bonds rings between ligand molecules in the crystal, as shown in Fig. 2c. The bands at 555 and 538 cm⁻¹ can be ascribed to stretching of the two non-equivalent Cu–S bonds (as reported in Table 1).^13c

Table 1 Selected distances (in Å) and angles (°) and DC electrical conductivity measurements at 298K and 373K for CPs 1–3. (See the ESI for atom labels)

CP	Cu–S	Cu–I	Cu–Cu	Cu–S–Cu	S–Cu–S	I–Cu–I	σ S cm^−1 (298 K)	σ S cm^−1 (373 K)
a For S1(b) site position.
1	2.197(2)		3.081(1)		120.83(7)		5.4 × 10^−5	8.3 × 10^−5
	2.295(2)		3.907(1)
2	2.480(7)		3.755(2)	110.6(3)	111.6(3)		6.1 × 10^−8
	2.326(7)		3.952(6)	110.1(3)	109.1(3)
	2.254(8)			113.1(3)	105.3(3)
	2.498(8)^a			111.3(3)^a	110.3(3)^a
	2.285(5)^a			112.4(3)^a	108.6(3)^a
	2.233(8)^a			113.2(3)^a	103.2(4)^a
3		Cu(1)–I(1)	Cu(1)–Cu(1)			Cu(1)	6.1 × 10^−8
		2.601(1)	3.218(2)			107.63(4)
		2.690(1)	Cu(2)–Cu(2)			105.80(4)
		2.724(1)	2.822(1)			105.11(4)
		Cu(2)–I(2)	3.420(1)			Cu(2)
		2.721(1)				117.37(4)
		2.709(1)				104.47(4)
		2.631(1)				100.57(4)

---

In CP2 the carbonyl band is observed at 1731 cm⁻¹, i.e. at higher frequency with respect to H6mna. This observation, together with the sharpness of the peak and the absence of the O–H bending signal at 920 cm⁻¹, confirms that the carboxyl acid group is not involved in H-bonds, as inferred from crystallographic analysis (Fig. 3c). The signal at 528 cm⁻¹ confirms the presence of Cu–S bonds.^13c

CP3 has two significant signals at 1706 and 1685 cm⁻¹ in the C=O stretching zone, which are almost completely overlapped due to the broadening of the signals caused by hydrogen bonds between the two carboxylic moieties of adjacent layers (Fig. 4a). The presence of two peaks correlates with slightly different lengths observed for the two carbonyl groups in the structural analysis. In fact, one carboxyl group is characterized by short and long C–O distances (1.23(1) Å and 1.28(1) Å, respectively) while the other carboxyl group presents almost equal C–O distances (1.25(1) Å and 1.27(1) Å, respectively). As in CP1, bending of the O–H bond is detected at 920 cm⁻¹, which is ascribable to the dimeric H-bond ring which forms between two adjacent ligands. CP3 is also characterized by an S–S stretching band at 764 cm⁻¹.

Optical characterization

Absorption and emission properties of the two ligands have been characterized in solution and in the solid state while those of CPs 1–3 have been analyzed only in the solid state, due to the lack of solubility of these materials in common organic solvents. Measurements have been performed both at room temperature and at 77 K.

The absorption spectrum of H6mna, collected both in EtOH and in DCM : MeOH 1 : 1, is shown in Fig. S17.† It displays two bands in the 250–400 nm region with ε of the order of 2–3 × 10⁴ M⁻¹ cm⁻¹ in EtOH (Table S4†), similarly to what was observed for 2-mercaptonicotinic acid.¹⁹ The absorption spectrum of H₂dtdn is confined below 300 nm (Fig. S18†), i.e. bathochromically shifted with respect to that of the monomer H6mna, a behaviour already reported for the dimers of mercaptonicotinic acids.^19,20 Both ligands were found to be non-emissive in solution at room temperature. Conversely, in a frozen DCM : MeOH 1 : 1 matrix at 77 K, they display emission, peaking at 480 nm and 440 nm for H6mna and H₂dtdn respectively (Fig. S17 and S18†). The large Stokes shift (12 210 cm⁻¹ and 6940 cm⁻¹, respectively) points to either fluorescence deriving from a distorted singlet excited state or to phosphorescence. The nature of the emitting excited state could not be assessed because of the weakness of the emission that precluded lifetime determination. In the solid state at room temperature, H6mna shows a weak and broad emission with a maximum at 582 nm (Fig. S17†) while H₂dtdn is non-emissive.

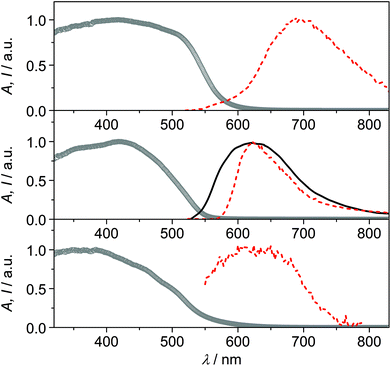
The solid samples of CPs 1–3 show broad absorption spectra with onset up to 550–600 nm (Fig. 5), accounting for their yellow to deep orange color. Only CP2 was found to be emissive at room temperature, with a broad emission spectrum peaking at 620 nm (Fig. 5).‡ Conversely, at 77 K, all compounds display orange-red luminescence, with maxima at 692 nm, 622 nm and 624 nm for CPs 1, 2 and 3, respectively (Fig. 5, in the case of CP3 the emission is very weak). The observed low-energy absorption and emission features of the complexes, bathochromically shifted with respect to those of the relevant bare ligands, can be ascribed to excited states involving orbitals from both the metal and the ligands.

Fig. 5 Absorption (circles) and emission spectra at room temperature (black full line) and at 77 K (red dashed line) of the solid samples of CP1 (top), CP2 (center) and CP3 (bottom). Excitation at 400 nm.

The emission features of CP1 at low temperature, with maximum at 692 nm and a broad spectrum extending in the near-infrared region, resemble those of Cu(I) phenanthroline complexes, where the typical metal-to-ligand charge-transfer (MLCT) emission arising from a distorted (flattened) excited state is observed.^21,22 The absence of the halide in the coordination sphere of Cu(I) in CP1 could, indeed, account for an MLCT nature of the emission, involving the π* orbitals of the 6mna ligand.

The emission of CP2 and CP3 appears, conversely, at higher energy, with maximum around 620 nm. This outcome can be ascribed to transitions involving the halide which is, in these cases, coordinating the metal ion. Halide-to-metal charge transfer (XMCT) excited states are most probably involved, as previously argued for CPs based on Cu(I) halides and a thiolated ligand.^29b The contribution from metal-centered (MC) excited states can be excluded by considering that the Cu⋯Cu distances are in all cases higher than the sum of the van der Waals radii (2.8 Å).^6b,22 The measured excited state lifetimes are in the μs range for all compounds (Table S5†), indicating a triplet nature of the emission.²³

The temperature dependence of the luminescence output cannot be discussed in terms of thermochromism,²⁴ but rather as a general increase in emission intensity due to the rigidification of the medium that disfavors thermal deactivation of the excited state (due to rotational or vibrational modes)^25,26 and/or suppresses bimolecular quenching given by molecular oxygen.^27,28 For CP2, indeed, it is possible to observe that there is no shift in the emission maximum, while an increase in the emission intensity and a narrowing of the emission band is observed by lowering the temperature. The distorted tetrahedral geometry of the copper complex in CP3 and the presence of solvent molecules within the voids of the structure, could account for the weak luminescence properties of this compound.

Electrical characterization

The electrical conductivity of the CPs 1, 2, and 3 has been measured in individual crystals at 300 K, using a two contact methodology. The crystals are contacted through the use of a graphite conductive ink and two platinum tips that are connected to a system that allows application of a voltage between the two tips, and measure the current intensity (amperes) through them (Fig. S19†). Using these experimental conditions, the obtained electrical conductivity values are of 5,4 × 10⁻⁵, 6.1 × 10⁻⁸ and 6.1 × 10⁻⁸ S cm⁻¹ respectively (Table 1 and Fig. S20–S22†). These values are in agreement with those found in the bibliography for this type of chains, belonging to the range of semiconductors materials.^3,29CP1 has a fairly high electrical conductivity value within the large coordination polymer family with electrical properties and within the family of CPs with Cu–S bonds.³ For this reason, we have also studied the variation of its conductivity with temperature (from 300 K to 373 K). The graph of conductivity versus temperature obtained for CP1 shows how this CP presents a different behavior between 300 K and 320 K, where the increase in temperature produces a slight increase in the electrical conductivity values. This should be indicative of a semiconductor behavior. However, from 330 K to 373 K the conductivity values decrease showing a metallic behavior (Fig. S23†).¹⁷ It seems evident from the graph obtained that at these temperatures there is a structural change. For this reason and in an attempt to understand what could happen, a thermogravimetric study of compound CP1 was carried out, showing that thermal decomposition takes place at temperatures over 423 K. In addition, X-ray powder diffractogram of CP1 heated up to 375 K confirms that there is no phase transformation. Therefore, the changes that occur upon heating the crystals could be due to small internal micro-fractures as a consequence of mechanical crystal elongations or contractions leading to a decrease in its conductivity. This behavior has been observed in measurements of crystals of related compounds.^10b,c

When trying to compare the optical band gap obtained from the visible spectra for CP1 (a value around 1.7 eV, Fig. 5), with the data obtained by the electrical conductivity measurements of the same compound (a value around 0.58 eV, Fig. S24†) we observed a big discrepancy. It is known that many materials show significant differences between the optical and electrical band gap, where the value of the optical gap is generally greater. Indeed, the discrepancies in the values may be greater depending on the measurement conditions. In this case, the absorbance of CP1 has been measured in the solid state by gently crushing the powder samples of the compound. This process produces a decrease in the crystal size and a considerable increase in the surface area and number of defects. These changes can cause an increase in the optical gap. On the other hand, the measurement of the electrical conductivity was carried out on a single crystal of micrometric dimensions, with much less defects, which considerably improves the value of the electrical conductivity, thereby reducing the experimental gap. In addition, the slope obtained from the graph of the variation of the napierian logarithm of the resistivity versus the inverse of the temperature (Fig. S24†), presents a linear regression coefficient (R²) for the least squares of 0.84021, which indicates that the experimental data are not very precise in calculating the activation energy.

To explain the differences found in the conductivity values of these compounds, we have studied in detail their crystalline structures and compared the Cu–Cu, Cu–S, or Cu–I distances as well as the Cu–S–Cu, S–Cu–S or I–Cu–I angles, which are the ones that mainly help to explain the path followed by the electrons along the chains or the sheets in these types of CPs.

CP1 only begins to have an ohmic behavior between 0 and 10 volts (Fig. S20†). Between −10 and 0 V, the compound shows a typical curve that can be ascribed to intrinsic resistance, however, for a correct interpretation in this voltage range, a deeper study, out of the scope of this work, is required. Its ohmic behavior can be related to the possible paths through which electrons can circulate (Fig. 6a and b). One (i) is along the chains formed by Cu–S–C–N–Cu–S bonds (Fig. 6a), but this is prevented by carbon and nitrogen atoms that do not possess vacant orbitals to provide accessible electron mobility, and another (ii) is a much more favorable option: the chains formed by the Cu–S–Cu bonds (Fig. 6b), with short Cu–S distances, 2.197(2) and 2.295(2) Å, and a trigonal planar geometry, with S–Cu–S and Cu–S–Cu angles close to 120°, where this value facilitates the overlap interaction between the copper “d” orbitals and the sulphur “p” orbitals.

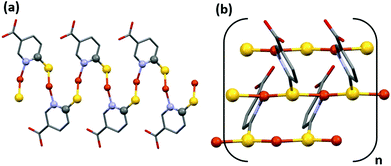Fig. 6 Two possible paths through which electrons can circulate. Along the chains formed by Cu–S–C–N–Cu–S bonds (a) and along the chains formed by the Cu–S–Cu bonds (b).

On the other hand, CP2 presents a unique path for the mobility of the electrons along the S–Cu–S bonds (Fig. 7a) that form the infinite hexagonal channel, where each copper is linked to three sulfurs by means of a distorted tetrahedric environment, with short Cu–S distances (2.254(8), 2.326(7), 2.480(7); 2.233(8), 2.285(5) and 2.498(8) at RT respectively for the two different sulfur positions) but with S–Cu–S angles between 112 and 105°, which worsens the overlap between the metal and sulfur orbitals. This characteristic can explain that its conductivity value is lower than that for CP1.

Fig. 7 Possible path for the mobility of the electrons, along the S–Cu–S bonds that form the infinite hexagonal channel, in CP2 (only one position of S atoms is drawn for the sake of clarity) (a). Possible path for the mobility of the electrons along infinite [Cu₂I₂] chains in CP3 (b).

The electric conductivity value obtained for CP3 is within the range obtained for many CPs of this type, and has to be explained according to the formation of infinite [Cu₂I₂] chains (Fig. 7b), where the bridging iodine anions are coordinated simultaneously to three Cu(I) metal centers with slightly different coordination bond lengths (Table 1).^10b,c

Experimental

Materials and methods

6-Mercaptonicotinic acid (H6mna), 6,6′-dithiodinicotinic acid (H₂dtdn), CuI and solvents were purchased from Sigma-Aldrich and used as received.

IR spectra were recorded on a PerkinElmer Spectrum BX spectrometer using KBr pellets in the range of 4000–400 cm⁻¹.

Elemental analyses were carried out by the microanalytical service of the Autónoma University of Madrid.

Powder X-ray diffractograms in the range of 2θ = 5–40° (step size 0.02°; time/step, 20 s; 40 mA × 40 kV) were collected on a Panalytical X'Pert PRO automated diffractometer equipped with an X'Celerator detector and in Bragg–Brentano geometry by using CuK_α radiation (λ = 1.54177 Å). The samples have been analyzed with scanning θ/θ. The diffractometer can be equipped with Anton Paar TTK450 for variable temperature measurement (VT-XRPD). The program Mercury was used to simulate PXRD patterns from single-crystal data.

Single crystals data of CP1 were collected on a Bruker Kappa Apex II diffractometer and those of CPs 2–3 were collected on an Oxford Xcalibur S diffractometer, and both instruments were equipped with a MoKα anode (λ = 0.71073 Å) and graphite monochromator. The measurements of all crystals were performed at room temperature (298 K). CP2 was also analyzed at 100 K, using a Cryostream 800 cooler. All the crystallographic data and further details on data collection and structure refinement are reported in the ESI.†

The experimental data were deposited within the Cambridge Crystallographic Data Centre. CCDC 1959835, 1960090, 1959681, 1959622 contain the supplementary crystallographic data for this paper.†

Two probe direct current (dc) electrical conductivity measurements at 300 K were performed in several single crystals of CPs 1–3. The conductivity values at 300 K were obtained by applying voltages from −10.0 to +10.0 V. We have performed dc conductivity measurements for at least three single crystals of each compound and the final conductivity value is given by the average value. The thermal dependence of the dc electrical conductivity was measured for CP1 in the voltage range where the crystals are ohmic conductors, in the temperature range of 300–400 K. The warming rate was 1.0 K min⁻¹. The contacts were made with Pt wires (25 μm diameter) using graphite paste. The samples were measured in a Quantum Design PPMS-9 equipment connected to an external voltage source (Keithley model 2400 source-meter) and amperometer (Keithley model 6514 electro-meter).

Absorption spectra of solutions were recorded with a PerkinElmer Lambda 950 UV/Vis/NIR spectrophotometer. Room temperature emission spectra were collected with an Edinburgh FLS920 fluorimeter, equipped with a Peltier-cooled Hamamatsu R928 PMT (280–850 nm), and corrected for the wavelength-dependent phototube response. Absorption and emission determinations on the solid samples were performed on gently crushed powder samples placed inside two quartz slides. Reflectance spectra were acquired with the spectrophotometer described above, equipped with a 60 mm integrating sphere. They were converted into absorption spectra by using the Kubelka–Munk function.¹⁶ Emission spectra were collected in front-face mode with the same Edinburgh FLS920 fluorimeter. For 77 K determinations the samples were placed inside quartz capillary tubes and immersed in liquid nitrogen in a homemade quartz Dewar. Excited state lifetimes were determined with an IBH 5000F time-correlated single-photon-counting apparatus by using a pulsed NanoLED excitation source at 373 nm. Analysis of the emission decay profiles versus time was accomplished by using the decay analysis software DAS6 provided by the manufacturer. Estimated errors are 10% on lifetimes and 2 nm on emission and absorption peaks.

Thermogravimetric analysis (TGA) measurements were performed using a PerkinElmer TGA7 in the temperature range of 35–400 °C under a N₂ gas flow, and heating was carried out at 5 °C min⁻¹.

Synthesis

[Cu(6mna)]_n (CP1).
Method A. A mixture of CuI (0.10 g, 0.52 mmol) and H₂dtdn (0.088 g, 0.26 mmol) was dissolved in 20 mL of acetonitrile (MeCN) and ethanol (EtOH) (1 : 1). The resulting yellow mixture was sealed in a 45 mL Teflon-lined steel autoclave, heated at 130 °C for 48 h and finally cooled to 20 °C in 24 h. The orange solid of CP1 was filtered from the yellow solution and washed with H₂O, MeCN and diethyl ether, and dried by vacuum (0.06 g, 53% yield based on Cu).
Method B. A mixture of CuI (0.05 g, 0.26 mmol) and H6mna (0.044 g, 0.26 mmol) was dissolved in 30 mL of a mixture of MeCN and methanol (MeOH) (1 : 1). The resulting mixture was stirred for 2 h at room temperature, to give a yellow solution. Over this yellow solution, H₂O was added to precipitate the orange solid of CP1. The orange solid was filtered off, washed with H₂O, MeCN and diethyl ether, and dried by vacuum (0.04 g, 70% yield based on Cu). Suitable crystals of CP1 were grown using solvothermal conditions where a mixture of CuI (0.05 g, 0.26 mmol) and H6mna (0.044 g, 0.26 mmol) was dissolved in 20 mL of MeCN and H₂O (1 : 1). The resulting yellow mixture was sealed in a 45 mL Teflon-lined steel autoclave, heated at 140 °C for 48 h and finally cooled to 20 °C in 30 h. The orange/red crystals of CP1 were filtered from the yellow solution, washed with H₂O, MeCN and diethyl ether, and dried by vacuum (0.025 g, 46% yield based on Cu).

Anal. calcd (found) for C₆H₄CuNO₂S: C, 33.10 (31.79); H, 1.85 (2.22); N, 6.43 (6.18); S, 14.70 (14.14). IR selected data (KBr, cm⁻¹): 3160–2710 (br), 1671 (s), 1585 (s) 1421 (w), 1359 (m), 1309 (m), 1265 (m), 1145 (m), 1101 (s), 1027 (w), 925 (w), 761 (m), 555 (w), 538 (w), 487 (w). The purity of the solid was confirmed by X-ray powder diffraction (see Fig. S1†).

[CuCl(H6mna)(H₂O)_0.33]_n (CP2). A mixture of CuI (0.05 g, 0.26 mmol) and H6mna (0.044 g, 0.26 mmol) was dissolved in 30 mL of MeCN and dichloromethane (CH₂Cl₂) (1 : 1). The resulting yellow mixture was sealed in a 45 mL Teflon-lined steel autoclave, heated at 140 °C for 2 days and finally cooled to 30 °C in 20 h. The o/red crystals were filtered from the resulting orange mixture, washed with H₂O, MeCN and diethyl ether, and dried by vacuum. The obtained amount of CP2 is 0.035 g (52% yield based on Cu). Anal. calcd (found) for C₆H_5.66ClCuNO_2.33S: C, 27.70 (28.35); H, 2.20 (1.98); N, 5.39 (5.51); S, 12.32 (12.59). IR selected data (KBr, cm⁻¹): 3431 (br), 3200–2800 (br), 1731 (s), 1680 (w), 1616 (s), 1585 (s) 1425 (w), 1369 (m), 1332 (m), 1195 (m), 1106 (s), 732 (m) 688 (m), 528 (m), 476 (w). The purity of the solid was confirmed by X-ray powder diffraction (Fig. S2†).

{[(CuI)₂H₂dtdn]·MeCN}_n (CP3).
Method A. A mixture of CuI (0.10 g, 0.52 mmol) and H₂dtdn (0.081 g, 0.26 mmol) was dissolved in 30 mL of EtOH/MeCN (1 : 1). The resulting yellow solution was refluxed for 2 h at 80 °C. The obtained yellow mixture was filtered to yield unknown material as a yellow solid (0.042 g) and yellow solution. Yellow crystals of CP3 were obtained by slow evaporation of the yellow solution at 25 °C. The obtained amount of CP3 is 0.071 g (38% yield based on Cu).
Method B. A mixture of CuI (0.05 g, 0.26 mmol) and H6mna (0.044 g, 0.26 mmol) was dissolved in 60 mL of (1 : 1) mixture of EtOH and MeCN. The resulting yellow solution was stirred for 2 h at RT. Then the yellow solution was filtered off and left to crystalize by slow evaporation at 25 °C and 4 °C. After a few days, an unknown yellow solid appeared (0.02 g). The solid was filtered off and washed by H₂O, EtOH, MeCN and dried by diethyl ether and vacuum. The rest of the yellow solution was left for crystallization at 25 °C. Orange/yellow crystals of CP3 (0.010 g, 10% based on Cu) started to appear after one week.

Anal. calcd (found) for C₁₄H₁₁Cu₂I₂N₃O₄S₂: C, 23.03 (22.68); H, 1.52 (1.87); N, 5.75 (5.30); S, 8.78 (8.88). IR selected data (KBr, cm⁻¹): 3100–2700 (bs), 1706 (s), 1685 (s), 1584 (s), 1412 (m), 1365 (m), 1289 (m), 1265 (m), 1145 (m), 1094 (m), 1029 (w), 920 (w), 764 (m), 551 (w), 516 (w). The purity of the solid was confirmed by X-ray powder diffraction (Fig. S3†).

Conclusions

Three novel coordination polymers have been prepared from copper(I) iodide and nitrogen−sulfur containing heterocyclic chelating ligands (6-mercaptonicotinic acid, H6mna, and 6,6′-dithionicotinic acid, H₂dtdn). Interestingly, CP1 and CP3 can be obtained starting from either H6mna or H₂dtdn: in the case of CP1, the high temperature favors 6mna⁽⁻⁾ and the formation of the Cu–S bonds. Conversely, the mild synthesis conditions clearly favor the H₂dtdn ligand that coordinates the metal with the pyridyl nitrogen. The three distinct structures originated from the different binding sites and possible coordination motifs of the ligands. X-ray characterization allowed determination of their crystal arrangement. The three CPs exhibited weak or null luminescence at room temperature in the solid state, whereas at low temperatures, CP1 and CP2 showed a fairly intense emission with maximum at 692 nm and 622 nm, respectively. The luminescence properties of these CPs have been discussed in terms of interplay between MLCT and XMCT transitions, depending on the structure of the emissive copper complex in the crystal. The electrical conductivities of CPs 1–3 were explored and the results point to a possible semiconductive behavior. Deeper studies related to the electrical behavior of CP1 are currently underway. The explored compounds can be considered as attractive copper(I)-based coordination polymers for sensing or optoelectronic applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

EC is acknowledged for the SmartMOFs project, grant no. 751175 under H2020-MSCA-IF-2016. The authors thank financial support from the Spanish Ministerio de Ciencia e Innovación (PID2019-108028GB-C22, MAT2016-77608-C3-1-P, MAT2016-75883-C2-2-P) and the Italian CNR (Project “PHEEL”).

References

1. J. Heine and K. Müller-Buschbaum, Chem. Soc. Rev., 2013, 42, 9232.
2. E. Coronado, M. Giménez-Marqués, G. M. Espallargas and L. Brammer, Nat. Commun., 2012, 3, 828.
3. G. Givaja, P. Amo-Ochoa, C. J. Gómez-Garcia and F. Zamora, Chem. Soc. Rev., 2012, 41, 115.
4. P. Amo-Ochoa, O. Castillo, C. J. Gómez-García, K. Hassanein, S. Verma, J. Kumar and F. Zamora, Inorg. Chem., 2013, 52, 11428.
5. A. Rana, S. Kumar Jana, T. Pal, H. Puschmann, E. Zangrando and S. Dalai, J. Solid State Chem., 2014, 216, 49.
6. (a) D. Braga, F. Grepioni, L. Maini, P. P. Mazzeo and B. Ventura, New J. Chem., 2011, 35, 339; (b) P. C. Ford, E. Cariati and J. Bourassa, Chem. Rev., 1999, 99, 3625; (c) D. Braga, L. Maini, P. P. Mazzeo and B. Ventura, Chem. – Eur. J., 2010, 16, 1553; (d) P. P. Mazzeo, L. Maini, D. Braga, G. Valenti, F. Paolucci, M. Marcaccio, A. Barbieri and B. Ventura, Eur. J. Inorg. Chem., 2013, 4459; (e) L. Maini, D. Braga, P. P. Mazzeo, L. Maschio, M. Rérat, I. Manet and B. Ventura, Dalton Trans., 2015, 44, 13003.
7. P. Amo-Ochoa, L. Welte, R. González-Prieto, P. J. Sanz Miguel, C. J. Gómez-García, E. Mateo-Martí, S. Delgado, J. Gómez-Herrero and F. Zamora, Chem. Commun., 2010, 46, 3262.
8. E. Cariati, E. Lucenti, C. Botta, U. Giovanella, D. Marinotto and S. Righetto, Chem. Rev., 2016, 306, 566.
9. R. Peng, M. Li and D. Li, Coord. Chem. Rev., 2010, 254, 1.
10. (a) P. Amo-Ochoa, K. Hassanein, C. J. Gómez-García, S. Benmansour, J. Perles, O. Castillo, J. I. Martínez, P. Ocón and F. Zamora, Chem. Commun., 2015, 51, 14306; (b) K. Hassanein, P. Amo-Ochoa, C. J. Gómez-García, S. Delgado, O. Castillo, P. Ocón, J. I. Martínez, J. Perles and F. Zamora, Inorg. Chem., 2015, 54, 10738; (c) K. Hassanein, J. Conesa-Egea, S. Delgado, O. Castillo, S. Benmansour, J. I. Martínez, G. Abellán, C. J. Gómez-García, F. Zamora and P. Amo-Ochoa, Chem. – Eur. J., 2015, 21, 17282; (d) J. C. Egea, F. Zamora and P. Amo-Ochoa, Coord. Chem. Rev., 2019, 381, 65; (e) J. Conesa-Egea, N. Nogal, J. I. Martínez, V. Fernández-Moreira, U. R. Rodríguez-Mendoza, J. González-Platas, C. J. Gómez-García, S. Delgado, F. Zamora and P. Amo-Ochoa, Chem. Sci., 2018, 9, 8000; (f) J. Conesa-Egea, C. D. Redondo, J. I. Martínez, C. J. Gómez-García, Ó. Castillo, F. Zamora and P. Amo-Ochoa, Inorg. Chem., 2018, 57, 7568; (g) J. Conesa-Egea, J. Gallardo-Martínez, S. Delgado, J. I. Martínez, J. González-Platas, V. Fernández-Moreira, U. R. Rodríguez-Mendoza, P. Ocón, F. Zamora and P. Amo-Ochoa, Small, 2017, 13, 1700965.
11. (a) A. Kobayashi and M. Kato, Chem. Lett., 2017, 46, 154; (b) X.-C. Shan, H.-B. Zhang, L. Chen, M.-Y. Wu, F.-L. Jiang and M.-C. Hong, Cryst. Growth Des., 2013, 13, 1377.
12. A. Gallego, O. Castillo, C. J. Gómez-García, F. Zamora and S. Delgado, Inorg. Chem., 2012, 51, 718.
13. (a) O. Veselska, D. Podbevšek, G. Ledoux, A. Fateeva and A. Demessence, Chem. Commun., 2017, 53, 12225; (b) K.-H. Low, V. A. L. Roy, S. S.-Y. Chui, S. L.-F. Chan and C.-M. Che, Chem. Commun., 2010, 46, 7328; (c) A. Pathak, J.-W. Shen, M. Usman, L.-F. Wei, S. Mendiratta, Y.-S. Chang, B. Sainbileg, C.-M. Ngue, R.-S. Chen, M. Hayashi, T.-T. Luo, F.-R. Chen, K.-H. Chen, T.-W. Tseng, L.-C. Chen and K.-L. Lu, Nat. Commun., 2019, 10, 1721.
14. (a) H.-B. Zhu and S.-H. Gou, Coord. Chem. Rev., 2011, 255, 318; (b) B. Mandala and B. Basu, RSC Adv., 2014, 4, 13854; (c) A. V. Joshi, S. Bhusare, M. Baidossi, N. Qafisheh and Y. Sasson, Tetrahedron Lett., 2005, 46, 3583.
15. (a) T. M. Ways, W. Lau and V. Khutoryanskiy, Polymers, 2018, 10, 267; (b) S.-M. Fang, M. Chen, X.-G. Yang, J.-Y. Hu and C.-S. Liu, Inorg. Chem. Commun., 2012, 22, 101; (c) Y.-N. Zhang, Y.-Y. Wang, L. Hou, P. Liu, J.-Q. Liu and Q.-Z. Shi, CrystEngComm, 2010, 12, 3840.
16. F. C. Jentoft, Chapter 3 Ultraviolet–Visible–Near Infrared Spectroscopy in Catalysis: Theory, Experiment, Analysis, and Application Under Reaction Conditions, in Advances in Catalysis, Academic Press, 2009, vol. 52, pp. 129–211.
17. S. Delgado, P. J. Sanz Miguel, J. L. Priego, R. Jiménez-Aparicio, C. J. Gómez-García and F. Zamora, Inorg. Chem., 2008, 47, 9128.
18. C. Hernandez, S. Dreisch, J. Horn and S. Neuenfeld, Chem. Eng. Trans., 2016, 48, 763.
19. L. Armijo and V. A. Arancibia, Anal. Chim. Acta, 1994, 298, 91.
20. X. Wang, J. Iqbal, D. Rahmat and A. Bernkop-Schnürch, Int. J. Pharm., 2012, 438, 217.
21. A. Barbieri, G. Accorsi and N. Armaroli, Chem. Commun., 2008, 2185.
22. P. C. Ford, Coord. Chem. Rev., 1994, 132, 129.
23. N. Armaroli, G. Accorsi, F. Cardinali and A. Listorti, Photochemistry and Photophysics of Coordination Compounds: Copper, in Photochemistry and Photophysics of Coordination Compounds I, ed. V. Balzani and S. Campagna, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007, pp. 69–115.
24. (a) J. Troyano, O. Castillo, J. I. Martínez, V. Fernández-Moreira, Y. Ballesteros, D. Maspoch, F. Zamora and S. Delgado, Adv. Funct. Mater., 2018, 28, 1704040; (b) C. M. Brown, V. Carta and M. O. Wolf, Chem. Mater., 2018, 30, 5786.
25. B. Sadowski, K. Hassanein, B. Ventura and D. T. Gryko, Org. Lett., 2018, 20, 3183.
26. Y. You, H. S. Huh, K. S. Kim, S. W. Lee, D. Kim and S. Y. Park, Chem. Commun., 2008, 34, 3998.
27. R.-B. Lin, S.-Y. Liu, J.-W. Ye, X.-Y. Li and J.-P. Zhang, Adv. Sci., 2016, 3, 1500434.
28. L. Shi, B. Li, S. Yue and D. Fan, Sens. Actuators, B, 2009, 137, 386.
29. (a) J. Troyano, J. Perles, P. Amo-Ochoa, J. I. Martínez, F. Zamora and S. Delgado, CrystEngComm, 2014, 16, 8224; (b) J. Troyano, J. Perles, P. Amo-Ochoa, F. Zamora and S. Delgado, CrystEngComm, 2016, 18, 1809; (c) J. Troyano, Ó. Castillo, P. Amo-Ochoa, V. Fernández-Moreira, C. J. Gómez-García, F. Zamora and S. Delgado, J. Mater. Chem. C, 2016, 4, 8545; (d) J. Troyano, E. Zapata, J. Perles, P. Amo-Ochoa, V. Fernández-Moreira, J. I. Martínez, F. Zamora and S. Delgado, Inorg. Chem., 2019, 58, 3290.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional crystallographic, spectroscopic and conductivity data. CCDC 1959622, 1959835, 1959681 and 1960090. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/D0DT01127D

‡ The absolute emission quantum yield was below the limit of detection of our system, i.e. 2%.

---