Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structural, magnetic, redox and theoretical characterization of seven-coordinate first-row transition metal complexes with a macrocyclic ligand containing two benzimidazolyl N-pendant arms†
Bohuslav
Drahoš
 *a,
Ivana
Císařová
*a,
Ivana
Císařová
 b,
Oleksii
Laguta
b,
Oleksii
Laguta
 c,
Vinicius T.
Santana
c,
Vinicius T.
Santana
 c,
Petr
Neugebauer
c,
Petr
Neugebauer
 c and
Radovan
Herchel
c and
Radovan
Herchel
 a
a
aDepartment of Inorganic Chemistry, Faculty of Science, Palacký University, 17. listopadu 12, 771 46, Olomouc, Czech Republic. E-mail: bohuslav.drahos@upol.cz; Fax: +420585 634 954; Tel: +420 585 634 429
bDepartment of Inorganic Chemistry, Faculty of Science, Charles University, Hlavova 2030, 128 00, Prague, Czech Republic
cCentral European Institute of Technology, CEITEC BUT, Purkyňova 656/123, 61200, Brno, Czech Republic
First published on 16th March 2020
Abstract
A structurally new heptadentate derivative of a 15-membered pyridine-based macrocycle containing two benzimidazol-2-yl-methyl N-pendant arms (L = 3,12-bis((1H-benzimidazol-2-yl)methyl)-6,9-dioxa-3,12,18-triazabicyclo[12.3.1]octadeca-1(18),14,16-triene) was synthesized and its complexes with the general formula [M(L)](ClO4)2·1.5CH3NO2 (M = MnII (1), FeII (2), CoII (3) and NiII (4)) were thoroughly investigated. X-ray crystal structures confirmed that all complexes are seven-coordinate with axially compressed pentagonal bipyramidal geometry having the largest distortion for NiII complex 4. FeII, CoII and NiII complexes 2, 3 and 4 show rather large magnetic anisotropy manifested by moderate to high obtained values of the axial zero-field splitting parameter D (7.9, 40.3, and −17.2 cm−1, respectively). Magneto-structural correlation of the FeII, CoII and NiII complexes with L and with previously studied structurally similar ligands revealed a significant impact of the functional group in pendant arms on the magnetic anisotropy especially that of the CoII and NiII complexes and some recommendations concerning the ligand-field design important for anisotropy tuning in future. Furthermore, complex 3 showed field-induced single-molecule magnet behavior described with the Raman (C = 507 K−n s−1 for n = 2.58) relaxation process. The magnetic properties of the studied complexes were supported by theoretical calculations, which very well correspond with the experimental data of magnetic anisotropy. Electrochemical measurements revealed high positive redox potentials for M3+/2+ couples and high negative redox potentials for M2+/+ couples, which indicate the stabilization of the oxidation state +II expected for the σ-donor/π-acceptor ability of benzimidazole functional groups.
Introduction
In the last decade, increased attention has been devoted to the seven-coordinate pentagonal bipyramidal complexes of transition metals1 and lanthanides2–6 due to their interesting magnetic properties, which was demonstrated in an increasing number of published articles and reviews concerning this topic.7–9 These seven-coordinate pentagonal bipyramidal complexes especially of FeII,10–16 CoII,12,17–22 and NiII,12,17,23 and more recently also 4d/5d metals like MoIV/III![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24,25 possess large magnetic anisotropy, which is commonly expressed in terms of axial and rhombic zero-field splitting (ZFS) parameters D and E for transition metal complexes.26 Due to their large axial magnetic anisotropy, they have been successfully employed in the construction of single-molecule magnets (SMMs).27,28 SMMs are compounds showing slow relaxation of magnetization based on pure molecular origin (no long range ordering typical of bulk magnets) and therefore they behave as “nanomagnets” which could find many applications in different fields of interest, e.g. in high-density storage media, spintronics, quantum computing etc.29 Unfortunately, SMMs operate at very low temperature. The greatest progress has been achieved for dysprosium metallocenes with a blocking temperature of 60 K,30 and the current record breaking the liquid nitrogen temperature is 80 K.31 In order to increase this temperature, it is necessary to (i) increase the energy of magnetic moment reversal (Ueff), which is defined for transition metal complexes as Ueff = |D|S2 or Ueff = |D|(S2 − ¼) for the integer or non-integer ground spin state, S,27,28 while for lanthanides with inner shell 4f electrons, large unquenched orbital moments and strong spin–orbit coupling (total momentum J is used) it is based on strong single-ion anisotropy and cannot be described in terms of ZFS spin Hamiltonian parameters, and to (ii) slow down the relaxation of magnetization by understanding all potential relaxation mechanisms including Orbach, direct and Raman mechanisms or quantum tunneling, and by their consequent elimination. Nevertheless, because the relaxation processes are rather complex, the approach (ii) is quite complicated and despite some first attempts,32 still many questions remain unclear in this field. On the other hand, it was found that for high Ueff, not the total spin (S) of the magnetic ground state, but the axial magnetic anisotropy (D) is in fact the key parameter, which has to be tuned and enlarged in order to construct more efficient SMMs.
24,25 possess large magnetic anisotropy, which is commonly expressed in terms of axial and rhombic zero-field splitting (ZFS) parameters D and E for transition metal complexes.26 Due to their large axial magnetic anisotropy, they have been successfully employed in the construction of single-molecule magnets (SMMs).27,28 SMMs are compounds showing slow relaxation of magnetization based on pure molecular origin (no long range ordering typical of bulk magnets) and therefore they behave as “nanomagnets” which could find many applications in different fields of interest, e.g. in high-density storage media, spintronics, quantum computing etc.29 Unfortunately, SMMs operate at very low temperature. The greatest progress has been achieved for dysprosium metallocenes with a blocking temperature of 60 K,30 and the current record breaking the liquid nitrogen temperature is 80 K.31 In order to increase this temperature, it is necessary to (i) increase the energy of magnetic moment reversal (Ueff), which is defined for transition metal complexes as Ueff = |D|S2 or Ueff = |D|(S2 − ¼) for the integer or non-integer ground spin state, S,27,28 while for lanthanides with inner shell 4f electrons, large unquenched orbital moments and strong spin–orbit coupling (total momentum J is used) it is based on strong single-ion anisotropy and cannot be described in terms of ZFS spin Hamiltonian parameters, and to (ii) slow down the relaxation of magnetization by understanding all potential relaxation mechanisms including Orbach, direct and Raman mechanisms or quantum tunneling, and by their consequent elimination. Nevertheless, because the relaxation processes are rather complex, the approach (ii) is quite complicated and despite some first attempts,32 still many questions remain unclear in this field. On the other hand, it was found that for high Ueff, not the total spin (S) of the magnetic ground state, but the axial magnetic anisotropy (D) is in fact the key parameter, which has to be tuned and enlarged in order to construct more efficient SMMs.
Such tuning can be achieved by modification of the coordination environment of the metal centre, i.e. rational ligand design. In the case of pentagonal bipyramidal complexes, two strategies have been successfully employed previously. In the first one, a pentadentate acyclic (L4,11,22,33L5)19 or macrocyclic ligand (L1, Fig. 1)21,34 is coordinated in the equatorial plane (these ligands differ in donor atoms, rigidity, electron distribution, and cavity size) while two apical monodentate co-ligands (varying in σ-donor/π-acceptor properties) are exchanged. The second strategy is based on the structural modification of the pentadentate macrocyclic ligand (e.g.L1 or 1,10-diaza-15-crown-5)35,36 with two pendant arms containing various functional groups with different coordination abilities (2-pyridylmethyl in L2,12,37 acetate in L3,38 2-aminobenzyl in L635 and 2-benzimidazolylmethyl in L7, Fig. 1).36 A significant influence on the magnetic anisotropy of the FeII/III, CoII and NiII complexes with L212 and L338 has been observed (Fig. 1), but unfortunately, no clear trend could be elucidated because of the very complex description of the bond character in the complexes and various contradictory structural parameters.
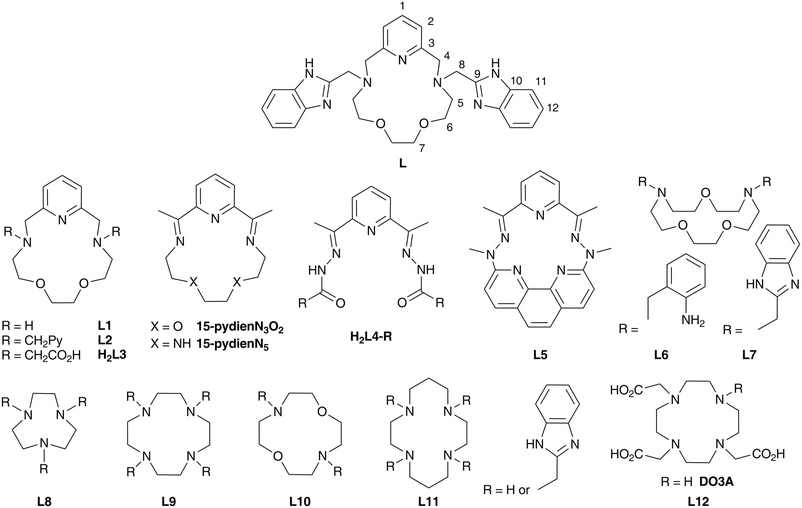 | ||
| Fig. 1 Structural formulas of studied ligand L together with its atom numbering (applied for assignment of NMR signals) and ligands discussed in the text. | ||
In order to further investigate the effect of different functional groups in pendant arms and to obtain any reasonable magneto-structural correlation,39 the macrocyclic ligand L1 has been modified with two 2-benzimidazolylmethyl pendant arms to give a structurally new ligand, L (Fig. 1). In fact, benzimidazolyl groups can act as better σ-donors in comparison with pyridine moieties40,41 and thus, they could provide a stronger axial ligand field, which according to the theoretical predictions17 could beneficially influence the magnetic anisotropy especially in the case of pentagonal bipyramidal FeII and NiII complexes.17 Moreover, this ligand is a new member of a relatively small family of rarely documented macrocycles modified with benzimidazolyl pendant arms (Fig. 1, L7,36 differently-substituted triazacyclononanes L8,42,43 tetraazacyclododecanes (cyclenes) L9,44,45 its dioxa-derivative L10,46 tetraazacyclotetradecanes (cyclames) L1147 and its DO3A derivative L12).48
Thus, in this paper, a structurally new ligand, L, has been synthesized and its MnII, FeII, CoII and NiII complexes have been prepared and studied in detail. Their structural, magnetic and redox properties were thoroughly investigated and compared with those of previously studied systems containing ligands L2 and L3. The obtained results were supported by extensive theoretical calculations.
Experimental section
Materials and methods
Ligand L112,49 and 2-chloromethylbenzimidazole50 were synthesized according to the literature procedures. All the solvents (VWR International, Fontenay-sous-Blois, France) and other chemicals were purchased from commercial sources (Acros Organics, Geel, Belgium and Sigma-Aldrich, St. Louis, MO, USA) and used as received.Elemental analysis (C, H, N) was performed using a Flash 2000 CHNO-S analyzer (Thermo Scientific, Waltham, MA, USA). The mass spectra (Fig. S1†) were collected using an LCQ Fleet mass spectrometer (Thermo Scientific, Waltham, MA, USA) equipped with an electro spray ion source and a three-dimensional (3D) ion-trap detector in the positive/negative mode. The infrared (IR) spectra of the ligand and the studied complexes (Fig. S2†) were recorded using a Thermo Nicolet NEXUS 670 FT-IR spectrometer (Thermo Nicolet, Waltham, MA, USA) or a Jasco FT/IR-4700 spectrometer (Jasco, Easton, MD, USA) using the ATR technique on a diamond plate in the range of 400–4000 cm−1. 1H and 13C NMR spectra were recorded using a 400-MR NMR spectrometer (Varian, Palo Alto, CA, USA) at 25 °C: 1H 399.95 MHz, chloroform-d (CDCl3, tetramethylsilane) δ = 0.00 ppm, and 13C 100.60 MHz, (CDCl3, residual solvent peak) δ = 77.0 ppm. The multiplicity of the signals is indicated as follows: s – singlet, d – doublet, t – triplet, m – multiplet, and bs – broad singlet. Deuterated solvent CDCl3 containing 0.03% of TMS purchased from Sigma Aldrich was used as received. The atom numbering scheme used for NMR data interpretation is shown in Fig. 1. The carbon and hydrogen atoms were assigned according to the spectra obtained from two-dimensional correlation experiments 1H–1H gs-COSY, 1H–13C gs-HMQC and 1H–13C gs-HMBS (see Fig. S3 and S4†). The temperature dependence of the magnetization at B = 0.1 T from 1.9 to 300 K and the isothermal magnetization at T = 2, 5, and 10 K up to B = 9 T were measured using PPMS Dynacool with the VSM module (Quantum Design Inc., San Diego, CA, USA). The experimental data were corrected for diamagnetism and the signal of the sample holder. Dynamic magnetic properties were studied by measuring AC susceptibility using an MPMS XL7 SQUID magnetometer (Quantum Design Inc., San Diego, CA, USA). High frequency/field electron paramagnetic resonance spectroscopy (HFEPR) was performed at CEITEC (Brno, CZ) using a home-built spectrometer equipped with a cryogen-free 16 T superconducting magnet (Cryogenics Ltd, London, UK), a microwave source for measurements from 90 GHz to 500 GHz (Virginia Diodes Inc., Charlottesville, VA, USA), and quasi-optical components in the same range (Thomas Keating Ltd, Billingshurst, UK). The samples were milled with 20% eicosane and made into a ∅5 mm pellet to be placed inside the sample holder for induction mode HFEPR with a modulation frequency of 10 kHz and an amplitude of 0.4 mT. The spectra were obtained at 4 K and 15 K. Simulations were performed using EasySpin51 in MATLAB.52 Cyclic voltammetry was measured using an electrochemical analyzer CHI600C (CH Instrument Inc., Austin, TX, USA). A conventional electrochemical three-electrode-type cell with a Ag/Ag+ reference electrode (0.01 M AgNO3 in 0.1 M TBAP), a platinum wire auxiliary electrode and a glassy carbon working electrode was used during the measurements with a scan rate of 100 mV s−1. The internal ferrocene/ferrocenium standard (E1/2 = 0.452/0.478 V vs. our Ag/Ag+ electrode, E1/2 = 0.624 V vs. SHE)53 was employed in order to obtain the final potential values referred to SHE. The measurements were performed under an inert argon atmosphere in acetonitrile solution containing tetrabutylammonium perchlorate (TBAP) as a supporting electrolyte (0.1 M) and an appropriate complex (2 × 10−3 M).
Crystal data
Single crystals of studied complexes 1–4 suitable for X-ray structure analysis were prepared as described in the experimental section. X-ray diffraction data were collected using a Nonius Kappa CCD diffractometer equipped with a Bruker APEX-II CCD detector with monochromatized MoKα radiation (λ = 0.71073 Å) at a temperature of 150(2) K. The molecular structures of the studied complexes were solved by direct methods and refined by full matrix least squares based on F2 (SHELXL 2014/07).54 The hydrogen atoms on carbon atoms were fixed in idealized positions (riding model) and assigned temperature factors either Hiso(H) = 1.2Ueq(pivot atom) or Hiso(H) = 1.5Ueq (pivot atom) for the methyl moiety. The hydrogen atoms of the H–N moieties were found using a difference electron density map and refined as riding on the corresponding pivot atom. All four crystals were isostructural, differing mostly in their quality with regard to the degree of disorder of perchlorate anions and solvated nitromethane molecules. One of the nitromethanes is situated near the inversion center of the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group and is disordered over four positions at least. To improve the precision of an important part of the structures, PLATON55/SQUEEZE procedures were applied to correct the diffraction data for its contribution to all structures. The molecular and crystal structures of the studied complexes, depicted in Fig. 2 and 4 were drawn using the Mercury software.56
space group and is disordered over four positions at least. To improve the precision of an important part of the structures, PLATON55/SQUEEZE procedures were applied to correct the diffraction data for its contribution to all structures. The molecular and crystal structures of the studied complexes, depicted in Fig. 2 and 4 were drawn using the Mercury software.56
Syntheses
MS m/z (+): 512.24 ([L + H+]+, calcd 512.28), 534.29 ([L + Na+]+, calcd 534.26), 550.22 ([L + K+]+, calcd 550.23).
1H NMR(CDCl3): δ 3.19 (H5, t, 3JHH = 4.9 Hz, 4H), 3.41 (H7, s, 4H), 3.50 (H6, t, 3JHH = 4.9 Hz, 4H), 3.94 (H4, s, 4H), 4.04 (H8, s, 4H), 6.93 (H2, d, 3JHH = 7.8 Hz, 2H), 7.14 (H12, m, 4H), 7.39 (H1, t, 3JHH = 7.8 Hz, 1H), 7.48 (H11, m, 2H), 7.60 (H11, m, 2H), 11.55 (NH, bs, 2H)
13C{1H} NMR (CDCl3): δ 53.75 (C8), 57.76 (C5), 62.85 (C4), 68.41 (C6), 69.79 (C7), 111.26 (C11), 118.66 (C11), 121.39 (C12), 121.82 (C2), 121.90 (C12), 133.77 (C10), 136.92 (C1), 143.96 (C10), 155.34 (C9), 158.50 (C3).
General procedure for the preparation of complexes 1–4
Ligand L (100 mg, 0.195 mmol) and an appropriate amount of M(ClO4)2·6H2O (0.186 mmol, 67 mg of Mn(ClO4)2·6H2O and Fe(ClO4)2·6H2O or 68 mg of Co(ClO4)2·6H2O and Ni(ClO4)2·6H2O) were dissolved in 4 mL of CH3OH and left to diethyl ether vapor diffusion at 5 °C. After several days, the well-shaped crystals of the complex formed, were isolated by filtration and re-dissolved in 1 mL of CH3NO2. The obtained solution was filtered via a Millipore syringe filter (0.45 μm). The diffusion of diethyl ether vapors into the filtrate at 5 °C resulted in the formation of well-shaped crystals, which were filtered off and dried in air at room temperature. These crystals were also suitable for X-ray diffraction analysis.Caution! Although we have experienced no difficulties, perchlorate salts of metal complexes with organic ligands are potentially explosive and should be handled with great care even in small quantities.
[MnL](ClO4)2·1.5CH3NO2 (1)
The product was isolated in the form of light yellow crystals (84 mg, 52.7%).
MS m/z (+): 565.11 ([Mn(L − H+)]+, calcd 565.20), 664.89 ([MnL + (ClO4)−]+, calcd 665.16).
MS m/z (−): 864.24 ([MnL + 3 × (ClO4)−]−, calcd 863.05), 1628.86 ([2 × (MnL) + 5 × (ClO4)−]−, calcd 1629.15).
Anal. calcd (%) for [MnL](ClO4)2·1.5CH3NO2 (C30.5H37.5Cl2MnN8.5O13, Mr = 857.02): C, 42.74; H, 4.41; N, 13.89. Found C, 43.12; H, 4.58; N, 13.80.
[FeL](ClO4)2·1.5CH3NO2 (2)
The product was isolated in the form of green-brown crystals (61 mg, yield 38.2%).
MS m/z (+): 566.09 ([Fe(L − H+)]+, calcd 566.20), 665.84 ([FeL + (ClO4)−]+, calcd 666.15).
MS m/z (−): 865.02 ([FeL + 3 × (ClO4)−]−, calcd 864.05), 1631.01 ([2 × (FeL) + 5 × (ClO4)−]−, calcd 1631.15).
Anal. calcd (%) for [FeL](ClO4)2·1.5CH3NO2 (C30.5H37.5Cl2FeN8.5O13, Mr = 857.92): C, 42.70; H, 4.41; N, 13.88. Found C, 42.22; H, 4.25; N, 13.40.
[CoL](ClO4)2·1.5CH3NO2 (3)
The product was isolated in the form of pink crystals (98 mg, yield 61.2%).
MS m/z (+): 569.12 ([Co(L − H+)]+, calcd 569.19), 668.83 ([CoL + (ClO4)−]+, calcd 669.15).
MS m/z (−): 869.27 ([CoL + 3 × (ClO4)−]−, calcd 869.05), 1637.11 ([2 × (CoL) + 5 × (ClO4)−]−, calcd 1637.15).
Anal. calcd (%) for [CoL](ClO4)2·1.5CH3NO2 (C30.5H37.5Cl2CoN8.5O13, Mr = 861.01): C, 42.55; H, 4.39; N, 13.83. Found C, 42.65; H, 4.32; N, 13.52.
[NiL](ClO4)2·1.5CH3NO2 (4)
The product was isolated in the form of green crystals (65 mg, yield 40.6%).
MS m/z (+): 568.17 ([Ni(L − H+)]+, calcd 568.20), 667.78 ([NiL + (ClO4)−]+, calcd 668.15).
MS m/z (−): 868.62 ([NiL + 3 × (ClO4)−]−, calcd 868.05), 1637.42 ([2 × (NiL) + 5 × (ClO4)−]−, calcd 1635.15).
Anal. calcd (%) for [NiL](ClO4)2·1.5CH3NO2 (C30.5H37.5Cl2N8.5NiO13, Mr = 860.77): C, 42.56; H, 4.39; N, 13.83. Found C, 42.30; H, 4.52; N, 13.72.
Theoretical methods
The ORCA 4.1 computational package was used for quantum chemical calculations.57,58 The calculations of ZFS parameters were done using state average complete active space self-consistent field (SA-CASSCF)59 wave functions complemented by the N-electron valence second-order perturbation theory (NEVPT2)60–62 using triple-ζ basis set def2-TZVP63 for all atoms. Using the state-averaged approach, all multiplets for a given electron configuration were equally weighted. The ZFS parameters, based on dominant spin–orbit coupling contributions from the excited states, were calculated through the quasi-degenerate perturbation theory (QDPT),64 in which an approximation to the Breit-Pauli form of the spin–orbit coupling operator (SOMF approximation)65 and the effective Hamiltonian theory66 were utilized. The calculations utilized the RIJCOSX approximation with the auxiliary basis sets def2/J67 and def2-TZVP/C.68 Increased integration grids (Grid5 and GridX5 in ORCA convention) and tight SCF convergence criteria were used in all calculations. Moreover, the recently introduced dynamic correlation dressed CAS with the second-order treatment (DCD-CAS(2)) was also utilized to calculate the ZFS parameters, where the spin–orbit and the spin–spin interactions were included.69 VESTA 3 program was used to visualize the results of the calculations.70Results and discussion
Syntheses and general characterizations
Ligand L was prepared by a common SN2 substitution reaction of parent macrocycle L1 and 2-chloromethylbenzimidazole in CH3CN with K2CO3 as a base. Synthesis of all studied complexes was simply based on mixing L with the perchlorate of the appropriate metal ion in CH3OH. The products in the crystalline form obtained after diethyl ether vapor diffusion at 5° C were sensitive to loose co-crystallized CH3OH solvent molecule(s) and therefore they were re-crystallized from CH3NO2. The obtained complexes with the co-crystallized CH3NO2 molecules were stable in air and were thoroughly characterized by elemental analysis, mass spectrometry (Fig. S1†) and IR spectroscopy. The measured IR spectra of studied complexes 1–4 are displayed in Fig. S2† and they are identical, which is in accordance with their similar composition and isostructurality (see later). The spectral pattern of all studied complexes 1–4 contains vibrations of the perchlorate anion at 1070 cm−1, stretching C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C
C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N aromatic vibrations at ∼1450 cm−1, vibrations of MeNO2 at 1550 cm−1, aliphatic CH stretching vibrations at 2880, 2920 and 3090 cm−1, and NH stretching vibrations at 3250 cm−1.
N aromatic vibrations at ∼1450 cm−1, vibrations of MeNO2 at 1550 cm−1, aliphatic CH stretching vibrations at 2880, 2920 and 3090 cm−1, and NH stretching vibrations at 3250 cm−1.
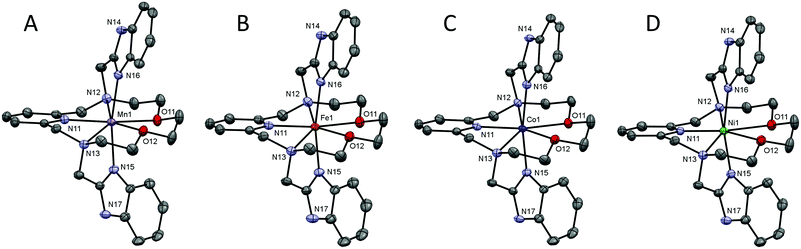
Crystal structure analysis
The molecular structures of the complex cations of all studied complexes 1–4 are shown in Fig. 2 and crystal data and structure refinements for studied complexes 1–4 can be found in Table S1 in the ESI.† All complexes 1–4 are isostructural, they all crystallized in the triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group and their molecular structures have a similar structural pattern. The macrocyclic part of the ligand is coordinated in the pentagonal equatorial plane, while the two benzimidazolyl pendant arms are coordinated in apical positions. Thus, all the central atoms are seven-coordinate with pentagonal bipyramidal geometry and a N5O2 donor atom set.
space group and their molecular structures have a similar structural pattern. The macrocyclic part of the ligand is coordinated in the pentagonal equatorial plane, while the two benzimidazolyl pendant arms are coordinated in apical positions. Thus, all the central atoms are seven-coordinate with pentagonal bipyramidal geometry and a N5O2 donor atom set.
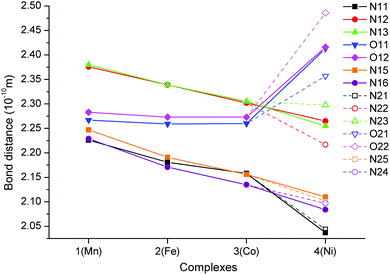
A comparison of the M-donor atom distances is shown in Fig. 3, listed in Table 1, and indicates several trends. The M–N(benzimidazole) distances are comparable to those of M–Npy and are much shorter than other bonds in the equatorial pentagonal plane, and thus, the pentagonal bipyramid can be considered as slightly axially compressed. Furthermore, in the order going from MnII to NiII complex 1 → 4 all M–N distances decrease, which is in agreement with the decreasing ionic radius of complexed metal ions. On the other hand, the M–O distances remain the same for 1–3 and significantly increase in the case of NiII complex 4 due to the Jahn–Teller effect,71 which is typical of structurally similar seven-coordinate pentagonal bipyramidal NiII complexes [NiL1Cl2],72 [NiL2](ClO4)2,12 [NiL3],38 [NiL6](ClO4)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 for which the Ni–O distances often exceed 2.5 Å. Thus, the pentagonal bipyramidal geometry of the NiII centre in 4 is the most distorted one (Ni–O is 2.413(2) and 2.416(2) Å) and this distortion for the second crystallographically independent molecules present in the asymmetric unit is even more pronounced (Ni–O is 2.357(2) and 2.486(2) Å, see Table 1 and Fig. 3 – empty symbols). This observation was confirmed by an analysis of the geometry of coordination polyhedra of all complexes 1–4 based on a comparison of continuous shape measures obtained by program Shape 2.1 (deviation between the real and ideal geometry of the polyhedron, Table S2†),73,74 because the lowest deviation values were obtained for the pentagonal bipyramidal arrangement.
35 for which the Ni–O distances often exceed 2.5 Å. Thus, the pentagonal bipyramidal geometry of the NiII centre in 4 is the most distorted one (Ni–O is 2.413(2) and 2.416(2) Å) and this distortion for the second crystallographically independent molecules present in the asymmetric unit is even more pronounced (Ni–O is 2.357(2) and 2.486(2) Å, see Table 1 and Fig. 3 – empty symbols). This observation was confirmed by an analysis of the geometry of coordination polyhedra of all complexes 1–4 based on a comparison of continuous shape measures obtained by program Shape 2.1 (deviation between the real and ideal geometry of the polyhedron, Table S2†),73,74 because the lowest deviation values were obtained for the pentagonal bipyramidal arrangement.
| Distances | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| a Values for one of the two crystallographically independent molecules present in the asymmetric unit of each complex are given. | ||||
| M–N11/21 | 2.230(3)/2.226(3) | 2.184(3)/2.181(3) | 2.166(2)/2.158(3) | 2.044(2)/2.037(2) |
| M–N12/22 | 2.381(3)/2.376(3) | 2.334(3)/2.339(3) | 2.300(2)/2.302(2) | 2.217(2)/2.265(2) |
| M–N13/23 | 2.378(3)/2.380(3) | 2.340(3)/2.339(3) | 2.304(2)/2.305(2) | 2.298(2)/2.255(2) |
| M–O11/21 | 2.278(2)/2.267(2) | 2.260(2)/2.259(2) | 2.264(2)/2.260(2) | 2.357(2)/2.413(2) |
| M–O12/22 | 2.281(2)/2.283(2) | 2.280(2)/2.273(2) | 2.281(2)/2.273(2) | 2.486(2)/2.416(2) |
| M–N16/24 | 2.241(3)/2.247(3) | 2.178(3)/2.191(3) | 2.147(2)/2.156(2) | 2.097(2)/2.110(2) |
| M–N15/25 | 2.251(3)/2.229(3) | 2.186(3)/2.171(3) | 2.145(2)/2.135(2) | 2.102(2)/2.084(2) |
| Anglesa | ||||
| N11–M–N12 | 71.54(9) | 71.95(9) | 72.09(9) | 76.10(8) |
| N12–M–O11 | 74.89(8) | 74.89(9) | 74.54(8) | 75.04(7) |
| O11–M–O12 | 72.00(8) | 70.69(8) | 70.74(7) | 66.44(6) |
| N13–M–O12 | 73.63(8) | 73.47(9) | 73.20(8) | 70.45(7) |
| N11–M–N13 | 70.99(9) | 71.54(9) | 71.75(9) | 74.08(8) |
| N11–M–N15 | 92.62(9) | 93.60(10) | 93.11(9) | 95.63(8) |
| N12–M–N15 | 104.57(9) | 104.88(9) | 103.06(9) | 103.57(8) |
| N13–M–N15 | 76.39(9) | 77.27(9) | 78.89(9) | 79.54(8) |
| O11–M–N15 | 84.43(9) | 84.78(9) | 84.66(9) | 82.46(8) |
| O12–M–N15 | 87.54(9) | 86.51(9) | 87.65(8) | 85.22(7) |
| N11–M–N16 | 97.83(9) | 97.76(9) | 97.07(9) | 99.13(8) |
| N12–M–N16 | 75.60(9) | 76.61(9) | 78.11(9) | 79.99(8) |
| N13–M–N16 | 110.42(9) | 108.59(9) | 106.42(9) | 104.64(8) |
| O11–M–N16 | 84.98(9) | 84.53(9) | 85.71(9) | 84.71(8) |
| O12–M–N16 | 86.19(9) | 85.69(9) | 85.42(8) | 82.98(7) |
| N15–M–N16 | 168.95(10) | 168.39(10) | 169.58(9) | 165.24(8) |
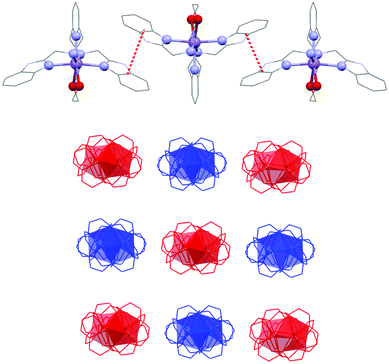
The final crystal packing of all studied complexes 1–4 is influenced by π–π stacking interactions between the benzimidazole units in the pendant arms (centroid⋯centroid distance Cg⋯Cg = 3.664/3.665/4.016/4.563 Å (1), 3.672/3.673/4.035/4.549 Å (2), 3.679/3.680/4.060/4.605 Å (3), and 3.668/3.678/4.057/4.620 Å (4)), which are responsible for the formation of supramolecular linear 1D chains along the c-axis (Fig. 4). Each supramolecular 1D chain contains only one enantiomeric form of the complex cation and these 1D chains regularly alternate in the final crystal packing as shown in Fig. 4. Furthermore, these 1D chains are connected to each other by a large number of hydrogen bonds (N–H⋯O–Cl, C–Haromatic⋯O–Cl, C–Haromatic⋯O–N) among the perchlorate counter-ions, complex cations and nitromethane solvent molecules.
Comparison of the obtained molecular structures with those of previously studied complexes containing L2 and L3
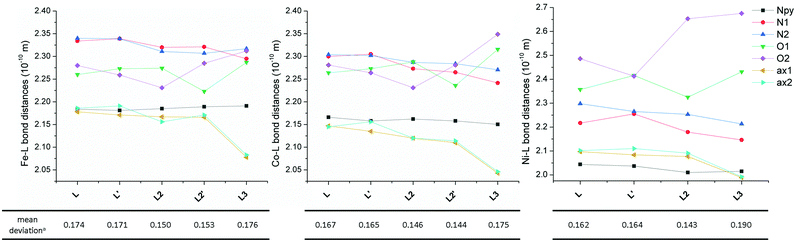
The molecular structure of metal complexes is crucial for understanding their magnetic anisotropy (see the next section Magnetic analysis) and therefore it is important to compare the obtained molecular structures of the FeII, CoII and NiII complexes containing L with those of previously studied complexes containing structurally similar ligands L2 and L3 (Fig. 5) in order to reveal any trends which could explain the observed magnetic properties.The Npy–M distance does not change much going from L to L3 for all three metals, but its value decreases from FeII to NiII according to the decreasing ionic radius. The N(1,2-aliphatic)–M distances almost always decrease for L → L3 (only the N2–M distance slightly increases in the case of the FeII complex when going from L2 to L3). On the other hand, the effect on the O–M distances is opposite. When going from L to L2, one distance decreases while the other increases for all metals (but the mean values for both crystallographically independent molecules slightly decrease), but both values increase when going from L2 to L3. The most significant increase is observed for the NiII complex due to the operating Jahn–Teller effect. The distances between the metal and axial donor atoms decrease when going from L to L3 for all three metals. This indicates, in comparison with L, stronger axial binding in the case of pyridine analogue L2 (both L and L2 are neutral) and a significant electrostatic contribution in the case of negatively charged carboxylate analogue L3.
Thus when going from L to L3 in all FeII, CoII and NiII complexes, the metal in the equatorial plane is shifted towards the N-donor containing part and moving away from the O-donor part of the macrocycle, and the axial donor atoms are getting closer to the metal atom. One has to also pursue the variation of the distances in the equatorial plane, because the observed axial compression of the pentagonal bipyramid (L → L3) resulted either in a more symmetric equatorial plane in the case of the FeII complex of L3 (the N–M and O–M distances are close to each other) or in a more asymmetric equatorial plane in the case of CoII and especially the NiII complex of L3 (the N–M and O–M distances are very different). From Fig. 5, it is also evident that the M–O distances in comparison with M–N(aliphatic) are shorter in the case of FeII complexes, are comparable in the case of CoII complexes and longer in the case of NiII complexes, which is in accordance with the oxophilic character of FeII and N-donors preference for NiII.
Moreover, an additional interesting parameter is the planarity of the equatorial plane, which can be described by the mean deviation of equatorial donor atoms (N3O2) from the least-squares plane defined by the central metal atom and all equatorial donor atoms (MN3O2). The complexes with the most planar equatorial plane form pyridine ligand L2 followed by benzimidazole ligand L and carboxylate ligand L3 (Fig. 5). In the case of complexes with L and L2, the planarity increases from FeII to NiII (the mean deviation decreases), while in the case of complexes with L3, the lowest planarity (the highest mean deviation) is observed for the NiII complex. But in general, it can be concluded that the equatorial planarity of all complexes (similar structural types) is comparable.
Magnetic analysis
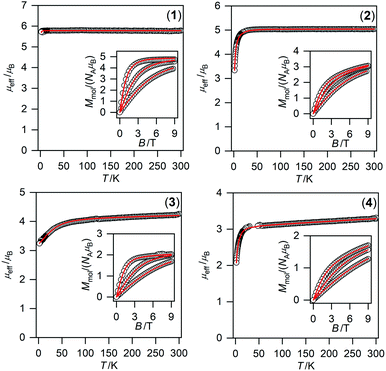 | ||
| Fig. 6 Magnetic data for compounds 1–4. Temperature dependence of the effective magnetic moment and the isothermal magnetizations measured at T = 2, 5, and 10 K. The empty circles represent the experimental data points and the full lines represent the best fits calculated by using eqn (1) with parameters listed in Table 2. | ||
Thus, the experimental magnetic data were treated with the spin Hamiltonian comprising ZFS terms describing the magnetic anisotropy and Zeeman term postulated as
| Ĥ = D(Ŝz2 − Ŝ2/3) + E(Ŝx2 − Ŝy2) + μBBgŜa | (1) |
To obtain reliable parameters, both temperature and field-dependent magnetic experimental data were fitted concurrently. The best-fitted parameters are listed in Table 2.76 The large and negative D-value was found for NiII compound 4 (−17.2 cm−1) whereas the large and positive D-values were found for CoII and FeII compounds 3 (40.3 cm−1) and 2 (7.9 cm−1), respectively. This is in accordance with the different low temperature values of μeff/μB observed for 2–4 (Fig. 6).
| Compound | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| a The theoretical calculations were done for both crystallographically independent molecules present in the asymmetric unit. b The detailed procedure for the calculation of standard deviations is described in ref. 76. | ||||
| Central metal atom | Mn(II) | Fe(II) | Co(II) | Ni(II) |
| Electron configuration | 3d5 | 3d6 | 3d7 | 3d8 |
| Spin state S | 5/2 | 2 | 3/2 | 1 |
| ZFS and g values based on CASSCF/NEVPT2 calculations | ||||
| D (cm−1) | –0.071/–0.076 | 7.41/7.55 | 34.4/34.0 | –23.8/–25.6 |
| E/D | 0.101/0.087 | 0.200/0.183 | 0.082/0.085 | 0.067/0.043 |
| g x | 2.000/2.000 | 2.079/2.081 | 2.320/2.312 | 2.251/2.245 |
| g y | 2.000/2.000 | 2.172/2.175 | 2.383/2.378 | 2.233/2.234 |
| g z | 2.000/2.000 | 2.017/2.016 | 2.042/2.041 | 2.404/2.414 |
| ZFS values based on CASSCF/DCD-CAS(2) calculations | ||||
| D (cm−1) | –0.114/–0.122 | 7.67/7.80 | 38.4/37.9 | –23.6/–25.5 |
| E/D | 0.069/0.070 | 0.145/0.122 | 0.067/0.074 | 0.062/0.040 |
| Magnetic analysis of the experimental datab | ||||
| D (cm−1) | –0.30(3) | 7.90(6) | 40.3(1.5) | –17.2(2) |
| E/D | 0.0 | 0.220(4) | 0.10(3) | 0.076(1) |
| g | 1.9538(9) | 2.057(1) | g xy = 2.156(6) gz = 2.00 | 2.165(3) |
| χ TIP (10−9 m3 mol−1) | 0.0 | 0.0 | 5.3(5) | 7.5(2) |
| Data for complexes with L212 | ||||
| D (cm−1) | 0 | –7.4 | 34.0 | –12.8 |
| E/D | 0.0 | 0.0 | 0.136 | |
| Data for complexes with L338 | ||||
| D (cm−1) | — | –9.6 | 29.1 | –8.5 |
| E/D | 0.006 | 0 | 0.19 | |
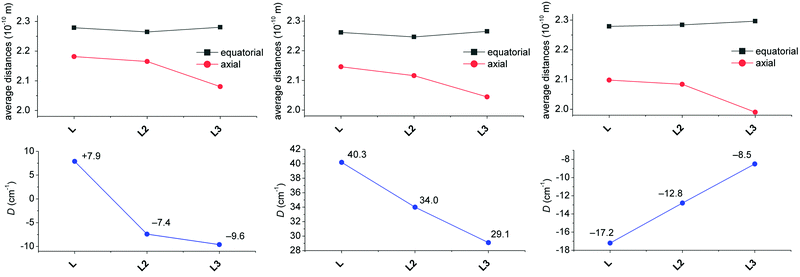
When the obtained D-values are compared with those of previously studied complexes with L2 and L3 (Table 2),12,38 they are very similar for MnII and FeII complexes 1 and 2, but they are much higher for CoII and NiII complexes 3 and 4 revealing their larger magnetic anisotropy. The sign of the D-value for 2 is positive and thus different from previously studied FeII complexes with L2 and L3 (Table 2), but it is in accordance with the CASSCF/NEVPT2 calculations for 2 (Table 2) and also with the previously performed calculations (see Fig. 10 in ref. 38). These calculations showed that the strong axial ligand field in the seven-coordinate FeII complex can provide small positive D-values while when this ligand field is reduced, D becomes larger and negative. Moreover, HF-EPR measurements (Fig. S5†) confirmed the positive sign of D. The data for 180 GHz, 321 GHz and 415 GHz at 4 K were successfully simulated for the spin S = 2 with D = +8.2 cm−1 and E/D = 0.29 and the g values from Table 2. The EPR signal vanishes at 15 K, in agreement with the simulated data, which indicates a significant decrease in the absorption intensity with increasing temperature. Both complexes 3 and 4 show the highest magnetic anisotropies among those reported for the pentagonal bipyramidal CoII (Table 3) or NiII complexes (Table 2). If the calculations previously reported by Sutter and Mallah are considered,17 the stronger axial ligand field should provide larger magnetic anisotropy in the case of NiII complexes, while an opposite effect on the magnetic anisotropy is expected for the CoII complexes. A similar trend as for the NiII complexes was recently observed for the FeII complexes,11 but the description/explanation was more complex concerning the contribution(s) to the D value from different excited states and also differential π-interactions of the FeII–axial ligands between the x and y directions. Thus, according to the large magnetic anisotropy of CoII complex 3, the axial field should be weaker, but on the other hand according to the large magnetic anisotropy of NiII complex 4 and the positive sign of D for FeII complex 3, the axial field should be stronger. So, not only the axial, but also the equatorial effect (a more symmetric field provides larger anisotropy) should be taken into account, which makes the elucidation of any trend for the complexes of N-pendant armed macrocycles not as straightforward as expected. We tried to establish such a magneto-structural correlation as shown in Fig. 7, where the average equatorial and the axial metal to the donor atom distances together with the values of the D-parameter are shown for each metal ion as a function of coordinated ligands (L, L2 and L3). The D value is becoming more positive for both FeII and CoII complexes, while D is becoming more negative for the NiII complexes considering the change of ligands, L3 → L (Fig. 7).
| Complex | ZFS | Orbach | Direct | Raman | Ref. | |||
|---|---|---|---|---|---|---|---|---|
| D/cm−1 | E/D | τ0/10−9 s | U eff/cm−1 (K) | A/K−1 s−1 | C/K−n s−1 | n | ||
| a im = imidazole, tbp = 4-tert-butylpyridne, isq = isoquinoline. b Calculated by a simplified model described in the corresponding literature. c Values correspond to 2πf/C (where f is the AC frequency). d In the unit Oe−2 K−1 s−1. e Fixed during the fitting procedure. | ||||||||
| [Co(H2L4-Ph)(H2O)(NO3)]NO3 | 32.4 | 0 | 0.6 | 56.3 (81.2) | 17,18 | |||
| [Co(15-pydienN5)(H2O)2]Cl2 | 24.6 | −0.014 | 1200 | 20.7 (29.8) | 18 | |||
| [Co(L4-Ph)(im)2]a | 24.8 | 0.0016 | 0.087 | 62.3 (89.6) | 18 | |||
| [Co(tbp)3(NO3)2]a | 35.8 | 0.006 | 768 | 17.7 (25.5) | 78 | |||
| [Co(isq)3(NO3)2]a | 35.7 | 0.0006 | 701 | 11.0 (15.8) | 78 | |||
| [Co(L5)(H2O)2](BF4)2 | 25.6 | −0.039 | 1100 | 42.2 (29.3) | 19 | |||
| [Co(L5)(CN)2]·2H2O | 17.4 | −0.034 | 3200 | 48.9 (34.0) | 19 | |||
| [Co(L5)(NCS)2] | 26.3 | −0.004 | 1000 | 49.2 (34.2) | 19 | |||
| [Co(L5)(SPh)2] | 34.5 | −0.052 | 2100 | 54.7 (38.0) | 19 | |||
| [Co(L1)Cl2]·2CH3OH | 38(3) | 0 | —b | 5.5–7.8 (7.9–11.2)b | 0.99–1.62b,c | 1.76–2.59b | 21 | |
| [Co(L1)Br2] | 41(1) | 0 | 1120 | 4.2 (6.1) | 613 | 2.79 | 21 | |
| [Co(L1)I2] | 35(1) | 0 | 1120 | 4.5 (6.5) | 500 | 2.82 | 21 | |
| [Co(L2)](ClO4)2 | 34 | 0 | 990 | 16.9 (24.3) | 47.3 | 2.84 | 12 | |
| [Co(L3)]·H2O | 29.0 | 0 | — | — | 96.9 | 0.535 | 5.49 | 38 |
| [Co(15-pydienN3O2)(CH3CN)2](BPh4)2 | 36.9 | 0.005 | 0.034(2) | 62 (89) | 131(9) | 2.1(1) | 79 | |
| [Co(L4-PhOH)(CH3OH)2] | 43.1 | 0.077 | 7400 | 23.3 (33.5) | 4.7 | 22 | ||
| [Co(H2L4-PhOH)(NCS)(CH3OH)]ClO4·CH3OH | 41.5 | 0.036 | 5600 | 19.7 (28.4) | 4.2 | 22 | ||
| [Co(H2L4-PhOH)(NCS)2]·2CH3OH | 38.8 | 0.54 | 4800 | 16.4 (23.6) | 3.7 | 22 | ||
| [Co(H2L4-NH2)(NCS)2]·0.5C2H5OH | 35.6 | 0.17 | — | — | 1.03 × 10−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
0.00106 | 9e | 33 |
| [Co(H2L4-NH2)(NCSe)2]·0.5C2H5OH | 38.2 | 0 | — | — | 4.10 × 10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
0.02 | 7.4 | 33 |
| [Co(H2L4-NH2){N(CN)2}2]·2H2O | 35.3 | 0.101 | — | — | 1.29 × 10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
0.017 | 7.3 | 33 |
| [Co(H2L4-NH2)(H2O){C(CN)3}]NO3·1.16H2O | 33.6 | 0.149 | — | — | 7.7 × 10−5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
0.4 | 5.6 | 33 |
| {[Co(H2L4-NH2)(H2O)(N3)][Co(H2L4-NH2)(N3)2]}N3·4H2O | 40.4 | 0 | — | — | 2.9 × 10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
0.26 | 5.8 | 33 |
| [Co(L)](ClO4)2·1.5CH3NO2 | 40.3 | 0.1 | 6040 | 6.0 (8.7) | 507 | 2.58 | This work | |
If we consider that the increasing average distance of axial donor atoms (L3 → L) can be interpreted in terms of a weaker axial ligand field (although benzimidazole is a stronger σ-donor than pyridine, it is also a weaker π-acceptor),40 the increasing magnetic anisotropy of the CoII complexes is in agreement with the theoretically predicted trend. This is in contrast to the behavior of the NiII complexes, where the magnetic anisotropy increased twice (L3 → L), which can be rather explained by the more symmetric equatorial ligand field (Fig. 5, right) and this can be quantified by deviations from the PBPY-7 ideal symmetry obtained by the program SHAPE (1.112 and 1.201 for L, Table S2,† 1.237 for L2,12 and 2.988 for L3).38 As the change in the equatorial ligand field has a more dramatic impact on the value of D than on the variation of the axial ligand field in the NiII complexes (see Fig. 12 later in the section, Theoretical calculations), the increase of negative D for the NiII complexes (L3 → L) is more likely governed by the decreasing deviation from the ideal D5h symmetry. The absolute values of D and |D| for the FeII complexes are almost the same, which is in agreement with our theoretical simulations (vide infra) showing a small impact of the ligand field change on the size of the magnetic anisotropy. Moreover, the variation of ZFS parameters for the FeII complexes must be considered with great care, because usually the low lying excited states reduce the validation of the spin Hamiltonian approach.
In conclusion, both axial and equatorial ligand fields have to be considered when analyzing the magnetic anisotropy, because the change in each field has a differently strong and sometimes opposite impact on the resulting anisotropy. Moreover these effects have different extents for different central metal ions and thus, general analysis for more metals appears to be intricate.
Dynamic magnetic measurements
The alternating current (AC) susceptibly measurement was performed for 2–4, however, the non-zero out-of-phase signal was found only for CoII compound 3 upon applying a weak static magnetic field (Fig. S6†). Therefore, temperature and frequency dependent AC susceptibility data were acquired at BDC = 0.1 T (Fig. 8) and clearly defined maxima of the out-of-phase signal of AC susceptibility dependent on the applied frequency were found for compound 3, which is the characteristic behavior of SMMs. Next, the one-component Debye's model was applied based on the equation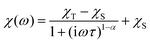 | (2) |
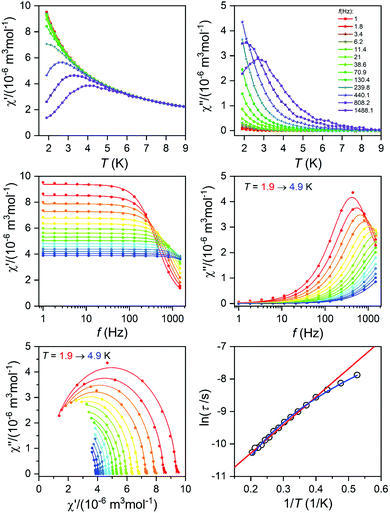 | ||
| Fig. 8 AC susceptibility data of 3. Top: in-phase χ′ and out-of-phase χ′′ molar susceptibilities at the applied external magnetic field BDC = 0.1 T (the full lines are only guides for the eye). Middle: frequency dependence of in-phase χ′ and out-of-phase χ′′ molar susceptibilities. The full lines represent the fitted data using eqn (2). Bottom: the Argand (Cole–Cole) plot with a full line fitted with eqn (2) and the fit of the resulting relaxation times τ with the Arrhenius law (red line) and Raman relaxation process (blue line). | ||
which resulted in isothermal (χT) and adiabatic (χS) susceptibilities, relaxation times (τ) and distribution parameters (α) (Table S3†). Afterwards, the Argand (Cole–Cole) plot was constructed as shown in Fig. 8. The application of the Arrhenius law to the temperature dependence of the relaxation times revealed τ0 = 6.04 × 10−6 s and Ueff = 6.0 cm−1 (8.7 K). Such a physically unreasonable value of Ueff can be ascribed to the fact that the D-parameter is positive and E/D is very small, hence, the easy-plane type of magnetic anisotropy is operational, which means that there is no energy barrier U defined by |D|(S2 − ¼). The origin of the slow relaxation of magnetization in Kramers ions (such as CoII) with dominant easy-plane magnetic anisotropy was investigated in detail by E. Ruiz, F. Luis et al.,77 and such spin–lattice relaxation was rather described by one-phonon direct processes and two-phonon Raman processes. Therefore, the temperature dependence of the relaxation times was successfully fitted considering the Raman relaxation mechanism described by the following equation
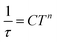 | (3) |
The obtained values of τ0 and Ueff for the Orbach relaxation process or C and n for the Raman relaxation process are compared with those of previously studied pentagonal bipyramidal CoII SMMs in Table 3. The Ueff values are comparable with those of the CoII complexes with structurally similar ligands L1, L2, and L3, but are smaller in comparison with those of other ligands having a more rigid macrocyclic part (15-pydienN3O2, L4-Ph, L5). This “equatorial rigidity” effect appears to have a more significant influence on the relaxation times than on the magnetic anisotropy represented by the D-value. Thus, there is no clear relationship between the magnetic anisotropy (D) and the values of relaxation times, which can be attributed to the fact that the Orbach relaxation mechanism is not active for such easy-plane systems and the direct and Raman relaxation processes should stand at the centre of our focus. Therefore, in order to increase the relaxation time, the C and n parameters of the Raman relaxation process should be decreased. However, the lack of these parameters from the literature means that further investigation of CoII complexes has to be done to better understand the relationship between the molecular structure and relaxation properties.
Electrochemistry
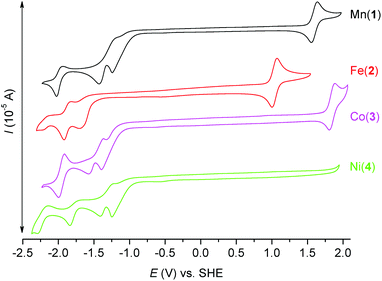
In order to investigate the electrochemical properties of prepared complexes 1–4, the measurement of cyclic voltammetry was performed in acetonitrile solution. The obtained cyclic voltammograms are depicted in Fig. 9 and the redox potentials are listed in Table 4. All E1/2 potentials for the Mn3+/2+, Fe3+/2+ and Co3+/2+ couples are very high (1.596, 1.043 and 1.853 V, respectively), which indicates that the lower oxidation states (Mn2+/Fe2+/Co2+) are stabilized due to the π-acceptor ability of axially coordinated two benzimidazolyl pendant arms. Moreover, the Ni3+/2+ redox couple is not even visible in the range of available potentials during the measurement. Thus, the oxidation state +III of the NiII complexes is not accessible, which is in accordance with the π-acceptor properties of benzimidazole functional groups. On the other hand, lower oxidation states Mn+/Fe+/Co+/Ni+ are accessible in quasi-reversible/quasi-reversible/reversible/quasi-reversible processes at relatively high negative potentials (see Table 4). Furthermore, irreversible reduction peaks at ca. −1.25 and −1.40 V were detected and they correspond to the reduction of the CH3NO2 co-crystallized solvent molecule as was confirmed by the measurement of MeCN solution with an extra addition of CH3NO2 (Fig. S7†).| Compound | Redox process | E 1/2 [V] vs. Fc/Fc+ | E 1/2 [V] vs. SHE | ΔE [mV] |
|---|---|---|---|---|
| 1 | Mn3+/Mn2+ | 0.972 | 1.596 | 84 |
| Mn2+/Mn+ | −2.604 | −1.980 | 91 | |
| 2 | Fe3+/Fe2+ | 0.419 | 1.043 | 70 |
| Fe2+/Fe+ | −2.496 | −1.872 | 93 | |
| 3 | Co3+/Co2+ | 1.229 | 1.853 | 76 |
| Co2+/Co+ | −2.584 | −1.960 | 80 | |
| 4 | Ni2+/Ni+ | −2.375 | −1.751 | 140 |
The cyclic voltammogram of the ligand L was measured as well and it shows one irreversible oxidation peak at Eox = 1.450 V (Fig. S8†), which may be assigned to the oxidation of both benzimidazolyl pendant arms, and one irreversible reduction peak at Ered = −2.063 V.
When the obtained results are compared with those of the complexes containing structurally similar pyridine analogue L2, several aspects can be found. The E1/2 potentials for the Mn3+/2+ and Fe3+/2+ couples are slightly lower than those found for the complexes with L2 (E1/2(Mn) = 1.624 V, E1/2(Fe) = 1.132 V vs. SHE, see Fig. S9 and S10†), but the E1/2 potential for the Co3+/2+ couple is slightly higher than that for the complex with L2 (E1/2(Co) = 1.744 V vs. SHE, see Fig. S11†).80 Therefore the oxidation states Mn2+ and Fe2+ are more stabilized in the complexes with L2, while the oxidation state Co2+ is more stabilized in the complex with L. On the other hand, lower oxidation states Mn+/Fe+/Co+ are easily accessible in the complexes with L2 because complexes 2–4 with L have more negative reduction potentials (see Fig. S9–S11†). This is in accordance with the weaker π-acceptor ability of the benzimidazole moiety in comparison with the pyridine one. In conclusion the electrochemical behavior of the complexes with L and L2 is rather similar, but in the case of the complexes with L the lower oxidation states are less accessible and thus, the oxidation state +II is more stabilized.
Theoretical calculations
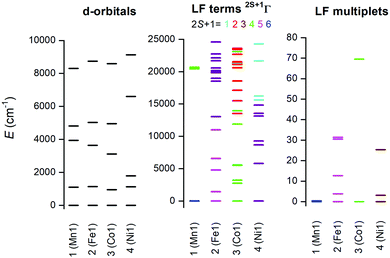
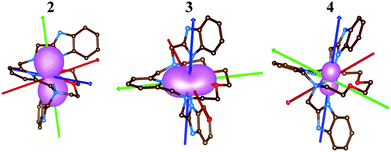
The electronic structure of the reported complexes was also studied by theoretical methods using computational package ORCA 4.1. First, the post-Hartree–Fock multireference calculations based on the state-averaged complete active space self-consistent field method (SA-CASSCF) were employed together with the def2-TZVP basis set to reveal the impact of the spin–orbit coupling and ligand field on the spin Hamiltonian parameters, especially on the zero-field splitting parameters D and E. The active space was defined by n-electrons in five d-orbitals, CAS(n,5), and we have used two methods to cover the dynamic electron correlation effect, namely, the well-known N-electron valence state perturbation theory (NEVPT) and also the recently introduced dynamic correlation dressed CAS with the second-order treatment (DCD-CAS(2)). The ab initio ligand field theory (AILFT)81,82 was used to calculate the energy of the d-orbitals as depicted in Fig. 10. The ideal D5h ligand field symmetry leads to splitting of the d-orbitals into three sets, e1′′ (dxz, dyz), e2′ (dxy, dx2−y2) and a1′ (dz2), and such a pattern is visible in the case of 1, but even in this complex, the degeneracy of the d-orbitals is removed due to the non-homogenous ligand field. Evidently, the pattern of the splitting of the d-orbitals is continuously changing from 1 to 4 and is interconnected with the weakening of M–O donor–acceptor bonds.Subsequently, the ligand-field terms are shown in Fig. 10 and it is evident that except for 1, there are close lying terms with the same or lower multiplicities which do contribute to the zero-field splitting of the ground spin state multiplet (Fig. 10, right). The calculated ZFS and g-tensor parameters are summarized in Table 2, where calculations for both metal complexes within asymmetric units were done. The reported values are in very good agreement with the fitted ones, especially for compounds 2 and 3, e.g. D = 38.4/37.9 cm−1 for 3 derived by DCD-CAS(2) and the fitted value of D is 40.2 cm−1. The main axes of the calculated D-tensors for the complexes with large magnetic anisotropy, 2–4, are shown in Fig. 11 together with a three-dimensional plot of the calculated molar magnetization. Evidently, the easy-plane type of the magnetic anisotropy is present in the CoII complex and coincides with the equatorial pentagonal plane, while the easy-axis type is found in both FeII and NiII complexes. In the case of NiII, this behavior is natural due to the negative value of the D-parameter, however, in the case of FeII, the D-parameter is positive but due to large rhombicity, the easy-axis type of the magnetic anisotropy is operational.
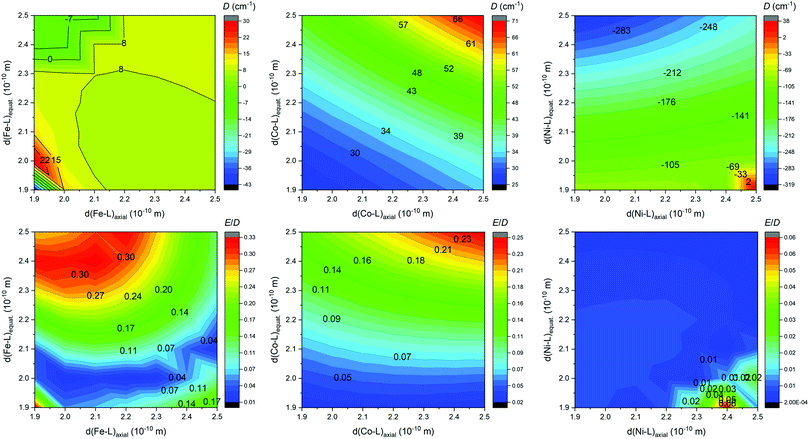
With the aim to get more insight into the role of the equatorial and the axial ligand field strength in the zero-field splitting of such pentagonal bipyramidal complexes of late transition metal complexes, we performed the CASSCF/DCD-CAS(2) calculations for model complexes [M(NH3)2(NCH)3(H2O)2]2+ (M = FeII, CoII and NiII) – Fig. 12. Both the in-plane and the axial metal-donor interatomic distances were varied in the range from 1.9 to 2.5 Å, which enabled the creation of the contour plots of the axial and rhombic ZFS parameters – Fig. 13.
Evidently, there is a small impact on the ZFS parameters in the FeII complexes, and a relatively small and positive D prevails, but the axial type of the magnetic anisotropy in the model complex can be achieved by increasing the rhombicity (E/D → 1/3) by weakening the ligand field in the equatorial plane and strengthening the ligand field in the axial positions. In the case of CoII complexes, D is definitively positive and large, and its value can be increased by weakening the ligand field in both axial and equatorial directions, which also leads to the escalation of E. The model of the NiII complex provided a very large and negative D value almost in the whole simulation range, which in general makes such complexes good candidates for observing the axial type of the magnetic anisotropy, also taking into the account very small rhombicity. The equatorial ligands show indisputably a larger impact on the value of D, thus weakening of the equatorial ligand field would increase |D| substantially. To summarize, the careful and rational design of macrocyclic ligands and axial pendant arms is crucial to prepare magnetically interesting complex compounds, however, the design of rigid ligands may be necessary to suppress the deformation of the ideal D5h symmetry induced by the Jahn–Teller effect.
Conclusions
A structurally new macrocyclic ligand with two 2-benzimidazolyl pendant arms (L) has been synthesized and it provided axially compressed pentagonal bipyramidal MnII, FeII, CoII and NiII complexes with the largest distortion observed for NiII complex 4 due to the Jahn–Teller effect. The large magnetic anisotropy was confirmed for FeII, CoII and NiII complexes 2–4 and CoII complex 3 behaved as a field-induced SMM with a preferential Raman mechanism of relaxation of magnetization. The obtained results were supported by theoretical CASSCF calculations, which very well correspond to the obtained values of magnetic anisotropy. The CASSCF/CAS-DCD(2) based theoretical simulations provided detailed information about the effect of the equatorial and axial ligand field on the magnetic anisotropy in this class of seven-coordinate FeII, CoII and NiII complexes. Furthermore, they provide important information on how to tune/increase the magnetic anisotropy in the future: (i) for the CoII complexes the equatorial and axial ligand field should be decreased and the effect of changing each of them is rather equal, (ii) for the NiII complexes the equatorial field should be decreased while the axial field should be increased, but the effect of the equatorial one is much more pronounced, (iii) for the FeII complexes, the changes in both ligand fields alter |D| to a lesser extent, but a large variation in the rhombicity E/D is observed. In this respect, a more rigid macrocycle containing five nitrogen donor atoms could be a reasonable proposition to fulfill the above-mentioned requirements for magnetic anisotropy enhancement. Furthermore, the deprotonization of L is even possible, so this could be another way to additionally increase the axial ligand field and enhance the magnetic anisotropy at least for NiII complexes, and to utilize these complexes as building blocks for the synthesis of more complex polymeric coordination compounds.According to the electrochemical measurements, ligand L stabilizes the oxidation state +II in contrast to +I or +III due to its weaker π-acceptor ability in comparison with its pyridine-analogue L2. The trend in redox potentials for the M3+/2+ couples (M = Mn, Fe, Co and Ni) in the complexes of L and L2 was found to be E1/2([ML2]3+/2+) > E1/2([ML]3+/2+ for M = Mn and Fe, while it is opposite for E1/2([CoL2]3+/2+) < E1/2([CoL]3+/2+ and could be related to the different stabilization of the high spin MnIII/FeIII and low spin CoIII complexes and the stronger σ-donor/weaker π-acceptor ability of the benzimidazole group.
In conclusion, modification of the macrocycle with two benzimidazolyl moieties has a beneficial effect on the magnetic anisotropy of especially CoII and NiII complexes and also alters the redox properties of the prepared complexes. But altogether it can be concluded that the tuning of magnetic anisotropy in seven-coordinate pentagonal bipyramidal late-first-row transition metal complexes with macrocyclic ligands modified by pendant arms is a rather complex problem. More factors including not only the strength of the axial ligand field, but also mainly the strength and symmetry of the equatorial ligand field have to be considered with great care during the rational design of new suitable ligands.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors gratefully acknowledge the Ministry of Education, Youth, and Sports of the Czech Republic - National Program of Sustainability (NPU LO1305) and the Czech Science Foundation (GAČR 17-08992S) for the financial support. The authors also acknowledge funding from the ERC under the European Union's Horizon 2020 research and innovation program (GA No. 714850). This work was also supported by the ESF under the project CZ.02.2.69/0.0/0.0/18_070/0009469. The authors also thank Prof. Z. Trávníček for initial preliminary X-ray diffraction data collection, Dr A. Klanicová for recording IR spectra and Mrs P. Richterová for performing elemental analysis.References
- E. L. Gavey and M. Pilkington, Coord. Chem. Rev., 2015, 296, 125–152 CrossRef CAS.
- J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 5441–5450 CrossRef CAS PubMed.
- Y.-S. Ding, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, Angew. Chem., Int. Ed., 2016, 55, 16071–16074 CrossRef CAS PubMed.
- Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 2829–2837 CrossRef CAS PubMed.
- Z. Zhu, M. Guo, X.-L. Li and J. Tang, Coord. Chem. Rev., 2019, 378, 350–364 CrossRef CAS.
- A. K. Bar, P. Kalita, J. P. Sutter and V. Chandrasekhar, Inorg. Chem., 2018, 57, 2398–2401 CrossRef CAS PubMed.
- A. K. Bar, C. Pichon and J.-P. Sutter, Coord. Chem. Rev., 2016, 308, 346–380 CrossRef CAS.
- J. Ferrando-Soria, J. Vallejo, M. Castellano, J. Martínez-Lillo, E. Pardo, J. Cano, I. Castro, F. Lloret, R. Ruiz-García and M. Julve, Coord. Chem. Rev., 2017, 339, 17–103 CrossRef CAS.
- M. Feng and M. L. Tong, Chem. – Eur. J., 2018, 24, 1–22 CrossRef.
- A. K. Bar, C. Pichon, N. Gogoi, C. Duhayon, S. Ramasesha and J.-P. Sutter, Chem. Commun., 2015, 51, 3616–3619 RSC.
- A. K. Bar, N. Gogoi, C. Pichon, V. M. L. Durga Prasad Goli, M. Thlijeni, C. Duhayon, N. Suaud, N. Guihéry, A.-L. Barra, S. Ramasesha and J.-P. Sutter, Chem. – Eur. J., 2017, 23, 4380–4396 CrossRef CAS PubMed.
- P. Antal, B. Drahoš, R. Herchel and Z. Trávníček, Inorg. Chem., 2016, 55, 5957–5972 CrossRef CAS PubMed.
- D. Shao, S. L. Zhang, X. H. Zhao and X. Y. Wang, Chem. Commun., 2015, 51, 4360–4363 RSC.
- D. Shao, X.-H. Zhao, S.-L. Zhang, D.-Q. Wu, X.-Q. Wei and X.-Y. Wang, Inorg. Chem. Front., 2015, 2, 846–853 RSC.
- B. Drahoš, R. Herchel and Z. Trávníček, Inorg. Chem., 2018, 57, 12718–12726 CrossRef PubMed.
- C. Pichon, N. Suaud, C. Duhayon, N. Guihery and J. P. Sutter, J. Am. Chem. Soc., 2018, 140, 7698–7704 CrossRef CAS PubMed.
- R. Ruamps, L. J. Batchelor, R. Maurice, N. Gogoi, P. Jiménez-Lozano, N. Guihéry, C. de Graaf, A.-L. Barra, J.-P. Sutter and T. Mallah, Chem. – Eur. J., 2013, 19, 950–956 CrossRef CAS PubMed.
- X.-C. Huang, C. Zhou, D. Shao and X.-Y. Wang, Inorg. Chem., 2014, 53, 12671–12673 CrossRef CAS.
- D. Shao, S. L. Zhang, L. Shi, Y. Q. Zhang and X. Y. Wang, Inorg. Chem., 2016, 55, 10859–10869 CrossRef CAS PubMed.
- D. Shao, L. Shi, S.-L. Zhang, X.-H. Zhao, D.-Q. Wu, X.-Q. Wei and X.-Y. Wang, CrystEngComm, 2016, 18, 4150–4157 RSC.
- B. Drahoš, R. Herchel and Z. Trávníček, Inorg. Chem., 2017, 56, 5076–5088 CrossRef PubMed.
- A. K. Mondal, A. Mondal, B. Dey and S. Konar, Inorg. Chem., 2018, 57, 9999–10008 CrossRef CAS PubMed.
- N. Gogoi, M. Thlijeni, C. Duhayon and J.-P. Sutter, Inorg. Chem., 2013, 52, 2283–2285 CrossRef CAS PubMed.
- V. S. Mironov, T. A. Bazhenova, Y. V. Manakin, K. A. Lyssenko, A. D. Talantsev and E. B. Yagubskii, Dalton Trans., 2017, 46, 14083–14087 RSC.
- Y. V. Manakin, V. S. Mironov, T. A. Bazhenova, K. A. Lyssenko, I. F. Gilmutdinov, K. S. Bikbaev, A. A. Masitov and E. B. Yagubskii, Chem. Commun., 2018, 54, 10084–10087 RSC.
- R. Boča, Zero-field splitting in metal complexes, Coord. Chem. Rev., 2004, 248, 757–815 CrossRef.
- D. Gatteshi, R. Sessoli and J. Villain, Molecular Nanomegnets, Oxford University Press, New York, 2006 Search PubMed.
- Molecular Nanomagnets and Related Phenomena, in Structure and Bonding, ed. S. Gao, Springer, Berlin, 2015, vol. 164 Search PubMed.
- J. S. Miller and D. Gatteschi, Molecule-based magnets themed issue No. 6, Chem. Soc. Rev., 2011, 40, 3065–3365 RSC.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–441 CrossRef CAS PubMed.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403 CrossRef CAS PubMed.
- M. Atanasov, D. Aravena, E. Suturina, E. Bill, D. Maganas and F. Neese, Coord. Chem. Rev., 2015, 289–290, 177–214 CrossRef CAS.
- V. A. Kopotkov, D. V. Korchagin, V. D. Sasnovskaya, I. F. Gilmutdinov and E. B. Yagubskii, Magnetochemistry, 2019, 5, 58 CrossRef.
- B. Drahoš, R. Herchel and Z. Trávníček, RSC Adv., 2016, 6, 34674–34684 RSC.
- C. Platas-Iglesias, L. Vaiana, D. Esteban-Gómez, F. Avecilla, J. A. Real, A. de Blas and T. Rodríguez-Blas, Inorg. Chem., 2005, 44, 9704–9713 CrossRef CAS PubMed.
- L. Vaiana, M. Regueiro-Figueroa, M. Mato-Iglesias, C. Platas-Iglesias, D. Esteban-Gómez, A. de Blas and T. Rodríguez-Blas, Inorg. Chem., 2007, 46, 8271–8282 CrossRef CAS PubMed.
- P. Antal, B. Drahoš, R. Herchel and Z. Trávníček, Dalton Trans., 2016, 45, 15114–15121 RSC.
- P. Antal, B. Drahoš, R. Herchel and Z. Trávníček, Eur. J. Inorg. Chem., 2018, 2018, 4286–4297 CrossRef CAS.
- I. Nemec, R. Herchel, I. Svoboda, R. Boca and Z. Travnicek, Dalton Trans., 2015, 44, 9551–9560 RSC.
- X. Xiaoming, M.-a. Haga, T. Matsumura-Inoue, Y. Ru, A. W. Addison and K. Kano, J. Chem. Soc., Dalton Trans., 1993, 16, 2477–2484 RSC.
- M. Boča, R. F. Jameson and W. Linert, Coord. Chem. Rev., 2011, 255, 290–317 CrossRef.
- Q.-X. Li, Q.-H. Luo, Y.-Z. Li, C.-Y. Duan and Q.-Y. Tu, Inorg. Chim. Acta, 2005, 358, 504–512 CrossRef CAS.
- A. Rodríguez-Rodríguez, I. Carreira-Barral, D. Esteban-Gómez, C. Platas-Iglesias, A. de Blas and T. Rodríguez-Blas, Inorg. Chim. Acta, 2014, 417, 155–162 CrossRef.
- A. El Majzoub, C. Cadiou, I. Déchamps-Olivier, F. Chuburu and M. Aplincourt, Eur. J. Inorg. Chem., 2007, 32, 5087–5097 CrossRef.
- A. E. Majzoub, C. Cadiou, I. Déchamps-Olivier, F. Chuburu, M. Aplincourt and B. Tinant, Inorg. Chim. Acta, 2009, 362, 1169–1178 CrossRef.
- M. Regueiro-Figueroa, D. Esteban-Gómez, C. Platas-Iglesias, A. de Blas and T. Rodríguez-Blas, Eur. J. Inorg. Chem., 2007, 15, 2198–2207 CrossRef.
- A. El Majzoub, C. Cadiou, I. Dechamps-Olivier, B. Tinant and F. Chuburu, Inorg. Chem., 2011, 50, 4029–4038 CrossRef CAS PubMed.
- C. M. Fisher, E. Fuller, B. P. Burke, V. Mogilireddy, S. J. Pope, A. E. Sparke, I. Dechamps-Olivier, C. Cadiou, F. Chuburu, S. Faulkner and S. J. Archibald, Dalton Trans., 2014, 43, 9567–9578 RSC.
- B. Drahoš, J. Kotek, P. Hermann, I. Lukeš and E. Tóth, Inorg. Chem., 2010, 49, 3224–3238 CrossRef PubMed.
- J. Prousek, Collect. Czech. Chem. Commun., 1991, 56, 1358–1360 CrossRef CAS.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- MATLAB, The Mathworks Inc., Natick, MA, USA.
- V. V. Pavlishchuk and A. W. Addison, Inorg. Chim. Acta, 2000, 298, 97–102 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155 CrossRef CAS PubMed.
- C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466–470 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- P. A. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189–194 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef CAS.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. Ganyushin and F. Neese, J. Chem. Phys., 2006, 125, 024103 CrossRef PubMed.
- F. Neese, J. Chem. Phys., 2005, 122, 034107 CrossRef PubMed.
- R. Maurice, R. Bastardis, C. de Graaf, N. Suaud, T. Mallah and N. Guihéry, J. Chem. Theory Comput., 2009, 5, 2977–2984 CrossRef CAS PubMed.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Theor. Chem. Acc., 2007, 117, 587–597 Search PubMed.
- S. Pathak, L. Lang and F. Neese, J. Chem. Phys., 2017, 147, 234109 CrossRef PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- M. Regueiro-Figueroa, L. M. Lima, V. Blanco, D. Esteban-Gomez, A. de Blas, T. Rodriguez-Blas, R. Delgado and C. Platas-Iglesias, Inorg. Chem., 2014, 53, 12859–12869 CrossRef CAS PubMed.
- B. Drahoš, R. Herchel and Z. Trávníček, Inorg. Chem., 2015, 54, 3352–3369 CrossRef PubMed.
- S. Alvarez, Dalton Trans., 2005, 13, 2209–2233 RSC.
- D. Casanova, P. Alemany, J. M. Bofill and S. Alvarez, Chem. – Eur. J., 2003, 9, 1281–1295 CrossRef CAS PubMed.
- R. Boča, Theoretical Foundations of Molecular Magnetism, Elsevier, Amsterdam, 1999 Search PubMed.
- The standard deviations were calculated as σi = (Pii−1·S/(N–k))−1/2, where Pij = Σ(δμn/δai·δμn/δaj) and S = Σ(μn − μexpn)2 with n = 1 to N; ai and aj are fitted parameters, N is the number of experimental points (the sum of temperature and field dependent data), μn and μexpn are the calculated and experimental effective magnetic moments for a given temperature and magnetic field. The σi was then multiplied by Student's t95% to provide confidence limits with 95% probabilities listed in the text.
- S. Gomez-Coca, A. Urtizberea, E. Cremades, P. J. Alonso, A. Camon, E. Ruiz and F. Luis, Nat. Commun., 2014, 5, 1–8 Search PubMed.
- L. Chen, S.-Y. Chen, Y.-C. Sun, Y.-M. Guo, L. Yu, X.-T. Chen, Z. Wang, Z. W. Ouyang, Y. Song and Z.-L. Xue, Dalton Trans., 2015, 44, 11482–11490 RSC.
- Y.-F. Deng, B. Yao, P.-Z. Zhan, D. Gan, Y.-Z. Zhang and K. R. Dunbar, Dalton Trans., 2019, 48, 3243–3248 RSC.
- MnII, FeII and CoII complexes of L2 were resynthesized according to ref. 12 and the E1/2 values were remeasured. The obtained data are in very good agreement with the previously published data in ref. 12 if these data were recalculated using the new value E1/2 = 0.624 V vs. SHE for ferrocene/ferrocenium standard and its potential E1/2 = 0.075 V vs. Ag/Ag+ during the measurement.
- M. Atanasov, D. Ganyushin, K. Sivalingam and F. Neese, in Molecular Electronic Structures of Transition Metal Complexes II, ed. D. M. P. Mingos, P. Day and J. P. Dahl, Springer, Berlin, Heidelberg, 2012, pp. 149–220 Search PubMed.
- S. K. Singh, J. Eng, M. Atanasov and F. Neese, Coord. Chem. Rev., 2017, 344, 2–25 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: IR and MS spectra of the ligand and studied complexes, 2D NMR spectra of the ligand L, HFEPR data, additional magnetic data and cyclic voltammograms, crystal data and structure refinements, results of continuous shape measures, parameters of one-component Debye model. CCDC 1942109–1942112. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/D0DT00166J |
| This journal is © The Royal Society of Chemistry 2020 |