Interaction of Np(V) with borate in alkaline, dilute-to-concentrated, NaCl and MgCl₂ solutions

Abstract

The interaction of Np(V) with borate was investigated in 0.1–5.0 M NaCl and 0.25–4.5 M MgCl₂ solutions with 7.2 ≤ pH_m ≤ 10.0 (pH_m = –log[H⁺]) and 0.004 M ≤ [B]_tot ≤ 0.16 M. Experiments were performed under an Ar-atmosphere at T = (22 ± 2) °C using a combination of under- and oversaturation solubility experiments, NIR spectroscopy, and extensive solid phase characterization. A bathochromic shift (≈5 nm) in the Np(V) band at λ = 980 nm indicates the formation of weak Np(V)–borate complexes under mildly alkaline pH_m-conditions. The identification of an isosbestic point supports the formation of a single Np(V)–borate species in dilute MgCl₂ systems, whereas a more complex aqueous speciation (eventually involving the formation of several Np(V)–borate species) is observed in concentrated MgCl₂ solutions. The solubility of freshly prepared NpO₂OH(am) remained largely unaltered in NaCl and MgCl₂ solutions with [B]_tot = 0.04 M within the timeframe of this study (t ≤ 300 days). At [B]_tot = 0.16 M, a kinetically hindered but very significant drop in the solubility of Np(V) (3–4 log₁₀-units, compared to borate-free systems) was observed in NaCl and dilute MgCl₂ solutions with pH_m ≤ 9. The drop in the solubility was accompanied by a clear change in the colour of the solid phase (from green to white-greyish). XRD and TEM analyses showed that the amorphous NpO₂OH(am) “starting material” transformed into crystalline solid phases with similar XRD patterns in NaCl and MgCl₂ systems. XPS, SEM–EDS and EXAFS further indicated that borate and Na/Mg participate stoichiometrically in the formation of such solid phases. Additional undersaturation solubility experiments using the newly formed Na–Np(V)–borate(cr) and Mg–Np(V)–borate(cr) compounds further confirmed the low solubility ([Np(V)]_aq ≈ 10⁻⁶–10⁻⁷ M) of such solid phases in mildly alkaline pH_m-conditions. The formation of these solid phases represents a previously unreported retention mechanism for the highly mobile Np(V) under boundary conditions (pH_m, [B]_tot, ionic strength) of relevance to certain repository concepts for nuclear waste disposal.

---

1. Introduction

Neptunium-237 is a relevant radionuclide in the context of nuclear waste disposal because of its inventory in spent nuclear fuel and long half-life (t_1/2 = 2.14 × 10⁶ a). Neptunium can be found in different redox states in the environment (+IV to +VI), which accordingly exhibit very different chemical properties. Np(IV) is expected to predominate under the reducing conditions found in anoxic near-surface groundwaters or those foreseen in deep underground repositories for the disposal of nuclear waste. Np(V), which is the predominant oxidation state under oxic conditions, can also play a role, e.g. in the early stages of repository closure, in the presence of oxidizing waste forms (i.e. high content of NO₃⁻) or in the direct vicinity of spent fuel as a result of radiolysis effects. Np(V) forms the very soluble NpO₂OH(am) solid phase and is characterized by weak sorption. The +V oxidation state holds the lowest effective charge (Z_eff ≈ +2.3) of all the oxidation states of Np that form in aqueous systems.¹ This accordingly results in weaker interactions with strong ligands (hard Lewis bases) such as hydroxide or carbonate.²

Boron is a relatively scarce element in the Earth's crust (≈0.001% of the crust mass), where it is mostly found in evaporates such as borax (Na₂B₄O₇·10H₂O) and kernite (Na₂B₄O₆(OH)₂·3H₂O).³ Indeed, borax is a natural inclusion in the Salado Formation and has been found at the Waste Isolation Pilot Plant (WIPP), an underground repository for transuranic (TRU) waste in New Mexico, USA. Borate concentrations in “weep” brines found in the WIPP are as high as 0.18 M (or 0.044 M if expressed as B₄O₇²⁻).⁴ Boron can be also present in repositories for radioactive waste as a component of the emplaced waste, mostly (but not exclusively) coming from vitrified high level waste (HLW).⁵ In the context of the accident at the Fukushima nuclear power plant, seawater supplemented with boron (as a neutron absorber) was pumped into the reactors during the first weeks after the emergency.⁶ Accordingly, some of the wastes resulting from the decommissioning of the Fukushima nuclear power plant are expected to contain high levels of salts and boron. Pessimistic concentration estimates reported in the literature refer to 0.6 M ≤ [NaCl] ≤ 6.0 M and 0.1 M ≤ [B]_tot ≤ 1.0 M (0.01 to 0.1 M in the original publication, referring to Na₂B₁₀O₁₆·10H₂O).⁷ The aqueous speciation of boron is strongly dependent on its total concentration. Monomeric species (B(OH)₃(aq) and B(OH)₄⁻) prevail at low boron concentrations, whereas polyborate species (e.g. B₃O₃(OH)₄⁻, B₄O₅(OH)₄²⁻ or B₅O₆(OH)₄⁻, among others) control the speciation of boron at higher [B]_tot in near-neutral to weakly alkaline pH conditions.^8,9

Only a very limited number of experimental studies available in the literature deal with the impact of borate on the solution chemistry of actinides.^10–15 Most of these studies focus on Nd(III), Eu(III) and Cm(III) as analogues of the trivalent actinides Am(III) and Pu(III).^10–13 Spectroscopic and solubility data indicated the formation of relatively weak Cm(III)–borate(aq) and Ln(III)–borate(aq) complexes in mildly alkaline aqueous solutions.^10–13 On the other hand, the most distinct feature observed in Hinz et al. (2015) was the formation of a previously unreported Nd(III)–borate(s) amorphous solid phase that defined solubility limits well below the solubility of Nd(OH)₃(s) in weakly alkaline solutions.¹³ In her PhD thesis, Hinz revealed also no (or very minor) impact of borate on the solubility of Th(IV), very likely as a result of the strong An(IV) hydrolysis that cannot be outcompeted by borate complexation.¹⁴ The formation of An(VI)–borate(aq) aqueous complexes was confirmed in solubility (for U(VI)¹⁴) and spectroscopic (for Pu(VI)¹⁵) studies. So far, no experimental studies dealing with the interaction of Np(V) with borates in aqueous solutions are available in the literature. Based on the systematics along the different oxidation states of the actinide series, it can be assumed that NpO₂⁺ may also form weak complexes with borate. The scarcity of investigations dedicated to actinide–borate interactions in aqueous systems is also reflected in the absence of any thermodynamic data selection for actinide–borate aqueous complexes or solid compounds in the current NEA–TDB reviews.¹⁶

There are no actinide–borate minerals reported to naturally occur in the environment. The first crystalline structure of a uranium–borate compound was only reported in the 80's by Behm,¹⁷ who synthesized K₆[UO₂(B₁₆O₂₄(OH)₈)]·12H₂O(cr) by slow evaporation at room temperature. Most of the actinide–borate compounds synthesized afterwards were prepared at elevated temperatures: using molten B₂O₃ in high temperature reactions (>1000 °C),^18–20 molten B(OH)₃ at T > 170 °C (ref. 21–24) or molten CH₃B(OH)₂ at T > 90 °C.²⁵ Several neptunium–borate compounds were prepared using molten B(OH)₃,^26,27 but this synthetic route resulted in a number of cases in borate compounds containing various oxidation states of Np.^28,29 Using instead molten CH₃B(OH)₂ at T = 120 °C, Wang et al. (2010) succeeded in preparing the first oxidation state pure Np(V)–borate compound, NpO₂[B₃O₄(OH)₂](cr).²⁵ Indeed, the same research group proved that Np(V)–borate compounds can be synthesized using B(OH)₃ if appropriate counterions are considered, and obtained K[(NpO₂)B₁₀O₁₄(OH)₄](cr) and K₂[(NpO₂)₂B₁₆O₂₅(OH)₂](cr) by using molten B(OH)₃ at T = 220 °C in chloride media.³⁰ From a solution chemistry perspective, it is, however, unclear if such crystalline compounds synthesized at elevated temperatures will be the solubility-controlling phase for Np(V) at ambient temperature.

The goal of the present study is to comprehensively investigate the interaction of borate with Np(V) in dilute-to-concentrated salt systems. The primary focus is on the aqueous speciation and the associated formation and in situ transformation of new solubility-controlling solid compounds. For this purpose, a combination of over- and undersaturation experiments, spectroscopic measurements and a systematic, multi-method solid phase characterization approach was used to investigate the solution chemistry of Np in NaCl and MgCl₂ solutions over a broad range of pH_m and [B]_tot. The boundary conditions investigated are of special relevance in the framework of underground repositories for the disposal of nuclear waste, but could be also of interest for more specific cases such as wastes arising from the decommissioning of the Fukushima nuclear power plant.

2. Materials and methods

2.1. Chemicals

All solutions were prepared with purified water (Milli-Q academic, Millipore) and purged for 2–3 hours with Ar before use. All samples were prepared and stored in an Ar glovebox with <10 ppm O₂ at T = (22 ± 2) °C. Sodium tetraborate Na₂B₄O₇·10H₂O, NaCl, HCl (Titrisol®), NaOH (Titrisol®) and MgCl₂·6H₂O were obtained from Merck (p.a.). Carbonate impurities in commercial Mg(OH)₂ (p.a., Merck) resulted in the predominance of NpO₂CO₃⁻ in MgCl₂–Mg(OH)₂ solutions with pH_m ≈ 9, as confirmed by the predominant band at λ = 990 nm in the NIR spectra of Np.³¹ This band disappeared when Mg(OH)₂ was obtained by the titration of a MgCl₂ solution with 1.0 M NaOH (Titrisol). The resulting Mg(OH)₂ solid phase was washed 4–5 times with Milli-Q water before its use in solubility experiments and spectroscopic measurements.

Sufficiently long equilibration times (∼1 month) were used for all initially-prepared inactive borate matrix systems in dilute to concentrated NaCl and MgCl₂ solutions before the addition of Np(V) solids (undersaturation solubility experiments) and aqueous Np(V) (oversaturation solubility experiments and spectroscopic measurements). A radiochemically well-characterized ²³⁷Np(V) stock solution of KIT-INE with [Np(V)]_aq = 0.32 M (in 0.01 M HCl) was used in all experiments.

2.2. pH measurements

A combination glass pH electrode (type ROSS, Orion), freshly calibrated against standard pH buffers (pH 7–10, Merck), was used to determine the molal H⁺ concentration, [H⁺] (with pH_m = −log[H⁺]). In aqueous solutions with I ≥ 0.1 M, the measured pH (pH_exp) is an operational value related to [H⁺] by pH_m = pH_exp + A_m, where A_m is an empirical parameter entailing the liquid junction potential of the electrode in a given background electrolyte concentration and the activity coefficient of H⁺. Values of A_m as a function of NaCl and MgCl₂ concentration were taken from Altmaier et al. (2003).³² Uncertainty in the pH measurements did not exceed 3 mV (ca. ±0.05 pH-units). In MgCl₂ solutions, the maximum pH_m is limited to pH_max ≈ 9 due to the precipitation and consequent pH-buffering of magnesium hydroxide or hydroxochloride phases (depending upon MgCl₂ concentration).³²

2.3. Solid phase preparation and solubility experiments

Solubility samples in NaCl (0.1, 0.5 and 5.0 M, 7.2 ≤ pH_m ≤ 9.9) and MgCl₂ (0.25, 3.5 and 4.5 M, 7.3 ≤ pH_m ≤ 9.1) solutions containing 0.01 ≤ [B]_tot ≤ 0.16 M were prepared in polyethylene vials with 5–10 mL matrix solution and 8–14 mg of Np(V) solid phase per sample. Four different solubility series were prepared:

I. Undersaturation solubility batch experiments with NpO₂OH(am) and varying pH_m: NpO₂OH(am) was precipitated by titration of a Np(V) stock solution with carbonate-free NaOH. The resulting greenish solid phase was separated from the solution by centrifugation and washed 3–4 times with water. The washed solid was contacted with 0.1/5.0 M NaCl (7.2 ≤ pH_m ≤ 9.9) and 0.25/3.5 M MgCl₂ (7.3 ≤ pH_m ≤ 9.1) solutions, pre-equilibrated with borate at [B]_tot = 0.04 and 0.16 M.

II. Undersaturation solubility batch experiments with Na/Mg–Np(V)–borate(cr) and varying pH_m: The amorphous NpO₂OH(am) “starting material” transformed into crystalline Na–Np(V)–borate(cr) and Mg–Np(V)–borate(cr) solid phases in NaCl and dilute MgCl₂ systems with [B]_tot = 0.16 M (see section 3.1). The transformed solid phases were used in a second series of undersaturation solubility experiments under experimental conditions analogous to approach I, except that no samples were prepared for the 3.5 M MgCl₂ system.

III. Undersaturation solubility batch experiments with Na/Mg–Np(V)–borate(cr) and varying [B]_tot: Na–Np(V)–borate(cr) and Mg–Np(V)–borate(cr) crystalline phases obtained in I were also used in a series of solubility experiments in 0.5/5.0 M NaCl and 0.25/4.5 M MgCl₂ at constant pH_m (≈8.5–8.7) and varying borate concentration (0.01 ≤ [B]_tot ≤ 0.16 M).

IV. Oversaturation solubility batch experiments with varying pH_m: For the system in 0.1 M NaCl with [B]_tot = 0.16 M, additional experiments were performed from oversaturation conditions with [Np(V)]₀ = 0.01 M (V_tot = 5 mL, total Np inventory ≈ 12 mg) and 8.2 ≤ pH_m ≤ 8.9. The aim of this experimental series was to confirm the formation of Na–Np(V)–borate(cr) solid phases when the system was approached from oversaturation conditions.

The Np concentration and pH_m of the solubility experiments were monitored at regular time intervals for up to 300 days until no further changes in Np concentration and pH_m were observed. The concentration of Np in the aqueous solution was quantified by liquid scintillation counting (LSC, PerkinElmer 1220 Quantulus) after ultrafiltration with 10 kDa filters (∼1.5 nm, Pall Life Sciences). An aliquot of the resulting filtrate was mixed with 10 mL of LSC-cocktail (PerkinElmer Ultima Gold XR), and the α activity was measured for 30 minutes using α/β-discrimination to eliminate the contribution from the ²³³Pa daughter nuclide.

2.4. Solid phase characterization

2.4.1 XRD, XPS, SEM and TEM. Solid phases of selected solubility experiments equilibrated in NaCl and MgCl₂ solutions were characterized by powder X-ray diffraction (XRD), X-ray photoelectron spectroscopy (XPS), scanning electron microscopy (SEM) and transmission electron microscopy (TEM).

Approximately 1 mg of the corresponding solid was separated from the solution by centrifugation (4000g) in the glovebox and washed 3 times with ethanol (2 mL) under an Ar-atmosphere. The washed solid was dried in the glovebox and characterized by XRD using a Bruker D8 Advance diffractometer (Cu Kα radiation) equipped with a Sol-X detector. XRD data were collected within 5° ≤ 2Θ ≤ 60°, with a step size of 0.04° and 6 seconds of accumulation time per step. An air-tight sample holder with a dome cover (Bruker) was used for the measurements.

Solid samples for XPS, SEM and TEM analysis were prepared using the same approach as described for XRD, but with a significantly reduced amount of sample (10–50 μg). After drying, the washed solid was pressed on an indium foil and analysed with an XP spectrometer (ULVAC-PHI, Inc., model PHI 5000 VersaProbe II) equipped with a scanning microprobe X-ray source (monochromatic Al Kα (1486.7 eV)). Survey scans were recorded with a source power of 31 W of the scanning microprobe X-ray source and a pass energy of 187.85 eV of the analyzer, step size 0.8 eV, to identify the elements and to determine their atomic concentrations at the sample surface. A FEI Quanta 650 FEG environmental scanning electron microscope (now Thermo Fisher Scientific Inc.) was applied to analyse the sample surfaces.

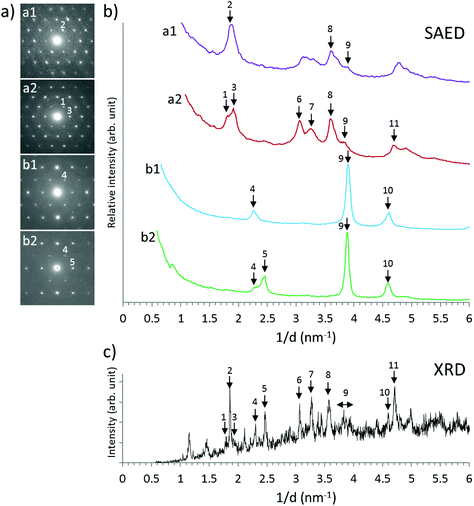
High-angle annular dark-field scanning TEM (HAADF-STEM), electron energy-loss spectroscopy (EELS), energy-dispersive X-ray spectroscopy (EDS), and selected-area electron diffraction (SAED) were performed using a FEI Tecnai G2 F20 X-TWIN equipment operated at 200 kV. EELS and EDS were performed with a STEM mode (STEM-EELS and STEM-EDS). SAED patterns were taken from a sample area of about 200 nm in diameter. Rotational profiles of the SAED patterns were obtained by using ImageJ software.

2.4.2 XAFS techniques. Neptunium L_III-edge X-ray absorption spectra were recorded at the INE-Beamline at the KARA synchrotron source (formerly ANKA), KIT Campus North, in Karlsruhe (Germany).³³ The beamline is equipped with a Ge(422) double crystal monochromator (DCM) coupled with a collimating and a focusing Rh-coated mirror before and after the DCM, respectively.

Approximately 1 mg of each investigated solid phase was transferred together with ≈300 μL of the supernatant solution to a polyethylene vial under an Ar atmosphere. The vials were centrifuged at 4000g for 5 minutes to compact the solid at the bottom of the vial. These were then mounted in a gas-tight cell with Kapton® film (polyimide) windows inside the Ar-glovebox and transported to the INE-beamline. XAFS measurements were performed under continuous Ar-flow within 1 day after sample preparation.

Bulk X-ray absorption spectroscopic (XAS) measurements at the Np L_III-edge at 17 610 eV were performed in fluorescence mode at room temperature using a Ge solid-state detector. The monochromator was calibrated for the Np-L_III edge by assigning the energy of 17 038 eV to the first inflection point of the K-edge absorption spectrum of the Y metal foil. Multiple scans were run on each sample.

Extended X-ray absorption (EXAFS) spectra were extracted from raw data with the ATHENA interface of the IFFEFIT software.³⁴ The Fourier transforms (FTs) were obtained from the k³-weighted χ(k) functions using a Kaiser–Bessel window function with an apodization parameter of 1. Multishell fits were performed in real space (FT⁻¹) across the range of the first two to three shells. Amplitude and phase shifts functions were calculated using the FEFF 8.4 code³⁵ and the self-consistency loop.³⁶ The amplitude reduction factor S₀² was set to the value of 0.8.³⁷ Structural information was obtained by following a multi-shell approach for EXAFS data fitting. The fit was limited to parameters describing the Np coordination to surrounding oxygen and boron atoms (neighbouring atomic distances (R), EXAFS Debye–Waller factors (σ²), coordination numbers (N) and relative shift in ionization energy E⁰ (ΔE⁰)).

2.5. Spectroscopic (NIR) measurements

NIR measurements were conducted with 0.25 and 3.5 M MgCl₂ solutions at pH_m ≈ 9 containing [B]_tot = 0, 0.004, 0.04 and 0.16 M. After 2 weeks of equilibration time, a small aliquot of the neptunium stock solution was spiked into the matrix solutions to give [Np(V)]_aq = 1 × 10^–4 M, and NIR spectra were collected within 2 hours after the addition of neptunium. All measurements were performed with ≈3 mL of sample solution in quartz cuvettes with d = 10 mm (Hellma, QS). Spectra were recorded on a Cary 5e (Varian) in the range 850–1250 nm with a data interval of 0.2 nm and a scan rate of 60 nm min⁻¹. Data were collected in double beam mode against a reference solution with the same background electrolyte and borate concentration present in the measured neptunium sample.

3. Results and discussion

3.1. Solubility of Np(V) in the presence of borate

Fig. 1 shows the solubility of Np(V) in the presence of borate in (a) 0.1 M NaCl, (b) 5.0 M NaCl, (c) 0.25 M MgCl₂ and (d) 3.5 M MgCl₂ solutions. The figure includes solubility data obtained from over- and undersaturation conditions. In the latter case either NpO₂OH(am) or ternary Na/Mg–Np(V)–borate(cr) solid phases were used as the “starting material”. Np(V) solubility data reported in the literature for borate-free systems under analogous pH_m and ionic strength conditions are appended to the figure for comparison purposes,^38–40 as well as the solubility curves of NpO₂OH(am,fresh) calculated with the thermodynamic data selected in the NEA–TDB.¹⁶

Fig. 1 Solubility of Np(V) in the presence of 0.04 M ≤ [B]_tot ≤ 0.16 M (coloured symbols) in (a) 0.1 M NaCl, (b) 5.0 M NaCl, (c) 0.25 M MgCl₂ and (d) 3.5 M MgCl₂ solutions. Solubility data obtained with NpO₂OH(am) (blue symbols) and Na/Mg–Np(V)–borate(cr) (yellow/orange/red symbols) as Np(V) “starting material” (see text). Comparison with experimental solubility data in the absence of borate (open symbols, black) as reported by Neck et al., (1992),³⁸ Petrov et al., (2017)³⁹ and Fellhauer et al., (2016).⁴⁰ Solid green line in figures (a)–(c) correspond to the solubility of NpO₂OH(am,fresh) calculated according with thermodynamic data selected in the NEA–TDB.¹⁶ Ionic strength in figure (d) extends well beyond the applicability of SIT, and thus the solid green line in the figure is only provided to help visualize the trend in data. In MgCl₂ solutions (figures c and d), the maximum pH_m (pH_max) is limited to ≈9 by the precipitation of Mg(OH)₂(cr) or Mg₂(OH)₃Cl·4H₂O(cr).

As shown in Fig. 1, borate has no significant impact on the solubility of NpO₂OH(am) in 5.0 M NaCl, 0.25 M MgCl₂ and 3.5 M MgCl₂ solutions with [B]_tot = 0.04 M. Concentrations of neptunium measured in these systems are in good agreement with the solubility of NpO₂OH(am) in borate-free solutions.^39,40 A slight increase in the solubility of NpO₂OH(am) is observed in 0.1 M NaCl solutions with pH_m = 9 and [B]_tot ≥ 0.04 M, which suggests that Np(V)–borate complexes are being formed in solution (Fig. 1a).

The most dramatic feature observed in NaCl systems is the significant decrease in the apparent solubility of NpO₂OH(am) occurring in solutions with [B]_tot = 0.16 M and pH_m ≤ 9 (Fig. 1a and b). The drop in the solubility is accompanied by a change in the colour of the Np(V) solid phase: from the initial greenish colour which corresponded to NpO₂OH(am) to a white-greyish coloured phase. These observations suggest the transformation of the initial amorphous Np(V) hydroxide phase into a previously unreported borate-containing Np(V) compound. This solid phase transformation was “fast” in 5.0 M NaCl solutions (significant drop in solubility observed at ≈2 weeks), but slower in 0.1 M NaCl solutions (≈270 days). In the latter case, the drop in solubility was observed only at pH_m ≤ 8.5. Fig. 1a also shows that samples prepared from oversaturation conditions in 0.1 M NaCl and [B]_tot = 0.16 M (red blue circles) resulted in very similar observations: a slight increase of Np(V) concentration at pH_m ∼ 8.8 and a drop in the Np(V) solubility at pH_m ≤ 8.5 accompanied by a change in the colour of the Np(V) solid phase. In both cases (under- and oversaturation conditions), the concentration of Np(V) in equilibrium with the newly formed solid phase is 2–4 log₁₀-units (depending upon pH_m and NaCl concentration) lower than the solubility of NpO₂OH(am) in borate-free systems. We note that similar observations were reported for Nd(III) in the presence of comparable borate concentrations and pH_m.¹³

A comparable decrease in the solubility of NpO₂OH(am) accompanied by a change in the colour of the solid phase from greenish to white-greyish occurs in dilute MgCl₂ systems at pH_m < 9 and [B]_tot = 0.16 M (dark blue symbols in Fig. 1c). Similar to the behaviour observed in 0.1 M NaCl solutions, the solubility of Np(V) using NpO₂OH(am) as “starting material” decreased slowly and attained a constant value (≈10^−6.5 M) only after 270 days. In contrast to dilute MgCl₂ systems, only a minor decrease in the solubility of NpO₂OH(am) is observed in 3.5 M MgCl₂ solutions with [B]_tot = 0.16 M, even after ≈300 days. This result can be explained by three different hypothesis: (i) the formation of borate-containing Np(V) solid phase has slower kinetics in concentrated MgCl₂ solutions, (ii) the predominance of Mg(II)–borate binary complexes in solution, which decrease [borate]_free in solution and accordingly prevents/limits the precipitation of a Np(V)–borate solid phase or, (iii) a combination of (i) and (ii).

The white-greyish solid phases formed in NaCl and dilute MgCl₂ solutions (identified as Na–Np(V)–borate(cr) and Mg–Np(V)–borate(cr) compounds, see section 3.2) were used in a second series of solubility experiments under analogous boundary conditions (pH_m, concentration of background electrolyte and [B]_tot; see yellow/orange/red symbols in Fig. 1a–c). In the three investigated systems, the concentration of neptunium in the presence of [B]_tot = 0.16 M at pH_m ≤ 8.5 agrees well with the solubility data obtained under analogous conditions with NpO₂OH(am) as the Np(V) “starting material”. This agreement establishes that thermodynamic equilibrium was attained, and that very likely the same Na/Mg–Np(V)–borate(cr) solid phases control the solubility of Np(V) at the end-point of both approaches. A significantly lower concentration of neptunium is measured in 0.1 M NaCl and 0.25 M MgCl₂ systems with pH_m > 8.5, compared to the solubility experiments initiated with NpO₂OH(am). This observation confirms that the transformation of NpO₂OH(am) in ternary Na/Mg–Np(V)–borate(cr) phases is kinetically hindered and less favoured with increasing alkalinity. The impact of borate concentration on the solubility of the ternary Na/Mg–Np(V)–borate(cr) phases remains unclear in Fig. 1. Hence, the solubility of Na–Np(V)–borate(cr) in 5.0 M NaCl solutions increases when increasing [B]_tot from 0.10 M to 0.16 M, whereas the solubility of Mg–Np(V)–borate(cr) in 0.25 M MgCl₂ solutions importantly decreases when increasing [B]_tot from 0.04 M to 0.10 M. This inconsistency was specifically addressed in a series of solubility experiments with Na/Mg–Np(V)–borate(cr) solid phases at pH_m ≈ constant ≈ 8.5–8.7 and varying borate concentration as 0.01 M ≤ [B]_tot ≤ 0.16 M (Fig. 2a and b).

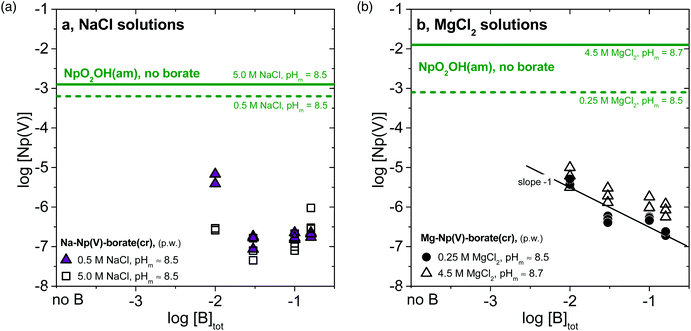Fig. 2 Solubility of Np(V) at constant pH_m (≈8.5–8.7) and varying borate concentration (−2.0 ≤ log[B]_tot ≤ −0.8 in (a) 0.5 and 5.0 M NaCl systems, and (b) in 0.25 and 4.5 M MgCl₂ systems. Solubility data obtained with (a) Na–Np(V)–borate(cr) and (b) Mg–Np(V)–borate(cr) solid phases as “starting material”. Solid and dashed green lines correspond to the solubility of NpO₂OH(am) determined in the absence of borate for NaCl^39,40 and MgCl₂ ⁴⁰ systems.

Fig. 2a shows that the solubility of Na–Np(V)–borate(cr) in 0.5 and 5.0 M NaCl decreases with increasing borate concentration from 0.01 M to 0.03 M, but increases slightly above [B]_tot ≈ 0.10 M. The decrease in solubility with increasing borate concentration can be rationalized using a generic expression for the apparent solubility constant of Na–Np(V)–borate(cr) (1):

From the expression of log K^app_s,0(Na–Np(V)–borate(cr)), it follows that at constant [NaCl] and pH_m, an increase in concentration of “borate” will result in a decrease of log[“Np(V)”]. On the other hand, at high borate concentrations, the formation of Np(V)–borate aqueous complexes must be taken into account and can be used to reasonably justify the observed increase in solubility.

The solubility of Mg–Np(V)–borate(cr) in 0.25 and 4.5 M MgCl₂ solutions at pH_m ≈ 8.5–8.7 decreases monotonically with increasing borate concentration following a slope ≈−1 (Fig. 2b). As in the case of Na–Np(V)–borate(cr), the decrease in solubility with increasing borate concentration can be properly rationalized through the use of log K^app_s,0(Mg–Np(V)–borate(cr)). In contrast to the NaCl systems, the solubility of Mg–Np(V)–borate(cr) does not increase above [B]_tot ≈ 0.10 M. Although Np(V)–borate aqueous complexes may form also in MgCl₂ solutions (see for instance section 3.4), they have a minor impact in the solubility possibly due to the decreased [“borate”]_free as a result of the binary Mg(II)–borate aqueous complexes formed.^41,42 Interestingly, the solubility of Mg–Np(V)–borate(cr) in 4.5 M MgCl₂ systems remains low within the investigated range of borate concentrations different to the data shown in Fig. 1d. This observation confirms that the lack of solid phase transformations in the solubility experiments using NpO₂OH(am) as the “starting material” in 3.5 M MgCl₂ solutions (Fig. 1d) was due to insufficient equilibration time: a full transformation to a Mg–Np(V)–borate(cr) solid should be expected in the long-term.

3.2 Solid phase characterization

3.2.1 XRD, XPS and SEM–EDS. Fig. 3 shows the XRD of the NpO₂OH(am) “starting material”, together with the diffractograms of the white-greyish phases formed in 0.1 M NaCl, 5.0 M NaCl and 0.25 M MgCl₂ solutions at pH_m ≈ 8.5 with [B]_tot = 0.16 M. In contrast to the amorphous character of NpO₂OH(am), diffractograms of the transformed solid phases show well-defined patterns with sharp peaks, indicating the crystalline structure of the newly-formed compounds. Although with certain similarities, the diffractograms obtained for the solid phases formed in NaCl and MgCl₂ solutions are markedly different, suggesting that the cation of the background electrolyte participates in the formation of these secondary solid phases. No positive match with any of the existing borate entries in the JCPDS database⁴³ or with XRD data reported by Wang and co-workers for Np(V)–borate compounds^25,30 was found for the collected diffractograms.

Fig. 3 Diffractograms of NpO₂OH(am) “starting material” and transformed Np(V) solid phases that form in NaCl and MgCl₂ solutions at pH_m ≈ 8.5 with [B]_tot = 0.16 M. Peaks marked with an asterisk “*” correspond to reflections of NaCl and result from the insufficient washing of the transformed Np(V) solids obtained in 5.0 M NaCl.

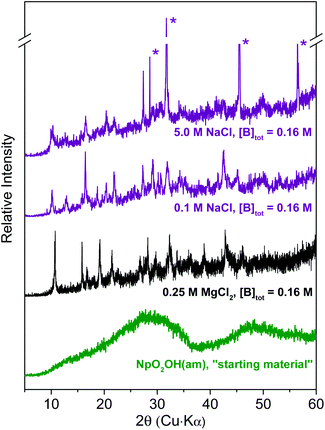
Results of XPS analyses of the Np(V) secondary phases formed in 0.1 M NaCl, 5.0 M NaCl and 0.25 M MgCl₂ solutions are summarized in Table 1. These data confirm the stoichiometric contribution of boron and Na/Mg in the investigated Np(V) solid phases. EDS results of the Np(V) solid equilibrated in 5.0 M NaCl shows the presence of Cl together with an excess of Na, compared to the Np(V) compound equilibrated in 0.1 M NaCl. This observation can be explained by the presence of NaCl resulting from incomplete removal of the 5.0 M NaCl matrix solution during sample preparation, as also confirmed by XRD (see Fig. 3). XPS data in Table 1 can be used to define tentative stoichiometries for the solid phases that formed in NaCl and MgCl₂ solutions, namely NpO₂[B₅O₆(OH)₄]·2NaOH(cr) and (NpO₂)₂[B₅O₆(OH)₄]₂·3Mg(OH)₂(cr). These proposed stoichiometries should be considered hypothetical until there is more definitive experimental evidence (e.g. single crystal analysis).

Table 1 Composition of the newly formed Np(V)–borate solids (in at%) based on XPS analyses (analytical uncertainties lie within 10–20% of the nominal value)

Sample	B	O	Na	Mg	Cl	Np
0.1 M NaCl, [B]tot = 0.16 M	24.4	62.0	9.4	—	—	4.2
5.0 M NaCl, [B]tot = 0.16 M	23.6	57.4	13.6	—	2.0	3.4
0.25 M MgCl2, [B]tot = 0.16 M	21.1	68.2	—	6.3	—	4.4

---

Fig. 4 shows SEM images of Np(V)–borate solid phases formed in NaCl and MgCl₂ solutions. Solid phases collected from samples in 0.1 M NaCl (Fig. 4a) and 0.25 M MgCl₂ solutions (Fig. 4b) show a homogeneous distribution of Np(V) in the entire investigated area. The sample equilibrated in 0.1 M NaCl contains very thin (∼20 nm) hexagonal platelets with a diameter of ∼500 nm. The structure of the sample equilibrated in 0.25 M MgCl₂ looks similar in shape but appears less crystalline. The Np(V)–borate solid phase formed in 5.0 M NaCl (Fig. 4c) clearly shows the co-existence of two phases. Here, massive, crystalline hexagonal blocks appear surrounded by platelet-like particles. EDS indicated the predominance of Na and Cl in the block structures, whereas the less crystalline phase corresponds to the newly formed Np(V)–borate phase whose composition was summarized in Table 1.

Fig. 4 SEM images of solid phases collected from Np(V) solubility experiments in the presence of borate (with [B]_tot = 0.16 M) in (a) 0.1 M NaCl, (b) 0.25 M MgCl₂, and (c) 5.0 M NaCl.

3.2.2 STEM–EELS, STEM–EDS and SAED. Fig. 5a and b show STEM–EELS and STEM–EDS spectra obtained from an individual platelet particle of the Np(V)–borate solid formed in 0.1 M NaCl. The HAADF–STEM image of the platelet particle indicated by an arrow is shown in the inset of Fig. 5a. Consistent with the XPS results summarized in Table 1, STEM–EELS and STEM–EDS spectra support the co-existence of Np, B, O and Na in the sample. On the other hand, SAED patterns taken along the normal directions of the platelet particles of the sample indicate at least four types of crystal structures as shown in Fig. 6a(a1, a2, b1 and b2). The SAED patterns show hexagonal-like grids with the clear presence of deformations, which lead to distinct diffraction peaks (Fig. 6b). This feature likely reflects the morphology of the hexagonal-like shaped particles seen in the SEM and HAADF-STEM images of the sample (Fig. 4 and 5a). Fig. 6b and c show radial intensity profiles of the SAED patterns (radial profiles) and the XRD profile, respectively. XRD patterns are shown in terms of reciprocal d-spacing (nm⁻¹) instead of degrees, to allow the comparison between XRD and radial profiles. This conversion is required since the wavelength of the Cu K-α X-ray (0.15406 nm) is different from that of the electron beam at 200 kV (0.00251 nm), causing differences in the Bragg angles in each case. Diffraction peaks marked as 1 to 11 in the radial profiles (Fig. 6b) show a good match with the peak positions in the XRD profile (Fig. 6c), although some diffraction peaks in the latter profile are not observed by SAED. This comparison shows that the Np(V)–borate solid formed in 0.1 M NaCl contain several (at least four) phases or polymorphs with clearly different SAED patterns, all sharing hexagonal-like grids with deformations present.

Fig. 5 EELS (a) and EDS (b) spectra of the Np(V) solid phase formed in the presence of borate (with [B]_tot = 0.16 M) in 0.1 M NaCl. Both spectra taken from the same particle area at the same time. Inset shows a HAADF-STEM image of a platelet particle of the sample. The carbon signal in the EELS spectrum mainly originates from a carbon thin film below the particle, which is not visible in the HAADF-STEM image. The copper signal originates from the Cu TEM grid.

Fig. 6 SAED patterns taken from individual particles of the Np(V) solid phase formed in the presence of borate (with [B]_tot = 0.16 M) in 0.1 M NaCl: (a) SAED patterns taken from four different platelet particles; (b) radial intensity profiles obtained from the corresponding SAED patterns; (c) XRD profile. The XRD profile is shown in terms of reciprocal d-spacing (nm⁻¹) to allow the comparison with the radial intensity profiles. Matching diffraction peaks between SAED and XRD are indicated by numbers 1 to 11.

3.2.3 EXAFS measurements. Np L_III-edge EXAFS spectra of the newly formed Np(V)–borate compounds were collected for the solid phases equilibrated in 0.1 M NaCl, 5.0 M NaCl and 0.25 M MgCl₂ solutions with [B]_tot = 0.16 M and pH_m ≈ 8.5. Fourier Transforms and the k³-weighted EXAFS spectra for the Np(V)–borate phases are shown in Fig. 7 together with the corresponding best fit models. The k³-weighted χ(k) spectra of the three investigated solids are very similar. The greatest differences are observed in the k-space ∼6–8 Å⁻¹, where the oscillation splits show a beat pattern between 6–7 Å⁻¹ and a maxima at ∼7.7 Å⁻¹ for the NaCl samples. In contrast, this oscillation is dampened in the MgCl₂ sample with a maxima at ∼7.4 Å⁻¹. This difference reflects the presence of different cations (Na⁺ or Mg²⁺) in the Np(V)–borate structure.

Fig. 7 Np L_III-edge spectra: (a) k³-weighted EXAFS spectra; (b) corresponding Fourier transform of the EXAFS spectra and (c) experimental (black solid line) and fitted (red line) k³-weighted EXAFS function of the Fourier back-transform spectra (range: ca. R + ΔR = 1.1–3.7 Å).

The differences of the spectral features observed in the k³-weighted χ(k) spectra are reflected in the k³-weighted EXAFS function of the Fourier back-transform spectra (Fig. 7c). The first two shells of the Radial Structure Functions (RSF) (modulus, |FT|, and imaginary parts, ImFT) described at R + Δ ∼ 1.4 and ∼1.9 Å represent the axial (O_ax) and equatorial oxygen atoms (O_eq) (Fig. 7b). The distances to the axial and equatorial oxygen atoms are very similar in all the samples analysed. A very small shift to longer distances is observed for the third shell (corresponding to B) depending upon the concentration and composition of background electrolyte. The structural parameters that result from the EXAFS fit and calculated paths of an atomic cluster based on a starting structure of Np(V)–borate (NpO₂[B₃O₄(OH)₂])²⁵ are shown in Table 2. For the fit, data were transformed in the k-space between ∼4.3–11.9 Å⁻¹ and in the R-space between ∼1.1–3.7 Å. A step-by-step approach was followed to model the experimental spectra. Each shell (O_ax, O_eq and B) were fitted separately and subsequently the best fits were used for the final structural model.

Table 2 Structural parameters obtained from the EXAFS evaluation of Np(V) solid phases formed in borate-bearing NaCl and MgCl₂ solutions. Multiple scattering: CN = 2; NpO_ax1–NpO_ax1&2 = 2 × R_Oax; σ²NpO_ax1–NpO_ax1 = 4 − σ²_Oax, σ²NpO_ax1–NpO_ax2 3 & 4 leg = 2 × σ²_Oax

Sample	Path	CN	R [Å]	σ ^2 [Å^2]	ΔE0 [eV]
Fit errors: CN: ±20%, R: 0.01 Å, σ^2: 0.001 Å^2.a Held constant during the fit.
0.1 M NaCl, [B]tot = 0.16 M	Np–Oax	2.4	1.82	0.001^a	−1.04
	Np–Oeq	5.9	2.50	0.010
	Np–B	3.2	3.00	0.012
5.0 M NaCl, [B]tot = 0.16 M	Np–Oax	2.2	1.84	0.001^a	1.93
	Np–Oeq	4.7	2.50	0.010
	Np–B	1.8	3.09	0.003
0.25 M MgCl2, [B]tot = 0.16 M	Np–Oax	2.3	1.84	0.001^a	2.68
	Np–Oeq	3.0	2.48	0.008
	Np–B	3.0	3.13	0.001

---

As already observed in the Radial Structure Functions (RSF) (Fig. 7b), the Np–O_ax distances are similar for all samples (1.82–1.84 Å). These values are in line with Np–O_ax distances in other Np(V)–borate compounds as determined by single-crystal analysis (Np^VO₂[B₃O₄(OH)₂], R_Np–Oax = 1.83 Å (CN = 5);²⁵ KNp^VO₂[B₁₀O₁₄(OH)₄], R_Np–Oax = 1.81 Å (CN = 6)³⁰). This contrasts with the significantly shorter Np–O_ax distances reported for the Np(VI)–borate compound Np^VIO₂[B₈O₁₁(OH)₄] (1.74 Å).⁴⁴ The Np–O_eq distances are comparable for all samples within error (2.48–2.50 Å), whereas the fit of the B-shell shows different Np–B distances depending on the composition and concentration of the background electrolyte. The shortest Np–B distance of ∼3.00 Å is found in the solid phase equilibrated in 0.1 M NaCl, whereas the longest Np–B distance (3.13 Å) is observed for the solid equilibrated in 0.25 M MgCl₂ solution. The sample from concentrated NaCl shows a distance of 3.09 Å, which is similar to the starting structure (3.11 Å). Debye Waller (DW) values that fit O_ax are relatively small and were fixed (in the case of solids equilibrated in 0.25 M MgCl₂ and 5.0 M NaCl solutions) to the value resulting from the fit using only O_ax. Debye Waller values of O_eq are generally higher (∼0.01) in the fits of all three samples indicating a less rigid structure.

3.3 Np(V) aqueous speciation by UV–Vis/NIR spectroscopy

Absorption spectra of Np(V) collected in 0.25 M and 3.5 M MgCl₂ solutions at pH_m ≈ 9 in the absence of borate and with [B]_tot = 0.004, 0.04 and 0.16 M are shown in Fig. 8. In 0.25 M MgCl₂, the absorption spectra of Np(V) in the absence of borate shows the characteristic NpO₂⁺ band with a peak maximum at λ ≈ 980 nm.⁴⁵ A peak shift to higher wavelengths (λ ≈ 983 nm) and peak broadening is observed in 3.5 M MgCl₂, indicating the formation of Np(V)–chloro complexes as previously described in CaCl₂ solutions of analogous pH_m and chloride concentrations.^46,47 A relatively minor bathochromic shift (≈0.5 nm) is observed at [B]_tot = 0.004 M in 0.25 and 3.5 M MgCl₂ solutions, suggesting the onset of Np(V)–borate complexation but indicating that aqueous speciation remains mostly controlled by NpO₂⁺ aqua-ion and Np(V)–chloro complexes, respectively, at this borate concentration. The slight increase in absorption intensity (≈5%) observed for this borate concentration in 3.5 M MgCl₂ solutions compared to the borate-free systems was attributed to experimental uncertainty.

Fig. 8 NIR absorption spectra of Np(V) in (a) 0.25 M and (b) 3.5 M MgCl₂ solutions at pH_m ≈ 9 in the absence of borate and with [B]_tot = 0.004, 0.04 and 0.16 M.

In 0.25 M MgCl₂ systems and for [B]_tot ≥ 0.04 M, the intensities of the absorption band decrease, the widths increase, and peak maxima are shifted to higher wavelengths by ≈5 nm. These results provide clear evidence on the formation of Np(V)–borate complex/es in dilute MgCl₂ systems. Furthermore, the presence of an isosbestic point strongly supports the presence of only two species: NpO₂⁺ and a yet undefined Np(V)–borate complex. As in the case of dilute MgCl₂ solutions, [B]_tot ≥ 0.04 M in 3.5 M MgCl₂ systems promotes a peak shift of the main absorption band to higher wavelengths and a pronounced increase of the FWHM (full width at half maximum). Here, no isosbestic point is observed which suggests a more complex aqueous speciation that may include several Np(V)–chloro, Np(V)–borate and/or mixed Mg/borate/chloro complexes of Np(V).

These results confirm that Np(V)–borate aqueous complexes form in dilute to concentrated MgCl₂ solutions. Although experimental data discussed in section 3.1 show that such complexes have a relatively minor impact on solubility, borate importantly impacts the aqueous speciation of Np(V) in weakly alkaline systems. Analogous spectroscopic studies on-going at LANL using NaCl instead of MgCl₂ as background electrolyte confirm this observation. As in the case of dilute MgCl₂ solutions, the observation of an isosbestic point in dilute to concentrated NaCl solutions confirms the formation of one main Np(V)–borate aqueous species. The more complex picture observed in the present work in concentrated MgCl₂ solutions reflects also the complexity of the Mg–borate binary system. As already proposed by Felmy and Weare (1986)⁴¹ and recently supported by Xiong et al. (2018),⁴² binary Mg–borate complexes (likely (MgB(OH)₄⁺) play a relevant role in the solution chemistry of borate in concentrated MgCl₂ solutions. Spectroscopic data obtained in the present work confirm that the formation of such binary complexes do not outcompete the complexation of borate with Np(V). This can be explained by the formation of strong Np(V)–borate complexes, or by the (likely) formation of ternary Mg–Np(V)–borate complexes. Note that the formation of the ternary complex Ca[NpO₂Cl]²⁺ in concentrated CaCl₂ solutions was recently proposed by Fellhauer and co-workers based on EXAFS evidence.⁴⁷ An analogous complex might be envisaged for borate, e.g. Mg[NpO₂′′borate′′]²⁺, where the undefined “borate” moiety can represent either monomeric or polynuclear boron species.

Due to the limited dataset collected in this work and to the complex aqueous speciation of boron in MgCl₂ solutions, no thermodynamic modelling of the spectroscopic data was attempted in this study.

4. Conclusions

Under- and oversaturation solubility experiments with Np(V) in combination with spectroscopic investigations and a comprehensive, multimethod solid phase characterization confirm the impact of borate on the aqueous speciation and especially on the solubility of Np(V) in mildly alkaline, dilute to concentrated NaCl and MgCl₂ solutions.

Spectroscopic data confirm the formation of at least one Np(V)–borate complex in MgCl₂ solutions with [B]_tot ≥ 0.04 M, although the exact stoichiometry of the complex/es formed remains so far undefined. In spite of forming the Np(V)–borate complex/es, the presence of borate does not significantly increase the solubility of Np(V) in alkaline NaCl and MgCl₂ solutions. On the contrary and similarly to Nd(III), a significant drop in the Np(V) solubility (3 to 4 log₁₀-units) occurs in borate-bearing NaCl and MgCl₂ solutions with pH_m ≤ 9. The drop in solubility is accompanied by a clear change in the colour of the initial solid (from green to white-greyish), supporting the formation of a new solid phase. Solid phase characterization using XRD, XPS, SEM–EDS, TEM and EXAFS confirms the formation of hitherto unknown Na–Np(V)–borate(cr) and Mg–Np(V)–borate(cr) solid phases in NaCl and dilute MgCl₂, respectively. Although the undersaturation solubility experiments with the Mg–Np(V)–borate(cr) phase exhibit a very low solubility in 4.5 M MgCl₂ solutions, the transformation of NpO₂OH(am) was kinetically hindered and was not observed (within the timeframe of this study) in such concentrated brines. The in situ formation of Na–Np(V)–borate(cr) and Mg–Np(V)–borate(cr) solid phases in aqueous solutions at ambient temperature conditions highlights a previously unreported retention mechanism for the highly mobile Np(V) under boundary conditions (pH_m, [B]_tot, ionic strength) that is potentially relevant in the context of nuclear waste disposal.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The contribution of M. Böttle (KIT–INE) to analytical methods and preparation of experiments is highly appreciated and gratefully acknowledged. We thank the colleagues at KIT, Institute of Applied Materials, particularly Dr H.-C. Schneider whose TEM was used for the measurements. We acknowledge the KIT light source for provision of instruments at the INE-Beamline station operated by the Institute of Nuclear Waste Disposal and we would like to thank the Institute for Beam Physics and Technology (IBPT) for the operation of the storage ring, the Karlsruhe Research Accelerator (KARA). This research has received partial funding from the German Federal Ministry of Economics and Technology (BMWi) under the project number: 02E11021. Support for the Los Alamos and Florida State University contributions was provided by the Waste Isolation Pilot Plant (WIPP) project (DOE-CBFO); both directly and through a DOE Oak Ridge Associated Universities (ORAU) fellowship. TEAS was supported by the Center for Actinide Science and Technology (CAST), an Energy Frontier Research Center (EFRC) funded by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES), under Award Number DE-SC0016568.

References

1. G. R. Choppin, Radiochim. Acta, 1999, 85, 89–95.
2. M. Altmaier, X. Gaona and T. Fanghänel, Chem. Rev., 2013, 113, 901–943.
3. T. Nakano and E. Nakamura, Phys. Earth Planet. Inter., 2001, 127, 233–252.
4. A. C. Snider, Verification of the definition of generic weep brine and the developent of a recipe for this brine, Sandia National Laboratory, 2003.
5. B. Grambow, Waste forms for actinides: borosilicate glasses, in Uranium - Cradle to Grave, ed. P. C. Burns and G. Sigmon, 2013, pp. 301–316.
6. IAEA Fukushima Daiichi Status Report, 4 November 2011; IAEA: 4 November 2011, 2011.
7. M. Ochs, B. Vriens and Y. Tachi, Prog. Nucl. Sci. Technol., 2018, 5, 208–212.
8. N. Ingri, G. Lagerstrom, M. Frydman and L. G. Sillen, Acta Chem. Scand., 1957, 11, 1034–1058.
9. N. Ingri, Acta Chem. Scand., 1962, 16, 439–448.
10. M. Borkowski, M. Richmann, D. T. Reed and Y. Xiong, Radiochim. Acta, 2010, 98, 577–582.
11. J. Schott, J. Kretzschmar, M. Acker, S. Eidner, M. U. Kumke, B. Drobot, A. Barkleit, S. Taut, V. Brendler and T. Stumpf, Dalton Trans., 2014, 43, 11516–11528.
12. J. Schott, J. Kretzschmar, S. Tsushima, B. Drobot, M. Acker, A. Barkleit, S. Taut, V. Brendler and T. Stumpf, Dalton Trans., 2015, 44, 11095–11108.
13. K. Hinz, M. Altmaier, X. Gaona, T. Rabung, D. Schild, M. Richmann, D. T. Reed, E. V. Alekseev and H. Geckeis, New J. Chem., 2015, 39, 849–859.
14. K. Hinz, Interaction of Ln(III) and An(III/IV/V/VI) with borate in dilute to concentrated NaCl, CaCl₂ and MgCl₂ solutions, Karlsruhe Institute of Technology, 2015.
15. M. A. Silver , in Assessment of PuO2²⁺ solubility in high borate media, Pu Futures the Conference, Baden-Baden (Germany), 2016; Baden-Baden (Germany), 2016, p 313.
16. R. Guillaumont, J. Fanghänel, V. Neck, J. Fuger, D. A. Palmer, I. Grenthe and M. H. Rand, Chemical Thermodynamics Vol. 5. Update on the Chemical Thermodynamics of Uranium, Neptunium, Plutonium, Americium and Technetium, Elsevier, Amsterdam, North Holland, 2003.
17. H. Behm, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1985, 41, 642–645.
18. M. Gasperin, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1987, 43, 2031–2033.
19. M. Gasperin, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1987, 43, 2264–2266.
20. M. Gasperin, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1990, 46, 372–374.
21. S. A. Wang, E. V. Alekseev, J. T. Stritzinger, W. Depmeier and T. E. Albrecht-Schmitt, Inorg. Chem., 2010, 49, 6690–6696.
22. S. A. Wang, E. V. Alekseev, J. T. Stritzinger, G. K. Liu, W. Depmeier and T. E. Albrecht-Schmitt, Chem. Mater., 2010, 22, 5983–5991.
23. S. Wang, E. V. Alekseev, W. Depmeier and T. E. Albrecht-Schmitt, Inorg. Chem., 2011, 50, 2079–2081.
24. S. Wang, J. Diwu, E. V. Alekseev, L. J. Jouffret, W. Depmeier and T. E. Albrecht-Schmitt, Inorg. Chem., 2012, 51, 7016–7018.
25. S. A. Wang, E. V. Alekseev, H. M. Miller, W. Depmeier and T. E. Albrecht-Schmitt, Inorg. Chem., 2010, 49, 9755–9757.
26. S. A. Wang, E. V. Alekseev, W. Depmeier and T. E. Albrecht-Schmitt, Chem. Commun., 2011, 47, 10874–10885.
27. S. Wang, E. V. Alekseev, J. Ling, S. Skanthakumar, L. Soderholm, W. Depmeier and T. E. Albrecht-Schmitt, Angew. Chem., 2010, 122, 1190–1190.
28. S. A. Wang, E. V. Alekseev, W. Depmeier and T. E. Albrecht-Schmitt, Chem. Commun., 2010, 46, 3955–3957.
29. S. A. Wang, E. V. Alekseev, J. Ling, S. Skanthakumar, L. Soderholm, W. Depmeier and T. E. Albrecht-Schmitt, Angew. Chem., Int. Ed., 2010, 49, 1263–1266.
30. S. A. Wang, E. V. Alekseev, W. Depmeier and T. E. Albrecht-Schmitt, Inorg. Chem., 2012, 51, 7–9.
31. V. Neck, T. Fanghänel and J. I. Kim, Radiochim. Acta, 1997, 77, 167–175.
32. M. Altmaier, V. Metz, V. Neck, R. Müller and T. Fanghänel, Geochim. Cosmochim. Acta, 2003, 67, 3595–3601.
33. J. Rothe, S. Butorin, K. Dardenne, M. A. Denecke, B. Kienzler, M. Löble, V. Metz, A. Seibert, M. Steppert, T. Vitova, C. Walther and H. Geckeis, Rev. Sci. Instrum., 2012, 83, 043105.
34. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
35. A. Ankudinov, C. Bouldin, J. Rehr, J. Sims and H. Hung, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104107.
36. J. M. Lozano, D. L. Clark, S. D. Conradson, C. Den Auwer, C. Fillaux, D. Guilaumont, D. W. Keogh, J. M. de Leon, P. D. Palmer and E. Simoni, Phys. Chem. Chem. Phys., 2009, 11, 10396–10402.
37. F. Heberling, A. C. Scheinost and D. Bosbach, J. Contam. Hydrol., 2011, 124, 50–56.
38. V. Neck, J. L. Kim and B. Kanellakopulos, Radiochim. Acta, 1992, 56, 25–30.
39. V. G. Petrov, D. Fellhauer, X. Gaona, K. Dardenne, J. Rothe, S. N. Kalmykov and M. Altmaier, Radiochim. Acta, 2017, 105, 1–20.
40. D. Fellhauer, X. Gaona, K. Dardenne and M. Altmaier, in Solubility, hydrolysis and chloride complexation of Np(V) in alkaline, dilute to concentrated NaCl, MgCl₂ and CaCl₂ solutions, Pu Futures the Conference, Baden-Baden, Germany, 2016; Baden-Baden (Germany), 2016.
41. A. R. Felmy and J. H. Weare, Geochim. Cosmochim. Acta, 1986, 50, 2771–2783.
42. Y. L. Xiong, L. Kirkes and T. Westfall, J. Solution Chem., 2018, 47, 595–610.
43. W. Wong-Ng, H. F. McMurdie, C. R. Hubbard and A. D. Mighell, J. Res. Natl. Inst. Stand. Technol., 2001, 106, 1013–1028.
44. S. A. Wang, E. M. Villa, J. A. Diwu, E. V. Alekseev, W. Depmeier and T. E. Albrecht-Schmitt, Inorg. Chem., 2011, 50, 2527–2533.
45. V. Neck, T. Fanghänel, G. Rudolph and J. Kim, Radiochim. Acta, 1995, 69, 39–48.
46. D. Fellhauer, Untersuchungen zur Redoxchemie und Löslichkeit von Neptunium und Plutonium, PhD Thesis, Universität Heidelberg, Heidelberg, 2013.
47. D. Fellhauer, J. Rothe, M. Altmaier, V. Neck, J. Runke, T. Wiss and T. Fanghänel, Radiochim. Acta, 2016, 104, 355–379.

---

Footnotes

† Current address: Brenk Systemplanung GmbH, Aachen, Germany.

‡ Current address: Institute of Micro- and Nanostructure Research, Friedrich-Alexander-Universität Erlangen-Nürnberg, Germany.

§ Current address: State Key Laboratory of Radiation Medicine and Protection School for Radiological and interdisciplinary Sciences (RAD-X) and Collaborative Innovation Center of Radiation Medicine of Jiangsu Higher Education Institutions Soochow University, China.

---