A quantitative empirical directing group scale for selectivity in iridium-catalysed hydrogen isotope exchange reactions

Abstract

A palette of commonly used directing groups, including various pharmaceutically relevant nitrogen-containing heterocycles, are quantitatively ranked based on the results of intermolecular hydrogen isotope exchange competition reactions using two iridium complexes: [Ir(COD)(IMes)(PPh₃)][BArF₂₄] and [IrCl(COD)(IMes)]. The directing group power scales that have been constructed from these data reveal a wide range of reactivity covering four orders of magnitude. Intramolecular competition experiments have demonstrated that the obtained reactivity scale provides accurate predictions of regioselectivity within molecules with multiple competing directing groups. This work contributes to our understanding and control of regioselectivity in metal-catalysed C–H activation reactions.

---

Introduction

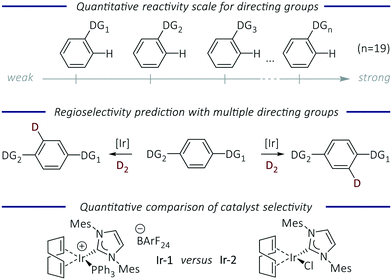
Transition metal-catalysed C–H functionalisation is a powerful synthetic tool to convert C–H bonds into carbon–carbon and carbon–heteroatom bonds without the need for substrates to be prefunctionalised.^1,2 Despite the developments in this area, understanding and control of site-selectivity in complex molecules with multiple C–H bonds is required in order for this approach to reach its full potential.³ The use of directing groups (DGs) has proved to be one of the most successful methods for inducing regiocontrol over C–H activation.⁴ DGs are typically coordinating Lewis bases, which guide the metal catalyst to a specific C–H bond in the molecule, allowing its selective cleavage and subsequent functionalisation. A diverse range of DGs are compatible with many C–H functionalisation processes, and most are ortho-directing. For the functionalisation of more complex molecules the presence of multiple directing groups can lead to reactions occurring at several sites, and control in these processes remains a central challenge to the development of C–H functionalisation reactions.

The prediction of regioselectivity in complex molecules depends on an understanding of relative directing group strength. Preliminary studies have been carried out in a small number of cases to assess directing group ability. The evaluation of relative DG ability in two specific metal-catalysed reactions (acetoxylation⁵ and halogenation)⁶ has been conducted. A quantitative reactivity scale for DGs (imines/N-heterocycles) in ruthenium-catalysed C–H arylation reactions was obtained from intermolecular competition experiments.⁷ More recently, a quantum chemical approach was used to develop a relative DG strength scale to predict regioselectivity in palladium-catalysed C–H activation reactions, based on the relative energies of the corresponding palladacycle intermediates.⁸ There are still very few quantitative studies in this area that allow the robust and quantitative prediction of regioselectivity. Herein, we tackle this issue using hydrogen isotope exchange (HIE) as a model C–H activation reaction due to its wide scope, mild reaction conditions, and operational simplicity.^9,10 The key aims of our work were to: develop a quantitative directing group scale; apply this to predict the regioselectivity of reactions of functionalised molecules; and quantify the difference in selectivity between HIE catalysts as a tool to evaluate current and future HIE catalysts (Fig. 1).

Fig. 1 Aims of this study.

Some empirical ranking of selectivity has been performed for HIE directed by N-heterocycles, but the use of excess D₂ resulted in very small differences in the conversion of each substrate and the resulting rankings were only qualitative.¹¹ Derdau and co-workers reported qualitative trends in the relative reactivity of several directing groups based on competition experiments and DFT calculations.¹² They were able to predict the major deuteration or tritiation positions based on comparison of the calculated free energies of activation.

Here, we describe the most detailed quantitative and systematic determination of DG ability to date, using HIE as a model C–H activation reaction; this is based on relative rate constants obtained experimentally from a structured set of competition experiments. The resulting reactivity scale spans nineteen directing groups that are often present in, for example, drug molecules and natural products, and ranks them in order of how effectively they deliver the iridium catalyst to the adjacent C–H bond. Competition experiments with two iridium complexes – cationic NHC/phosphine complex [Ir(COD)(IMes)(PPh₃)] Ir-1 and neutral NHC/chloride complex [IrCl(COD)(IMes)] Ir-2 – were conducted to reveal the differences in reactivity and selectivity between these species. Intramolecular experiments show that these data can be used to not only predict the preferred site of labelling, but also to quantify the ratio of deuteration at each site.

Results and discussion

Experimental approach

Kerr's suite of catalysts have proven to be highly effective and selective catalysts in C–H activation and H/D and H/T exchange reactions of substrates with a variety of directing groups, and so they were deployed for this study. Complexes of the type [Ir(COD)(IMes)(PR₃)]PF₆ have been successfully applied to homogeneous, ortho-directed HIE processes using a range of O- and N-donor directing groups (COD = 1,5-cyclooctadiene; IMes = 2,6-bis(2,4,6-trimethylphenyl)imidazol-2-ylidene); these include ketones, amides, esters, and nitroarenes, as well as various heterocycles, such as pyridines, pyrimidines, pyrazoles, imidazole(in)es, thiazole(in)es, oxazole(in)es and their benzo-fused analogues.^11,13–15 The PF₆ counterion was replaced with tetrakis(3,5-bis(trifluoromethyl)phenyl)borate (BArF₂₄) to produce a second generation of complexes, further improving reactivity and broadening the range of applicable solvents.^16,17 Additionally, neutral [IrCl(COD)(NHC)] complexes were shown to be effective catalysts in the HIE of aryl ketones and nitrogen-based heterocycles,¹⁸ and excelled in the labeling of secondary sulfonamides,¹⁹ and the formyl HIE of aldehydes.²⁰ However, there are subtle differences between the reactivity of these complexes, depending on the nature of the ancillary ligands, and as a result, this area would benefit from a rigorous and quantitative understanding of directing group ability, as well as serving as an appropriate model reaction for the much larger field of C–H activation.

The relative rates of hydrogen–deuterium exchange reactions were determined by competition experiments. In these experiments, equimolar quantities of each of the two substrates, bearing different DGs, were exposed to substoichiometric amounts of Ir-1 or Ir-2 and a limiting amount of D₂ in DCM at 25 °C (see Experimental section). The use of less than one equivalent of deuterium gas ensured that full conversion for both substrates was not possible, and therefore that meaningful differences in deuteration at each site should be observed. The two different Ir(I) catalysts were used for these reactions because of the distinct and complementary reactivity that has been observed previously for these complexes (vide supra).

The competition constants κ, which reveal the relative rates of two competing labelling reactions of the substrates R1 and R2 with rates k₁ and k₂, respectively, can be expressed by eqn (1) (Scheme 1).²¹ Each substrate combination was analysed at least three times, and in each case the ratio of the initial [R]₀ and remaining [R]_t concentrations of non-deuterated substrates were determined by integration of the ¹H NMR spectra. The initial concentrations of substrates are defined by eqn (2) (mass balance). This approach has been successfully used by Mayr and Knochel to quantify relative reactivities in palladium-catalysed cross-coupling reactions of substituted aryl bromides and organozinc reagents²² and the relative rates of halogen-magnesium exchange.²³

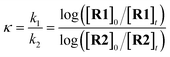
Scheme 1 Competition experiments to access reaction selectivity.

[R]₀ = [R]_t + [P]_t (2)

A quantitative reactivity scale for directed HIE

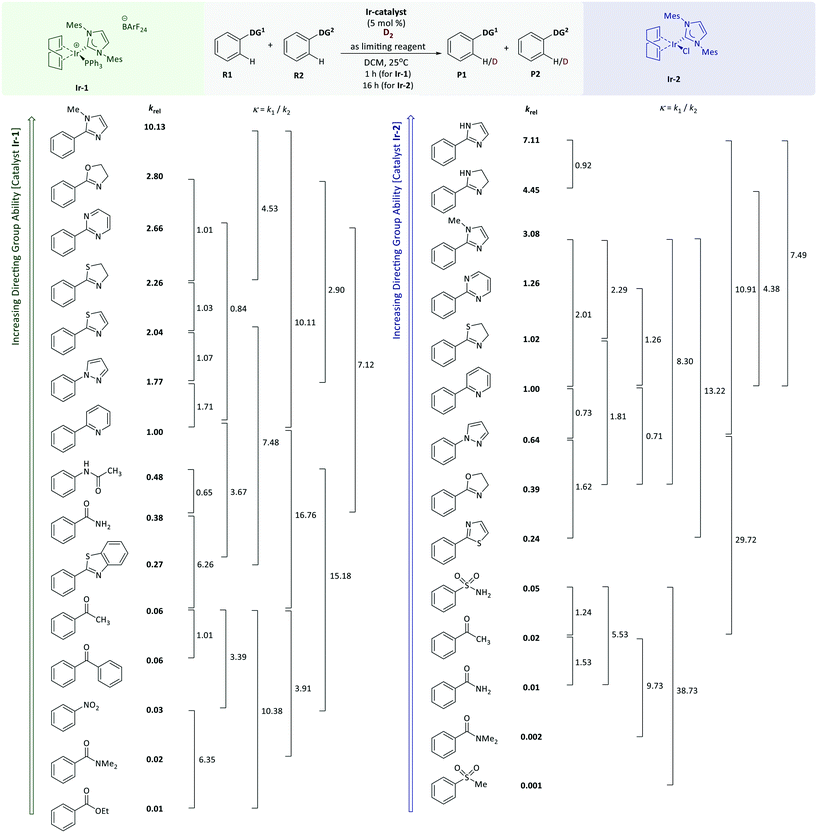
The competition HIE reactions between phenylpyridine and phenylpyrazole were used as a model system to evaluate the effects of various parameters such as reaction time, catalyst loadings and solvents. The competition constants (κ) were found to be time-independent, as confirmed by repeating the same experiment over shorter periods of time. For instance, the competition experiment with phenylpyridine and phenylpyrazole (with Ir-2) gave κ = 1.29–1.44 at different time points. Competition reactions between phenylpyridine and phenylpyrazole with different catalyst loadings (2.5 to 10 mol% Ir-2) gave similar results (κ = 1.05–1.35). A representative series of chlorinated, ethereal, ester, and aromatic solvents were used to perform competition experiments with the same model reaction; phenylpyrazole was found to be more reactive than phenylpyridine in DCM, THF, Et₂O and toluene (κ = 1.71, 1.33, 1.38, and 1.75, respectively), whereas in ethyl acetate the order of reactivity was reversed (κ = 0.90). For the remainder of our studies, DCM was used as the reaction solvent. Each model substrate listed in Fig. 3 was utilised in multiple competition labelling reactions with several different model substrates. A total of 20 competition experiments were conducted with Ir-1, and 19 competition experiments were carried out with Ir-2; each competition experiment was performed in triplicate. For each substrate pair, κ formally relates the relative rates of the reactions of two different substrates (eqn (3)).

log κ = log k₁ − log k₂ (3)

Linear regression analysis of the dataset from a series of the HIE competition reactions was performed to find optimised relative rate constants (k_rel) by minimising the sum of squares errors (∑Δ² = ∑(κ^exptl − κ^calcd)²) for each competition experiment, where κ is expressed by eqn (3). The pyridine directing group was assigned as the reference substrate with k_rel = 1 (i.e. k_{rel(substrate)} = k_(substrate)/k_{(phenylpyridine)}). The k_rel values obtained from least squares minimisation were used to derive κ^calcd for each competition experiment that was carried out. A comparison of κ^calcd and experimentally-determined values of κ^exptl is important because a good correlation means that the values of k_rel from linear regression are reliable and are consistent across experiments. As depicted in Fig. 2, a plot of the experimental κ^exptl against κ^calcd shows an excellent correlation, indicating the robustness of our approach.

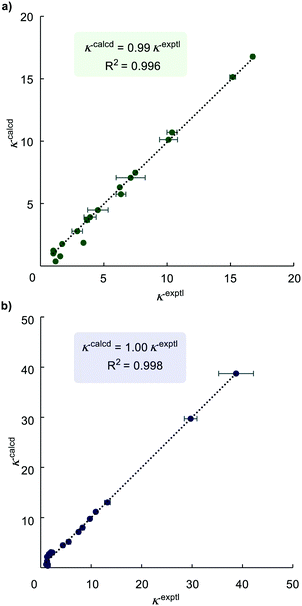Fig. 2 Plots of experimental versus calculated (from linear regression) competition constants κ. a) For catalyst Ir-1; b) for catalyst Ir-2.

With relative rate constants k_rel in hand, a quantitative directing group reactivity scale was constructed, comprising nineteen directing groups. Fig. 3 shows a reactivity range covering four orders of magnitude, from ethyl benzoate, methyl phenyl sulfone, and benzamide as the least reactive substrates, to phenylimidazol(in)es as the most reactive substrates of the series.

Fig. 3 A quantitative directing group power scale for HIE catalysed by iridium(I) complexes Ir-1 (left, green) and Ir-2 (right, purple). The values of k_rel are derived from linear regression of the entire dataset, while the values next to each bracket indicate the value of κ measured experimentally for that substrate pair.

The directing groups follow almost the same reactivity trends with the two different catalysts, Ir-1 and Ir-2. In general, the strongest coordination to iridium takes place through a nitrogen atom, whereas groups that bind through an oxygen or sulfur atom are weaker. Benzenesulfonamide and acetanilide were found to be the most reactive of the non-heterocyclic directing groups. N-Heterocyclic directing groups proved to be the most effective of those studied, with both catalysts. Fully unsaturated six-membered nitrogen heterocycles are less reactive compared to their five-membered ring analogues, and pyrimidine is a more effective than pyridine as a directing group. Even though for Ir-2 the individual competition constants (κ = 1.4) showed pyrazole and oxazoline to be slightly more reactive when compared to pyridine, the linear regression based on the whole data set placed these directing groups below pyridine in the reactivity scale. Within the saturated five-membered heteroaromatic directing groups, oxygen and sulfur analogues showed lower reactivity compared to imidazole. Thiazoline demonstrates higher reactivity than thiazole (k_rel = 1.1 for Ir-1; k_rel = 4.2 for Ir-2). The fusion of a benzene ring with a five-membered aromatic heterocycle appears to decrease the reactivity by seven-fold (benzothiazole versus thiazole; k_rel = 0.27 vs. 2.04). The methyl substituted derivative of imidazole is less reactive, presumably due to the steric hindrance introduced by N-methylation. A similar effect was observed when benzamide was compared to N,N-dimethyl benzamide, suggesting that the sterically larger N-methyl substituents are detrimental to the reaction. This observation might also be due to hindered rotation within the molecule, which will affect the conformations that can be readily adopted by the substrate during binding and catalysis.

Predicting selectivity in substrates with multiple directing groups

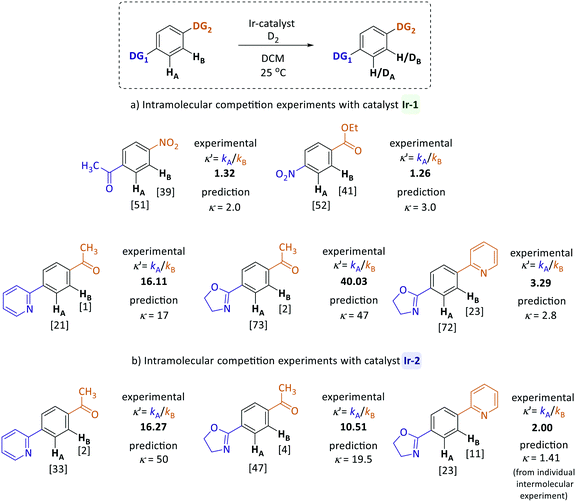
To examine the applicability of the directing group reactivity scale obtained in our work, a series of intramolecular HIE competition studies of model substrates were conducted, where multiple potential directing groups can compete for coordination (and subsequent C–H activation) at the iridium centre. Several representative substrates were examined under the same reaction conditions as previously used for competition experiments with two substrates (Scheme 2). The competition constants κ′, which reveal the relative labelling rates of two competing sites (H_Aversus H_B), were calculated as the ratio of deuterium incorporation at each position (κ′ = %D_A/%D_B). Competition rate constants κ′ obtained for reactions with both catalysts (Ir-1 and Ir-2) were then compared to the prediction based on the quantitative reactivity scale in Fig. 3.

Scheme 2 Intramolecular competition studies. The numbers in brackets next to H atoms are deuterium incorporations, reported as the average of three experiments. Unless stated otherwise predicted κ are based on k_rel from linear regression.

The calculated (predicted) competition constants are derived from the corresponding k_rel values for each directing group; the exception is the pyridine–oxazoline comparison for catalyst Ir-2, where the experimental constant κ from intermolecular competition experiments was used for comparison, because there is not a clear order of reactivity for these substrates with catalyst Ir-2. Pleasingly, the inter- and intramolecular competition reaction are in good agreement. The experimental and predicted from reactivity scale competition constants are not expected to be exact, as the two directing groups present in each molecule are linked to the same aromatic system and can affect each other and the core aromatic ring electronically, whereas in the intermolecular experiments only mono-substituted systems were investigated. Future work will investigate how these effects can be decoupled from the intrinsic directing ability of each group.

For example, according to the reactivity scale for catalyst Ir-1, pyridine and oxazoline are very strong DGs with k_rel = 1.0 and k_rel = 2.80 respectively, whereas acetophenone is significantly weaker (k_rel = 0.06). As expected, the HIE reactions of para-pyridyl and para-oxazolyl acetophenones labelled almost exclusively ortho to the heterocyclic directing groups and show excellent correlation between the calculated and experimental competition constants for catalyst Ir-1. In case of iridium complex Ir-2, the prediction is less accurate, as for this catalyst there was only one competition experiment linking the strength of heterocyclic systems and other less reactive directing groups. For the competition between pyridine and oxazoline directing groups, the scale yields accurate predictions for both catalysts. As illustrated in Fig. 3, the nitro group is two times more reactive than the ketone, and the ester is three times less reactive than the nitro group, which matches the experimental results.

Fig. 4 shows the correlation between the predicted and observed competition constants for the intramolecular competition experiments. As discussed above, predictions for the site-selectivity of reactions catalysed by Ir-1 not only show the reliable identification of the preferred site of labelling but also quantify the correct ratio of the deuterium incorporation; this is clearly illustrated by the correlation between prediction and measurement having a gradient close to 1.0. The much greater gradient (2.69) obtained for catalyst Ir-2 shows that our scale overestimates the predicted ratios of the deuterium incorporations, especially when groups with high reactivity difference are compared. However, this may be as a result of the relatively low incorporation of deuterium in some sites and the limits in the accuracy and precision with which we can determine the extent of deuteration by ¹H NMR integration.

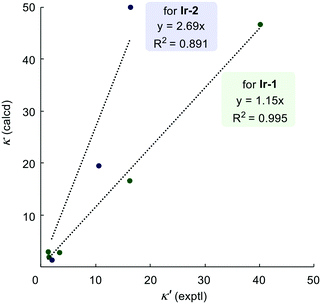Fig. 4 Plots of experimental versus calculated (from reactivity scale) competition constants for intramolecular reactions.

With our quantitative DG activity scale in hand we can predict not only the main site of the hydrogen isotope exchange reactions, but also estimate the ratio of deuteration at different sites within substrates bearing multiple directing groups.

Finally, we have considered the order of reactivity identified (and quantified) here in the context of previous work to quantify and understand directing group ability in metal-catalysed C–H functionalization reactions (Fig. 5). Most of the literature scales are qualitative or semi-quantitative, but a comparison of the order of directing group ability is achievable.

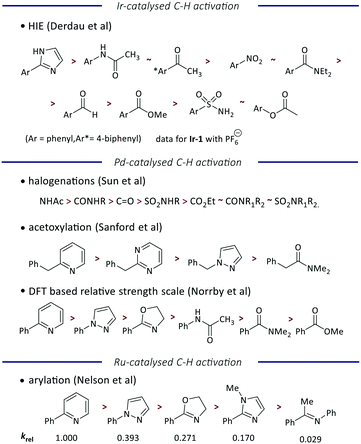Fig. 5 Comparison of the directing group abilities reported for different transition-metal catalysed C–H activation reactions.

Unsurprisingly, the recent study by Derdau and co-workers using an analogue of Ir-1 (with the PF₆ rather than BArF₂₄ counterion) reveals the same order of reactivity as observed here, although our scale is able to differentiate between acetamide and acetophenone, and between nitrobenzene and N,N-diethylbenzamide.¹² A slightly different order of reactivity is observed in palladium-catalysed reactions, with studies of halogenation,⁶ acetoxylation,⁵ and a broad DFT-driven study⁸ giving a consistent order that ranks heterocycles ahead of carbonyl-containing groups. However, we note that this differs from the behavior of iridium in the relative directing group ability of different heterocycles. Finally, our recent study of ruthenium-catalysed arylation yields an order of directing group ability that correlates well with the order identified for palladium.⁷ While further work is required to interrogate these reactivity trends and understand where and why they differ, we note that palladium and ruthenium are 4d transition metals, while iridium is a 5d transition metal, and so this may explain some of the contrasting behaviour.

Conclusions

In summary, we have quantitatively ranked the commonly used directing groups, including various pharmaceutically relevant nitrogen-containing heterocycles, based on the results of intermolecular competition HIE reaction using a cationic NHC/phosphene complex (Ir-1) and a neutral NHC/chloride complex (Ir-2). The directing group power scales constructed for a robust and structured series of competition experiments reveal a wide range of reactivity that spans four orders of magnitude (k_rel = 10⁻³ to 10¹). Intramolecular competition experiments have demonstrated that our reactivity scales provide accurate predictions of preferred labelling site within molecules that possess multiple competing directing groups. Our relative strength scale includes nineteen common directing groups and can be used for semi-quantitative regioselectivity predictions in hydrogen isotope exchange reactions of complex molecules, as well as designing new substrates with combinations of directing groups for late stage functionalization in medicinal chemistry.

Experimental

General procedure for competition experiments: the two substrates of interest (0.10 mmol each) were added to a J. Young Schlenk flask (of ca. 8 mL volume), along with the catalyst of choice (0.005 mmol) in air. DCM (6 mL) was added in such a way to rinse the inner walls of the flask. The flask was then sealed (with the gas inlet left open) under air before being cooled in a dry ice–acetone bath. The flask was evacuated and flushed with deuterium three times via a balloon. The gas inlet was then closed with fast thread tap, creating a sealed atmosphere of deuterium. After sealing the flask, it was placed in a thermostated water bath, and the reaction timer was started. The reaction mixture was stirred at 25 °C (1 h for catalyst Ir-1 and 16 h for catalyst Ir-2) before the removal of excess deuterium and the opening of the flask to air. The reaction mixture was quenched by the addition of a few drops of MeCN and transferred to a single-necked flask together with washings (DCM) before removing the solvent under reduced pressure. For NH-containing substrates (benzamide, benzenesulfonamide, acetanilide, phenylimidazol(in)e) the residue was directly analysed by ¹H NMR spectroscopy. For other substrates, the residue was dissolved in a small portion of a 1 : 1 mixture of petroleum ether and diethyl ether or ethyl acetate and passed through a short plug of silica, eluting with a 1 : 1 petroleum ether/diethyl ether solution or a 1 : 1 ethyl acetate/petroleum ether solution (3 × 2 mL). The solvent was evaporated again under reduced pressure and the residue was analysed by ¹H NMR spectroscopy.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the Leverhulme Trust for a Research Project Grant (RPG-2018-207). We thank Mr. Gavin Bain (now retired), Mr. Alexander Clunie, Mr. Craig Irving, Ms. Patricia Keating, and Dr. John Parkinson for assistance with technical and analytical facilities, and Mr. Jamie McIntyre for the synthesis of some starting materials.

Notes and references

1. D. Y. K. Chen and S. W. Youn, Chem. – Eur. J., 2012, 18, 9452–9474.
2. J. Yamaguchi, A. D. Yamaguchi and K. Itami, Angew. Chem., Int. Ed., 2012, 51, 8960–9009.
3. J. A. Labinger and J. E. Bercaw, Nature, 2002, 417, 507–514.
4. C. Sambiagio, D. Schönbauer, R. Blieck, T. Dao-Huy, G. Pototschnig, P. Schaaf, T. Wiesinger, M. F. Zia, J. Wencel-Delord, T. Besset, B. U. W. Maes and M. Schnürch, Chem. Soc. Rev., 2018, 47, 6603–6743.
5. L. V. Desai, K. J. Stowers and M. S. Sanford, J. Am. Chem. Soc., 2008, 130, 13285–13293.
6. X. Sun, G. Shan, Y. Sun and Y. Rao, Angew. Chem., Int. Ed., 2013, 52, 4440–4444.
7. J. McIntyre, I. Mayoral-Soler, P. Salvador, A. Poater and D. J. Nelson, Catal. Sci. Technol., 2018, 8, 3174–3182.
8. A. Tomberg, M. É. Muratore, M. J. Johansson, I. Terstiege, C. Sköld and P.-O. Norrby, iScience, 2019, 20, 373–391.
9. J. Atzrodt, V. Derdau, W. J. Kerr and M. Reid, Angew. Chem., Int. Ed., 2018, 57, 1758–1784.
10. J. Atzrodt, V. Derdau, W. J. Kerr and M. Reid, Angew. Chem., Int. Ed., 2018, 57, 3022–3047.
11. J. Atzrodt, V. Derdau, W. J. Kerr, M. Reid, P. Rojahn and R. Weck, Tetrahedron, 2015, 71, 1924–1929.
12. M. Valero, T. Kruissink, J. Blass, R. Weck, S. Güssregen, A. T. Plowright and V. Derdau, Angew. Chem., Int. Ed., 2020, 59, 5626–5631.
13. J. A. Brown, S. Irvine, A. R. Kennedy, W. J. Kerr, S. Andersson and G. N. Nilsson, Chem. Commun., 2008, 1115–1117.
14. J. A. Brown, A. R. Cochrane, S. Irvine, W. J. Kerr, B. Mondal, J. A. Parkinson, L. C. Paterson, M. Reid, T. Tuttle, S. Andersson and G. N. Nilsson, Adv. Synth. Catal., 2014, 356, 3551–3562.
15. J. Devlin, J. W. Kerr, M. D. Lindsay, J. D. T. McCabe, M. Reid and T. Tuttle, Molecules, 2015, 20, 11676–11698.
16. A. R. Kennedy, W. J. Kerr, R. Moir and M. Reid, Org. Biomol. Chem., 2014, 12, 7927–7931.
17. W. J. Kerr, R. J. Mudd, P. K. Owens, M. Reid, J. A. Brown and S. Campos, J. Labelled Compd. Radiopharm., 2016, 59, 601–603.
18. A. R. Cochrane, S. Irvine, W. J. Kerr, M. Reid, S. Andersson and G. N. Nilsson, J. Labelled Compd. Radiopharm., 2013, 56, 451–454.
19. W. J. Kerr, M. Reid and T. Tuttle, ACS Catal., 2015, 5, 402–410.
20. W. J. Kerr, M. Reid and T. Tuttle, Angew. Chem., Int. Ed., 2017, 56, 7808–7812.
21. R. Huisgen, Angew. Chem., Int. Ed. Engl., 1970, 9, 751–762.
22. Z.-B. Dong, G. Manolikakes, L. Shi, P. Knochel and H. Mayr, Chem. – Eur. J., 2010, 16, 248–253.
23. L. Shi, Y. Chu, P. Knochel and H. Mayr, Org. Lett., 2012, 14, 2602–2605.

---

Footnotes

† Dedicated to the memory of Professor Rolf Huisgen.

‡ All data underpinning this publication are openly available from the University of Strathclyde Knowledge Base at https://doi.org/10.15129/46bc02ea-f605-44f5-978c-fd7852fbdc19.

§ Electronic supplementary information (ESI) available: Synthetic procedures, characterisation data, competition experiment methodology, and outcomes thereof. See DOI: 10.1039/d0cy01597k

---