On the behaviour of structure-sensitive reactions on single atom and dilute alloy surfaces

Abstract

Materials that are composed of atomically dispersed platinum group metal (PGM) atoms on coinage metal surfaces show remarkable catalytic performance in a number of chemical reactions. On these single atom alloy (SAA) surfaces, the isolated PGM atoms exhibit unique reactivity features owing to their distinctive, and often limited, interactions with the surrounding coinage metal atoms. In this work, we use density functional theory to investigate the reactivity of numerous SAA(100) and (111) surfaces, focusing on typically structure-sensitive reactions, which include the direct dissociations of NO, CO₂ and N₂. Our results suggest that the structure-sensitivity of these three reactions is considerably reduced on SAA surfaces as compared to pure platinum group metal surfaces (Rh, Pt, Pd and Ni). Additionally, we examine the reactivity of small Rh and Ni ensembles doped on Cu(100) and (111) facets. We determine that Ni–Ni dimers and Ni trimers outperform the studied SAAs in the activation of N=O, C=O and N≡N bonds, and are also capable of performing facile association reactions. This work can guide future theoretical and surface science studies on SAAs, as well as the development of highly dilute alloys, which can efficiently catalyse chemistries of industrial significance.

---

1. Introduction

The importance of developing catalytic materials with high activity, stability and selectivity towards the desired product, in conjunction with the need for minimising the usage of expensive platinum group metals (PGMs) have motivated the development of single atom alloy (SAA) catalysts.^1,2 In these alloys, the host material is a relatively inert metal (i.e. Au, Ag and Cu), whereon embedded PGM atoms (e.g. Ni, Pt, Rh and Pd), known as the dopants, exist as isolated surface species. The dopant atoms are capable of first activating chemical bonds, thereby enabling highly selective catalysis to happen on the host metal sites at a later stage.³

Surface science and catalysis studies underline the excellent catalytic properties of SAAs for a number of chemistries, such as hydrogenation and dehydrogenation reactions,^2,4–6 C–H activation,^7,8 C–C coupling,⁹ and catalytic oxidations.¹⁰ Remarkably, studies by Zhang et al.¹¹ have unveiled that Pt/Cu SAA catalysts exhibit an unprecedented catalytic performance (i.e. extremely high activity, selectivity and stability) during the hydrogenolysis of glycerol to 1,2-propanediol; we note that the activation of pertinent reactions usually requires the presence of large PGM metal ensembles on the alloy surface.¹² Accordingly, the work of Zhang et al.¹¹ is a testament to the unique catalytic properties offered by isolated reactive atoms doped on less reactive host materials.¹³ In addition, very recent studies by Furukawa and co-workers highlight that Pd/Cu SAA nanoparticles supported on Al₂O₃ are exceptional catalysts for the catalytic NO reduction by CO.¹⁴ The latter reaction is crucial for stripping out harmful gases from catalytic converters.¹⁵ In particular, the authors demonstrated that on a Pd/Cu SAA catalyst, NO was fully converted to N₂ at low temperatures (e.g. 200 °C) and, remarkably, this occurred without the formation of other undesired products such as N₂O.¹⁴

The extraordinary catalytic performance of SAAs is ascribed to the distinctive electronic structure of the isolated dopant atom amid the host metal atoms. Photoemission spectroscopy and density functional theory (DFT) show that, for a number of SAA surfaces, the d band of the doped atom is very narrow, resembling that of a gas phase metal atom.^16,17 This electronic characteristic is attributed to the occasionally limited electronic interactions between the dopant atom and its coordination environment, and brings about the high reactivity of SAAs.¹⁶ Furthermore, calculations performed by our group suggested that CO exhibits very similar binding strengths on the top dopant site of two low-index SAA surfaces, (100) and (111),¹⁸ which are the most commonly exposed surfaces on face-centred cubic metals.¹⁹ This finding implies that adsorbate binding is not affected by the geometry of the host (at least for CO), and gives rise to questions of far-reaching significance for future surface science and theoretical investigations: are isolated dopant atoms on flat (111) and (100) surfaces equivalent in terms of reactivity? Do dopant atoms on different flat facets have comparable electronic structures? Could typically structure-sensitive reactions (e.g. N≡N,²⁰ C=O,²¹ N=O (ref. 22) bond-breaking) exhibit similar behaviour on the two aforementioned flat surfaces?

To shed light on these questions, we have employed periodic DFT and investigate the catalytic activity of numerous single atom and pure metal (100) and (111) surfaces toward a number of structure-sensitive reactions that include the dissociations of CO₂, N₂ and NO. Although these dissociations are used as prototypical reactions in our work, they are ubiquitous steps in chemistries of fundamental importance (e.g. NO reduction reaction, CH₃OH synthesis, NH₃ synthesis).

According to our data, the reactivity of the more open (100) SAA facet is higher as compared to the reactivity of the (111) SAA facet. This observation is also corroborated by our computed density of states (DOS) projected onto the d states of the single atom. However, we observe that the investigated reactions show a noticeably lower structure-sensitivity on the SAA surfaces than that observed on pure PGM metal surfaces. This is a finding that may have a great impact upon the search of optimum SAA catalysts, as it indicates that surface science studies on a flat facet may yield valid conclusions for a different flat facet, not under investigation. Besides SAA surfaces, we also study the reactivity of highly dilute Ni/Cu and Rh/Cu alloy surfaces, whereon Ni and Rh atoms form small ensembles (Ni–Ni and Rh–Rh dimers, and Ni trimers). We find that Ni/Cu binary alloys are remarkably competent in activating chemical bonds, while being capable of performing facile association reactions (e.g. N + N → N₂). Therefore, we underline that Ni/Cu dilute alloys may be promising catalytic materials for a number of applications (e.g. NO reduction by CO and CH₃OH synthesis).

2. Computational details

Periodic DFT calculations were performed within the generalised gradient approximation (GGA).²³ For these calculations, we used the Vienna ab initio simulation package (VASP),^24,25 which solves the Kohn–Sham equations in an iterative manner.²⁶ The projector augmented wave (PAW) method was employed to model the interaction between the core and valence electrons, and the kinetic energy cut-off was set at 400 eV.²⁷ Exchange and correlation effects were treated with the optB86b-vdW functional,^28–30 which accounts for dispersive van der Waals (vdW) interactions. Spin-polarised calculations were performed for gas-phase NO and O₂, but also for Ni surfaces and Ni-containing alloys; however on the latter surfaces, we noticed that the magnetic moment of Ni atoms was quenched during the simulation, which is consistent with previous works.^16,31 The low-index (100) and (111) surfaces were modelled by a 5-layer p(3 × 3) cell, and periodic images along the z-direction were separated by a vacuum of 10 Å. The presence of a small number of dopant atoms (i.e. up to three) on the surface layer of the highly dilute and SAA surfaces will, in all probability, have an unimportant effect on the lattice constant of the host material. Therefore, the lattice constant of the alloy materials was the optB86b-vdW computed lattice constant of the host metal (i.e. Au, Ag or Cu). These lattice constants are reported in the ESI of ref. 32. During geometry optimisation the three top layers of the DFT slab and any adsorbed species were allowed to relax, whilst the two bottom layers were fixed at the calculated lattice constant. The electronic self-consistency threshold was set to 10⁻⁷ eV, the Hellman–Feynman forces were relaxed to less than 10⁻² eV Å⁻¹ and the first Brillouin zones of the (111) and (100) surfaces were sampled with a 9 × 9 × 1 Monkhorst–Pack k-point mesh. Our k-point convergence check shows that this simulation setup affords a good accuracy (see section I in the ESI†). In turn, this permits us to compare our computed activation barriers for the dissociation of CO₂ reaction on the (100) surface to those previously obtained on the (111) surface using a 13 × 13 × 1 k-mesh (see Fig. S2†).³² The adsorption energy of a NO and N₂ species bound to the surface (E_ads (A), where A = NO or N₂) was calculated using the following expression:where E^A+slab_tot is the DFT total energy of a slab with the adsorbed species thereon, E^slab_tot is the DFT total energy of the clean slab, and is the DFT total energy of the adspecies in the gas phase. The corresponding adsorption energies of O adatoms on the different surfaces are computed relative to O₂ in the gas-phase:where E^O+slab_tot is the DFT total energy of a slab with an O adspecies thereon, and is the DFT total energy of O₂ in the gas phase.

The transition states (TSs) of the elementary reactions studied, were located using the dimer method,³³ and vibrational frequency analyses verified that each TS found was a first-order saddle point on the potential energy surface. The activation barrier (E_a) and the reaction energy (ΔE_rxn) of an elementary step are found from eqn (3) and (4), respectively.

E_a = E_TS − E_IS, (3)

ΔE_rxn = E_FS − E_IS, (4)

where E_TS, E_FS and E_IS are the DFT-computed energies for the TS, final state (FS) and initial state (IS), respectively.

Finally, the presented d projected DOS were computed using LOBSTER version 3.2.0,^34–37 and the reported d-band centres were calculated as the first moment of the obtained d DOS:³⁸

where ρ(ε) is the electronic density of states distribution.

3. Results and discussion

3.1. Adsorption energies on SAA(111) and (100) surfaces

In our previous studies, we have explored the adsorption of CO on the top dopant site of a number of Cu-, Ag-, and Au-based SAA surfaces.^18,39 A highlight of our work was that the binding strength of CO on SAA(111) and (100) surfaces is almost identical.¹⁸ Therefore, our results suggested that isolated dopant atoms on flat facets show very similar reactivity, which appears to be independent of the geometry of the catalytic surface. To some extent, this phenomenon can be attributed to the limited electronic and spatial overlap between the dopant atom and its surrounding host metal atoms.^16,31

Herein, we further investigate and compare the reactivity of SAA(100) and (111) surfaces by calculating the adsorption energy of other common adsorbates thereon. We compute and report the adsorption energies of N₂, NO and O on the top dopant site of Cu-, Ag- and Au-based SAA(100) and (111) surfaces, with Pt, Pd, Rh and Ni as dopants. With regard to the most stable adsorption structure of the adsorbates under investigation, our DFT calculations show that both N₂ and NO prefer to adsorb in an upright linear configuration, with N being closer to the alloy surface for the latter species (i.e. the dopant atom) – (see Tables S5 and S6 in the ESI†).

Fig. 1(a) shows a parity between the computed adsorption energies of the three adspecies on the (111) and (100) SAA surfaces. For greater clarity, we do not show which alloy corresponds to which point in the plot, but a full list of the adsorption energy values is provided in section IX of the ESI.† A first observation is that there is a strong correlation between E_ads(111) and E_ads(100) for the SAA surfaces, with the vast majority of the plot points lying close to the parity line (Fig. 1(a)). We also observe that the binding strength is systematically stronger on the more open SAA(100) surfaces than on the SAA(111) surfaces, by ca. 0.10 eV on average (Fig. 1(a)). As noted earlier, one may expect a small electronic interaction between the PGM atom and its coordination environment.¹⁶ Yet, the narrow dopant–host interactions do not rule out the transfer of charge between these two types of surface species.¹⁶ Consequently, the observed disparate reactivity in Fig. 1(a) may be the result of dopant–host charge transfer, which occurs to a different extent on the SAA(100) and (111) surfaces, given their different geometry.

Fig. 1 (a) Parity plot between E_ads(100) and E_ads(111) for the adsorption of N₂, NO and O on the top dopant site of a number of SAA surfaces; for clarity, we also show the adsorption energies of the three species on the most stable adsorption site of the corresponding monometallic (MM) surfaces which include Pt, Pd, Rh, Ni, Ag, Au and Cu surfaces (points without outline). (b) Linear correlation between ε_d(100) and ε_d(111) of the dopant d states of the SAA surfaces. The parity line is shown as a dashed black line in panels (a) and (b); determination coefficients (R²) and fitting lines are shown in both panels (a) and (b). In the linear fit in panel (a) only the SAA surfaces are considered (points with black outline). (c) d DOS plots for all the SAA(100) and (111) surfaces, whereby the DOS are projected onto the d states of the single atom.

The reactivity of pure metal and alloy surfaces is conventionally explained by the position of the d band centre (ε_d) relative to the Fermi level: the higher the d band centre the higher the reactivity of a catalytic surface.³⁸ In an effort to better understand the generally higher reactivity of the SAA(100) facet as compared to the SAA(111) facet, we proceed by computing the d band centres of the isolated PGM atoms on the examined SAA surfaces (Fig. 1(b)). Interestingly, our results reveal a strong correlation between ε_d(100) and ε_d(111). In addition, we observe that ε_d(100) are always at higher energy than ε_d(111), suggesting that the d band model can rationalise the disparate reactivity exhibited by different SAA facets. On the contrary, we realise that the same model cannot explain the reactivity of different SAA surfaces that belong to the same facet. In particular, we note that there exists a poor correlation between the adsorption energies of the investigated adspecies (i.e. E_ads(O), E_ads(N₂) and E_ads(NO)) and the d band centres of the PGM for a specific facet (see Fig. S3 in the ESI†).

Next, we study the electronic structure of the dopant on the two low-index surfaces. To this end, we present the corresponding d projected DOS plots for a number of dopant atoms on coinage metal surfaces (Fig. 1(c)). As observed in Fig. 1(c), the d band of the single atom exhibits very sharp features close to the Fermi level for all Au- and Ag-based SAA surfaces for both low-index facets.³¹ Conversely, Cu-based SAA surfaces deviate, to some extent, from this behaviour, probably because of a better electron density mixing between the dopant and Cu atoms (Fig. 1(c)).³¹ We also note that the DOS plots of SAA(100) surfaces are shifted slightly closer to the Fermi level as compared to those of SAA(111) surfaces (Fig. 1(c)). This shift in d DOS is consistent with the data displayed in Fig. 1(b), and implies a higher electron density available close to the Fermi level for the PGM atoms on SAA(100). The end result is an enhanced interaction between the SAA(100) dopants and the adsorbate species (Fig. 1(a)).

3.2. Assessing the reactivity of SAA surfaces by calculating kinetic barriers

We continue by assessing the reactivity of SAA(100) and SAA(111) surfaces by means of TS calculations. We compute and report effective activation barriers with respect to the most stable initial states for three typically structure-sensitive reactions (for the definition of the effective barrier see section VIII in the ESI†), which include the direct dissociations of NO, CO₂ and N₂,^40–43 over the same SAA surfaces as before (Fig. 2). We also compute the same barriers over seven (100) and (111) pure metal surfaces (i.e. Pt, Pd, Rh, Ni, Ag, Cu and Au surfaces) – (Fig. 2). We point out that the presented kinetic barriers for the CO₂ dissociation reaction on (111) SAA and pure metal surfaces are taken from ref. 32 (Fig. 2(b)).

Fig. 2 E _a(100) and E_a(111) parity for SAA surfaces (red circles), pure metal surfaces (green squares) and Ni ensembles on Cu (orange diamonds) for (a) the direct dissociation of NO; (b) the dissociation of CO₂, and (c) the dissociation of N₂. (d) Cu nanoparticles whereon the geometry of Ni and Rh ensembles (Ni₂Cu, Rh₂Cu and Ni₃Cu) on the (100) and (111) surfaces is highlighted. Cu and Ni or Rh atoms are shown in orange and purple, respectively. The red lines in panels (a)–(c) are linear fits of only the SAA data (red circles).

To verify the reliability of our calculations, we first compare our results to data reported in the literature. The direct dissociation of NO is underscored as a crucial step for the NO reduction with CO. According to theoretical and experimental studies, under some circumstances this reaction step can be the rate determining step (RDS) of the NO + CO reaction.^44,45 Among the commonly employed pure metal catalysts in three-way catalytic converters (i.e. Rh, Pt and Pd), Rh is the only metal that is capable of activating the N=O bond at low temperatures.⁴¹ This observation is in line with our DFT calculations, which show that the activation barriers for the NO dissociation reaction over Rh surfaces (i.e. E_a = 0.44 eV and 1.42 eV for Rh(100) and Rh(111), respectively) are considerably lower than those over Pd and Pt surfaces (E_a = 1.44 eV, 2.25 eV, 0.81 eV and 2.05 eV for Pd(100), Pd(111), Pt(100) and Pt(111), respectively) – (Fig. 2(a)). Based on our simulations, the initial state of this reaction involves a nitric oxide molecule, which is adsorbed in an upright linear configuration with the N atom closer to a hollow site (3-fold and 4-fold for (111) and (100) surfaces, respectively) – (see Fig. S14 and S15†). The only exception to that is Rh(100), where we find that a different adsorption configuration, with NO almost parallel to the surface, is thermodynamically more stable than the upright linear adsorption structure. This is consistent with previous theoretical studies;⁴⁶ in addition, our computed NO dissociation barriers on Rh(100), Rh(111), Pd(100) surfaces are consistent with activation barriers reported in previous theoretical and experimental works.^41,47–51

Regarding the dissociation of CO₂ on Cu(100), we compute E_a = 0.95 eV, namely a value which is in excellent agreement with the experimentally determined value by Chorkendorff and co-workers of E_a = 0.96 ± 0.05 eV.⁵² We also note that there is also an excellent match between our calculated E_a for Ni(100) and Rh(100) surfaces and those reported by Liu et al. (Fig. 2(c)).⁴² Furthermore, in Fig. S5 of the ESI,† we provide the activation barriers for the reverse reaction (i.e. CO oxidation to CO₂). Our data, in line with other studies, suggest that the catalytic CO oxidation is very facile on pure metal Ag and Au surfaces,^53,54 while relatively low activation barriers are calculated for Cu(111) and Cu(100) surfaces (0.48 eV and 0.73 eV, respectively) – (Fig. S5†).

An important observation in Fig. 2(a)–(c) is that all three dissociation reactions are, in most of the cases, more facile on (100) SAA and pure metal surfaces than on the corresponding (111) surfaces. Indeed, according to Liu and Hu,⁵⁵ one should, in general, expect more facile bond activation on more open surfaces and on those containing under-coordinated sites (e.g. steps and kinks). This is not true, however, for association reactions, which often show little or no structure-sensitivity.⁵⁵ In our results, the structure-sensitivity of reactions that involve N=O, C=O and N≡N bond-breaking is clear for PGM surfaces (i.e. Pt, Pd, Rh and Ni), for which there is a significant scatter in the data (Fig. 2(a)–(c)). By contrast, the dissociation barrier differences between the (111) and (100) SAA surfaces are relatively small, and noticeably less accentuated in comparison to monometallic PGM surfaces (Fig. 2(a)–(c)). The same is true for coinage metal surfaces as well.

In order to quantify the average difference between the computed kinetic barriers on the two low-index surfaces, we define the following metric, :

k ∈ {SAAs, PGMs, Coinage Metals, All Pure Metal Surfaces} (6)

where N_k is the number of surfaces in group k (where k ∈ {SAA surfaces, PGM surfaces, coinage metal surfaces, all pure metal surfaces}), E_a,k,i are the computed activation barriers for surface i that belongs to group k, and N_S is the total number of surfaces in group k. Thus, for each catalyst group k, is indicative of the average extent by which the dissociation barriers computed for (111) surfaces deviate from those for the more open (100) surfaces.

Table 1 summarises values of for the dissociations of NO, CO₂ and N₂. We note that and show similar values for the three dissociation reactions, and an average 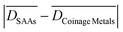of just 0.11 eV (Table 1). Along these lines, bond scission processes seem to exhibit low structure sensitivity on both pure coinage and SAA low-index surfaces.

Table 1 values for SAA and pure metal surfaces for the three examined dissociation reactions

Reaction	(eV)	(eV)	(eV)	(eV)
1. NO* → N* + O*	0.27	0.94	0.15	0.60
2. CO*2 → CO* + O*	0.13	0.42	0.33	0.39
3. N*2 → N* + N*	0.39	0.55	0.36	0.49

---

On the other hand, we find that the deviation between E_a(100) and E_a(111) for PGM surfaces () is, on average, larger by ca. 0.38 eV than that for SAA surfaces. Accordingly, it appears that a significant “part of the structure-sensitivity” of dissociation reactions is diminished on SAA surfaces as compared to the PGM surfaces, and this is an important observation from a surface science standpoint. The “retained structure-sensitivity” of SAAs can be ascribed to two factors: (i) the slightly different electronic d-band structure of the dopant on SAA(100) and (111) (see Fig. 1(b) and (c)), and (ii) geometric effects that arise as a result of the extended nature of the TS structure. Indeed, the TS geometries for the N₂ and NO dissociations are quite extended, and involve mainly mixed metal sites (see Fig. 3 for SAA(100) surfaces, Fig. S6, S7 and S12 in the ESI†).⁵⁶ Yet, the scission of the C=O bond of CO₂ appears to happen closer to the top dopant site, hence the relatively small for this reaction (see Fig. 3, Table 1 and Fig. S9 in the ESI†).

Fig. 3 Top view of representative IS, FS and TS structures on SAA(100) surfaces for the (a) dissociation of CO₂; (b) dissociation of NO and (c) dissociation of N₂. Dopant and host metal atoms are shown in dark green and orange, respectively. N, O and C atoms are shown in blue, red and grey, respectively. The structures of this figure correspond to the Pd/Cu(100) system, but they are representative for the majority of the SAA(100) surfaces.

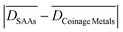Finally, the group all pure metals (Table 1) includes all the pure metal surfaces (i.e. PGM and coinage metals). Although this group contains the coinage metal surfaces which do not exhibit pronounced structure sensitivity for the bond cleavage reactions, we compute values that are always larger than and an average over the three reactions of ca. 0.23 eV.

3.3. Highly reactive Ni and Rh ensembles on Cu-based alloys

Another noteworthy feature of Fig. 2 is that, in general, Cu-based SAAs show considerably lower dissociation barriers as compared to Ag- and Au-based SAA surfaces (Fig. 2(a)–(c)). The high activity of Cu-based SAAs toward numerous chemical reactions has been experimentally confirmed.^4,11,14 We determine that, among the Cu-based SAAs, Ni/Cu and Rh/Cu bimetallic alloys exhibit the lowest dissociation barriers. The most facile bond cleavage reactions are predicted to occur on Ni/Cu surfaces (Fig. 2(a)–(c)). This behaviour may be explained by: (1) the more localised d states of the isolated Ni atom on Cu as compared to the broader d states of Rh, Pt and Pd atoms on the same host metal (Fig. 1(c)), and (2) the closer position of the d DOS peak of Ni on Ni/Cu to the Fermi level than the corresponding Pt and Pd peaks on Pt/Cu and Pd/Cu, respectively (Fig. 1(c)).

Yet, our simulations show that the computed kinetic barriers on pure metal Ni and Rh surfaces are always lower than those of the Ni/Cu and Rh/Cu SAA surfaces (Fig. 2(a)–(c)). For example, the activation barriers for the direct dissociation of NO on Rh(111) and (100) surfaces are 1.42 eV and 0.44 eV, respectively, while on Ni/Cu(111) and (100) SAA surfaces are 1.47 eV and 1.07 eV (Fig. 2(a)). Along the same lines, the dissociation of CO₂ appears to be more facile on Rh(100) (E_a = 0.28 eV) than on Ni/Cu(100) (E_a = 0.64 eV) – (Fig. 2(b)). Finally, the same trend holds true for the dissociation of N₂ for which our computed barriers for SAA surfaces are very large (i.e. E_a > 3.0 eV), and large for pure metal surfaces (i.e. E_a > 2.0 eV) – (Fig. 2(c)).

In an effort to circumvent the “kinetic barrier gap” between SAA and pure metal surfaces, we proceed by investigating the reactivity of small PGM “ensembles” (i.e. dimers and trimers), on Cu surfaces. PGM ensembles embedded on coinage host surfaces have recently drawn the attention of the catalysis community. For example, Wang et al.⁵⁷ demonstrated that Pd–Pd dimers on a Au host matrix exhibit optimal catalytic performance during the electroreduction of CO₂. Qiu et al.⁵⁸ proposed that Co trimers and tetramers on a Cu host are highly active and selective for the synthesis of CH₃OH via the hydrogenation of CO₂. Kim and Henkelman argued that only ensembles of more than three Pd atoms can catalyse the oxidation of CO on Pd/Au alloys.⁵⁹ Finally, recent ab initio Monte Carlo and machine learning studies reveal that the size and geometry of dopant ensembles can be tuned under reactive conditions, thereby providing the means for tailoring the catalytic performance of dilute alloys.^60,61 Herein, we focus our attention on Ni and Rh ensembles on a Cu host (i.e. Ni–Ni dimers and Ni trimers, which will be denoted as Ni₂Cu and Ni₃Cu, and Rh dimers Rh₂Cu) – (Fig. 2(d)). This is because Ni/Cu and Rh/Cu SAA surfaces demonstrate the highest capability of activating chemical bonds (Fig. 2(a)–(c)), and because Ni/Cu alloys are composed of relatively inexpensive metals and are therefore attractive from a practical standpoint. Regarding the Rh/Cu dilute alloys, we focus on the performance of Rh–Rh dimers on Cu, as previous works indicate that the SAA phase on Rh/Cu exhibits high thermodynamic stability under both vacuum and reactive conditions.⁶¹ Along these lines, we assume negligible formation of clusters larger than Rh–Rh dimers at low concentration of Rh over these surfaces.

Our data suggests that the kinetic barriers for NO or CO₂ dissociation on Rh–Rh dimers are comparable to or higher than those on the Rh/Cu SAA surfaces (Fig. 2(a) and (b)). On the contrary, the breaking of N=O, C=O and N≡N bonds is easier on Ni ensembles than on isolated dopant atoms on coinage metals (Fig. 2(a)–(c)). Therefore, the presence of small Ni aggregates on the catalytic surface appears to be beneficial for the catalytic activity toward dissociation reactions. Remarkably, we realise that Ni₂Cu, Ni₃Cu surfaces perform almost equivalently to commonly employed PGMs in catalysis, such as Ni, Pt and Rh (Fig. 2(a)–(c)). For the direct dissociation of NO, which is a key reaction step for the NO + CO reaction,⁴⁴ Ni₂Cu(111) and Ni₃Cu(111) demonstrate moderate kinetic barriers of 1.30 eV and 1.37 eV, respectively. These barriers are lower than the corresponding barriers for Rh(111) (E_a = 1.42 eV) as well as than those for Pd(111), and Pt(111) (E_a = 2.25 eV and 2.08 eV, respectively) – (Fig. 2(a)). Additionally, the desorption energies of NO from Ni dimers and trimers are larger (within the range of 2.7–3.1 eV for both low-index surfaces; see Table S1†) than the corresponding NO dissociation kinetic barriers, indicating a high probability for NO dissociation over Ni ensembles. This dissociation probability will also be large on the Ni(111) surface (where we find E_a = 1.29 eV and a desorption energy of NO of 2.84 eV; see Table S1†), but not that large for pure Cu(111) whereon the NO dissociation barrier (E_a = 1.56 eV) is almost identical to the corresponding desorption barrier (1.55 eV). Finally, it should be mentioned that on the (100) surface the lowest kinetic barrier is observed for Rh(100) – (E_a = 0.44 eV), justifying the extensive use of Rh in catalytic converters.

Moreover, the cleavage of the C=O bond is quite facile on Ni₃Cu and Ni₂Cu surfaces (E_a < 0.5 eV for both Ni ensemble surfaces). Regarding their pure metal counterparts, our calculations imply that the desorption of CO₂ will be preferred to its dissociation over Ni(111), Cu(111) and Cu(100) (see Tables S2 and S3 in the ESI†). Remarkably, the same is not true for Ni–Ni dimers and trimers, where we compute CO₂ desorption energies that are larger than the CO₂ dissociation barriers on these surfaces (see Table S4 in the ESI†). Accordingly, we conclude that CO₂ dissociation will be generally favoured against CO₂ desorption over that Ni ensemble surfaces. The only exception to that is the Ni₂Cu(111) surface for which the dissociation and desorption energies are 0.47 eV and 0.37 eV, respectively.

The better efficiency of Ni₂Cu and Ni₃Cu in cleaving chemical bonds compared to the Ni/Cu SAA, can be rationalised by the electronic structure of these systems (Fig. 4). Based on the IS and TS structures of the examined dissociation reactions, we realise that, with the exception of the Ni₃Cu(111) surface, the adsorbate species mainly interact with mixed sites on the Ni/Cu surfaces (i.e. sites that are surrounded by both Cu and Ni atoms) – (see Fig. 3, and S8, S10 and S13 in the ESI†). These mixed sites, whereon the bond breaking occurs, are composed of three and four surface atoms for (111) and (100) dilute alloy surfaces, respectively, and are displayed in the insets on the right of Fig. 4 for the Ni/Cu dilute alloy and SAA surfaces.

Fig. 4 d DOS plots for the Ni/Cu SAA and dilute alloy (a) (111) and (b) (100) surfaces, whereby the DOS are projected onto the d states of the mixed active sites shown on the right inset of each DOS plot. The mixed active sites are highlighted in the same colours as those of the corresponding DOS curves.

Also shown in Fig. 4(a) and (b) are the d DOS projected onto the atoms of the mixed active sites of SAA and dilute alloy surfaces. Almost all DOS plots exhibit bimodality; the first peak on the right (between 0 eV and −1.3 eV) is related to the d states of the embedded Ni atoms, while the broader peak on the left (between −1.5 eV and −4.5 eV) corresponds to the d states of Cu atoms (Fig. 4(a) and (b)). On the other hand, the Ni₃Cu(111) surface is hardly bimodal, and this stems from the fact that the active site for the dissociation thereon is composed only of Ni atoms (Fig. 4(a)).

Importantly, we observe that the right DOS peaks of Ni₃Cu and Ni₂Cu exhibit higher intensity and are closer to the Fermi level than the corresponding peaks of the two SAA low-index surfaces (Fig. 4). Along these lines, one may expect that electron back-donation from the mixed active site of the former surfaces to the antibonding orbitals of the adsorbates will be more pronounced compared to that on the Ni/Cu SAA surfaces. Charge transfer in this direction leads to the formation of dissociation precursors (e.g. CO₂^δ− during CO₂ dissociation),⁴² and thus is a crucial process in bond breaking reactions. This observation explains the generally higher efficiency of small Ni ensembles (i.e. dimers and trimers) than isolated Ni atoms in activating chemical bonds (Fig. 2(a)–(c)).

3.4. On the performance of Ni and Rh ensembles in association reactions

According to our discussion in the previous section, small Ni, and Rh to a smaller extent, ensembles on Cu surfaces show promising performance in relation to the activation of chemical bonds. The next step is to examine the performance of the Rh₂Cu, Ni₂Cu and Ni₃Cu surfaces toward association reactions, which are often equally important to dissociation reactions. We focus on the reverse reactions to those presented in Fig. 2, namely the formation of NO, N₂ and CO₂. Besides the aforementioned highly dilute alloy surfaces, we also investigate the performance of pure Cu, Ni and Rh surfaces, as these catalysts are the monometallic counterparts of the dilute alloys. Before proceeding to our results, we briefly discuss some fundamental principles with regard to association reactions. This discussion will help us in deciphering the observed trends in our simulation data.

In general, the barrier of an association reaction (e.g. A* + B* ↔ AB*) can be decomposed into terms that are associated with the geometric and electronic effects on the kinetic barrier as follows:⁶²

where E^TS_A, E^TS_B, E^IS_A and E^IS_B are the chemisorption energies of A and B in the TS and IS positions, respectively, and E^TS_int and E^IS_int account for the interactions between the reactants A and B in the TS and IS, respectively.⁶³ The latter terms are often positive as a result of repulsive interactions between the two reactants.

The chemisorption energies in eqn (7) are strongly related to the local electronic environment (i.e. the position of the d band centre) of the surface whereon the reactant species are bound to. These terms may be considerably different for chemisorption on under-coordinated sites (e.g. steps, kinks) than for chemisorption on flat surfaces (e.g. sites on the (111) surface), and quantify the contribution of the electronic effects to the association barrier.⁵⁵ Importantly, a large number of association reactions, including these examined here, exhibit early TSs. In such cases, the IS structure closely resembles the TS structure (e.g. see panels in Fig. 3 in the reverse order), thereby rendering E^TS_A and E^TS_B similar to E^IS_A and E^IS_B, respectively. On this basis, it is generally true that the contribution of electronic effects to the structure sensitivity of association reactions is small,⁵⁵ but not necessarily negligible.

Furthermore, the contribution of the geometric effects to E^as_a is described by E^TS_int and E^IS_int,⁵⁵ which quantify the interactions between the two reactants in the TS and in the IS. These interactions arise as a result of: (i) bonding competition effects,⁶⁴ and (ii) the direct Pauli repulsion between the reactant species.⁶² The former effects are important when the reactants are bonded to the same metal atom in the TS and/or IS structures.⁶² A good example is the activation of CH₄ over a Pt/Ag(111) SAA surface, where CH₃ and the activated H adatom share the top Pt site in the TS.³² Accordingly, we expect that bonding competition effects will be alleviated for the NO, N₂ and CO₂ formation reactions on Rh, Cu, Ni, Rh₂Cu Ni₂Cu and Ni₃Cu(100) and (111) surfaces, for which in the TS and IS, the reactants are located in different hollow sites and are not competing for the same metal top site (see Fig. S8, S10 and S13–S18†).

Regarding the direct Pauli repulsions, we note that these effects are important when the distance between the reactant species is less than 2.5 Å.⁶² Within this range of distance there will be a direct overlap between the wavefunctions of the reactants.⁶⁵Fig. 5, panels (a) and (b) summarise these distances (d_A–B) for the three studied reactions on dilute and pure metal surfaces for the TS and IS structures, respectively. It is noted that for all the ISs d_A–B > 2.5 Å, while for all the TSs the opposite is true and in the vast majority of the cases d_A–B < 2.0. Therefore, the magnitude of direct Pauli repulsions in the IS will be small, and E^IS_int in eqn (7) will be approximately zero.^55,62 Conversely, Pauli repulsions will be significant in the TSs and the magnitude of a computed association barrier will be heavily dependent on E^TS_int

Fig. 5 Reactant distances in the (a) TS and (b) IS structures for the three association reactions on the dilute alloy and pure metal (111) and (100) surfaces. The dashed line marks the 2.5 Å distance, below which Pauli repulsions become significant. Top view of the TS structures for the three reactions on the (111) and (100) pure metal surfaces (panels (c)–(e) for N₂, NO, CO₂, respectively) and dilute alloy surfaces (panels (f)–(h) for N₂, NO, CO₂, respectively). O, N and C atoms are shown by red, blue and grey, respectively. Ni, Cu and Rh atoms are shown in purple, orange and dark green, respectively.

Our computed barriers for the formation of N₂, NO and CO₂ are shown in Fig. 6(a)–(c) from where we note that these association reactions exhibit significant structure-sensitivity (Fig. 6(a)). This behaviour can be loosely attributed to the fact that, in many cases, the reaction intermediate species reside in high coordination sites (i.e. threefold and fourfold sites) – (Fig. 5(c)–(h)).⁶⁶ The lowest structure-sensitivity is seen for the oxidation of CO, where CO and O in the TS are always bound to low coordination sites (i.e. top and bridge sites) – (Fig. 5(e) and (h)).⁶⁶ Importantly, for all the association reactions, we observe that the Cu and dilute alloy surfaces follow the same trend by which the computed barriers on the (111) surfaces are lower than those of the corresponding (100) surfaces. The exact opposite trend is observed for Rh surfaces (Fig. 6(a)–(c)). These trends are associated with the extent of the direct Pauli repulsions between the reactants in the TS on these surfaces (we discuss this in the following paragraphs).

Fig. 6 Computed barriers for the formation of (a) N₂; (b) NO and (c) CO₂ on different (100) and (111) dilute alloy and pure metal surfaces (colour coding shown in the legend below the bar charts). Panels (d) and (e) show the 2p-projected DOS of an N atom adsorbed on Ni₂Cu and Rh surfaces, respectively. Panels (f) and (g) show the 2p-projected DOS of an O atom adsorbed on Ni₂Cu and Rh surfaces, respectively. The insets in panels (d)–(g) show the top view of the DFT slabs where the positions of the adatoms (N and O) is highlighted. Cu, Ni, Rh, O and N atoms are shown in orange, purple, dark green, red and blue, respectively. The area shaded in green in panels (d)–(g) is the p–d bonding area.

Particular attention is paid to the formation of N₂ as this reaction is a crucial elementary step for the NO reduction by CO because of the following reasons: (i) this association reaction frees up active sites that can catalyse subsequent surface reactions, and (ii) it is the RDS of the NO + CO reaction at high temperatures.⁴⁴ The IS of this reaction involves two N adatoms on hollow sites, whilst in the FS, N₂ is vertically adsorbed on a top site (see Fig. S13, S16 and S17†).^22,67 In order to verify the reliability of our data, we compare our computed kinetic barrier on Rh(111) – (E_a = 1.84 eV) to the value reported by Ishikawa and Tateyama for the same reaction pathway of N₂ formation (E_a = 1.78 eV),⁴⁴ and we find a reasonable agreement.

Our simulations show that the N₂ association reaction proceeds with similar kinetic barriers on the Rh₂Cu(100), Ni ensemble (100) – (i.e. Ni₂Cu & Ni₃Cu), Cu(100) and Rh(100) surfaces (Fig. 6(a)). These barriers are large, being within the range of 1.5–2.0 eV, and the lowest values are observed for Rh(100) and Ni₂Cu(100) (1.50 eV and 1.57 eV, respectively) – (Fig. 6(a)). We also find a very large association barrier on Ni(100) (E_a = 2.82 eV), whereon the formation of N₂ will be an extremely rare event.

Interestingly, the formation of N₂ is dramatically more facile on Ni ensembles, Rh–Rh dimers and Cu(111) surfaces as compared to the Rh(111) and Ni(111) surfaces. For example, the kinetic barrier for the Ni₂Cu(111) surface (E_a = 0.62 eV) is lower than that for Rh(111) (E_a = 1.85 eV) by 1.23 eV and that for Ni(111) (E_a = 1.54 eV) by 0.92 eV (Fig. 6(a)). This observation, along with the ability of Ni ensembles to dissociate the N=O bond, and the relatively low CO oxidation barriers of Cu surfaces (Fig. 6(c)), make us envision a bifunctional Ni/Cu alloy suitable for the reduction of NO. On this alloy catalyst, Cu atoms will be the active sites for the oxidation of CO,⁶⁸ while Ni ensembles will provide the sites for the N=O bond cleavage and the formation of N₂.

As pointed out earlier, an interesting observation is that the kinetic barrier for the formation of N₂ for Rh(100) is lower than that for Rh(111) – (i.e. E_a(111) > E_a(100)), while the opposite trend is true for the rest of the examined surfaces (i.e. E_a(111) < E_a(100)) – (Fig. 6(a)). This is true for the other association reactions as well (Fig. 6(b) and (c)), namely bond formation is more facile on the most densely packed dilute alloy (111) surfaces (Ni₂Cu, Ni₃Cu and Rh₂Cu).

According to our previous discussion the preponderant contribution to the computed association barriers stems from the direct Pauli repulsion between the reactants in the TS. Qualitative insights into the magnitude of the Pauli repulsion can be provided by the local DOS of the reactant species in the TS position.⁶² To this end, we analyse the N 2p-projected DOS of a single N atom adsorbed on the same position as in the TS structure for the following four surfaces: Ni₂Cu(111), Ni₂Cu(100), Rh(111) and Rh(100) – (Fig. 6(b) and (c)). The former two surfaces are representative of the E_a(111) < E_a(100) trend, while the latter two follow the E_a(111) > E_a(100) trend. Our DFT calculations show that the TS position for the N atom is near a bridge site for Rh(100), Rh(111) and Ni₂Cu(111) surfaces and near a mixed 4-fold site for Ni₂Cu(100) – (Fig. 5(c) and (f)).

The DOS plots are displayed in Fig. 6(d) and (e), and the main difference between the DOS curves is observed in the region between −7.0 eV and −5.0 eV; this is the region where the p orbitals of the N adatom mix with the d states of the catalytic surface (i.e. the p–d bonding region).⁶² We realise that the 2p-projected DOS in the p–d bonding region of the Ni₂Cu(100) surface has much higher intensity and appears more localised than on the Ni₂Cu(111) surface (Fig. 6(d)). Therefore, we expect a larger Pauli repulsion between the N adatoms on Ni₂Cu(100) than on Ni₂Cu(111), thereby explaining the large difference in the computed barriers (E_a = 1.57 eV and 0.62 eV for Ni₂Cu(100) and Ni₂Cu(111), respectively). Similarly, the N 2p-projected DOS for Rh(111) and Rh(100) show an overall higher density of states in the p–d bonding region for the former surface than for the latter (the total areas below the DOS curves in the p–d bonding region are 1.62 for Rh(111) and 1.35 for Rh(100); Fig. 6(e)). However, in this case the intensity of the peaks is similar (Fig. 6(e)), and consequently there is no dramatic difference in the barriers exhibited by the two surfaces (E_a = 1.85 eV and 1.50 eV for Rh(111) and Rh(100), respectively).

The observed trends for the formation of NO can be rationalised along the same lines as for the formation of N₂. We find that for the former reaction E_a(100) > E_a(111) on the three dilute alloy surfaces, and that the TS structures on both Ni₂Cu(111) and Ni₂Cu(100) facets involve an O adatom on a mixed bridge site (Fig. 5(g)). By analysing the 2p-projected DOS of the O adatom in the mixed bridge sites of the two aforementioned surfaces, we note that the DOS peaks in the p–d bonding area are similar in terms of intensity and width (Fig. 6(f)). This may be an indication that the observed differences between the barriers of the NO formation on (111) and (100) dilute alloy surfaces arise largely from the disparate electronic structure of the N atoms on these surfaces (Fig. 6(d)), and not from both reactants. Accordingly, the barrier differences between the (111) and (100) surfaces for the association of NO are much smaller than that for the formation of N₂ (Fig. 6(a) and (b)). Finally, Fig. 6(g) shows the 2p-projected DOS of an O adatom on Rh(111) and Rh(100) surfaces. The O DOS on Rh(111) exhibit a higher intensity and are more localised than the DOS for Rh(100), thereby explaining the E_a(100) < E_a(111) trend in Fig. 6(b).

As a final remark, regardless of the showcased capability of Ni ensembles to perform facile N₂ formation and N=O bond scission, we acknowledge that further studies are required to establish Ni/Cu dilute alloys as promising NO reduction catalysts. In particular, additional reaction steps that take place during the NO + CO reaction have to be examined (e.g. the formation of N₂O).^69–71 Moreover, in the presence of CO, the formation of harmful Ni(CO)₄ species is a common problem for Ni-based catalysts, and this would also have to be taken into account. Finally, kinetic Monte Carlo simulations, which account for adsorbate–adsorbate interactions,^72–76 should be performed in order to unveil phenomena occurring at the mesoscale. This will also enable an accurate comparison between the Ni/Cu dilute alloy and currently employed metals in catalytic converters (Pd, Pt and Rh). Ongoing research activities in our lab are dedicated to these additional considerations.

4. Concluding remarks

In summary, we have presented and discussed a large amount of data, which can serve as a guide for future experimental and theoretical studies that aim at developing SAA catalysts.

Our work focused on the reactivity of numerous SAA(100) and SAA(111) surfaces. By means of adsorption and TS calculations, we demonstrated that the reactivity of isolated PGM atoms doped on these two low-index coinage facets is, to some extent, dissimilar. This disparity in reactivity is mainly attributed to the distinct electronic structure demonstrated by dopant atoms when exposed to different coordination environments. Remarkably, however, our results underscore that (dissociation) reactions that exhibit significant structure-sensitivity on PGM surfaces, appear to a large extent structure-insensitive when they take place on (111) and (100) SAA and coinage metal surfaces. This is a result with far-reaching implications for future single-crystal and catalysis studies where the activation of chemical bonds is of central importance. In more precise terms, this result implies that works over the (111) SAA facet may give insight into the behaviour of the (100) SAA facet, and vice versa, thereby accelerating the development and design of optimal SAA catalysts. From a catalysis standpoint, the reduced structure-sensitivity of reactions on SAA surfaces may eliminate the need for precise engineering of the structure and geometry of catalytic nanoparticles.

Finally, we have examined the reactivity of small Ni and Rh ensembles (i.e. Rh–Rh dimers, Ni–Ni dimers and Ni trimers) on a Cu host toward the cleavage of N=O, C=O and N≡N chemical bonds. The Ni ensembles show increased capability in activating the aforementioned chemical bonds as compared to the SAA surfaces studied herein. By contrast, small Rh ensembles offer no significant benefit as compared to isolated Rh atoms on Cu. Importantly, the performance of Ni₂Cu and Ni₃Cu surfaces with respect to association and dissociation reactions was found similar (or even better in some cases) to those of well-established pure metals in heterogeneous catalysis (e.g. Rh, Pt and Pd), thereby underlining the potential of these materials for the catalysis of important reactions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

K. G. P. is funded by the Department of Chemical Engineering at University College London. The authors acknowledge the use of the UCL High Performance Computing Facilities Myriad@UCL, Kathleen@UCL and Grace@UCL in the completion of the simulations of this work. We are grateful to the U.K. Materials and Molecular Modelling Hub, which is partially funded by EPSRC (EP/P020194/1), for computational resources (HPC facility Thomas). We also thank Prof. Charlie Sykes, Dr Matt Darby and Dr Julia Schumann for helpful discussions.

References

1. H. L. Tierney, A. E. Baber, J. R. Kitchin and E. C. H. Sykes, Phys. Rev. Lett., 2009, 103, 246102.
2. G. Kyriakou, M. B. Boucher, A. D. Jewell, E. A. Lewis, T. J. Lawton, A. E. Baber, H. L. Tierney, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Science, 2012, 335, 1209–1212.
3. M. B. Boucher, B. Zugic, G. Cladaras, J. Kammert, M. D. Marcinkowski, T. J. Lawton, E. C. H. Sykes and M. Flytzani-Stephanopoulos, Phys. Chem. Chem. Phys., 2013, 15, 12187–12196.
4. F. R. Lucci, J. Liu, M. D. Marcinkowski, M. Yang, L. F. Allard, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Nat. Commun., 2015, 6, 8550.
5. G. Giannakakis, A. Trimpalis, J. Shan, Z. Qi, S. Cao, J. Liu, J. Ye, J. Biener and M. Flytzani-Stephanopoulos, Top. Catal., 2018, 61, 475–486.
6. J. Liu, J. Shan, F. R. Lucci, S. Cao, E. C. H. Sykes and M. Flytzani-Stephanopoulos, Catal. Sci. Technol., 2017, 7, 4276–4284.
7. M. D. Marcinkowski, M. T. Darby, J. Liu, J. M. Wimble, F. R. Lucci, S. Lee, A. Michaelides, M. Flytzani-Stephanopoulos, M. Stamatakis and E. C. H. Sykes, Nat. Chem., 2018, 10, 325–332.
8. J. Shan, J. Liu, M. Li, S. Lustig, S. Lee and M. Flytzani-Stephanopoulos, Appl. Catal., B, 2018, 226, 534–543.
9. R. Réocreux, M. Uhlman, T. Thuening, P. Kress, R. Hannagan, M. Stamatakis and E. C. H. Sykes, Chem. Commun., 2019, 55, 15085–15088.
10. C. J. Wrasman, A. Boubnov, A. R. Riscoe, A. S. Hoffman, S. R. Bare and M. Cargnello, J. Am. Chem. Soc., 2018, 140, 12930–12939.
11. X. Zhang, G. Cui, H. Feng, L. Chen, H. Wang, B. Wang, X. Zhang, L. Zheng, S. Hong and M. Wei, Nat. Commun., 2019, 10, 5812.
12. J. Sinfelt, J. L. Carter and D. J. C. Yates, J. Catal., 1972, 24, 283–296.
13. M. Jørgensen and H. Grönbeck, J. Am. Chem. Soc., 2019, 141, 8541–8549.
14. F. Xing, J. Jeon, T. Toyao, K. Shimizu and S. Furukawa, Chem. Sci., 2019, 10, 8292–8298.
15. B. Cho, B. H. Shanks and J. E. Bailey, J. Catal., 1989, 115, 486–499.
16. M. T. Greiner, T. E. Jones, S. Beeg, L. Zwiener, M. Scherzer, F. Girgsdies, S. Piccinin, M. Armbrüster, A. Knop-Gericke and R. Schlögl, Nat. Chem., 2018, 10, 1008–1015.
17. I.-C. Oğuz, T. Mineva and H. Guesmi, J. Chem. Phys., 2018, 148, 024701.
18. K. G. Papanikolaou, M. T. Darby and M. Stamatakis, J. Phys. Chem. C, 2019, 123, 9128–9138.
19. J. K. Nørskov, F. Studt, F. Abild-Pedersen and T. Bligaard, in Fundamental Concepts in Heterogeneous Catalysis, John Wiley & Sons, Inc, Hoboken, NJ, USA, 2014, pp. 6–25.
20. G. A. Somorjai, Catal. Lett., 1991, 7, 169–182.
21. M. P. Andersson, F. Abild-Pedersen, I. N. Remediakis, T. Bligaard, G. Jones, J. Engbæk, O. Lytken, S. Horch, J. H. Nielsen and J. Sehested, J. Catal., 2008, 255, 6–19.
22. B. Hammer, J. Catal., 2001, 199, 171–176.
23. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
24. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
25. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
26. W. Kohn and L. J. Sham, Phys. Rev. [Sect.] A, 1965, 140, A1133–A1138.
27. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
28. J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131.
29. J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 022201.
30. M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401.
31. H. Thirumalai and J. R. Kitchin, Top. Catal., 2018, 61, 462–474.
32. M. T. Darby, R. Réocreux, E. C. H. Sykes, A. Michaelides and M. Stamatakis, ACS Catal., 2018, 8, 5038–5050.
33. G. Henkelman and H. Jónsson, J. Chem. Phys., 1999, 111, 7010–7022.
34. R. Dronskowski and P. E. Blochl, J. Phys. Chem., 1993, 97, 8617–8624.
35. V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466.
36. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567.
37. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035.
38. J. K. Nørskov, F. Studt, F. Abild-Pedersen and T. Bligaard, in Fundamental Concepts in Heterogeneous Catalysis, John Wiley & Sons, Inc, Hoboken, NJ, USA, 1st edn, 2014, pp. 114–137.
39. M. T. Darby, E. C. H. Sykes, A. Michaelides and M. Stamatakis, Top. Catal., 2018, 61, 428–438.
40. S. Dahl, A. Logadottir, R. C. Egeberg, J. H. Larsen, I. Chorkendorff, E. Törnqvist and J. K. Nørskov, Phys. Rev. Lett., 1999, 83, 1814–1817.
41. D. Loffreda, D. Simon and P. Sautet, J. Catal., 2003, 213, 211–225.
42. X. Liu, L. Sun and W.-Q. Deng, J. Phys. Chem. C, 2018, 122, 8306–8314.
43. G. A. Somorjai and J. Carrazza, Ind. Eng. Chem. Fundam., 1986, 25, 63–69.
44. A. Ishikawa and Y. Tateyama, J. Phys. Chem. C, 2018, 122, 17378–17388.
45. M. Daté, H. Okuyama, N. Takagi, M. Nishijima and T. Aruga, Surf. Sci., 1996, 350, 79–90.
46. K. Tian, X.-Y. Tu and S.-S. Dai, Surf. Sci., 2007, 601, 3186–3195.
47. J. S. Villarrubia and W. Ho, J. Chem. Phys., 1987, 87, 750–764.
48. B. Hammer, Faraday Discuss., 1998, 110, 323–333.
49. D. Mei, Q. Ge, M. Neurock, L. Kieken and J. Lerou, Mol. Phys., 2004, 102, 361–369.
50. M. Mavrikakis, L. B. Hansen, J. J. Mortensen, B. Hammer and J. K. Nørskov, in Transition State Modeling for Catalysts, 1999, pp. 245–258.
51. M. J. P. Hopstaken and J. W. Niemantsverdriet, J. Phys. Chem. B, 2000, 104, 3058–3066.
52. P. B. Rasmussen, P. A. Taylor and I. Chorkendorff, Surf. Sci., 1992, 269–270, 352–359.
53. B. K. Min, A. R. Alemozafar, D. Pinnaduwage, X. Deng and C. M. Friend, J. Phys. Chem. B, 2006, 110, 19833–19838.
54. H.-Y. Su, Z. Zeng, X.-H. Bao and W.-X. Li, J. Phys. Chem. C, 2009, 113, 8266–8272.
55. Z.-P. Liu and P. Hu, J. Am. Chem. Soc., 2003, 125, 1958–1967.
56. J. K. Nørskov, T. Bligaard, B. Hvolbæk, F. Abild-Pedersen, I. Chorkendorff and C. H. Christensen, Chem. Soc. Rev., 2008, 37, 2163.
57. Y. Wang, L. Cao, N. J. Libretto, X. Li, C. Li, Y. Wan, C. He, J. Lee, J. Gregg, H. Zong, D. Su, J. T. Miller, T. Mueller and C. Wang, J. Am. Chem. Soc., 2019, 141, 16635–16642.
58. M. Qiu, H. Tao, Y. Li, Y. Li, K. Ding, X. Huang, W. Chen and Y. Zhang, Appl. Surf. Sci., 2018, 427, 837–847.
59. H. Y. Kim and G. Henkelman, ACS Catal., 2013, 3, 2541–2546.
60. Z. Lu, S. Yadav and C. V. Singh, Catal. Sci. Technol., 2020, 10, 86–98.
61. K. G. Papanikolaou, M. T. Darby and M. Stamatakis, ACS Catal., 2020, 10, 1224–1236.
62. Z.-P. Liu, P. Hu and M.-H. Lee, J. Chem. Phys., 2003, 119, 6282–6289.
63. A. Michaelides, Z. P. Liu, C. J. Zhang, A. Alavi, D. A. King and P. Hu, J. Am. Chem. Soc., 2003, 125, 3704–3705.
64. P. J. Feibelman, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 12133–12138.
65. B. Hammer and J. K. Nørskov, in Advances in Catalysis, 2000, vol. 45, pp. 71–129.
66. G. A. Somorjai, J. Mol. Struct.: THEOCHEM, 1998, 424, 101–117.
67. M. Mavrikakis, J. Rempel, J. Greeley, L. B. Hansen and J. K. Nørskov, J. Chem. Phys., 2002, 117, 6737–6744.
68. S. Kandoi, A. A. Gokhale, L. C. Grabow, J. A. Dumesic and M. Mavrikakis, Catal. Lett., 2004, 93, 93–100.
69. R. Burch, S. T. Daniells and P. Hu, J. Chem. Phys., 2004, 121, 2737.
70. J.-F. Paul, J. Pérez-Ramírez, F. Ample and J. M. Ricart, J. Phys. Chem. B, 2004, 108, 17921–17927.
71. A. Bogicevic and K. C. Hass, Surf. Sci., 2002, 506, L237–L242.
72. C. Wu, D. J. Schmidt, C. Wolverton and W. F. Schneider, J. Catal., 2012, 286, 88–94.
73. M. Stamatakis and S. Piccinin, ACS Catal., 2016, 6, 2105–2111.
74. D. J. Schmidt, W. Chen, C. Wolverton and W. F. Schneider, J. Chem. Theory Comput., 2012, 8, 264–273.
75. A. Bajpai, K. Frey and W. F. Schneider, Langmuir, 2020, 36, 465–474.
76. K. G. Papanikolaou, M. T. Darby and M. Stamatakis, J. Chem. Phys., 2018, 149, 184701.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cy00904k

---