Total oxidation of methane over Pd/Al₂O₃ at pressures from 1 to 10 atm

Abstract

The kinetics of total methane oxidation over a 0.15 wt% Pd/Al₂O₃ monolith catalyst has been measured during temperature programmed methane oxidation experiments at total pressures from 1 to 10 atm and compared with multiscale simulations. The methane conversion can be significantly enhanced by increasing the total pressure at temperatures above 350 °C, which is thanks to a longer residence time that dominates over decreased bulk gas diffusion rates and product inhibition. For the present catalyst, the external mass transfer impacts the methane conversion above 4 atm. With increasing total pressure, the observed methane reactions order decreases at 350 °C whereas it increases at 450 °C due to a more pronounced product inhibition at the lower temperatures. This is also reflected in the apparent activation energy, which increases with increasing total pressure. The multiscale simulations capture the general trends of the experimental results but overestimate the methane conversion at higher temperatures and total pressures. The overestimated activity indicates of an overestimated number of active sites and/or an underestimated external mass transfer resistance.

---

1 Introduction

Many catalytic processes are operated at high pressures because the chemical reaction may be thermodynamically more favourable and/or the elevated pressure enhances the reaction kinetics. Catalytic cracking of alkenes,¹ ammonia production² and methanol synthesis³ are three important examples. Elevated pressures can also be used to enhance the rate of oxidation reactions. A well-known example is the total oxidation of methane^4–11 that is used in the high-temperature catalytic combustion for heat and power generation. For catalytic emission control in general, and exhaust aftertreatment for natural gas vehicles in particular, the total oxidation of methane has almost exclusively been studied at atmospheric pressure conditions. The focus has been on understanding the catalytically active phase and how to formulate more active and durable catalysts.^12–26 For large gas engines, which is the main motivation for this work, the possibility of installing catalytic aftertreatment devices between the engine and the turbo charger, as to take advantage of the higher pressure to reduce the overall size of the catalytic system, is tempting.^27,28

In a recent experimental study including also kinetic modelling, Stotz et al. report a slight suppression of the methane oxidation over Pd/Al₂O₃ upon increased pressure as compared to atmospheric pressure.²⁹ Our recent theoretical studies, however, indicate that for certain temperatures, an increased pressure may govern the methane turn-over frequency³⁰ and, in the case of a Pd/Al₂O₃ monolith catalyst, the methane conversion.³¹ With these possible discrepancies as a starting point, we here focus on whether or not an increased total pressure facilitates the total oxidation of methane over a Pd/Al₂O₃ monolith catalyst at low temperatures using both experiments and simulations. The experiments were carried out using a chemical reactor designed for operating pressures between 1 and 15 atm and the product stream was continuously monitored with mass spectrometry. The simulation code is based on a multiscale kinetic model free of fitted parameters as described in detail elsewhere.^30–32 We show that the methane oxidation indeed can be enhanced but equally well suppressed by increased pressure depending on foremost operational temperature.

2 Material and methods

2.1 Catalyst preparation

The 0.15 wt% Pd/Al₂O₃ catalyst used for the activity tests was prepared by incipient wetness impregnation where γ-alumina (Puralox SBa 200, Sasol) was mixed with aqueous 10 wt% tetraaminepalladium(II) nitrate solution (Alfa Aesar). The slurry was mixed and frozen, using liquid nitrogen, before being freeze-dried over night. The dry sample was then calcined in air at 600 °C for 2 h. During the calcination the temperature was linearly increased from room temperature to the final value with a rate of 5 °C min⁻¹. A monolith substrate of cordierite (corning) was washcoated with 31 mg of the Pd/Al₂O₃ catalyst. During the washcoating procedure the monolith was repeatedly dipped in a slurry and dried under a heating gun until the final weight was achieved. The slurry contained 16 wt% powder catalyst, 4 wt% binder material (Boehmite, Disperal P2, Sasol) and 80 wt% of a 50/50 mix of ethanol and Milli-Q water (18 MΩ cm). The monolith dimensions were 15 and 12 mm in length and diameter, respectively, with the cell density of 400 cells per square inch (cpsi). The coated monolith was finally calcined in air at 600 °C for 2 h with a temperature increase of 5 °C min⁻¹ before cooling to room temperature by natural convection.

2.2 Catalyst characterization

2.2.1 Chemisorption. The dispersion of Pd and the mean Pd particle diameter were determined by chemisorption of carbon monoxide using a Micrometrics ASAP 2020 instrument. 200 mg of catalyst sample, packed between quartz wool was firstly degassed at 250 °C for 3 h to determine the dry weight of the sample. Subsequently, an oxidative pretreatment (2 vol% O₂) at 500 °C for 1 h and a reductive pretreatment (4 vol% H₂) at 500 °C for 1 h were performed. To finalize the pretreatment, the measurement cell was cooled to 35 °C and evacuated for 1 h. The CO-chemisorption measurement was carried out at 35 °C by carefully increasing the CO dosage. Assuming the ratio of adsorbed CO molecules and surface Pd atoms is 1 : 2,³³ the Pd dispersion and the mean hemispherical Pd particle diameter were calculated.

2.2.2 Nitrogen physisorption measurements. The specific surface area (SSA) of the sample was determined by nitrogen physisorption at −196 °C with a Micrometrics Tristar 3000 instrument using 200 mg of sample for the measurement. The sample was initially dried for 3 h at 225 °C under a nitrogen flow to remove weakly adsorbed species. After the physisorption experiments were performed, the specific surface area was calculated using the multipoint Brunauer–Emmett–Teller (BET) model,³⁴ considering five equally spaced points in the p/p₀ range from 0.05 to 0.2. The pore size distribution was determined from the isotherm (range 0.35 < p/p₀ < 1) by means of the Barrett–Joyner–Halenda (BJH) method.^35,36

2.2.3 Elemental analysis. The Pd loading of the powder catalyst was measured using inductively coupled plasma-optical emission spectrometry (ICP-OES, iCAP 600 series by Thermo Scientific). The sample was dissolved in aqua regia (3 : 1 ratio of hydrochloric acid and nitric acid, for Trace Metal Analysis, Fisher Chemical), heated up for two hours to 100 °C and was kept in the acid to digest overnight. Then the solution was diluted 1 : 10 with Milli-Q water and was filtered (syringe filter, PTFE-membrane with 0.2 μm pore diameter) to subsequently be analyzed.

2.3 Catalytic activity tests

2.3.1 Reactor setup. All kinetic experiments were performed in an in-house built reactor setup. The flow reactor is a modified version of a portable water generation reactor.³⁷ The coated monolithic sample was fixed with quartz wool in a stainless steel tube (ID = 15 mm, L = 480 mm). The steel tube is heated by an electrical heating coil which is fixed directly upstream of the coated monolith sample to ensure a constant gas feed and reaction temperature. The temperature of the feed gas is measured by a K-type thermocouple placed 5 mm in front of the catalyst. The flow of each gas component is controlled by a mass flow controller (Bronkhorst model FG-201CV). A control valve (Bronkhorst F-001) is implemented at the reactor outlet to control the pressure of the reactor system. The total pressure of the system is monitored by an in-line mounted gauge pressure transmitter (Yokogawa, model EJA530E). The gas concentration of the gas components at the reactor outlet is analyzed by mass spectroscopy (V&F Analysetechnik, Airsense Compact).

2.3.2 Methane oxidation. Prior to each experiment, the sample was pretreated at 500 °C with 4 vol% H₂ for 20 min and with 2 vol% O₂ for 40 min. After the oxidative pretreatment the sample was cooled to 280 °C in 2 vol% O₂ and Ar. The procedure was carried out at the same total pressure as for the following temperature programmed reaction (TPR) experiment to ensure reproducible results.

For the TPR experiments the temperature was linearly increased by 2 °C min⁻¹ to reach a maximum temperature of 450 °C, followed by a dwell of 30 min and cooling with a rate of 2 °C min⁻¹. The conversion of methane was measured for a gas flow rate of 100 mL min⁻¹, with 1000 vol ppm CH₄ and 2 vol% O₂ balanced with Ar. Five different TPR experiments were performed in which the total pressure of the experiment was varied (1, 2, 4 and 10 atm). Furthermore, two TPR experiments were performed in presence of 10 vol% CO₂ at 1 and 4 atm. The apparent activation energies for methane oxidation in each TPR experiment were calculated using data points between 7 and 15% methane conversion. Reaction orders were determined by varying the methane concentration from 400 to 1600 ppm with steps of 200 ppm at fixed temperatures and total pressures of 350, 400 and 450 °C and 1, 2 and 4 atm, respectively.

2.3.3 Multiscale simulations of methane oxidation. Simulations of methane conversions were performed using a previously developed 2D multiscale reactor model where the surface kinetics inside a porous catalyst layer is described by first-principles calculations and coupled with mass and heat transport equations.^30–32 Under lean conditions palladium oxide is reported to be the active phase of palladium and PdO(101) as the most reactive surface for methane dissociation.^38,39 The reaction network is determined by density functional theory and the surface kinetics are described by transition state theory, where a dual site pair mechanism between the under-coordinated palladium and oxygen atoms of the PdO(101) surface is utilized. The multiscale model contains no fitting parameters but uses physical system properties and flow conditions as input variables. The multiscale model contains no fitting parameters but uses physical system properties and flow conditions as input variables. The model does not account for structural changes of the PdO(101) surface during reaction. A single-channel adiabatic reactor model is used to model the complete methane oxidation reaction inside the coated monolith. The procedure has been successfully used by other groups.^40,41 The coated monolith is discretized by the tanks-in-series method while the porous catalyst is divided into layers to obtain axial and radial gradients. Here, a model of 10 tanks and 12 layers is used, which provides a sufficient trade-off between accuracy and computational time. The single-channel geometry represents a monolith with 400 cpsi. Details of the computational approach are published elsewhere.^31,42

3 Results and discussion

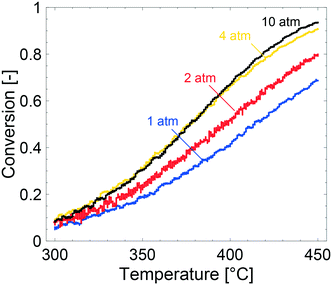
Key physical properties of the catalyst, i.e., specific surface area, porosity and palladium loading and dispersion, were characterised with established methods. The specific surface area of the powder catalyst was determined to be 172 m² g⁻¹ with an average pore diameter of 9 nm, which is in line with previously published values.^15,43,44 The porosity of the catalyst is ascribed to the alumina onto which the Pd particles are supported. CO-Chemisorption revealed a palladium dispersion of 41% assuming hemispherical Pd particles and bridged configuration³³ between the Pd and CO. The mean Pd diameter was determined to be 1.9 nm, which is comparable to published values.⁴⁴ A palladium loading of 0.15 wt% was determined by ICP-OES analysis of three different samples. The determined values of palladium loading and dispersion were used as input parameters for the simulations and can be found in Table 1.

Table 1 Key physical properties for a catalyst with 0.15 wt% Pd dispersed on γ-alumina, 31 mg of catalyst powder deposited on cordierite substrate of 15 mm length, 12 mm width and 400 cpsi

Property type	This work	Literature	Ref.
Pd dispersion (%)	41	51–56	33, 44
Pd mean diameter (nm)	1.9	1–4	44
Specific surface area (m^2 g^−1)	172	144–165	15, 43
Average pore diameter (nm)	9	9.3	44

---

Fig. 1 shows the methane conversion as a function of temperature during the cooling phase of the TPR experiments. Considering the experiments, the methane conversion clearly increases with increased total pressure from 1 to 4 atm whereas a further increase to 10 atm only results in a slight increase of the methane conversion above 400 °C. Due to the low flow rate of 100 mL min⁻¹ in the experiments, which corresponds to a gas hourly space velocity of 3500 h⁻¹, it is reasonable to assume that mass transport effects are not significant at the examined conditions. This will be discussed in detail later. It is commonly accepted that kinetics control the reaction below ca. 20% conversion, but for the experiment performed at 1 atm it can be assumed that kinetics are not affected by internal mass transport due to a very thin washcoat thickness (as determined by optical microscopy, see ESI†). When the total pressure is increased from 1 to 2 atm the activity increases for all temperatures, except the lowest where the reaction is not significantly affected. The increased methane conversion is attributed to an increasing residence time, due to a constant molar flow. The same arguments explain the enhanced methane conversion between 2 and 4 atm. Similar observations are reported elsewhere.^45,46 At 10 atm the methane conversion is not affected except at temperatures above 400 °C where a slight increase is seen. The fact that the methane conversion is not affected is most likely due to steep concentration gradients of methane in the bulk gas. Hence, external mass transfer resistances are present in the system at 10 atm and at temperatures above 400 °C. This is explained by a linearly decreasing bulk gas diffusion for increasing total pressures. Below 400 °C, where the methane conversion is not affected, it is most likely that the temperature is not sufficient to show an increased conversion for increasing total pressures. Hence, the positive effect of total pressure on methane conversion, at present catalyst properties and reaction conditions, is a combined result between the trade-offs between the positive effect of an increased residence time and the negative effect of stronger external mass transfer resistances. An inevitable feature of the Pd/Al₂O₃ catalyst for complete oxidation of methane, is the product inhibition by water and carbon dioxide. The inhibition effect by water has been thoroughly discussed before where water promotes long-term sintering of the alumina support and formation of inactive Pd(OH)₂. Furthermore, the long-term effect of water on the alumina support is reported to be stronger at elevated total pressures.⁴⁵ The increased external mass transfer resistance and stronger inhibition of water can explain the low activity enhancement between 4 and 10 atm.

Fig. 1 Methane conversion for temperature programmed reaction experiments over a 0.15 wt% Pd/Al₂O₃ monolith catalyst for a gas composition of 1000 vol ppm CH₄, 2 vol% O₂ and Ar as balance at 1 (blue), 2 (red), 4 (yellow) and 10 (black) atm.

The effects of product inhibition can be indirectly observed by evaluating how the reaction order for methane changes when the total pressure is increased. The reaction order with respect to methane was obtained by a set of steady-state measurements at different temperatures and total pressures. The experimentally determined reaction orders may not, even in the absence of transport resistances, represent the true orders of the reaction because they are not in all cases calculated at differential reactor conditions. They do however serve to compare the sensitivity of the methane conversion and indirectly reaction rates to methane concentration at the same conditions for experiments. The experimentally determined reaction orders for methane are shown in Fig. 2. The reaction order decreases slightly with increasing total pressures at 350 °C and increases at 400 and 450 °C, at which the reaction order converges towards unity. Further, the measured reaction orders are within the range of published values of 0.7–1 in total oxidation of methane over Pd and PdO for varying methane concentrations.^47–49 Based on the results from estimating if internal mass transport may affect the reaction rate using Weisz–Prater's method, it is reasonable to assume that the internal mass transport is not significantly affecting the reaction rate at 350 °C for the investigated total pressures (see ESI†). Product inhibition and an increasing external mass transport resistance are probable causes for the decreasing methane reaction order. The same observation are seen from the apparent activation energies. The apparent activation energy for each TPR experiment in Fig. 1 is estimated by using experimental values between 7 and 15% methane conversion. The Arrhenius plots, with corresponding linear regressions, are included in the ESI.† The apparent activation energy is determined to be 70, 63, 73 and 80 kJ mol⁻¹ for 1, 2, 4 and 10 atm, respectively. The apparent activation energy increases with increasing total pressure, except for 2 atm where the apparent activation energy showed a local minimum. The increasing apparent activation energy originates from readsorbed reaction products. As previously mentioned, water inhibits the palladium particles by formation of Pd(OH)₂ but also promotes loss of active sites due to sintering of the alumina support. Such structural changes may contribute to the increased apparent activation energy. Carbon dioxide is reported to show an inhibiting effect by formation of formates and carbonates. However, the effect of carbon dioxide is less severe than the effect of water. For increasing temperature and ultimately at 450 °C, the reaction orders show an increasing trend since the higher temperature can sustain a faster reaction rate and inhibitory effects of water, and especially carbon dioxide, are small at 450 °C.

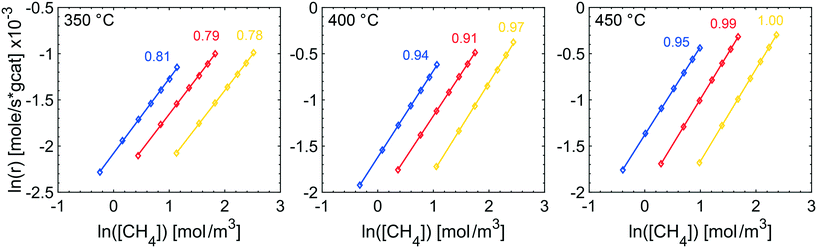Fig. 2 Experimentally determined reaction orders with respect to methane at 350 (left), 400 (center) and 450 °C (right) and 1 (blue), 2 (red) and 4 atm (yellow).

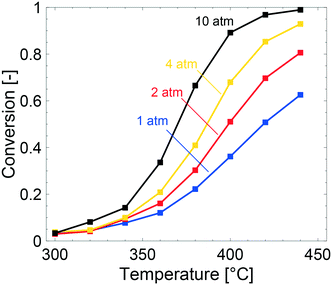
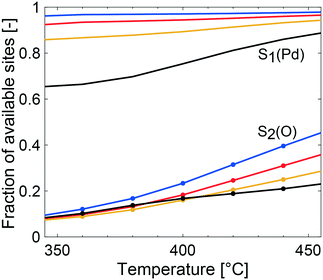
The multiscale simulations reproduce the experimental trends well, but underestimate the methane conversion at low temperatures and overestimate the same at high temperatures (see Table 2). The underestimated simulated activity in Fig. 3 up to around 400 °C, depending on the total pressure, is argued to be either caused by a too low predicted inherent reactivity of the active sites or an over-prediction of the adsorbate coverages by the model. The latter lowers the rate of methane dissociation. The reaction network in the model is based on a dual-site mechanism where both the palladium and oxygen atoms are required as adsorption sites on the active PdO surface. Thus, both the palladium and the oxygen site are important in the catalytic cycle to activate and oxidize methane. Fig. 4 shows the fraction of available palladium (S₁(Pd)) and oxygen sites (S₂(O)) in the coated monolith calculated by the microkinetic model, averaged over the monolith length. The fraction of available S₁(Pd) and S₂(O) sites increases with increasing temperature and decreases with increasing total pressure. The availability of S₁(Pd) sites is generally high on the catalyst surface for all examined reaction conditions. According to the simulations, the most abundant surface species on the S₁(Pd) sites are adsorbed water, hydroxyl and bicarbonates in dry conditions. Adsorbed water comes from the adsorption of produced water from the reaction while hydroxyl species are formed after the dissociation of adsorbed water and as a reaction byproduct. This is similar to the results of previous studies where the negative influence of water on the conversion of methane over Pd/Al₂O₃, is ascribed to be due to blocking of active sites by adsorbed water species or hydroxyl groups which could explain the observed effect.^50–52 Bicarbonates originate from adsorbed carbon dioxide which reacts with surface hydroxyl into bicarbonate species. A discussion about the most abundant surface species is included in the ESI.† Interestingly, the fraction of available S₂(O) sites at 350 °C is low where the conversion of methane is underestimated, due to a high coverage of hydrogen atoms (see ESI†). As for S₁(Pd), the coverage of S₂(O) sites increases with increasing temperatures and decreases with increasing total pressure. The observation of a low availability of S₂(O) sites is interesting since no support effects of the alumina are accounted for in the model. Support effects could affect the availability of S₂(O) sites or reactivity in terms of oxygen storage capacity, regeneration of the S₂(O) sites or interface sites and explain the underestimated simulated methane conversion. For the simulations at temperatures above 400 °C, the positive effect of increased total pressure on the conversion of methane is due to an increased residence time and higher methane impingement rate. The residence time increases, since the inlet mass flow is constant, and a positive effect of impingement rate is due to a sufficiently high number of available S₂(O) sites. The simulated methane conversions are in fairly good agreement with the corresponding experimental results except at total pressures of 10 atm, where the simulated methane conversion is overestimated. The overestimated conversion could be caused by an overestimation of the fraction of available active sites and/or insufficiently described external mass transfer process.

Table 2 Comparison between experimental (Exp.) and simulated (Sim.) methane conversions at low (340 °C), moderate (380 °C) and high (440 °C) temperatures (T) for 1, 2, 4 and 10 atm pressure

Pressure (atm)	Low T		Moderate T		High T
	340 °C		380 °C		440 °C
	Exp.	Sim.	Exp.	Sim.	Exp.	Sim.
1	0.15	0.08	0.32	0.22	0.63	0.63
2	0.18	0.09	0.40	0.30	0.75	0.81
4	0.26	0.10	0.52	0.41	0.87	0.93
10	0.24	0.14	0.51	0.67	0.91	0.99

---

Fig. 3 Simulated methane conversions for temperature programmed reaction experiments over 0.15 wt% Pd/Al₂O₃ monolith for a gas composition of 1000 vol ppm CH₄ and 2 vol% O₂ at 1 (blue), 2 (red), 4 (yellow) and 10 (black) atm.

Fig. 4 Fraction of available palladium site (S₁(Pd)) and available oxygen site (S₂(O)) according to the multiscale model in the Pd/Al₂O₃ coated monolith at 1 (blue), 2 (red), 4 (yellow) and 10 (black) atm. If there is a free S₁(Pd) site next to a free S₂(O) site, a free Pd–O site pair is available. Methane dissociation occurs most easily on the free Pd–O site pair.

We recall that the model contains no description of support effects nor structural changes that may influence the active sites⁵³ and the overall methane conversion. Experimentally, such effects cannot be avoided. Further, the reactor model assumes an adiabatic vessel with heat radiation losses only from the reactor inlet and outlet whereas in the experiments, other heat losses are present as well. Hence, the heat losses in the simulations are most likely underestimated, which leads to an overestimation of the activity at conditions where the exothermic reaction heat is significant. In contrast to adiabatic simulations, isothermal simulations neglecting the evolved reaction heat and assuming a uniform temperature throughout the monolith showed a severely underestimated methane conversion, see ESI.† The two types of simulations, however, indicate that the experiments most likely are best described by an adiabatic model.

4 Conclusions

The study shows that the total oxidation of methane over a Pd/Al₂O₃ catalyst is affected by an increased total pressure of the system. In dry conditions and at fixed molar flows, increasing the total pressure results in a higher impingement rate and increased residence time, which have a positive effect on the methane conversion. However, the external mass transfer resistance is more pronounced at higher total pressures due to a linearly decreasing bulk gas diffusion with increasing total pressure. This explains the diminishing effect of increasing the total pressure between 4 and 10 atm. Hence, increasing the total pressure creates a trade-off between the positive effect of a longer residence time and the negative effect of a decreased bulk diffusion. Furthermore, the positive effect requires a sufficiently high fraction of available active sites and a sufficient temperature to sustain the reaction rate of methane oxidation. Here an increased apparent activation energy is observed with increasing total pressure (from 70 to 80 kJ mol⁻¹ at 1 and 10 atm, respectively) probably due to an increased product adsorption which results in adsorbed water, hydroxyl species and to some extent bicarbonates on the active site surface. The reaction order of the system decreases with increasing total pressure at low temperatures (350 °C) whereas at higher temperatures the opposite trend is observed since product adsorption is less frequent.

The multiscale simulations captures the general experimental trends. At the lower temperatures the methane conversion is underestimated and the first-principles based microkinetic reaction mechanism shows a low availability of the oxygen sites compared to the palladium sites at all temperatures. The observation is interesting since the model simulations do not account for any support effects or interface sites that can affect the activity. At higher temperatures, and total pressures, the simulated activity is overestimated which indicates of an overestimation of active sites and/or an underestimated external mass transfer resistance.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been performed within the Competence Centre for Catalysis, which is hosted by Chalmers University of Technology and financially supported by the Swedish Energy Agency (No. 22490-4) and the member companies AB Volvo, ECAPS AB, Johnson Matthey AB, Preem AB, Scania CV AB, Umicore Denmark ApS and Volvo Car Corporation AB. Additional support from the Swedish Research Council is acknowledged as well as computational resources at C3SE (Göteborg) via an SNIC grant. The authors would also like to thank Professor Liberato Manna for valuable comments and support.

Notes and references

1. A. V. Nikitin, A. S. Dmitruk and V. S. Arutyunov, Russ. Chem. Bull., 2016, 65, 2405–2410.
2. M. Appl, in Ammonia, 2. Production Processes, American Cancer Society, 2011.
3. Y. Hartadi, D. Widmann and R. J. Behm, J. Catal., 2016, 333, 238–250.
4. A. Ersson, H. Kušar, R. Carroni, T. Griffin and S. Järås, Catal. Today, 2003, 83, 265–277.
5. M. Reinke, J. Mantzaras, R. Schaeren, R. Bombach, A. Inauen and S. Schenker, Combust. Flame, 2004, 136, 217–240.
6. K. Persson, A. Ersson, A. M. Carrera, J. Jayasuriya, R. Fakhrai, T. Fransson and S. Järås, Catal. Today, 2005, 100, 479–483.
7. P. Piermartini, T. Schuhmann, P. Pfeifer and G. Schaub, Top. Catal., 2011, 54, 967.
8. P. S. Barbato, A. Di Benedetto, V. Di Sarli, G. Landi and R. Pirone, Ind. Eng. Chem. Res., 2012, 51, 7547–7558.
9. A. D. Benedetto, G. Landi, V. D. Sarli, P. Barbato, R. Pirone and G. Russo, Catal. Today, 2012, 197, 206–213.
10. A. Di Benedetto, P. S. Barbato and G. Landi, Energy Fuels, 2013, 27, 6017–6023.
11. F. Sen, T. Kasper, U. Bergmann, R. Hegner and B. Atakan, Z. Phys. Chem., 2015, 229, 955–976.
12. W. S. Epling and G. B. Hoflund, J. Catal., 1999, 182, 5–12.
13. F. H. Ribeiro, M. Chow and R. A. Dalla Betta, J. Catal., 1994, 146, 537–544.
14. M. R. Lyubovsky and L. D. Pfefferle, Catal. Today, 1999, 47, 29–44.
15. P. Thevenin, E. Pocoroba, L. Pettersson, H. Karhu, I. Väyrynen and S. Järås, J. Catal., 2002, 207, 139–149.
16. I. E. Beck, V. I. Bukhtiyarov, I. Y. Pakharukov, V. I. Zaikovsky, V. V. Kriventsov and V. N. Parmon, J. Catal., 2009, 268, 60–67.
17. P. Gélin and M. Primet, Appl. Catal., B, 2002, 39, 1–37.
18. P. Gélin, L. Urfels, M. Primet and E. Tena, Catal. Today, 2003, 83, 45–57.
19. R. Abbasi, L. Wu, S. E. Wanke and R. E. Hayes, Chem. Eng. Res. Des., 2012, 90, 1930–1942.
20. Z. Li and G. B. Hoflund, J. Nat. Gas Chem., 2003, 12, 153–160.
21. J. B. Miller and M. Malatpure, Appl. Catal., A, 2015, 495, 54–62.
22. N. M. Kinnunen, J. T. Hirvi, K. Kallinen, T. Maunula, M. Keenan and M. Suvanto, Appl. Catal., B, 2017, 207, 114–119.
23. M. M. Pakulska, C. M. Grgicak and J. B. Giorgi, Appl. Catal., A, 2007, 332, 124–129.
24. R. S. Monteiro, D. Zemlyanov, J. M. Storey and F. H. Ribeiro, J. Catal., 2001, 199, 291–301.
25. R. J. Farrauto, J. K. Lampert, M. C. Hobson and E. M. Waterman, Appl. Catal., B, 1995, 6, 263–270.
26. R. Ramírez-López, I. Elizalde-Martinez and L. Balderas-Tapia, Catal. Today, 2010, 150, 358–362.
27. O. Kröcher, M. Elsener, M.-R. Bothien and W. Dölling, MTZ worldwide, 2014, 75, 46–51.
28. R. Bank, U. Etzien, B. Buchholz and H. Harndorf, MTZ Industrial, 2015, 3, 14–21.
29. H. Stotz, L. Maier, A. Boubnov, A. Gremminger, J.-D. Grunwaldt and O. Deutschmann, J. Catal., 2019, 370, 152–175.
30. C.-R. Florén, M. Van den Bossche, D. Creaser, H. Grönbeck, P.-A. Carlsson, H. Korpi and M. Skoglundh, Catal. Sci. Technol., 2018, 8, 508–520.
31. C.-R. Florén, P.-A. Carlsson, D. Creaser, H. Grönbeck and M. Skoglundh, Catal. Sci. Technol., 2019, 9, 3055–3065.
32. M. Van Den Bossche and H. Grönbeck, J. Am. Chem. Soc., 2015, 137, 12035–12044.
33. P. Canton, G. Fagherazzi, M. Battagliarin, F. Menegazzo, F. Pinna and N. Pernicone, Langmuir, 2002, 18, 6530–6535.
34. S. Brunauer, P. H. Emmett and E. Teller, J. Am. Chem. Soc., 1938, 60, 309–319.
35. E. P. Barrett, L. G. Joyner and P. P. Halenda, J. Am. Chem. Soc., 1951, 73, 373–380.
36. L. G. Joyner, E. P. Barrett and R. Skold, J. Am. Chem. Soc., 1951, 73, 3155–3158.
37. P. Velin, U. Stenman, M. Skoglundh and P.-A. Carlsson, Rev. Sci. Instrum., 2017, 88, 115102.
38. A. Hellman, A. Resta, N. M. Martin, J. Gustafson, A. Trinchero, P.-A. Carlsson, O. Balmes, R. Felici, R. van Rijn, J. W. M. Frenken, J. N. Andersen, E. Lundgren and H. Grönbeck, J. Phys. Chem. Lett., 2012, 3, 678–682.
39. A. Trinchero, A. Hellman and H. Grönbeck, Phys. Status Solidi RRL, 2014, 8, 605–609.
40. C. Ericson, B. Westerberg and I. Odenbrand, SAE World Congress & Exhibition, 2008.
41. D. Creaser, X. Karatzas, B. Lundberg, L. J. Pettersson and J. Dawody, Appl. Catal., A, 2011, 404, 129–140.
42. M. M. Azis, H. Härelind and D. Creaser, Chem. Eng. J., 2013, 221, 382–397.
43. S. C. Shekar, K. R. Rao and E. Sahle-Demessie, Appl. Catal., A, 2005, 294, 235–243.
44. J. Kim, M. J. Kelly, H. H. Lamb, G. W. Roberts and D. J. Kiserow, J. Phys. Chem. C, 2008, 112, 10446–10452.
45. B. Torkashvand, A. Gremminger, S. Valchera, M. Casapu, J.-D. Grunwaldt and O. Deutschmann, SAE Technical Paper Series, 2017.
46. T. Rammelt, B. Torkashvand, C. Hauck, J. Böhm, R. Gläser and O. Deutschmann, Emiss. Control Sci. Technol., 2017, 3, 275–288.
47. R. Monteiro, D. Zemlyanov, J. Storey and F. Ribeiro, J. Catal., 2001, 199, 291–301.
48. G. Zhu, J. Han, D. Y. Zemlyanov and F. H. Ribeiro, J. Phys. Chem. B, 2005, 109, 2331–2337.
49. R. E. Hayes, S. T. Kolaczkowski, P. K. Li and S. Awdry, Chem. Eng. Sci., 2001, 56, 4815–4835.
50. R. Gholami, M. Alyani and K. J. Smith, Catalysts, 2015, 5, 561–594.
51. T. Choudhary, S. Banerjee and V. Choudhary, Appl. Catal., A, 2002, 234, 1–23.
52. R. Burch, F. Urbano and P. Loader, Appl. Catal., A, 1995, 123, 173–184.
53. J. J. Willis, A. Gallo, D. Sokaras, H. Aljama, S. H. Nowak, E. D. Goodman, L. Wu, C. J. Tassone, T. F. Jaramillo, F. Abild-Pedersen and M. Cargnello, ACS Catal., 2017, 7, 7810–7821.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cy00813c

‡ These authors contributed equally to this work.

---